HEP ML LAB: An end-to-end framework for applying machine learning to phenomenology studies

In recent years, the continuous accumulation of data from the Large Hadron Collider experiments has intensified the demand for new developments in physics. Because of their outstanding capabilities in data analysis and pattern recognition, machine learning techniques have been widely researched and applied in high-energy physics, such as jet tagging tasks [1−34] and rapid generation of simulated events [35−40]. Additional applications are discussed in a review paper on this topic [41].

Typically, the process of research involving machine learning models in high-energy physics comprises four steps: data generation, dataset construction, model training, and performance evaluation. In this process, cooperation between various types of software is often required. For instance, MADGRAPH5_AMC [42] is used for generating simulated events, PYTHIA8 [43] for simulating parton showering, DELPHES [44] for fast simulation of detector effects, ROOT [45] for data processing, and deep learning frameworks such as PYTORCH [46] and TENSORFLOW [47] for subsequently building the neural networks. Researchers new to high-energy physics find it challenging to learn and use these software tools, whereas experienced researchers find it tedious to switch between different types of software. Such a process inevitably increases the complexity of the computational results, which makes them potentially difficult to replicate, leading to difficulties in comparing the results in subsequent research.

Lately, some efforts have been made to simplify the entire process, as follows. PD4ML [48] includes five datasets — Top Tagging Landscape, Smart Background, Spinodal or Not, EoS, and Air Showers — and provides a set of concise application programming interfaces (APIs) for importing them. MLANALYSIS [49] can convert LHE and LHCO files generated by MADGRAPH5_AMC into datasets, and has three built-in machine learning algorithms: isolation forest (IF), nested isolation forest (NIF), and k-means anomaly detection (KMAD). MADMINER [50] offers a complete process for inference tasks [51], and internally encapsulates the necessary simulation software as well as neural networks based on PYTORCH. These frameworks significantly reduce the workload related to specific tasks but have scope for further improvement.

HEP ML LAB, developed in Python, encompasses an end-to-end process. All modules are listed in Fig. 1. MADGRAPH5_AMC is minimally encapsulated for event generation, such as defining processes, generating Feynman diagrams, and launching runs. In the transition from events to datasets, we introduced an observable naming convention that directly links physical objects with observables, facilitating users to directly use the names of the observables to retrieve the corresponding values. This convention can be further applied to the definitions of cuts. Inspired by the expression form of cuts in UPROOT [52], we expand the corresponding syntax to support filtering at the event level, using veto to define events that need to be removed and define custom observables of greater complexity. This naming rule also applies to the creation of datasets with different representations. In the current version, users can easily create set and image datasets. In addition, we offer a rich set of functions for preprocessing and displaying of images.

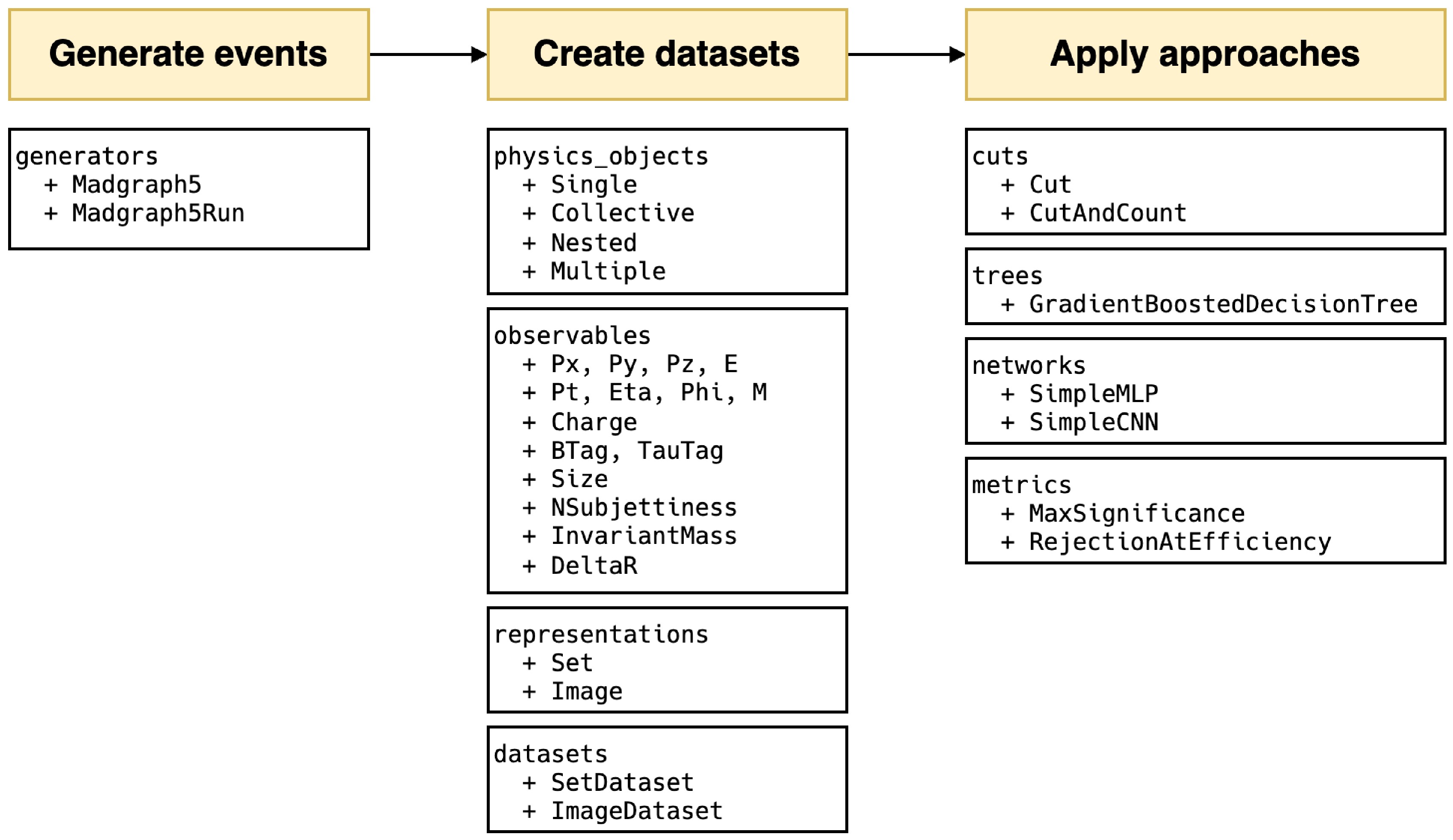
Figure 1.  (color online) All modules in the $ \mathrm{hml}$ framework and main classes in each module.

In the context of machine learning, we introduce two basic deep learning models: simple multi-layer perceptron and simple convolutional neural network. Both have fewer than ten thousand parameters, providing a baseline for classification performance. These models are implemented using KERAS [53] without any custom modifications, making it easy to expand to other existing models. Additionally, we integrated two traditional approaches, cut-and-count, and gradient boosted decision tree, ensuring compatibility with KERAS. After the different approaches were trained, we provided physics-based evaluation metrics — signal significance and background rejection rate — at a fixed signal efficiency to assess their performance.

This package is publicly available through the Python Package Index (PyPI) and can be installed using the standard pip package manager with the command $ \mathrm{pip install hep-ml-lab}$. It supports Python 3.9+ and is compatible with Linux, MacOS, and Windows operating systems. The source code is open-sourced on Github ¹.

The structure of the paper is as follows. Sec. II introduces the wrapper class of MADGRAPH5_AMC to generate events. In Sec. III, we describe the observable naming convention and demonstrate step by step its use in extracting data from events as well as its extension to filter data and to the creation of datasets. Three types of approaches — cut and count, decision trees, and currently available neural networks — are discussed in Sec. IV. Physics-inspired metrics are also discussed. In Sec. V, we demonstrate the effectiveness of the framework using a simple and complete W boson tagging as a case study. Finally, we conclude the paper and discuss the scope for future research in Sec. VI.

All phenomenological studies generally begin by simulating collision events, for example, by using MADGRAPH5_AMC. The $ \mathrm{generators}$ module provides a wrapper for specific parts of its core functionalities, aiming to facilitate its integration into Python scripts for customized setting requirements.

Code example 1: Initialize $ \mathrm{Madgraph5}$.

In code example 1, users need to pass the executable path to the $ \mathrm{executive}$ parameter to ensure that commands can be sent to it. The $ \mathrm{verbose}$ parameter decides whether to display the intermediate outputs. The default value is 1, indicating that the intermediate outputs are displayed, consistent with the output obtained when using MADGRAPH5_AMC in the terminal. After initialization, we can use its various methods to simulate commands entered in the terminal, as shown in code example 2.

Code example 2: Methods of $ \mathrm{Madgraph5}$ to generate processes.

During the process generation, we first need to use the $ {\mathrm{import}}{\_}{\mathrm{model}}$ method to import the model file. This method supports passing the path or name of the model (MADGRAPH5_AMC will search for the model in the models folder or download the model based on its name). Next, use the $ \mathrm{define}$ method to define multi-particles, for example, ${\mathrm{define ("j = }} $ $ { \mathrm{j b b}}\sim {\mathrm "})$. Then, in the $ \mathrm{generate}$ method, pass all the processes to be generated without having to input $ \mathrm{add process}$ as in the case of the terminal. Here, the asterisk represents the unpacking operation in Python, and multiple processes can be directly entered, separated by commas, $ \mathrm{g.generate("p p > } \mathrm{w+ z", "p p > } \mathrm{w- z")} $ without constructing a list with square brackets. Usually, to confirm that processes have been generated as expected, we need to view the Feynman diagrams, for which the ${ \mathrm{display}}\_{ \mathrm{diagrams}}$ method can be used. It saves the generated Feynman diagrams to the ${ \mathrm{diagram}}\_{ \mathrm{dir}}$ folder. Prior to this, it converts the default EPS files into the PDF format for convenience. Finally, use the $ \mathrm{output}$ method to export the processes to a folder.

Code example 3: Use the $ \mathrm{launch}$ method and set up all possible parameters for generating the events.

With the process folder ready, we can begin producing runs to generate the simulated events, as shown in code example 3. The $ \mathrm{launch}$ method includes parameters that may need to be configured for the run, where $ \mathrm{shower}$, $ \mathrm{detector}$, and $ \mathrm{madspin}$ represent switches for PYTHIA8, DELPHES, and MADSPIN, respectively, consistent with the options in the prompt of the terminal. $ \mathrm{settings}$ includes parameters configured in the run card, for example, $ \mathrm{settings = \{"nevents":1000, "iseed":} \mathrm{42\}}$. Furthermore, $ \mathrm{iseed}$ is the random seed used by MADGRAPH5_AMC to control the randomness of the sub-level events. It does not affect PYTHIA8 and DELPHES. You can specify the $ \mathrm{seed}$ parameter to uniformly configure these three, ensuring the cross section, error, and events are fully reproducible. The $ \mathrm{decays}$ method is used to set the decay of the particles; for example, $ \mathrm{decays = ["w+ > j j", "z > } \mathrm {vl vl}\sim{\mathrm{"}}]$. The $ \mathrm{cards}$ parameter accepts the path to the pre-configured parameter files; for example, ${ \mathrm{cards=["delphes}}\_{ \mathrm{card.dat"}}$, $ { \mathrm{"pythia8}}\_{ \mathrm{card.}}{\mathrm{dat"]}}$. In this version, only Pythia8 and Delphes cards with "pythia8" and "delphes" in their file names can be recognized correctly. It currently does not support the cards that have external folders as dependencies, such as the muon collider delphes card. When numerous events need to be generated, the $ {\mathrm{multi}}\_{ \mathrm{run}}$ parameter can be set to create multiple sub-runs for a single run, for example, by setting $ {\mathrm{multi}}\_{\mathrm{run}} = 2$. The final event files will be named as $ {\mathrm{run}}\_01\_1$, $ {\mathrm{run}}\_01\_2$, which is controled by $ \mathrm{MadEvent}$. Note that because MADGRAPH5_AMC does not recommend generating more than one million events in a single run, the $ \mathrm{nevents}$ parameter in $ \mathrm{settings}$ should also be set appropriately, as the total number of events is the result of $ \mathrm{nevents}$ multiplied by $ {\mathrm{multi}}\_{\mathrm{run}}$. $ \mathrm{hml}$ will generate the corresponding valid commands based on the settings and send them to MADGRAPH5_AMC running in the background. To check the actual commands before the beginning of the run, set $ {\mathrm{dry}} ={\mathrm{ True}}$, which returns the generated commands instead of starting the run.

Code example 4: All the information in the table can be accessed.

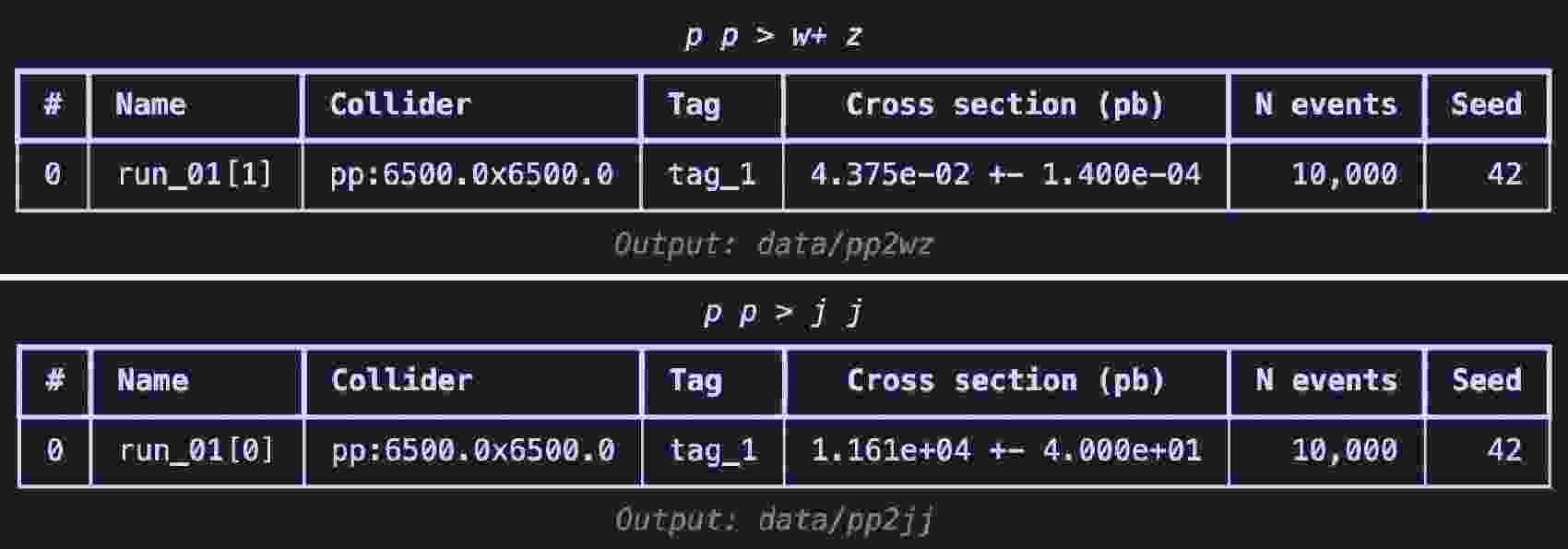
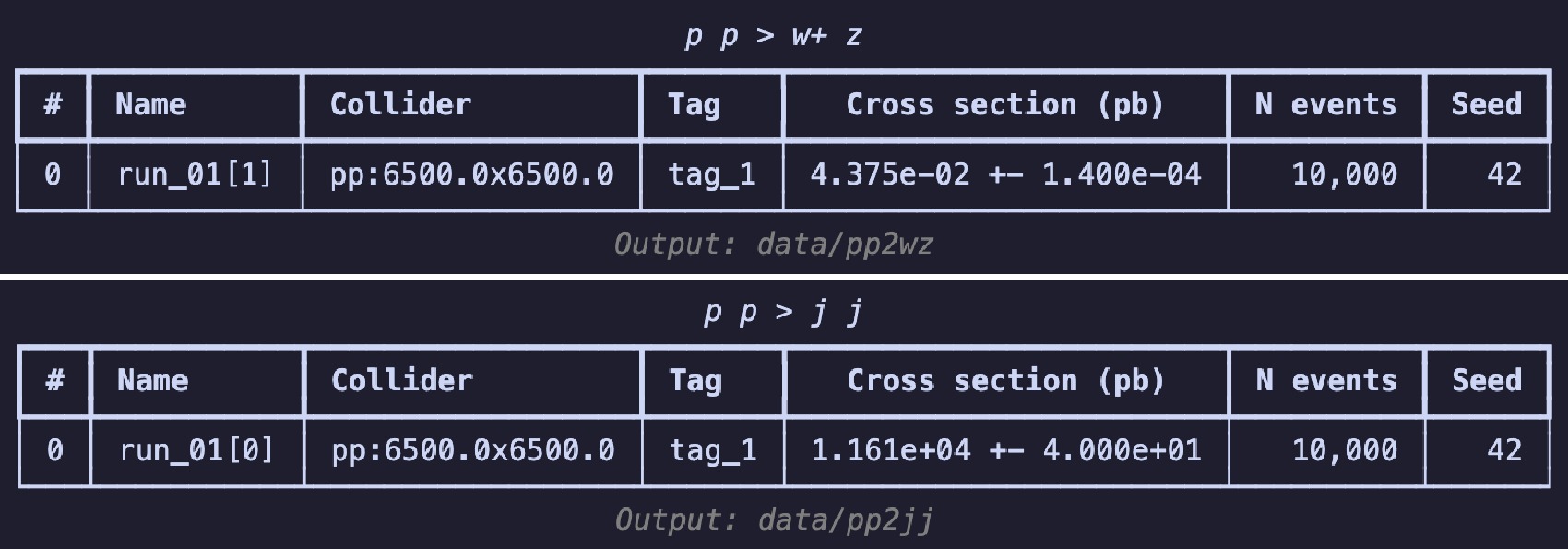
After generating the events, the $ \mathrm{summary}$ method, i.e., $ \mathrm{g.summary()} $ can be used to print the results in a table, as shown in Fig. 2. The table includes the name of each run, number of sub-runs in brackets, colliding particle beam information, tags, cross-section, error, total number of events, and the random seed. The header displays the process information, and the footnote shows the relative path of the output; these are essentially consistent with the results seen on the web page.

Figure 2.  Output of the $ \mathrm{summary}$ method.

To continue experimenting with different parameter combinations, the $ \mathrm{launch}$ method can be used again, or the loop statements in Python can be employed to generate a series of combinations to observe the differences in the cross-section under various conditions. When doing so, it is recommended to set short label names to facilitate subsequent search and analysis, as in code example 5.

Code example 5: Use a loop to scan the mass of a particle called "nh2" and show the summary.

If output files are already available, $ \mathrm{hml}$ can be used to extract the necessary information for subsequent use. The class method ${ \mathrm{Madgraph5.from}}\_{\mathrm{output}}$ and $ \mathrm{Madgraph5Run}$ will be of great assistance, as shown in code example 6. The former accepts the path to the output folder, which is the path entered in the $ \mathrm{output}$ command of $ \mathrm{MadGraph5}$, as well as the path to the executable file. The latter requires the output folder path and name of the run to access information such as the cross section and error. The $ \mathrm{events}$ method enables the retrieval of the paths to all event files under a run, including those of the sub-runs. Currently, it supports only files in the root format. $ \mathrm{uproot}$ can be used to open these files for subsequent processing.

Code example 6: Use $ {\mathrm{Madgraph5.from}}\_{\mathrm{output}}$ and $ \mathrm{Madgraph5Run}$ to access the information.

The mass of the leading fat jet, angular distance between the primary and secondary jets, total transverse momentum of all jets, number of electrons, etc., demonstrate that observables are always connected to certain physical objects. Therefore, we propose the following observable naming convention: the name of an observable is a combination of the name of the physical object and type of the observable, connected by a dot, that is, $ \mathrm{<physics} \mathrm{object>. <observable type>}$. In this section, starting from physical objects, we gradually refine this representation, eventually extending it to the acquisition of observables, construction of data representations, and definitions of cuts.

Physical objects in DELPHES are stored in different branches and represent a category rather than a specific instance. Considering that the calculation of multiple observables involves different types and numbers of physical objects, often utilizing their fundamental four-momentum information, we have categorized physical objects into four types based on their quantity and category:

1. $ \mathrm{Single}$ physical objects, which precisely refer to a specific physical object. For example:

– $ \mathrm{"jet0"}$ is the leading jet.

– $ \mathrm{"electron1"}$ is the secondary electron.

2. $ \mathrm{Collective}$ physical objects, representing a category of physical objects. For example:

– $ \mathrm{"jet"}$ or $ \mathrm{"jet:"}$ represents all jets.

– $ \mathrm{"electron:2"}$ represents the first two electrons.

3. $ \mathrm{Nested}$ physical objects, formed by free combinations of single and collective physical objects. It currently supports the combination of "FatJet/Jet" and "Constituents":

– $ \mathrm{"jet.constituents"}$ represents all constituents of all jets.

– $ \mathrm{"fatjet0.constituents:100"}$ represents the first 100 constituents of the leading fat jet.

4. $ \mathrm{Multiple}$ physical objects, comprising the previous three types and separated by commas. For example:

– $ \mathrm{"jet0,jet1"}$ represents the leading and secondary jets.

This naming convention is inspired by the syntax of Python lists. To minimize the input cost for the user, we discard the original requirement to use square brackets for receiving indexes or slices: for single physical objects, the type name is directly connected to the index value; for collective physical objects, a colon is used to separate the start index from the end index, and the type name alone represents the entire set of objects. The ${ \mathrm{parse}}\_{\mathrm{physics}}\_ {\mathrm{object}}$ method can be used to obtain the branch and the required index values based on the name of the physical objects, as shown in code example 7. This design makes users focus on the physical objects, rather than on how the corresponding classes should be initialized. In Table 1, we summarize all types of physical objects along with their initialization parameters and provide examples.

Type	Initialization parameters	Name examples
$\mathrm{Single}$	$\mathrm{branch: str,}$ $\mathrm{index: int}$	$\mathrm{"jet0", "muon0"}$
$\mathrm{Collective}$	$\mathrm{branch: str,}$ $\mathrm{start: int|None}$	$\mathrm{"jet", "jet1:", "jet:3", "jet1:3}$
$\mathrm{Nested}$	$\mathrm{main: str|PhysicsObject,}$ $\mathrm{sub: str|PhysicsObject}$	$\mathrm{"jet.constituents", "jet0.constituents:100}$
$\mathrm{Multiple}$	$\mathrm{all: list[str|Physicsobject]}$	$\mathrm{"jet0,jet1", "jet0,jet"}$

Table 1.  Types of physics objects and their examples.

Code example 7: Use the $ {\mathrm{parse}}\_{\mathrm{physics}}\_{\mathrm{object}}$ method to obtain the branch and slices of physics objects.

In this version, physical objects are merely tools for parsing the user input and do not contain any information about the observables. Unlike other software packages, we strictly separate the acquisition of observables from the physical objects. Physical objects store only the information on the connection between the observables and their data sources, and not the data.

After defining the physical objects, the task of the observables is to extract information from them. In code example 7, we store all useful information from a physical object in $ \mathrm{branch}$ and $ \mathrm{slices}$: the former refers to the corresponding branch name, and the latter means specific parts of array-like data. The advantage of this is that when encountering certain physical objects, such as the hundredth jet, which does not exist, it returns a list of length zero instead of an error. An empty list will automatically be judged as $ \mathrm{False}$ when applying cuts, thereby being skipped.

Table 2 lists all the currently available observables. To avoid remembering the exact name of an observable, its name is case-insensitive and common aliases are added. For example, $ \mathrm{Mass}$ can be written as $ \mathrm{mass}$ or $ \mathrm{m}$, and $ \mathrm{NSubjettinessRatio}$ has the alias $ \mathrm{tau{m}{n}}$, where the values of $ \mathrm{m}$ and $ \mathrm{n}$ are passed as parameters to the corresponding class. For the transverse momentum, considering the style in different types of software, we have assigned a greater number of aliases for its symbol representation. Moreover, different observables support different types of physical objects. For example, the $ \mathrm{Size}$ observable supports collective physical objects, whereas the $ \mathrm{AngularDistance}$ observable supports all combinations of multi-body objects.

Type	Alias	Single	Collective	Nested	Multiple
$\mathrm{MomentumX, Px}$	${\mathrm{momentum}}\_{\mathrm{x, px}}$	$\checkmark$	$\checkmark$	$\checkmark$
$\mathrm{MomentumY, Py}$	${\mathrm{momentum}}\_{\mathrm{y, py}}$	$\checkmark$	$\checkmark$	$\checkmark$
$\mathrm{MomentumZ, Pz}$	${\mathrm{momentum}}\_{\mathrm{z, pz}}$	$\checkmark$	$\checkmark$	$\checkmark$
$\mathrm{Energy, E}$	$\mathrm{energy, e}$	$\checkmark$	$\checkmark$	$\checkmark$
$\mathrm{TransverseMomentum, Pt}$	${\mathrm{transverse}}\_{\mathrm{momentum, pt, pT, PT}}$	$\checkmark$	$\checkmark$	$\checkmark$
$\mathrm{PseudoRapidity, Eta}$	${\mathrm{pseudo}}\_{\mathrm{rapadity, eta}}$	$\checkmark$	$\checkmark$	$\checkmark$
$\mathrm{AzimuthalAngle, Phi}$	${\mathrm{azimuthal}}\_{\mathrm{angle, phi}}$	$\checkmark$	$\checkmark$	$\checkmark$
$\mathrm{Mass, M}$	$\mathrm{mass, m}$	$\checkmark$	$\checkmark$	$\checkmark$
$\mathrm{Charge}$	$\mathrm{charge}$	$\checkmark$	$\checkmark$
$\mathrm{BTag}$	${\mathrm{b}}\_{\mathrm{tag}}$	$\checkmark$	$\checkmark$
$\mathrm{TauTag}$	${\mathrm{tau}}\_{\mathrm{tag}}$	$\checkmark$	$\checkmark$
$\mathrm{NSubjettiness, TauN}$	${\mathrm{n}}\_{\mathrm{subjettiness,tau}}\_{\mathrm{n},}{\mathrm{ tau{n}}}$	$\checkmark$	$\checkmark$
$\mathrm{NSubjettinessRatio, TauMN}$	${\mathrm{n}}\_{\mathrm{subjettiness}}\_{\mathrm{ratio, tau}}\_{\mathrm{{m}{n}, tau{m}{n}}}$	$\checkmark$	$\checkmark$
$\mathrm{Size}$	$\mathrm{size}$		$\checkmark$
$\mathrm{InvariantMass}$	${\mathrm{invariant}}\_{\mathrm{mass, inv}}\_{\mathrm{mass, inv}}\_{\mathrm{m}}$	$\checkmark$			$\checkmark$
$\mathrm{AngularDistance, DeltaR}$	${\mathrm{angular}}\_{\mathrm{distance, delta}}\_{\mathrm r}$	$\checkmark$	$\checkmark$	$\checkmark$	$\checkmark$

Table 2.  Types of observables and their supported types of physical objects.

In code example 8, we show how to use such an observable. First, initialize the corresponding observables using the $ {\mathrm{parse}}\_{\mathrm{observable}}$ function from the $ \mathrm{observables}$ module. Then, use the $ \mathrm{read}$ method to extract the values from an event. As the $ \mathrm{read}$ returns the object itself, method chaining can be used to define an observable, directly followed by the reading of an event. Additional information, namely, the observable name, shape, and data type, is added when the observable is printed. Internally, $ \mathrm{awkward}$ [54] is used for manipulating variable-length jagged arrays. The question mark in the data type indicates missing values ($ \mathrm{None}$). The $ \mathrm{var}$ appearing in the shape indicates inconsistent lengths; for example, each event has a varying number of jets and each jet has a varying number of constituents.

The first dimension of the observable value always represents the number of events, but the shape is generally determined by the related physical objects. For example, the shape of the transverse momentum and other kinematic variables is identical to its physics obsject. However, this also depends on the computation of the observable. For instance, the shape of the $ \mathrm{Size}$ observable is the number of physics objects and the second dimension is always $ 1 $, whereas the shape of $ \mathrm{AngularDistance}$ depends on the type of physical objects: when calculating the distance between all jets and the leading fat jet, we will obtain an array of shape ${ \mathrm{(n}}\_{\mathrm{events, var, 1)}}$, where ${ \mathrm{n}}\_{\mathrm{events}}$ represents the number of events, $ \mathrm{var}$ represents a variable number of jets, and $ 1 $ represents the leading fat jet; when calculating the distance between the first ten fat jets and all constituents of all the jets, we obtain an array of shape $ {\mathrm{(n}}\_{\mathrm{events, 10, var)}}$. The value of $ \mathrm{var}$ now originates from the number of constituents and number of jets; the two dimensions are compressed into one. For events that do not have sufficient physics objects, the missing values are filled with $ \mathrm{None}$.

Code example 8: Use $ {\mathrm{parse}}\_{\mathrm{observable}}$ and $ \mathrm{read}$ to obtain the values of the observables. $ \mathrm{events}$ are opened by $ \mathrm{uproot}$.

The built-in observables are very basic and may not be sufficient for every use case. Therefore, we show three examples of building your own observables. In the first example 9, when the needed observable is already stored under a certain branch, only the name of this observable needs to be declared as a class that inherits from $ \mathrm{Observable}$. $ \mathrm{hml}$ will search for the branch based on the physical object name and extract the corresponding value based on the slices. Here, we take the observable $ \mathrm{MET}$ as an example, which is originally stored under the branch $ \mathrm{MissingET}$. To use the $ {\mathrm{parse}}\_{\mathrm{observable}}$ function, the ${\mathrm{register}}\_ $ $ {\mathrm{observable}}$ function can be called to register an alias for it. Please note that this implementation requires a physical object, which means that only by entering $ \mathrm{"missinget0.met"}$ or $ \mathrm{"MissingET0.MET"}$ can the ${ \mathrm{parse}}\_{\mathrm{observables}}$ function normally. Only $ \mathrm{"MET"}$ or $ \mathrm{"met"}$ without a physics object is not allowed. As each event has only one missing energy physical object, $ \mathrm{"MissingET"}$ is followed by 0.

Code example 9: Inheriting from $ \mathrm{Observable}$ will automatically retrieve the corresponding value if the physics object has it.

If a computation process has been already established and the physical objects need not be considered, we recommend referring to the second example 10. For this, the $ \mathrm{read}$ method should be overwritten by specifying the process for computing the values of the observables. $ \mathrm{events}$ is the return value of $ \mathrm{uproot.open}$. You may need to adjust the calculation because of $ \mathrm{events}$ and the underlying $ \mathrm{awkward}$ array. It is important to note that $ \_\mathrm{value}$ must be an iterable object, such as a list or array, to be correctly converted into an $ \mathrm{awkward}$ array by $ \mathrm{hml}$. Additionally, $ \mathrm{self}$ should be returned at the end, enabling chain calls similar to those of other observables.

Code example 10: Overwrite the $ \mathrm{read}$ method to specify the process for calculating the value of the observable.

The third example 11 changes the initialization. We add constraints on the physical objects, i.e., it can be related only to a single physics object. In addition, a new parameter is introduced for greater flexibility. The $ \mathrm{read}$ part is the same as that in the second example. This is the strictest observable but also the safest one.

Currently, the naming convention is built upon the output of DELPHES and does not support other formats yet. However, considering that different analyses require data at different levels and in different formats, we plan to gradually add support for other event formats in the future versions, such as HEPMC, LHE, etc.

To make high-energy physics data compatible with different analysis approaches, it is necessary to convert the data into various representations. The review paper [55] summarizes six representations of jets: ordered sets, images, sequences, binary trees, graphs, and unordered sets. Built upon the observable naming convention, we extend the representation to an event. Currently, $ \mathrm{hml}$ supports the (ordered) set and image representations. In future versions, we will prioritize adding the graph representation and the corresponding neural networks.

Code example 11: Define an observable with constraints on the type of physical objects and with a new parameter.

The ordered set is one of the most commonly used representations. It arranges physics-inspired observables in an arbitrary order to form a vector that describes an event. The vectors from all events are then assembled into one matrix by event, with the shape $ {\mathrm{(n}}\_{\mathrm{events}}, {\mathrm{n}}\_{\mathrm{observables)}}$. By following the naming convention, such a set can be constructed in a straightforward and concise manner, as illustrated in code example 12.

Code example 12: Use $ \mathrm{Set}$ to represent the ordered set of observables.

The observable names must be packaged into a list and passed to the $ \mathrm{Set}$. Next, the $ \mathrm{read}$ method must be called to obtain the values from the events. The values will be stored in the $ \mathrm{values}$ attribute. Here, it can be seen that the $ \mathrm{awkward}$ arrays are used to store the data. For observables that have the correct physical object name but do not exist (for example, $ \mathrm{muon0.charge}$, when there are no muons produced in the event), the value is set to $ \mathrm{None}$. This approach of handling missing values allows us to follow the matrix operation sequence: first build the data matrix, then deal with the missing values.

For the image representation, the observable names are used to specify the method for fetching the data for its height, width, and channel, as shown in code example 13. The $ \mathrm{read}$ method is used to read events as before. Here, we construct an image of the leading fat jet, along with the pseudorapidity, azimuthal angle, and transverse momentum of all its constituents. Considering that similar preprocessing processes have been employed in a large number of studies, we add them as the methods of the $ \mathrm{Image}$ class. Because preprocessing often relates to sub-jets, it is necessary to add the information on sub-jets via the method $ {\mathrm{with}}\_{\mathrm{subjets}}$; its parameters include the name of the constituents, clustering algorithm, radius, and minimum momentum of the jet. The $ \mathrm{translate}$ method moves the position of the leading sub-jet to the origin, which reduces the complexity of the position information and expedites the learning process. Next, the position of the sub-leading sub-jet can be rotated right below the origin, making the features of the entire image more pronounced. Lastly, the $ \mathrm{pixelate}$ method is used to pixelate the data to obtain a real image. Because pixelation reduces the data precision, this step is removed. Further studies are needed to determine when this method should be applied and the effect of the order of its application.

Code example 13: Use $ \mathrm{Image}$ to represent a fat jet and preprocess it via sub-jets.

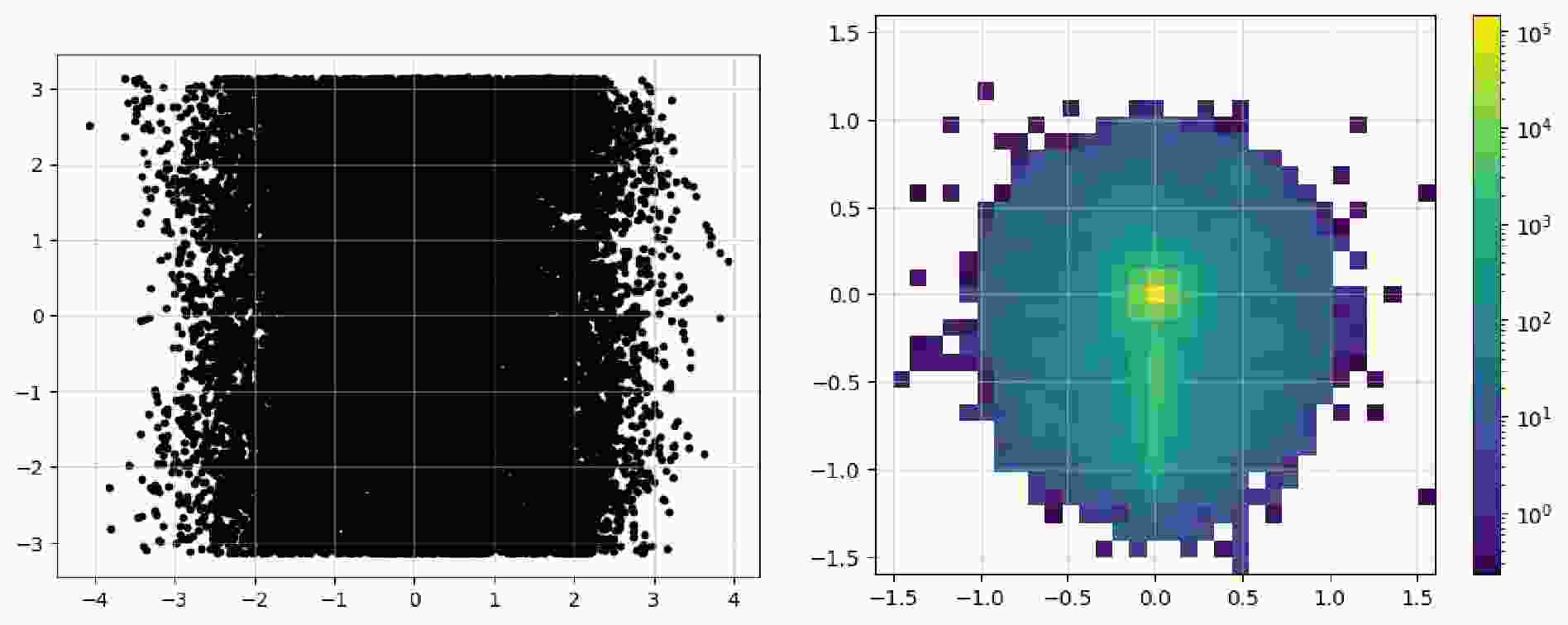
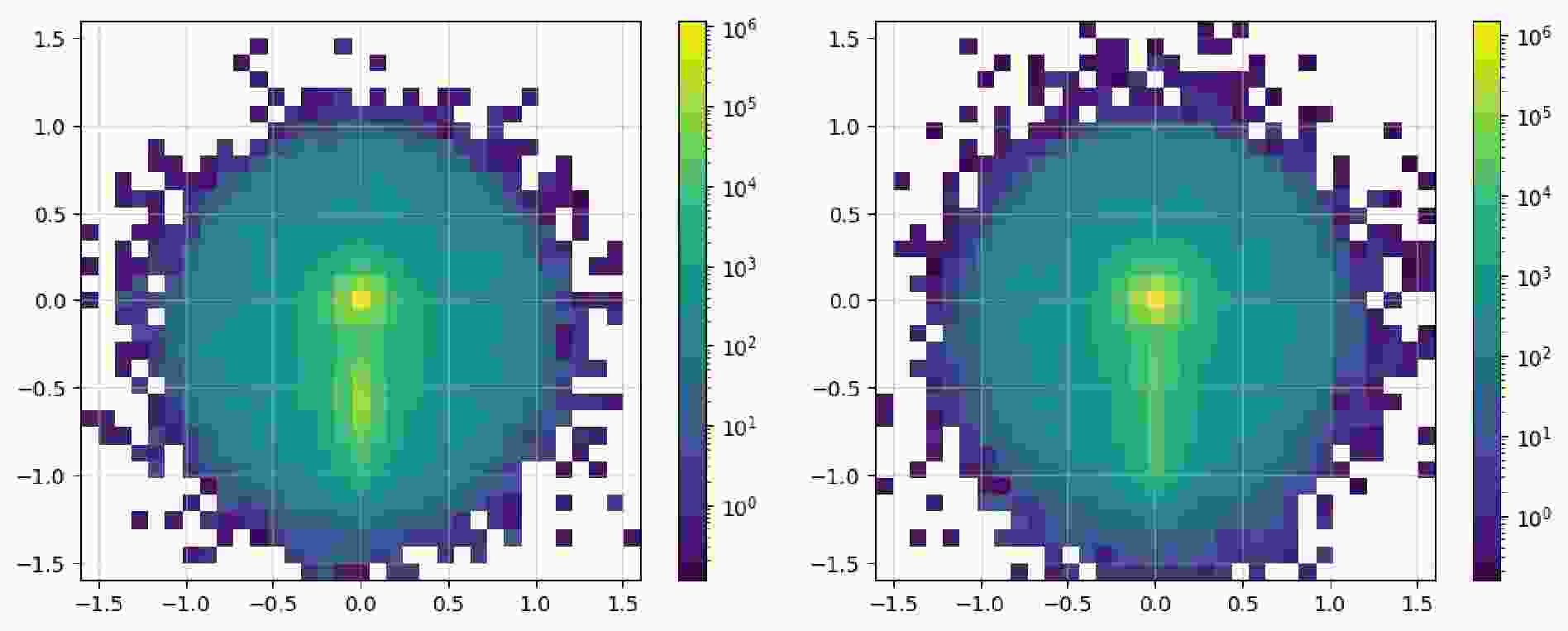
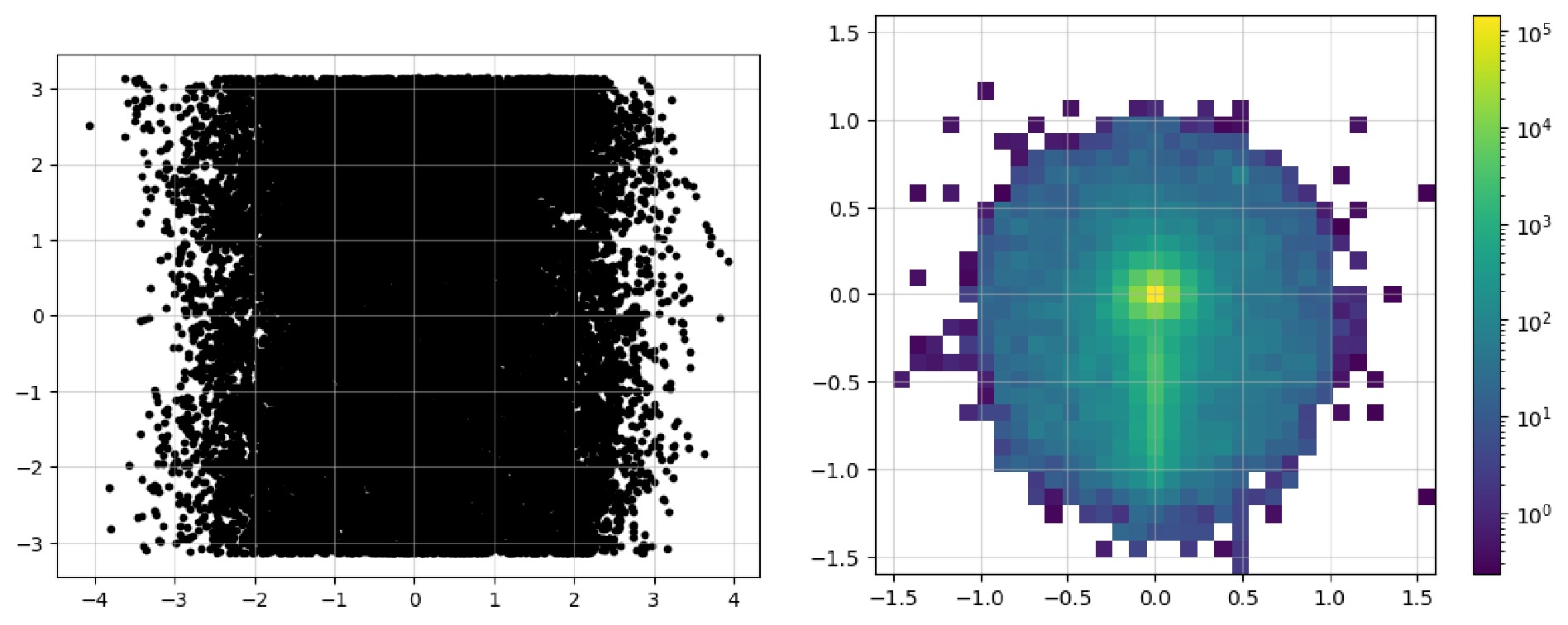
For convenience in displaying the images, the $ \mathrm{Image}$ class contains the $ \mathrm{show}$ method, which can directly plot it as an image. Code example 14 shows all the available parameters: the first two are used to show the image as dots; the last three parameters display a pixel-level grid, enable the grid by default, and apply normalization over the entire image, respectively. Figure 3 shows the image representations before and after the preprocessing steps. In the raw image, the observables used for "height" and "width" are directly plotted as a 2D scatter image. In addition, $ \mathrm{norm="log"}$ enhances the features of the final pixelated image to make them more distinct. The data can be accessed via the $ \mathrm{.values}$ property as a list of awkward arrays (before pixelation) or one awkward array (after pixelation). These can be converted and saved in formats such as a numpy array and JSON files to allow for their handling with common tools.

Figure 3.  (color online) Raw image and pixelated image after preprocessing.

Code example 14: Use $ \mathrm{show}$ to plot the image as a 2d heatmap if it has been pixelated or as a 2d scatter plot.

After acquisition, the original event data are filtered to obtain events that satisfy specific criteria. In the previous workflow, during the event loop, it was common to manually include the calculation of the observables and then apply conditionals to filter the events. We note that the $ ($array) method in $ \mathrm{uproot}$ supports the $ \mathrm{cut}$ parameter. In $ \mathrm{hml}$, we utilize a matrix-oriented programming style to change the filtering procedure into Boolean indexing; furthermore, we add the logical operation syntax to the observable naming convention to make the definitions of cuts intuitive, as shown in code example 15. $ \mathrm{Cut}$ continues to have a similar $ \mathrm{read}$ method. The values form a one-dimensional Boolean matrix, the length of which is equal to the number of events, allowing its direct use to filter other observables via Boolean indexing.

For the extend syntax of the logical operations, i.e., how to combine multiple conditions, we refer to the implementation of $ \mathrm{uproot}$: it uses the bitwise logical operators of the matrices, & and $ \mathrm{|}$, to replace $ \mathrm{and}$ and$ \mathrm{or}$, respectively, and adds parentheses to ensure priority. For example, $ \mathrm{(pt1 > 50) }$ & $ \mathrm{ ((E1>100) | (E1<90))}$ expresses the condition that $ \mathrm{pt1}$ is greater than 50 and $ \mathrm{E1}$ is either greater than 100 or less than 90. The expression is then parsed directly by Python: it is purely a matrix operation, without considering the case of the DELPHES output. It cannot handle cuts such as "all jets are required to have a transverse momentum greater than 10 GeV," where the data have the shape ${ \mathrm{n}}\_{\mathrm{events, var}}$. It undoubtedly requires users to rearrange the original data to make the dimensions of the matrices consistent, as the number of jets is not necessarily the same among the events. This essentially filters only the values that meet the conditions, not the events that meet the conditions. In conjunction with the observable naming convention, we advocate simplifying the matrix logical operation syntax to facilitate the user input.

Code example 15: Cut values are Boolean arrays that can be used to filter other observables.

1. Logical AND and logical OR are represented by $ \mathrm{and}$ and $ \mathrm{or}$, respectively. They are automatically converted to bitwise logical operators & and $ \mathrm{|}$, respectively, avoiding too many parentheses.

2. The result of the logical expression acts on the first dimension, that is, the dimension of the events, to filter the events.

3. The involved observables must have the same dimensions to ensure the correctness of the logical operations.

4. At the end of a cut, default $ \mathrm{[all]}$ represents a logical AND operation on all values of all observables in each event. It can be ignored and need not be written; $ \mathrm{[any]}$ represents a logical OR operation on all values of all observables in each event. This syntax is suitable for cases where all of a certain observable or any one observable in the events must meet the conditions.

5. Add support for $ \mathrm{veto}$ at the beginning of a cut for cases where certain events need to be excluded.

Below, we demonstrate and explain the new syntax by referring to literature. The original text will be presented first, followed by the corresponding cut in the next line. We assume that the data are stored in the same units as indicated in the description. In [56]:

1. Muons $ \mu^{ \pm} $ are identified with a minimum transverse momentum $ p_T^\mu>10~ \mathrm{GeV} $ and rapidity range $ \left|\eta^\mu\right|<2.4 $...

$ \mathrm{muon.pt > = 10 and -2.4 < muon.eta < 2.4}$

Here, we take all the muons and simplify the syntax for pseudorapidity within a certain range, which can be written consecutively. Here, $ \mathrm{and}$ represents the bitwise logical operator of the matrix. For each event, if $ \mathrm{[any]}$ is absent at the end of the expression, all values must satisfy the condition;

2. Only events with reconstructed di-muons having the same sign are selected.

$ \mathrm{muon0.charge = = muon1.charge}$

Here, we only need to judge whether the charges of the two muons are the same, without determining whether the number of muons is two. When there are fewer than two muons, the charge of one muon will be $ \mathrm{None}$, and such a judgment will be automatically treated as $ \mathrm{False}$;

3. We identify the hardest fat-jet with the $ W^{ \pm} $ candidate jet ($ J $), which is required to have $ p_T^J>100 ~\mathrm{GeV} $.

$ \mathrm{fatjet0.pt > = 100}$

In [57]:

1. C3: we veto the events if the OS di-muon invariant mass is less than 200 GeV.

${ \mathrm{muon0.charge ! = muon1.charge and muon0,muon1.inv}}$ $\_{\mathrm{mass > 200}} $

2. C4: we apply a b-veto.

$ {\mathrm{veto jet.b}}\_{\mathrm{tag = = 1 [any]}}$

Use $ \mathrm{veto}$ and $ \mathrm{[any]}$ to indicate that for all jets, if any jet is b-tagged, then the event is excluded.

3. C5: we consider only events with a maximum MET of 60 GeV.

$ \mathrm{MissingET0.PT < 60}$

The case used (uppercase or lowercase) is inconsequential because there is only one missing energy; hence, it is represented by 0. The MET observable in this case also refers to the transverse momentum; hence, it can be represented by PT.

4. C8: we choose events with $ N $-subjettiness $ \tau_{21}^{J_0}<0.4 $.

$ \mathrm{fatjet0.tau21 < 0.4}$

The definition of this observable is provided by the DELPHES card. We have already defined its parsing method in the observables module; therefore, its name can be directly used here.

In [58], the cuts of CBA-I for $ M_N = 600-900 $ GeV:

1. Jet-lepton separation $ 2.8<\Delta R(j, \ell)<3.8 $

$ {\mathrm{ 2.8 < jet0,lepton0.delta}}\_{\_{\mathrm{mass > 200}}{r < 3.8}}$

In [59]:

1. The basic selections in our signal region require a lepton ($ e $ or $ \mu $) with $ |\eta_{\ell}|<2.5 $ and $ p_{T, \ell}>500 $ GeV...

$ \mathrm{ -2.5 < muon0.eta < 2.5 and muon0.pt > 500}$.

We take the example of the muon.

2. ... veto events that contain additional leptons with $ \left|\eta_{\ell}\right|<2.5 $ and $ p_{T, \ell}>7 \mathrm{GeV} $

$ \mathrm{veto -2.5 < muon.eta < 2.5 and muon.pt >}$ $ \mathrm{7 [any]} $

In this cut, it is easier to use $ \mathrm{veto}$ to exclude events with additional leptons.

3. ... and impose a jet veto on the subleading jets with $ \left|\eta_j\right|<2.5 $ and $ p_{T, j}>30 \mathrm{GeV} $.

$ \mathrm{veto -2.5 < jet1.eta < 2.5 and jet1.pt > }$ $\mathrm {30 [any]}$

In [60]:

1. Photon-veto: Events having any photon with $ p_T>15 $ GeV in the central region, $ |\eta|<2.5 $, are discarded.

$ \mathrm{veto -2.5 < photon.eta < 2.5 and photon.pt }$ $\mathrm{> 15 [any] }$

2. $ \tau $ and b-veto: No tau-tagged jets in $ |\eta|<2.3 $ with $ p_T>18 $ GeV and no b-tagged jets in $ |\eta|<2.5 $ with $ p_T>20 $ GeV are allowed.

$ {\mathrm{ veto jet.tau}}\_{\mathrm{tag = = 1 and -2.3 < jet.eta < }}$ ${\mathrm{2.3 and jet.pt > 18 [any] }}$

3. Alignment of MET with respect to the jet directions: Azimuthal angle separation between the reconstructed jet with the MET to satisfy $ \min (\varDelta \phi({\bf{p}}_T^{\mathrm{MET}}, {\bf{p}}_T^j))>0.5 $ for up to four leading jets with $ p_T>30 ~\mathrm{GeV} $ and $ |\eta| < 4.7 $.

${\mathrm{jet:4,missinget0.min}}\_{\mathrm{delta}}\_{\mathrm{phi > 0.5 and }}$ ${\mathrm{jet:4.pt >}} {\mathrm{30 and -4.7 < jet:4.eta < 4.7}} $

Users need to define the observable $ \mathrm{MinDeltaPhi}$ in advance and register it with the alias $ {\mathrm{min}}\_{\mathrm{delta}}\_{\mathrm{phi}}$.

With the previously defined data representation and cuts, we can now proceed to construct the dataset. Corresponding to the data representations, we currently offer two datasets: $ \mathrm{SetDataset}$ and $ \mathrm{ImageDataset}$. Code example 16 shows the use of the dataset of an ordered set. Its initialization requires the names of the observables. Next, use the $ \mathrm{read}$ method to read the events. For this $ \mathrm{read}$, we introduced two additional parameters: $ \mathrm{targets}$ is the integer label assigned to the event, which is the target of the convergence. Here, we assign $ 1 $ to denote the events as signals; $ \mathrm{cuts}$ are the filtering criteria. Here, we require the number of jets to be greater than $ 1 $, and the number of leading fat jets to be greater than $ 0 $. When multiple cuts are used, the result of each cut is applied to the dataset sequentially, which means they are connected by a logical AND. The $ \mathrm{split}$ method can be used to split the dataset. Its parameters are the ratios for the training, test, and validation sets. Here, we used 70% of the data as the training set, 20% as the test set, and 10% as the validation set. Before saving the dataset, $ \mathrm{samples}$ and $ \mathrm{targets}$ can be accessed to view the stored data, which have already been converted into $ \mathrm{numpy}$ arrays. Finally, use the $ \mathrm{save}$ method to save the dataset to a zip compressed file with the $ \mathrm{.ds}$ suffix. Such a file can be loaded by the ${ \mathrm{load}}\_ {\mathrm{dataset}}$ function or $ \mathrm{SetDataset.load}$ class method.

The $ \mathrm{show}$ method can be used to quickly view the distributions of the entire dataset. Code example 17 shows all the available parameters: ${ \mathrm{n}}\_{\mathrm{feature}}\_{\mathrm{per}}\_{\mathrm{line}}$ is the number of observables to display per line, $ {\mathrm{n}}\_{\mathrm{samples}}$ is the number of events to display, and $ \mathrm{target}$ is the label of the events to display.

Code example 16: Use $ \mathrm{SetDataset}$ to build a dataset representing each event as a set of observables.

Code example 17: Use $ \mathrm{show}$ to display the distribution of observables of a set dataset.

The construction process of an image dataset is similar to that of an ordered set, as shown in code example 18. When initializing an $ \mathrm{Image}$, you can directly configure the necessary preprocessing steps in method chaining. When the dataset reads the events later, these steps will be performed in sequence.

Code example 18: Use $ \mathrm{ImageDataset}$ to build a dataset representing each event as an image

The $ \mathrm{show}$ method of an image dataset can be used to display the events as an image, as shown in Example 19. By default, the images of the entire dataset are compressed into one image. If the original dimensions are $ {\mathrm{n}}\_{\mathrm{events}}, {\mathrm{height, width, channel}}$, the compressed dimensions will be $ \mathrm{height, width, channel}$, respectively. Most parameters are the same as those in the $ \mathrm{show}$ method of $ \mathrm{Image}$ with the exception of two additional parameters: $ {\mathrm{n}}\_{\mathrm{samples}}$ representing the number of events to display, and $ \mathrm{target}$ representing the label of the events to display.

Code example 19: Use $ \mathrm{show}$ to plot the image of the dataset.

With well-prepared datasets, we can apply different approaches to identify rare new physics signals. The $ \mathrm{approaches}$ module includes cut-and-count, trees, and neural networks. We will gradually enhance it in the future versions. The basic design principle of this module is ensuring minimal encapsulation to interface with current frameworks, such as SCIKIT-LEARN [61], TENSORFLOW, and PYTORCH. Considering simplicity, we adopted the Keras-style interface design: decide approach structure at initialization, $ \mathrm{compile}$ for configuring the training process, $ \mathrm{fit}$ for training the approach, and $ \mathrm{predict}$ for prediction using new data. KERAS was originally a high-level encapsulation of TENSORFLOW. However, after the release of version 3, it supports multiple backends, thus offering unprecedented flexibility, which is one of the reasons for choosing it. Note that to date, we have tested only its compatibility with the TensorFlow backend.

Cut-and-count (or cut-based analysis) is fundamental and widely used when studying the effect of various observables on the final sensitivity. It provides evidence to support the discovery of new particles and verification of new theories.

As the name suggests, it involves two steps: applying a series of cuts to distinguish the signal from the background as much as possible, followed by counting the number of events that pass the cuts. The subsequent distribution, such as an invariant mass, is used to determine the nature of the particles involved. These cuts can be applied to the properties of specific particles, such as kinematic quantities, charge, other observables, or other characteristics associated with simulated collision events, such as the particle states in decay chains. Filtering the data allows focusing on the areas of interest, increasing the possibility of discovering new physics.

Applying cuts requires a technique to make the final signal more evident. Typically, the distribution of the observables that reflect the signal characteristics would be plotted and the area with a higher signal ratio would be selected as the cut range based on manual judgment. There are two issues here: 1) manual judgment is subjective and cannot guarantee the effect of the cut; 2) the observable distributions observed by users are sometimes the source data without any cuts. If there is an unavoidable association between the observables, applying a cut will affect the distribution of the next observable. Therefore, a more rigorous method is to apply one cut first, plot the distribution of the next observable, and then determine the next cut.

Users can use $ \mathrm{CutAndCount}$ to implement these two different strategies of applying cuts. In code example 20, we demonstrate how to initialize a $ \mathrm{CutAndCount}$ method. The number of involved observables must be specified. Subsequently, an internal $ \mathrm{CutLayer}$ is created to automatically search for the optimal cut values. For each observable, four possible conditions are considered: the signals on the left side, right side, middle, and both sides of the cut. Then, the user-specified loss function for each case is calculated, and the one with the minimum loss is selected as the final cut. $ {\mathrm{n}}\_{\mathrm{bins}}$ sets the granularity of the data when searching, i.e., the number of bins for the distribution of each observable. A higher number of bins can make the cut more precise but increases the cost of calculation, which also affects the data size and complexity of its distribution. The principle here is that as long as the data distributions remain stable, the number of bins can be appropriately reduced without affecting the final result. $ \mathrm{topology}$ sets the order or strategy of applying the cuts: $ \mathrm{parallel}$ indicates that all cuts are independent, and the distributions are considered to originate from the original data, whereas $ \mathrm{sequential}$ considers the correlation among the cuts, with each cut applied on the basis of the previous one.

Code example 20: Initialize the CutAndCount approach

In code example 21, we show how to configure and train the $ \mathrm{CutAndCount}$ approach. In the $ \mathrm{compile}$ method, you can specify the optimizer, loss function, and evaluation metrics. The optimizer is unnecessary for $ \mathrm{CutAndCount}$ because it does not use the gradient descent methods internally but rather finds the optimal cut values through a search process. The loss function is used to evaluate the effectiveness of each cut, whereas the evaluation metrics will be used to reveal the performance scores during the training. It is better to evaluate the performances simultaneously after the training. The setting $ {\mathrm{run}}\_{\mathrm{eagerly = True}}$ is necessary. By default, KERAS uses a computational graph for the calculations, which is very efficient for training neural networks. However, $ \mathrm{CutAndCount}$ includes some custom calculations that are not yet fully compatible within the computational graph; hence, it needs to be set to $ \mathrm{True}$. In the $ \mathrm{fit}$ method, the samples and targets of the training set must be input, where the batch size should be the minimum number that can reflect the distribution pattern of the data. If the user dataset is relatively small and can fit entirely into the GPU memory, the batch size can be set to the size of the entire training set. Moreover, the $ \mathrm{epochs}$ parameter is unnecessary, and the $ \mathrm{callbacks}$ parameter has not been implemented yet but will be gradually added in future versions.

Code example 21: Configure and train the $ \mathrm{CutAndCount}$ approach

Decision trees are a common method of classification, and several mature frameworks are available, such as TMVA [62], XGBOOST [63], and SCIKIT-LEARN. TENSORFLOW DECISION FORESTS [64] is also a good choice, as it too adopts the KERAS training style. Considering our preference for the multi-backend support, we modify parts of the $ \mathrm{GradientBoostingClassifier}$ code from SCIKIT-LEARN to conform to the same style.

Firstly, the original $ \mathrm{fit}$ method is enhanced to handle the input targets in a one-hot encoded format. Secondly, support for the $ \mathrm{Keras}$ metrics, such as the commonly used $ \mathrm{"accuracy"}$, is provided during the training process. Thirdly, the output of its $ \mathrm{predict}$ method is changed to predict the probabilities, aligning it with $ \mathrm{Keras}$. Despite these changes, many parameters are not supported yet: many of the original initialization parameters are related to early stopping, learning rate adjustments, etc., which are implemented in $ \mathrm{Keras}$through the callback functions. Moreover, loss functions are not uniformly customizable in $ \mathrm{scikit-learn}$; hence, we do not support changing it in the $ \mathrm{compile}$ method. In code example 22, we demonstrate the basic usage.

A starting point of $ \mathrm{hml}$ is to provide researchers with existing deep learning models so that they can conduct benchmark tests on their datasets and select the optimal model. At this early development stage, we offer only two basic models: $ \mathrm{SimpleMLP}$ (multi-layer perceptron) and $ \mathrm{SimpleCNN}$ (convolutional neural network). In future versions, after thorough testing, we will gradually introduce additional existing models to provide a larger range of selection.

Code example 22: Basic usage of the modified $ \mathrm{GradientBoostedDecisionTree}$ approach.

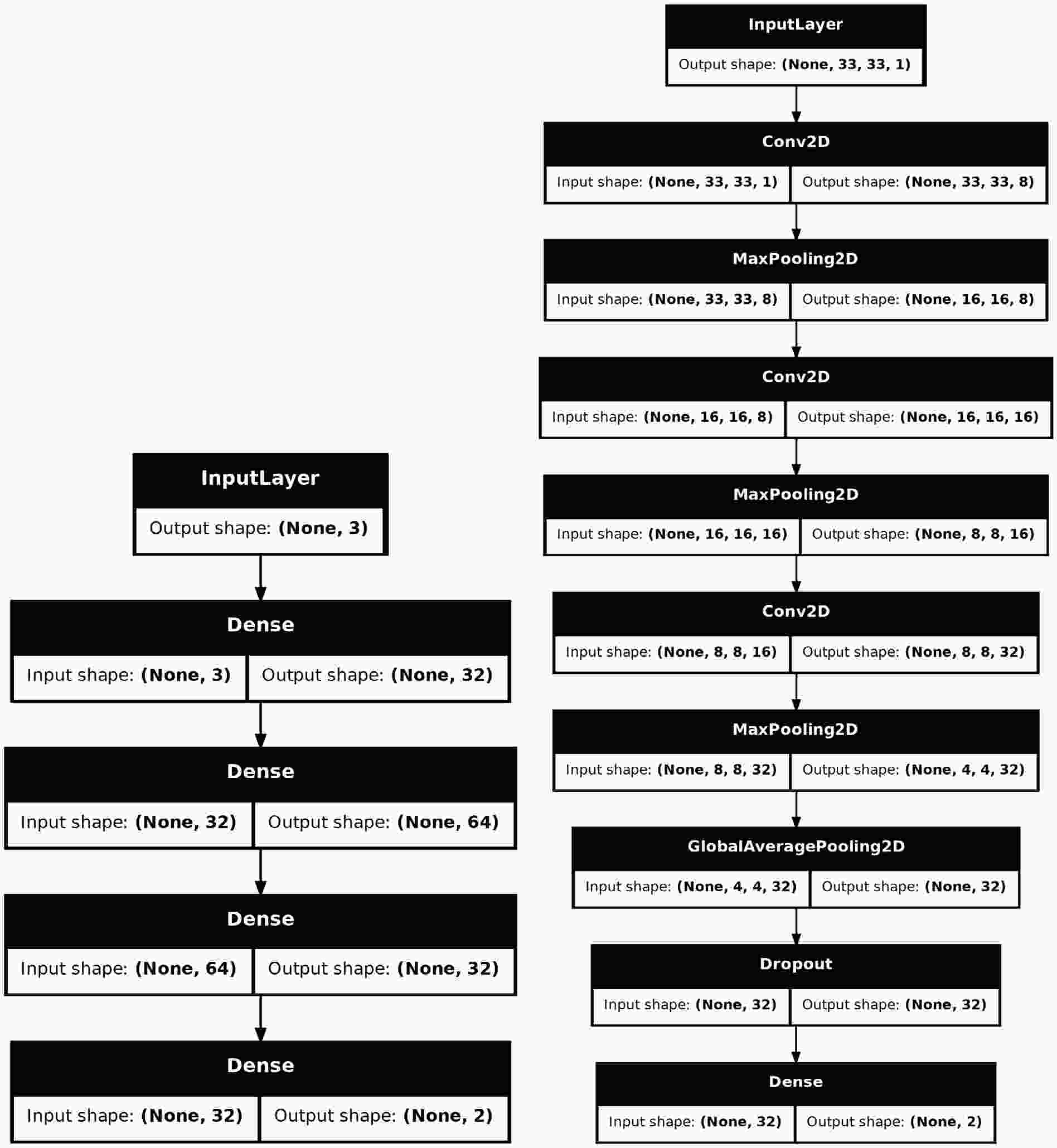
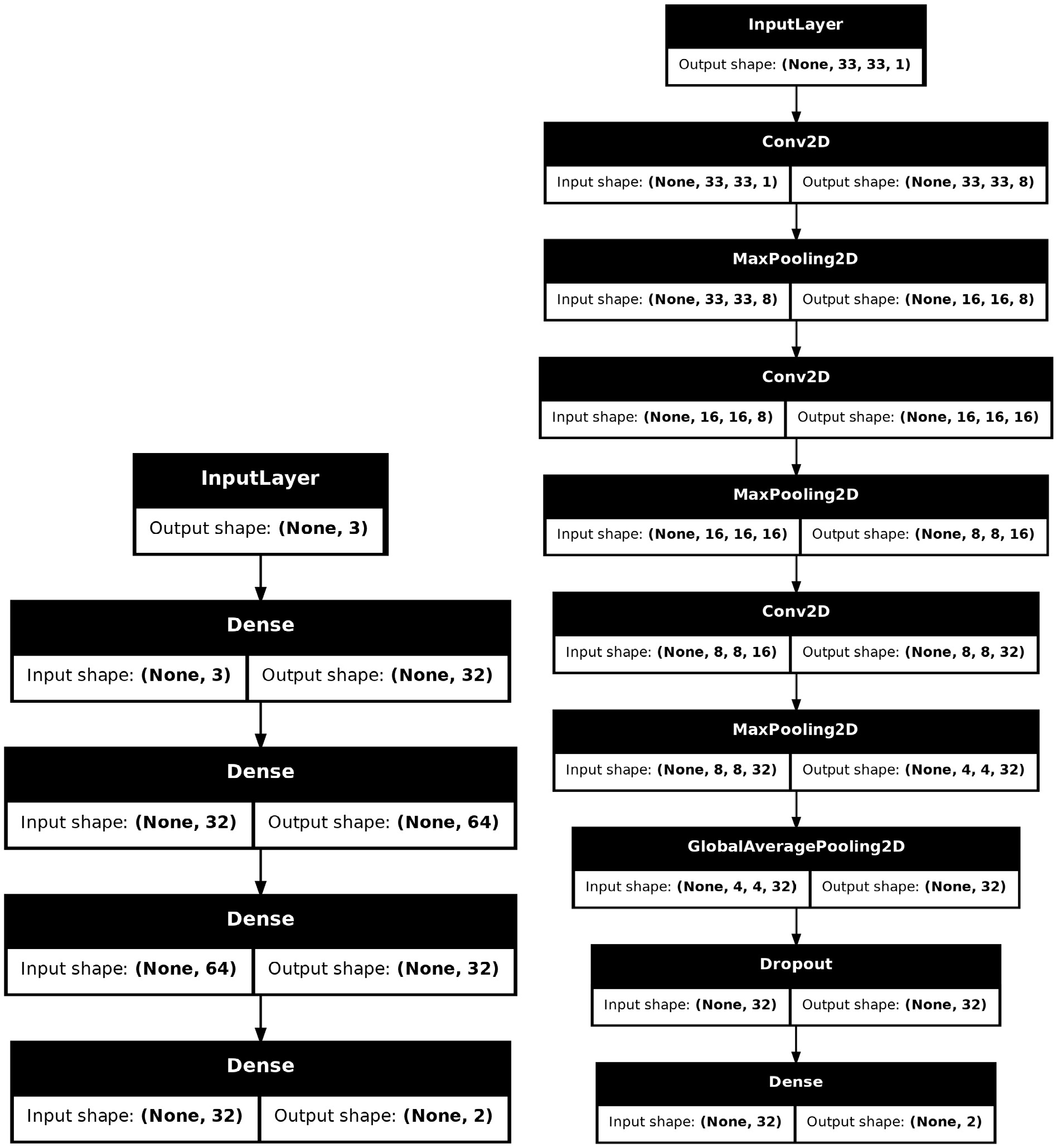
In KERAS, a model can be built in three ways: 1. Using $ \mathrm{Sequential}$ to stack the layers, 2. Using the Functional API to construct more complex topologies, 3. Inheriting from $ \mathrm{Model}$to declare a subclass for greater flexibility. Considering that the construction of many models is highly complex and requires exposing a certain number of hyper-parameters for tuning, we used the third approach to build the models. Fig. 4 shows the structures of the two models.$ \mathrm{SimpleMLP}$ has $ 4386 $ parameters and the inputs are three observables. $ \mathrm{SimpleCNN}$ has $ 5960 $ parameters and the inputs are images of the shape $ (33, 33, 1) $. Both models are shallow and simple, resulting in low consumption of computing resources during the training and testing stages.

Figure 4.  Structures of the $ \mathrm{SimpleMLP}$ and $ \mathrm{SimpleCNN}$ models.

After training an approach on a dataset, it is often necessary to use various metrics to assess its effectiveness. Unlike the classical accuracy score, which is commonly used in classification tasks, in high-energy physics, the scarcity of signals shifts the focus toward the signal significance, denoted by $ \sigma $. A higher value indicates a lower probability that the observed signal is a result of background fluctuations alone. For instance, 3$ \sigma $ is often considered as an evidence of a signal, indicating that there is approximately a 0.27% chance of the signal being a statistical fluke. Further, 5$ \sigma $ is the gold standard in high-energy physics for claiming a discovery, corresponding to a probability of roughly 1 in 3.5 million that the observed signal is due to background noise. Equation 1 is the formula for calculating the significance in $ \mathrm{hml}$. Note that $ S $ represents the number of signals, and $ B $ represents the number of backgrounds, which indicates the number of simulated events when the cross section of the corresponding process and integrated luminosity are not specified. We demonstrate its use in code example 23.

Code example 23: Use the $ \mathrm{MaxSignificance}$ metric to evaluate the performance of a trained approach.

The outputs of the built-in approaches are the probabilities for the signal and background. By default, only when the probability exceeds 0.5 do we consider it as a signal or background. In $ \mathrm{MaxSignificance}$, this threshold can be changed by setting $ \mathrm{thresholds}$. By default, data with ${\mathrm{class}}\_{\mathrm{id = 1}}$ are viewed as the signal and 0 as the background. This can be changed if the targets for the signal and background in the user dataset are different.

In addition to significance, some studies have also included the background rejection at a fixed signal efficiency as an evaluation metric. Hence, this metric was adopted in our study as well and is expressed as equation 2. The higher the background rejection rate, the fewer are the background events that are mistakenly classified as signals. Example 24 demonstrates its use. Note that multiple calls to both the metrics will result in the values being averaged. Therefore, the $ {\mathrm{reset}}\_{\mathrm{state}}$ method should be called to calculate them from scratch.

Code example 24: Use the $ \mathrm{RejectionAtEfficiency}$ metric to evaluate the performance of the model.

To enable users to gain a complete understanding of the entire workflow, this section shows how to integrate various modules to complete the task of jet tagging. This example serves merely as a proof of concept; users must conduct a more personalized analysis on this basis.

We simulated the production of highly boosted $ W^{+} $ bosons that decay into two jets, resulting in a single fat jet during event reconstruction. This jet has distinct characteristics of mass and spatial distributions, making it easier to identify using all built-in approaches.

In code example 25, we first import the event generator module from $ \mathrm{Madgraph5}$ using the $ \mathrm{generate}$ method to create the signal process, and then use the $ \mathrm{output}$ method to save it to a designated folder. To make $ W^{+} $ bosons highly boosted, we leave the decay chain unfinished here and constrain its $ p_T $ range in code example 26. After the $ \mathrm{output}$ command is completed, the output Feynman diagrams can be viewed in the $ \mathrm{Diagrams}$ folder within the output folder.

Then, the $ \mathrm{launch}$ method in code example 26 is used to start the simulation, turning on the $ \mathrm{shower}$ and $ \mathrm{detector}$. To boost the $ W^+$ boson, we set the spin mode as "none" to apply the following cuts ² in the settings. Following [3], we set the $ p_T $ range for the $ W^{+} $ boson to $ 250 $ to $ 350 $ GeV. When using the default CMS delphes card with $ R = 0.8 $ and the anti-$ k_T $ algorithm to cluster the jets, a fat jet is expected to originate from the decay of the $ W^{+} $ boson. The $ \mathrm{decay}$ method is used for further specific decays. The random seed ($ \mathrm{seed}$) is set to 42 to ensure the reproducibility of the results. When the simulation ends, the $ \mathrm{summary}$ method is used to review the results (shown in Fig. 5). This is akin to viewing the results on the website of $ \mathrm{Madgraph5}$.

Figure 5.  Summary table of the signal (upper) and background (lower) events.

Code example 25: Generate $ W^{+}$ boson events using $ \mathrm{Madgraph5}$

Code example 26: Launch the simulation of $ W^+$ boson events.

The generation process for the background events is similar to that in code example 27, with the difference lying in the $ p_T $ range settings. Because the jets in this case do not originate from the decay of a single particle, we directly restrict the $ p_T $ range of the jets.

Code example 27: Generate background events using $ \mathrm{Madgraph5}$

After the event generation is complete, we begin preparing the dataset. First, in code example 28, we use $ \mathrm{uproot}$ to open the root file output by DELPHES, which stores the branches categorized according to the physical objects. The $ \mathrm{generators}$ module includes $ \mathrm{Madgraph5Run}$, which conveniently retrieves information about the run, such as the cross section and generated event files. Because it searches for files produced in all sub-runs of a given run, even though the files for the signal events are stored in the sub-runs, $ {\mathrm{run}}\_{\mathrm{01}}$ can also retrieve the corresponding path correctly.

Code example 28: Use $ \mathrm{uproot}$ to open the DELPHES output root file.

In code example 29, to avoid missing values of the desired observables, we use the previously mentioned extended logical operations to apply the cuts. For both types of datasets, that is, $ \mathrm{SetDataset}$ and $ \mathrm{ImageDataset}$, it is required to have at least one fat jet and two regular jets. The $ \mathrm{read}$ method supports entering multiple cuts. Thus, there is no need to use the $ \mathrm{Cut}$ class to parse the expressions first. When reading the events, integer labels are assigned separately for the signal and background events. Before saving locally, the data are split into training and testing sets at a 7:3 ratio.

Code example 29: Prepare the set dataset.

For the image dataset, the representation of the data is first decided, namely, which observables should constitute the images and which preprocessing steps should be taken. In code example 30, $ \phi $, $ \eta $, and $ p_T $ of all constituents from the leading fat jet are used as the data source for the height, width, and channel of an image. Before preprocessing, ${ \mathrm{with}}\_{\mathrm{subjets}}$ is used to recluster the constituents to add information about the subjets. Because the distance between the two sub-jets will not be less than $ 0.3 $ according to the previous equation, it is safe to use the $ k_T $ algorithm with $ R = 0.3 $. Then, $ \mathrm{translate}$ and $ \mathrm{rotate}$ are used to translate and rotate the image, aligning the information of the two sub-jets. Finally, $ \mathrm{pixelate}$ is used to pixelate the image; the size here is $ 33 \times 33 $, with a range of $ (-1.6, 1.6) $ and an equivalent precision of around $ 0.1 $. This precision does not match the precision in the detector card. For simplicity, we take this fixed precision. In code example 31, we show how to prepare the image dataset.

Code example 30: Construct the representation of the image dataset.

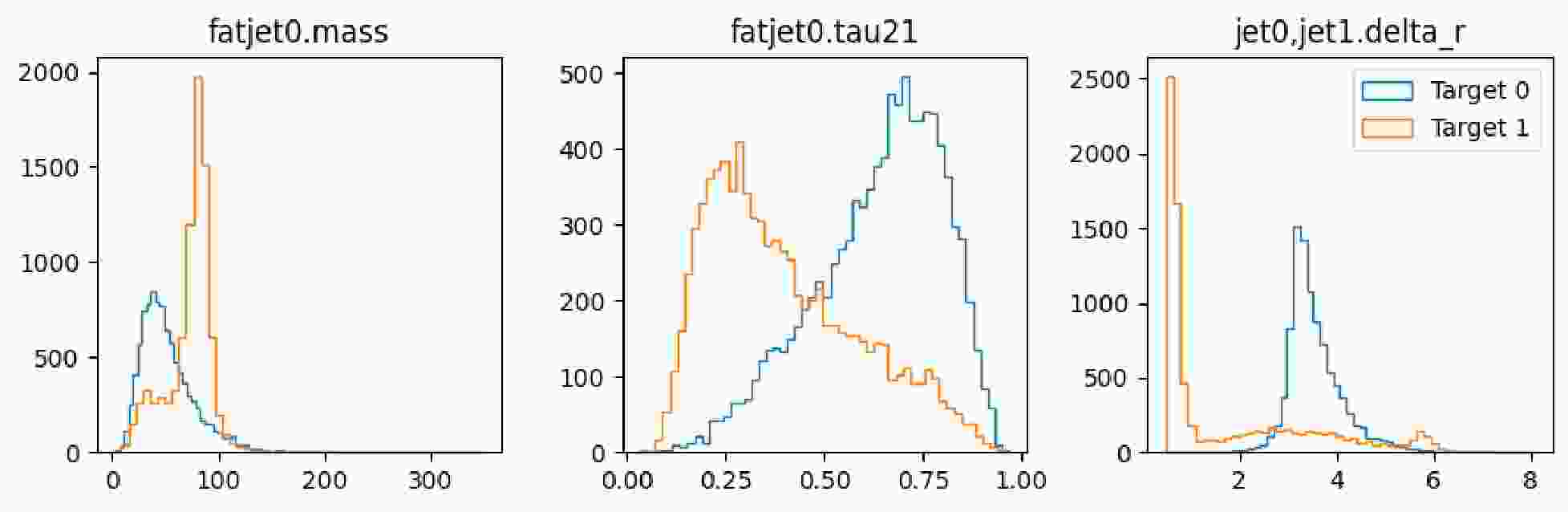
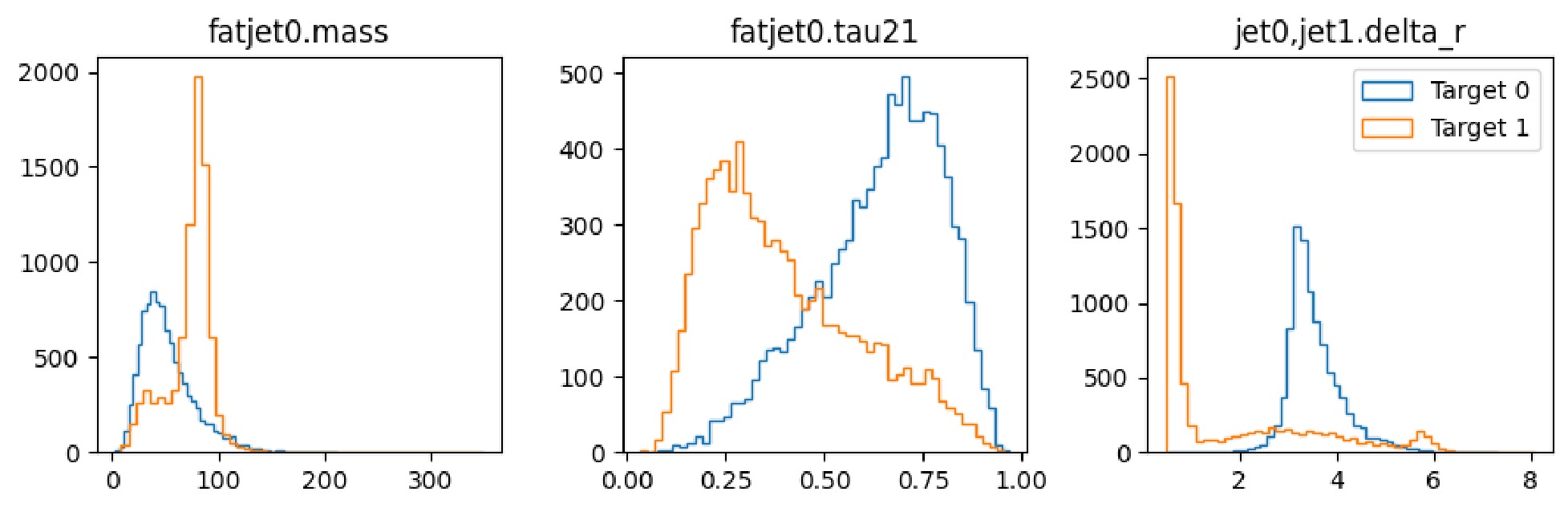
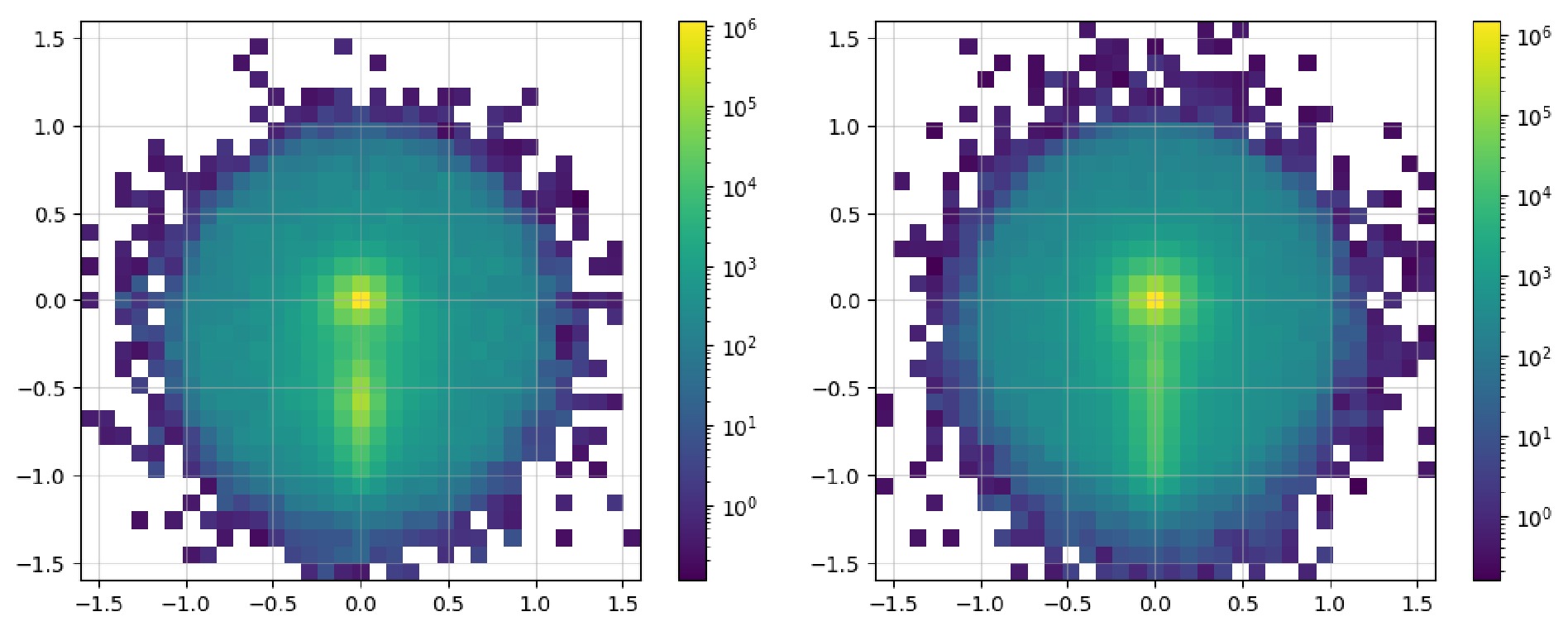
After constructing the datasets, we count the signal and background samples in code example 32 to avoid introducing an artificial bias. Then, we use the $ \mathrm{show}$ method of the dataset to display the distribution of the observables, as illustrated in Fig. 6 and Fig. 7.

Figure 6.  (color online) Feature distributions of the set dataset.

Figure 7.  (color online) Combined images of signal (left) and background (right) events.

Code example 31: Prepare the image dataset.

Code example 32: Count the number of signals and backgrounds and show the distribution of the datasets.

It is observed that the number of signals and number of background instances are approximately equal, and the observables used clearly reflect the distinct characteristics of each, which is beneficial for our subsequent classification tasks. In the display of the image dataset, we show a merged image of the signal and background. It can be seen that the fat jet image of the signal prominently features two sub-jets, whereas the sub-jets in the background are less distinct.

After preparing the datasets, all the available approaches are imported for training. These approaches learn the differences between the signal and background. Subsequently, a dictionary and the built-in metrics are used to assess their performance, which will then be presented as a benchmark test. First, import all the necessary packages, as shown in code example 33; the packages have been roughly categorized to facilitate the understanding of their purposes.

The selected evaluation metrics are accuracy, Area Under the Curve (AUC), signal significance, and background rejection rate at a fixed signal efficiency. These metrics are commonly used in high-energy physics and help us better understand the performance of the approaches. In code example 34, we define a function to retrieve the evaluation metrics of an approach.

The cut-and-count and decision tree approaches are not sensitive to the scale of features. Hence, we can directly import the dataset (code example 35) and start the training (code example 36). Two different topologies of the cut-and-count are used to demonstrate how the order of applying the cuts affects the performance.

Code example 33: Import necessary packages for the benchmark test.

Code example 34: Define a function to obtain the evaluation metrics of a model.

The input for the multilayer perceptron requires the use of $ \mathrm{MinMaxScaler}$ to scale the features within the 0-1 range, as detailed in code example 38, which aids in the rapid convergence of the model. We trained the model for 100 epochs with a batch size of 128. Code example 39 illustrates the training process.

Code example 35: Load the set dataset for training the cut-and-count and decision tree approaches.

Code example 36: Train the cut-and-count approaches with two different topologies.

Code example 37: Train the decision tree approach.

For the convolutional neural network, we employ two different preprocessing methods. One scales each image by its maximum value, whereas the other applies a logarithmic transformation to each pixel value. Given the large variations in the pixel intensity in the jet images, scaling directly by the maximum value might result in excessively small pixel values, whereas logarithmic transformation preserves the information better. In code example 40 and 42, we load the image dataset and demonstrate these two distinct preprocessing techniques.

Code example 38: Load the set dataset for training the multilayer perceptron approach.

Code example 39: Train the multilayer perceptron approach.

Finally, we present a performance comparison using code example 43. The results are shown in Table 3.

Name	ACC	AUC	Significance	R50	R99
${\mathrm{cnc}}\_{\mathrm{parallel}}$	0.750323	0.728121	33.660892	4.005174	1.000000
${\mathrm{cnc}}\_{\mathrm{sequential}}$	0.787784	0.769440	36.557026	4.712174	1.000000
$\mathrm{bdt}$	0.902011	0.955063	44.368549	117.804291	2.146139
$\mathrm{mlp}$	0.900904	0.956274	44.205276	117.804291	2.124265
${\mathrm{cnn}}\_{\mathrm{max}}$	0.806827	0.867769	38.444225	17.089737	1.188322
${\mathrm{cnn}}\_{\mathrm{log}}$	0.809452	0.876692	38.732323	19.042860	1.276514

Table 3.  Comparison of different approaches.

The significance column shows that for the cut-and-count method, the sequential topology, which considers the impacts among the cuts, performs better than the parallel topology. For convolutional neural networks, the performance of logarithmic scaling is roughly equivalent to that using maximum value scaling. Multilayer perceptron and decision trees, which utilize features with clear distinctions, exhibit the best performance. For more practical problems, we can apply different approaches to the dataset and then select the most suitable one based on various performance metrics.

Code example 40: Load the image dataset and normalize the pixel values with the maximum value.

Code example 41: Train the convolutional neural network approach with the maximum value normalization.

In the current era of rapid evolution of machine learning models, it is worthwhile to explore methods to use them more conveniently in high-energy physics for searching new physical signals. In this paper, we introduced the $ \mathrm{hml}$ Python package, which offers a streamlined workflow from event generation to performance evaluation. The simplified process and control over random seeds significantly enhance the reproducibility of the final analysis results.

Code example 42: Normalize the pixel values by using the logarithm. $ \mathrm{"..."}$ indicates the same code as in code examples 40 and 41.

Code example 43: Compare the performances of different approaches.

We proposed a naming convention for observables, which enables users to easily extract the required data from the events output by DELPHES. Additionally, we extended the cut expression syntax, originally in UPROOT, to make it more user-friendly and compatible with the DELPHES output formats. This convention is also utilized in our dataset construction process, helping users to quickly and conveniently build datasets. Based on this naming convention, we implemented a transformation from the outputs of event generators to datasets usable by various analysis approaches. Moreover, the $ \mathrm{show}$ method included in the datasets enables users to display the data either as 1D distributions or 2D images, facilitating the adjustment of observable selections based on the observed differences.

We adopted the interface style of KERAS to standardize traditional methods such as the cut-and-count technique and decision trees. Furthermore, the cut-and-count approach supports automatic searching for the optimal cut positions, significantly reducing the workload for users. Additionally, we incorporated the commonly used evaluation metrics in high-energy physics, such as signal significance and background rejection rate at a fixed signal efficiency. These metrics help users to better understand the performance of the models.

We demonstrated the complete workflow through a practical example, which intuitively showcased the usage of $ \mathrm{hml}$. $ \mathrm{hml}$ is continuously being updated. We plan to incorporate additional existing deep learning models and datasets, and extend it to graph representations of data to further enhance its capabilities.