Investigation on cluster states around ²⁰Ne including spin-orbit coupling and its extension to heavier nuclei

Clustering is an intriguing phenomenon inside nuclear many-body systems appearing abundantly in different mass regions across the nuclide chart. The clustering phenomenon unveils an alternative perspective on the basic structures within the atomic nucleus [1, 2]. Due to the strongly correlated nucleon motions, some particles with high degrees of symmetry under certain circumstances can be regarded as substructures, like the enormously stable α particle [3]. In fact, the α-cluster concept has been applied to investigate a series of typical nuclei above double shell closures [4−10], giving good descriptions of electromagnetic transitions, energy spectra, α scatting and α-emission widths. However, the explorations on the cluster structures of heavy nuclei are more challenging because of both the mean-field effects and the limitations of experimental technology. Therefore, much more attention has been paid to clustering phenomena for the systems of $ n\alpha $ or $ n\alpha $ plus other particles in light-mass region [11−13], especially for the exotic cluster states. Recently, plenty of 4α events were recorded with full particle identification providing new evidence for the Hoyle-like structure in ¹⁶O [14]. The excited 0⁺ state with a gas-like characteristic was found via the microscopic five-body calculations implying the existence of 5α condensate state in ²⁰Ne [15].

Despite the α-clustering being a common occurrence throughout above regions, the measurements of energy levels and electromagnetic transition rates for cluster states appear to be more difficult when it comes to odd-mass nuclei owing to the interaction in collective excitations of few-body [16] and quite small cross sections corresponding to the astrophysical energies. Fortunately, the widely discussed cluster states close to the thresholds in favorable nuclei ¹⁹F and ²¹Ne can be identified via the three-nucleon and α-particle transfer reactions [17, 18]. From the theoretical point of view, new insight into the clustering phenomena in odd-A nuclei with the spin-orbit coupling effects can be obtained by studying the weak-coupling interplay [19] between the cluster and residual core. On the other hand, the energy spectra and electromagnetic transitions around ²⁰Ne have been observed experimentally with implications for nuclear astrophysical field [16, 20−32]. Besides, the existence of cluster states in heavier odd-mass nuclei is a topic of interest in recent years. The spectroscopic properties including spin parities and α-particle partial widths of possible cluster states in these nuclei, like ⁴³Sc, ⁵⁹Cu and ⁹³Mo [33, 34], have a significant impact on the astrophysical nucleosynthesis process.

In the recent decades, some progress has been achieved in the microscopic comprehension of clustering phenomena rooted in the configuration mixing. Starting from the generator coordinate method (GCM), orthogonality condition model (OCM) and resonating group method (RGM), various new microscopic models and methods have been developed to interpret the α-cluster states for light nuclei, such as the Tohsaki-Horiuchi-Schuck-Röpke (THSR) wave function [12, 15], the antisymmetrized molecular dynamics (AMD) [35−37], the Monte Carlo Shell Model (MCSM) [38], and so on. In addition to these cluster models, the binary cluster-core model [7−9, 39−41], treating the picture of target nucleus as the cluster constituted by strongly correlated nucleons orbiting the inert core, has been used successfully to describe the spectroscopic properties from light to heavy nuclei, including several odd-A nuclei [39, 42]. In our previous work [7, 8], we have systematically investigated the parity doublet bands and the electromagnetic transitions for α-cluster states above double shell closures within the BCM and the Monte Carlo bootstrap method, resulting in a good agreement with the available data plus uncertainty evaluation.

One objective of this study is to give satisfactory calculations of energy bands, $ B(E1) $ and $ B(E2) $ values in the field of astrophysical interest with the extra cluster spin-orbit potential in the same framework of "three-nucleon or α-cluster + core" configurations for ¹⁹F and ²¹Ne to verify the reliability of such binary cluster-core model. The other aim is to check or prove the role of cluster degrees of freedom played in the heavier odd-mass nuclei, such as ⁴³Sc, ⁵⁹Cu and ⁹³Mo. The rest sections of this article are organized in the following way. Section II presents the theoretical framework of the calculations of energy spectra and electromagnetic transition strengths. In Sec. III, the numerous results and discussions for cluster states in above nuclei are given. A brief summary with additional remarks will be shown in the last section.

As mentioned before, the BCM is a clear and effective cluster model, in which the target nucleus is assumed as the strongly correlated cluster orbiting the inert core composed of the residual nucleons. The wave functions and corresponding energies of relative motion between the cluster and core can be determined by direct solution of the two-body radial Schrödinger equation, which is given by

Here μ, n and l are the reduced mass of the two-body system, the principal and orbital quantum numbers, respectively. The total interaction potential $ V(r) $ is the key point of the cluster-core structure, containing the local nuclear potential, repulsive Coulomb part, cluster spin-orbit interaction and centrifugal term, as follows:

The Coulomb potential $ V_{C}(r) $ is regarded as that of the uniformly charged spherical core of radius $ R_C $ interacting with a point cluster. In terms of the nuclear potential $ V_N(r) $, it is to be noted that the conventional Woods-Saxon (W.S.) potentials often behave inverse feature in high-lying levels. There is also a typical shortcoming of compressed spectra in describing the ground-state rotational bands caused by the semi-microscopic double folding potentials [43−45]. To get rid of these dilemmas, the W.S. + W.S.³ approach is developed to refine the shape of nuclear potential in accordance with the energy spectra and half-lives of charged-particle emissions simultaneously [46]. A slightly modified variant of the W.S. potential mixture plus the terms of λ and σ subsequently optimizes these circumstances, leading to a good description of the excitation energies and $ B(E2) $ transition rates. The cluster-core potential of (1 + Gaussian)(W.S. + W.S.³) shape is therefore chosen as the nuclear part the same as our previous studies [7, 8], namely,

where the values of depth $ V_0 $, the diffuseness a, the mixing parameter b, the parameters λ and σ are to be introduced in the following process. The nuclear parameter R is assumed to be equivalent to the Coulomb radius $ R_C $ for minimizing the number of adjustable parameters, which is obtained by reproducing the experimental bandhead of the parity doublet bands. In general, spin-orbit splitting is not considered in the even-even nuclei because of the zero spins of the cluster and residual core, while the spin-orbit coupling potential cannot be neglected in the calculations of the odd-mass region, which is related to the nuclear potential $ V_N(r) $ of Eq. (3) in the usual way [39, 42] by

Here ($ \hbar $/$ m_{\pi}c $)² = 2 fm², $ \mathit{\boldsymbol{\sigma}} $ is the spin of triton or ³He and odd-mass core in the different configurations. $ V_{so} $ is the potential depth of spin-orbit part, which can adjust the ordering and spacing of energy levels.

Based on the shell-model theory, the nucleons inside the cluster should lie completely in the certain orbitals outside the frozen core, which are characterized by the orbital angular momentum l, and the internal node n of wave function, namely the principal quantum number in the Eq. (1). The values of n and l are allowed by the Wildermuth condition,

The global quantum number G, identifying the energy bands of states, can be obtained after fixing the values of the oscillator and interior quantum numbers $ g_i^{A_d+A_c} $ and $ g_i^{A_c} $. Subsequently, the node n can be determined by the orbital angular momentum l. The condition G $ \geqslant $ $ G_{\mathrm{g.s.}} $ is taken into account when describing the parity doublet bands for odd-A nuclei, where $ G_{\mathrm{g.s.}} $ is connected with the ground states. In the present study, the global quantum numbers G, employed to the α-core structures in ¹⁹F, ²¹Ne, ⁴³Sc, ⁵⁹Cu and ⁹³Mo, are separately fixed as 8, 8, 12, 12 and 16. As for the triton or ³He cluster states, the values of G are set to 6, 6, 9, 9 and 12 in the systems of "t + ¹⁶O", "³He + ¹⁸O", "t + ⁴⁰Ca", "t + ⁵⁶Ni" and "³He + ⁹⁰Zr", respectively.

In the framework of BCM, the electromagnetic transitions of the cluster states belong to a special case of "single-particle" transition. For example, the entire α cluster is viewed as a single particle during the transition instead of four separate nucleons undergoing the change of shell-model states. In this way, the reduced dipole transition strength $ B(E1) $ [42] for the cluster-core relative motion from the initial state $ j_i $ of $ K_i $-band to the final state $ j_f $ of $ K_f $-band is evaluated by:

with

and

The quadrupole transition rate $ B(E2) $ [42] is given by:

with

and

The $ Z_c $ and $ A_c $ are respectively the proton and mass numbers of the cluster, and $ Z_d $, $ A_d $ are for the residual core. The $ u_{lj}(r) $ is the radial wave function associated with the momenta l and j for the cluster states. It is convenient to compare the calculated results of electromagnetic transition rates with the observed data by using the Weisskopf unit (W.u.) in the following forms:

for B(E1) values and

for B(E2) values. Here these two transition strengths in the Weisskopf units vary with the mass numbers of the target nuclei.

As mentioned above, the nuclear properties of cluster states in ¹⁹F and ²¹Ne have been reported by three-nucleon and α transfer reactions in the past decades. Nevertheless, some experimental information around the A = 20 region, like energy levels, electromagnetic transition rates, spins and parities, remains somewhat ambiguous owing to the intricate structures within the odd-A nuclei and the limitations of experimental techniques. These spectroscopic properties are vital to the generation of heavy elements in astrophysical environments [20−32] and deepening the theoretical understanding of many-body physics, with particular relevance to the clustering phenomena in odd mass nuclei. Furthermore, the ¹⁷O + α reaction rates have great influence on the efficiency of the weak s process occurring in the massive stars and asymptotic giant branch stars. The rates of ¹⁷O(α, γ)²¹Ne and ¹⁷O(α, n)²⁰Ne reactions [30−32] strongly depend on the energy levels of α-cluster states approaching the thresholds in ²¹Ne [20], which have attracted more attention in the region of interest to astrophysics.

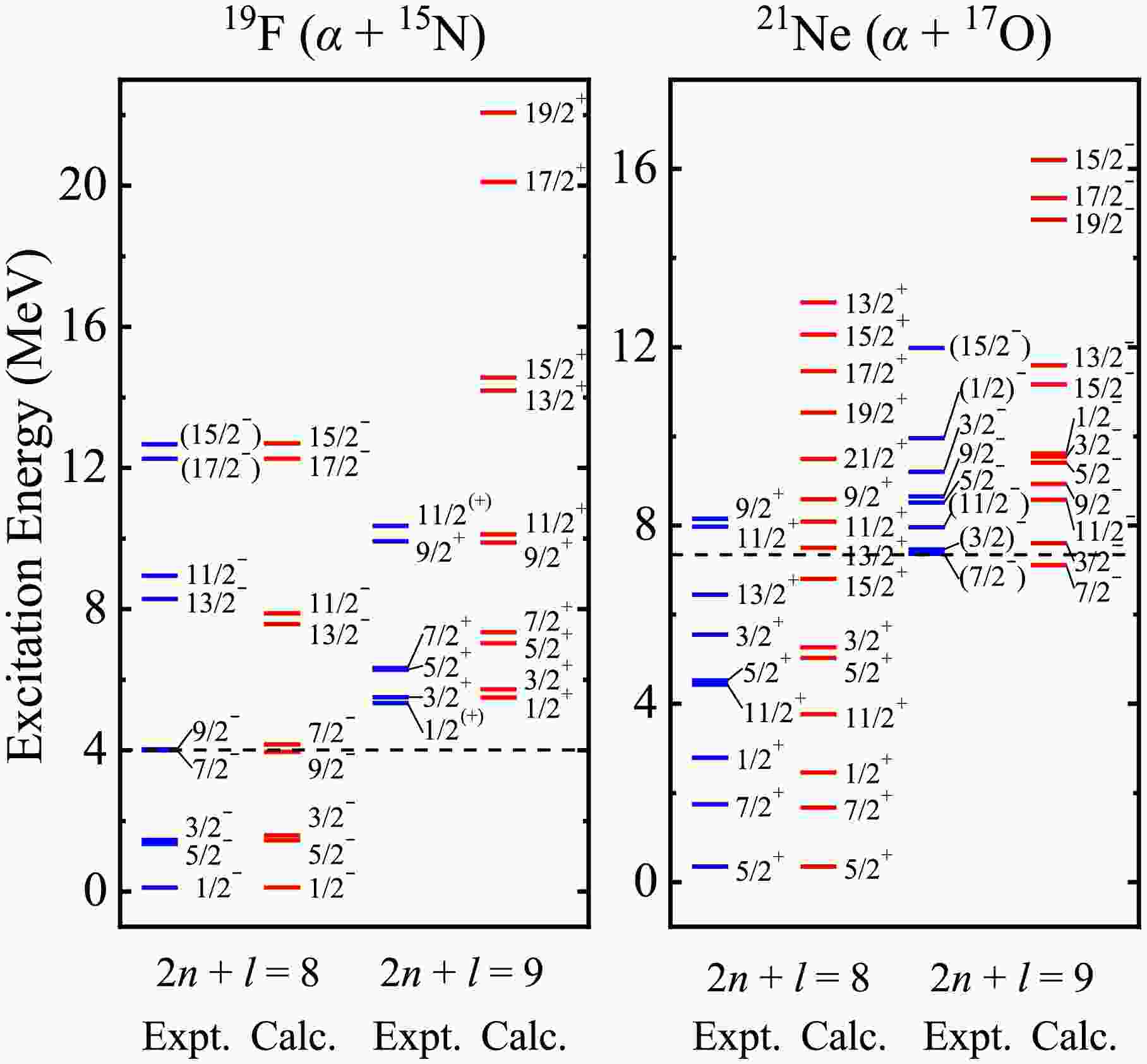
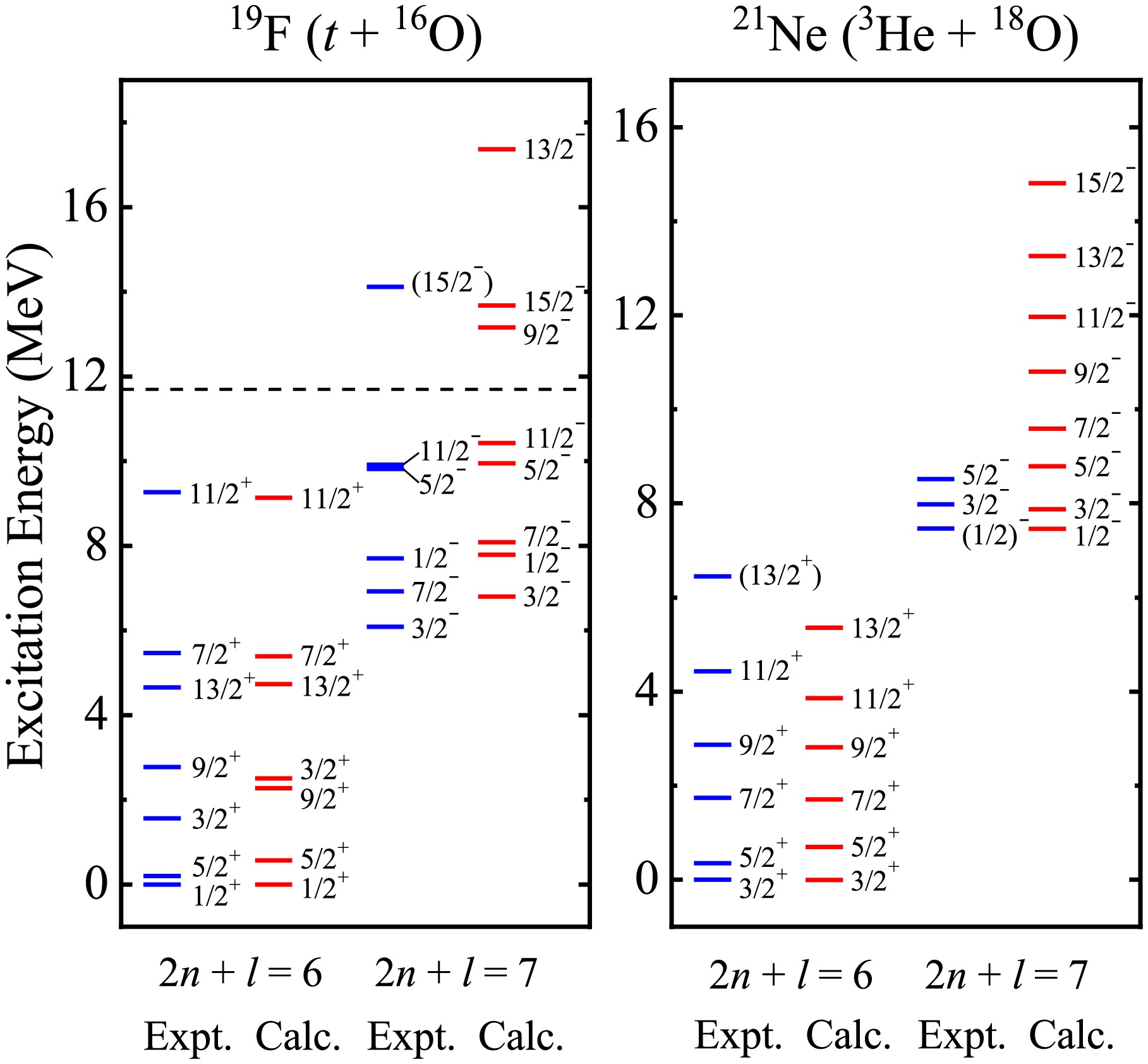
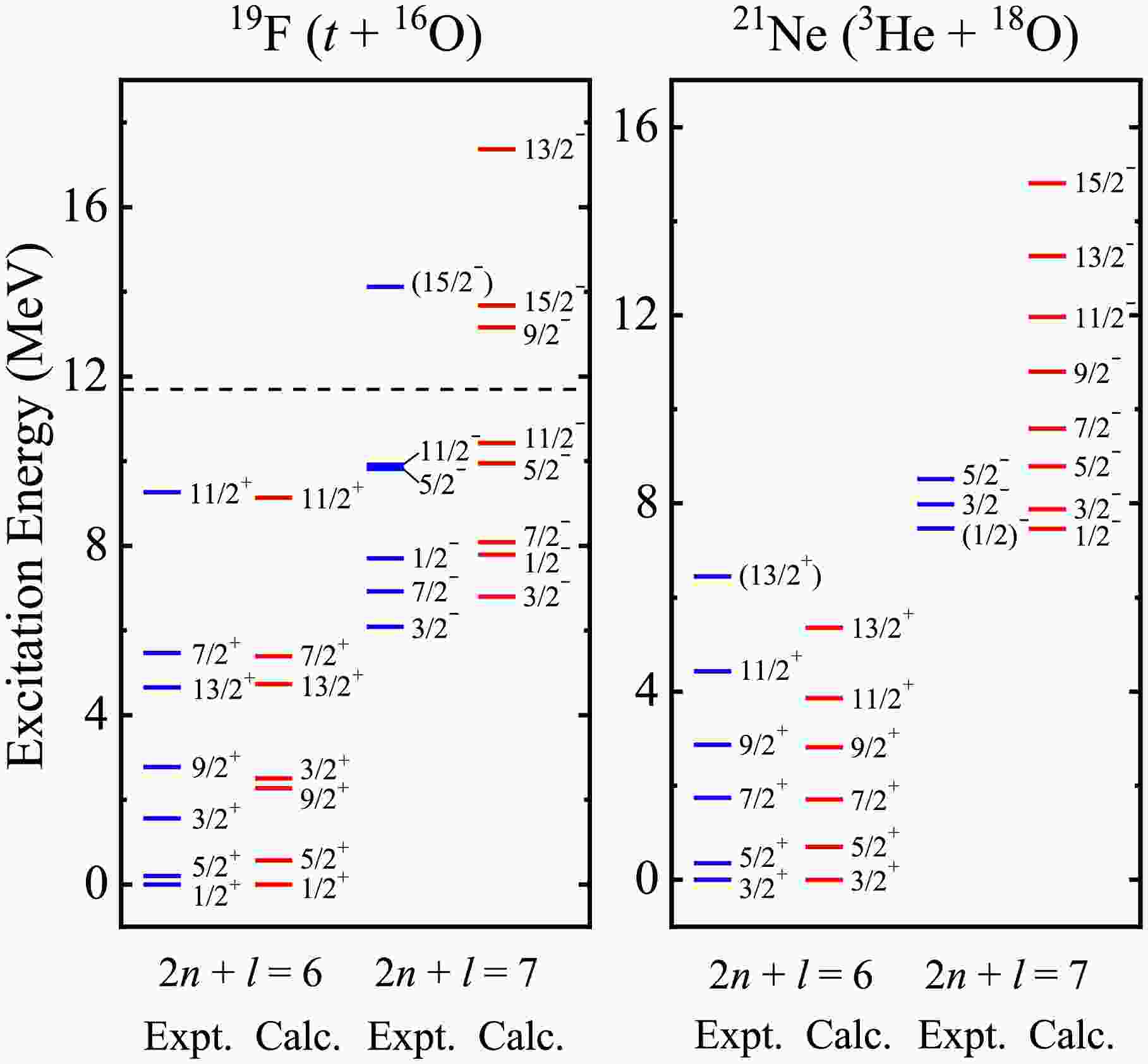
With this in mind, the energy spectra, $ B(E1) $ and $ B(E2) $ values of cluster states around ²⁰Ne are initially calculated, serving as a test on the binary cluster-core model. The theoretical energy levels of α-cluster and three-nucleon structures for ¹⁹F and ²¹Ne compared with the observed data are shown in Figs. 1 and 2, in which the dash lines denote the cluster thresholds. The nuclear parameters for ¹⁹F (α + ¹⁵N) and ²¹Ne (α + ¹⁷O) in Eq. (3) are respectively $ V_0 $ = 235.00 MeV, a = 0.70 fm, b = 0.19, λ = 0.10 and σ = 0.20 fm, which are consistent with our previous work [8]. The values of b, λ and σ remain constant in all cases of this work to reduce the number of free parameters. According to the previous empirical systematics and constant reasonable attempts, the $ V_0 $ = 190.00 MeV and a = 0.90 fm are applied to describe the three-nucleon cluster states in the following process, which are close to other studies [40, 47−49]. The key point is the inclusion of the spin-orbit coupling potential, which gives rise to the splitting of energy levels with the same orbital angular momentum l. With the bootstrap method [7, 8], the depths $ V_{so} $ can be then separately fixed as 0.058 MeV, 0.005 MeV and -0.018 MeV for t-cluster states in ¹⁹F, α-cluster and ³He-cluster states in ²¹Ne. As for "α + ¹⁵N" configuration of ¹⁹F, $ V_{so} $ = 0.003 MeV is corresponding to 2n + l = 8 band, and $ V_{so} $ = -0.018 MeV is for 2n + l = 9 band. The complete parity doublet bands have been compared with Ref [42], where the spin-orbit coupling effect was not introduced in the α-core structure for ¹⁹F. The energy spectra of cluster states for ¹⁹F and ²¹Ne have been well reproduced within the BCM, along with reasonable predictions for further levels without experimental counterparts. It is observed that the degree of energy level splitting, very sensitive to spin-orbit potential depth, rises with growth of the absolute value of $ V_{so} $. Moreover, the energy spacing coming from the same l is found to increase with the increasing of l in a certain energy band as well. The agreement of our results with experimental data proves that the BCM is equally reliable for describing the cluster states and possesses robust model predictive capability in light odd-A nuclei, thereby offering assistance in theoretical analysis of cluster phenomena and experimental design about the essential reactions of (α, n) and (α, γ) in the astrophysical s process. It is noted that the calculations of above two configurations are performed based on mutually orthogonal wave functions and two disjoint bases. In addition, the assignments of energy levels and electromagnetic transition strengths are related to Wildermuth condition, which contributes to different global quantum numbers G of different configurations in the same nucleus. Hence, there will be no conflicts in the assignment of energy levels and electromagnetic transitions in these two cluster states. The calculations here can be serve as a preliminary attempt to explore the possible cluster states in odd-A nuclei with two configurations in the framework of BCM plus the spin-orbit coupling. In fact, there may exist some possible mixed states between triton and α-cluster, which deserve further investigations within the coupled-channels formalism in the future work.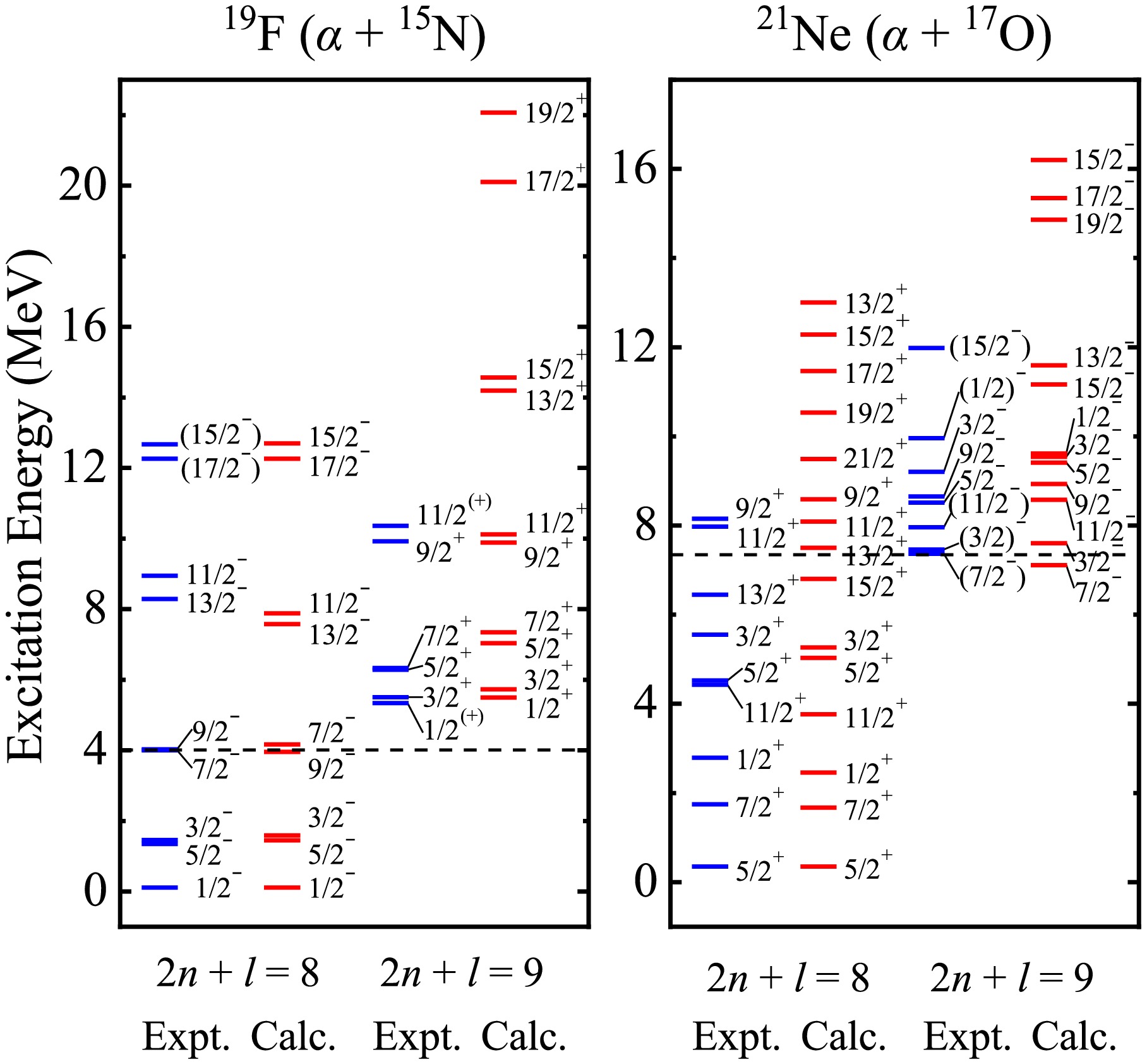

Figure 1.  (color online) The comparisons of the calculated parity doublet bands of 2n + l = 8 and 9 for α-cluster states in ¹⁹F (α + ¹⁵N) and ²¹Ne (α + ¹⁷O) with the experimental data [20, 42, 50], where the dash lines dictate the α-cluster breakup thresholds. The intrinsic spins of ¹⁵N and ¹⁷O are 1/2^- and 5/2⁺, respectively.

Figure 2.  (color online) Same as Fig. 1 but for the t-cluster states in ¹⁹F (t + ¹⁶O) and ³He-cluster states in ²¹Ne (³He + ¹⁸O) with 2n + l = 8 and 9. The experimental data is from Ref [42, 50]. The intrinsic spins of t and ³He are both 1/2⁺.

As is well known, analyzing the spectra is a direct way to study the spectroscopic properties of cluster states. The enhancement of reduced electromagnetic transition rates is an effective symbol of cluster states. Once the wave functions are generated in above procedure, the $ B(E1) $ and $ B(E2) $ transition probabilities between successive band members can be then obtained with Eqs. (6) and (9). For further examination on the BCM, the comparison of obtained reduced quadrupole transition strengths with available data and other related calculations for cluster states in ¹⁹F and ²¹Ne is presented in Table 1. The first column denotes the target nuclei with the clusters. The third and forth columns separately indicate the theoretical $ B(E2) $ values and experimental data. As for ¹⁹F, the $ B(E2)_{1} $ values of fifth column is from the vibron-fermion model with SU(3) $ \times $ U(2) limit [56], $ i.e. $, the extension of the U(3) vibron model. The calculated results for $ B(E2)_{2} $ based on the GCM [57] with "α + ¹⁵N" configuration are plotted in the last column. Obviously, the $ B(E2) $ values have been well reproduced within the BCM for both nuclei despite the overestimation for the transition 11/2^- $ \rightarrow $ 7/2^- in ¹⁹F (α + ¹⁵N), which can be comparable with $ B(E2)_1 $ and $ B(E2)_2 $ values. The present $ B(E2) $ values are in accordance with these two calculations except for the 11/2⁺ $ \rightarrow $ 7/2⁺ and 11/2⁺ $ \rightarrow $ 13/2⁺ transitions for ¹⁹F in Ref [57]. This implies that there are some mixed cluster states of triton and α-particle in the low-lying energy region, which makes difficulties in both experimental detection and theoretical research. The transition rates of 5/2⁺ $ \rightarrow $ 1/2⁺ with 5.36 W.u., 3/2⁺ $ \rightarrow $ 5/2⁺ with 2.40 W.u. and 9/2⁺ $ \rightarrow $ 5/2⁺ with 6.21 W.u. in ¹⁹F are very close to the recently results of 6.45 W.u., 2.65 W.u. and 6.41 W.u. in Ref [59], respectively, where the $ B(E2) $ values are determined by using the USDB nuclear shell model interaction. The calculations of $ B(E2) $ values in this study for ²¹Ne agree with the $ B(E2)_{1} $ values of the fifth column in Table 1, which are obtained in the framework of CSM [58]. Additionally, reasonable predictions of $ B(E2) $ values for these two nuclei are displayed in the Table 1, especially for α-cluster states approaching the thresholds in the region of astrophysical interest. These selected levels of negative-parity bands in ²¹Ne maybe belong to the α-cluster states due to large $ B(E2) $ strengths.

Nuclei	Transition	$ B(E2)_{{\rm{calc.}}} $	$ B(E2)_{{\rm{expt.}}} $	$ B(E2)_{1} $	$ B(E2)_{2} $
19F(α)	5/2− $ \rightarrow $ 1/2−	19.53	21.60 $ \pm $ 0.40	20.00	18.10
19F(α)	3/2− $ \rightarrow $ 1/2−	19.69		21.89	18.00
19F(α)	3/2− $ \rightarrow $ 5/2−	8.54			7.50
19F(α)	7/2− $ \rightarrow $ 5/2−	2.68		3.13	2.20
19F(α)	7/2− $ \rightarrow $ 3/2−	24.30		25.71	21.00
19F(α)	9/2− $ \rightarrow $ 5/2−	26.36	28.00 $ \pm $ 6.00	22.51	23.70
19F(α)	9/2− $ \rightarrow $ 7/2−	1.66			1.30
19F(α)	13/2− $ \rightarrow $ 9/2−	23.56	19.00 $ \pm $ 2.00
19F(α)	11/2− $ \rightarrow $ 7/2−	23.80	8.10 $ \pm $ 2.00	23.88	18.80
19F(α)	11/2− $ \rightarrow $ 9/2−	0.91		1.28	0.60
19F(α)	11/2− $ \rightarrow $ 13/2−	0.84
19F(t)	5/2+ $ \rightarrow $ 1/2+	5.36	6.95 $ \pm $ 0.08	6.95	6.20
19F(t)	3/2+ $ \rightarrow $ 1/2+	5.77		6.95	8.00
19F(t)	3/2+ $ \rightarrow $ 5/2+	2.40		3.10	2.80
19F(t)	9/2+ $ \rightarrow $ 5/2+	6.21	8.20 $ \pm $ 0.90	8.09	5.80
19F(t)	13/2+ $ \rightarrow $ 9/2+	3.93	3.20 $ \pm $ 0.40	5.27	2.90
19F(t)	7/2+ $ \rightarrow $ 5/2+	0.72		0.81	0.90
19F(t)	7/2+ $ \rightarrow $ 3/2+	6.70		7.28	12.80
19F(t)	7/2+ $ \rightarrow $ 9/2+	0.55		0.78	0.50
19F(t)	11/2+ $ \rightarrow $ 9/2+	0.20			0.50
19F(t)	11/2+ $ \rightarrow $ 13/2+	0.21			0.07
19F(t)	11/2+ $ \rightarrow $ 7/2+	4.91			22.8
21Ne(α)	7/2+ $ \rightarrow $ 5/2+ $ ^{\rm{a}} $	14.62	11.00 $ \pm $ 4.00
21Ne(α)	1/2+ $ \rightarrow $ 5/2+ $ ^{ \rm a} $	42.22
21Ne(α)	11/2+ $ ^{\rm{c}} $ $ \rightarrow $ 7/2+ $ ^{\rm{a}} $	15.75
21Ne(α)	5/2+ $ ^{\rm{b}} $ $ \rightarrow $ 5/2+ $ ^{\rm{a}} $	0.69
21Ne(α)	5/2+ $ ^{\rm{b}} $ $ \rightarrow $ 7/2+	18.90
21Ne(α)	5/2+ $ ^{\rm{b}} $ $ \rightarrow $ 1/2+	13.50
21Ne(α)	3/2+ $ \rightarrow $ 5/2+ $ ^{\rm{a}} $	0.08
21Ne(α)	3/2+ $ \rightarrow $ 7/2+	19.12
21Ne(α)	3/2+ $ \rightarrow $ 1/2+	13.68
21Ne(α)	3/2+ $ \rightarrow $ 5/2+ $ ^{\rm{b}} $	36.16
21Ne(α)	13/2+ $ \rightarrow $ 11/2+ $ ^{\rm{c}} $	3.53
21Ne(α)	3/2− $ ^{\rm{d}} $ $ \rightarrow $ 7/2−	49.31
21Ne(α)	11/2− $ \rightarrow $ 7/2−	41.01
21Ne(α)	5/2− $ \rightarrow $ 7/2−	52.52
21Ne(α)	5/2− $ \rightarrow $ 3/2− $ ^{\rm{d}} $	68.43
21Ne(α)	9/2− $ \rightarrow $ 7/2−	23.83
21Ne(α)	9/2− $ \rightarrow $ 11/2−	20.27
21Ne(α)	9/2− $ \rightarrow $ 5/2−	43.41
21Ne(3He)	5/2+ $ \rightarrow $ 3/2+	20.58	24.30 $ \pm $ 2.00	24.16
21Ne(3He)	7/2+ $ \rightarrow $ 3/2+	7.04	9.30 $ \pm $ 0.80	10.08
21Ne(3He)	7/2+ $ \rightarrow $ 5/2+	10.54	11.00 $ \pm $ 4.00	15.10
21Ne(3He)	9/2+ $ \rightarrow $ 5/2+	10.90	15.70 $ \pm $ 2.20	15.10
21Ne(3He)	9/2+ $ \rightarrow $ 7/2+	7.94	9.00 $ \pm $ 5.00	9.87
21Ne(3He)	11/2+ $ \rightarrow $ 7/2+	7.50		17.94
21Ne(3He)	11/2+ $ \rightarrow $ 9/2+	2.85	6.00 $ \pm $ 4.00	6.91
21Ne(3He)	13/2+ $ \rightarrow $ 9/2+	8.57		19.72
21Ne(3He)	13/2+ $ \rightarrow $ 11/2+	3.69		5.05
$ ^{\rm{a}} $$ E(5/2^{+}) $ = 0.351 MeV. $ ^{\rm{b}} $$ E(5/2^{+}) $ = 4.526 MeV. $ ^{\rm{c}} $$ E(11/2^{+}) $ = 4.433 MeV. $ ^{\rm{d}} $$ E(3/2^{-}) $ = 7.465 MeV.

Table 1.  Comparison of the theoretical $ B(E2) $ values with the experimental data [50−52] and other associated studies for ¹⁹F and ²¹Ne. The comparative theoretical results of the $ B(E2)_1 $ and $ B(E2)_2 $ values in ¹⁹F are respectively from Ref [56] and Ref [57], where the $ B(E2)_{1} $ values are based on the SU(3) $ \times $ U(2) limit of the vibron-fermion model and the $ B(E2)_{2} $ values are obtained within the generator coordinate method (GCM). The comparative results of $ B(E2)_{1} $ values for ²¹Ne are based on the cluster shell model (CSM) [58]. All the quadrupole transition probabilities are presented here in the Weisskopf units (W.u.).

The electromagnetic dipole transitions are often considered as another important indicator of cluster states. In the past decades, some interesting events of enhanced $ B(E1) $ values [60−64] have been observed from light to heavy nuclei, attracting widespread attention in nuclear physics. In this study, the $ E1 $ transitions occur in ¹⁹F from G = 9 band to G = 8 band of α-cluster states and from the negative-parity levels to positive-parity levels of t-cluster states. Table 2 shows the $ B(E1) $ values for ¹⁹F in comparison with measured quantities and aforementioned calculations. The general agreement with experimental data is obtained for the "α + ¹⁵N" configuration except for the transition 5/2⁺ $ \rightarrow $ 3/2^-, which is close to the theoretical $ B(E1)_1 $ and $ B(E1)_2 $ values. Nonetheless, the strong dipole transition probabilities of triton states are given within the BCM with approximately two orders of magnitude larger than the available data. As the Ref [42] discussed, the quite large difference between two configurations come from the recoil terms of Eqs. (7) and (10), giving rise to larger $ B(E1) $ rates for triton states by a factor of 16 than the case of α-core structure. On the other hand, these states may have impure cluster structures, namely the mixing states between α and t cluster levels or between cluster and non-cluster states, leading to the uncertainties in the measurements. Such an enhancement of $ B(E1) $ values of t-cluster states in ¹⁹F we calculated have not yet been experimentally observed. Similarly, the reproduction of $ E1 $ transitions by other models is generally unsatisfactory [42, 56, 57], like the quite small results in the calculations with the algebraic approach [56]. A consistent investigation of this problem in odd mass nuclei relies on the additional experimental data, which is hoped to be useful for the on going or forthcoming experiments on the nuclear structures.

Nuclei	Transition	$ B(E1)_{{\rm{calc.}}} $	$ B(E1)_{{\rm{expt.}}} $	$ B(E1)_{1} $	$ B(E1)_{2} $
19F(α)	3/2+ $ \rightarrow $ 1/2−	18.20	7.00	4.83	11.20
19F(α)	3/2+ $ \rightarrow $ 5/2−	31.10	9.80	5.06	8.70
19F(α)	3/2+ $ \rightarrow $ 3/2−	3.56			2.00
19F(α)	5/2+ $ \rightarrow $ 5/2−	0.86	2.10 $ \pm $ 0.50	0.24	1.20
19F(α)	5/2+ $ \rightarrow $ 3/2−	12.62	1.20 $ \pm $ 0.40	5.80	16.80
19F(α)	5/2+ $ \rightarrow $ 7/2−	18.06
19F(α)	7/2+ $ \rightarrow $ 5/2−	16.94
19F(α)	7/2+ $ \rightarrow $ 7/2−	0.60
19F(α)	7/2+ $ \rightarrow $ 9/2−	19.24
19F(t)	1/2− $ \rightarrow $ 1/2+	269.90
19F(t)	1/2− $ \rightarrow $ 3/2+	43.83
19F(t)	3/2− $ \rightarrow $ 1/2+	302.24	5.10 $ \pm $ 1.40
19F(t)	3/2− $ \rightarrow $ 5/2+	448.23	3.2 $ \pm $ 1.00
19F(t)	3/2− $ \rightarrow $ 3/2+	49.80
19F(t)	5/2− $ \rightarrow $ 5/2+	26.52
19F(t)	5/2− $ \rightarrow $ 3/2+	371.31
19F(t)	5/2− $ \rightarrow $ 7/2+	257.23
19F(t)	7/2− $ \rightarrow $ 5/2+	462.97	12.00 $ \pm $ 2.00	0.03	5.20
19F(t)	7/2− $ \rightarrow $ 9/2+	316.95	1.7 $ \pm $ 0.50	0.002	4.00
19F(t)	7/2− $ \rightarrow $ 7/2+	9.06			0.08
19F(t)	11/2− $ \rightarrow $ 9/2+	510.58	3.90 $ \pm $ 1.20
19F(t)	11/2− $ \rightarrow $ 13/2+	133.48	0.33 $ \pm $ 0.16

Table 2.  Same as Table 1 but for the $ E1 $ reduced transition probabilities in 10^-3 Weisskopf units (10^-3 W.u.). The experimental data are taken from Ref [50, 51].

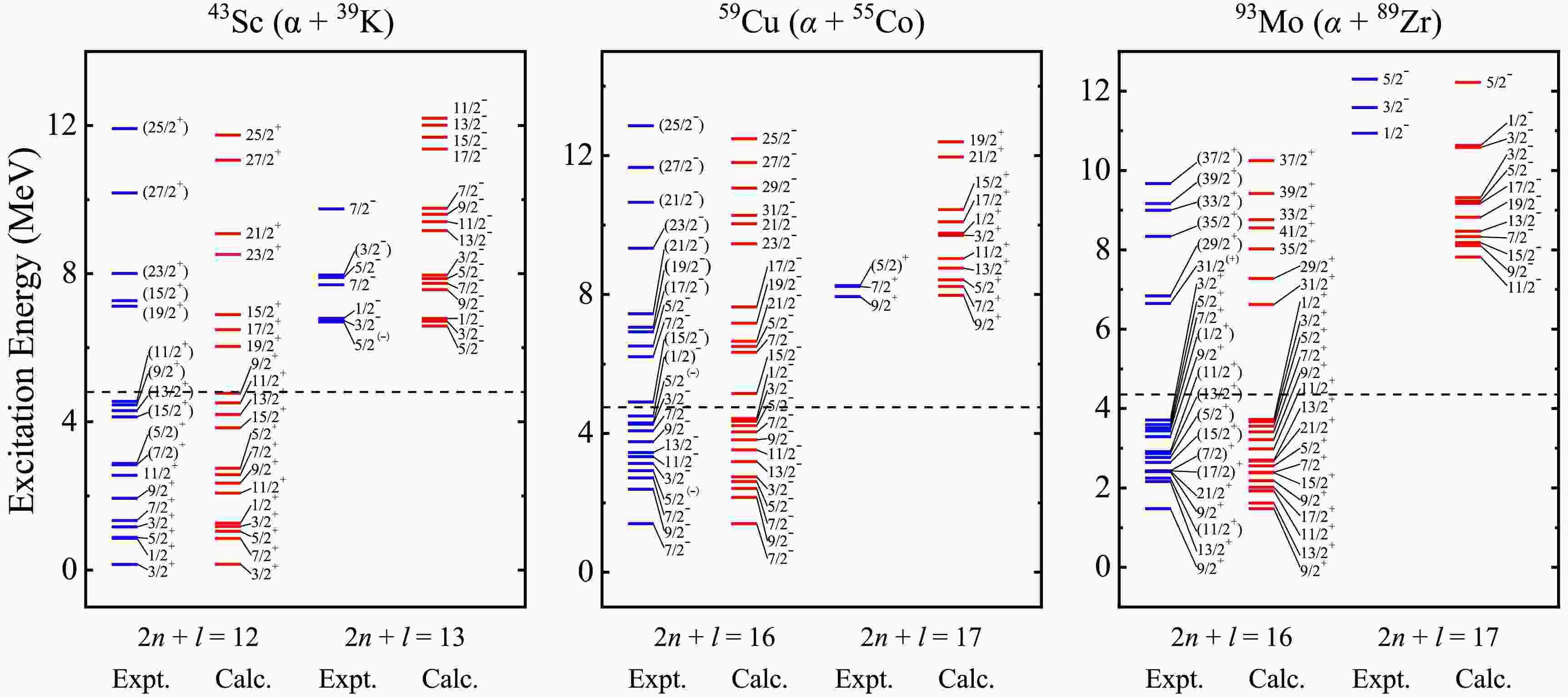
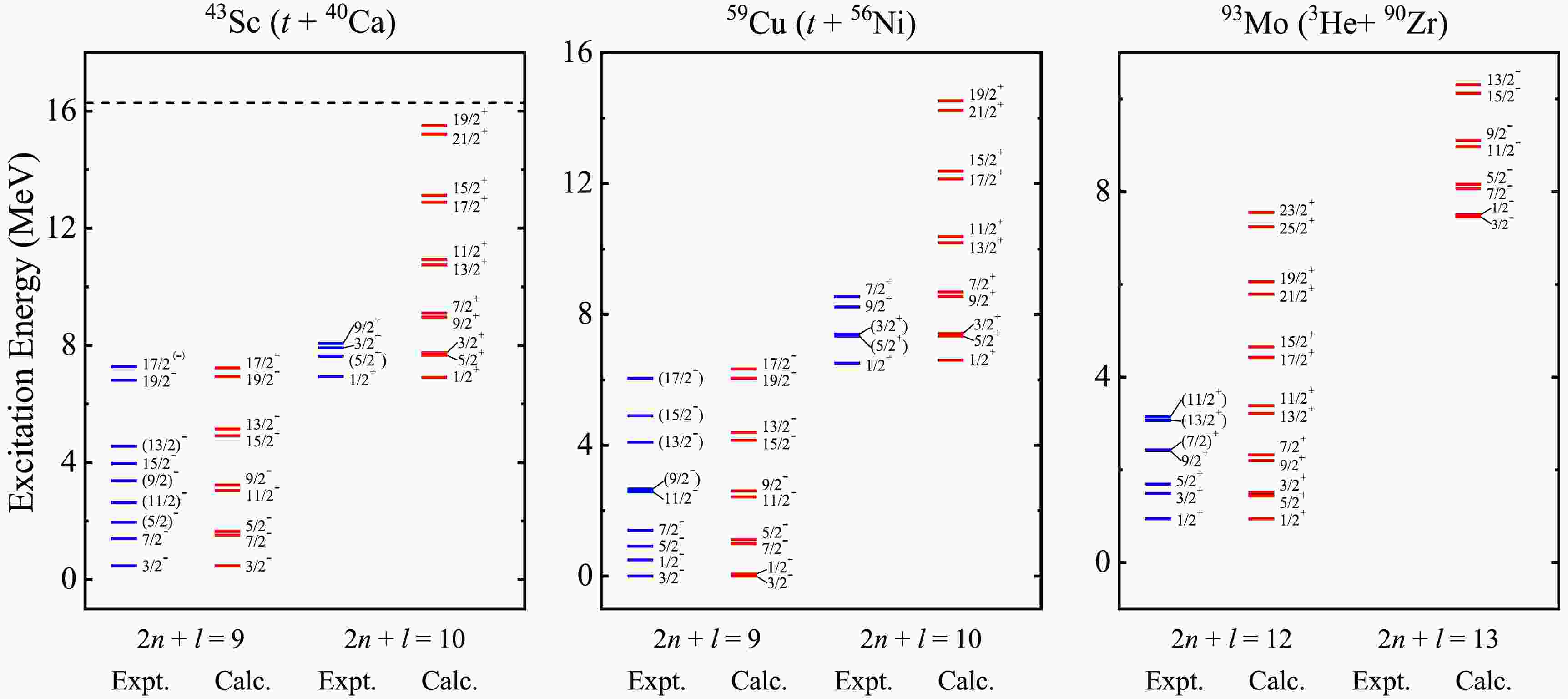
In fact, the excited states of atomic nuclei, especially in light even-even nuclei, are strongly characterized by α clustering, contributing to a variety of α-cluster configurations as the excitation energy increases. When it comes to heavier nuclei, the picture of clusters becomes unclear resulting from the complex interactions among nucleons, not to mention the interplay with nucleon degree. On the other hand, the symmetry breaking [65] coming from the spin-orbit force and the mean-field effect would be stronger, suppressing the α-like correlations in this region. Therefore, it is of great significance to extend the α-cluster concept to heavier nuclei. Inspired by the successful application of cluster-core structures around ²⁰Ne, the BCM is generalized to heavier nuclei approaching to the shell closures, such as ⁴³Sc, ⁵⁹Cu and ⁹³Mo, which can provide a good testing ground to confirm the persistence of cluster states. The obtained energy spectra for nuclei ⁴³Sc, ⁵⁹Cu and ⁹³Mo with α and three-nucleon clusters are compared with the suggested experimental counterparts in Figs. 3 and 4, respectively. For the purpose to ensure the applicability of BCM within the same parameterization, the nuclear parameters in Eq. (3) are the same as before, and the spin-orbit parameter $ V_{so} $ = 0.003 MeV, consistent with the case of the negative-parity band in ¹⁹F (α + ¹⁵N), is employed in both configurations of these three nuclei. The satisfactory theoretical parity doublet bands and predictions have been obtained in the framework of BCM, as is shown in the Figs. 3 and 4, which suggest the available levels correspond to possible cluster states in heavier nuclei with odd mass. It should be noted that ⁹³Mo exhibits rich information of energy levels below 5 MeV, but no corresponding energy levels have been observed in the region from 5 to 10 MeV [55]. This reflects the theoretical prediction of $ 2n + l $ = 13 band for ³He-cluster states awaiting additional experimental confirmation. Meanwhile, the energy bands of α-cluster states are more intricate than other configurations on account of the inclusion of the spin-orbit coupling effect. For example, the number of energy levels coming from one certain orbital angular momentum l is 2 for the ³He-cluster states in ⁹³Mo, while the maximum number could even reach 10 for the α-cluster states. This seems to indicate that the α cluster tends to form more easily than other cluster within nuclei and plays a dominant role in the mixed states.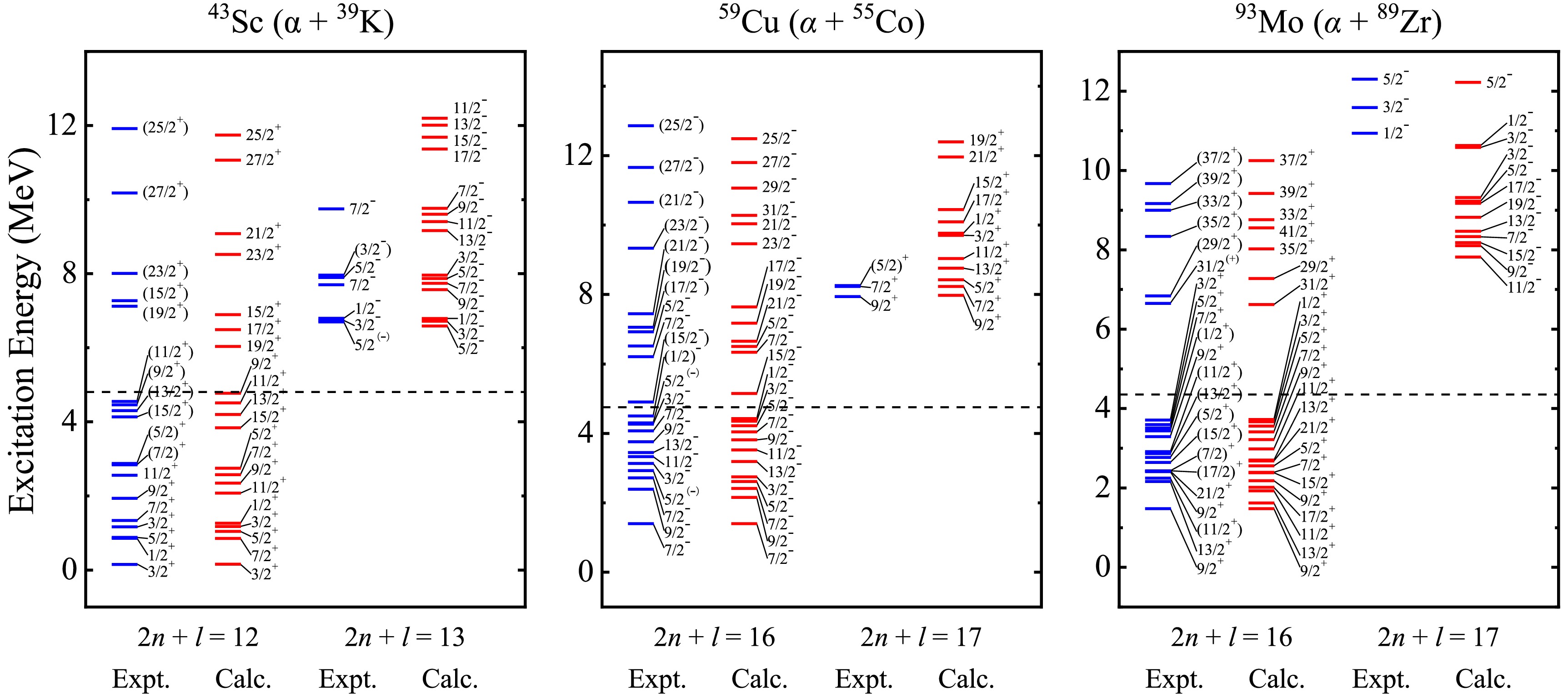

Figure 3.  (color online) The comparisons of the calculated doublet parity bands with the available candidates [50] for α-cluster states in heavier nuclei, where the dash lines denote the α-cluster thresholds. The intrinsic spins of ³⁹K, ⁵⁵Co and ⁸⁹Zr are 3/2⁺, 7/2^- and 9/2^-, respectively.

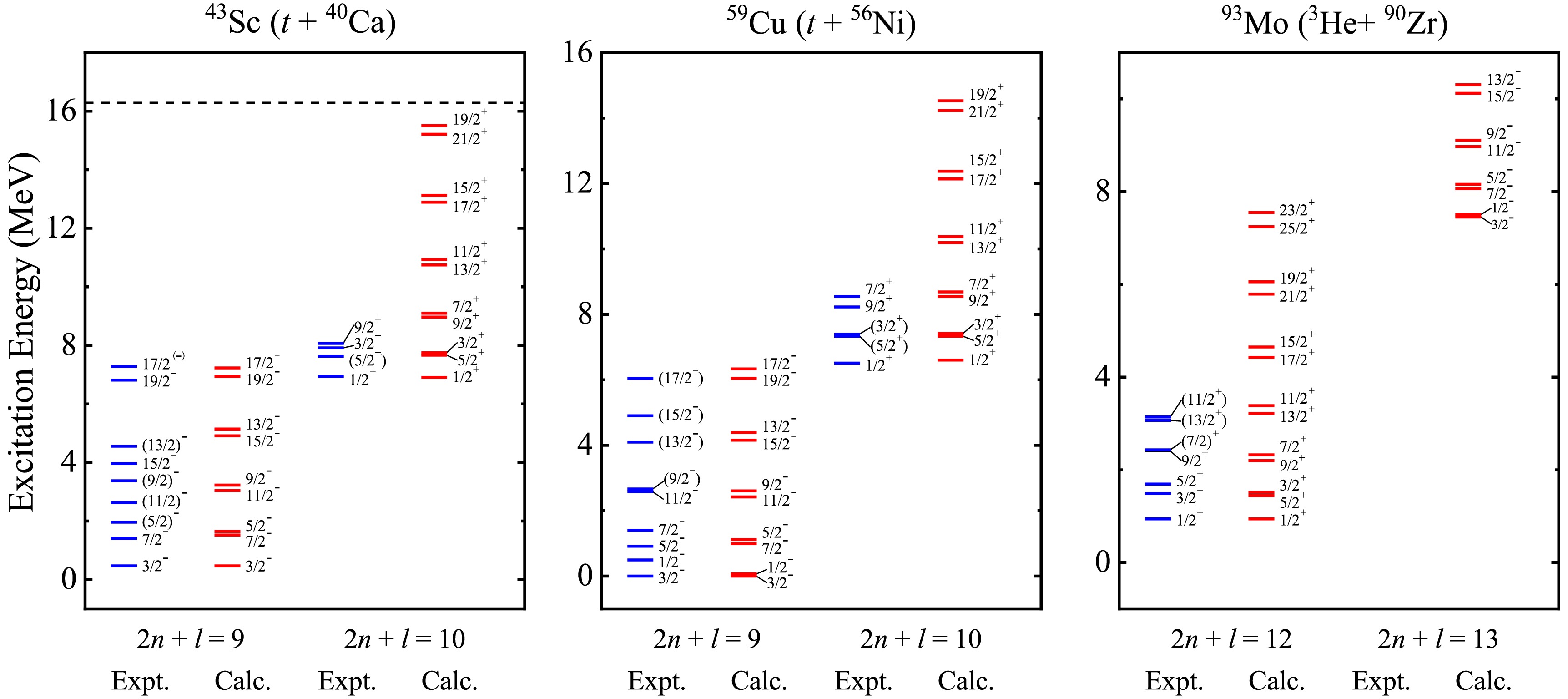
Figure 4.  (color online) Same as Fig. 3 but for triton and ³He cluster states.

In the same vein as ¹⁹F and ²¹Ne, we have systematically investigated the electromagnetic quadrupole transitions with two different configurations for ⁴³Sc, ⁵⁹Cu and ⁹³Mo within the BCM. The calculated $ B(E2) $ values are displayed in Table 3, where one can get overall agreement of the results and the experimental data despite the underestimation in the transitions of 7/2^- $ \rightarrow $ 3/2^- and 11/2^- $ \rightarrow $ 7/2^- in ⁴³Sc (t + ⁴⁰Ca). All the results verify α clustering is a stable feature from light to heavier nuclei, including the odd-A nuclei. There might be fewer cluster structures of ³H and ³He in this region. Additionally, the existence of clustering phenomena in heavy nuclei is still an open question, which deserves further study within the coupled-channels formalism in our future work. We hope this study can give new sight into the nuclear structures.

Nuclei(cluster)	$ J^{\pi}_i(E^{\rm{expt.}}_i) $	$ J^{\pi}_f(E^{\rm{expt.}}_f) $	$ B(E2)_{{\rm{calc.}}} $	$ B(E2)_{{\rm{expt.}}} $
43Sc(α)	5/2+(0.881)	3/2+(0.152)	23.08	13.00 $ \pm $ 5.00
43Sc(α)	3/2+(1.159)	1/2+(0.856)	13.56	$< 180.00 $
43Sc(α)	3/2+(1.159)	5/2+(0.881)	34.80	$< 180.00 $
43Sc(α)	7/2+(1.338)	3/2+(0.152)	9.56	20.00 $ \pm $ 9.00
43Sc(α)	7/2+(1.338)	5/2+(0.881)	14.42	46.00 $ \pm $ 24.00
43Sc(α)	9/2+(1.933)	5/2+(0.881)	13.79	15.00 $ \pm $ 4.00
43Sc(α)	9/2+(1.933)	7/2+(1.338)	9.00	3.30 $ \pm $ 1.60
43Sc(α)	11/2+(2.554)	7/2+(1.338)	16.17	20.00 $ \pm $ 3.00
43Sc(t)	7/2-(1.408)	3/2-(0.473)	2.62	24.00 $ \pm $ 9.00
43Sc(t)	5/2-(1.963)	3/2-(0.473)	6.30	4.40 $ \pm $ 2.50
43Sc(t)	11/2-(2.635)	7/2-(1.408)	4.09	43.00 $ \pm $ 16.00
59Cu(t)	1/2-(0.492)	3/2-(0)	4.83	$< 300.00 $
59Cu(t)	5/2-(0.914)	3/2-(0)	0.66	$< 2.90 $
59Cu(t)	7/2-(1.399)	3/2-(0)	2.98	17.00 $ \pm $ 8.00
59Cu(t)	7/2-(1.399)	5/2-(0.914)	0.34	1.30 $ \pm $ 0.80
93Mo(α)	13/2+(2.162)	9/2+(1.477)	12.26	3.30 $ \pm $ 0.50
93Mo(α)	11/2+(2.247)	9/2+(1.477)	4.32	3.70$ ^{+1.90}_{-2.10} $
93Mo(α)	17/2+(2.430)	13/2+(2.162)	12.95	4.48 $ \pm $ 0.23

Table 3.  Comparison of the calculated $ B(E2) $ values of cluster states with available data [50, 53−55] for ⁴³Sc, ⁵⁹Cu and ⁹³Mo in the Weisskopf units (W.u.). The $ E^{\rm{expt.}}_i $ and $ E^{\rm{expt.}}_f $ are the measured data in MeV consistent with the energies of initial and final states.

In summary, the investigations of parity doublet bands and electromagnetic transition properties have been extended to the odd mass region around ²⁰Ne within the binary cluster-core model plus the extra nuclear spin-orbit potential. These nuclear properties approaching to α thresholds are crucial inputs for origins of heavy elements from the s process in the massive stars. The good agreement of our results for cluster states based on the "α + core" and "t or ³He + core" configurations, except for the $ B(E1) $ values of t-cluster states, with available data and other calculations in ¹⁹F and ²¹Ne coming from the GCM, the phenomenological algebraic model and CSM, demonstrates the reliability and model predictive capacity of BCM. Moreover, the better theoretical $ B(E1) $ values of α-cluster states reveal that the α-cluster ingredients occupy a prominent position in the mixed states constituted with t or ³He clusters. Encouraged by this, the present physical picture is applied to describe the cluster states for ⁴³Sc, ⁵⁹Cu and ⁹³Mo. The calculated energy spectra and $ B(E2) $ values are found to be consistent with measured data, implying the persistence of cluster states in the heavier odd-A nuclei and the reasonableness of present framework. It is expected to be helpful to comprehend the role of cluster degree of freedom played in the structural knowledge of odd mass nuclei.