-
To date, a rich spectrum of exotic mesons, including charmonium-like and bottomonium-like states, has emerged, and more new states are expected from continuous experimental efforts [1-10]. However, in the baryon sector, only three narrow pentaquark states,
$ P_c(4312) $ ,$ P_c(4440) $ , and$ P_c(4457) $ , were discovered by the LHCb collaboration in$ \Lambda_{b}\to J/\psi pK^- $ decay [11, 12]. It is essential to study these known states and search for new ones resulting from other decay and reaction channels to disentangle different models. Recently, D0 and GlueX collaborations searched for these states in inclusive$ p \overline p $ collisions [13] and photoproduction [14], respectively. The D0 collaboration found an enhancement from the joint contribution of$ P_c(4440) $ and$ P_c(4457) $ in$ J/\psi p $ invariance mass spectrum with low significance [13], serving as the first and only confirmatory evidence for these pentaquark states.Various interpretations were proposed for the nature of hidden charm pentaquark states before and after their observation, e.g., molecular states [15, 16], compact diquark-diquark-antiquark states [17-19], and hadro-charmonium states [20]. In addition, it was pointed out that the peaks of pentaquark in the decay and reaction with multi-particle final states could be induced by a triangle singularity considering that their masses locate close to the
$ \Sigma_c\bar{D} $ and$ \Sigma_c\bar{D}^* $ threshold [21-27]. To survey this non-resonance explanation, the reactions with two-body final states induced by beams of photon, electron [28-34], and pion [23, 35-37] are suggested to be decisive. At present, and in the near future, the high energy pion beam seems to be unavailable, so photo- and electroproduction reactions would play the central role and are expected to attract much interest. These reactions are also useful to search for other$ P_c $ , for instance, those among seven states in spin multiplets anticipated by heavy-quark spin symmetry [38-40], and$ P_b $ , i.e., the bottom analogs of$ P_c $ , expected by heavy quark flavor symmetry in many models [29, 41-43].The observation of hidden-charm pentaquark states encourages researchers to investigate the hidden-bottom pentaquark state that contains a bottom quark pair and three light quarks. There are several studies about the nature of the hidden-bottom pentaquark state in different models [44-46]. Photoproduction of the hidden-bottom pentaquark state was investigated in Refs. [47, 48]. It is natural to predict the production of hidden-bottom pentaquark states in electron-proton scattering in future EICs.
An Electron-Ions Collider (EIC) is an important platform to explore nuclear structure and exotic particle nature in the coming decade. In electron-proton scattering, the initial electron emits a virtual photon that interacts with the initial proton to produce vector mesons. There are several proposed EICs, for instance, EicC (EIC in China) [49, 50], EIC-US (EIC in US) [51], and LHeC (EIC in LHC) [52], ranging from intermediate to extremely high energies.
The simulation of production in EICs is very important before EICs are built. Such simulation can help us estimate the particles cross sections for the proposed EICs. In this regard, eSTARlight is a Monte-Carlo package to simulate production of vector mesons in electron-proton scattering for EICs [53]. It can describe the vector meson production well for HERA in the t-channel. The production of exotic particles was also studied in eSTARlight [54]. The cross sections of photon-proton to vector mesons are necessary to calculate the cross sections of vector mesons in electron-proton scattering. In the eSTARlight package, the glauber model is employed to obtain the
$ \gamma A\to VA $ [55]. With the help of eSTARlight, we can obtain the four momenta of final state particles, which are important for the detector systems. Then, we can rebuild the four momenta of short-life particles. Simulation can provide some distributions of the physical process. In previous versions of eSTARlight, only the t-channel was investigated. In this study, we analyze the s-channel vector meson production in electron-proton scattering using eSTARlight. In particular, we investigate the electroproduction of pentaquark$ P_c $ in$ e p\to e J/\psi p $ and$ P_b $ in$ e p\to e \Upsilon(1S) p $ scattering comprehensively in this study. Specifically, we focus on EicC and EIC-US, comparing the cross sections and the rapidity distributions of final particles.The main objective of this study is the adoption of eSTARlight to simulate the production of charm and bottom vector mesons in the s-channel and t-channel; eSTARlight can describe vector meson cross sections of HERA well in the t-channel. We extend this to vector meson production in the s-channel in eSTARlight. This paper is organized as follows. The theoretical framework is given in Sec. II. The numerical results are presented in Sec. III. The paper concludes with a summary in Sec. IV.
-
In electron-proton scattering, diffractive production of vector mesons is important given that the photon in electro-production is off-mass-shell. It is interesting to analyze how the internal structures of the particles influence the vector meson production in electron-proton scattering. The diagrams for the s-channel and t-channel of
$ ep\to eVp $ are depicted in Fig. 1. In the s-channel (left graph), the virtual photon and initial proton produce resonances (e.g.,$ P_c $ and$ P_b $ states), and then, the pentaquark resonance states decay into vector mesons and a proton. In the t-channel (right graph), the virtual photon interacts with protons via exchanging pomerons or gluons and then converts into the final vector mesons. In this study, we made use of exchanging of pomerons in the t-channel. We treat the t-channel contribution as a background of resonance contributions of pentaquark states. We parameterized the cross section of$ \gamma p\to Vp $ as the basic input to the simulation of the$ ep\to eVp $ reaction. This can be recognized by the eSTARlight package.
Figure 1. Diagrams for
$ J/\psi $ and$ \Upsilon (1S) $ production in electron-proton scattering via$ P_c $ and$ P_b $ pentaquark resonance in the s-channel (left graph) and pomeron exchange in the t-channel (right graph).In the electron proton scattering, the cross section of
$ ep\to eVp $ is expressed in terms of the cross section of$ \gamma^* p\to Vp $ . In particular, it is written as follows [53]:$ \sigma(ep\to eVp) = \int {\rm d}k{\rm d}Q^2\frac{{\rm d}N^2(k,Q^2)}{{\rm d}k{\rm d}Q^2}\sigma_{\gamma^* p\to Vp}(W,Q^2), $

(1) where k is the momentum of the photon emitted from the initial electron in the target rest frame, W is the center of mass (c.m.) energy of the virtual photon and proton system, and
$ Q^2 $ is the virtuality of the virtual photon. The photon flux is expressed as follows [56]:$ \frac{{\rm d}^2N(k,Q^2)}{{\rm d}k{\rm d}Q^2} = \frac{\alpha}{\pi kQ^2}\Bigg[1-\frac{k}{E_e}+\frac{k^2}{2E^2_e}-\Bigg(1-\frac{k}{E_e}\Bigg)\Bigg|\frac{Q^2_{\rm min}}{Q^2}\Bigg|\Bigg], $

(2) where
$ E_e $ is the energy of the incoming electron in the proton rest frame, and$ Q^2_{\rm min} $ is defined as follows:$ Q^2_{\rm min} = \frac{m_e^2k^2}{E_e(E_e-k)}. $

(3) The maximum
$ Q^2 $ is determined by the energy loss of the initial electron as follows:$ Q^2_{\rm max} = 4E_e(E_e-k). $

(4) The
$ Q^2 $ dependence of$ \sigma_{\gamma^*p\to Vp}(W,Q^2) $ is factorized as follows:$ \sigma_{\gamma^*p\to Vp}(W,Q^2) = \sigma_{\gamma p\to Vp}(W,Q^2 = 0)\Bigg(\frac{M_V^2}{M_V^2+Q^2}\Bigg)^\eta, $

(5) where
$ \eta = c_1+c_2(M_V^2+Q^2) $ with the values of$ c_1 = 2.36\pm0.20 $ and$ c_2 = 0.0029\pm 0.43\quad\mathrm{ GeV}^2 $ , which are determined by the data of$ \gamma^*p\to Vp $ with$ Q^2 \neq 0 $ [53]. We used the same$ Q^2 $ dependence for pentaquark and pomeron channels, as these values are unknown for pentaquark resonance channels. Because of the very strong$ Q^2 $ dependence of photon flux in Eq. (2), the impact of this prescription is expected not to be large in the final results.For the resonance channel of the pentaquark states , the cross sections of
$ \gamma p{\to}Vp $ can be written in a compact Breit-Wigner form [29, 30]:$ \sigma^{P_X}_{\gamma p{\to}Vp}(W) = \frac{2J+1}{2(2s_2+1)}\frac{4\pi}{k^2_{in}}\frac{\Gamma^2_{P_X}}{4} \frac{\mathcal{B}(P_X\to\gamma p)\mathcal{B}(P_X\to Vp)}{(W-M_{P_X})^2+\Gamma^2_{P_X}/4}, $

(6) where
$ P_X $ denotes pentaquark states, such$ P_c $ and$ P_b $ ,$ s_1 $ is the spin of the initial proton, and J is the total spin of the$ P_c $ and$ P_b $ pentaquark states. Here,$ M_{P_X} $ and$ \Gamma_{P_X} $ denote the mass and total decay width of the$ P_c $ and$ P_b $ states, respectively;$ k_{\rm in} $ is the magnitude of three momenta of initial states in the c.m. frame. The branching ratio of$ P_X\to \gamma p $ is calculated by the vector meson dominant model:$ \mathcal{B}(P_X\to \gamma p) = \frac{3\Gamma(V \to e^+e^-)}{\alpha M_V} \left(\frac{k_{\rm in}}{k_{\rm out}}\right)^{2L+1}\mathcal{B}(P_X\to Vp), $

(7) where
$ \alpha $ is the fine structure constant, and$ \Gamma (V\to e^+e^-) $ is the dilepton decay width of vector mesons. Besides,$ k_{\rm out} $ is the magnitude of three momenta of the final state in the c.m. frame. In this study, we used the lowest orbital excitation$ L = 0 $ for the$ J/\psi+ p $ system and$ J = 1/2 $ . Other quantum numbers of$ P_X $ can be similarly calculated. We adopted$ \mathcal{B}(P_c\to J/ \psi p) $ = 5% and$ \mathcal{B}(P_b\to \Upsilon(1S)p) $ = 5% for the calculations in this study; these values concide with the upper limits from the GlueX group [14]. A comparison of our values for$ \sigma^{P_c}_{\gamma p{\to}J/\psi p}(W) $ with the GlueX data can be found in Ref. [57].To study the rapidity distributions and transverse momentum distributions of the vector mesons and proton in final states, we need angular distributions of the decay process
$ P_X \to Vp $ . In the process of$ P_X\to Vp $ , the angle distribution of$ P_X\to Vp $ has the following general expression:$ \frac{{\rm d}\sigma}{{\rm d}\cos\theta}\propto 1+\beta \cos^2\theta. $

(8) Here,
$ \theta $ is the polar angle of the vector meson or proton in the rest frame of$ P_c $ and$ P_b $ states, and$ \beta $ depends on the quantum number$ J^p $ of the$ P_X $ pentaquark, only if the lowest partial wave is considered. However, several partial waves were usually presented in this study. Thus, the actual value of$ \beta $ deviates from these values. The relation of$ \beta $ and$ J^p $ are listed in Table 1. These results are employed in the calculations of$ J/\psi $ and$ \Upsilon(1S) $ rapidity distributions.$ J^p $ 

$ \frac{1}{2}^- $ 

$ \frac{1}{2}^+ $ 

$ \frac{3}{2}^- $ 

$ \frac{3}{2}^+ $ 

$ \beta $ 

−1 0 0 1 Table 1.
$ \beta $ for different quantum numbers of$ P_c $ and$ P_b $ states.For the contribution of Pomeron exchange in the t-channel, the cross section of
$ \gamma p\to Vp $ is expressed as follows [58]:$ \sigma^t_{\gamma p\to Vp}(W) = \sigma_p\cdot\Bigg(1-\frac{(m_p+m_{V})^2}{W^2}\Bigg)\cdot W^\epsilon, $

(9) with
$ \sigma_p $ = 4.06 nb and$ \epsilon $ = 0.65 for$ J/\psi $ and$ \sigma_p $ = 6.4 pb and$ \epsilon $ = 0.74 for$ \Upsilon(1S) $ . These values were determined by the experimental data of$ \gamma p\to Vp $ with$ Q^2 = 0 $ and applied successfully to previous studies of$ J/\psi $ and$ \Upsilon(1S) $ electroproduction [58].In this study, we first employed eSTARlight to simulate resonance production processes of pentaquark states via photon-proton interaction. Then, the decay process of
$ P_c\to J/\psi+p $ and$ P_b\to \Upsilon(1S)+p $ was implemented in eSTARlight. Finally, the vector mesons to dilepton was simulated. The resonance channel production in eSTARlight was newly studied. It can be applied to other resonance channels considered in the next step. -
In this study, two pentaquark states,
$ P_c(4312) $ and$ P_b(11120) $ , were selected to analyze the production of vector mesons. The properties of$ P_c(4312) $ and$ P_b(11120) $ are listed in Table 2, in which the decay width of$ P_b(11120) $ is taken from Ref. [48]. Throughout this study, we used the central values of the masses of two pentaquark states. We investigated their production in proposed EICs, including EicC and EIC-US, whose collider energies are also listed. A detailed comparison of the proposed EICs is presented in Refs. [49, 54].States Properties [12, 48] Collider EicC EIC-US Energy (e.vs. p) 3.5 GeV vs 20 GeV 18 GeV vs 275 GeV $ P_c(4312) $ 

Mass $ 4.311\pm0.7^{+6.8}_{-0.6} $ GeV

$\sigma_t(ep\to eJ/\psi p)$ 

0.69 nb 9.1 nb Width $ 9.8\pm2.7^{+3.7}_{-4.5} $ MeV

$\sigma_s(ep\to eJ/\psi p)$ 

0.89 pb 1.3 pb $ P_b(11120) $ 

Mass 11.120 GeV $\sigma_t(ep\to e \Upsilon p)$ 

0.13 pb 15 pb Width 30 - 300 MeV $\sigma_s(ep\to e \Upsilon p)$ 

9.3 - 82 fb 0.022-0.19 pb Table 2. Cross sections of
$ J/\psi $ and$ \Upsilon(1S) $ vector mesons in two channels for proposed EicC and EIC-US. The s-channel is the resonance channel of pentaquark states.First, we present the estimated
$ J/\psi $ and$ \Upsilon(1S) $ cross sections in the s-channels and t-channel in Table 2. The cross sections of the t-channel is viewed as the background of the t-channel pentaquark production. For all the calculations in this study, we employed$ 0<Q^2<5 $ $ \mathrm{GeV}^2 $ and$ \beta = -1 $ . According to Table 2, the$ J/\psi $ cross section in the t-channel is much larger than that in the s-channel in both EicC and EIC-US. However, the cross sections of$ \Upsilon(1S) $ in the t-channel are not significantly larger than that in the s-channel during$ J/\psi $ production. This conclusion is crucial for the study of pentaquark states because the t-channel can be viewed as a background to identify pentaquark states in experiments.Second, we present the pseudo-rapidity distributions of
$ J/\psi $ in two channels for the proposed EicC and EIC-US in Fig. 2. Given that the cross section of$ J/\psi $ in the t-channel is much larger than that in the s-channel, the s-channel cross section is smaller than that of the t-channel. Consequently, we can neglect the interference between the t-channel and the s-channel because the amplitude in the s-channel is much smaller than that of the t-channel.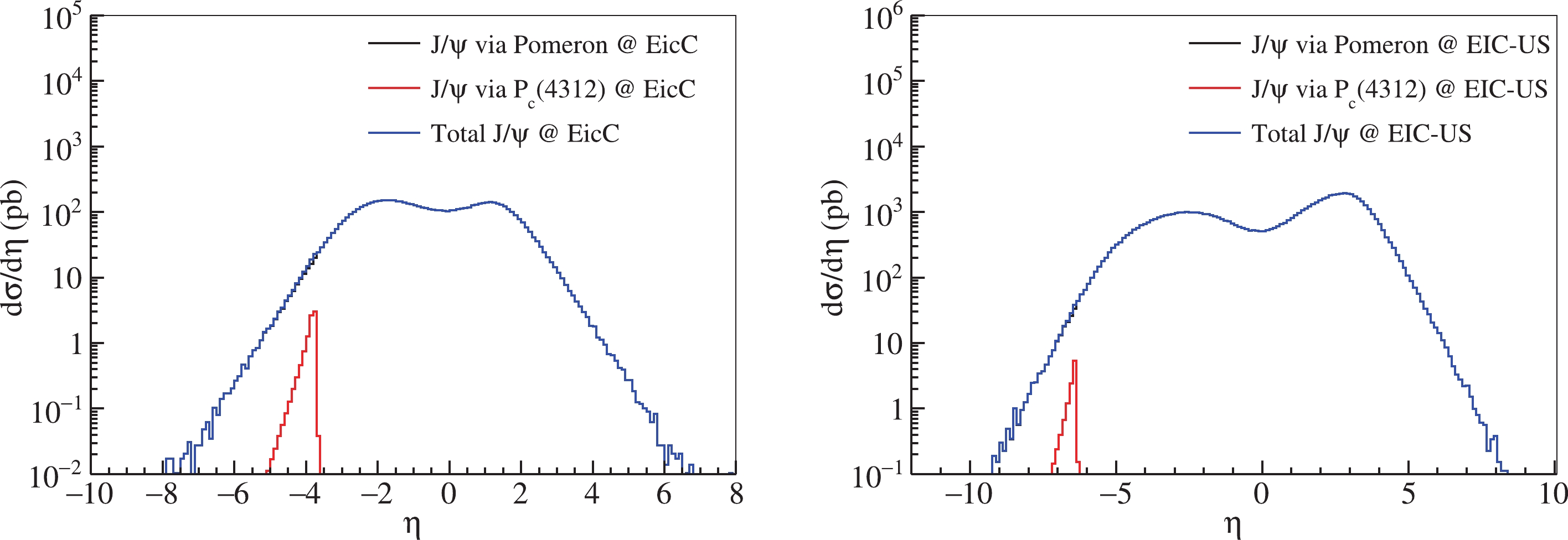
Figure 2. (color online) Pseudo-rapidity distributions of
$ J/\psi $ in two channels for EicC (left graph) and EIC-US (right graph).The rapidity distributions of
$ J/\psi $ in the two channels for the proposed EicC and EIC-US are depicted in Fig. 3. It indicates that s-channel is too weak to identify the pentaquark states in rapidity distributions. According to Fig. 2 and Fig. 3, it is difficult to distinguish the contributions from pentaquark resonance channels as the background. It is also difficult to identify the pentaquark states in$ J/\psi $ +p production.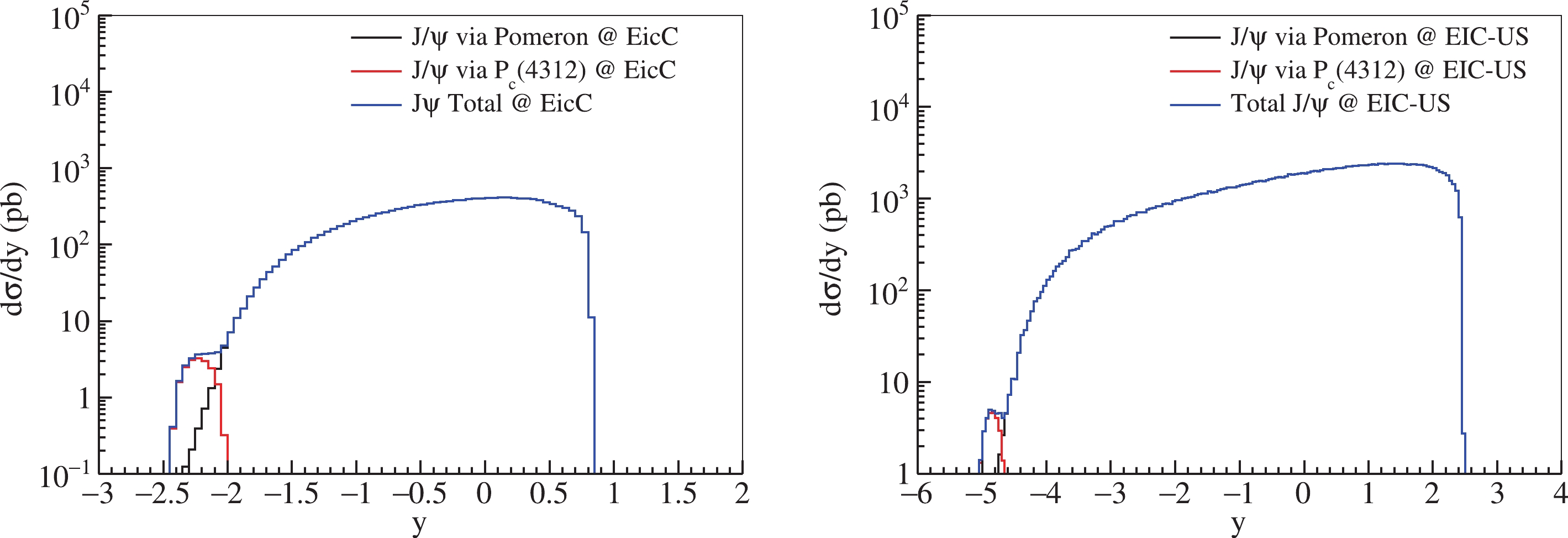
Figure 3. (color online) Rapidity distributions of
$ J/\psi $ produced in two channels for the proposed EicC (left graph) and EIC-US (right graph).Moreover, the distributions of
$ \Upsilon(1S) $ are shown in Fig. 4 to Fig. 7. Given that the width of$ P_b(11120) $ is not determined in this case, we used 30-300 MeV as the range of width [48]. In Fig. 4, the pseudo-rapidity distributions of$ \Upsilon(1S) $ are shown in two channels with a lower limit of width. The upper limit of$ P_b(11120) $ is applied for the calculations, and the results are depicted in Fig. 5. According to Fig. 4 and Fig. 5, the peak of$ \Upsilon(1S) $ in the pentaquark resonance exchange channel is remarkable compared to the background of the pomeron exchange channel, especially in EicC. The reason is that the cross section of$ \Upsilon(1S) $ in the t-channel in EicC is much smaller than the cross section in EIC-US, as listed in Table 2.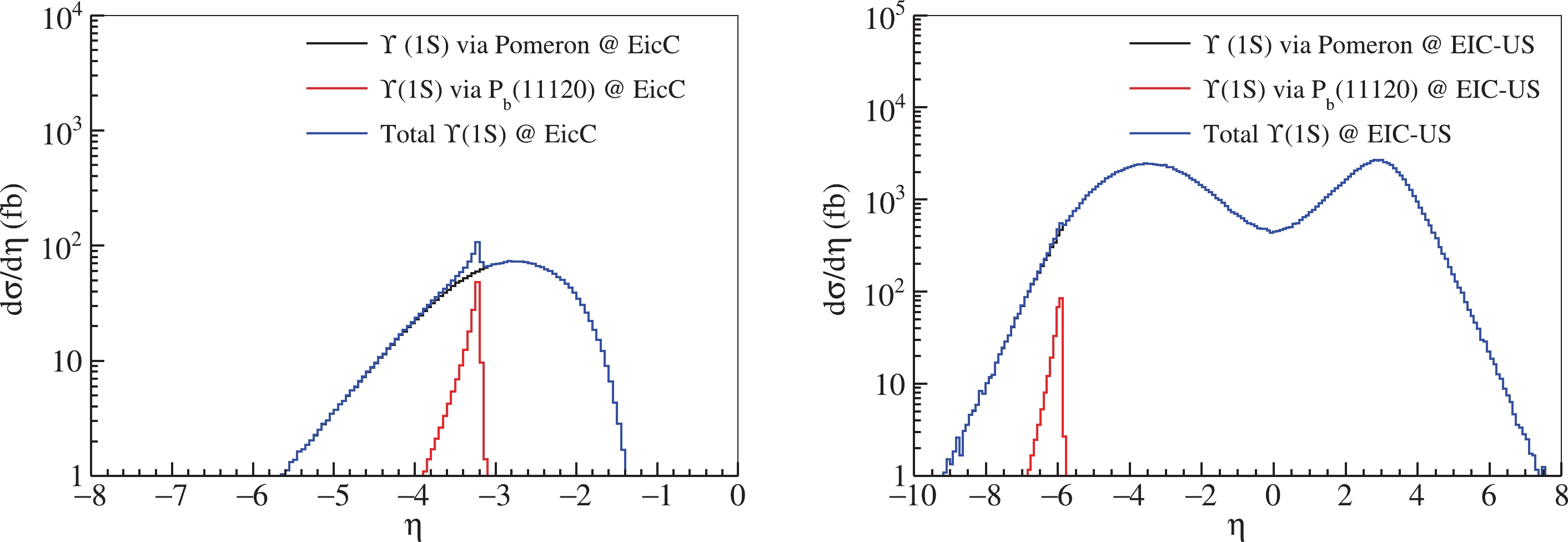
Figure 4. (color online) Pseudo-rapidity distributions of
$ \Upsilon(1S) $ in two channels for the proposed EicC (left graph) and EIC-US (right graph). A width of$ P_b(11120) $ 30 MeV was assumed in the calculations.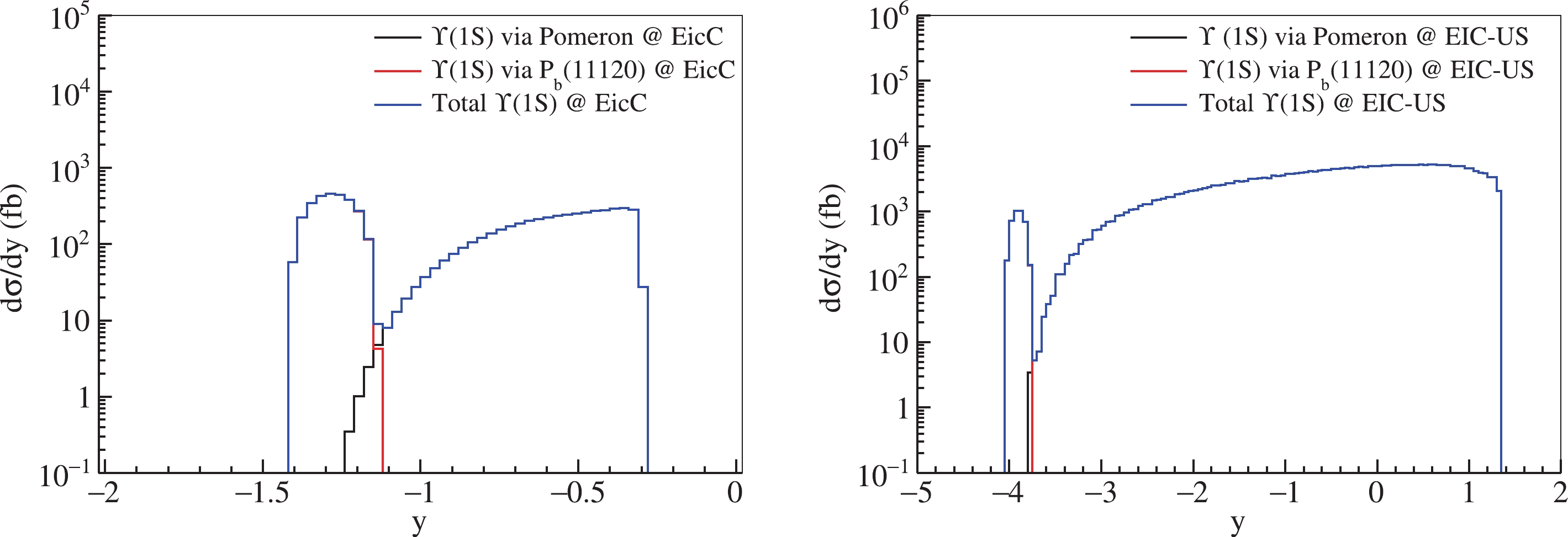
Figure 7. (color online) Rapidity distributions of
$ \Upsilon (1S) $ in two channels for the proposed EicC (left graph) and EIC-US (right graph). A width of$ P_b(11120) $ 300 MeV was assumed in the calculations.
Figure 5. (color online) Pseudo-rapidity distributions of
$ \Upsilon(1S) $ in two channels for the proposed EicC (left graph) and EIC-US (right graph). A width of$ P_b(11120) $ 300 MeV was assumed in the calculations.Furthermore, the rapidity distributions of
$ \Upsilon(1S) $ in two channels in lower and upper limits of width of$ P_b(11120) $ are presented in Fig. 6 and Fig. 7. The same conclusions can be drawn from the rapidity distributions compared to the pseudo-rapidity distributions. These results indicate that the$ P_b $ pentaquark states of EicC are produced near the mid-rapidity region. However, the$ P_b $ pentaquark states are produced at large rapidity regions in EIC-US because the collider energies of EIC-US is much higher than those of EicC. Hence, it is easy to identify$ P_b $ states in the EicC platform given that the detector system can observe$ P_b $ easily at the mid-rapidity region.
Figure 6. (color online) Rapidity distributions of
$ \Upsilon (1S) $ in two channels for the proposed EicC (left graph) and EIC-US (right graph). A width of$ P_b(11120) $ 30 MeV was assumed in the calculations.Finally, from above discussions, it can be concluded that
$ P_c(4312) $ is difficult to identify in electron-proton scattering process in the proposed EicC and EIC-US because of the strong background of the t-channel. By contrast, the signals of$ P_b(11120) $ are remarkable in electron-proton scattering, especially in the proposed EicC. Thus, EicC is a good platform to search for$ P_b $ pentaquark states in the future, according to the predictions from this study. -
In this study, the hidden-charm and hidden-bottom pentaquark states were investigated via photoproduction in electron-proton scattering. The pseudo-rapidity and rapidity distributions of two vector mesons for EicC and EIC-US were compared under various energy configurations. The
$ P_c(4312) $ pentaquark resonance state was difficult to identify via pseudo-rapidity distributions in EicC and EIC-US. It can be concluded that the$ P_b(11120) $ resonance state can be identified via pseudo-rapidity distributions in EicC and EIC-US. Moreover, EicC is a good platform to study the$ P_b $ pentaquark resonance states.Generally speaking, we found that the production cross sections increase slowly with growing c.m. energies in the EIC machine. At high-energy colliders such as the proposed EIC-US, the final states are produced at the far forward rapidity region. For lower energy colliders such as EicC, the systems are produced closer to the mid-rapidity region, facilitating the detection of the final states by the central detectors. Our study is a good starting point for further simulations of
$ P_c $ and$ P_b $ electroproduction processes. Such simulations will be helpful for the design of experimental methods and detector systems in future EICs.Given that the EICs are expected to be in operation in the near future, but they are unavailable at present, alternative procedures would be ultra-peripheral pA collisions at STAR and ALICE [59, 60]. The vector meson production in heavy ion ultra-peripheral collisions can be simulated by the STARlight package [58], and the production of pentaquarks can be included by a similar extension of the kinematic condition in this study.
-
The authors gratefully thank Dr. J. J. Xie, Dr. Z. Yang, Dr. X.Y.Wang, and Dr. J. J. Wu for fruitful discussions.
Production of hidden-charm and hidden-bottom pentaquark states in electron-proton collisions
- Received Date: 2020-09-29
- Available Online: 2021-04-15
Abstract: Electro-production of several pentaquark states is investigated in this study. The eSTARlight package is adapted to study the electro-production of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: