Fixing effective range parameters in elastic α-¹²C scattering: impact on resonant 2₄⁺ state of ¹⁶O and S_E2 factor of ¹²C(α,γ)¹⁶O

The radiative α capture on ¹²C and ¹²C(α,γ)¹⁶O is one of the fundamental reactions in nuclear astrophysics. It determines, along with the triple α reaction, the C/O ratio in the core of a helium-burning star [1]. It also provides an initial condition for computer simulations of star evolution [2, 3] and significantly influences the results of star explosions and nucleosynthesis [4]. However, the reaction rate or, equivalently, the astrophysical S factor of ¹²C(α,γ)¹⁶O at the Gamow-peak energy, $ E_G=0.3 $ MeV, has not been measured in an experimental facility because of the Coulomb barrier. One needs to employ a theoretical model, fit the model parameters to experimental data measured at an energy scale of a few MeV, and extrapolate the reaction rate to $ E_G $. Meanwhile, it is known that E1 and E2 transitions of ¹²C(α,γ)¹⁶O are dominant owing to the subthreshold $ 1_1^- $ and $ 2_1^+ $ ($ l^\pi_{ith} $) states of ¹⁶O, whose binding energies with respect to the α-¹²C breakup energy are $ B_1=0.045 $ MeV and $ B_2=0.245 $ MeV, respectively [5]. During the past half-century, many experimental and theoretical studies on the reaction have been carried out. For a review, refer, e.g., to Refs. [6−10] (for a brief review, see Ref. [11]).

We previously studied reactions related to ¹²C(α,γ)¹⁶O by constructing a low-energy effective field theory (EFT) based on the methodology of quantum field theory [12−14]. When constructing an EFT, one first chooses a typical scale of a reaction to study and then introduces a large scale for relevant degrees of freedom at low energy to separate from irrelevant degrees of freedom from high energy. We chose the Gamow-peak energy, $ E_G=0.3 $ MeV, as a typical energy scale; a typical momentum scale would be $ Q=\sqrt{2\mu E_G}=40 $ MeV, where μ is the reduced mass of α and ¹²C ¹. Because the typical wavelength of the reaction is larger than the size of the nuclei, nucleons inside the nuclei would be irrelevant; we assigned α and ¹²C as structure-less (point-like) spin-0 scalar fields. We then chose the energy difference between p-¹⁵N and α-¹²C breakup energies of ¹⁶O; $ \Delta E = 12.13 - 7.16 = 4.97 $ MeV, as the high energy (separation) scale; the high momentum scale was set as $ \Lambda_H = \sqrt{2\mu \Delta E} = 160 $ MeV. The theory provides us with a perturbative expansion scheme featuring an expansion parameter of $ Q/\Lambda_H = 1/4 $. The p-¹⁵N system is now regarded to have irrelevant degrees of freedom and is integrated out of the effective Lagrangian, whose effects are embedded in the coefficients of terms of the Lagrangian. In principle, these coefficients can be determined from the mother theory; in practice, they are fixed by using experimental data or empirical values. Because of the perturbative expansion scheme of EFT, by truncating the terms up to a given order, one can obtain an expression of reaction amplitudes in terms of a few parameters for each of the reaction channels. This approach was recently used for the study of important reactions in nuclear astrophysics, such as elastic p-¹²C scattering [15], elastic d-α scattering [16], and radiative proton capture on ¹⁵N [17, 18].

Previuosly, we studied various cases of elastic α-¹²C scattering at low energies [19−23], E1 transition of ¹²C(α,γ)¹⁶O, and an estimate of the $ S_{E1} $ factor of ¹²C(α,γ)¹⁶O at $ E_G $ [24], as well as β delayed α emissions from ¹⁶N [10] up to the sub-leading order within the cluster EFT. The experimental data of each of the reactions are well reproduced by the fitted values of the parameters of reaction amplitudes. However, we observed a problem in a previous study (see Fig. 6 in Ref. [22]): when applying the fitted parameters to the precise phase shift data up to the p-¹⁵N breakup energy, $ E_\alpha = 6.62 $ MeV ($ E_\alpha $ is the α energy in the laboratory frame), reported by Tischhauser et al. (2009) [25], a path of the inverse of dressed ¹⁶O propagator for $ l=2 $ cannot be uniquely determined in the low-energy region, where the $ S_{E2} $ factor is extrapolated to $ E_G $. In this study, we analyzed this issue by introducing conditions applied to the effective range parameters in the low-energy region and by employing two types of experimental data: the phase shift of the elastic α-¹²C scattering explicitly including the resonant $ 2_4^+ $ state of ¹⁶O and the $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O below the energy of sharp resonant $ 2_2^+ $ state of ¹⁶O.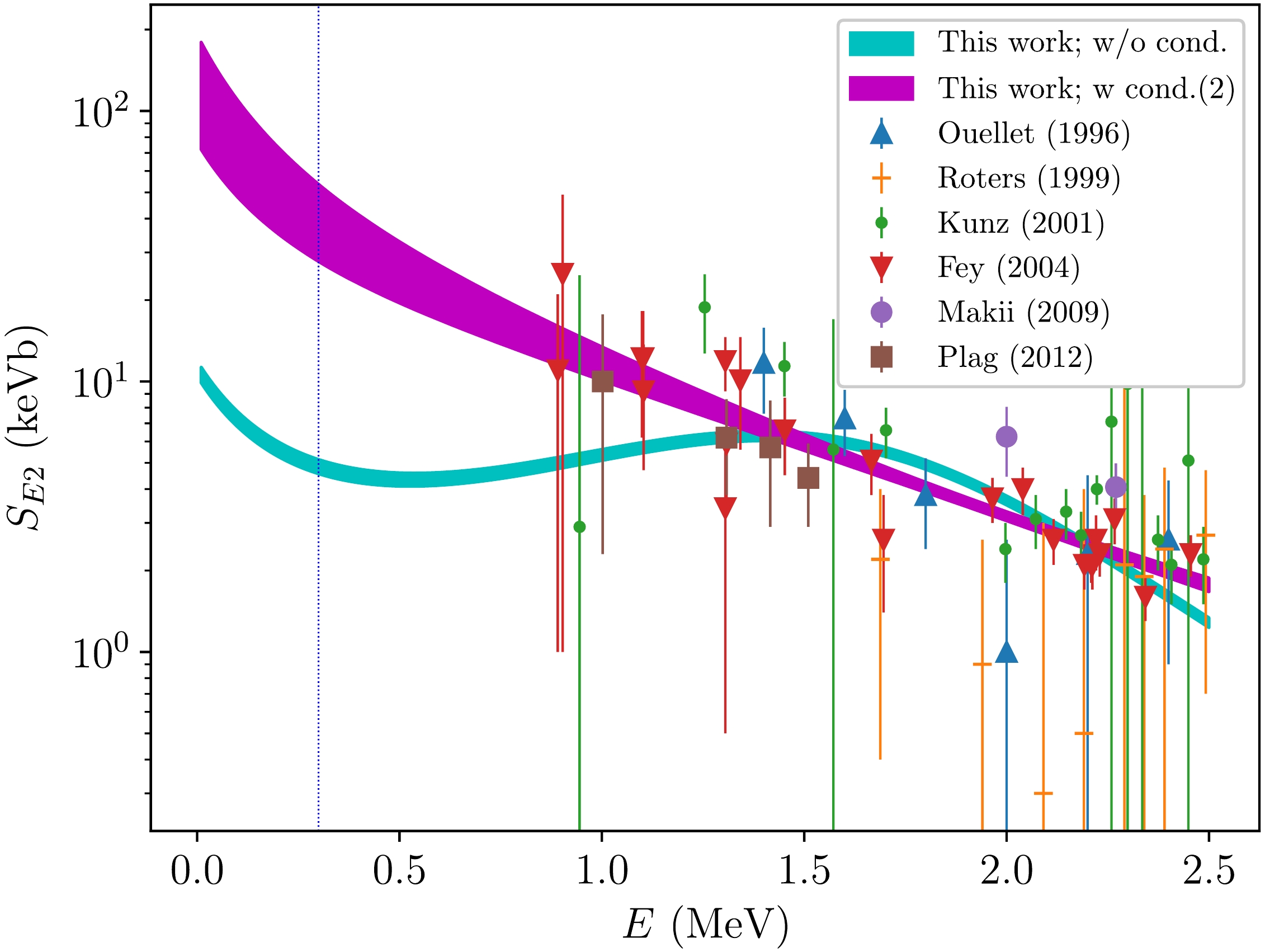

Figure 6.  (color online) $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O represented as a function of the energy E of the initial α-¹²C state in the center-of-mass frame. The two bands are plotted using the fitted parameters presented in Table 3. The bands, which correspond to the 16% to 84% distributions of the $ S_{E2} $ factor, are calculated from the samples of the parameters $ h_2^{(R)} $ and $ y^{(0)} $ in the MCMC analysis. The experimental data (see the text) are included in the figure as well. The vertical blue line marks $ E_G=0.3 $ MeV.

A known problem in the study of the elastic α-¹²C scattering for $ l=2 $ at low energy is that the asymptotic normalization coefficient (ANC) of the subthreshold $ 2_1^+ $state of ¹⁶O calculated from the effective range parameters is significantly smaller than the values deduced from other reactions, such as α transfer reactions. An estimate of the ANC of the subthreshold $ 2_1^+ $ state of ¹⁶O, $ |C_b|_2 $, using the effective range parameters was reported by König, Lee, and Hammer to be $ |C_b|_2 = (2.41\pm 0.38)\times 10^4 $ fm^−1/2 [26], which is smaller by approximately a factor of five than the value of $ |C_b|_2 = (1.11\pm 0.11)\times 10^5 $ fm^−1/2 deduced from the α-transfer reactions, ¹²C(⁶Li, d)¹⁶O and ¹²C(⁷Li,t)¹⁶O [27]. Meanwhile, a large uncertainty of the ANC of the $ 2_1^+ $ state deduced from the elastic α-¹²C scattering within a potential model, with values ranging from 2 to $ 18\times 10^4 $ fm^−1/2, was reported by Sparenberg, Capel, and Baye [28] (the values of the ANC for the $ 2_1^+ $ state of ¹⁶O reported in literature are summarized in Table 2 in Ref. [29]). As will be discussed in the following, the inverse of the dressed ¹⁶O propagator for $ l=2 $ is expressed in terms of the three effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $, which approximately configure a cubic polynomial function. Fig. 6 in Ref. [22] features three types of lines: 1) those having a maximum point and a minimum point, 2) those having a plateau, and 3) those simply decreasing, obtained from the cubic function in the low energy region, where no data points exist to determine which line is correct, even though those sets of fitted values of the effective range parameters evenly reproduce the phase shift data accurately. Thus, we introduced the aforementioned conditions into the effective range parameters. This made the value of the ANC of the $ 2_1^+ $ state larger and caused the line of the inverse of the dressed ¹⁶O propagator for $ l=2 $ to simply decrease. Because no verification of the conditions has been reported, we analyzed their reliability by studying the effects of the conditions on the observable of the resonant $ 2_4^+ $ state of ¹⁶O and the estimate of the $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O at $ E_G $.

	Bruno (1975)	TWC (1993)	deBoer (2012)	This work w/o cond.	This work w cond.(1)
$ E_{R(24)} $/MeV	5.83(3)	5.858(10)	5.805(2)	5.92(2)	5.90(2)
$ \Gamma_{R(24)} $/keV	520(200)	150(10)	349(3)	$300 ^{+60}_{-40} $	235(20)

Table 2.  Resonant energy and width of the $ 2_4^+ $state of ¹⁶O. The values in the second, third, and fourth columns are extracted from literature: Bruno et al. (1975) [30], the compilation edited by Tilley, Weller, and Cheves (TWC) (1993) [5], and deBoer et al. (2012) [36], respectively. Those in the fifth and sixth columns are the fitted values obtained in this study without and with the conditions applied to the effective range parameters.

In this study, we first investigated the elastic α-¹²C scattering at low energies including the resonant $ 2_4^+ $ state of ¹⁶O in the cluster EFT. A set of the experimental data of the phase shift up to $ E_\alpha = 10 $ MeV, reported by Bruno et al. (1975) [30], was employed along with the precise phase shift data reported by Tischhauser et al. (2009) [25]. The resonant $ 2_4^+ $ state of ¹⁶O appears at $ E_\alpha = 4/3 E_{R(24)} = 7.9 $ MeV, where $ E_{R(24)} $ is the resonant energy of the $ 2_4^+ $ state of ¹⁶O, $ E_{R(24)}=5.86 $ MeV [5]. We introduced the conditions to restrict the parameter space of the effective range parameters in the low-energy region, $ E_\alpha = 0 $ – 2.6 MeV, and parameters of the S matrix of the elastic α-¹²C scattering for $ l=2 $ were fitted to the two sets of the phase shift data for three cases: one without applying the conditions to the effective range parameters and the other two applying the conditions in the parameter fit. For one of these two latter cases, we employed a value of the ANC of the $ 2_1^+ $ state of ¹⁶O to fix a value of one of the effective range parameters. For all cases, the fitted parameters reproduced the phase shift data well. However, we found a large difference in the values of the ANC of the $ 2_1^+ $ state of ¹⁶O; this confirmed that the ANC of the $ 2_1^+ $ state of ¹⁶O cannot be determined by the phase shift data of the elastic α-¹²C scattering for $ l=2 $. We also found noticeable differences in the values of parameters for the resonant $ 2_4^+ $ state of ¹⁶O. We compared the fitted values of the resonant energy and width of the $ 2_4^+ $state of ¹⁶O with those reported in literature.

We also employed experimental data of the $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O. First, we studied the energy dependence of the inverse of the dressed ¹⁶O propagator for $ l=2 $ in the low-energy region. We fixed one of the effective range parameters for the large value of the ANC to reproduce a value of the ANC of the $ 2_1^+ $ state of ¹⁶O deduced from the α-transfer reactions. Then, using the fitted values of the effective range parameters for two of the three aforementioned cases, two additional parameters, $ y^{(0)} $ and $ h_R^{(2)} $, of E2 transition amplitudes of ¹²C(α,γ)¹⁶O were fitted to the experimental data of the $ S_{E2} $ factor. We found the $ \chi^2 $ values to be $ \chi^2/N = 1.18 $ and 1.55 for the cases with and without applying the conditions, respectively, where N is the number of data points of the $ S_{E2} $ factor. The $ S_{E2} $ factor was extrapolated to be $ E_G=0.3 $ MeV; we found notably different values of the $ S_{E2} $ factor at $ E_G $. We analyzed the significance of introducing the conditions in the observables of the $ 2_4^+ $ state of ¹⁶O and the estimate of the $ S_{E2} $ factor at $ E_G $, concluding that it is necessary to adopt the value of the ANC of the $ 2_1^+ $ state of ¹⁶O deduced from the α-transfer reactions to reduce the uncertainty in fixing the effective range parameters of the $ 2_1^+ $ state of ¹⁶O ².

This paper is organized as follows. In Section II, we review the expression of the S matrix of the elastic α-¹²C scattering for $ l=2 $ in the cluster EFT. In Section III, the numerical results of this study are presented; in Section III.A, the conditions applied to the effective range parameters are discussed; in Section III.B, the fitting of the parameters of the S matrix for $ l=2 $to the experimental phase shift data is presented, and the fitted values of the resonant energy and width of the $ 2_4^+ $ state of ¹⁶O are compared with those reported in literature. In Section III.C, the energy dependence of the inverse of the dressed ¹⁶O propagator for $ l=2 $ on the conditions in the low energy region is studied. Then, the fitting of two additional parameters of the E2 transition amplitudes of ¹²C(α,γ)¹⁶O to the experimental data of the $ S_{E2} $ factor is presented, and we describe how the $ S_{E2} $ factor is extrapolated to $ E_G $. The numerical results for the $ S_{E2} $ factor are presented and discussed. Finally, in Section IV, more results of this study are presented and discussed. In Appendix A, the expansion formulas of the digamma function and the inverse of the dressed ¹⁶O propagator for $ l=2 $ are summarized; in Appendix B, the expression and derivation of the E2 transition amplitudes of ¹²C(α,γ)¹⁶O in the cluster EFT are briefly discussed.

In this section, we review the expression of the S matrices of the elastic α-¹²C scattering at low energies and its brief derivation in the cluster EFT [23]. The S matrices of the elastic α-¹²C scattering for lth partial wave states are expressed in terms of phase shifts, $ \delta_l $, and elastic scattering amplitudes, $ \tilde{A}_l $, as

Let us assume that the phase shifts can be decomposed as

where $ \delta_l^{(bs)} $ is a phase shift generated from a bound state, and $ \delta_l^{(rsN)} $, with $ N=1,2,3 $, are phase shifts generated from the first, second, and third resonant states and may have a relation with a corresponding scattering amplitude as

where $ ch(annel) = bs, rsN $, and $ \tilde{A}_l^{(bs)} $ and $ \tilde{A}_l^{(rsN)} $, with $ N=1,2,3 $, are the amplitudes for the binding part and the first, second, and third resonant parts of the amplitudes, derived from the effective Lagrangian in Ref. [23]. The total amplitudes $ \tilde{A}_l $ for the nuclear reaction part in terms of the four amplitudes, $ \tilde{A}_l^{(bs)} $ and $ \tilde{A}_l^{(rsN)} $, with $ N=1,2,3 $, read

Note that the total amplitudes are not obtained as the summation of amplitudes; the additional phase factors appear in front of them.

The amplitudes were calculated using the diagrams shown in Figs. 1 and 2 [19, 20, 22]. In the present study, for the elastic α-¹²C scattering for $ l=2 $, we included the subthreshold bound $ 2_1^+ $ state and three resonant $ 2_2^+ $, $ 2_3^+ $, $ 2_4^+ $ states of ¹⁶O. For the bound state amplitude, that is, $ \tilde{A}_l^{(bs)} $ with $ l=2 $, one has

Figure 1.  Diagrams for dressed ¹⁶O propagators. Thick and thin double dashed lines with or without a filled circle represent the dressed or bare ¹⁶O propagators, respectively. A thick (thin) dashed line represents a propagator of ¹²C (α), and a shaded blob in the loop diagrams represents the Coulomb Green's function.

Figure 2.  Diagram for elastic α-¹²C scattering amplitudes. A shaded blob represents the initial or final Coulomb wave function, and a thick and thin double-dashed line with a filled circle represents a dressed ¹⁶O propagator. Refer also to the caption of Fig. 1.

where $ C_\eta^2 W_2(p) $ in the numerator is calculated from the initial and final state Coulomb interactions for $ l=2 $ in Fig. 2; p is the magnitude of relative momentum of the α-¹²C system in the center of mass frame, $ p=\sqrt{2\mu E} $, where E is the energy of the α-¹²C system, and

where η is the Sommerfeld parameter, $ \eta=\kappa/p $, with κ being the inverse of the Bohr radius, $ \kappa = Z_\alpha Z_{12C} \alpha_E\mu $, where $ Z_A $ is the number of protons in a nucleus, and $ \alpha_E $ is the fine structure constant. One has $ \kappa=245 $ MeV, which is regarded as a large scale of the theory given that $ \kappa > \Lambda_H $. The function $ -2\kappa H_2(p) $ in the denominator of the amplitude is the Coulomb self-energy term, which is calculated from the loop diagram in Fig. 1, and one has

where $ \psi(z) $ is the digamma function. As discussed in Ref. [20], large and significant contributions to the series of effective range expansions, compared to the terms calculated using a phase shift datum at the lowest energy of the data, $ E_\alpha=2.6 $ MeV [25], appear from the Coulomb self-energy term, $ -2\kappa H_l(p) $, with $ l=0,1,2 $. In addition, for $ l=2 $, the large terms appear by expanding the self-energy term, $ 2\kappa H_2(p) $, in terms of $ 1/\eta^2=(p/\kappa)^2 $ at the $ p\to 0 $ limit. Expressions of the function $ H_2(p) $ expanded in powers of $ (p/\kappa)^2 $ are presented in Appendix A. Thus, one has

where large terms proportional to $ \kappa^3 $ and κ appear in the first and second terms on the right-hand side of the equation. These terms do not obey the counting rules and need to be subtracted by the counter terms [32, 33].

Nuclear interaction is represented in terms of the effective range parameters in the function $ K_2(p) $ in the denominator of the amplitude in Eq. (5). We introduced two terms proportional to $ p^2 $ and $ p^4 $ as leading order contributions to subtract the two large contributions from the self-energy term mentioned above, and a term proportional to $ p^6 $ as a sub-leading one. The effective range terms up to $ p^6 $ order are included for $ l=2 $, and we have

where $ a_2 $, $ r_2 $, $ P_2 $, and $ Q_2 $ are the effective range parameters for $ l=2 $.

We fixed a parameter among the four effective range parameters, $ a_2 $, $ r_2 $, $ P_2 $, and $ Q_2 $, using the condition that the inverse of the scattering amplitude $ \tilde{A}_2^{(bs)} $ vanishes at the binding energy of the $ 2_1^+ $ state of ¹⁶O. Thus, the denominator of the scattering amplitude,

vanishes at $ p={\rm i}\gamma_{2} $, where $ \gamma_{2} $ denotes the binding momentum of the $ 2_1^+ $ state of ¹⁶O; $ \gamma_{2} = \sqrt{2\mu B_{2}} = 37.0 $ MeV. Fixing the scattering length $ a_2 $ using this condition allows rewriting the expression of the function $ K_2(p) $ as

At the binding energy, the wave function normalization factor $ \sqrt{Z_{2}} $ for the bound $ 2_1^+ $ state of ¹⁶O in the dressed ¹⁶O propagator for $ l=2 $ can be expressed as

where the dots denote the finite terms at $ E=-B_{2} $, and one has

The wave function normalization factor $ \sqrt{Z_{2}} $ is multiplied by a reaction amplitude when the bound state appears in the initial or final state of a reaction.

The ANCs $ |C_b|_{l} $ for the bound states of ¹⁶O are calculated using the formula of Iwinski, Rosenberg, and Spruch [34],

where $ \Gamma(x) $ is the gamma function. Comparing Eqs. (13) and (14), it can be observed that the ANCs are proportional to the wave function normalization factor $ \sqrt{Z_{l}} $. The ANC of the $ 2_1^+ $ state of ¹⁶O, $ |C_b|_2 $, can be calculated by using the fitted values of the effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $.

The amplitudes for the resonant $ 2_2^+ $, $ 2_3^+ $, $ 2_4^+ $ states may be obtained in the Breit-Wigner-like expression as

with

where $ E_{R(2i)} $ and $ \Gamma_{R(2i)} $ are the energy and width of the resonant $ 2_{i}^+ $ states (where $ i=N+1 $ with $ N=1,2,3 $), and $ p_r $ and $ \eta_r=\kappa/p_r $ are the momenta and Sommerfeld factors at the resonant energies; we suppressed the i indices for them. The functions $ R_{(2i)}(E) $ have the second and third order corrections expanded around $ E=E_{R(2i)} $, where the coefficients $ a_{(2i)} $ and $ b_{(2i)} $ are fitted to the shapes of resonant peaks.

Using the relations for the amplitudes in Eqs. (5) and (15), the S matrix for $ l=2 $ in Eq. (1) can be rewritten as a simple and transparent expression,

where we represented the part of the subthreshold state as a function of momentum, p, and the parts of the resonant states as functions of energy, E; they are related by the non-relativistic equation $ E=p^2/(2\mu) $.

In this section, we first introduce the conditions to apply to the effective range parameters when fitting them to the phase shift data. We then consider two types of experimental data, namely the phase shift of the elastic α-¹²C scattering for $ l=2 $ up to $ E_\alpha= 10 $ MeV and the $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O up to $ E=2.5 $ MeV. Employing the phase shift data, we fitted the parameters of the S matrix of the elastic α-¹²C scattering for $ l=2 $ with and without applying the conditions, and compared the fitted values of resonant energy and width of the $ 2_4^+ $ state of ¹⁶O with those in literature. We also studied the energy dependence of the inverse of the dressed ¹⁶O propagator for $ l=2 $ in the low-energy region by using the fitted values of the effective range parameters. Then, employing the experimental data of the $ S_{E2} $ factor, we fitted additional parameters of the E2 transition amplitudes of ¹²C(α,γ)¹⁶O, and the $ S_{E2} $ factor was extrapolated to $ E_G $.

The inverse of the propagator, $ D_2(p) $, is approximately represented as a cubic equation in powers of $ p^2 $, whose coefficients are given by the effective range parameters $ r_2 $, $ P_2 $, and $ Q_2 $. In general, it can have a minimum point and a maximum point or a flat plateau; else, it can simply decrease in the low-energy region, as mentioned above. To make it a simple decreasing function, which results in a large value of the ANC of the $ 2_1^+ $ state of ¹⁶O, we introduced the conditions when fitting the effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $, in the low energy region, $ 0\le E_\alpha \le 2.6 $ MeV.

We first expanded the function $ H(\eta) $ in terms of $ 1/\eta $ in the asymptotic limit, $ \eta \to \infty $; the formulas for the expansion of the digamma function $ \psi(z) $ are summarized in Appendix A. Thus, the real part of the inverse of the propagator, $ {\rm Re} D_2(p) $, in Eq. (10) becomes expanded around the binding energy, $ E=-B_2 $, i.e., $ p^2 = -\gamma_2^2 $, yielding

with

and the conditions $ C_n<0 $ for $ n=1, 2, 3 $ are introduced, which make $ {\rm Re} D_2(p) $ simply decrease in the low energy region (one may notice that $ C_4 $, $ C_5<0 $above). These conditions lead to restrictions on the effective range parameters,

where the terms are expanded in powers of $ (\gamma_2/\kappa)^2 = $ 0.023 [$ <(Q/\Lambda_H)^2 = 0.0625 $]; the truncation of higher-order terms would be a good approximation. From those conditions, the minimum or maximum values of the effective range parameters are

Note that the wave function normalization factor $ Z_2 $ in Eq. (13) is obtained from $ C_1 $ in Eq. (20) as $ Z_2^{-1} = -2\mu C_1 $ (note that $ C_1 $ is negative), and the ANC of the $ 2_1^+ $ state of ¹⁶O is expressed as

Thus, if one adopts the ANC of the $ 2_1^+ $ state of ¹⁶O, $ |C_b|_2 $, as an input, one of the three effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $, in $ C_1 $can be fixed by this equation.

In a previous study of ours [22], we employed precise phase shift data up to $ E_\alpha = 6.62 $ MeV reported by Tischhauser et al. (2009) [25] to fit the parameters, including the resonant $ 2_2^+ $ and $ 2_3^+ $ states of ¹⁶O. (They appear at $ E_\alpha(2_2^+) = 3.58 $ MeV and $ E_\alpha(2_3^+)=5.81 $ MeV.) We obtained six sets of values for the effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $, which fitted the precise phase shift data for $ l=2 $ well (see Tables 1 and 2 in Ref. [23]). However, these values yielded different values of the ANC of the $ 2_1^+ $ state of ¹⁶O and different paths of the real part of the inverse of the dressed ¹⁶O propagator for $ l=2 $, $ {\rm Re} D_2(p) $, in the low energy region where the $ S_{E2} $ factor was extrapolated to $ E_G $ (see Fig. 6 in Ref. [23]). In the present study, we employed and included a set of phase shift data for $ l=2 $ up to $ E_\alpha = 10 $ MeV reported by Bruno et al. (1975) [30] to refit the parameters, explicitly including the resonant $ 2_4^+ $ state of ¹⁶O in the S matrix of the elastic α-¹²C scattering for $ l=2 $. There are 13 parameters (12 parameters when $ r_1 $ is fixed by $ |C_b|_2 $), $ \theta =\{r_2, P_2, Q_2, E_{R(22)},\, \Gamma_{R(22)},\, E_{R(23)},\, \Gamma_{R(23)},\, a_{(23)},\, b_{(23)},\, E_{R(24)},\, \Gamma_{R(24)},\, a_{(24)},\, b_{(24)} \} $, which were fitted to the two sets of phase shift data; we introduced the conditions to the effective range parameters by means of the $ \chi^2 $ fit using an MCMC ensemble sampler [35].

	Prev. work w/o cond.	This work w/o cond.	This work w cond.(1)	This work w cond.(2)
$ r_2 $/fm−3	0.149(4)	0.150(6)	0.1586(3)	0.1575*
$ P_2 $/fm−1	−1.19(5)	−1.18(8)	−1.047(2)	−1.049(2)
$ Q_2 $/fm	0.081(16)	0.084(3)	0.138(2)	0.141(2)
$ E_{R(22)} $/MeV	2.68308(5)	2.68308(1)	2.68308(1)	2.68308(1)
$ \Gamma_{R(22)} $/keV	0.75(2)	0.76(1)	0.76(1)	0.76(1)
$ E_{R(23)} $/MeV	4.3545(2)	4.3533(3)	4.3537(1)	4.3536(1)
$ \Gamma_{R(23)} $/keV	74.61(3)	74.5(1)	74.5(1)	74.5(1)
$ a_{(23)} $/MeV−1	0.46(12)	0.6(2)	1.1(1)	1.2(1)
$ b_{(23)} $/MeV−2	0.47(9)	0.5(2)	0.6(1)	0.6(1)
$ E_{R(24)} $/MeV	5.858*	5.92(2)	5.90(2)	5.89(2)
$ \Gamma_{R(24)} $/keV	150*	300$ ^{+60}_{-40} $	235(20)	237(19)
$ a_{(24)} $/MeV−1	–	0.3(4)	0.6(1)	0.67(9)
$ b_{(24)} $/MeV−2	–	0.96$ ^{+0.79}_{-0.50} $	0.3(1)	0.2(1)
$ |C_b|_2 $/fm$ ^{-1/2} $	3.1(6)$ \times 10^4 $	3.24$ \times 10^4 $	22.8$ \times 10^4 $	$ 10\times 10^{4*} $
$ \chi^2/N $ (N)	0.66 (245)	3.02 (271)	3.04 (271)	3.05 (271)

Table 1.  Fitted values of the parameters of the S matrix of the elastic α-¹²C scattering for $ l=2 $ to the two sets of phase shift data [25, 30]. The second column lists values from column (I) in Table 2 from a previous study of ours [22]; the third column lists values obtained in this study without applying the conditions; the fourth and fifth columns list values obtained in this study applying the conditions to the effective range parameters in Eqs. (25), (26), and (27); and the fifth column lists the values of the ANC of the $ 2_1^+ $ state of ¹⁶O, $ |C_b|_2 = 10 \times 10^4 $ fm^−1/2, employed to fix the corresponding values of $ r_2 $ (marked by *). The second row from the bottom includes values of the ANC of the $ 2_1^+ $ state of ¹⁶O calculated using the values of $ r_2 $, $ P_2 $, and $ Q_2 $. The last row presents values of $ \chi^2/N $ (where N is the number of data). In the aforementioned previous study, $ E_{R(24)} $ and $ \Gamma_{R(24)} $ were included as fixed values (marked by *) using the experimental data [5]; the parameters $ a_{(24)} $ and $ b_{(24)} $ were not included.

Table 1 presents values of the parameters fitted to the phase shift data. The second column lists values from a previous study of ours (column (I) in Table 2) [22]. The third column lists values obtained in the present study without applying the conditions. The fourth and fifth columns list values obtained in this study by applying the conditions in Eqs. (25), (26), and (27) to the effective range parameters. The fifth column lists the values of the ANC of the $ 2_1^+ $ state of ¹⁶O, $ |C_b|_2 = 10\times 10^4 $fm^−1/2, adopted to fix one of the effective range parameters, $ r_2 $. In the aforementioned previous study, we employed experimental data reported by Tischhauser et al. (2009) [25] (number of data points: $ N=245 $); we included the $ 2_4^+ $ state as a background from high energy, where the resonant energy and width were fixed by using experimental data [5], and the parameters $ a_{(24)} $ and $ b_{(24)} $ were not included. One can see that the values in the second and third columns are in good agreement except for those of $ \Gamma_{R(24)} $ and $ \chi^2/N $. We discuss the values of $ \Gamma_{R(24)} $ later on. The larger values of $ \chi^2/N $ are due to the inclusion of the phase shift data reported by Bruno et al. (1975) [30] (number of data points: $ N=26 $). We found that the conditions applied to the effective range parameters change the values of $ r_2 $, $ P_2 $, and $ Q_2 $ significantly, as shown in the third to fifth columns. Note that the values of the effective range parameters in the second and third columns do not satisfy the bounds owing to the conditions in Eq. (28), whereas those in the fourth and fifth columns do satisfy them. The values of ANC, $ |C_b|_2 $, are altered largely; we obtained $ |C_b|_2 = 3.24\times 10^4 $ fm^−1/2 when the conditions were not applied, which is larger by approximately a factor of 1.6 than the value reported by König, Lee, and Hammer. This may be due to the inclusion of the $ 2_4^+ $ state of ¹⁶O (see Ref. [22]). We obtained $ |C_b|_2 = 22.8\times 10^4 $ fm^−1/2 when applying the conditions in the fourth column, which is larger by approximately a factor of 2 than the values deduced from the α-transfer reactions. This range of values of the ANC, $ |C_b|_2 = (3.2 -22.8)\times 10^4 $ fm^−1/2, agrees with that reported by Sparenberg, Capel, and Baye in their study employing a potential model, $ (2-18)\times 10^4 $ fm^−1/2 [28]. In addition, the values of $ \chi^2/N $ in the third to fifth columns are similar. We confirmed that the ANC of the $ 2_1^+ $ state of ¹⁶O cannot be determined by the phase shift data of the elastic α-¹²C scattering for $ l=2 $. Note also that the values of the shape parameter, $ a_{(23)} $, of the $ 2_3^+ $ state and the width and shape parameters, $ \Gamma_{R(24)} $, $ a_{(24)} $, and $ b_{(24)} $, of the $ 2_4^+ $ state are altered between the third column and the fourth and fifth columns in Table 1.

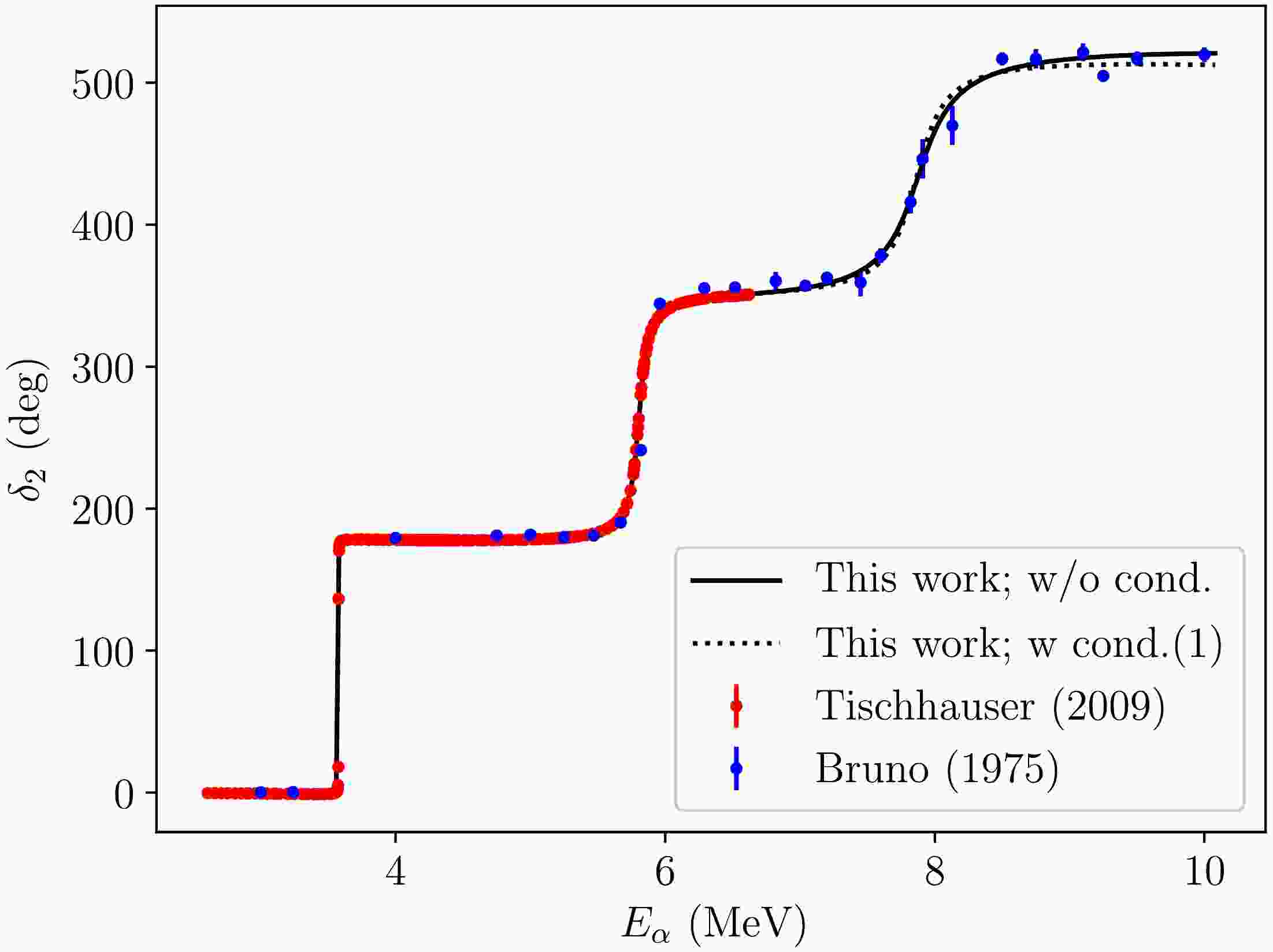
In Fig. 3, the phase shifts of the elastic α-¹²C scattering for $ l=2 $ are represented as functions of the α energy $ E_\alpha $. The solid line represents the values of the parameters in the third column in Table 1. The dotted line represents the values in the fourth column of the same table. The experimental data reported by Tischhauser et al. (2009) [25] (accurate data up to the p-¹⁵N breakup energy, $ E_\alpha=6.62 $ MeV) and Bruno et al. (1975) [30] (data covering the high-energy region for the resonant $ 2_4^+ $ state of ¹⁶O up to $ E_\alpha = 10 $ MeV) are also represented in the figure. Note that both lines reproduce the experimental data well.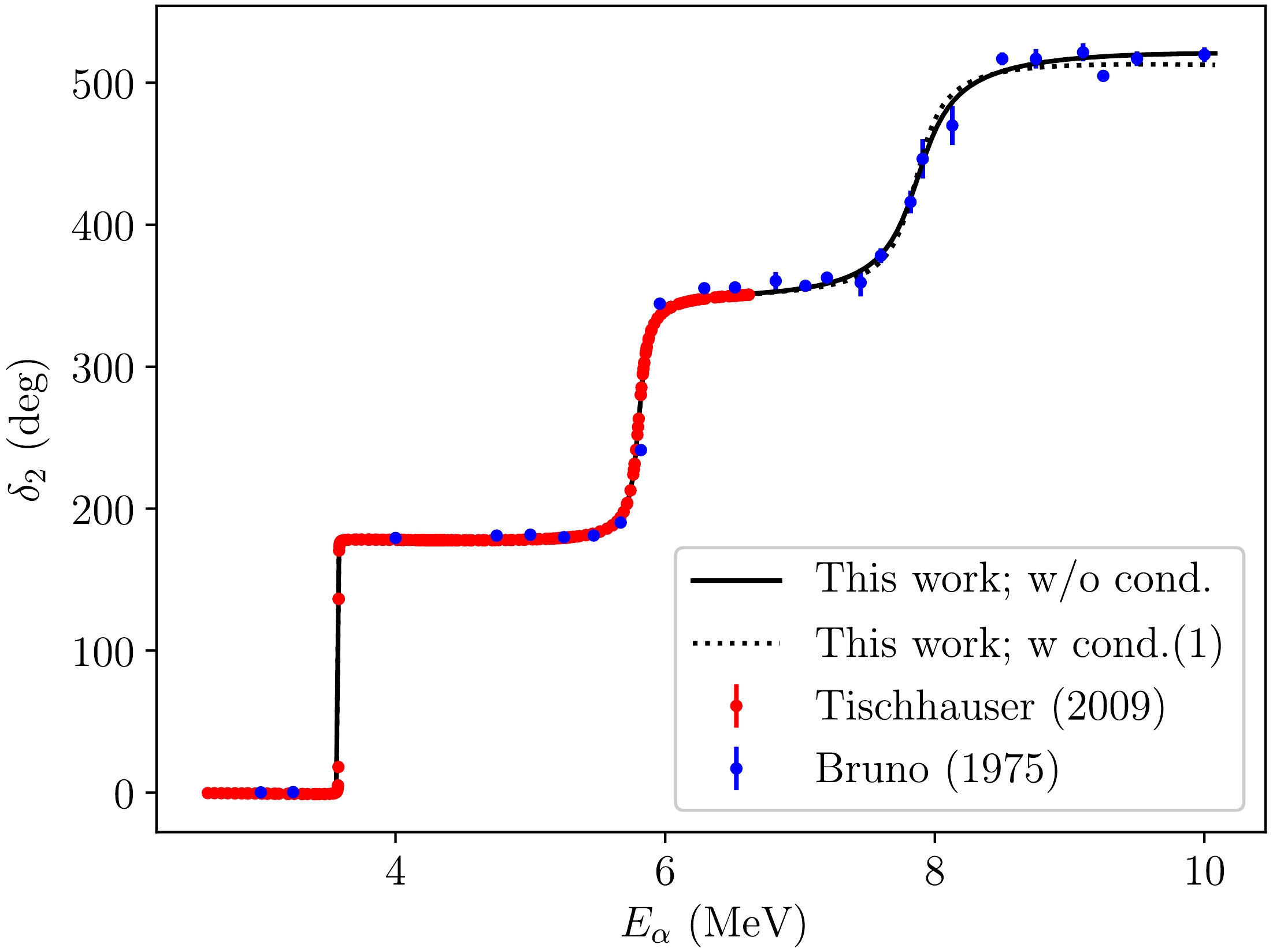

Figure 3.  (color online) Phase shifts of the elastic α-¹²C scattering for $ l=2 $ represented as functions of the α energy $ E_\alpha $ in the laboratory frame. The solid line represents the values of the parameters in the third column in Table 1, whereas the dotted line represents the values in the fourth column in the same table. The experimental data reported by Tischhauser et al. (2009) [25] and Bruno et al. (1975) [30] are represented in the figure as well.

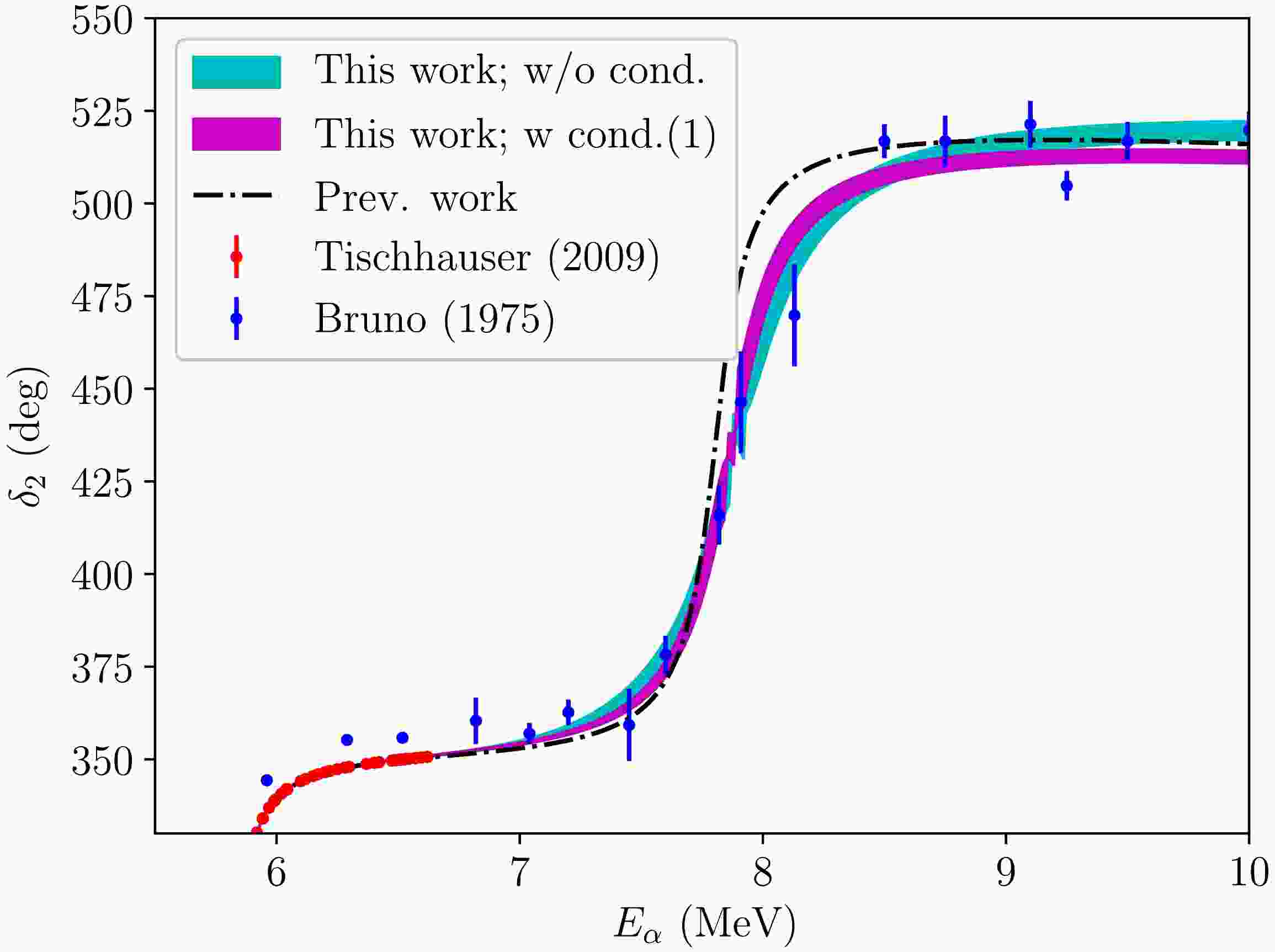
In Fig. 4, the same lines with the bands and data shown in Fig. 3 are represented in the energy region for the resonant $ 2_4^+ $ state of ¹⁶O. The dashed-dotted line represents the parameters obtained in the previous study (those in the second column in Table 1). The bands represent the uncertainty of the phase shifts, which are calculated as the band from 16% to 84% distribution of a phase shift calculated from the samples of the parameters in the MCMC analysis. Note that the bands fitted to the data in this study are more accurate than those in the previous study. The two bands in this study are distinguishable. However, the data exhibit large error bars; it is not easy to determine which line is more accurate. As discussed above, this difference is also observed in the different values of the parameters of the $ 2_4^+ $ state of ¹⁶O in the third and fourth columns of Table 1.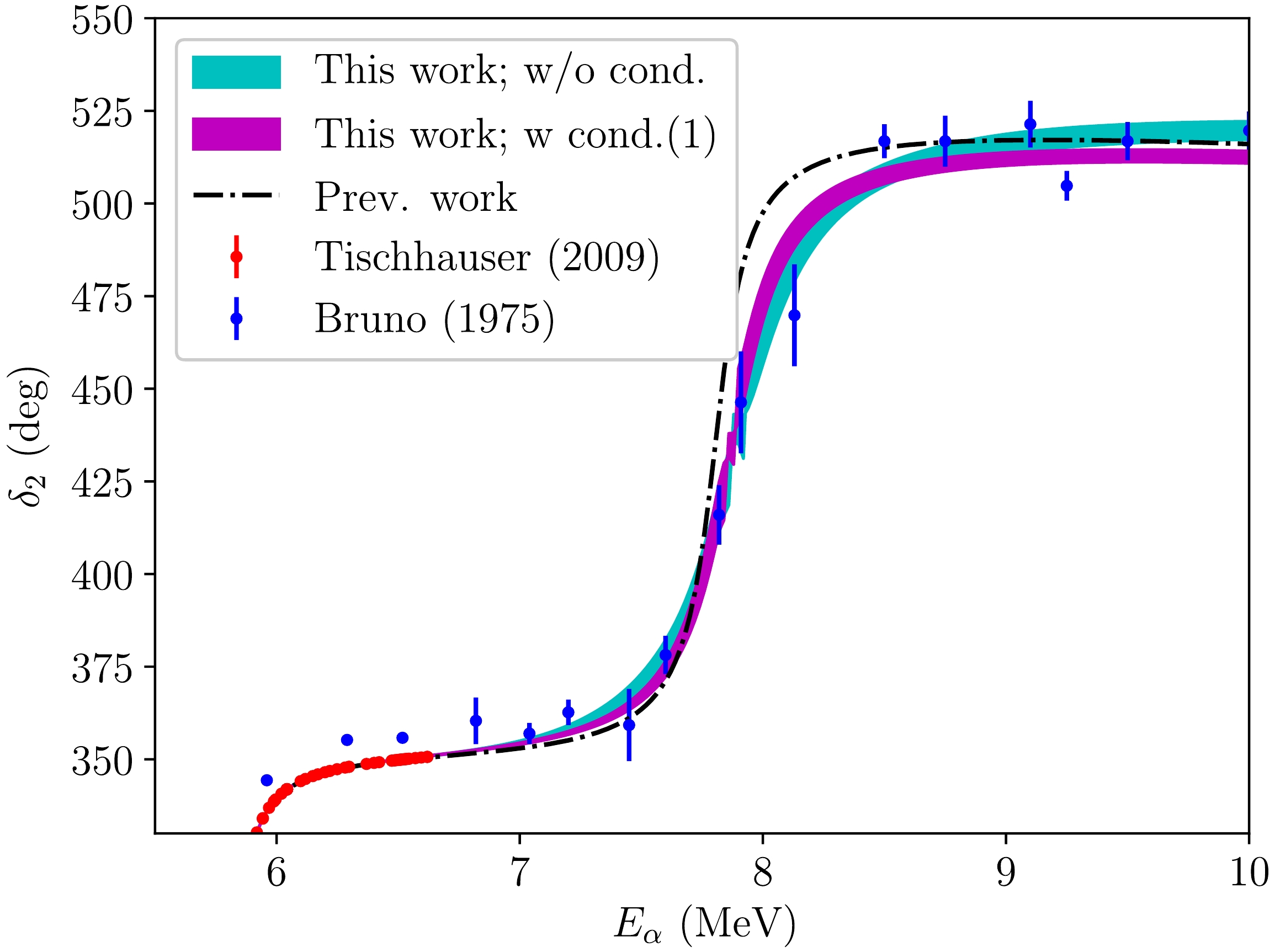

Figure 4.  (color online) Same phase shifts with the bands represented in Fig. 3 in the energy region of the resonant $ 2_4^+ $ state, represented as functions of the α energy $ E_\alpha $. The bands, spanning 16% to 84% distribution of a phase shift, are calculated from the samples of the parameters in the MCMC analysis. The dashed-dotted line represents the parameters obtained in the previous study (those in the second column in Table 1). Refer also to the caption of Fig. 3.

In Table 2, we summarize the values of the resonant energy and width of the $ 2_4^+ $ state of ¹⁶O, $ E_{R(24)} $ and $ \Gamma_{R(24)} $, reported in literature and our results presented in Table 1. We obtained larger values of the resonant energy, $ E_{R(24)} $, by two sigma deviation with respect to the value of Bruno et al. (1975) [30]. Note that the values of $ \Gamma_{R(24)} $ reported in literature are still scattered, and their uncertainties are significant; these values are in good agreement within the error bars, except for the compilation edited by Tilley, Weller, and Cheves (1993) [5], with $ \Gamma_{R(24)}=150(10) $ keV, which is significantly smaller than the others. To improve this situation, it may be helpful to have a more precise data set of the phase shift in the energy region for the resonant $ 2_4^+ $ state of ¹⁶O. Note that because two channels, α-¹²C^*($ 2_1^+ $) and p-¹⁵N states, open in this energy region, the inelastic channels of the scattering start contributing. Thus, it is necessary to improve the theoretical framework as well.

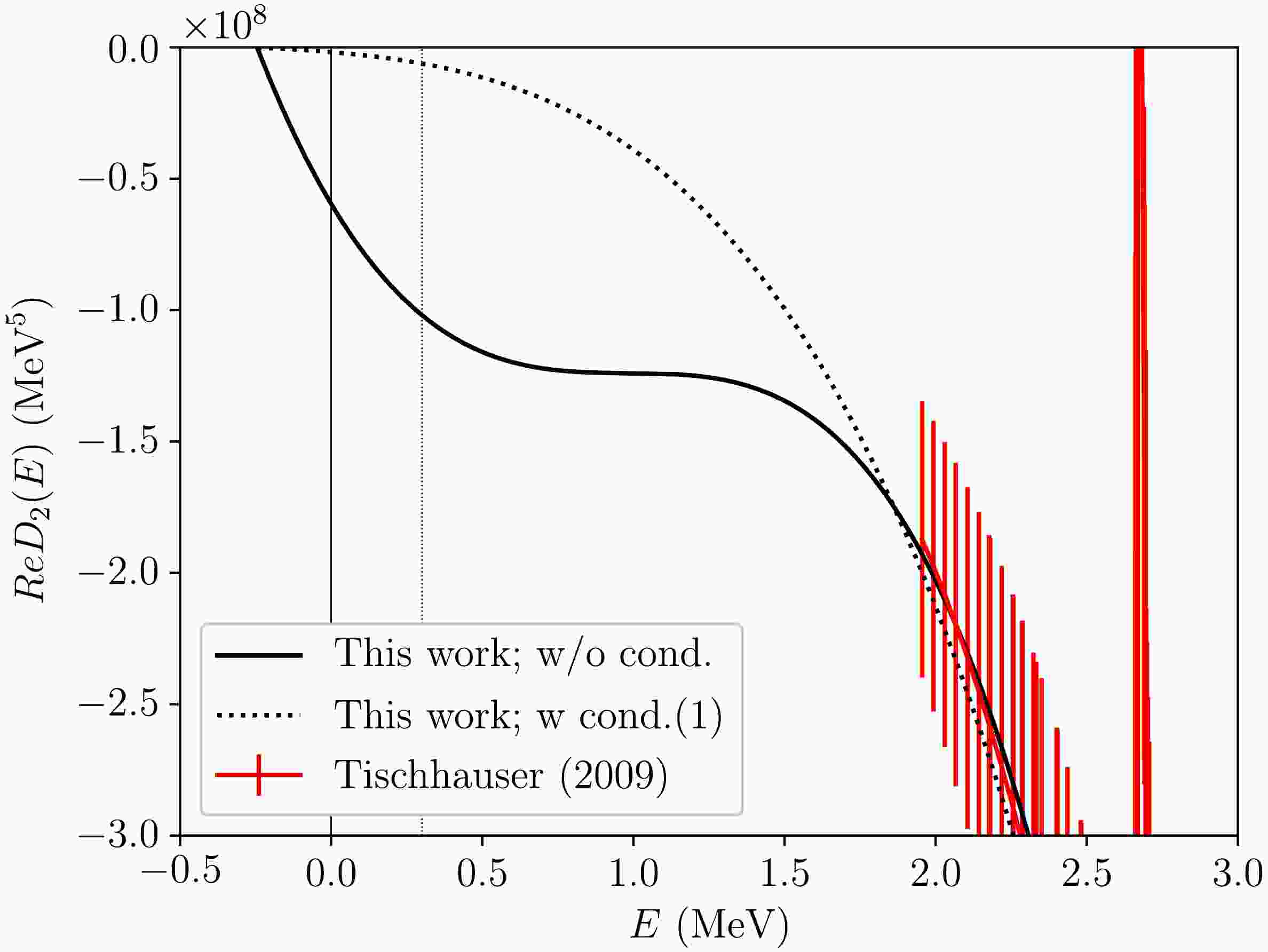
We can now study the effect of the conditions applied to the effective range parameters on the inverse of the propagator, $ D_2(p) $, and on the calculation of the $ S_{E2} $ factor of the E2 transition of ¹²C(α,γ)¹⁶O. In Fig. 5, we represent the real part of $ D_2(E) $ [$ =D_2(p) $] as a function of the energy E of the α-¹²C system in the center-of-mass frame of the low-energy region. The solid line was obtained using the values of $ r_2 $, $ P_2 $, and $ Q_2 $ in the third column of Table 1, whereas the dotted line was obtained using the values in the fourth column of the same table. The experimental data of the phase shift reported by Tischhauser et al. (2009) [25] were converted to $ {\rm Re} D_2(E) $ through the relation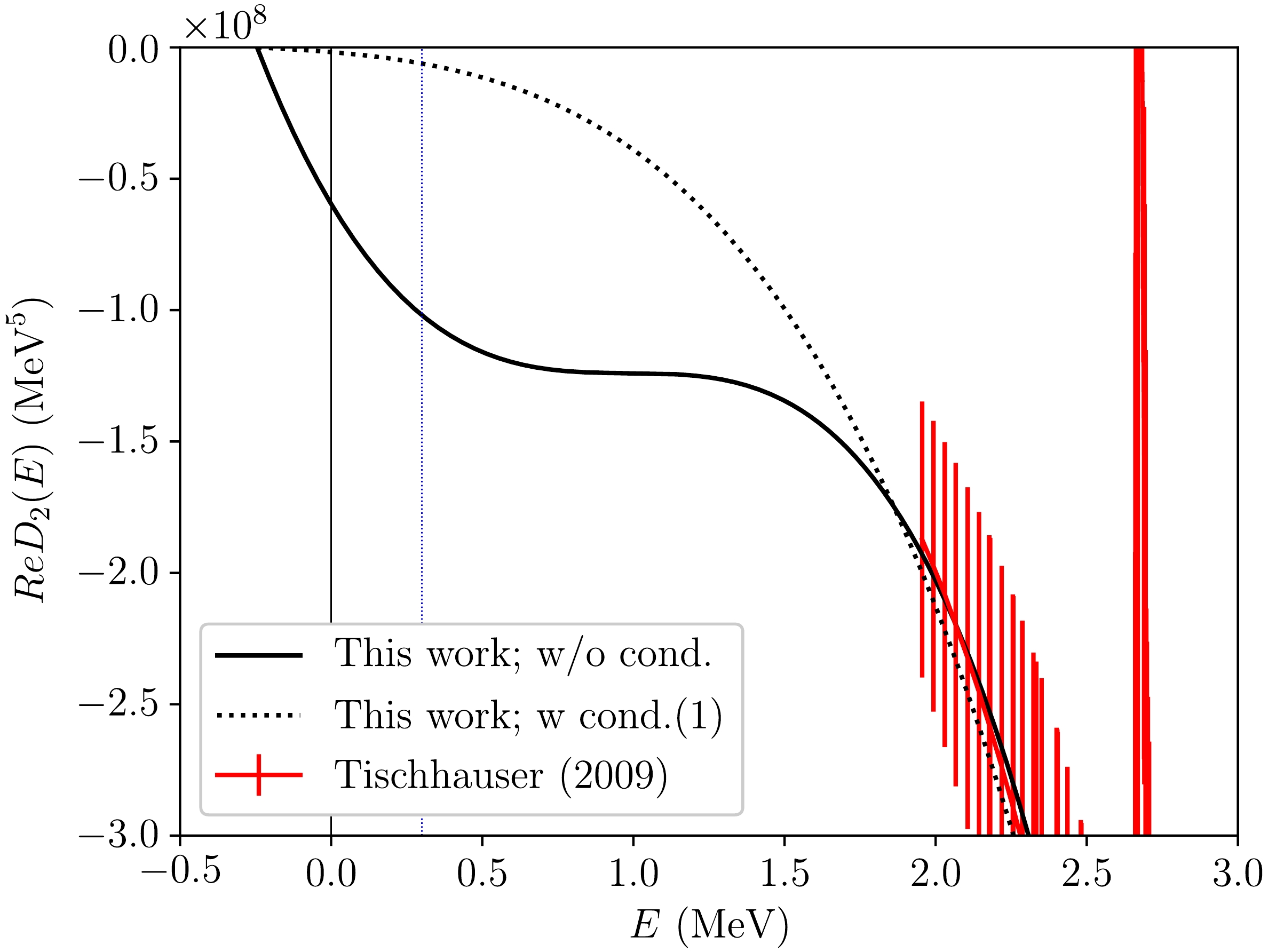

Figure 5.  (color online) Real part of the inverse of the propagator, $ {\rm Re} D_2(E) $ [$ ={\rm Re} D_2(p) $], represented as a function of the energy E of the α-¹²C system in the center-of-mass frame. The solid line is represented using the values of the effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $, in the third column in Table 1, whereas the dotted line is represented using the values in the fourth column in the same table. The phase shift data reported by Tischhauser et al. (2009) [25] are converted and represented in the figure as well. A vertical blue line is drawn at $ E_G = 0.3 $ MeV.

and represented in the figure as well. Note that the paths of both lines are notably different because of the conditions applied (or not applied) to the effective range parameters. The solid line exhibits a plateau in the low energy region, $ 0<E<1.95 $ MeV, whereas the dotted line decreases smoothly. Both lines reproduce the experimental data equally well. In addition, at the top of the figure, both lines start at the same point, i.e., at the binding energy of the $ 2_1^+ $ state of ¹⁶O, $ E=-B_2 $, where $ D_2(-B_2)=0 $. Note also that the gradients of the lines at this point are also notably different; they are related to the values of the ANC of the $ 2_1^+ $ state of ¹⁶O, $ |C_b|_2 $, in Eq. (14). Because the square of the root of the gradient appears in the denominator of the formula of $ |C_b|_2 $, a large negative angle associated with the horizontal line at this point leads to a small value of the ANC, whereas a small negative angle leads to a large value of the ANC. Thus, we obtained notably different values: small and large values of the ANC, as shown in Table 1. Both lines go through different paths between the point at $ E=-B_2 $ and the datum of phase shift whose lowest energy is $ E= 3/4 E_\alpha = 1.95 $ MeV. Because the inverse of the propagator $ D_2(p) $ appears in the denominator of the E2 transition amplitudes of ¹²C(α,γ)¹⁶O, the energy dependence of $ D_2(E) $ [$ =D_2(p) $] in the low energy region is crucial when extrapolating the $ S_{E2} $ factor to $ E_G=0.3 $ MeV.

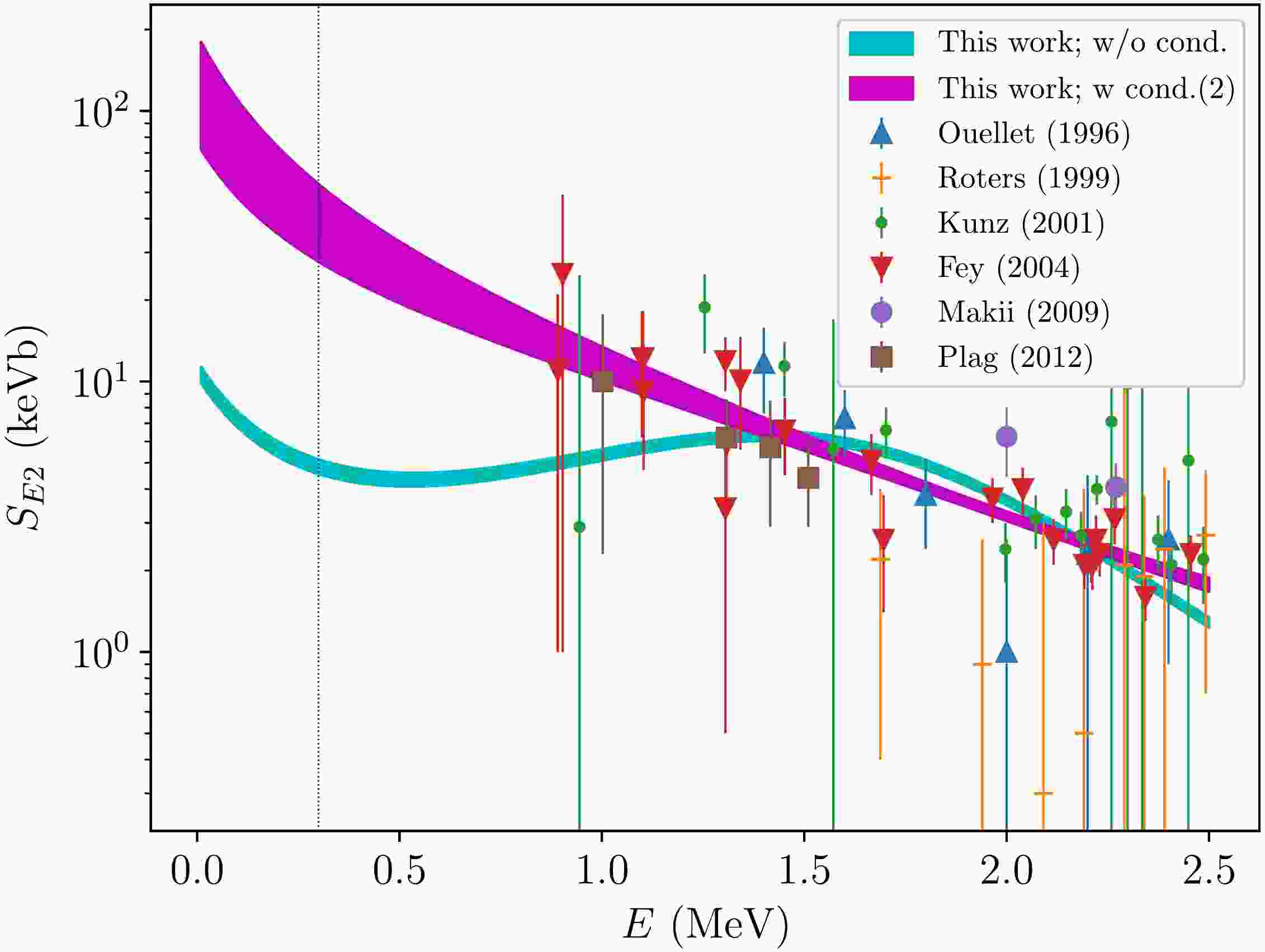
By employing the two sets of fitted values of the effective range parameters in the third and fifth columns in Table 1, we fitted additional parameters in the E2 transition amplitudes of ¹²C(α,γ)¹⁶O to the experimental data of the $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O. The expression of the E2 transition amplitudes and its brief derivation are presented in Appendix B; we have two additional parameters, $ h_R^{(2)} $ and $ y^{(0)} $, in the amplitudes. The experimental data of the $ S_{E2} $ factor below the resonant energy of $ 2_2^+ $ of ¹⁶O, up to $ E=2.5 $ MeV, reported by Ouellet et al. (1996) [37], Roters et al. (1999) [38], Kunz et al. (2001) [39], Fey (2004) [40], Makii et al. (2009) [41], and Plag et al. (2012) [42], were employed for fitting.

In Table 3, fitted values of the parameters $ h_R^{(2)} $ and $ y^{(0)} $ are presented along with the $ \chi^2/N $ values. When fitting these parameters, we used the values of the effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $, listed in the third and fifth columns in Table 1. Values of the $ S_{E2} $ factor at $ E_G=0.3 $ MeV were calculated using the fitted values of the parameters $ h_R^{(2)} $ and $ y^{(0)} $ and included in the table as well. Note that the fitted values of the parameters $ h_R^{(2)} $ and $ y^{(0)} $ are still scattered for both cases. The $ \chi^2/N $ values in the last two columns are $ \chi^2/N= 1.55 $ and 1.18, and the deduced values of $ S_{E2} $ at $ E_G $ show a difference of a factor of ten. We obtained $ S_{E2} = 4.1 \pm 0.2 $ and $ 40^{+14}_{-12} $ keVb, respectively. These two values are still within the range of previously reported values of the $ S_{E2} $ factor summarized in Table IV in Ref. [9].

$ |C_b|_2 $/fm−1/2	This work (w/o cond.) $ 3.2\times 10^4 $	This work (w cond.(2)) $ 10\times 10^4 $
$ h_R^{(2)}\times 10^{-11} $/MeV4	$ 50.6\pm 0.4 $	$ 45.53^{+0.04}_{-0.03} $
$ y^{(0)} $/MeV−1/2	$ 1.99\pm 0.01 \times 10^{-3} $	$5.9 \pm 0.1\times 10^{-2} $
$ \chi^2/N $ ($ N=51 $)	1.55	1.18
$ S_{E2} $/keVb at $ E_G $	$ 4.1\pm 0.2 $	$ 40^{+14}_{-12} $

Table 3.  Values of $ h_R^{(2)} $ and $ y^{(0)} $ fitted to the experimental data of the $ S_{E2} $ factor using two sets of values of the effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $. We used the values of $ r_2 $, $ P_2 $, $ Q_2 $ listed in the third column of Table 1 for the values in the second column. For those in the third column, we used the values of $ r_2 $, $ P_2 $, and $ Q_2 $ listed in the fifth column of Table 1. The $ \chi^2/N $ values for fitting are included in the table as well. $ S_{E2} $ at $ E_G=0.3 $ MeV was calculated using the fitted parameters.

In Fig. 6, two bands of the $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O are represented as functions of the energy E of the initial α-¹²C state in the center-of-mass frame. The experimental data of the $ S_{E2} $ factor are included in the figure as well. The cyan band for the $ S_{E2} $ factor, which exhibits a minimum point and a maximum point, was calculated using the fitted values of the parameters for which the conditions set to the effective range parameters were not applied. The magenta band of the $ S_{E2} $ factor, which decreases, was calculated using the fitted values for which the conditions were applied; one of the three effective range parameters was constrained by the value of the ANC, $ |C_b|_2 = 10\times 10^4 $ fm^−1/2, according to Eq. (29). Note that the energy dependence of the $ S_{E2} $ factor mainly results from that of $ D_2(E) $, which appears in the denominator of the E2 transition amplitudes of ¹²C(α,γ)¹⁶O, shown in Fig. 5. The $ \chi^2/N $ values of the bands are 1.55 and 1.18, respectively, which indicates that the magenta band is better to fit the data than the cyan one.

In this study, we first analyzed the elastic α-¹²C scattering for $ l=2 $ introducing conditions applied to the effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $, when fixing them to the phase shift data. We employed two data sets for elastic scattering: one featuring precise phase shift data up to the p-¹⁵N breakup energy, $ E_\alpha=6.62 $ MeV, reported by Tischhauser et al. (2009) [25], and the other featuring data up to $ E_\alpha=10 $ MeV, covering the resonant $ 2_4^+ $ state of ¹⁶O, as reported by Bruno et al. (1975) [30]. We fitted the parameters of the S matrix of the elastic α-¹²C scattering for $ l=2 $ to the phase shift data for three cases: one without applying the conditions and the other two applying the conditions to the effective range parameters in the low-energy region, where no experimental data have been reported. In one of the two cases with the conditions applied, the value of the ANC of the $ 2_1^+ $ state of ¹⁶O, $ |C_b|_2 = 10\times 10^4 $fm^−1/2, was used to fix one of the effective range parameters, $ r_2 $. We found larger values of the width of the $ 2_4^+ $ state of ¹⁶O, $ \Gamma_{R(24)}= 235(20) $ and $ 300^{+60}_{-40} $ keV, than those listed in the compilation, $ \Gamma_{R(24)}=150(10) $ keV [5]. We also found large and small values of the ANC of the $ 2_1^+ $ state of ¹⁶O, $ |C_b|_2 = 23.3\times 10^4 $ and $ 3.24\times 10^4 $fm^−1/2, for two of the three cases. The three sets of fitted parameters reproduced the phase shift data equally well. The fitted values of the effective range parameters for two sets of the three cases were employed for the study of the $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O. First, we studied the energy dependence of the inverse of the ¹⁶O propagator for $ l=2 $ in the low energy region where the $ S_{E2} $ factor is extrapolated to $ E_G $. Then, we fitted two additional parameters, $ h_R^{(2)} $ and $ y^{(0)} $, of the E2 transition amplitude of ¹²C(α,γ)¹⁶O to the experimental data of the $ S_{E2} $ factor with the following two $ \chi^2/N $ values: $ \chi^2/N= $ 1.18 and 1.55. We extrapolated the $ S_{E2} $ factor to $ E_G $, where, as mentioned, we fixed one of the effective range parameters for the case of the large ANC by adopting the ANC of the $ 2_1^+ $ state of ¹⁶O deduced from the α-transfer reactions, $ |C_b|_2=10\times 10^4 $ fm^−1/2. We obtained $ S_{E2}= 40^{+14}_{-12} $ and $ 4.1 \pm 0.2 $ keVb at $ E_G=0.3 $ MeV, respectively. We found that both values are within the range of previously reported values of $ S_{E2} $ at $ E_G $ reported in literature.

There is no restriction on whether one should apply the conditions to the effective range parameters or not when fitting to the phase shift data because the phase shift data were equally well-fitted for all cases. In other words, for the phase shift data for $ l=2 $, it is not possible to determine which line drawn in Fig. 5 is better, while it is crucial to extrapolate the $ S_{E2} $ factor to $ E_G $. One may argue that it is necessary to introduce the conditions because of the simplicity of natural laws, as once stated by Poincaré: ''natural laws must be simple'' [43]. For the present case, one may regard that the dotted line (which simply decreases) is simpler than the solid line (which exhibits a plateau) in Fig. 5; the appearance of such a bump in the $ S_{E2} $ factor in Fig. 6 might indicate interference with an unknown bound or resonant state at low energies. This assumption should be tested experimentally or using other possible methods.

A quantity that could test a verification of the conditions may be the width of the resonant $ 2_4^+ $ state of ¹⁶O. The reported values listed in Table 2 are still scattered. Nevertheless, the value $ \Gamma_{R(24)}= 349(3) $ keV recently reported by deBoer et al. (2012) could support the result of $ \Gamma_{R(24)} = 300^{+60}_{-40} $ keV, which was obtained without applying the conditions. Meanwhile, as discussed above, we need to improve the theoretical framework because new channels start opening in this energy region.

The experimental data of the $ S_{E2} $ factor of ¹²C(α,γ)¹⁶O may provide another quantity to test the verification of the conditions because the data cover a lower energy region, $ E=0.9- $$ 1.95 $ MeV ($ E_\alpha = 4/3 E=1.2 -$$ 2.6 $ MeV), than those of the elastic α-¹²C scattering. However, the data of the $ S_{E2} $ factor exhibit large error bars, especially in the lower energy region, $ E=0.9 - 1.2 $ MeV. After fitting the parameters $ h_R^{(2)} $ and $ y^{(0)} $ of the E2 transition amplitudes of ¹²C(α,γ)¹⁶O, we obtained the $ \chi^2/N $ values for two of the three cases: $ \chi^2/N=1.18 $ and 1.55. This may support the application of the conditions in the low-energy region although the data of the $ S_{E2} $ factor still present large uncertainties. More accurate measurements of the $ S_{E2} $ factor in the energy range $ E=0.9 -1.5$ MeV would be helpful to obtain a clear conclusion.

The values of the ANC of the $ 2_1^+ $ state of ¹⁶O obtained in this study are notably different for the cases $ |C_b|_2 = 3.24\times 10^4 $ and $ 23.3\times 10^4 $ fm^−1/2. As previously mentioned, the values of $ |C_b|_2 $ are deduced from α-transfer reactions such as ¹²C(⁶Li,d)¹⁶O [44]; the value of $ |C_b|_2 $ was recently updated by Hebborn et al. to be $ |C_b|_2 = 10.7(3)\times 10^4 $ fm^−1/2 [45]. They used the ANC of the ground state of ⁶Li as d-α system deduced from ab initio calculations [46]. As discussed above, we employed a value of the ANC, $ |C_b|_2=10\times 10^4 $ fm^−1/2, adopted from α-transfer reactions to constrain the values of the effective range parameters according to Eq. (29) when fitting them to the phase shift data applying the conditions. We obtained $ S_{E2}=40^{+14}_{-12} $ keV b with $ \chi^2/N=1.18 $. This $ \chi^2 $ value is small but the error of the $ S_{E2} $ factor is significantly large, approximately 35%. This may also result from the large errors of the data of the $ S_{E2} $ factor. Thus, it would be important to reduce the error bar of the $ S_{E2} $ factor theoretically estimated using the other available experimental data. A study in this direction is now being conducted.

The author would like to thank D. Phillips, T. Kajino, R. deBoer, and C. H. Hyun for discussions.

In this appendix, we discuss the relations related to the function $ H_2(p) $ in Eq. (7) in the low energy limit, $ p\to 0 $. Let us consider two formulas of the digamma function $ \psi(z) $; one is Eq. 6.3.18 in Ref. [47],

for $ |z|\to \infty $ and $ |arg z| <\pi $, where $ B_{2n} $ are Bernoulli numbers,

and the other is Eq. 5.4.16 in Ref. [48],

allowing us to rewrite the imaginary and real parts of the function $ H(\eta) $ in Eq. (7) as

This allows obtaining the expression of $ 2\kappa {\rm Re} H_2(p) $ in Eq. (8).

The expressions of $ {\rm Re} D_2(p) $ in Eq. (19) is calculated as follows. First, one may expand the $ H(\eta) $ function using the equation above. We obtain an expression of $ {\rm Re} D_2(p) $,

where a, b, c, d, and e are coefficients. Explicitly, we have

Then, one may use the relations

obtaining

with

Finally, we obtain the expressions of the coefficients $ C_i $, with $ i=1,2,3,4,5 $, in Eqs. (20)−(24).

In this appendix, we present the expression of the E2 transition amplitudes of ¹²C(α,γ)¹⁶O and briefly discuss its derivation. Figure B1 shows the diagrams of the reaction. The vertex functions and propagators are derived from the effective Lagrangian. We obtain the E2 transition amplitude of ¹²C(α,γ)¹⁶O as

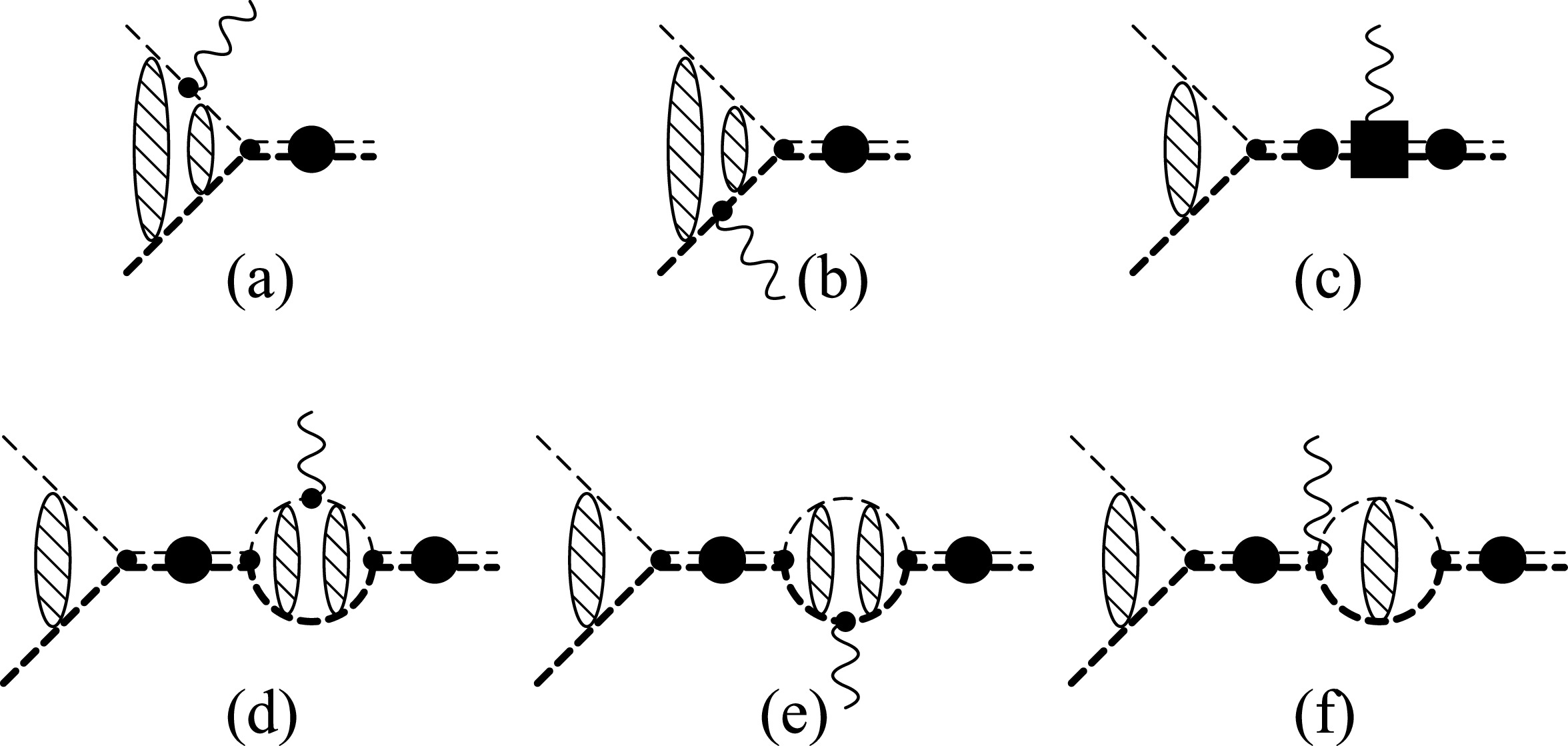
Figure B1.  Diagrams of amplitudes for radiative α capture on ¹²C. The wavy and thin (thick) dashed lines denote the outgoing photon and α (¹²C) state, respectively. The double thin-and-thick lines with a filled circle denote the dressed ¹⁶O propagators for the $ 2_1^+ $ state in the intermediate state and for the $ 0_1^+ $ state in the final state. Please, refer also to the caption in Fig. 1. The $ O\gamma O^* $vertex in diagram (c) is a counter term proportional to $ h_R^{(2)} $ to renormalize the infinities from loop diagrams in (d), (e), and (f).

where $ \vec{\epsilon}^*_{(\gamma)} $ is the polarization vector of the outgoing photon, $ \hat{k}' $ is the unit vector of the photon three-momentum, and $ \hat{p} $ is the unit vector of the relative momentum of the initial α-¹²C system. The amplitude $ X^{(l=2)} $ is decomposed as

where each amplitude corresponds to the diagrams depicted in Fig. B1. Thus, we have

where $ m_\alpha $, $ m_C $, and $ m_O $ ($ Z_\alpha $, $ Z_C $, and $ Z_O $) are the masses (numbers of protons) of α, ¹²C, and ¹⁶O, respectively; μ and κ are the reduced mass and the inverse of the Boer radius of the α-¹²C system; $ k' $and p are the magnitude of the three momentum of the outgoing photon and that of the relative momentum of the α-¹²C system in the center-of-mass frame; η is the Sommerfeld parameter, $ \eta = \kappa/p $; $ \gamma_0 $ is the binding momentum of the ground state of ¹⁶O, with $ \gamma_0 = \sqrt{2\mu B_0} $, where $ B_0 $ is the binding energy of the α-¹²C system in the ground state of ¹⁶O; and $ \eta_{0b} = \kappa/({\rm i}\gamma_0) $. $ \Gamma(z) $, $ j_l(x) $, $ F_l(\eta,\rho) $, and$ W_{\kappa,\mu}(z) $are the gamma, spherical Bessel, regular Coulomb, and Whittaker functions, respectively; $ \sigma_2 $ is the Coulomb phase shift for $ l=2 $.

The three loop diagrams of the $ O\gamma O^* $ vertex in Figs. B1(d), (e), and (f) diverge. The log divergence appears in the r-space integral at the $ r\to 0 $ limit in Eq. (52) for diagrams (d) and (e); we introduce a cutoff $ r_C $in the r-space integral and the infinite part is renormalized by the counter term $ h^{(2)} $ in Eq. (51). The divergence appearing in diagram (f) was regulated in the momentum space integral as $ J_0^{div} $ by means of dimensional regularization [49, 50]. Those infinities are renormalized by the renormalized coefficient $ h_R^{(2)} $ as

with

where we performed the integration in $ d=4-2\epsilon $ dimensions, $ \mu_{RD} $ is the scale of dimensional regularization, and $ C_E $ is Euler's constant, $ C_E = 0.5771\cdots $; we set $ \mu_{DR} = \Lambda_H = 160 $ MeV. We found a minor cutoff $ r_C $dependence and set $ r_C = 0.01 $ fm. The E2 transition amplitudes up to this order have two additional parameters, $ h_R^{(2)} $ and $ y^{(0)} $, along with the effective range parameters, $ r_2 $, $ P_2 $, and $ Q_2 $, in the function of $ K_2(p) $.

The total cross-section is expressed as

where $ E_\gamma' (=k') $ is the energy of the outgoing photon,

and the $ S_{E2} $ factor is defined as