STORI’24: In-ring nuclear reaction induced by light-ions at the HIRFL-CSR

Nuclear size measurements have a long history since the Geiger-Marsden alpha scattering experiment in 1908 [1]. Based on the experiment, atomic nucleus with a small size of $ \sim 10 ^{-15} $ m was discovered, consequently, the Rutherford atomic model was established in 1911 [2]. Since then, the open issue of how the nucleus is assembled by nucleons, namely protons and neutrons, continues attracting much attention.

Among nuclear fundamental properties, the root-mean-square (rms) proton distribution radii ($ R_p $) and neutron distribution radii ($ R_n $) characterize the spatial distribution sizes of protons and neutrons inside nuclei, respectively. They play an extremely important role in nuclear structure and astrophysics investigations. The global trend of nucleon radii is proportional to the cube root of mass number ${\rm{A}} ^{1/3} $, which reflects the saturation of nuclear force. Owing to the well-known electromagnetic interaction, the charge radii of about 1000 isotopes have already been measured with a high precision of around 0.01 fm [3]. With these precise radius data, for instance, the observed odd-even staggering and shape-staggering effects were applied to constrain microscopic theories [4, 5]. Combining with the proton distribution radii deduced from the measured charge radii, the neutron radii can be extracted from the measured matter (neutron+proton) radii ($ R_m $) via $ R_n = \sqrt{\dfrac{A}{N}R_m^2-\dfrac{Z}{N}R_p^2} $, where N, Z, and A are the neutron, proton, and mass numbers, respectively. However, the matter radius measurements are model-dependent and have relatively large uncertainties of around 0.05 fm due to the poorly known strong interaction [6].

Compared to the charge radii, as shown in Fig. 1, the experimental matter radius data are still scarce, and only about 200 isotopes were measured [7−11]. However, in recent decades, with the development of theories, different experimental methods, for instance, interaction cross sections [12], antiprotonic atoms [13], hadron scatterings [14], and parity-violation electron scatterings [15] are adopted to get insights into the physical quantities associated with nucleon spatial distributions in nuclei. The famous halo structure in weakly-bound nucleus $ ^{11} {\rm{Li}}$ was found through the abnormal deviation of the measured matter radii by the interaction cross section experiments [12]. The neutron radii also play an important role in searching new physics via atomic and particle physics experiments related to the weak interaction, e.g., the atomic parity violation [16] and the coherent elastic neutrino-nucleus scattering [17]. Additionally, the difference between the neutron and proton radii in nucleus, $ \Delta R_{np} = R_n-R_p $, known as neutron skin thickness, has also been widely employed to constrain the symmetry energy slope L at the saturation density [18]. Recently, the experimental neutron skin data for the stable Ca, Ni, Sn, and Pb isotopes were compiled, and the evaluated neutron skin values have a precision of around 0.02 fm [9]. With these evaluated data, separate trends of neutron skins versus relative neutron excess, $ \delta = (N-Z)/A $, were observed for the Ca, Ni, Sn, and Pb isotopic chains [9]. Moreover, the CREX-PREX neutron skin puzzle [19, 20], that is to say, the discrepancy between the parity-violation electron scattering measurements [15, 21] with other experimental results, may also indicate new physics, more details see Refs. [19, 20].

Figure 1.  (color online) Upper: The nuclides with experimental charge radius data are indicated by the filled blue squares. Lower: The filled red squares show the nuclides whose matter radii have been determined by experiments. The charge radius data can be found in Ref. [3]. See Refs. [7−11] for the matter radius data.

It is well known that proton probe not only interacts with protons in nucleus, but also interacts with neutrons inside nucleus. With the development of ion accelerators, the wavelength of high-energy proton probe can be comparable with the spatial distributions of nucleons in nucleus. Therefore, proton-nucleus elastic scattering is widely used to determine the matter radii of nuclei [14, 17, 22− 29]. In particular, compared to other methods, proton-nucleus elastic scattering is also sensitive to the matter density distribution profile [22, 27, 28]. For example, the nucleon rearrangements for the magic number $ ^{56} {\rm{Ni}}$- and $ ^{90} {\rm{Zr}}$-cores were found recently through the matter density distribution differences obtained by the proton-nucleus elastic scattering experiments [27, 28]. Additionally, matter density profiles are also sensitive to cluster structures in nuclei [30]. Considering $ ^{20} {\rm{Ne}}$ with the α+$ ^{16} {\rm{O}}$ configuration, the resulting theoretical matter density diffuseness parameter a of 0.585 fm [30] agrees with a measured result of 0.592(30) fm from the proton-$ ^{20} {\rm{Ne}}$ elastic scattering experiment [31].

We note that, most of proton-nucleus elastic scattering experiments have been performed in normal kinematics based on solid target [25, 29], which are limited to the stable or very long-lived nuclides. Furthermore, based on the thick solid-target method, it is also challenging to precisely measure the low momentum transfer scattering, because the ejectiles from multiple scattering would have different orbits and large energy losses. As known, compared to the inelastic scattering, the small-angle differential cross sections of proton-nucleus elastic scattering in the center-of-mass (c.m.) frame resulted by the low momentum transfer are relatively high in general. Therefore, the low momentum transfer measurements would be helpful to reduce the effects of inelastic scatterings associated with low excitation energies [17]. In addition, the low momentum transfer elastic scatterings are from the peripheral collisions, and the reaction mechanism is relatively simple compared to the large-angle scatterings [29, 32]. For example, the effects of spin-orbit term can be neglected for the description of small-angle differential cross sections of proton-nucleus elastic scattering, therefore, the matter radius extractions using the Glauber multiple-scattering model can be performed with less parameters [29, 32]. As a result, the radius uncertainties caused by the input parameters would be smaller.} Therefore, novel experimental methods based on active gas target and internal gas-jet target are developed to determine the matter radii by measuring the small-angle differential cross sections of proton-nucleus elastic scattering at low momentum transfer [22, 23, 32]. Such kinds of experiments are performed in inverse kinematics, they are suitable for the matter radius studies of gaseous and chemically active isotopes owing to avoiding the difficulty of producing targets, as shown by our in-ring $ ^{78}{\rm{Kr}} $ and $ ^{133} {\rm{Cs}}$ experiments [17, 23].

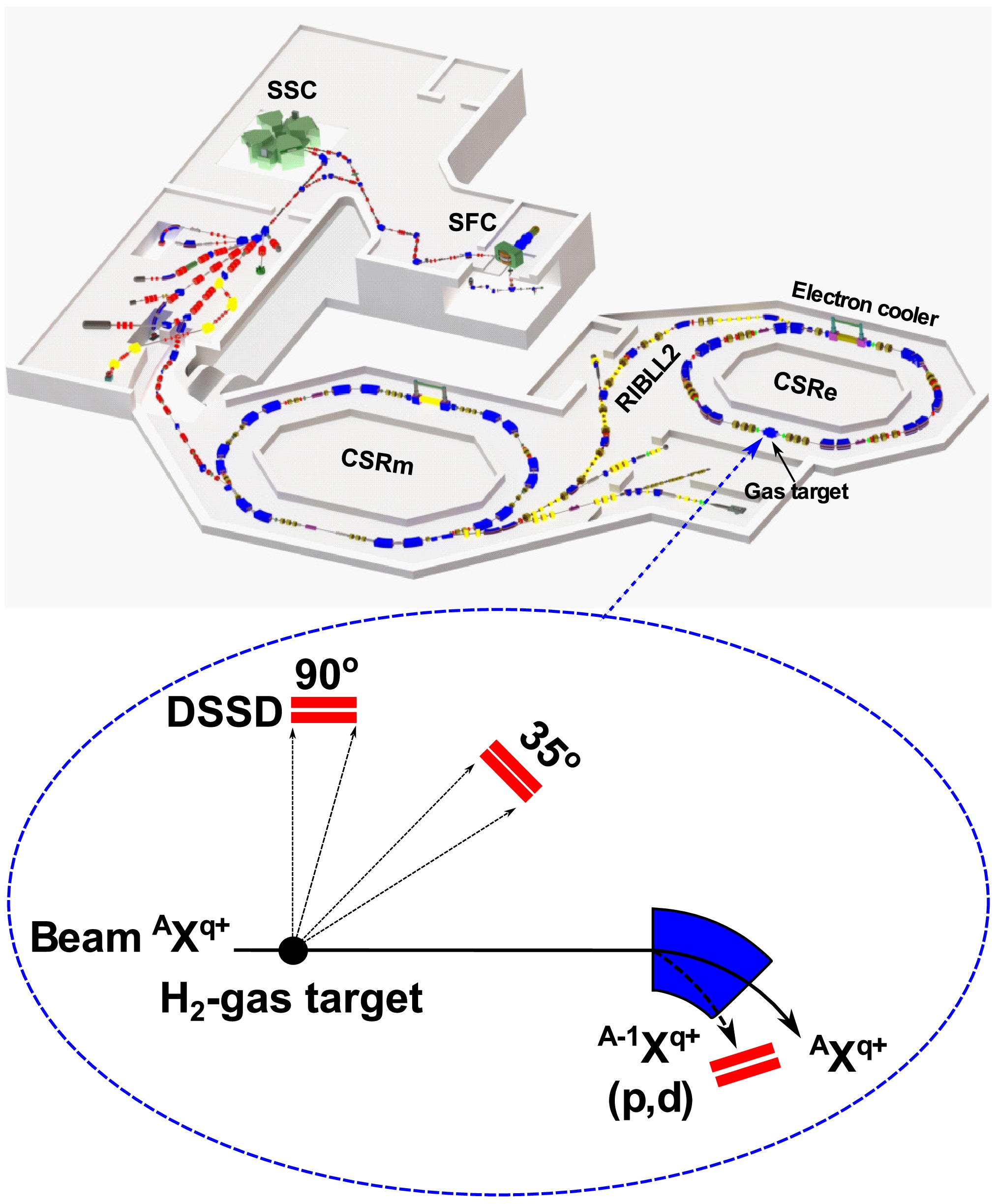
The EXL cooperation group as a pioneer has already shown that various nuclear reactions induced by light ions, e.g., elastic scattering [22], inelastic scattering [33], and transfer reaction [34, 35], can be effectively addressed by the in-ring experimental method based on the internal gas-jet target. The storage ring nuclear physics group at the Institute of Modern Physics (IMP) has started to develop the in-ring nuclear reaction techniques based on the Cooler Storage Ring at the Heavy Ion Research Facility in Lanzhou (HIRFL-CSR) since 2016 [36]. The HIRFL-CSR [37], as shown in Fig. 2, consists of the main storage ring (CSRm) and the experimental storage ring (CSRe). The two rings are connected by the radioactive beam line (RIBLL2). The primary beam with an energy of several MeV/u from the sector focusing cyclotron (SFC) can be accelerated to an energy of several hundred MeV/u by the CSRm. Secondary beam can be produced by the projectile fragmentation, and subsequently purified by the RIBLL2 through the $ B\rho $-$ \Delta E $-$ B\rho $ method. The primary or secondary beam is injected and stored in the CSRe for atomic and nuclear experiments. The CSRe is equipped with the electron cooler [38] and the internal gas-jet target facilities [39]. The momentum spread of stored ions can be reduced by the electron cooler [38]. Although it will take several seconds (depend on ions number and charge state) to reduce the momentum spread of stored ions, the in-ring nuclear reaction experiments can still cover many isotopes, see Fig. 3. In order to produce hydrogen-gas-jet target, the hydrogen gas at a few atmospheres is cooled to low temperature around 40 K by the internal gas-jet target facility. Subsequently, the cooled gas is expanded into the vacuum environment through a conical nozzle. As a result, the gas-jet beam is formed owing to the adiabatic expansion inside the nozzle. With the extraction of a set of skimmers, the produced hydrogen-gas-jet target in the collision region has a typical diameter of about 4 mm and a thickness of about $10 ^{12} $ atoms/cm². More details on the internal gas-jet target at the CSRe can be found in Ref. [39]. The stored ions interact repeatedly with the gas-jet target based on inverse kinematics in the CSRe. Various nuclear reactions, e.g., elastic scattering, inelastic scattering, and transfer reaction, are induced by the collisions with the protons in the hydrogen-gas-jet target.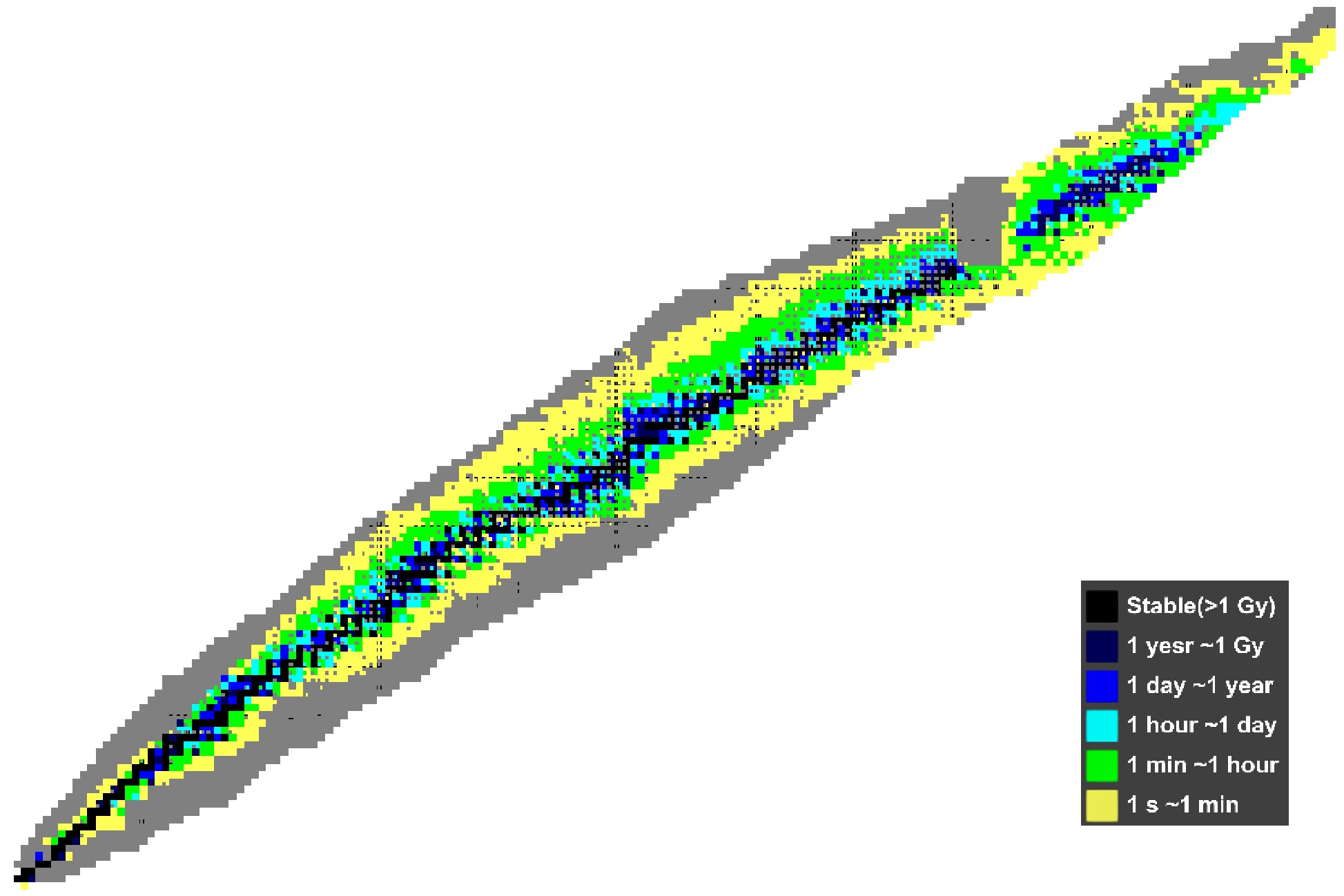

Figure 2.  (color online) The layout of HIRFL-CSR (upper) [37] and the schematic illustration of the detector system installed for the in-ring nuclear reaction experiments (lower) [36].

Figure 3.  (color online) The nuclei with half-lives greater than 1s in the nuclide chart, which generally can be measured by the in-ring nuclear reaction experiments. The figure is obtained by the software NucleusPlus [40].

For the proton-nucleus elastic scattering experiment performed in inverse kinematics (high-energy ions collide with proton target), as shown in Fig. 2, the elastic recoil protons from the low momentum transfer are measured by the Si-strip detector installed at around 90 degree in laboratory frame [36] to determine the small-angle differential cross sections in the center-of-mass frame. To measure the low energy protons, the Si-strip detector have to be installed in the CSRe ring. As a result, the adopted Si-strip detector needs to meet the requirements of ultra-high vacuum and high temperature conditions in storage ring. See Ref. [36] for more details on the development of ultra-high vacuum compatible Si-strip detector at the CSRe. The energy resolution for the used Si-strip detector after high-temperature degassing at about 150 °C is about 1% (FWHM), which was measured by a $ ^{241} {\rm{Am}}$ alpha source. In addition, the measured relative detection efficiencies are consistent in the energy range from about 0.5 to 5.5 MeV [23].

As shown in Fig. 3 in Ref. [39], the available flanges of the CSRe gas-target chamber at forward angle are at around 35 degree. We can also mount the Si-strip detector at the flanges to measure the small-angle inelastic scattering protons in the center-of-mass frame, see Fig. 2. Note that, in order to measure the small-angle inelastic scattering protons in this angular region, the beam energy need to be optimized according to reaction kinematics. With the measurements of inelastic scattering proton at small angles, the isovector giant dipole resonance (IVGDR) can be studied [41]. Moreover, this detector system also can be employed to measure the light recoil particles from the transfer reactions. Due to lack of decelerating facility at the CSRe, the secondary beam produced by the intermediate-high energy projectile fragmentation can not be decelerated to the low energy approaching the Gamow Window. However, the (low charged) primary beam with an energy of around 20 MeV/u from the CSRm can be injected and stored at the CSRe. Consequently, the low energy transfer reaction experiments associated with astrophysics can also be carried out for the stable and long-lived isotopes at least. As known, the trajectories of projectile-like products from the transfer reactions, e.g., (p, d) and (d, p), would be changed in the dipole magnetic field, because the mass numbers of projectile-like products are different from the stored ions. Therefore, the projectile-like products from the low energy transfer reactions can also be detected by the Si-strip detector installed behind the first dipole magnet at the CSRe, see Fig. 2. To determine absolute cross sections, the reaction luminosities for the inelastic scattering and transfer reaction can be determined through comparing the measured elastic scattering differential cross sections with the calculated results by the experimentally deduced global phenomenological optical model potentials [42].

Currently, the small-angle differential cross sections for proton-nucleus elastic scattering have been successfully measured to determine matter radii using the in-ring nuclear reaction facility at the HIRFL-CSR [17, 23, 24]. The Si-strip detector installed at around 90 degree in laboratory frame is used to measure the counts and energies of the elastic recoil protons from the low momentum transfer, see Fig. 2. The flight paths and energies of recoil protons are hardly altered by secondary collisions with the very thin gas-jet target, therefore, the differential cross sections of proton-nucleus elastic scattering can be precisely obtained by the measured proton counts and energies [17, 23]. Especially, the effects of thin target on the reaction luminosity can also be compensated by the high revolution frequencies of stored ions. Subsequently, the matter radii are extracted by fitting the measured small-angle differential cross sections with the Glauber model [43]. As known, the slope parameters β are one of important input quantities for the Glauber model fitting [32]. In order to reduce the model-dependent error, the energy-dependent slope parameters were calibrated through fitting the reported small-angle differential cross sections of proton-nucleus elastic scatterings at different energies to reproduce the determined matter radii by other experiments [44]. For more details on the experiments and data analyses for the in-ring radius measurements at the HIRFL-CSR, see Refs. [17, 23].

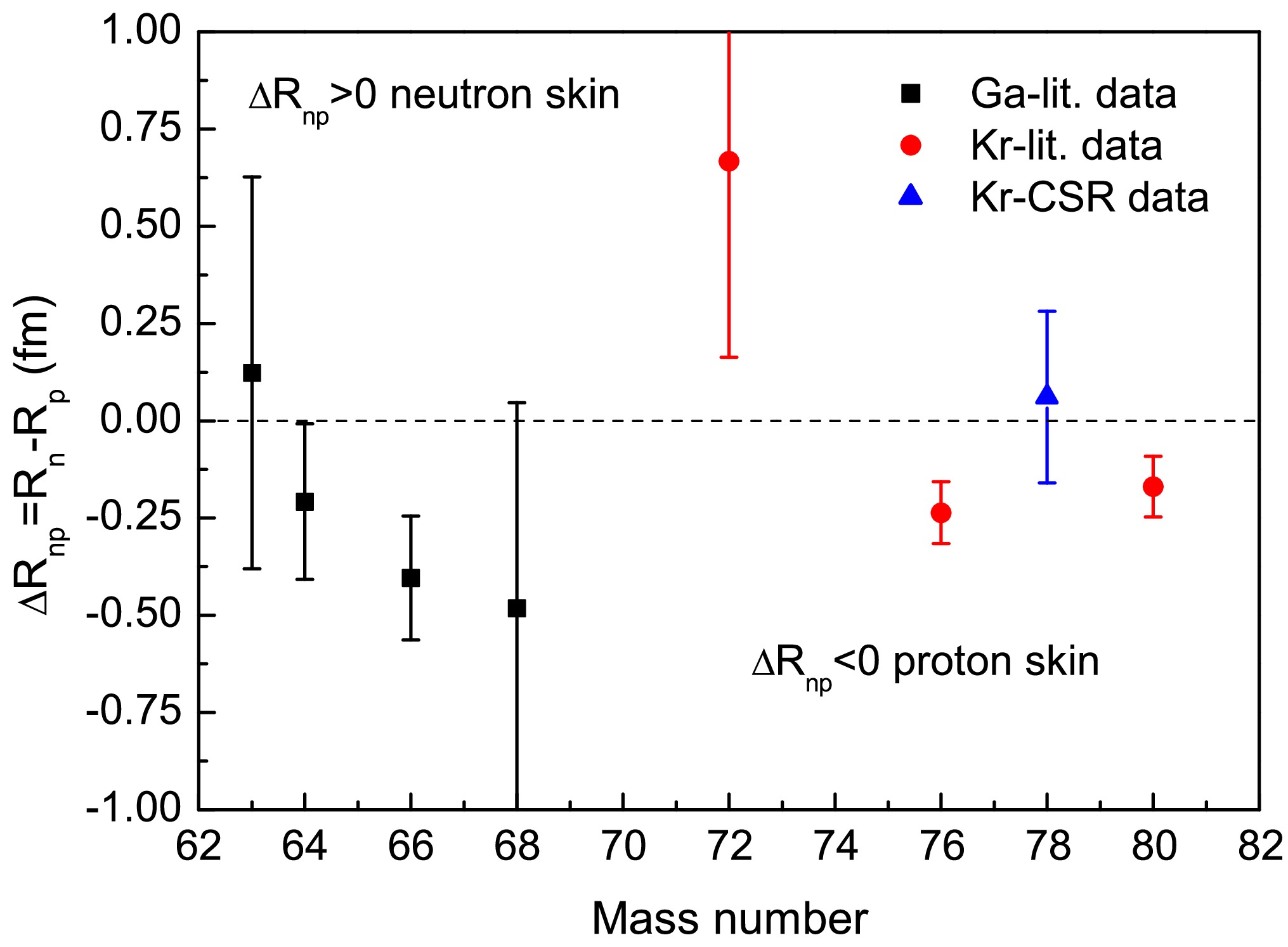
In the region of mass number around 70, the matter radii for the proton-rich Ga and Kr isotopes have been determined by the measured reaction cross sections and interaction cross sections [11, 45], respectively. Combining with proton distribution radii, the differences between neutron and proton radii can be extracted from the measured matter radii via $ \Delta R_{np} = \sqrt{\dfrac{A}{N}R_m^2-\dfrac{Z}{N}R_p^2}-R_p $. Obviously, as shown in Fig 4, the negative $ \Delta R_{np} $ values indicate that there are proton skin structures in this mass region. However, the proton skin structures in this mass region would result in a tension with other observables and methodologies. For example, as known, the linear relationship between the $ \Delta R_{np} $ value and the symmetry energy slope L at the saturation density can be established by the self-consistent mean-field models [46]. However, the proton skin structures with negative $ \Delta R_{np} $ values in this mass region can not be reproduced by the L values in the range of 30 MeV to 110 MeV, which are constrained by different observables and methodologies [47]. In order to address the possible proton skin structures, a different experimental method was adopted to measure the matter radius of $ ^{78} {\rm{Kr}}$ at the HIRFL-CSR. We measured the small-angle differential cross sections of proton-$ ^{78} {\rm{Kr}}$ elastic scattering} with a collision energy of 152.7 MeV/u using the in-ring nuclear reaction facility at the CSRe [23]. A rms point-matter radius of 4.16(12) fm for the $ ^{78} {\rm{Kr}}$ nucleus was obtained by fitting the measured small-angle differential cross sections with the Glauber model [23]. In the fitting procedure, the relative differential cross section analysis method [10] was employed to reduce the effects of reaction luminosity on the radius precision. The resulting $ \Delta R_{np} $ of 0.06(22) fm for $ ^{78} {\rm{Kr}}$ is consistent with a value of 0.03 fm predicted by the DD-ME2 interaction with a L value of 51 MeV, which is close to the world-averaged L value of 57 MeV obtained by different observables and methodologies [47]. Our results do not obviously indicate that there is a proton skin structure in $ ^{78} {\rm{Kr}}$.

Figure 4.  (color online) The difference between neutron and proton radii, $ \Delta R_{np}$, for the Ga and Kr isotopes in the region with mass number around 70. The literature data for matter radii are taken from Refs. [11, 45].

Besides nuclear structure, the $ \Delta R_{np} $ data also find their applications in atomic and particle physics. The measurements of atomic parity violation for $ ^{133} {\rm{Cs}}$ have been carried out precisely [48]. As known, the parity violation in atom is dominated by the Z-boson exchange between atomic electrons and neutrons [49]. However, the reference many-body Coulomb-correlated amplitude for the parity-nonconserving (PNC) is usually determined using the proton distribution in nucleus [49]. Therefore, the effects of neutron-proton radius difference on the parity-nonconserving amplitude, $ \frac{\delta E^{n.s.}_{PNC}}{E_{PNC}} $, need to be considered via [49]

where α is the fine-structure constant.

Due to the low melting point of 28 degrees Celsius and spontaneous ignition in air, the neutron radius of $ ^{133} {\rm{Cs}}$ is still not precisely measured. Based on the observed coherent elastic neutrino-nucleus scattering by the CsI[Na] detector [50], the extracted neutron radius values for $ ^{133} {\rm{Cs}}$ have a large spread, which depends on the adopted data analysis methods, more details see Ref. [17] and references cited therein. Recently, the point-neutron radius of $ ^{133} {\rm{Cs}}$ was also determined to be 4.86(21) fm by measuring the proton-$ ^{133} {\rm{Cs}}$ elastic scattering at low momentum transfer at the CSRe [17]. With our neutron radius, the weak mixing angle sin$ ^2 \theta_W $ was independently extracted to be 0.227(28) by fitting the coherent elastic neutrino-nucleus scattering data [17]. Combining with the proton distribution radius, a $ \Delta R_{np} $ value of 0.12(21) fm for $ ^{133} {\rm{Cs}}$ was obtained, which is consistent with the calculated value of 0.13(4) fm by the empirical linear relationship from the antiprotonic atom experiment [13]. In the present work, we address the impact of our $ \Delta R_{np} $ result for $ ^{133} {\rm{Cs}}$ on the parity-nonconserving amplitude correction. As known, the extracted folded-neutron radius values of $ ^{133} {\rm{Cs}}$ from the coherent elastic neutrino-nucleus scattering experiments [50] spread from 4.6 fm through 6.6 fm [17]. These neutron radii associated with different $ \Delta R_{np} $ values would result in different parity-nonconserving amplitude corrections with a standard deviation of 0.006, see the histogram in Fig. 5. With our $ \Delta R_{np} $ value of $ ^{133} {\rm{Cs}}$, the neutron skin correction on the parity-nonconserving amplitude is determined to be -0.0017(30). Obviously, the correction precision is improved by our $ \Delta R_{np} $ data, as shown in Fig. 5.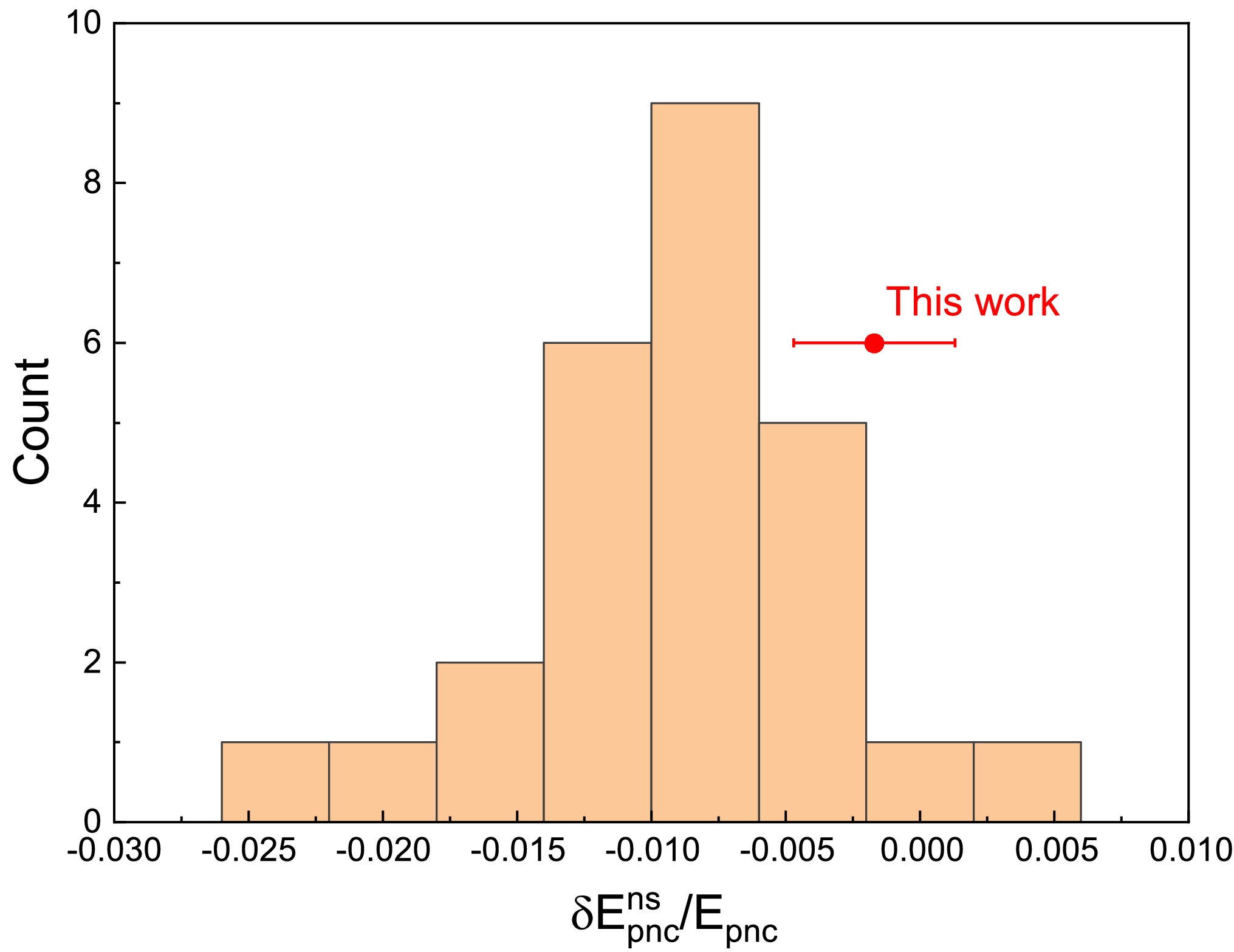

Figure 5.  (color online) The neutron skin correction for the parity-nonconserving amplitude. The histogram was obtained using different neutron radii, which were extracted from the coherent elastic neutrino-nucleus scattering data, details can be found in Ref. [17] and references cited therein.

Direct reactions at low momentum transfer induced by light ions provide important information for studying nuclear structure and astrophysics. Recently, a novel in-ring nuclear reaction technique based on the stored beam and the internal gas-jet target has attracted much interest. This method is characterized by the low-momentum sensitivity and low background. As one of the existing facilities, the HIRFL-CSR is equipped with the electron cooler and the internal gas-jet target, also provides an opportunity to perform such kinds of experiments based on inverse kinematics. In this proceeding, we present the progress of in-ring nuclear reaction investigations at the HIRFL-CSR. Especially, the recent matter radius determinations for $ ^{78} {\rm{Kr}}$ and $ ^{133} {\rm{Cs}}$ and their impacts on the skin structure and the parity-nonconserving amplitude correction were also discussed. In the near future, the one-day experiment for the (p, p') inelastic scattering at the CSRe will be performed.