Moments from momentum derivatives in lattice QCD

In high-energy scattering, the structure of hadrons is characterized by quantities such as parton distribution functions (PDFs), which describe the momentum distributions of quark and gluon partons inside a hadron. Although these functions are essential for interpreting experimental data in hadron-hadron or lepton-hadron collisions, calculating them from first principles has been challenging because of their intrinsic nonperturbative nature and the fact that their definition involves lightcone correlations.

Phenomenologically, PDFs are determined through global fits to a wide range of experimental data from high-energy collisions. As different fitting groups may choose different data sets and PDF parametrizations, such global fits can lead to ambiguities in the extracted PDFs, especially in certain kinematic regions where experimental data are sparse. On the other hand, lattice quantum chromodynamics (QCD) offers a reliable first-principles approach that can provide important complementary information about PDFs. Traditionally, PDFs are accessed indirectly on the lattice through operator product expansion (OPE), where lightcone correlators are expanded in terms of local operator matrix elements that define the Mellin moments of PDFs. Although these moments can be computed on the lattice, only the first few orders are obtainable because of the potential power-divergent operator mixings at higher orders. Nevertheless, considerable efforts have been made to calculate the Mellin moments, and the results have had a valuable impact on phenomenological analyses (see, e.g., Ref. [1] for a recent review). A notable example is the global analysis of the quark transversity PDF in the nucleon [2], which incorporates the lattice result on the isovector tensor charge $ g_T $ with experimental data from semi-inclusive deep-inelastic scattering. The inclusion of the former has significantly reduced the uncertainty bands of the fit.

In addition to calculating moments, recent theoretical developments [3−10] have enabled the direct calculations of the Bjorken-x dependence of PDFs from the lattice. A commonly used quantity in these approaches is the equal-time Euclidean correlation function, which can be linked to PDFs either through a short distance factorization in coordinate space [8] or through a large momentum factorization in momentum space [6, 7, 11], where the latter has been formulated as the large-momentum effective theory (LaMET) [7, 11]. The LaMET approach has shown promise in determining the Bjorken-x dependence of PDFs in the moderate x region, whereas the prediction is not reliable in the small and large x regions because power-suppressed higher-twist contributions become important there and must be considered. As a result, it is difficult to obtain moments in a reliable manner from the integration of extracted PDFs over the momentum fraction x. In contrast, the short distance factorization approach relies on a global fit of moments to lattice matrix elements [12−14], which often used correlations at large distances where factorization is expected to fail. Furthermore, such a global fit suffers from similar ambiguities as those encountered in phenomenological fits to experimental data.

In this study, we show that, by leveraging recent theoretical developments, the traditional moments approach based on OPE can be realized such that it utilizes the difference in momenta instead of distances. This also avoids power divergent mixings, and thus allows to extract moments order by order, to all orders in principle. Moreover, by exploiting the symmetry of lattice matrix elements, we can determine the even and odd moments separately. This approach avoids using long distance correlations and focuses on relatively small momenta. As a result, it significantly reduces the computational cost of higher-order moments on the lattice, which greatly facilitates the reconstruction of PDFs across the full kinematic range from their Mellin moments and complementing ongoing efforts to extract PDFs from LaMET.

We briefly review the traditional approach for calculating moments on the lattice by taking the transversity structure function as an example. The local operators from OPE that measure the $ (n-1) $-th moments $ \left<x^{n-1}\right> $ take the form

where an antisymmetrization between $ \mu_1 $ and $ \perp $ indices is assumed, and the bracket indicates that the enclosed indices are symmetric and traceless. $ \psi, \bar\psi $ denote the quark fields, and the covariant derivative

is realized on the lattice as

where $ U_\mu(x) $ represents the link variable joining points x and $ x+a\hat\mu $ with $ \hat\mu $ being a unit vector.

Although the operators in Eq. (1) belong to irreducible representations of the Lorentz group in the continuum, they are reducible on the lattice and become linear combinations of irreducible representations of the hypercubic group, and therefore, they lead to operator mixings. For higher dimensional operators, the mixing coefficient can be power divergent, making the calculation of moments beyond the first few orders very challenging [15].

In this section, we outline our proposal in which we use the difference in momenta rather than distances as a leverage to extract moments at a given order. The discussion below is based on the so-called quasi-light-front (quasi-LF) correlations, which are equal-time nonlocal quark and gluon bilinear operator matrix elements used in LaMET and short distance factorization. However, the same strategy can be applied to other correlations used, e.g., in current-current correlations [4] and lattice cross sections [9], provided that a similar factorization formula exists. In the following, we take the isovector quark transversity PDF as an example. The discussion can be readily extended to other nonsinglet quark PDFs, as well as singlet quark and gluon PDFs, with minor modifications.

We consider the following quasi-LF correlation

where $ \psi, \bar\psi $ represent quark fields, $ W(z,0) = {\cal P}\exp [-{\rm i}\, g\int_0^z {\rm d}u\, n\cdot A(u n)] $ represents the gauge link along the z direction with $ n^\mu = (0,0,0,1) $, $ |PS_\perp\rangle $ represents an external hadron state with momentum $ P^\mu = (P^t,0,0,P^z) $ and transverse polarization $ S_\perp $, and $ \lambda = z P^z $ is the so-called quasi-LF distance. $ N = 1/(2P^t) $ is a normalization factor. The nonlocal quark bilinear operator defining $ \tilde h $ has been shown to renormalize multiplicatively [16−18]. Therefore, $ \tilde h $ can be nonperturbatively renormalized by dividing by the same correlation in a zero-momentum hadron state

which is known as the ratio scheme [8]. As long as z is within the perturbative region, this is a legitimate renormalization scheme, and it has been used in many lattice calculations of PDFs. For recent examples, see, e.g., [19−23]. The renormalized quasi-LF correlation at small z can then be factorized into the LF correlation defining the leading-twist PDF, denoted as h, as [8, 24−26]

where μ represents the renormalization scale in the $ \overline{\rm{MS}} $ scheme, and $\rm p.c. $ represents power corrections. Using OPE, the above equation can be turned into an equation for the moments of PDFs [25, 27]

where

are the $ (n-1) $-th moments of the isovector quark transversity PDF $ \delta q(x,\mu) $ and perturbative matching kernel $ C(u, z^2\mu^2) $, respectively; $ g_T = \int_{-1}^1 {\rm d}x\,\delta q(x,\mu) $ represents the the tensor charge, and $ C^{(0)} = 1 $. The power correction $ {\rm p.c.} $ in Eq. (7) consists of target mass corrections and genuine higher-twist contributions. Both have less powers in $ P^z $ than the leading term as they arise from trace terms. Although the leading target mass corrections have been calculated to all orders for unpolarized, helicity, and transversity quark PDFs in Ref. [28], genuine higher-twist contributions can be kept small by requiring $ z^2\Lambda_{\rm{QCD}}^2\ll 1 $.

Our proposal is based on the observation of different momentum dependencies in moments of different orders, as well as in the leading and subleading power terms in the expansion above. Furthermore, the symmetry of real and imaginary parts of the quasi-LF correlation $ \tilde h_R $ provides a practical advantage that considerably simplifies the calculation.

To show how to extract the moments order by order, we separate the real and imaginary parts of $ \tilde h_R $ as

They are even and odd functions of $ P^z $, respectively. Therefore, we can define a new variable $ \zeta = (P^z)^2 $. Then, the even and odd moments are given by the following derivatives w.r.t. ζ at a fixed z

where $ {\rm p.c.} $ denotes $ {\cal O}(z^2M^2, z^2\Lambda_{\rm{QCD}}^2) $ corrections that can be kept small by keeping the distance $ z\ll 1/\Lambda_{\rm{QCD}} $. In addition, these power corrections will be further suppressed by extra combinatorial factors at each order, and therefore, they will only have a minor impact on the extraction of the moments at a given order. One great advantage of using Eq. (10) is that by using symmetry of the renormalized matrix elements and defining the new variable ζ, the even and odd moments can be determined separately, and therefore, it is considerably easier to go to higher orders.

Following the same spirit, the even moments can be extracted with a reduced number of derivatives:

where $ k\geq0 $. A special case is the extraction of the second moment, which is free from taking derivatives:

We use the combination $ \text{Re}\tilde{h}_{R}-1 $ in (11) to subtract the mass corrections of $ {\cal{O}}({\zeta^0}) $ in $ \text{Re}\tilde{h}_{R} $ following Ref. [28] so that $ d\dfrac{\text{Re}\tilde{h}_{R}-1}{\zeta}/d^{k}\zeta $ is regular at $ \zeta = 0 $.

Using the approach above, we extract the first three moments beyond $ g_T $ of the isovector quark transversity PDF in the nucleon based on the renormalized matrix elements at a single lattice spacing $ a = 0.094 $ fm with a pion mass 358 MeV and various momenta in Ref. [19]. All moments presented here have been normalized by $ g_T $. The next-to-leading order Wilson coefficients needed in Eq. (9) have also been given in Ref. [19] as

where $ \alpha_s $ represents the strong coupling constant and $ \gamma_E $ represents the Euler constant.

In our approach, the derivatives of lattice matrix elements are taken w.r.t. the momentum square ζ. Data at different perturbative distances z can be combined together to determine moments at a given order. This is also the strategy we adopt here due to the limited data quality. Taking the extraction of $ \langle x^{2}\rangle/g_{T} $ as an example, we start from the following formula based on OPE:

where we have truncated the expansion up to terms of $ O(\lambda^4) $ in the leading-twist OPE and included leading higher-twist contributions as well. $ C^{(n)} $s are defined by Eq. (8), and their dependence on $ \mu^{2}z^{2} $ is not shown for simplicity. To extract $ \langle x^{2}\rangle/g_{T} $, an extrapolation to $ \lambda = 0 $ (or equivalently, to $ P_z = 0 $) needs to be carried out, similar to the continuum extrapolation to $ a = 0 $. We have tested that including higher-order terms in Eq. (14) only has a minor impact on the fitting result. Besides $ \langle x^{2}\rangle/g_{T} $, $ b,c,d,e $ in the above equation are also free fitting parameters depending on the scale μ, whose variation provides an important source of systematic errors. For extractions of $ \langle x^{1}\rangle/g_{T} $ and $ \langle x^{3}\rangle/g_{T} $, we use formulas similar to Eq. (14), including the first three (two) terms at the twist-2 (twist-4) level.

We have selected lattice data at $ z = 2a ,3a $ for our analysis, as $ z = a $ data suffer from discretization effects while $ z\ge4a $ is too large so that the validity of factorization in Eq. (6) becomes questionable [29]. We take the difference between including $ z = a $ data or not as part of our systematic uncertainties. Our results are shown in Fig. 1 with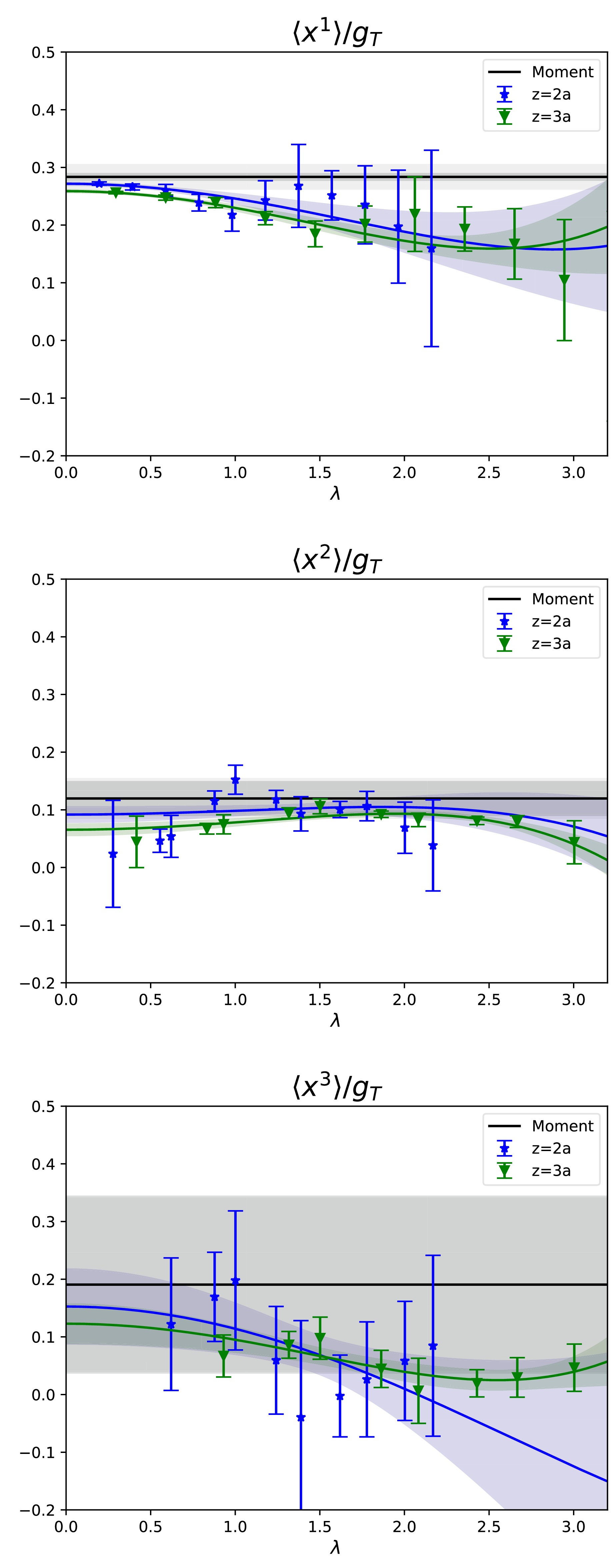

Figure 1.  (color online) First three moments beyond the tensor charge $g_T$ of the isovector quark transversity PDF in the nucleon. All results are normalized by $g_T$. The renormalization scale is $\mu=\sqrt 2$ GeV. The blue stars and green inverted triangles represent the raw data for joint fit lines of $z=2a$ and $z=3a$, respectively, while the black line and gray band show the results of $\langle x^n\rangle/g_T$.

where the renormalization scale has been selected as $ \mu = \sqrt 2 $ GeV, and the numbers in the two parentheses represent statistical and systematic errors, respectively. The sources of systematic errors are composed of two parts: 1) Inclusion of data at $ z = a $: The lattice data at $ z = a $ have large discretization errors. We consider the difference in our results with and without including these data as part of our systematic uncertainties. 2) Perturbative running: We change the renormalization scale to $ \mu = 2 $ GeV and include the difference in the results as systematic uncertainties. This scale dependence reflects the impact of missing higher-order perturbative corrections. Our final results for $ \langle x^1\rangle $ and $ \langle x^2\rangle $ are slightly larger; however, they are still consistent within $ 1\sim 2 \sigma $ with those extracted in Ref. [19] through global fits. In Ref. [19], the transversity PDF was fitted (at $ \mu = \sqrt{2} $ GeV) based on the OPE of $ \tilde{h}_{R} $ using lattice data ranging from from $ z = 0.188 $ fm to $ z = 0.94 $ fm. Then, the first and second moments beyond $ g_T $ were obtained through the fitted transversity PDF. This yields slightly different numbers and the appearance of smaller uncertainties in their results. However, when $ z\gtrsim 0.2 $ fm, the errors of Wilson coefficients become large under scale variation, and the OPE cannot be trusted when $ z\gtrsim 0.4 $ fm. Our $ \langle x^3\rangle $ has relatively large errors because of the limited data points and quality, which can be improved in future by increasing statistics and collecting more data points at small momenta. Note that our approach does not require using lattice data at large distances, as done in [12−14, 19], and our results do not suffer from ambiguities of global fits.

In contrast to the traditional moments approach, our method offers several advantages. First, by leveraging the multiplicative renormalizability of equal-time nonlocal bilinear operators, the potential power divergent mixing between higher- and lower-order moments operators is avoided. Second, the usual differentiation w.r.t. distance is replaced by a differentiation w.r.t. momentum, which is computationally much cheaper. Third, by using the symmetry of the lattice matrix elements, the even and odd moments can be computed separately, making it considerably easier to go to higher orders. Fourth, there is no need to use long distance correlations where factorization is expected to fail, and the determination of higher-order moments is independent of the lower-order ones.

To facilitate lattice calculations using the presented method, we need lattices with a large box size L so that the step in momentum $ \Delta P = 2\pi/L $ is small, and we can focus on the small λ region ($ \lambda\lesssim1 $). We can reliably take the derivatives and extrapolate to zero momentum, whereas a small lattice spacing is less important. In practical calculations, we can combine matrix elements at different perturbative distances to determine moments at a given order.

In the discussion above, we focused on quasi-LF correlators employed in LaMET and short-distance factorization. However, the methodology we outlined can be applied to other types of nonlocal correlators such as current-current correlations and lattice cross sections, where a factorization similar to Eq. (6) holds. These nonlocal correlators form a universality class of operators, whose matrix elements can be combined together to compute the same moments effectively.

In conclusion, we showed that the traditional moments approach based on OPE can be realized such that it utilizes derivatives w.r.t. momentum rather than distance. This is computationally much cheaper and avoids power divergent mixings, enabling moments calculations to be performed order by order, to all orders in principle. Taking the isovector quark transversity PDF of the nucleon as an example, we illustrated how its first three moments beyond $ g_T $ can be computed through differentiating renormalized quasi-LF correlations w.r.t. the momentum square. Furthermore, we showed how the real and imaginary parts of the correlations can be used to separately extract even and odd moments. We also outlined the main advantages and requirements for the lattice setup in our proposal. It will be intriguing to explore the extent to which we can extend the computation of moments to higher orders using the proposed approach. The results will provide valuable complementary insights into the partonic structure of hadrons along with other approaches.

After this paper was submitted, we noticed that similar strategies (taking differentiation of $ \tilde{h}_R $ w.r.t. λ) were also discussed in Ref. [30], whereas our proposal to take differentiation w.r.t. $ \zeta = (P^z)^2 $ rather than $ \lambda = z P^z $ enabled faster convergence in the extrapolation to zero momentum and more efficient determination of higher moments. Moreover, the authors of Ref. [30] discussed extracted moments as a function of $ z^2 $, ranging from $ z = a $ to nonperturbative z. In contrast, we only used data points at $ z = 2a $ and $ z = 3a $for our joint fit, which avoids heavy contaminations from discretization errors and higher-twist effects. We leave a more detailed analysis (with resummed Wilson coefficients) using data points generated by lattices with a larger box size to future work. Further, we discussed the universality class of operators in our paper.

We are grateful to Jiunn-Wei Chen for valuable discussions at the early stage of this project. We also thank Joe Karpie for sharing their lattice data with us, and Huey-Wen Lin and Yi-Bo Yang for helpful discussions.