-
The elastic scattering process has been widely used to investigate nuclear surface properties and halo structures in light nuclei [1]. Experimental and theoretical researches have revealed that strong coupling effects can profoundly influence the elastic scattering angular distributions, which provide an effective tool to probe the specific nuclear structure properties of a projectile or target [2−4]. Although such effects have been observed for stable nuclei [5, 6], they are considerably more striking in the elastic scattering reactions induced by proton or neutron rich radioactive projectiles [7, 8]. Furthermore, high-precision heavy ion elastic scattering measurements can provide reliable information on the optical potential (OP) of the interaction [9].
Reactions induced by carbon isotopes have been studied both experimentally and theoretically to understand the evolution of the nuclear structure near the drip line. For instance, data on the elastic scattering of the proton-rich
$ ^{9} $ C isotope on a lead target at three times the Coulomb barrier has been reported in Ref. [10]. The data were analyzed with continuum-discretized coupled-channels (CDCC), assuming that$ ^{9} $ C can have both$ ^{7} $ Be+2p and$ ^{8} $ B+p cluster structures. Assuming both configurations, the calculated results reproduced the data well, indicating that elastic scattering at such high incident energies is not sensitive to the single-particle structure of light proton-rich nuclei. Another carbon proton-rich isotope,$ ^{10} $ C, is considered to have a Brunnian (super-borromean) structure given by a four-body α+α+$ p+p $ configuration [11]. Removing any of the particles will leave the remaining nuclei,$ ^{9} $ B,$ ^{6} $ Be,$ ^{8} $ Be, and$ ^{5} $ Li, unbound. The full angular distributions for the elastic scattering of$ ^{10} $ C+$ ^{58} $ Ni [12] and$ ^{10} $ C+$ ^{208} $ Pb [13] have been measured at energies close to the Coulomb barrier. Although the couplings to the continuum, analyzed via CDCC calculations, were not relevant, the cluster configurations for$ ^{10} $ C,$ ^{9} $ B+p, and$ ^{6} $ Be +α were important in the description of the data. These results show that elastic scattering can be a useful tool in investigating target-projectile effects on the nuclear reaction mechanism at energies close to the barriers. Elastic scattering measurements for$ ^{10,11} $ C+$ ^{208} $ Pb systems were performed at three times the Coulomb barriers at the Radioactive Ion Beam Line in Lanzhou (RIBLL) [14]. The data were effectively reproduced by optical model (OM) calculations with systematic nucleus-nucleus potentials. Moreover, the contribution from the inelastic scattering channels owing to the excitation of$ ^{11} $ C was found to be negligible via coupled-channel (CC) calculations. Because a$ ^{11} $ C projectile is as tightly-bound as that of$ ^{12} $ C, where$ S_{\alpha} $ =7.544 MeV and$ S_{\alpha} $ =7.367 MeV, respectively, CDCC calculations were not performed.For the neutron-rich side of the carbon isotopes chain,
$ ^{13,14,15} $ C, several elastic scattering experiments have previously been performed on heavy targets. To date, there is only one elastic scattering measurement of$ ^{13} $ C on a heavy$ ^{208} $ Pb target performed at 30 MeV/A [15]. They used a simplified Glauber approach, with a$ ^{12} $ C density to analyze the data with good results. A$ ^{14} $ C projectile is a strongly-bound nucleus ($ S_n $ =8.177 MeV). Interestingly, it is found to be associated with the possibility of the extra valence neutrons acting as covalent bonds to stabilize the α-chain [16]. Elastic scattering angular distribution data of$ ^{14} $ C on medium- to heavy-mass targets have been reported [17, 18]. OM and distorted wave Born approximation (DWBA) analyses using collective model form factors provided good fits to most of the scattering and one- and two-neutron stripping reaction data. For$ ^{15} $ C, the scattering dynamics at energies around the Coulomb barrier were first studied on a$ ^{208} $ Pb target at 65 MeV [19]. The data revealed a strong long-range absorption pattern in the elastic scattering angular distribution. The total interaction cross-section of$ ^{15} $ C was found to be approximately 30% larger than that of$ ^{14} $ C. Combining the large cross section with the fact that$ ^{15} $ C is described as$ ^{14} $ C plus a “pure” 2s$ _{1/2} $ single-neutron can be a clear indication of a halo configuration for this nucleus. Keeley and Alamanos performed coupled-reaction channel (CRC) calculations on the$ ^{15} $ C+$ ^{208} $ Pb elastic scattering data at 54.07 MeV, and the results revealed a significant coupling effects due to the dominant 2s$ _{1/2} $ halo nature of the ground state [20].To complete the systematic analysis of elastic scattering measurements for carbon isotopes projectiles, we present new experimental data for
$ ^{13,14} $ C on$ ^{208} $ Pb at energies around five times the Coulomb barriers. This paper is organized as follows. In Sec. II, we describe the experimental procedure and detection setups used in the measurements. Then, the results of the experiment and theoretical analysis with OM and CDCC calculations are presented and discussed in Sec. III. Finally, the main conclusions of this study are summarized in Sec. IV. -
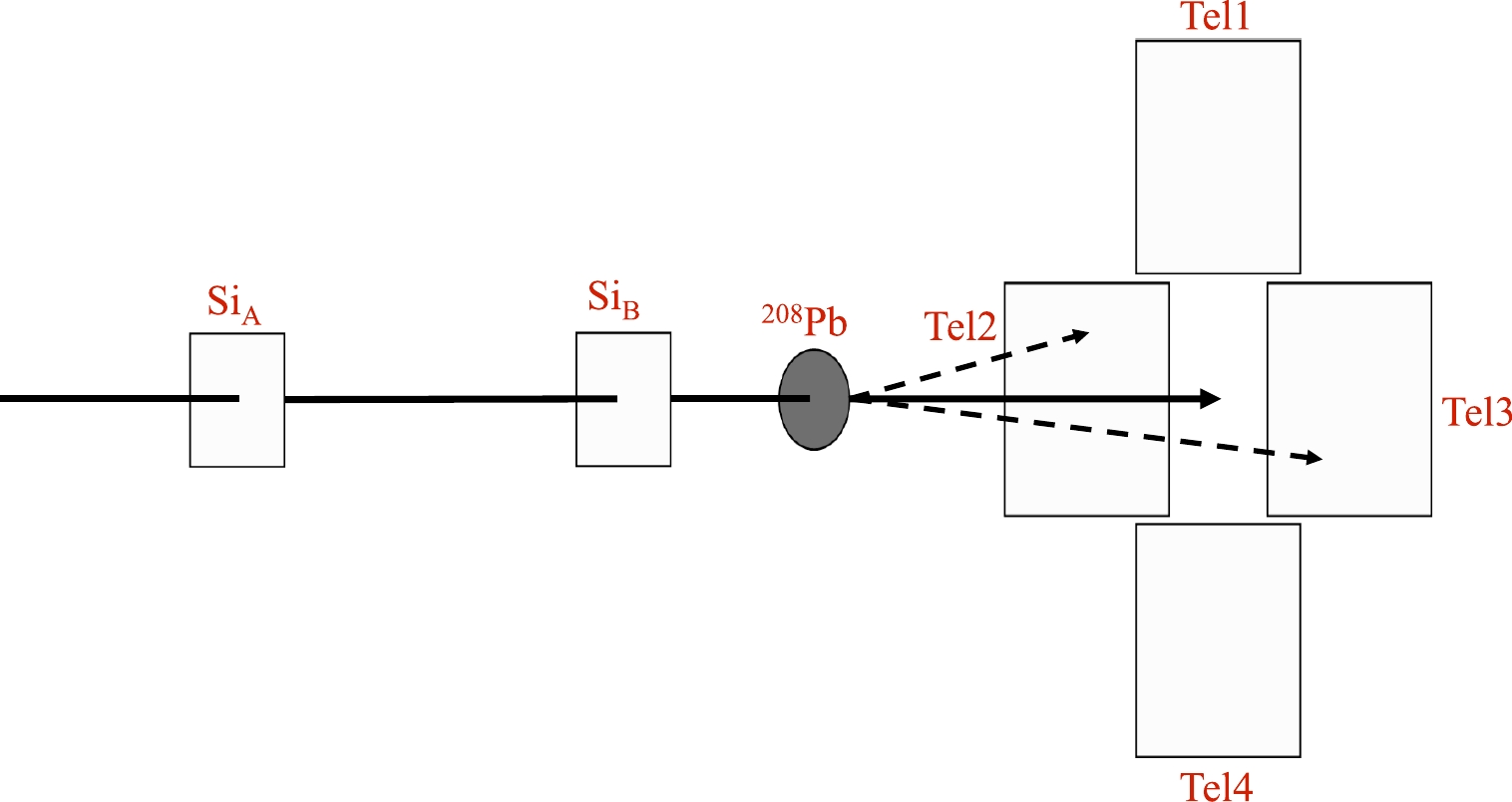
Measurements were performed at the National Laboratory of Heavy Ion Research of the Institute of Modern Physics. The radioactive beams of the carbon isotopes
$ ^{13,14} $ C were provided by the RIBLL facility [21, 22]. The secondary beams were produced using a primary$ ^{16} $ O beam at 59.5 MeV/u from the Heavy-Ion Research Facility in Lanzhou (HIRFL) [23, 24] impinged on a$ ^{9} $ Be target (2.0-mm-thick). The secondary beams of interest were selected and optimized by adjusting the magnetic rigidity. In addition, we used two double-sided silicon detectors (DSSDs), Si$ _{\rm A} $ and Si$ _{\rm B} $ , 87 μm and 65 μm thick, respectively, to provide the accurate location and orientation of the incident particles with respect to the target alignment. Both DSSDs have 16 junction and 16 ohmic strips, 3 mm wide. They were placed 669 mm and 69 mm upstream of the$ ^{208} $ Pb target. The thicknesses of the$ ^{208} $ Pb targets were 13.30 mg/cm$ ^2 $ for the$ ^{14} $ C beam at 294 MeV and 12.24 mg/cm$ ^2 $ for the$ ^{13} $ C beam at 340 MeV and the$ ^{14} $ C beam at 342 MeV. To detect the scattering particles, four$ {\Delta}E $ -$ \mathit{E} $ telescopes (Tel1, Tel2, Tel3, and Tel4) were installed 267 mm downstream of the target, covering an angular range from$ \sim $ 3° to$ \sim $ 27° in the laboratory reference. A schematic view of the detection setup is shown in Fig. 1. The telescopes Tel2 and Tel3 were symmetrical from left to right, covering an angular range of 3°$ \le \theta \le $ 21°, whereas Tel1 and Tel4 were symmetrical from top to bottom, covering an angular range of 12°$\le \theta \le $ 27°. The angular overlap could be used to cross-check the differential cross sections measured by these telescopes. The$ {\Delta}E $ detectors in each telescope have an active area of 64 mm×64 mm,$ \sim $ 150 μm thick, and with both the front and back sides segmented into 32 strips. The single-pad$ \mathit{E} $ detectors have the same active area but a thickness of$ \sim $ 1500 μm. A detailed description of the experimental setup is provided in Ref. [25].The scattering particles were identified and selected using the two-dimensional
$ {\Delta}E $ -$ \mathit{E} $ spectra obtained with the telescopes, as shown in Fig. 2, for$ ^{13} $ C+$ ^{208} $ Pb at 340 MeV (Fig. 2 (a)),$ ^{14} $ C+$ ^{208} $ Pb at 294 MeV (Fig. 2 (b)), and$ ^{14} $ C+$ ^{208} $ Pb at 342 MeV (Fig. 2 (c)). As clearly shown in the figures, the$ ^{13} $ C and$ ^{14} $ C scattering particles were well separated from the contaminants. Moreover, as shown in Fig. (Fig. 2 (b)), there was indication of the presence of$ ^{13} $ C particles (from breakup or transfer) near the$ ^{14} $ C scattering particles; however, they were not statistically sufficient for further analysis. -
The results of the elastic scattering angular distributions normalized to the Rutherford cross sections for
$ ^{13} $ C and$ ^{14} $ C on a$ ^{208} $ Pb target are shown in Fig. 3, where the error bars of the cross sections are statistical only. The elastic scattering angles were determined using the position and direction of the incident particles, provided by the Si$ _{\rm A} $ and Si$ _{\rm B} $ detectors, combined with the hit positions of the scattering particles in the Si-telescopes. Considering the broadening and non uniformity of the beam profile on the target, Monte Carlo simulation was required to evaluate the differential cross sections. More detailed descriptions of the procedure for obtaining the cross sections, data normalization, and angle determination are given in Refs. [26−28]. The overall final normalization factor for the measured cross sections of$ ^{13} $ C+$ ^{208} $ Pb at$ \mathit{E} _{\rm lab}$ =340 MeV and$^{14}$ C+$^{208}$ Pb at$\mathit{E} _{\rm lab}$ =342 MeV was determined on the assumption that the elastic scattering of$ ^{11} $ C+$ ^{208} $ Pb at$ \mathit{E}_{\rm lab}$ =275 MeV, which was also measured, is pure Rutherford scattering at forward angles. This method was also applied in the data analysis of$^{13}$ B and$^{13}$ O [25]. The final normalization constant for$^{14}$ C+$^{208}$ Pb at$\mathit{E} _{\rm lab} $ =294 MeV was determined by considering that$ ^{14} $ C elastic scattering is pure Rutherford scattering at very forward angles [27].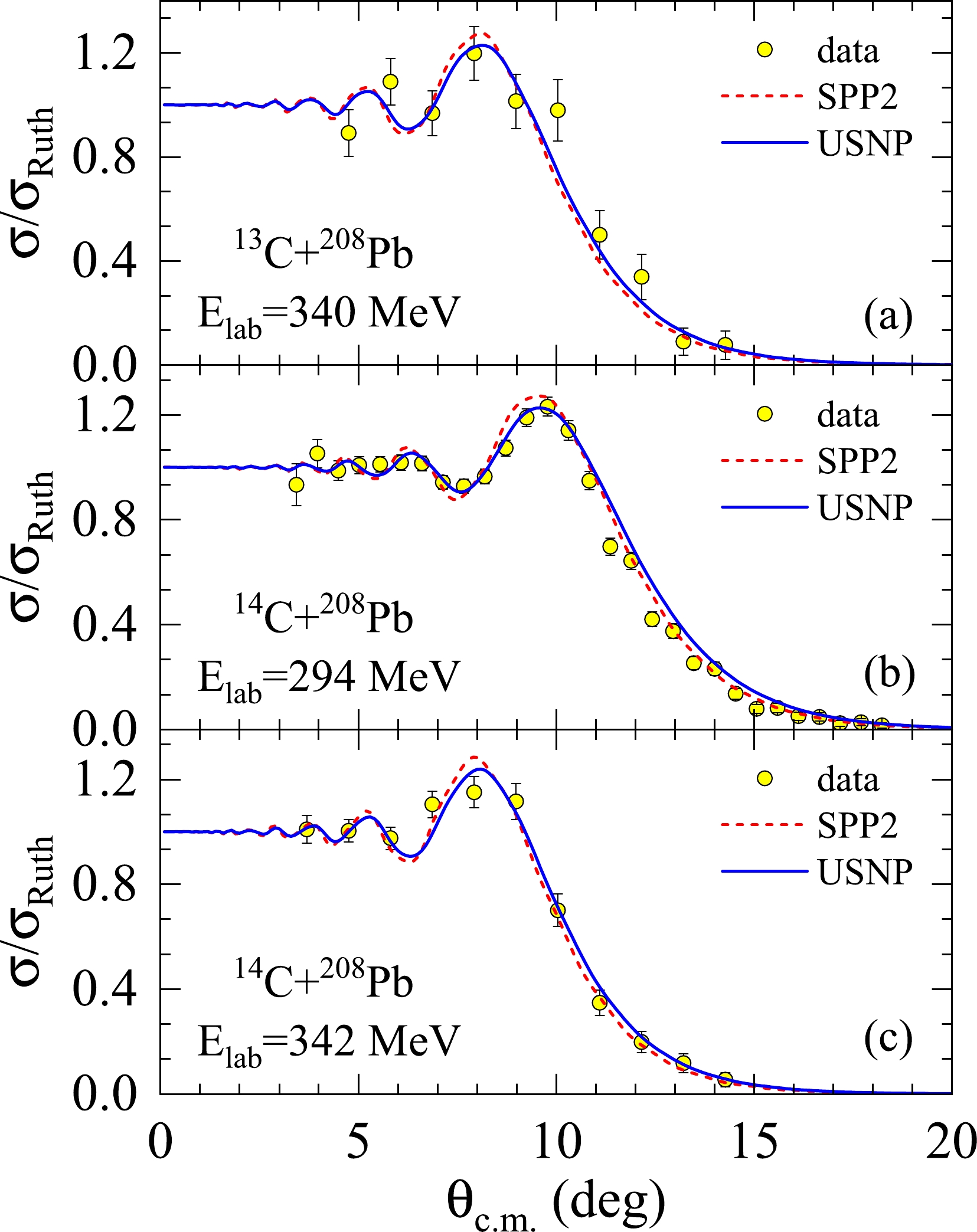
Figure 3. (color online) Experimentally measured elastic scattering angular distributions for (a)
$^{13}$ C+$^{208}$ Pb at 340 MeV, (b)$^{14}$ C+$^{208}$ Pb at 294 MeV, and (c)$^{14}$ C+$^{208}$ Pb at 342 MeV. The solid and dashed curves represent the results of the optical model calculations with the USNP [30] and SPP2 [31], respectively.The angular distributions revealed Fresnel patterns and Coulomb nuclear interference peaks (CNIPs) [29], typical for tightly-bound projectiles on heavy targets and similar to that observed for
$ ^{13} $ B scattered by a$ ^{208} $ Pb target [25]. The measured angular distributions for$ ^{13} $ C and$ ^{14} $ C were analyzed in terms of the OM with different approaches based on the complex nuclear potentials, in which the imaginary parts represented the coupling effects of different channels. The Coulomb potential had the usual form for the uniform charge distributions of spherical nuclei, with charge radii given by$R_C= 1.3\times(A_P^{1/3}+A_T^{1/3})$ fm (where$ A_P $ and$ A_T $ are the mass numbers of the projectile and target, respectively). For the nuclear complex potential in the OM, we used an updated version of a systematic nucleus-nucleus potential (USNP) proposed in Ref. [30]. This potential corresponds to a single-folding model based on the Bruy$ \grave{\text{e}} $ res Jeukenne-Lejeune-Mahaux (JLMB) model nucleon-nucleus potential [32, 33], with renormalization factors determined by the stable nuclei [30]. The proton and neutron density distributions required to obtain the potential were taken from Hartree-Fock calculations based on SkX parameterization [34]. Spin-orbit potentials were neglected because they are not usually important for the description of heavy-ion–heavy-ion scattering [35]. The details of calculations can be found in Ref. [30]. The results of OM calculations with the USNP are shown in Fig. 3 as solid blue curves (Fig. 3 (a) for$ ^{13} $ C +$ ^{208} $ Pb at 340 MeV, Fig. 3 (b) for$ ^{14} $ C +$ ^{208} $ Pb at 294 MeV, and Fig. 3 (c) for$ ^{14} $ C +$ ^{208} $ Pb at 342 MeV). The calculations with the USNP can effectively describe the data for almost the entire angular range, except for the overestimation of differential cross sections at the backward angles of$ ^{14} $ C +$ ^{208} $ Pb at 294 MeV.We also considered the S
$ \tilde{\text{a}} $ o Paulo potential version 2 (SPP2) [31] in the OM analysis, which is an improvement on the previous double-folding S$ \tilde{\text{a}} $ o Paulo potential (SPP) [36]. The improvement is related to the possibility of using experimental charge densities obtained from electron scattering experiments, or nuclear densities calculated through the Dirac-Hartree-Bogoliubov model. It also includes a dependence on the relative velocity between nuclei. These features are important for elastic scattering involving radioactive projectiles with the nucleus far from the valley of stability and at incident energies considerably higher than the Coulomb barrier. Calculations were performed with the code REGINA [31] assuming renormalization factors of$ N_{r} $ = 1 and$ N_{i} $ = 0.78 for the real and imaginary parts of the potential, respectively. The results of these calculations are shown in Fig. 3 as red dashed curves. The SPP2 results could also account for the experimental data with larger cross sections at approximately CNIP angles and smaller cross sections at backward angles. The total reaction cross sections obtained from the OM calculations with SPP2 for$ ^{13} $ C +$ ^{208} $ Pb at 340 MeV,$ ^{14} $ C +$ ^{208} $ Pb at 294 MeV and 342 MeV were 3648 mb, 3664 mb, and 3742 mb, respectively, which are similar to those computed with the USNP (3659 mb, 3665 mb, and 3730 mb, respectively). This can be considered a good achievement because it is not an adjusted but parameter free calculation.The neutron separation energies for
$ ^{13} $ C ($ S_n $ =4.946 MeV) and$ ^{14} $ C ($ S_n $ =8.177 MeV) were large. However, because of the high incident energies, there was a possibility that these projectiles could have a large breakup probability. To account for the possible breakup coupling effects in the elastic scattering angular distributions, we performed CDCC calculations with the code FRESCO [37]. In these calculations, the$ ^{13,14} $ C projectiles were composed of a$ ^{12,13} $ C core plus a valence neutron. The$ ^{208} $ Pb target has spin zero, and no explicit target excitation was included in the calculation. Furthermore, for simplicity, the spins of both cores and valence nucleons were ignored, and the wave functions describing the relative motion between these cores and valence particles were calculated using Woods-Saxon potentials, assuming a reduced radius$ r_{0} $ = 1.25 fm, diffuseness parameter$ a_{0} $ = 0.65 fm, and a depth parameter adjusted to reproduce the neutron separation energy in the ground state. The continuum states of the subsystems, n+$ ^{12} $ C for$ ^{13} $ C and n+$ ^{13} $ C for$ ^{14} $ C, were discretized up to a maximum excitation energy of$ \varepsilon_{\text{max}} $ = 18 MeV for$ ^{13} $ C and 20 MeV for$ ^{14} $ C, with width bins of 2 MeV. Neutron-core relative orbital angular momenta up to$ l_{\text{max}} $ = 4 were included with all couplings up to a maximum multipolarity$ \lambda_{\text{max}} $ = 8. With such model space, the results for the elastic scattering cross sections reached convergence. Furthermore, for the effective interactions between the core-target and neutron-target subsystems, the systematic nucleus-nucleus folding potentials of Ref. [30] and the systematic nucleon-nucleus potentials of Koning and Delaroche [38] were considered.The calculated elastic scattering cross sections with the CDCC couplings are shown in Fig. 4. For comparison, the results of "no coupling" are also displayed in the figure. It is important to emphasize that the "no coupling" calculation corresponds to the cluster folding model where the
$ ^{14} $ C and$ ^{13} $ C projectiles are described as$ ^{13} $ C+n and$ ^{12} $ C+n, respectively. This can be interpreted as good achievement of the model in describing the elastic scattering of these systems. We qualitatively observed good agreement between the experimental data and the calculation results, including the coupling effects from the breakup channels for both the$ ^{13} $ C and$ ^{14} $ C projectiles. Although there was a small reduction in the Fresnel peak for$^{13,14}$ C +$ ^{208} $ Pb, which improved the agreement with the data, the couplings to the continuum had little effect in the description of the elastic scattering data; thus, the contribution from the breakup channels to the angular distributions of elastic scattering for$ ^{13,14} $ C +$ ^{208} $ Pb systems was negligibly small at these relatively high incident energies.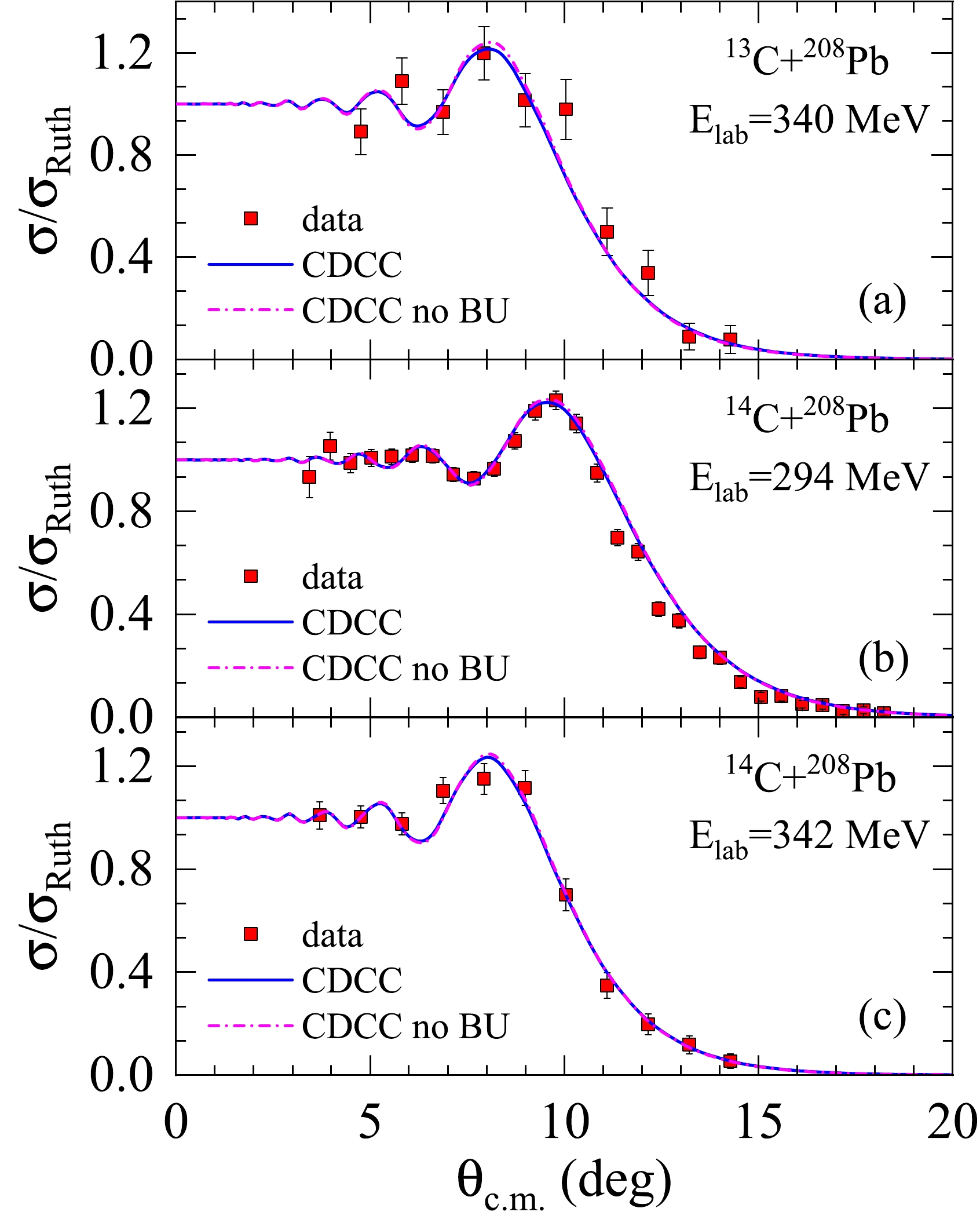
Figure 4. (color online) Elastic scattering cross sections from CDCC calculations for (a)
$^{13}$ C+$^{208}$ Pb at 340 MeV, (b)$^{14}$ C+$^{208}$ Pb at 294 MeV, and (c)$^{14}$ C+$^{208}$ Pb at 342 MeV and their comparisons with experimental data. Solid and dashed-dotted curves represent the results of CDCC calculations with and without couplings to continuum states, respectively.For the
$ ^{14} $ C+$ ^{208} $ Pb system, further considerations were introduced to the CDCC analysis. The$ ^{14} $ C projectile has a large separation energy of the valence neutron in the ground state and several bound excited states below the breakup threshold. The inelastic scattering events were not distinguished from elastic ones in this experiment owing to the beam energy resolution. To consider the inelastic channel, we included the contributions of all bound excited states in the CDCC calculations ($ J^{\pi} $ = 1$ ^{-} $ , 3$ ^{-} $ , 0$ ^{-} $ , 2$ ^{+} $ , 2$ ^{-} $ at$ \mathit{E} ^{*}$ =6.094, 6.728, 6.903, 7.012, 7.341 MeV, respectively.), except the 0$^{+}$ bound excited state at 6.590 MeV. We omitted this particular state because in the CDCC formalism, the excited states are constructed as the single-particle states of a valence particle bound to its remaining core in the ground state. Without considering dynamic core excitation, the 0$^{+}$ excited state could not be reproduced correctly; instead, the same quantum state was constructed as the ground state, a situation that was difficult to manage in FRESCO. The coupling effect of the inelastic scattering of the 0$^{+}$ excited state on the angular distribution of elastic scattering was thus neglected. The contribution of the excited states of the lead target was also omitted based on a previous study [39]. The results of the CDCC calculations, with all the considered excited states (dashed-dotted curve) as well as the prediction when not considering the excited states (dashed-double-dotted curve) are presented in Fig. 5. As shown, the couplings to the inelastic states of the$^{14}$ C projectile did not have a significant influence on the elastic cross sections. Similar phenomena were also observed for$^{10}$ B,$^{10}$ C, and$^{11}$ C scattered by$^{208}$ Pb at energies approximately four times the Coulomb barriers [14], and$^{12}$ C scattered by zirconium isotopes at energies approximately twice the Coulomb barriers [40]. The results of CDCC calculation excluding the continuum coupling effects but considering the effects of coupling to excited states are also shown in Fig. 5 as a dashed curve, indicating that the contributions of the continuum states to the elastic scattering angular distribution were somewhat larger than those of the excited states for$^{14}$ C +$^{208}$ Pb at an energy of 294 MeV.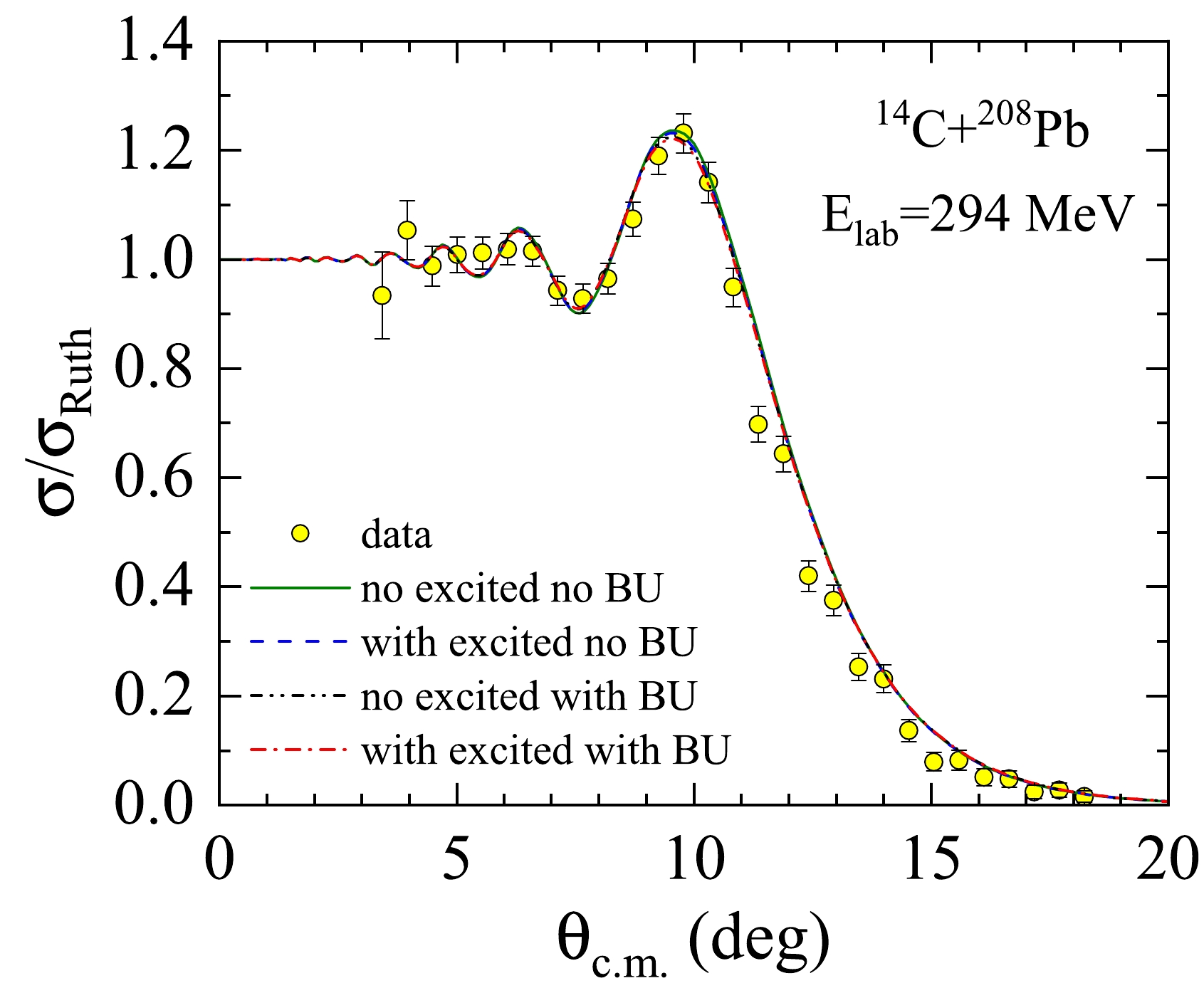
Figure 5. (color online) Comparisons between the experimental data and CDCC calculations with and without the contributions of bound excited states (labeled as "with excited" and "no excited," respectively) or continuum states (labeled as "with BU" and "no BU," respectively) for
$^{14}$ C+$^{208}$ Pb at 294 MeV. See text for details.A phenomenological analysis of the interaction distances was performed to gain further insights into the systematic behavior of angular distributions for the carbon isotope chain. The present data for
$^{13,14}$ C+$^{208}$ Pb and the data from literature involving$^{10}$ C+$^{208}$ Pb at$\mathit{E}_{\rm lab} $ =66 MeV [13],$ ^{10} $ C+$ ^{208} $ Pb at$ \mathit{E} _{\rm lab}$ =226 MeV [14], and$^{15}$ C+$^{208}$ Pb at$\mathit{E} _{\rm lab} $ =65 MeV [19] were converted from σ/$ \sigma_{\text{Ruth}} $ as a function of angle for a given energy to σ/$ \sigma_{\text{Ruth}} $ as a function of the reduced distance of closest approach on a Rutherford trajectory, expressed as [41−43]$ d=\frac{Z_{P}Z_{T}{\rm e}^{2}}{2E_{\text{c.m.}}} \left[ 1+\frac{1}{\text{sin}(\theta_{\text{c.m.}}/2)} \right] \frac{1}{A_{P}^{1/3}+A_{T}^{1/3}} , $

(1) where
$ Z_{P} $ and$ Z_{T} $ are the charge number of the projectile and target, respectively, and$ E_{\text{c.m.}} $ and$ \theta_{\text{c.m.}} $ are the incident energy and scattering angle in the center of mass coordinate. The data results using this procedure are presented in Fig. 6. For all datasets, σ/$ \sigma_{\text{Ruth}} $ was close to unity at larger distances but rapidly fell off when tending toward shorter distances owing to the strong absorption of the elastic flux into non-elastic channels [42]. The large differences between$ ^{15} $ C and other carbon isotopes can be understood in terms of the combination of the reduced critical interaction distance${d}_{\text{I}}$ and reduced strong interaction distance${d}_{\text{S}}$ . In this study, a modified exponential function [43] was adopted with two free parameters to extract these distances,
Figure 6. (color online) Ratio of elastic cross section to the Rutherford value, σ/
$\sigma_{\text{Ruth}}$ , as a function of the reduced distance of closest approach d for the carbon isotopes scattered by the$^{208}$ Pb target at the energies indicated. The different curves represent the fitting results using Eq. (2).${d}_{\text{I}}$ and${d}_{\text{S}}$ are indicated for reference. The experimental data for$^{10}$ C+$^{208}$ Pb at$\mathit{E} _ {\rm lab} $ =66 MeV and$ ^{15} $ C+$ ^{208} $ Pb at$ \mathit{E} _{\rm lab}$ =65 MeV are taken from Refs. [13] and [19], respectively. See text for details.$ \sigma/\sigma_{\text{Ruth}}=\frac{1}{1+3 e ^{a_{1}(d-a_{2})}} ,$

(2) where
$ a_{1} $ and$ a_{2} $ are adjustable parameters to fit the data of the same reaction system at various incident energies. The fitting procedure was applied to the scattering data of carbon isotopes, with the results illustrated in Fig. 6 as different curves. The reduced distance${d}_{\text{I}}$ , the$ \sigma/\sigma_{\text{Ruth}} $ ratio of which was 0.98, and${d}_{\text{S}}$ , the$ \sigma/\sigma_{\text{Ruth}} $ ratio of which was 0.25, were obtained taking into account the uncertainty of the cross sections, that is,${d}_{\text{I}}$ = 1.97, 1.84, 1.99, 3.07 fm and${d}_{\text{S}}$ = 1.49, 1.39, 1.46, 1.53 fm for$ ^{10} $ C,$ ^{13} $ C,$ ^{14} $ C,$ ^{15} $ C+$ ^{208} $ Pb, corresponding to differences between these two distances of$\Delta {d}$ =${d}_{\text{I}}$ –${d}_{\text{S}}$ = 0.48, 0.45, 0.53, 1.54 fm, respectively. The strong interaction distances were approximately close to each other for these systems, whereas the critical interaction distance for$ ^{15} $ C+$ ^{208} $ Pb was significantly larger than those of the other three. Similar trends can be found in Refs. [42, 43], where larger values of${d}_{\text{I}}$ were observed for exotic nuclei compared with weakly and tightly bound nuclei. Note that the incident energies of$ \sigma/\sigma_{\text{Ruth}} $ were higher for$ ^{13,14} $ C+$ ^{208} $ Pb, close to the barrier for$ ^{15} $ C+$ ^{208} $ Pb, and both for$ ^{10} $ C+$ ^{208} $ Pb. However, besides the incident energy difference, isospin asymmetry and valence particle separation energy were also different for these systems:$ ^{10} $ C (S$ _p $ =4.006 MeV),$ ^{13} $ C (S$ _n $ =4.946 MeV),$ ^{14} $ C (S$ _n $ =8.177 MeV), and$ ^{15} $ C (S$ _n $ =1.218 MeV). The larger values of$\Delta {d}$ , as also observed in the suppression of the Fresnel diffraction peak in the corresponding angular distributions [13, 19], could be attributed to the low binding energies and/or couplings to other reaction channels [42, 43]. However, note that the angular distribution of$ ^{15} $ C+$ ^{208} $ Pb had fewer data points and larger error bars in the regions of interest. Moreover, there are no reported measurements for$ ^{13,14} $ C+$ ^{208} $ Pb at energies close to the barriers. More detailed and extensive measurements of the angular distributions across the entire angular range would be required in further studies on the static and dynamic effects in the elastic scattering process, especially for a$ ^{15} $ C projectile, through reduced critical and strong interaction distances. -
The angular distributions for the elastic scattering of
$ ^{13,14} $ C on$ ^{208} $ Pb were measured at energies of approximately five times the Coulomb barriers at the HIRFL-RIBLL. The obtained angular distributions were analyzed within the OM using the systematic nucleus-nucleus potential of Ref. [30] and SPP2 [31]. The results of the calculations showed good agreement with experimental data. The coupling effects of breakup reactions on elastic scattering were investigated using CDCC, revealing negligible contributions at these relatively high incident energies. A semi-classical approach [41−43] of plotting the elastic cross sections normalized to those of Rutherford scattering as a function of the reduced distance of closest approach was performed to discuss different behaviors of the angular distributions of elastic scattering data involving carbon isotope projectiles. -
We would like to acknowledge the staff at the HIRFL for the operation of the cyclotron and their friendly collaboration.
Elastic scattering of 13C and 14C isotopes on a 208Pb target at energies of approximately five times the Coulomb barriers
- Received Date: 2023-10-20
- Available Online: 2024-03-15
Abstract: The elastic scattering angular distributions of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: