Constraint on symmetry energy slope using neutron skins of ⁴⁸Ca, ⁶⁴Ni, ¹²⁴Sn, and ²⁰⁸Pb and its impact on neutron star radius

The equation of state (EoS) of isospin asymmetric nuclear matter plays an important role in research on nuclear reaction and structure as well as astrophysics [1]. For example, bulk properties of neutron stars are mainly governed by the EoS [1−4]. Many investigations indicate that there are significant correlations between neutron star radii and EoS parameters, namely, the symmetry energy slope L at the saturation density $ \rho_{0} $, nuclear matter incompressibility coefficient $ K_0 $, and skewness parameter $ Q_0 $ [4−9]. In particular, the radii of neutron stars with density $ \rho\sim\rho_0 $ are primarily determined by the slope L [4]. These findings are important, and many attempts have been made to precisely determine EoS parameters [7, 10]. $ K_0 $ was constrained with a precision of approximately 10% to be 240(20) MeV by giant resonance [11, 12], which agrees with recent results [13]. However, the deduced L values at $ \rho_{0} $ by different methodologies have a large spread from approximately 30 to 110 MeV. For more details, see the review article in Ref. [14]. In particular, due to a lack of sensitive observables, $ Q_0 $ is still poorly understood. Theoretical values for $ Q_0 $ are in the range of $ \sim - 1000$ to $ \sim 1000$ MeV [15].

Similar to neutron star radii, it is well known that neutron skins formed in heavy nuclei with an excess of neutron over proton are sensitive to the slope L at $ \rho_{0} $ [16]. Because the linear relationships were established based on different effective nucleon-nucleon interactions of the self-consistent mean-field models [16], neutron skin thicknesses $\Delta{{\rm{R}}} _{ {\rm{np}}} $, as the difference of neutron and proton distribution rms radii in nuclei, namely, $\Delta{{\rm{R}}} _{ {\rm{np}}} = {{\rm{R}}} _ {\rm{n}}- {{\rm{R}}} _ {\rm{p}} $, have been widely employed to constrain the slope L. Theoretical progress has also promoted the development of novel experimental methods for neutron distribution radius measurements [17−26]. Recently, model-dependent $\Delta{{\rm{R}}} _{ {\rm{np}}} $ data for the stable Ca, Ni, Sn, and Pb isotopes were compiled, and the evaluated $\Delta{{\rm{R}}} _{ {\rm{np}}} $ values showed a high precision of approximately 0.02 fm [27]. These compiled $\Delta{{\rm{R}}} _{ {\rm{np}}} $ data [27] are taken from different experiments related to hadron scatterings [18, 24, 28], interaction cross sections [25, 29], giant resonances [30, 31], and antiprotonic atoms [22, 32]. Based on the compiled $\Delta{{\rm{R}}} _{ {\rm{np}}} $ data, separate trends of $\Delta{{\rm{R}}} _{ {\rm{np}}} $ versus relative neutron excess, $ \delta = (N-Z)/A $, were observed for the Ca, Ni, Sn, and Pb isotopic chains [27], where N, Z, and A reperesent neutron, proton, and mass numbers, respectively. In addition, parity-violating electron scattering provides a so-called mode-independent approach to determine $\Delta{{\rm{R}}} _{ {\rm{np}}} $ in nuclei [23, 33]. With this method, the $\Delta{{\rm{R}}} _{ {\rm{np}}} $ of $ ^{48} {\rm{Ca}}$ and $ ^{208} {\rm{Pb}}$ were determined by the CREX and PREX collaboration groups [23, 33], respectively. Although the tension of the CREX-PREX neutron skins with other experimental and theoretical results has been widely discussed from a physics perspective [34−37], the possibility of statistical fluctuations was also mentioned in Refs. [38−40]

The $\Delta{{\rm{R}}} _{ {\rm{np}}} $ data from different experimental methods would be helpful to reduce the model-dependent effects of single experimental data [41]. For instance, using the $\Delta{{\rm{R}}} _{ {\rm{np}}} $ of Sn isotopes from different experiments, highly precise L values at different densities have already been obtained in Refs. [42, 43]. We note that the compiled neutron skin data from different experimental methods reproduce the separate $\Delta{{\rm{R}}} _{ {\rm{np}}} $ structures of Ca, Ni, Sn, and Pb isotope chains predicted by the SLy4 interaction [27]. This would indicate that these compiled neutron skin data are reliable. Therefore, it is interesting to precisely constrain the symmetry energy slopes L at the saturation density using the compiled $\Delta{{\rm{R}}} _{ {\rm{np}}} $ data [27] and to address their impacts on the neutron star radii at 1.4 solar-mass ($ 1.4\,M_{\odot} $).

As known, the symmetry energy slope L at the saturation density can be sensitively constrained by the $\Delta{{\rm{R}}} _{ {\rm{np}}} $ value of heavy nuclei with large neutron-to-proton values [43, 44]. Therefore, for each isotope chain tabulated in Ref. [27], we only adopt the $\Delta{{\rm{R}}} _{ {\rm{np}}} $ data of magic nucleus with the maximum neutron-to-proton value, namely $ ^{48} {\rm{Ca}}$, $ ^{64} {\rm{Ni}}$, $ ^{124} {\rm{Sn}}$, and $ ^{208} {\rm{Pb}}$, to determine the slope L. It would also be helpful to reduce the effects of possible $\Delta{{\rm{R}}} _{ {\rm{np}}} $ isotope-dependent deviation on the L extraction through balancing the contribution of each isotope chain. To constrain L in this study, the $\Delta{{\rm{R}}} _{ {\rm{np}}} $ values are analyzed via the chi-square $ \chi _{j}^{2} $ value defined here as

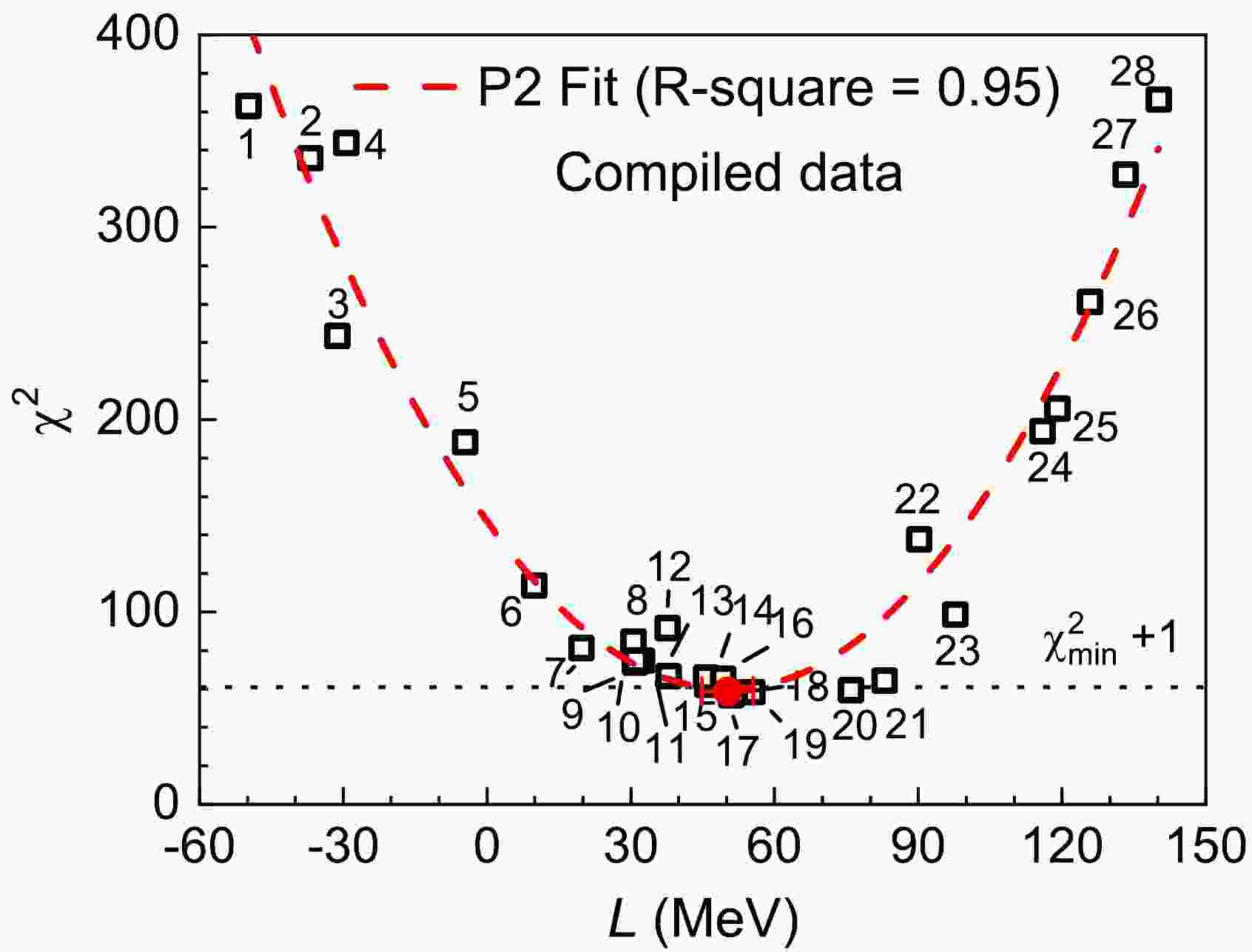
where $ k = 1, 2......M $ represent $ ^{48} {\rm{Ca}}$, $ ^{64} {\rm{Ni}}$, $ ^{124} {\rm{Sn}}$, and $ ^{208} {\rm{Pb}}$, respectively. $ i = 1, 2......N $, where N is the number of adopted neutron skin thicknesses for nucleus k. $ \Delta {\rm{R}}_{ {\rm{np}}}^{ {\rm{th}}}(k, j) $ ($ j = 1, 2......28 $) is the theoretical neutron skin thickness of nucleus k corresponding to the effective interaction j. The randomly adopted effective interactions are Z, Es, E, Zs, Zs* [45], SIII [46], SkP [47], SkS1 [48], SkT6, SkT7 [49], RATP [50], SGII [51], SkS2 [48], SkM$ ^{*} $ [52], SLy4 [53], SkM [54], DD-ME2 [55], SkS3 [48], TW99 [56], PKO2, PKO3 [57], PKDD [58], PKO1 [59], PK1 [58], NL3 [60], NL-Z2 [61], NL-Z [62], and NL1 [63]. They are labeled with numbers from 1 to 28, respectively, as shown in Fig. 1. Each effective interaction corresponds to a specific L value. These interactions cover a large L range from approximately $ - $50 to 140 MeV. $\Delta{{\rm{R}}} _{ {\rm{np}}}^{ {\rm{exp}}}(k, i) $ and $ \delta\Delta {{\rm{R}}} _{ {\rm{np}}}^{ {\rm{exp}}}(k, i) $ are the ith experimental neutron skin thickness and error for nucleus k, respectively.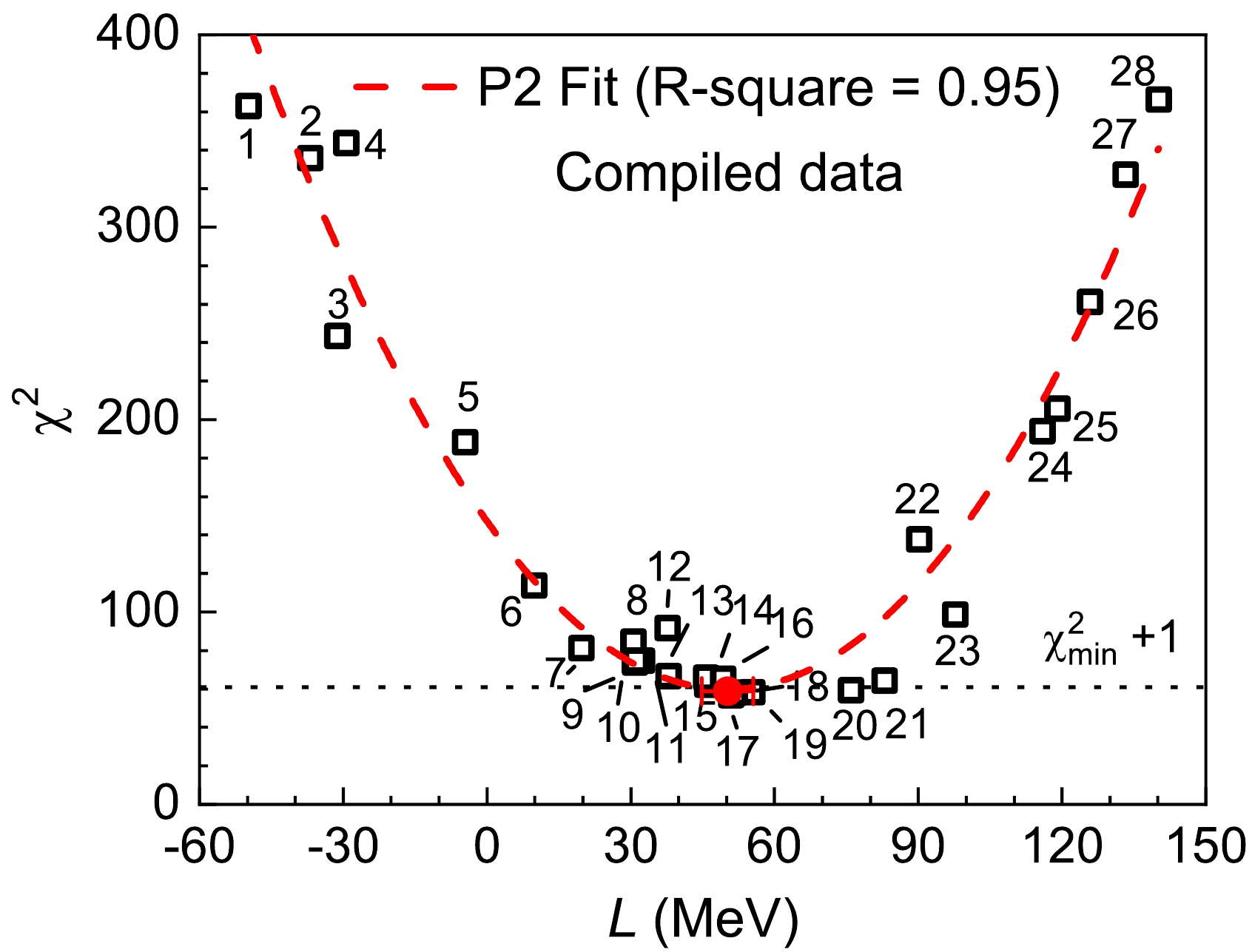

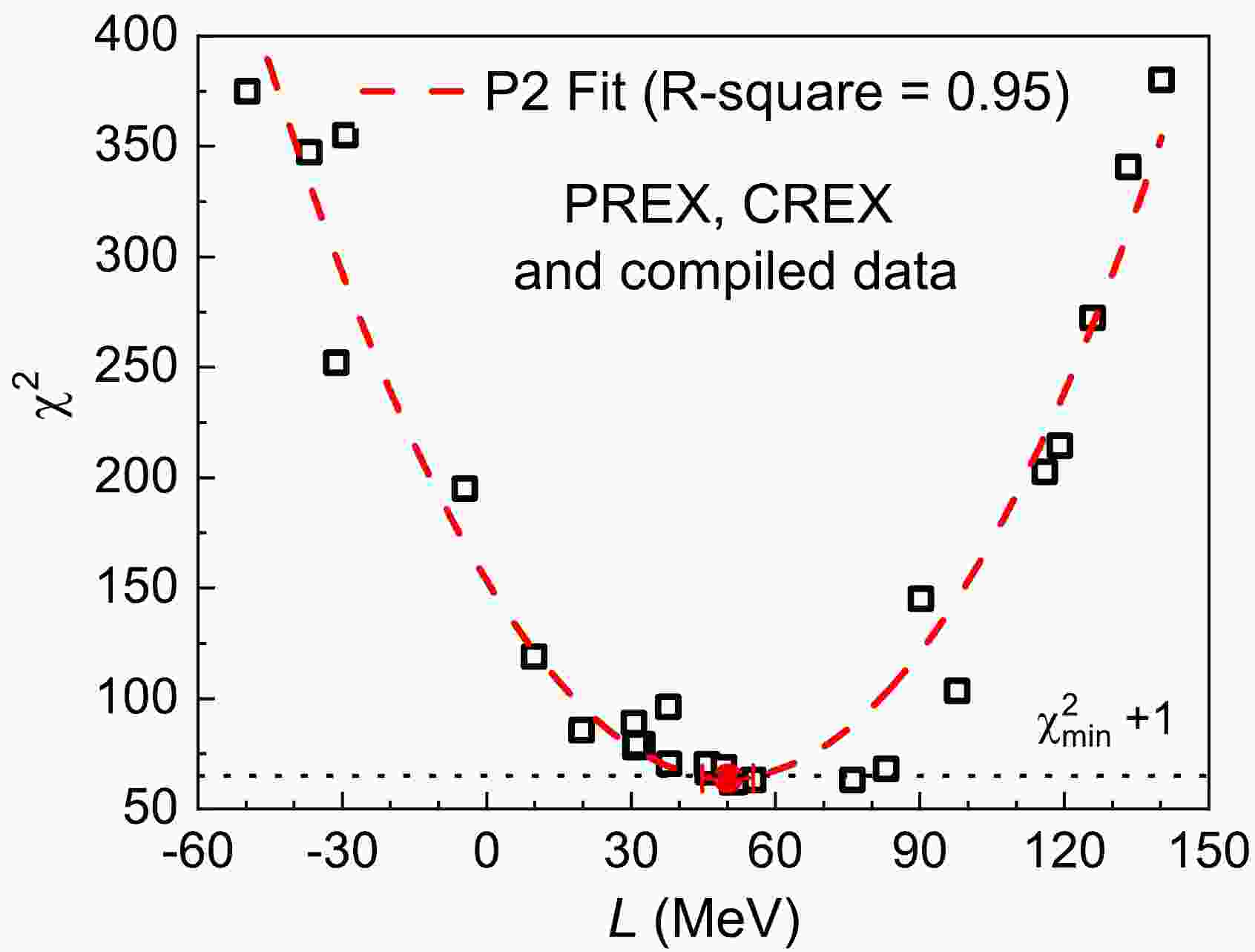
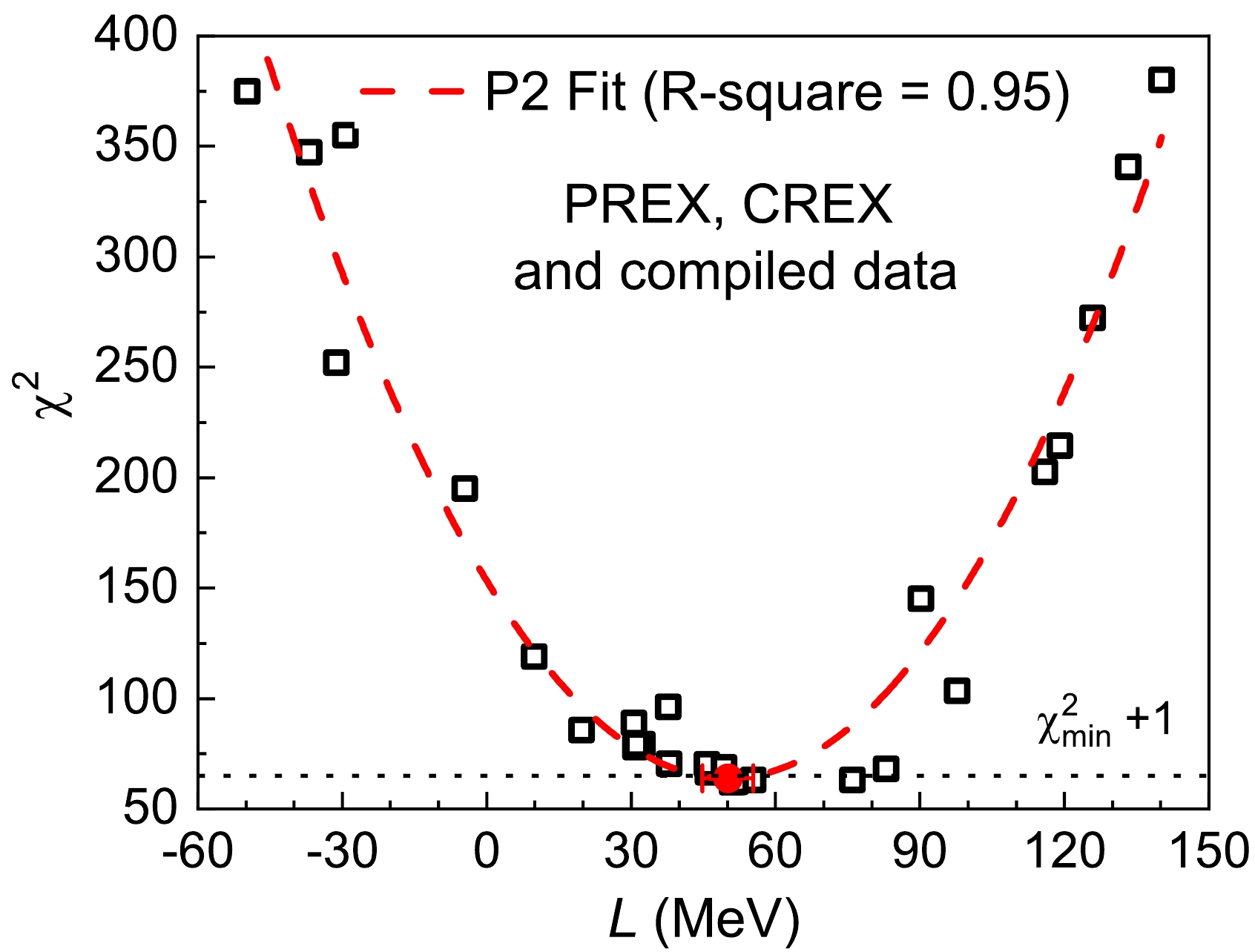
Figure 1.  (color online) Slope L versus $\chi ^{2}$ obtained by the compiled 49 model-dependent $\Delta{\rm{R}}_{\textrm{np}}$ values of $^{48}{\rm{Ca}}$, $^{64}{\rm{Ni}}$, $^{124}{\rm{Sn}}$, and $^{208}{\rm{Pb}}$; see Table I in Ref. [27] for details on the $\Delta{\rm{R}}_{\textrm{np}}$ data. The dashed line denotes the quadratic polynomial (P2) fit with an R-Square value of 0.95. The filled red circle with error bar represents the extracted L result at the minimum $\chi ^{2}$. The interaction parameter sets used are labeled with numbers 1 to 28; see text for details.

First, the 49 compiled model-dependent $\Delta{{\rm{R}}} _{ {\rm{np}}} $ values of $ ^{48} {\rm{Ca}}$, $ ^{64} {\rm{Ni}}$, $ ^{124} {\rm{Sn}}$, and $ ^{208} {\rm{Pb}}$ [27] are adopted to constrain L. These data are available in Table I in Ref. [27], which were obtained by various experiments; see Ref. [27] and references therein for details. The obtained $ \chi ^{2} $ as a function of L is plotted in Fig. 1. In the $ \chi ^{2} $ calculations (Eq. (1)), only the reported experimental errors of neutron skins are considered. The scattering of the $ \chi ^{2} $ data points would be mainly caused by the difference of interaction models. Subsequently, the obtained $ \chi ^{2} $ as a function of L is fitted by the quadratic polynomial (P2) function, namely, $ \chi ^{2} = aL^2+bL+c $. Then, an L value of 50(6) MeV is deduced at the minimum $ \chi ^{2} $, $ \chi _{ {\rm{min}}}^{2} $, via the P2 fit function. The final error of L includes the uncertainties from fitting parameters and statistics. The L uncertainty caused by fitting parameters mainly originates from the model difference. As shown in Fig. 1, the obtained $ \chi _{ {\rm{min}}}^{2} $ value for the 49 $\Delta{{\rm{R}}} _{ {\rm{np}}} $ is approximately 60. As a result, our normalized $ \chi_n $ of 1.1$ \pm $0.1 is close to 1 within the error bar, which means that there are no significant unidentified systematic uncertainties. Therefore, similar to Ref. [42], the statistical error with a confidence level of 68.3% for the slope L is obtained using the $ \chi _{ {\rm{min}}}^{2} +1 $ method.

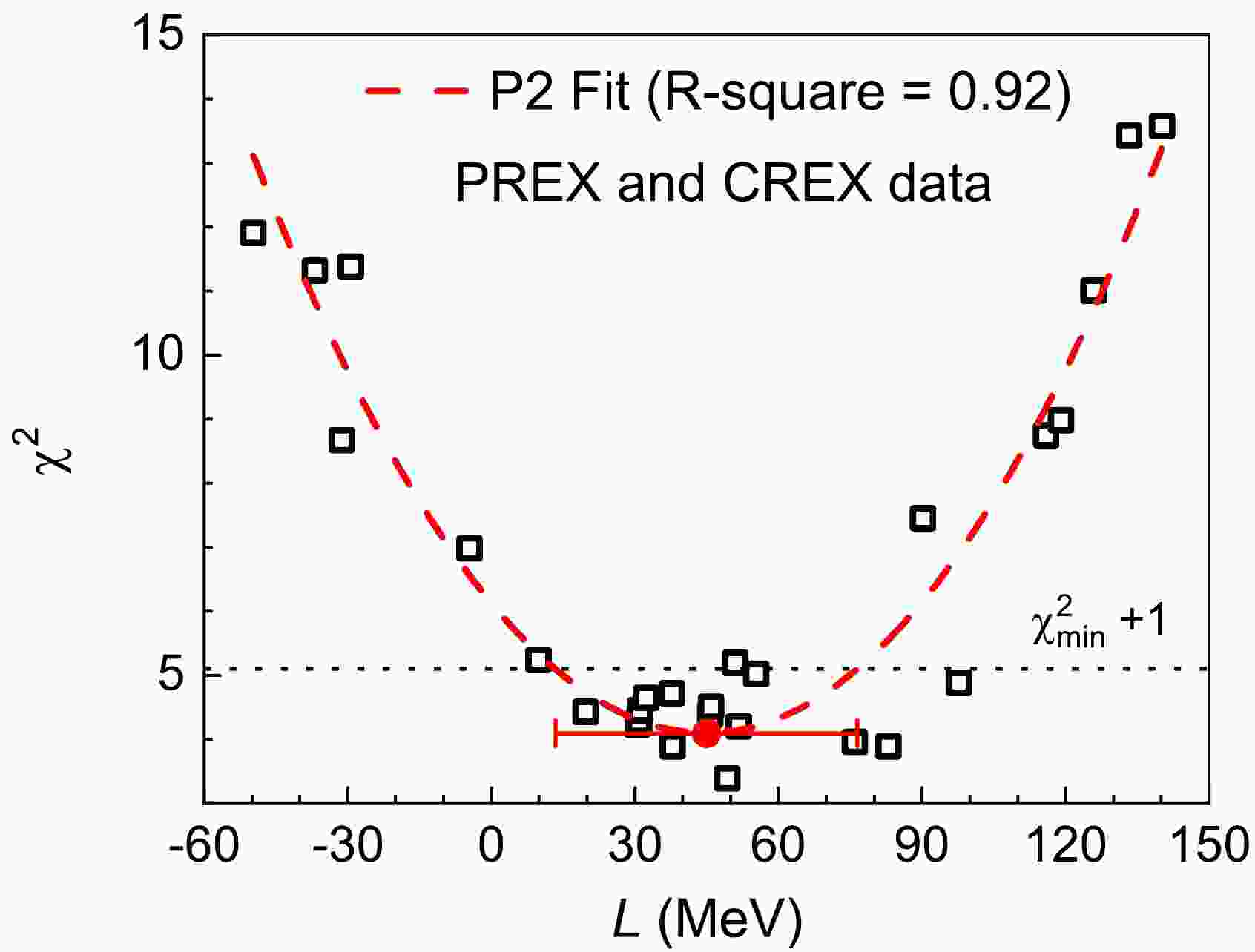
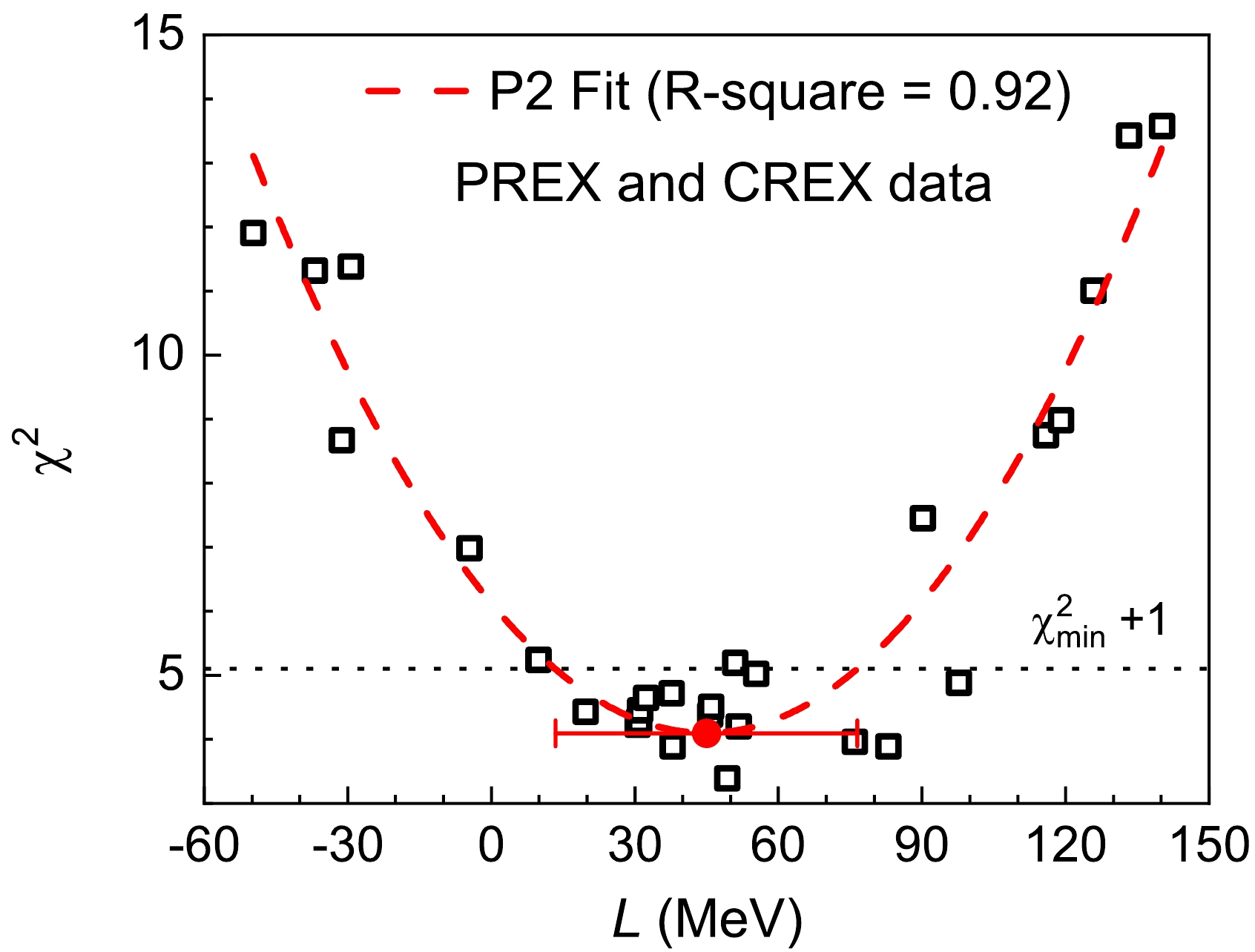
Furthermore, we also constrain the slope L using the so-called model-independent $\Delta{{\rm{R}}} _{ {\rm{np}}} $ value of $ ^{48} {\rm{Ca}}$ and $ ^{208} {\rm{Pb}}$ determined by the CREX and PREX experiments [23, 33], as shown in Fig. 2. The obtained L of 45(32) MeV is very consistent with the result of 50(6) MeV determined by the compiled model-dependent $\Delta{{\rm{R}}} _{ {\rm{np}}} $ of $ ^{48} {\rm{Ca}}$, $ ^{64} {\rm{Ni}}$, $ ^{124} {\rm{Sn}}$, and $ ^{208} {\rm{Pb}}$ [27]. The difference of their center values is only approximately 5 MeV, which demonstrates the consistency of $\Delta{{\rm{R}}} _{ {\rm{np}}} $ from different experiments.

Figure 2.  (color online) Same as Fig. 1, but $\chi ^{2}$ values are obtained by the two model-independent $\Delta{\rm{R}}_{\textrm{np}}$ values from the CREX and PREX experiments [23, 33].

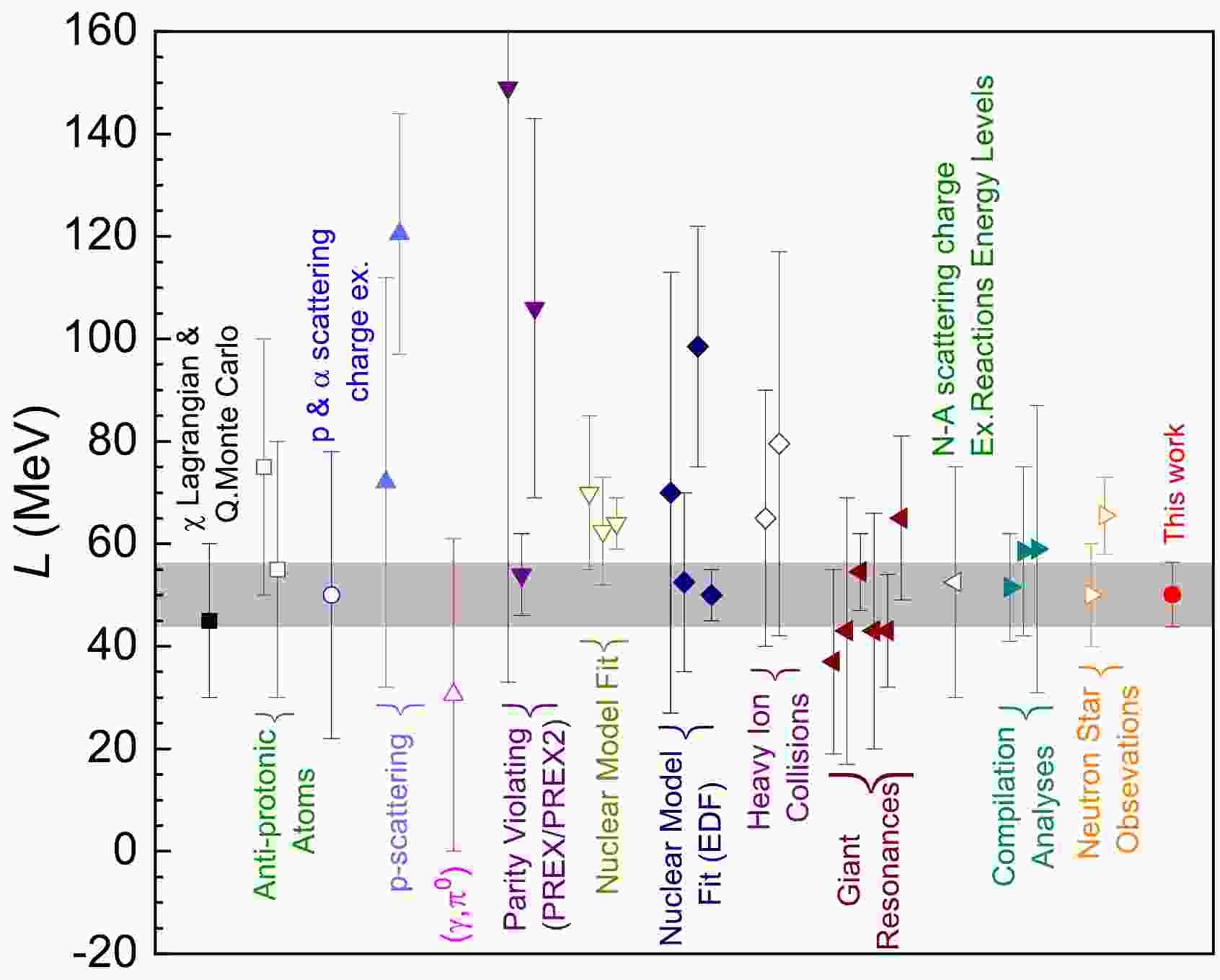
Finally, in Fig. 3, the slope L is constrained to be 50(6) MeV using all fifty-one $\Delta{{\rm{R}}} _{ {\rm{np}}} $ values, including the model-dependent and -independent data used in Figs. 1 and 2. Figure 4 shows a comparison of the obtained L in this work with the reported data from different observables and methodologies; see the review article in Ref. [14] and references therein for more details. Our L result constrained by the abundant $\Delta{{\rm{R}}} _{ {\rm{np}}} $ data from various experiments has high precision. In particular, our L value is consistent with the so-called world-averaged result, namely, a weighted mean value of 57.2(22) MeV obtained using literature data, as shown in Fig. 4. Their difference is only approximately 7.2(64) MeV.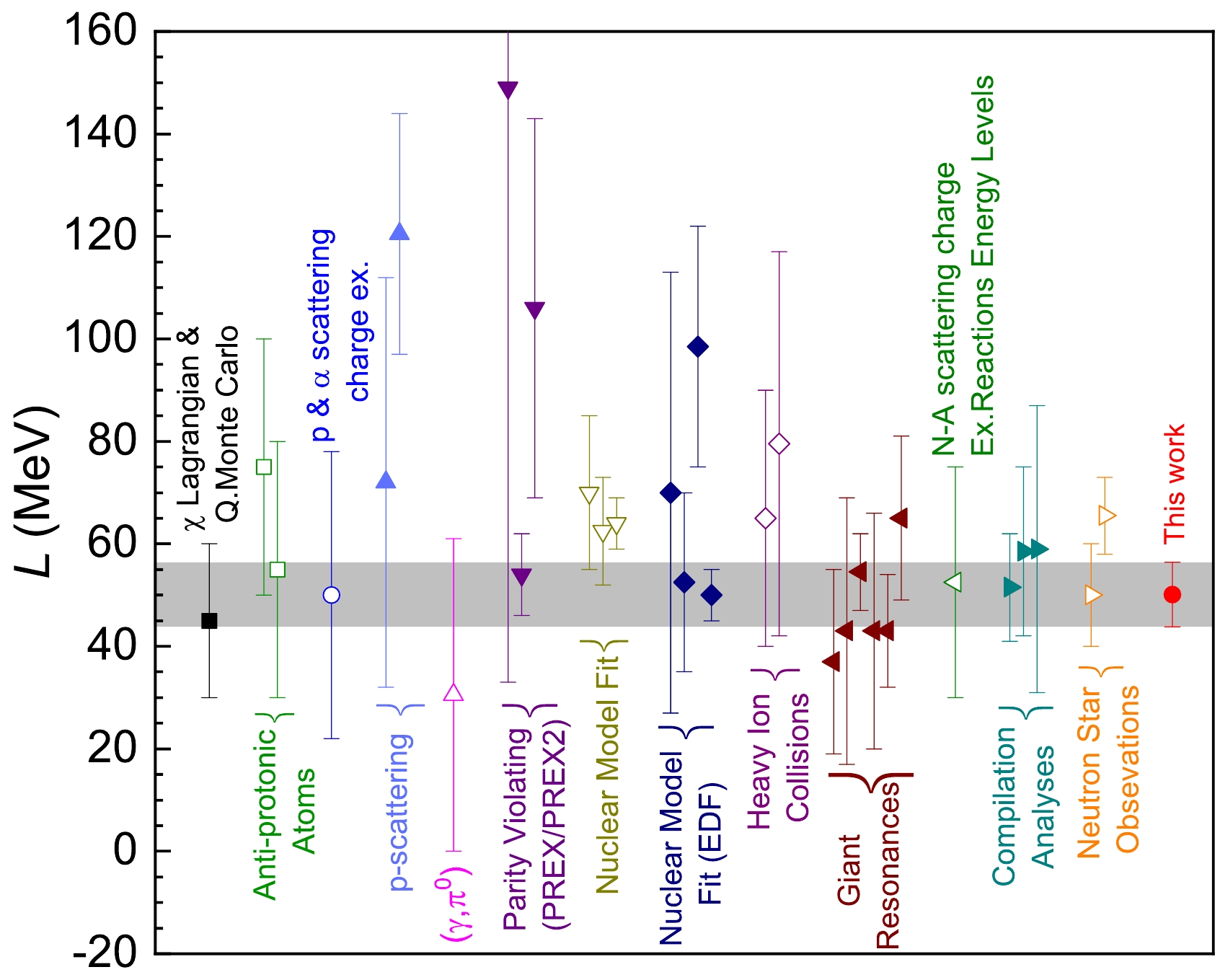

Figure 3.  (color online) Same as Fig. 1, but $\chi ^{2}$ values are determined by all data used in Figs. 1 and 2.

Figure 4.  (color online) Comparison of the L value obtained in this study with the reported results from various methods, taken from Ref. [14]. The gray area indicates the uncertainty of our L.

We further revisit the effects of our L on the neutron star radii $ R_{1.4} $ at 1.4 solar-mass ($ 1.4\,M_{\odot} $). To easily understand the effects of the EoS parameters, the neutron star radii R can be empirically expressed as [4]

where $ \delta = (\rho_n-\rho_p)/\rho $ is the asymmetry parameter, and $ \rho_n $ and $ \rho_p $ are the neutron and proton densities, respectively. The $ R_{1.4} $-L correlation deduced from various EoS parameter sets is relatively weak [4], and there is a model-dependent $ R_{1.4} $ spread of approximately 2 km at one given L [4, 15]. Consequently, as indicated by Eq. (2), the L value alone is insufficient to characterize $ R_{1.4} $.

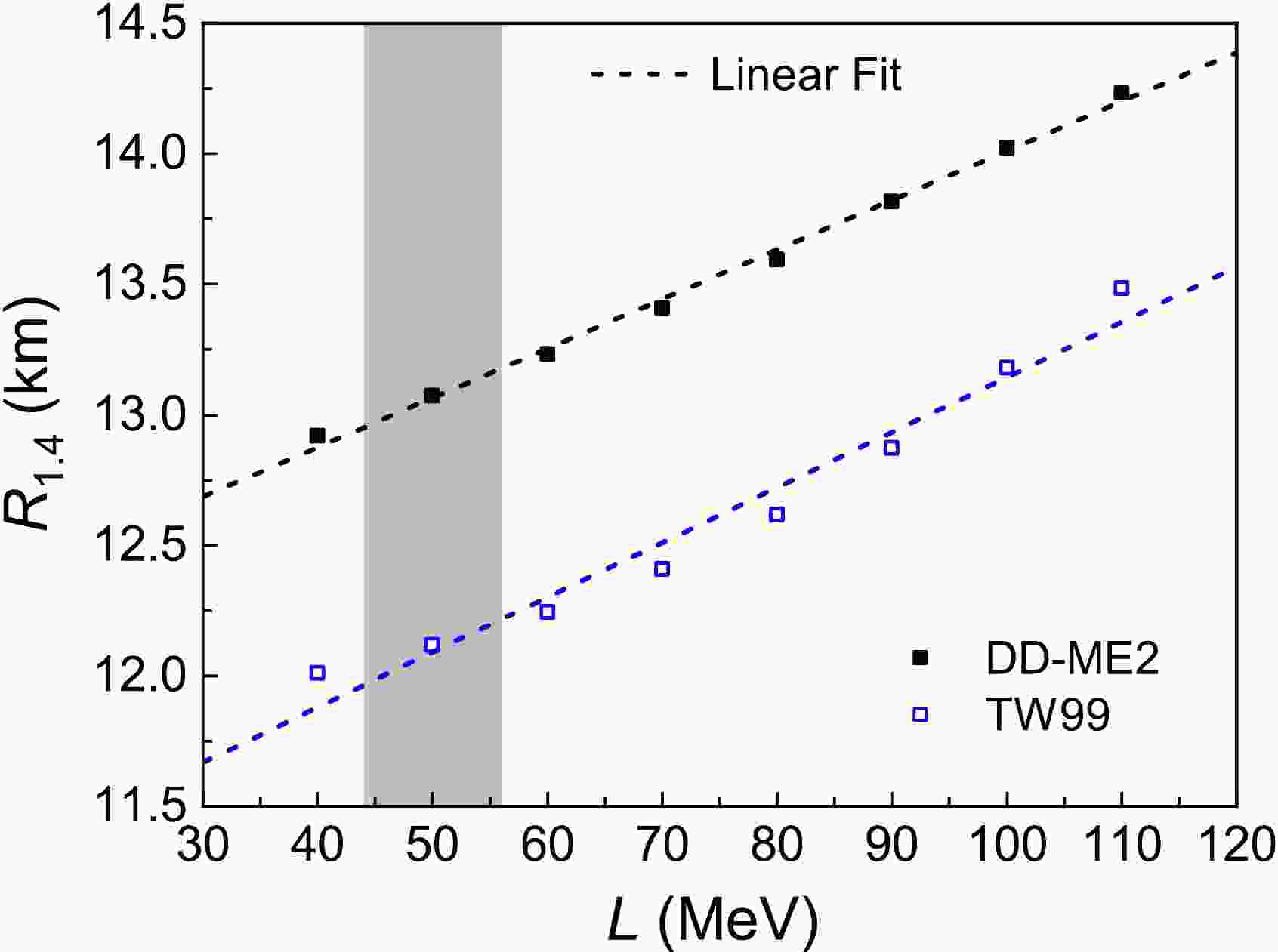
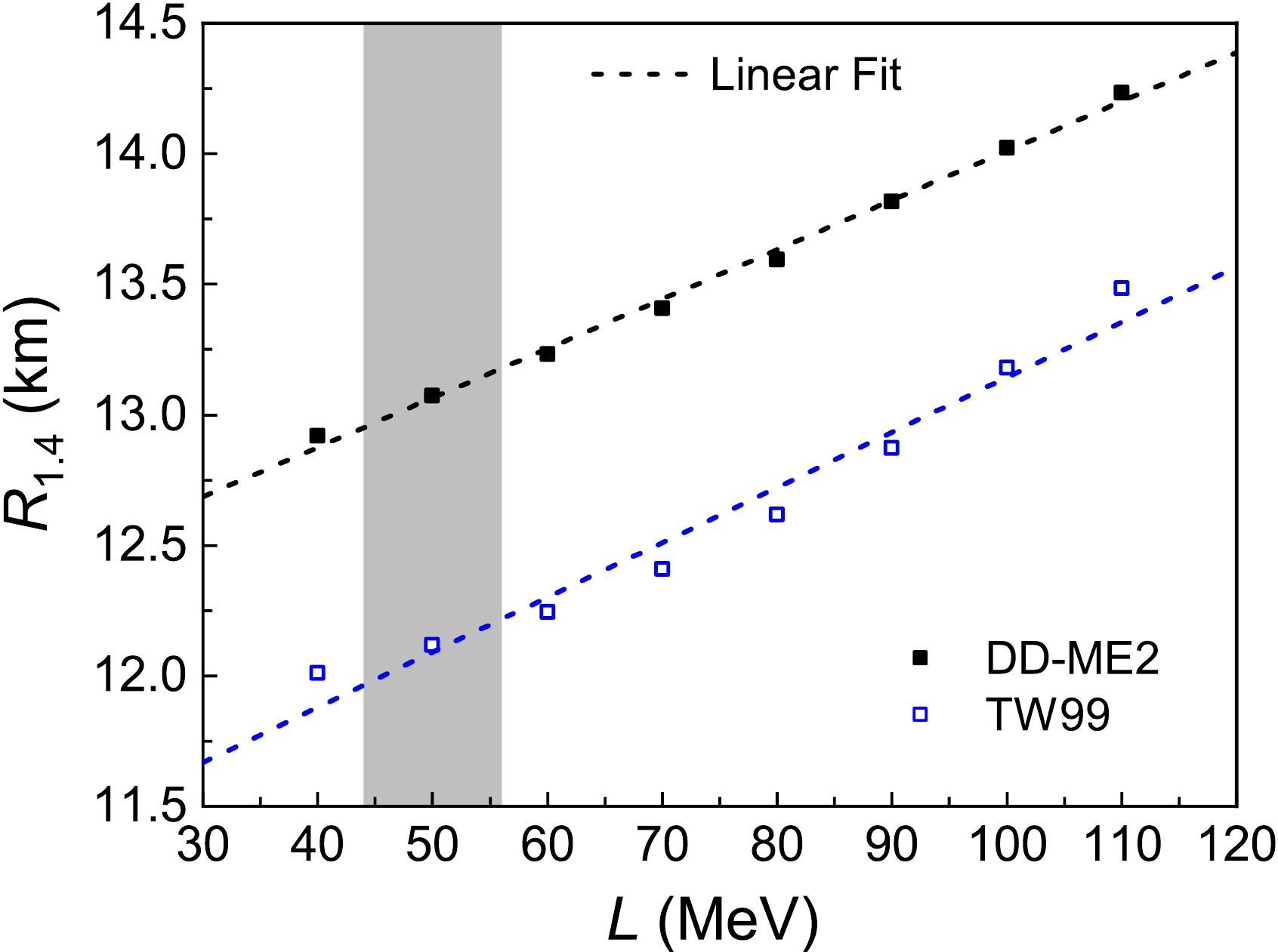
However, the effects of L on $ R_{1.4} $ can be evaluated by adjusting the coupling constants associated with the vector-isovector meson ρ in the relativistic mean-field Lagrangian, while the coupling strengths of isoscalar mesons are kept; for more details, see Ref. [5]. For instance, the linear $ R_{1.4} $-L relationships were established using such methods based on the TM1 and IUFSU EoS families [5]. Similarly, we also deduced the $ R_{1.4} $-L relationships from the DD-ME2 and TW99 EoS families. The matter in the core of a neutron star is composed of neutrons, protons, electrons, and muons and is assumed to be in β-equilibrium. For the core, we describe the EoS of uniform neutron star matter using the DD-ME2 and TW99 models. For the inner and outer crust regions, the EoSs of nonuniform matter are generated by the Thomas-Fermi approximation and Baym-Pethick-Sutherland, respectively. By fitting the deduced $ R_{1.4} $-L relationships (see Fig. 5) linear functions of $ R_{1.4} = 12.12+0.0189L $ and $ R_{1.4} = 11.03+ 0.0211L $ were obtained for the DD-ME2 and TW99 families, respectively. These linear functions are helpful to evaluate the effects of L on the $ R_{1.4} $ determinations. The spread of 30−110 MeV for L leads to an $ R_{1.4} $ uncertainty of approximately 1.6 km under the same theoretical framework (see Fig. 5). This is comparable to the model-dependent $ R_{1.4} $ uncertainty of approximately 2 km for the different EoS families [4, 15]. Compared to the $ R_{1.4} $ uncertainty of approximately 1.6 km caused by the L spread of 30−110 MeV, the obtained L of 50(6) MeV in this study from the finite nucleus system improves the $ R_{1.4} $ precision (resulted only by L) by a factor of approximately 7 to be around 0.24 km under the same theoretical framework (see Fig. 5). Therefore, at the precision level of our L, the model-dependent $ R_{1.4} $ uncertainty of approximately 2 km becomes more obvious [4, 15]. Furthermore, as shown in Fig. 5, there is an obvious model-dependent $ R_{1.4} $ difference of approximately 1 km between the DD-ME2 and TW99 EoS families. For the model-dependent $ R_{1.4} $ difference between the TM1 and IUFSU EoS families, as shown in Fig. 15 in Ref. [5], which was explained by the difference of incompressibility coefficient $ K_0 $ [5], the $ Q_{0} $ value of $ - $285 MeV for the TM1 is very close to that of $ - $290 MeV for the IUFSU EoS family [15]. Compared to $ K_0 $ and L, the poorly understood $ Q_0 $ has a large spread from $ \sim - 1000$ to $ \sim 1000$ MeV [15]. We note that the DD-ME2 and TW99 families have almost the same $ K_0 $, but the $ Q_0 $ values are completely different: 478 MeV and $ - $544 MeV, respectively [15]. Therefore, it would also be interesting to further study the $ R_{1.4} $ deviation caused by the poorly understood $ Q_0 $ using the DD-ME2 and TW99 EoS families. Besides, $ K_0 $ and $ Q_0 $ largely influence the high-density behaviors of EoSs and the magnitude of $ R_{1.4} $ of neutron stars.

Figure 5.  (color online) $R_{1.4}$-L correlations obtained by the DD-ME2 and TW99 EoS families. The dashed lines show the linear fit curves. The shaded area is the range of L constrained by this study.

The symmetry energy slope L at the saturation density was constrained by neutron skins from various experiments. The determined L of 50(6) MeV is consistent with the so-called world-averaged result from different observables and methodologies. Furthermore, based on the DD-ME2 and TW99 EoS families, the linear $ R_{1.4} $-L relationships were established to study the effects of the newly constrained L on the radius determinations of 1.4 solar-mass neutron stars. Significant model-dependence of neutron star radius was observed as a result of varying skewness parameter $ Q_0 $. Our L value effectively reduces the $ R_{1.4} $ uncertainty of neutron stars caused by the L spread by a factor of approximately 7 to be around 0.24 km under the same theoretical framework, which is smaller than the uncertainty of approximately 2 km from the different EoS families.

We would like to thank J. J. Li for the useful discussions and calculations.