Rotating and non-linear magnetic-charged black hole with an anisotropic matter field

From the prediction of black holes by general relativity to the release of the first image of a black hole shadow in Virgo A* galaxy (M87) by the Event Horizon Telescope Collaboration in April 2019 [1], more than a hundred years have passed. Although we have made significant advancements in both observation and black hole theory, the unavoidable issue of singularities in black hole theory still remains. The singularity of a black hole has a series of peculiar properties, including infinite density and curvature, where currently known physical laws fail [2]. The black hole singularity problem originates from general relativity, but general relativity does not apply at the singularity, highlighting the incomplete development of our current theory of gravity. It is generally believed that solving this problem requires a complete theory of quantum gravity, through which the black hole singularity can be fully resolved. However, given that a complete theory of quantum gravity has not yet been discovered, using semiclassical theories to address the singularity problem remains extremely valuable.

In 1968, Bardeen presented the first solution for a regular black hole [3]. It avoids the singularity by incorporating a de Sitter core that generates negative pressure, thereby preventing a singular end-state of the gravitationally collapsed matter [4, 5]. Afterwards, Ayón-Beato and García considered the coupling between the gravitational field and a non-linear electromagnetic field [6]. Then, the Bardeen black hole solution could be recovered, indicating that the Bardeen model can be interpreted as a non-linear magnetic monopole in non-linear electrodynamics. Subsequently, more regular black holes, such as Ayón-Beato and García [7], Hayward [8], and Berej-Matyjasek-Trynieki-Wornowicz [9] black holes, were obtained by coupling non-linear electrodynamics with gravitational theory.

In astrophysical research, the spherically symmetric model is one of the simplest models. It can be divided into isotropic and anisotropic spherically symmetric celestial models based on whether the pressure is isotropic or anisotropic. Currently, most research focuses on isotropic fluids because astrophysical observations support isotropy [10, 11]. For example, the perfect Pascalian-fluid (isotropic-fluid) assumption is supported by theory and observation [12–14].

However, compared to isotropic models, studies on anisotropic models are relatively limited. Increasing theoretical evidence suggests that various interesting physical phenomena may occur within certain density ranges, leading to local anisotropy [15]. This has led to increased research on anisotropy. For instance, at the galactic level, dark force effects allow for an effective description in terms of general relativity sourced by an anisotropic fluid [16]. Local anisotropy in self-gravitating systems affects the physical properties, stability, and structure of stellar matter [17–19].

The electromagnetic field outside the Reissner-Nordström (R-N) black hole is the simplest anisotropic matter field, where the equation of state satisfies $ p_{r}=-\varepsilon $ in the radial direction and $ p_{\theta}=p_{\phi}=\varepsilon $ in the angular directions within a local reference frame. Cho and Kim extended the R-N black hole solution to obtain a Schwarzschild black hole with an anisotropic matter field [20]. The anisotropic matter field in this black hole is described by the parameters ω and K, related as $ r_{0}^{2 \omega _{2}} \equiv \left(1-2 \omega _{2}\right) K \geq 0 $. Subsequently, a rotating charged black hole with an anisotropic matter field [21] was proposed, and its geometry, thermodynamic properties, and energy extraction were studied. For further research related to anisotropic matter fields, see Refs. [22–27].

We have reviewed research and developments on regular black holes and anisotropic matter fields. In this paper, we consider both to obtain the solution of a non-linear magnetic-charged black hole with an anisotropic matter field and the corresponding rotating black hole. We then further study the geometric and thermodynamic properties of this rotating black hole.

The structure of this paper is as follows. In Sec. II, we obtain the solution for a non-linear magnetic-charged black hole with an anisotropic matter field. In Sec. III, we extend this solution using the modified Newman-Janis algorithm to obtain a solution for a rotating and non-linear magnetic-charged black hole with an anisotropic matter field and study its energy-momentum tensor and weak energy condition. In Secs. IV and V, we explore the geometric and thermodynamic properties of the rotating black hole, respectively. In Sec. VI, we examine the efficiency of the Penrose process for extracting energy from the rotating black hole. Finally, in Sec. VII, we present the conclusion and discussion of this study.

We consider the coupling between Einstein gravity and a non-linear electromagnetic field in the presence of an anisotropic matter field, which is described by the following equations:

Here, $ {\cal{L}} $ is a function of the invariant $ F \equiv \frac{1}{4} F_{\mu \nu} F^{\mu \nu} $ with $ F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu} $, given by [5, 28]

where Q is the magnetic charge. In this study, we consider black holes with an anisotropic matter field. The energy-momentum tensor of an anisotropic matter field obtained from Ref. [20] is given by

where $ p_{r}=-\varepsilon(r) $ and $ p_{\theta}=p_{\phi}=\omega \varepsilon(r) $. The energy density is

where $ r_0 $ is a charge-like quantity of dimension of length defined by $ r_{0}^{2 \omega }=(1-2 \omega ) K $.

To obtain a static spherically symmetric black hole solution, we assume that the line element is

and use the ansatz for Maxwell field,

Using Eqs. (2) and (3), we can simplify Eq. (9) to obtain

where Q is the integration constant. Furthermore, we obtain $ F=Q^{2} / 2 r^{4} $. Note that the magnetic charge Q is defined in the following integral form:

where $ S_{2}^{\infty} $ is a two-sphere at the infinity. From the above results, it is possible to simplify the time component of Eq. (1) as

By integrating Eq. (12) from r to $ \infty $ and using the relation $ M=\lim\limits_{r \rightarrow \infty}\left(m(r)-\dfrac{K}{2} r^{-2\omega +1}\right) $, one finally obtains

For the above equation for $ K=0 $, we can derive the metric function $ f(r) $ of the Hayward-like black hole [8]. When $ Q=0 $ and $ \omega=1 $, we can derive the metric function $ f(r) $ of the R-N black hole. It is found that K and q (q is the charge in the R-N black hole) have similar status in the metric function $ f(r) $. Therefore, K is the global charge, and $ r_0 $ is a charge-like quantity of dimension of length defined by $ r_{0}^{2\omega} = (1 - 2\omega)K $.

In the introduction, we mentioned the non-linear magnetic-charged black hole, which is a regular black hole without a curvature singularity. Now, we consider whether an anisotropic matter field in the non-linear magnetic-charged black hole will alter this property. To investigate this, we calculate the curvature of the black hole as follows:

From the above results, we find that the curvature diverges at $ r=0 $ owing to the influence of the anisotropic matter field, which indicates that the non-linear magnetic-charged black hole with an anisotropic matter field is not a regular black hole and has a singularity.

In 1965, the Newman-Janis algorithm (NJA) [29] was first proposed by Newman and Janis. This algorithm obtains the Kerr metric by performing a complex coordinate transformation on the Schwarzschild line element. The NJA has been widely applied in the scientific community [21, 28, 30–38]. Later, Azreg-Aïnou modified the NJA [39, 40]; the only difference from the original one is that they skipped the complexification of coordinates.

In this section, we use the modified NJA to generalize the solution of the spherically symmetric non-linear magnetic-charged black hole with an anisotropic matter field to obtain the corresponding rotating black hole solution. First, let us review the modified NJA for deriving a general rotating black hole line element from a general static spherically symmetric black hole line element. The line element for a static spherically symmetric spacetime in Boyer-Lindquist (BL) coordinates is

where

Considering the coordinate transformation

the line element in Eddington-Finkelstein (EF) coordinates $ (u, r, \theta, \phi) $ is obtained as

Concerning the null tetrads that satisfy the relations $ l_{\mu} l^{\mu}= n_{\mu} n^{\mu}=m_{\mu} m^{\mu}=l_{\mu} m^{\mu}= n_{\mu} m^{\mu}=0 $ and $ l_{\mu} n^{\mu}=-m_{\mu} \bar{m}^{\mu}= 1 $, the contravariant metric tensor in Eq. (20) can be expressed in terms of the null tetrads as

where

The key step of the modified NJA is the consideration of complex coordinate transformations in the $ u-r $ plane,

As a result of the transformation of Eq. (22), the metric function also takes a new form: $ f(r) $ $ \rightarrow $ $ F(r, a, \theta) $, $ g(r) $ $ \rightarrow G(r, a, \theta) $, and $ h(r) $ $ \rightarrow $ $ \Sigma=r^{2}+a^{2} \cos ^{2}\theta $ [39, 40]. Thus, the new form of null tetrads is given by

Then, from Eq. (21), the contravariant components of the metric $ g^{\mu\nu} $ can be obtained as

The following transformation is used to convert from EF to BL coordinates:

where the functions $ \lambda(r) $ and $ \chi(r) $ can be determined by ensuring that all the nondiagonal components of the metric tensor other than the coefficient $ g_{t \phi}\left(g_{\phi t}\right) $ are equal to zero. Therefore, we obtain that [39]

with

and

Finally, the rotating solution corresponding to the spherically symmetric line element Eq. (17) is obtained as follows:

Above, we mentioned the modified NJA algorithm, which provides a general expression for a rotating black hole metric. Using the metric function from Eq. (8) in the previous section, we obtain

Substituting Eq. (31) into Eq. (30), we obtain the line element of a rotating and non-linear magnetic-charged black hole with an anisotropic matter field as

where

The nonvanishing components of the Einstein tensor $ G_{\mu \nu} $ are given by

where the prime $ \prime $ denotes the derivative with respect to r and

To obtain the components of the energy-momentum tensor, we use the standard orthonormal basis [28, 41]:

The components of the energy-momentum tensor derived from Eqs. (34) and (36) and the Einstein field equation $ G_{\mu \nu} = 8 \pi T_{\mu \nu} $ are as follows:

from which we obtain

When $ Q=0 $ and $ K=\omega =0 $, Eq. (39) corresponds to rotating black holes with an anisotropic matter field and non-linear magnetic-charged black holes, respectively.

The weak energy condition ensures that the behavior of matter and energy is physically reasonable, preventing phenomena such as negative energy density. It states that, for any timelike vector $ \xi^{\mu} $ at any point in spacetime, the stress-energy tensor $ T_{\mu \nu} $ satisfies

With the decomposition of the energy-momentum tensor $ T_{\mu \nu} $, the weak energy condition is equivalent to

where $ i=r $, θ, φ. Substituting Eqs. (33), (38), and (39) into Eq. (41), we obtain

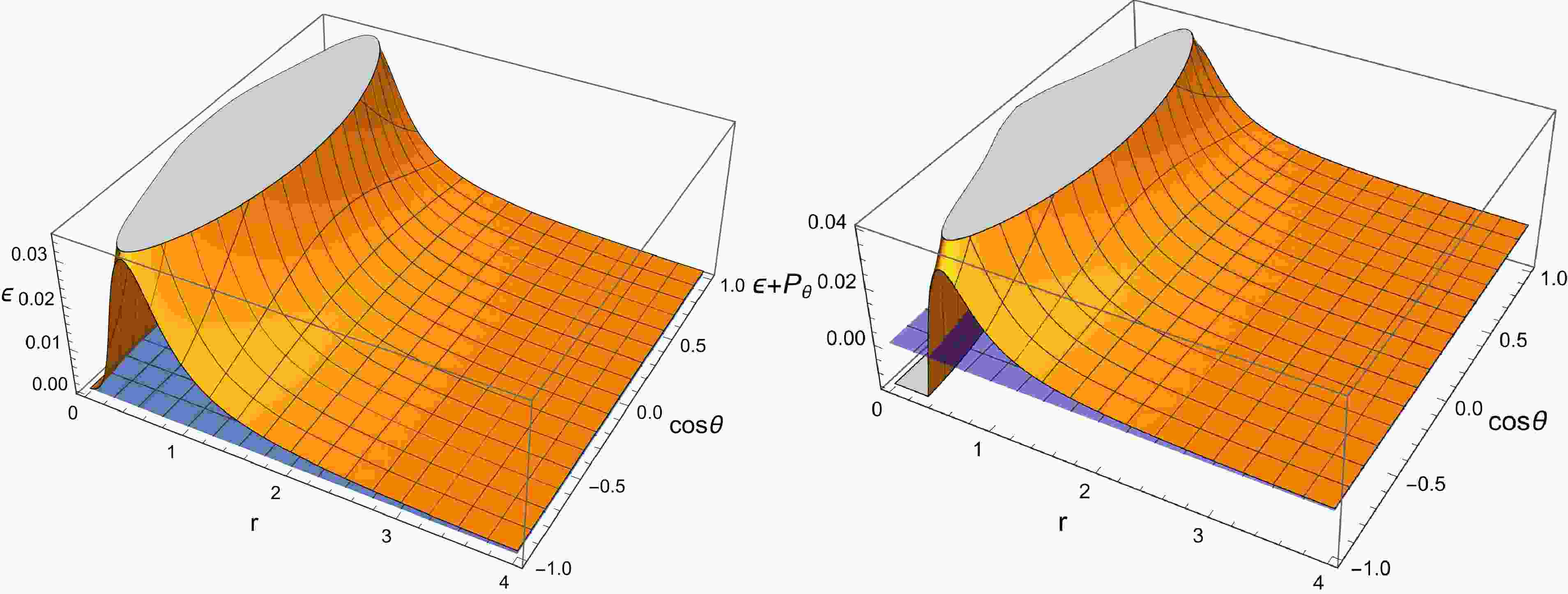
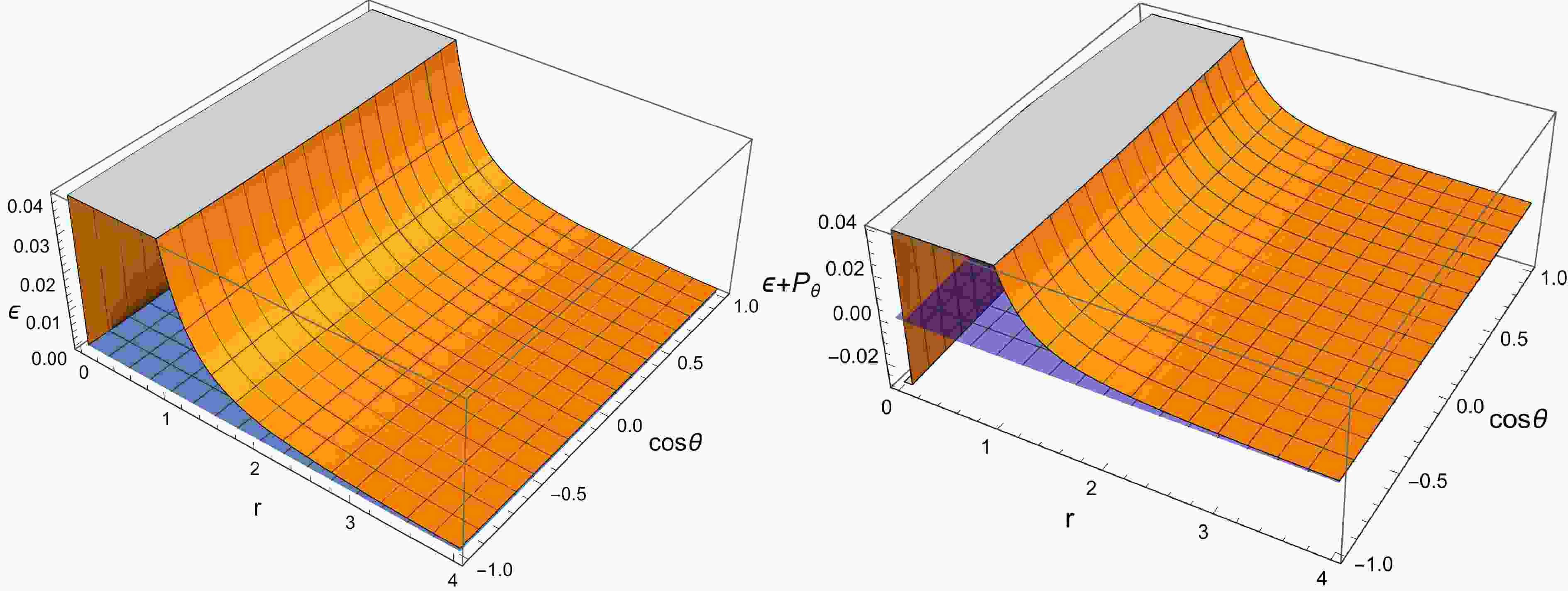
From Eqs. (42), (43), and (44), we present the variations of $ \epsilon $ and $ \epsilon+p_{\theta}/\epsilon+p_{\varphi} $ with r and $ \cos\theta $ under two sets of parameters in Figs. 1 and 2. It can be concluded from Figs. 1 and 2 that the weak energy condition is violated in a rotating, non-linear magnetic-charged black hole with an anisotropic matter field.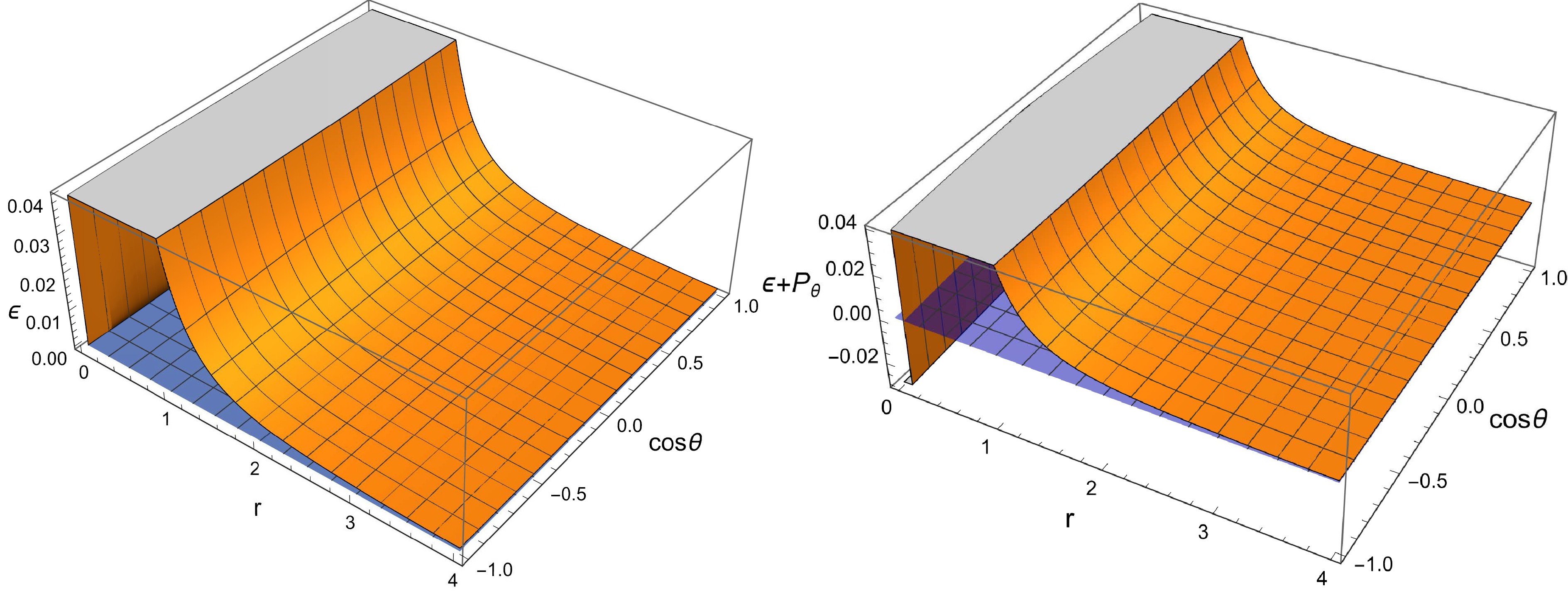

Figure 1.  (color online) Dependence of matter density $ \epsilon $ and $ \epsilon+p_{\theta} $ on radius and angle for rotating and nonlinear magnetic-charged black hole with an anisotropic matter field for $ M=1 $, $ Q=0.5 $, $ a=0.2 $, $ K=1 $, and $ \omega =0.2 $.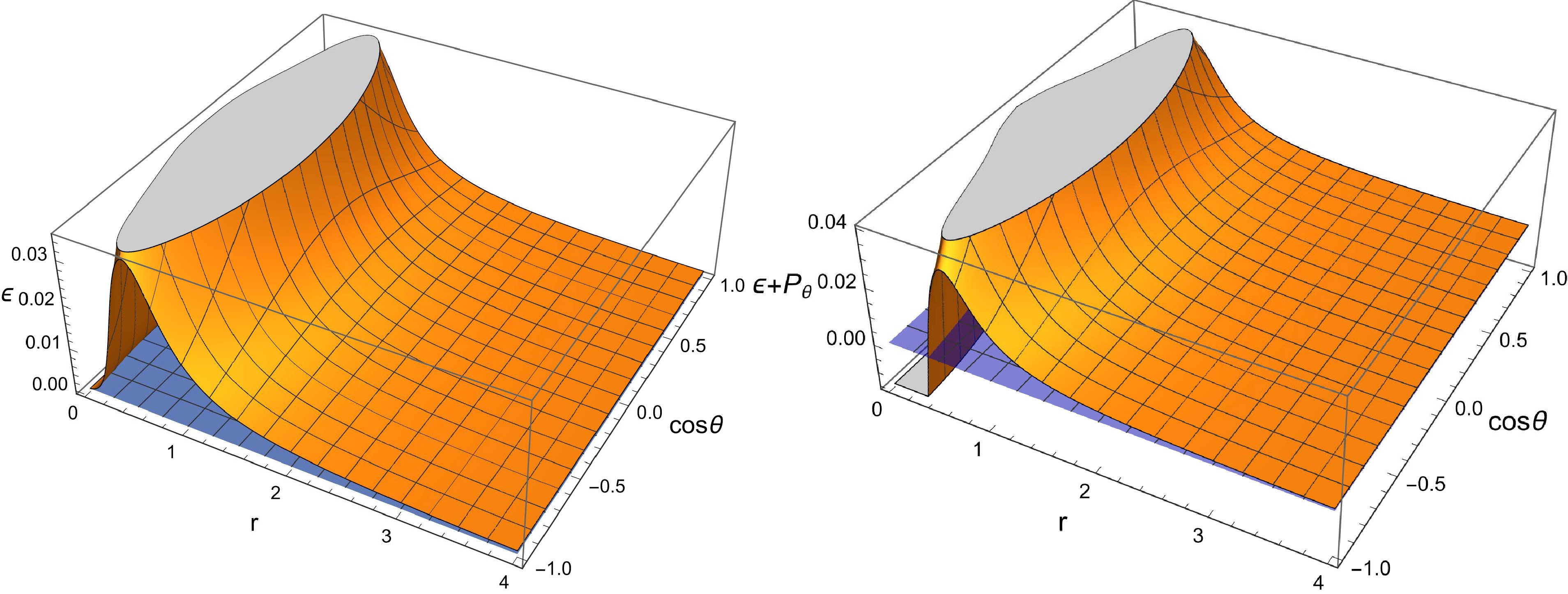

Figure 2.  (color online) Dependence of matter density $ \epsilon $ and $ \epsilon+p_{\theta} $ on radius and angle for a rotating and nonlinear magnetic-charged black hole with an anisotropic matter field for $ M=1 $, $ Q=0.5 $, $ a=0.9 $, $ K=1 $, and $ \omega =0.2 $.

Based on the analysis of parameter ω in Ref. [21], when $ 0 \leq \omega \leq \dfrac{1}{2} $, the energy density is not sufficiently localized, causing the total mass to diverge as $ r \to \infty $. As a result, subsequent studies primarily focused on systems with $ \omega > \dfrac{1}{2} $ to ensure that the spacetime asymptotically approaches flatness at infinity.

The event horizon corresponds to the Killing horizon, which defines the "surface" of a black hole as a three-dimensional hypersurface. The line element Eq. (32) is singular at $ \Delta= 0 $, which corresponds to the event horizon of the black hole and satisfies

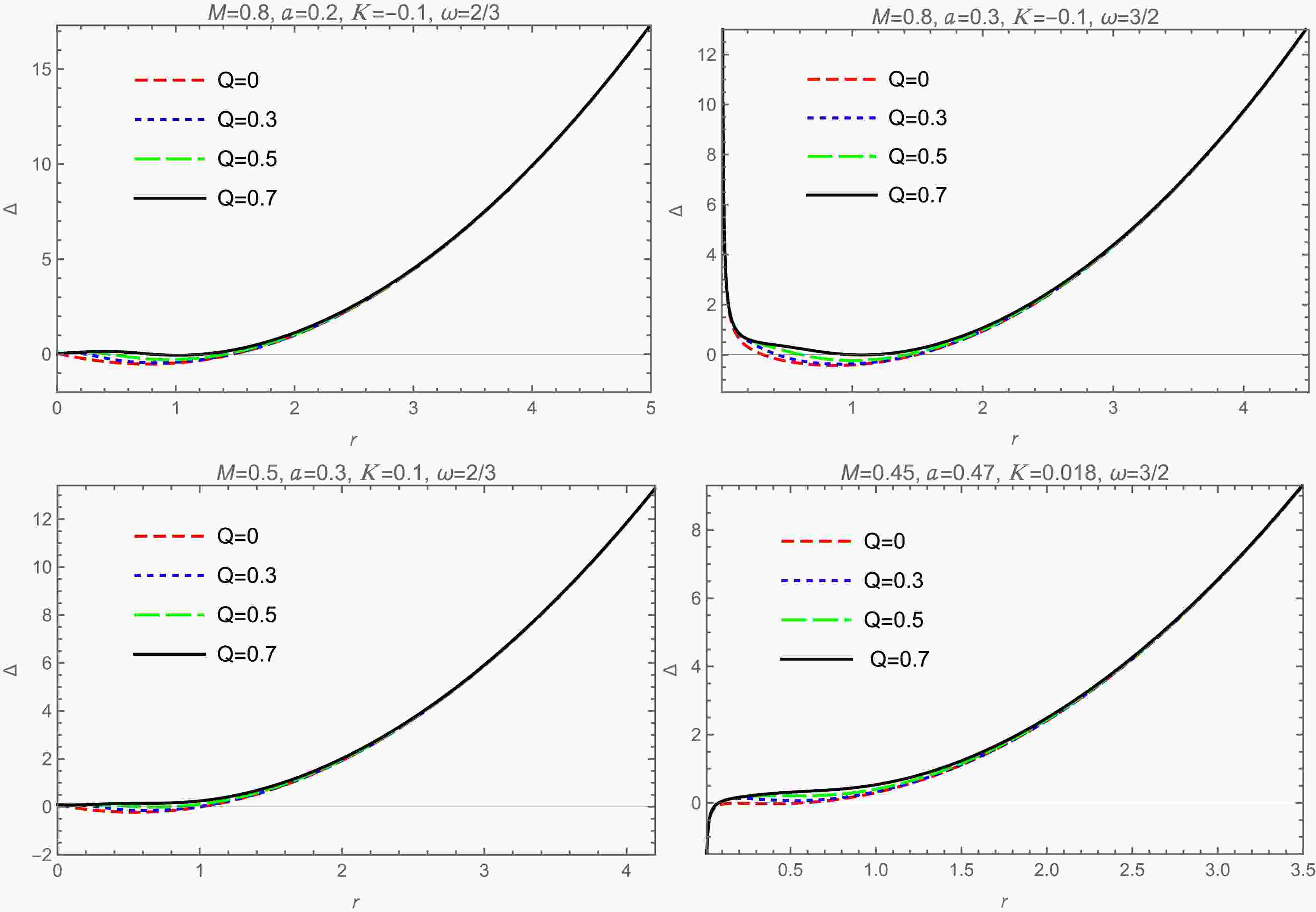
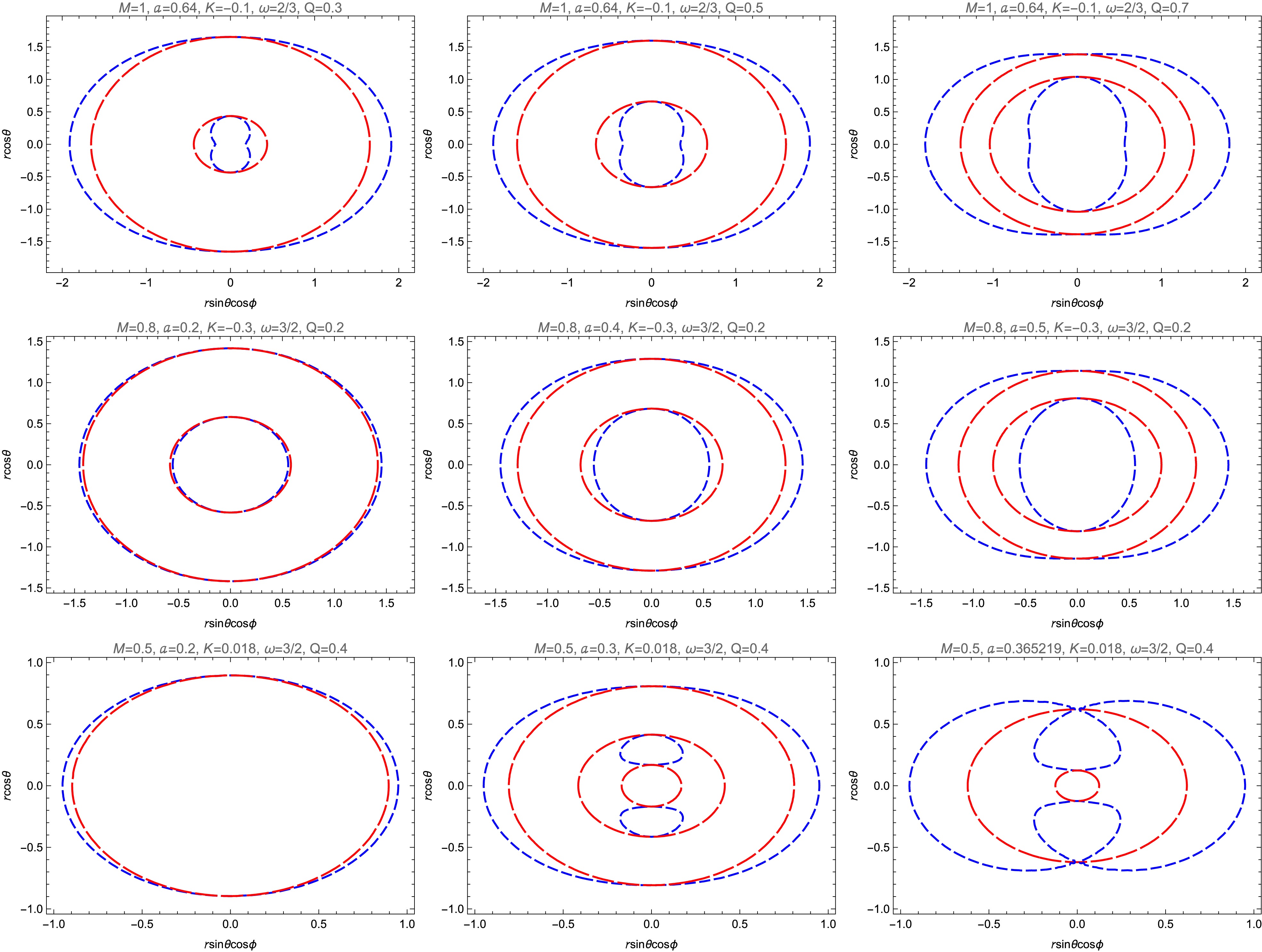
Based on the above equation, Fig. 3 shows the behavior of Δ as a function of r for different values of the parameters a, K, and ω with Q taking values of $ 0 $, $ 0.3 $, $ 0.5 $, and $ 0.7 $, respectively. In Fig. 3, the first and second graphs correspond to the case of $ K<0 $, while the third and fourth graphs correspond to the case of $ K>0 $. According to the first and third graphs in Fig. 3, for $ \dfrac{1}{2} < \omega < 1 $, the influence of Q on Δ is weakened as r increases, and this influence becomes negligible when r is large. This effect is noticeable within a small interval starting from $ 0 $. According to the second and fourth graphs in Fig. 3, for $ \omega > 1 $, the influence of Q on Δ is insignificant for both small and large values of r, with a noticeable effect only within a small interval of r. Therefore, the influence of Q on Δ mainly occurs within a small interval. The above analysis shows that we can analyze the possible roots of Δ by considering the case when $ Q = 0 $ [21]. By analyzing Eq. (45) and Fig. 3, we draw the following conclusions: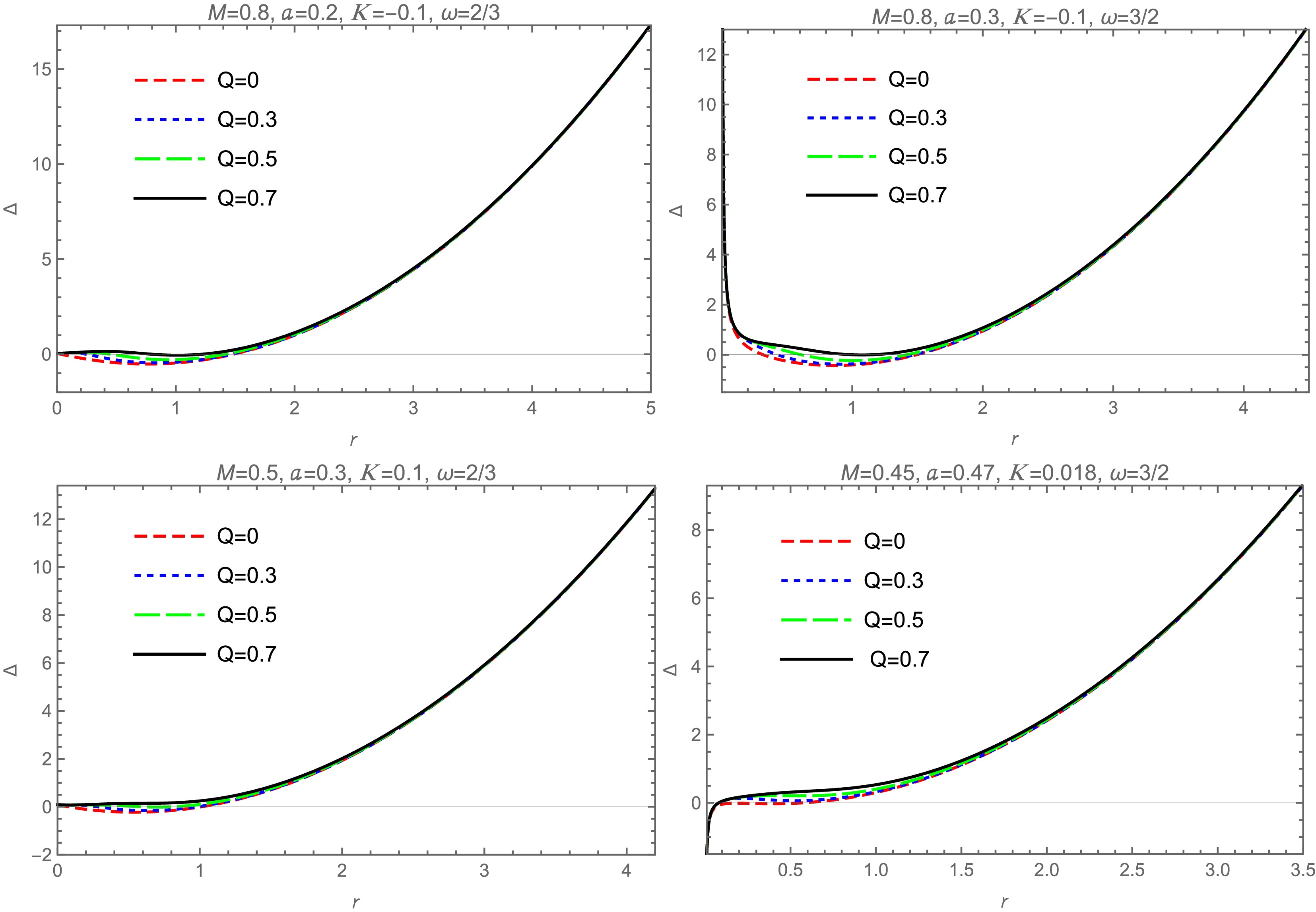

Figure 3.  (color online) Behavior of Δ as a function of r for different values of the parameters a, K, and ω when Q takes the values of 0, 0.3, 0.5, and 0.7.

● For $ \dfrac{1}{2} < \omega < 1 $, Δ is mainly dominated by the $ r^2 $ term for large r, while for smaller r, it is mainly influenced by $ r^2 $ and the non-linear magnetic-charged term. The influence of the nonlinear magnetic charge term causes Δ ($ Q \neq 0 $) to deviate from the case Δ ($ Q = 0 $) in a small interval starting from $ r = 0 $. For both cases, $ K < 0 $ and $ K > 0 $, the rotating black hole may have two horizons, namely the Cauchy and event horizons. For example, in the first and third graphs in Fig. 3, the Δ graphs correspond to the cases of $ K = -0.1 $, $ \omega = \dfrac{2}{3} $ and $ K = 0.1 $, $ \omega = \dfrac{2}{3} $, respectively.

● For $ \omega>1 $, Δ is mainly dominated by the $ r^2 $ term for large r, while for smaller r, it is primarily influenced by the anisotropic matter field term. The influence of the non-linear magnetic-charged term causes Δ ($ Q \neq 0 $) to deviate within a small range of r compared to the case Δ ($ Q = 0 $). For $ K < 0 $, Δ starts from positive infinity at $ r \to 0 $, decreases rapidly, and then increases again. Therefore, for $ \omega >1 $ and $ K < 0 $, the black hole may have two horizons. For $ K > 0 $, Δ starts from negative infinity at $ r \to 0 $, increases rapidly, then decreases, and then increases again, or Δ starts from negative infinity at $ r \to 0 $, increases rapidly, and then increases with the $ r^2 $ term. Therefore, for $ \omega >1 $ and $ K > 0 $, the black hole may have three horizons. For example, in the second and fourth graphs in Fig. 3, they correspond to Δ images for $ K = -0.1 $, $ \omega = \dfrac{3}{2} $ and $ K = 0.018 $, $ \omega = \dfrac{3}{2} $, respectively.

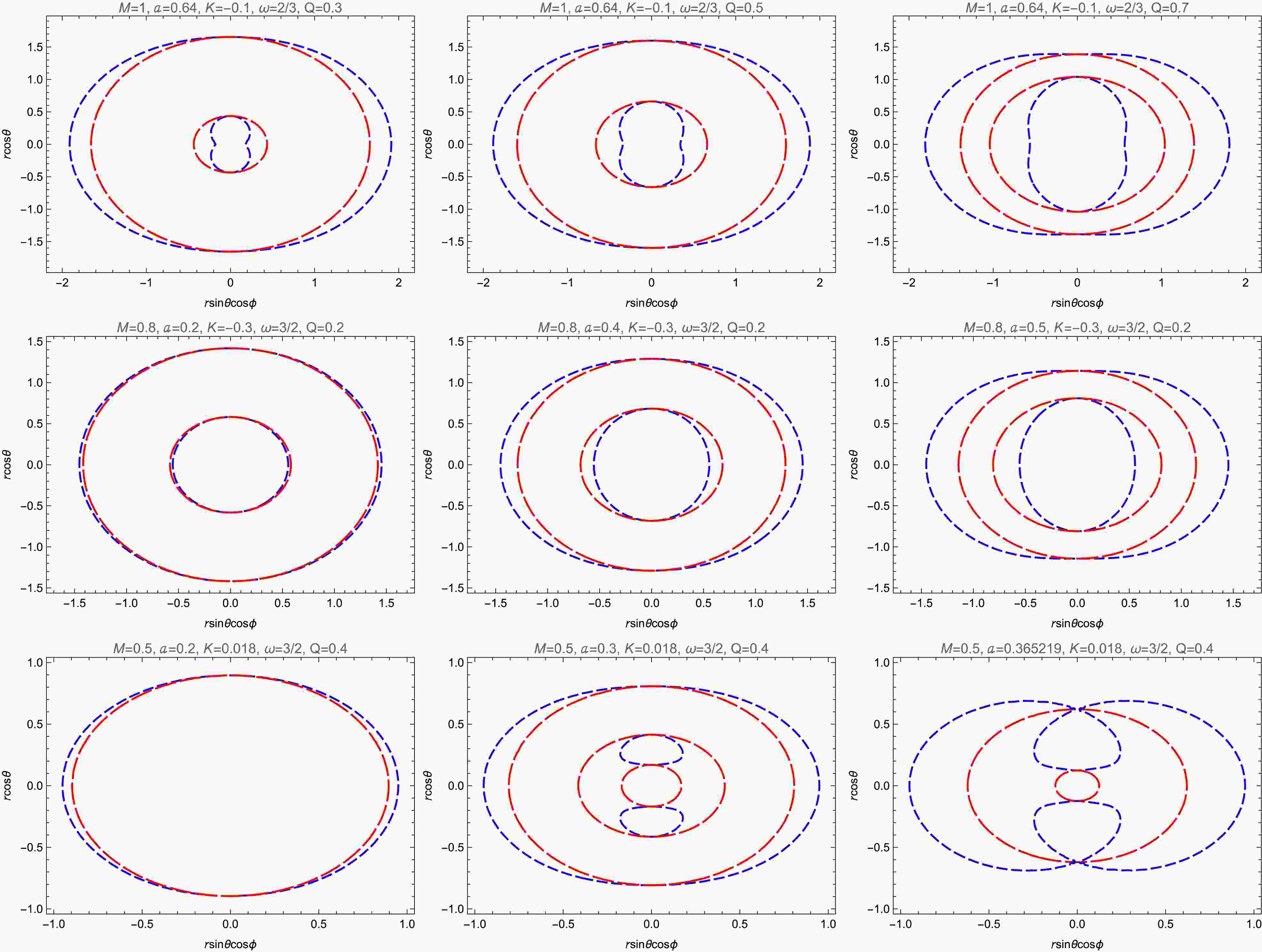
The stationary limit surface, also known as the infinite redshift surface, is where the timelike Killing vector $ K^\mu = \partial_t $ satisfies $ K^\mu K_\mu = 0 $. Therefore, we obtain

The ergosphere is a region outside the black hole, bounded by the event horizon and the outer stationary limit surface. Energy extraction from a rotating black hole relies on the ergosphere, which corresponds to the area between the outermost red curve and the blue curve in each graph in Fig. 4. Using Eqs. (45) and (46), we present the behavior of the ergosphere in the xz-plane for different values of the parameters a, K, ω, and Q in Fig. 4. In the first row of ergosphere graphs in Fig. 4, we show that, when other parameters are kept constant and the parameter Q is varied, the area of the ergosphere increases with the parameter Q. In the second and third rows of ergosphere graphs in Fig. 4, we show that, when other parameters are kept constant and parameter a is varied, the area of the ergosphere increases with the parameter a. In the third row of ergosphere graphs in Fig. 4, we show that, for $ K > 0 $ and $ \omega >1 $, as the parameter a increases, the black hole transitions from having a single horizon to three horizons, and then to two horizons.

Figure 4.  (color online) Behavior of ergosphere in the xz-plane for different values of the parameters M, a, K, ω, and Q.

We now understand that a black hole is not just a gravitational system but also a thermodynamic system. This insight originates from the proposal of black hole entropy [42, 43] and Hawking temperature [44, 45]. The Bekenstein-Hawking entropy is one-quarter of the event horizon area. Therefore, the entropy of a rotating and non-linear magnetic-charged black hole with an anisotropic matter field is given by

where $ r_{H} $ is the event horizon, which satisfies Eq. (45). On the event horizon, the Hawking temperature is proportional to the surface gravity κ:

The angular velocity of a rotating black hole at the event horizon is

Above, we directly derived the entropy, temperature, and angular velocity of the rotating black hole through the relationship between thermodynamic and classical mechanical quantities. However, other thermodynamic quantities of the black hole, such as the electric potential, are not easily obtained using similar methods. Below, we use the first law of thermodynamics and the squared-mass formula of a rotating and non-linear magnetic-charged black hole with an anisotropic matter field to solve for various thermodynamic quantities of the rotating black hole.

For a rotating and non-linear magnetic-charged black hole with an anisotropic matter field, we consider S, Q, J, and $ r_{0} $ as four independent thermodynamic quantities and express its first law of thermodynamics as [46]

where Φ is the magnetic charge potential for Q, J is the angular momentum, and $ \Phi_{0} $ is the electric potential for $ r_0 $. From Eqs. (45) and (48) and $ J=Ma $, we obtain the squared-mass formula for a rotating and non-linear magnetic-charged black hole with an anisotropic matter field as [47, 48]

From Eqs. (50) and (51), we obtain the following two thermodynamic quantities:

and

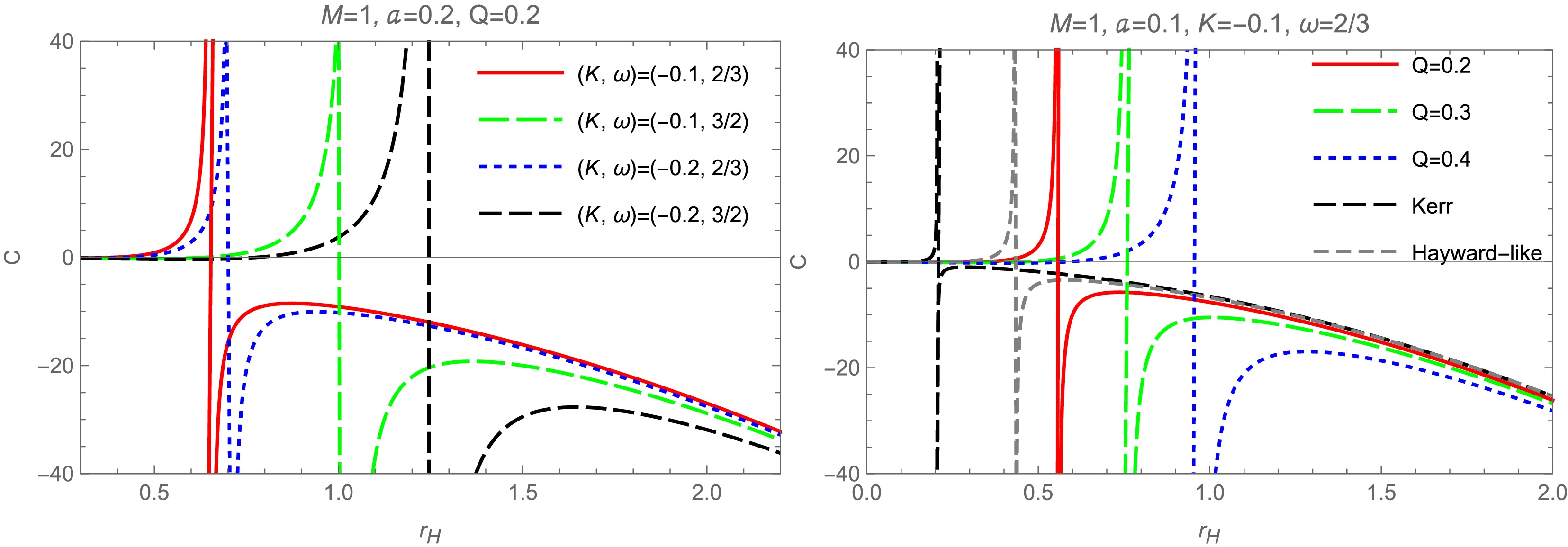
For Eq. (53), when $ Q=a=0 $ and $ Q =0 $ ($ a\ne 0 $), it degenerates into a Schwarzschild black hole with an anisotropic matter field [20] and rotating black hole with an anisotropic matter field [21], respectively. For a thermodynamic black hole system, the thermodynamic stability can be studied through its heat capacity. Therefore, we obtain the heat capacity of a rotating and non-linear magnetic-charged black hole with an anisotropic matter field and analyze the stability of the rotating black hole. The heat capacity C, calculated at constant angular momentum and charge in the canonical ensemble, is given by

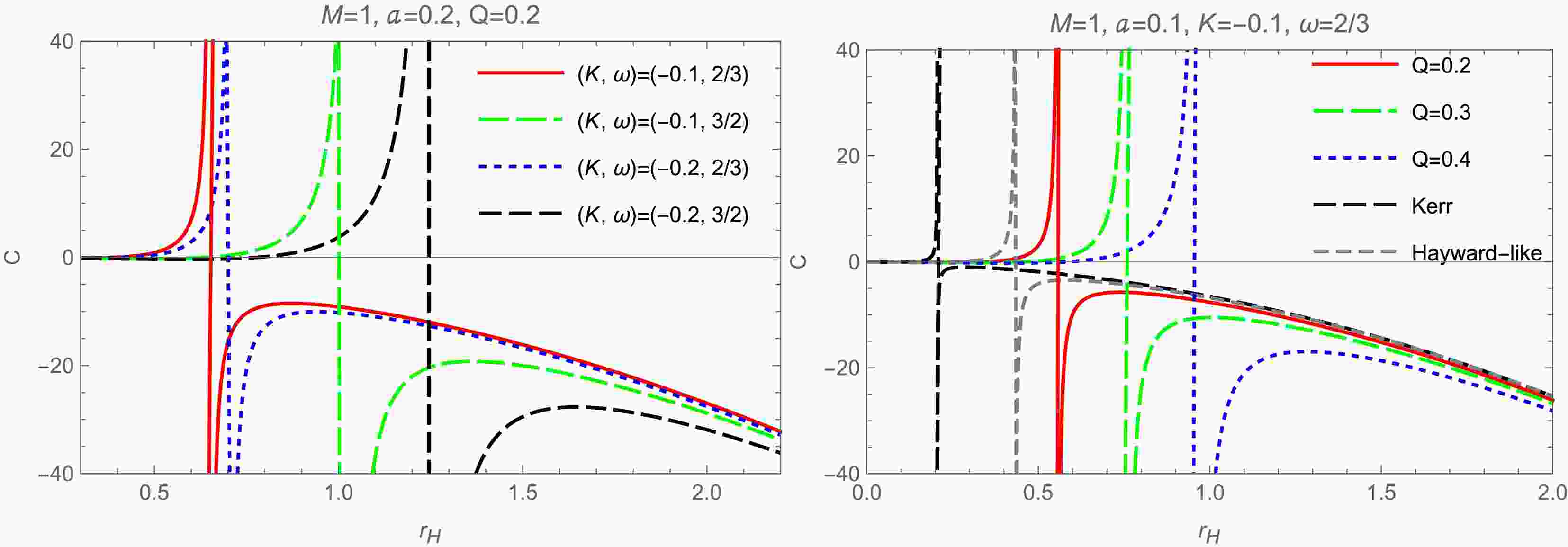
When $ Q = 0 $, the above equation degenerates into the heat capacity of a rotating black hole with an anisotropic matter field [21]. Based on Eq. (54), we plot the behavior of heat capacity as a function of $ r_{H} $ for different values of the parameters Q, a, K, and ω in Fig. 5. For a black hole thermodynamic system, the positive and negative values of the black hole heat capacity correspond to local thermodynamic stability and instability, respectively. In Fig. 5, the left and right graphs correspond to the heat capacity graphs for different values of the (K, ω) parameters and Q parameter, respectively. Note that, when the black hole event horizon radius satisfies $ 0 < r_{H} < r_{H}^{C} $, the system is thermodynamically stable, while for $ r_{H} > r_{H}^{C} $, it is thermodynamically unstable. At $ r_{H}=r_{H}^{C} $, the black hole heat capacity diverges, which indicates a second-order phase transition.

Figure 5.  (color online) Behavior of the heat capacity as a function of $ r_{H} $ for different values of the parameters a, K, ω, and Q.

In 1969, British physicist Penrose proposed a theoretical process for extracting energy from a rotating black hole, known as the Penrose process. Here, we calculate the Penrose process for a rotating and non-linear magnetic-charged black hole with an anisotropic matter field [49–51] and obtain the energy gain and extraction efficiency of this process.

The basic idea of the Penrose process is that a particle A moving on the equatorial plane ($ \theta =\pi/2 $, $ u^\theta =0 $) of the black hole enters the ergosphere, where it decays into two massless particles, B and C. The massless particle B falls into a negative energy orbit, while massless particle C escapes to infinity. According to energy conservation, the energy of massless particle C exceeds the initial energy of particle A. The four-momentum of a particle is

where $ u^{\nu} $ is the four-velocity of a particle. Considering that particles moving on the equatorial plane of a black hole satisfy energy and momentum conservation, we obtain

where E and L are the energy and angular momentum of the test particle, respectively. The radial equation for the geodesic motion of a test particle, derived from Eqs. (56) and (57), under the condition $ P_{\nu} P^{\nu}=-\delta $ , where $ \delta=-1 $, $ 0 $, $ 1 $, corresponding to time-like, null, and space-like geodesics, respectively, is as follows:

Assuming that the decay of particle A occurs at the turning point of the geodesic ($ u^{r}=0 $), we can derive from Eq. (58) and the condition $ u^{r} = 0 $ that

and

To have negative energy, the angular momentum must satisfy $ L < 0 $. Therefore, from Eq. (60), we obtain

Given that $ g_{tt}(\theta=\dfrac{\pi}{2})=-\left(1 - \dfrac{2\rho}{r}\right) $, it is evident from the inequality that this phenomenon can occur within the ergosphere. We consider a particle A ($ \delta=-1 $) with energy $ E_A=1>0 $ and angular momentum $ L=L_A $ entering the ergosphere. It then decays into two massless particles B and C ($ \delta=0 $), with energies and angular momenta ($ E_B $, $ L_B $) and ($ E_C $, $ L_C $), respectively. The massless particle B that falls into the event horizon has negative energy, while the massless particle C that escapes to infinity has positive energy. From Eq. (60), we obtain the relationship between the angular momentum and energy for A, B, and C as

The conservation of energy and angular momentum is expressed as follows:

and

The energies of two massless particles B and C obtained from Eqs. (62), (63), and (64) are given by

and

We conclude from Eq. (66) that the energy of the massless particle C escaping to infinity is higher than the energy of the particle A that initially entered the ergosphere of the black hole. The energy gain $ \Delta E $ can be obtained as

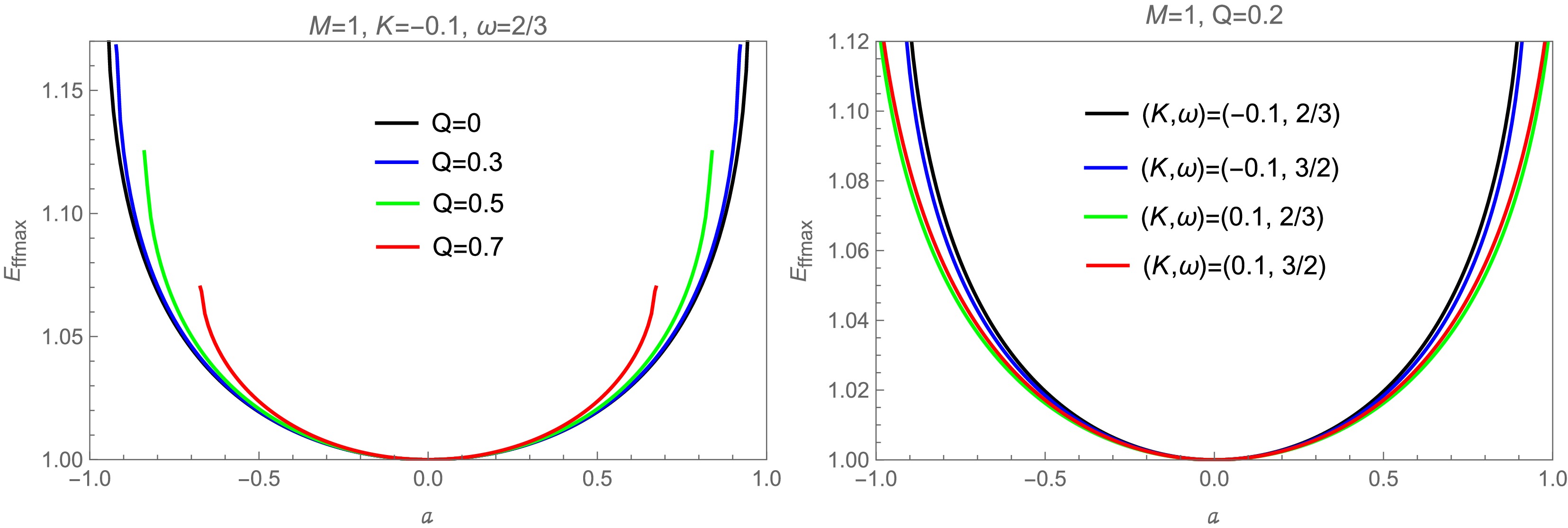
According to Eq. (65), the maximum energy gain occurs at the event horizon, and the maximum efficiency of the Penrose process is then given by

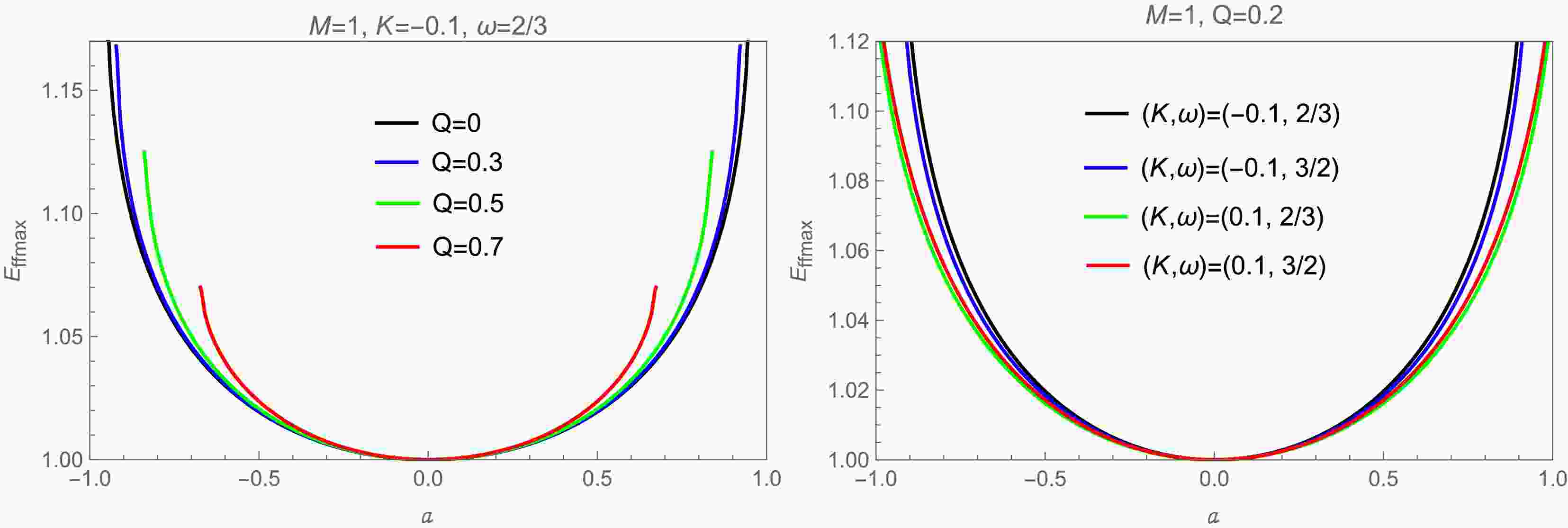
The behavior of the maximum efficiency of the Penrose process as a function of a for different values of the parameters K, ω, and Q is shown in Fig. 6. Note that $ E_{f f \max } $ increases with the spin parameter a and magnetic charge Q. The influence of the anisotropic matter field on $ E_{f f \max } $ is realized through its effect on the event horizon $ r_{H} $.

Figure 6.  (color online) Behavior of the maximum efficiency of the Penrose process as a function of a for different values of the parameters K, ω, and Q.

In this study, we first obtained the exact solution of the static, spherically symmetric non-linear magnetic-charged black hole with an anisotropic matter field and further calculated the curvature of the black hole. The results show that the curvature diverges at $ r=0 $, indicating that a non-linear magnetic-charged black hole with an anisotropic matter field has a singularity. We used a modified Newman-Janis algorithm to obtain the solution for a rotating and non-linear magnetic-charged black hole with an anisotropic matter field. Subsequently, we studied the energy-momentum tensor and weak energy condition for the rotating black hole, finding that this black hole violates the weak energy condition.

We investigated the geometric and thermodynamic properties of a rotating and nonlinear magnetic-charged black hole with an anisotropic matter field. Regarding the geometric properties, we first analyzed the influence of the spin parameter a and magnetic charge Q on Δ in Fig. 3. We found that the influence of Q mainly occurs within a small interval. Further analysis of Fig. 3 and Δ ($ Q = 0 $) [21] revealed that the rotating black hole may have two horizons for $ \dfrac{1}{2} < \omega < 1 $, regardless of whether K is positive or negative. For $ \omega > 1 $ and $ K < 0 $, Δ can have at most two roots, while for $ \omega > 1 $ and $ K > 0 $, the black hole can have at most three roots, indicating the possible existence of three horizons. Further analysis of the influence of various parameters on the ergosphere of the black hole showed that the area of the ergosphere increases with the spin parameter a and magnetic charge Q.

Regarding thermodynamic properties, we obtained the entropy, Hawking temperature, and angular velocity of the rotating and non-linear magnetic-charged black hole with an anisotropic matter field. To further derive other thermodynamic quantities, we presented the first law of thermodynamics for the black hole. Using $ \Delta= 0 $, we derived the squared mass formula and calculated other thermodynamic quantities. We further studied the stability of this black hole through its heat capacity and found that the black hole is thermodynamically stable when the event horizon radius satisfies $ 0 < r_{H} < r_{H}^{C} $. However, when $ r_{H} > r_{H}^{C} $, the black hole becomes thermodynamically unstable. At $ r_{H} = r_{H}^{C} $, the heat capacity diverges, which indicates a second-order phase transition.

Finally, we calculated the energy extraction efficiency of the Penrose process for a rotating and non-linear magnetic-charged black hole with an anisotropic matter field and found that the maximum efficiency increases with the spin parameter a and magnetic charge Q. The influence of the anisotropic matter field on the maximum efficiency of the Penrose process is realized through its impact on the event horizon.

In this study, we primarily analyzed black hole properties across various parameter values without imposing constraints on these parameters. The shape of the black hole shadow is sensitive to parameter changes. By combining observational data from the Event Horizon Telescope (EHT) and others, we can effectively eliminate parameter regions that do not match the measurements. In future research, we will constrain the parameter space of this black hole using observational features of the black hole shadow, such as the axis ratio and angular diameter.