Theoretical study of Strong gravitational lensing around Dyonic ModMax black hole: constraints from EHT observations

The study of strong gravitational lensing provides a profound window into the nature of spacetime and the properties of black holes. This phenomenon, predicted by Einstein's theory of general relativity[1, 2], occurs when light from a distant source is bent by the gravitational field of a massive object, such as a black hole, resulting in multiple images or highly magnified and distorted images of the source[3]. Strong gravitational lensing not only offers insights into the structure and dynamics of black holes but also serves as a powerful tool for probing fundamental physics under extreme conditions[4].

In recent years, the Event Horizon Telescope (EHT) has revolutionized our understanding of black holes by capturing the images of the shadow of a supermassive black holes at the center of the galaxy $ M87^* $[5, 6] and at the center of Milky Way [7, 8]. These unprecedented observations provide a unique opportunity to test various black hole models and theories of gravity[9]. Previous research has investigated the lensing properties of black holes in various modified gravity frameworks[10−14]. However, the gravitational lensing effects of black holes described by non-linear electrodynamics, such as the Dyonic ModMax model, remain underexplored.

Recent studies have explored gravitational lensing in non-linear electrodynamics, including the Dyonic ModMax model, focusing on weak lensing, plasma effects, and black hole shadows [15−20]. However, strong lensing and the interplay of dual charges with rotation remain underexplored [21, 22]. The Dyonic ModMax model’s duality and conformal invariance offer unique lensing signatures [23, 24]. This study investigates strong lensing in Dyonic ModMax black holes, proposing novel observational tests to constrain model parameters using future telescope data [16, 17], addressing primary and relativistic images in the strong gravitational field regime.

The Dyonic ModMax black hole model extends the conventional Maxwell theory by incorporating a modification through nonlinear electrodynamics, leading to distinct spacetime features that are absent in other modified gravity models[25]. Among the intriguing models that have emerged is the Dyonic ModMax black hole, which incorporates modifications to Maxwell's electrodynamics, leading to novel predictions about the behavior of light and matter in the vicinity of the black hole[26−29].

This article presents a theoretical investigation of strong gravitational lensing around Dyonic ModMax black holes. By analyzing the lensing effects and comparing them with the EHT observations, we aim to place constraints on the parameters of the Dyonic ModMax black hole model. We begin by reviewing the key aspects of gravitational lensing theory[30] and the Dyonic ModMax black hole solution[29, 31−34]. Subsequently, we derive the lensing observables, such as the angular position and magnification of the lensed images, and examine how these are influenced by the unique features of the Dyonic ModMax black hole.

Our study is motivated by the need to explore alternative gravity theories and to understand how deviations from classical general relativity manifest in observational phenomena[35−43]. The Dyonic ModMax black hole serves as a test case for these explorations, providing insights that could extend to other modified gravity theories. By comparing our theoretical predictions with the empirical data from the EHT[44−53], we aim to identify distinctive signatures of the Dyonic ModMax black hole and determine the feasibility of this model in explaining the observed characteristics of black hole shadows and lensing patterns.

The results of this investigation will not only shed light on the viability of the Dyonic ModMax black hole model but also contribute to the broader effort to test the limits of general relativity and explore new physics in the strong gravity regime[40, 54−57]. Through this theoretical and observational synergy, we seek to deepen our understanding of black holes and the fundamental laws governing our universe[58−60].

In this paper, we estimate the deflection angle of the light rays and the time delay of the signals from two relativitic images. We show that time delays between relativistic images are indeed measurable in most supermassive black holes cases. Moreover, it turns out that in a first approximation, the time delay between consecutive relativistic images is proportional to the minimum impact angle. The ratio between these two observables is nothing but the distance of the lens, which can be estimated in a very precise way and without bias. This paper is structured as follows: in Sect. II we will give brief explanation about Dyonic ModMax black hole solution and obtain horizon properties, III, we will provide the main results of the gravitational lensing in the case of strong field regime. In Sect. IV we will derive a general expression for the time delay, also we will consider Dyonic ModMax spacetime case and calculate time delay for supermassive black holes at the center of several galaxies such as Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA). Finally, in Sect. V, we will give several conclusion.

Dyonic ModMax black hole space-time singularities have been extensively studied in GR with NED[17, 28, 61−63]. However, here we focus on a new black hole solution in GR with NED, involving an exotic field referred to as the Dyonic ModMax field. The action can be written as

where

are the electromagnetic Lorentz invariants in terms of the electromagnetic tensor $ F_{\mu\nu} $ and its dual $ \tilde F_{\mu\nu} : = \frac 12 \epsilon_{\mu\nu\sigma\rho} F^{\sigma\rho} $. From the ModMax Lagrangian the Plebański dual variable reads [31, 64]

Its dual is

Modified Maxwell field equations is given by[29]:

Also the Einstein equations can be expressed as

Here, the energy momentum tensor $ T^\mu_\nu $ is given by [29, 31]

To solve the einstein equation, we choose following anzats

In this paper we consider only asymptotically flat configurations, so that we choose $ \Lambda = 0 $ in Eq.(5). First we take $ A_\mu = (\Phi(r), 0, 0, Q_m \cos \theta) $ to consider dyonic solution. In this case we get

In consequence

and it is straightforward to show that, the only non-vanishing Pleban'ski variables are

For the electric potential, we can write

This condition leads to set conservation low for $ P_{01} $. In this case, the gravitational field equations read

the solution of this system of equations is

Finally, we can find the lapse function of the metric Eq.(7)

where $ Q_e $ and $ Q_m $ are the electric and magnetic charge of the black hole respectively, γ is related to a constant screening factor for the charge of the black hole, corresponds to the nonlinear parameter [29, 34]. If we choose $ \gamma = 0 $, Maxwell's theory is recovered. Also, by choosing $ Q_e = Q_m = 0 $ we can easily get the Schwarzschild case. To analyse horizon properties such a black hole, we set $ f(r) = 0 $. Under this condition we can find the event horizon radius:

Throughout this paper we study only photon motion which is neutral, massless particle. So we can define Q as $ Q_e^2 + Q_m^2 = Q^2 $.From Eq.(15) we can obtain the maximum value of black holes charge:

From Eq.(15) one can easily find that Q and γ parameters negatively affect on the horizon radius. Also, Eq.(16) gives boundary values for charge Q in terms of M and γ.

In this section, we have investigated strong gravitational lensing effect in the spacetime described as Eq.(7). To find photon sphere radius we can use following expression [65]:

where $ \prime $ is the differentiation with respect to the radial coordinate r. From Eqs.(7) and (17), we get

The specific energy and angular momentum can be written as

and

where $ \Delta = f(r)\cdot r^2 $ and $ \kappa_\mu $ is the killing vector. One of the important quantity is impact parameter which is defined as

We also assume the motion occurs in the equatorial plane, $ \theta = \pi/2 $. With this assumption, equations of motion in the radial direction can be obtained as

or

where $ V(r) $ is the effective potential for the motion of the photon and it reads

We consider that light beam coming from infinity is deflected at the closest distance $ r = r_0 $ and goes to infinity. At the closest distance, $ \dot{r} $ vanishes and from Eq.(22) we get following formula for the critical impact parameter at the closest distance as [65]

By using the above equation, we can define critical impact parameter as

The meaning of critical impact parameter is that if the photons that have an impact parameter $ b < b_c $ fall into the black hole. Parameter $ b(r_0) $ can be expanded in the power of $ r_0-r_m $ as

From Eq.(22), we can find following relationship between r and ϕ

or we can write in terms of the deflection angle $ \alpha(r_0) $ of the light beam

where

By introducing a variable z defined as

$ I(r_0) $ can be rewritten as

where

$ I(r_0) $ can be splitted into two parts, i.e., a divergent part $ I_D $($ r_0 $) and a regular part $ I_R $($ r_0 $): I($ r_0 $) = $ I_D $($ r_0 $)+ $ I_R $($ r_0 $). The divergent part is expressed as

where

and the result is

In the strong deflection limit $ r_0\rightarrow r_m $ Eq.(40) is formulated as

where $ \bar{a} $ is given by

Additionally, the regular part $ I_R $ is defined as

where

Since we are investigating deflection angle in the strong field limit $ r_0 \rightarrow r_m $, we consider

After some calculations, the analytical expression can be taken as

Eventually, the bending angle of the light rays $ \alpha(b) $ in the strong deflection limit $ b\rightarrow b_c $ is given by [65]

where $ \overline{a} $ and $ \overline{b} $ as

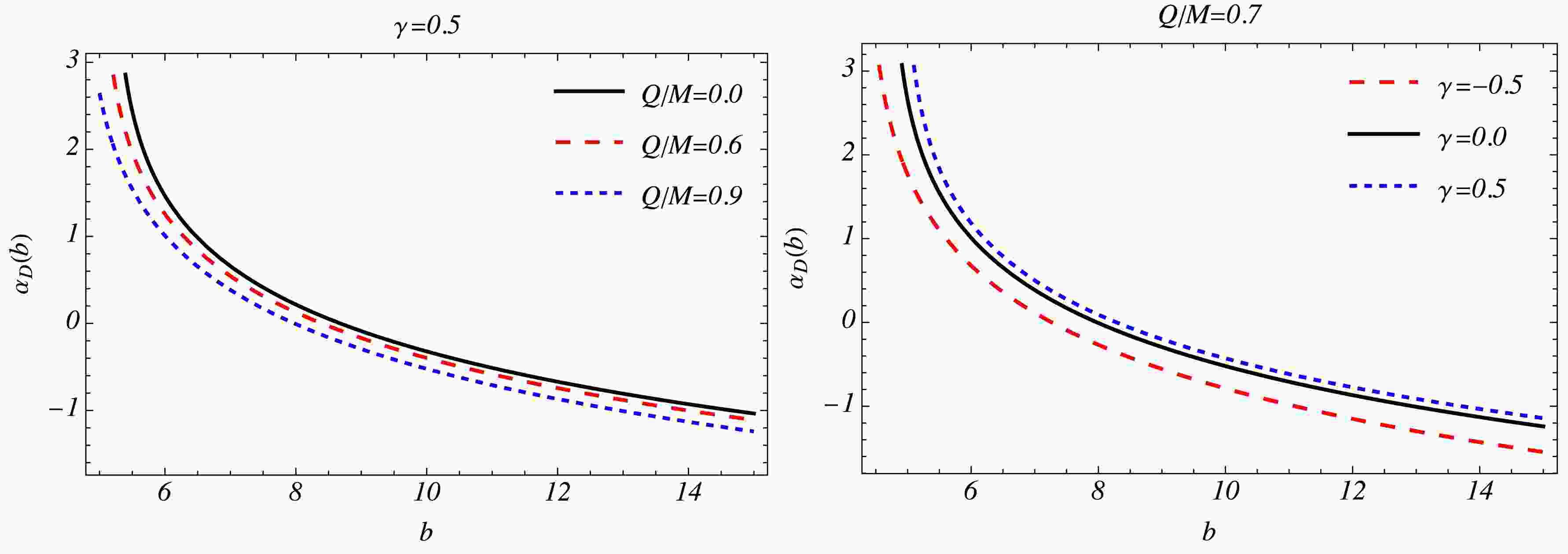
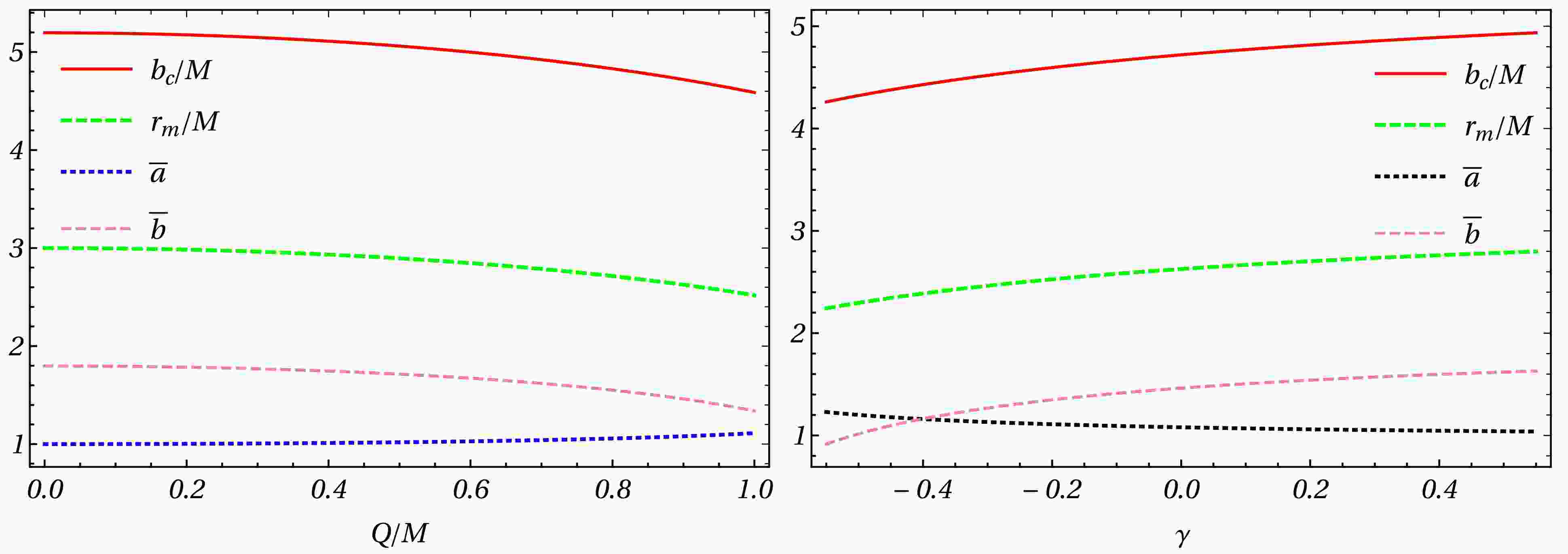
respectively. Table 1 gives information about $ b_c/M $, $ \overline{a} $ and $ \overline{b} $ are the lensing coefficients as the functions of the charge of the black hole Q/M and γ parameters. When the black hole non-charged $ (Q/M = 0) $, we obtain $ b_c = 3\sqrt{3}M $, $ \overline{a} = 1 $, and $ \overline{b} = -0.40023 $. When the black hole has $ Q/M = 0.6 $, we obtain $ b_c = 4.59M $, $ \overline{a} = 1.1092 $ and $ \overline{b} = -0.4085 $ which means in the case of Dyonic ModMax black hole, the quantity $ b_c $ will be smaller than the Schwarzschild case. From Fig. 1, One can see that the coefficient $ \overline{a} $ increases while $ \overline{b} $, $ b_c $, $ r_m $ decrease with the increased value of $ Q/M $. The deflection angle $ \alpha_D(b) $ as a function of b for different Q/M and γ is depicted in Fig. 2 The deflection angle for Dyonic ModMax black holes (see Fig. 2) is monotonically decreasing with impact parameter b and deflection angle $ \alpha_D(b)\rightarrow \infty $ as $ b\rightarrow b_c $. Interestingly, the deflection angle for Dyonic ModMax black holes decreases with the increasing value of parameter b whereas for an impact parameter close to the critical impact parameter (see Fig. 2), the deflection angle $ \alpha_D(b) $ decreases in both cases increasing values of Q/M and γ parameters.

γ	$ {Q/M} $	$ \bar{a} $	$ \bar{b} $	$ {b_c/R_s} $
0	0.0	1	-0.40023	2.59808
-0.5	0.4	1.03512	-0.396203	2.47728
-0.5	0.8	1.58337	-1.08685	1.94022
0.0	0.4	1.01974	-0.397184	2.49912
0.0	0.8	1.12317	-0.413638	2.27299
0.5	0.4	1.01147	-0.398215	2.55523
0.5	0.8	1.05727	-0.396916	2.41483

Table 1.  Estimated for the strong lensing coefficients $ \overline{a} $, $ \overline{b} $ and the critical impact parameter $ b_c/R $ for Dyonic ModMax Black hole Spacetime. The values for $ Q/M=0 $ and $ \gamma=0 $ correspond to a Schwarzschild black hole.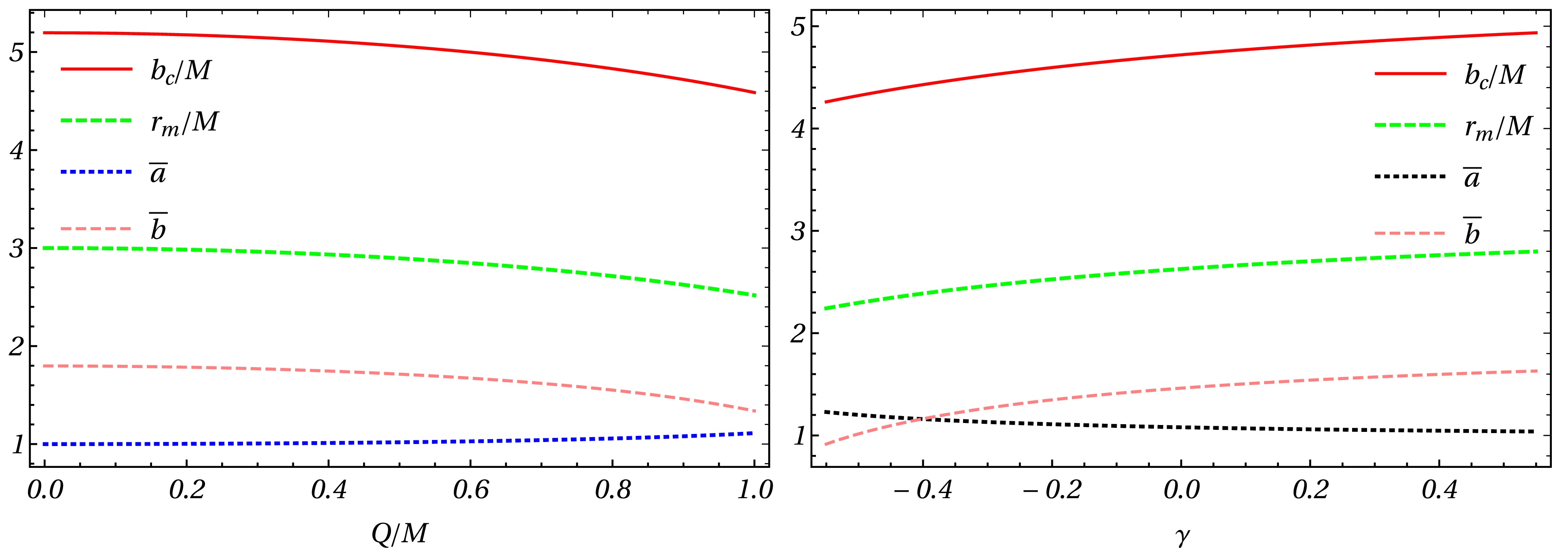

Figure 1.  The quantities $ b_c/M , r_m/M, \overline{a}, $ and $ \overline{b} $ in the Dyonic ModMax spacetime as the functions of Q/M and γ. $ \overline{a} = 1 $ and $ \overline{b} = -0.4002 $ at $ Q/M = 0, \gamma = 0 $ correspond to the values of a Schwarzschild black hole.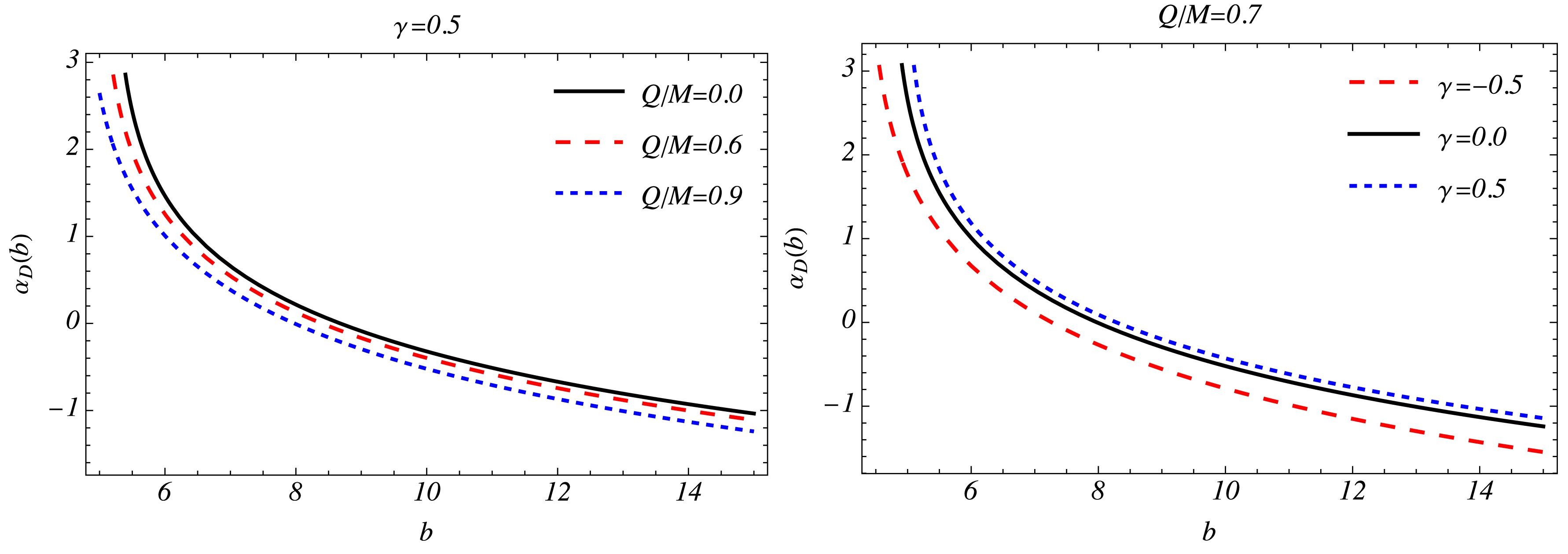

Figure 2.  Variation of deflection angle for Dyonic ModMax black hole spacetime as a function of the impact parameter b for different values of parameters $ Q/M $(left) and γ (right)

Where $ \Delta\alpha = \alpha-2n\pi $ is the offset of deflection angle looping over $ 2n\pi $ and n is an integer. Here, β is the angular position of the source while θ is the angular position of the image from the optic axis. The distance between the observer and the lens and between the observer and the source are $ D_{OL} $ and $ D_{OS} $, respectively. Using Eqs. (47) and (50), the position of the nth relativistic image can be approximated as [65]

Where

$ \theta^0_n $ are are the image positions corresponding to $ \alpha = 2n\pi $.As gravitational lensing conserves surface brightness, the magnification is the quotient of the solid angles subtended by the nth image and the source ([66],[65], [67]). The magnification of the nth relativistic image reads as [65]

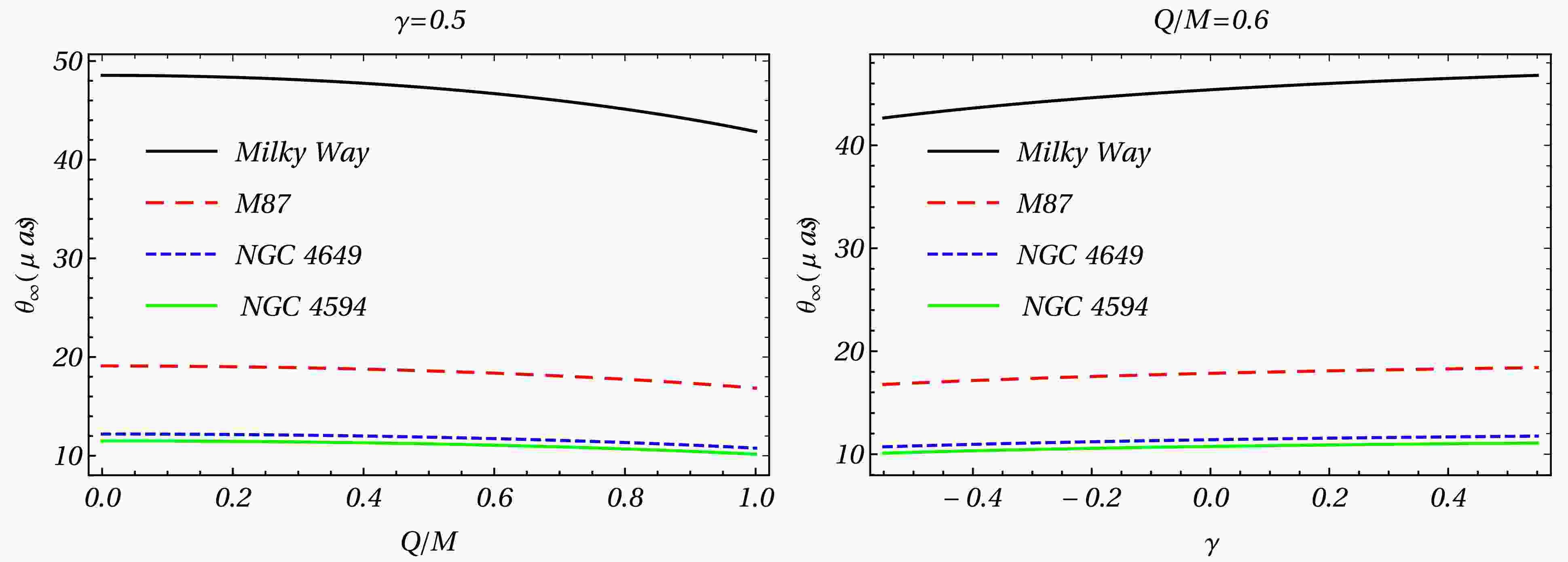
The first relativistic image is the brightest one, and the magnifications decrease exponentially with n. The magnifications are proportional to $ 1/D^2_{OL} $ which is a very small factor and thus the relativistic images are very faint, unless β has values close to zero, i.e., nearly perfect alignment. Having obtained the deflection angle (Eq.(47), (48), and (49)), we calculate three observables of relativistic images (see Table 3, Fig. 3,4 and 5), the angular position of the asymptotic relativistic images ($ \theta_\infty $), the angular separation between the outermost and asymptotic relativistic images($ s_\infty $), (see Fig. 4) and relative magnification of the outermost relativistic image with other relativistic images ($ r_{mag} $)(see Fig. 5)[65].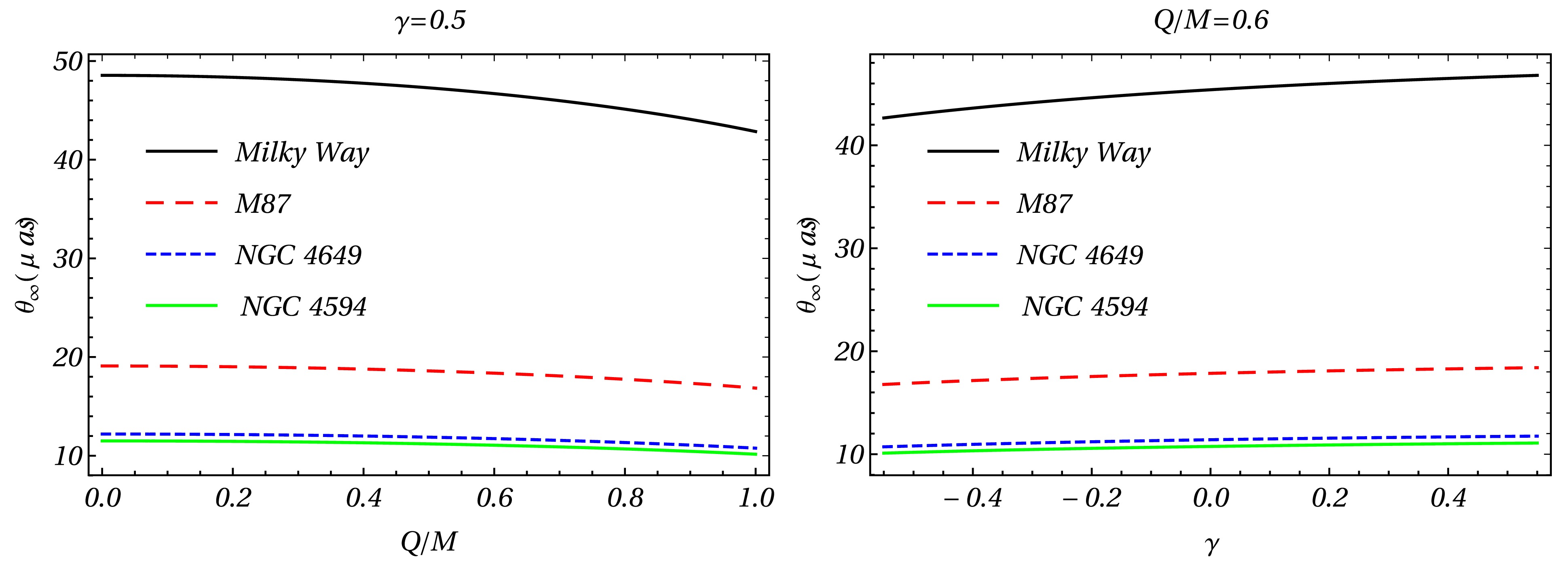

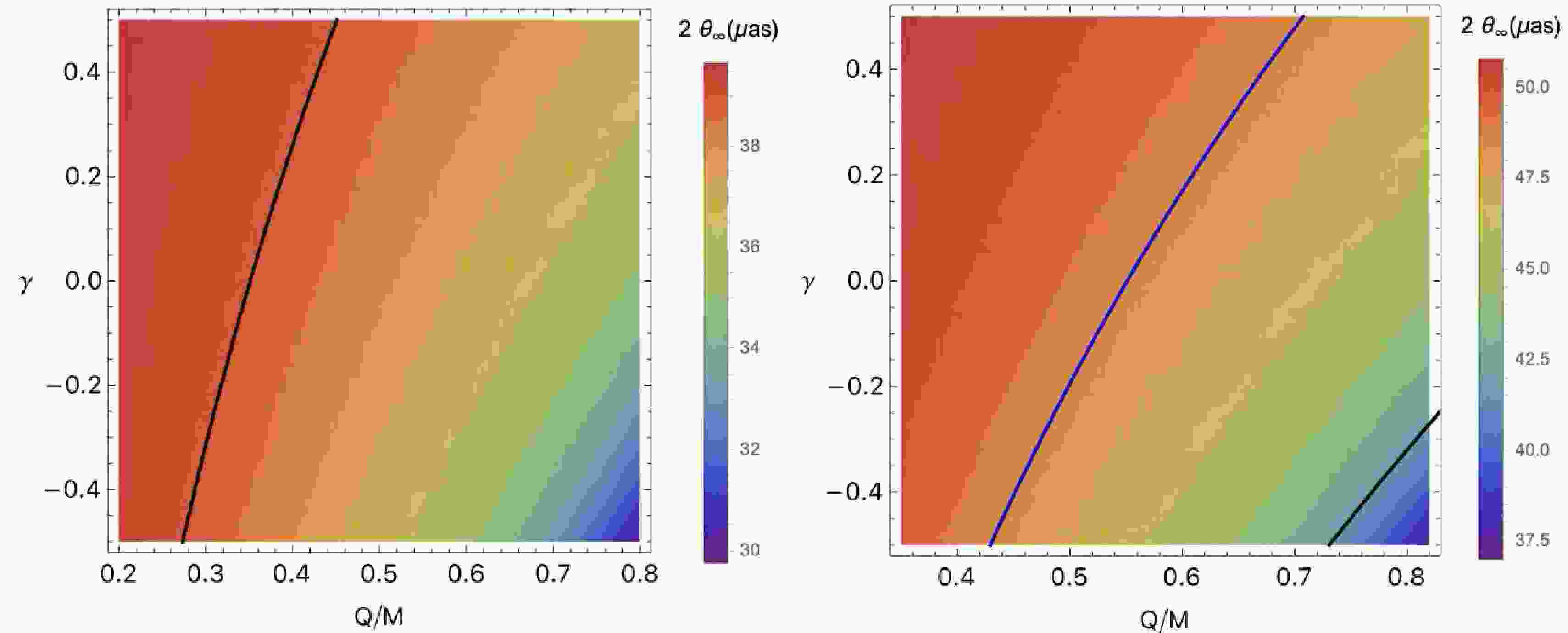
Figure 3.  Behavior of lensing observables $ \theta_\infty $ as a function of parameters Q/M and γ in strong field limit by considering that the spacetime around the compact object.

Galaxy	M($ M_\odot $)	$ D_{OL} $(Mpc)	$ M/D_{OL} $	$ \Delta T^S_{2,1}(Schw) $	$ \Delta T^S_{2,1}(DM) $
Milky Way	$ 3.61 \times10^6 $	0.00762	$ 2.26467\times10^{-11} $	11.4968	8.748
"NGC4486(M87)"	$ 3.0 \times10^9 $	16.1	$ 8.90733 \times10^{-12} $	8021	7270
NGC4649	$ 2.0 \times10^9 $	16.8	$ 5.6908 \times10^{-12} $	8021	7270
NGC4697	$ 1.7 \times10^8 $	11.7	$ 6.94569 \times10^{-13} $	5347.34	4846.67
NGC5128(cenA)	$ 2.4\times10^8 $	4.2	$2.73158 \times10^{-12} $	454.53	411.97

Table 3.  The time delay between two relativistic images of different galaxies.

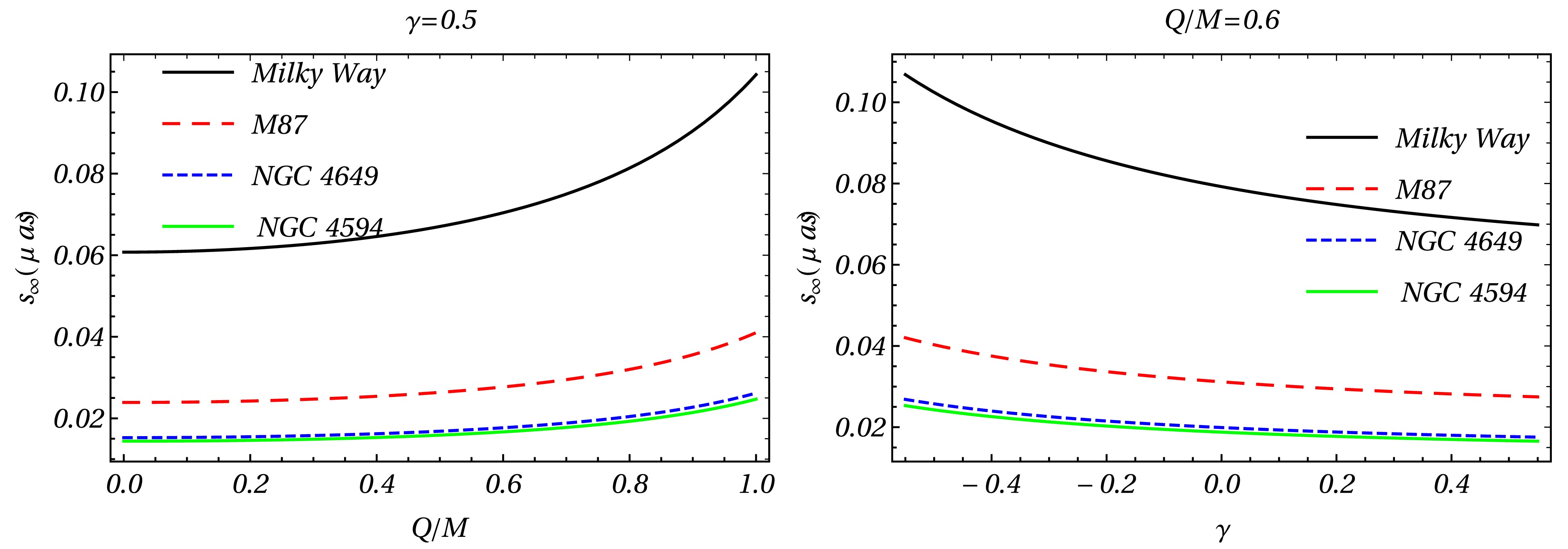
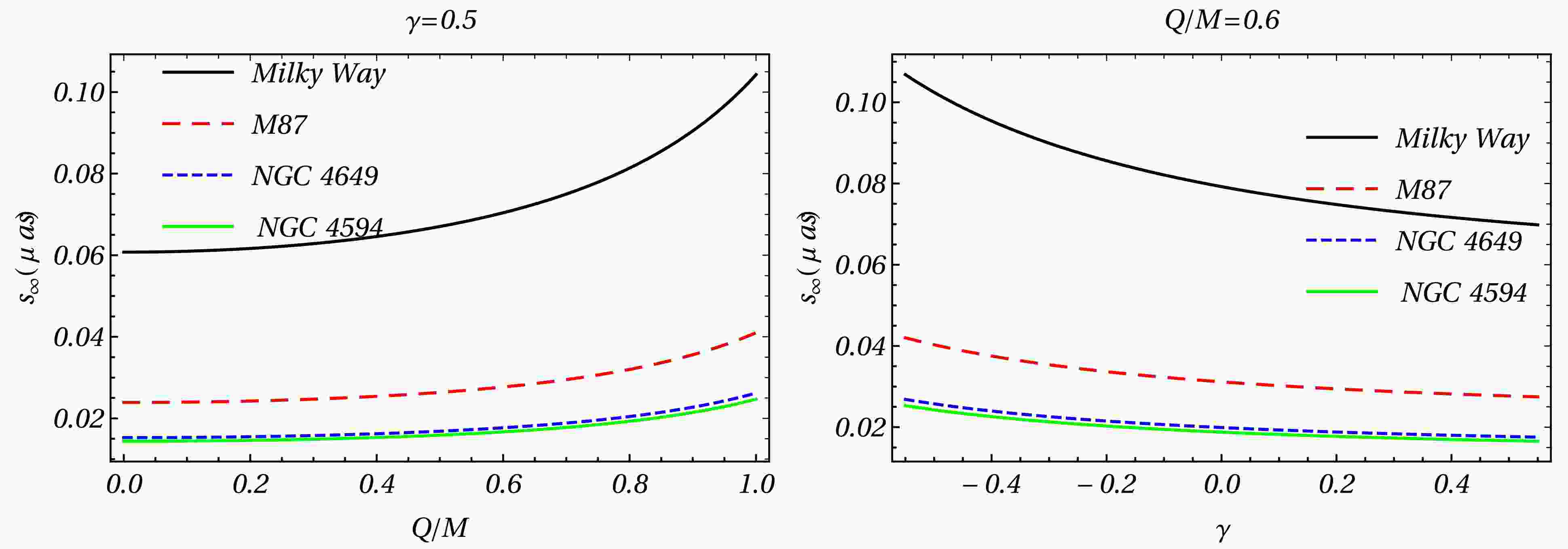
Figure 4.  Behavior of lensing observables $ s_\infty $ as a function of parameters Q/M and γ in strong field limit by considering that the spacetime around the compact object.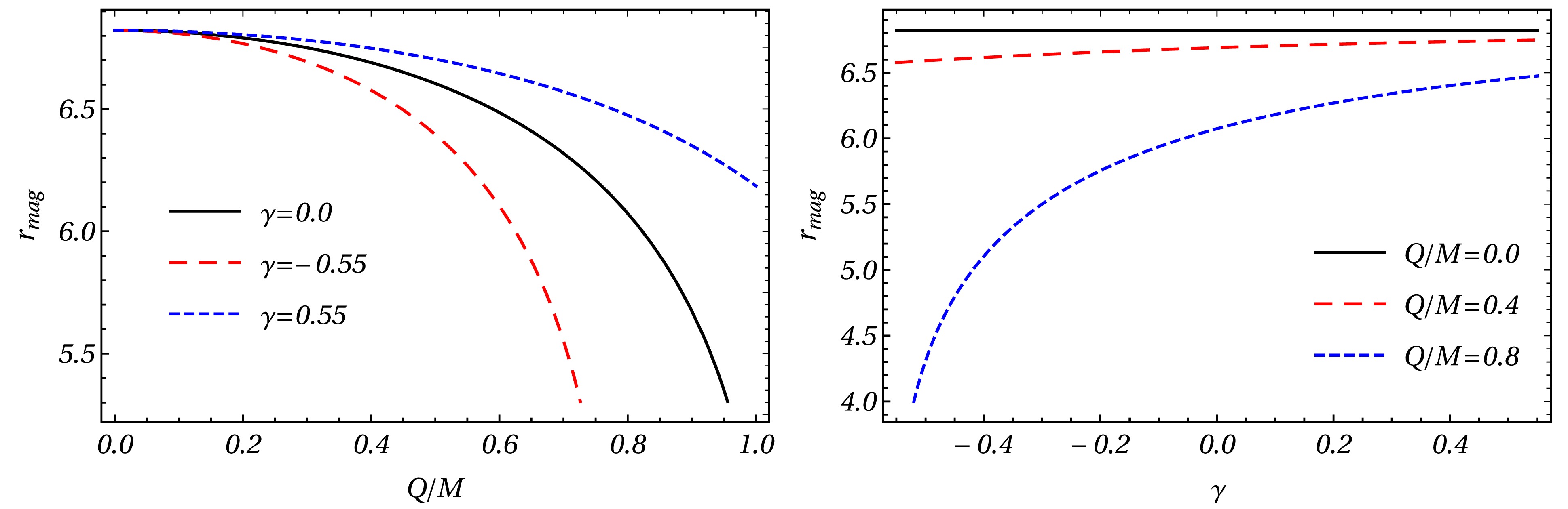

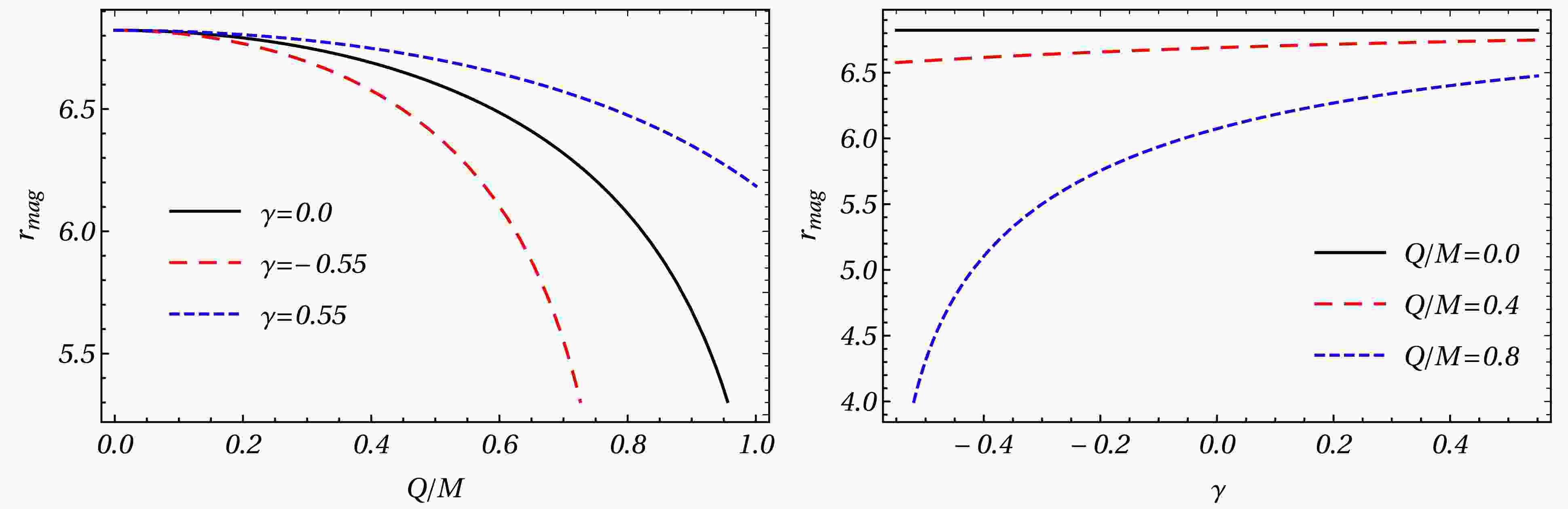
Figure 5.  This graph shows the relationship between the contact parameter $ r_{mag} $ and the parameter ϵ.

γ	Q/M	Milky Way		NGC4486		NGC4649		$ r_{mag} $
		$ \theta_{\infty}(\mu as) $	$ S(\mu as) $	$ \theta_{\infty}(\mu as) $	$ S(\mu as) $	$ \theta_{\infty}(\mu as) $	$ S(\mu as) $
0.0	0.0	48.5447	0.0607535	19.0935	0.0238954	12.1986	0.0152665	6.82188
-0.5	0.4	46.2876	0.0729555	18.2057	0.0286946	11.9974	0.0183327	6.59044
-0.5	0.8	36.2528	0.345028	14.2589	0.135705	11.3382	0.0867007	4.30845
0.0	0.4	47.2071	0.067439	18.5674	0.0265249	11.8625	0.0169465	6.68985
0.0	0.8	42.4706	0.109304	16.7044	0.0429911	10.6723	0.0274666	6.07378
0.5	0.4	47.744	0.0645842	18.7786	0.0254021	11.9974	0.0162291	6.74453
0.5	0.8	45.1208	0.081358	17.7468	0.0319995	11.3382	0.0204441	6.45234

Table 2.  The angular position of the asymptotic relativistic images ($ \theta_\infty $), the angular separation between the outermost and asymptotic relativistic images ($ s_\infty $), and relative magnification of the outermost relativistic image with other relativistic images ($ r_{mag} $) for Milky Way, NGC4486, and NGC4649 in the case of fixed the charge of the black hole Q/M and γ parameters.

The strong deflection limit coefficients $ \overline{a} $, $ \overline{b} $ and the critical impact parameter ups can be obtained after measuring s, $ r_{mag} $, and $ \theta_\infty $. If $ \theta_\infty $ represents the asymptotic position of a set of images in the limit $ n \rightarrow\infty $, we consider that only the outermost image $ \theta_1 $ is resolved as a single image and all the remaining ones are packed together at $ \theta_\infty $. The values obtained from measurements can be compared with those predicted by the theoretical models to check the nature of the black hole. Table 3 presents the observable values corresponding to various parameters γ and Q. It is evident from these results that the Dyonic ModMax black hole exhibits unique and distinguishable observable characteristics compared to other configurations.

One of the important conclusions in study of deflection angle is that we can constrain Dyonic ModMax spacetime parameter by using EHT observation. From Eq.(54), we can ascertain the specific values of these parameters that may be used to align the diameters of the M87* and Sgr A* BH, as determined by the EHT. The angular size of the image of BH M87* is reported to be $ \theta_d = 42\pm3 \mu as $. The mass and distance of M87* from the solar system are given as $ M = 6.5\times 10^9 M_\odot $ and $ d = 16.8 $ Mpc, respectively, as mentioned in Refs[7, 68]. The constraints on M87* are depicted in the left panel of Fig. 6. This figure reveals that the allowed region for the charge is quite limited when the γ parameter is negative, whereas it becomes significantly broader for positive values of γ. More specificly, the parameter constraints are: $ 0.7\ge Q>0.4 $ and $ \gamma\ge-0.5 $. The observational data of the supermassive BH Sgr A* may be analyzed using the same methodology. A study conducted by Akiyama et al. (2019) determined that the angular diameter of the shadow of the BH Sgr A* is around $ \theta_d = 48.7\pm7\mu as $, and its mass is estimated to be around $ M\simeq4\times10^6M_\odot $. The distance from Earth is approximately estimated to be $ d\simeq 8 kpc $. The results for Sgr A* are demonstrated in Fig. 6, right panel. Analyzing this graph, it is evident that the allowed parameter region for Sgr A* is broader compared to that of the M87* observational results which are : $ Q \geqslant 0.3 $ and $ \gamma \geqslant -0.5 $. This broader range can likely be attributed to the greater observational uncertainties associated with Sgr A*.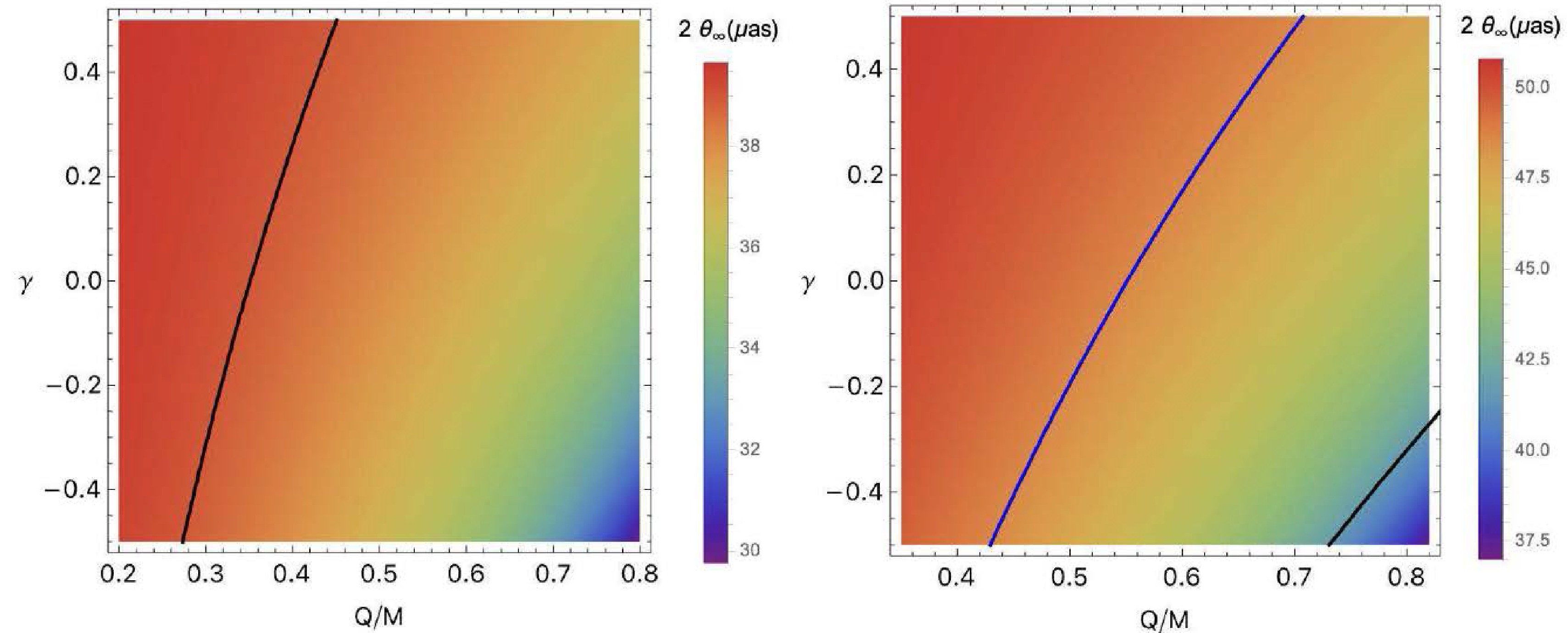

Figure 6.  Constraining parameter by using EHT observation for $ M87^* $ (left panel) and $ Sgr A^* $ (right panel). The black thick line corresponds to the maximum values of parameters which consistent with observational results $ 39 \mu as $ for $ M87^* $(left panel) and $ 41.7 \mu as $ for $ Sgr A^* $(right panel) while the blue one represents the middle value of observational results($ 48.7 \mu as $ for $ Sgr A^* $).

The time difference is caused by the photon taking different paths while winding the black hole, so there is a time delay between different images. If we can distinguish the time signals of the first image and other packed images. The time spent by the photon to wind around the black hole is [69]

The images are highly demagnified, and the separation between the images is of the order of microarcseconds, so we must at least distinguish the outermost relativistic image from the rest, and we assume the source to be variable, which generally is abundant in all galaxies, otherwise, there is no time delay to measure. For spherically symmetric black holes, the time delay between the first and second relativistic image [69]

Using Eq.(58), if we can measure the time delay with an accuracy of and the critical impact parameter with negligible error, we can obtain the distance of the black hole with an accuracy of. In Table 3, we compare several galaxies representing Schwarzschild and Dyonic ModMax spacetime. In the Dyonic ModMax spacetime spacetime, the time delays $ \Delta T^s_{2.1} $ between two distinct relativistic images are comparatively smaller than the fixed value of Q/M and γ in the Schwarzschild cases. We have also analytically derived the time delays $ \Delta T^s_{2.1} $ between the first and second-order relativistic images for various astronomical objects including the Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA) with the help of data are obtained from [67]. From this analysis, we have shown that if we have an independent observation for the time delay, we can strongly constrain the Dyonic ModMax space time parameters Q and γ due to measurable difference on the value of time delay.

Through this investigations, we can show several important notices as a conclusion:

● The radius of the spherical photon orbit $ r_m $, the critical impact parameter $ b_c $, the lensing coefficient $ \bar{b} $, the deflection angle $ \alpha_D(b) $, and the angular position $ \theta_\infty $ all decrease as Q increases, while the lensing coefficient $ \bar{a} $ and angular separation $ s_\infty $ exhibit the opposite trend. Consequently, the parameter γ behaves inversely to Q.

● Additionally, we have shown the constraining Dyonic ModMax spacetime with EHT observations. We represent it as parametric space graphs.

● We have also analytically derived the time delays $ \Delta T^s_{2.1} $ between first and second-order relativistic images for the Milky Way, M87, NGC4649, NGC4697, and NGC5128(cenA). One can observe that for supermassive black hole with higher mass, the time delay is higher than for the case of lighter black holes.

● Based on the graphical and tabular results, the dependence of the deflection angle on the parameters Q and γ was revealed. In particular, it was observed that when γ takes negative values, the deflection angle decreases more sharply, while positive values of γ tend to smooth out this variation. Observations from the EHT, especially those related to the shadow diameters of the $ M87^* $ and $ SgrA^* $ black holes, were used to establish experimental constraints on these parameters. For $ M87^* $, the parameters are constrained by $ 0.7\ge Q>0.4 $ and $ \gamma\ge-0.5 $, whereas for $ SgrA^* $, the allowed parameter space is broader, i.e $ Q \geqslant 0.3 $ and $ \gamma \geqslant -0.5 $, due to larger observational uncertainties.