Study of QCD critical point with the effect of three-nucleon correlations on light nuclei yield ratios using PYTHIA8/Angantyr

The creation of a state of matter known as the quark-gluon plasma (QGP), characterized by deconfined quarks and gluons, is believed to occur under extreme conditions of temperature and/or density during heavy-ion collisions at ultra-relativistic energies. Understanding the phase structure of strongly interacting matter described by quantum chromodynamics (QCD) is a key objective in nuclear physics. The QCD phase diagram, typically represented in a two-dimensional graph of temperature (T) versus baryon chemical potential ($ \mu_{\mathrm{B}} $), offers critical insights into the behavior of strongly interacting matter.

Lattice QCD calculations have shown that the transition from the hadronic phase to the QGP at low values of $ \mu_{\mathrm{B}} $ occurs as a smooth crossover [1–2]. However, at higher values of $ \mu_{\mathrm{B}} $, QCD-based model calculations predict a first-order phase transition [3−6]. If this prediction holds true, a critical point must exist on the phase diagram, marking the endpoint of the first-order phase boundary. Despite ongoing theoretical discussions on the location and even the existence of the QCD critical point, the relativistic heavy-ion collisions, by recreating the extreme conditions required to probe the QCD phase structure, provide an experimental platform to search for this critical point [7−17]. As the system approaches the QCD critical point, the correlation length of fluctuations grows, leading to enhanced density fluctuations. Conserved quantities, such as net-baryon, net-charge, and net-strangeness, exhibit fluctuations that are sensitive to the correlation length. The STAR experiment has conducted extensive measurements of high-order cumulants and second-order off-diagonal cumulants of net-proton, net-charge, and net-kaon multiplicity distributions [18]. Notably, a non-monotonic behavior in the fourth-order net-proton cumulant ratio was observed, with a minimum of approximately 19.6 GeV for Au+Au collisions spanning a broad energy range ($ \sqrt{s_{\mathrm{NN}}} = 7.7 $–200 GeV). This behavior cannot be accounted for by existing theoretical models without invoking the physics associated with the QCD critical point [10].

In addition to cumulant measurements, baryon density fluctuations arising from critical phenomena during a first-order phase transition are predicted to influence the production of light nuclei [19−24]. For example, the light nuclei yield ratio, $ N_p N_t / N_d^2 $, involving protons $ (p) $, deuterons $ (d) $, and tritons $ (t) $, can be related to the relative neutron density fluctuation, $ \langle (\delta n)^2\rangle / \langle n\rangle^2 $ (denoted as $ \Delta n $ in Ref. [19]). Measurements by the STAR experiment revealed an evident non-monotonic energy dependence of this yield ratio for central Au+Au collisions, with a peak observed at $ \sqrt{s_{\mathrm{NN}}}=20-30 $ GeV [25–26].

Our previous study [27], based on the PYTHIA8 Angantyr model, investigated the effect of two-body neutron-proton density correlations $ (C_{np}) $ on light nuclei yield ratios. However, a critical factor was not considered: the three-nucleon correlation $ (C_{n^2p}) $ involving two neutrons and one proton, which directly impacts triton production and, consequently, the overall yield ratio. Given that tritons form via coalescence processes requiring multiple nucleons, incorporating $ C_{n^2p} $ is essential to comprehensively understand light nuclei formation dynamics and extract relative neutron density fluctuations from experimental data.

In this study, we expand on our earlier findings by incorporating the three-nucleon correlation $ C_{n^2p} $ into the analysis of light nuclei yield ratios for Au+Au collisions. Using the PYTHIA8 Angantyr model, we simulated collisions at $ \sqrt{s_{\mathrm{NN}}} = 7.7 $, 11.5, 14.5, 19.6, 27, 39, 62.4, and 200 GeV. We take the notation $ R = N_p N_t / N_d^2 $ in this study. The Angantyr model extends PYTHIA8 by enabling the construction of heavy-ion collisions as a superposition of binary nucleon-nucleon collisions. Our findings highlight the critical importance of $ C_{n^2p} $ in interpreting light nuclei yield ratios and neutron density fluctuations. By providing an improved methodology for extracting neutron density fluctuations from experimental data, this study offers new insights into the search for the QCD critical point.

This paper is organized as follows. Section II.A provides an overview of the PYTHIA8 Angantyr model. Section II.B discusses the relationship between neutron density fluctuations and light nuclei yield ratios for heavy-ion collisions. The results and discussions on neutron density fluctuations and neutron-proton correlations are presented in Section III. Finally, we summarize our findings and conclusions in Section IV.

PYTHIA [28] is an extensively utilized event generator designed for simulating particle collisions, particularly proton-proton (pp) and proton-lepton interactions. For pp collisions, multi-parton interactions (MPI) are generated under the assumption that every partonic interaction is almost independent. However, in its default configuration, PYTHIA8 does not natively support heavy-ion collision simulations.

To overcome this limitation, the PYTHIA8 Angantyr model [29] was introduced. This extension enables the extrapolation of pp dynamics into heavy-ion collisions, facilitating the study of proton-nucleus (pA) and nucleus-nucleus (AA) interactions. The Angantyr model achieves this by combining multiple nucleon-nucleon collisions to simulate a single heavy-ion collision. It incorporates theoretical frameworks to describe both hard and soft interactions, along with key features, such as initial- and final-state parton showers, particle fragmentation, MPI, and color reconnection (CR) mechanisms. Notably, the Angantyr model does not include mechanisms to account for the formation of the QGP, which is widely believed to occur in AA collisions.

In the current version of the PYTHIA8 Angantyr model [30], heavy-ion collisions are modeled using the Glauber approach to determine the number of participating nucleons based on the geometric overlap of the colliding nuclei. The model introduces algorithms to distinguish between different types of nucleon-nucleon interactions, such as elastic, diffractive, and absorptive processes. The model can describe final-state observables effectively, including particle multiplicity distributions and transverse momentum spectra in AA collisions [31–32].

In this study, we utilized version 8.308 of PYTHIA8 for the simulation of Au+Au collisions at various energies. Approximately one million events were generated for each collision energy, employing multiple PYTHIA tunes with distinct configurations for MPI and CR. To remove the influence of system volume and density fluctuations inherent in heavy-ion collisions, we introduced two dimensionless statistical quantities: $ \langle (\delta p)\rangle /\langle p\rangle $ and $ \langle (\delta n)\rangle /\langle n\rangle $ (described in detail in Sec. II.B). Nucleons were analyzed across various rapidity ranges and centrality classes. The centrality intervals were defined based on the transverse momentum sum of charged particles ($ \sum E_T $) at the final state of the collisions within the pseudorapidity range of $ [-0.5, 0.5] $.

The production of light nuclei, such as deuterons and tritons, has been extensively studied to understand the underlying nucleon coalescence mechanism, which plays a pivotal role in high-energy nuclear collisions [24, 33, 27]. This mechanism assumes that nucleons, protons, and neutrons within close spatial and momentum proximity can coalesce to form light nuclei. The theoretical yield of light nuclei can be derived by applying the coalescence model, neglecting the effects of binding energy. The expression for the abundance of a cluster containing A nucleons is given by

where $ g_c = \dfrac{2S+1}{2^A} $ is the coalescence factor for a cluster with $ A = A_n + A_p $ nucleons and total spin S. The terms $ m_0 $, $ T_{\rm eff} $, and V represent the nucleon mass, effective kinetic freeze-out temperature, and system volume, respectively. $ \langle \rho_n \rangle $ and $ \langle \rho_p \rangle $ denote the average neutron and proton densities, respectively, whereas $ C_{A_p}^i $ and $ C_{A_n}^j $ are combinatorial factors representing possible configurations of $ A_p $ protons and $ A_n $ neutrons, respectively. The factor $ C_{n^j p^i} $ accounts for the correlation between i-protons and j-neutrons, defined as

where $ \delta \rho_p^i $ and $ \delta \rho_n^j $ represent the density fluctuations for protons and neutrons, respectively.

Among these correlations, the relative neutron density fluctuation $ \Delta \rho_n = \sigma_n^2 / \langle \rho_n \rangle^2 $ corresponds to $ C_{n^2 p^0} $. Similarly, the two-nucleon correlation $ C_{np} $ can be expressed as

For higher-order correlations, such as the three-nucleon correlation, $ C_{n^2 p} $, the expression becomes

The yields of specific light nuclei can now be explicitly formulated. In Eq. (3) and Eq. (4), the nucleons considered are the initial nucleons. For deuterons $ ( N_d ) $ and tritons $ ( N_t ) $, the yields are

From these equations, the ratio of light nuclei yields, R, can be expressed as

The term $ C_{n^2 p} $, representing three-nucleon correlations, introduces a significant contribution to the light nuclei yield ratio. By assuming $ C_{n^2 p} = 0 $, the yield ratio can be simplified to

In the absence of both two- and three-nucleon correlations ($ C_{np} = C_{n^2 p} = 0 $, $ C_{np} $ and $ C_{n^2p} $ are the parameters of nucleon correlation), the expression can be further simplified to

In this simplified scenario, the yield ratio becomes directly proportional to the relative neutron density fluctuation $ \Delta \rho_n $, which forms the experimental basis for extracting $ \Delta \rho_n $ from the yield ratios of light nuclei.

In addition to the physical parameters employed in the model calculations, as detailed in the last paragraph of Sec. 2.1, the analysis also incorporates the option to activate or deactivate the multiple-parton interactions (MPI) based color reconnection (CR) mechanism. This can be achieved by enabling or disabling the parameters $\mathrm{ColourReconnection:reconnect} $ and ${ \mathrm{PartonLevel: }} \mathrm{ MPI}$ within the PYTHIA8 Angantyr model framework.

The results presented in Figs. 1, 2, 3, 4, and 6 are obtained by applying the PYTHIA8 Angantyr model, with the inclusion of the MPI-based CR mechanism. These results provide significant insights into the interplay between nucleon density fluctuations and light nuclei yield ratios in high-energy nuclear collisions.

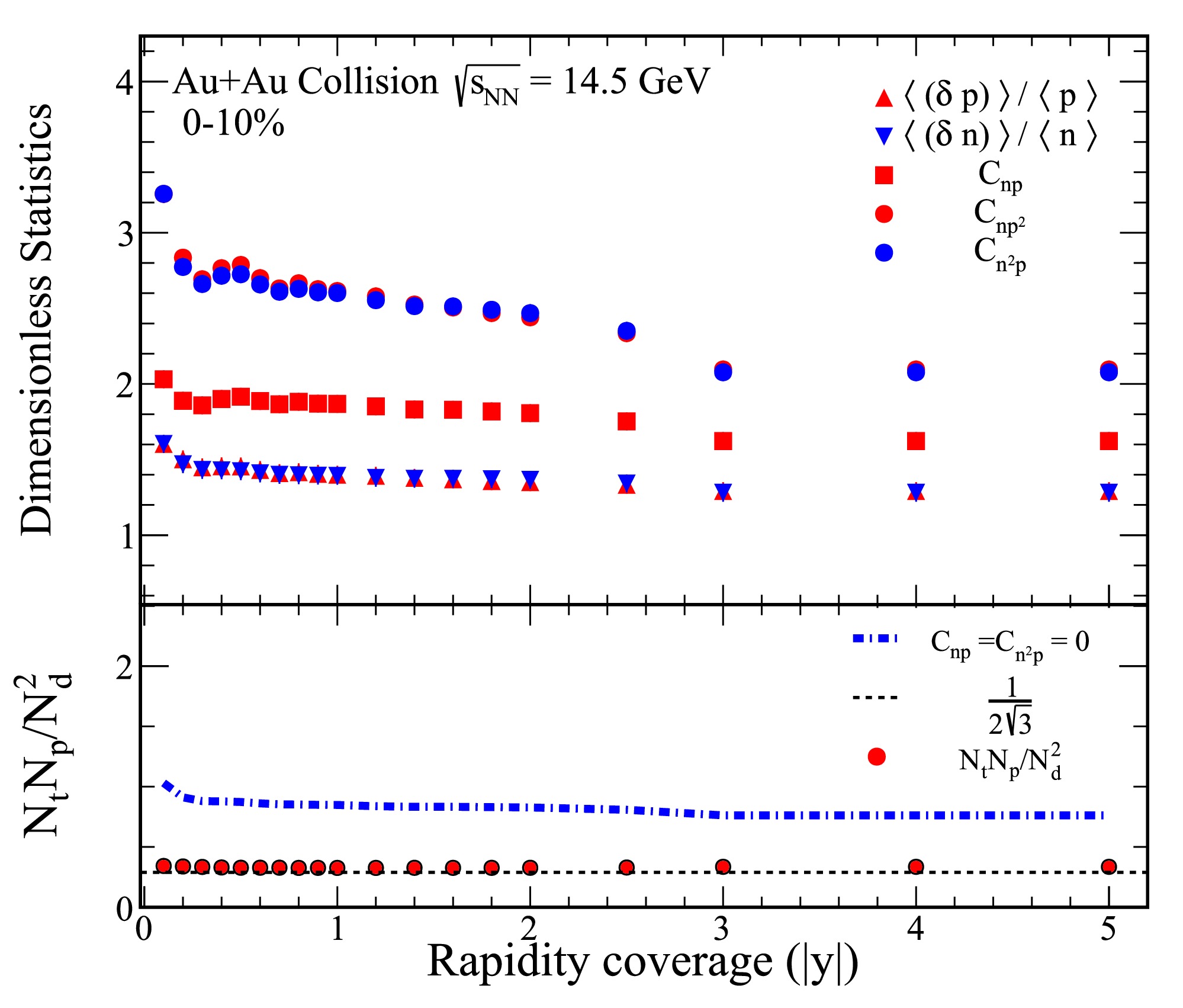
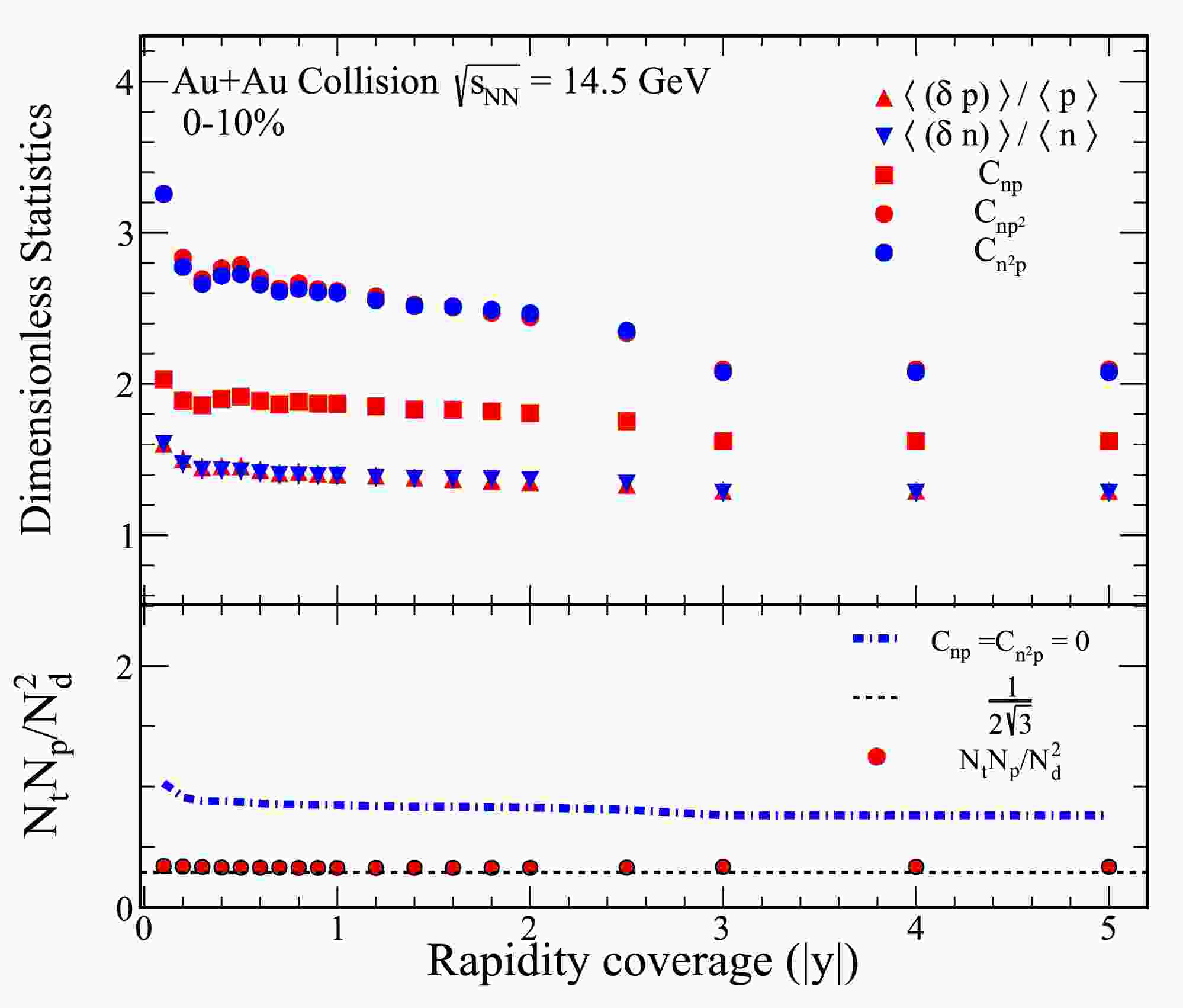
Figure 1.  (color online) The top panel of the figure presents various dimensionless statistical quantities, including $ \langle (\delta p) \rangle /\langle p \rangle $, $ \langle (\delta n) \rangle /\langle n \rangle $, $ C_{np} $, $ C_{np^2} $, and $ C_{n^2 p} $, derived from 0−10% Au+Au collisions at a center-of-mass energy of $ \sqrt{s_{{\rm{NN}}}}= $ 14.5 GeV. The bottom panel illustrates the yield ratio for light nuclei, $ N_tN_p/N_d^2 $, which is calculated using the results from the top panel. The solid circles represent values obtained through Eq. (7), and the dash-dot lines indicate calculations based on Eq. (9).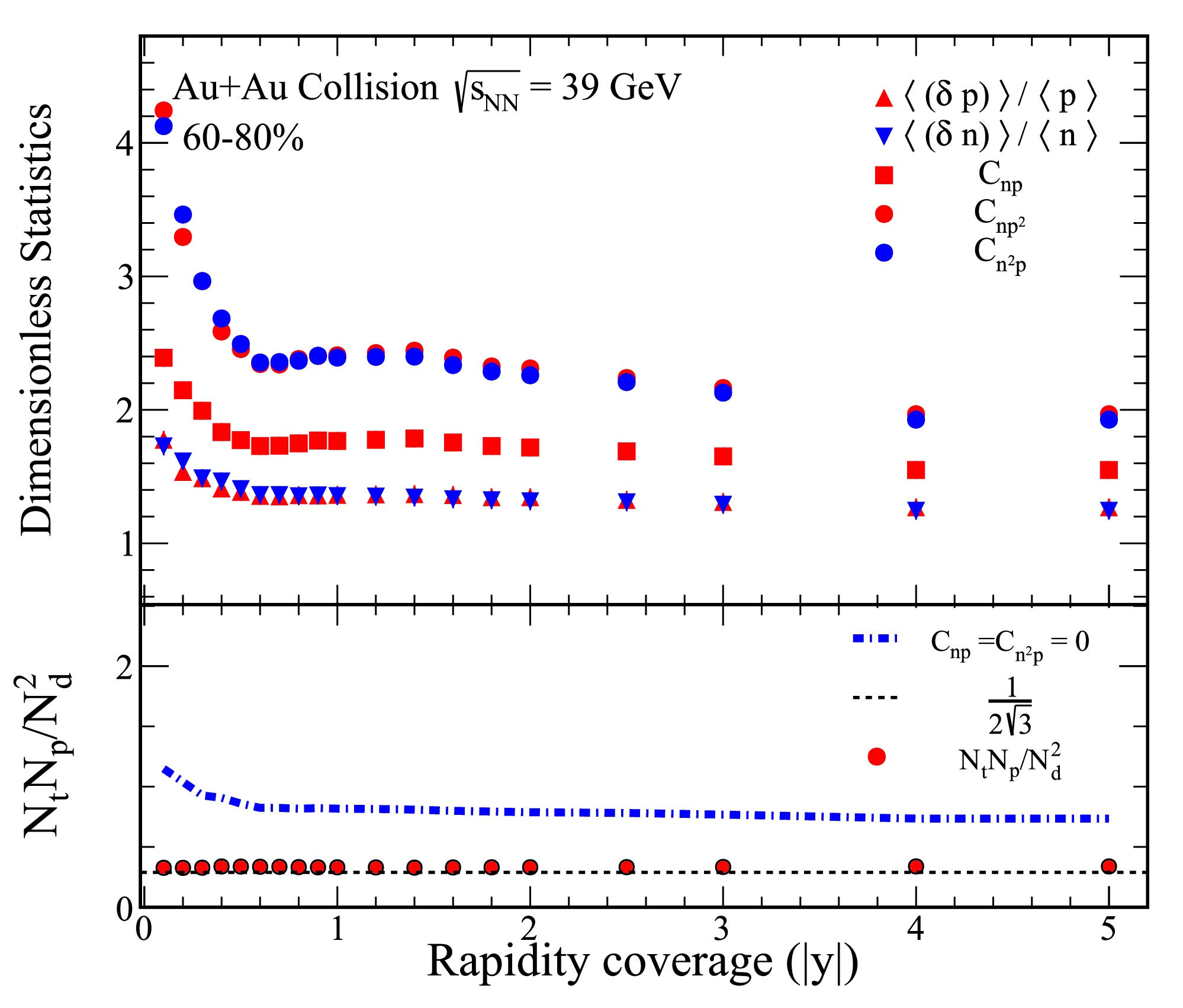

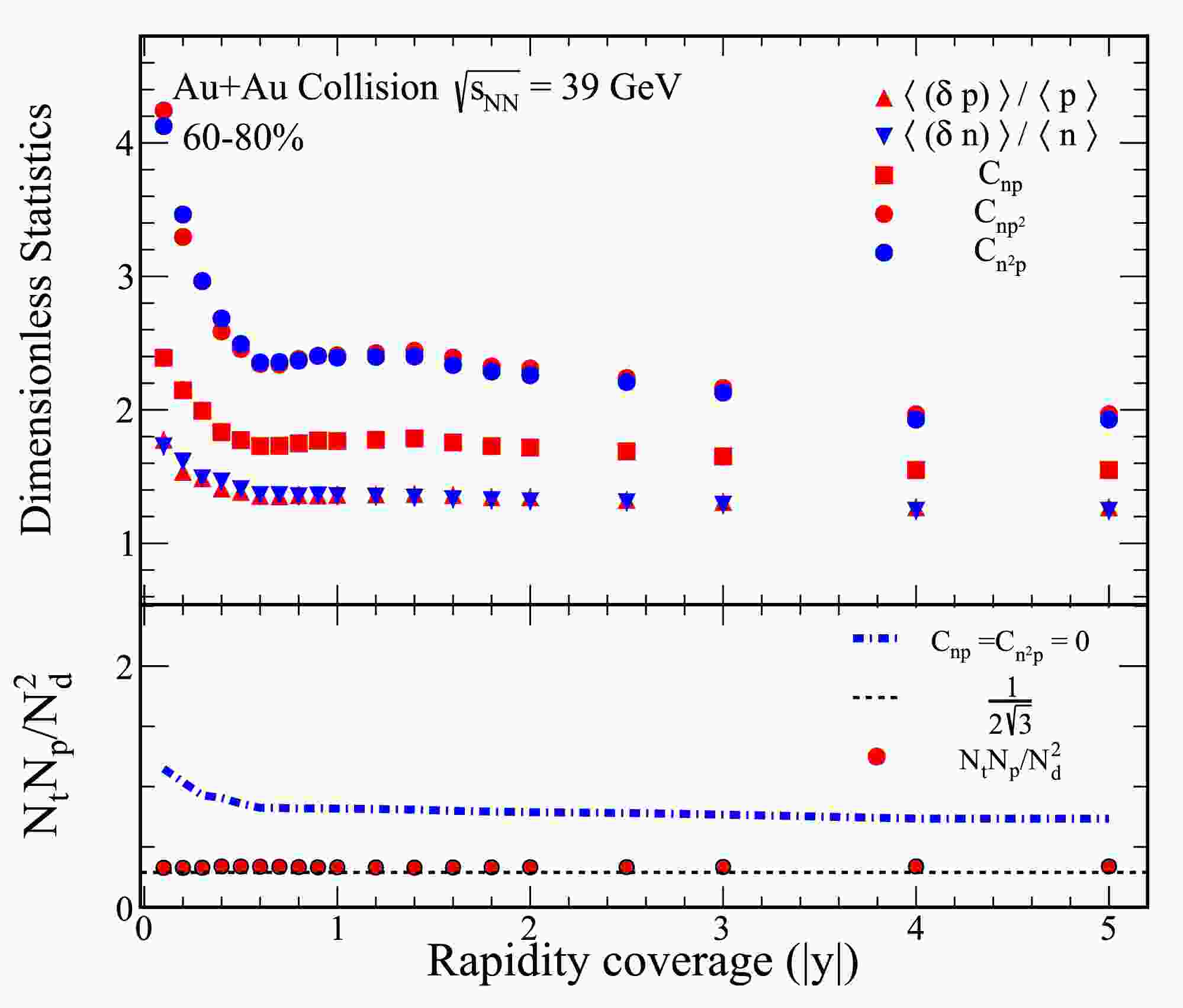
Figure 2.  (color online) The figure presents various dimensionless statistics and the ratio of light nuclei yields for 60%−80% Au+Au collisions at a center-of-mass energy of $ \sqrt{s_{{\rm{NN}}}} = $$ 39 $GeV. The top panel presents the dimensionless statistics $ \langle (\delta p)\rangle /\langle p\rangle $, $ \langle (\delta n)\rangle /\langle n\rangle $, $ C_{np} $, $ C_{np^2} $, and $ C_{n^2 p} $. The bottom panel illustrates the yield ratio for light nuclei, given by $ N_tN_p/N_d^2 $. This ratio is calculated using the data presented in the top panel. The solid circles represent the light nuclei yield ratio, calculated according to Eq. (7), and the dash-dot line corresponds to the calculation based on Eq. (9).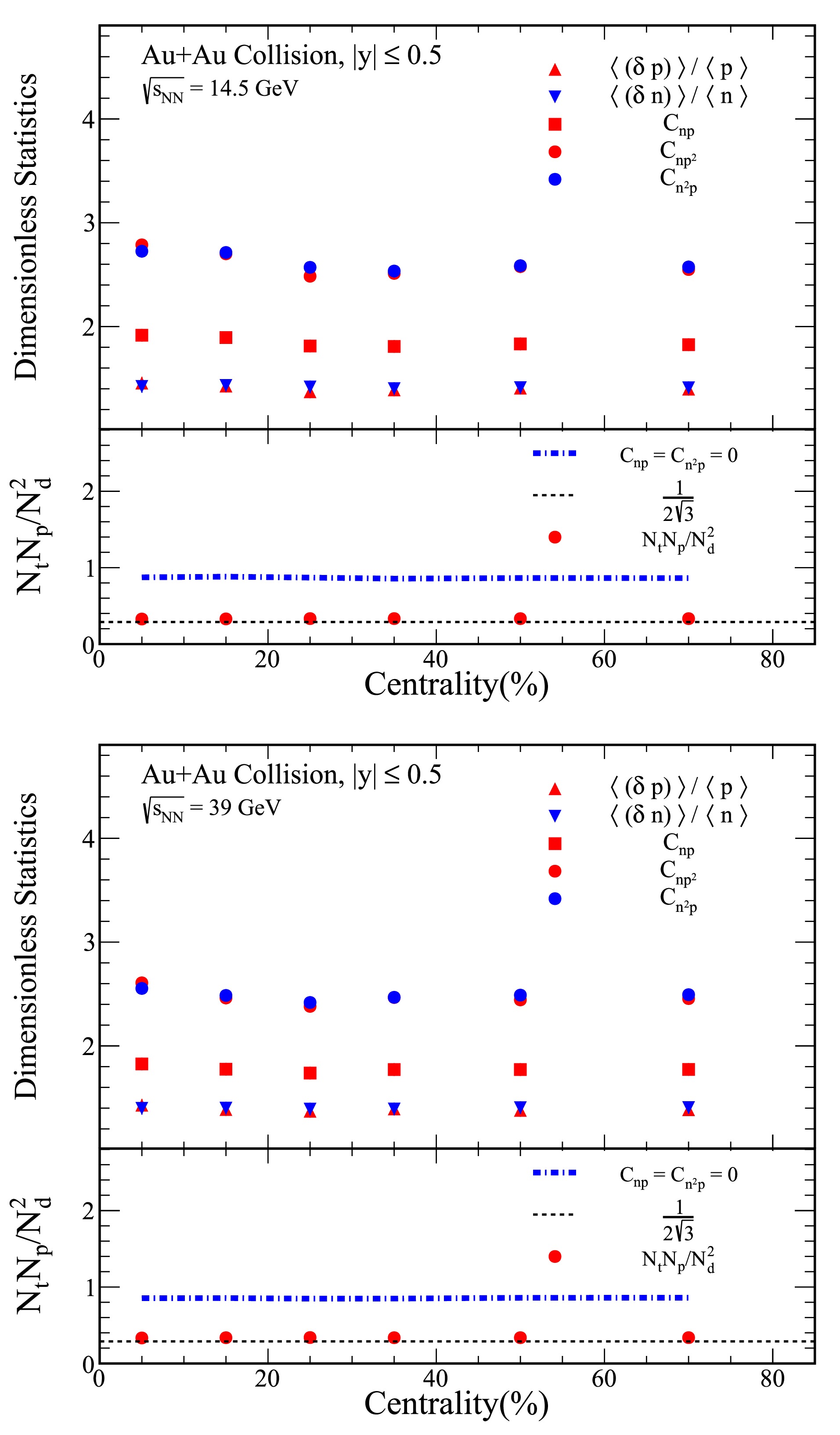

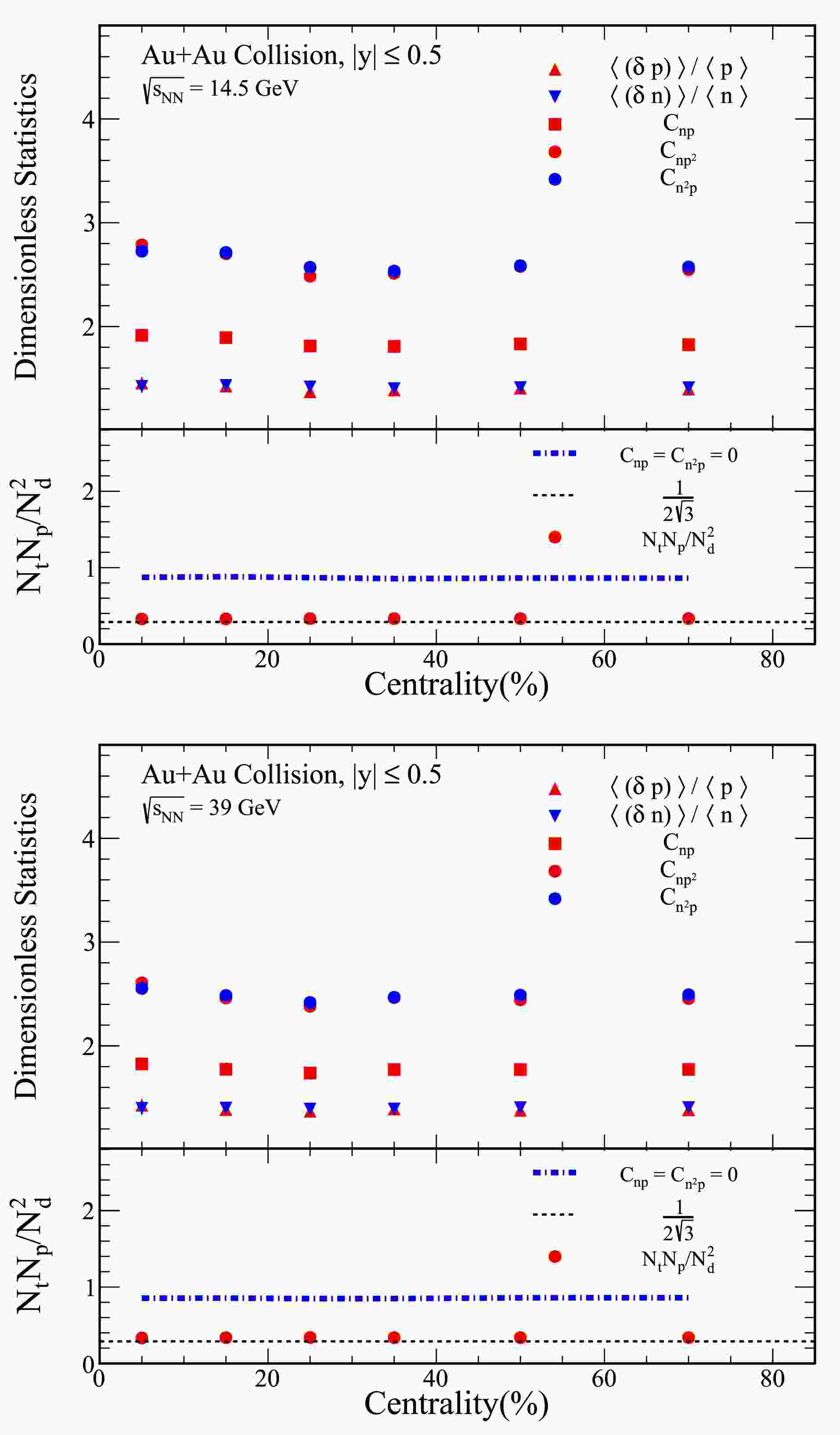
Figure 3.  (color online) The figures present the centrality dependent $ \langle (\delta p)\rangle /\langle p\rangle $, $ \langle (\delta n)\rangle /\langle n\rangle $, $ C_{np} $, $ C_{np^2} $, and $ C_{n^2 p} $ for Au+Au collisions at center-of-mass energies of $ \sqrt{s_{{\rm{NN}}}}= $ 14.5 and 39 GeV, with rapidities confined to the range $ |y|\leq 0.5 $. Additionally, the yield ratio for light nuclei, given by $ N_tN_p/N_d^2 $, is shown. This ratio is represented by solid circles, calculated according to Eq. (7), and the dash-dot line corresponds to the result obtained from Eq. (9).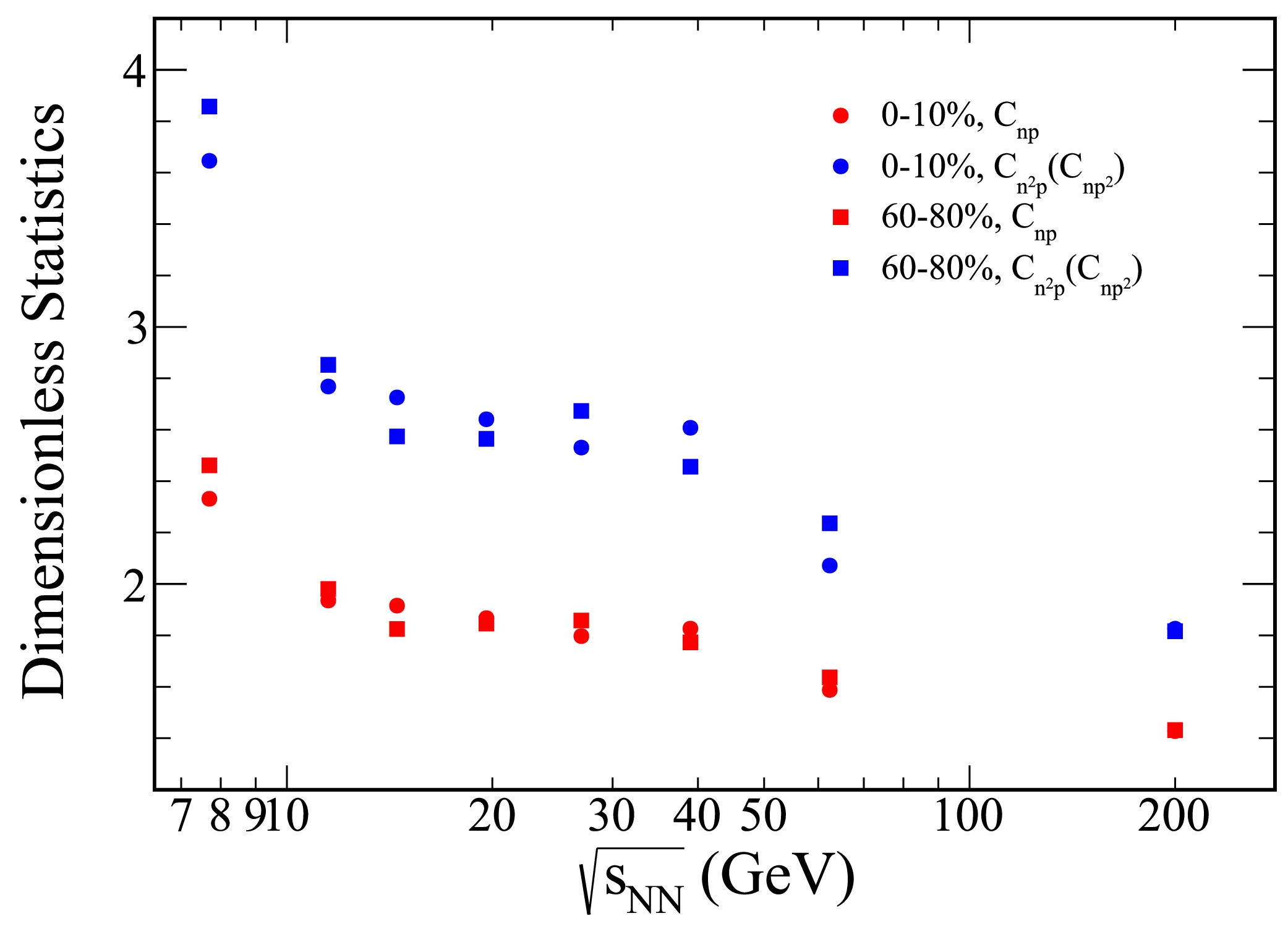

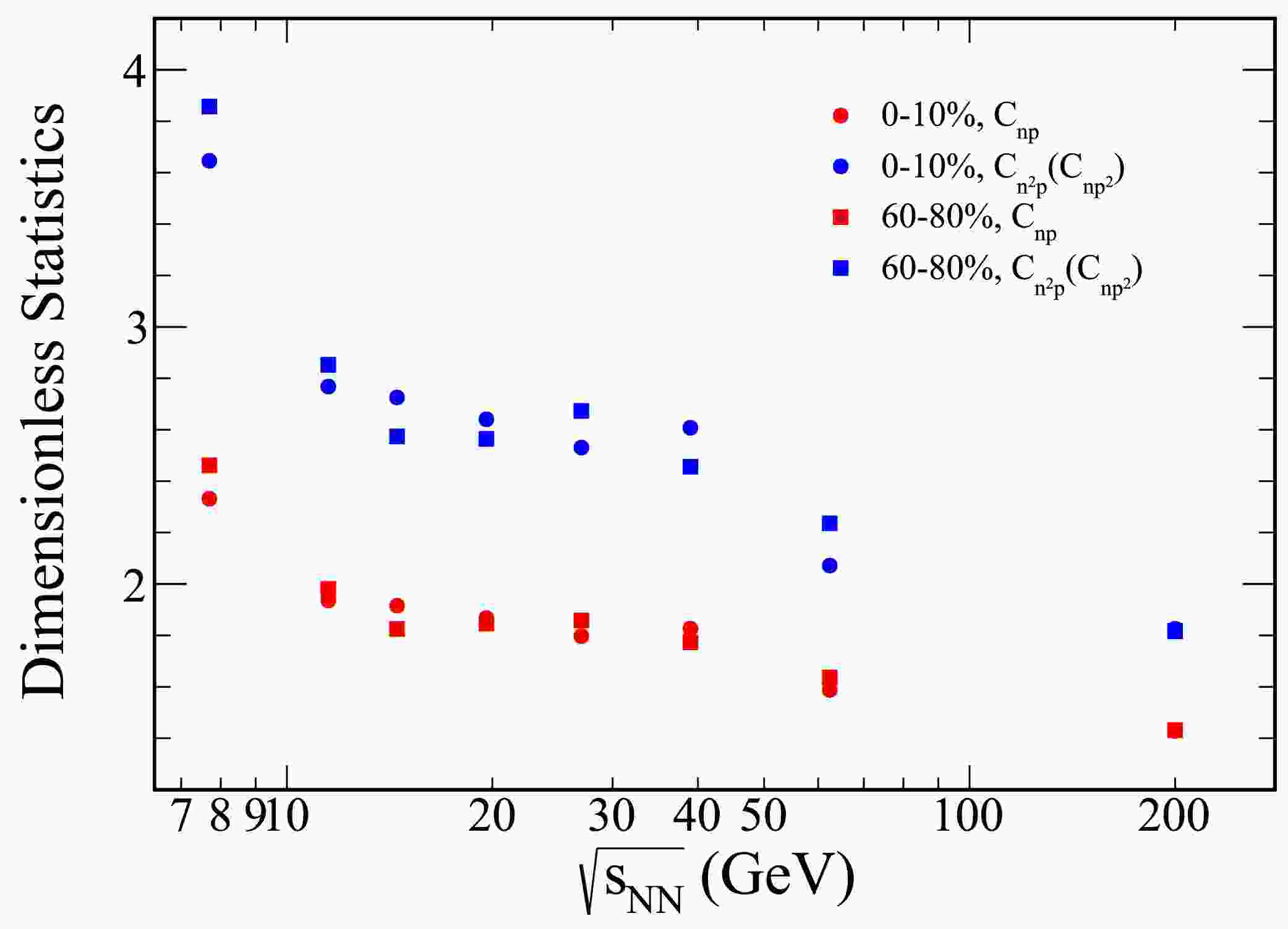
Figure 4.  (color online) The figures present the collision energy dependence of $ C_{np} $, $ C_{np^2} $, and $ C_{n^2 p} $ for Au+Au collisions, with rapidities confined to the range $ |y|\leq 0.5 $. The results for 0−10% central collisions are represented by solid circles, whereas those for 60%−80% peripheral collisions are depicted as squares.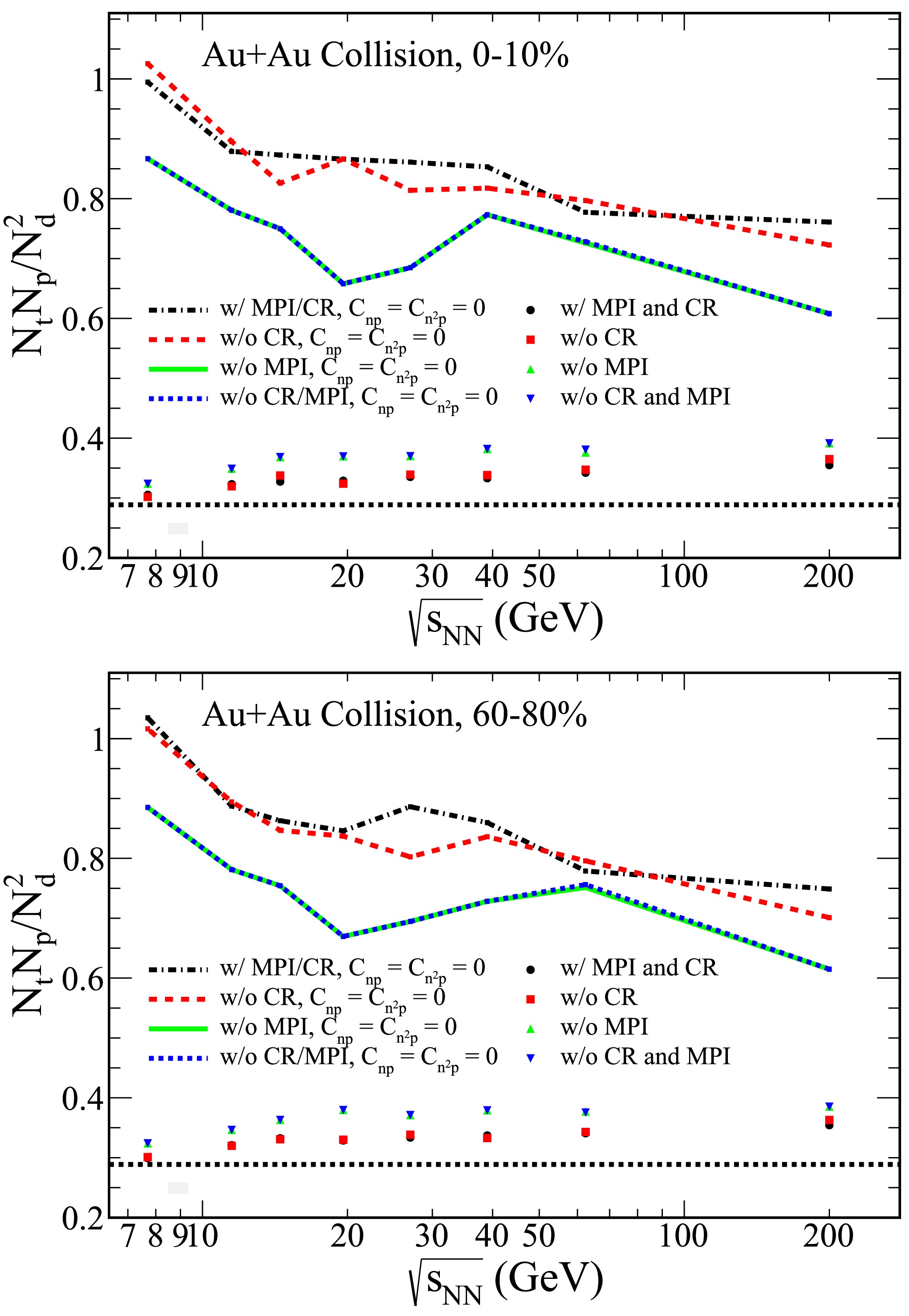

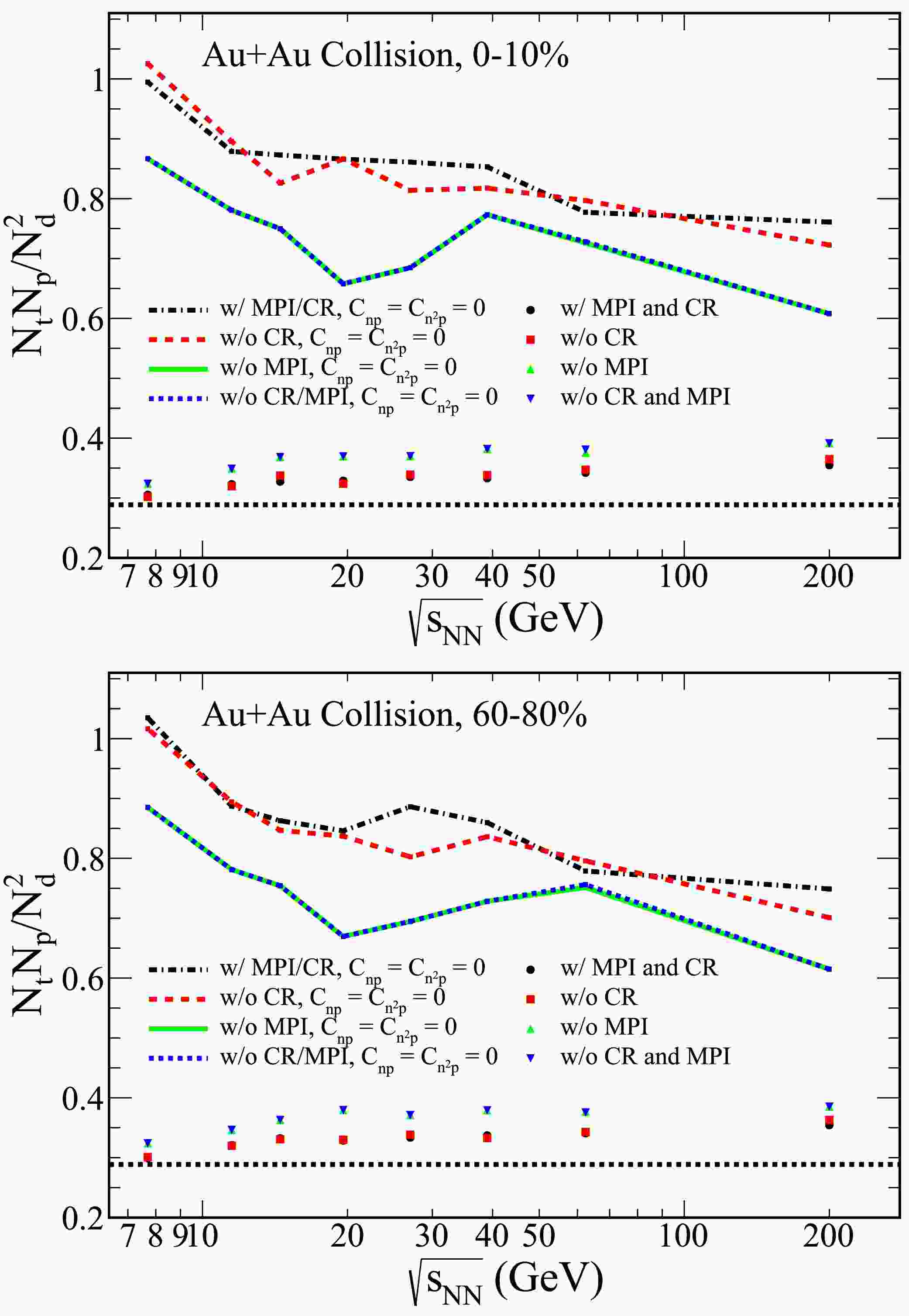
Figure 6.  (color online) The collision energy dependence of the light nuclei yield ratio $ N_tN_p/N_d^2 $ for Au+Au collisions with $ |y|\leq 0.5 $ was investigated using the PYTHIA8 Angantyr model across different model tunes. The results, displayed in the upper and lower panels of Fig. 6, correspond to 0−10% central and 60%−80% peripheral collisions, respectively.

Focusing on the top panel of Fig. 1, the rapidity dependence of the dimensionless statistics $ \langle (\delta p) \rangle /\langle p \rangle $ and $ \langle (\delta n) \rangle /\langle n \rangle $ is shown for 0−10% Au+Au collisions at $ \sqrt{s_{{\rm{NN}}}}= $ 14.5 GeV. As the rapidity coverage increases, both $ \langle (\delta p) \rangle /\langle p \rangle $ and $ \langle (\delta n) \rangle /\langle n \rangle $ demonstrate an evident decreasing trend, suggesting that relative nucleon density fluctuations reduce with wider rapidity coverage. Furthermore, these fluctuations appear to converge toward a constant value as the rapidity coverage is extended. Notably, $ \langle (\delta p) \rangle /\langle p \rangle $ and $ \langle (\delta n) \rangle /\langle n \rangle $ are consistent in Fig. 1. The correlations $ C_{np} $, $ C_{np^2} $, and $ C_{n^2 p} $ exhibit a trend similar to that of the relative nucleon density fluctuations with respect to rapidity coverage for 0−10% Au+Au collisions at $ \sqrt{s_{{\rm{NN}}}}= $ 14.5 GeV.

To provide a baseline for comparison, a reference line at $ 1/2\sqrt{3} $ is plotted, corresponding to the scenario where both density fluctuations and correlations vanish. The light nuclei yield ratio, $ N_tN_p/N_d^2 $, calculated using Eq. (7), is depicted as solid circles in the bottom panel of Fig. 1. This ratio consistently exceeds the reference line of $ 1/2\sqrt{3} $ for 0–10% central Au+Au collisions at $ \sqrt{s_{{\rm{NN}}}} = 14.5 $ GeV. The results further reveal that, when the correlations $ C_{np} $ and $ C_{n^2 p} $ are neglected (as represented by the dash-dot lines derived from Eq. (9)), the calculated yield ratio becomes significantly higher than the reference line. This observation highlights the critical role of $ C_{np} $ and $ C_{n^2 p} $ in determining the relative neutron density fluctuations through the light nuclei yield ratio. Similar trends are observed at other collision energies for central collisions, underscoring the generality of these results.

Figure 2 presents the rapidity dependence of various dimensionless statistics and the light nuclei yield ratio for 60%−80% Au+Au collisions at a center-of-mass energy of $ \sqrt{s_{{\rm{NN}}}} = 39 $ GeV. The top panel displays the ratios $ \langle (\delta p)\rangle /\langle p\rangle $ and $ \langle (\delta n)\rangle /\langle n\rangle $, along with the correlations $ C_{np} $, $ C_{np^2} $, and $ C_{n^2 p} $. In the top panel, it is evident that both $ \langle (\delta p)\rangle /\langle p\rangle $ and $ \langle (\delta n)\rangle /\langle n\rangle $ decrease as the rapidity coverage increases. Furthermore, the correlations $ C_{np} $, $ C_{np^2} $, and $ C_{n^2 p} $, shown in the same panel, are dependent on the rapidity coverage. These correlations follow a trend similar to that of the relative fluctuations in nucleon density.

In the bottom panel of Fig. 2, we show the yield ratio for light nuclei, specifically $ N_tN_p/N_d^2 $. This ratio is calculated using the data from the top panel and is represented by solid circles in accordance with Eq. (7), whereas the dash-dot line corresponds to the calculation using Eq. (9). Our results indicate that the exclusion of the $ C_{np} $ and $ C_{n^2 p} $ parameters leads to a significant increase in the light nuclei yield ratio. This indicates that neglecting the $ C_{np} $ and $ C_{n^2 p} $ parameters reduces the relative fluctuations in neutron density, thereby resulting in a higher light nuclei yield ratio.

Figure 3 presents the centrality dependence of the dimensionless statistics $ \small\langle (\delta p) \small\rangle /\small\langle p\small\rangle $ and $ \small\langle (\delta n)\small\rangle /\small\langle n\small\rangle $ for Au+Aucollisions at $ \sqrt{s_{{\rm{NN}}}} = 14.5 $ and 39 GeV, with the rapidity coverage of $ |y|\leq 0.5 $. As shown in the top panel, both quantities remain flat across central to peripheral collisions.

In the bottom panel of Fig. 3, the yield ratios for light nuclei, as defined by Eq. (7) and Eq. (9), are also observed to be flat across central, mid-central, and peripheral collisions. However, note that the relative nucleon density fluctuation cannot be directly extracted from the light nuclei yield ratios alone. The effects of neutron-proton correlations, particularly $ C_{np} $ and $ C_{n^2 p} $, must be considered for a comprehensive understanding of the fluctuation behavior at different centralities.

Figure 4 illustrates the collision energy dependence of the two- and three-nucleon correlations ($ C_{np} $, $ C_{np^2} $ and $ C_{n^2 p} $) for Au+Au collisions with rapidities confined to $ |y|\leq 0.5 $, spanning from 0–10% central to 60%–80% peripheral collisions. As shown in the figure, the light nuclei yield ratio exhibits a decrease with rising collision energy.

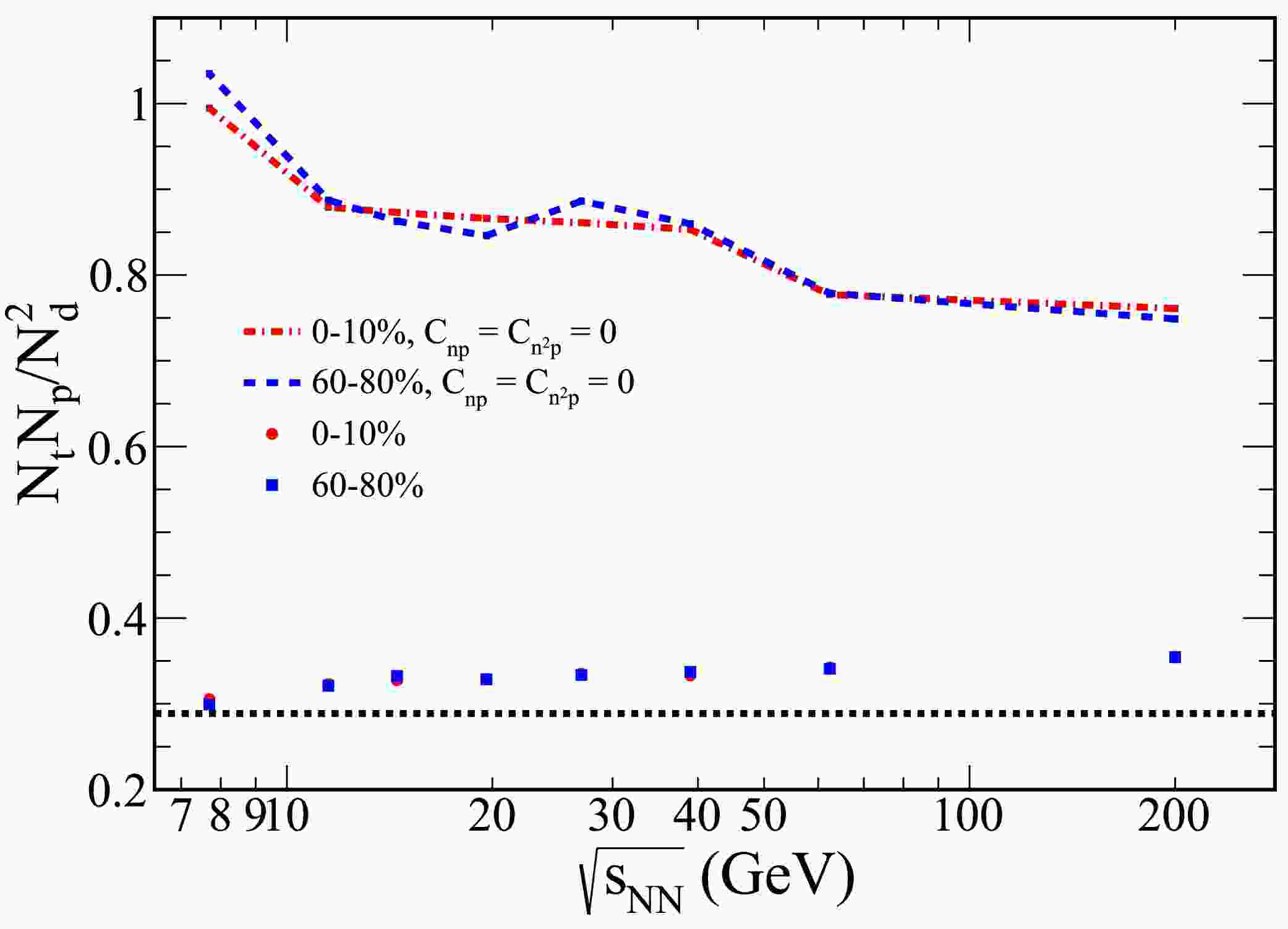
Figure 5 illustrates the collision energy dependence of the light nuclei yield ratio, $ N_tN_p/N_d^2 $, for Au+Au collisions with rapidities confined to $ |y|\leq 0.5 $, spanning from 0–10% central to 60%−80% peripheral collisions. As shown in the figure, the light nuclei yield ratio exhibits a slight increase with rising collision energy.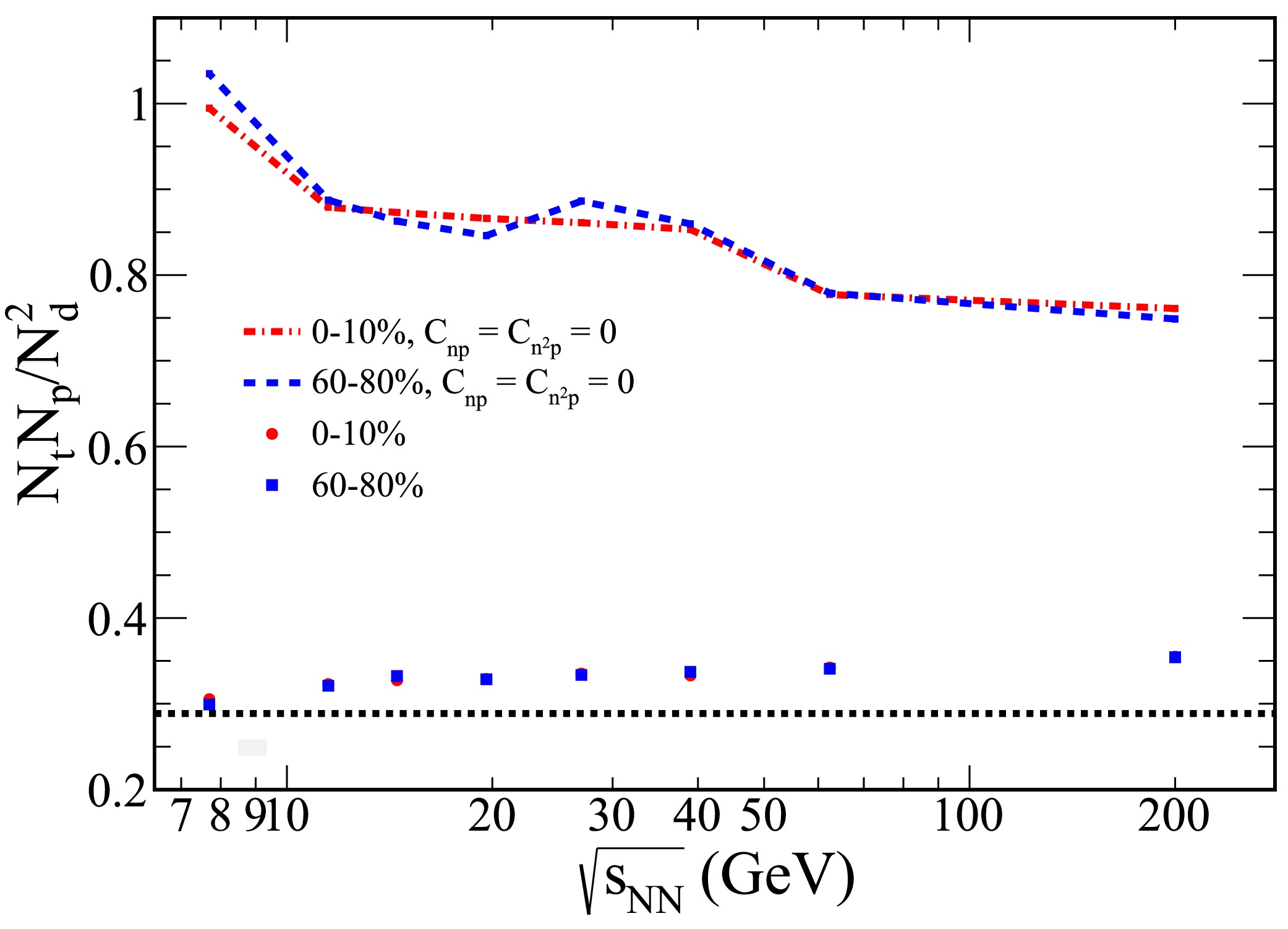

Figure 5.  (color online) The PYTHIA8 Angantyr model was employed to investigate the collision energy dependence of the light nuclei yield ratio, $ N_tN_p/N_d^2 $, for Au+Au collisions with rapidities restricted to $ |y|\leq 0.5 $. The results for 0−10% central collisions are represented by solid circles, whereas those for 60%−80% peripheral collisions are depicted as squares. Additionally, the dash-dot lines show the corresponding results when the correlations $ C_{np} $ and $ C_{n^2 p} $ are excluded.

Note that the yield ratio for peripheral collisions is comparable to that of central collisions, with both ratios exceeding $ 1/2\sqrt{3} $. Additionally, the results for the case excluding correlations $ C_{np} $ and $ C_{n^2 p} $ are also presented in the figure, indicated by the dash-dot lines. These results reveal a decrease in the light nuclei yield ratio as the collision energy increases.

To investigate the effect of different PYTHIA8 Angantyr model tunes, we explore several configurations: MPI with CR, no CR, no MPI, and both MPI and CR turned off. The collision energy dependence of the light nuclei yield ratio $ N_tN_p/N_d^2 $ for Au+Au collisions with rapidity coverage $ |y|\leq 0.5 $ is displayed in Fig. 6, which shows results for both 0−10% central and 60%−80% peripheral collisions.

From Fig. 6, it is apparent that the light nuclei yield ratio increases slightly as the collision energy increases across the different configurations of the PYTHIA8 Angantyr model. This trend is observed for both central and peripheral collisions. Furthermore, the results for the cases in which $ C_{np} $ and $ C_{n^2 p} $ are excluded, represented by dash-dot lines, reveal a decrease in the light nuclei yield ratio as the collision energy increases. In the context of Au+Au collisions, the absence of CR does not produce a significant effect when MPI is turned off, regardless of the PYTHIA8 Angantyr model tune.

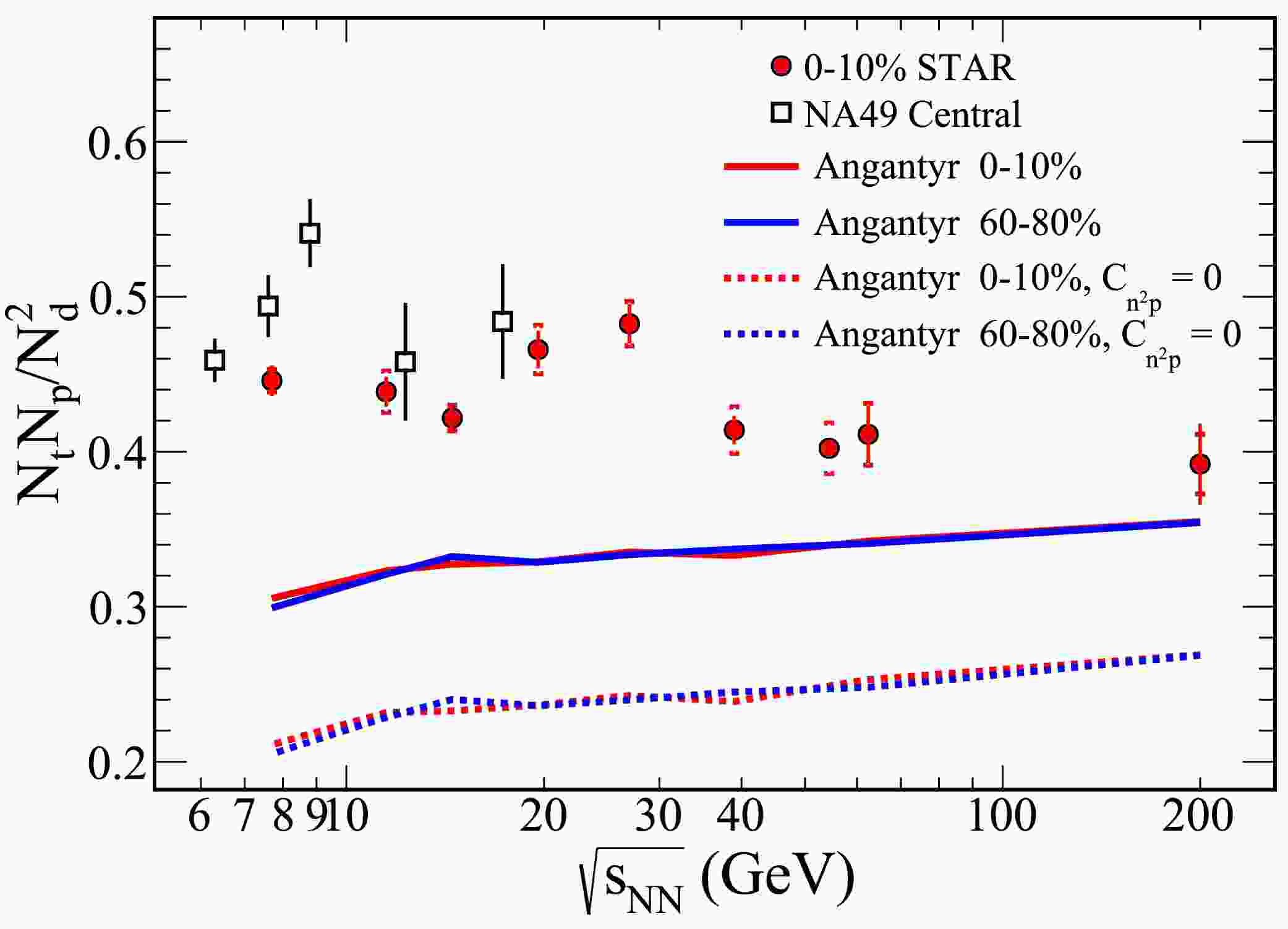
When $ C_{n^2p} $ and $ C_{np} $ are considered, a reduction in the yield ratio is observed for both central and peripheral collisions in Fig. 5 and Fig. 6. This suggests that neglecting these correlation terms may lead to an overestimation of neutron density fluctuations. In the lower energy regime, the influence of $ C_{n^2p} $ and $ C_{np} $ on the yield ratio is significant. However, the underlying mechanisms remain unclear and represent an important direction for future research.

Figure 7 presents the experimental results of light nuclei yield ratios from the STAR detector for 0−10% central Au+Au collisions [26, 34] and NA49 for central Pb+Pb collisions [24, 35]. These results are compared with theoretical predictions from the PYTHIA8 Angantyr model. A striking feature observed in the experimental data is the non-monotonic energy dependence of the yield ratios. Specifically, the yield ratio of light nuclei exhibits a pronounced peak in the energy range of $ \sqrt{s_{\rm{NN}}}=20-30 $ GeV, which indicates the most significant relative neutron density fluctuations occurring within this range.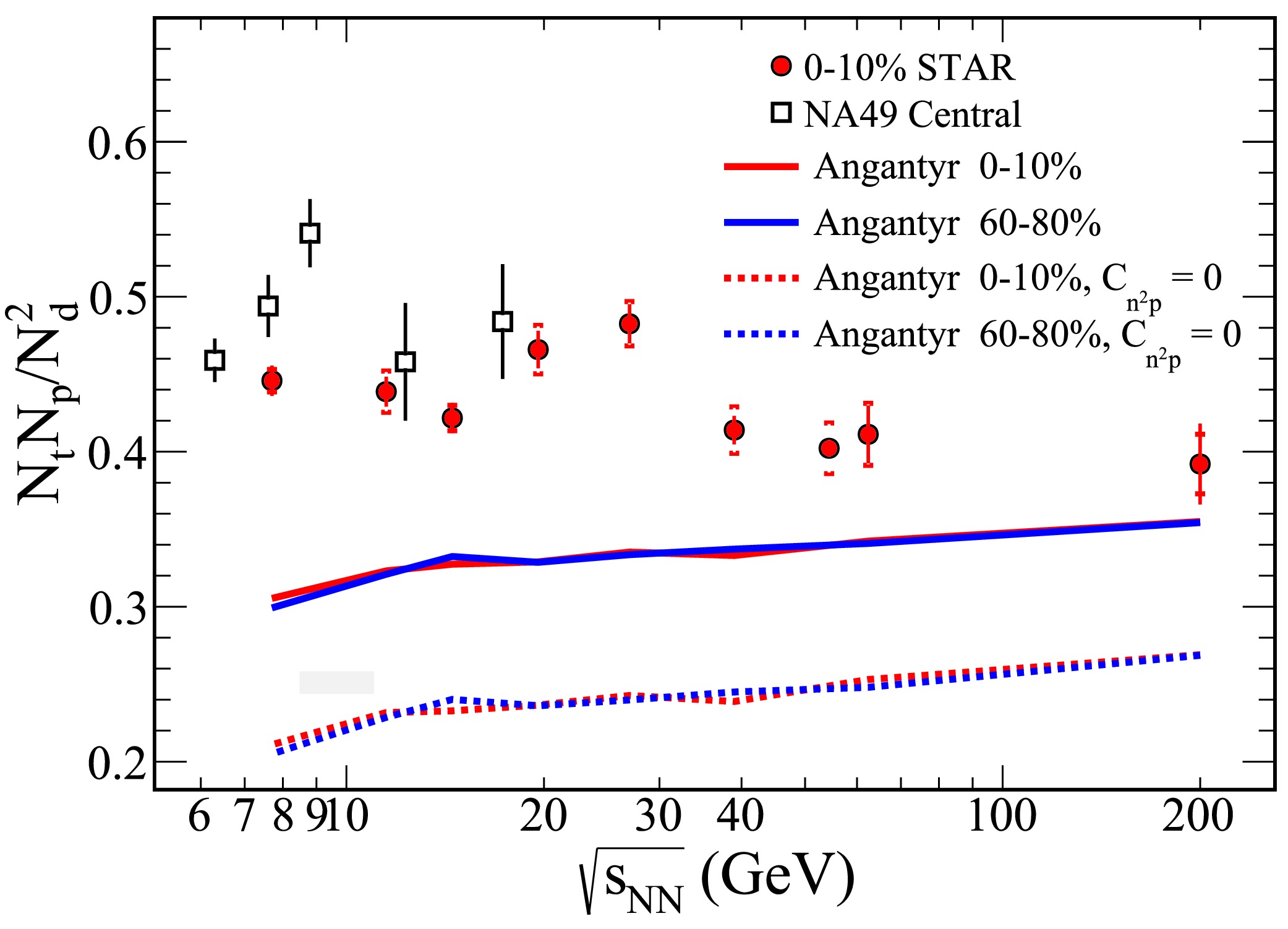

Figure 7.  (color online) The yield ratio of $ N_tN_p/N_d^2 $, considering both collision energy and centrality, was analyzed using the PYTHIA8 Angantyr model within the rapidity range $ |y|\leq 0.5 $. The results from the PYTHIA8 Angantyr model are represented as solid lines under the MPI and RC mode, whereas the dashed lines indicate the results from the same model by ignoring the three-nucleon correlation ($ C_{n^2p} = 0 $), as detailed in [27]. Experimental results from the STAR detector for 0–10% central Au+Au collisions [26, 34] are shown as solid circles, whereas data from the NA49 experiment for central Pb+Pb collisions [24, 35] are presented as open squares.

In contrast, the PYTHIA8 Angantyr model underestimates the experimental results across the entire energy range. This discrepancy arises because the PYTHIA8 Angantyr model lacks mechanisms involving critical phenomena and the QGP medium, making it unable to reproduce the observed non-monotonic energy dependence.

Furthermore, Fig. 7 highlights the role of three-nucleon correlations, denoted as $ C_{n^2p} $, which lead to an overall enhancement of the light nuclei yield ratios, irrespective of whether the collisions are central or peripheral.

The light nuclei ratios in our results show a weak dependence on collision energy, with a slight increase observed at higher energies. Our results underestimate the experimental results, which include all the real physics, such as the QCD critical point effect around 20 GeV and a possible spinodal effect around 8 GeV [24]. Both of these effects might cause a larger light nuclei ratio at lower collision energies. However, our model currently cannot address these effects. So the discrepancy between our results and the experimental results is large at low energies but small at high energies.

In summary, this study employs the PYTHIA8 Angantyr model to investigate the dependence of the relative neutron density fluctuation, neutron-proton correlations ($ C_{np} $ and $ C_{n^2p} $), and the corresponding light nuclei yield ratio ($ N_tN_p/N_d^2 $) on rapidity, centrality, and collision energy.

A critical observation from the study is the effect of MPI and CR on light nuclei yield ratios. The analysis demonstrates that CR has no impact on the yield ratios if MPI is turned off. Regardless of whether the collisions are central or peripheral, the three-nucleon correlation, $ C_{n^2p} $, leads to a consistent enhancement in the light nuclei yield ratios.

Comparing the predictions of the PYTHIA8 Angantyr model with experimental data, the experimental results exhibit a prominent peak in the light nuclei yield ratio at $ \sqrt{s_{\rm{NN}}}=20-30 $GeV. This peak is indicative of significant fluctuations in the relative neutron density, which are linked to critical phenomena in the collision dynamics. However, the observed non-monotonic energy dependence in the experimental results is underestimated by the PYTHIA8 Angantyr model. This discrepancy arises owing to the inability of the model to incorporate critical physics and QGP medium effects. Despite its limitations, the PYTHIA8 Angantyr model serves as a useful baseline for scenarios where critical phenomena and QGP medium mechanisms are absent. Our study provides a baseline for understanding nucleon coalescence effects in the absence of a QGP phase. As such, it should serve as a useful reference for models that incorporate critical dynamics.

The authors appreciate the referee for his/her careful reading of the paper and valuable comments.