-
A system is called chiral if it is not invariant under mirror reflection. The imbalance of right- and left-handed particles in a chiral system can be quantified by the chiral chemical potential (
$ \mu_5 $ ). In a system of charged fermions with finite$ \mu_5 $ , an electric current can be generated in the presence of a strong magnetic field ($ \overrightarrow{B} $ ),$ \overrightarrow{J_e} \propto \mu_5\overrightarrow{B}, $

(1) which is theorized as the chiral magnetic effect (CME) [1, 2]. CME physics encompasses a wide range of systems and has generated significant interdisciplinary interest (Refs. [3-6]). For example, this has been observed in condensed matter systems using Dirac and Weyl semimetals with emergent chiral quasiparticles such as ZrTe5 [7], Na3Bi [8], TaAs [9], and TaP [10]. In this paper, we present methods studies in search of the CME in high-energy nuclear collisions.
Ultra-relativistic heavy-ion collisions have been performed in experimental facilities such as the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC). These experiments aim to create a new phase of hot and dense nuclear matter called the quark-gluon plasma (QGP), which has a temperature higher than several trillion Kelvin and consists of deconfined quarks and gluons [11-14]. Inside the QGP, the chiral symmetry is approximately restored, and the light-flavor quarks
$ u $ and$ d $ become nearly massless and hence chiral. The two preconditions (finite$ \mu_5 $ and the$ \overrightarrow{B} $ field) for the CME could be realized in heavy-ion collisions as described below.Topological configurations of color-SU(3) gluon fields in quantum chromodynamics (QCD) can generate a chirality imbalance in light quarks through the chiral anomaly [15, 16]; thus, forming local chiral domains with finite
$ \mu_5 $ in a QGP [1, 2, 17-20]. Note that the global chirality imbalance vanishes when averaged over an infinite number of domains. In non-central heavy-ion collisions, extremely strong magnetic fields (B ~ 1014 T) can be formed [1, 17] by energetic protons. By convention, the participating nucleons in the overlap region are called participants, and the rest, spectators.Therefore, the CME can occur in heavy-ion collisions and cause an electric current along the
$ \overrightarrow{B} $ direction. As$ \overrightarrow{B} $ is approximately perpendicular to the reaction plane ($ \Psi_{\rm{RP}} $ ) that contains the impact parameter and the beam momenta of a collision, the CME will manifest itself as an electric charge transport phenomenon across the reaction plane.In view of the CME-induced charge transport and other modes of the collective motion of the QGP, the azimuthal distribution of particles is often Fourier-decomposed for a given transverse momentum (
$ p_T $ ) and pseudorapidity ($ \eta $ ) in an event:$\begin{aligned}[b] \frac{{\rm d}N_{\alpha}}{{\rm d}\phi^*} \approx& \frac{N_\alpha}{2\pi} \Big [1 + 2v_{1,\alpha}\cos(\phi^*) + 2v_{2,\alpha}\cos(2\phi^*) \\&+ 2v_{3,\alpha}\cos(3\phi^*) + ... + 2a_{1,\alpha}\sin(\phi^*) + ... \Big ], \end{aligned} $

(2) where
$ \phi $ is the azimuthal angle of a particle, and$ \phi^* = \phi - { \Psi_{{\rm{RP}}}} $ . The subscript$ \alpha $ ($ + $ or$ - $ ) denotes the charge sign of a particle. Conventionally, the coefficients$ v_1 $ ,$ v_2 $ , and$ v_3 $ correspond to "directed flow," "elliptic flow," and "triangular flow," respectively. They reflect the hydrodynamic response of the QGP medium to the initial collision geometry and its fluctuations [21]. Here "RP" does not necessarily signify the reaction plane, but rather a flow symmetry plane obtained from the collective motion of final particles. For simplicity, we still use RP in the following discussions, where RP denotes a specific flow plane. The coefficient$ a_1 $ (with$ a_{1,-} = -a_{1,+} $ in a charge-symmetric system) characterizes the electric charge separation with respect to the flow plane, e.g., due to the CME. It is tempting to average the$ a_{1,\pm} $ coefficient in Eq. (2) over events to measure the CME signal. However, since$ \mu_5 $ changes sign on a domain-by-domain basis with equal probability (the global chirality should be balanced), the event-averaged$ a_{1,\pm} $ is zero by construction. Therefore, most experimental observables have been designed to measure the$ a_{1,\pm} $ fluctuations with respect to the flow plane.Experimental confirmation of the CME in heavy-ion collisions will open new windows for accessing fundamental aspects of strong interaction physics such as QCD chiral symmetry restoration and the topological configurations of non-Abelian gauge fields. New information could also be extracted on the dynamical evolution of the extremely strong magnetic fields in these collisions, which provides crucial inputs for studying many other nontrivial effects of the magnetic field. Community-wide interest in the search for the CME at the RHIC [22-32] and the LHC [33-37] has increased over the past two decades. However, there is currently no conclusive evidence for the existence of the CME in heavy-ion collisions. The main challenge in the CME search lies in the background contributions to the experimental observables; for example, mechanisms such as resonances with finite elliptic flow can also enhance charge fluctuations across flow planes [38-47]. To better gauge the background, the STAR experiment at the RHIC has collected a large data sample of isobar collisions and performed the corresponding CME-related analyses.
Two isobaric systems,
$ ^{96}_{44} {\rm{Ru}} + ^{96}_{44} {\rm{Ru}}$ and$ ^{96}_{40} {\rm{Zr}} + ^{96}_{40} {\rm{Zr}}$ , have the same number of nucleons and hence similar quantities of elliptic flow; however, they contain different numbers of protons, which causes a difference in the magnetic field strength and, in turn, a difference in the CME signal [48-51]. By keeping the background unchanged and varying the signal level, the two isobaric systems provide an ideal test ground for the CME study. The STAR Collaboration implemented a blind-analysis procedure [52] to eliminate unintentional biases in data analyses, and all analysis codes were frozen as part of the blinding procedure before unblinding the isobar species. As the isobar collisions will be examined with multiple observables, it is desirable to learn the connection and the difference between them, as well as their sensitivities to the CME signals. The objective of this paper is to perform direct comparisons between method kernels. For the sensitivity test of the final observables used in STAR blind analyses, we shall apply the STAR frozen codes to simulated events with various CME inputs. This study will provide an important reference point for the interpretation of isobar-collision data that were recently obtained from blind analyses [53].The paper is structured as follows. In Sec. II, we focus on three observables in search of the CME: the
$ \gamma $ correlator [54], the$ R $ correlator [32, 55], and the signed balance functions [56, 57]. We shall uncover the relations between them. Sec. III describes simple Monte Carlo calculations, as well as a more realistic event generator: Event-By-Event Anomalous-Viscous Fluid Dynamics (EBE-AVFD) [58-60]. These simulations are deployed in Sec. IV to compare the core components of the experimental observables. In Sec. V, EBE-AVFD is used for the isobar collisions under study to estimate the sensitivities of the final observables to the CME signal. Sec. VI presents the summary and outlook. -
Several observables have been proposed to search for the CME in heavy-ion collisions, including the
$ \gamma $ correlator [54], the$ R(\Delta S_m) $ correlator [32, 55], and signed balance functions [56, 57]. It is not a surprise that these methods provide largely overlapping information, as they all make use of similar particle azimuthal correlation inputs. We will review these approaches and reveal the relations among them. -
The three-point
$ \gamma $ correlator (later specified as$ \gamma_{112} $ ) measures the fluctuation in charge separations or$ a_{1,\pm} $ coefficients with respect to a flow plane [54] as follows:$ \begin{aligned}[b] \gamma_{112} \equiv & \langle \cos(\phi_\alpha + \phi_\beta -2{\Psi_{{\rm{RP}}}}) \rangle \\ = & \langle\cos(\phi^*_{\alpha})\cos(\phi^*_{\beta}) - \sin(\phi^*_{\alpha})\sin(\phi^*_{\beta})\rangle \\ = & (\langle v_{1,\alpha}v_{1,\beta}\rangle + B_{\rm{IN}}) -(\langle a_{1,\alpha}a_{1,\beta}\rangle + B_{\rm{OUT}}), \end{aligned} $

(3) where the averaging is performed over all combinations of the
$ \alpha $ and$ \beta $ particles in an event and over all events. The trigonometric expansion reveals the difference between the in-plane and out-of-plane projections of azimuthal correlations. The third term in Eq. (3),$ \langle a_{1,\alpha}a_{1,\,\beta}\rangle $ , represents the fluctuations of$ a_{1,\pm} $ coefficients, the main target of the CME search. The other terms are presumed irrelevant to the CME:$ \langle v_{1,\alpha}v_{1,\,\beta}\rangle $ is related to directed flow and expected to be charge-independent and unrelated to the electromagnetic field in symmetric A+A collisions;$ B_{\rm{IN}} $ and$ B_{\rm{OUT}} $ represent other possible background correlations in and out of the flow plane, respectively. When we take the difference between the opposite-sign and same-sign$ \gamma_{112} $ correlators,$ \Delta \gamma_{112} \equiv \gamma^{\rm{OS}}_{112} - \gamma^{\rm{SS}}_{112}, $

(4) the
$ \langle v_{1,\alpha}v_{1,\,\beta}\rangle $ terms cancel out, as well as a large portion of ($ B_{\rm{IN}}-B_{\rm{OUT}} $ ). A residual flow-plane dependent background in ($ B_{\rm{IN}}-B_{\rm{OUT}} $ ) still exists at a level proportional to elliptic flow, which is the major background source in the$ \Delta \gamma_{112} $ measurements. In practice, the flow plane is approximated by reconstructing the "event plane" ($ \Psi_{{\rm{EP}}} $ ) with detected particles, and then the measurement is corrected for the finite event plane resolution [61]. The main advantages of$ \gamma_{112} $ lie in its direct connection to$ a_1 $ and a straightforward procedure that corrects for the finite event plane resolution.The flow-plane-related backgrounds in
$ \Delta\gamma_{112} $ can be understood with the example of resonance decays. While resonances flow with the QGP medium, their decay daughters generate random (if the parents possess no global spin alignment) event-by-event charge separation across the flow plane [44, 45]. The flowing resonance picture can be generalized as transverse momentum conservation (TMC) [42, 43] and local charge conservation (LCC) [44]. Ideally, the two-particle correlator$ \begin{aligned}[b] \delta \equiv& \langle \cos(\phi_\alpha -\phi_\beta) \rangle \\ =& (\langle v_{1,\,\alpha}v_{1,\,\beta}\rangle + B_{\rm{IN}}) +(\langle a_{1,\, \alpha}a_{1,\,\beta}\rangle + B_{\rm{OUT}}), \end{aligned} $

(5) should also reflect
$ \langle a_{1,\,\alpha} a_{1,\,\beta} \rangle $ ; however, in reality, it is dominated by short-range two-particle correlations. For example, the TMC effect contributes the following relevant correlations in$ \delta $ and$ \gamma_{112} $ [42]:$ \delta^{\rm{TMC}} \approx -\frac{1}{N} \frac{\langle p_T \rangle^2_{\Omega}}{\langle p_T^2 \rangle_{\rm{F}}} \frac{1+({\bar v}_{2,{\Omega}})^2-2{\bar{\bar v}}_{2,{\rm{F}}}{\bar v}_{2,{\Omega}}} {1-({\bar{\bar v}}_{2,{\rm{F}}})^2}, $

(6) $ \begin{aligned}[b] \gamma^{\rm{TMC}}_{112} \approx& -\frac{1}{N} \frac{\langle p_T \rangle^2_{\Omega}}{\langle p_T^2 \rangle_{\rm{F}}} \frac{2{\bar v}_{2,{\Omega}}-{\bar{\bar v}}_{2,{\rm{F}}}-{\bar{\bar v}}_{2,{\rm{F}}}({\bar v}_{2,{\Omega}})^2} {1-({\bar{\bar v}}_{2,{\rm{F}}})^2} \\ \approx& \kappa^{\rm{TMC}}_{112} \cdot v_{2,{\Omega}} \cdot \delta^{\rm{TMC}}, \end{aligned} $

(7) where
$ N $ is the total number of particles,$ \kappa^{\rm{TMC}}_{112} = $ $ (2{\bar v}_{2,{\Omega}}-{\bar{\bar v}}_{2,{\rm{F}}})/v_{2,{\Omega}} $ , and$ {\bar v}_{2} $ and$ {\bar{\bar v}}_{2} $ represent the$ p_T $ - and$ p_T^2 $ -weighted moments of$ v_2 $ , respectively. The subscript "F" denotes an average over all produced particles in the full phase space, whereas the actual measurements only sample a fraction of the full space, denoted by "$ {\Omega} $ ." The background contribution due to the LCC effect has a similar characteristic structure as in Eqs. (6) and (7) [43, 44]. This motivates the following normalization of$ \Delta \gamma $ by$ v_2 $ and$ \Delta \delta $ :$ \kappa_{112} \equiv \frac{\Delta \gamma_{112}}{v_2 \cdot \Delta \delta}. $

(8) A CME signal will cause
$ \kappa_{112} $ to become larger than the background baseline,$ \kappa^{\rm{TMC/LCC}}_{112} $ . Although a reliable estimate of$ \kappa^{\rm{TMC/LCC}}_{112} $ is still elusive, the comparison of$ \Delta\gamma_{112} $ (and$ \kappa_{112} $ ) between isobar collisions may provide a more definite conclusion for the CME signal.It is intuitive to introduce several derivative
$ \gamma $ correlators and their corresponding$ \kappa $ observables [35]; for example,$ \gamma_{123} \equiv \langle \langle \cos(\phi_\alpha + 2\phi_\beta -3{\Psi_{3}}) \rangle\rangle,\;\; \ \kappa_{123} \equiv \frac{\Delta \gamma_{123}}{v_3 \cdot \Delta \delta}, $

(9) $ \gamma_{132} \equiv \langle \langle \cos(\phi_\alpha - 3\phi_\beta + 2{\Psi_{2}}) \rangle\rangle,\;\; \ \kappa_{132} \equiv \frac{\Delta \gamma_{132}}{v_2 \cdot \Delta \delta}, $

(10) where
$ \Psi_{2} $ and$ \Psi_{3} $ represent the$ 2^{\rm{nd}} $ - and$ 3^{\rm rd} $ -order flow planes, respectively. However, these observables may not serve as good background estimates for$ \gamma_{112} $ or$ \kappa_{112} $ . Indeed, background-only AMPT calculations show that$ \kappa_{123} $ and$ \kappa_{132} $ are not equal to$ \kappa_{112} $ in Au+Au collisions at 200 GeV [62]. Therefore, in the following sections, we will not extend our method study to these derivative correlators. -
The
$ R(\Delta S_m) $ correlator [32, 55] takes the double ratio of four event-by-event distributions,$ R(\Delta S_m) \equiv \frac{N(\Delta S_{m,{\rm{real}}})}{N(\Delta S_{m,{\rm{shuffled}}})} \Bigg/ \frac{N(\Delta S^{\perp}_{m,{\rm{real}}})}{N(\Delta S^{\perp}_{m,{\rm{shuffled}}})}, \; \ m = 2,3,..., $

(11) where, in a real event, the charge separation perpendicular to the
$ m^{\rm{th}} $ -order flow plane ($ \Psi_m $ ) is expressed as$ \Delta S_{m,{\rm{real}}} = \langle\sin\left(\frac{m}{2}\phi^*_m\right)\rangle_{N_+} - \langle\sin\left(\frac{m}{2}\phi^*_m\right)\rangle_{N_-}. $

(12) Here,
$ \phi^*_m = \phi - {\Psi}_m $ , and$ N_+ $ ($ N_- $ ) is the number of positively (negatively) charged particles in a specific event. Weighted averages could be used to consider the azimuthal acceptance of the detector.$ \Delta S^{\perp}_m $ denotes the charge separation parallel to$ \Psi_m $ and is defined similar to$ \Delta S_m $ ; however,$ {\Psi}_m $ is replaced with$ ({\Psi}_m + \pi/m) $ to provide a baseline unrelated to the magnetic field. The$ \Delta S^{(\perp)}_{m,{\rm{shuffled}}} $ distributions are obtained via random charge reassignment (shuffling) of the reconstructed tracks in each real event, while respecting the multiplicities of positive and negative charges. Ideally, the CME will cause a concave shape in the double ratio of the$ R(\Delta S_2) $ distribution, which is presumed to differ from the$ R(\Delta S_3) $ shape [55]. The latter is intended as a background estimate similar to the role of$ \gamma_{123} $ .The
$ R(\Delta S_2) $ distribution is fit with a Gaussian (inverse-Gaussian) function if it bears a convex (concave) shape, and the Gaussian width ($ \sigma_{R2} $ ) is used to reflect the CME signal. As the four core components,$ \Delta S^{(\perp)}_{2,{\rm{real}}({\rm{shuffled}})} $ , roughly follow Gaussian distributions, we can establish the relation between$ \sigma_{R2} $ and the RMS values of the core-component distributions:$ \begin{aligned}[b] \frac{S_{{\rm{concavity}}}}{\sigma_{R2}^2} =& \frac{1}{\langle (\Delta S_{2,{\rm{real}}})^2 \rangle} - \frac{1}{\langle (\Delta S_{2,{\rm{shuffled}}})^2\rangle} \\&- \frac{1}{\langle (\Delta S_{2,{\rm{real}}}^{\perp})^2 \rangle} + \frac{1}{\langle (\Delta S_{2,{\rm{shuffled}}}^{\perp})^2 \rangle}.\end{aligned} $

(13) The sign of concavity,
$ S_{{\rm{concavity}}} $ , is positive if the double ratio is convex and negative if concave. First, the meaning of each term on the right must be understood. For simplicity, we use unity weights, and the first term can be expanded as$ \begin{aligned}[b] (\Delta S_{2,{\rm{real}}})^2 \equiv& \left(\frac{\displaystyle\sum\nolimits_{i = 1}^{N_+}\sin(\phi^*_i)}{N_+}-\frac{\displaystyle\sum\nolimits_{i = 1}^{N_-}\sin(\phi^*_i)}{N_-}\right)^2 \\ = & \frac{\displaystyle\sum\nolimits_{i = 1}^{N_+}\sin^2(\phi^*_i)+\displaystyle\sum\nolimits_{i\neq j}^{N_+}\sin(\phi^*_i)\sin(\phi^*_j)}{N_+^2}\\&+\frac{\displaystyle\sum\nolimits_{i = 1}^{N_-}\sin^2(\phi^*_i)+\displaystyle\sum\nolimits_{i\neq j}^{N_-}\sin(\phi^*_i)\sin(\phi^*_j)}{N_-^2}\\&-\frac{2\displaystyle\sum\nolimits_{i = 1,j = 1}^{N_+,N_-}\sin(\phi^*_i)\sin(\phi^*_j)}{N_+N_-} \\ =& \frac{\langle \sin^2(\phi^*_i)\rangle_{N_+} +(N_+-1) \langle \sin(\phi^*_i)\sin(\phi^*_j)\rangle_{N_+N_+}}{N_+}\\&+\frac{\langle \sin^2(\phi^*_i)\rangle_{N_-} +(N_- -1) \langle \sin(\phi^*_i)\sin(\phi^*_j)\rangle_{N_-N_-}}{N_-} \\ &-2\langle \sin(\phi^*_i)\sin(\phi^*_j) \rangle_{N_+N_-} . \end{aligned} $

(14) Using the trigonometric identities,
$ \sin^2(x) = $ $ [1-\cos(2x)]/2 $ and$ 2\sin(x)\sin(y) = \cos(x-y)-\cos(x+y) $ , the average of Eq. (14) over all events is$ \begin{aligned}[b] \langle(\Delta S_{2,{\rm{real}}})^2\rangle = & \frac{1-v_2^+}{2N_+} + \frac{N_+-1}{2N_+}(\delta^{++}-\gamma^{++}_{112})\\&+\frac{1-v_2^-}{2N_-} + \frac{N_- -1}{2N_-}(\delta^{--}-\gamma^{--}_{112}) - (\delta^{+-}-\gamma^{+-}_{112}), \end{aligned}$

(15) $\quad\quad\quad\quad\quad \approx \frac{2(1-v_2-\delta^{\rm{SS}}+\gamma_{112}^{\rm{SS}})}{M} - \Delta\delta + \Delta\gamma_{112}. $

(16) The final line assumes
$ v_2^+ \approx v_2^- $ and$ N_+ \approx N_- = M/2 $ . Even prior to conducting the approximations, it is clear that$ \langle(\Delta S_{2,{\rm{real}}})^2\rangle $ can be expressed by$ N_{+(-)} $ ,$ v_2 $ ,$ \delta $ , and$ \gamma_{112} $ . Similarly,$ \begin{aligned}[b] \langle(\Delta S_{2,{\rm{real}}}^\perp)^2\rangle =& \frac{1+v_2^+}{2N_+} + \frac{N_+-1}{2N_+}(\delta^{++}+\gamma^{++}_{112})+\frac{1+v_2^-}{2N_-} \\&+ \frac{N_- -1}{2N_-}(\delta^{--}+\gamma^{--}_{112}) - (\delta^{+-}+\gamma^{+-}_{112}), \end{aligned} $

(17) $\quad\quad\quad\quad\quad \approx \frac{2(1+v_2-\delta^{\rm{SS}}-\gamma_{112}^{\rm{SS}})}{M} - \Delta\delta - \Delta\gamma_{112}. $

(18) For the shuffled terms,
$ v_2^+ $ and$ v_2^- $ will be roughly replaced with$ (v_2^+ + v_2^-)/2 $ , all the$ \delta $ correlators will be replaced with$ (\delta^{\rm{OS}}+\delta^{\rm{SS}})/2 $ , and all the$ \gamma $ correlators with$ (\gamma^{\rm{OS}}+\gamma^{\rm{SS}})/2 $ . Therefore,$ \langle(\Delta S_{2,{\rm{shuffled}}})^2\rangle \approx \frac{2(1-v_2)-\delta^{\rm{SS}}-\delta^{\rm{OS}}+\gamma_{112}^{\rm{SS}}+\gamma_{112}^{\rm{OS}}}{M}, $

(19) $ \langle(\Delta S_{2,{\rm{shuffled}}}^\perp)^2\rangle \approx \frac{2(1+v_2)-\delta^{\rm{SS}}-\delta^{\rm{OS}}-\gamma_{112}^{\rm{SS}}-\gamma_{112}^{\rm{OS}}}{M}. $

(20) It is appealing to construct a double-subtraction observable based on the four core components of
$ R(\Delta S_2) $ , which shows an apparent link to$ \Delta\gamma_{112} $ as follows:$ \begin{aligned}[b] \Delta_{R2} \equiv& \langle (\Delta S_{2,{\rm{real}}})^2 \rangle - \langle (\Delta S_{2,{\rm{shuffled}}})^2 \rangle - \langle (\Delta S^{\perp}_{2,{\rm{real}}})^2 \rangle \\&+ \langle (\Delta S^{\perp}_{2,{\rm{shuffled}}})^2 \rangle \approx 2\left(1-\frac{1}{M}\right)\Delta \gamma_{112}. \end{aligned} $

(21) This relation will be tested in Sec. IV. To make the connection between the final observables,
$ \sigma^2_{R2} $ and$ \Delta\gamma $ , we combine Eqs. (16), (18), (19) and (20) with Eq. (13) and obtain$ \frac{S_{{\rm{concavity}}}}{\sigma_{R2}^2} \approx -\frac{M}{2}(M-1)\Delta\gamma_{112}. $

(22) Here, we further assume that in each of the four
$ \langle (\Delta S_2)^2\rangle $ terms,$ \dfrac{2}{M} $ is much larger than other contributions, among which$ \Delta\delta $ typically has the largest magnitude. This assumption may not always hold true, depending on collision details such as beam energy and centrality. The relation in Eq. (22) implies that if$ \Delta\gamma $ is positively (negatively) finite, the$ R(\Delta S_2) $ distribution will exhibit a concave (convex) shape and vice versa.The above derivation is with respect to the known flow plane
$ \Psi_m $ , which is not precisely known experimentally, and is assessed by the reconstructed event plane with a finite resolution. The empirical correction for the event plane resolution used in the experiment for$ \Delta_{R2} $ and$ \sigma^2_{R2} $ [55] is nontrivial. An analytical resolution correction has been derived in Ref. [63]. Eqs. (21) and (22) can provide approximate approaches to examine the resolution correction factor.Multiplicity fluctuations widen the
$ R(\Delta S_2) $ distributions. To reduce this effect, a scaling was proposed in Ref. [55], which was used in experimental data analyses and included in the frozen code of the STAR isobar blind analysis. The$ R(\Delta S_2) $ distribution is converted into the$ R(\Delta S'_2) $ distribution by dividing the horizontal axis by the RMS of the$ N(\Delta S_{2, {\rm{shuffled}}}) $ distribution, i.e.,$ \Delta S_2' = $ $ \Delta S/\sqrt{\langle(\Delta S_{2,{\rm{shuffled}}})^2\rangle} $ (see Sec. V for details). Then, the width of$ R(\Delta S'_2) $ becomes$ \begin{aligned}[b] \frac{S_{{\rm{concavity}}}}{\sigma_{R2'}^2} =& \frac{S_{{\rm{concavity}}}}{\sigma_{R2}^2} \langle(\Delta S_{2,{\rm{shuffled}}})^2\rangle \\ \approx& -\frac{M}{2}(M-1)\Delta\gamma_{112} \times \frac{2}{M} \approx -M \Delta\gamma_{112} . \end{aligned} $

(23) -
Another method was recently proposed that invokes signed balance functions [56],
$ \begin{aligned}[b] \Delta B_y \equiv& \Bigg[\frac{N_{y(+-)}-N_{y(++)}}{N_+} - \frac{N_{y(-+)}-N_{y(--)}}{N_-}\Bigg] \\&- \Bigg[\frac{N_{y(-+)}-N_{y(++)}}{N_+} - \frac{N_{y(+-)}-N_{y(--)}}{N_-}\Bigg] \\ =& \frac{N_+ + N_-}{N_+N_-}\Big[N_{y(+-)} - N_{y(-+)}\Big], \end{aligned} $

(24) where
$ N_{y(\alpha\beta)} $ is an event-by-event quantity and denotes the number of pairs in which particle$ \alpha $ is ahead of particle$ \beta $ in the direction perpendicular to the reaction plane ($ p_y^\alpha > p_y^\beta $ ). Similarly, we can construct a$ \Delta B_x $ to count the number of pairs along the in-plane direction. Then, the final observable is based on the widths of the$ \Delta B_y $ and$ \Delta B_x $ distributions:$ r \equiv \sigma(\Delta B_y) / \sigma(\Delta B_x). $

(25) Intuitively, the CME will lead to
$ r>1 $ because the CME-induced charge separation will cause more fluctuations of pair ordering across the reaction plane. The ratio$ r $ can be calculated in both the laboratory frame ($ r_{{\rm{lab}}} $ ) and the pair's rest frame ($ r_{{\rm{rest}}} $ ). It is argued that the rest frame is the most appropriate frame for r to study charge separations, and the ratio,$ R_{{\rm{B}}} = r_{{\rm{rest}}} / r_{{\rm{lab}}}, $

(26) can help differentiate the background from the real CME signal [56]. Similar to the
$ \gamma_{112} $ correlator, a lower event plane resolution will lead to a lower magnitude of the observed$ r $ . Extra care is also needed to correct the$ r $ observables for the event plane resolution.In each event, we can rewrite the core component of
$ \Delta B_y $ as follows:$ N_{y(\alpha\beta)}-N_{y(\beta\alpha)} = \sum\limits_{\alpha,\beta} {\rm{Sign}}[p_{T,\alpha}\sin(\phi^*_\alpha)-p_{T,\,\beta}\sin(\phi^*_\beta)]. $

(27) Compared with other methods, the signed balance functions may be more sensitive to the local CME domains that move with the expanding medium because this method considers the transverse-momentum ordering instead of only the azimuthal angle. For example, a pair of particles traveling in the same direction can still be regarded as a case of charge separation by signed balance functions but not by other methods that only consider the azimuthal angle. However, this advantage will likely not make a significant difference if the local domains merge into a global charge separation for the whole event after full hydrodynamic evolution. Thus, to make a connection with the other observables, we take the first approximation by replacing
$ p_T $ with the mean$ p_T $ ; hence,$ p_T $ can be removed, and only the azimuthal angle is used as in other methods. Next, we unpack the Sign() function and directly use$ [\sin(\phi^*_\alpha) - \sin(\phi^*_\beta)] $ , which requires a normalization factor,$ C_y $ . In view of the event average,$\begin{aligned}[b] \langle N_{y(\alpha\beta)}-N_{y(\beta\alpha)} \rangle \approx& C_y \Big\langle \sum\limits_{\alpha,\beta} \big [\sin(\phi^*_\alpha) - \sin(\phi^*_\beta)\big ] \Big\rangle \\ =& C_y \Big\langle \big [N_\beta \sum\limits_{\alpha}\sin(\phi^*_\alpha) - N_\alpha \sum\limits_{\beta}\sin(\phi^*_\beta)\big ] \Big\rangle \\ =& C_y N_\alpha N_\beta \langle \langle \sin( \phi^*)\rangle _{N_\alpha}-\langle \sin(\phi^*)\rangle_{N_\beta} \rangle. \end{aligned} $

(28) The constant can be determined by explicitly counting the pairs with
$ \dfrac{{\rm d}N}{{\rm d}\phi^*} $ from Eq. (2).$\begin{aligned}[b] \langle N_{y(\alpha\beta)}-N_{y(\beta\alpha)} \rangle = & 2\int_{-\pi/2}^{\pi/2} \Bigg[\int_{-\pi/2}^{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta+\int_{\pi-\phi^*_\alpha}^{3\pi/2} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta\\&-\int^{\pi-\phi^*_\alpha}_{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta\Bigg]\frac{{\rm d}N}{{\rm d}\phi^*_\alpha}{\rm d}\phi^*_\alpha \\ \approx& \frac{8}{\pi^2}\left(1+\frac{2}{3}v_2\right)N_\alpha N_\beta (a_{1,\alpha}-a_{1,\beta}). \end{aligned} $

(29) By comparing Eqs. (28) and (29), we learn that
$ C_y = $ $ 8(1+2v_2/3)/\pi^2 $ . Therefore, if we ignore the$ p_T $ weight,$ \langle\Delta B_y\rangle $ becomes$ \dfrac{8M}{\pi^2}\left(1+\dfrac{2}{3}v_2\right) \langle\langle \sin(\phi^*) \rangle_{N_+} - $ $ \langle \sin(\phi^*)\rangle_{N_-} \rangle $ , which displays a function form akin to$ \langle S_{2,{\rm{real}}}\rangle $ . Similarly, we assume$ \langle N_{x(\alpha\beta)}-N_{x(\beta\alpha)} \rangle \approx C_x N_\alpha N_\beta \langle\langle \cos(\phi^*) \rangle _{N_\alpha}-\langle \cos(\phi^*)\rangle_{N_\beta} \rangle, $

(30) and the explicit counting gives
$ \begin{aligned}[b] \langle N_{x(\alpha\beta)}-N_{x(\beta\alpha)} \rangle = & 2\int_{0}^{\pi} \Bigg[\int_{\phi^*_\alpha}^{2\pi-\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta\\&-\int^{\phi^*_\alpha}_{-\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta\Bigg]\frac{{\rm d}N}{{\rm d}\phi^*_\alpha}d\phi^*_\alpha \\ \approx& \frac{8}{\pi^2}\left(1-\frac{2}{3}v_2\right)N_\alpha N_\beta (v_{1,\alpha}-v_{1,\,\beta}). \end{aligned} $

(31) Thus,
$ C_x = 8(1-2v_2/3)/\pi^2 $ , and$ \langle\Delta B_x\rangle $ becomes$ \dfrac{8M}{\pi^2}\left(1-\dfrac{2}{3}v_2\right) $ $ \langle\langle \cos(\phi^*)\rangle_{N_+} -\langle \cos(\phi^*)\rangle_{N_-} \rangle $ , resembling$ \langle \Delta S_{2,{\rm{real}}}^{\perp}\rangle $ .In reality, both
$ \langle\Delta B_{y(x)}\rangle $ and$ \langle \Delta S_{2,{\rm{real}}}^{(\perp)}\rangle $ are zero, but the derivation of$ C_y $ and$ C_x $ provides insight into the meaning of signed balance functions. Our goal is to relate the RMS values of the$ \Delta B_y $ and$ \Delta B_x $ distributions to the other observables. Below, we directly provide the relations, with the details of the analytical derivations explained in Appendix A.$ \sigma^2(\Delta B_y) \approx \frac{4M}{3}+ \frac{64M^2}{\pi^4}\left(1+ \frac{4}{3} v_2\right)(a_{1,+}-a_{1,-})^2 , $

(32) $ \sigma^2(\Delta B_x) \approx \frac{4M}{3}+ \frac{64M^2}{\pi^4}\left(1-\frac{4}{3}v_2\right)(v_{1,+}-v_{1,-})^2 . $

(33) Then, we define an observable that further connects the signed balance function to the
$ \gamma $ correlator:$ \Delta_{\rm{SBF}} \equiv \sigma^2(\Delta B_y) - \sigma^2(\Delta B_x) \approx \frac{128M^2}{\pi^4}\left(\Delta\gamma_{112}-\frac{4}{3}v_2\Delta\delta\right). $

(34) Note that signed balance functions consider both the azimuthal angles of particles and their momenta. If the ratio definition in Eq. (25) is transformed to
$ \sigma^2(\Delta B_y) - \sigma^2({\Delta B_x}) $ , this method is approximately equivalent to$ (\Delta \gamma_{112}-\dfrac{4}{3}v_2\Delta\delta) $ with momentum weighting. -
We now describe a toy model that uses simple Monte Carlo calculations as well as the more realistic event generator, EBE-AVFD [58-60].
-
We invoke a toy model to verify the mathematical relation between different methods using simplified Monte Carlo calculations. In this setup, particle spectra, collective flow, and charge-separation signals are well constrained and conveniently adjusted such that the response of each method to the signal and the background can be understood in a controlled manner. In the simulations, each event consists of 195
$ \pi^+ $ and 195$ \pi^- $ mesons to match the total multiplicity at midrapidities within 2 units of rapidity in 30%-40% central Au+Au collisions at$ \sqrt{s_{NN}} = $ 200 GeV [64]. In the background-free case, all pions are treated as primordial (none from resonance decays), and their azimuthal angle distribution is configured according to Eq. (2) with$ a_1 $ ,$ v_2 $ , and$ v_3 $ . The elliptic flow ($ v_2 $ ) is introduced by an NCQ-inspired function [65],$ v_2/{\cal{N}} = a/(1+{\rm e}^{-[(m_T-m_0)/{\cal{N}} -b]/c}) - d, $

(35) where
$ {\cal{N}} = 2 $ is the number of constituent quarks in a pion, and$ m_T $ and$ m_0 $ are its transverse mass and rest mass, respectively. The parameters ($ a $ ,$ b $ ,$ c $ , and$ d $ ) are obtained by fitting Eq. (35) to the experimental data [46]. To add the resonance background, a fraction of primordial pions (33$ \pi^+ $ and 33$ \pi^- $ ) are replaced with 33$ \pi^+ $ -$ \pi^- $ pairs from$ \rho $ -meson decays using PYTHIA6 [66]. The$ \rho $ -meson$ v_2 $ is described by Eq. (35) with the corresponding$ \rho $ masses.$ v_3 $ is fixed at$ 1/5 $ of$ v_2 $ at any given$ p_T $ for both primordial pions and$ \rho $ resonances [67]. The primordial-pion spectra follow the Bose-Einstein distribution,$ \frac{{\rm d}N_{\pi^\pm}}{{\rm d}m_T^2} \propto ({\rm e}^{m_T/T_{\rm{BE}}}-1)^{-1}, $

(36) where
$ T_{\rm{BE}} = 212 $ MeV is set to match the experimentally observed$ \langle p_T \rangle $ of 400 MeV [64]. The$ \rho $ -resonance spectra obey$ \frac{{\rm d}N_\rho}{{\rm d}m_T^2} \propto \frac{{\rm e}^{-(m_T-m_\rho)/T}}{T(m_\rho+T)}, $

(37) where
$ T = 317 $ MeV is used to match its$ \langle p_T \rangle $ of 830 MeV, as observed in data [67]. Pseudorapidity (Rapidity) is uniformly distributed in the range of [-1, 1] for primordial pions ($ \rho $ resonances). -
The EBE-AVFD model [58-60] is a comprehensive simulation framework that dynamically describes the CME in heavy-ion collisions. This state-of-the-art tool has been developed over the past few years as an important part of efforts within the Beam Energy Scan Theory (BEST) Collaboration, aiming to address the needs of the ongoing experimental program at RHIC collision energies. Critical to the success of the CME search is a quantitative and realistic characterization of the CME signals as well as the relevant backgrounds. Accordingly, EBE-AVFD implements the dynamical CME transport for quark currents on top of the relativistically expanding viscous QGP fluid and properly models major sources of background correlations, such as LCC and resonance decays.
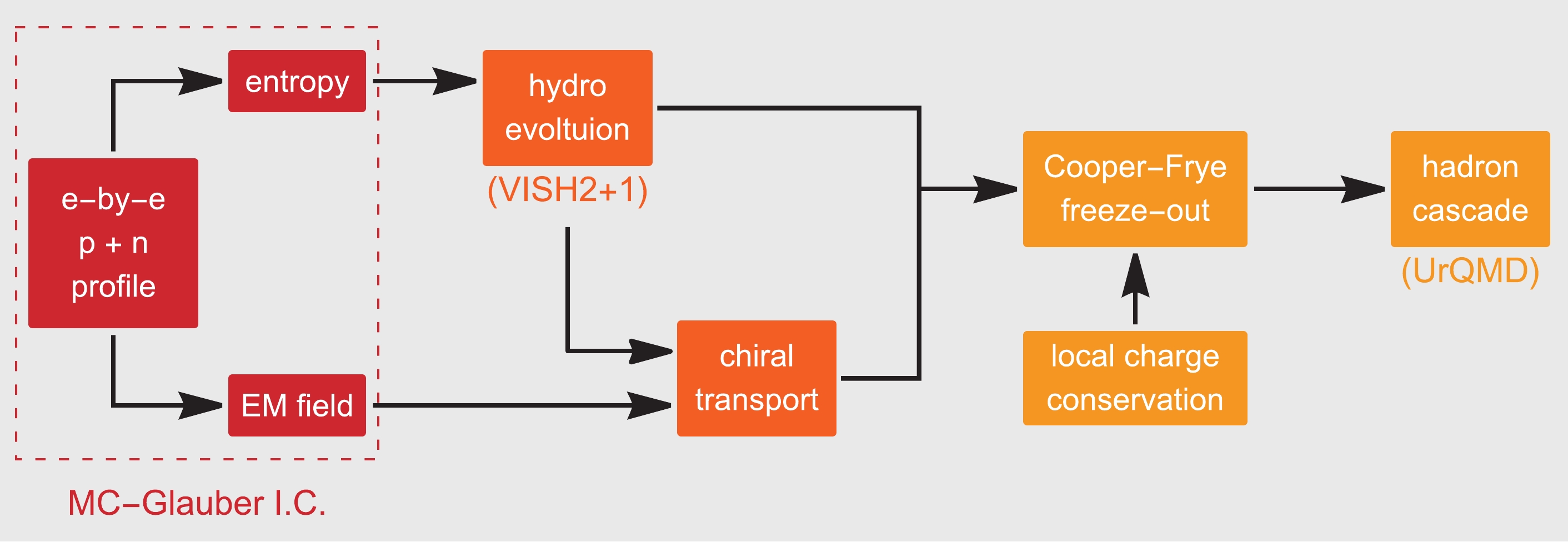
More specifically, the EBE-AVFD framework starts with event-wise fluctuating initial conditions, and solves the evolution of chiral quark currents as linear perturbations in addition to the viscous bulk flow background provided by data-validated hydrodynamic simulation packages. The LCC effect is incorporated in the freeze-out process, followed by hadron cascade simulations. This is illustrated in Fig. 1.
The fluctuating initial conditions for entropy density profiles are generated by the Monte-Carlo Glauber model, with the switching time
$ \tau_0 = 0.6\; {\rm{fm}}/c $ and mixing parameter$ \alpha_{\rm{glb}} = 0.118 $ . The latter factorizes the contributions of the participant density ($ n_{\rm{part}} $ ) and binary collision density ($ n_{\rm{coll}} $ ) in the local entropy density,$ s = \alpha_{\rm{glb}}\, n_{\rm{coll}} + $ $ (1-\alpha_{\rm{glb}})n_{\rm{part}}/2 $ . The initial axial charge density ($ n_5 $ ) is approximated in such a way that it is proportional to the corresponding local entropy density with a constant ratio. This ratio parameter can be varied to sensitively control the strength of the CME transport. For example, one can set$ n_5/s $ to$ 0 $ ,$ 0.1 $ , and$ 0.2 $ in the simulations to represent scenarios of zero, modest, and strong CME signals, respectively. The initial electromagnetic field,$ \overrightarrow{B}_{\rm ini}(\overrightarrow{x}) $ , is computed according to the event-wise proton configuration in the Monte-Carlo Glauber initial conditions. Then, the space-time evolution is modeled as the product of the time-independent initial condition and a space-independent function characterizing its decay in time,$ \overrightarrow{B}(\overrightarrow{x},\tau) = \overrightarrow{B}_{\rm ini}(\overrightarrow{x}) \times F(\tau) $ . With the medium effects taken into account, the time-dependence is chosen to be$ F(\tau) = 1/(1+\tau^2/\tau_{\rm B}^2) $ with$ \tau_{\rm B} = 0.6 \;{\rm{fm}}/ c $ being the lifetime of the B-field.The hydrodynamic evolution is solved through two components. The bulk-matter collective flow is described by the VISH2+1 simulation package [68] with the lattice equation of state s95p-v1.2, shear-viscosity
$ \eta/s = 0.08 $ , and freeze-out temperature$ T_{\rm{fo}} = 160\; $ MeV. Such hydrodynamic simulations of bulk flow have been extensively tested and validated with relevant experimental data. The dynamical CME transport is described by anomalous hydrodynamic equations for the quark chiral currents on top of the bulk flow background, where the magnetic-field-induced CME currents lead to a charge separation in the fireball. Additionally, conventional transport processes such as diffusion and relaxation of quark currents are consistently included, with the diffusion constant chosen to be$ \sigma = 0.1\,T $ and the relaxation time chosen to be$ \tau_r = 0.5/T $ . Further discussions on hydrodynamic equations and their relevant details can be found in Refs. [58-60].After the hydrodynamic stage, hadrons are locally produced in all fluid cells on the freeze-out hypersurface using the Cooper-Frye freeze-out formula
$ E \frac{{\rm d}N}{{\rm d}^3p} (x^\mu, p^\mu) = \frac{g}{(2\pi)^3} \int_{\Sigma_{\rm{fo}}} p^\mu {\rm d}^3\sigma_\mu f(x,p) \,\, . $

(38) Here, the local distribution function automatically includes the charge separation effect owing to the CME as well as non-equilibrium corrections. In the freeze-out process, the LCC effect is implemented by extending an earlier method from Ref. [69]. The approach in Ref. [69] chooses to produce all charged hadron-antihadron pairs in the same fluid cell, while their momenta are sampled independently in the local rest frame of the fluid cell. This treatment implicitly assumes the charge-correlation length to be smaller than the cell size, and hence provides an upper limit for the correlations between opposite-sign pairs. In the EBE-AVFD package, the aforementioned procedure is generalized and improved to more realistically mimic the impact of a finite charge-correlation length; a new parameter
$ P_{\rm{LCC}} $ is introduced to characterize the fraction of charged hadrons that are sampled in positive-negative pairs in the same way, as in Ref. [69], while the rest of the hadrons are sampled independently. Varying the parameter$ P_{\rm{LCC}} $ between 0 and 1 tunes the LCC contributions from none to its maximum. Finally, all the hadrons produced from the freeze-out hypersurface are further subject to hadron cascades through UrQMD simulations [70], which account for various hadron resonance decay processes and automatically include their contributions to the charge-dependent correlations. The tuning of the EBE-AVFD calculations to the experimental measurements of$ \Delta\delta $ and$ \Delta\gamma_{112} $ in Au+Au collisions suggests that an optimal value of$ P_{\rm{LCC}} $ is approximately$ 1/3 $ , and that roughly half of the background correlations arise from LCC and the other half from resonance decays. -
We use the toy model and the EBE-AVFD model to simulate the core components of the experimental observables introduced in Sec. II:
$ \Delta \gamma_{112} $ for the$ \gamma $ correlator,$ \Delta_{R2} $ for the$ R $ correlator, and$ \Delta_{\rm{SBF}} $ for signed balance functions. Our objective is to examine the responses of the core components to the CME signal and the background, and to verify the relations between these methods (Eqs. (21) and (34)). For a fair comparison with other observables, the momentum weighting is not applied in the$ \Delta_{\rm{SBF}} $ results. For simplicity, the true reaction plane is used in all the simulations in this section. The particles of interest are selected with$ |\eta|<1 $ and$ 0.2 < p_T < 2 $ GeV/c. -
We consider the three core components equally by plotting
$ 2\Delta\gamma_{112} $ ,$ \Delta_{R2} $ , and$ \Delta'_{\rm{SBF}}\equiv\left(\dfrac{\pi^4}{64M^2}\Delta_{\rm{SBF}}+ $ $ \dfrac{8}{3}v_2\Delta\delta\right) $ as function of the input$ a_1^2 $ in Fig. 2 for two scenarios: with and without resonance decays (LCC is not implemented in the toy model). In the background-free case without decays, the three observables produce highly similar results (open markers); they fall on the linear function of$ 4a_1^2 $ . Therefore, all three methods are sensitive to the same amount of the CME signal. When resonance decays are turned on with finite elliptic flow, sizeable background effects appear alongside the pure-signal contributions for all three approaches (solid markers); this is more prominent at smaller input$ a_1^2 $ values. Note that each final observable can be approximately regarded as a weighted average of the correlations due to the CME, the resonance background, and the cross terms. At unrealistically large$ a_1^2 $ values, the CME contribution in an observable may be diluted by the resonance contribution because the latter becomes smaller than the former. The three core components exhibit similar responses to the backgrounds owing to flowing resonances in this toy model. In this scenario, there are subtle differences between the results from these three approaches, likely because of higher-order effects that were omitted in the derivation of Eqs. (21) and (34). Although the background contributions depend on spectra and, in particular, the elliptic flow of resonances [43, 44, 47], in the first order, we expect the three observables to have similar responses to resonance decays for a wide range of spectra or elliptic flow. A recent study [63] also found that the$ R $ correlator and the$ \Delta\gamma_{112} $ correlator have similar sensitivities to the CME signal and background.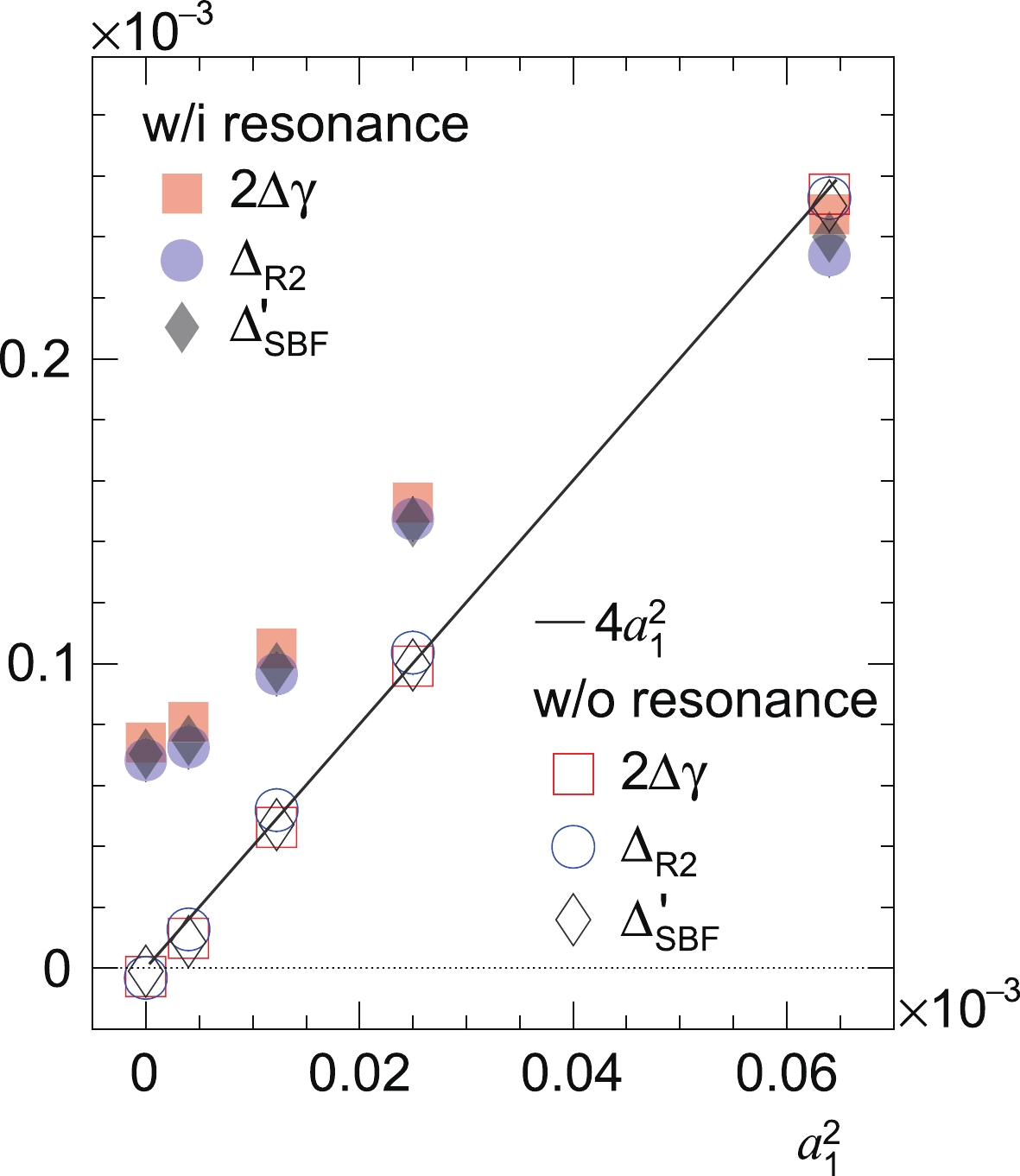
Figure 2. (color online) The toy-model simulations of
$ 2\Delta\gamma_{112} $ ,$ \Delta_{R2} $ , and$ \Delta'_{\rm{SBF}}\equiv\left(\dfrac{\pi^4}{64M^2}\Delta_{\rm{SBF}}+\dfrac{8}{3}v_2\Delta\delta\right) $ as a function of the input$ a_1^2 $ . The open markers represent the pure-signal scenario without resonances, and the solid markers denote the scenario with resonance decays. For comparison, the linear function of$ 4a^2_1 $ is also added. -
The EBE-AVFD model applies the CME and the backgrounds more realistically. In the following simulations, we generate the EBE-AVFD events of the 30%-40% Au+Au collisions at
$ \sqrt{s_{{{NN}}}} = 200 $ GeV, with$ n_{5}/s $ = 0, 0.1 and 0.2. The background effects remain approximately the same, whereas the CME signal is varied according to the input$ n_{5}/s $ . Figure 3(a) presents the corresponding calculations of$ 2\Delta\gamma_{112} $ ,$ \Delta_{R2} $ , and$ \Delta'_{\rm{SBF}} $ as a function of$ n_{5}/s $ . The three methods yield similar results at each input$ n_{5}/s $ value, supporting the relations expressed in Eqs. (21) and (34).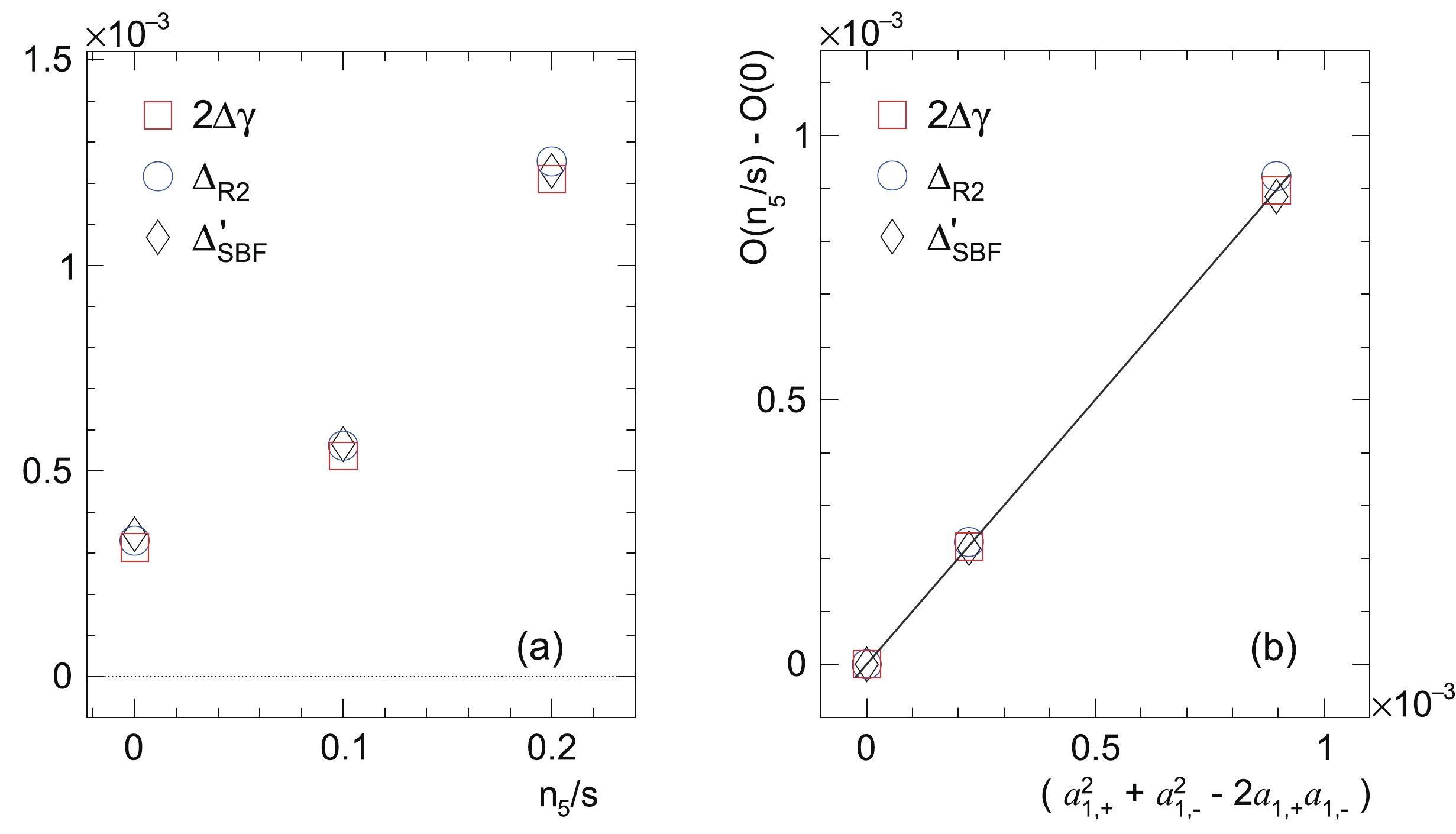
Figure 3. (color online) (a) The EBE-AVFD simulations of
$ 2\Delta\gamma_{112} $ ,$ \Delta_{R2} $ , and$ \Delta'_{\rm{SBF}}\equiv \left (\dfrac{\pi^4}{64M^2}\Delta_{\rm{SBF}}+\dfrac{8}{3}v_2\Delta\delta \right) $ as a function of$ n_5/s $ in the 30%-40% Au+Au collisions at 200 GeV. (b) The same results with the subtraction of the pure-background case vs$ (a_{1,+}^2 + a_{1,-}^2 - 2a_{1,+}a_{1,-}) $ . For comparison, a linear function of$ y = x $ is drawn to verify the relation in Eq. (39).With the known reaction plane angle in each EBE-AVFD event, we can readily calculate
$ a_{1,\pm} $ and verify whether this CME contribution explains the difference between the cases with different$ n_{5}/s $ values.$ a_{1,\pm} $ is consistent with zero for$ n_{5}/s = 0 $ , and$ a_{1,+} $ and$ a_{1,-} $ are finite with opposite signs for finite$ n_{5}/s $ values. Note that$ a_{1,+} $ and$ a_{1,-} $ do not necessarily have the same magnitude because the collision system always carries extra positive charges. Based on the expansion of the$ \gamma_{112} $ correlator in Eq. (3) and the equivalence between the three observables, we expect the following equation for any of these observables,$ O(n_{5}/s) $ :$ O(n_{5}/s) - O(0) = a_{1,+}^2 + a_{1,-}^2 - 2a_{1,+}a_{1,-}. $

(39) Figure 3(b) shows that the results for each observable after the subtraction of the pure-background case fall on the straight line representing the relation in Eq. (39). Thus, the EBE-AVFD calculations reveal the linear superposition of the CME signal and the background contribution in the experimental observables. This property is implicitly assumed by most of the analysis techniques that attempt to separate the CME signal and the backgrounds, and it is now corroborated by the EBE-AVFD model.
The core-component comparison using both the toy model and the EBE-AVFD model supports the idea that, in the first order, the three observables are equivalent because of their similar responses to the CME signal as well as the backgrounds.
-
The validity of Eq. (39) for the three experimental observables reveals that the disentanglement of the CME signal from the backgrounds using isobar collisions is feasible. To eliminate unintentional biases in the analyses of the isobar-collision data, the STAR Collaboration followed a blind-analysis procedure [52]. One important step in this procedure requires the analysis codes from all analyzers to be frozen before the mass production of the isobar-collision data. In this section, we shall apply these frozen codes to the EBE-AVFD events of isobar collisions to investigate the realistic sensitivity of each method to the CME signal. The particles of interest are chosen based on the acceptance of
$ |\eta|<1 $ , with$ 0.2 < p_T < 2 $ GeV/c for the$ \gamma $ correlator and signed balance functions, or with$ 0.35 < p_T < 2 $ GeV/c for the$ R $ correlator, as implemented in the frozen codes. Owing to the different kinematic cuts used in different methods, this sensitivity study cannot guarantee the direct comparisons that were assured in the core-component comparisons in Sec. IV. Nevertheless, we will obtain a reliable benchmark for interpreting experimental data.For each of the two isobaric collision systems, Ru+Ru and Zr+Zr at
$ \sqrt{s_{{{NN}}}} = 200 $ GeV, four cases of the EBE-AVFD events have been generated, with$ n_5/s = 0, $ $ 0.05,\; 0.1, \; {\rm{and}} \; 0.2 $ . The centrality selection for all the cases focuses on the 30%-40% central collisions, in which the potential CME signal is relatively easy to detect owing to good event plane resolutions. 200 million events are produced for each case of$ n_5/s = 0 $ and$ n_5/s = 0.2 $ , and 400 million events are produced for each of the other cases. To mimic the detection performance of the STAR Time Projection Chamber, the simulated particles in the EBE-AVFD events are randomly rejected according to a transverse-momentum dependent tracking efficiency. The event plane resolution for these EBE-AVFD events is matched to that of the real isobar data (Isobar Mixed Analysis in Ref. [53]).Table 1 lists
$ a_{1,\pm} $ calculated using EBE-AVFD at different$ n_5/s $ values.$ a_{1,\pm} $ displays a linear function of$ n_5/s $ , and$ a_{1,+} $ is approximately 4% larger than$ a_{1,-} $ for all the cases, reflecting the collision systems' charge asymmetry. Meanwhile,$ a_{1,\pm} $ is approximately 7% larger in Ru+Ru than in Zr+Zr collisions, which confirms the expectation from the difference in the corresponding magnetic fields [50]. For the experimental observables under study, the background levels are approximately the same for the two isobaric systems, and the ratio of the Ru+Ru measurement to the Zr+Zr measurement is expected to be larger than unity in the presence of a positive CME signal. Hence, the sensitivity of each method can be defined by the statistical significance of this ratio's deviation from unity.$n_{5}/s$ 

$a_{1,+}$ (%)

$a_{1,-}$ (%)

Ru+Ru Zr+Zr Ru+Ru Zr+Zr 0 0 0 0 0 0.05 0.37 0.35 0.35 0.33 0.10 0.74 0.69 0.71 0.66 0.20 1.48 1.38 1.42 1.32 Table 1. The
$a_{1,\pm}$ values calculated for the EBE-AVFD events for the 30%-40% isobar collisions at$\sqrt{s_{{NN}}} = 200$ GeV.Figure 4 presents the EBE-AVFD calculations of
$ \gamma_{112}^{{\rm{OS}}({\rm{SS}})} $ (a) and$ \Delta \gamma_{112} $ (b) as functions of$ n_{5}/s $ for the 30%-40% isobar collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV. The ratios of$ \Delta \gamma_{112} $ between Ru+Ru and Zr+Zr is delineated in panel (c). The$ 2^{\rm{nd}} $ -order event plane is reconstructed from the same kinematic region as the particles of interest, and the observed$ \gamma $ correlators and$ v_2 $ (to be shown later) have been corrected with the corresponding event plane resolution. At each$ n_5/s $ value,$ \gamma_{112}^{\rm{OS}} $ remains positive and$ \gamma_{112}^{\rm{SS}} $ stays negative, both with larger magnitudes at higher$ n_5/s $ . Although the CME expects$ \gamma_{112}^{\rm{OS}} $ and$ \gamma_{112}^{\rm{SS}} $ to be symmetric around zero, there are charge-independent backgrounds, such as momentum conservation and elliptic flow, that shift$ \gamma_{112}^{\rm{OS}} $ and$ \gamma_{112}^{\rm{SS}} $ upward or downward [24]. Therefore, we shall focus on$ \Delta\gamma_{112} $ , which shows a finite background contribution at$ n_5/s = 0 $ and increases with the CME signal. The difference between Ru+Ru and Zr+Zr is better viewed with the ratio$ \Delta\gamma_{112}^{{\rm{Ru+Ru}}}/\Delta\gamma_{112}^{{\rm{Zr+Zr}}} $ ; this ratio is consistent with unity at$ n_5/s = 0 $ and increases quadratically with$ n_5/s $ , as demonstrated by the$ 2^{\rm{nd}} $ -order-polynomial fit function that passes (0, 1) (dashed line). The quadratically-increasing trend is expected because this ratio is a linear function of the CME signal fraction in$ \Delta\gamma_{112} $ in a two-component perturbative framework [50]; the the latter is proportional to$ (n_5/s)^2 $ or$ a_1^2 $ , as shown in Fig. 3.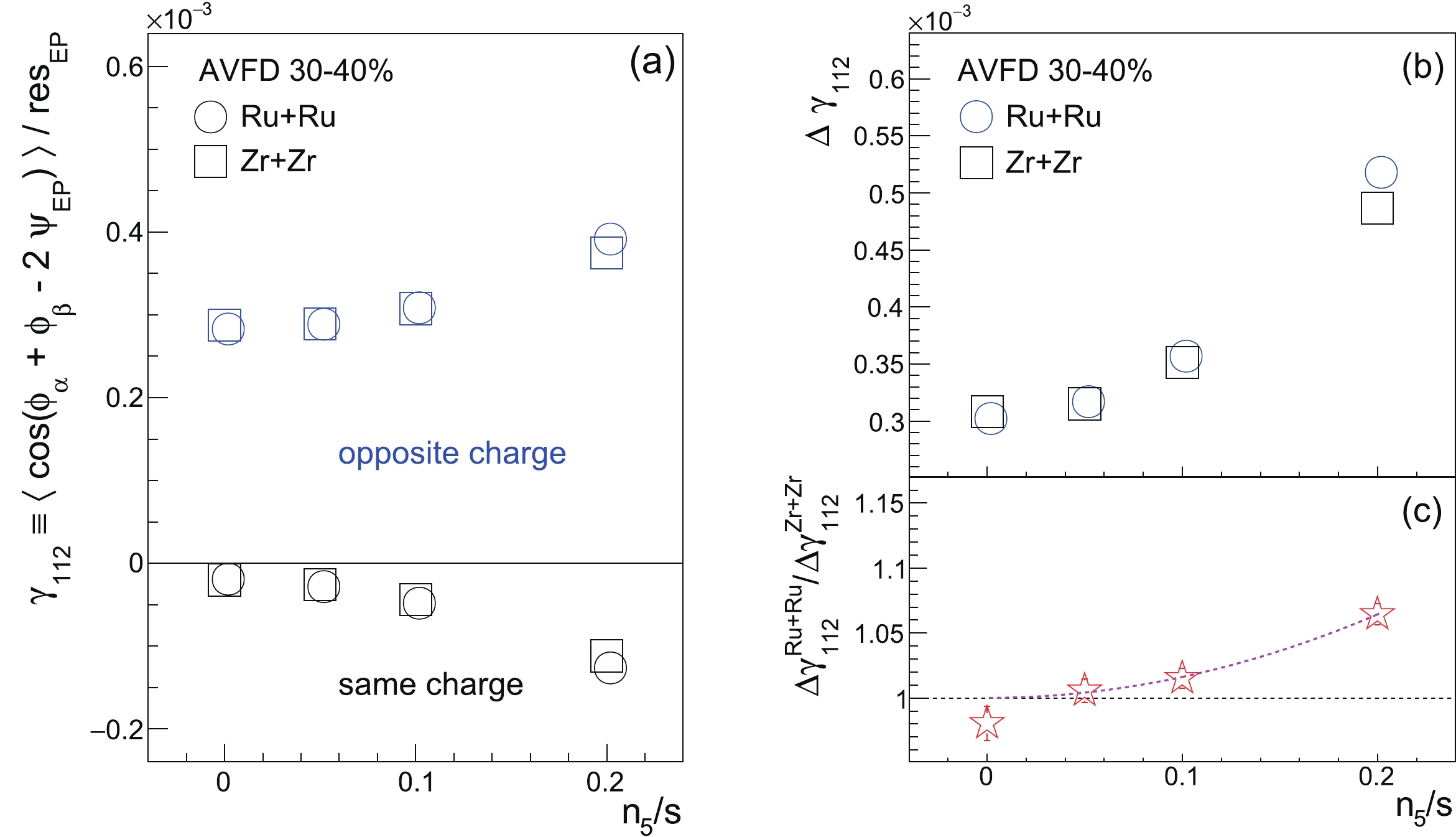
Figure 4. (color online) EBE-AVFD calculations of
$ \gamma_{112}^{ {\rm{OS}}({\rm{SS}})} $ (a) and$ \Delta \gamma_{112} $ (b) as functions of$ n_{5}/s $ for the 30%-40% isobar collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV, with the ratio of$ \Delta \gamma_{112} $ (c) between Ru+Ru and Zr+Zr. In panel (c), the$ 2^{\rm{nd}} $ -order-polynomial fit function illustrates the rising trend starting from (0, 1).Potentially, the
$ \delta $ correlator could also contain the CME signal as Eq. (5) suggests, which would be manifested in the$ \Delta\delta $ ratio between Ru+Ru and Zr+Zr [60]. Figure 5 depicts the EBE-AVFD results of$ \delta^{ {\rm{OS}}({\rm{SS}})} $ (a) and$ \Delta \delta $ (b) as functions of$ n_{5}/s $ for the 30%-40% isobar collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV. The ratio of$ \Delta \delta $ between Ru+Ru and Zr+Zr is shown in panel (c). For all cases,$ \delta^{\rm{OS}} $ is larger than$ \delta^{\rm{SS}} $ , leading to a positive$ \Delta\delta $ because the background contributions to$ \delta^{\rm{OS}} $ are larger than those to$ \delta^{\rm{SS}} $ . It is argued that, although overshadowed by the background contributions, the CME signal in$ \Delta\delta $ could be even larger than that in$ \Delta\gamma_{112} $ measured with respect to the participant plane [60]. This is because the magnetic field difference between the two isobar systems is maximal with respect to the reaction plane and is reduced when measured otherwise. Indeed, the EBE-AVFD simulations support this idea; at each$ n_5/s $ value in Fig. 5(c), the deviation of the$ \Delta\delta $ ratio from unity is at a similar level to that of the$ \Delta\gamma_{112} $ ratio. As$ \Delta\delta $ is typically larger than$ \Delta\gamma $ by an order of magnitude, this similar deviation in their respective ratios indicates a significantly larger CME effect in$ \Delta\delta $ than in$ \Delta\gamma $ . A$ 2^{\rm{nd}} $ -order polynomial fit function is added to guide the eye. As a result of the smaller relative statistical uncertainties of$ \Delta\delta $ than those of$ \Delta\gamma_{112} $ , the former may yield even better CME signal significance levels than the latter in the isobar-collision data, provided equal background contributions to$ \Delta\delta $ in the two systems. The caveat is that the two-particle correlation background contributions to$ \Delta\delta $ are significantly larger than those to$ \Delta\gamma $ ; hence, any difference in the background between the two isobaric systems would have a stronger impact on$ \Delta\delta $ . However likely or unlikely this scenario is to occur, we retain these results for completeness and to the test with real data.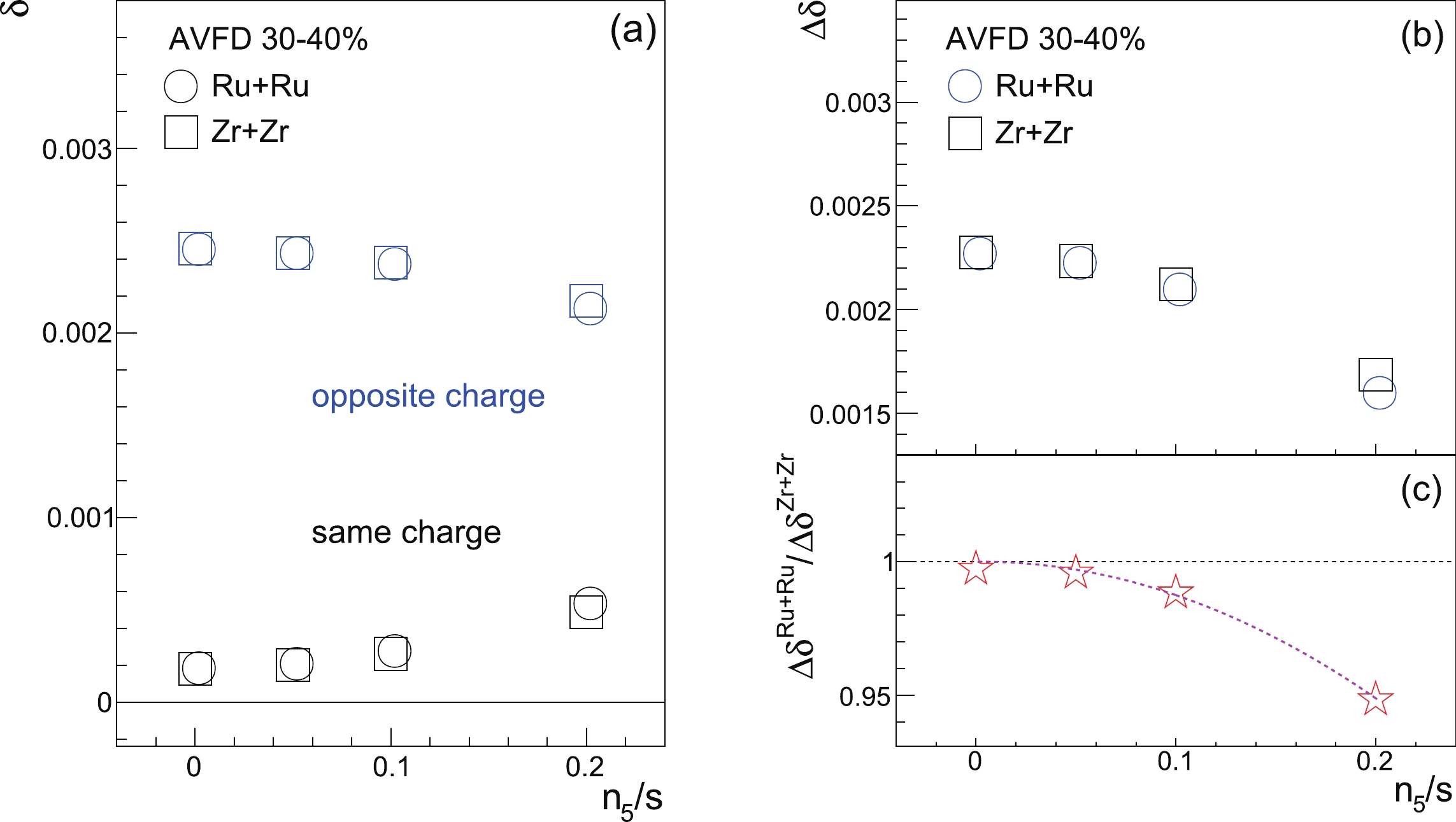
Figure 5. (color online) EBE-AVFD calculations of
$ \delta^{ {\rm{OS}}({\rm{SS}})} $ (a) and$ \Delta \delta $ (b) as functions of$ n_{5}/s $ for the 30%-40% isobar collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV, with the ratios of$ \Delta \delta $ (c) between Ru+Ru and Zr+Zr. In panel (c), the$ 2^{\rm{nd}} $ -order-polynomial fit function is added to demonstrate the rising trend starting from (0, 1).Between Ru+Ru and Zr+Zr, the difference in the background contributions to
$ \Delta\gamma_{112} $ may be small but may still be finite owing to the potentially different$ v_2 $ values. The normalization of$ \Delta\gamma_{112} $ using$ v_2 $ would be a more robust variable for the CME search. The EBE-AVFD simulations of$ v_2 $ (a) and$ \Delta\gamma_{112}/v_2 $ (c) are presented in Fig. 6 as functions of$ n_{5}/s $ for the 30%-40% isobar collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV, with the corresponding$ v_2 $ ratio (b) and$ \Delta\gamma_{112}/v_2 $ ratio (d) between Ru+Ru and Zr+Zr. The$ v_2 $ values are very close to each other between the Ru+Ru and Zr+Zr collisions, with the relative difference at the level of 0.1%. Therefore, the Ru+Ru/Zr+Zr ratio of$ \Delta\gamma_{112}/v_2 $ in Fig. 6(d) is approximately identical to that of$ \Delta\gamma $ in Fig. 4(c). Besides the possible$ v_2 $ difference, the two-particle correlation strength (which is part of the CME background) could also differ between the Ru+Ru to Zr+Zr collisions. Although$ \Delta\delta $ is sensitive to the CME, it is overwhelmed by background correlations and thus may be used as an approximate gauge for the two-particle correlation strength. As a result, the additional normalization of$ \Delta\gamma_{112}/v_2 $ using$ \Delta\delta $ in$ \kappa_{112} $ could further suppress this difference and enhance the sensitivity to the CME signal. There are two potential scenarios where$ \kappa_{112} $ has the advantage over$ \Delta\gamma_{112} $ . First, in reality, the$ \Delta\delta $ ratio may disfavor the CME interpretation; hence, the$ \kappa_{112} $ ratio is less prone to a false CME signal than the$ \gamma_{112} $ ratio. Second,$ \Delta\delta $ may also contain the CME signal as shown in Fig. 5(c), while the relative statistical uncertainty of$ \Delta\delta $ is smaller than that of$ \Delta\gamma_{112} $ . In that case,$ \kappa_{112}^{\rm{Ru+Ru}}/\kappa_{112}^{\rm{Zr+Zr}} $ could yield a larger ratio than$ \Delta\gamma_{112}^{\rm{Ru+Ru}}/\Delta\gamma_{112}^{\rm{Zr+Zr}} $ , with a similar relative statistical uncertainty, which results in a better significance of the CME signal. Indeed, panel (f) also shows a quadratically increasing trend, with larger magnitudes than panel (d) at finite$ n_5/s $ values, and the calculated significance values for$ \kappa_{112}^{\rm{Ru+Ru}}/\kappa_{112}^{\rm{Zr+Zr}} $ are approximately double those for$ \Delta\gamma_{112}^{\rm{Ru+Ru}}/\Delta\gamma_{112}^{\rm{Zr+Zr}} $ , as documented later in Table 2. In general, the EBE-AVFD simulations show good responses to the signal for$ \Delta\gamma_{112}^{\rm{Ru+Ru}} / \Delta\gamma_{112}^{\rm{Zr+Zr}} $ ,$ \Delta\delta^{\rm{Ru+Ru}} / \Delta\delta^{\rm{Zr+Zr}} $ , and$ \kappa_{112}^{\rm{Ru+Ru}} / \kappa_{112}^{\rm{Zr+Zr}} $ , and these promising features await verification by the isobar-collision data.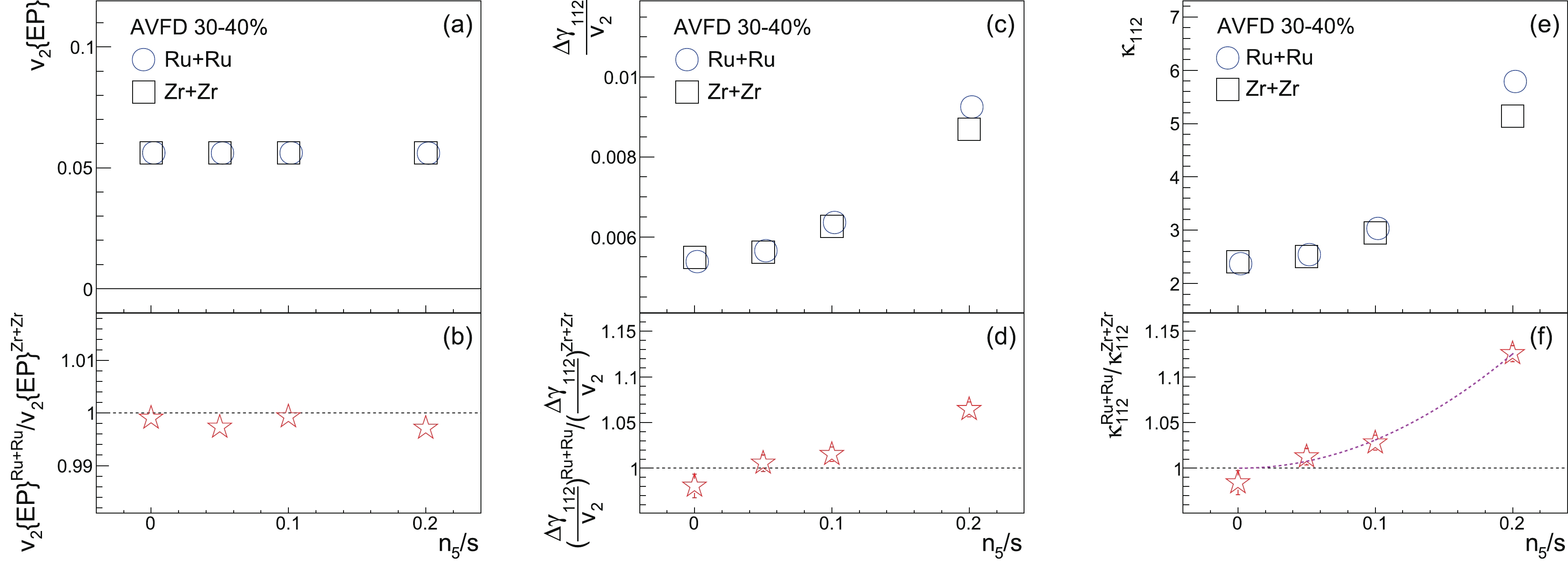
Figure 6. (color online) EBE-AVFD calculations of
$ v_2 $ (a),$ \Delta\gamma_{112}/v_2 $ (c), and$ \kappa_{112} $ (e) as functions of$ n_{5}/s $ for the 30%-40% isobar collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV, with the ratios of$ v_2 $ (b),$ \Delta\gamma_{112}/v_2 $ (d), and$ \kappa_{112} $ (f) between Ru+Ru and Zr+Zr. In panel (f), the$ 2^{\rm{nd}} $ -order-polynomial fit function illustrates the rising trend starting from (0, 1).$ n_{5}/s $ 

$ N_{\rm{event}} $ 

$ \Delta \gamma_{112} $ 

$ \Delta\delta $ 

$ \kappa_{112} $ 

$ r_{\rm{lab}} $ 

$ \sigma_{R2}^{-1} $ 

$ \Delta\gamma_{112}\{{\rm{RP}}\} $ 

$ \sigma_{R2}^{-1}\{{\rm{RP}}\} $ 

0 $ 2\times 10^8 $ 

−1.50 −2.89 −1.21 −0.77 1.33 0.67 0.56 0.05 $ 4\times 10^8 $ 

0.62 −6.16 1.37 0.47 0.29 2.84 3.33 0.10 $ 4\times 10^8 $ 

1.91 −16.81 3.43 3.11 0.62 11.78 10.85 0.20 $ 2\times10^8 $ 

7.73 −42.96 14.07 5.96 1.84 37.48 27.90 Table 2. The statistical significance of
$ (O^{\rm{Ru+Ru}}/O^{\rm{Zr+Zr}} -1) $ for different experimental observables. In contrast with other observables, the$ \Delta\delta $ ratio expects negative significance values owing to the CME signal.$ N_{\rm{event}} $ denotes the number of events used for each isobaric system in the simulation. For completeness, the final two columns list the significance values for$ \Delta\gamma_{112} $ and$ \sigma^{-1}_{R2} $ with respect to the reaction plane (not following the frozen code).A similar frozen-code analysis is performed for the
$ R(\Delta S_2) $ correlator, and the results are presented in Fig. 7. To minimize the influence of particle number fluctuations, the$ R(\Delta S_2) $ distribution is converted to the$ R(\Delta S_2') $ distribution by dividing the horizontal axis by the RMS of the$ N(\Delta S_{2,{\rm{shuffled}}}) $ distribution, i.e.,$ \Delta S_2' = \Delta S_2/\sqrt{\langle(\Delta S_{2,{\rm{shuffled}}})^2\rangle} $ . Then,$ \Delta S_2' $ is further modified to correct for the event plane resolution, i.e.,$ \Delta S'' = \Delta S'/\delta_{{\rm{Res}}} $ , where$ \delta_{{\rm{Res}}} $ is the correction factor (details can be found in Ref. [55]). Panels (a) and (b) show the$ R(\Delta S_2'') $ distributions from the EBE-AVFD events of the 30%-40% Ru+Ru and Zr+Zr collisions, respectively, at$ \sqrt{s_{{NN}}} = 200 $ GeV with different$ n_{5}/s $ inputs. As$ n_{5}/s $ increases, the concavity of the$ R(\Delta S_2'') $ distribution increases, qualitatively representing more CME contributions. To quantify the distribution shape, the Gaussian width ($ \sigma_{R2} $ ) is obtained by fitting each$ R(\Delta S_2'') $ distribution with an inverse Gaussian function, and the resultant$ \sigma^{-1}_{R2} $ values with increasing$ n_{5}/s $ are presented in panel (c). The$ \sigma^{-1}_{R2} $ ratios between Ru+Ru and Zr+Zr are shown in panel (d). According to Eq. (22),$ \sigma^{-1}_{R2} $ is proportional to$ \sqrt{\Delta\gamma_{112}} \propto $ $ \big [(\sigma^{-2}_{R2})^{\rm{CME}}+(\sigma^{-2}_{R2})^{{\rm{BG}}}\big ]^{1/2} $ ; hence, the$ \sigma^{-1}_{R2} $ ratio is expected to follow a quadratic trend against$ n_5/s $ , assuming the CME signal is small compared with the background. Despite large statistical uncertainties, we fit the$ \sigma^{-1}_{R2} $ ratios with a$ 2^{\rm{nd}} $ -order polynomial function starting from (0, 1). The significance values of these ratios are stored in Table 2 for later discussions.
Figure 7. (color online) Distributions of
$ R(\Delta S_2'') $ from the EBE-AVFD events of 30%-40% Ru+Ru (a) and Zr+Zr (b) at 200 GeV with different$ n_{5}/s $ inputs. Panel (c) lists$ \sigma^{-1}_{R2} $ vs$ n_{5}/s $ , extracted from panels (a) and (b), and the$ \sigma^{-1}_{R2} $ ratios between Ru+Ru and Zr+Zr are shown in panel (d), where the$ 2^{\rm{nd}} $ -order-polynomial fit function shows the rising trend starting from (0, 1).Figure 8 presents the sensitivity study for signed balance functions. This approach is not part of the STAR blind analysis, but follows the same procedure as used in the Quark Matter 2019 Conference proceedings [57]. The observables
$ r_{\rm{lab}} $ and$ R_{{\rm{B}}} $ , as defined in Eqs. (25) and (26) (with$ p_T $ weighting), respectively, are exhibited in panels (a) and (c) as function of$ n_{5}/s $ from the EBE-AVFD model for the 30%-40% Ru+Ru and Zr+Zr collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV. The corresponding ratios between Ru+Ru and Zr+Zr are shown in panels (b) and (d), respectively.$ r_{\rm{lab}} $ increases with the CME signal in each isobar collision. According to Eqs. (25) and (34) and the core-component comparisons,$ r_{\rm{lab}} $ is related to$ \sqrt{\Delta\gamma_{112}} $ ; therefore, the$ r_{\rm{lab}} $ ratio between the two systems should approximately obey a$ 2^{\rm{nd}} $ -order polynomial function that starts from (0, 1). This relation is demonstrated with the corresponding fit in Fig. 8(b). Panel (d) does not show a clear trend for the ratio of$ R_{\rm{B}}^{\rm{Ru+Ru}}/R_{\rm{B}}^{\rm{Zr+Zr}} $ , which is not a complete surprise as$ R_{\rm B} $ considers a higher-order effect in the difference between$ r_{\rm{lab}} $ and$ r_{\rm{rest}} $ and thus requires more statistics than$ r_{\rm{lab}} $ .
Figure 8. (color online)
$ r_{{\rm{lab}}} $ (a) and$ R_{\rm{B}} $ (c) as a function of$ n_{5}/s $ from the EBE-AVFD model for the 30%-40% Ru+Ru and Zr+Zr collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV, with their ratios between Ru+Ru and Zr+Zr in panels (b) and (d), respectively. In panel (b), the$ 2^{\rm{nd}} $ -order-polynomial fit function demonstrates the rising trend starting from (0, 1).The sensitivity relating to the statistical significance of
$ (O^{\rm{Ru+Ru}}/O^{\rm{Zr+Zr}} -1) $ is listed in Table 2 for the observables,$ \Delta\gamma_{112} $ ,$ \Delta\delta $ ,$ \kappa_{112} $ ,$ r_{\rm{lab}} $ , and$ \sigma_{R2}^{-1} $ . This table serves as a reference point to interpret the STAR data on isobar collisions. In our convention, a statistical significance within (-3, 3) is regarded as "not significant" or "consistent with no difference between the two systems." Note that, in contrast with other observables, the$ \Delta\delta $ ratio must be lower than unity in the presence of the CME. Therefore, the more negative the statistical significance of$ (\Delta\delta^{\rm{Ru+Ru}}/\Delta\delta^{\rm{Zr+Zr}}-1) $ , the more sensitive this observable is to the CME signal. The high sensitivities of the$ \Delta\delta $ ratio reported in Table 2 could be a special feature of EBE-AVFD instead of a universal truth; this awaits verification or falsification from real data. In general,$ \kappa_{112} $ approximately doubles the sensitivity of$ \Delta\gamma_{112} $ , which should be mainly due to the contribution of$ \Delta\delta $ ; this must be tested using experimental data.$ \Delta\gamma_{112} $ and$ r_{\rm{lab}} $ show similar significance values because of the approximate equivalence between them. Note that neither the toy model nor the EBE-AVFD model considers the separate CME domains that move independently in the fireball rather than merging into a global charge separation for the whole event. Thus, from these models,$ r_{\rm{lab}} $ is expected to respond to the CME signal in a similar way as$ \Delta\gamma_{112} $ that only deals with the azimuthal angle. Should the isobar-collision data show a better$ r_{\rm{lab}} $ senstivitity than that of$ \Delta\gamma_{112} $ , it may reveal that the CME domains undergo incomplete hydrodynamic evolution owing to its short duration.In the analysis of the
$ R $ correlator using the STAR frozen code,$ \sigma_{R2}^{-1} $ yields lower significance than other observables; this is worth noting in anticipation of the STAR blind analysis results. However, this is largely due to two factors in this particular implementation. First, this analysis uses the sub event plane instead of the full event plane, as in the$ \Delta\gamma_{112} $ analysis, which leads to worse event plane resolutions and hence larger statistical uncertainties. Second, the particles of interest in the$ R(\Delta S_2) $ analysis come from narrower kinematic regions than other analyses, which further enlarges its statistical errors and reduces its sensitivities. When we repeat the calculations of the$ R $ correlator and the$ \gamma_{112} $ correlator with the true reaction plane and the same kinematic cuts (not following the frozen code anymore),$ \sigma_{R2}^{-1}\{{\rm{RP}}\} $ and$ \Delta\gamma_{112}\{{\rm{RP}}\} $ exhibit comparable significance values, as shown in the final two columns of Table 2; these are consistent with the findings in Ref. [63]. Therefore, this result, the toy model studies, and Eqs. (21) and (34) all demonstrate that, on general grounds, the$ \gamma_{112} $ correlator,$ R $ correlator, and signed balance functions have similar sensitivities when used on the same set of particles. -
Several experimental approaches have been developed to search for the CME in heavy-ion collisions. In this paper, we focus on three: the
$ \gamma_{112} $ correlator, the$ R(\Delta S_2) $ correlator, and signed balance functions. We established the relation between these methods via analytical derivation and employed simple Monte Carlo simulations and the EBE-AVFD model to verify the equivalence between the core components of these observables. Our study also supports the assumption that the CME signal and the background contributions can be linearly summed in these core components. For the observables of$ \Delta\gamma_{112} $ ,$ \Delta\delta $ ,$ \kappa_{112} $ ,$ r_{\rm{lab}} $ , and$ \sigma_{R2}^{-1} $ , we extracted their sensitivities to the difference between the Ru+Ru and Zr+Zr collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV from the 30%-40% central events generated using EBE-AVFD.$ \Delta\delta $ and$ \kappa_{112} $ may produce better sensitivities than other observables, which could be a model-dependent feature instead of a universal truth; this needs to be further scrutinized by data. The same significance level has been corroborated for$ \Delta\gamma_{112} $ ,$ r_{\rm{lab}} $ , and$ \sigma_{R2}^{-1} $ in equal conditions; however, the implementation details in the STAR frozen code can cause apparent differences in their sensitivities. Therefore, this study provides a reference point to gauge STAR isobar-collision data. -
This investigation was initiated in and agreed upon by the CME focus group of the STAR Collaboration and was motivated by the desire to benchmark the various CME observables planned for use in the STAR isobar blind analysis against the well-established model, EBE-AVFD. We thank the STAR Collaboration for permitting the use of the corresponding isobar blind analysis frozen code in this simulation study and the many collaborators who have contributed to previous STAR CME related studies besides the authors. We are especially grateful to the following people for their substantial help: Kenneth Barish, Helen Caines, Jinhui Chen, William Christie, Frank Geurts, Huanzhong Huang, Hongwei Ke, William Llope, Xiaofeng Luo, Rongrong Ma, Yugang Ma, Bedanga Mohanty, Grigory Nigmatkulov, Lijuan Ruan, Ernst Sichtermann, Yuanfang Wu, Nu Xu, Zhangbu Xu, and Zhenyu Ye.
We thank the STAR Collaboration, the RHIC Operations Group, and the RCF at the RHIC for their support.
-
To estimate the RMS of
$ \Delta B_y $ ,$ \sigma(\Delta B_y) $ , we first go through the following expansion:$\tag{A1}\begin{aligned}[b] (N_{x(\alpha\beta)}-N_{x(\beta\alpha)})^2 = & \Bigg\{\sum\limits_{\alpha,\beta} {\rm{Sign}}\big [\sin(\phi^*_\alpha)-\sin(\phi^*_\beta)\big ] \Bigg\}^2 = \Bigg\{\sum\limits_{\alpha,\beta} {\rm{Sign}}\big [\sin(\phi^*_\alpha)-\sin(\phi^*_\beta)\big ] \Bigg\} \Bigg\{\sum\limits_{\alpha',\beta'} {\rm{Sign}}\big [\sin(\phi^*_{\alpha'})-\sin(\phi^*_{\beta'})\big ] \Bigg\} \\ = & \sum\limits_{\alpha\neq\alpha'}\sum\limits_{\beta\neq\beta'} {\rm{Sign}}\big [\sin(\phi^*_\alpha)-\sin(\phi^*_\beta)\big ]\times{\rm{Sign}}\big [\sin(\phi^*_{\alpha'})-\sin(\phi^*_{\beta'})\big ] \\& + \sum\limits_{\alpha}\sum\limits_{\beta\neq\beta'} {\rm{Sign}}\big [\sin(\phi^*_\alpha)-\sin(\phi^*_\beta)\big ]\times{\rm{Sign}}\big [\sin(\phi^*_{\alpha})-\sin(\phi^*_{\beta'})\big ] \\& + \sum\limits_{\alpha\neq\alpha'}\sum\limits_{\beta} {\rm{Sign}}\big [\sin(\phi^*_\alpha)-\sin(\phi^*_\beta)\big ]\times{\rm{Sign}}\big [\sin(\phi^*_{\alpha'})-\sin(\phi^*_{\beta})\big ] + \sum\limits_{\alpha}\sum\limits_{\beta} 1. \end{aligned} $ 
Then, the average of each term in Eq. (A2) is computed separately, similar to Eq. (29). The first one reads
$\tag{A2}\begin{aligned}[b]& \Big\langle\sum\limits_{\alpha\neq\alpha'}\sum\limits_{\beta\neq\beta'} {\rm{Sign}}\big [\sin(\phi^*_\alpha)-\sin(\phi^*_\beta)\big ]\times{\rm{Sign}}\big [\sin(\phi^*_{\alpha'})-\sin(\phi^*_{\beta'})\big ]\Big\rangle \\ = & N_\alpha(N_\alpha-1)N_\beta(N_\beta-1)\times \Bigg\{ \int_{-\pi/2}^{\pi/2} \Bigg[\int_{-\pi-\phi^*_\alpha}^{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta-\int^{\pi-\phi^*_\alpha}_{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta\Bigg]\frac{{\rm d}N}{{\rm d}\phi^*_\alpha}{\rm d}\phi^*_\alpha \\ & +\int_{\pi/2}^{3\pi/2} \Bigg[\int_{\pi-\phi^*_\alpha}^{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta-\int^{3\pi-\phi^*_\alpha}_{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta\Bigg]\frac{{\rm d}N}{{\rm d}\phi^*_\alpha}{\rm d}\phi^*_\alpha \Bigg\}^2 = N_\alpha(N_\alpha-1)N_\beta(N_\beta-1)\Bigg[\frac{8}{\pi^2}(1+\frac{2}{3}v_2)(a_{1,\alpha}-a_{1,\,\beta}) \Bigg]^2. \end{aligned}$

The second term becomes
$\tag{A3}\begin{aligned}[b]& \Big\langle\sum\limits_{\alpha}\sum\limits_{\beta\neq\beta'} {\rm{Sign}}\big [\sin(\phi^*_\alpha)-\sin(\phi^*_\beta)\big ]\times{\rm{Sign}}[\sin(\phi^*_{\alpha})-\sin(\phi^*_{\beta'})]\Big\rangle \\ = & N_\alpha N_\beta(N_\beta-1)\times \Bigg\{ \int_{-\pi/2}^{\pi/2} \Bigg[\int_{-\pi-\phi^*_\alpha}^{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta-\int^{\pi-\phi^*_\alpha}_{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta\Bigg]^2\frac{{\rm d}N}{{\rm d}\phi^*_\alpha}{\rm d}\phi^*_\alpha \\ & +\int_{\pi/2}^{3\pi/2} \Bigg[\int_{\pi-\phi^*_\alpha}^{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta-\int^{3\pi-\phi^*_\alpha}_{\phi^*_\alpha} \frac{{\rm d}N}{{\rm d}\phi^*_\beta}{\rm d}\phi^*_\beta\Bigg]^2\frac{{\rm d}N}{{\rm d}\phi^*_\alpha}{\rm d}\phi^*_\alpha \Bigg\} = N_\alpha N_\beta(N_\beta-1)\Bigg[\frac{1}{3}-\frac{8}{\pi^2}(1+v_2)a_{1,\beta}(a_{1,\alpha}-a_{1,\,\beta}) \Bigg]. \end{aligned}$

Similarly, the third term gives
$\tag{A4} \Big\langle\sum\limits_{\alpha\neq\alpha'}\sum\limits_{\beta} {\rm{Sign}}\big [\sin(\phi^*_\alpha)-\sin(\phi^*_\beta)\big ]\times{\rm{Sign}}[\sin(\phi^*_{\alpha'})-\sin(\phi^*_{\beta})]\Big\rangle = N_\alpha(N_\alpha-1) N_\beta\Bigg[\frac{1}{3}+\frac{8}{\pi^2}(1+v_2)a_{1,\alpha}(a_{1,\alpha}-a_{1,\,\beta}) \Bigg]. $

The last term is simply
$\tag{A5} \sum\limits_{\alpha}\sum\limits_{\beta} 1 = N_\alpha N_\beta. $

According to the definition in Eq. (24), we have
$\tag{A6} \sigma^2(\Delta B_y) = \frac{M^2}{N_+^2 N_-^2} \langle (N_{x(+-)}-N_{x(-+)})^2 \rangle. $

For simplicity, we assume
$ N_+ = N_- = M/2 \gg 1 $ and$ v_2 \ll 1 $ , and put Eqs. (A3)-(A6) into Eq. (A7), so that$\tag{A7} \sigma^2(\Delta B_y) \approx \frac{4(M+1)}{3}+ \frac{64M^2}{\pi^4}\Bigg[\left(1+\frac{2}{3}v_2\right)^2+\frac{\pi^2(1+v_2)}{4M}\Bigg](a_{1,+}-a_{1,-})^2 \\ \approx \frac{4M}{3}+ \frac{64M^2}{\pi^4}\left(1+ \frac{4}{3}v_2\right)(a_{1,+}-a_{1,-})^2. $

Similarly, we also obtain
$\tag{A8} \sigma^2(\Delta B_x) \approx \frac{4(M+1)}{3}+ \frac{64M^2}{\pi^4}\Bigg[\left(1-\frac{2}{3}v_2\right)^2+\frac{\pi^2(1-v_2)}{4M}\Bigg](v_{1,+}-v_{1,-})^2 \\ \approx \frac{4M}{3}+ \frac{64M^2}{\pi^4}\left(1- \frac{4}{3}v_2\right)(v_{1,+}-v_{1,-})^2. $

Then, the difference between
$ \sigma^2(\Delta B_y) $ and$ \sigma^2(\Delta B_x) $ gives$\tag{A9} \sigma^2(\Delta B_y) - \sigma^2(\Delta B_x) \approx \frac{128M^2}{\pi^4}\Bigg[\left(1+\frac{\pi^2}{4M}\right)\Delta\gamma_{112}-\left(\frac{4}{3}+\frac{\pi^2}{4M}\right)v_2\Delta\delta\Bigg] \approx \frac{128M^2}{\pi^4}\left(\Delta\gamma_{112}-\frac{4}{3}v_2\Delta\delta\right). $

Investigation of experimental observables in search of the chiral magnetic effect in heavy-ion collisions in the STAR experiment
- Received Date: 2021-07-17
- Available Online: 2022-01-15
Abstract: The chiral magnetic effect (CME) is a novel transport phenomenon, arising from the interplay between quantum anomalies and strong magnetic fields in chiral systems. In high-energy nuclear collisions, the CME may survive the expansion of the quark-gluon plasma fireball and be detected in experiments. Over the past two decades, experimental searches for the CME have attracted extensive interest at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC). The main goal of this study is to investigate three pertinent experimental approaches: the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: