Synthesis of unknown ^287−290Og isotopes infusion-evaporation reactions

The synthesis of superheavy nuclei is one of the most challenging and fascinating research topics in nuclear physics [1−4]. Superheavy nuclei have been continuously studied for decades due to their extremely high atomic numbers and unique properties [5−7]. To date, superheavy nuclei with atomic numbers ranging from 104 to 118 have been discovered [8], all of which are neutron-deficient. Although these nuclides, located in the upper-right region of the nuclear map, generally exhibit short half-lives [9, 10], the synthesis and study of superheavy nuclei provide critical insights into nuclear forces, nuclear structure, decay exotic modes, and the fundamental principles of nuclear stability [11].

Due to the extremely low formation probability of superheavy elements, scientists have adopted two different approaches to synthesize them over the past few decades. One method is cold fusion reactions, which use $^{208}\text{Pb}$ or $^{209}\text{Bi}$ as target nuclei [12–13]. These reactions can produce compound nuclei with relatively low excitation energies, maximizing the survival probability by suppressing fission. The other method involves hot fusion reactions, using $^{48}\text{Ca}$ as the projectile to bombard actinide targets [14−16], which can effectively increase the formation probability of compound nucleus. Experimentally, elements with $ Z = 107-113 $ were synthesized using cold fusion reactions. However, as the synthesis of $ Z = 113 $ element was proved challenging due to extremely low cross sections [17], scientists turned to hot fusion reactions. Elements with $ Z = 114-118 $ were successfully synthesized using this approach [18]. The shell structure plays a crucial role in the stability of superheavy nuclei. Since the prediction of the island of stability, many scientists have explored it using various models. Oganesson (Og) is located in the seventh period and the last position of the noble gases in the periodic table, with a fully filled electron configuration [19]. Additionally, it lies at the edge of the island of stability, and its existence and stability can provide significant experimental evidence to support shell theory [20−23]. Scientists have made numerous attempts to discover isotopes of Og [24–25]. However, only one Og isotope, $^{294}\text{Og}$, has been discovered [26], while its neighboring unknown isotopes remain undiscovered.

Experimental research has lead to significant progress in the production of superheavy nuclei. These advancements have aided in the development of theoretical models to describe the fusion reactions involved. Macroscopic models, including the dinuclear system (DNS) model [27−32], two-step model [33], fusion-by-diffusion model [34–35], and nucleon collectivization model [36], can be used to study fusion reaction mechanisms and predict the synthesis of superheavy nuclei. In addition, microscopic models, such as the improved quantum molecular dynamics model [37−39] and time-dependent Hartree-Fock model [40−42], can effectively simulate the dynamical evolution of the nuclear fusion process.

The remainder of this paper is organized as follows. In Sec. II, we briefly introduce the DNS model. In Sec. III, the production cross sections of Og isotopes in different reactions are calculated. Finally, the conclusion is given in Sec. IV.

Within the DNS framework, the fusion-evaporation process can be divided into three stages: capture, fusion, and evaporation. In the capture stage, the system overcomes the Coulomb barrier to form a DNS. During the fusion stage, the DNS undergoes nucleon transfer to form a compound nucleus, competing with the quasifission process. In the evaporation stage, the compound nucleus undergoes light-particle evaporation to achieve deexcitation, thereby synthesizing the goal nucleus [43]. The evaporation residue (ER) cross section of superheavy nuclei can be expressed as

where $ E_{\text{c.m.}} $ represents the incident energy in the center-of-mass frame. $ T $ and $ P_{\text{CN}} $ are the capture and fusion probabilities, respectively [44]. $ W_{\text{sur}} $ is the survival probability of the compound nucleus during the deexcitation process [45].

The capture cross section can be written as follows:

Here, the penetration probability can be expressed as [46]

Here, $ \hbar \omega(J) $ represents the width of the parabolic barrier, μ is the reduced mass of the system, and $ R_B $ is the position of the barrier. Due to factors such as vibration, rotation, and dynamic deformation, the Coulomb barrier becomes distributed. The barrier distribution function $ f(B) $ is taken to be an asymmetric Gaussian form [36, 47].

Here, N is the normalization factor. $ \Delta_2 = (B_0 - B_{\text{s}})/2 $, $ \Delta_1 = \Delta_2 - 2 $ MeV, and $ B_{\text{m}} = (B_0 + B_{\text{s}})/2 $. $ B_{\text{s}} $ and $ B_0 $ represent the barrier heights at the saddle point and for the waist-waist collision, respectively.

Subsequently, nucleon transfer occurs at the bottom of the potential energy pocket of the DNS [48], leading to the fusion or quasifission processes. The nucleon diffusion process is strongly influenced by the potential energy surface (PES), which is defined as

Here, $\Delta(Z_1, N_1)$ and $\Delta(Z_2, N_2)$ represent the mass excesses of fragments 1 and 2, respectively, taken from Möller’s mass table [49].

$R$ is the distance between the two fragments at the bottom of the potential pocket. $ V_{\text{C}} $ and $ V_{\text{N}} $ denote the Coulomb potential and nuclear potential calculated using the Wong formula and double-folding potential, respectively [50–51].

$ V_{\text{C}} $ can be expressed as

Here, $ R_i $ (for $ i = 1, 2 $) is the nuclear radius, and $ \beta_i $ represents the quadrupole deformations of the projectile and target.

$ V_{\text{N}} $ can be expressed as

Here, $ \rho_1 $ and $ \rho_2 $ represent the nucleon density distributions of the projectile and target, respectively. The parameters are chosen as follows: $ C_0 = 300\ \text{MeV} \cdot \text{fm}^3 $, $ f_{\text{in}} = 0.09 $, $ f_{\text{ex}} = -2.59 $, $ f_{\text{in}}' = 0.42 $, and $ f_{\text{ex}}' = 0.54 $. $ F_{\text{in,ex}} $ are defined as

$ \rho_1 $ and $ \rho_2 $ are typically described by the Woods–Saxon form, as follows:

where $ \rho_0 = 0.16\ \mathrm{fm}^{-3} $, and $ a_1 $ and $ a_2 $ are the surface diffuseness parameters of the two nuclei. In this study, $ a_1 = a_2 = 0.45\ \mathrm{fm} $.

The time evolution of the probability distribution of the fragment with proton number $ Z_1 $ and neutron number $ N_1 $ can be described by the following master equation:

Here, $W_{Z_1, N_1; Z_1', N_1}$ (or $W_{Z_1, N_1; Z_1, N_1'}$) represents the transition rate from channel $(Z_1, N_1)$ to $(Z_1', N_1)$ [or from $(Z_1, N_1)$ to $(Z_1, N_1')$] [52], and the microscopic dimension $ \mathrm{d}_{Z_1,N_1} $ denotes the number of microscopic states contained within the macroscopic state $(Z_1, N_1)$ of the fragment [53]. $ \Theta(t) $ is the local temperature, given by $ \Theta(t) = \sqrt{\varepsilon^*/a} $, where a is the level density parameter, taken to be $ a = A/12 $. $ \varepsilon^* $ is the local excitation energy of the DNS. $\Lambda_{\text{qf}}$ and $\Lambda_{\text{fis}}$ represent the quasifission rate and fission rate, respectively, which are calculated by the one-dimensional Kramers equation [54–55].

The highest point of the driving potential is called the Businaro Gallone (BG) point. The difference in the driving potential between the injection point and the BG point represents the inner fusion barrier [56]. To form a compound nucleus, the DNS must have sufficient internal excitation energy to overcome the inner fusion barrier. Within the framework of the DNS model, the sum of the distribution probabilities of fragments that exceed the BG point is assumed to be the fusion probability and is expressed as follows:

Here, $ \tau_{\text{int}} $ denotes the interaction time [57], which is calculated using the deflection function method.

The compound nucleus formed through the fusion process is deexcited by emitting gamma rays, light particles, and fission. This process can be described using a statistical model [58]. For the deexcitation of superheavy nuclei, neutron evaporation and fission are the dominant competing channels. The neutron evaporation width can be expressed as [59]

where $ S_{{n}} $, $ m_{{n}} $, and $ B_{{n}} $ are the spin, mass, and binding energy of the evaporated neutron, respectively. ρ represents the level density and is derived from the Fermi-gas model. δ represents the pairing correction energy, with values of $ 12/\sqrt{A} $ for even-even nuclei, 0 for odd-A nuclei, and $-12/\sqrt{A} $ for odd-odd nuclei. For odd-A nuclei, $ \delta_{{n}} $ is $ 12/\sqrt{A} $; otherwise, $ \delta_{{n}} $ is 0 [60]. $ \sigma_{\text{inv}}(\epsilon) $ is the inverse cross section.

The fission decay width can be expressed as follows [61]:

where $ B_{\text{f}} $ is the fission barrier, and $ \rho_{\text{f}} $ is the level density at the fission barrier. If the compound nucleus is even-even or odd-odd, $ \delta_{\text{f}} = \delta $; otherwise, $ \delta_{\text{f}} = 0 $.

The fission barrier $ B_{\text{f}} $ can be expressed as

Here, $ B_{\text{f}}^{\text{M}} $ is the shell correction energy of the nucleus in its ground state and is obtained from the data tables provided by Möller [49]. $ E^* $ represents the excitation energy of the compound nucleus, and $ E_{\text{D}} $ is the shell damping factor, which is taken to be 20 MeV in this study. $ {\cal{J}}_{\text{g.s.}} $ and $ {\cal{J}}_{\text{s.d.}} $ represent the moments of inertia of the compound nucleus at the ground state and saddle point, respectively, and are given by the following expressions:

Here, M and R represent the mass and radius of the compound nucleus, respectively. The parameter k is taken as 0.4. The quadrupole deformation at the saddle point is calculated as $ \beta_2^{\text{s.d.}} = \beta_2^{\text{g.s.}} + 0.2 $.

$ B_{\text{f}}^{\text{LD}} $ is the macroscopic fission barrier obtained from the liquid-drop model:

where the fissility parameter $ x = E_{c0}/2E_{s0} $. $ E_{s0} $ and $ E_{c0} $ are the surface energy and Coulomb energy of a spherical nucleus, respectively, defined as

and

The level density ρ can be expressed as

Here,

where $ \bar{m}^2 \approx 0.24A^{2/3} $. For the fission level density $ \rho_f $, the level density parameter is taken as $ a_f = 1.05a $ in this study.

Considering only neutron evaporation and fission during the deexcitation process, the survival probability of the compound nucleus is expressed as [62]

Here, $J$ and $E^*_{\text{CN}}$ are the angular momentum and excitation energy of the compound nucleus, respectively. $ E_{\text{CN}}^* = E_{\text{c.m.}} + Q $. $P(E^*_{\text{CN}}, x, J)$ represents the probability of realizing the $x{n}$ evaporation channel. $E^*_{i}$ is the excitation energy of the superheavy nucleus before the evaporation of the ${\text{i}}$-th neutron, satisfying the following relationship:

Here, $B_{i}^{{n}}$ is the separation energy of the $i$-th evaporated neutron. $ E_i^* = aT_i^2 $, where $T_i$ is the nuclear temperature before the evaporation of the $i$-th neutron.

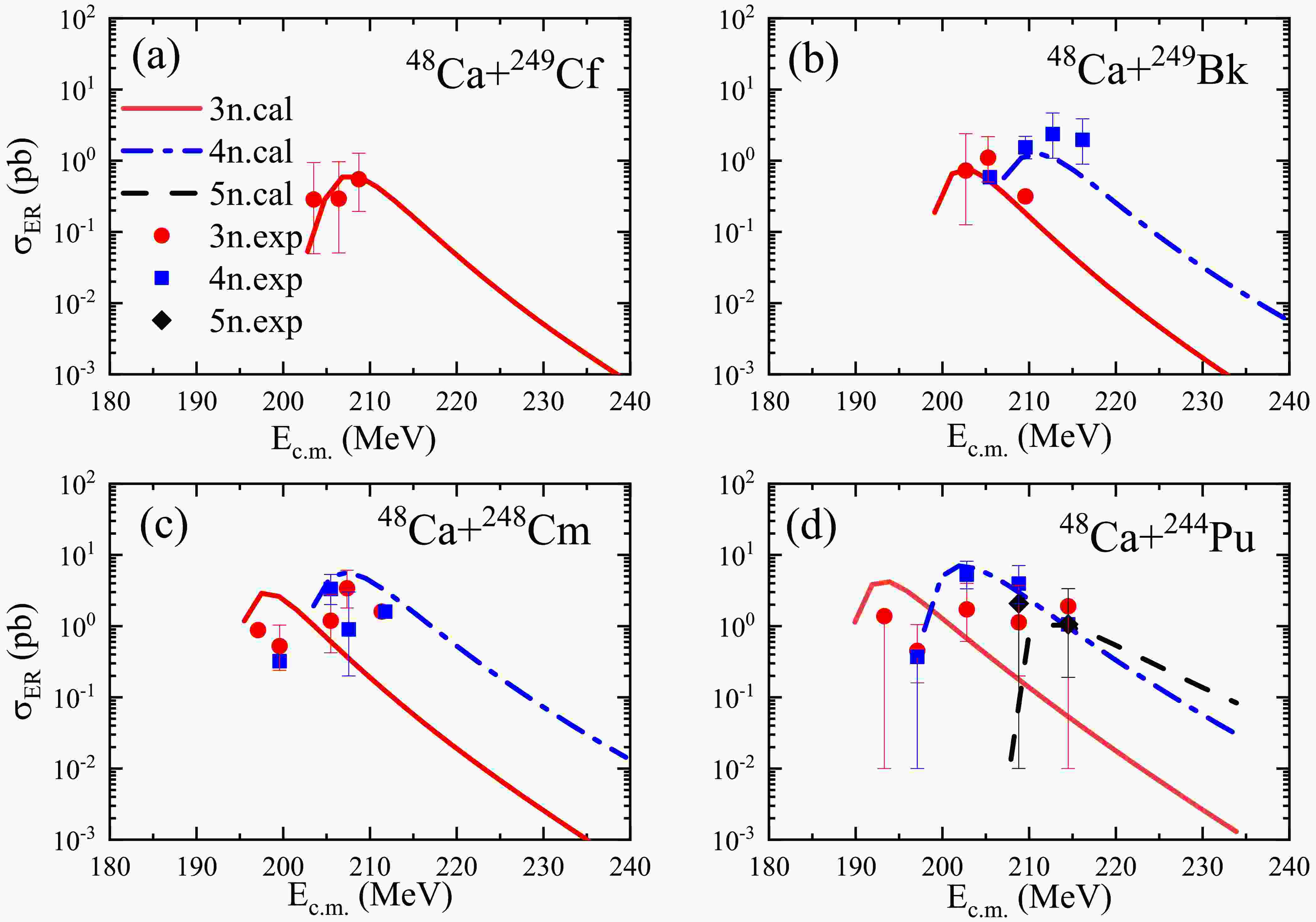
To evaluate the accuracy of our model in predicting the production of superheavy nuclei, we present the calculated ER cross sections for the reactions $ ^{48} \text{Ca}$ +$ ^{249} \text{Cf}$, $ ^{48} \text{Ca}$ +$ ^{249} \text{Bk}$, $ ^{48} \text{Ca}$ +$ ^{248} \text{Cm}$, and $ ^{48} \text{Ca}$ +$ ^{244} \text{Pu}$ and compare them with experimental data, as shown in Fig. 1. The solid, dash-dotted, and dashed lines represent the calculated ER cross sections for the 3n, 4n, and 5n evaporation channels, respectively. The circles, squares, and diamonds indicate the experimental data for the 3n, 4n, and 5n channels, respectively.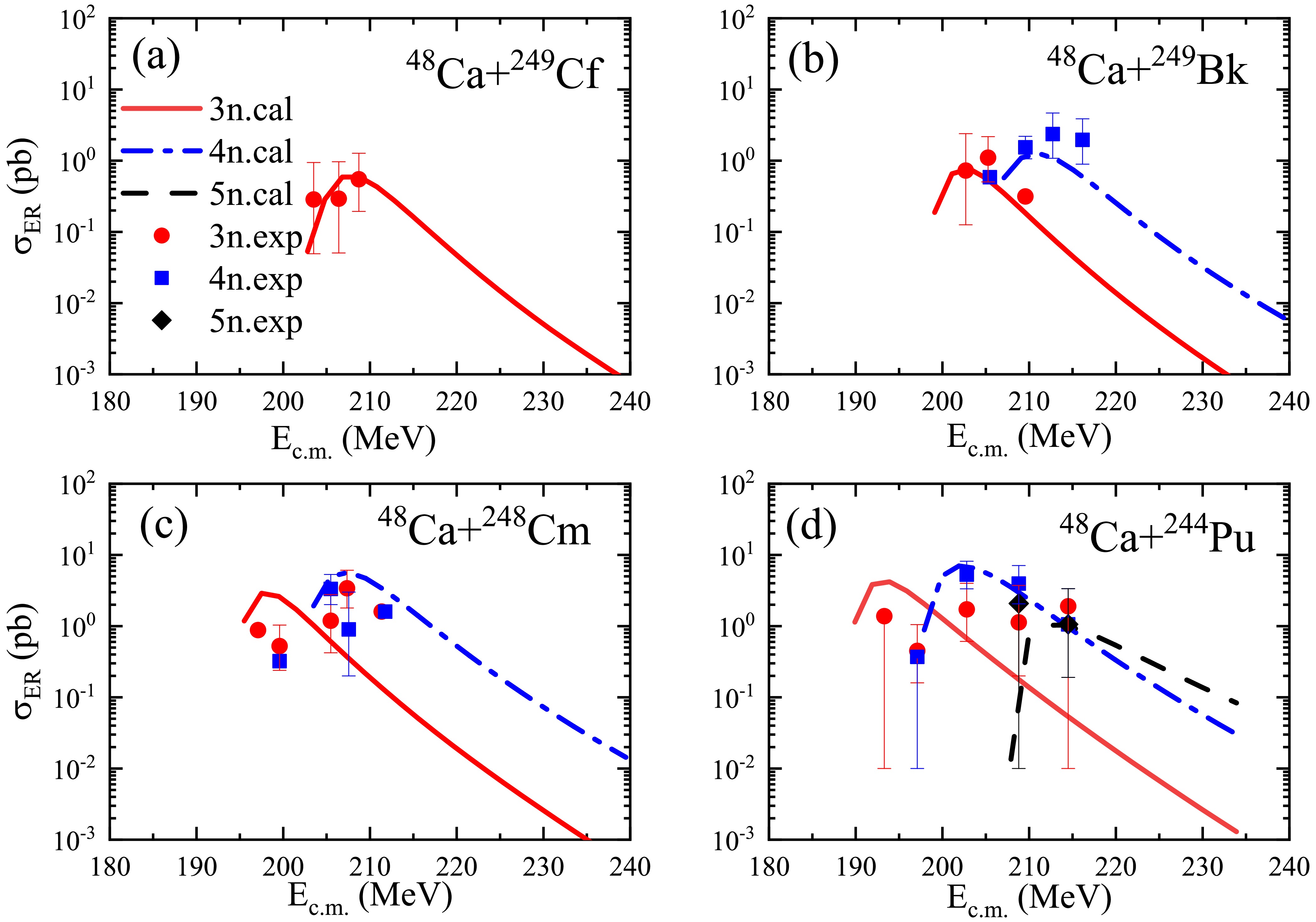

Figure 1.  (color online) Comparison of the calculated ER cross sections with experimental data for the reactions (a) $ ^{48} \text{Ca}$ +$ ^{249} \text{Cf}$, (b) $ ^{48} \text{Ca}$ +$ ^{249} \text{Bk}$, (c) $ ^{48} \text{Ca}$ +$ ^{248} \text{Cm}$, and (d) $ ^{48} \text{Ca}$ +$ ^{244} \text{Pu}$. The circles, squares, and diamonds represent the experimental data for the 3n, 4n, and 5n channels, respectively. The experimental data are obtained from the references [63−66]. The calculated results for the 3n, 4n, and 5n channels are represented by solid, dash-dotted, and dashed lines, respectively.

The ER cross sections decrease with increasing proton number of the compound nucleus, and the calculated results show the same trend. Among the reactions, the calculated 4n cross sections for $ ^{48} \text{Ca}$ +$ ^{249} \text{Bk}$, $ ^{48} \text{Ca}$ +$ ^{248} \text{Cm}$, and $ ^{48} \text{Ca}$ +$ ^{244} \text{Pu}$ reach the highest values, achieving good agreements with the experimental data. Specifically, for the reaction $ ^{48} \text{Ca}$ +$ ^{249} \text{Cf}$, the calculated cross section for the 3n channel aligns well with the experimental data. These results validate the applicability of the DNS model in predicting the synthesis of new Og isotopes using fusion-evaporation reactions.

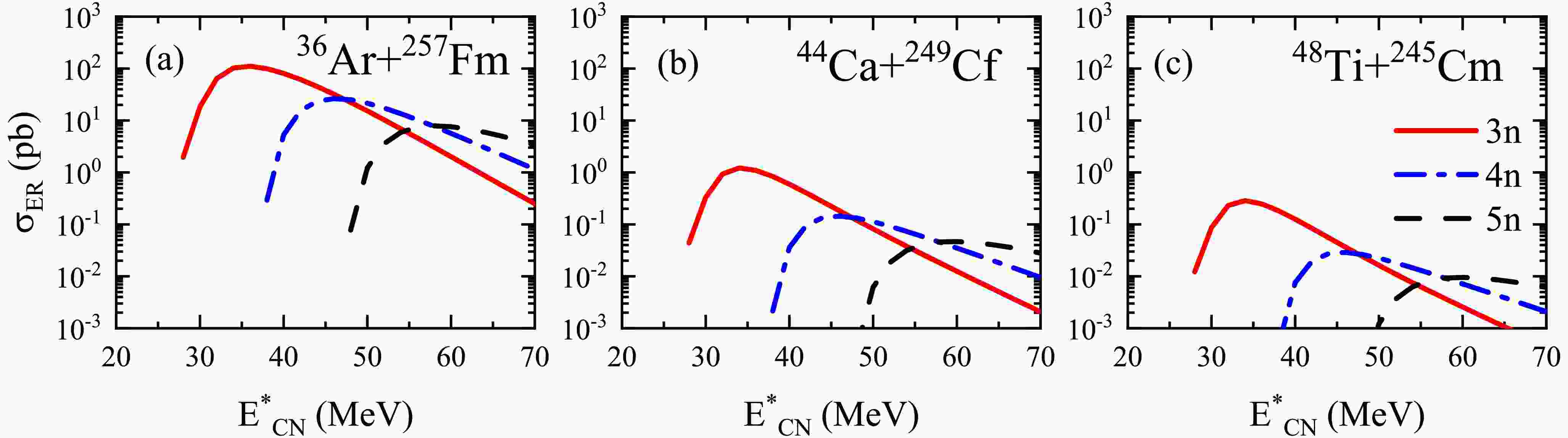
To explore systems more suitable for synthesizing new Og isotopes, we present the calculated ER cross sections for the reactions $^{36}\text{Ar} + ^{257}\text{Fm}$, $^{44}\text{Ca} + ^{249}\text{Cf}$, and $^{48}\text{Ti} + ^{245}\text{Cm}$, all of which lead to the formation of the same compound nucleus, displayed in Fig. 2. It is noteworthy that, as the projectile charge increases, the ER cross sections of the compound nucleus decrease progressively. This trend is primarily attributed to a reduction in the fusion probability.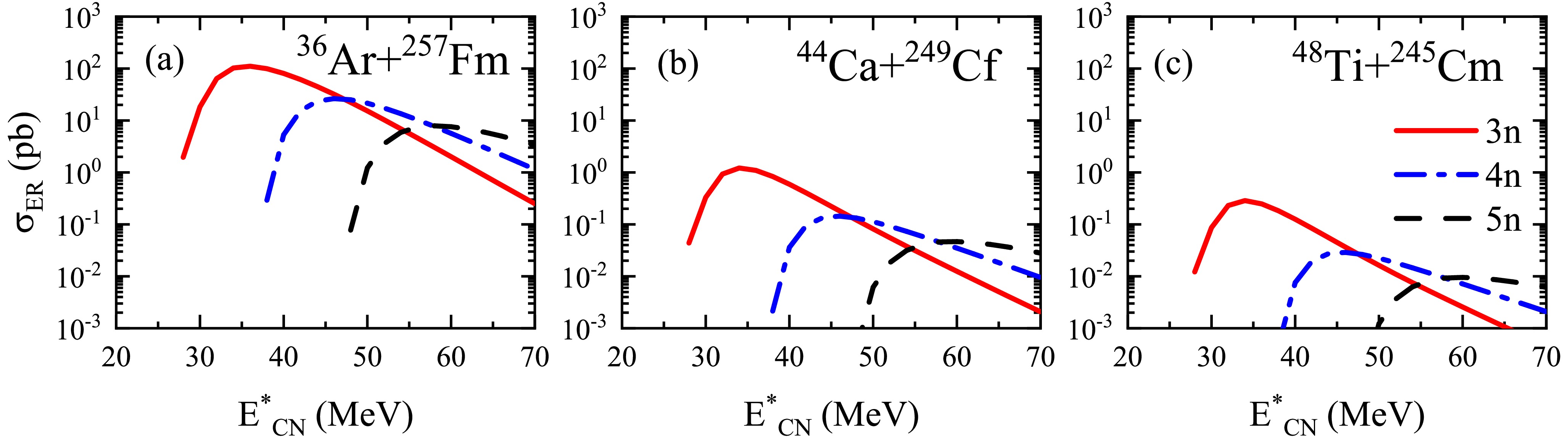

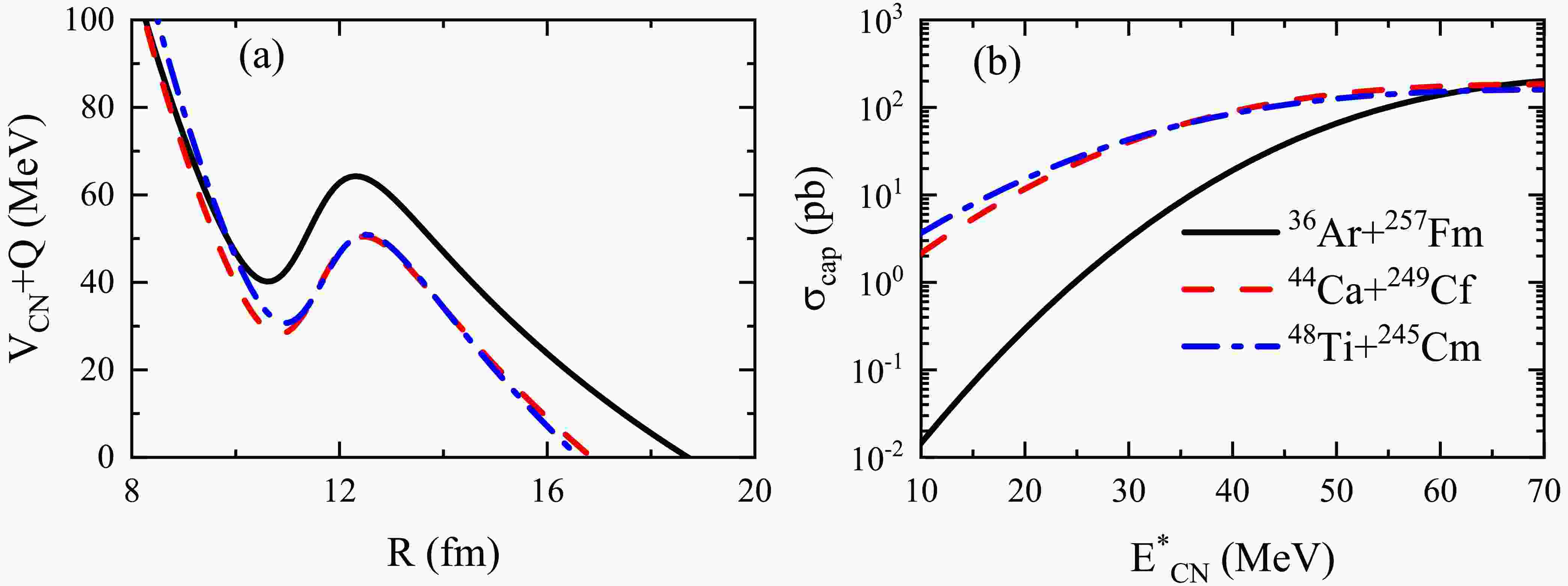
Figure 2.  (color online) Predicted ER cross sections for the reactions (a) $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, (b) $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and (c) $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$. The calculated results for the 3n, 4n, and 5n channels are represented by solid, dash-dotted, and dashed lines, respectively.

In the following, we provide a detailed analysis of the results from three processes involved in fusion-evaporation reactions. The Coulomb barrier plays a crucial role in the capture process. Fig. 3(a) shows the $ V_{\text{CN}} + Q $ values as a function of the distance between the projectile and target nuclei. It is clear that the $ V_{\text{B}} + Q $ ($ V_{\text{B}} $ is the Coulomb barrier) values for the $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$ and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$ reactions are quite close, approximately 50 MeV. In contrast, the $ V_{\text{B}} + Q $ value for the $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ reaction is approximately 14 MeV higher than those of the other two reactions.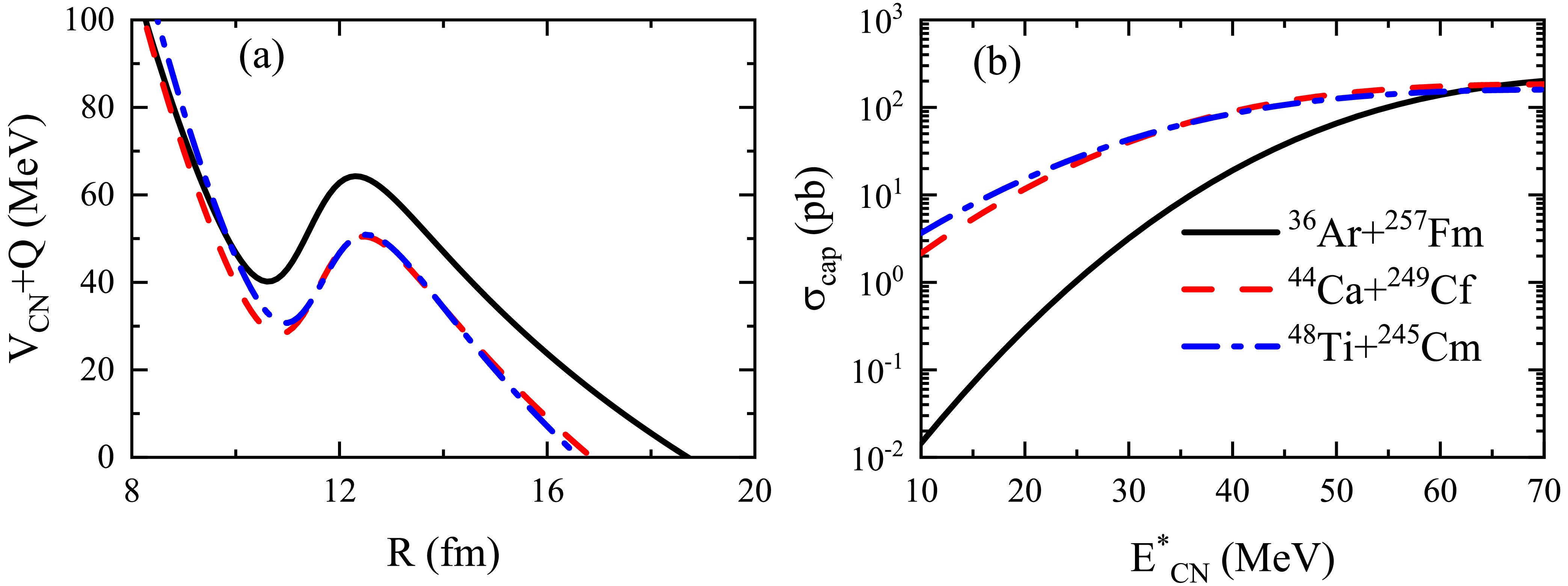

Figure 3.  (color online) (a) $ V_{\text{CN}} + Q $ values as a function of the distance between the centers of mass of the projectile and target nuclei for the reactions $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$. (b) Capture cross sections for these reactions as a function of the excitation energy of the compound nucleus. The reactions $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$ are represented by solid, dashed and dash-dotted lines, respectively.

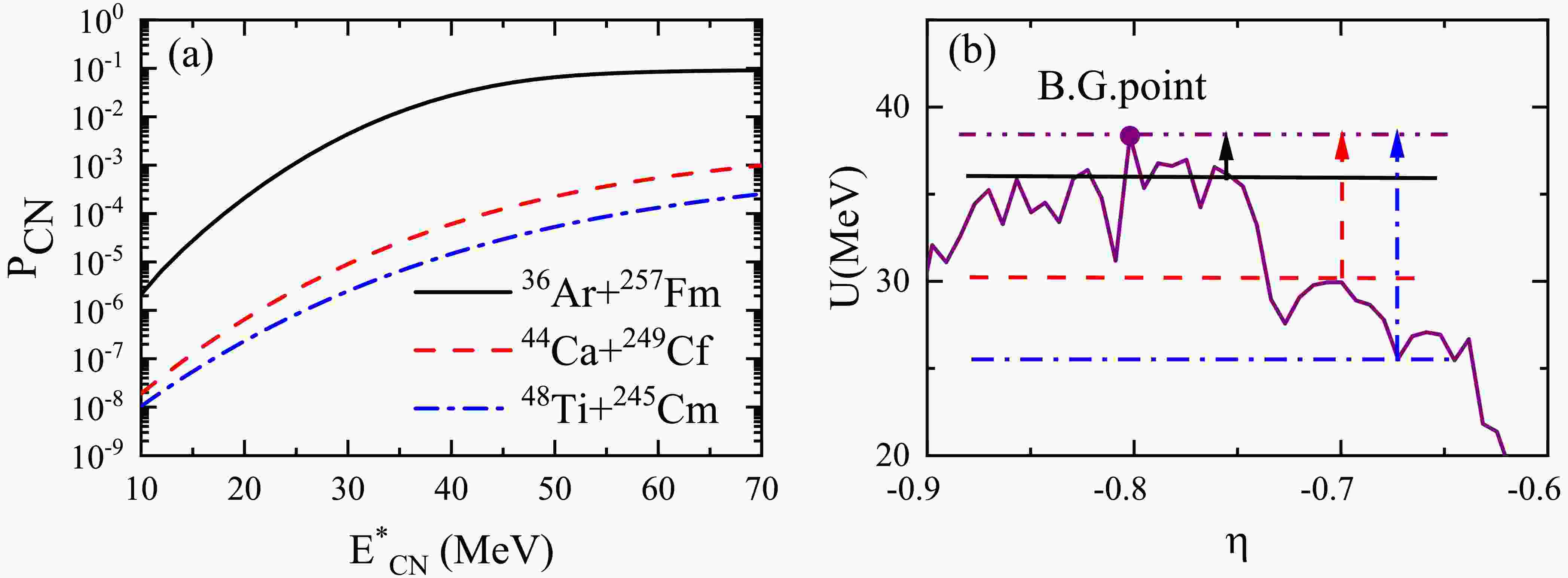
Figure 3(b) presents the capture cross sections for these reactions as a function of excitation energy. It can be noticed that, as the excitation energy increases, the capture cross sections rise sharply when the excitation energy is below $ V_{\text{B}} + Q $. This process is primarily driven by quantum tunneling effects. The higher the $ V_{\text{B}} + Q $ value of the reaction system, the more difficult it is for the system to overcome the Coulomb barrier, which reduces the capture probability. When the excitation energy exceeds $ V_{\text{B}} + Q $, the increase in the capture cross section is mainly due to the contribution of partial waves with larger angular momenta. At lower excitation energies, the capture cross sections of the $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$ and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$ reactions are comparable and higher than that of the $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ reaction. This is because the $ V_{\text{B}} + Q $ value of the reaction $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ is relatively high.

The fusion process is highly complex, and different models provide varying descriptions. However, the importance of the fusion probability is widely recognized. In Fig. 4(a), we present the fusion probabilities for the reactions $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$. The fusion probabilities of the three reactions increase with increasing excitation energy. This is because higher incident energy makes it easier for the DNS to overcome the inner fusion barrier. Additionally, it is evident that the fusion probabilities for the $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$ systems decrease in sequence.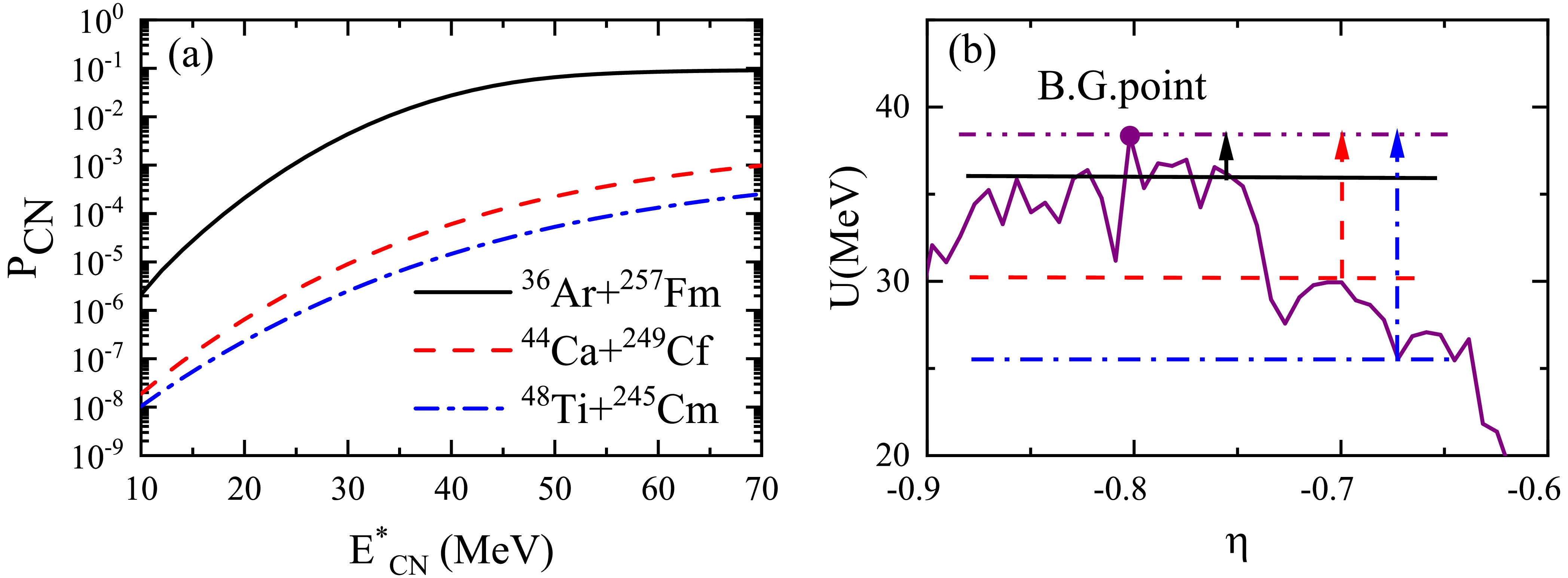

Figure 4.  (color online) (a) Calculated fusion probabilities for the reactions $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$. (b) Driving potentials for these reactions as a function of mass asymmetry. The reactions $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$ are represented by solid line arrow, dashed line arrow, and dash-dotted line arrow, respectively.

To further investigate the effect of mass asymmetry on the fusion reaction, we present the driving potential of the reaction system in Fig. 4(b). It can be noticed that, as the mass asymmetry of the reaction system decreases, the position of the entrance channel moves further away from the BG point, resulting in a higher inner fusion barrier. Its value for the $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ reaction is 2.26 MeV, which is lower than the values of 8.41 MeV and 12.79 MeV for the $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$ and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$ reactions, respectively. Therefore, the $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ reaction is more likely to overcome the internal fusion barrier, resulting in an increased fusion probability.

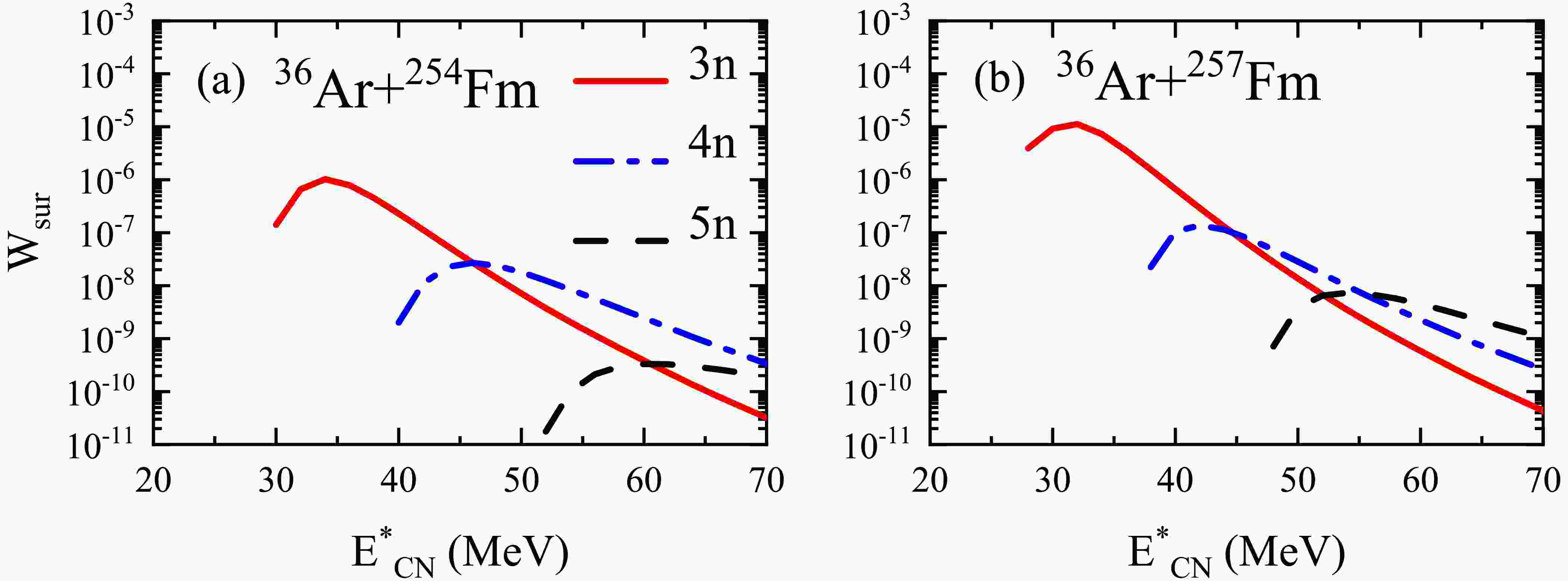
Figure 5 shows the survival probabilities for the reactions $ ^{36} \text{Ar}$ +$ ^{254} \text{Fm}$ and $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ with the evaporation of 3 to 5 neutrons. It can be noticed that the peak intervals are approximately 10 MeV, which is due to each neutron evaporation carrying away approximately 8–10 MeV of energy. As the number of evaporated neutrons increases, the peak values decrease rapidly, primarily because fission becomes more significant at higher excitation energies. A comparison of Fig. 5(a) and 5(b) reveals that, for the same neutron evaporation channels, the maximum ER cross sections for the $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ reaction are significantly higher than those for the $ ^{36} \text{Ar}$ +$ ^{254} \text{Fm}$ reaction. This is because a more neutron-rich compound nucleus has a higher fission barrier. Therefore, the compound nucleus formed in the $ ^{36} \text{Ar}$ +$ ^{254} \text{Fm}$ reaction, which has a lower fission barrier than that formed in the $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ reaction, is prone to fission, resulting in a lower survival probability.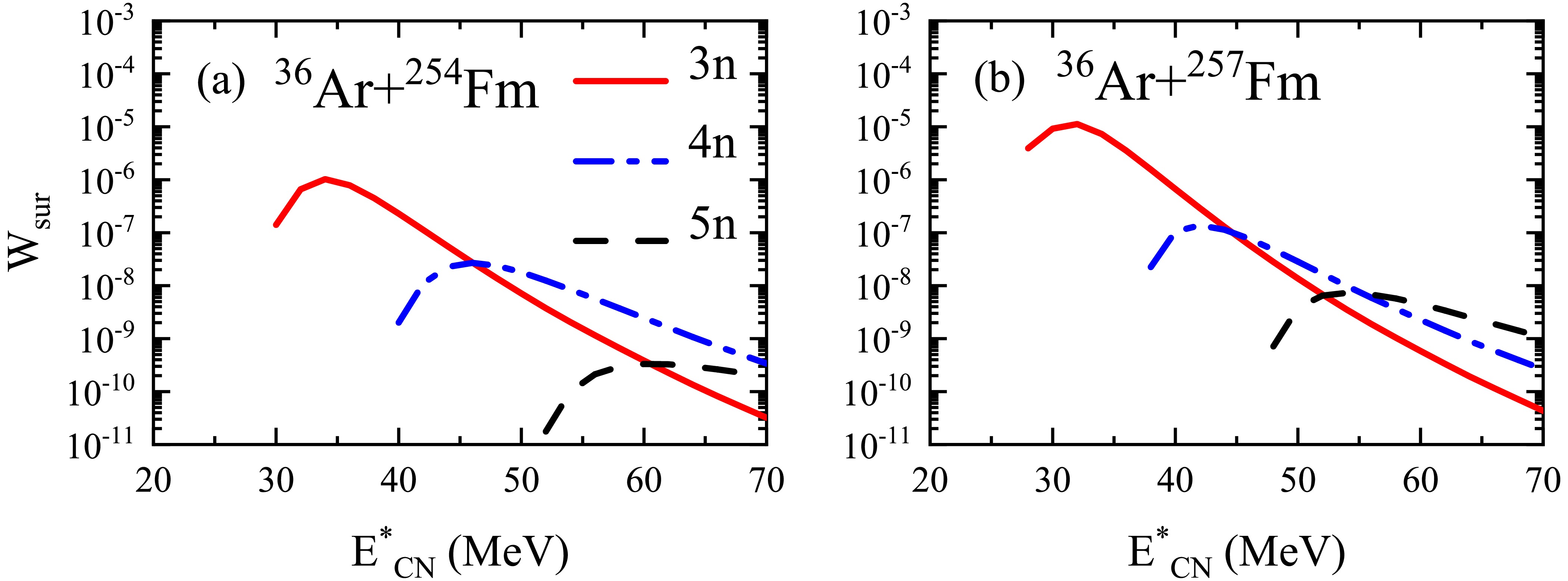

Figure 5.  (color online) Survival probabilities for the reactions (a) $ ^{36} \text{Ar}$ +$ ^{254} \text{Fm}$ and (b) $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ with the evaporation of 3–5 neutrons. The calculated results for the 3n, 4n, and 5n channels are represented by solid, dash-dotted, and dashed lines, respectively.

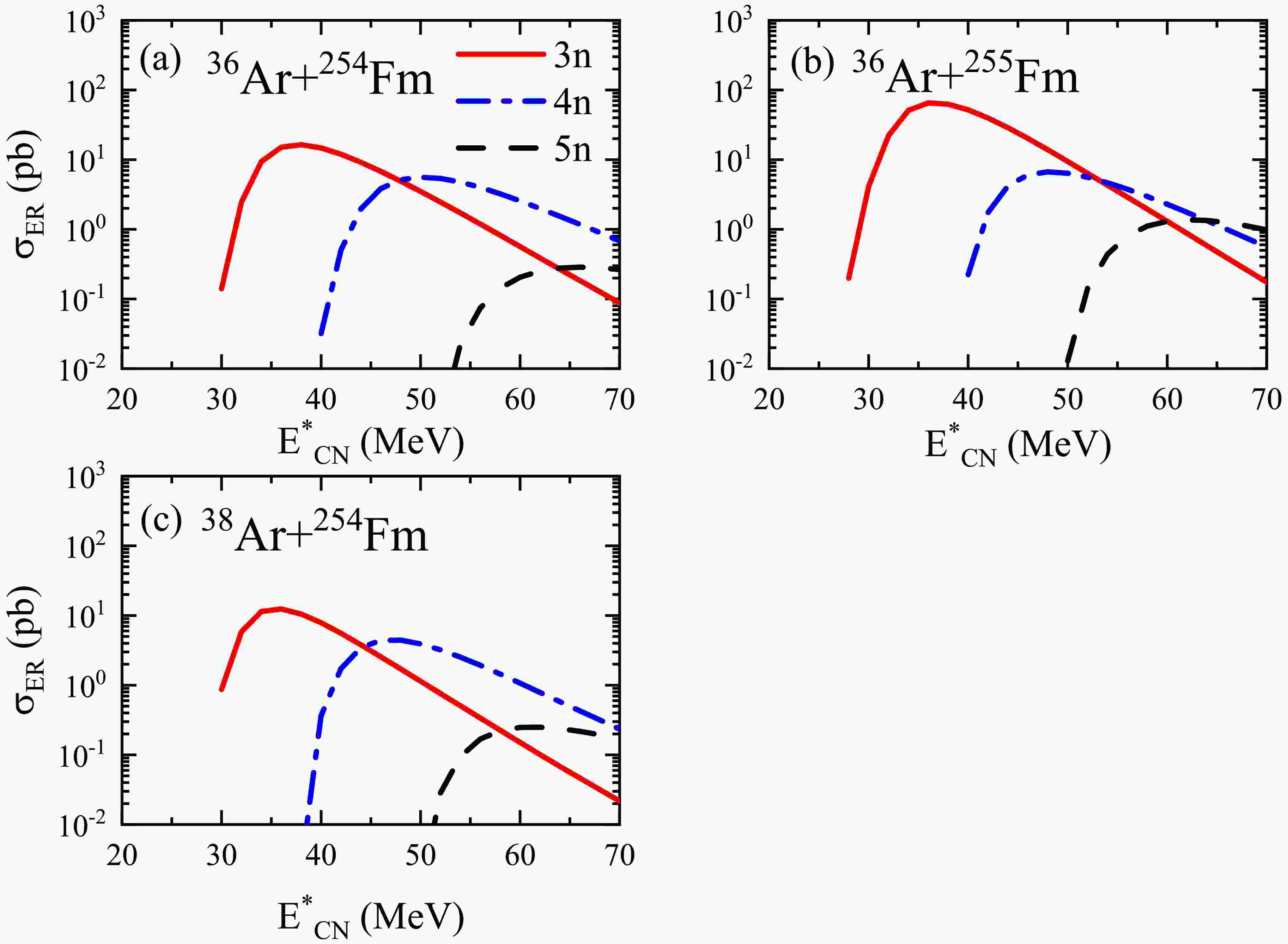
By analyzing the calculated results in the reactions $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$, it can be noticed that the $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ reaction is more favorable for synthesizing unknown Og isotopes due to its higher fusion probability. Therefore, we use the Ar + Fm system to predict the synthesis of new nuclides. The ER cross sections for the reactions $ ^{36} \text{Ar}$ +$ ^{254,255,257} \text{Fm}$ and $ ^{38} \text{Ar}$ +$ ^{254} \text{Fm}$ are shown in Fig. 2(a) and Fig. 6. Among the reactions $ ^{36} \text{Ar}$ +$ ^{254,255,257} \text{Fm}$, it can be noticed that, as the neutron number of the target nucleus gradually increases, the ER cross sections increase. This is because neutron-rich compound nuclei evaporate neutrons more easily. The highest cross sections for the reactions appear in the 3n channel because this channel has the highest survival probabilities. In the reactions $ ^{36} \text{Ar}$ +$ ^{254} \text{Fm}$, $ ^{36} \text{Ar}$ +$ ^{255} \text{Fm}$, $ ^{38} \text{Ar}$ +$ ^{254} \text{Fm}$, and $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, the unknown isotopes $^{287-290}\text{Og}$ can be produced through the 3n channel. The corresponding maximum cross sections for these reactions are 16.4, 65.1, 12.4, and 111.1 pb, respectively.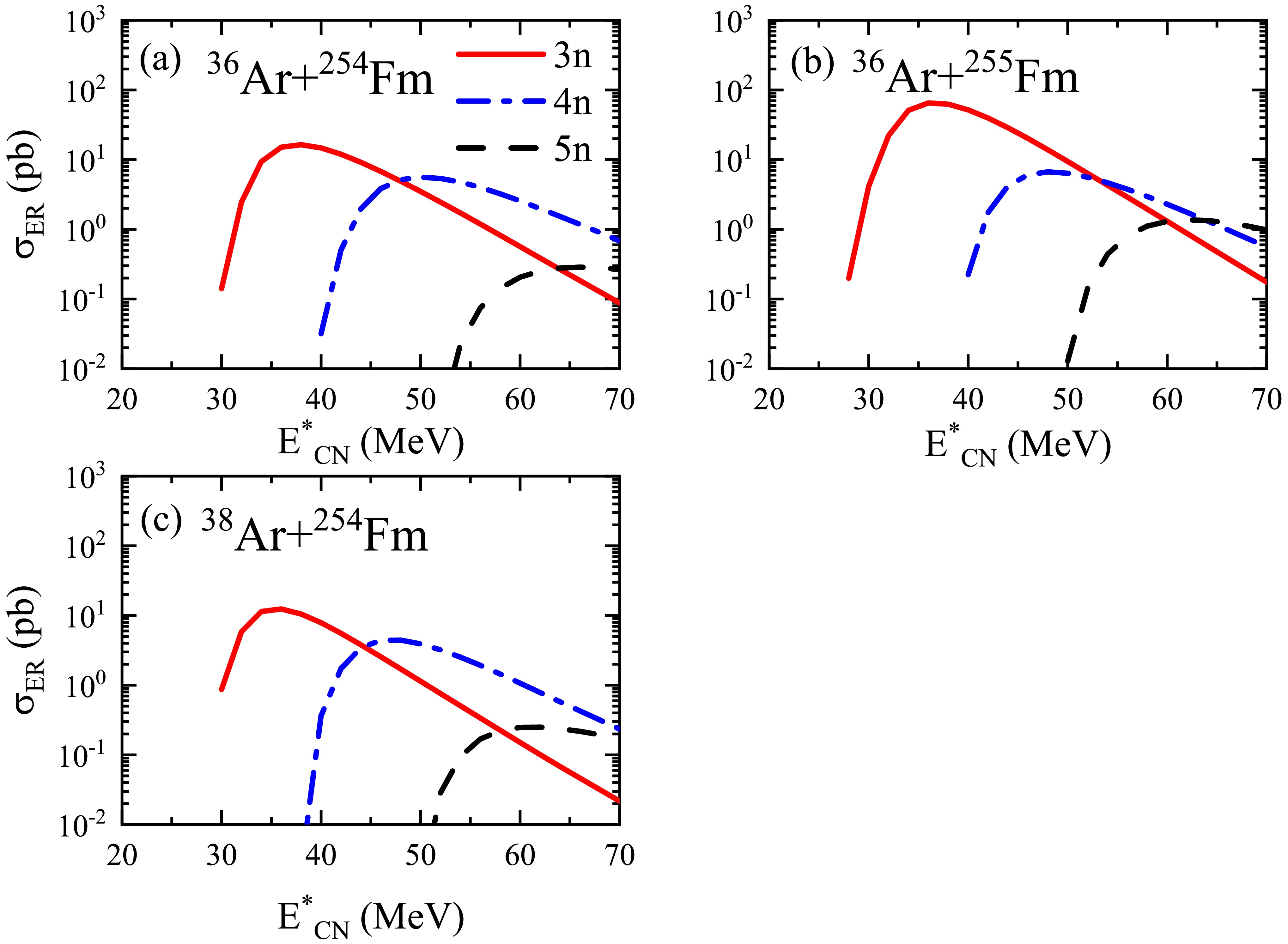

Figure 6.  (color online) Calculated ER cross sections for the reactions (a) $ ^{36} \text{Ar}$ +$ ^{254} \text{Fm}$, (b) $ ^{36} \text{Ar}$ +$ ^{255} \text{Fm}$, and (c) $ ^{38} \text{Ar}$ +$ ^{254} \text{Fm}$. The calculated results for the 3n, 4n, and 5n channels are shown as solid, dash-dotted, and dashed lines, respectively.

Due to the limitations in target fabrication technology and the current production yield of Fm targets, an experimental fusion-evaporation reaction using Fm as a target is not yet feasible. However, with the continuous advancement of target fabrication techniques, such as thin film deposition and material synthesis, as well as the improvement in Fm target production yield, significant progress is being made. For instance, the High Flux Isotope Reactor is continuously upgrading its equipment to enhance isotope production capacity, and the U.S. Department of Energy (DOE) has instructed Oak Ridge National Laboratory to develop plans to expand its radioactive isotope handling capacity to support the rapidly growing DOE isotope production and research programs [67]. Therefore, we believe that, in the near future, Fm targets will become feasible for use in experimental fusion-evaporation reactions.

The synthesis of the unknown Og isotopes in the fusion-evaporation reactions was investigated using the DNS model. The calculated ER cross sections in the reactions $ ^{48} \text{Ca}$ +$ ^{249} \text{Cf}$, $ ^{48} \text{Ca}$ +$ ^{249} \text{Bk}$, $ ^{48} \text{Ca}$ +$ ^{248} \text{Cm}$, and $ ^{48} \text{Ca}$ +$ ^{244} \text{Pu}$ are in good agreement with the experimental data. By comparing the reactions $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$, and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$, it was found that the reaction $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ exhibits the highest ER cross section, and the ER cross section decreases with increasing projectile charge number. Further investigation into the capture and fusion processes revealed that the capture cross sections of $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$ and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$ are larger than those in the reaction $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$. This is because the $ V_{\text{B}} + Q $ values of $ ^{44} \text{Ca}$ +$ ^{249} \text{Cf}$ and $ ^{48} \text{Ti}$ +$ ^{245} \text{Cm}$ are close to each other and lower than that of $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$. However, the fusion probability of $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ is the highest due to its largest mass asymmetry and lowest inner fusion barrier. The survival probabilities of the compound nuclei formed in the $ ^{36} \text{Ar}$ +$ ^{254} \text{Fm}$ and $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ reactions were also studied. It was found that the survival probability in the reaction $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$ is higher because the neutron-rich compound nucleus has a higher fission barrier, making fission less likely and neutron evaporation more likely. By analyzing the ER cross sections for the reactions $ ^{36} \text{Ar}$ +$ ^{254} \text{Fm}$, $ ^{36} \text{Ar}$ +$ ^{255} \text{Fm}$, $ ^{38} \text{Ar}$ +$ ^{254} \text{Fm}$, and $ ^{36} \text{Ar}$ +$ ^{257} \text{Fm}$, it was found that the 3n evaporation channel exhibits the maximum cross section, and these reactions were predicted to synthesize the new isotopes $^{287-290}\text{Og}$ with maximum ER cross sections of 16.4, 65.1, 12.4, and 111.1 pb, respectively.