Pear Shape and Tetrahedral Shape Competition in Actinide Nuclei

Studies of stable deformed nuclei have been a long-standing focus in nuclear structure research and continues to attract growing attention. According to Bohr formulation, the nuclear shapes can be described by employing spherical harmonic $ \{Y_{\lambda\mu}(\vartheta, \varphi)\} $ expansion of the nuclear surface Σ, c.f. Ref. [1]:

where the expansion coefficients $ \alpha_{\lambda \mu} $ are usually called 'deformation parameters' or 'deformations' for short. They are generally complex but we limit ourselves, as many other authors do, to the real parametrisation. The radius parameter $ R_0 \equiv r_0 A^{1/3} $, where $ r_0 \approx 1.2 $ fm, gives an approximation of the effective nuclear spherical radius in fermi, and the auxiliary function $ c(\alpha) $ assures that the volume encompassed by the nuclear surface is constant and independent of deformation.

Existence of nuclear shapes resembling axial-, and reflection-symmetric spheroids was confirmed by the observations of the rotational band structures and the measurements of their properties already in the middle of the previous century. Nuclei with quadrupole deformations $ \alpha_{\lambda=2,\mu=0,\pm 2} $ together with other even-λ shape components are symmetric under the space inversion. In contrast, nuclei with deformations involving odd-multipolarities, such as pear-shape octupole $ \alpha_{\lambda=3,0} $ related to the spherical harmonic $ Y_{3,0} $, break inversion invariance, and manifest presence of low-lying negative-parity bands, Ref. [2]. The low-lying bands with $ K^{\pi}=1^{-} $ or $ 3^{-} $ band-heads in even-even nuclei and sizeable octupole transition probabilities have been found in many cases, Ref. [3].

It turns out that pear-like shapes occur in nuclei with single nucleonic levels of opposite parities and orbital and total angular momenta that differ by 3$ \hbar $ – lying close to the Fermi energies. This phenomenon, resulting from the so-called residual octupole-octupole interaction, is observed among others close to proton numbers $ Z\approx $ 34, 56, and 88 and neutron numbers $ N\approx $ 34, 56, 88, and 134, Ref. [4]. The largest collection of $ Y_{30} $-type shapes has been seen at proton numbers $ Z\approx88 $ and $ N\approx134 $, Ref. [5]. The pear-shape deformed nuclei have been studied extensively in particular in Refs. [6−8].

Another important realisation of octupole deformations leading to deep minima on the nuclear potential energy surfaces corresponds to $ Y_{32} $ shape components. One demonstrates easily employing elementary properties of spherical harmonics that these shapes represent tetrahedral symmetry. They have been studied recently using various modelling approaches, focussing in particular on possible tetrahedral ground states and isomeric states. One of the most frequently used approaches involves the so-called macroscopic-microscopic method (MMM), cf. Refs. [9−16] and references therein.

So far unique, experimental evidence of rotational bands in a nucleus with tetrahedral symmetry was reported in Refs. [16] and [17]. According to theory predictions, the strongest tetrahedral effects appear at the so called tetrahedral magic numbers $ Z/N\approx $32, 40, 56, 64, 70, 90,136 (analogues of the well-known spherical magic numbers), cf. Ref. [10]. A recent article using similar methods extended the tetrahedral symmetry studies to the super-heavy region and the results show that tetrahedral shape is dominant also at $ N=196 $, cf. Ref. [18]. Besides that, tetrahedral equilibrium deformations were studied by non-relativistic density functional theory employing self-consistent Hartree-Fock techniques in Refs. [19−24], and multidimensionally constrained relativistic Hartree-Bogolyubov modelling in Refs. [25, 26]. Moreover the covariant density functional theories were used in studying the tetrahedral deformed nuclei in neutron-rich Zr isotopes and $ N=184 $ isotones in Refs. [27, 28]. Other authors used relativistic density functional theory on a three-dimensional lattice space, see Refs. [29−31]. Independently, algebraic cluster model, Ref. [32] and the lattice effective field theory, Ref. [33] presented the evidence of the tetrahedral symmetry in an α-cluster nucleus ¹⁶O.

Recent calculations addressing exotic geometrical symmetries around the 'fourfold octupole magic numbers', cf. Ref. [34], demonstrated simultaneous presence of the four octupole multipolarities, $ Y_{30} $, $ Y_{31} $, $ Y_{32} $ and $ Y_{33} $, wherefrom the term 'fourfold' – in deformations of actinide nuclei with neutron numbers around $ N=136 $. To provide more detailed information about possible forms of the shape competition and coexistence involving octupole deformations, the present article will focus on the interplay between pear-shape and tetrahedral shape deformations in the light actinide region. We are going to construct the criteria of identification of nuclear tetrahedral symmetry in this region of nuclei and encourage in this way possible experimental advancement of our knowledge of new exotic symmetries in heavy nuclei.

Nuclear potential energies will be calculated using the so-called macroscopic-microscopic method of Strutinsky, Refs. [35, 36]. Following standard today definitions and notation, the corresponding energy can be expressed as:

The first term represents the classical macroscopic liquid-drop model contribution, which in the present realisation follows the Finite-Range Liquid-Drop Model (FRLDM) including the surface energy term from Yukawa-plus-exponential finite range approach of Ref. [37]. The two microscopic terms are defined as the sums of the so-called shell-correction, and pairing correction energies within Strutinsky method.

To calculate the shell-correction one needs the single nucleon energies; they are calculated using realistic phenomenological mean-field approach with the deformed Woods-Saxon potential in its "universal" parametrisation. The reader interested in the concept of universality in this context and its evolution in the past is invited to consult Refs. [38, 39]. The adjective "universal" refers to a unique parameter set for all nuclei in the entire nuclear Mass Table. The corresponding parameters were recently re-examined employing the Inverse Problem Theory methods addressing predictive power, parametric correlations and model parameter uncertainties, cf. Refs. [40−42], whereas the numerical parameter values can be found in Ref. [43].

The expression of the nuclear mean-field Woods-Saxon Hamiltonian can be considered very standard today. It is given by:

where $ \hat{T} $ represents the nucleonic kinetic energy operator and $ \hat{\mathcal{V}}_{WS} $, the central Woods-Saxon potential, the latter defined via the equation of the nuclear surface, Σ of Eq. (1), as follows

in which $ V^{c} $ is the central potential depth parameter, $ r^{c} $ (in $ R^{c}=r^{c}A^{1/3} $), the central radius parameter, and $ a^{c} $ the central-potential diffusivity parameter. Function $ {\rm dist}_\Sigma(\vec{r},R^c; \alpha) $ represents the geometrical distance between the nucleon position, $ \vec{r}\equiv\{x,y,z\} $ and the nuclear surface Σ. This latter function is calculated with the help of an auxiliary one, $ f(\theta,\varphi) $ related to $ \vec{r}\equiv\{x,y,z\} $ and the nuclear surface Σ introduced in Eq.(1) as follows

One can calculate the distance function by minimizing the above auxiliary function over θ and φ, respectively,

Thus the problem can be solved numerically by finding the solutions for the system with two nonlinear equations

The spin-orbit potential as usual involves the gradient of the central one

where

Above, $ \lambda^{so} $ is a dimensionless spin-orbit strength scaling factor, $ r^{so} $ (in $ R^{so}=r^{so}A^{1/3} $) is the spin-orbit radius, and $ a^{so} $ is the spin-orbit diffusivity parameter.

In principle, this definition of the phenomenological mean-field Hamiltonian with the deformation-dependent Woods-Saxon proton and neutron potentials explicitly introduces two sets of 6 parameters each,

one for protons π, and one for neutrons ν, respectively.

As it is well known, nuclear interactions are of the short-range so that the corresponding potential decreases to zero fast in the nuclear surface area; one can demonstrate that this dependence is approximately exponential, cf. Eq. (4).

It follows that the shapes of the nuclear matter density distributions and these of the mean-field potentials are closely related and as the direct consequence, the symmetries of the nuclei and the symmetries of their mean fields can be identified. This facilitates the mathematical description of the problem since the spherical harmonics entering definition of nuclear surfaces via Eq. (1) are particularly well adapted mathematical tools employed also in group representation theory.

The single nucleon energies are obtained with the help of the Schrödinger equation with the Hamiltonian of Eq. (2)

which is solved using standard diagonalization methods with a matrix representation of the Hamiltonian within anisotropic Harmonic Oscillator (HO) basis. The HO basis cut-off conditions have been adjusted in such a way that the calculated single nucleon energies remain stable within three decimal places even for the extreme ranges of variations of the deformation parameters; see Ref. [43] for details.

In the light Actinide region, the ground-state equilibrium deformations contributed by quadrupole, hexadecapole and octuple degrees of freedom have been discussed in the literature both from experimental and theoretical viewpoints. Stable octupole shapes have been observed experimentally among others in ²²⁰Rn, and in ^222,224,228Ra, Refs. [44, 45]. As noticed earlier, the strong octupole shell effects at $ N=134 $ are confirmed for both the pear-shape in Ref. [5], and the tetrahedral-shape in ¹⁵²Sm, in Ref. [11] and more recently [17].

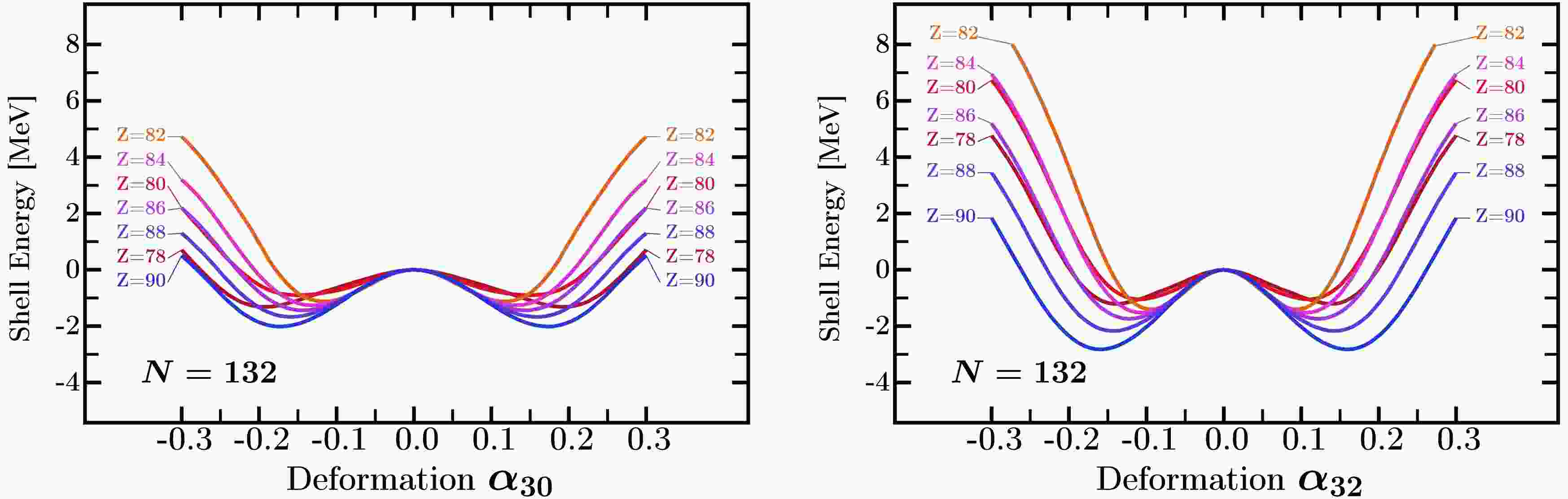
In Fig. 1 we show the nuclear shell energies, composed of Strutinsky and BCS pairing correlation energies, as functions of octupole deformations $ \alpha_{30} $ and $ \alpha_{32} $ for isotones with $ N=132 $ and proton number varying from $ Z = 78 $ to $ Z = 90 $. Comparing the shell effects induced by $ \alpha_{30} $ and $ \alpha_{32} $ deformations, one can notice that the octupole minima in both octupole deformations with $ \alpha_{30}\approx\pm0.15 $ and $ \alpha_{32}\approx\pm0.10 $ are present in all studied nuclei. The tetrahedral equilibrium deformation increases with increasing proton numbers, the strongest effect occurs at $ Z=90 $.

Figure 1.  (color online) Comparison of the nuclear shell-energies with varying number of protons from $Z = 78$ to $Z = 90$ for fixed neutron number $N = 132$ as functions of pear-shape octupole $\alpha_{30}$ deformation, left, and the tetrahedral octupole deformation $\alpha_{32}$, right. To better see the effects of the octuple deformations, all the shell energy curves are normalized to zero at the zero deformation. The nuclear deformation-driving effects appear in both deformations for all nuclei, with the strongest effect at $Z=90$. All other deformations are set to zero.

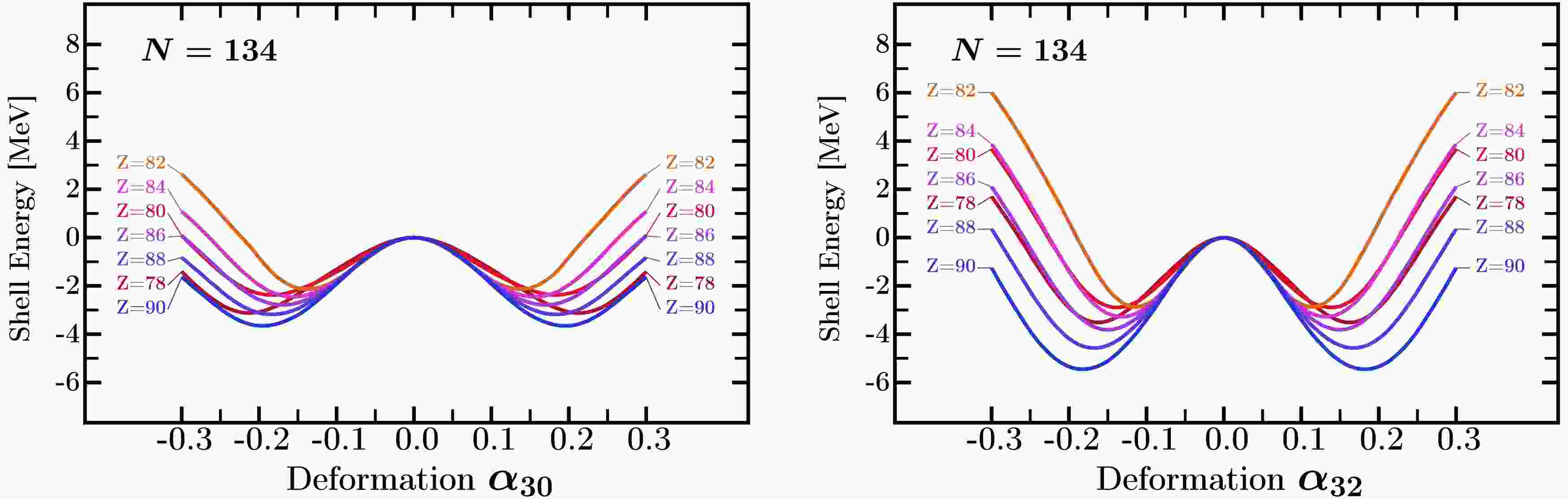
Figure 2 shows the comparison of the shell energies between $ \alpha_{30} $ and $ \alpha_{32} $ for the isotones $ N=134 $ – similar to the comparison for $ N=132 $. One significant difference is that the energy barriers between the twin octuple minima are larger for all nuclei with $ N=134 $. In particular, the tetrahedral minima are predicted to be more stable than the pear-shape minima for all nuclei due to the higher energy barriers. Moreover, the effects of both types of octuple deformations increase when the proton number increases from $ Z=82 $ to $ Z=90 $.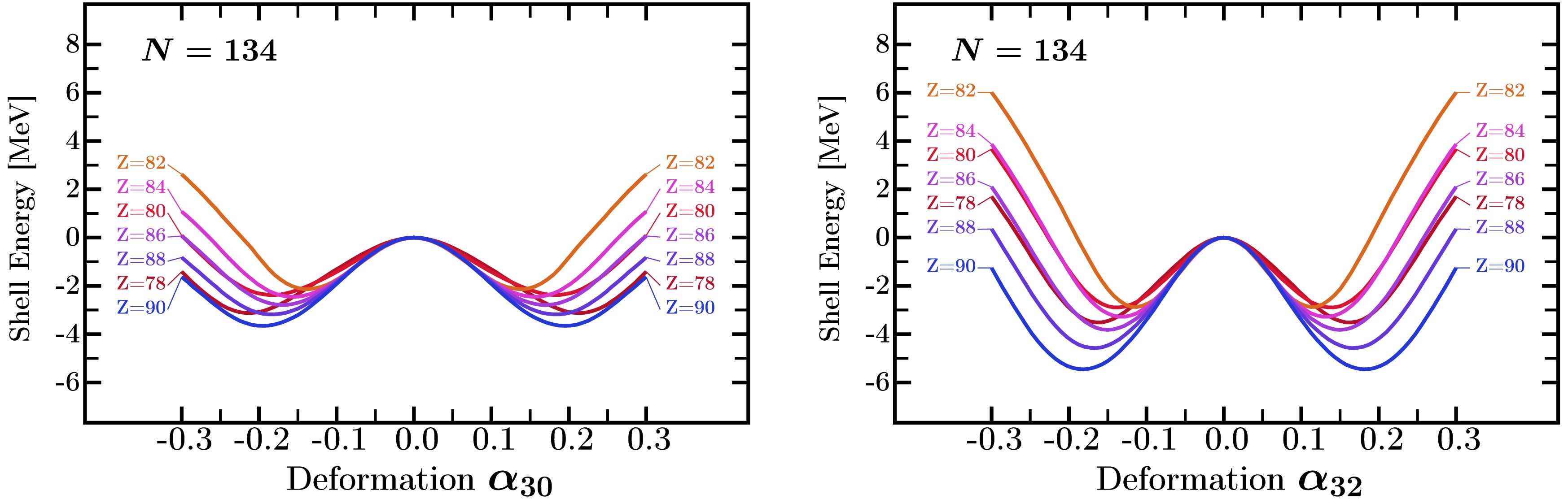

Figure 2.  (color online) Comparison similar to that in Fig.1, but for neutron number $N=134$ with proton numbers varying also from $Z = 78$ to $Z = 90$. The most pronounced nuclear shell effects appear for the tetrahedral-$\alpha_{32}$ deformation for $Z=90$. All other deformations are set to zero.

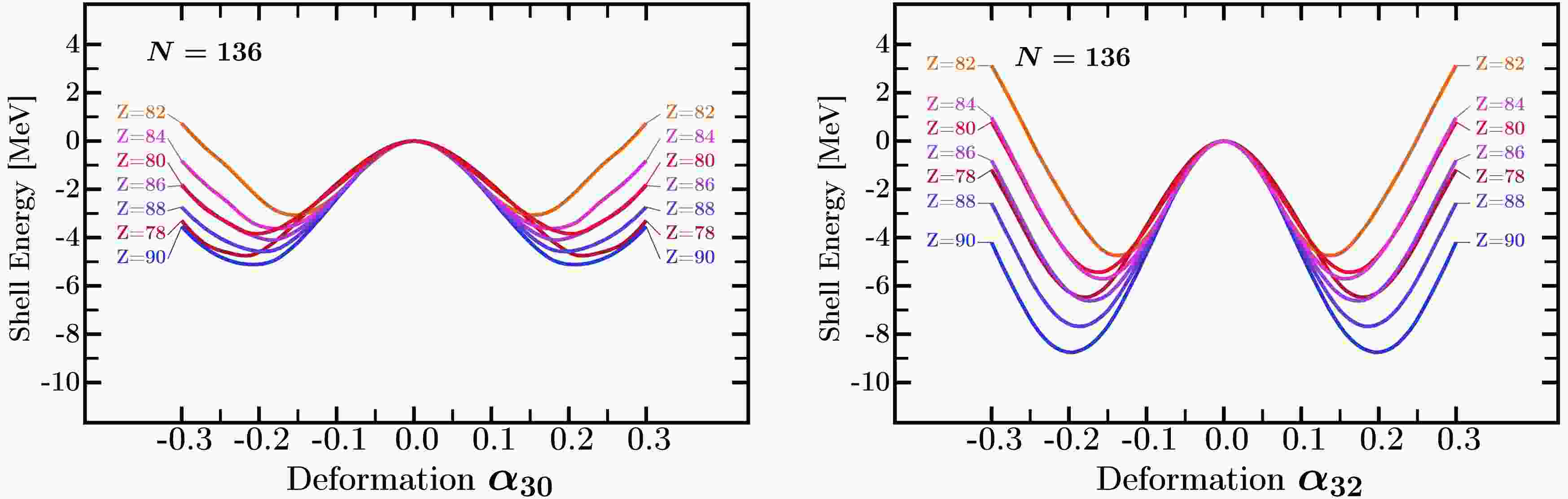
In the recent Ref. [18], it has been shown that $ N=136 $ is the magic number for all four octuple multipolarities, whereas $ Z=90 $ is identified as the proton tetrahedral magic number, Ref. [10]. This is supported by the strongest tetrahedral shell effects visible in Fig. 3, which exhibit separating energy barriers of the order of 9 MeV. While the shell energy barriers for tetrahedral deformation are higher than for the pear-shape ones, the equilibrium deformations remain comparable for both families of shapes.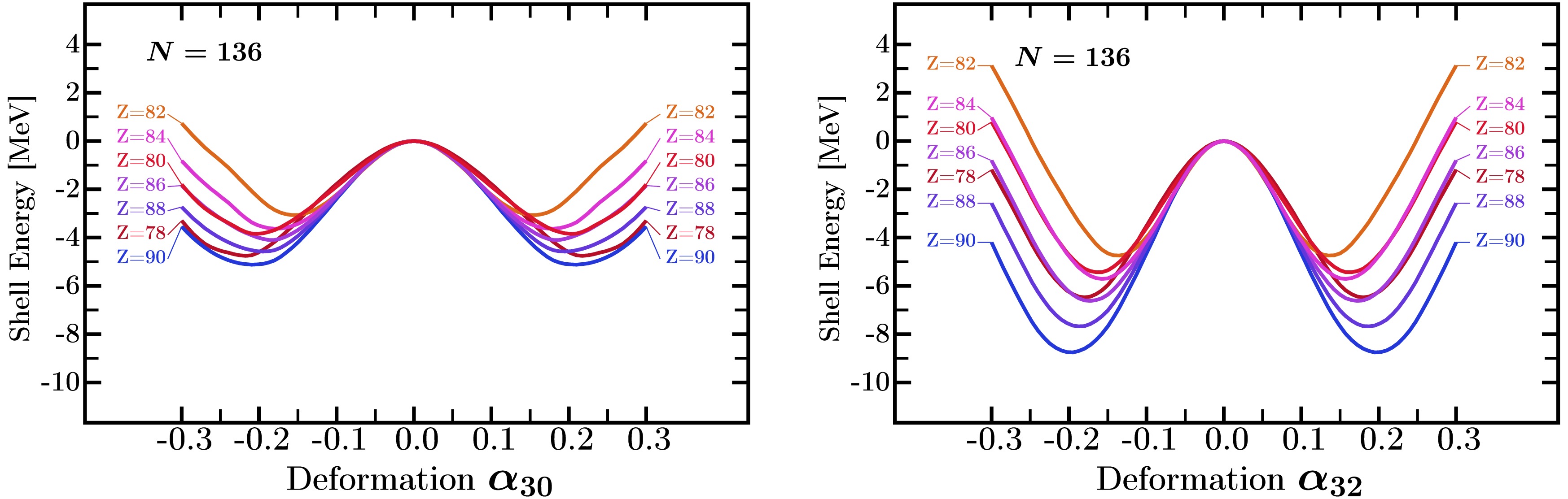

Figure 3.  (color online) Comparison similar to that in Fig.1, but for isotones $N=136$. The shell effects for the tetrahedral-$\alpha_{32}$ deformation are stronger than the shell effects for pear-shape deformation for all nuclei, with the strongest effect at $Z=90$. All other deformations are set to zero.

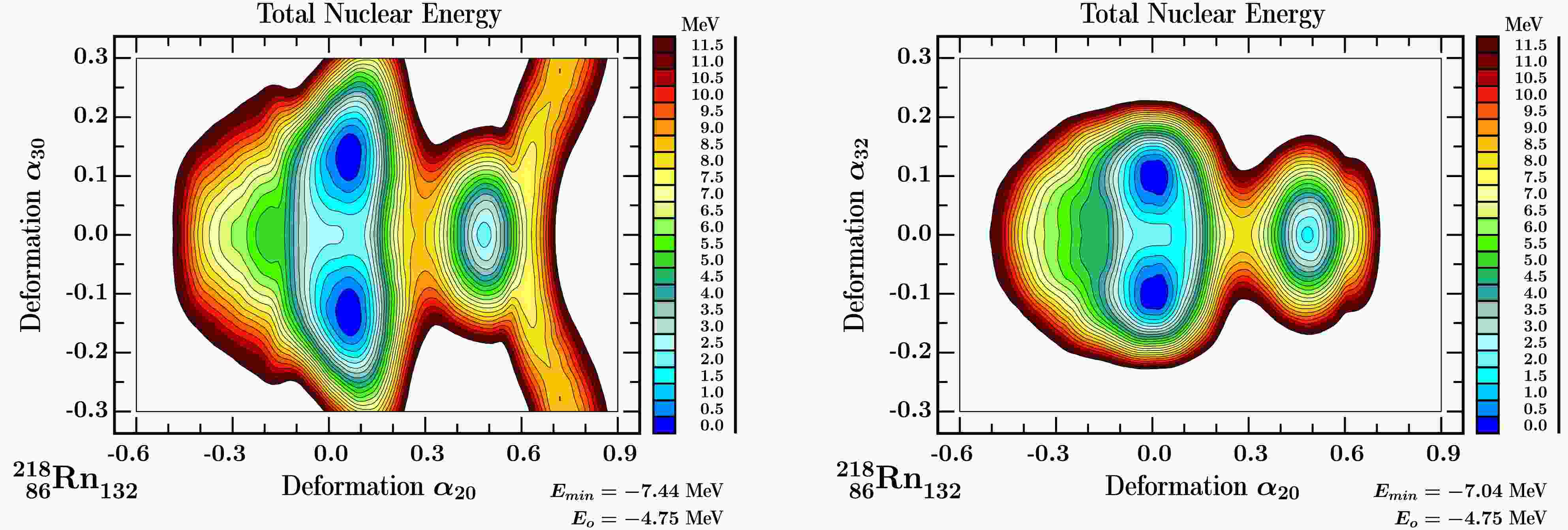
To give a comparative illustration of the octupole shell effects, we present the mesh calculations including multi-dimensional deformation spaces $ \{\alpha_{20} $, $ \alpha_{30} $, $ \alpha_{40}\} $ and $ \{\alpha_{20} $, $ \alpha_{32} $, $ \alpha_{40}\} $, separately. Examples of the nuclear potential energies projected on ($ \alpha_{20} $, $ \alpha_{30} $) plane and the ($ \alpha_{20} $, $ \alpha_{32} $) plane are given in Fig. 4. At point of the rectangle, minimisation over hexadecapole deformation $ \alpha_{40} $ is performed. Comparison shows that the pear-shape deformation with $ \alpha_{30}\approx\pm 0.15 $ and the tetrahedral one with $ \alpha_{32}\approx\pm 0.15 $ are predicted in ²¹⁸Rn.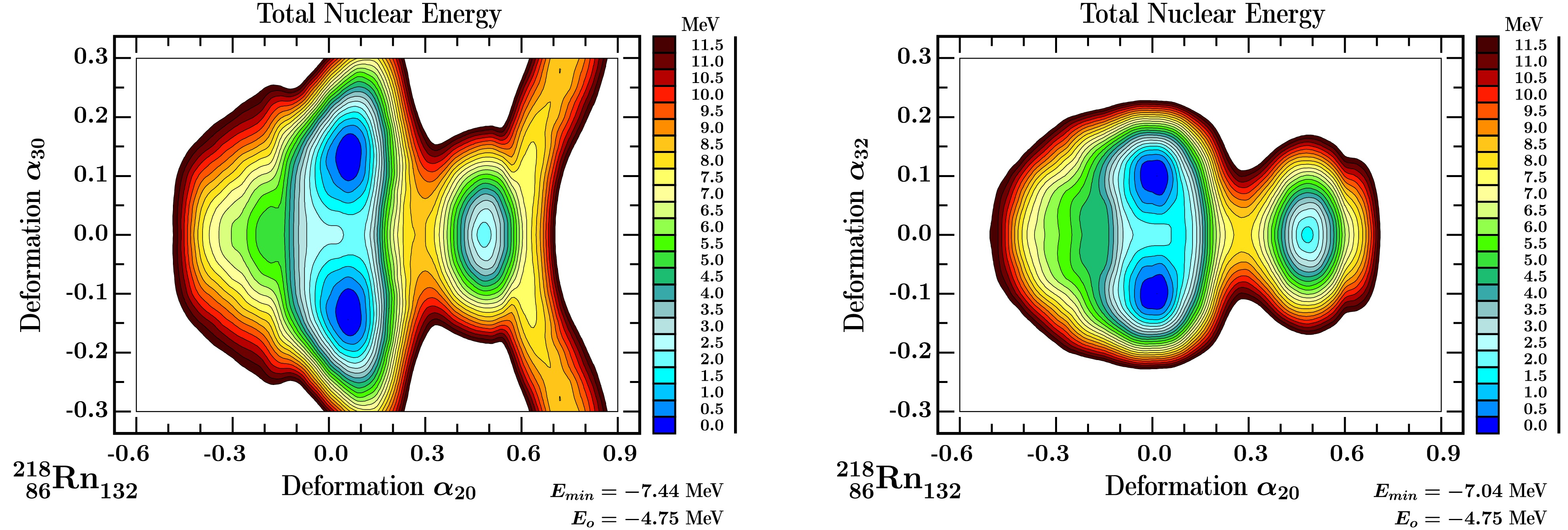

Figure 4.  (color online) Examples of nuclear potential energy 2D maps projected from the 3D mesh energies with $\{\alpha_{20}$, $\alpha_{30}$, $\alpha_{40}\}$ and $\{\alpha_{20}$, $\alpha_{32}$, $\alpha_{40}\}$. The BCS pairing was used for the Strutinsky-type calculations. Our focus is on the difference between the ($\alpha_{20}$, $\alpha_{30}$) and the ($\alpha_{20}$, $\alpha_{32}$) projections, in both cases minimised at each point over hexadecapole deformation $\alpha_{40}$, here for the example of ₈₆²¹⁸Rn₁₃₂. The comparison shows that both pear-shape and tetrahedral deformation minima are predicted in ²¹⁸Rn, at comparable energies.

Illustrations of the nuclear surfaces corresponding to these two types of minima are presented in Fig. 5. The corresponding equilibrium deformations exhibit comparable energy minima with $ E^{\alpha_{30}}_{min}=-7.44 $ MeV and $ E^{\alpha_{32}}_{min}=-7.04 $ MeV. Please note: The lower the energy minimum, the stronger the nuclear stability.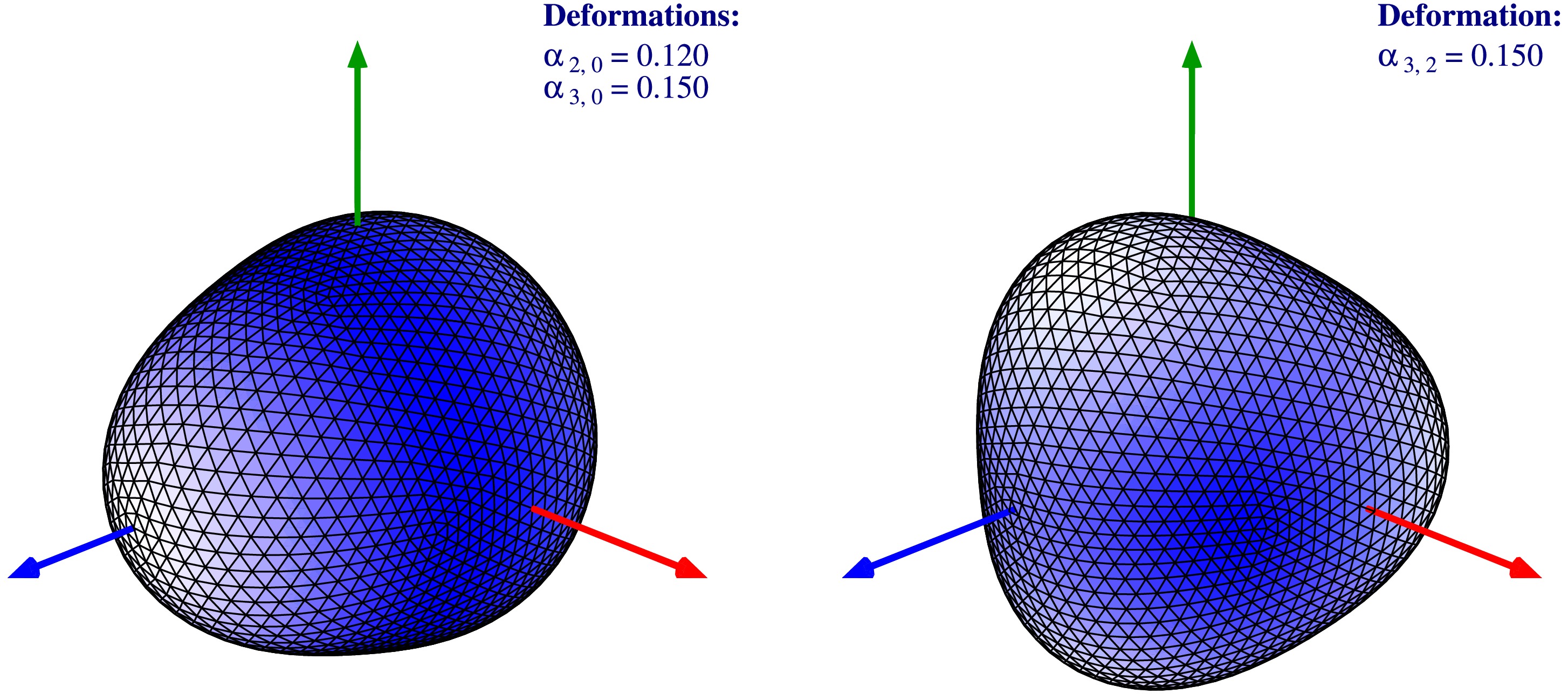

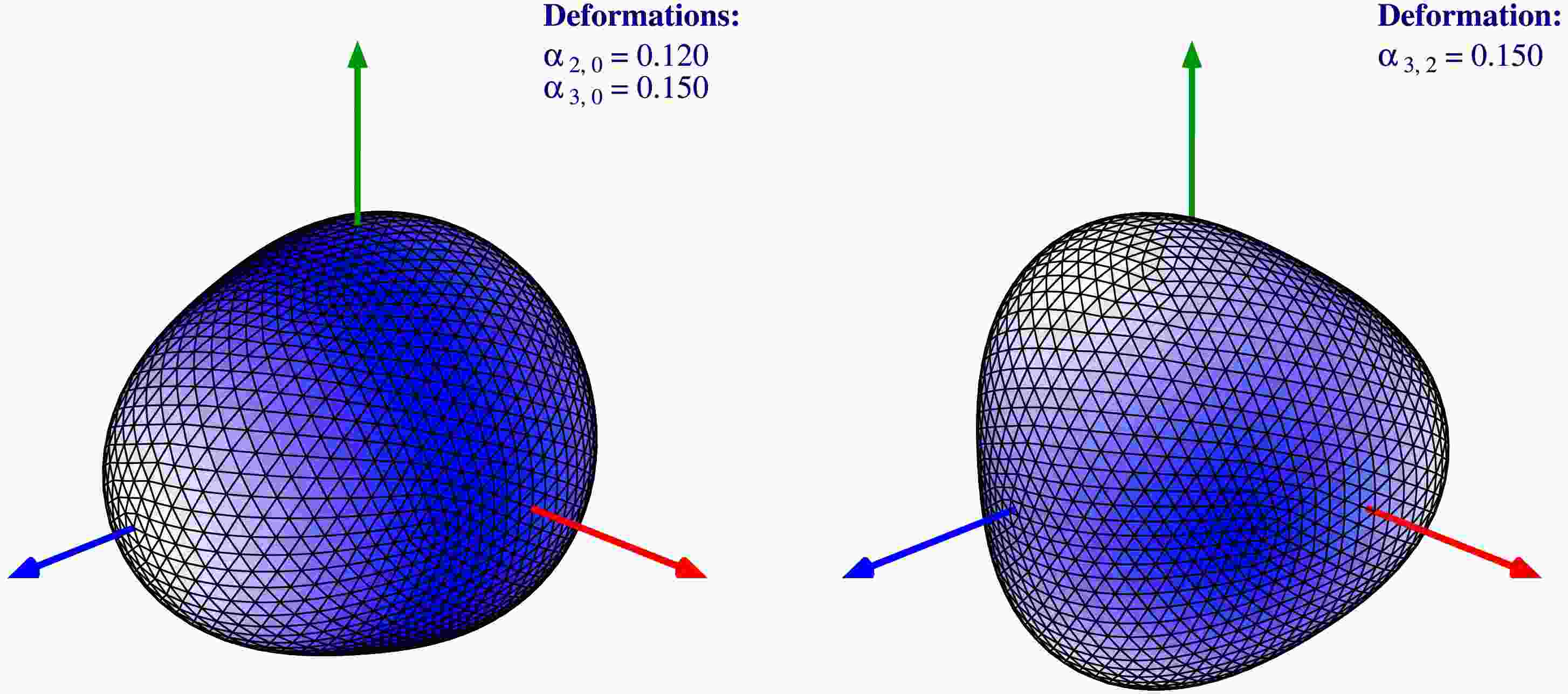
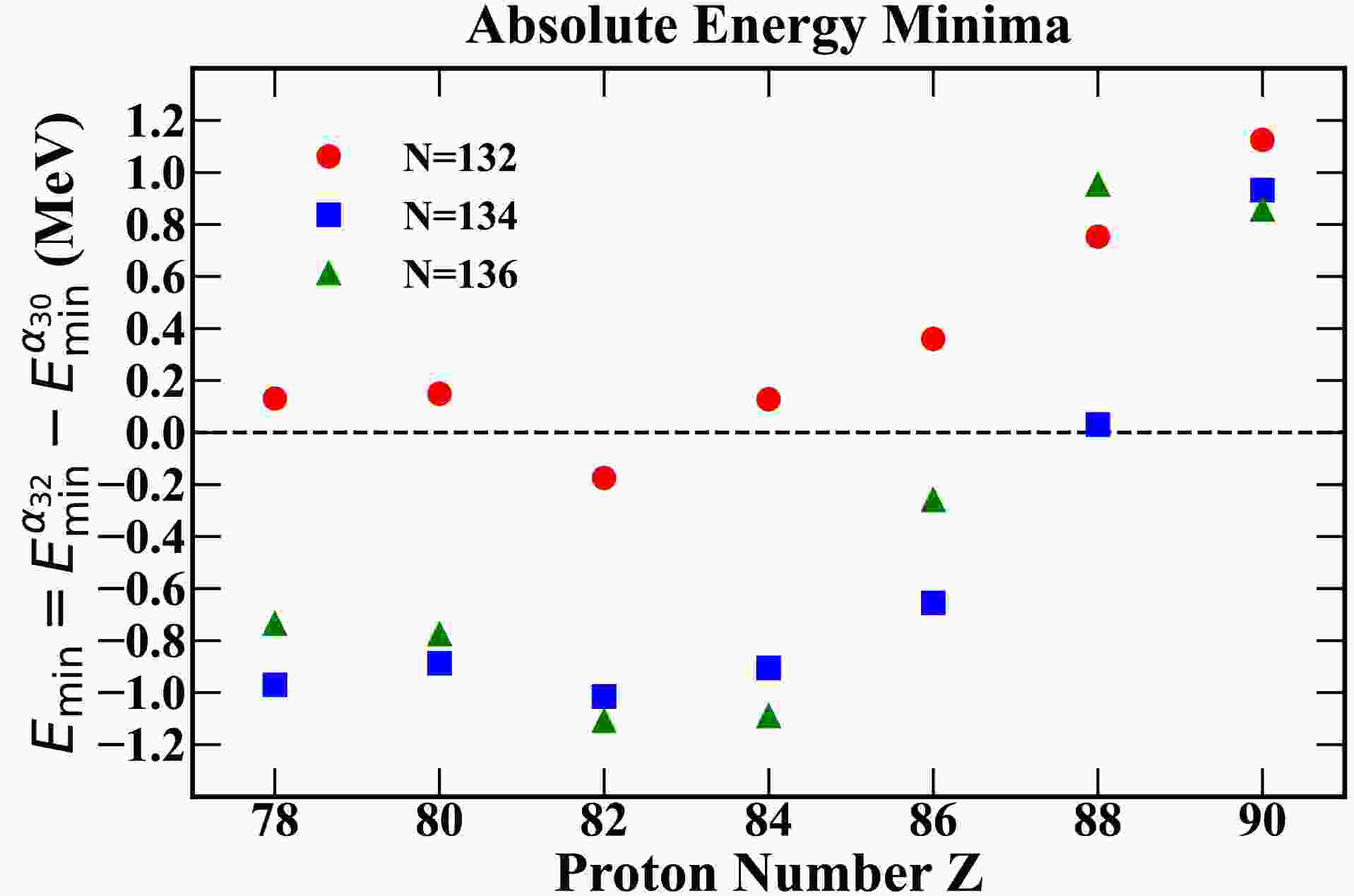
Figure 5.  (color online) Illustrations of the nuclear surfaces corresponding to the discussed two types of minima. Left: the pear-shape deformation corresponding to the minimum at $\alpha_{20}=0.12$, $\alpha_{30}=0.15$ and $\alpha_{40}=0.0$. Right: similar for the minimum at tetrahedral deformation $\alpha_{20}=0.0$, $\alpha_{32}=0.15$ and $\alpha_{40}=0.0$; compare with the maps in Fig. 4.

Figure 6 combines the information about potential energy minima, deduced from the results like the ones shown in Fig. 4, for both pear-, and tetrahedral-shape deformations. For convenience reasons, the tetrahedral minima are normalized to the pear-shape minima, showing directly the relative depth of the former. We observe that for nuclei with $ N=132 $ and $ Z=78-86 $, the absolute energy minima are close to zero, implying the possible shape competition between these two types of octuple symmetries. For nuclei with $ N=134 $ and $ N=136 $, the dominating minima correspond to tetrahedral deformation, with the exception of ₈₈²²²Ra₁₃₄ and ₈₆²²²Rn₁₃₆.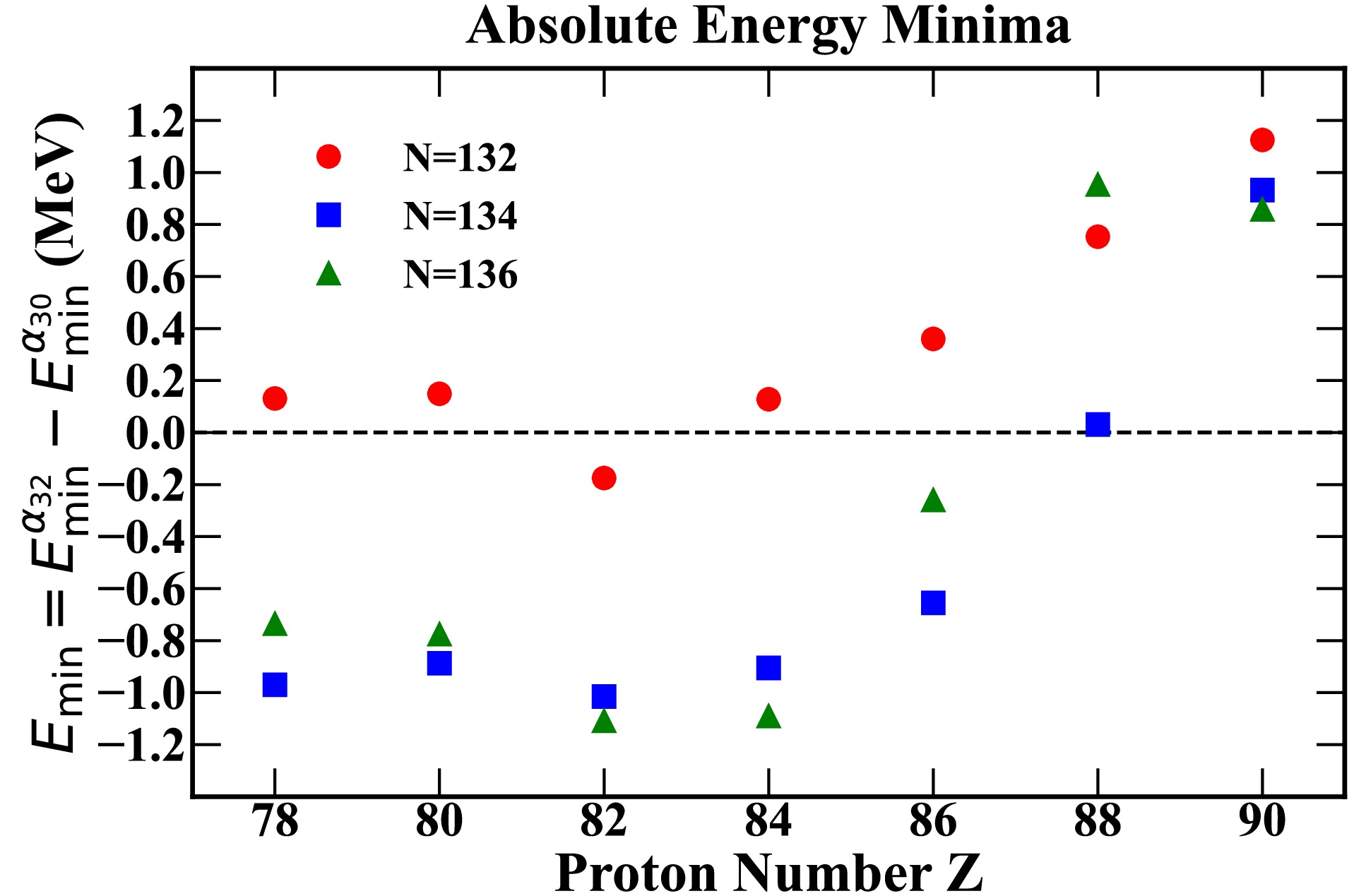

Figure 6.  (color online) Comparison of the absolute energy minima $E_{\rm min}=E^{\alpha_{32}}_{\rm min}-E^{\alpha_{30}}_{\rm min}$, deduced from the potential energy maps, see examples in Fig. 4, for $N=132$, $N=134$ and $N=136$ isotones, respectively.

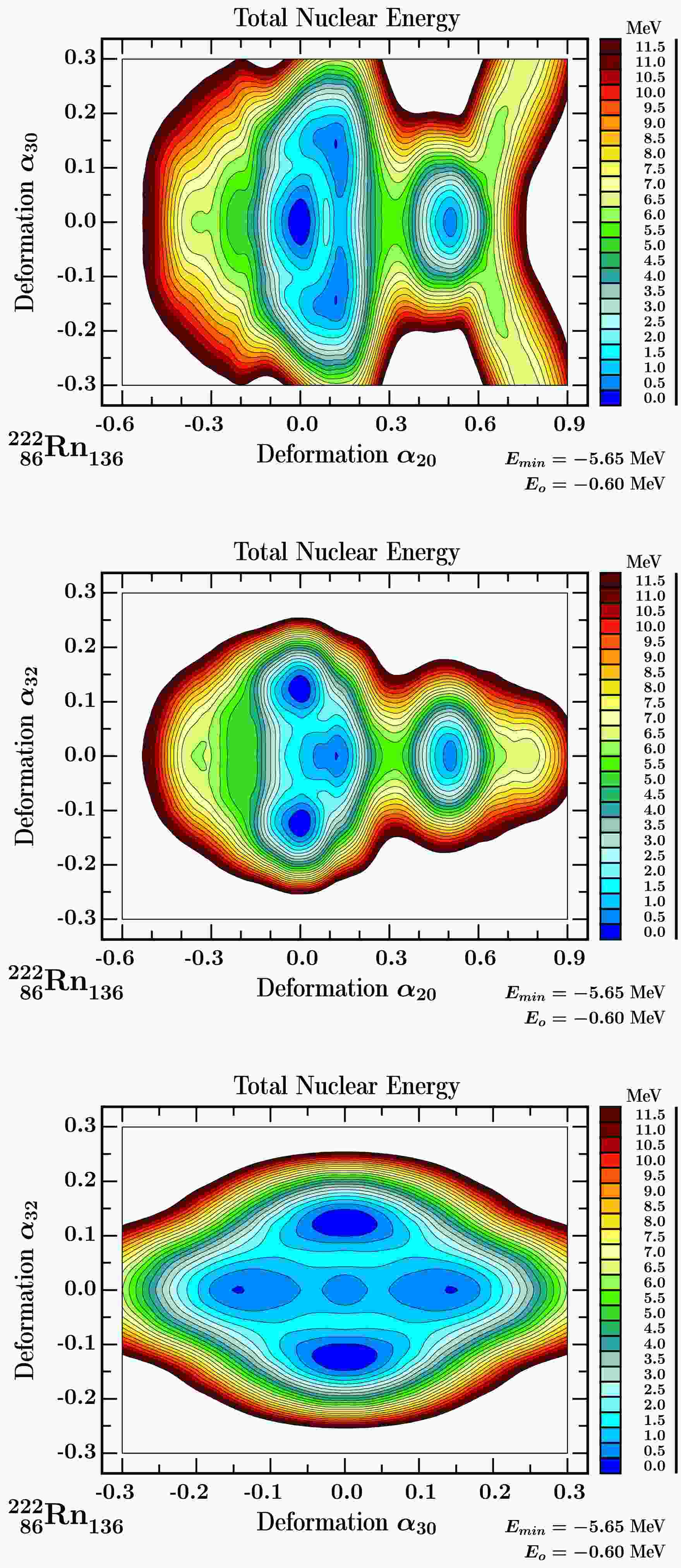
To give a richer illustration of the predicted competition and coexistence between pear-, and tetrahedral-shape symmetries, we continue with the comparison of illustrative results of the mesh calculations including four deformations $ \{\alpha_{20} $, $ \alpha_{30} $, $ \alpha_{32} $, $ \alpha_{40}\} $ simultaneously. The projections on ($ \alpha_{20} $, $ \alpha_{30} $), ($ \alpha_{20} $, $ \alpha_{32} $), and ($ \alpha_{30} $, $ \alpha_{32} $) planes are illustrated in Figs. 7-9. Comparing the potential energy surfaces in Fig. 4 with those in Figs. 7-9, we notice that both the axial octupole and the tetrahedral octupole minima are present in the same potential energy projection, with the octupole-$ \alpha_{30} $ minima exhibiting greater softness. The competition between these two types of symmetry is shown on the ($ \alpha_{30} $, $ \alpha_{32} $) projection, where the separation energy is approximately 1 MeV.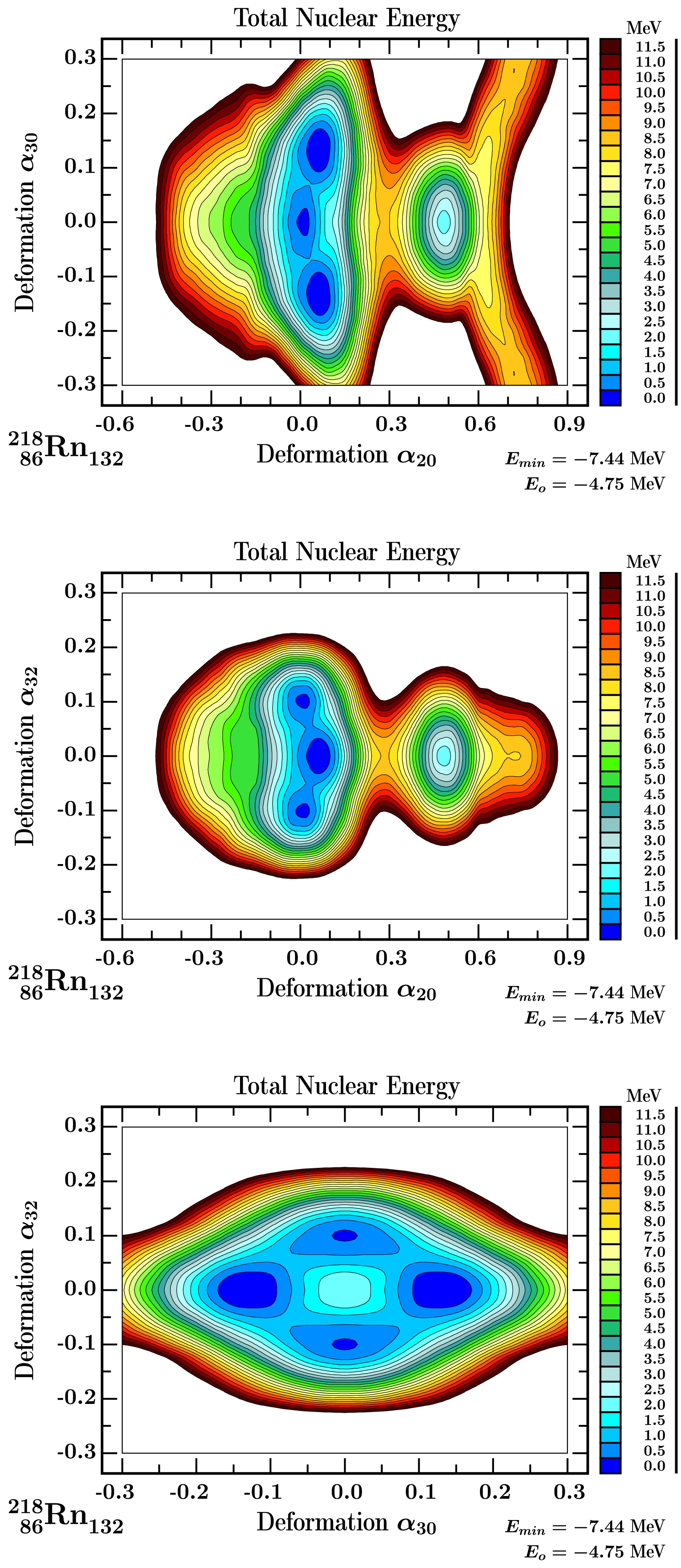

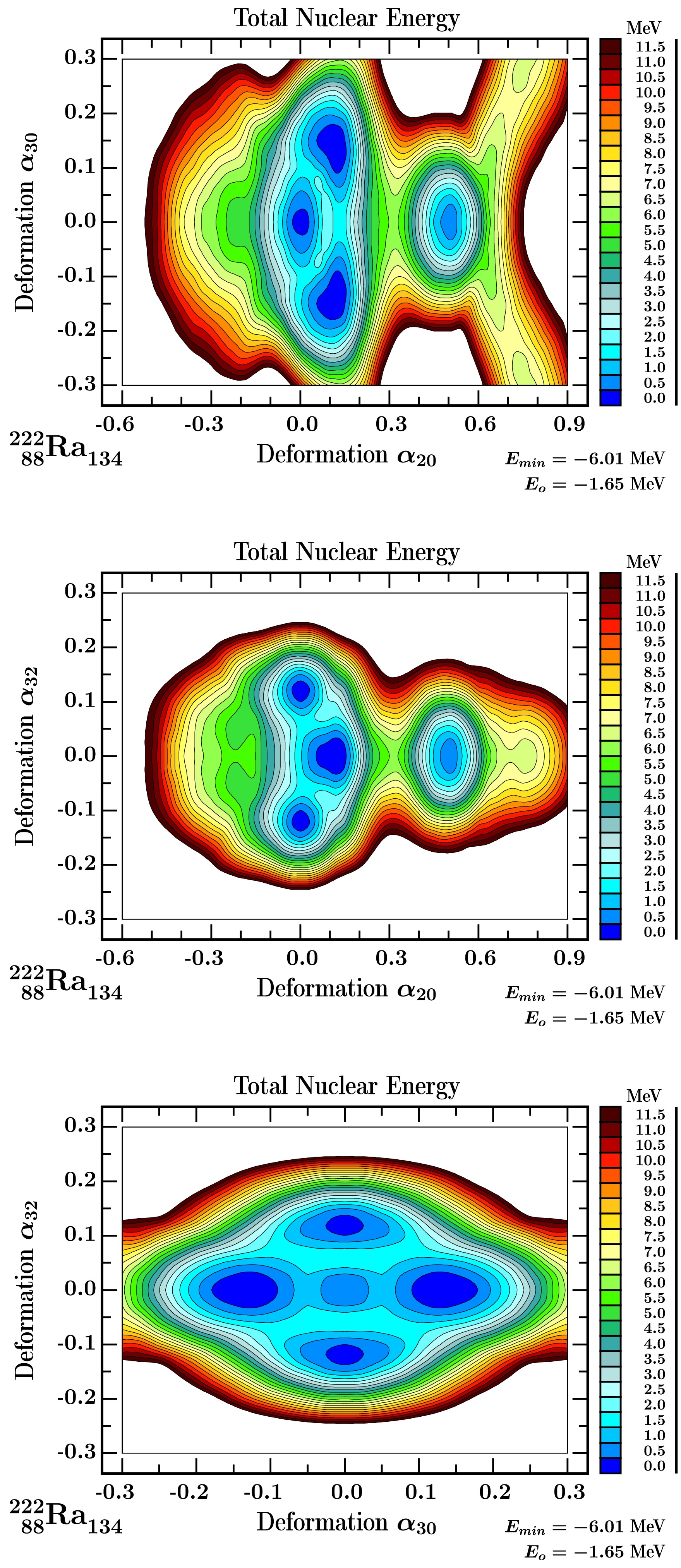
Figure 7.  (color online) Results structurally similar to those in Fig. 4, here obtained from the 4D deformation space $\{\alpha_{20}$, $\alpha_{30}$, $\alpha_{32}$, $\alpha_{40}\}$. Potential energy surfaces for ₈₆²¹⁸Rn₁₃₂, projections onto the ($\alpha_{20}$, $\alpha_{30}$) and ($\alpha_{20}$, $\alpha_{32}$) planes, two upper diagrams, showing a competition between octupole and spherical shapes, and ($\alpha_{30}$, $\alpha_{32}$) plane, bottom diagram. The latter one illustrates a competition between $\alpha_{30}$ and $\alpha_{32}$ deformations taking into account minimisation over ($\alpha_{20}$, $\alpha_{40}$) deformations.

Figure 8.  Results structurally similar to those in Fig. 7 but for the case of ₈₈²²²Ra₁₃₄. The quadrupole deformation $\alpha_{20}\approx0.18$ obtained from the $\{\alpha_{20}, \alpha_{30}\}$ projection is comparable with the experimental deformation $\beta_2\approx0.19$ from Ref. [46].

Figure 9.  Results structurally similar to those in Fig. 7 but for the case of ₈₆²²²Rn₁₃₆. Theoretical quadrupole deformation $\alpha_{20}\approx0.125$ is close to the experimental quadrupole deformation $\beta_2\approx0.142$ from Ref. [46].

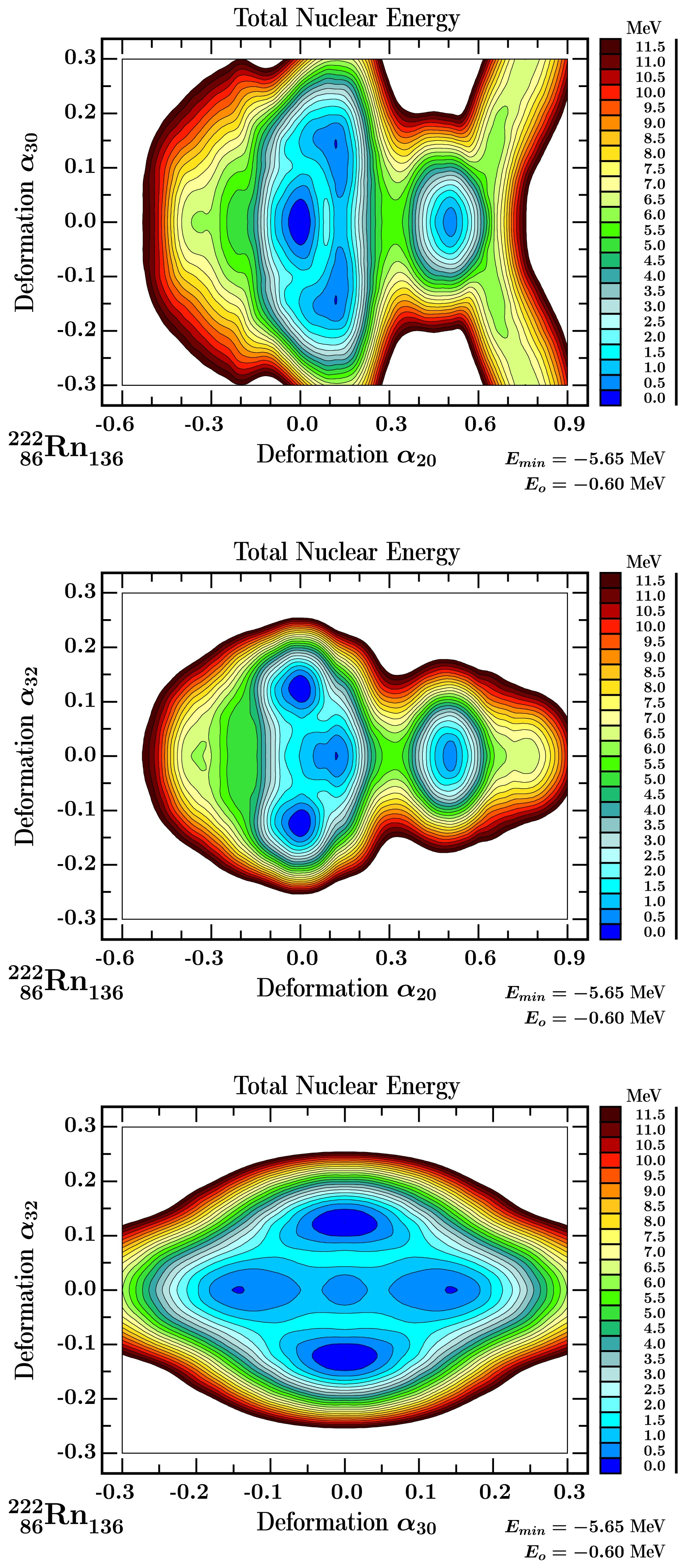
Figure 8 shows the results for ₈₈²²²Ra₁₃₄. It follows that the pear-shape deformation with $ \alpha_{30} \approx0.15 $ is associated with a quadrupole deformation of $ \alpha_{20} \approx 0.18 $, which is comparable with the experimental quadrupole deformation $ \beta\approx0.19 $ from Ref. [46]. Compared to this: the tetrahedral minimum at $ \alpha_{32} \approx 0.10 $ corresponds to vanishing quadrupole deformation, $ \alpha_{20} \approx0.0 $.

The potential barrier between the two types of octupole minima is approximately 2 MeV, similar for ₈₈²²²Ra₁₃₄, and ₈₆²²²Rn₁₃₆ compared to 1 MeV for ²¹⁸Rn. Let us note that the theoretical quadrupole deformation for $^{222}_{\;\;86}{\rm{Rn}}_{136} $ is about $ \alpha_{20}\approx0.125 $ and is comparable with the experimental quadrupole deformation $ \beta_2\approx0.142 $ from Ref. [46]. In addition, the super-deformed minimum at $ \alpha_{20}\approx 0.45 $ is predicted in all three studied nuclei and it is about 1 MeV above the ground states of ₈₈²²²Ra₁₃₄ and ₈₆²²²Rn₁₃₆ nuclei and about 1 MeV lower than the one in ²¹⁸Rn.

Octupole collectivity is generally manifested by the presence of low lying negative parity bands and enhanced $ \Delta I=3 $ octupole transitions. A new experimental evidence of the octupole collectivity in radioactive isotopes ^222,224,226Rn $ (Z = 86) $ and ^222,228Ra $ (Z = 88) $, has been interpreted recently in terms of the pear-shape deformation in Ref. [8].

It will be instructive to introduce the issue of the mean field rotation and the concept of the cranking mechanism and cranking frequency by considering first the elementary mean-field approximation as the one represented by the Hamiltonian of Eq. (2). In the simplest form of modelling, collective rotational motion of nuclei is traditionally described by the so-called rotor Hamiltonian, similar to the analogous classical expression, in which the classical angular momentum components are replaced by the corresponding quantum operators whereas the moments of inertia remain the parameters of the Hamiltonian ¹. The easiest populated rotational bands are the ones which are the lowest in energy – thus corresponding to the rotation about an axis perpendicular to the symmetry, say $ \mathcal{O}_z $- axis, and associated with the biggest component of the moment inertia.

The presence of collective rotation introduces formal complication of the mean field description of the motion since the originally stationary wave functions become formally time dependent in the laboratory frame. It has been noticed by Inglis that transforming the equations of the motion to the rotating reference frame can be used to simplify the description by profiting from the fact that for slow rotation the spatial form of the wave functions in both rotating and original, static reference systems can be represented by the same time-independent mathematical realisations. One can demonstrate that the mean-field Hamiltonian in the rotating reference frame takes the form:

in which $ \hat{H}_{WS} $ is given by Eq. (2), $ \vec{\omega}=\{\omega_x, \omega_y, \omega_z\} $ is the rotational frequency vector, whereas $ \hat{\jmath} $ stands for the nucleonic angular momentum operator. The new object, $ \hat{H}^{\omega}_{WS} $, is the energy operator in the rotating reference frame traditionally called Routhian and denoted alternatively by $ \hat{\mathcal{R}} $; interested reader may consult Ref. [47] for mathematical details and discussion.

In what follows, attempting the more realistic description, we are going to consider collective rotation with the mean field of Eq. (2) supplemented with the monopole pairing Hamiltonian. We are not going to reintroduce the whole pairing formalism at this point, the subject presented in many publications in the past. Instead we will limit ourselves to recalling the basic definitions and notation. Our calculation results discussed below were obtained according to the formalism very close to the one described in Ref. [47] using pairing Hamiltonian (see below) which takes a particular form of the more general two-body interaction written as usual

where $ \hat{c}^+ $ and $ \hat{c} $ are single nucleon creation and annihilation operators according to the standard definitions and notation. The pairing Hamiltonian with the two-body interaction defined as the particular case of the general one above takes the form

where the 'bar" over the symbol refers to the result of the time-reversal operation $ | \bar{\alpha} \rangle\equiv \hat{T} | \alpha \rangle $. We are going to solve the pairing problem for the rotating nuclei in a standard manner assuming the particle number and angular momentum constraints

The corresponding cranking Hamiltonian in the rotating reference frame (pairing Routhian analogous to the one in Eq. (12)) takes the form

The so far unknown Lagrange multipliers λ and ω are associated with the constraints in Eq. (15) and are traditionally referred to as Fermi energy and rotational cranking frequency, respectively. The problem of the nucleonic motion represented by the above Hamiltonian can be solved after application of the well known Bogolyubov transformation and following the so-called Hartree-Fock-Bogolyubov Cranking (HFBC) method. Interested reader may follow the details and illustrations in Ref. [48] and/or Ref. [47].

It turns out that an ideal tetrahedral symmetry rotor is characterised by a 'spherically symmetric tensor of inertia', with the effect that the cranking results do not depend on the tilting axis or positioning of the cranking axis with respect to the rotor, see Section IV in Ref. [23] for details, or Ref. [1] for a more general discussion. It follows that the orientation of the axis with respect to a tetrahedral rotor can be selected arbitrarily. Interested reader can find a detailed discussion of the generalised quantum rotor formalism in Refs. [49] and [50].

In the case of the octupole pear-shape symmetry we are going to consider rotation about an axis perpendicular to the elongation axis, the latter fixed as $ \mathcal{O}_z $ and select axis $ \mathcal{O}_y $ as the rotation axis, traditionally called 'cranking' axis. We will introduce the symbols $ E_{\rm total}(I) $, $ \mathcal{R}(I) $ and $ I_y(I) $ for the laboratory energy, Routhian and expectation values of the y-component of angular momentum, respectively.

It follows from the HFBC formalism, that the energy in the laboratory system can be calculated as follows

The corresponding results were obtained by employing HFBC method after slight adjustments of the pairing strength constant G, cf. Eq. (14). We calculated among others the nuclear energy as function of the cranking frequency with the mean-field deformations corresponding to the energy minima presented earlier.

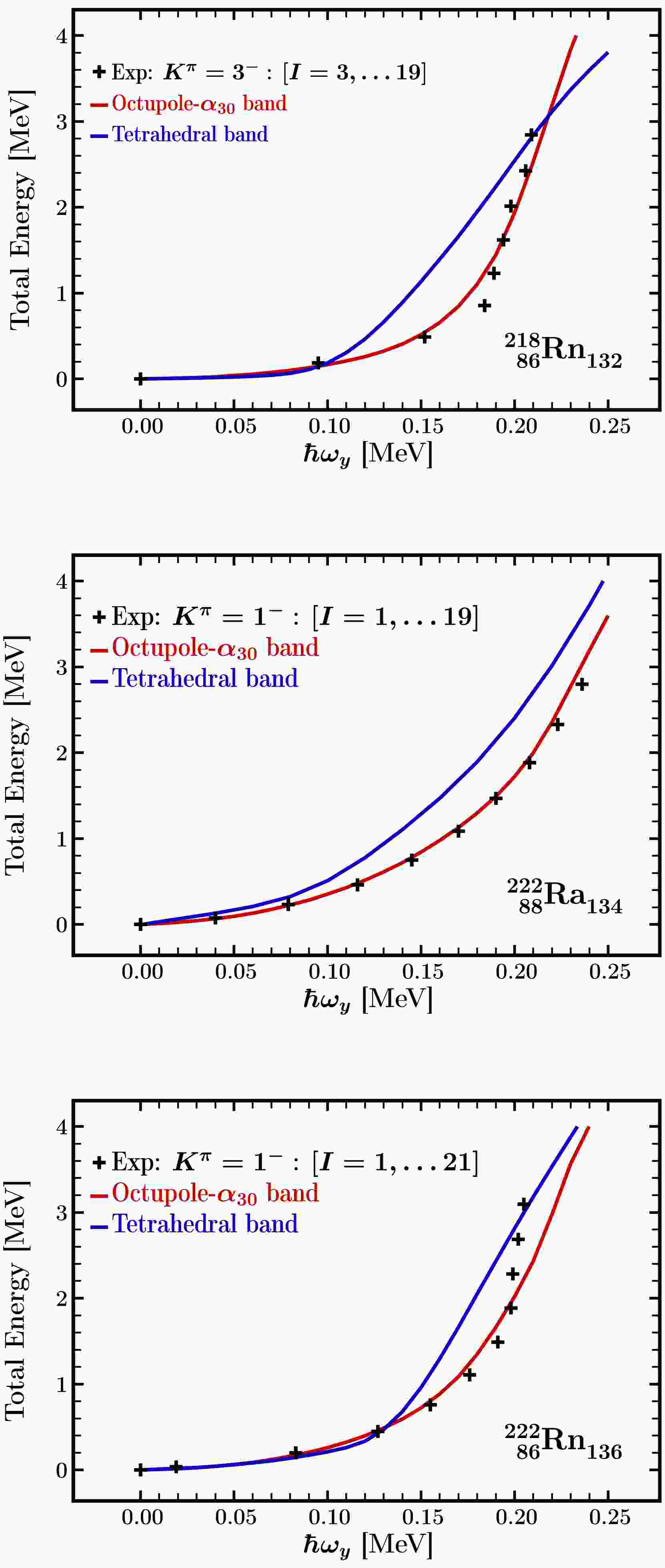
Cranking calculation results illustrated in Fig. 10 were performed for theoretically predicted equilibrium deformations with pear-shape and the tetrahedral deformations for selected illustrative cases: ₈₆²¹⁸Rn₁₃₂, ₈₈²²²Ra₁₃₄ and ₈₆²²²Rn₁₃₆ nuclei. The results for the nucleus ₈₆²¹⁸Rn₁₃₂ were calculated at the energy minima with $ \alpha_{20}=0.15,\, \alpha_{40}=-0.025 $ and $ \alpha_{30}=0.13 $ and another one at $ \alpha_{20}=0.0,\, \alpha_{40}=-0.025 $ with $ \alpha_{32}\approx0.13 $, cf. Fig. 7. Results for ₈₈²²²Ra₁₃₄, were obtained with $ \alpha_{20}=0.18,\, \alpha_{40}=0.075 $ and $ \alpha_{30}=0.15 $ for the pear-shape and $ \alpha_{20}=0.0, \,\alpha_{40}=0.075 $ with $ \alpha_{32}\approx 0.13 $ for the tetrahedral one, cf. Fig. 8. Similarly, for ₈₆²²²Rn₁₃₆ we found the shape coexisting minima at $ \alpha_{20}=0.12, \,\alpha_{40}=0.075 $, with $ \alpha_{30}=0.15 $ together with $ \alpha_{20}=0.0,\, \alpha_{40}=0.075 $ and $ \alpha_{32}\approx 0.13 $, cf. Fig. 9.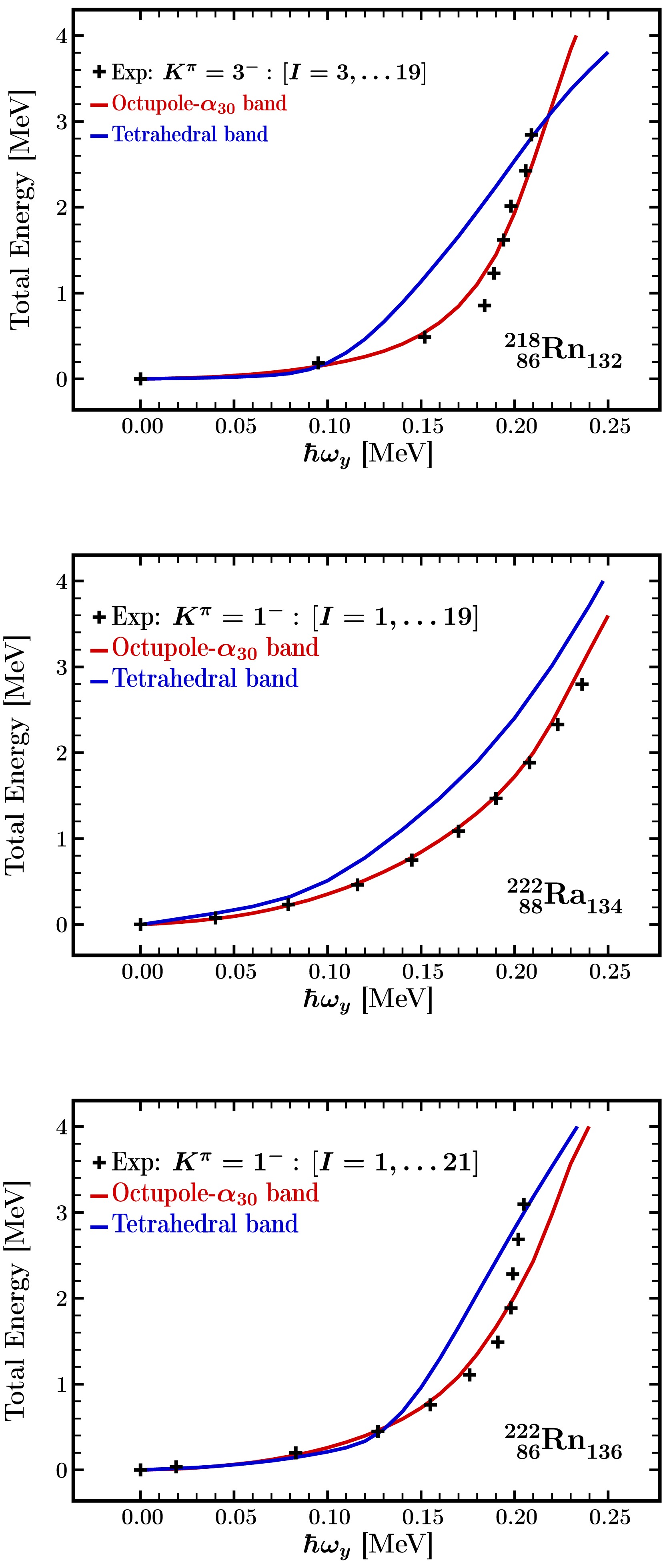

Figure 10.  Comparison of the pear-shape (red) and the tetrahedral (blue) energy vs. rotational frequency dependence with the experimental data (crosses) for ₈₆²¹⁸Rn₁₃₂, ₈₈²²²Ra₁₃₄ and ₈₆²²²Rn₁₃₆ nuclei. Experimental energies are taken from Ref. [46]. The experimental bands are normalized to 0 MeV at $\hbar\omega=0.0$. The Hamiltonian parameters employed for the pear-shape nuclear configurations, were used without modifications for the tetrahedral ones. The predictions for the tetrahedral symmetry cases were obtained at the equilibrium deformations discussed in the preceding sections.

Our HFBC modelling results are composed of two series of runs. Firstly, we calculate the total energies as functions of rotational frequency at pear-shape potential energy minima profiting from the fact that the corresponding octupole bands are known experimentally.

The resulting comparison allows verifying to what extent our Universal Woods-Saxon Hamiltonian combined with the associated HFBC pairing treatment can be considered realistic. This is an important element of the project since as the next step we wish to employ the same Hamiltonian in order to predict the analogous rotational behaviour but this time in the competing tetrahedral minima. In this way we will determine the moments of inertia with which we intend to address the modelling of the tetrahedral symmetry bands including the degeneracies predicted by the group theory – see below. These bands were never observed so far, so that predictions of this kind could be helpful in proposing a possible experiment theory collaboration.

Comparisons of the three octupole rotational bands for ²¹⁸Rn, ²²²Ra, and ²²²Rn are presented in separate diagrams in Figure 10. The results indicate that the calculated pear-shape bands reproduce closely experiment.

In the case of ²²²Rn nucleus, at the high spin limit, we note the presence of an up-bending, which is a reduced form of the well-known back-bending mechanism observed in many nuclei so far. Both the back-bending and up-bending are caused by the so-called quasiparticle alignment usually accompanying the Coriolis anti-pairing mechanism (lowering of the pairing correlations due to increasing rotation). We did not address this aspect since it depends on a specific quasiparticle structure which in turn depends on the single nucleon energy spectra, and such aspects depend strongly on nuclear shapes. Thus, these kinds of details deduced from the pear-shape configuration will perturb the image of predictions intended for tetrahedral bands in which case we focus on the turning tetrahedral ground-state (the lowest lying configuration unperturbed by any particle-hole (quasi-particle) excitations). Since the experimental information about tetrahedral symmetry does not exist at this time, we believe that the calculations addressing the simplest structures will be the most useful for experiment planning.

To advance the discussion we will remind the reader about the well-known results based on the group representation theory, which address the spin-parity rules for rotational bands generated by quantum objects with a given particular point group symmetry, here T_d. Recall that the well-known rotational sequences for the axially symmetric ellipsoidal objects e.g. quadrupole deformed even-even nucleus, here treated as a reference to compare with, satisfy:

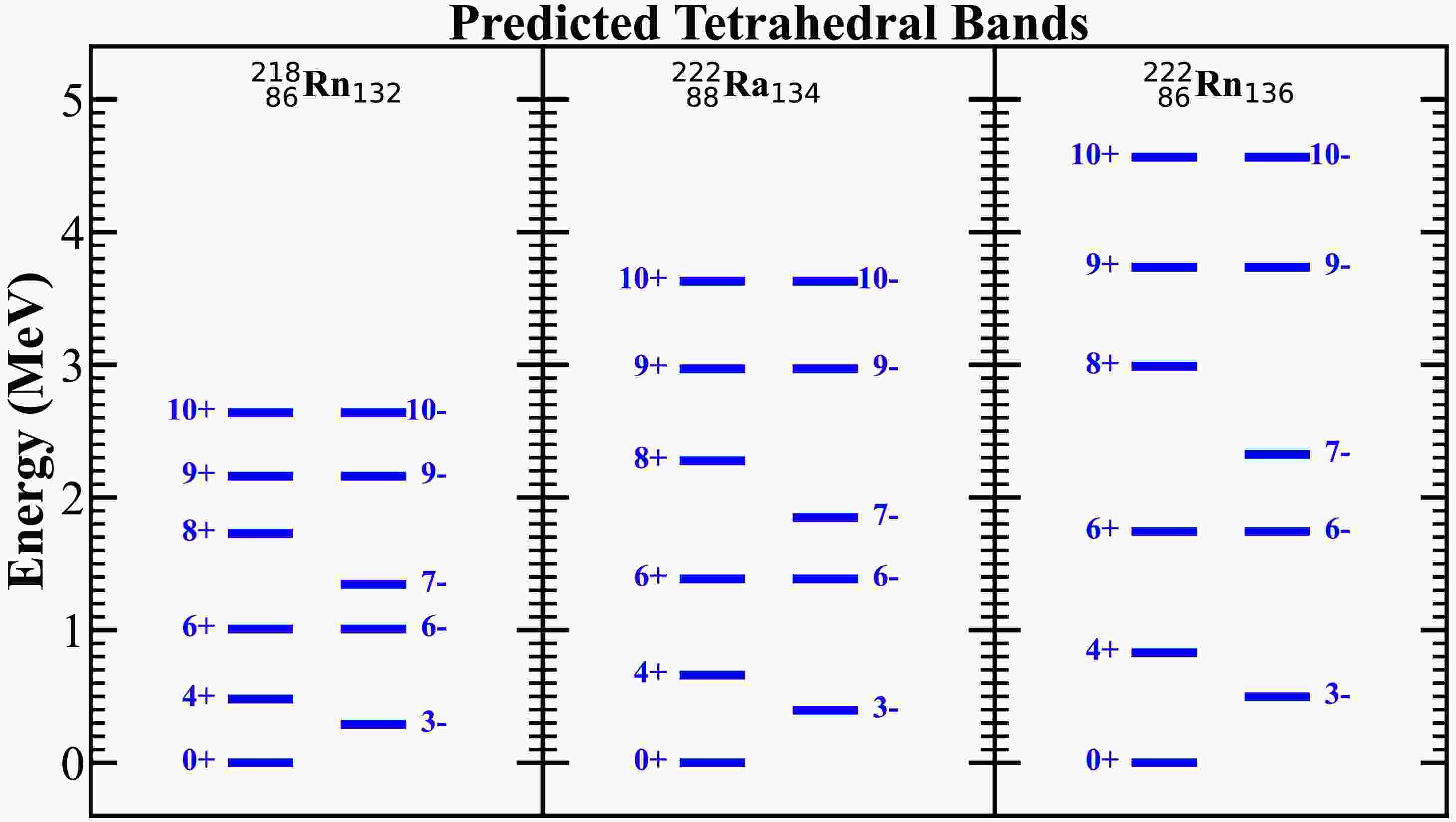
These bands are composed of states with even spins ($ \Delta I=2 $) and of positive parity only and are very different from the exotic symmetry bands, see below. In particular, following Ref. [16], we find that the lowest tetrahedral symmetry band in an even-even nucleus, built on the $ I^\pi=0^+ $ configuration (treated as the tetrahedral symmetry ground-state) is composed of states forming the so-called $ A_1 $-irreducible representation whose spins and parities are given by the sequence

Observe that the states with spins $ I=1,\,2 $, and 5 are totally missing, whereas the states with spin $ I=6, 9, 10, \ldots $ form degenerate parity doublets. Generally one can show that tetrahedral symmetry bands are formed of the $ E_I = a I(I+1) $ sequences with constant coefficient a related to the effective moment of inertia $ \mathcal{J}_T $, $ a =1 /{(2 \mathcal{J})_T} $, in which angular momentum I can be even or odd and both parities can be present.

The bands predicted with the help of the moments of inertia, $ \mathcal{J}_T $, deduced form the blue curves in Fig. 10, following Eq. (19), are presented in Fig. 11.

Figure 11.  Illustration of the tetrahedral $I^\pi=0^+$ bands predicted according to Eq. (19) for ₈₆²¹⁸Rn₁₃₂, ₈₈²²²Ra₁₃₄ and ₈₆²²²Rn₁₃₆ nuclei; we arbitrarily limit the sequences to $I\leq10$. Observe the presence of the degenerate parity doublets at spins $I=6,\,9$, and 10. Identification of such bands in nature will require specifically designated experiments like the one in Ref. [17].

By construction, these sequences follow prediction of Eq. (19), i.e., the tetrahedral symmetry bands involve the presence of both positive and negative parity states, the existence of degenerate states, as well as totally missing states, but they are related by the common moment of inertia.

These illustrations define criteria for experimental identification of tetrahedral symmetry. Let us mention in passing that in this article, we discuss merely one irreducible representation as a band sequence indicator, but the physics in question is much richer. According to group theory, there are 4 other irreducible representations generating different spin-parity sequences showing yet unexplored richness of the related phenomena.

Although figures 10 and 11 address information about rotation of the pear-, and the tetrahedral-shape nuclei, they address two different aspects. Figure 10 serves determining the effective moments of inertia, which allow learning about the slopes of the energy-vs.-cranking frequency curves. This information is based on the well-known HFBC cranking method, while Fig. 11 is constructed following the general group theory based theorem about band structures with degeneracies. Such a construction requires the knowledge of the moment of inertia. The only way to test the correctness of these predictions is to compare them with (future) experimental results.

Competition between pear- and tetrahedral-shape deformations in actinide nuclei, for isotones with $ N=132,134 $, and 136, is investigated using the macroscopic-microscopic method (MMM) of Strutinsky, supplemented with description of rotation in the presence of the paring interactions using yet another standard approach – the Hartree-Fock-Bogolyubov Cranking (HFBC) method. Both types of shape degrees of freedom exhibit significant deformation-stabilising effects deduced from the total energy minima within the deformation spaces composed of $ \{\alpha_{20}, \alpha_{30}, \alpha_{40}\} $ and $ \{\alpha_{20}, \alpha_{32}, \alpha_{40}\} $. The tetrahedral deformation effects generally lead to deeper energy minima in most nuclei with $ N=134 $ and $ N=136 $. This is due to the fact that many nucleonic levels in the presence of tetrahedral symmetry are four-fold degenerate (in contrast to double (Kramers) degeneracy of levels present in all other nuclear shapes). It follows that the average level spacing is higher leading to stronger shell-corrections. In nuclei ₈₆²¹⁸Rn₁₃₂, ₈₈²²²Ra₁₃₄, and ₈₆²²²Rn₁₃₆, specifically selected for the illustrations of the present project, somewhat exceptionally the effects of pear-shape octupole deformation are comparable to those of tetrahedral octupole deformation.

Potential energy surfaces projected onto the ($ \alpha_{20}, \alpha_{30} $), ($ \alpha_{20}, \alpha_{32} $), and ($ \alpha_{30}, \alpha_{32} $) planes for these nuclei demonstrate the coexistence of both octupole shapes. To encourage the possible experimental verifications of the new predictions presented in this article especially focussing on the exotic (T_d) symmetries, we have constructed the precise spin-parity sequences characteristic for the tetrahedral bands as predicted using well-known methods of the group representation theory.

To test the prediction capacity of our modelling methods the calculated properties of the pear-shape associated bands were compared with the experimental data available in the literature. This comparison can be considered satisfactory thus strengthening the conclusions encouraging collaboration between theory and experiment to develop the studies of the exotic symmetry properties in heavy nuclei.