-
Neutrinos, described by the Dirac equation and considered as
$S U(2)_{L}$ gauge invariant fields, were accepted in the standard model (SM) as massless left-handed Dirac fermions after the experimental measurement of neutrino helicity as –1 in 1958 [1]. However, the Solar Neutrino Experiment, Sudbury Neutrino Observatory, and Super-Kamioka Neutrino Detection Experiment have observed neutrino oscillation [2−5], indicating that neutrinos have an extremely small mass.If the antiparticle of a neutrino is itself, the solution to the Dirac equation can produce a Majorana particle. In the theory of Majorana [6], neutrinos can potentially possess mass. Some theories, such as the seesaw mechanism [7, 8], provide a natural framework for generating a small Majorana mass. If neutrinos are indeed Majorana fermions, this would lead to a violation of lepton number conservation by two units. Hence, the discovery of lepton number violating processes might be relevant to the properties of neutrinos. Furthermore, baryon number violation (BNV) is a key aspect of some grand unified theories (GUTs) and is essential for understanding the early Universe. The connection between BNV and lepton number violation (LNV) in various theories and models [9−12] suggests that the search for the LNV decay is one of the important approaches to establish a theory beyond the SM.
Various LNV signals have been sought after, and the search for neutrinoless double-beta (
$ 0\nu \beta \beta $ ) decay [13−16], which was first proposed by Furry [17] in 1939, is considered to be the most sensitive. Many collider experiments have searched for LNV decays, such as$ B^- $ decays by LHCb [18, 19],$ q\bar{q}\to l^{\pm}l'^{\pm}q'\bar{q} $ and$ q\gamma\to l^{\pm}l^{\pm}q''q'\bar{q} (l=e,\mu) $ channels by CMS [20],$ X_{c}^{+}\to h^{\pm}l^{\mp}l^{(\prime)+}\; (X_{c}=D,D_{s},\; \Lambda_{c}^{+}, h=\pi,K,p) $ decays by BaBar [21], decays with final states consisting of two charged leptons and two jets by ATLAS [22], decays of charm and charmed-strange mesons to final states$ h^{\pm}e^{\mp}e^{+}\; (h=\pi,K) $ by CLEO [23], 3-body di-muon decays of$ D^+,D_{s}^+ $ by FOCUS [24], and D meson LNV decays by BESIII [25, 26]. The E865 [27], NA62 [28], and BESIII [29] experiments also searched for LNV with non-first generation quark decays in K and ϕ meson decays, but only negative results have been reportedto date.The world's largest
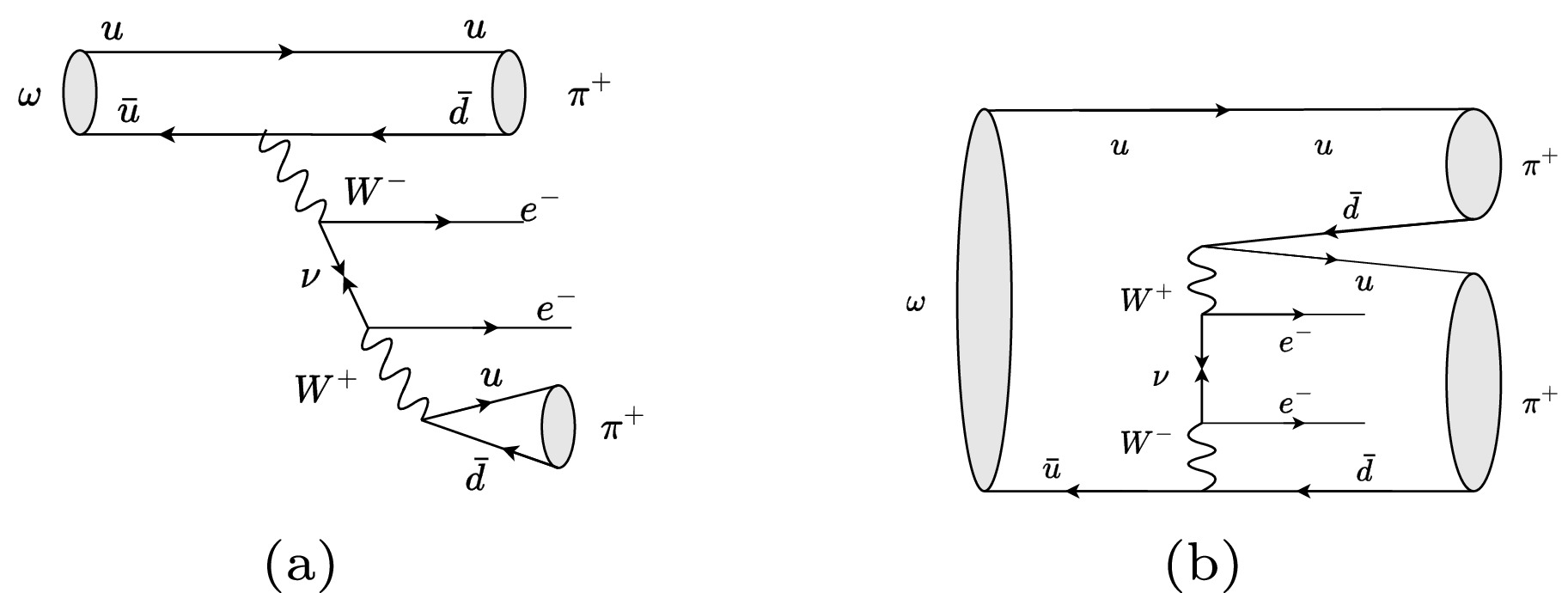
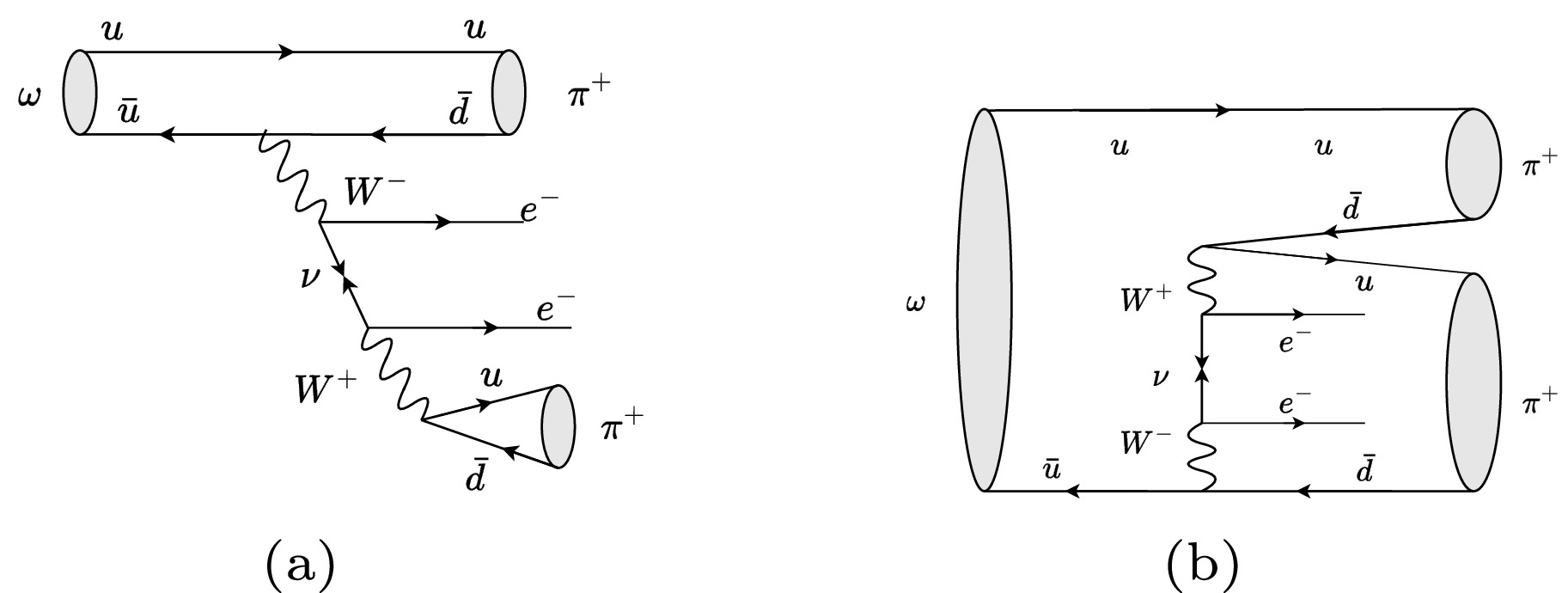
$ J/\psi $ dataset taken at BESIII offers a good opportunity to search for possible LNV decays of various light hadrons, e.g.,$ \omega\to \pi^+\pi^+l^{-}l^{-} $ . To avoid backgrounds from pion-muon misidentification and utilize a larger phase space, we focus on the$ \pi^+\pi^+e^-e^- $ final states in this work. Figure 1 shows two possible Feynman diagrams for$ \omega \to \pi^+ \pi^+ e^- e^- $ in the Majorana neutrino scenario, analogous to those in Ref. [30], with suppression owing to the large mass of the$ W^{\pm} $ bosons. The LNV decay of the ω meson in the process$ \omega\to \pi^+\pi^+e^-e^- $ has a unique phase space coverage compared with other measurements and low background contamination. Its discovery will indicate the existence of new physics.In this paper, we present the first search for the LNV decay
$ \omega \to \pi^+ \pi^+ e^- e^- $ via$ J/\psi\to\omega\eta $ decay based on$ (1.0087\pm 0.0044)\times 10^{10} $ $ J/\psi $ events [31] collected by the BESIII [32] detector at the Beijing Electron-Positron Collider II (BEPCII) [33]. The charge-conjugated decay mode$ \omega \to \pi^- \pi^- e^+ e^+ $ is included and implicitly assumed throughout. -
BESIII [32] is a symmetric cylindrical particle detector located around the interaction point of BEPCII [33], which is an
$ e^{+}e^{-} $ collider employing a double storage ring. The center-of-mass collision luminosity of BEPCII reached a peak of$ \rm 1.1\times 10^{33} \ cm^{-2}s^{-1} $ at$ 3.773\; \rm GeV $ . The BESIII detector consists of four detector sub-components [32]: a helium-based multilayer drift chamber (MDC), plastic scintillator time-of-flight counter (TOF), CsI(Tl) electromagnetic calorimeter (EMC), and muon counter, providing a coverage of 93% of the total solid angle. The superconducting solenoid supported by an octagonal flux-return yoke provides a magnetic field of 1.0 T for the MDC for most of the$ J/\psi $ data. The magnetic field was 0.9 T in 2012, which affects 11% of the total$ J/\psi $ data. The momentum resolution of the MDC for charged particles at 1 GeV/c is 0.5%, and the ionization energy loss (${\rm d}E/{\rm d}x$ ) resolution for electrons from Bhabha scattering is 6%. The time resolution of the TOF barrel region is 68 ps, and the time resolution of the end cap region was 110 ps. The end cap TOF system was upgraded in 2015 using multigap resistive plate chamber technology, providing a time resolution of 60 ps [34], which benefits 87% of the data used in this analysis. The EMC achieves an energy resolution of 2.5% at 1 GeV.Monte Carlo (MC) samples are used to analyze backgrounds and determine the detection efficiency. The detector response, geometric description [35, 36], and signal digitization models are simulated using the software GEANT4 [37]. For the inclusive MC sample, the known
$ J/\psi $ decay modes are generated using EVTGEN [38] with average branching fractions taken from the Particle Data Group (PDG) [39], whereas the remaining unknown decays modes from the charmonium states are generated using LUNDCHARM [40]. The$ J/\psi $ resonance is produced via$ e^+e^- $ annihilations using KKMC [41], which includes the effects of beam energy spread and initial state radiation. The final state radiation from charged final-state particles is incorporated using PHOTOS [42]. Signal MC events of$ J/\psi\to \omega\eta $ , with$ \eta \to \gamma\gamma $ and$ \omega \to \pi^{+}\pi^{-}\pi^{0} $ or$ \omega\to \pi^{+}\pi^{+} e^{-}e^{-} $ , are also generated. The$ J/\psi\to \omega\eta $ decays are modeled using a helicity amplitude model [38], and the$ \omega \to \pi^{+}\pi^{-}\pi^{0} $ decays are modeled using an ω Dalitz model [43]. Other decays are modeled using a phase space model. -
To avoid the large uncertainty (11.5%) [39] from the world average value of
$ {\cal{B}}(J/\psi\to\omega\eta) $ , we measure the branching fraction of the decay$ \omega\to\pi^+\pi^+e^-e^- $ relative to the reference decay$ \omega\to\pi^+\pi^-\pi^0 $ $ \begin{equation} \begin{split} {\cal{B}}(\omega\to\pi^+\pi^+e^-e^-)&={\cal{B}}(\omega\to\pi^+\pi^-\pi^{0})\\ \times{\cal{B}}(\pi^{0}\to\gamma\gamma)&\times\frac{N^{\rm sig}_{\pi^+\pi^+e^-e^-}/\epsilon_{\pi^+\pi^+e^-e^-}}{N^{\rm ref}_{\pi^+\pi^-\pi^0}/\epsilon_{\pi^+\pi^-\pi^0}}, \end{split} \end{equation} $

(1) where
$ {\cal{B}}(\omega\to\pi^{+}\pi^{-}\pi^{0}) $ and$ {\cal{B}}(\pi^{0}\to\gamma\gamma) $ are the branching fractions of$ \omega\to\pi^{+}\pi^{-}\pi^{0} $ and$ \pi^{0}\to\gamma\gamma $ , respectively.$ N^{\rm sig}_{\pi^+\pi^+e^-e^-} $ and$ N^{\rm ref}_{\pi^+\pi^-\pi^0} $ are the numbers of signal and reference channel events, respectively.$ \epsilon_{\pi^+\pi^+e^-e^-} $ and$ \epsilon_{\pi^+\pi^-\pi^0} $ are the detection efficiencies of signal and reference decays, respectively.All charged tracks are reconstructed in the detector acceptance region of the MDC. Their polar angles θ are required to satisfy
$ \left| \cos\theta \right| < 0.93 $ , where θ is measured relative to the z-axis, the symmetry axis of the MDC. The distances of closest approach to the interaction point of the charged tracks, along the z direction and in the plane perpendicular to the z-axis,$ \left|V_z\right| $ and$ \left|V_{xy}\right| $ , are required to be less than 10 cm and 1 cm, respectively.For charged particle identification (PID), we utilize a combination of
$ {\rm d}E/{\rm d}x $ in the MDC, the time of flight in the TOF, and the information of clusters in the EMC to calculate the confidence level (CL) for the pion, kaon, and electron hypotheses ($ {\rm CL}_{\pi} $ ,$ {\rm CL}_K $ ,$ {\rm CL}_e $ ). Pion candidates are required to satisfy$ {\rm CL}_{\pi}>0.001 $ and$ {\rm CL}_{\pi}>{\rm CL}_K $ , whereas electron candidates are required to satisfy$ {\rm CL}_e>0.001 $ and$ {\rm CL}_e/({\rm CL}_e+{\rm CL}_K+{\rm CL}_{\pi})>0.8 $ .Photons are reconstructed using isolated clusters in the EMC. The deposited energies in the barrel region (
$ \lvert \cos\theta \rvert<0.8 $ ) and endcap region ($ 0.86<\lvert \cos\theta \rvert<0.92 $ ) are required to be larger than$ 25\; \rm MeV $ and$ 50\; \rm MeV $ , respectively. To suppress electronic noise and unrelated encodings, the EMC timing of the photon candidate must be within 700 ns after the event start time. To eliminate photons emanating from charged tracks, the opening angle between the photon and the nearest charged track must be larger than 10 degrees. -
For the reference channel
$ J/\psi\to\omega\eta $ , with$ \eta\to\gamma\gamma $ ,$ \omega\to\pi^{+}\pi^{-}\pi^{0} $ , and$ \pi^{0}\to\gamma\gamma $ , at least four reconstructed photons and two reconstructed charged tracks with zero net charge are required. To select the photons of the$ \pi^0 $ and η candidates, we calculate the value of$\Delta m_{2\gamma}^{2} = \dfrac{(M_{\gamma\gamma}-M_{\pi^{0}})^{2}}{\sigma_{\pi^{0}}^{2}}+\dfrac{(M_{\gamma\gamma}-M_{\eta})^{2}}{\sigma_{\eta}^{2}}$ for all possible sets of four photons, where$ M_{\gamma \gamma} $ is the$ \gamma \gamma $ invariant mass,$ M_{\pi^0} $ and$ M_{\eta} $ are the known$ \pi^0 $ and η masses [39], and$ \sigma_{\pi^{0}} $ and$ \sigma_{\eta} $ are the corresponding mass resolutions determined from the MC simulation. The$ \pi^0 $ and η candidates with the smallest$ \Delta m_{2\gamma}^{2} $ are kept for further analysis.To reduce backgrounds and improve the mass resolution, we perform a five-constraint (5C) kinematic fit [44] to all the tracks enforcing energy and momentum conservation and constraining
$ M_{\gamma\gamma} $ to$ M_{\pi^0} $ .$ \chi^2_{\rm 5C} $ from the kinematic fit is required to be less than 20, which is determined by optimizing the figure of merit$\dfrac{S}{\sqrt{S+B}}$ , where S is the number of signal events, and B is the number of background events from the inclusive MC sample. The requirement vetoes 84% of background contributions and retains 67% of the reference channel.Backgrounds are investigated using the
$ 1.0011\times 10^{10} $ inclusive$ J/\psi $ MC events. Backgrounds with peaks in the invariant mass distributions of both$ \pi^+\pi^-\pi^0 $ ($ M_{3\pi} $ ) and$ M_{\gamma\gamma} $ are negligible. The remaining backgrounds include non-peaking backgrounds (BKGI) and those with peaks in either the$ M_{3\pi} $ or$ M_{\gamma\gamma} $ distributions (BKGII). The contributions of these backgrounds are determined by performing a two-dimensional (2D) fit to the invariant mass distributions of$ M_{3\pi} $ and$ M_{\gamma\gamma} $ .We use the sum of the two crystal ball (CB) functions (
$ F_{\rm sig}^{\omega} $ ) with the same σ and μ values but different tail parameters to describe the signal of$ M_{3\pi} $ and a signal MC shape convolved with a Gaussian function ($ F_{\rm sig}^{\eta} $ ) to describe$ M_{\gamma\gamma} $ . The non-peaking background contributions in the$ M_{3\pi} $ and$ M_{\gamma\gamma} $ distributions are described by a reversed ARGUS function [45] ($ F_{\rm bkg}^{\omega} $ and$ F_{\rm bkg}^{\eta} $ ). Consequently, the total signal shape is described by$ F_{\rm sig}^{\omega}\otimes F_{\rm sig}^{\eta} $ , backgrounds such as$ \pi^+\pi^-\pi^0\eta $ and$ \pi^0\pi^0\omega $ (BKGII) are described by$ F_{\rm bkg}^{\omega}\otimes F_{\rm sig}^{\eta} $ and$ F_{\rm bkg}^{\eta}\otimes F_{\rm sig}^{\omega} $ , and the BKGI is described by$ F_{\rm bkg}^{\omega}\otimes F_{\rm bkg}^{\eta} $ .The fit range is selected to be$ [0.70,\; 0.86] {\rm\; GeV/c^2} $ for$ M_{3\pi} $ , and$ [0.45,\; 0.65] {\rm\; GeV/c^2} $ for$ M_{\gamma\gamma} $ . We float the parameters of probability density functions (PDFs) during the fit, and the signal yield is determined to be$ N^{\rm ref}_{\pi^+\pi^-\pi^0}=941,336\pm 1,352 $ , where the uncertainty is statistical. The projections of the 2D fit to the$ M_{3\pi} $ and$ M_{\gamma\gamma} $ distributions are shown in Fig. 2. The detection efficiency of the reference channel is determined by the dedicated MC sample to be$ \epsilon_{\pi^+\pi^-\pi^0}=(12.80\pm0.03) $ %. By considering the signal yield$ N^{\rm ref}_{\pi^+\pi^-\pi^0} $ , detection efficiency$ \epsilon_{\pi^+\pi^-\pi^0} $ , and decay branching fractions of$ \omega\to \pi^+\pi^-\pi^0 $ and$ \pi^0\to\gamma\gamma $ from the PDG [39], we measure the branching fraction of$ J/\psi\to\omega\eta $ to be consistent with its world average value quoted from the PDG [39] within two standard deviation.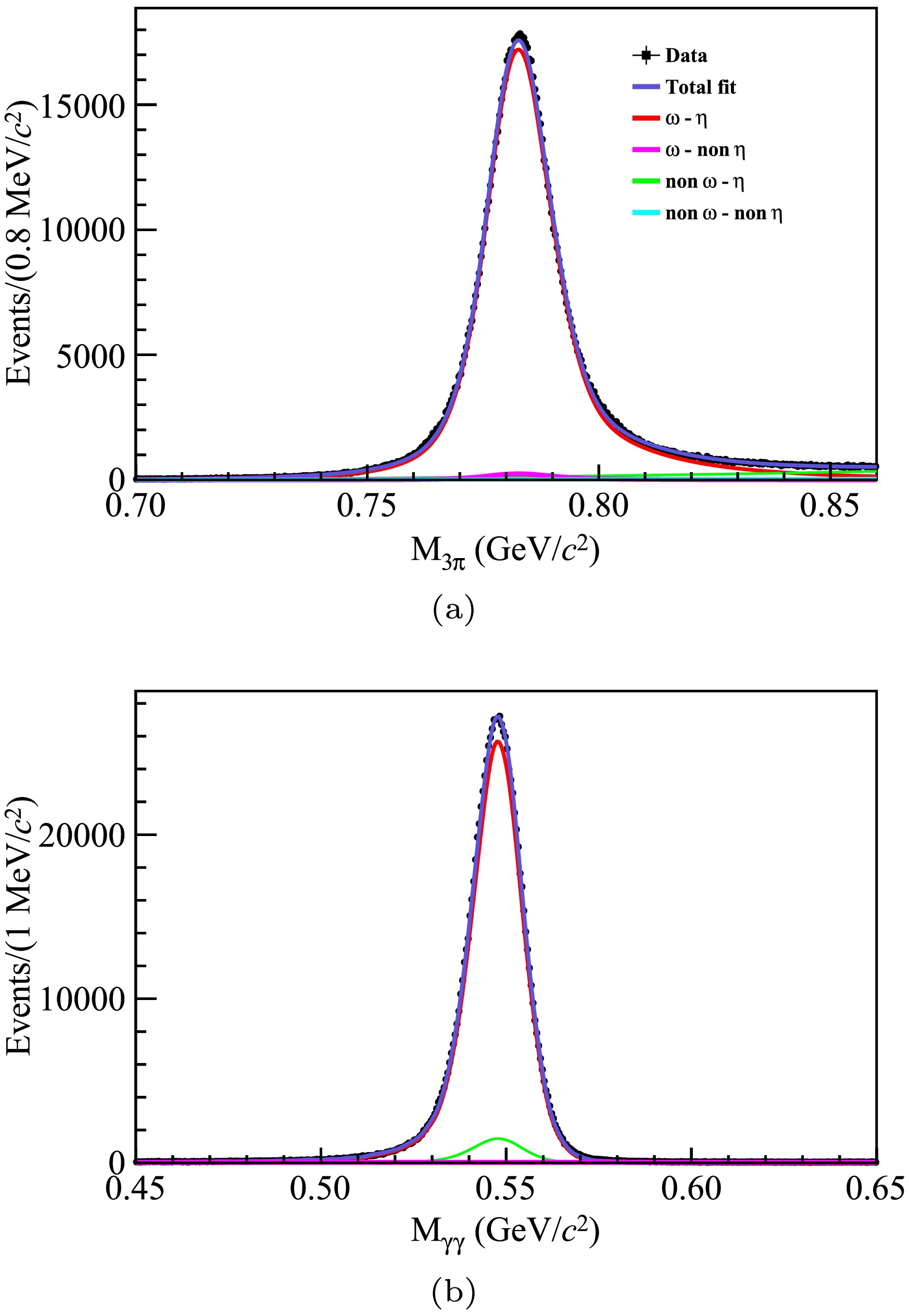
Figure 2. (color online) Projections of the 2D fit of the (a)
$ M_{3\pi} $ and (b)$ M_{\gamma\gamma} $ distributions, where the total PDF is shown by a blue solid curve. The signal PDF is shown by a red solid curve and labeled as$ \omega - \eta $ . The non-peaking background distribution is shown by a cyan solid curve and labeled as non-ω – non-η. The peaking background in$ M_{3\pi} $ is shown by a pink solid curve and labeled as ω – non-η. The peaking background in$ M_{\gamma\gamma} $ is shown by a green solid line and labeled as non-ω – η. -
For the signal channel
$ J/\psi\to\omega\eta $ with$ \eta\to\gamma\gamma $ and$ \omega\to\pi^+\pi^+e^-e^- $ , at least two reconstructed photons and four reconstructed charged tracks with zero net charge are required. The selection criteria of charged and neutral tracks that are consistent with those used in the reference channel.To reduce backgrounds and improve the mass resolution, we perform a four-constraint (4C) kinematic fit [44] by constraining the energy and momentum of the four charged tracks (
$ \pi^+\pi^+e^-e^- $ ) and two photons to those of the initial state. If more than two photons exist, we keep the candidate with the lowest$ \chi^{2}_{\rm 4C} $ for further analysis. To further suppress backgrounds,$ \chi^2_{\rm 4C} $ must be less than 10, which is determined by the Punzi figure-of-merit method [46], with the figure of merit$\dfrac{\epsilon}{1.5+\sqrt{B}}$ , where$ \epsilon $ is the detection efficiency, and B is the number of background events. This selection criterion can remove 99% of background events while retaining 56% of the signal events. To further suppress misidentification from processes with four charged tracks, we re-calculate the$ \chi^{2} $ of the 4C kinematic fit with different mass assignments ($ \chi^{2}_{\rm re} $ ):$ \pi^+\pi^-\pi^+\pi^-\gamma\gamma $ ,$ K^+K^-K^+K^-\gamma\gamma $ ,$ \pi^+\pi^-K^+K^-\gamma\gamma $ , and$ \pi^+\pi^-p \bar{p}\gamma\gamma $ . If any of the$ \chi^{2}_{\rm re} $ s is less than$ \chi^{2}_{\rm 4C} $ , the event is considered as background and rejected.The signal region is determined by fitting the
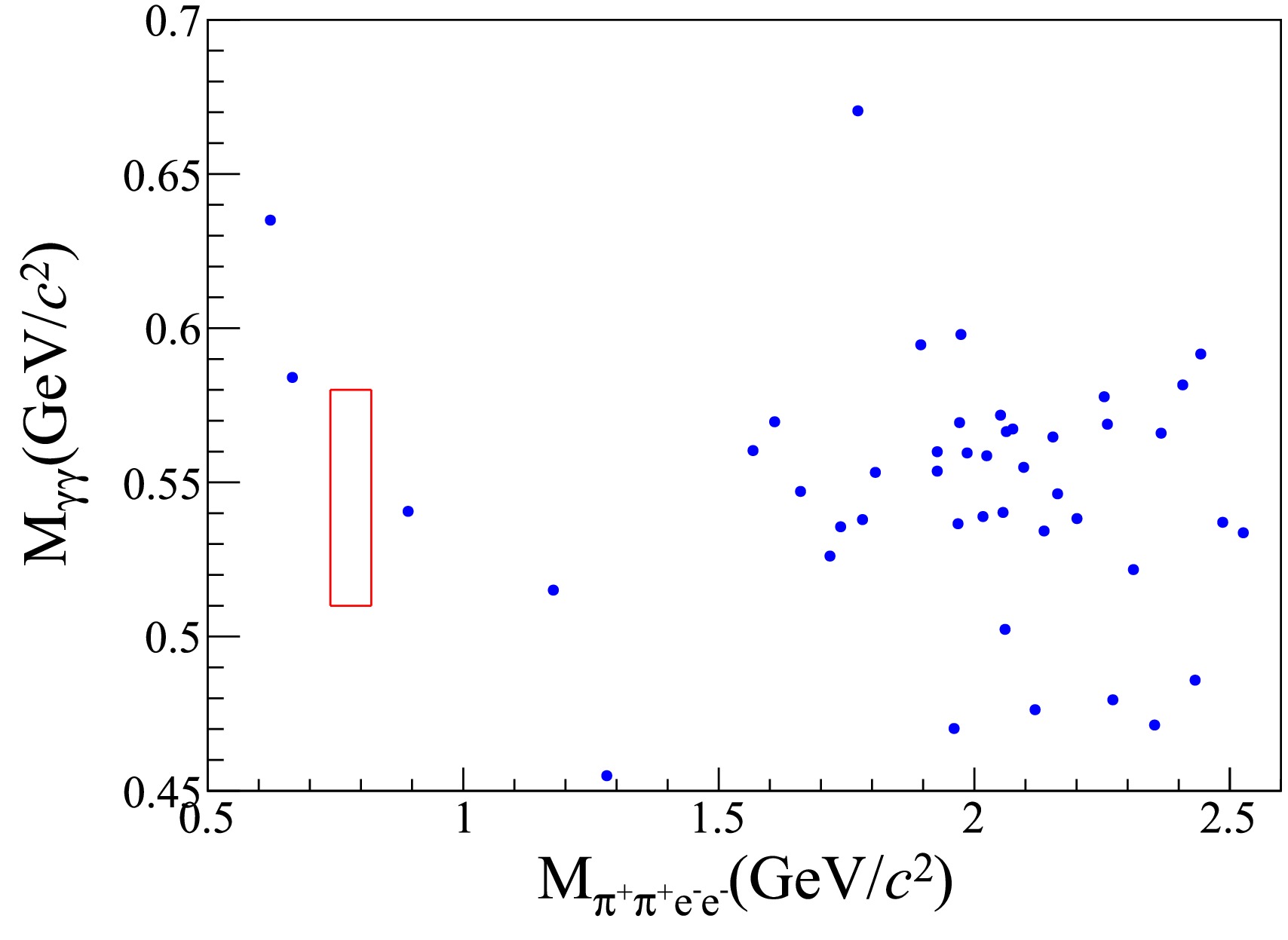
$ M_{\pi^+\pi^+e^-e^-} $ and$ M_{\gamma\gamma} $ distributions of signal MC samples, where the signal shape is modeled by a double Gaussian function and the background shape by a second-order polynomial function. The fitted regions are determined as$ [0.72,0.84]\; {\rm GeV}/c^2 $ for$ M_{\pi^+\pi^+e^-e^-} $ and$ [0.51,0.59]\; {\rm GeV}/c^2 $ for$ M_{\gamma\gamma} $ . These intervals correspond to$ \pm5\sigma $ ranges centered on the composite mean position of the double Gaussian function, where σ is the effective resolution parameter derived from the fit. The detection efficiency is$ \epsilon_{\pi^+\pi^+e^-e^-}=(11.52\pm0.03) $ % based on the simulated signal MC samples.Figure 3 shows the 2D scatter plot of
$ M_{\gamma\gamma} $ versus$ M_{\pi^+\pi^+e^-e^-} $ for the candidate events from$ J/\psi $ data. In the scatter plot, no candidates are found inside the defined signal region. Thus, the number of observed events is$ N^{\rm obs}_{\pi^+\pi^+e^-e^-}=0 $ . To study the possible backgrounds, we analyze$ 1.0011\times 10^{10} $ inclusive$ J/\psi $ MC events. We find that no event is located near the signal region, and the number of background events is determined to be$ N^{\rm bkg}_{\pi^+\pi^+e^-e^-}=0 $ . -
The systematic uncertainties for the signal and reference decays include the uncertainties in the MDC tracking, PID,
$ \pi^0 $ reconstruction, kinematic fit and$ \chi^{2} $ requirement, signal window, 2D fit, MC modeling,$ N^{\rm ref}_{\pi^+\pi^-\pi^0} $ determination, and input branching fractions. The systematic uncertainties of the η reconstruction with$ {\cal{B}}(J/\psi\to\omega\eta) $ and$ {\cal{B}}(\eta\to\gamma\gamma) $ cancel when calculating the relative branching fraction ratio.The systematic uncertainties of MDC tracking and PID for charged pions and electrons are 1.0% [47, 48] per charged track. Because the reference channel has two charged tracks and the LNV channel has four, the systematic uncertainties are assigned to be 2.0% and 4.0%, respectively. The individual systematic uncertainty for both MDC tracking and PID of charged tracks is calculated to be
$ \sqrt{(2.0{\text{%}})^2+(4.0{\text{%}})^2}=4.5 $ %.The systematic uncertainty of
$ \pi^0 $ reconstruction is 1.0% [49]. The systematic uncertainty in the kinematic fit and$ \chi^{2} $ requirement of the signal (reference) decay is estimated with the control sample$ J/\psi\rightarrow \pi^{+}\pi^{-}\pi^{+}\pi^{-}\eta, \eta\rightarrow \gamma\gamma $ ($ J/\psi\rightarrow \omega\pi^{0}, \omega\rightarrow \pi^{+}\pi^{-}\pi^{0} $ ). The relative difference of the selection efficiencies between data and MC simulation is taken as the uncertainty. The systematic uncertainties due to the kinematic fit are 2.7% for the LNV channel and 0.1% for the reference channel. The uncertainty of the kinematic fit is calculated to be 2.7%. The systematic uncertainty of signal window is studied by changing the ranges to$ \pm 4.9\sigma $ ,$ \pm 5.1\sigma $ , etc. The maximum relative difference 0.2% is taken as the systematic uncertainty.The uncertainties from the background (signal) shapes in the 2D fit are estimated by changing the reverse ARGUS function (sum of two CB function) to a second-order polynomial function (sum of a CB function and the signal MC shape obtained from the MC simulation). The maximum differences of 3.3% and 1.1% between the signal yields are taken as the uncertainties due to background and signal shapes, respectively. Therefore, the total uncertainty for 2D fit is calculated to be 3.5%.
The systematic uncertainty of the MC modeling is studied by generating events with a Majorana intermediate state in two different modes: one with two Majorana neutrinos (
$ \omega\rightarrow \nu_{M}\nu_{M}, \nu_{M}\rightarrow \pi^{+}e^{-} $ ), and the other with one Majorana neutrino ($ \omega\rightarrow \nu_{M}\pi^{+}e^{-}, \nu_{M}\rightarrow \pi^{+}e^{-} $ ), where the mass of the Majorana neutrino can range from the$ \pi e $ mass threshold to the largest phase space of ω decay. The largest difference between the average detection efficiencies in the nominal analysis and in these two modes, 0.3%, is taken as the systematic uncertainty.The statistical uncertainty in
$ N^{\rm ref}_{\pi^+\pi^-\pi^0} $ determination is calculated to be 0.2%. The uncertainty due to MC statistics is given by$ \sqrt{\dfrac{1-\epsilon}{\epsilon N_{\rm total}^{\rm MC}}} $ , where$ \epsilon $ is the detection efficiency of$ \omega\rightarrow \pi^+\pi^+e^-e^- $ , and$ N_{\rm total}^{\rm MC} $ is the total number of produced signal MC events. It is determined to be 0.3%. The uncertainty of the input branching fraction$ {\cal{B}}(\omega \to \pi^{+}\pi^{-}\pi^{0}, \pi^{0}\to \gamma \gamma) $ is 0.8% [39].Table 1 summarizes the systematic uncertainties. The total systematic uncertainty (
$ \Delta_{\rm sys} $ ) is calculated by adding the individual contributions in quadrature.Source Uncertainty (%) MDC tracking 4.5 PID 4.5 $ \pi^0 $ reconstruction

1.0 Kinematic fit and $ \chi^{2} $ requirement

2.7 Signal window 0.2 2D fit 3.5 MC modeling 0.3 $ N^{\rm ref}_{\pi^+\pi^-\pi^0} \;{\rm{ determination}}$ 

0.2 MC statistics 0.3 $ {\cal{B}}(\omega \to \pi^{+}\pi^{-}\pi^{0}, \pi^{0}\to \gamma \gamma) $ 

0.8 Total 7.9 Table 1. Relative systematic uncertainties.
-
Because we do not observe any signal or background events, we set an upper limit on the signal yield at the 90% CL using Feldman-Cousins intervals [50]. Both the number of observed events and background yield are assumed to follow Poisson distributions, and the upper limit on the signal yield is calculated to be
$ 2.44 $ at the 90% CL. Beause the Feldman-Cousins method does not consider the systematic uncertainty ($ \Delta_{\text{sys}}=7.9 $ %), the upper limit is shifted up to$ 2.44/(1-\Delta_{\text{sys}})=2.65 $ . Thus, the upper limit on the branching fraction of$ \omega\to \pi^+\pi^+e^-e^- $ at the$ 90 $ % CL is calculated using Eq. (1) to be$ \begin{equation*} {\cal{B}}(\omega\to \pi^+\pi^+e^-e^-)<2.8 \times 10^{-6}. \end{equation*} $

-
In this paper, we search for the LNV decay
$ \omega \to \pi^{+} \pi^{+} e^{-} e^{-} $ for the first time by analyzing$ 1.0087\times 10^{10} $ $ J/\psi $ events collected using the BESIII detector. No signal is observed, and the upper limit on its decay branching fraction is set to be$ {\cal{B}}(\omega \to \pi^+\pi^+e^-e^-+c.c.)< 2.8\times10^{-6} $ at the 90% CL. This is the first experimental constraint on the LNV decay of the ω meson. Our result enriches the searches for$ 0\nu \beta \beta $ decay in collider experiments, which are complimentary to the specially designed$ 0\nu \beta \beta $ searching experiments. The upper limit may be further improved with other advanced methodologies, such as the partial reconstruction strategy, which is based on inclusive ω signal finding; it introduces a higher background but can also yield higher statistics. In the future, the constraint can be further improved with an expected increase of over 100 times$ J/\psi $ events from the super τ-charm facility [51]. -
The BESIII Collaboration thanks the staff of BEPCII and the IHEP computing center for their strong support.
Search for the lepton number violation decay ω→π+π+e−e−+c.c.
- Received Date: 2025-04-30
- Available Online: 2025-10-15
Abstract: Lepton number violation decay






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: