Characterizing the CJPL’s site-specific neutrino floor as the neutrino fog boundary

The search for dark matter (DM) constitutes one of the most significant endeavors in modern physics [1]. Among the various DM candidates, Weakly Interacting Massive Particles (WIMPs) have been a leading hypothesis [2, 3]. Direct detection experiments aim to observe the scattering of WIMPs off atomic nuclei in a detector. However, these experiments face a fundamental challenge in the form of the neutrino floor.

The neutrino floor, originally defined as the theoretical sensitivity limit for WIMPs in direct DM detection experiments, has long been regarded as an insurmountable barrier owing to irreducible neutrino-induced backgrounds [4]. However, recent advances have revealed that there is no strict theoretical ''floor'' for DM direct searches but a dynamic transition zone — termed the neutrino fog — where statistical and systematic uncertainties obscure DM signals [5]. This means that the neutrino fog delineates regions of parameter space where WIMP-nucleus interactions become indistinguishable from coherent elastic neutrino-nucleus scattering (CEνNS) events, primarily sourced from solar (e.g., $ ^8 {\rm{B}} $), atmospheric, and diffuse supernova neutrino fluxes. The new definition of neutrino fog emphasizes its statistical nature. The transition from Poisson-statistic-dominated to systematic uncertainty-limited regimes is quantified by the gradient index n, where $ n = 2 $ marks the boundary of the fog (the neutrino floor). For $ n>2 $, sensitivity improvements require an exponential increase in exposure, making conventional detection strategies ineffective.

In fact, after numerous years of fruitless searches for DM particles, researchers have first detected a genuine signal emanating from a stream of neutrinos produced by nuclear reactions in the Sun. Notably, in 2024, the PandaX [6] and XENON [7] collaborations reported that their detectors had likely begun detecting this elusive neutrino fog ($ ^8 {\rm{B}}$ solar neutrinos). Recently, several theoretical studies on this subject have also been conducted, (see Refs. [8−14]), significantly advancing our understanding of the implications of this irreducible neutrino background for DM searches.

Critically, the morphology of the neutrino fog exhibits strong geographic dependence, as local neutrino flux variations—modulated by geomagnetic latitude, cosmic-ray modulation, and detector depth — directly influence background kinematics and systematics.

China Jinping Underground Laboratory (CJPL), with its unique geographic profile ($ 18.06^\circ {\rm{N}}$ geomagnetic latitude, 2400 m rock overburden), constitutes an exceptional case for studying the neutrino fog. Among all existing direct detection experiments, CJPL exhibits the largest crustal geoneutrino flux [15] and smallest reactor neutrino background [16]. More crucially, the atmospheric neutrino flux at CJPL is notably lower [17], which has a significant impact on the neutrino floor in the high-mass region of DM. Considering these distinctive site-specific attributes, it is imperative to conduct localized fog calculations.

This study delves into two primary questions. First, we examine how the unique neutrino flux characteristics at CJPL alter the landscape of the neutrino fog and floor compared to established benchmarks, such as xenon-based detectors located at Laboratori Nazionali del Gran Sasso (LNGS). Second, we calculate the prospective sensitivities and estimated the necessary exposure to reach the neutrino floor in the PandaX experiment conducted at CJPL.

The structure of this paper is as follows: In Sec. II, we delve into the neutrino fluxes at CJPL. Sec. III is dedicated to deriving the neutrino floor and fog specific to CJPL. In Sec. IV, we present the calculation of the sensitivity of the PandaX-xT experiment, aiming to determine the required exposure to reach the new neutrino floor in the high DM mass region. Finally, in Sec. V, we present our conclusions.

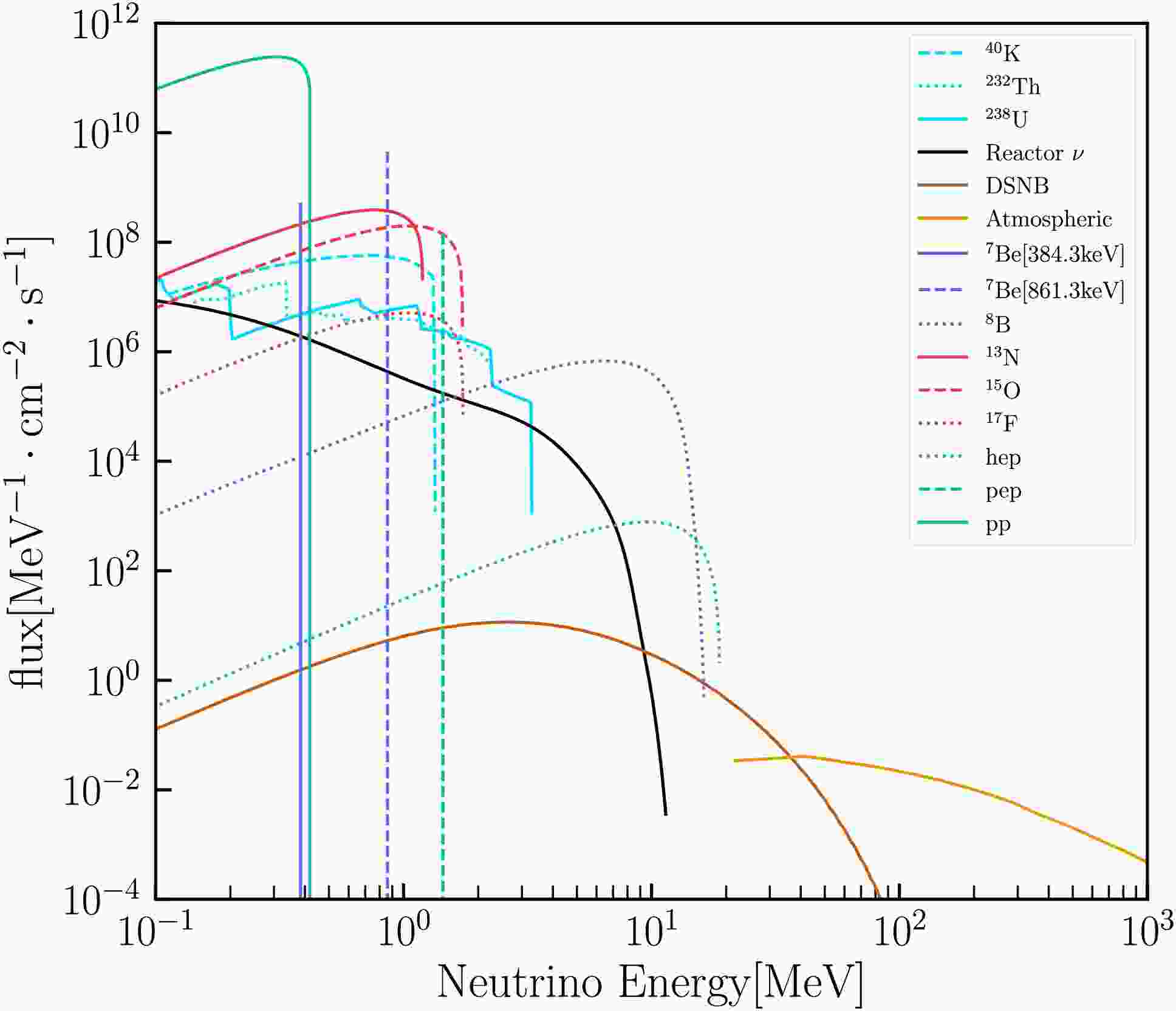
The neutrino fluxes, especially those of atmospheric neutrinos, geoneutrinos, and reactor neutrinos, are highly dependent on geographic location. CJPL is uniquely positioned with several unparalleled features that distinguish it from other sites. It has the thickest overburden, providing exceptional shielding against cosmic rays, and has the lowest reactor neutrino flux owing to its remote location from nuclear power plants [18]. Additionally, CJPL has the largest crustal geoneutrino flux, which is highly advantageous for geoneutrino studies. The laboratory also benefits from the lowest environmental radioactivity, ensuring a cleaner experimental environment, and has the longest solar neutrino path through the Earth, which is particularly beneficial for solar neutrino research. Therefore, the specific geographic and environmental features of CJPL contribute to its specialized neutrino background. Next, we elaborate on the pertinent constituents of the neutrino fluxes at CJPL, which are summarized in Fig. 1.

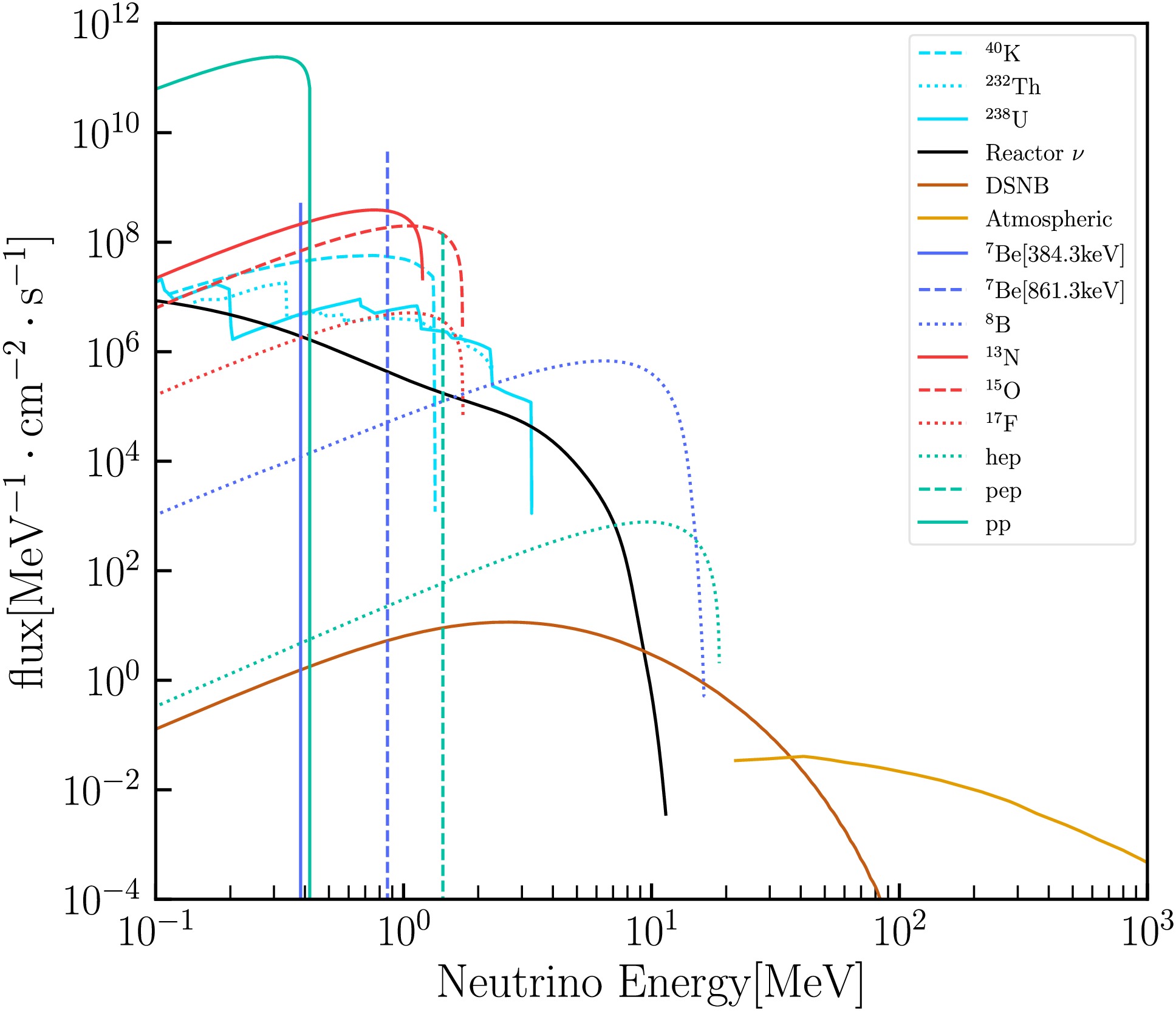
Figure 1.  (color online) Neutrino fluxes at CJPL. Fluxes from different neutrino sources are represented by different colors: geoneutrinos [22] are represented by light blue lines, neutrinos from reactors [16] are represented by black lines, solar neutrinos are represented by blue, red, and green lines corresponding to different reaction chains [20], DSNB neutrinos [5] are represented by brown lines, and atmospheric neutrinos [17] are represented in orange lines.

1. Solar neutrino

The Sun produces neutrinos through two primary nuclear reaction chains: the proton-proton (pp) chain and carbon-nitrogen-oxygen (CNO) cycle. Solar neutrinos dominate the flux at energies $ E_\nu \leq 18.77 $ MeV [19]. These neutrinos constitute the principal source of CEνNS events in DM detectors and constrain sensitivity to DM candidates with masses near $ m_{\rm{DM}} \sim 10 $ GeV. Recently, the PandaX [6] and XENON [7] collaborations independently reported tentative observations of CEvNS signals from solar neutrinos.

In this study, we combined the GS98 high-metallicity Standard Solar Model with the Barcelona 2016 calculations [20]. For all components, we maintained the published normalization uncertainties, with the exception of $ ^{8}\text{B} $, for which a 2% uncertainty was assigned based on comprehensive fits of global neutrino data [21]. Subsequent to $ ^{8}\text{B} $, the $ ^{7}\text{Be} $ electron-capture neutrino lines — which are pivotal for enhancing sensitivity to sub-GeV DM — were assigned a normalization uncertainty of 6%.

2. Geoneutrinos

Geoneutrinos are antielectron neutrinos released during the decay processes of radioactive isotopes such as uranium ($ ^{238} {\rm{U}}$), thorium ($ ^{232}{\rm{Th}} $), and potassium ($ ^{40} {\rm{K}}$). Their flux directly reflects the radioactive heat production rate and thermal evolution history of the Earth's interior. The location-dependent geoneutrino flux is particularly sensitive to the amount of crust beneath the laboratory site, which contains the largest portion of heat producing elements. CJPL is situated near the Himalayan Mountains in China, where the crust is the thickest. The uranium and thorium abundances in the local crustal composition significantly influence the spatial distribution of the geoneutrino flux in this region. This has been previously identified as a favorable location for geoneutrino detection [15].

For concreteness, we used the geoneutrino flux reported in Ref. [22], with corresponding uncertainties for each component.

3. Reactor neutrinos

This is another source of antineutrinos, which influences the background at slightly higher masses. Jinping is far from all nuclear power plants [18] in operation and under construction.

The reactor neutrino background at Jinping is the lowest among all the direct detection experiments. In this study, we used the total differential reactor neutrino flux at Jinping reported in Ref. [16].

4. Diffuse supernova neutrino background (DSNB)

DSNB is a relic flux of neutrinos and antineutrinos resulting from core-collapse supernovae throughout cosmic history and emerges as a critical astrophysical background for DM direct detection. For DM experiments, the DSNB-induced CEνNS creates an irreducible “neutrino floor” near $m_\chi \sim 20 \, \text{GeV}$ [5]. A 50% uncertainty on the all-flavor flux accounts for cosmic variance in supernova rates, progenitor mass-dependent spectral ambiguities, and neutrino oscillation effects [23]. We used the same flux as that reported in Ref. [5].

5. Atmospheric neutrinos

Atmospheric neutrinos exhibit significant geographic dependence due to variations in cosmic ray flux, Earth's geometry, and magnetic field effects. At high latitudes (e.g., polar regions), weaker geomagnetic shielding results in higher cosmic ray flux and neutrino production, while low latitudes (e.g., equatorial regions) experience reduced flux due to stronger magnetic deflection.

CJPL is situated in a geomagnetic low-latitude region (with a geomagnetic latitude of 18.06°N), where the atmospheric neutrino flux is predominantly driven by higher-energy cosmic rays. The flux at CJPL is suppressed compared to LNGS, primarily owing to the relatively high rigidity cutoff energy.

The atmospheric flux used in this study is the average of the solar minimum and maximum fluxes calculated in [17], with a recommended 25% theoretical uncertainty applied.

In this section, we initially revisit the newly introduced definition of the neutrino floor, as presented in Ref. [5]. Subsequently, we derive our novel neutrino floor specifically for CJPL.

We focus on the standard spin-independent (SI) interactions between DM and nucleons and consider only elastic scattering. The scattering rate can be expressed as [24, 25]

which is the scattering rate summed over all target nuclides; $ {\sigma }_{n} $ is the WIMP-nucleon cross-section. In this study, we set $ \rho = 0.3\; \text{GeV/cm}^{3} $ for the local DM density; $ {\mu }_{n} $ is the reduced mass of the WIMP-nucleon system; $ {\zeta }_{T} $ is the mass fraction of the isotope T in the detector; Z is the atomic number of the target nucleus; A is the atomic mass number of the target nucleus; and $ {f}_{n}/{f}_{p} $ is the ratio between the neutron and proton couplings to the WIMP. Following the standard assumption, we set $ {f}_{p} = {f}_{n} $ to ensure that the DM–proton and DM–neutron couplings are isosinglet; $ {F}_{SI}^{2}\left({E}_{R}\right) $ is assumed to be the Helm form factor [26]; and ${\eta}\left({v}_{\min}\left({E}_{R}\right)\right)\equiv\int_{v\geq v_{\min}} {\rm d}\vec{v} f(\vec{v})/v$ is the integral of the DM velocity distribution.

For the sake of completeness, the rate for CEνNS can be found in Appendix A. Additionally, the case for the spin-dependent (SD) interaction is analyzed in Appendix B.

The neutrino fog refers to the obscured region in direct DM detection experiments where the neutrino background and DM signal energy spectra overlap significantly, rendering them indistinguishable. This phenomenon leads to a stagnation in experimental sensitivity. The underlying mechanism arises when the DM signal strength falls below the combined effects of systematic uncertainties and statistical fluctuations of the neutrino background, thereby masking the signal entirely. The neutrino floor, defined as the dynamic boundary of the neutrino fog, represents the critical hypersurface in parameter space where a DM signal transitions from a detectable regime to an indistinguishable one. This boundary is not static but evolves with experimental statistics, systematic errors, and target material properties.

The statistical inference is based on a binned likelihood function, incorporating Poissonian probabilities and Gaussian distributions to model the background interference:

where the Poissonian term describes the probability in each energy bin for the observed event count $ N_{i}^{\text{obs}} $, given the expected signal events $ N_{i}^{\chi} $ and the total expected neutrino events $ N_{i}^{\nu} $ summed over neutrino fluxes $ \Phi_{j} $. The Gaussian term introduces neutrino flux normalization parameters, which are considered as the nuisance parameters, with standard deviations $ \delta\Phi $ quantifying systematic uncertainties in flux calculations. The DM mass and cross section are parameters.

Hypothesis testing compares the null background-only model ($ {\cal{M}}_{\sigma = 0} $) with the signal-plus-background model ($ {\cal{M}} $). A discovery threshold of $ q_{0} > 9 $ (corresponding to $ 3\sigma $ significance) defines the exclusion limit [5], where the test statistic is defined as

We maximize the likelihood function at $ {\hat{\hat{\bf{\Phi}}}} $ for the background-only model and at $ ( \hat{\sigma},{\hat{\bf{\Phi}}}) $ for the signal-plus-background model. In this context, the Chernoff's theorem [27] applies, and under the null hypothesis where $ {\cal{M}} $ is true, the test statistic $ {q}_{0} $ asymptotically follows a mixture distribution of $ \dfrac{1}{2}{\chi }_{1}^{2} + \dfrac{1}{2}\delta\left( 0\right) $ [28]. The statistical significance of the DM signal above background corresponds to $ \sqrt{q_0} $.

The sensitivity evolution as a function of N (the number of observed background events) exhibits four distinct regimes [5]: (a) background independent regime ($ N \ll1 $), in which the sensitivity scales as $ \sigma \propto N^{-1} $ and the neutrino background is small; (b) Poisson statistic dominated regime ($ N\gg1 $), in which the sensitivity follows $ \sigma \propto N^{-1/2} $, governed by statistical fluctuations; (c) systematics uncertainty dominated regime ($ N \geq 1/\delta\Phi^{2} $), in which the sensitivity stagnates as $ \sigma\propto \sqrt{{(1 + N\delta\Phi^{2})}/{N}} $ and systematic errors dominate [4]; (d) when exposures are very high and observed event counts large, the experiment can effectively measure its own background, reinstating the Poissonian regime.

These features result in the mathematical characterization of the neutrino fog, known as the ''opacity'', which is defined by the gradient index:

For $ n = 2 $ (Poisson statistic dominated regime), the sensitivity adheres to $ \sigma \propto N^{-1/2} $. When $ n > 2 $ (systematics uncertainty dominated regime), the experiment enters the saturation phase of the neutrino fog, where sensitivity plateaus.

By mapping the $ n = 2 $ contour, the neutrino floor is identified as the critical hypersurface in the DM mass $ m_{\chi} $ and cross-section σ parameter space where sensitivity degradation becomes irreversible.

Building upon the public code [29] developed by O'Hare, this study pioneers the integration of neutrino flux data from CJPL to derive geographically characterized neutrino floor curves, as shown in Fig. 2. The comparative analysis reveals key findings through the following comparisons.

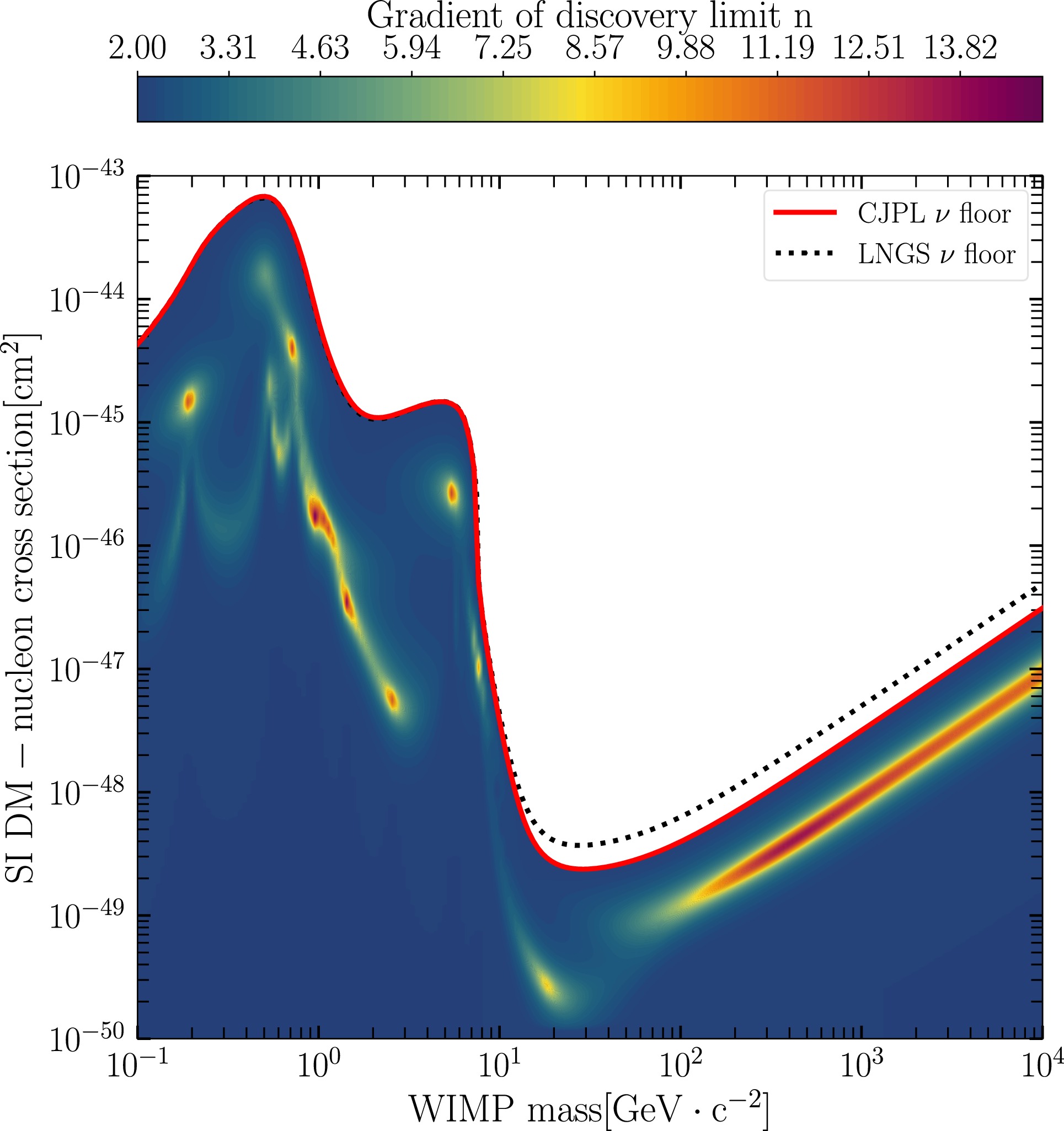
Figure 2.  (color online) Neutrino floor and fog for CJPL. The red dashed curve represents the neutrino floor as the boundary of the neutrino fog for $ n=2$ obtained in this study; the black dotted line is the neutrino floor at LNGS derived in Ref. [5]. The color scale represents the value of n.

Regarding location effects, in the high-mass region (WIMP mass $ >10 $ GeV), the neutrino floor of CJPL exhibits a $ 30 $% lower background limit compared to LNGS, marked by the red solid curve. For LNGS, the neutrino fluxes and uncertainties used are identical to those in the calculation reported in Ref. [5]. This advantage stems from the unique geological profile of CJPL. Its atmospheric neutrino flux is reduced by approximately ($ 20\%-40\% $) relative to LNGS, attributable to its lower geomagnetic latitude. Consequently, high-energy nuclear recoil backgrounds — dominant in this mass range — are suppressed. Future research should aim to optimize the treatment of atmospheric neutrinos to improve the accuracy of neutrino background limits.

Below 10 GeV, the neutrino floors at CJPL and LNGS display a remarkable degree of consistency. This convergence is primarily attributed to the dominance of solar neutrinos, which contribute approximately 90% of the overall neutrino flux, with minimal variation observed across different geographic locations. Although the crustal geoneutrino flux at CJPL is notably higher than at LNGS — a disparity linked to regional variations in uranium and thorium concentrations — the impact of geoneutrinos in the low-mass region is negligible.

To visualize the neutrino fog, a color-mapping technique across the DM parameter space based on the gradient index n was implemented. This methodology is demonstrated in Fig. 2, where the color scale above the plot explicitly indicates the n-value for each point within the fog.

The opacity of the neutrino fog quantifies the resistance to experimental progress through parameter space, revealing regions where overlapping neutrino backgrounds obscure DM discovery. This metric highlights zones where spectral degeneracies between DM and neutrino-induced recoils are most pronounced. Darker regions in Fig. 2 correspond to $ n > 2 $, signifying enhanced spectral degeneracy where DM and neutrino event rates become nearly indistinguishable.

While subtle differences between DM and neutrino signals persist in most scenarios, these distinctions can be statistically resolved in high-exposure regimes. Notably, once the accumulated event count N surpasses a critical threshold, the sensitivity scaling reverts to $ n = 2 $ for extremely low cross-sections, reflecting a transition back to Poisson-statistics-dominated sensitivity.

A comparison reveals distinct characteristics between the neutrino fog at CJPL and LNGS. These differences stem from site-specific variations in neutrino flux components and their associated systematic uncertainties. Such geographic disparities underscore the necessity of site-specific fog modeling to optimize future DM detection strategies.

Given the establishment of the new neutrino floor at CJPL, it is crucial to explore the potential detection prospects of the PandaX experiment. We estimate the direct detection capabilities of the PandaX-xT experiment at CJPL [30], focusing on a liquid xenon detector with a mass of 40 tonnes. Our calculation assumes an exposure duration spanning several years, as detailed in [30].

To accurately reproduce the event rate measured by the experiments, we need to account for the detection efficiency. The total number of events is given by

Here, $ \epsilon \left ( {E_R} \right ) $ is the detection efficiency. We used the efficiency curve of the current PandaX-4T detector [31], which covers the energy range from approximately 4 to 110 keV. To ensure completeness of all detectable events, we set the upper limit of the energy window to a sufficiently large value, covering the maximum energy range the experiment can detect.

Based on the aforementioned statistical methods, the likelihood function is modified as follows to perform the detection simulation:

where $ {n}_{i}^{\rm{bkg}} $ represents the background events in the PandaX detector, following the results reported in [30]. Additionally, we assumed that background events are uniformly distributed within the detector. It should be noted that we updated the neutrino nuclear recoil background event rate using our calculated results from the earlier part of this study.

Applying the likelihood ratio test (Eq. (3)), the projected 90% confidence level exclusion sensitivity reach of the PandaX-xT experiment is shown in Fig. 3. For benchmark validation, we initially computed the sensitivity curve at 200 tonne-years (ty) exposure (black dot-dashed line), obtaining good consistency with the baseline simulations of the PandaX Collaboration [30]. This agreement confirms the validity of our treatment. The orange and pink dot-dashed curves represent the sensitivities for 500 ty and 1000 ty exposures, respectively. We also include the neutrino floor and fog in the plot. When the exclusion sensitivity reaches the neutrino floor, further improvement would require a significant increase in experimental exposure.

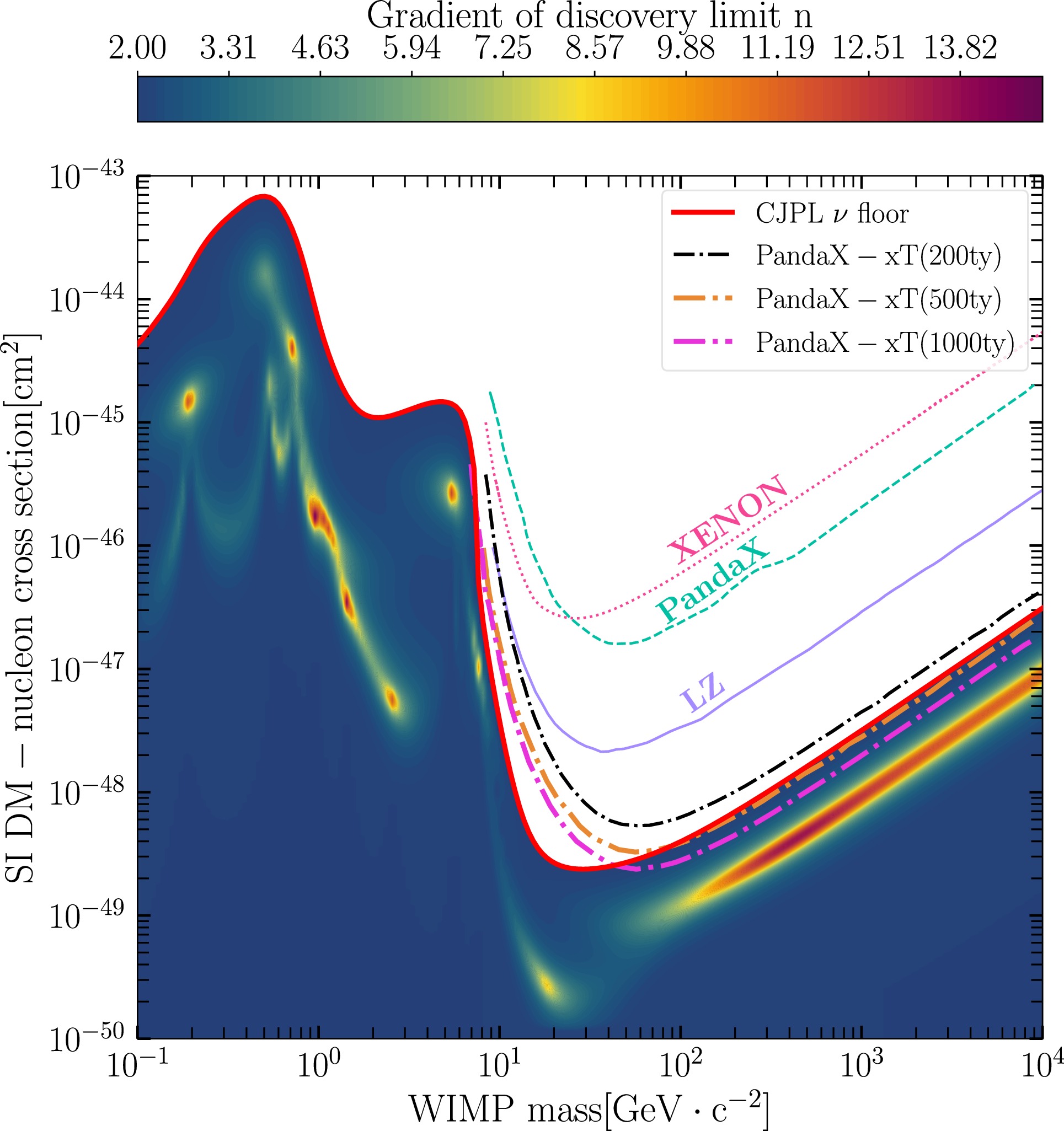
Figure 3.  (color online) Sensitivity and neutrino background. The latest excluded limits are represented by a purple solid line for LZ [32], green dashed line for PandaX4T [33], and magenta dotted line for XENONnT [34]. The prospective sensitivities are also shown in this figure: the black dash-dotted line represents the prospect from PandaX-xT with a 200 ty exposure, which is consistent with Ref. [30]; the orange dash dotted and pink solid lines correspond to the sensitivities for 500 ty and 1000 ty exposures at the PandaX-xT experiment, respectively.

For WIMP mass smaller than 10 GeV/$c^{2}$, the sensitivity barely enhances with more exposure. This is owing to the much lower detection efficiency in this region. In future detections, the PandaX-xT experiment would achieve a much better sensitivity in this low mass region by lowering the detection threshold [6]. Specially, it is expected to measure the solar $^{8}{\rm{B}}$ solar neutrinos with a precision higher than 10% [30].

Our central finding reveals that penetrating the neutrino floor requires accumulated exposures exceeding 500 ty for WIMP masses above 70 GeV/$c^{2}$ (see the orange dot-dashed curve). At this threshold, the sensitivity of PandaX-xT approaches cross-sections of $\sigma_{n} \sim 3\times 10^{-49}$ cm² at a WIMP mass of 70 GeV/$c^{2}$, marking the onset of neutrino floor dominance. We further present the results for a 1000 ty exposure. In the “saturation region” of the neutrino fog, systematic uncertainties—such as those related to neutrino flux calculations—become the dominant factors. Consequently, experimental sensitivity cannot be effectively improved by increasing exposure.

This study presents the first site-specific characterization of the neutrino floor and fog at CJPL, driven by its unique geographic and environmental conditions. By integrating the suppressed atmospheric neutrino flux of CJPL ($ \sim30 $% lower than LNGS) and the enhanced geoneutrino contributions into a gradient-based statistical framework, we redefined the neutrino fog boundary as a dynamic transition zone governed by Poisson-statistical and systematic uncertainties. These features reduce the neutrino floor by nearly 30% for high-mass WIMPs ($ m_ {\rm{DM}} > 10 \, \text{GeV}$), enhancing sensitivity through reduced neutrino backgrounds. Below $10 \; \text{GeV}$, solar neutrino dominance homogenizes sensitivity limits across sites. The sensitivity estimation of the PandaX-xT experiment shows that a 500 ty exposure reaches cross-sections as low as $\sigma_{n} \sim 3\times 10^{-49} \, \text{cm}^2$ at a WIMP mass of 70 GeV$ /c^2 $, intersecting the neutrino floor of CJPL. Critical challenges persist, particularly systematic uncertainties in neutrino flux normalization, underscoring the need for refined models and multi-detector synergies.

Neutrinos can scatter elastically off nuclei, producing recoils with spectra very similar to those from DM-nucleus scattering. To date, measurements of CEνNS have been performed by the COHERENT collaboration [35, 36] and the CONUS+ experiment [37], and it is also well-understood in the context of the Standard Model [38, 39]. Similar to the WIMP event rate calculation, the neutrino event rate is computed by convolving the differential CEνNS cross section with the neutrino flux,

where we cut off the integral at the minimum neutrino energy that can cause a recoil with $ E_r $: $ E_{\nu}^{\min } = \sqrt{m_{N} E_{r} / 2} $. The differential neutrino-nucleus cross section as a function of the recoil and neutrino energies was reported in Refs. [4, 40−42],

where $ m_N $ is the nucleus mass, $ G_f $ is the Fermi coupling constant, and $ Q_{\omega} = N - (1-4\sin^2\theta_{\omega})Z $ is the weak nuclear hypercharge, where N is the number of neutrons, Z is the number of protons, and $ \theta_{\omega} $ is the weak mixing angle, being $ \sin^2{\theta_W} = 0.2387 $. The form factors account for the loss of coherence at higher momentum transfer and are assumed to be the same as those for WIMP-nucleus SI scattering, for which we used the standard Helm form factor [43].

In general, the cross section for SD interaction between DM and nucleus can be expressed as [24, 44]

where J is the total nuclear angular momentum, $ G_{F} $ is the Fermi coupling constant, $ \mu_{N} $ is the reduced mass of the DM-nucleus system, $ \left \langle S_{p} \right \rangle $ and $ \left \langle S_{n} \right \rangle $ are the expectation values of the total spin operators for proton and neutron [45], and $ a_{p,n} $ are the couplings to proton and neutron. In typical experimental setups, the scattering cross-section of the entire nucleus with DM is considered to involve only protons or neutrons within the nucleus by setting $ a_{p} $ or $ a_{n} $ to zero, respectively. Then, we have

where $ \sigma _{p} $ and $ \sigma _{n} $are scattering cross sections of protons or neutrons with DM.

Employing the same procedure used in the SI case above, we derived the neutrino fog and sensitivities of the PandaX-xT experiment for DM-proton/neutron SD interactions; the results are presented in Fig. B1. Additionally, the latest excluded limits are represented by a purple solid line for LZ [32], green dashed line for PandaX-4T [33], gray solid line for PICO-60 [46], and pink dotted line for XENONnT [47].

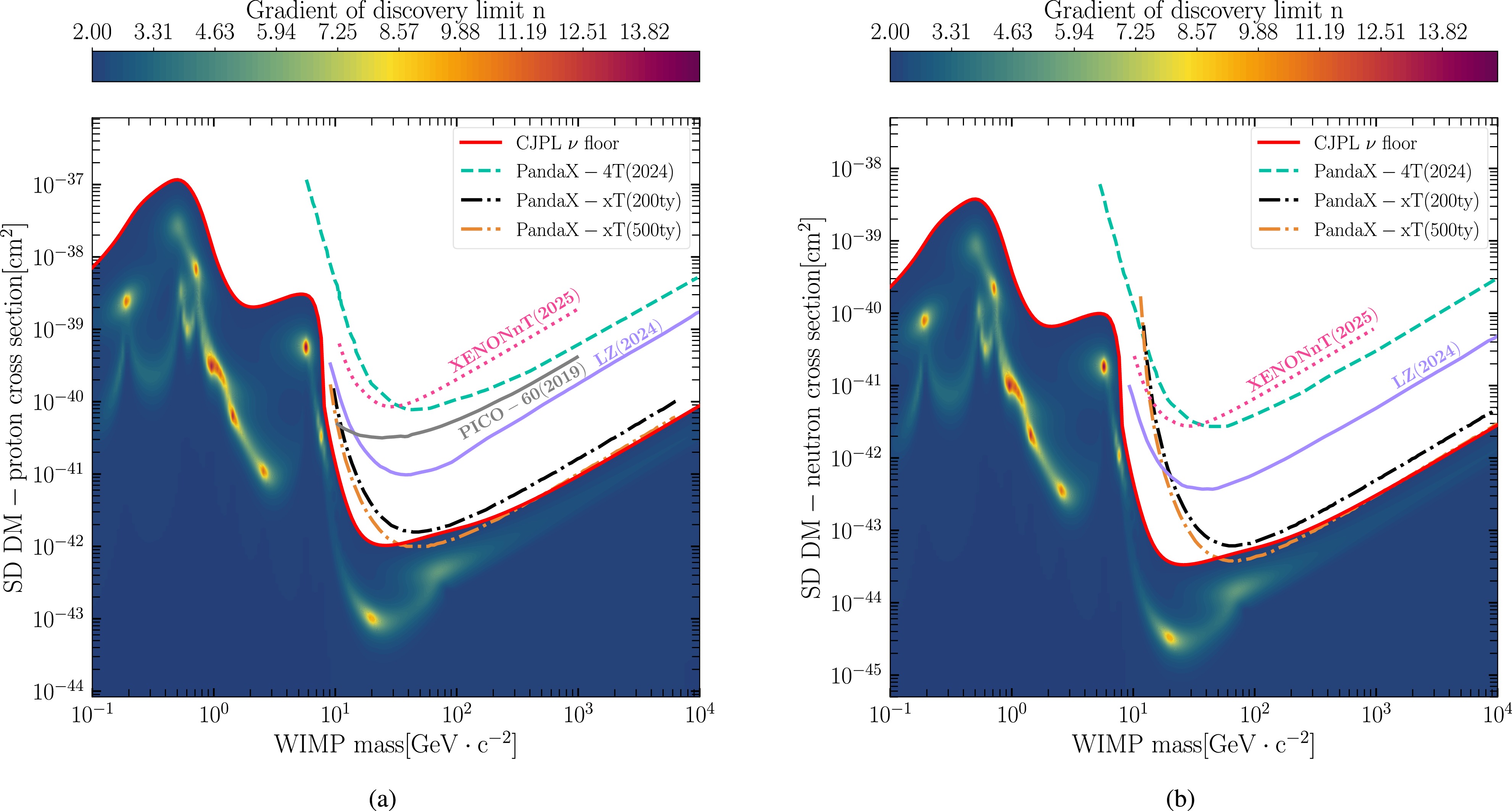
Figure B1.  (color online) Neutrino fog and exclusion sensitivities for SD DM-nucleon interactions at CJPL: (a) DM-proton interaction; (b) DM-neutron interaction. The latest exclusion limits are shown in each panel: purple solid line for LZ [32], green dashed line for PandaX-4T [33], gray solid line for PICO-60 [46], and pink dotted line for XENONnT [47]. Additionally, the black (orange) dot-dashed lines in both (a) and (b) represent the sensitivity curves of PandaX-xT for a 200(500) ty exposure.

Our results reveal that the PandaX-xT detector with a 500 ty exposure will encounter neutrino fog for both the DM-proton and DM-neutron SD scattering, represented by the orange dot-dashed lines in Fig. B1.