-
Recently, researchers have exhibited increasing interest in unraveling the secrets of the universe and its components. Stars occupy a central role in astronomy, serving as critical contributors to galaxy formation. Their development and evolution, along with that of planets, rely heavily on the process of nuclear fusion. A star's stability is maintained by the balance between the gravitational forces pulling inward and the outward pressure produced by fusion. When its nuclear fuel is exhausted, the star collapses and may transform into a dense object, such as a white dwarf, neutron star, or black hole, depending on its original mass. Compact stars differ fundamentally from ordinary stars, as they have large masses and small radii. These unique properties have captivated the interest of numerous researchers. In 1972, Ruderman [1] pioneered the study of anisotropy in the internal geometry of compact stars, establishing a foundation for future research in the field. This anisotropic behavior can result from various factors. Herrera et al. [2] provided a comprehensive review of the local anisotropic nature of self-gravitating systems [3], whereas Kalam et al. [4] investigated the properties of neutron stars with anisotropic structures influenced by dark energy. The authors of [5] introduced a novel solution describing the equilibrium state of compact stars, offering critical insights into their internal dynamics. Key astrophysical phenomena associated with quark and neutron stars, including their behavior under extreme conditions, are discussed in [6, 7]. Additionally, Rahaman et al. [8] utilized the MIT bag model to explore strange stars, focusing on their mass and redshift characteristics.
Furthermore, Einstein's theory of General Relativity (GR) has been highly successful in describing a wide range of gravitational phenomena. However, it encounters significant challenges when confronted with cosmological observations, particularly those related to the phenomena of dark energy and dark matter. Two primary approaches are often pursued to address these challenges. The first approach seeks to modify the matter sector of the theory by introducing additional dark energy components to the universe's energy composition. The second approach focuses on extending the geometric framework of GR, particularly through modifications to the Einstein-Hilbert action. Among the various geometric extensions of GR,
$ f(R) $ gravity, which is based on modifications to the curvature of spacetime, has attracted the most interest. Alternatively, the geometric structure of GR can be altered through the inclusion of torsion or nonmetricity. Theories that incorporate torsion and remain equivalent to GR are referred to as the Teleparallel Equivalent of GR (TEGR), whereas those that involve nonmetricity are known as the Symmetric Teleparallel Equivalent of GR (STEGR). Research focusing on compact stars in the context of$ f(R) $ gravity is extensively discussed in the literature [9−19], providing important insights into their structure, evolution, and the effects of modified gravity on astrophysical phenomena. Additionally, recent research indicates that the modified gravity theory has the potential to explain a range of cosmic and astrophysical phenomena [20−29].Moreover, metric-affine gravity introduces a geometric framework based on an affine connection, which is essential for defining covariant derivatives. Weyl [30] advanced this concept by integrating electromagnetism and gravitation into a generalized geometry characterized by the vanishing covariant divergence of the metric tensor. This advancement led to the introduction of nonmetricity, a novel geometric quantity. However, Einstein criticized Weyl's theory, arguing that it was inconsistent with experimental observations [31]. Subsequently, Cartan [32] extended GR by formulating the Einstein-Cartan theory, which incorporates torsion as an additional geometric feature. Weitzenböck later proposed a distinct mathematical framework known as Weitzenböck space [33], which is characterized by zero curvature. In this formulation, nonmetric variables are expressed through the nonmetricity scalar Q, which defines symmetric teleparallel gravity. In the context of STEGR, gravity is characterized by nonmetricity instead of curvature and torsion. An extension of STEGR is
$ f(Q) $ gravity, which was developed by Jimenez et al. [34]. For an in-depth examination of the geometrical representations of this gravity, refer to [35], where the authors describe them as the geometrical trinity of gravity. This theoretical framework has been rigorously evaluated using a diverse array of observational data, such as the Cosmic Microwave Background (CMB), Supernovae Type Ia (SNIa), Baryonic Acoustic Oscillations (BAO), Redshift Space Distortion (RSD), and growth rate data [36−42]. The outcomes suggest that$ f(Q) $ gravity can pose a significant challenge to the standard$ \Lambda\rm CDM $ model. Additionally,$ f(Q) $ gravity effectively navigates the constraints imposed by Big Bang Nucleosynthesis (BBN) [43]. In [44], the authors conducted an observational test for$ f(Q) $ gravity with weak gravitational lensing. They considered$ f(Q) $ gravity to be a realistic theory. Furthermore, the solar system has been tested in this gravity framework [45].The exploration of compact stars through the framework of
$ f(Q) $ gravity is underpinned by its potential to elucidate the gravitational dynamics of dense and exotic astrophysical systems. This theoretical construct presents a viable alternative that may more effectively address the extreme physical conditions prevalent in the interiors of dense stellar environments. By transitioning from the curvature-centric paradigms of GR to focus on the nonmetricity of spacetime,$ f(Q) $ gravity introduces a robust framework for investigating the gravitational interactions of compact stellar objects. This departure from established gravitational theories enables the exploration of novel astrophysical phenomena and provides a platform for rigorously testing the limits of contemporary gravitational paradigms, thereby facilitating the potential discovery of new physics at the forefront of astrophysical research. Thus, the impetus for employing$ f(Q) $ gravity in the study of compact stars lies in its capacity to yield transformative insights and enhance our understanding of the fundamental principles of gravity and the intricate physics of dense matter in the cosmos. Numerous interesting aspects of compact stars have been explored in the context of symmetric teleparallel gravity and discussed in literature [46−55].Dark matter is a theoretical type of substance that is believed to account for approximately 27% of the mass-energy content of the universe. While various candidates, such as axions and Weakly Interacting Massive Particles (WIMPs), have been proposed within the frameworks of supersymmetric string theory and particle physics, no direct detection of dark matter has occurred thus far. However, recent experimental observations indicate that several astronomical phenomena, including the creation of galactic rotation curves [56], the dynamics of galaxy clusters [57], and the anisotropies in the cosmic microwave background identified by the PLANCK satellite [58], may be influenced by dark matter. This makes dark matter one of the most significant unresolved questions in contemporary science. It is considered one of the largest scientific mysteries of the modern era, with numerous hypotheses regarding its identity owing to the limited knowledge of its microphysical properties.
The quantum statistics of particles with integer spin, known as bosons, have been a central focus of research in both theoretical and experimental physics since Bose's seminal work [59] and Einstein's subsequent generalization [60, 61]. One of the defining features of bosonic systems is their transition to a condensed phase, termed a Bose-Einstein condensate, in which all particles occupy the same quantum ground state. Physically, such systems exhibit a pronounced peak in both coordinate and momentum space distributions against a broader background, reflecting mutual correlations and overlapping wavelengths. The Bose-Einstein condensation process is crucial for understanding many phenomena in condensed matter physics; for instance, superfluidity in low-temperature liquids such as
$ {}^{3}He $ can be explained by this mechanism [62]. Furthermore, the possibility of Bose-Einstein condensation occurring on astrophysical or cosmological scales cannot be dismissed, as it has been extensively studied in terrestrial systems. Dark matter, often modeled as a cold bosonic gravitationally bound system, plays a vital role in explaining the dynamics of neutral hydrogen clouds located far from galactic centers, suggesting that dark matter could potentially exist in a Bose-Einstein condensed state [63−65]. A detailed investigation of the characteristics of galactic dark matter halos modeled as Bose-Einstein condensates is available in literature [66], and recent research has explored the cosmological and astrophysical implications of Bose-Einstein condensed dark matter [67−74]. Moreover, it has long been proposed that various forms of Bose-Einstein condensation may occur in neutron stars [75], which raises compelling questions about their internal structure and dynamics, emphasizing the importance of exploring models that include such phenomena.Motivated by these considerations, we present an innovative framework for modeling anisotropic compact stars that incorporates the density profile of Bose-Einstein condensate dark matter within the
$ f(Q) $ gravity framework. This approach aims to enhance our understanding of compact star dynamics and the role of dark matter in their structure. Recently, the authors of references [76, 77] explored a relativistic model for an anisotropic compact star featuring a Bose-Einstein density to examine the star's physical properties. The remainder of this paper is organized as follows. Section II presents a comprehensive formulation of the mathematical framework underlying symmetric teleparallel gravity. In Sec. III, we analyze the Bose-Einstein condensate matter density profile with a linear equation of state within the context of$ f(Q) $ gravity. Section IV derives the metric potentials and determines the unknown parameters of the solution by matching the internal and external spacetimes at the boundary. Section V provides a detailed investigation of the physical characteristics of compact stars, including a rigorous evaluation of the model's stability and consistency. Finally, Section VI concludes the paper with a summary of the findings and insightful remarks. -
In this section, we provide a brief overview of the fundamental principles underlying
$ f(Q) $ gravity, a novel geometric theory of gravity that is formulated using a non-metric compatible connection. This approach is characterized by the absence of both torsion and curvature and is also known as symmetric teleparallel gravity. The$ f(Q) $ gravity theory is an extension of Einstein's GR that modifies the gravitational action by incorporating a general function of the non-metricity scalar Q. The Einstein-Hilbert action for$ f(Q) $ gravity can be expressed as [34]$ \begin{aligned} S=\int\left[\frac{1}{16\pi}f(Q)+L_m\right]\sqrt{-g}{\rm d}^4x, \end{aligned} $

(1) where
$ f(Q) $ is an arbitrary function of the non-metricity scalar Q,$ L_m $ is the matter Lagrangian, and g is the determinant of the metric$ g_{\mu\nu} $ . The non-metricity tensor and its two independent traces are given by$ \begin{aligned} Q_{\lambda\mu\nu} = \nabla_\lambda g_{\mu\nu}, \end{aligned} $

(2) $ \begin{aligned} Q_\alpha = Q^{\;\;\;\mu}_{\alpha\;\;\mu}, \quad \tilde{Q}_\alpha = Q{^\mu}_{\alpha\mu}. \end{aligned} $

(3) We also define the non-metricity conjugate related to the non-metricity tensor as follows:
$ \begin{aligned} {P^\alpha} _{\mu\nu} = \frac{1}{4}\left[-Q^\alpha_{\;\;\mu\nu} + 2Q^{\;\;\;\alpha}_{\left(\mu\;\;\nu\right)}+ Q^\alpha g_{\mu\nu} -\tilde{Q}^\alpha g_{\mu\nu} -\delta^\alpha_{(\mu}Q_{\nu)}\right]. \end{aligned} $

(4) From this equation, the non-metricity scalar is expressed as
$ \begin{aligned}[b] Q &= -Q_{\alpha \mu \nu} P^{\alpha \mu \nu}\\ &=-\frac{1}{4}\left(-Q^{\alpha\nu\sigma} Q_{\alpha\nu\sigma}+2 Q^{\alpha\nu\sigma} Q_{\sigma\alpha\nu}-2 Q^{\sigma}\tilde{Q_\sigma}+Q^\sigma Q_\sigma\right). \end{aligned} $

(5) By varying the action (1) with respect to the fundamental metric, we obtain the governing equation for symmetric teleparallel gravity:
$ \begin{aligned}[b] &\frac{-2}{\sqrt-g} \nabla_\alpha \left(\sqrt -g f_Q P^\alpha _{\;\;\mu \nu}\right) \\ &- \frac{1}{2} g_{\mu\nu} f - f_Q \left(P_{\mu \alpha \beta} Q^{\;\;\alpha \beta} _{\nu} -2Q^{\alpha \beta} _{\;\;\mu} P_{\alpha \beta\nu}\right) = 8\pi T_{\mu\nu}, \end{aligned} $

(6) and
$ \begin{aligned} \nabla_\mu \nabla_\nu\left(\sqrt-gf_Q P^\alpha _{\;\;\mu \nu}\right)=0. \end{aligned} $

(7) For notational brevity, we define the shorthand notation
$ f_Q=f'(Q) $ . Furthermore, the stress-energy tensor$ T_{\mu\nu} $ is explicitly defined as$ \begin{aligned} T_{\mu \nu} = \frac{-2}{\sqrt-g} \frac{\delta(\sqrt -g \mathscr{L}_m)}{\delta g^{\mu \nu}}. \end{aligned} $

(8) Now, we must define the static spherically symmetric spacetime to examine stellar structures, as follows:
$ \begin{aligned} {\rm d}s^2=-{\rm e}^{\alpha(r)} {\rm d}t^2+{\rm e}^{\beta(r)} {\rm d}r^2+r^2 ({\rm d}\theta^2+\sin^2\theta \,{\rm d}\phi^2). \end{aligned} $

(9) We assume the anisotropic matter distribution as
$ \begin{aligned} T_{\mu\nu}=(\rho+P_t) \eta_\mu \eta_\nu+(P_r-P_t)\zeta_\mu \zeta_\nu+P_t g_{\mu \nu}, \end{aligned} $

(10) where
$ \rho, P_r, P_t $ are the energy density, radial, and tangential pressures, respectively. Here,$ \eta_\mu $ is the time-like vector defined as$ \eta_\mu=[1, 0, 0, 0] $ , and$ \zeta_\mu $ is the unit space-like vector in the radial direction defined as$ \zeta_\mu=[0, 1, 0, 0] $ such that$ \zeta_\mu\zeta^\mu=-\eta_\mu \eta^\mu=1 $ . Therefore, we can represent the components of the stress-energy tensor for an anisotropic fluid in matrix form as$ \mathcal{T}_\mu^\nu = \text{diag}(-\rho, P_r, P_t, P_t) $ .Using Eq. (10), the non-metricity scalar becomes
$ \begin{aligned} Q=-\dfrac{2\, {\rm e}^{-\beta(r)}}{r^2}\left[1+r\, \alpha'(r)\right]. \end{aligned} $

(11) Substituting the metric (9) and non-metricity scalar (11) into the field Eq. (6) under the anisotropic matter (10), we obtain the following expressions [78]:
$ \begin{aligned} \rho&=\frac{f}{2}-f_Q \left[Q+\frac{1}{r^2}+\dfrac{{\rm e}^{-\beta} \left(\beta '+\alpha'\right)}{r}\right], \end{aligned} $

(12) $ \begin{aligned} P_r&=f_Q \left[Q+\frac{1}{r^2}\right]-\frac{f}{2}, \quad {\rm and} \end{aligned} $

(13) $ \begin{aligned} P_t&=f_Q \left[\frac{Q}{2}-{\rm e}^{-\beta} \left(\left(\frac{\alpha'}{4}+\frac{1}{2 r}\right) \left(\alpha'-\beta'\right)+\frac{1}{2} \alpha''\right)\right]-\frac{f}{2}. \end{aligned} $

(14) -
Existing literature highlights that the high density observed in anisotropic compact stars has prompted researchers to thoroughly investigate the nature of matter distribution within these celestial entities. In pursuit of this objective, several recent studies have proposed diverse models for anisotropic compact stars composed of dark matter. Contributing to this ongoing discourse, we aim to examine the Bose-Einstein dark matter density profile in conjunction with a linear equation of state (EoS) to develop a novel and suitable model for anisotropic compact stars within the framework of
$ f(Q) $ gravity, particularly focusing on the implications of dark matter in their formation and evolution. The expressions for the Bose-Einstein density profile and the linear equation of state can be written as$ \begin{aligned} \rho(r)&=\frac{\xi}{k \,r}\sin(k\,r) \quad {\rm and} \end{aligned} $

(15) $ \begin{aligned} P_r(r)&=X\,\rho-Y, \end{aligned} $

(16) where
$\xi({\rm km}^{-1}),\, k,\, X$ , and$Y({\rm km}^{-2})$ are constants. Chavanis and Harko [79] identified that certain compact celestial entities may possess a considerable amount of their mass in the form of a Bose-Einstein condensate. Meanwhile, Pethik et al. [80] and Mosquera et al. [81] examined the existence of Bose-Einstein condensates in neutron stars and helium white dwarf stars, respectively. Furthermore, Li et al. [82] investigated the potential configurations of matter that could emerge from the Bose-Einstein condensation of dark matter. The study of Bose-Einstein condensates, which result from the quantum statistics of bosons, has profoundly influenced both theoretical and experimental physics. Beyond terrestrial applications, Bose-Einstein condensates are speculated to exist on astrophysical scales, potentially providing insights into phenomena such as dark matter halos and the interiors of neutron stars. Additionally, a thorough examination of Eqs. (15) and (16) concerning a compact star within the framework of$ f(Q) $ gravity has not yet been conducted, signaling a compelling avenue for further investigation.Now, let us select a linear function for
$ f(Q) $ gravity, which is expressed as$ \begin{aligned} f(Q)=\mu Q, \end{aligned} $

(17) where μ is the model parameter. Notably, when
$ \mu=1 $ , the scenario reduces to STEGR, which is dynamically equivalent to GR. By employing Eq. (17), we can rewrite the expression for matter density ρ, radial pressure$ P_r $ , and tangential pressure$ P_t $ as$ \begin{aligned} \rho&=\frac{\xi}{k \,r}\sin(k\,r), \end{aligned} $

(18) $ \begin{aligned} P_r&=\frac{\xi X \sin (k r)}{k r}-Y, \end{aligned} $

(19) $ \begin{aligned} P_t&=\frac{4 \pi\, \xi \,\mu }{k \,r}[\sin (k\, r)+k r \cos (k\, r)]. \end{aligned} $

(20) Furthermore, the mass of a matter configuration is determined by the energy density and can be expressed as
$ M(r)=4\pi\int_0^r r^2\,\rho(r) \,{\rm d}r =\frac{4 \pi \xi}{k^3} \left[\sin (k\, r)-k \,r \cos (k\, r)\right]. $

(21) Bose-Einstein condensation has been extensively observed and analyzed in terrestrial systems, suggesting the possibility that it can also manifest in bosonic systems on astrophysical or cosmic scales. Dark matter, widely regarded as a cold bosonic system bound by gravity, is essential to account for the dynamics of neutral hydrogen clouds at significant distances from galactic centers. This has led to the hypothesis that dark matter may exist in the form of a Bose-Einstein condensate [63−65]. A comprehensive examination of the characteristics of Bose-Einstein condensed galactic dark matter halos is available in [66].
-
In this section, we effectively match the interior solutions to the external Schwarzschild solutions of the celestial matter configuration at the boundary
$ r=R $ . Importantly, this matching process enables us to determine the values of certain constants that depend on the model. Wang et al. [83] demonstrated that the exterior solution of the field equations yields the exact Schwarzschild solution if and only if$ fQQ=0 $ . From Eq. (17), we deduce that$ fQQ=0 $ . Consequently, we confirm that the Schwarzschild solution is only valid in linear$ f(Q) $ gravity, which recovers STEGR. Thus, the exterior region of the compact star has no deviations from GR, and the Schwarzschild solution is applicable. In [84], the author examined the deviations from the Schwarzschild solution within the context of$ f(Q) $ gravity. The exterior Schwarzschild solution is given as$ \begin{aligned} {\rm d}s^2=-g_{tt}(r)\, {\rm d}t^2+g_{rr}(r)\, {\rm d}r^2+r^2 ({\rm d}\theta^2+\sin^2\theta\,{\rm d}\phi^2), \end{aligned} $

(22) where
$ g_{tt}=g_{rr}^{-1}=(1-\frac{2M}{R}) $ .Hence, comparing Eq. (9) and Eq. (22) with mass function (21), we obtain
$ \begin{aligned} {\rm e}^{\alpha(r)}& = \left(1 - \frac{2M}{R}\right) = 1 + \dfrac{8 \pi \xi}{k^3\, R} \left[k R \cos (k \,R) - \sin (k\, R)\right], \end{aligned} $

(23) $ \begin{aligned} {\rm e}^{\beta(r)}& = \left(1 - \frac{2M}{R}\right)^{-1} = \frac{k^3 \,R}{k^3 R - 8 \pi \,\xi \,\sin (k \,R) + 8 \pi\, \xi\, k \,R \cos (k\, R)}. \end{aligned} $

(24) Applying the natural logarithm to both sides of the equation yields
$ \begin{aligned} \alpha(r)& = \ln \Bigg[1 + \dfrac{8 \pi \xi}{k^3\, R} \left[k R \cos (k \,R) - \sin (k\, R)\right]\Bigg] \quad {\rm and} \end{aligned} $

(25) $ \begin{aligned} \beta(r)& = \ln \Bigg[\frac{k^3 \,R}{k^3 R - 8 \pi \,\xi \,\sin (k \,R) + 8 \pi\, \xi\, k \,R \cos (k\, R)}\Bigg]. \end{aligned} $

(26) Furthermore, the vanishing of the radial pressure at the boundary of the matter configuration implies
$ \begin{aligned} P_r(R)=0. \end{aligned} $

(27) Using the previously mentioned Eqs. (23), (24), and (27), we evaluate the constants ξ and X in terms of k, radius R, and mass M of the fluid sphere as follows:
$ \begin{aligned} \xi&=\frac{k^3 M}{4 \pi (\sin (k \,R)- k\, R \cos (k\, R))}, \end{aligned} $

(28) $ \begin{aligned} X&=\frac{Y\, k\, R \csc (k\, R)}{\xi}. \end{aligned} $

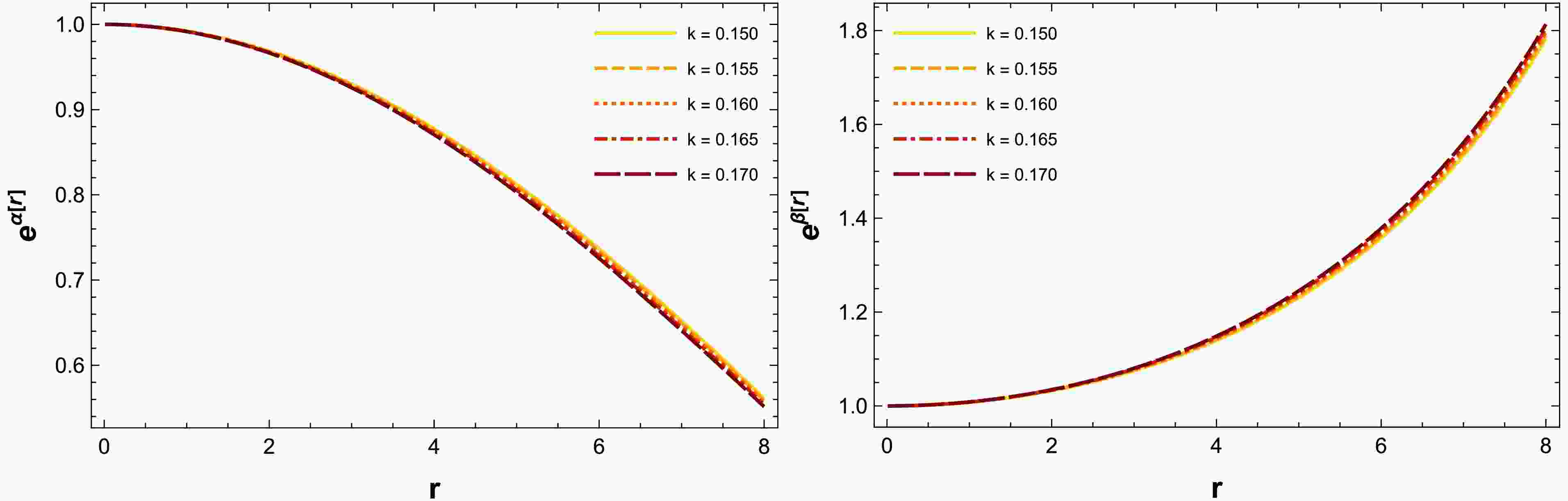
(29) The remaining parameters are selected arbitrarily to ensure a well-behaved solution (for more details, see Table 1). Figure 1 shows the evolution of the metric potential functions as a function of the radial coordinate. Evidently, both obtained metric potentials exhibit positive and regular behavior throughout the stellar core.
$ k $ 

$\xi({\rm km}^{-1})$ 

$ X $ 

$\rho^c (10^{15} {\rm g/cm}^3)$ 

$P_r^c (10^{35} {\rm g/cm}^2)$ 

$\rho(R)(10^{14} {\rm g/cm}^3)$ 

$ u(R) $ 

$ Z_s(R) $ 

$ 0.150 $ 

$ 0.00094821 $ 

$ 0.13274 $ 

$ 1.27862 $ 

$ 1.52817 $ 

$ 8.73639 $ 

$ 0.29987 $ 

$ 0.58062 $ 

$ 0.155 $ 

$ 0.00096284 $ 

$ 0.13447 $ 

$ 1.29835 $ 

$ 1.57198 $ 

$ 8.62393 $ 

$ 0.29987 $ 

$ 0.58062 $ 

$ 0.160 $ 

$ 0.00097826 $ 

$ 0.13632 $ 

$ 1.31914 $ 

$ 1.61913 $ 

$ 8.50662 $ 

$ 0.29987 $ 

$ 0.58062 $ 

$ 0.165 $ 

$ 0.00099451 $ 

$ 0.13831 $ 

$ 1.34105 $ 

$ 1.67005 $ 

$ 8.38431 $ 

$ 0.29987 $ 

$ 0.58062 $ 

$ 0.170 $ 

$ 0.00101164 $ 

$ 0.14045 $ 

$ 1.36415 $ 

$ 1.7251 $ 

$ 8.25692 $ 

$ 0.29987 $ 

$ 0.58063 $ 

Table 1. Numerical values of constants, central density
$ \rho^c $ , central pressure$ P_r^c $ , surface density$ \rho(R) $ , compactness factor$ u(R) $ , and surface redshift function$ Z_s(R) $ for the compact star PSR J1614-2230$(M=1.97 M_\odot, R=9.69 ~{\rm km})$ with$Y =0.86\times 10^{-4} {\rm km}^{-2}$ .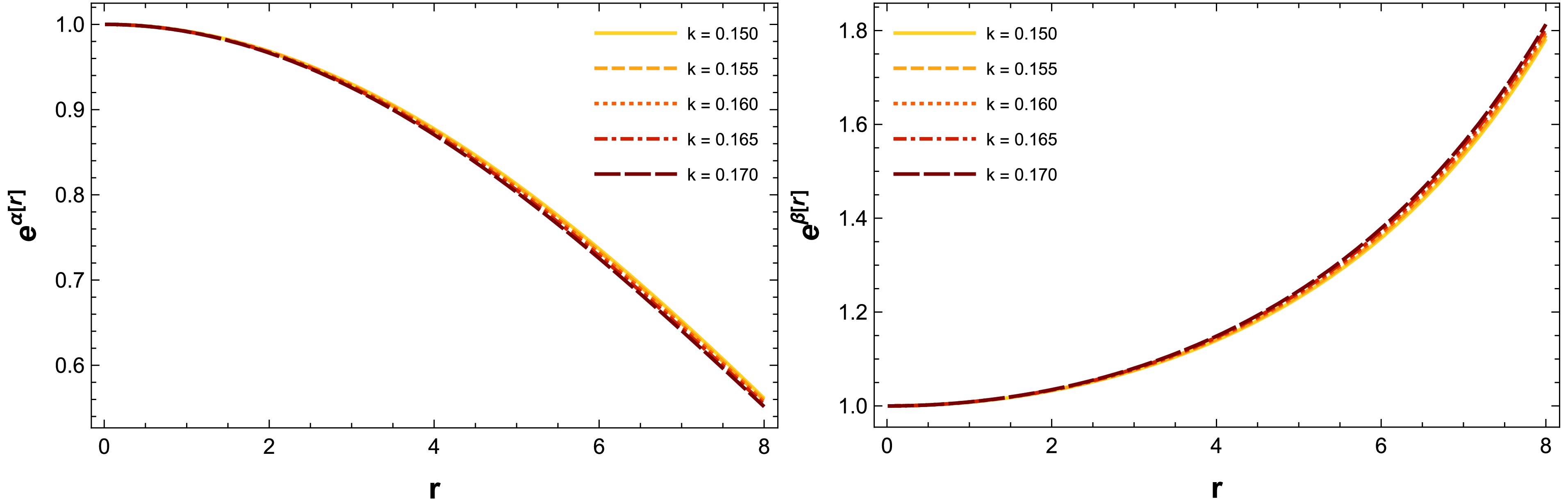
Figure 1. (color online) Graphical representation of the metric potentials for the compact star PSR J1614-2230 based on the numerical values of constants listed in Table 1.
-
In this section, we analyze the key physical properties of anisotropic objects, such as energy density, radial and transverse pressures, anisotropy factor, mass function, compactification factor, surface redshift, and adiabatic index. This analysis is conducted within the framework of
$ f(Q) $ gravity to assess the physical validity and stability of our stellar system. Furthermore, we aim to explore the behavior of these physical parameters using both analytical methods and graphical representations to offer a thorough understanding of the characteristics of our proposed model. -
In this subsection, we explore the behavior of various physical parameters, including energy density, radial pressure, and transverse pressure. This analysis is conducted both analytically and graphically for the compact star PSR J1614-2230, considering values of k in the range of
$ \{0.150,~ 0.155,~ 0.160,~ 0.165, ~0.170\} $ . Evidently, Eqs. (18)−(20) reach their maximum values at the core of the stellar sphere and decrease toward zero at the boundary$ r=R $ . This characteristic is visually represented in Fig. 2.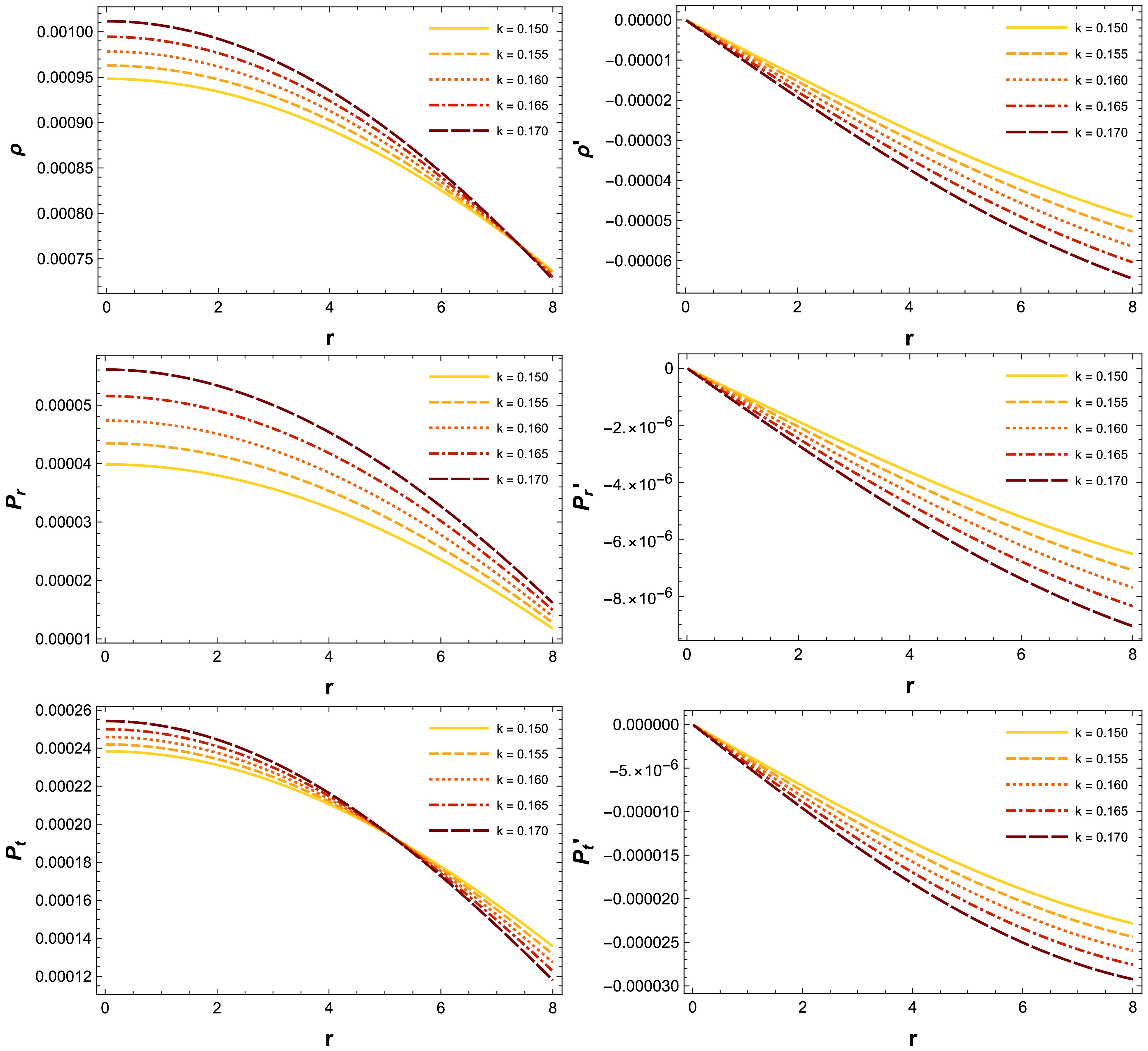
Figure 2. (color online) Visual representation of the density and pressure profiles for the compact star PSR J1614-2230, derived from the numerical values in Table 1.
-
This subsection analyzes the gradients of energy density and pressure components as they pertain to the radial coordinate. For the compact star model to be effectively constructed, these gradients must satisfy the following criteria:
$ \begin{aligned}[b] & \rho'(r)<0, \quad P_r'(r)<0, \quad P_t'(r)<0 \quad {\rm and} \\ & \rho'(r)=0, \quad P_r'(r)=0, \quad P_t'(r)=0\quad at \,r=0. \end{aligned} $

(30) The gradient conditions previously discussed are fulfilled, as depicted in the right panel of Fig. 2. These gradients take on a negative characteristic and diminish to zero at the center of the compact star. Thus, we can assert that the gradients satisfy the fundamental requirements for a stable stellar model.
-
To ensure the physical viability of the solutions, the energy density along with the radial and transverse pressures, must be both finite and positive. Therefore, the central values of energy density and pressures should also satisfy these conditions of positivity and finiteness. We have subsequently calculated the central values of these quantities in our solutions, which are outlined as follows:
$ \begin{aligned} \rho^c|_{r=0}&=\xi>0, \end{aligned} $

(31) $ \begin{aligned} P_r^c|_{r=0}&=X \,\xi-Y. \end{aligned} $

(32) Furthermore, Zeldovich's condition is relevant to the interior of a compact star. It states that the ratio of central pressure to central density must not exceed one. Now, applying this criterion to our solution, we obtain
$ \begin{aligned} \dfrac{X \,\xi-Y}{\xi}\leqslant 1. \end{aligned} $

(33) From Eqs. (31) and (33), we obtain
$ \begin{aligned} 0<\xi\leqslant\frac{Y}{1-X}. \end{aligned} $

(34) The variations in central density, central pressure, and surface density with changes in the k-parameter are given in Table 1.
-
In this subsection, we determine the EoS parameters for pressure components, which are presented by
$ \begin{aligned} \omega_r=\frac{P_r}{\rho} \quad {\rm and} \quad \omega_t=\frac{P_t}{\rho}. \end{aligned} $

(35) Substituting Eqs. (18)−(20) into Eq. (35), we can obtain
$ \begin{aligned} \omega_r&= X -\frac{Y \,k\, r \csc (k \,r)}{\xi}, \end{aligned} $

(36) $ \begin{aligned} \omega_t&=4\, \pi\, \mu [k\, r \cot (k \,r)+1]. \end{aligned} $

(37) Here, the EoS parameters for our derived solutions fall within the interval
$ 0 < \omega_r(r), \omega_t(r) < 1 $ , as shown in Fig. 3. Consequently, the solutions we present are consistent with a physical matter configuration.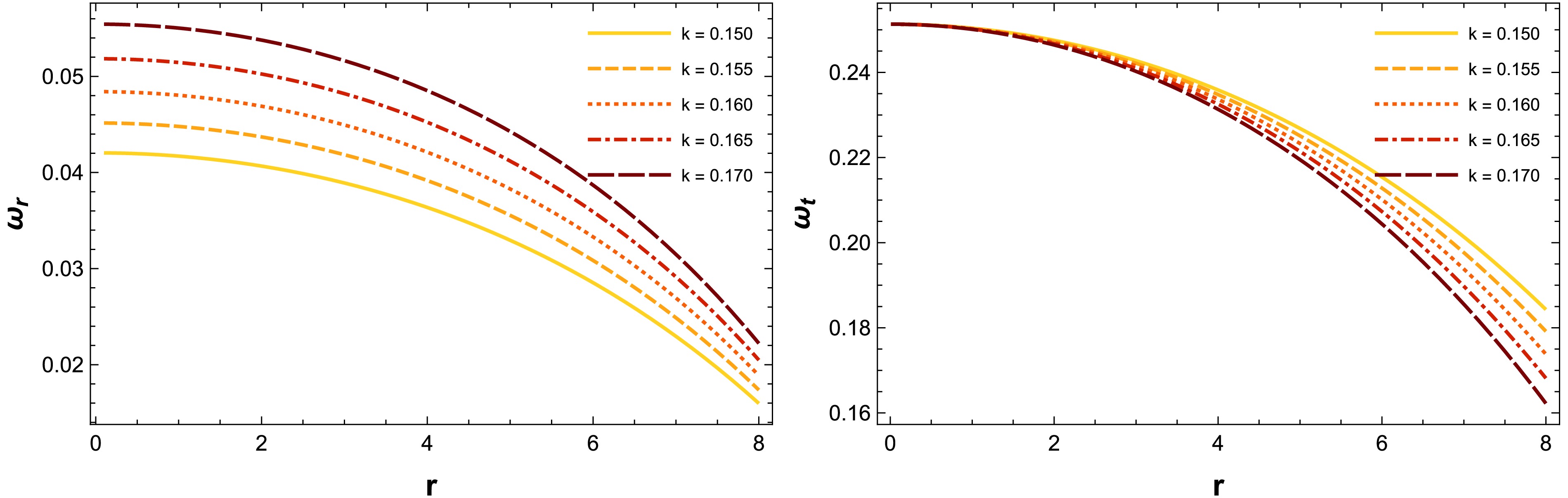
Figure 3. (color online) Variations in the EoS parameters with respect to the radial coordinate r for the compact star PSR J1614-2230, corresponding to the numerical values of constants given in Table 1.
-
Energy conditions are critical for assessing the stability of stellar structures, as they aid in defining the permissible behavior of matter and energy in GR. These conditions are formulated as inequalities involving the energy-momentum tensor, with each condition addressing different aspects of matter distribution, such as energy density and pressure. By verifying these inequalities within a star's interior, we can determine whether the matter behaves as typical baryonic matter or exhibits properties indicative of exotic forms of matter, such as negative energy density. The validity of these energy conditions also offers insights into potential scenarios for gravitational collapse and the formation of compact objects like neutron stars or black holes. Ultimately, a thorough understanding of energy conditions is vital for unraveling the complexities of stellar dynamics and the underlying physics governing these cosmic entities. These energy conditions are articulated as follows:
$ \circ $ $ NEC_r $ :$ \rho+P_r\ge0 $ .$ \circ $ $ NEC_t $ :$ \rho+P_t\ge0 $ .$ \circ $ $ WEC_r $ :$ \rho\ge0 $ ,$ \rho+P_r\ge0 $ .$ \circ $ $ WEC_t $ :$ \rho\ge0 $ ,$ \rho+P_t\ge0 $ .$ \circ $ SEC:$ \rho+P_r+2P_t\ge 0 $ .Next, we evaluate all of these energy conditions using graphical representations, as depicted in Fig. 4. The solutions clearly fulfill all energy conditions relevant to the matter configuration. Consequently, we can assert that all the physical parameters of our reported solutions are well-defined and adhere to the necessary criteria.
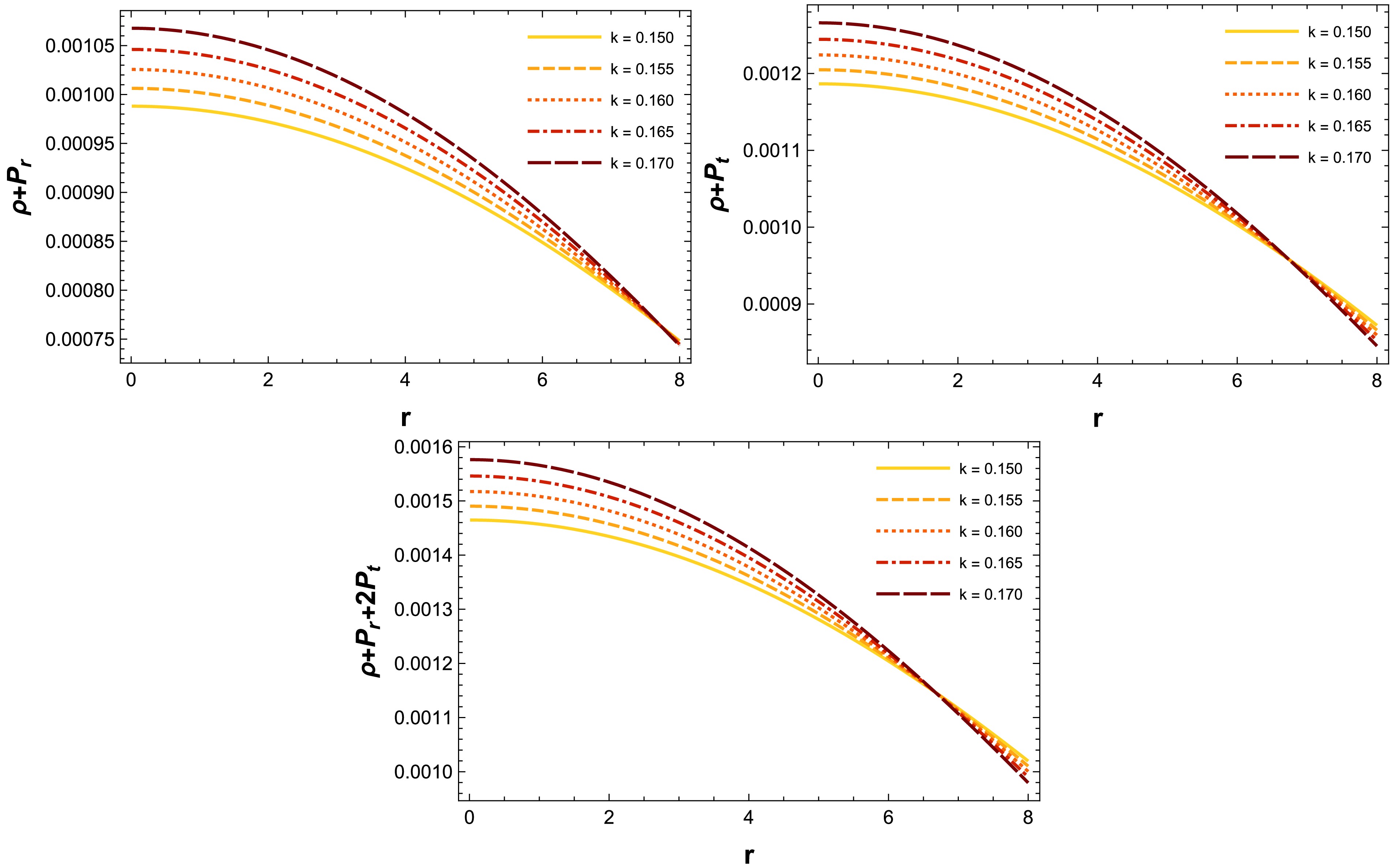
Figure 4. (color online) Characteristics of the energy conditions influenced by the Bose-Einstein density profile for the compact star PSR J1614-2230 corresponding to the numerical values of the constants provided in Table 1.
-
We have established the total mass function of the compact star in Eq. (21), and using this expression, we can evaluate the feasibility of our compact stellar structure by examining a physical parameter defined as the mass and radius ratio, commonly referred to as the compactness factor, expressed as
$ \begin{aligned} u(r) = \frac{M(r)}{r}=\frac{4\, \pi \, \xi}{k^3 r} [\sin (k\, r)-k\, r \cos (k\,r)]. \end{aligned} $

(38) For a well-behaved compact stellar configuration, this mass and compactness factor should be zero at the center and increase steadily throughout the interior region. Additionally, for the stability of the model, the compactness must remain below the limit of
$ u < 4/9 $ , which is known as Buchdahl's limit [85]. The visual representation of the mass function and compactness factor is shown in Fig. 5. From this figure, we can observe that both functions are monotonically increasing, with their minimum values occurring at the core of the star. This behavior indicates that the mass and compactness are well-behaved throughout the interior of the star, consistent with the requirements for a stable compact stellar configuration.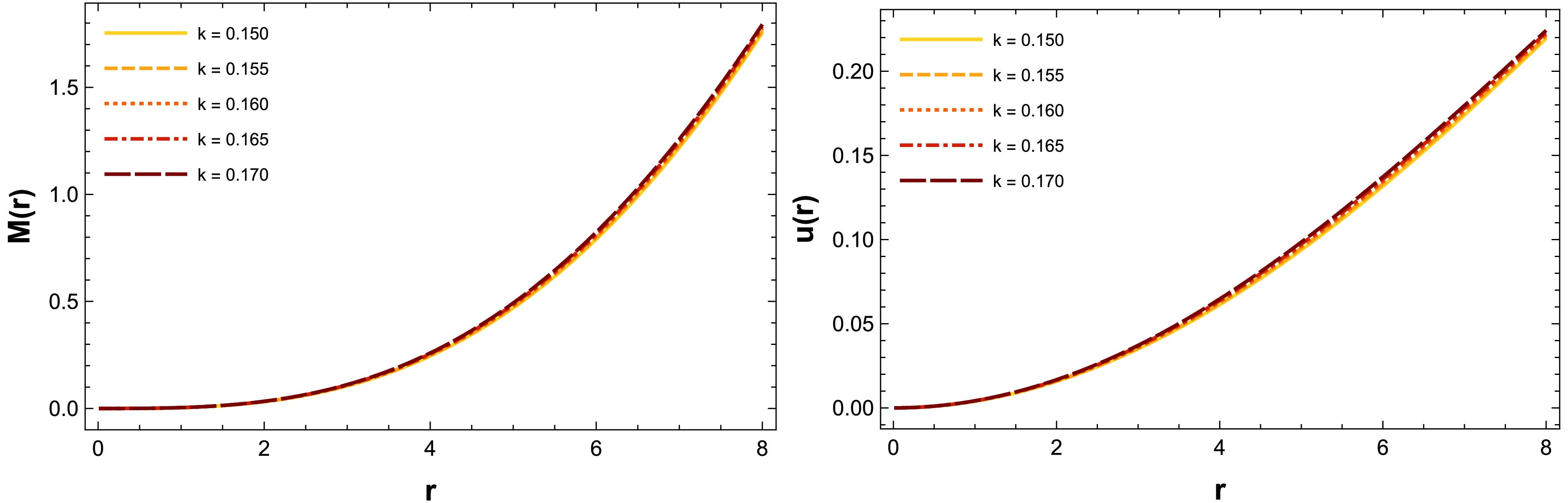
Figure 5. (color online) Visual representation of the mass function and compactness factor for the compact star PSR J1614-2230 corresponding to the numerical values of the constants provided in Table 1.
-
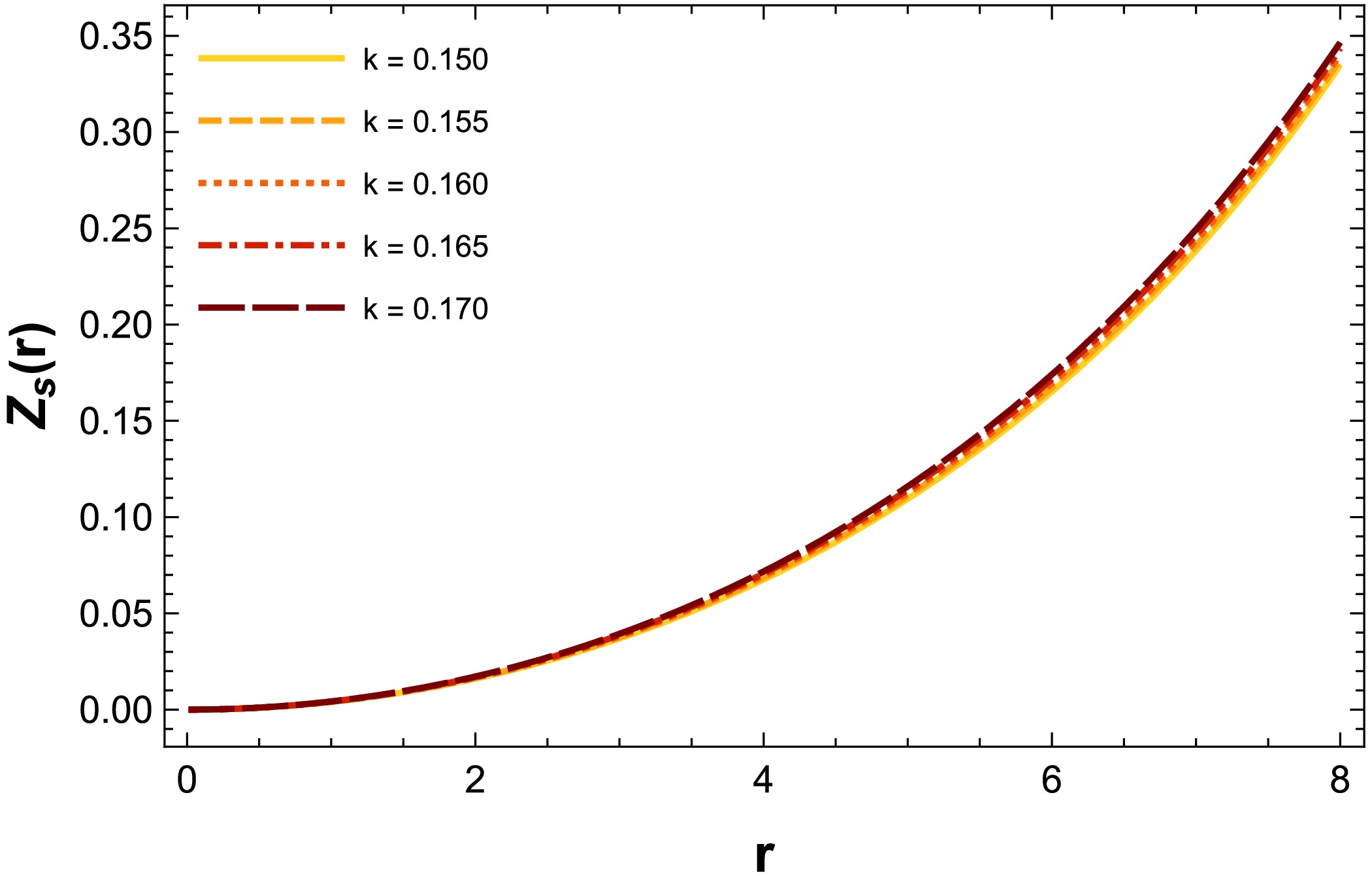
In this segment, we evaluate the validity of our stellar system by examining a physical parameter called surface redshift, which quantifies the influence of a strong gravitational field on light. The surface red-shift can be determined using
$ \begin{aligned}[b] Z_s(r)&=(1-2\,u(r))^{-1/2}-1\\ &=\frac{1}{\sqrt{\dfrac{8 \,\pi \, \xi (k\, r \cos (k\, r)-\sin (k \,r))}{k^3 r}+1}}-1. \end{aligned} $

(39) We have also plotted the profile of the surface redshift, as depicted in Fig. 6, and it falls well within the acceptable limit, specifically
$ Z_s(r) \leqslant 2 $ . -
In this section, we evaluate the stability of our compact stellar model. The analysis will be conducted through an examination of four essential factors: (i) the causality condition, (ii) the adiabatic index, (iii) the static stability criterion, and (iv) the effect of anisotropy.
-
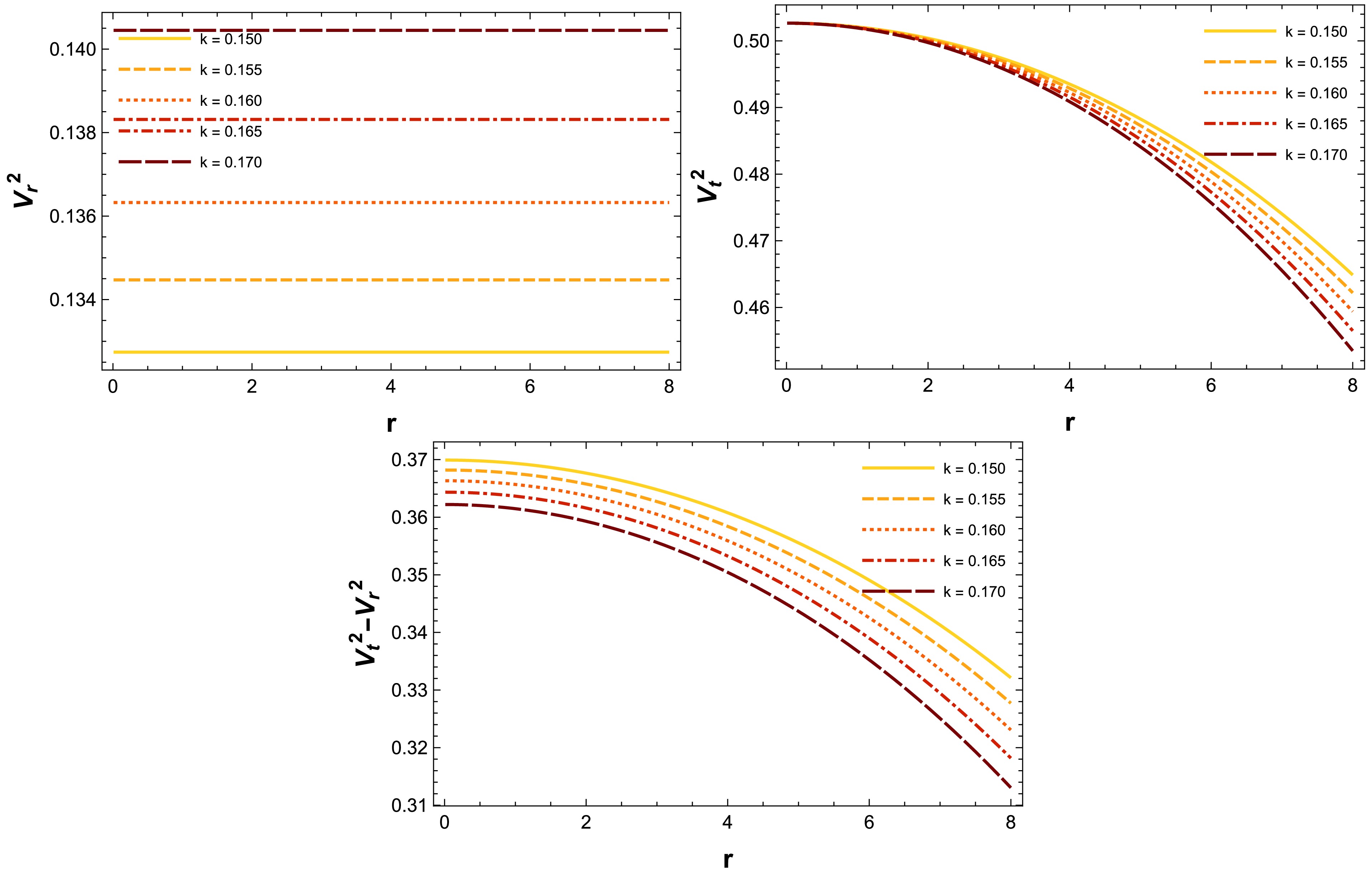
A compact stellar structure model is considered physically valid only if the conditions of causality hold true at every point throughout its complete interior. The principle of causality fundamentally asserts that, for an anisotropic distribution of matter, both the radial and tangential sound speeds must remain below the speed of light. Therefore, we define the sound speed as follows:
$ \begin{aligned} V_r^2= \frac{P_r'(r)}{\rho'(r)} \quad {\rm and} \quad V_t^2= \frac{P_t'(r)}{\rho'(r)}. \end{aligned} $

(40) Consequently, the principle of causality is expressed as
$ 0 < V_r, V_t < 1 $ , given that the speed of light$ c=1 $ is adopted throughout this model. Furthermore, stability can be assessed using an alternative method based on anisotropic matter distribution, known as Herrera's cracking concept [86]. According to this theory, the condition$ 0 < |V_t^2-V_r^2 < 1 $ must be satisfied at every point in a stable stellar region with such a matter distribution, indicating that cracking does not occur in that area.Figure 7 presents the graphical representation of sound speed velocities and the difference
$ ( V_t^2 - V_r^2 ) $ with respect to the radius r. Our analysis confirms that the values of radial sound speed lie within the interval$ (0,1) $ for PSR J1614-2230 across various values of k. Consequently, we assert that the causality conditions hold true throughout the interior regions of the stellar configurations defined by our proposed model. Furthermore, we can demonstrate that the difference$ ( V_t^2 - V_r^2 ) $ fulfills the cracking condition$ 0 < |V_t^2 - V_r^2| < 1 $ within the stars. Thus, we can confidently state that our proposed model exhibits physical stability. -
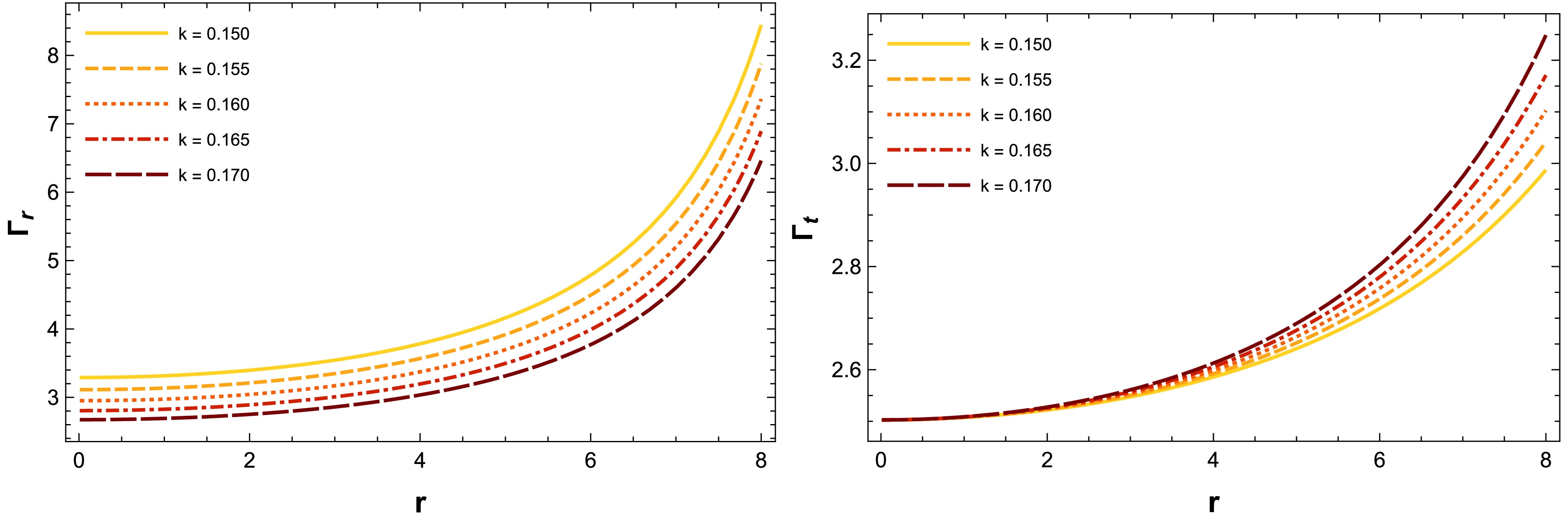
The adiabatic index is essential for ensuring stable equilibrium against gravitational collapse and is fundamental to analyzing the dynamical stability of compact star configurations. However, in the context of anisotropic matter distributions, the adiabatic index must be greater than the Chandrasekhar limit within the interior region of the star i.e.,
$ \Gamma> {4}/{3} $ . The mathematical expressions for the radial and tangential adiabatic indices in the context of anisotropic stellar matter can be represented as follows:$ \begin{aligned} \Gamma_r =\frac{\rho+P_r}{P_r} V_r^2 \quad {\rm and} \quad \Gamma_t =\frac{\rho+P_t}{P_t} V_t^2. \end{aligned} $

(41) In this study, we explore the radial and tangential adiabatic indices within the interior of the spheres. To highlight the significance of
$ \Gamma_r $ and$ \Gamma_t $ within our model, we analyze their graphical representation in Fig. 8. Our investigation reveals that the adiabatic indices remain greater than${4}/{3}$ throughout the interior region and progressively increase with the radial coordinate r. These findings confirm that the model represents a dynamically stable configuration, underscoring the validity of our theoretical framework and its critical role in understanding anisotropic stellar structures. -
An important approach for evaluating the stability of compact stellar structures is the Harrison-Zeldovich-Novikov static stability condition. Initially, Chandrasekhar analyzed radial perturbations to investigate stellar stability through the pulsation equation [87]. The Harrison-Zeldovich-Novikov criterion was later developed as an enhancement and simplification of Chandrasekhar's method. According to this criterion, the gravitational mass M must increase as the central density
$ \rho_c $ increases. Specifically, a stellar structure is considered stable if$\dfrac{{\rm d}M(\rho^c)}{{\rm d}\rho^c} > 0$ . Conversely, if this condition is not satisfied (i.e.,$\dfrac{{\rm d}M(\rho^c)}{{\rm d}\rho^c} < 0$ ), it signifies an unstable distribution of matter. The mass and surface radius in terms of$ \rho^c $ are obtained as$ \begin{aligned} M(\rho^c)=\frac{4\,R\,\rho^c}{k^3}[\sin(k\,R)-k\,R\cos(k\,R)]. \end{aligned} $

(42) Therefore,
$ \begin{aligned} \dfrac{{\rm d} M(\rho^c)}{{\rm d}\rho^c}=\frac{4\,R}{k^3}[\sin(k\,R)-k\,R\cos(k\,R)]. \end{aligned} $

(43) Clearly, for
$ R=9.69 $ km and$ k = \{0.150, 0.155, 0.160,0.165, 0.170\} $ , we observe that$ (\sin(k\,R)-k\,R\cos(k\,R))>0 $ , which implies$\dfrac{{\rm d}M(\rho^c)}{{\rm d}\rho^c} > 0$ . This result demonstrates that our stellar configuration is stable. -
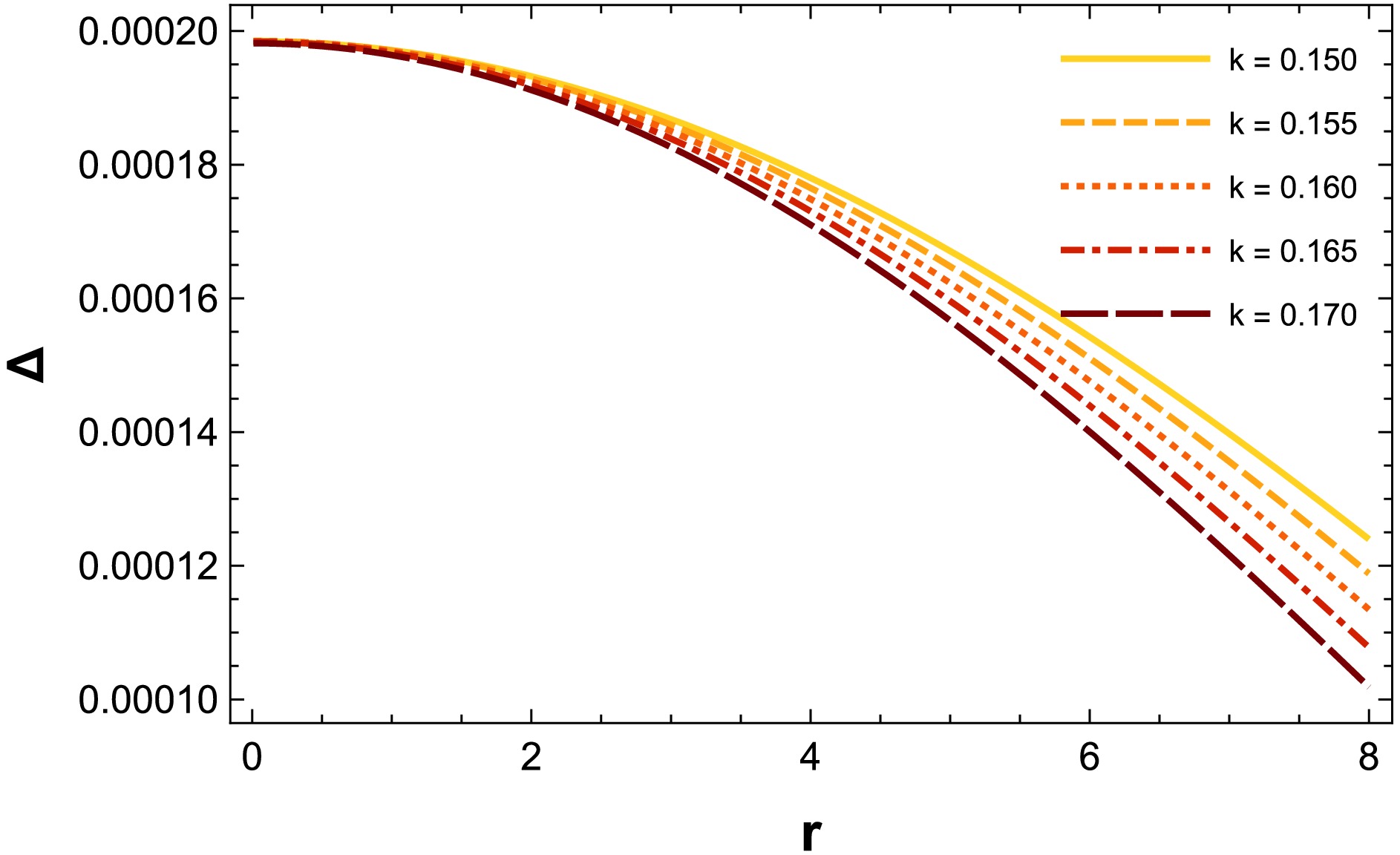
This article explores the final aspect, highlighting the role of anisotropy in determining the internal structure of a relativistic stellar configuration. Anisotropy is characterized by
$ \begin{aligned} \Delta=P_t(r)-P_r(r)=\frac{\xi (4 \pi \mu-X ) \sin (k \,r)}{k\, r}+4 \pi \xi \mu \cos (k \,r)+Y, \end{aligned} $

(44) where
$ P_t(r) $ is the tangential pressure and$ P_r(r) $ is the radial pressure. The anisotropic factor significantly influences the geometry of compact stars. If the tangential pressure exceeds the radial pressure, the star's structure exhibits a repulsive nature, producing an outward anisotropic force. Conversely, if the radial pressure is greater, the star's structure demonstrates an attractive nature, leading to an inward anisotropic force. At the core of the star, where$ \Delta(r=0) $ equals zero, tangential and radial pressures are balanced.Figure 9 depicts anisotropy, showing that Δ within the star's interior remains positive and increases steadily. This indicates a repulsive anisotropic effect directed outward. Therefore, our compact stellar model remains stable under the influence of the Bose-Einstein density profile within the framework of symmetric teleparallel gravity.
-
In this article, we introduce an innovative framework for modeling anisotropic compact stars in the context of
$ f(Q) $ gravity, which considers the influence of physical dark matter. Our approach employs a Bose-Einstein density profile to characterize the dark matter and uses a linear EoS to describe the properties of the stellar matter. This combination enables a deeper understanding of the interactions between dark matter and the structural dynamics of compact stars within the$ f(Q) $ gravity framework. To ensure the physical validity of our model, we examine the solutions in relation to the well-known compact star PSR J1614-2230, particularly focusing on the constant values k within the range of$ [0.150, 0.170] $ . Furthermore, we match our interior solutions with the exterior Schwarzschild metric to determine the metric potentials and to find the values of the parameters ξ and X listed in Table 1. Moreover, we conduct both analytical and graphical analyses of the physical properties of the compact star to evaluate the stability of the model in the background of symmetric teleparallel gravity. A detailed explanation is provided below:• Initially, we examine the nature of the density and pressure components using the Bose-Einstein density and a linear EoS within the framework of
$ f(Q) $ gravity. These components are found to be positive, finite, and decreasing throughout the matter configuration. Furthermore, their gradients exhibit negative and decreasing trends. The graphical representation of the evolution of energy density, pressure, and their gradients are shown in Fig. 2. This illustration shows that the maximum values of energy density and pressure occur at the core of the stellar spheres. Toward the surface boundary, both the energy density and the radial and tangential pressures diminish to zero. This observation highlights the exceptionally dense nature of stellar spheres and confirm that the presented configurations are free of singularities. Additionally, these gradients satisfy the required conditions for a stable stellar model, ultimately vanishing at the star's center.• For our solution, the radial and tangential EoS parameters lie within the range of 0 and 1. This is visually depicted in Fig. 3. Compact stars composed of physical matter satisfy the NEC, WEC and SEC. These findings are clearly shown in Fig. 4, indicating that our solutions represent physically viable matter distributions.
• We have conducted a thorough investigation of the mass function, compactness factor, and redshift characteristics. As shown in Figs. 5 and 6, the graphs for the mass function, compactness factor, and surface redshift indicate a consistent increasing trend. This behavior confirms that our model adheres to the stability criteria.
• Finally, we have conducted a stability analysis of the compact star PSR J1614-2230, employing various criteria including the causality condition, adiabatic index, static stability criterion, and effects of anisotropy. Our findings indicate that the compact stellar model remains stable under the influence of Bose-Einstein density in the context of
$ f(Q) $ gravity. The graphical representation of these criteria is presented in Figs. 7 to 9.Upon a thorough examination of our previous discussions, we observe that the solutions derived for anisotropic spheres with a Bose-Einstein density profile within the framework of
$ f(Q) $ gravity comply with all relevant physical constraints. Through a combination of graphical representations and analytical scrutiny, we have firmly established the efficacy and stability of our theoretical framework.
Impact of the Bose-Einstein density profile on anisotropic compact stars under f (Q) gravity
- Received Date: 2024-12-10
- Available Online: 2025-05-15
Abstract: This paper presents an innovative framework for modeling anisotropic compact stars by incorporating the density profile of Bose-Einstein condensate dark matter within the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: