Effect of nucleus deformation on final-state flow harmonics

The relativistic heavy-ion collision is an important tool for extracting crucial information on quark-gluon plasma (QGP) [1−3]. As a state of matter subject to extreme conditions, QGP is characterized by high temperature and density created at the moment of collision. On the experimental side, among others, the collective phenomenon, notably the elliptic flow, plays a significant role in forming the research community's consensus on the fluid nature of the strongly interacting system. The latter is demonstrated in terms of the observations of nuclear collisions performed at the relativistic heavy-ion collider [4] (RHIC) and large hadron collider [5−7] (LHC), including that for “small” systems [8−12].

While applicable to physical systems of distinct scales, the transport, particularly the hydrodynamic model, provides an effective and intuitive description of the temporal evolution of a system produced in heavy-ion collision experiments [13−18]. In practice, it has become one of the standard tools for analyzing relevant experimental data [19−23]. A complete and systematic approach to the collision process mostly consists of four stages: pre-collision, collision, temporal evolution, and decoupling. Scholars have extensively developed numerical implementations of the underlying theoretical models. These typically involve the initial conditions (ICs) [24, 25], relativistic hydrodynamical evolution [26, 27], and hadronization and final-state interactions [28]. With numerical simulations, the results can be compared with measurements from various experimental collaborations at the RHIC and LHC.

Recently, the implications of the geometric deformation of nuclei have attracted much interest. Researchers [29, 30] have speculated that such a deformation might have a considerable effect on some experimental observables. Specifically, when described using a few parameters, the deviation from isotropic nuclei has been demonstrated to result in a relevant impact on the initial eccentricity [31], momentum-dependent particle correlations, and collective flow [32], particularly elliptic flow.

The eccentricities of the IC for Au+Au and U+U collisions were first studied in Ref. [31] using the Glauber Monte Carlo approach. The relation between the initial state geometry and fluctuations was investigated [33] for Au+Au, Cu+Au, and U+U collisions using the Glauber and IP-Glasma approaches. The study observed that elliptic flow as a function of multiplicity in central collisions can be used to discriminate between models with qualitatively different particle production mechanisms. On the experimental side, the STAR Collaboration [34] explored such an effect. The dependence of elliptic flow on multiplicity was measured by selecting entirely overlapping collisions of Au+Au and at $ \sqrt{s_{NN}} = 200 $ GeV and those of U+U collisions at $ \sqrt{s_{NN}} = 193 $ GeV. The data appear to favor models for which the multiplicity does not strongly depend on the number of binary nucleon-nucleon collisions. The density of the initial nucleus shape was modeled using a deformed Woods-Saxon profile to estimate the initial system's eccentricities. In particular, when integrating over different nuclear orientations, the Woods-Saxon parameters are no longer appropriate, and the deformation parameter $ \beta_2 $ derived from the reduced electric quadrupole transition probability does not coincide with that from the spherical harmonic expansion. The appropriate Woods-Saxon and deformation parameters were evaluated in Ref. [35] in a consistent manner.

Additionally, analyses [36, 37] have indicated the importance of the multipole deformations. In addition to$ \beta_2 $, which measures the quadrupole, such deformation is also characterized by $ \beta_3 $ and $ \beta_4 $, namely, the octupole and hexadecapole parameters. These parameters are relevant for the multipole expansion of the Woods-Saxon distribution for non-spherical nuclei. In literature, the values of these parameters typically vary significantly [38−42].

Moreover, over the past few years, isobar collisions such as Zr+Zr and Ru+Ru have been introduced to explore the skin and shape of atomic nuclei. The quantitative analysis becomes feasible as the relevant bulk observables such as $ v_2 $ and $ v_3 $ ratios have been obtained with unprecedented precision [43−49]. Additionally, these isobars collisions are distinct in terms of the shapes of the participant nuclei, which are characterized by different deformations. For the latter, the quadrupole and hexadecapole deformations play significant roles [50, 51].

Based on this background, this study investigates the effect of multipole nuclear deformation in flow harmonics. Hence, we focus on Au+Au collisions at $ \sqrt{s_{NN}} = 200 $ GeV and U+U collisions at $ \sqrt{s_{NN}} = 193 $ GeV. The non-spherical Woods-Saxon profile is employed to describe the nuclear density. We primarily focus on the quadrupole and hexadecapole deformations in terms of the parameters $ \beta_2 $ and $ \beta_4 $. The hydrodynamic simulations were conducted using the Complete Hydrodynamical Evolution System (CHESS) [52], a hybrid code unifying different stages of the relativistic heavy-ion collisions. Specifically, the CHESS code comprises $ T_RENT_o $ [24] to provide the IC, vHLLE [26] to simulate the hydrodynamic evolution, and THERMINATOR 2 [28] to govern the hadronization process.

The remainder of this paper is organized as follows. In Sec II, we briefly introduce the CHESS code and discuss the specific configuration for this study. In Sec III, we present the numerical results and elaborate, among others, the effect of the initial-state geometric shape on the flow harmonics in terms of the deformation parameters. The final section is dedicated to further discussions and concluding remarks.

As mentioned earlier, relativistic heavy-ion collisions have four main stages: pre-collisions, collisions, relativistic hydrodynamics, and decoupling. In this section, we elaborate on implementing the above elements in this study while providing a brief overview of hydrodynamics and the hadronization process.

The Glauber model [53] is one of several conventional candidates for the IC. Following its theoretical framework, nuclear collisions are primarily governed by the underlying geometry, typically given by the Woods-Saxon profile. Moreover, the Glauber model assumes that the collision between two nuclei can be considered a superposition of a series of binary nucleon collisions. As an individual nucleon can be considered as a pancake, collision only occurs if the distance between the center of two nucleons reaches the minimum, given by

where $ \sigma_{NN} $ is the total cross-section of elementary nucleon-nucleon collisions.

The two nuclei, denoted by A and B, are the target and projectile, respectively. They travel in opposite directions along the z-axis. To study the effect of deformed nuclei, in addition to symmetric ones, we consider nuclei subject to quadrapole and hexadecapole deformations, which are parameterized in terms of the deformation parameters in the Woods-Saxon profiles.

Specifically, the Woods-Saxon profile for a symmetric nucleus satisfies

where the subscripts A and B denote the two nuclei, ρ is the initial density, $ r = \sqrt{x^2 + y^2 + z^2} $, a is the diffusion parameter, and $ R_{A, B} $ are the radii of the nuclei.

In contrast, for a deformed nucleus, we follow the Woods-Saxon profile provided by [38, 54], which is expressed as

where we have considered quadrupole and hexadecapole deformations governed by the parameters $ \beta_2 $ and $ \beta_4 $, and $ Y_{2 0} $ and $ Y_{4 0} $ are the spherical harmonics.

Recent studies [46, 55] have proposed different implementations for deformation parameters and their respective associated spherical harmonics according to the degree of deformation used in Eq. (3). In this work, our primary focus is the impact on the observables originating from the deformations related to parameters $ \beta_2 $ and $ \beta_4 $. By imposing different conditions, we aim to verify the sensitivity of the relevant observables on these deformation parameters.

Fig. 1 shows the shapes of the nuclei according to different quadrupole and hexadecapole deformation parameters $ \beta_2 $ and $ \beta_4 $. The collisions are assumed to occur on the z-axis. Visually, a variation in $ \beta_2 $ leads to a deformation of essentially oblate or prolate shapes, whereas parameter $ \beta_4 $ implies further ondulation along the zenithal direction, characterizing a shape illustrated in the bottom-right panel of Fig. 1. The nucleus is spherically symmetric if no deformation parameter is associated with the collision, i.e., $ \beta_2 = \beta_4 = 0 $. In this study, we do not consider deformation degrees of freedom related to rotations in the axis such as those presented in Ref. [56].

Figure 1.  (color online) Different deformations of the nuclei used as the IC in this study: Top-left: Symmetric sphere representing $\beta_2=\beta_4=0$. Top-right: Oblate nucleus owing to a negative $\beta_2$. Center-left: Prolate nucleus associated with a positive $\beta_2$. Center-right: Deformed nuclei owing to nonvanishing $\beta_4$. Bottom-left: 2D view of deformed nuclei with vanishing $\beta_4$, aiming at oblate (dotted line) and prolate (solid line) deformations. Bottom-right: 2D view of deformed nuclei owing to nonvanishing $\beta_4$. The arrows indicate the deformation parameters increase.

Using the Wood-Saxon profile of the two nuclei A and B, we can also obtain information on nuclear thickness function, differential and total cross sections, the number of nucleon-nucleon collisions, and the total number of participants $ N_\mathrm{part} $.

As a venerable approach, the Glauber model facilitates the study of deformed nuclei owing to its flexibility in encoding the information on deformation via the model parameters. Studies have also been conducted using different ICs such as IP-glasma [25], an approach based on Color Glass Condensate (CGC) [57].

Relativistic hydrodynamics has become a prominent tool for describing the collective phenomenon observed in the heavy-ion collisions [13−17, 23, 58]. Although the system behaves close to an ideal fluid, viscous hydrodynamics is primarily employed. Some pedagogic studies on the specific numerical algorithm are available in Refs. [59, 60].

In this study, we employ a specific implementation, dubbed vHLLE [26]. The code uses a subset of the High-Resolution Shock-Capturing (HRSC) algorithms, known as the Godunov-type algorithm [61]. The HRSC algorithm treats the shock waves in their conservation form; it also generalizes to non-conservative shock waves including the treatment of non-continuous changes of variables such as pressure, density, and velocity [62, 63].

The algorithm's mathematical framework consists of using solutions to Riemann problems that consider cell boundaries. The constituent solutions can be exact or approximated. The algorithm then computes the fluxes through the cell boundaries.

As the system evolves hydrodynamically, it eventually cools down, and hadronization, known as decoupling, occurs. We use the THERMINATOR 2 [28], a Monte Carlo approach, in the CHESS code to implement hadron decoupling using the Cooper-Frye prescriptions [64, 65]. The Cooper-Frye formula describes hadronic decoupling as follows:

where $ {\rm d} \Sigma_{\mu} $ is an element of the freezeout hypersurface, and $ f(x,p) $ is the distribution function, which can be properly modified to consider the effect of the bulk and shear viscosities. In addition to hadronization, the model considers the two- and three-body decays of resonances. Although the explicit space-time evolution of hadronic degree of freedom is not considered under the current theoretical framework, we understand that the main results on anisotropy drawn in this study are largely unaffected.

Technically, THERMINATOR 2 provides the freedom to select whether the freeze-out surface is parameterized in a 2+1 plus boost invariant symmetry or a genuine 3+1 fashion. In this study, we adopt a boost invariant scheme for the hydrodynamic evolution and hadronization.

In this study, we employ the CHESS code [52], which is a conjunction of the IC implemented using $ T_RENT_o $, relativistic hydrodynamics governed by vHLLE, and decoupling using THERMINATOR 2. Different code ingredients are united by implementing a series of Python scripts. The flowchart for the CHESS code is presented inFig. 2.

Figure 2.  (color online) Flowchart of the CHESS code.

The green boxes in Fig. 2 indicate the auxiliary scripts implemented in Python, namely, ''aux,'' ''main,'' and ''post.'' The blue boxes are the employed numerical packets, and the pink boxes indicate the configurations and parameters for individual codes. The ''aux'' scripts invoke the ''main'' script responsible for the specific housekeeping tasks. Among others, it separates the input file into three parts, denoted by I, II, and III.

These separated files are then returned to ''aux'' and serve as part of the input files for $ T_RENT_o $, vHLLE, and THERMINATOR 2. The IC is generated by $ T_RENT_o $ using the parameters governed by input file I. Subsequently, vHLLE is invoked for the relativistic hydrodynamical evolution. The results obtained from $ T_RENT_o $together with the input file part II are fed to vHLLE as the parameters. Subsequently, the output from vHLLE is combined with input file III, which is input to THERMINATOR 2 to perform the hadronization. Finally, the postscript is utilized to evaluate the relevant observables, such as the particle spectrum and collective flow. The calculations are conducted on an event-by-event fluctuating basis.

This study considers collisions of gold (Au) and three types of uranium targets [24] as shown in Table 1, where the uranium nuclei are denoted as U, U2, and U3, respectively. In addition to the original nuclei, we introduce further modifications to the deformation parameters $ \beta_2 $ and $ \beta_4 $ of the Woods-Saxon profile based on Eq. (3). In particular, we further consider different geometric deformations for the given nuclei. By performing a systematic variation of these parameters, we evaluate the resulting collective flow, particularly the elliptic flow $ v_2 $.

Symbol	R	a	$\beta_2$	$\beta_4$
Au	6.37	0.535	0.0	0.0
U	6.81	0.60	0.280	0.093
U2	6.86	0.42	0.265	0.0
U3	6.67	0.44	0.280	0.093
Au$\langle 0\rangle$	6.37	0.535	0.0	0.0
Au$\langle 1\rangle$	6.37	0.535	−0.065	−0.031
Au$\langle 2\rangle$	6.37	0.535	−0.131	−0.031
Au$\langle 3\rangle$	6.37	0.535	−0.196	−0.031
Au$\langle 4\rangle$	6.37	0.535	−0.262	−0.031
Au$\langle 5\rangle$	6.37	0.535	−0.131	−0.015
Au$\langle 6\rangle$	6.37	0.535	−0.131	−0.046
Au$\langle 7\rangle$	6.37	0.535	−0.131	−0.062
U$\langle 0\rangle$	6.81	0.60	0.0	0.0
U$\langle 1\rangle$	6.81	0.60	0.070	0.093
U$\langle 2\rangle$	6.81	0.60	0.140	0.093
U$\langle 3\rangle$	6.81	0.60	0.210	0.093
U$\langle 4\rangle$	6.81	0.60	0.280	0.093
U$\langle 5\rangle$	6.81	0.60	0.560	0.093
U$\langle 6\rangle$	6.81	0.60	0.280	0.046
U$\langle 7\rangle$	6.81	0.60	0.280	0.139
U$\langle 8\rangle$	6.81	0.60	0.280	0.186
U2$\langle 0\rangle$	6.86	0.42	0.0	0.0
U2$\langle 1\rangle$	6.86	0.42	0.265	0.0
U3$\langle 0\rangle$	6.67	0.44	0.0	0.0
U3$\langle 1\rangle$	6.67	0.44	0.070	0.093
U3$\langle 2\rangle$	6.67	0.44	0.140	0.093
U3$\langle 3\rangle$	6.67	0.44	0.210	0.093
U3$\langle 4\rangle$	6.67	0.44	0.280	0.093
U3$\langle 5\rangle$	6.67	0.44	0.560	0.093
U3$\langle 6\rangle$	6.67	0.44	0.280	0.046
U3$\langle 7\rangle$	6.67	0.44	0.280	0.139
U3$\langle 8\rangle$	6.67	0.44	0.280	0.186

Table 1.  Woods-Saxon profile. Left: Original Au and U nuclei provided by $T_RENT_o$. Right: Implemented Au and U nuclei including the $\beta_2$ and $\beta_4$ variations.

The remaining parameters, such as R and a, are kept unchanged for these calculations. By varying the initial nucleus deformation, we aim to explore their impact on the resultant observables, particularly the collective flow. The specific Woods-Saxon profile parameters adopted for the present study are given in Table 1, which are indicated by an index number enclosed by a pair of angle brackets following the name of the nucleus. For instance, U$ 2\langle 3 \rangle $ indicates the third parameter set for the nucleus U2.

The energy profiles in the radial direction are shown in Fig. 3, where the solid black curves represent the symmetric nuclei, whereas the dashed red ones are the deformed nuclei. We observe that the deviation in the profile is more apparent for the uranium nucleus, particularly if we assume a higher degree of deformation being present at the bottom of Fig. 3. However, visually, the deformation does not considerably modify the Woods-Saxon profile. Nonetheless, the potential impact on the collective flow regarding observational implications is significant.

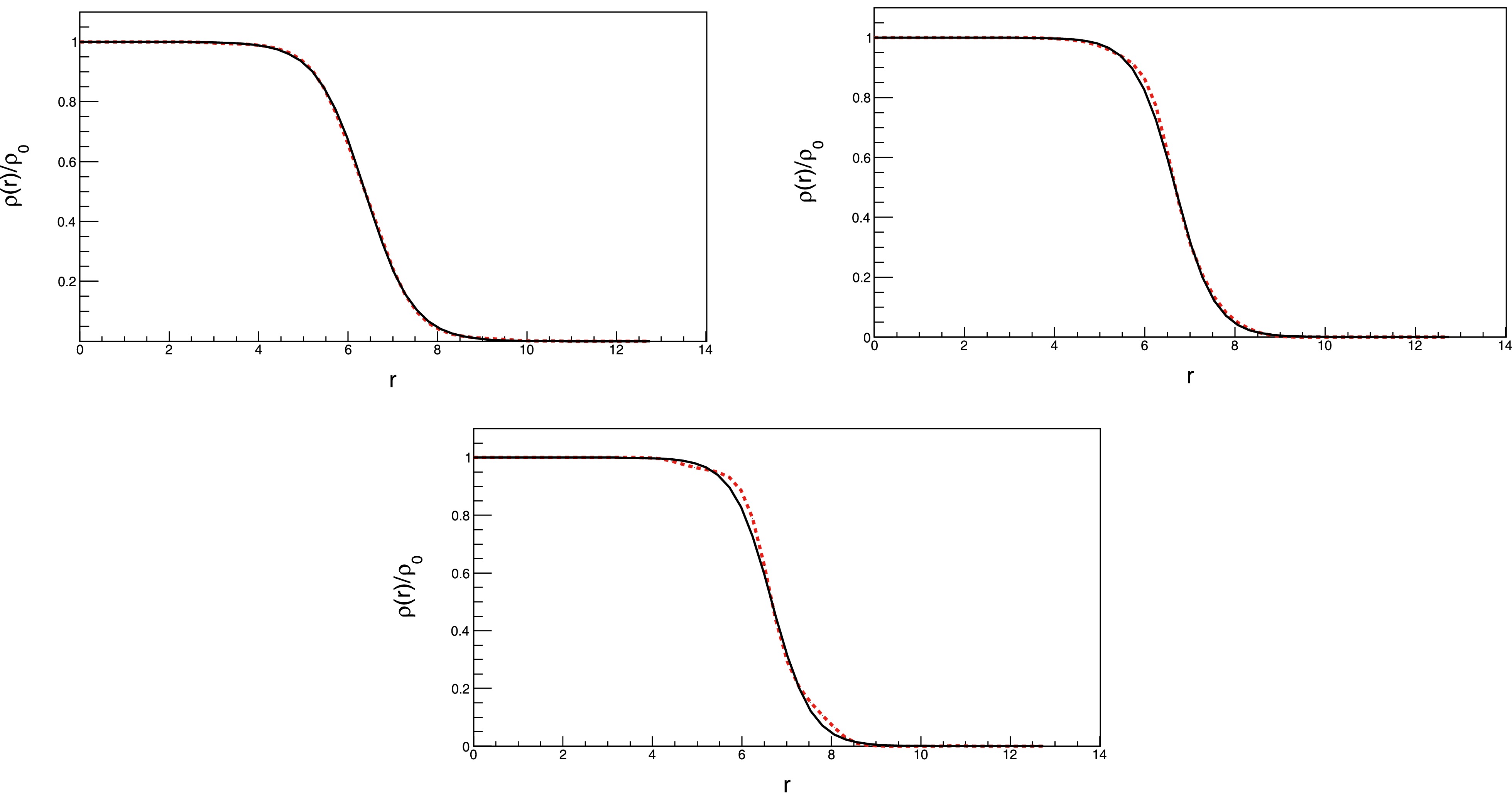
Figure 3.  (color online) Woods-Saxon profile for Au (top left), U2 (top right), and U3 (bottom) nuclei. The solid black curves are for the symmetric nuclei, whereas the dashed red ones represent the deformed nuclei. For the deformed nuclei, the profile is evaluated along the transverse plane $z=0$, with $\beta_2=-0.131$ and $\beta_4=-0.031$ for Au, $\beta_2=0.265$ and $\beta_4=0.0$ for U2, and $\beta_2=0.280$ and $\beta_4=0.093$ for U3.

We now calibrate our model to produce the correct multiplicity distribution $ {\rm d} N_{ch}/{\rm d}\eta $. The experimental results indicate that the charged particle multiplicity as a function of centrality fraction $ x\in [0,1] $ can be parameterized as follows [34]:

where $ c_i $ denotes constants. Specifically, we have $ c_1 = 5.0670 $, $ c_2 = 3.923 $, $ c_3 = 0.2310 $, $ c_4 = 18.37 $, and $ c_5 = 0.4842 $ for Au+Au collisions and $ c_1 = 5.3473 $, $ c_2 = 4.298 $, $c_3 = 0.2959$, $ c_4 = 18.21 $, and $ c_5 = 0.4541 $ for U+U collisions. Note that the centrality fraction x, the inverse of Eq. (5), can be estimated from the data because it is essentially defined as a cumulative distribution function as presented in [38]:

where $f(\mathrm{d}N_{ch}/\mathrm{d}\eta)$ is the probability density function, which is the negative of the reciprocal of the derivative of Eq. (5).

We generate 3200 events to perform the calibration and compare the resultant probability density functions f against those extracted by the STAR Collaboration for both the Au+Au and U+U collisions. Subsequently, the parameters $ p, k $, and w of $ T_RENT_o $ are tuned to adapt to the experimental data. We observe that relevant parameters mostly fall in the following range: $-2\leq r p\leq 2; 0 \leq k \leq 2$, and $ 0.2\leq w \leq 0.6 $. The parameters of the event generator are obtained by minimizing the sum of the squares of the deviations. As shown in Fig. 4, the $ T_RENT_o $ code can reproduce the multiplicity yields, where an overall normalization factor is properly introduced in the initial profiles. The specific values of the parameters are given in Table 2.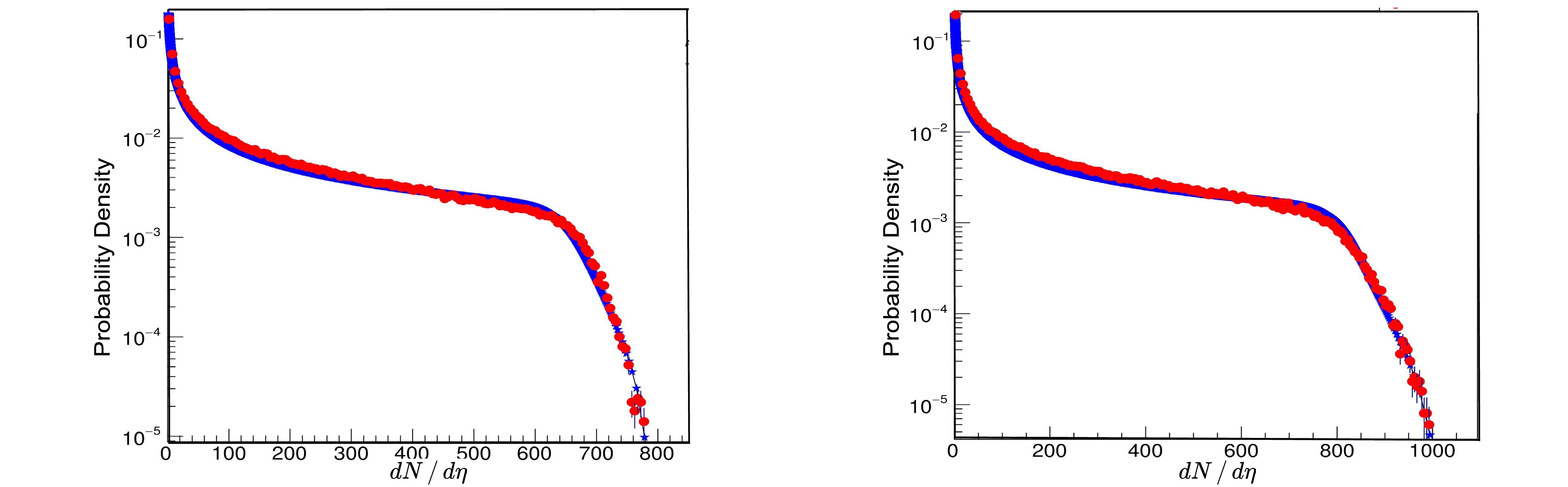

Figure 4.  (color online) Probability density distribution for Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV (left) and U+U collisions at $\sqrt{s_{NN}}=193$ GeV (right). The blue stars represent the results extracted from the STAR data, and the red filled circles are the results using $T_RENT_o$.

Nucleus	p	k	w	$\chi^2$
Au	−0.4	1.3	0.4	0.156
U	−0.7	1.7	0.2	0.287

Table 2.  Optimized parameters utilized by the $T_RENT_o$ event generator.

The initial geometry of the nucleus is implemented in $ T_RENT_o $ using the Woods-Saxon profile $ \rho(r) $governed by Eqs. (2) and (3). Note that, in literature, different profiles have been employed by some authors. For example, only the quadrupole expansion is considered in Refs. [39−42]. In contrast, in Ref. [43], quadrupole and octupole deformations are considered for the Woods-Saxon profile in a study on Zr+Zr and Ru+Ru collisions. In this study, we consider quadrupole and hexadecapole deformations in terms of the parameters $ \beta_2 $ and $ \beta_4 $.

Finally, to ensure that we have sufficient statistical power for the numerical analysis, we perform tentative simulations for U$ \langle 2\rangle $+U$ \langle 2\rangle $ collisions at $ \sqrt{s_{NN}} = 193 $ GeV while varying the number of events (NE). The flow harmonics evaluated for different NEs are presented in Fig. 5. In the left panel of Fig. 5, the differential elliptic flow $ v_2 $ and its standard error are shown as a function of transverse momentum. Additionally, the dependence of average elliptic flow on the NE is analyzed in the right panel of Fig. 5.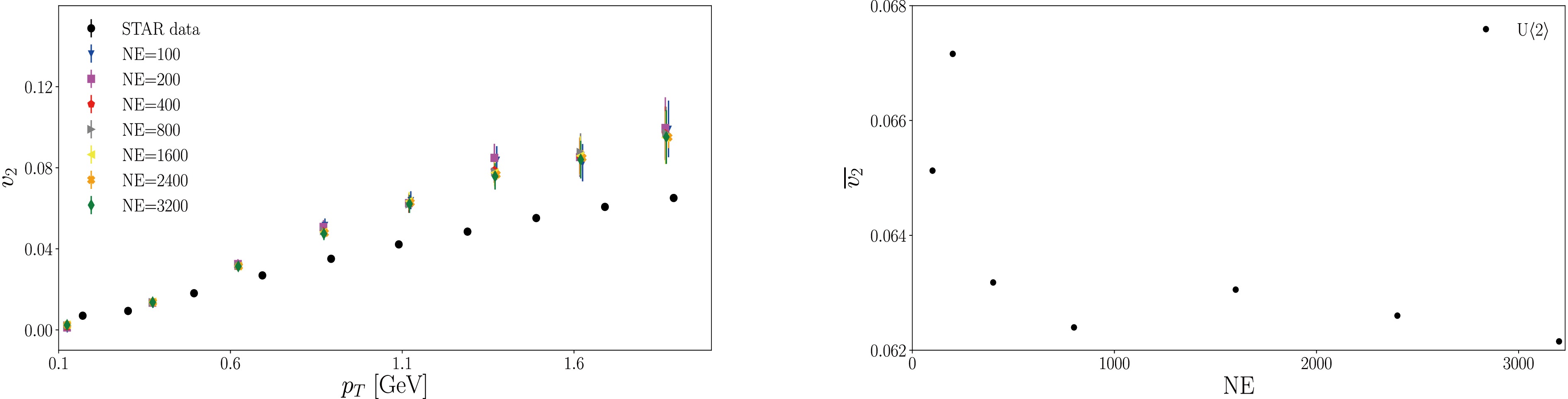

Figure 5.  (color online) Tentative simulations to guarantee the statistical power of the results. Left: Elliptic flow for U$\langle 2\rangle$+U$\langle 2\rangle$ collisions at $\sqrt{s_{NN}}= 193$ GeV, evaluated using different NEs. Right: Average elliptic flow $\overline{v_2}$ evaluated as a function of NE.

We observe that both $ v_2 $and its fluctuation increase with increasing transverse momentum. For the calculations of differential flows, reasonable numerical convergence is achieved for NE $ \ge 1000 $. Therefore, we adopt the value NE$ = 1600 $ for a given collision setup, which is sufficient for our purpose. Moreover, in our calculations, the number of Monte Carlo events is selected to be 1000.

In this section, we describe numerical simulations to explore the effect of nucleus deformation on the resultant collective flow. The obtained results on flow harmonics are compared with the experimental data from the STAR Collaboration [66] for Au+Au collisions at $ \sqrt{s_{NN}} = 200 $ GeV and U+U collisions at $ \sqrt{s_{NN}} = 193 $ GeV.

Using the IC generated using $ T_RENT_o $, we performed hydrodynamics simulations using the CHESS code. Two factors involve the IC. The first is intrinsic to the nuclei, namely, the nucleus's radius R and skin depth a, particularly for the various uranium nuclei. The second factor is the nucleus's initial geometry for different types of nuclei involved in the collisions. This study primarily focuses on the second factor and explores its impact on the observables.

Before analyzing the flow harmonics, we present the results of the multiplicity spectra. In Fig. 6, we show the transverse momentum spectra of Au+Au and U+U collisions, which are compared with the PHOBOS data [67] when applied for Au+Au collisions at 200 GeV. The results indicate that reasonable agreement is achieved for both collision systems. The lower transverse momentum region $p_T < 0.5\, \mathrm{GeV}$ is more relevant for us. The significance of the emanated lower $ p_T $ particles is related to not only the overall multiplicity but also the collective flow, which is primarily governed by the momentum anisotropy transformed from the initial state deformation and fluctuations via the hydrodynamic evolution.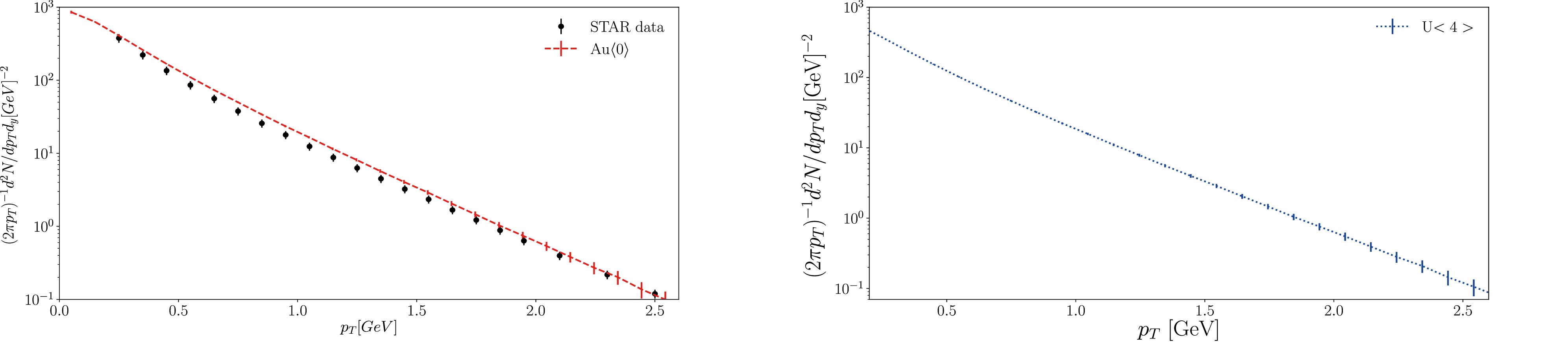

Figure 6.  (color online) Transverse momentum spectra obtained using CHESS. Left: Numerical results for Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV (red curve) compared with the PHOBOS data [67] (black symbols). Right: Numerical results for U+U collisions at $\sqrt{s_{NN}}= 193$ GeV (blue dotted curve).

Regarding the collective flow, we first explore the elliptic flow $ v_2 $ and its dependence on the initial geometric deformation. Ref. [38] indicates that initial-state anisotropy $ \epsilon_2 $ affects the final-state elliptic flow through a largely linear relation

where $ v_2\{2\} $ is the elliptic flow evaluated using the two-particle cumulant, $ \epsilon_2\{2\} $ is the eccentricity second order cumulant, and $ \kappa_2 $ is a constant. However, for higher-order harmonics, such a relation no longer holds [68].

In terms of quadrupole and hexadecapole deformations, we are unclear on how much the initial geometric deformation of an individual nucleus affects the eccentricities and the resulting collective flows on an event-by-event basis. Hence, both the overall deformation and individual effects associated with quadrupole and hexadecapole deformations are interesting to study.

In Fig. 7, we show the elliptic flows for Au+Au collisions by varying $ \beta_2 $ and $ \beta_4 $ while keeping the remaining parameters unchanged. Moreover, we elaborate on a scenario in which the overall deformation of the nucleus increases gradually. Specifically, for this case, the symmetric nucleus ($ 0 $%), $ 0.1 $%, $ 1 $%, $ 10 $%, and $ 100 $% percent of deformation are considered. The relative deformations are implemented as an interpolation between the symmetric and Au<2> nuclei and performed simultaneously for $ \beta_2 $ and $ \beta_4 $. The resulting elliptic flows are presented as functions of $ p_T $ and are compared with the STAR data [66].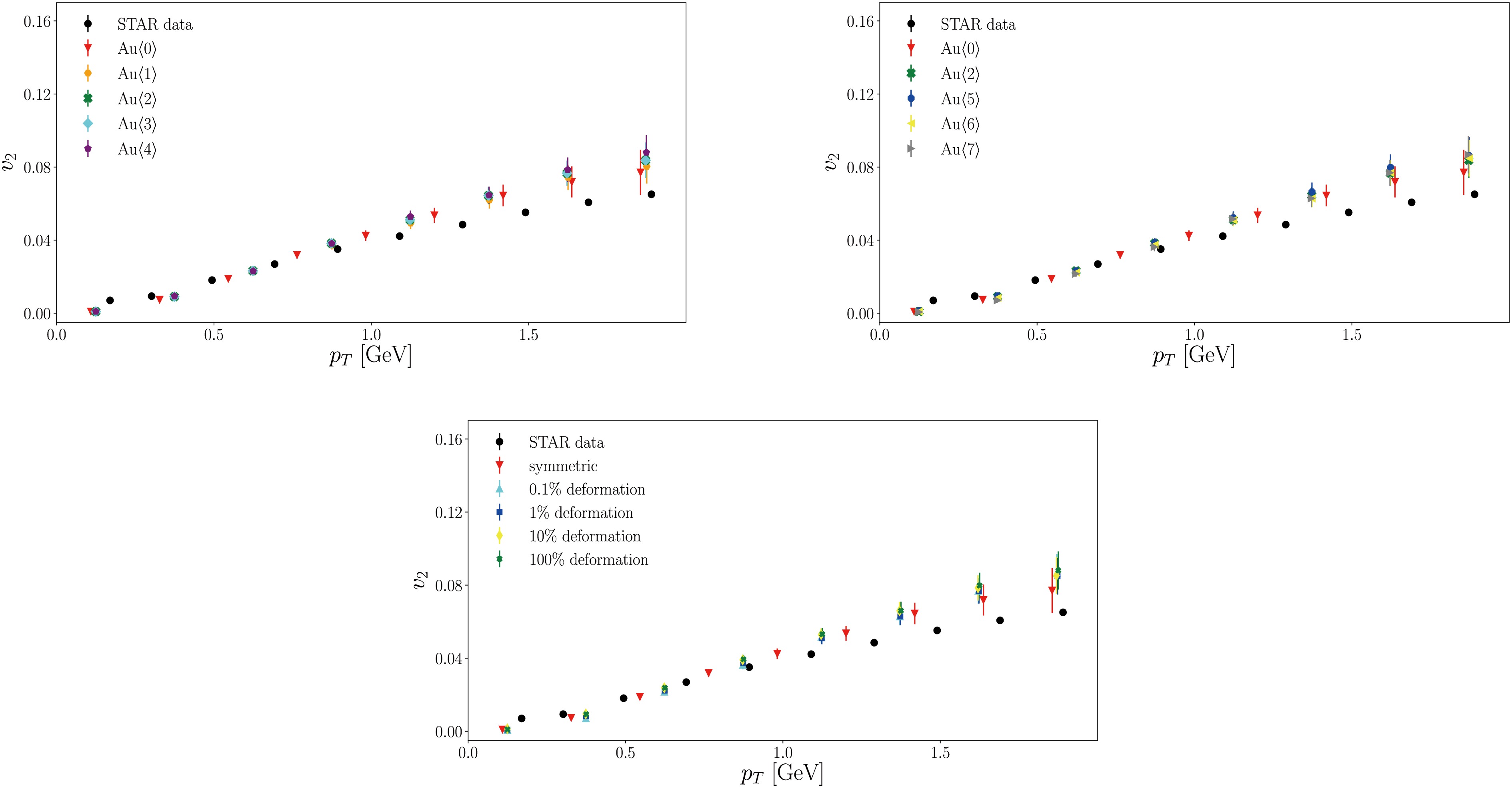

Figure 7.  (color online) Differential elliptic flow $v_2$using the centrality 0-6% for Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV with different degrees of nucleus deformation. The numerical results obtained using the CHESS code are compared with the STAR data [66]. Top-left: The results obtained by varying the quadrupole deformation parameter $\beta_2$; the specific parameters are given in Table 1. Top-right: Results obtained by varying the hexadecapole deformation parameter $\beta_4$; the specific parameters are given in Table 1. Bottom: Results obtained by varying the overall deformations of the Au nucleus. For all the plots, the red triangles represent the results for symmetric Au nuclei. The error bars indicate the standard errors.

We observe that the initial geometrical deformations affect the resulting elliptic flow. As shown in the bottom panel of Fig. 7, the resulting differential flow slightly increases as the overall deformation increases. The relation between the size of the deformation and the resulting impact on the elliptic flow is primarily linear. This is understood regarding existing results, which show that the elliptic flow $ v_2 $ is primarily proportional to the second cumulant of initial space anisotropy $ \epsilon_2 $ [68−72], except that the elliptic flow persists for ultra-central collisions [72−75]. Nonetheless, the model cannot faithfully reproduce the data at large transverse momenta. Through tuning individual deformation parameters, the above results mostly hold. Specifically, the elliptic flow generally becomes more suppressed, particularly in the region with larger transverse momenta, as $ \beta_2 $ or $ \beta_4 $ increases. In contrast, at smaller $ p_T $ values, the dependence of elliptic flow on these parameters is complex. An explicit study on the dependence of $ v_2 $ on the deformation parameters is presented in Fig. 10, where the average flow is analyzed.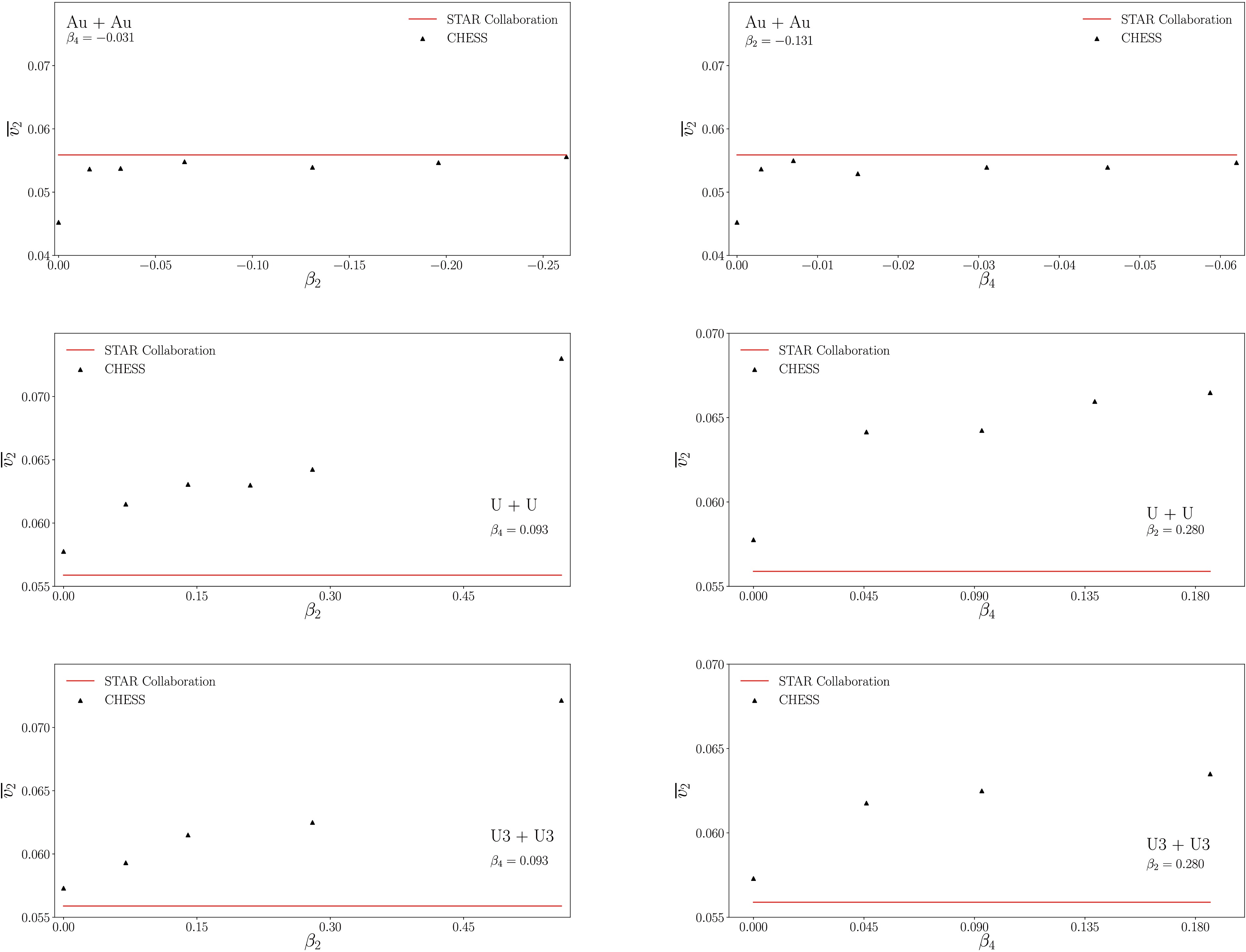

Figure 10.  (color online) Average elliptic flow $v_2$ for Au+Au and U+U collisions with centrality 0-6% as a function of nucleus deformation parameter. The numerical results obtained using the CHESS code are compared with the STAR data [66]. Top-left: Resulting flow as a function of $\beta_2$ for Au+Au collisions. Top-right: Resulting flow as a function of $\beta_4$ for Au+Au collisions. Middle-left: Resulting flow as a function of $\beta_2$ for U+U collisions. Middle-right: Resulting flow as a function of $\beta_4$ for U+U collisions. Bottom-left: Resulting flow as a function of $\beta_2$ for U3+U3 collisions. Bottom-right: Resulting flow as a function of $\beta_4$ for U3+U3 collisions. The specific parameters are given in Table 1 for all the plots. The red horizontal line indicates the average flows obtained by the STAR Collaboration.

A similar procedure is also performed for various types of U+U collisions. In Fig. 8, we present the flow harmonics for the three uranium nuclei while tuning the respective parameters regarding the quadrupole and hexadecapole deformations. The numerical results obtained using CHESS are also compared with the STAR data [66]. Generally, the initial geometric deformation plays a role in the final elliptic flow. As expected, the differential elliptic flow primarily increases with increasing $ \beta_2 $ or $ \beta_4 $, which is apparent, particularly for the region with a large transverse momentum.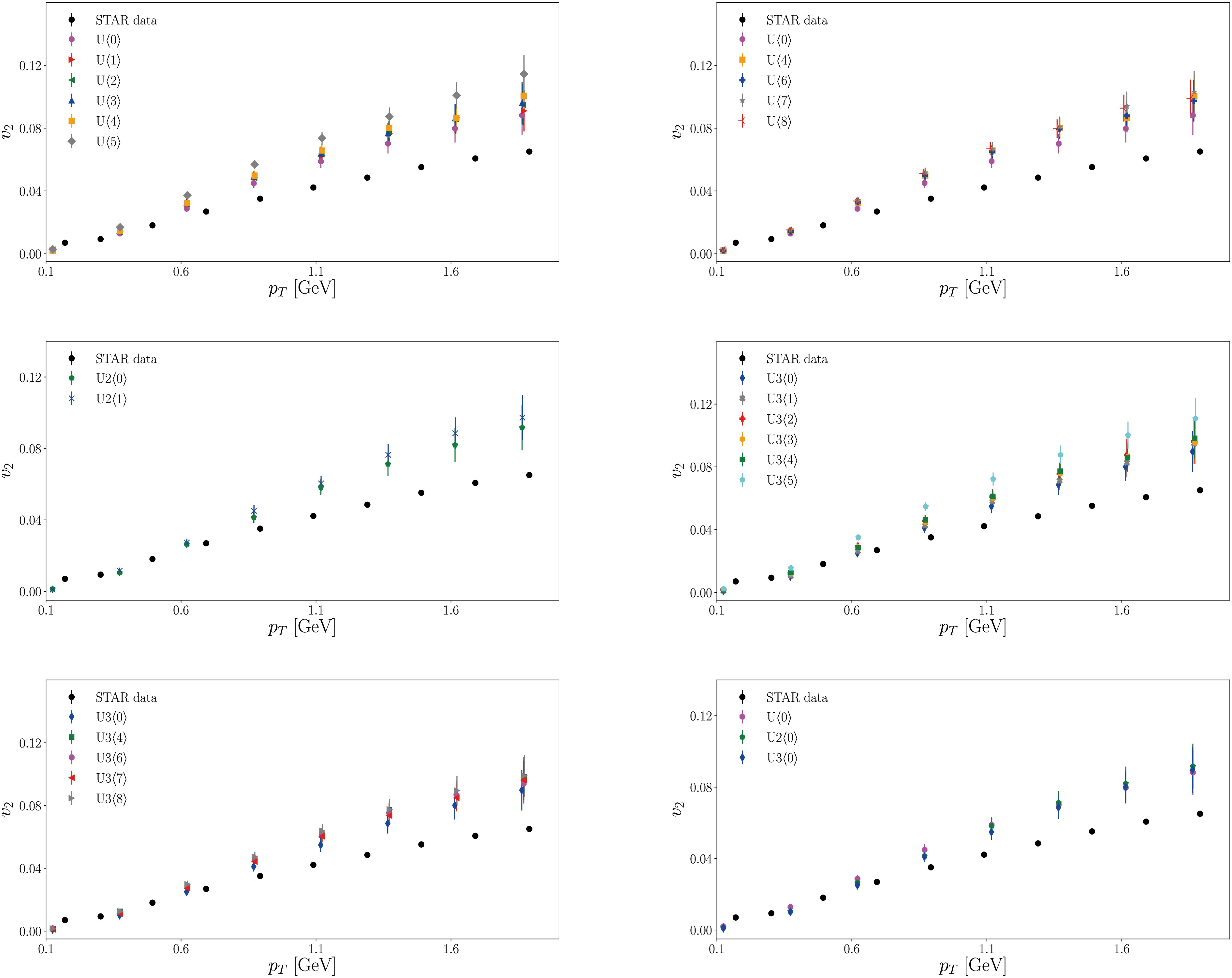

Figure 8.  (color online) Differential elliptic flow $v_2$ for U+U collisions at $\sqrt{s_{NN}}=193$GeV with a centrality of 0-6% and different degrees of nucleus deformation. The numerical results obtained using the CHESS code are compared with the STAR data [66] for Au+Au collisions at 200 GeV. Top-left: Results obtained by varying quadrupole deformation parameter $\beta_2$for U. Top-right: Results obtained by varying hexadecapole deformation parameter $\beta_4$for U. Middle-left: Results obtained by varying quadrupole deformation parameter for U2. Middle-right: Results obtained by varying hexadecapole deformation parameter $\beta_2$for U3. Bottom-left: Results obtained by varying the hexadecapole deformation parameter $\beta_4$for U3. Bottom-right: Results obtained for symmetric U+U, U2+U2, and U3+U3 collisions. The specific parameters are given in Table 1 for all the plots. The error bars indicate the standard errors.

This characteristic is universal to all three types of U+U collisions. However, in the region with insignificant $ p_T $, the dependence of $ v_2 $ on the deformation parameter is more subtle, which is explored further below. Regarding the magnitude of the effect, we conclude that hexadecapole deformation has a less significant impact when compared with that of quadrupole deformation. Although $ \beta_2 $ does not affect the initial eccentricity $ \epsilon_2 $ in a straightforward fashion, it is understood that $ \beta_4 $ is likely to have a minor effect compared with $ \beta_2 $. The obtained results agree reasonably with the STAR data for the low $ p_T $ region.

However, deviations occur at larger transverse momenta, where the numerical simulations systematically overshot the data. In the bottom-right panel of Fig. 8, we also perform a comparison for the three types of uranium nuclei when eliminating their geometric deformations. We find that the resultant elliptic flows are somewhat similar for the three systems, whereas U$ \langle 0\rangle $+U$ \langle 0\rangle $ collisions remain slightly closer to the experimental data.

By comparing the results of Au+Au and U+U collisions, we observe slightly different behaviors of the effect of deformation on the collective flow. On the one hand, for U+U collisions, we have observed that the increase in deformation mostly promotes the elliptic flow $ v_2 $ according to Eq. (7). On the other hand, for Au+Au collisions, the observable effect is less significant. In particular, in the high transverse momentum region, while the numerical results overshoot the data, flow harmonics only increase slightly as the deformation becomes more significant. In other words, we find that the elliptic flow in U+U collisions is more sensitive to the deformation. We attribute the difference in the magnitude of the effect to the highly nonlinear nature of the underlying hydrodynamic evolution and the strongly interacting system's equation of state.

It is also interesting to validate the relation given by Eq. (7), particularly regarding the apparently opposite effects of the deformation. Hence, we present the IC, inclusively the initial geometric deformation, generated using $ T_RENT_o $ in Table 3 on an event-by-event basis.

Nucleus	b	$N_\mathrm{part}$	$\epsilon_2$
Au$\langle 0\rangle$	9.82	104	0.432
Au$\langle 3\rangle$	9.90	104	0.429
Au$\langle 7\rangle$	10.04	99	0.446
U$\langle 0\rangle$	10.69	121	0.489
U$\langle 4\rangle$	10.94	118	0.498
U$\langle 8\rangle$	10.81	118	0.495
U2$\langle 0\rangle$	10.09	123	0.513
U2$\langle 1\rangle$	10.28	121	0.525
U3$\langle 0\rangle$	9.86	127	0.503
U3$\langle 4\rangle$	10.05	126	0.509
U3$\langle 8\rangle$	9.99	124	0.505

Table 3.  IC generated using $T_RENT_o$ for the collisions investigated in this study. For specific types of nuclei, the information on impact parameter b, number of participants $N_\mathrm{part}$, and spatial eccentricity $\epsilon_2$ are presented. Where applicable, the table gives average values evaluated on an event-by-event basis.

From Table 3, the observed results on flow and nucleus deformation can be readily understood in terms of Eq. (7) as a result of the system's initial geometry. Specifically, the eccentricity of the IC increases as the impact parameter increases and the number of participants decreases. Consequently, elliptic flow deviates from the value of symmetric nuclei in alignment with the initial state eccentricity. These results are largely consistent with the linear response dictated by Eq. (7) [68−70]. We have also observed that the effect of deformation factor $ \beta_4 $ on the initial state and final observables appears to be less significant than that of $ \beta_2 $, as directly indicated in Table 3.

We compare the elliptic flow data from symmetric Au+Au collisions with symmetric and deformed U+U data; the results are visualized in Fig. 9.

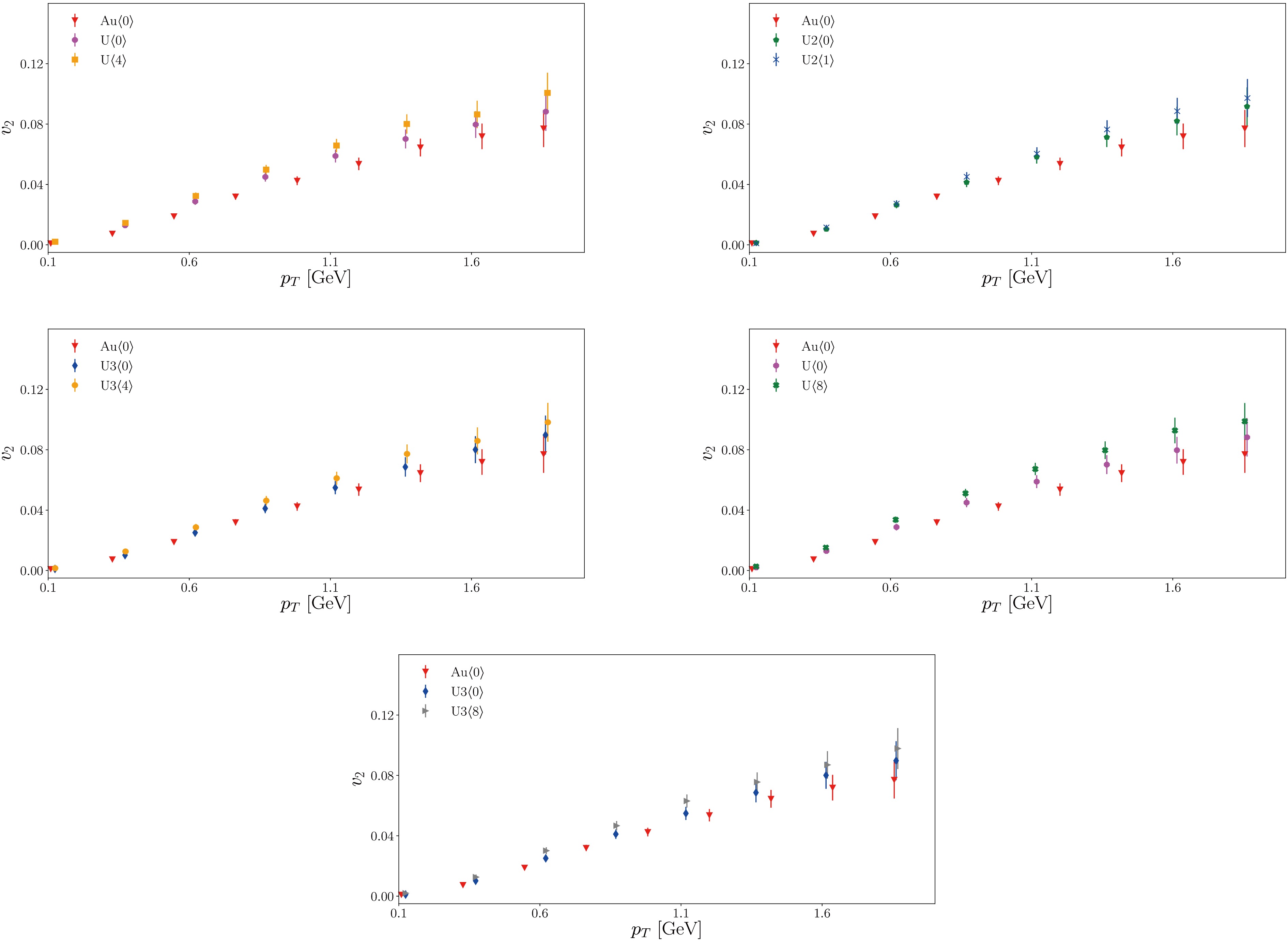
Figure 9.  (color online) Elliptic flow $v_2$ comparison for Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV and different U+U collisions at $\sqrt{s_{NN}}=193$ GeV. Top-left: Symmetric Au nuclei compared with symmetric and deformed U nuclei in terms of $\beta_2$. Top-right: Symmetric Au nuclei compared with symmetric and deformed U2 nuclei. Middle-left: Symmetric Au nuclei compared with symmetric and deformed U3 nuclei in terms of $\beta_2$. For all the plots, the red triangles represent the results for symmetric Au nuclei. Middle-right: Symmetric Au nuclei compared with symmetric and deformed U nuclei in terms of $\beta_4$. Bottom: Symmetric Au nuclei compared with symmetric and deformed U3 nuclei in terms of $\beta_4$. The error bars indicate the standard errors.

Comparing Au+Au with U+U data, we observe that the elliptic flow for Au+Au collisions is below the U+U data for the three types of U nuclei. In the top-left panel of Fig. 9, the elliptic flow of Au+Au collisions is compared with that of U+U collisions. The top-right panel of Fig. 9 compares the elliptic flow from Au+Au collisions with that from U2+U2 collisions. In the middle-left panel of Fig. 9, we compare the $ v_2 $ values of Au+Au and U3+U3 collisions. These figures are intrinsically related to the deformation factor $ \beta_2 $ effect. We also compare the results obtained for deformed uranium nuclei according to variations in the $ \beta_4 $ parameter. In the middle-right of Fig. 9, we compare the symmetric Au+Au collisions with symmetric and deformed U+U collisions in terms of $ \beta_4 $ parameter. Finally, at the bottom of Fig. 9, the symmetric Au+Au collision data are compared with U3+U3 collisions in terms of $ \beta_4 $ variations.

We can observe a similar behavior for elliptic flow for $ p_T<0.6 $ GeV. In this regime, Au, U, U2, and U3 essentially assume the same form, wheras for $ p_T>0.6 $ GeV, the results computed for Au+Au, U+U, U2+U2, and U3+U3 differ, with uranium collisions exhibiting high $ v_2 $. These results are found for different degrees of deformation in terms of parameters $ \beta_2, \,\beta_4 $. The behavior observed in the present study is the same as that in Ref. [38].

Finally, we discuss the effect of deformation on elliptic flow in the low transverse momentum region. We evaluate the average $ v_2 $ as a function of deformation parameters $ \beta_2 $ and $ \beta_4 $. As the average elliptic flow receives contribution primarily from the lower $ p_T $ region, the calculations are primarily aimed at the relevant region where the dependence on transverse momentum is more sensitive. When one of the deformation parameters varies for a given nucleus, the remaining parameters are held constant at their original values given in Table 1. The results are presented in Fig. 10, where both Au+Au and U+U collisions have been considered.

For Au+Au collisions, we observe that the elliptic flow is rather sensitive when the deformation is small. When compared with Fig. 7, the outstanding value of $ \bar{v_2} $ appears to be primarily due to the contribution from the anisotropy of low $ p_T $ particles. Here, the average is taken among all the emitted particles and on an event-by-event basis. As the deformation increases, the impact on the elliptic flow primarily follows a linear relation. The elliptic flow does not go to zero at vanishing $ \beta_2 $, which is largely attributed to non-vanishing geometric fluctuations. For this study, we find that the value $ \beta_2\approx-0.26 $ gives the average elliptic flow that is in reasonable agreement with the experimental data. Additionally, regarding Fig. 10, the value $ \beta_4 \approx-0.031 $ provides the best fit to the experimental data, which was originally adopted by $ T_RENT_o $. As a comparison, Giacalone [40] observed a relatively smaller value $ \beta_2\approx-0.15 $ by considering only the quadrupole deformation. We attribute such a difference mostly to that of the hydrodynamic model and IC.

For U+U collisions, the average values of $ \bar{v_2} $ exhibit a very similar behavior to those for the differential flow, analyzed in Fig. 8. This is expected, as the differential flows are found to be monotonical functions of transverse momentum, and the magnitudes of the effect monotonically increase with increasing deformation parameters. When comparing the effect of $ \beta_2 $ and that of $ \beta_4 $, the latter is found to play a slightly more significant role.

In this study, we explore the effect of nucleus deformation on flow harmonics using a hybrid code CHESS. By implementing the initial quadrupole and hexadecapole geometric deformations into the Woods-Saxon profile through $ T_RENT_o $, we simulate viscous hydrodynamic evolutions for Au+Au and U+U collisions. The particle spectrum and collective flow are evaluated. In particular, we analyze the collective flow as a function of the deformation parameters $ \beta_2 $ and $ \beta_4 $.

Our numerical results prompt a comparison between Au+Au and U+U nuclear collisions, revealing subtle differences in the resulting behavior. For Au+Au collisions, the simulations for both symmetric and deformed nuclei provide reasonable results regarding the experimental data from the STAR Collaboration, as shown in Fig. 7. The results for deformed nuclei with slightly augmented flow harmonics closely resemble the experimental data. In contrast, as shown in Fig. 10, the transition from symmetric to deformed nuclei indicates a shift in the average elliptic flow, $ \overline{v_2} $, owing to the contributions from high transverse momentum $ p_T\sim 2 $ GeV. For symmetric nuclei, $ \overline{v_2} $ significantly overestimates the data, and as deformation increases, the average elliptic flow converges to the experimental data. Conversely, for U+U nucleus collisions, numerical simulations diverge further from the STAR data as deformation factors increase. These results are explicitly shown in Fig. 8, where the elliptic flow increases in response to the deformation factors. The computation of the average elliptic flow, presented in Fig. 10, supports the linear behavior described in Eq. (7) that is extensively documented in the literature.

Studies regarding the effect of initial geometric deformation have been primarily motivated to answer the following questions: whether such deformation is observable and which deformation factor, $ \beta_2 $ or $ \beta_4 $, predominantly influences collective flow. From this study, the answer remains elusive, aligning with the results obtained by other authors [38−40, 50]. Nonetheless, for collisions of almost symmetric Au nuclei, the resulting integrated flow is observed to be somewhat sensitive to the initial quadrupole and hexadecapole deformations. Hence, the topic should be scrutinized by employing advanced analysis tools, such as Bayesian analysis [75−77] and maximum likelihood estimator [78, 79]; in particular, emulators [80−82] and variational autoencoders should be employed, whose significant potential has been recently demonstrated [83−86].