-
General relativity (GR) is regarded as the most successful and tested theory of gravity. However, it has notable challenges in explaining fundamental questions such as the occurrence of singularities inside black holes (BHs) [1, 2]. Additionally, GR still cannot explain phenomena such as dark matter (DM) and dark energy. These challenges indicate that GR is an incomplete theory and must be modified. Issues faced by GR might be resolved by proposing modified theories of gravity and exploring their properties to explain astrophysical phenomena that remain outside the reach of GR. It is worth noting that recent modern observations of phenomena such as gravitational waves (GWs) [3, 4] and BH shadows [5, 6] will be crucial in providing accurate and promising insights into the limitations of GR. Taken together, it is important to explore the nature of existing gravitational fields in the context of alternative theories of gravity to provide comprehensive explanations of phenomena that GR cannot explain.
From an astrophysical view point, BHs cannot be found in a vacuum because of the presence of matter fields sorrounding them. For example, observations of supernova explosions (SNIa) have confirmed the accelerated expansion of the universe with the cosmological constant Λ acting as vacuum energy and providing a repulsive gravitational effect. In this regard, the effect of the cosmological constant plays a pivotal role at large scales and in the environments sorrounding BHs, causing accelerating space expansion with vacuum energy Λ, which is interpreted as dark energy in the Einstein equations. The cosmological constant can be estimated to be of the order of
$ \Lambda \sim 10^{-52}m^{-2} $ . However, it is widely believed that the repulsive effect of the cosmological constant has a significant impact on the accelerating expansion rate of the universe at large scales [7, 8], and its impact has since been extensively investigated in various astrophysical contexts [9−16]. Additionally, it is important to note that the behavior of dark energy has alternative explanations. For example, the quintessence field, proposed by Kiselev [17], has been considered as an alternative model to explain the the expansion of the universe[7, 18, 19]. In this solution, the quintessence field is defined by the equation of state$ p = \omega_{q}\rho $ with$ \omega_q\in (-1;-1/3) $ [17] and$ (-1;-2/3) $ [20].It is a well-established fact that the motion of massive particles can be strongly affected by the geometry in the strong field regime, while their geodesics, together with the background geometry, can be altered by matter fields sorrounding BHs. From this viewpoint, DM would be important in explaining such phenomena, leading to the introduction of DM through the observation of the flat rotation curves of giant spiral and elliptical galaxies. Later, relying on astrophysical data, it was found that the elusive DM can only explain the rotational velocity of stars orbiting giant spiral galaxies, resulting in DM contributing to nearly 90% of the entire mass of the galaxy, with approximately 10% luminous matter formed by baryonic matter [21]. In the early evolution of the universe, stars were formed with contributions from these regions, especially very close to galaxy centers. Interestingly, observations have revealed that, owing to various dynamics, DM gradually drifted outward to form a galactic dark matter halos surrounding host galaxies. Therefore, based on the galaxy formation scenario, in most cases, all giant elliptical and spiral galaxies have a supermassive BH at their center and are sorrounded by a DM halo (see, e.g., [5, 6]). Various black hole solutions incorporating a DM profile have been proposed in the context of DM scenarios. For example, inspired by a quintessential scalar field developed by Kiselev [17], Li and Yang [22] presented a BH solution with a DM distribution using a phantom scalar field without a cosmological role. Following this line of thought, various extensive analyses for varying scanorios have been conducted since then [23−29]. In addition, models for determining DM halo solutions have been developed (see, e.g., [30−32]). Interestingly, a new DM halo solution has recently been proposed using a Dehnen-(1, 4, 0) type DM halo density profile [33], in which the spherically symmetric BH spacetime is considered to be immersed in a DM halo profile [34]. It should be noted that the phenomenological Dehnen DM density profile has been extensively investigated for various astrophysical phenomena, including galaxies [33]. Following Refs. [17, 34], this study considers a spherically symmetric BH with a Dehnen-(1, 4, 0) type DM halo together with a quintessence field. We explore the BH along with its and features using BH astrophysical observational properties in contexts such as shadow, deflection angle, and quasinormal modes (QNMs).
The event horizon telescope (EHT) obtained a photograph of the BH Sagittarius A* (SgrA*) at the center of the Milky Way galaxy and discovered that the radius of the ring around SgrA* is within 10% of GR's prediction [35−38]. This image clearly shows a bright ring-like structure outside the BH's shadow, which corresponds to the light emitted by the BH's accretion disk. The BH shadow appears as a dark region surrounded by a ring of light. Therefore, studying BH accretion disks can help us understand the characteristics of BHs and the impact of the dark sector, which includes Dehnen-type DM and the quintessence field. This dark sector/disk contributes to the formation of a BH shadow by trapping light in a strong deflection [39, 40]. Analyzing the BH shadow and gravitational lensing effects is crucial for exploring the geometry near the BH horizon. Numerous studies have extensively analyzed BH shadows in various contexts [see 41−56]. Gravitational lensing effects have been used to demonstrate the effectiveness of GR for describing the unique aspects of BH geometry [57]. Therefore, using GR to investigate BH geometries remains essential. However, other models of gravity have also been used to study gravitational lensing around BHs [see58−69].
QNMs are important characteristics of a BH's late-time response to external perturbations. Gravitational interferometers are used to detect quasinormal waves caused by spacetime perturbations [3−5]. Since the discovery of QNMs, the study of BH perturbations has become increasingly important in the last decade [70, 71]. QNMs dominate the late-time gravitational wave signals of BHs and other compact objects. QNMs are described by complex frequencies, with the real component corresponding to the oscillation frequency and the imaginary part relating to the damping rate caused by radiation emission. QNMs are also useful for determining the stability of black holes. In the case of positive imaginary parts of the quasinormal frequencies, the BH becomes unstable to perturbations, while in the case of negative imaginary parts, it remains stable.
This paper is structured as follows: Sec. II provides a description of the Schwarzschild BH embedded in a Dehnen-type DM halo in the background of a quintessence field. Sec. III analyzes BH shadows and the impact of BH parameters. In Sec. IV, we investigate the deflection angle by adapting the Gauss-Bonnet theorem. Next, in Sec. V, we evaluate and examine the QNMs. Finally, our conclusions are presented in Sec. VI.
-
This study derives a static BH with a Dehnen-type DM halo exhibiting a quintessence field. We first construct the density profile of the Dehnen dark matter halo, which is a specific example of a double power-law profile defined by [72]:
$ \begin{aligned} \rho =\rho _{s}\left( \frac{r}{r_{s}}\right) ^{-\sigma }\left[ \left( \frac{r}{r_{s}}\right) ^{\alpha }+1\right] ^{\tfrac{\sigma -\beta }{\alpha }}, \end{aligned} $

(1) where
$ \rho _{s} $ and$ r_{s} $ are the central halo density radius. σ is the specific variant of the profile with values in the set$ [0, 3] $ , where$ \sigma = 3/2 $ is used to fit the surface brightness profiles of elliptical galaxies that closely resemble the de Vaucouleurs$ r^{1/4} $ profile [73]. In this paper, we use the parameters$ \left( \alpha ,\beta ,\sigma \right) =\left( 1,4,0\right) $ [34]. Therefore, Eq. (1) becomes$ \begin{aligned} \rho _{D}=\frac{\rho _{s}}{\left( \dfrac{r}{r_{s}}+1\right) ^{4}}. \end{aligned} $

(2) Next, we determine the mass distribution of the dark matter profile. Thus, the mass profile can be estimated using the relation
$ \begin{aligned} M_{D}=4\pi \int\limits_{0}^{r}\rho \left( r^{\prime }\right) r^{\prime 2} {\rm d} r^{\prime }=\frac{4\pi \rho _{s}r_{s}^{3}r^3}{3\left( r+r_{s}\right) ^{3}}. \end{aligned} $

(3) In a spherically symmetric spacetime, the mass distribution at the center of the dark matter halo can be used to calculate the tangential velocity of the particle moving within it:
$ \begin{aligned} v_{D}^{2}=\frac{M_{D}}{r}=\frac{4\pi \rho _{s}r_{s}^{3}r^2}{3r\left( r+r_{s}\right) ^{3}}. \end{aligned} $

(4) A pure dark matter halo can be described by a spherically symmetric line element:
$ \begin{aligned} {\rm d} s^{2}=-F\left( r\right) {\rm d}t^{2}+\frac{{\rm d}r^{2}}{F\left( r\right) }+r^{2}\left( {\rm d}\theta ^{2}+\sin ^{2}\theta {\rm d}\phi ^{2}\right). \end{aligned} $

(5) where the metric function
$ F(r) $ is related to the tangential velocity through the expression$ \begin{aligned} v_{D}^{2}=r\frac{{\rm d}}{{\rm d}r}\left( \ln \sqrt{F(r)}\right) . \end{aligned} $

(6) Solving for
$ F(r) $ , we obtain$ \begin{aligned} F(r)=exp\left[- \frac{4\pi \rho _{s}r_{s}^{3}\left( 2r+r_{s}\right) }{ 3\left( r+r_{s}\right) ^{2}}\right] \approx 1-\frac{4\pi \rho _{s}r_{s}^{3}\left( 2r+r_{s}\right) }{3\left( r+r_{s}\right) ^{2}}, \end{aligned} $

(7) where the leading order terms of the equation were retained. The final step is to combine the DM profile encoded in
$ F(r) $ with the BH metric function. To do so, we used Xu et al.'s formalism [74], which has also been used by others [34, 75−77], to write the metric line element in this scenario. Therefore, the metric of a static and spherically symmetric BH embedded in a DM halo in the background of quintessential field is described by the line element [17, 34]$ \begin{aligned} {\rm d}s^{2}=-f\left( r\right) {\rm d}t^{2}+\frac{{\rm d}r^{2}}{f\left( r\right) }+r^{2}\left( {\rm d}\theta ^{2}+\sin ^{2}\theta {\rm d}\phi ^{2}\right) , \end{aligned} $

(8) where
$ \begin{aligned} f\left( r\right) =1-\frac{2M}{r}-\frac{4\pi \rho _{s}r_{s}^{3}\left( 2r+r_s\right) }{3\left( r+r_{s}\right) ^{2}}-\frac{\gamma}{r^{3\epsilon+1}}, \end{aligned} $

(9) where γ represents the quintessential state parameter and
$ \epsilon $ is the positive normalization factor depending on the density of the quintessence matter. We can explore the BH solution's behavior by taking advantage of curvature scalars. The Kretschmann scalar for the metric (8) is$ \begin{aligned}[b] R^{\mu \nu \alpha \beta }R_{\mu \nu \alpha \beta }= & \dfrac{4\left( r_{s}+r\right) ^{4}\left( 6M\left( r_{s}+r\right) ^{2}+3r^{-3\epsilon }\left( r_{s}+r\right) ^{2}\gamma +4\pi r_{s}^{3}r\left( r_{s}+2r\right) \rho _{s}\right) ^{2}}{9r^{6}\left( r_{s}+r\right) ^{8}}\\& +\frac{\left( 12M\left( r_{s}+r\right) ^{3}+3r^{-3\epsilon }\left( r_{s}+r\right) ^{4}\gamma \left( 1+3\epsilon \right) \left( 2+3\epsilon \right) -32\pi r_{s}^{3} r^2(r_s+r)\rho + 24 r_{s}^{3} \pi r^3 (r_s +2r)\rho \right)^2}{9r^{6}\left( r_{s}+r\right) ^{8}} \\& +\frac{4\left( r_{s}+r\right) ^{2}\left( 6M\left( r_{s}+r\right) ^{3}+3r^{-3\epsilon }\left( r_{s}+r\right) ^{3}\gamma \left( 1+3\epsilon \right) -8\pi r_{s}^{3} r^2(r_s +r)\rho +8 r_{s}^{3} \pi r^2 (r_s +2r)\rho \right)^2}{9r^{6}\left( r_{s}+r\right) ^{8}}. \end{aligned} $

(10) The Kretschmann scalar exhibits a singularity at
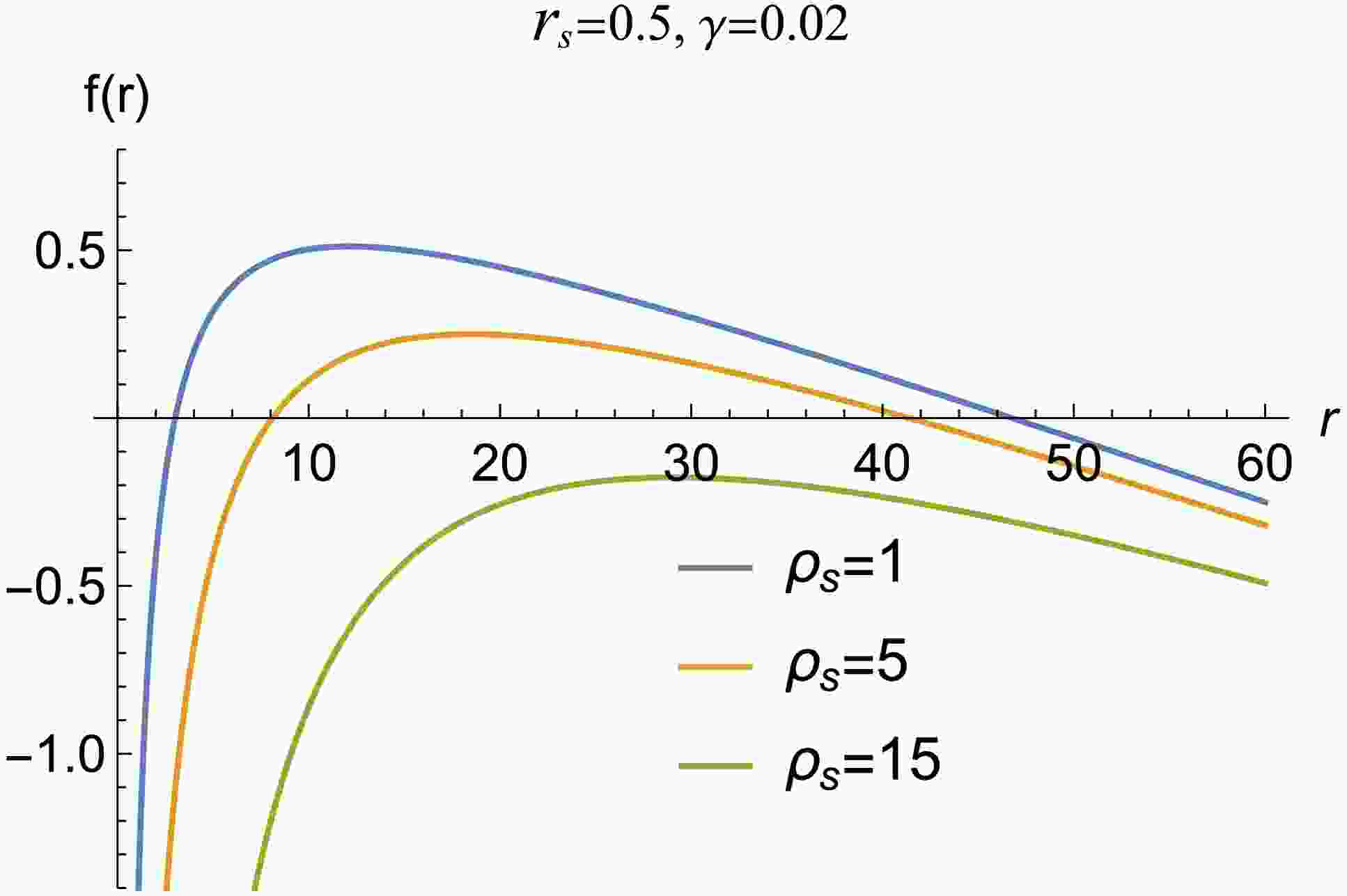
$ r = 0 $ . Thus, the BH solution's singularity at$ r = 0 $ is an essential singularity that no coordinate transformation can eliminate.To visualize the metric function (9), we display it as a function of r, as illustrated in Fig. 1. The graphic indicates that there are two horizons for the conjunction of the Dehnen type DM halo and the quintessence field. For core density large values, there is no horizon that indicates a naked singularity. In addition to event horizons, cosmological horizons become apparent when the quintessence term is taken considered. Spacetime horizons can be determined using the condition
$ f(r) = 0 $ i.e.,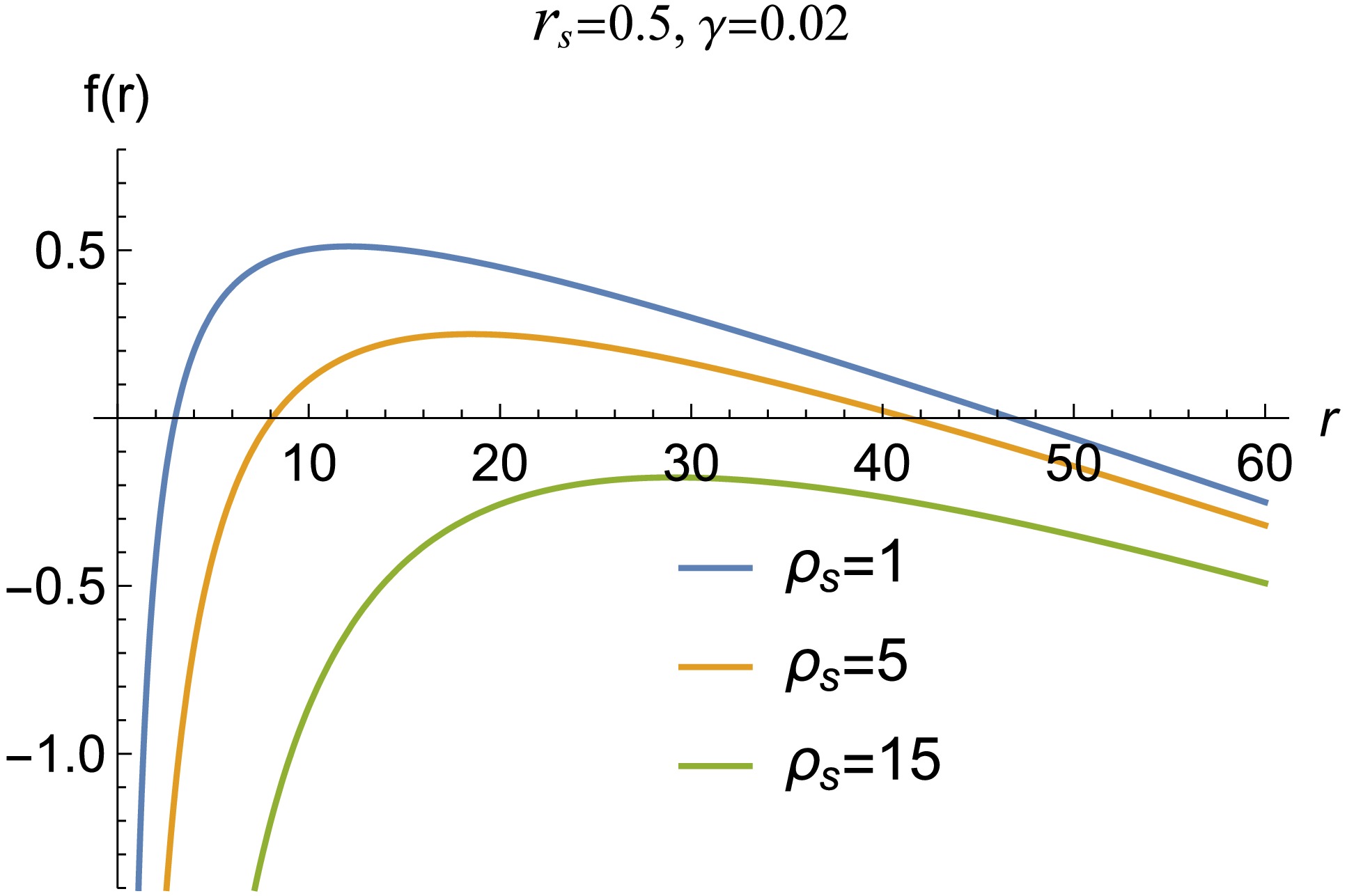
Figure 1. (color online) Metric function is plotted for different values of the BH parameters. Here,
$ M=1 $ and$ \epsilon=-2/3 $ .$ \begin{aligned} 1-\frac{2M}{r}-\frac{4\pi \rho _{s}r_{s}^{3}\left( 2r+r_s\right) }{3\left( r+r_{s}\right) ^{2}}-\frac{\gamma}{r^{3\epsilon+1}}=0. \end{aligned} $

(11) This equation (11) does not have an analytical solution. To derive the event and cosmological horizons, we employ numerical solutions. As we proceed, we will focus on the special case
$ \epsilon=-2/3 $ . The numerical results of these two horizons are tabulated in Table 1.γ $ \rho_s =0.8 $ 

$ r_{s}=0.4 $ 

$ r_{s} $ 

$ r_{h} $ 

$ r_{c} $ 

$ \rho _{s} $ 

$ r_{h} $ 

$ r_{c} $ 

$ 0.01 $ 

$ 0.2 $ 

$ 2.0905 $ 

$ 97.9026 $ 

$ 0.2 $ 

$ 2.12843 $ 

$ 97.8471 $ 

$ 0.6 $ 

$ 3.22949 $ 

$ 96.4389 $ 

$ 0.6 $ 

$ 2.30714 $ 

$ 97.6238 $ 

$ 1 $ 

$ 8.36711 $ 

$ 90.506 $ 

$ 1 $ 

$ 2.49217 $ 

$ 97.3995 $ 

$ 0.02 $ 

$ 0.2 $ 

$ 2.13839 $ 

$ 47.8547 $ 

$ 0.2 $ 

$ 2.17849 $ 

$ 47.797 $ 

$ 0.6 $ 

$ 3.36132 $ 

$ 46.3073 $ 

$ 0.6 $ 

$ 2.3674 $ 

$ 47.5636 $ 

$ 1 $ 

$ 9.6502 $ 

$ 39.2229 $ 

$ 1 $ 

$ 2.56399 $ 

$ 47.3277 $ 

$ 0.03 $ 

$ 0.2 $ 

$ 2.19111 $ 

$ 31.1353 $ 

$ 0.2 $ 

$ 2.23373 $ 

$ 31.0752 $ 

$ 0.6 $ 

$ 3.51788 $ 

$ 29.4842 $ 

$ 0.6 $ 

$ 2.43463 $ 

$ 30.8298 $ 

$ 1 $ 

$ 13.4464 $ 

$ 18.7599 $ 

$ 1 $ 

$ 2.64503 $ 

$ 30.5801 $ 

Table 1. Numerical results for the event horizon
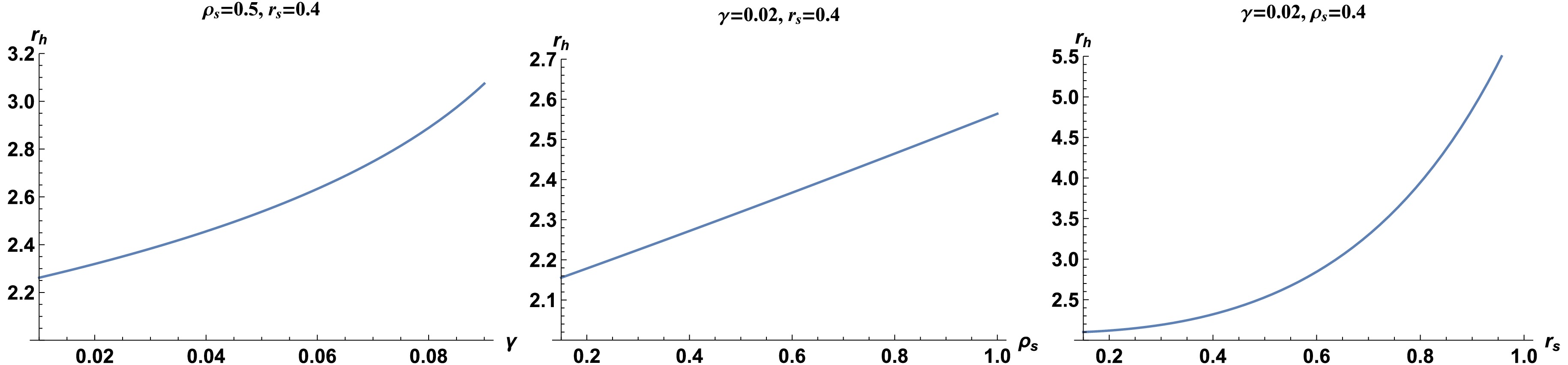
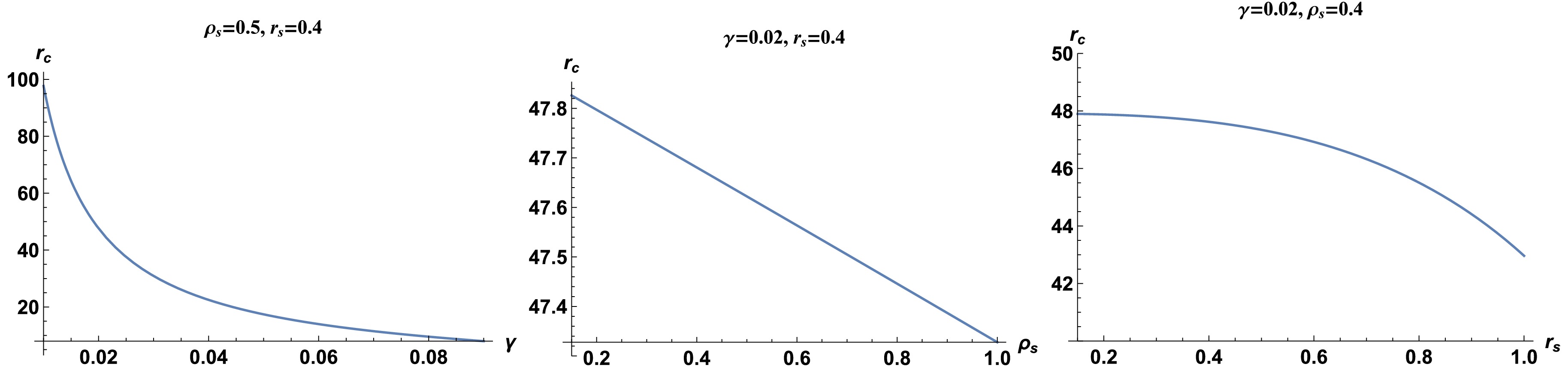
$ r_h $ and cosmological horizon$ r_c $ of the Dehnen-type DM BH in the background of quintessence field.Table 1 shows that a Dehnen-type DM halo with two parameters (core radius
$ r_s $ and core density$ \rho_s $ ) has similar effects on the event horizon, increasing$ r_h $ and decreasing$ r_c $ . (see Fig. 2). However, the event horizon is more influenced by the core radius than the density. The cosmological horizon decreases dramatically as the quintessence field value increases but only marginally with$ \rho_s $ and$ r_s $ (see Fig. 3). -
Shadow analysis relies on null geodesics, which is the motion of photons around black holes. Thus, the Lagrangian in the background of the Dehnen-type DM BH surrounded by a quintessence field is given by
$ \begin{aligned} {\cal{L}}(x,\dot{x})=\frac{1}{2}\,g_{\mu\nu}\dot{x}^{\mu}\dot{x}^{\nu}, \end{aligned} $

(12) where over-dot is differentiation with respect to the affine parameter τ, and we confine ourselves to the equatorial plane
$ (\theta=\pi/2) $ . With the metric independent of both t and ϕ, we get two conserved quantities of motion – energy E and angular momentum L.$ \begin{aligned} E=f(r)\dot{t}, \quad L=r^2 \dot{\phi}. \end{aligned} $

(13) Thus, we obtain the following equation for radial coordinates:
$ \begin{aligned} \dot{r}^2=E^2 -f(r)\frac{L^2}{r^2}=E^2-V_{\rm eff}(r), \end{aligned} $

(14) where the effective potential is
$ \begin{aligned} V_{\rm eff}=\frac{f(r)}{r^2}\left( \frac{L^2}{E^2}-1\right). \end{aligned} $

(15) Figure 4 shows the behaviour of the effective potential with respect to the radial distance r. It demonstrates that the potential peak values increase with increasing DM halo parameters (
$ \rho_s, r_s) $ and quintessence parameter γ.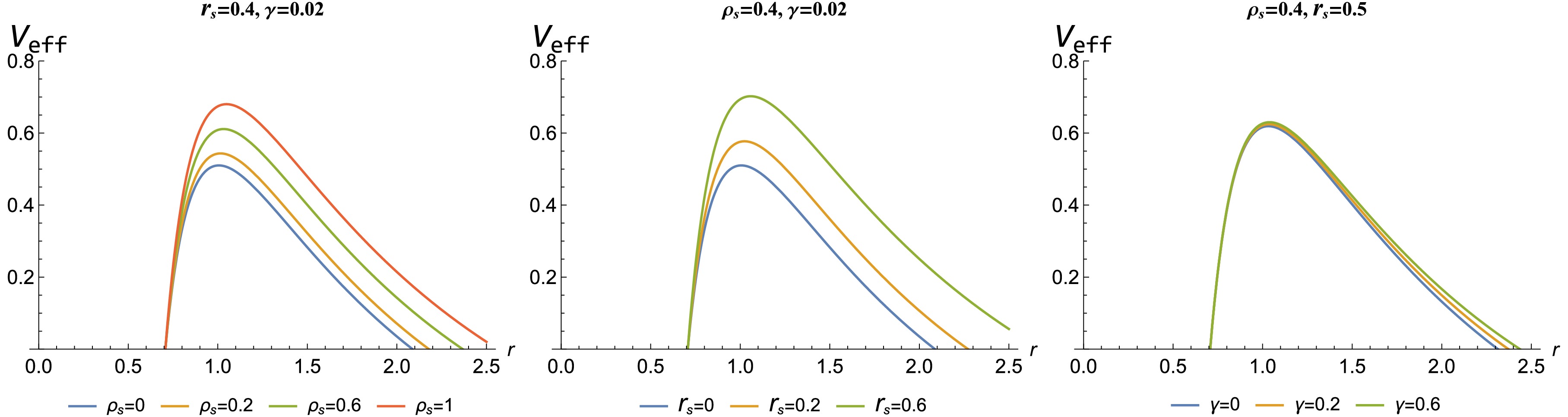
Figure 4. (color online) Behaviours of the effective potential
$ V_S $ with respect to the radial distance r for different core density, core radius, and quintessence parameter values.The radius of an unstable photon orbit can be obtained using the following condition:
$V_{\rm eff}=0=V'_{\rm eff}$ . To determine the BH shadow radius, we only need the photon sphere radius and critical impact parameter. The equation of the photon sphere radius is given by$ \begin{aligned} r_{ps}f'(r_{ps})-2f(r_{ps})=0. \end{aligned} $

(16) A critical impact parameter
$ b_{ps} $ corresponding to the photon orbit, also known as the shadow radius$ (R_s) $ of the BH, can be identified as follows:$ \begin{aligned} b_{ps}=R_s=\dfrac{r_{ps}}{\sqrt{f(r_{ps})}}. \end{aligned} $

(17) Substituting the metric function (9) in Eq. (16), we obtain
$ \begin{aligned} (18M+r(3r\gamma -6))(r_s +r)^3-8r^3_{s}\pi(r^2_{s}+3r_{s}r+3r^2)\rho_s=0. \end{aligned} $

(18) We observe that the photon radius cannot be expressed analytically. We will thus obtain its values numerically. Table 2 shows the numerical values of the photon sphere, and consequently, the shadow radius. In Table 2, we examined the impact of the quintessence parameter γ and the Dehnen-type dark matter halo with two parameters
$ r_s $ and$ \rho_s $ on the BH shadow.γ $ \rho_s =1 $ 

$ r_{s}=0.4 $ 

$ r_{s} $ 

$ r_{ps} $ 

$ R_{s} $ 

$ \rho _{s} $ 

$ r_{ps} $ 

$ R_{s} $ 

$ 0.01 $ 

$ 0.2 $ 

$ 3.1382 $ 

$ 5.61977 $ 

$ 0.2 $ 

$ 3.17799 $ 

$ 5.70235 $ 

$ 0.4 $ 

$ 3.72768 $ 

$ 6.77653 $ 

$ 0.6 $ 

$ 3.44847 $ 

$ 6.23092 $ 

$ 0.6 $ 

$ 5.34526 $ 

$ 10.0413 $ 

$ 1 $ 

$ 3.72768 $ 

$ 6.77653 $ 

$ 0.02 $ 

$ 0.2 $ 

$ 3.19095 $ 

$ 5.92313 $ 

$ 0.2 $ 

$ 3.23244 $ 

$ 6.0157 $ 

$ 0.4 $ 

$ 3.80555 $ 

$ 7.23178 $ 

$ 0.6 $ 

$ 3.51394 $ 

$ 6.6105 $ 

$ 0.6 $ 

$ 5.52092 $ 

$ 11.1272 $ 

$ 1 $ 

$ 3.80555 $ 

$ 7.23178 $ 

$ 0.03 $ 

$ 0.2 $ 

$ 3.24751 $ 

$ 6.27496 $ 

$ 0.2 $ 

$ 3.29088 $ 

$ 6.38009 $ 

$ 0.4 $ 

$ 3.89042 $ 

$ 7.77988 $ 

$ 0.6 $ 

$ 3.58475 $ 

$ 7.05941 $ 

$ 0.6 $ 

$ 5.72208 $ 

$ 12.6021 $ 

$ 1 $ 

$ 3.89042 $ 

$ 7.77988 $ 

Table 2. Numerical results for the photon sphere
$ r_{ps} $ and shadow radius$ R_s $ of the Dehnen-type DM BH in a quintessence field background.Figures 5 and 6 visualize the effects of the BH parameters. The figures demonstrate that both the photon sphere and shadow radii increase with the core density and core radius. Both radii increase roughly linearly with the core density but nonlinearly with the core radius. Similarly, as the quintessence parameter increases, both radii increases. We infer that the presence of Dehnen type DM and a quintessence field enhances the size of the shadow. This behavior is also reflected in Fig. 7. As demonstrated in Fig. 7, the shadow size eventually grows with increasing DM parameters and the quintessence parameter γ.
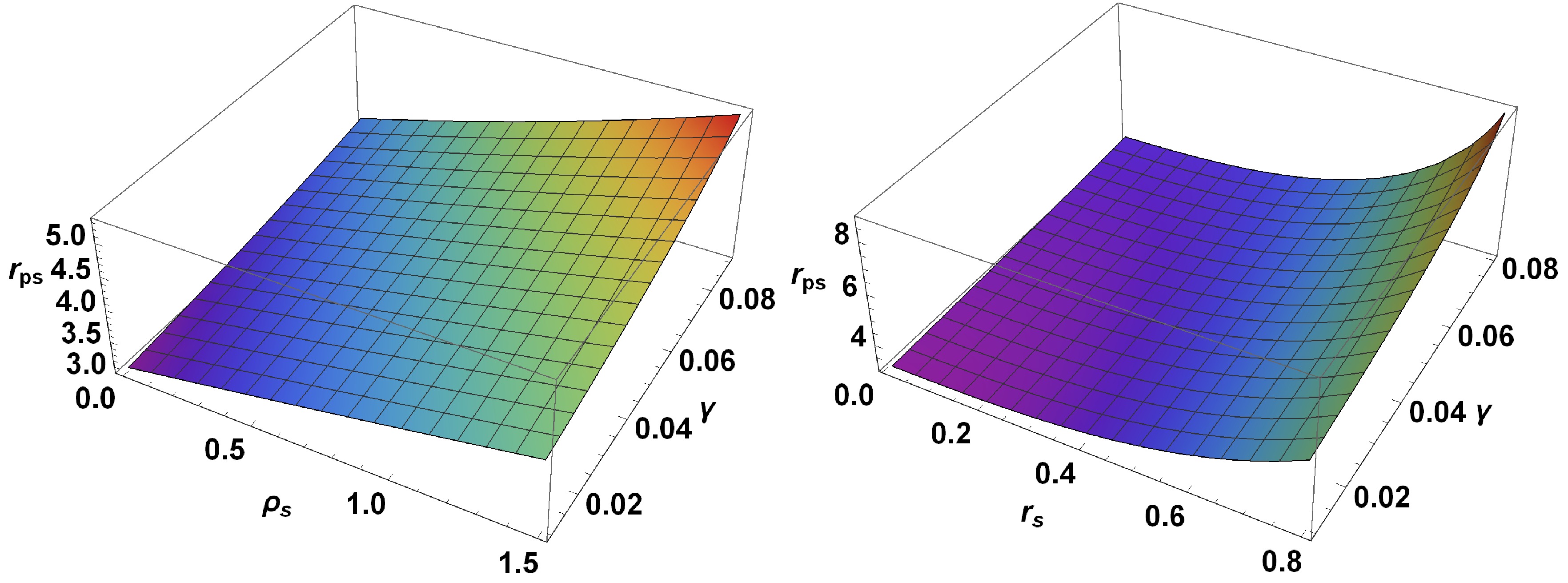
Figure 5. (color online)Variation of the photon sphere radius with
$ \rho_s $ and γ for$ r_s = 0.4 $ (left) and with$ r_s $ and γ for$ \rho_s = 0.5 $ (right).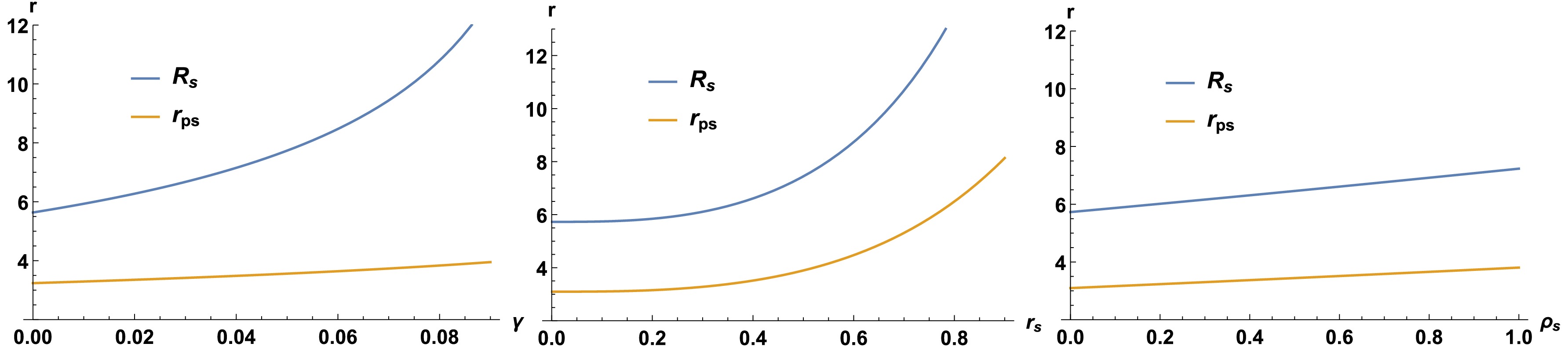
Figure 6. (color online)Variation of
$ r_{ps} $ and$ R_s $ with the quintessence parameter for$ r_s = 0.5 $ and$ \rho_s=0.2 $ (left), with core radius for$ \gamma = 0.02 $ and$ \rho_s=0.6 $ (middle), and with core density for$ \gamma = 0.02 $ and$ r_s=0.4 $ (right).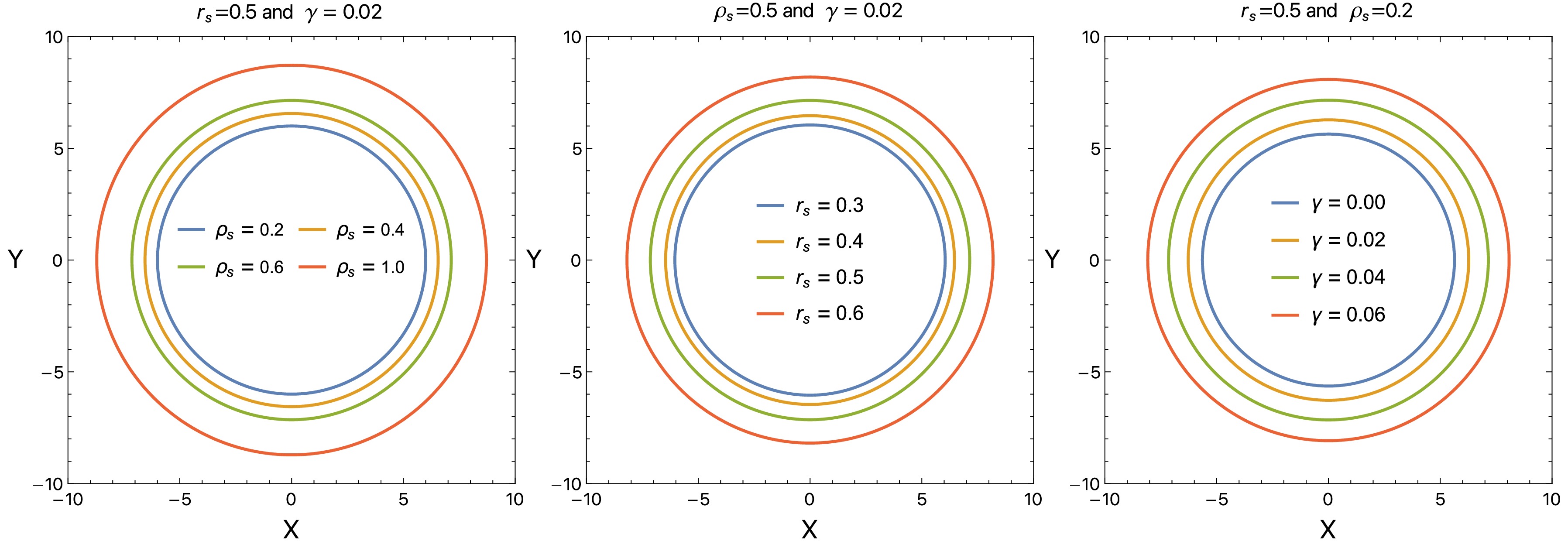
Figure 7. (color online)The BH shadow profile for different values of the DM density
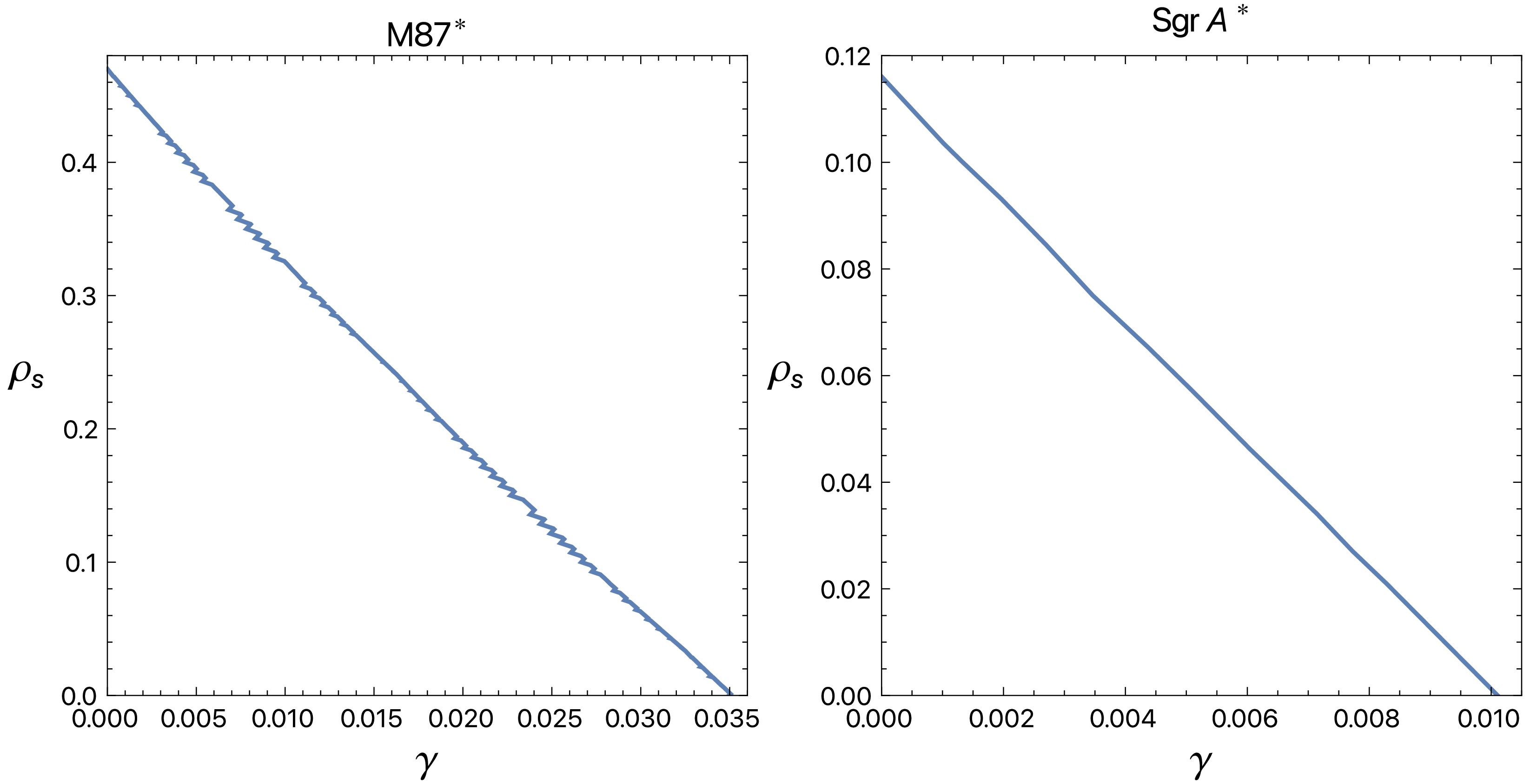
$ \rho_s $ (left) and the core radius$ r_s $ (middle) and the quintessence parameter γ (right).We then turn to provide insights into the BH parameters using recent EHT observations [5, 6]). For that we explore the obtained theoretical results to obtain precise constraints on these parameters. For astrophysical implications, two sources, Sgr A
$ ^{\star} $ and M87$ ^{\star} $ which can provide upper constraints for the BH parameters considered here, are assumed to be candidates to describe static and spherically symmetric BHs for our theoretical approach. Using EHT observational data, we can obtain the upper limits of the DM halo density$ \rho_s $ and quintessence parameter γ. For our approach, we adapt the observational shadow's angular diameter θ, the distance D, and the mass of Bhs at the center of the Sgr A$ ^{\star} $ and M87$ ^{\star} $ galaxies. Recent EHT observations have reported the angular daimeters of M87$ ^{\star} $ and Sgr A$ ^{\star} $ as$ \begin{array}{*{20}{l}} \theta_{\rm M87^{\star}}=42 \pm 3 \mu ~~~ \rm{and}~~~ \theta_{\rm Sgr A^{\star}}=48.7 \pm 7 \mu\, , \end{array} $

(19) with the distances
$D_{\rm M87^{\star}}= 16.8 \pm 0.8~\rm M pc$ and$D_{\rm M87^{\star}}= 8277 \pm 9 \pm 33~\rm pc$ between Earth and M87$ ^{\star} $ and Sgr A$ ^{\star} $ , respectively. The masses of the BHs have been measured to be$M_{\rm M87^{\star}} = (6.5 \pm 0.7) \times 10^9 M_{\odot}$ and$D=8277 \pm 9 \pm 33~\rm pc$ and$M_{\rm Sgr A^{\star}} = (4.297 \pm 0.013) \times 10^6 M_{\odot}$ (see, e.g., in Refs. [5, 6]). One can then evaluate the shadow diameter per unit mass by adopting the equation given by$ \begin{array}{*{20}{l}} d_{sh}=\dfrac{D\,\theta}{\,M}\, , \end{array} $

(20) which corresponds to
$d^{\rm M87^{\star}}_{sh}=(11 \pm 1.5)M$ for M87$ ^{\star} $ and$d^{\rm Sgr^{\star}}_{sh}=(9.5 \pm 1.4)M$ for Sgr A$ ^{\star} $ . Considering these values for Sgr A$ ^{\star} $ and M87$ ^{\star} $ , we obtain the possible values of$ \rho_s $ and γ, which are demonstrated in Fig. 8. From observational data of M87$ ^{\star} $ , one can deduce that$ \rho_s $ and γ may have larger values compared to those from Sgr A$ ^{\star} $ . Subsequently, EHT observational data for M87$ ^{\star} $ and Sgr A$ ^{\star} $ can provide precise constraints on the DM density parameter$ \rho_s<0.48,\, 0.12 $ and the quintessence parameter$ \gamma<0.035,\, 0.01 $ , respectively, for the Dehnen-type DM BH system with a quintessence field background. -
Unlike the previous section, we determine the deflection angle around Schwarzschild BHs embedded in a Dehnen type DM halo with a quintessential background field. To accomplish this, we adapt the method developed by Gibbons and Werner into a new thought experiment. This method refers to the Gauss-Bonnet theorem (GBT), which evaluates the deflection angle for spherically symmetric spacetimes (see [78, 79]). The GBT method was extended to axisymmetric [80], non-asymptotically flat spacetimes [81, 82]. To evaluate the weak deflection angle, this thought experiment has since been widely extended to various various situations and gravity models [83−89]. It is worth noting, however, that we consider the weak deflection angle in the background field of the BH embedded in a Dehnen type DM halo surrounded by the quintessential field. Taking the GBT method into consideration, we must determine the weak deflection angle by restricting null geodesics for photon motion. Hence, we use the optical metric for BH spacetime, which is written as follows:
$ \begin{array}{*{20}{l}} \text{d}\sigma^{2} = g_{kl}^{\text{opt}}\text{d}x^{k} \text{d}x ^{l} = {\rm d}r_{*}^2+{\cal{F}}^2(r_{*}){\rm d}\phi^2\, , \end{array} $

(21) where
$ \begin{aligned} {\cal{F}}\big(r_{*}(r)\big)=\frac{r}{\sqrt{f(r)}}, \end{aligned} $

(22) with
$f(r)=1-{2M}/{r}-{4\pi \rho _{s}r_{s}^{3}\left( 2r+ r_s\right) }/ {3\left( r+ r_{s}\right) ^{2}}-{\gamma}/ {r^{3\epsilon+1}}$ and$ r_{*} $ referring to the tortoise coordinate and given by$ \begin{aligned} r_{*}=\int{\dfrac{\text{d}r}{1-\dfrac{2M}{r}-\dfrac{4\pi \rho _{s}r_{s}^{3}\left( 2r+r_s\right) }{3\left( r+r_{s}\right) ^{2}}-\dfrac{\gamma}{r^{3\epsilon+1}}}}\, . \end{aligned} $

(23) For the optical metric in Eq. (21), we further evaluate the Gaussian curvature
$ \cal{K} $ by determining the non-vanishing components of Christoffel symbols associated with the BH spacetime [90]. We then write non-vanishing components of Christoffel symbols as$ \begin{array}{*{20}{l}} \Gamma_{\phi \phi}^{r_{*}}=-{\cal{F}}(r_{*})\dfrac{\text{d}{\cal{F}}(r_{\star})}{\text{d}{r_{\star}}}, \end{array} $

(24) $ \begin{array}{*{20}{l}} \Gamma_{r_{*}\phi}^{\phi}=\dfrac{1}{{\cal{F}}(r_{*})}\dfrac{\text{d}{\cal{F}}(r_{\star})}{\text{d}{r_{\star}}}, \end{array} $

(25) with the determinant
$ \det\tilde{g}_{kl}={\cal{F}}^{2}(r^{\star}) $ . Thus, the Gaussian curvature$ {\cal{K}} $ can be defined as [87]$ \begin{array}{*{20}{l}} {\cal{K}}=-\dfrac{R_{r_{*}\phi r_{*}\phi}}{\det\tilde{g}_{r\phi}}=-\dfrac{1}{{\cal{F}}(r_{\star})}\dfrac{\text{d}^{2}{\cal{F}}(r_{\star})}{\text{d}{r_{\star}}^{2}}\, . \end{array} $

(26) It must also be noted that the Gaussian curvature
$ {\cal{K}} $ can also be obatined in the context of the variable r [78, 91, 92] as$ \begin{array}{*{20}{l}} {\cal{K}} = -\dfrac{1}{{\cal{F}}(r^{\star})} \left[\dfrac{\text{d}r}{\text{d}r^{\star}}\dfrac{\text{d}}{\text{d}r}\left(\dfrac{\text{d}r}{\text{d}r^{\star}}\right)\dfrac{\text{d}f(r)}{\text{d}r}+\left(\dfrac{\text{d}r}{\text{d}r^{\star}}\right)^{2}\dfrac{\text{d}^{2}f(r)}{\text{d}r^{2}}\right] . \end{array} $

(27) Here, recalling Eq. (27) and employing Eqs. (22) and (23), we derive the Gaussian curvature with the equatorial plane area
$ \text{d}S=\sqrt{|\det{g}_{kl}^{opt}|}\text{d}r \text{d}\phi $ in the optical metric:$ \begin{aligned}[b] {\cal{K}}\text{d}S = & -\dfrac{9 \big[9 M^2 (r_s + r)^4 + 12 r_s^3 \pi r^3 \big(2 M r - r_s (r-4 M)\big) \rho_s + 16 r_s^6 \pi^2 r^4 \rho_s^2\big]\lambda}{2 \big(3 (2 M - r) (r_s + r)^2 + 4 r_s^3 \pi r (r_s + 2 r) \rho_s\big)^2 \bigg( 9 - \dfrac{18M}{r} - \dfrac{12 r_s^3 \pi (r_s + 2 r) \rho_s}{(r_s + r)^2}\bigg)^{1/2}}\\ & + \Big(48 \pi r_s^3 r \rho_s (r_s+r)^2 \left(2 r_s^3 M+8 r_s^2 M r+r^3 (r_s+6 M)+6 r_s M r^2-2 r^4\right)-64 \pi ^2 r_s^6 r^4 \rho_s^2 \left(r_s^2-3 r^2\right)\\ &+36 M (r_s+r)^6 (3 M-2 r) \Big) \times \dfrac{4 \bigg(9-\dfrac{18 M}{r}-\dfrac{12 \pi r_s^3 \rho_s (r_s+2 r)}{(r_s+r)^2}\bigg)^{-1/2}}{r^2 (r_s+r)^4 \Big(3 (r_s+r)^2 (r-2 M)-4 \pi r_s^3 r \rho (r_s+2 r)\Big)}\,\text{d}r\,\text{d}\phi\, . \end{aligned}$

(28) Taking the contribution of the Dehnen-type DM BH spacetime to the Gaussian curvature, we write the geodesic curvature as [78, 88]
$ \begin{array}{*{20}{l}} \dfrac{\text{d}\sigma}{\text{d}\phi}\bigg|_{C_{R}}= \left( \dfrac {r^2}{f(R)} \right)^{1/2}\, . \end{array} $

(29) Here, we note that
$ C_{R} $ refers to a curve defined by$r(\phi) = R = \rm constant$ with radius R. To determine the deflection angle using the GBT we further consider the limiting case$ {R} \rightarrow \infty $ that produces the relation$ \theta_{0}+\theta_{S}=\pi $ between the object and source. Consequently, the above equation in the limiting case can be rewritten as$ \begin{array}{*{20}{l}} \lim\limits_{R\to\infty} \kappa_g\dfrac{\text{d}\sigma}{\text{d}\phi}\bigg|_{C_R}\approx 1\, . \end{array} $

(30) Considering an spatial infinity,
$ R\to\infty $ , and imposing the straight light approximation$ r=b/\sin\phi $ , the equation for determining the small deflection angle$ \tilde{\delta} $ using the GBT method reads as follows [78, 88]:$ \begin{array}{*{20}{l}} \int^{\pi+\tilde{\delta}}_0 \left[\kappa_g\dfrac{\text{d}\sigma}{\text{d}\phi}\right]\bigg|_{C_R}\text{d}\phi-\pi =-\lim\limits_{R\to\infty}\displaystyle\int^\pi_0\displaystyle\int^{\infty}_{\tfrac{b}{\sin\phi}}{\cal{K}}\,\text{d}S\, . \end{array} $

(31) Here, b is defined as the impact parameter of of the deflection angle equation. Consequently, the deflection angle around the Dehnen-type DM BH with a quintessence field background in the weak limit approximation can be computed explicitly using the following approximate form:
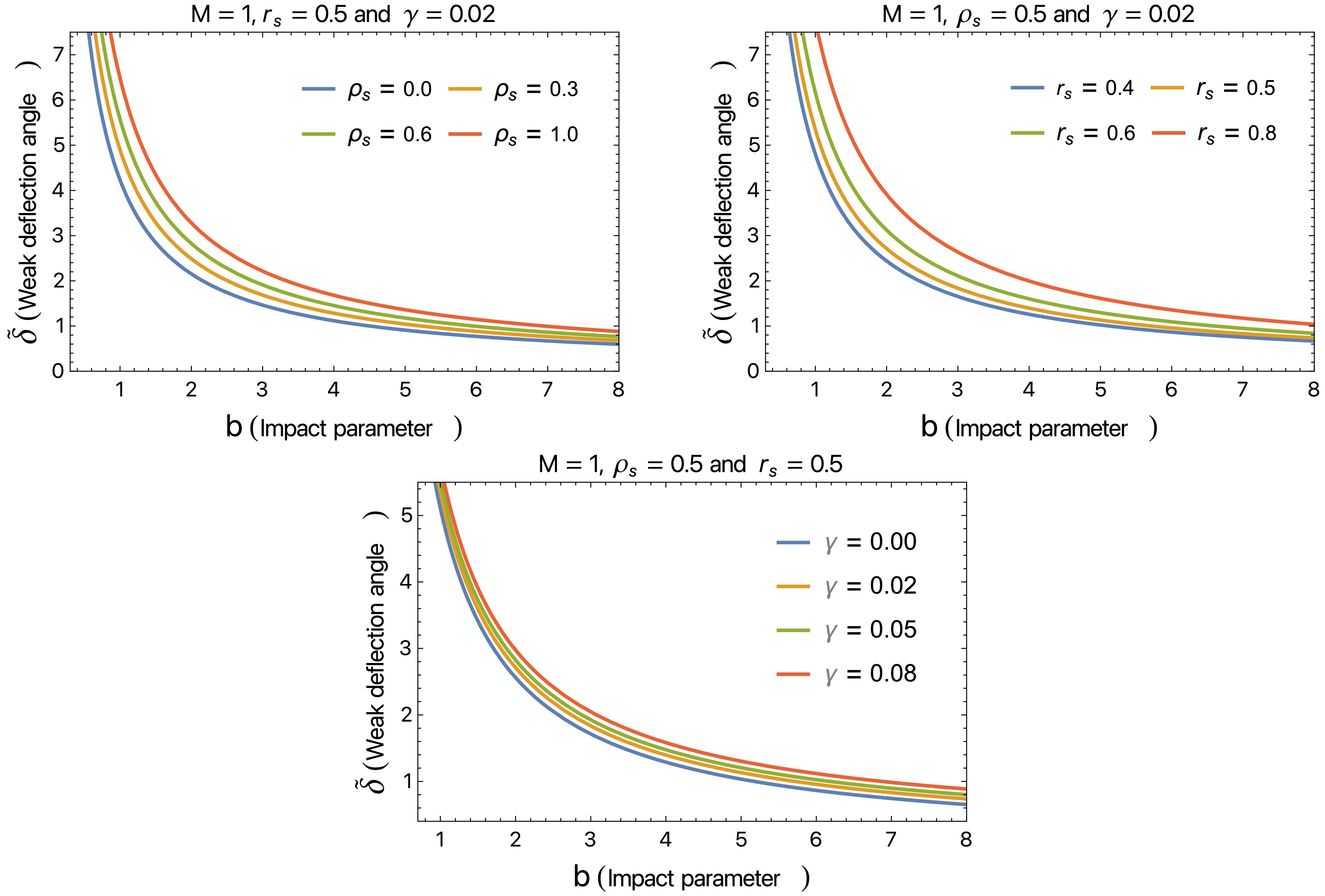
$\begin{aligned}[b] \tilde{\delta} \approx & \dfrac{4 M}{b}-\dfrac{4 \pi \gamma r_s^4 \rho_s}{b}+\dfrac{8 \pi \gamma r_s^3 M \rho_s}{b}+\dfrac{3 \gamma M^2}{b}\\&+\dfrac{\pi \gamma M}{2}+\dfrac{16 \pi r_s^3 \rho_s}{3 b}+\dfrac{16 \pi ^2 \gamma r_s^6 \rho_s^2}{3 b}\, . \end{aligned}$

(32) As demonstrated in Eq. (32), the deflection angle is influenced by the quintessential field parameter γ, DM halo density
$ \rho_s $ , and halo core radius$ r_s $ . We then analyze the deflection angle within the context of the optical metric for the considered BH spacetime, which fascilitates a deeper understanding of the impact of BH parameters on the deflection angle in the weak form. In Fig 9, we depict the deflection angle profile against the impact parameter b. As demonstrated in Fig 9, the left and right panels in the top row reflect the role of the DM density parameter$ \rho_s $ and halo core radius$ r_s $ on the deflection angle profile while keeping the quintessence field parameter γ fixed. The bottom panel reflects the role of the parameter γ for constant$ \rho_s $ and$ r_s $ under various conditions. The figure also shows that the deflection angle is inversely proportional to the impact parameter b. Interestingly, the deflection angle has a changing rate similar to that of the impact parameter, increasing with the parameters$ \rho_s $ and$ r_s $ . Similarly, the quintessence parameter γ has the same influence on the deflection angle as ρ and$ r_s $ . The impact of the DM parameters$ \rho_s $ and$ r_s $ on the deflection angle is much more prominent around the BH compared to a distance away from the BH. This happens because the Dehnen-type DM profile is well distributed around the BH. Thus, one can infer that the parameters$ \rho_s $ and$ r_s $ , together with the quintessence parameter γ, have similar effects that can be interpreted as repulsive gravitational charges, increasing the deflection angle to larger values. For a more complete analysis, we consider quasinormal modes to explore the unique aspects of Dehnen-type DM BH spacetime with a quintessence background field. -
This section consideres the scalar and electromagnetic field perturbations of the Dehnen-type DM BH in a quintessence field background to investigate the behaviour of QNMs. The gravitational waves emitted by BH coalescence provide valuable information about the nature of spacetime and are independent of any given initial stage. They also provide information about the BH system's stability in the presence of perturbations. The QNMs of scalar and electromagnetic field perturbations are wave equation solutions that fulfil particular boundary requirements both near the BH horizon and away from it. The solution must meet the requirements for purely ingoing waves at the event horizon and purely outgoing waves at the cosmological horizon or spatial infinity.
Since the current system has spherical symmetry, the general master equation for computing QNMs is
$ \begin{aligned} \frac{\text{d}^{2}\Psi}{\text{d}r_{\ast }^{2}}+\left( \omega^{2}-V(r_{\ast })\right) \Psi=0, \end{aligned} $

(33) where the tortoise coordinate
$ r_{\ast } $ is defined by$r_{\ast } = \displaystyle\int \dfrac{{\rm d}r}{f}$ . The effective potentials$ V(r_{\ast }) $ for scalar ($ V_S $ ) and electromagnetic ($V_{\rm EM}$ ) types of perturbation fields in Eq. (33) are$ \qquad\begin{aligned} V_{S}(r)=f \left( \left(\frac{1}{2}+l\right)\frac{1 }{r^{2}}+\frac{f^{\prime }}{r} \right), \qquad \end{aligned} $

(34) $ \qquad\begin{aligned} V_{\rm EM}(r)=\left(\frac{1}{2}+l\right)\frac{f }{r^{2}}, \end{aligned} $\qquad

(35) where l is the multipole moment. Figures 10 and 11 show graphs of the potentials in Eqs. 34 and 35 demonstrate both the effect of the DM halo density and quintessence parameter. The figures show that the DM halo (core density and radius parameters) and quintessence parameter both have a large impact on the potentials, albeit in similar ways. Potential peak values decrease with increasing DM halo parameters (
$ \rho_s, r_s) $ and the quintessence parameter γ. Compared to the impact of the BH parameters on the scalar (35) and EM (34) potentials, the parameters have opposite effects on the effective potential (15). The effects of the neglected terms in the metric function (7) on the peak of the perturbation potential are small enough to lead to variations in the QNM spectrum.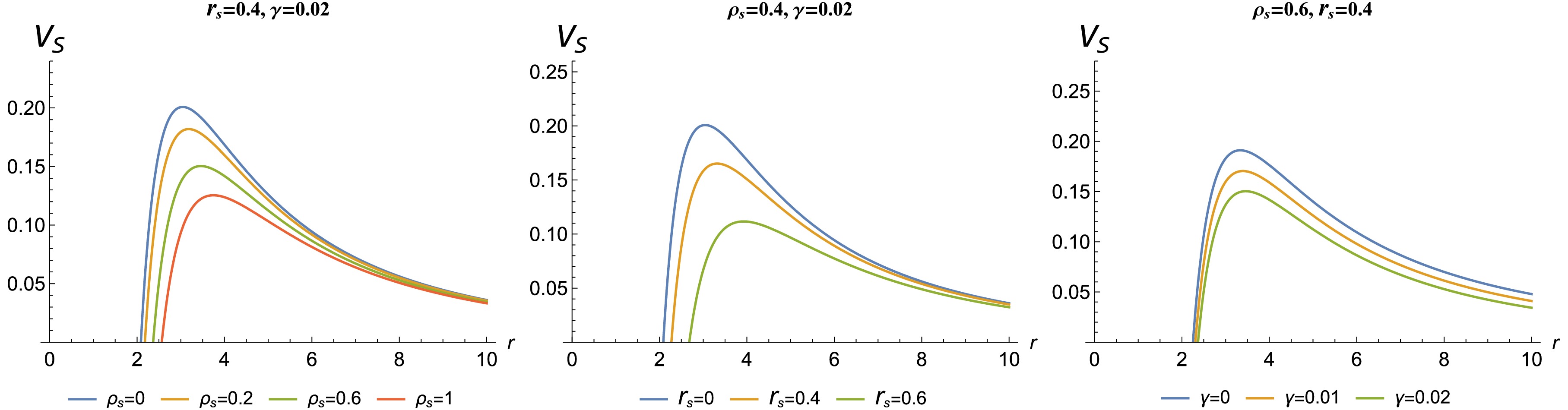
Figure 10. (color online) Behaviours of the scalar potential
$ V_S $ with respect to the radial distance r for different core density, core radius, and quintessence parameter values.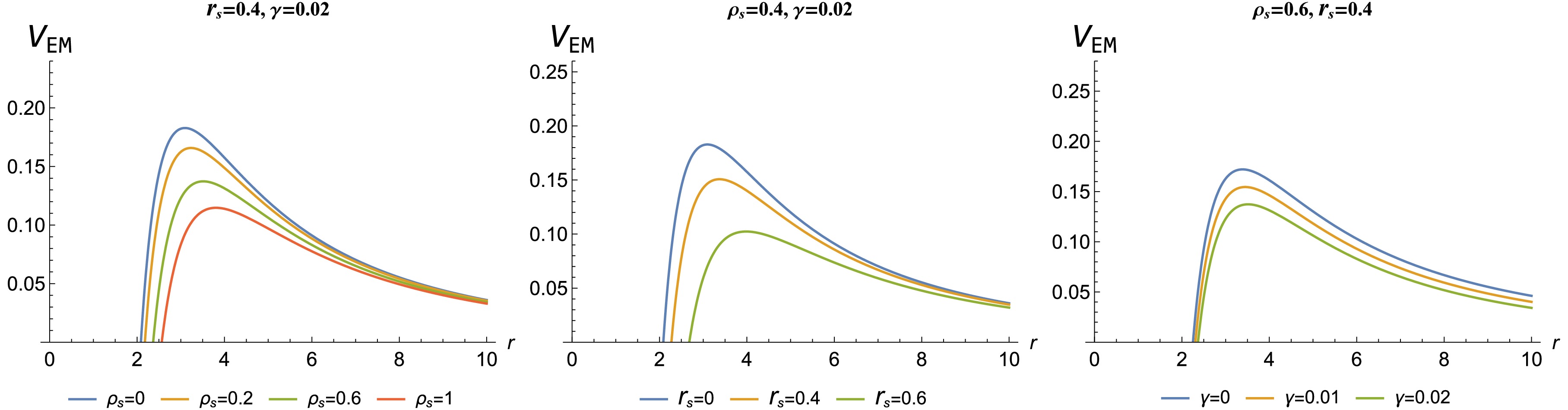
Figure 11. (color online)Behaviours of scalar potential
$ V_{EM} $ with respect to radial distance r for different values of core density, core radius, and the quintessence parameter.The WKB approximation approach is commonly used for calculating QNMs. It was initially introduced by Iyer [93] and later expanded by Konoplya [94]. The WKB approach is successful for low overtone numbers n, particularly
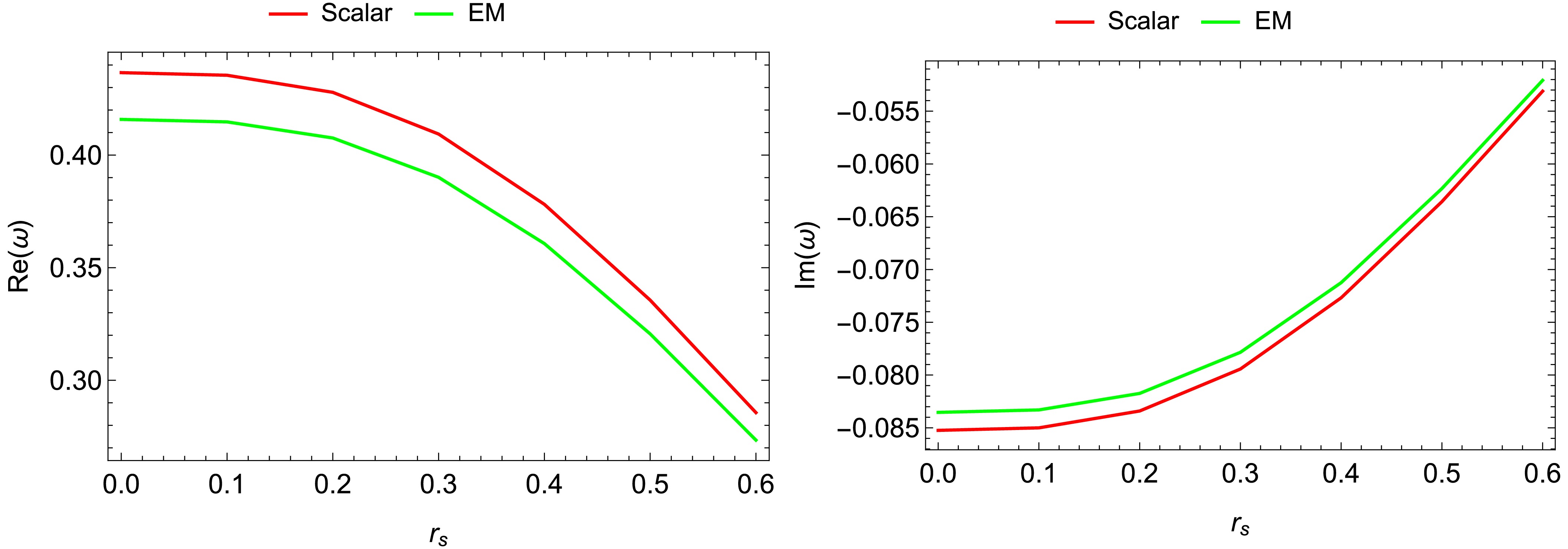
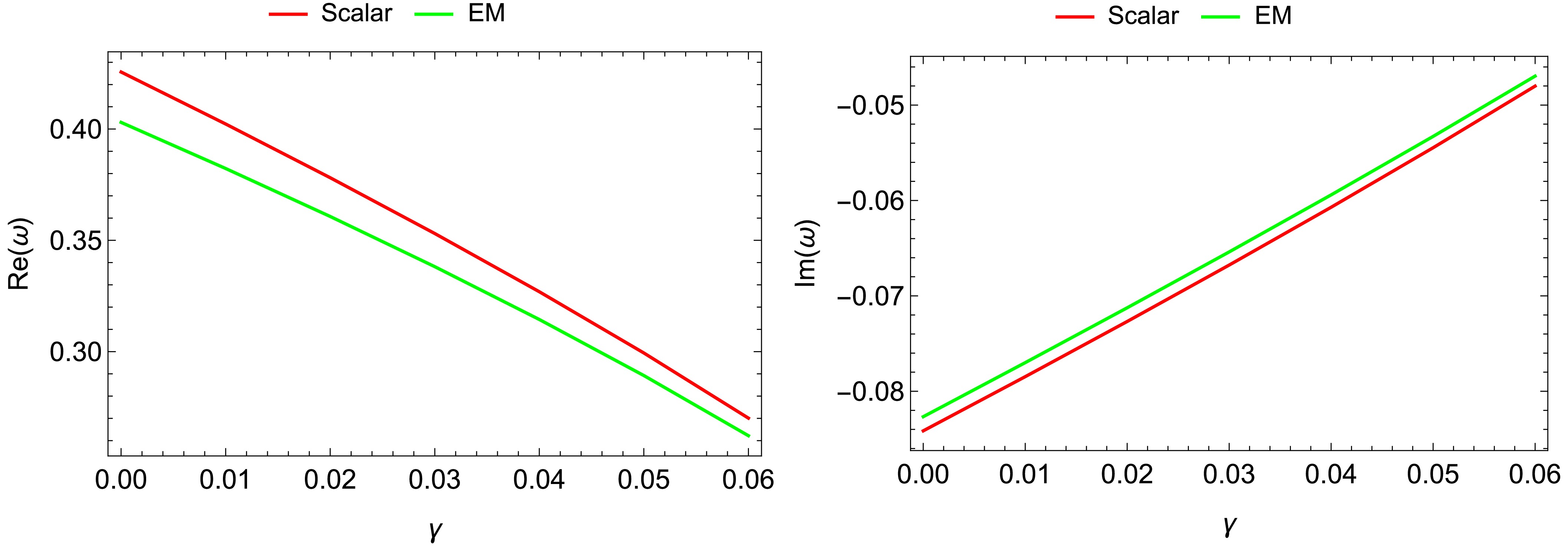
$ n <l $ .Using the effective potentials, we numerically determine the quasinormal frequencies for scalar and electromagnetic perturbations using the 6th order WKB approximation. Tables 3−5 show the quasinormal frequencies produced by altering the parameters
$ \rho_s $ ,$ r_s $ , and γ. The results from Tables 3, 4, and 5 are summarised in Figs. 12, 13, and 14, respectively. For both perturbations, increasing the DM halo parameters ($ \rho_s $ and$ r_{s} $ ) and quintessence parameter γ, decreases the magnitudes of both the imaginary and real parts of the quasinormal frequencies. In general, gravitational waves emitted from BHs surrounded by DM halo and a quintessence field have a lower frequency and decay rate compared to those emitted from BHs in a vacuum.$ r_{s}=0.4 $ ,

$ \gamma=0.02 $ ,

$ n=0 $ ,

$ l=2 $ ,

$ M=1 $ 

$ \rho _{s} $ 

$\rm Scalar$ 

EM $ 0 $ 

$0.436613-0.085241\,{\rm i}$ 

$ 0.415851-0.083537\,{\rm i} $ 

$ 0.2 $ 

$ 0.415693-0.08069\,{\rm i} $ 

$ 0.39614-0.079091\,{\rm i} $ 

$ 0.4 $ 

$ 0.39624-0.076523\,{\rm i} $ 

$ 0.37780-0.075007\,{\rm i} $ 

$ 0.6 $ 

$ 0.37813-0.072683\,{\rm i} $ 

$ 0.36072-0.071248\,{\rm i} $ 

$ 0.8 $ 

$ 0.36125-0.069141\,{\rm i} $ 

$ 0.34478-0.067779\,{\rm i} $ 

$ 1 $ 

$ 0.34550-0.065867\,{\rm i} $ 

$ 0.32990-0.06457\,{\rm i} $ 

Table 3. Variations of the amplitude and damping of QNMs with respect to the central halo density parameter.
$ \rho=0.6 $ ,

$ \gamma=0.02 $ ,

$ n=0 $ ,

$ l=2 $ ,

$ M=1 $ 

$ r_{s} $ 

$\rm Scalar$ 

EM $ 0 $ 

$ 0.436613-0.085241\,{\rm i} $ 

$ 0.41585-0.083537\,{\rm i}$ 

$ 0.1 $ 

$ 0.43545-0.085003\,{\rm i}$ 

$ 0.41475-0.083303\,{\rm i} $ 

$ 0.2 $ 

$ 0.42787-0.083407\,{\rm i} $ 

$ 0.40760-0.081740\,{\rm i} $ 

$ 0.3 $ 

$ 0.40935-0.079428\,{\rm i} $ 

$ 0.39014-0.077846\,{\rm i} $ 

$ 0.4 $ 

$ 0.37813-0.072683\,{\rm i} $ 

$ 0.36072-0.071248\,{\rm i} $ 

$ 0.5 $ 

$ 0.33561-0.063575\,{\rm i} $ 

$ 0.32062-0.062334\,{\rm i}$ 

$ 0.6 $ 

$ 0.28566-0.053108\,{\rm i}$ 

$ 0.27344-0.052083\,{\rm i}$ 

Table 4. Variations of the amplitude and damping of QNMs with respect to the central halo radius parameter.
$ r_{s}=0.4 $ ,

$ \rho_s=0.6 $ ,

$ n=0 $ ,

$ l=2 $ ,

$ M=1 $ 

γ $\rm Scalar $ 

EM $ 0 $ 

$ 0.42563-0.084147\,{\rm i}$ 

$ 0.40300-0.082665\,{\rm i}$ 

$ 0.01 $ 

$ 0.40227-0.078470\,{\rm i} $ 

$ 0.38228-0.077000\,{\rm i} $ 

$ 0.02 $ 

$ 0.37813-0.072683\,{\rm i} $ 

$ 0.36072-0.071248\,{\rm i} $ 

$ 0.03 $ 

$ 0.35307-0.066770\,{\rm i}$ 

$ 0.33817-0.065393\,{\rm i} $ 

$ 0.04 $ 

$ 0.32690-0.060710\,{\rm i} $ 

$ 0.31443-0.059415\,{\rm i} $ 

$ 0.05 $ 

$ 0.29938-0.054472\,{\rm i}$ 

$ 0.28924-0.053285\,{\rm i} $ 

$ 0.06 $ 

$ 0.27011-0.048012\,{\rm i}$ 

$ 0.26221-0.046964\,{\rm i} $ 

Table 5. Variations of the amplitude and damping of QNMs with respect to the quintessence parameter.
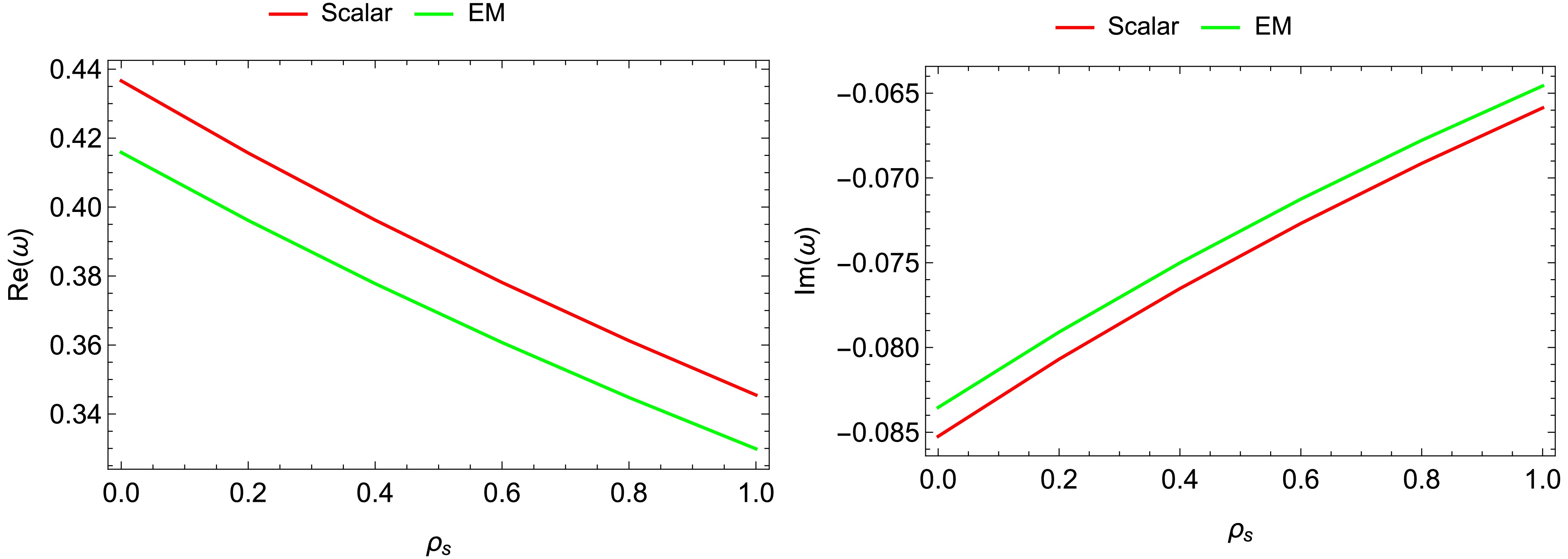
Figure 12. Variations of the amplitude and damping of QNMs with respect to the central density of the DM halo parameter for scalar and EM perturbations.
-
In this article, we considered a Schwarzschild BH embedded in a Dehnen-type DM halo with a quintessential field background. To accomplish this, we first derived the metric function and then discussed the impact of the DM and quintessence field components in three scenarios. The first important attribute of BHs is their singularity and horizons. We discovered that the solution of the BH singularity at
$ r = 0 $ is a necessary singularity that cannot be removed by coordinate translation. It is notable that the BH described by the metric (8) has two horizons: the event and cosmological horizons. Both horizons are mostly dependent on the parameters of the dark sector. It was found that all dark sector parameters$ (\rho_s,r_s, \gamma) $ increase$ r_h $ while lowering$ r_c $ .We then performed BH shadow analysis. After determining the effective potential, we estimated the photon and shadow radii. We demonstrated that the photon sphere and shadow radii grow with the core density and radius. Similarly, both radii expand in proportion to the quintessence parameter. We hypothesised that the presence of Dehnen type DM and the quintessence field increase the size of the shadow. Additionally, relying on EHT observations of M87
$ ^{\star} $ and Sgr A$ ^{\star} $ , we estimated the best-fit constraints on the DM density parameter$ \rho_s $ and the quintessence parameter γ. Our estimations showed that the DM density$ \rho_s $ can have values up to$ <0.48 $ and$ <0.12 $ in the quintessence field background with the parameter$ \gamma<0.035 $ and$ <0.01 $ for the observational data of M87$ ^{\star} $ and Sgr A$ ^{\star} $ , respectively.Further, we delved into the role of the Dehnen-type BH parameters in the presence of a quintessence field on the deflection angle under weak approximation. We explored this scenarios to investigate the unique aspects of BH parameters by elucidating their combined effects on the deflection angle around the Dehnen type DM BH surrounded by the quintessence field. We found that the deflection angle changes at a similar rate due to the impacts of the BH parameters
$ (\rho, r_s, \gamma) $ , resulting in the deflection angle shifting upward and increasing to larger values. Furthermore, through analysis, we provided a physical interpretation of the parameters$ (\rho, r_s, \gamma) $ with similar effects that increase the deflection angle. This is consistent with the physical interpretation of these parameters acting as repulsive gravitational charges that can weaken gravity in the BH background.Finally, QNMs are investigated using the 6th order WKB approach. Since we have limited ourselves to the case of
$ n = 0 $ and$ l=2 $ , the 6th order WKB approach yields accurate results. We considered both scalar and electromagnetic perturbations, and found that increasing the DM halo parameters ($ \rho_s $ and$ r_s $ ) and quintessence parameter γ, reduces the magnitudes of both the imaginary and real parts of the quasinormal frequencies. In addition, we showed that this BH is stable under perturbations. We conclude that the presence of the DM halo and quintessence field causes gravitational waves to propagate slower than for a Schwarzschild BH in a vacuum.In conclusion, our results show that the simultaneous presence of stretch type DM and the quintessence field leads to interesting effects on the horizon, shadow, deflection angle, and QNMs of Schwarzschild BHs.
Astrophysical properties of static black holes embedded in a Dehnen type dark matter halo with the presence of quintessential field
- Received Date: 2024-10-29
- Available Online: 2025-05-15
Abstract: From an astrophysical perspective, the composition of black holes (BHs), dark matter (DM), and dark energy can be an intriguing physical system. In this study, we consider Schwarzschild BHs embedded in a Dehnen-type DM halo with a quintessential field. This study examines the horizons, shadows, deflection angle, and quasinormal modes (QNMs) of the effective BH spacetime and how they are affected by the dark sector. The Schwarzschild BH embodied in a Dehnen-type DM halo with a quintessential field possesses two horizons: the event and cosmological horizons. We demonstrate that all dark sector parameters increase the event horizon while decreasing the cosmological horizon. We analyze the BH shadow and emphasize the impact of DM and quintessence parameters on the shadow. We show that the dark sector casts larger shadows than a Schwarzschild BH in a vacuum. Further, we delve into the weak gravitational lensing deflection angle using the Gauss-Bonnet theorem (GBT). We then investigate the system's QNMs using the 6th order WKB approach. To visually demonstrate the dark sector parameters, we present figures that illustrate the impact of varying the parameters of the Dehnen-type DM halo as well as the quintessence background. Our findings show that the gravitational waves emitted by BHs with a dark sector have a lower frequency and decay rate compared to those emitted by BHs in a vacuum.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: