Investigation of spectral properties of ¹¹Be in breakup reactions

Breakup reactions, in which the valence neutron is removed from the projectile by its interaction with a target nucleus, have played a valuable role in probing exotic nuclear structures, such as those of halo nuclei [1−3]. During the breakup reactions of these nuclei, the angular distributions of neutrons measured in conjunction with the core nuclei [4] are strongly forward peaked, and the parallel momentum distributions of the core fragment have very small widths [5−7], thus providing a confirmation of their halo structure. $ ^{11} {\rm{Be}}$ is a prominent example of a one-neutron halo nucleus, where the loosely bound valence neutron has a large spatial extension with respect to the corresponding core.

The breakup of halo nuclei has been investigated theoretically by several authors using various approaches: time-dependent (TD) models [8−13], the coupled-channel technique with a discretized continuum (CDCC) [14, 15], and models based on the eikonal approximation [16], particularly the dynamical eikonal approximation (DEA) [17, 18]. Each model has its own peculiarities. In particular, an advantage of the non-perturbative time-dependent model [11, 13] is the inclusion in the calculation of all higher-order effects in the relative motion of the breakup fragments, which provides a fully dynamical description of the projectile excitation caused by both the Coulomb and the nuclear interactions between the projectile and the target.

In our previous studies [19, 20], we employed the extended quantum-quasiclassical model based on the non-perturbative time-dependent approach [11, 13], a comprehensive analysis of the influence of resonant states on the breakup of a $ ^{11} {\rm{Be}}$ halo nucleus on a heavy target ($ ^{208} {\rm{Pb}}$) in a wide energy region (5−70 MeV/nucleon). It has been demonstrated that including the low-lying resonances ($ 5/2^{+} $, $ 3/2^{-} $, and $ 3/2^{+} $) of the $ ^{10} {\rm{Be}}$+n system made a significant contribution to the breakup cross section, which provides a better agreement with existing experimental data [21].

Here, we perform calculations of the breakup cross section of $ ^{11} {\rm{Be}}$ on a light carbon target at beam energies 5−67 MeV/nucleon with the curvilinear trajectory of the projectile and including low-lying resonances ($ 5/2^{+} $, $ 3/2^{-} $, $ 3/2^{+} $) of the $ ^{10} {\rm{Be}}$+n system. The obtained results are in good agreement with existing experimental data at 67 MeV/nucleon [21]. In the low energy region, there are only a few theoretical results [22, 23], with which we compare our calculations. The performed analysis demonstrates the possibility of studying spectral properties of halo nuclei in their breakup reactions.

The remainder of this paper is organized as follows. In Section II, we describe the non-perturbative time-dependent model with linear trajectories and a quantum-quasiclassical approach with “real” trajectories of $ ^{11} {\rm{Be}}$ in breakup reactions. In Section III, we demonstrate the convergence of the computational scheme and present the results. The investigation of the spectral structure of $ ^{11} {\rm{Be}}$ in breakup reactions is presented in Section IV. Finally, Section V provides concluding remarks.

This approach is based on the integration of the time-dependent three-dimensional Schrödinger equation for halo neutron for describing its dynamics during collision of $ ^{11} {\rm{Be}}$ with a target [11, 13].

The halo neutron is treated as a structureless particle weakly bound by the potential U(r) to the $ ^{10} {\rm{Be}}$ core nucleus, where r is the the relative variable between the neutron and the core. The time-dynamics of the halo neutron relative to the $ ^{10} {\rm{Be}}$ core in the breakup reaction $ ^{11} {\rm{Be}}$+$ ^{12} {\rm{C}}$ $ \rightarrow ^{10} {\rm{Be}}$+n+$ ^{12} {\rm{C}}$ is depicted by the time-dependent Schrödinger equation

in the projectile rest frame, where $ \Psi({\boldsymbol{r}},t) $ is the wave packet of the neutron relative to the $ ^{10} {\rm{Be}}$ core. In this expression

is the Hamiltonian describing the halo nucleon-core system with reduced mass $ \mu = m_{n}m_{c}/M $, where $ m_{n}, m_{c} $, and $ M = m_{n}+m_{c} $ are the neutron, $ ^{10} {\rm{Be}}$-core, and $ ^{11} {\rm{Be}}$ masses, respectively. The potential $ U({\boldsymbol{r}}) $ consists of the sum of the l-dependent Woods-Saxon potential $ V_{l}(r) $ and the spin-orbit interaction $V_{l}^{s}(r)({\boldsymbol{l}} \cdot {\boldsymbol{s}}) = -V_{l}^{s}\dfrac{1}{r}\dfrac{\rm d}{{\rm d}r} f(r)({\boldsymbol{l}} \cdot {\boldsymbol{s}})$, where $f\left(r\right) = 1/\left[1+{\rm exp}\left(\dfrac{r-R_{0}}{a}\right)\right]$. The parameters of potential have a standard value: $ R_{0} $ = 2.585 fm, a = 0.6 fm, and depth $ V_{l}^{s} $ = 21 MeV·fm².

The parameters of the spherical Woods-Saxon potentials $V_{l}\left(r\right) = -V_{l}/\left[1+\exp\left(\dfrac{r-R_{0}}{a}\right)\right]$, describing the energy spectrum of $ ^{11} {\rm{Be}}$ nucleus, had been determined as $ V_{l} $ = 62.52 MeV (l-even) and $ V_{l} $ = 39.74 MeV (l-odd) [17] to reproduce the $ 1/2^{+} $ ground state of $ ^{11} {\rm{Be}}$ at −0.503 MeV, the $ 1/2^{-} $ excited state at −0.183 MeV, and two resonance states $ 5/2^{+} $ and $ 3/2^{+} $ with the position of peaks at $ E_{5/2^{+}} $ = 1.232 MeV and $ E_{3/2^{+}} $ = 3.367 MeV [24, 25]. For these states, the radius is $ R_{0} $ = 2.585 fm and the diffuseness is a = 0.6 fm. To fix the position of the $ 3/2^{-} $ resonance (l = 1) close to the experimental [24] and theoretical [25] value $ E_{3/2^{-}} $ = 2.789 MeV, we tuned the set of parameters as $ V_{l} $ = 6.8 MeV, $ R_{0} $ = 2.5 fm, and a = 0.35 fm in our recent studies [19, 20]. For $ l\geqslant3 $, the spherical potential $ V_{l}(r) $ was set to zero. More details on parameterization of potentials between the neutron and $ ^{10} {\rm{Be}}$core and how the resonant states are included in the analysis of the breakup reaction are discussed in Table 1 of [19].

Here, as in our previous studies [19, 20, 26] (and also, for example, studies reported in [11, 13, 14, 17, 18]), we use the approximation of an inert $ ^{10} {\rm{Be}}$ core in which the ground $ 1/2^{+} $ and excited $ 1/2^{-} $ states of $ ^{11} {\rm{Be}}$, as well as the low-lying resonance $ 5/2^{+} $, are described reasonably well as single-particle configurations relative to $ ^{10} {\rm{Be}}$. However, it is known (see, for example, [27]) that, as the first excited state 2$ ^{+} $ of the $ ^{10} {\rm{Be}}$ core with the energy $ E_{2^{+}} $ = 3.368 MeV is approached, this state makes a significant contribution to the resonances $ 3/2^{-} $ and $ 3/2^{+} $ of $ ^{11} {\rm{Be}}$. Therefore, the excitation of the core in our model can be considered by following the scheme proposed in [27], adding to the Hamiltonian (2), i.e., the internal Hamiltonian of the core, and the quadrupole deformation of the Woods-Saxon potential. It is based on the particle-rotor model of Bohr and Mottelson with the $ ^{11} {\rm{Be}}$ Hamiltonian from [28]. This possibility is the subject of our further research.

The time-dependent potential $ V({\boldsymbol{r}},{\boldsymbol{R}},t) $ in Eq. (1) simulates the interaction of the target with the projectile. It was assumed to be purely Coulombic for breakup reactions with a heavy target ($ ^{208} {\rm{Pb}}$) at collision energies of approximately 70 MeV/nucleon [11, 13, 19], which is defined as $V_{C}({\boldsymbol{r}},{\boldsymbol{R}},t) = \dfrac{Z_{c}Z_{t}{\rm e}^{2}}{|m_{n} {\boldsymbol{r}}/M+{\boldsymbol{R}}(t)|}-\dfrac{Z_{c}Z_{t}{\rm e}^{2}}{R(t)}$, where $ Z_{c} $ and $ Z_{t} $ are charge numbers of the core and target, respectively, and $ {\boldsymbol{R}}(t) $ is the relative coordinate between the projectile and the target. As shown in previous studies with a time-dependent non-perturbative approach [19, 20], the contribution of the nuclear part of the projectile-target interaction in the breakup cross sections on a heavy target is significant for lower beam energies (30−5 MeV/nucleon). In this study, we evaluate this effect in the case of a light target ($ ^{12} {\rm{C}}$) using the approach of optical potential $ \Delta V_{N}({\boldsymbol{r}},{\boldsymbol{R}},t) = V_{cT}({\boldsymbol{r}}_{cT}(t))+V_{nT}({\boldsymbol{r}}_{nT}(t)) $ for the nuclear interaction between the target and projectile:

Here, $ {\boldsymbol{r}}_{cT}(t) $ and $ {\boldsymbol{r}}_{nT}(t) $ are the core-target $ {\boldsymbol{r}}_{cT}(t) = {\boldsymbol{R}}(t)+ m_{n}{\boldsymbol{r}}/M $ and neutron-target $ {\boldsymbol{r}}_{nT}(t) = {\boldsymbol{R}}(t)-m_{c}{\boldsymbol{r}}/M $ relative variables, and optical potentials $ V_{cT} $ and $ V_{nT} $ have the form

with Woods-Saxon form-factors $f_{x}\left(r_{xT},R_{R},a_{R}\right) = 1/ \left[1+\exp\left(\dfrac{r_{xT}-R}{a}\right)\right]$, where x stands for either core or neutron.

The analytical expressions of such potentials were obtained by selecting the parameters of general form-factors so as to fit the calculated scattering cross sections onto experimental data. A compilation of optical potentials for different projectiles and targets can be found in Refs. [22, 29, 30]. Here, we apply the parameters of the optical potentials (4) from the work, which are presented in Table 1. The potential of the core-target interaction is proposed by Al-Khalili, Tostevin, and Brooke [31], consistent with the elastic scattering of $ ^{10} {\rm{Be}}$ on $ ^{12} {\rm{C}}$ (denoted as ATB in the following). For the n- $ ^{12} {\rm{C}}$ interaction, the commonly used parametrization of Becchetti and Greenlees [30] (BG) is considered. The expediency of using this parameterization of the nuclear part of the interaction was analyzed in the study reported in [30].

c or n	$ V_{x} $ /MeV	$ W_{x} $/MeV	$ R_{R} $/fm	$ R_{I} $/fm	$ a_{R} $/fm	$ a_{I} $/fm
$ ^{10} {\rm{Be}}$	123.0	65.0	3.33	3.47	0.80	0.80
n	34.54	13.40	2.68	2.88	0.75	0.58

Table 1.  Parameters of the core-target [31] and neutron-target [30] optical potentials at 67 MeV/nucleon.

In early studies on non-perturbative time-dependent approach [11, 13], straight-line trajectories $ {\boldsymbol{R}}(t) = {\boldsymbol{b}}+ {\boldsymbol{v}}_{0}t $ were used, where $ {\boldsymbol{b}} $ is the impact parameter orthogonal to the initial velocity of the projectile $ {\boldsymbol{v}}_{0} $. However, advancement into the region of low collision energies, where the deviation of the projectile trajectory from a straight line increases, requires going beyond this approximation [19].

In our previous study [19], we extended the description of the $ ^{11} {\rm{Be}}$ breakup on $ ^{208} {\rm{Pb}}$ to low energies using the quantum-quasiclassical approach developed in [32−35] and successfully applied previously in various problems of atomic physics. This made it possible to calculate with satisfactory accuracy the cross section of this reaction at low collision energies of up to 5 MeV/nucleon. Here, we apply this approach to describe the breakup of $ ^{11} {\rm{Be}}$ on a light target $ ^{12} {\rm{C}}$. Therefore, note that employing a more realistic projectile trajectory is not a new approach. Thus, classical Coulomb trajectories were used in the study of Fallot et. al on the breakup of $ ^{11} {\rm{Be}}$ [12] and in the study of Melezhik and Baye on the breakup of $ ^{17} $F [34].

In this approach, simultaneously with the time-dependent Schrödinger Eq. (1) for the halo-nucleon wave function $ \Psi({\boldsymbol{r}},t) $ we integrate the set of Hamilton equations

describing relative projectile-target dynamics. Here, the classical Hamiltonian $ H_{BP}({\bf{P}}, {\bf{R}}, t) $ is denoted by

where the term $ \langle\Psi({\boldsymbol{r}},t)|V_{C}( {\boldsymbol{r}}, {\boldsymbol{R}}, t)|\Psi({\boldsymbol{r}},t)\rangle $ represents the quantum-mechanical average of the projectile-target interaction over the halo-nucleon density instantaneous distribution $ |\Psi({\boldsymbol{r}},t)|^2 $ during the collision. To construct the effective classical Hamiltonian $ H_{BP} $, which is supposed to be the real one, we neglected the optical potential (4), having an imaginary part and acting for impact parameters below $ b\sim $ 10 fm, in the region where the breakup cross section drops sharply with decreasing b [13, 19]. Thus, the Hamiltonian (6) can be defined as a parametric dependence on the halo-neutron position $ {\boldsymbol{R}}(t) $ at every time moment. This quantum-quasiclassical model permits to include in the computational scheme the deformation of the projectile trajectories and energy transfer between the target and projectile and vice versa during collisions. The required stability and accuracy of the integration of Eq. (5) simultaneously with the time-dependent Schrödinger equation (1) with the same step of integration over time were ensured by using a computational finite-difference scheme developed in [33] based on the Störmer–Verlet method.

The total breakup cross section is calculated as a function of the relative energy E between the emitted neutron and the core nucleus, including neutron interaction with the core in the final state of the breakup process by the formula [11, 13, 19, 34]:

Here, $\Psi({\boldsymbol{r}},T_{\rm out})$ is the neutron wave packet at the end of the collision process $ ^{11} {\rm{Be}}$+$ ^{12} {\rm{C}}$ $ \rightarrow ^{10} {\rm{Be}}$+n+$ ^{12} {\rm{C}}$ (at $t = T_{\rm out}$), which is found by numerical integration of the hybrid system of equations consisting of the time-dependent Schrödinger equation (1) and the classical Hamilton Eq. (5). $ \phi_{ljm}(k,r) $ is the radial part of the eigenfunction of the Hamiltonian $ H_{0}({\bf{r}}) $ (2) in the continuum spectrum ($ E = k^2\hbar^2/(2\mu)>0 $), normalized to a spherical Bessel function $ j_{l}(kr) $ as $ kr\rightarrow\infty $ if U(r) = 0; $ Y_{lm}(\hat{r}) $ are the spherical harmonics. Summation over ($ l, m $) in (7) includes all 16 partial waves up to $l_{\rm max}$ = 3, inclusive, as in [19].

The time evolution starts at initial time $ T_{\rm in} $ and stops at final time $ T_{\rm out} $ by iteration over $ N_{T} $ time steps $ \bigtriangleup t $ as explained in [11, 13]. The initial (final) time $ T_{\rm in} (T_{\rm out}) $ has to be sufficiently big $ \vert T_{\rm in}\vert, T_{\rm out}\rightarrow+\infty $, fixed from the demand for the time-dependent potential $ V({\boldsymbol{r}},{\boldsymbol{R}},t) $ to be negligible at the beginning (end) of the time evolution at t = $T_{\rm in}$($T_{\rm out}$). Following the investigation performed in [36], the time interval is fixed as $ T_{\rm in} $ = −10 $ \hslash $/MeV and $ T_{\rm out} $ = 10 $ \hslash $/MeV, the time step $ \bigtriangleup t $ equals to 0.02 $ \hslash $/MeV. The challenge when numerically integrating the system of equations (1), (5) is obtaining $ \Psi( {\boldsymbol{r}}, t) $ - solving the three-dimensional time-dependent Schrödinger equation (1). To solve it, a two-dimensional discrete-variable representation (2D DVR) is used to approximate the desired wave function $ \Psi (r,\Omega,t) $ in terms of angular variables $ \Omega = (\theta,\varphi) $ [11, 13, 37]. Moreover, as shown in our previous study [19], as the collision energy of $ ^{11} {\rm{Be}}$ with a heavy target decreases, the convergence of this approach in the number of basis functions N of the 2D DVR (which is equal to the number of grid points in angular variables $ N = N_{\theta}\times N_{\varphi} $) slows down. In the next section, we investigate the convergence of the 2D DVR in N for our problem of the breakup of $ ^{11} {\rm{Be}}$ on a light target in the entire energy range under study.

For discretizing with respect to the radial variable r, a sixth-order (seven point) finite-difference approximation on a quasiuniform grid has been used on the interval $ r\in[0,r_{m}] $ with $ r_{m} $ = 600 fm. The grid has been realized by the mapping $ r\rightarrow $x of the initial interval onto $ x\in[0,1] $ by the formula $r = r_{m}({\rm e}^{8x}-1)/(({\rm e}^{8}-1))$ [19, 37]. The choice of the edges of integration over radial variables and convergence of the method with respect to radial meshes was discussed in [36].

In the calculation of the breakup cross section, the choice of the edges of integration over impact parameters $b_{\rm min}$ and $b_{\rm max}$ must be carefully tested. For the breakup reaction $ ^{11} {\rm{Be}}$+$ ^{12} {\rm{C}}$ $ \rightarrow ^{10} {\rm{Be}}$+n+$ ^{12} {\rm{C}}$, the evolution is computed from impact parameters $b_{\rm min}$ = 0 fm up to $b_{\rm max}$. The step $ \vartriangle{b} $ is chosen to ensure the convergence of the integral in Eq. (7). It varies from $ \bigtriangleup b $ = 0.25 fm at small b up to $ \bigtriangleup b $ = 2 fm at large b as in [22]. The inclusion of a strong interaction between the target and the projectile using the optical potential causes a faster convergence of the integral (7) along the upper limit $b_{\rm max}$ (as it was shown in [36] at $b_{\rm max}$ = 150 fm). More details of numerical integration can be found in previous studies [11, 13, 19].

In our recent study [36], the convergence with respect to N of the time-dependent approach with linear trajectories of projectiles for the breakup of the $ ^{11} {\rm{Be}}$ nucleus on a light target ($ ^{12} {\rm{C}}$) was investigated at 67 MeV/nucleon, along with discussing the accuracy of the numerical technique. Here, we investigate the convergence in N of the quantum-quasiclassical approach, including the curvature of the trajectory of $ ^{11} {\rm{Be}}$ in collision with $ ^{12} {\rm{C}}$-target (effect important at low collision energies of $ ^{11} {\rm{Be}}$ on $ ^{208} {\rm{Pb}}$-target) [19]. The main task of our investigation is to extend a quantum-quasiclassical approach for calculation of the breakup cross sections at low beam energies.

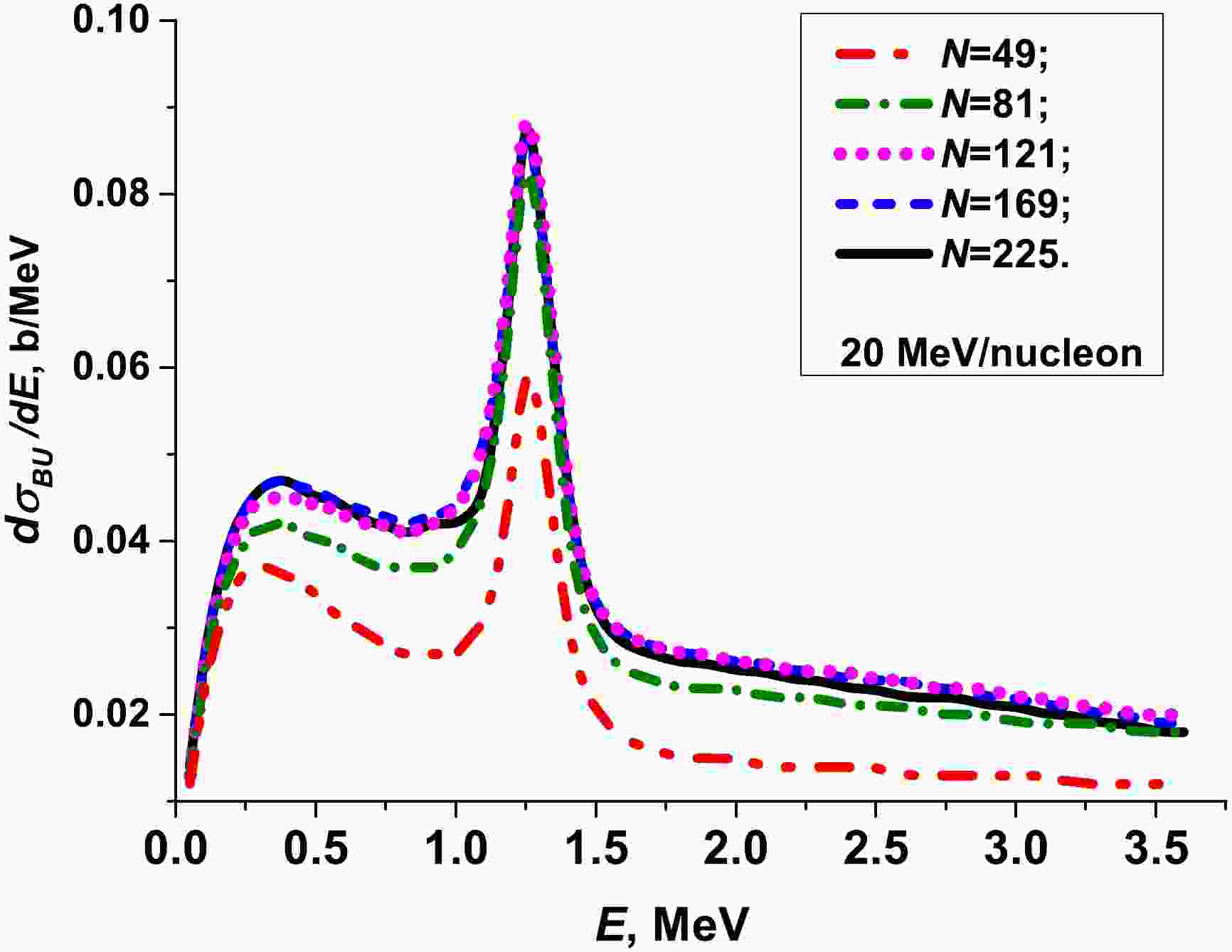
Therefore, the breakup cross sections ${\rm d}\sigma_{bu}(E)/{\rm d}E$ were computed with this approach on the 2D DVR basis functions extended from N = 49 ($ N_{\theta} = N_{\varphi} = $7) to N = 225 ($ N_{\theta} = N_{\varphi} = $15), including two bound states (ground $ 1/2^{+} $ and first excited $ 1/2^{-} $ states) and three low-lying resonances ($ 5/2^{+} $, $ 3/2^{-} $, $ 3/2^{+} $) of $ ^{11} {\rm{Be}}$ at beam energy of E = 20 MeV/nucleon. Fig. 1 shows that it is sufficient to use ($ N_{\theta} = N_{\varphi} = $15) angular grid points N = 225 (2D DVR basis functions) for computing the breakup cross section of $ ^{11} {\rm{Be}}$ on a $ ^{12} {\rm{C}}$ with the demanded accuracy on the order of a few percent. This number of 2D DVR basis functions was used in the subsequent calculations.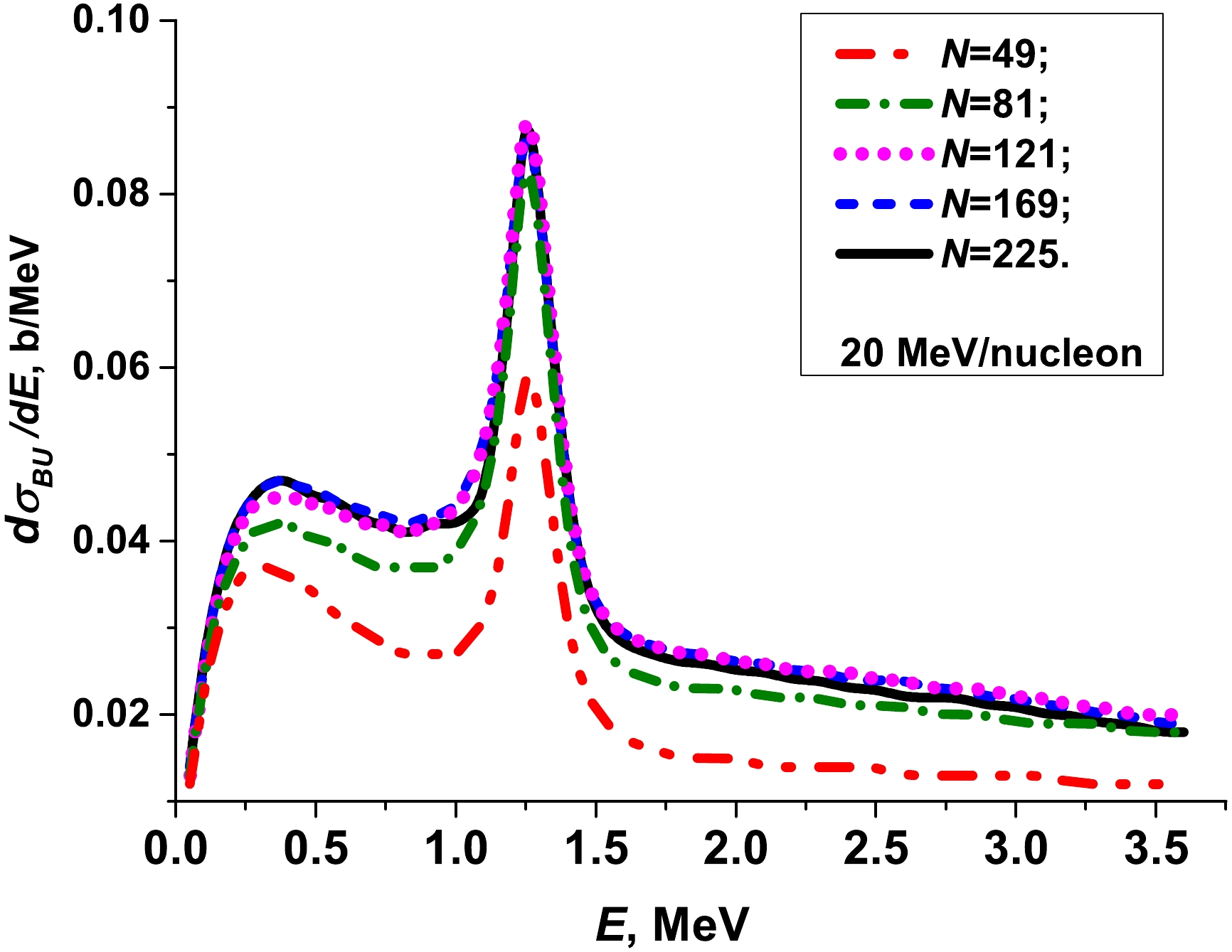

Figure 1.  (color online) Convergence of the calculated value with quantum-quasiclassical approach (1), (5): breakup cross section ${\rm d}\sigma_{bu}(E)/{\rm d}E$ (7) of $ ^{11} {\rm{Be}}$ at 20 MeV/nucleon as a function of the number $ N = N_{\theta}\times N_{\varphi} $ of angular grid points (2D DVR basis functions).

In Fig. 2, we demonstrate the influence of the projectile curvature on the breakup cross sections. Here, the breakup cross sections calculated with the hybrid quantum-quasiclassical approach (realistic trajectories) and with time-dependent approach with linear trajectories are presented for beam energies 5 MeV/nucleon (graph a) and 67 MeV/nucleon (graph b). In both calculations, two bound states ($ 1/2^{+} $, $ 1/2^{-} $) and three low-lying resonances ($ 5/2^{+} $, $ 3/2^{-} $, $ 3/2^{+} $) of the $ ^{10} {\rm{Be}}$+n system were included. The Coulomb and nuclear interactions between the projectile and the target (3) were also included. The results provided in Fig. 2 show that, in the energy range 10−67 MeV/nucleon, the contribution of the nonlinearity of the projectile curve does not exceed two percent. Nevertheless, at low beam energy (5 MeV/nucleon), a decrease in the (${\rm d}\sigma_{bu}(E)/{\rm d}E$) cross section calculated with real trajectories in the region 0.3 MeV $ \leqslant E \leqslant $1.1 MeV is on the order of 6% −7 % and approximtely 3 % at $ E \geqslant $1.7 MeV (in the region of low-lying resonances $ 3/2^{-} $ and $ 3/2^{+} $ with resonant energies $ E_{3/2^{-}} $ = 2.789 MeV and $ E_{3/2^{+}} $ = 3.367 MeV, graph (a)). By considering the deformation of projectile trajectory, it slightly decreases the maximum of the resonance $ 5/2^{+} $ at $ E_{5/2^{+}} $ = 1.232 MeV. In our previous studies on the influence of low-lying resonances on the breakup of $ ^{11} {\rm{Be}}$ on $ ^{208} {\rm{Pb}}$, it was found that, for incident beam energies of 5−30 MeV/nucleon, the contribution of the $ 5/2^{+} $ resonance state of $ ^{11} {\rm{Be}}$ to the breakup cross sections is visible, while at energies of $ \sim $70 MeV/nucleon, resonant states $ 3/2^{-} $ and $ 3/2^{+} $ make the largest contribution [19]. Note that, in the case of a heavy target ($ ^{208} {\rm{Pb}}$), the differences between the cross sections calculated with the linear and realistic trajectories of the projectile were approximately several percent in the energy range of 30−20 MeV/nucleon; for 10 MeV/nucleon, the discrepancy was 10% and reached a value of more than 20% at 5 MeV/nucleon, which exceeded the effect of nuclear interaction [19]. Here, for a breakup of the light target ($ ^{12} {\rm{C}}$), the influence of the projectile trajectory curvature on the breakup cross section with decreasing collision energy is significantly less than in case of a heavy target ($ ^{208} {\rm{Pb}}$) owing to weaker Coulomb interaction between $ ^{11} {\rm{Be}}$ and $ ^{12} {\rm{C}}$ than between $ ^{11} {\rm{Be}}$ and $ ^{208} {\rm{Pb}}$, as we assume.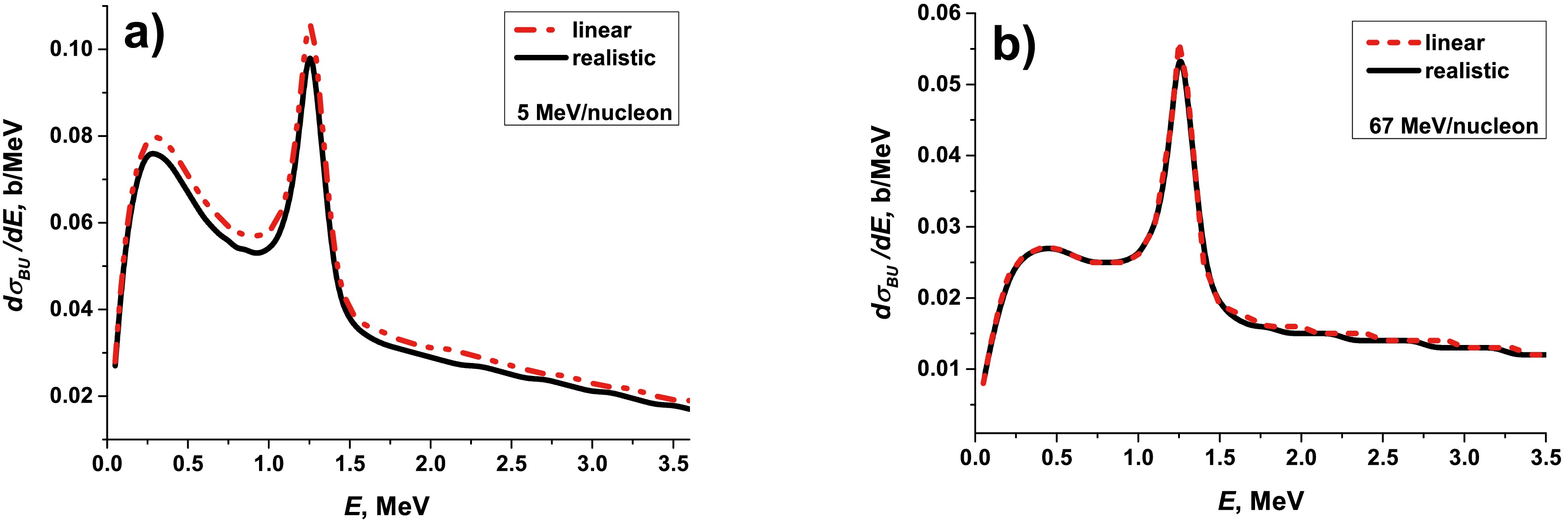

Figure 2.  (color online) Comparison of breakup cross sections calculated with the time-dependent approach with linear trajectories of the projectile and with the quantum-quasiclassical approach with realistic trajectories of the projectile for beam energies of 5 and 67 MeV/nucleon.

Figure 3 illustrates the comparison of calculated breakup cross section of $ ^{11} {\rm{Be}}$ on $ ^{12} {\rm{C}}$ with the experimental data measured by Fukuda et al. at 67 MeV/nucleon [21] and with the results of calculations from an earlier study performed with the non-perturbative time-dependent approach [11, 13]. Both the theoretical breakup cross sections at energy $ E_{0} $ are convoluted with the instrumental energy resolution $(E_{0}^{-1/2}/0.48 {\rm exp}[-(E-E_{0})^{2}/0.073 E_{0}]$, with $ E_{0} $ and E in MeV) to obtain a value at energy E comparable to experiment. The major effect of this convolution is to resize the peaks, which are broadened and slightly shifted toward lower energies. In both computations, the parameters of optical potentials and the edge parameters of integral (7) are the same except the angular basis functions, as we use an angular grid with the equal numbers $ N_{\theta} = N_{\varphi} = $15 of grid return $ N = N_{\theta} \times N_{\varphi} $ over θ and φ, whereas the authors applied an angular basis with $ N_{\theta} = $12 and $ N_{\varphi} = $23. Our results (red full line) were obtained by including two bound ($ 1/2^{+} $, $ 1/2^{-} $) and three resonance ($ 5/2^{+} $, $ 3/2^{-} $, and $ 3/2^{+} $) states of $ ^{11} {\rm{Be}}$ into the hybrid quantum-quasiclassical approach, accounting for the curvilinear trajectories of the projectile. The cross-sections calculated by us in relation to the experimental cross-section in the region of 2−3.4 MeV were underestimated because the excitation of the core was not considered in our model of the $ 3/2^{-} $ and $ 3/2^{+} $ resonances in this region.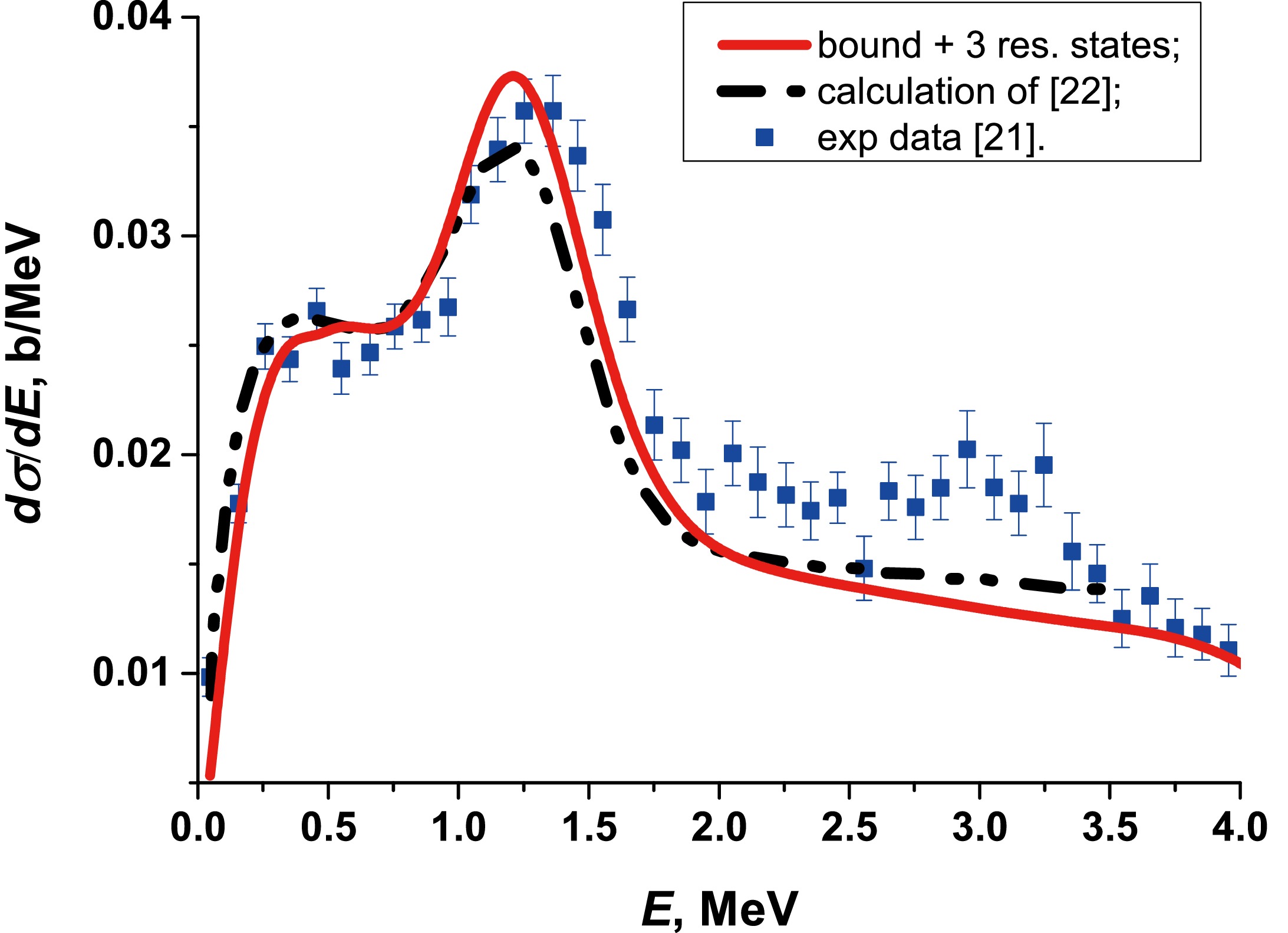

Figure 3.  (color online) Comparison of theoretical and experimental [21] breakup cross sections with our results, obtained with the quantum-quasiclassical approach, including two bound ($ 1/2^{+} $, $ 1/2^{-} $) and three resonance ($ 5/2^{+} $, $ 3/2^{-} $, $ 3/2^{+} $) states of $ ^{11} {\rm{Be}}$ at 67 MeV/nucleon.

Currently, there are no experimental data for low beam energies for the breakup reaction of $ ^{11} {\rm{Be}}$ on carbon and on lead targets. Nevertheless, attempts of calculations at lower energies have already been conducted within the framework of CDCC, DEA, and eikonal approaches [22, 23]. However, it was concluded by Hebborn and Capel [23] that they did not improve the description of the breakup of halo nuclei with the eikonal approaches down to 20 MeV/nucleon and that "CDCC exhibits convergence issues in this range of energies.” Nevertheless, in the absence of other results, we compared these calculations.

In Fig. 4, we present breakup cross sections of $ ^{11} {\rm{Be}}$ on $ ^{12} {\rm{C}}$ calculated at 20 MeV/nucleon as a function of the $ ^{10} {\rm{Be}}$+n relative energy. They are plotted in comparison with those obtained using the CDCC approach (purple dot-dashed line), the eikonal model (red dashed line), and the DEA (blue dotted line) [23]. Our results, highlighted with a solid line, are obtained, including two bound ($ 1/2^{+} $, $ 1/2^{-} $) and three resonant ($ 5/2^{+} $, $ 3/2^{-} $, $ 3/2^{+} $) states of the $ ^{10} {\rm{Be}}$+n system in the frame of the quantum-quasiclassical approach with curvilinear trajectories of the projectile. Theoretical calculations from [23] were performed by including only one resonance $ 5/2^{+} $ and two bound ($ 1/2^{+} $, $ 1/2^{-} $) states of the core-neutron system. As shown in Fig. 4, the CDCC result [23] exceeds our cross sections by approximately 30% over the whole energy range. Otherwise, the DEA result exceeds the values of breakup cross sections at the peak (corresponding to the resonance position of $ 5/2^{+} $), calculated with the eikonal approximation [23] and our quantum-quasiclassical approach. Our results agree well with the eikonal approximation [23] at $ ^{10} {\rm{Be}}$+n relative energies up to 1.3 MeV and with DEA at energies above 1.4 MeV. Note that transition in our approach to the straight-line trajectory causes visible exceeding of our cross sections below 1.5 MeV (see Fig. 2(a)). In the case of the eikonal approximations [23], the corrections to the straight-line trajectories progress in the same direction as that in our quasi-classical approach.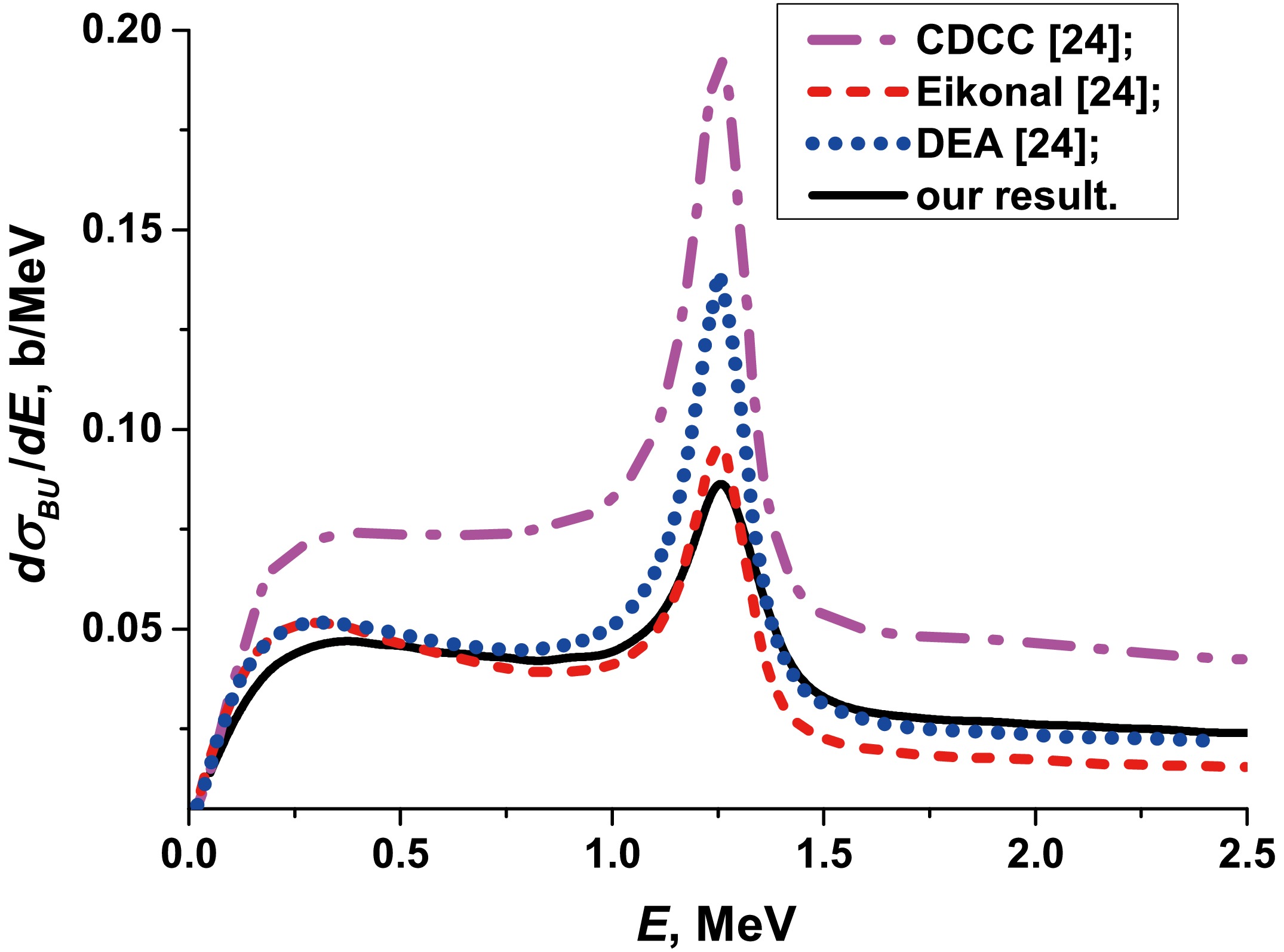

Figure 4.  (color online) Breakup cross sections of $ ^{11} {\rm{Be}}$ on $ ^{12} {\rm{C}}$ at 20 MeV/nucleon calculated within the quantum-quasiclassical approach in comparison with other theoretical approaches from [23].

In Fig. 5, we present the breakup cross sections of $ ^{11} {\rm{Be}}$ on the $ ^{12} {\rm{C}}$ target calculated for two bound states ($ 1/2^{+} $, $ 1/2^{-} $) at a broad range of beam energies, 5−67 MeV/nucleon. We considered the influence of the resonant states ($ 5/2^{+} $, $ 3/2^{-} $, $ 3/2^{+} $) and the effect of the deformation of the projectile trajectory, as well as the transfer of energy from the target to the projectile and vice versa during the breakup process [19].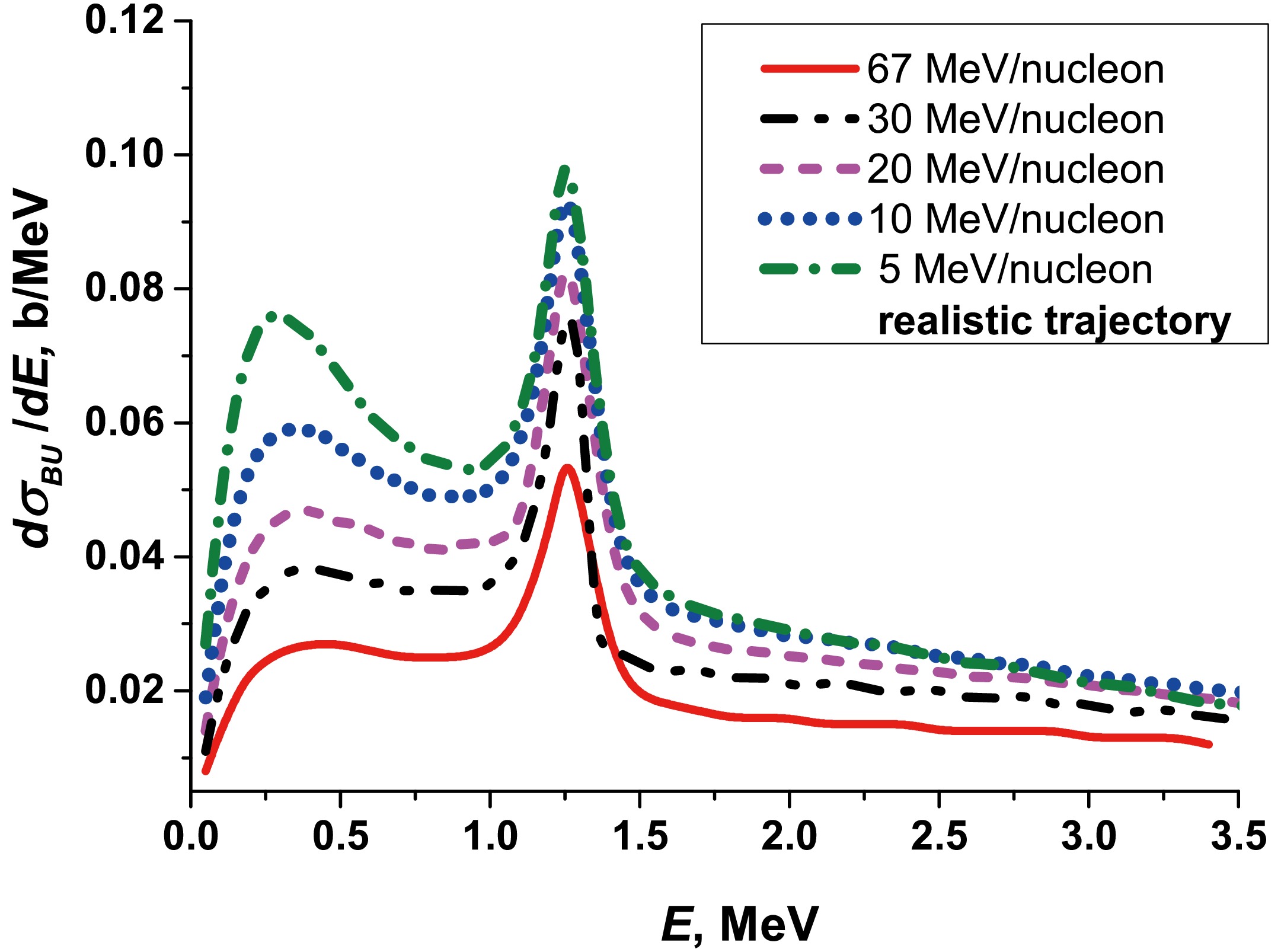

Figure 5.  (color online) Breakup cross section ${\rm d}\sigma_{bu}(E)/{\rm d}E$ calculated as a function of beam energy and the energy between $ ^{10} {\rm{Be}}$ and the neutron, including two bound ($ 1/2^{+} $, $ 1/2^{-} $) states and three resonances ($ 5/2^{+} $, $ 3/2^{-} $, $ 3/2^{+} $) of $ ^{11} {\rm{Be}}$.

Let us note two features in the dynamics of the breakup cross section of $ ^{11} {\rm{Be}}$ with decreasing colliding energy (see Fig. 5): a dramatic increase in the $ 5/2^{+} $ resonance at 1.25 MeV and the transformation of the plateau in the 0.3−1.0 MeV region into a broad peak at 0.3 MeV as the colliding energy decreases to 5 MeV/nucleon. To clarify the physical nature of these two peaks, we compared the calculated cross section $ ^{11} {\rm{Be}}$+$ ^{12} {\rm{C}}$ $ \rightarrow ^{10} {\rm{Be}}$+n+$ ^{12} {\rm{C}}$ at 5 MeV/nucleon with the cross section $ ^{11} {\rm{Be}}$+$ ^{208} {\rm{Pb}}$ $ \rightarrow ^{10} {\rm{Be}}$+n+$ ^{208} {\rm{Pb}}$ calculated in our previous study [19] at the same energy (see Fig. 6). In the latter case, the peak at 1.25 MeV is only slightly noticeable, although the breakup cross section on the heavy target is significantly higher than the cross section on the light target at the region below 2 MeV. However, because the positions of the 1.25 MeV and 0.3 MeV peaks do not depend on the type of target, the natural conclusion is that they are related to the spectral structure of the $ ^{11} {\rm{Be}}$ nucleus. The quantum-quasiclassical computational scheme allows one to manipulate the spectrum of $ ^{11} {\rm{Be}}$, i.e., by removing the excited state $ 1/2^{-} $ from the corresponding partial interaction n-$ ^{10} {\rm{Be}}$ and varying the binding energy of the ground state $ 1/2^{+} $ [19]. This allows us to study the influence of these bound states on the peak in the cross section of approximately 0.3 MeV. The results of this investigation are presented in Fig. 7. Here, it can be observed that the elimination of the excited state $ 1/2^{-} $ from the n-$ ^{10} {\rm{Be}}$ interaction causes an increase in the peak at 0.3 MeV, because the breakup from the ground state $ 1/2^{+} $ moves directly into the continuous spectrum without intermediate population of the excited state $ 1/2^{-} $. A further change in the interaction, leading to an increase in the binding energy of the ground state of $ ^{11} {\rm{Be}}$ from $ E_{1/2^{+}} $ = −0.503 MeV, causes the transformation of the peak and to a plateau of the cross section at $ E_{1/2^{+}} $ = −1 MeV and then to the elimination of the plateau at $ E_{1/2^{+}} $ $ \leqslant $−2 MeV. The influence of the position of the ground state energy level on the resonance amplitude is also noticeable for the $ 5/2^{+} $ resonance at 1.25 MeV.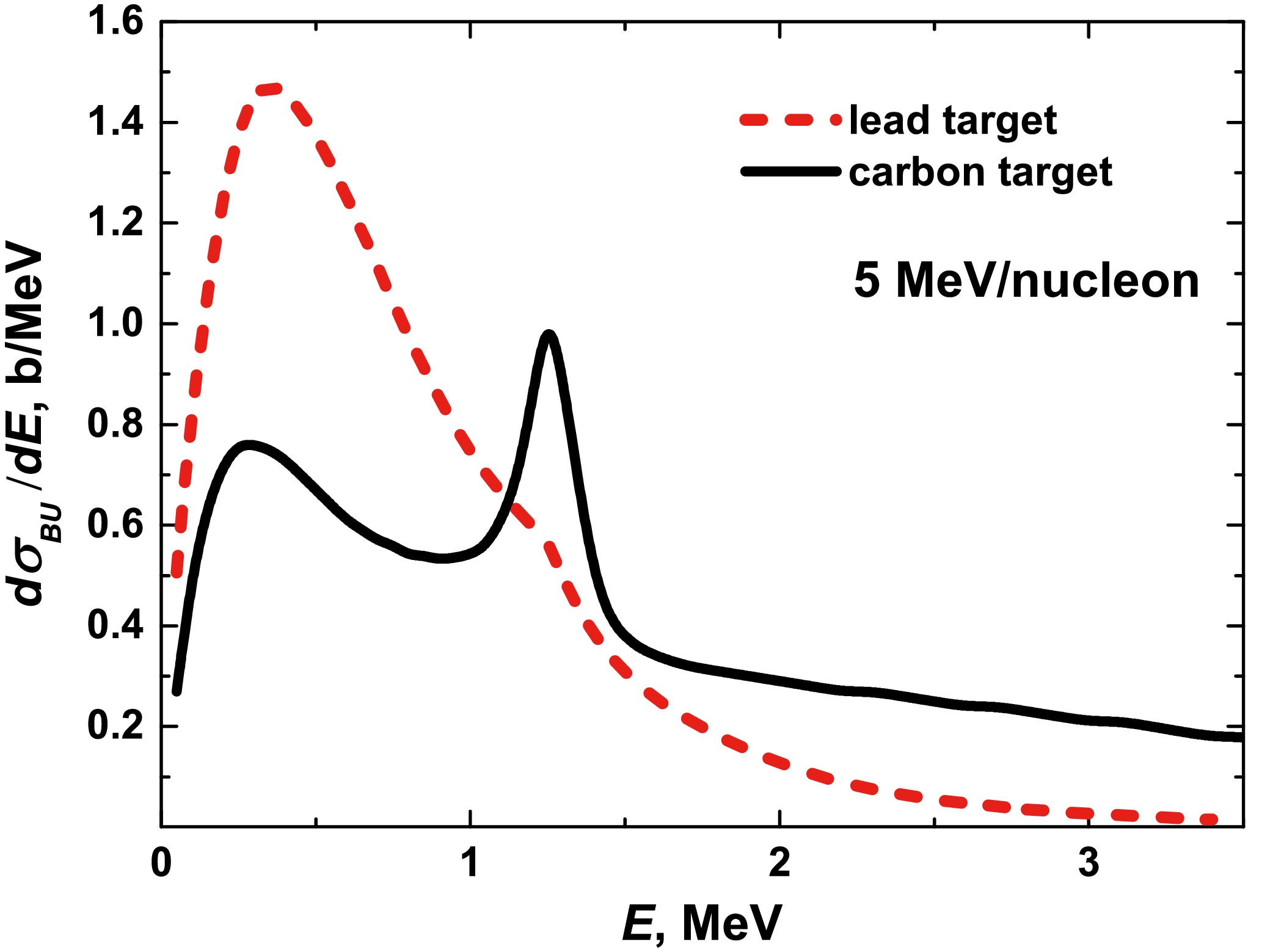

Figure 6.  (color online) Breakup cross sections of $ ^{11} {\rm{Be}}$ impinging on light ($ ^{12} {\rm{C}}$) (multiplied by 10) and heavy ($ ^{208} {\rm{Pb}}$) targets calculated within the quantum-quasiclassical approach at 5 MeV/nucleon.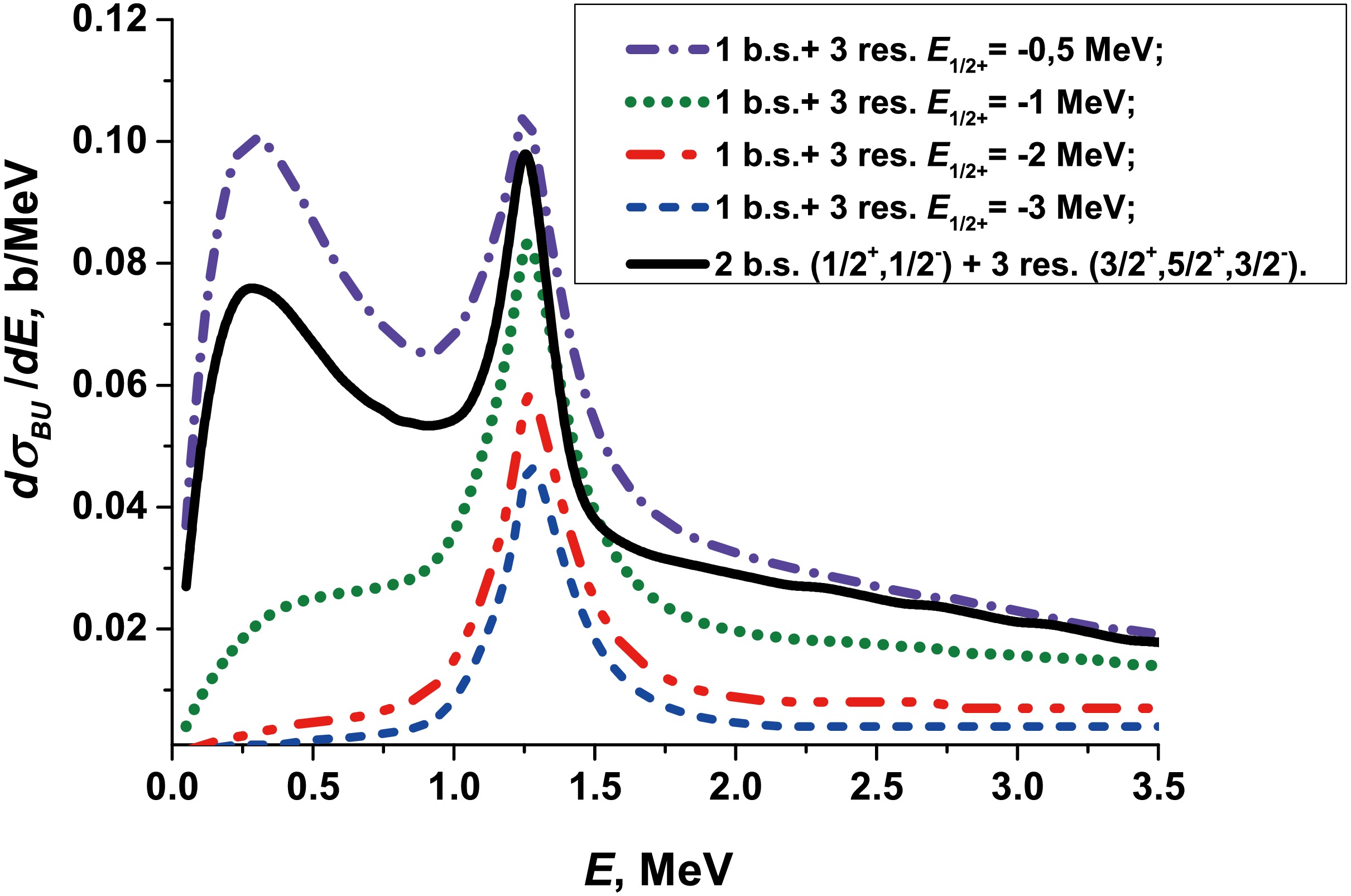

Figure 7.  (color online) Breakup cross sections of $ ^{11} {\rm{Be}}$ on $ ^{12} {\rm{C}}$ with different spectral structures of $ ^{11} {\rm{Be}}$ nucleus calculated at 5 MeV/nucleon.

The results in Fig. 8 illustrate the contribution of different partial waves in the continuum to the breakup cross sections at 5 MeV/nucleon calculated according to Eq. (7). We separated this study into two parts. In Fig. 8(a), we demonstrate the convergence of the breakup cross section over partial waves in the continuum, calculated with a successive increase in the number of partial waves l in Eq. (7) for the case of two bound states 1/2$ ^+ $ and 1/2$ ^- $ in the $ ^{11} {\rm{Be}}$ Hamiltonian Eq. (2). In Fig. 8(b), the case of one bound state 1/2$ ^+ $ in the $ ^{11} {\rm{Be}}$ Hamiltonian is illustrated. We can observe that the p-wave provides the main contribution to the peak at low energy below 0.5 MeV, and the d-wave mainly contributes in the 5/2$ ^+ $ resonance and above (see Fig. 8(a)). The contribution of the s-wave is insignificant in the entire energy range considered. The influence of the f-wave becomes significant only above 1.6 MeV.

Figure 8.  (color online) Breakup cross section ${\rm d}\sigma_{bu}(E)/{\rm d}E$ of $ ^{11} {\rm{Be}}$ at 5 MeV/nucleon calculated with increasing number of partial waves $ lm $ in the sum of Eq. (7). The calculations were performed with the complete number of m for every l-shell. Panel (a) shows the calculation results for the case of two bound states 1/2$ ^+ $ and 1/2$ ^- $ in the $ ^{11} {\rm{Be}}$ Hamiltonian Eq. (2). The case of one bound state 1/2$ ^{+} $ in the $ ^{11} {\rm{Be}}$ Hamiltonian is shown in Panel (b). Panels (c) and (d) illustrate the calculation of breakup cross sections for deeper energy levels of 1/2$ ^+ $ as $ E_{1/2^{+}} $ = -1 MeV (c) and $ E_{1/2^{+}} $ = -2 MeV (d), including one bound (1/2$ ^+ $) and three resonance states.

Excluding the excited state 1/2$ ^- $ from the $ ^{11} {\rm{Be}}$ Hamiltonian practically does not change the contribution of the s-wave in the entire energy range under consideration and slightly decreases the contributions of the p- and d- waves (see Fig. 8(b)). Thus, a comparison of the two calculations provided in Fig. 8(a) and Fig. 8(b) shows that the emitted neutron ends up in the p- and d- waves of the continuum spectrum owing to direct transitions 1/2$^+ \rightarrow kp$ and 1/2$ ^+ \rightarrow kd $ from the ground state of the $ ^{11} {\rm{Be}}$ nucleus ("$ kp $," "$ kd $," and "$ kf $" are the continuum states of the p-, d-, and f- partial waves, respectively). The transitions 1/2$ ^+ \rightarrow $ 1/2$ ^-\rightarrow kp $ and 1/2$ ^+\rightarrow $ 1/2$ ^- \rightarrow kd $ through the excited state 1/2$ ^- $ of $ ^{11} {\rm{Be}}$ provide an insignificant contribution to the population of the states $ kp $ and $ kd $. Therefore, the mechanism of population of the $ kf $ state by a neutron is important owing to the visible essential effect of the excited state 1/2$ ^- $ of $ ^{11} {\rm{Be}}$ on the population of the f-wave of the continuum at the energies below 1.6 MeV. In particular, from Fig. 8(b), we can observe that the direct transition 1/2$ ^+\rightarrow kf $ provides approximately 35% of the contribution from the transition 1/2$ ^+\rightarrow kp $ to the total breakup section, near the peak at 0.3 MeV (see Fig. 8(b)). However, the inclusion of the excited state 1/2$ ^- $ in the $ ^{11} {\rm{Be}}$ Hamiltonian leads to complete suppression of the contribution of the f-wave to the total breakup cross section below 1.6 MeV (see Fig. 8(a)). We interpret this small contribution of the f-wave in the total breakup cross section as mutual compensation of the direct transition 1/2$ ^+\rightarrow kf $ and the transition 1/2$ ^+\rightarrow $ 1/2$ ^- \rightarrow kf $ through the intermediate excited state 1/2$ ^- $ of $ ^{11} {\rm{Be}}$.

We explain the anomalously large contribution of the $ kf $ states of the continuum to the breakup cross section (7) (see Fig. 8(b)) by the anomalously long tail of the weakly-bound state s1/2$ ^+ $ with energy $ E_{1/2^{+}} $ = −0.5 MeV for the halo nucleus $ ^{11} {\rm{Be}}$. To confirm this, we performed calculations for cases when the potential $ V_{0}(r) $ has deeper energy levels $ E_{1/2^{+}} $ with $ E_{1/2^{+}} $ = −1 and −2 MeV, and the potential $ V_{1}(r) $ is zero. In these cases, the halo effect disappears (i.e., the tail of the wave function of the weakly-bound state s1/2$ ^+ $ is pulled under the potential barrier): the anomalously large contribution of the wave $ kf $ to the breakup cross section disappears with an increase in the nuclear binding energy (see Fig. 8(c) and (d)).

The study shows that the broad peak in the breakup cross section of $ ^{11} {\rm{Be}}$ on $ ^{12} {\rm{C}}$ near 0.3 MeV at 5 MeV/nucleon beam energy is caused by a weakly-bound ground state $ 1/2^{+} $ of $ ^{11} {\rm{Be}}$ with the energy $ E_{1/2^{+}} $= −0.503 MeV owing to the transition $ 1/2^{+} $ $ \rightarrow kp $ to the p-state of the continuum, and the presence of the excited state $ 1/2^{-} $ decreases its maximum by an order of 35% owing to the destructive interference between the transitions $ 1/2^{+} $ $ \rightarrow kf $ and $ 1/2^{+} $ $ \rightarrow $ $ 1/2^{-} $ $ \rightarrow kf $.

In this study, a theoretical investigation is performed on the breakup of the $ ^{11} {\rm{Be}}$ halo nucleus on a light target ($ ^{12} {\rm{C}}$) from intermediate (67 MeV/nucleon) to low (5−30 MeV/nucleon) energies within the quantum-quasiclassical approach, in which the three dimensional time-dependent Schrödinger equation for the halo nucleon was integrated simultaneously with the classical Hamiltonian equations describing relative projectile-target dynamics. In this hybrid quantum-quasiclassical approach, the time-dependent Schrödinger equation is integrated numerically with a technique developed to study the Coulomb breakup of halo nuclei [11, 13].

In the frame of the quantum-quasiclassical approach, we calculated the breakup cross sections of $ ^{11} {\rm{Be}}$ on a carbon target at energies of 5−67 MeV/nucleon, including Coulomb and nuclear interactions between the projectile and target. The performed study demonstrates that the model with straight-line projectile trajectories provides a satisfactory accuracy in calculating the breakup cross sections of $ ^{11} {\rm{Be}}$ while decreasing the beam energy down to 5−10 MeV/nucleon. The uniqueness of our calculations lies in the inclusion of low-lying resonances ($ 5/2^{+} $, $ 3/2^{-} $, and $ 3/2^{+} $) in the breakup cross section of the $ ^{11} {\rm{Be}}$ nucleus [19, 20, 26, 36]. Furthermore, we demonstrated that the analysis with our quantum-quasiclassical approach allows investigation of spectral properties of the $ ^{11} {\rm{Be}}$ nucleus from the breakup reactions. Our results describe well the existing experimental data of Fukuda et al. [21] at 67 MeV/nucleon and are in comparative agreement with other existing calculations performed with alternative theoretical models at 67 MeV/nucleon and 20 MeV/nucleon [23].

In summary, the results obtained by the quantum-quasiclassical approach can potentially be useful in further investigations of breakup reactions at low energies. In particular, the region around 20−10 MeV/nucleon is of great interest, because this is the energy range of HIE-ISOLD at CERN and the future ReA12 at MSU, and has hardly been investigated theoretically.