-
Superheavy nuclei have been one of the research frontiers and popular topics in nuclear physics since the prediction of the existence of a stable island of superheavy nuclei in the 1960s [1]. The study of superheavy nuclei is significant for extending the periodic table of elements, climbing the island of stability of superheavy nuclei, and exploring the stability of nuclei under extreme conditions. Over the past decades, experimentally, superheavy elements with
$ Z = 107-112 $ and$Z = 113-118$ have been synthesised in cold-fusion and hot-fusion reactions [2−7], respectively.α decay, one of the main decay modes of superheavy nuclei, is extremely important in the study of superheavy nuclei. On the one hand, it is an important method of identifying newly synthesized superheavy nuclei by measuring the cascade α decay of newly synthesized superheavy nuclei to known nuclei [2−7]. On the other hand, α decay, as an important probe for studying superheavy nuclei, provides abundant information about nuclear structures, such as magic numbers, islands of stability, and shell effects [6, 7]. Currently, the major superheavy nuclei laboratories around the world are attempting to synthesize new elements with
$ Z = 119 $ and 120 to break through the eighth period of the periodic table of elements [8−16]. If reliable theoretical predictions can be made about the properties of α decay of superheavy nuclei, they will provide a useful reference for the experimental synthesis and identification of new elements with$ Z = 119 $ and 120 [17−22]. Because α decay is dominated by quantum tunneling effects, the α decay energy is very important in the study of α decay [23−30]. An uncertainty of 1 MeV in α decay energy results in an uncertainty in the α decay half-life of$ 10^3 $ to$ 10^5 $ times for nuclei [31]. Therefore, accurate predictions of α decay energies would be useful in predicting the α decay half-lives of$ Z = 119 $ and 120 superheavy nuclei.The Finite-Range Droplet Model 2012 (FRDM) [32], a macroscopic-microscopic mass model, has been successfully and widely used to describe the fundamental properties of nuclei [33, 34]. In this study, we investigate the root mean square deviation between the α decay energies of nuclei given by the FRDM and those of 947 nuclei reported by the evaluated atomic mass table AME 2020 (AME) [35] with
$ 50\leqslant{Z}\leqslant 118 $ as 0.37 MeV. Although the FRDM can describe the α decay energies of heavy and superheavy nuclei relatively well, room for improvement remains.Recently, machine learning techniques have demonstrated their ability to analyze large amounts of data to find hidden correlations and have had widespread success in nuclear physics research, such as predicting the mass [36−38], charge radius [39, 40], α decay [41−44], fission barrier [45], and nuclear reaction [46]. In this study, first, we determine the differences between the α decay energies of the FRDM [32] and AME [35] using a neural network method and optimize the α decay energies of the FRDM by combining these learned differences with the predictions of the FRDM. Second, the α decay energies of unknown superheavy nuclei, in particular, those with
$ Z = 119 $ and 120, are predicted by combining the neural network approach and FRDM. Third, using the optimized α decay energy as input, we calculate the α decay half-lives of the known superheavy nuclei using the Generalized Liquid Drop Model (GLDM) and Royer formula of α decay half-lives [47]. The calculations are compared with experimental α decay half-lives. Fourth, the α decay half-lives of unknown superheavy nuclei, in particular those with$ Z = 119 $ and 120 are predicted using the GLDM and Royer formula with the optimized α decay energy as input. Finally, the relative errors of predictions and superposition are analyzed, and the average predictions are given to provide a theoretical reference for experiments synthesizing new elements.The remainder of this article is organized as follows. Sec. II presents the theoretical framework of the neural network details, GLDM, and Royer formula of α decay half-lives. Detailed calculations and discussion are given in Sec. III. Sec. IV provides a brief summary.
-
In this study, we design and implement a simple neural network model to predict the difference between the theoretical and experimental α decay energies. The model uses a three-layer fully connected network structure, with the input layer containing two features: the number of protons and mass number. It includes two hidden layers, each with 128 neurons, and uses the rectified linear unit (ReLU) activation function. The output layer consists of a single neuron to generate the predicted value. We divide the 947 nuclei dataset into three parts: 60% training set (569 nuclei), 20% validation set (189 nuclei), and 20% test set (189 nuclei). The training set is used to train the model. During this phase, the model learns the relationship between the input data and corresponding labels to adjust its parameters and minimize the loss function. The validation set is used to adjust the model's hyperparameters and select the best model architecture. During training, we regularly evaluate the model's performance on the validation set to assess its ability to generalize. If the model performs poorly on the validation set, this may indicate overfitting or underfitting. By monitoring the loss on the validation set, we can select the best training rounds and hyperparameters. The test set is used to evaluate the performance of the final model. The data in the test set are not used during training or validation; therefore, they provide a true assessment of the model.
We use the root mean square error
$ \sigma_{Q_{\alpha}} $ as a loss function to accurately assess the predictive accuracy of the model.$ \sigma_{Q_{\alpha}} = \sqrt{\frac{1}{n}\sum (Q_{\alpha,i}^{\text{FRDM-NN}}-Q_{\alpha,i}^{\text{AME}})^2} , $

(1) where
$ n = 947 $ represents the total number of data points,$ Q_{\alpha,i}^{\text{AME}} $ the desired output, and$ Q_{\alpha,i}^{\text{FRDM-NN}} $ the output from the neural network. We use the Adam optimizer to update the model parameters, which speeds up the training process. During training, the model undergoes 50000 iterations to reduce the loss for the training, validation, and test sets. Every 100 iterations, we output the loss value to monitor the training progress in real time. -
The α decay half-life can be obtained using the decay constant λ as
$ \ T_{1/2} = \frac{\ln{2}}{\lambda} . $

(2) Within Gamow's picture [48, 49], the α decay constant λ can be calculated using the product of α-particle preformation factor
$ P_{\alpha} $ , the assault frequency ν, and the barrier penetrating probability P:$ \ \lambda = P_{\alpha}{\nu}P . $

(3) The α-particle preformation factor
$ P_{\alpha} $ can be estimated using the analytic formula proposed in our previous work [50, 51]. It is expressed as$ \ \log_{10}P_{\alpha} = a+b(A_1^{1/6}+A_2^{1/6})+c\frac{N}{\sqrt{Q_{\alpha}}}+d\sqrt{l(l+1)}+h , $

(4) with
$ A_1 $ and$ A_2 $ being the mass numbers of the α-particle and daughter nucleus, respectively. N and$ Q_{\alpha} $ denote the neutron number and α decay energy of the parent nucleus, respectively. l is the angular momentum carried by the α-particle, which can be obtained using the conservation laws of angular momentum and parity [52]. The h represents the blocking effect of unpaired nucleons. The adjustable parameters values are$ a = 37.421 $ ,$ b = -10.900 $ ,$ c = 0.040 $ , and$ d = -0.088 $ .$ h = 0 $ ,$ -0.323 $ , and$ -0.851 $ for even-even, odd-A, and doubly odd nuclei, respectively [50].The assault frequency ν can be calculated as
$ \ \nu = \frac{1}{2R}\sqrt{\frac{2E_{\alpha}}{M_{\alpha}}} , $

(5) where
$ E_{\alpha} = \dfrac{A-4}{A}Q_{\alpha} $ is the kinetic energy of the α-particle, with A and$ Q_{\alpha} $ being the mass number and α decay energy of the parent nucleus, respectively.$ M_{\alpha} $ denotes the mass of the α-particle. R is the radius of the α decay parent nucleus obtained by Refs. [53, 54], and it is expressed as$ \ R = 1.28A^{1/3}-0.76+0.8A^{-1/3} , $

(6) with A being the mass number of the parent nucleus.
The barrier penetrating probability P can be obtained using Wentzel-Kramers-Brillouin (WKB) approximation as
$ \ P = \exp\left[-\frac{2}{\hbar}{\int_{r_{\text{in}}}^{r_{\text{out}}} \sqrt{2B(r)(E_{r}-E(\text{sphere}))} {\rm d}r}\right] , $

(7) with r being the center of mass distance between the preformed α-particle and daughter nucleus. The classical turning points
$ r_{\text{in}} $ and$ r_{\text{out}} $ are obtained using$ r_{\text{in}} = R_1+R_2 $ and$ E(r_{\text{out}}) = Q_{\alpha} $ .$ B(r) = \mu $ represents the reduced mass between the preformed α-particle and daughter nucleus.The total interaction potential E in the GLDM has been introduced in detail in previous works [54−58]. It consists of five parts: volume energy
$ E_V $ , surface energy$ E_S $ , Coulomb energy$ E_C $ , proximity energy$ E_{\text{Prox}} $ , and centrifugal potential$ E_l $ .$ \ E = E_V+E_S+E_C+E_{\text{Prox}}+E_l . $

(8) Although both the α-particle preformation factor
$ P_{\alpha} $ in Eq. (4) and centrifugal potential$ E_l $ in Eq. (8) consider the contribution of the angular momentum carried by the α-particle, this is not a double counting of the centrifugal effect. l reflects the difference in$ P_{\alpha} $ of the favored and unfavored α decays [50, 51]. Figs. 2–4 of our previous work present our findings on the effect of$ P_{\alpha} $ on α decay half-lives [59]. The previous study showed that the calculated α decay half-lives using Eq. (8), without considering$ P_{\alpha} $ , were smaller than the experimental data by more than an order of magnitude. When$ P_{\alpha} $ was considered, the experimental data were well reproduced [59]. This demonstrated that considering the contribution of the centrifugal potential only in the nuclear potential does not fully reflect the effect of angular momentum for α decay and preformation of α-particle. Therefore, the centrifugal effect is not double counted in Eqs. (4) and (8).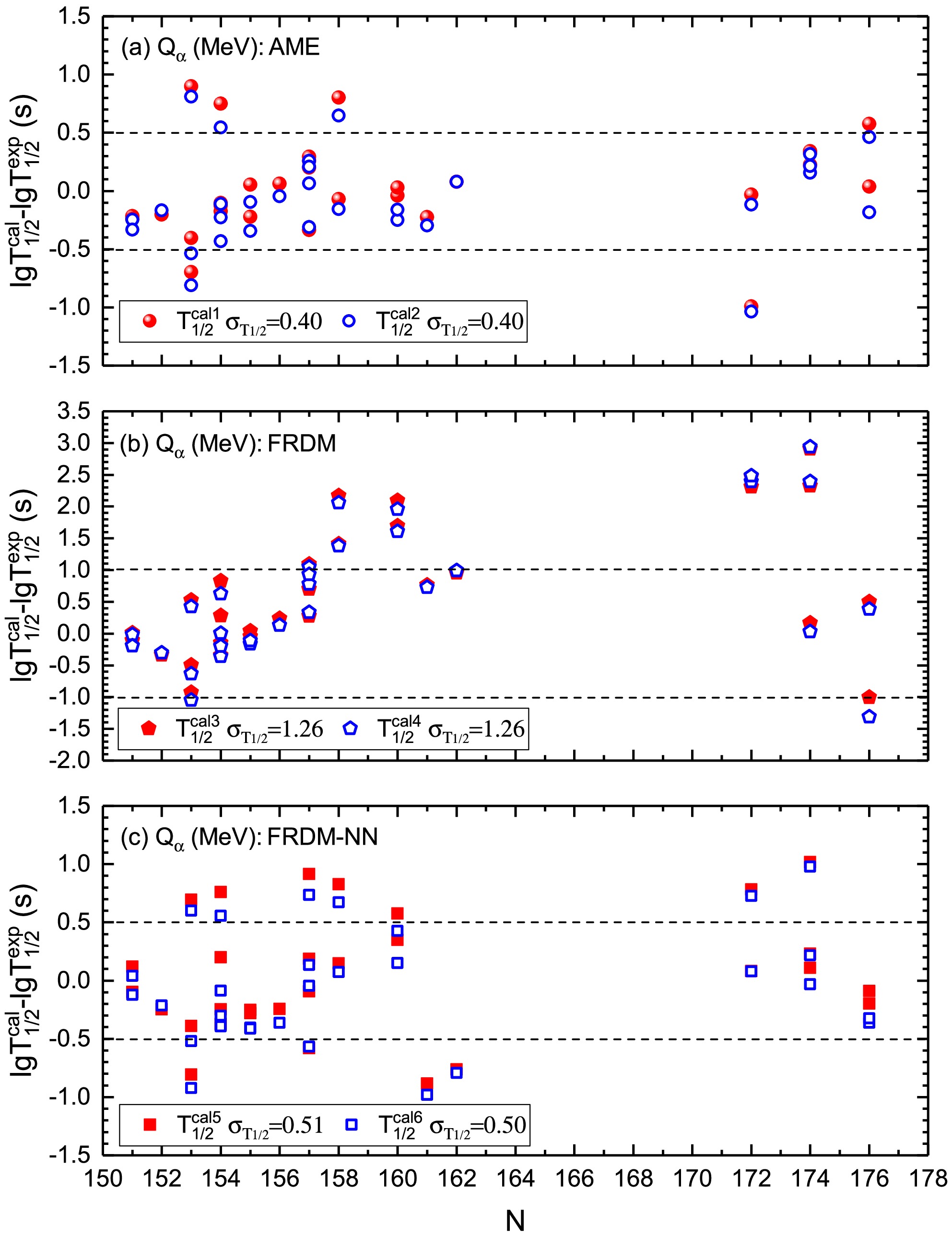
Figure 3. (color online) Logarithmic differences between the calculations of α decay half-lives using the GLDM and Royer formula [47] and the experimental data for 30 known superheavy nuclei, which are denoted by solid and open symbols, respectively.
${j^{\pi}_{p}}$ and${j^{\pi}_{d}}$ are available and obtained from NUBASE [61]. Subfigures (a), (b), and (c) denote the differences between the calculations when inputting the α decay energies obtained using AME [35], FRDM [32], and FRDM-NN and the experimental data, respectively.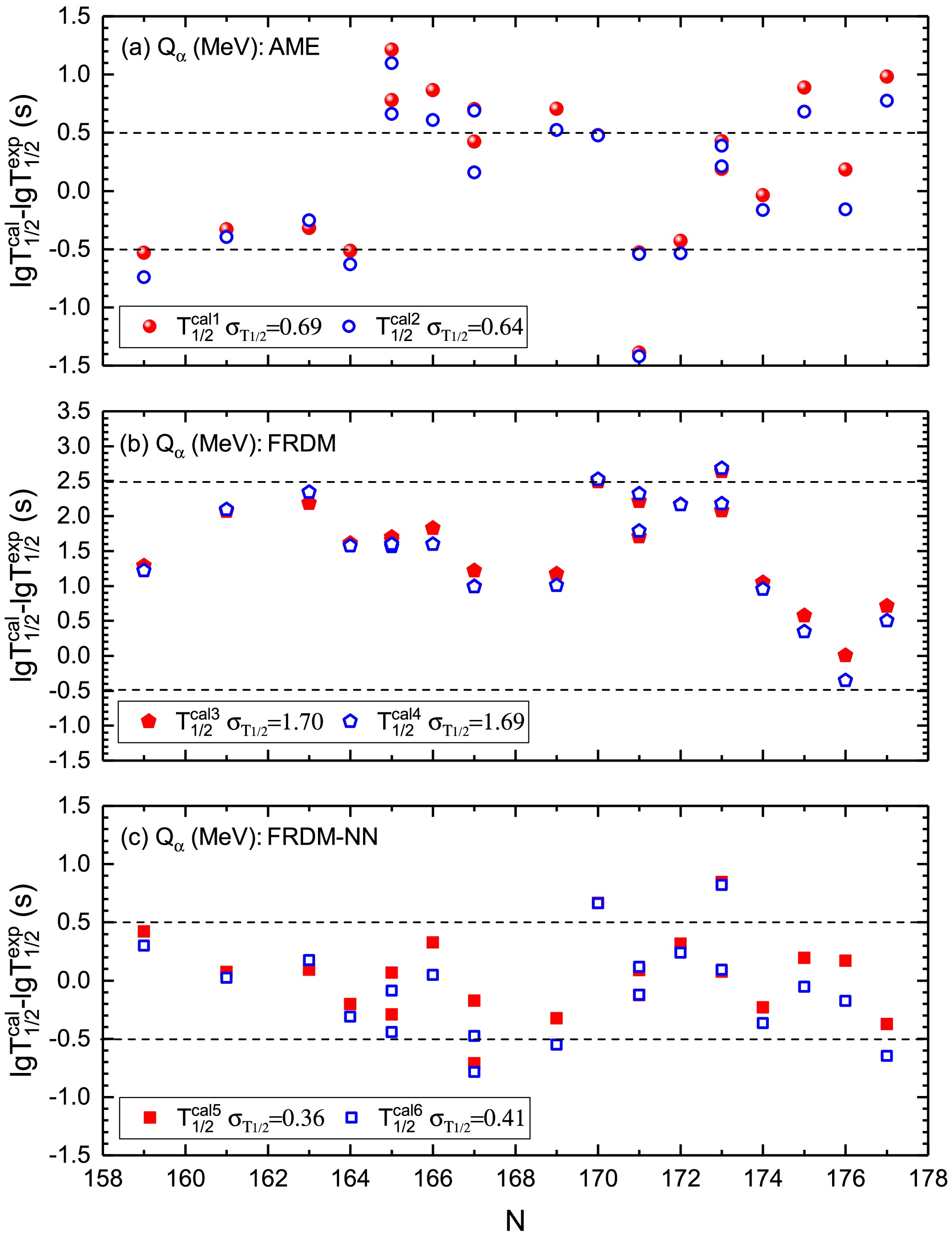
Figure 4. (color online) Same as Fig. 3, but depicting the logarithmic differences between the calculations of α decay half-lives using the GLDM and Royer formula [47] and the experimental data for 20 known odd-A superheavy nuclei, where
${j^{\pi}_{p}}$ and/or${j^{\pi}_{d}}$ are not available in NUBASE [61] but obtained using the FRDM [32]. -
The Royer formula [54] is widely used to calculate and predict α decay half-lives because it approximates the Universal Decay Law [27] when the reduced mass is approximately constant and the mass of the daughter is much larger than that of the α-particle [60]. This approximation is excellent for superheavy nuclei [60]. In a previous study [47], we further improved the Royer formula of α decay half-life by considering the contribution of centrifugal potential and the blocking effect of unpaired nucleons; it is expressed as
$ \log_{10}{T_{1/2}} = a+bA^{1/6}\sqrt{Z}+c\frac{Z}{\sqrt{Q_{\alpha}}}+{\rm d}l(l+1)+h , $

(9) where A, Z, and
$ Q_{\alpha} $ are the mass number, proton number, and α decay energy of parent nuclei, respectively. l is the angular momentum carried by the α-particle. h represents the blocking effect of unpaired nucleons. The values of adjustable parameters are$ a = -26.8125, b = -1.1255, c = 1.6057, d = 0.0513 $ . The values of h for different α decay cases are expressed as$ \ h = \left\{\begin{array}{llll} 0,&\text{for even-even nuclei},\\ 0.3625,&\text{for even } Z \;\text{-odd } N \text{ nuclei},\\ 0.2812,&\text{for odd } Z \;\text{-even } N \text{ nuclei},\\ 0.7486,&\text{for doubly odd nuclei}. \end{array}\right. $

(10) -
Accurate α decay energies must be employed to achieve a theoretically accurate description of α decay half-lives. Herein, the α decay energies given by the FRDM [32] are examined. The discrepancies between the α decay energies calculated using the FRDM [32] and ones reported by AME [35] for 947 heavy and superheavy nuclei are denoted as red square and plotted in Fig. 1. As shown in this figure, the discrepancy caused by the FRDM is typically in the range of
$ \pm 0.8 $ MeV for the majority of nuclei. However, for a significant number of nuclei, the discrepancy exceeds 1 MeV. Specifically, for$ 52<Z<54 $ , the difference is greater than 0.5 MeV and even close to 2 MeV, indicating that the α decay energies obtained using the FRDM are overestimated. In the region of$ 96<Z<116 $ , the difference increased further toward the superheavy nuclei region, biased toward negative values. This suggests that the FRDM underestimates the α decay energy in the region of superheavy nuclei. Consequently, the FRDM is likely to predict lower α decay energies for superheavy nuclei with$ Z = 119 $ and 120. Improving the accuracy of α decay energy calculations based on the FRDM alone is challenging. The introduction of neural networks can effectively compensate for these limitations within the FRDM [32]. Therefore, the α decay energies must be optimized using the neural networks to improve the accuracy of predicting the α decay energies of unknown superheavy nuclei, particularly with$ Z = 119 $ and 120. The deviations between the optimized α decay energies obtained using the neural network approach, i.e., FRDM-NN, and the α decay energies reported by AME [35] are marked as blue circles in Fig. 1. This figure shows that, after optimization using a neural network, the α decay energy discrepancy caused by the FRDM-NN is significantly smaller than that caused by the FRDM. Furthermore, for the majority of nuclei, the deviations caused by the FRDM-NN are within a range of$ \pm 0.3 $ MeV. For superheavy nuclei, the deviations caused by the FRDM-NN are significantly lower than those caused by the FRDM, indicating that the FRDM-NN effectively improves the accuracy in describing the α decay energy of superheavy nuclei. In addition, Fig. 1 depicts the root mean square errors$ \sigma_{Q_{\alpha}} $ between the α decay energies provided by the FRDM and FRDM-NN and those presented by AME. The$ \sigma_{Q_{\alpha}} $ values are reduced from 0.37 MeV in the FRDM to 0.21 MeV in the FRDM-NN, which means that the accuracy in describing the α decay energy improves by$ \dfrac{0.37-0.21}{0.37} = 43.24 $ % when the neural network approach is applied.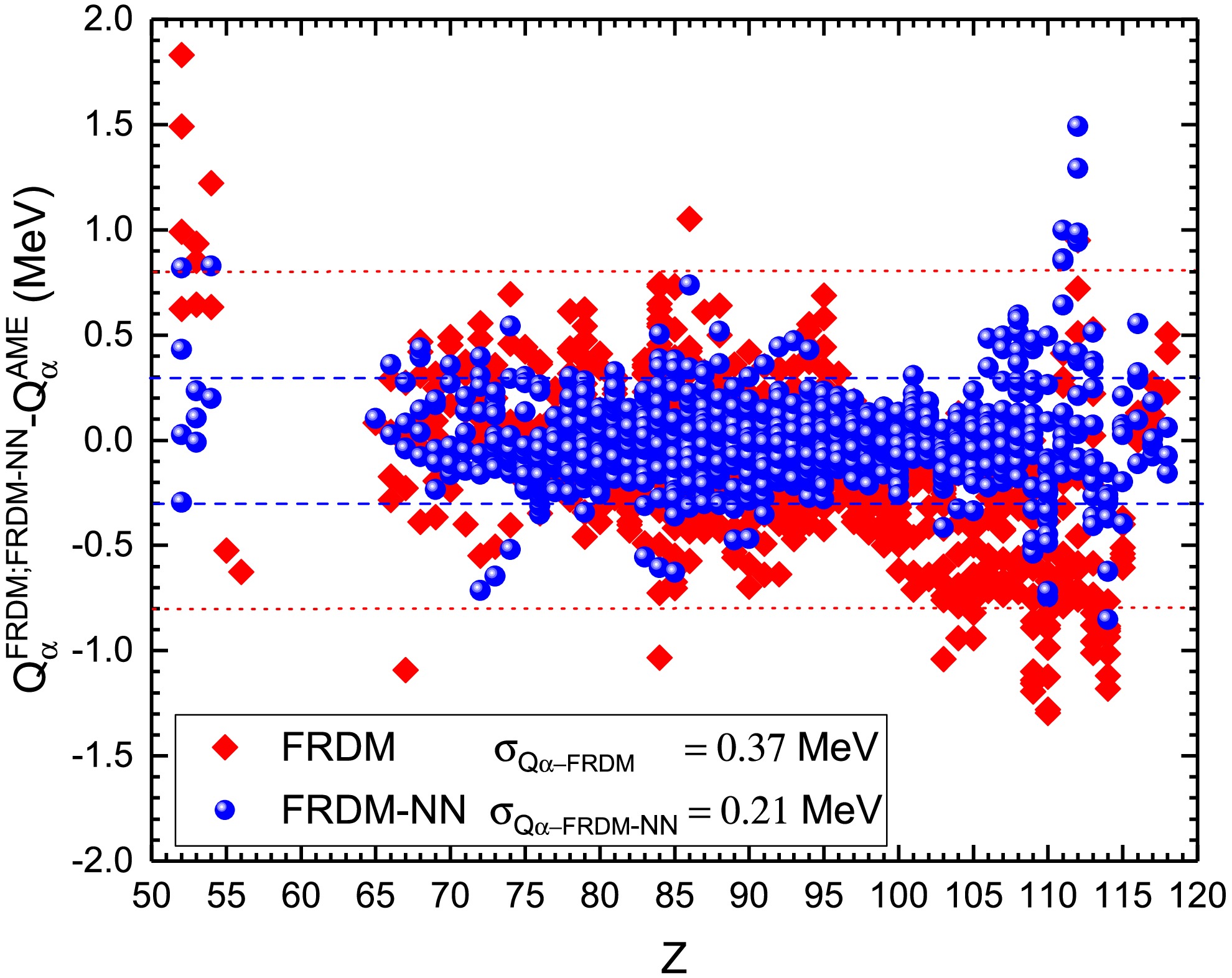
Figure 1. (color online) Differences between the α decay energies obtained using the FRDM [32] and FRDM-NN and the α decay energies reported by AME [35] for 947 known heavy and superheavy nuclei. The red square and blue circle denote the differences caused by
$Q_{\alpha}^{\text{FRDM}}$ and$Q_{\alpha}^{\text{FRDM-NN}}$ , respectively.The ability of the FRDM [32] and FRDM-NN to describe the α decay energies of superheavy nuclei with
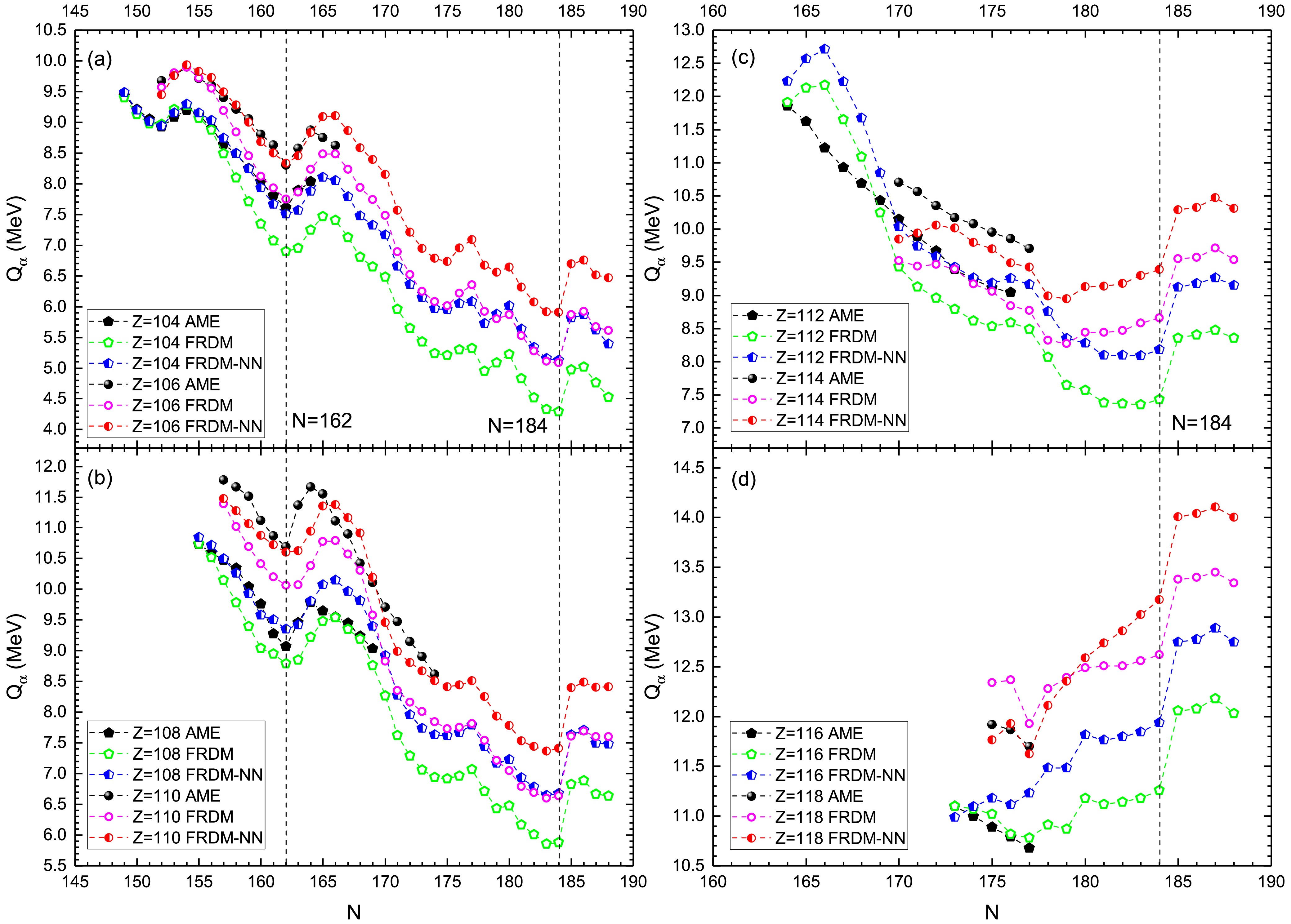
$ Z = 104 $ , 106, 108, 110, 112, 114, 116, and 118 is tested. Figure 2 shows the α decay energies of the superheavy nuclei given by AME [35], FRDM [32], and FRDM-NN, denoted by the solid, open, and semi-solid symbols, respectively. The α decay energies obtained with the FRDM are significantly different from those obtained with AME [35] (Fig. 2(a)−(d)). The optimized α decay energies obtained using the FRDM-NN are significantly improved in the reproduction of those given by AME [35]. In addition, consistent with the results shown in Fig. 1, the α decay energies of the superheavy isotope chains given by the FRDM [32] are mostly lower than the experimental values of AME [35]. The FRDM-NN method effectively solves this problem. Furthermore, Fig. 2 (a) and (b) show that the three types of α decay energies all have a valley at$ N = 162 $ , and the α decay energies of$ N = 164 $ increase dramatically. Evidence exists for a shell effect at$ N = 162 $ , based on the α decay energies obtained by AME [35], in particular, for the FRDM and FRDM-NN. The shell effect at$ N = 162 $ has been demonstrated experimentally [6, 7]. The FRDM-NN shows the shell effect at$ N = 162 $ , indicating that the neural network approach does not interfere with the revelation of the microscopic shell effect, which is important for exploring the island of stability for superheavy nuclei. In particular, Fig. 2(a)−(d) show that, when the neutron number exceeds$ N = 184 $ , the α decay energies predicted by the FRDM and FRDM-NN change sharply, and at$ N = 186 $ , the α decay energy increases by almost 1 MeV. This suggests that strong shell effect is reflected, implying that the next neutron magic number after$ N = 126 $ may be$ N = 184 $ .The experimental α decay half-lives and calculations based on the α decay energies data from AME [35], FRDM [32], and FRDM-NN are presented in Tables 1–3, respectively. Table 1 shows the calculated α decay half-lives for the 30 known superheavy nuclei for which the spin and parity values of the parent and daughter nuclei, i.e.,
$ {j^{\pi}_{p}} $ and$ {j^{\pi}_{d}} $ , are available, obtained from the evaluated nuclear properties table NUBASE 2020 (NUBASE) [61]. Table 2 presents the calculations of 20 known odd-A superheavy nuclei, where$ {j^{\pi}_{p}} $ and/or$ {j^{\pi}_{d}} $ are not available in NUBASE [61] but obtained using the FRDM [32]. For the favored and unfavored α decay shown in Tables 1 and 2, the angular momentum l is obtained using the conservation laws of angular momentum and parity [52]. In addition, the unfavored α decay with zero angular momentum transfer is also calculated to attest the possibility of favored α decay. Table 3 lists the calculations of 17 known doubly odd superheavy nuclei, where$ {j^{\pi}_{p}} $ and/or$ {j^{\pi}_{d}} $ are not available in NUBASE [61].$ l = 0 $ is assumed to study the possibility of favored α decay. In Tables 1–2, the first column shows the α decay including the parent and daughter nuclei. The second column represents the spin and parity transition of the parent and daughter nuclei. The third column provides the minimum angular momentum taken away by the α particle. The fourth column shows the experimental α decay half-lives and the error uncertainties given by NUBASE [61], except for the experimental α decay half-life and error uncertainties of the nucleus$ ^{264} {\rm{Hs}}$ listed in Table 1, which are obtained from the National Nuclear Data Center (NNDC) [62]. The fifth column is the α decay energy reported by AME [35]. The sixth and seventh columns are the calculated α decay half-lives using the GLDM and Royer formula [47], respectively, where the α decay energy given by AME [61] is inputted. The eighth column is the α decay energy calculated using the FRDM [32]. The ninth and tenth columns are the calculated α decay half-lives by using the GLDM and Royer formula [47], respectively, where the α decay energy given by the FRDM [32] is inputted. The eleventh column is the α decay energy calculated using the FRDM-NN. The last two columns are the α decay half-lives calculated using the GLDM and Royer formula [47], respectively, where the α decay energy given by the FRDM-NN is inputted. Each column in Table 3 is the same as those in Tables 1 and 2, except for the column that does not list the$ {j^{\pi}_{p}} $ $ \to $ $ {j^{\pi}_{d}} $ changes.α transition ${j^{\pi}_{p}}\to{j^{\pi}_{d}}$ 

l $\text{lg}T^{\text{exp}}_{1/2}$ 

$Q_{\alpha}^{\text{AME}}$ 

$\text{lg}T^{\text{cal1}}_{1/2}$ 

$\text{lg}T^{\text{cal2}}_{1/2}$ 

$Q_{\alpha}^{\text{FRDM}}$ 

$\text{lg}T^{\text{cal3}}_{1/2}$ 

$\text{lg}T^{\text{cal4}}_{1/2}$ 

$Q_{\alpha}^{\text{FRDM-NN}}$ 

$\text{lg}T^{\text{cal5}}_{1/2}$ 

$\text{lg}T^{\text{cal6}}_{1/2}$ 

$^{254}{\rm{Rf}} \to ^{250}{\rm{No}}$ 

${0^+\to0^+}$ 

0 $>-2.82^{}_{}$ 

$9.21\#$ 

$-0.70$ 

$-0.67$ 

$9.13$ 

$-0.47$ 

$-0.43$ 

$9.20$ 

$-0.67$ 

$-0.64$ 

$^{255}{\rm{Rf}} \to ^{251}{\rm{No}}$ 

${(9/2^-)}\to{(7/2^+)}$ 

0 $0.49^{+0.01}_{-0.01}$ 

$9.06$ 

$0.07$ 

$0.14$ 

$8.98$ 

$0.29$ 

$0.37$ 

$9.02$ 

$0.18$ 

$0.26$ 

$^{255}{\rm{Rf}} \to ^{251}{\rm{No}}$ 

${(9/2^-)}\to{(7/2^+)}$ 

1 $0.49^{+0.01}_{-0.01}$ 

$9.06$ 

$0.27$ 

$0.24$ 

$8.98$ 

$0.50$ 

$0.48$ 

$9.02$ 

$0.39$ 

$0.37$ 

$^{256}{\rm{Rf}} \to ^{252}{\rm{No}}$ 

${0^+\to0^+}$ 

0 $0.33^{+0.003}_{-0.003}$ 

$8.93$ 

$0.13$ 

$0.16$ 

$8.97$ 

$-0.01$ 

$0.02$ 

$8.94$ 

$0.08$ 

$0.12$ 

$^{257}{\rm{Rf}} \to ^{253}{\rm{No}}$ 

${(1/2^+)\to9/2^-}$ 

0 $0.75^{+0.02}_{-0.02}$ 

$9.08$ 

$-0.03$ 

$0.02$ 

$9.21$ 

$-0.40$ 

$-0.37$ 

$9.15$ 

$-0.24$ 

$-0.19$ 

$^{257}{\rm{Rf}} \to ^{253}{\rm{No}}$ 

${(1/2^+)\to9/2^-}$ 

5 $0.75^{+0.02}_{-0.02}$ 

$9.08$ 

$1.65$ 

$1.56$ 

$9.21$ 

$1.27$ 

$1.17$ 

$9.15$ 

$1.44$ 

$1.35$ 

$^{258}{\rm{Rf}} \to ^{254}{\rm{No}}$ 

${0^+\to0^+}$ 

0 $-0.59^{+0.02}_{-0.02}$ 

$9.20$ 

$-0.70$ 

$-0.70$ 

$9.28$ 

$-0.94$ 

$-0.95$ 

$9.29$ 

$-0.97$ 

$-0.99$ 

$^{259}{\rm{Rf}} \to ^{255}{\rm{No}}$ 

${3/2^+\#\to(1/2^+)}$ 

0 $0.49^{+0.04}_{-0.05}$ 

$9.13\#$ 

$-0.19$ 

$-0.16$ 

$9.07$ 

$-0.01$ 

$0.02$ 

$9.15$ 

$-0.25$ 

$-0.22$ 

$^{259}{\rm{Rf}} \to ^{255}{\rm{No}}$ 

${3/2^+\#\to(1/2^+)}$ 

2 $0.49^{+0.04}_{-0.05}$ 

$9.13\#$ 

$0.27$ 

$0.15$ 

$9.07$ 

$0.44$ 

$0.33$ 

$9.15$ 

$0.21$ 

$0.09$ 

$^{261}{\rm{Rf}} \to ^{257}{\rm{No}}$ 

${3/2^+\#\to(3/2^+)}$ 

0 $1.07^{+0.04}_{-0.04}$ 

$8.65$ 

$1.27$ 

$1.33$ 

$8.49$ 

$1.77$ 

$1.85$ 

$8.74$ 

$0.97$ 

$1.02$ 

$^{256}{\rm{Db}}$ 

$\to ^{252}{\rm{Lr}}$ 

${9^-\#\to7^-\#}$ 

0 $0.39^{+0.09}_{-0.12}$ 

$9.34$ 

$0.14$ 

$0.05$ 

$9.29$ 

$0.28$ 

$0.19$ 

$9.21$ 

$0.50$ 

$0.43$ 

$^{256}{\rm{Db}}$ 

$\to ^{252}{\rm{Lr}}$ 

${9^-\#\to7^-\#}$ 

2 $0.39^{+0.09}_{-0.12}$ 

$9.34$ 

$0.60$ 

$0.36$ 

$9.29$ 

$0.73$ 

$0.50$ 

$9.21$ 

$0.96$ 

$0.73$ 

$^{257}{\rm{Db}}$ 

$\to ^{253}{\rm{Lr}}$ 

${9/2^+\#\to(7/2^-)}$ 

0 $<0.39^{}_{}$ 

$9.21$ 

$-0.03$ 

$-0.04$ 

$9.26$ 

$-0.18$ 

$-0.21$ 

$9.15$ 

$0.13$ 

$0.12$ 

$^{257}{\rm{Db}}$ 

$\to ^{253}{\rm{Lr}}$ 

${9/2^+\#\to(7/2^-)}$ 

1 $<0.39^{}_{}$ 

$9.21$ 

$0.18$ 

$0.06$ 

$9.26$ 

$0.02$ 

$-0.10$ 

$9.15$ 

$0.33$ 

$0.22$ 

$^{258}{\rm{Db}}$ 

$\to ^{254}{\rm{Lr}}$ 

${0^-\#\to4^+\#}$ 

0 $0.53^{+0.07}_{-0.08}$ 

$9.44$ 

$-0.17$ 

$-0.28$ 

$9.52$ 

$-0.40$ 

$-0.52$ 

$9.48$ 

$-0.28$ 

$-0.39$ 

$^{258}{\rm{Db}}$ 

$\to ^{254}{\rm{Lr}}$ 

${0^-\#\to4^+\#}$ 

5 $0.53^{+0.07}_{-0.08}$ 

$9.44$ 

$1.50$ 

$1.26$ 

$9.52$ 

$1.27$ 

$1.02$ 

$9.48$ 

$1.39$ 

$1.15$ 

$^{259}{\rm{Db}}$ 

$\to ^{255}{\rm{Lr}}$ 

${9/2^+\#\to(1/2^-)}$ 

0 $-0.29^{+0.12}_{-0.16}$ 

$9.62$ 

$-1.21$ 

$-1.29$ 

$9.59$ 

$-1.13$ 

$-1.21$ 

$9.61$ 

$-1.20$ 

$-1.28$ 

$^{259}{\rm{Db}}$ 

$\to ^{255}{\rm{Lr}}$ 

${9/2^+\#\to(1/2^-)}$ 

5 $-0.29^{+0.12}_{-0.16}$ 

$9.62$ 

$0.46$ 

$0.25$ 

$9.59$ 

$0.54$ 

$0.33$ 

$9.61$ 

$0.47$ 

$0.26$ 

$^{263}{\rm{Db}}$ 

$\to ^{259}{\rm{Lr}}$ 

${9/2^+\#\to1/2^-\#}$ 

0 $1.89^{+0.12}_{-0.16}$ 

$8.83\#$ 

$1.01$ 

$1.00$ 

$8.41$ 

$2.37$ 

$2.41$ 

$8.83$ 

$1.03$ 

$1.03$ 

$^{263}{\rm{Db}}$ 

$\to ^{259}{\rm{Lr}}$ 

${9/2^+\#\to1/2^-\#}$ 

5 $1.89^{+0.12}_{-0.16}$ 

$8.83\#$ 

$2.70$ 

$2.54$ 

$8.41$ 

$4.06$ 

$3.95$ 

$8.83$ 

$2.72$ 

$2.57$ 

$^{259}{\rm{Sg}} \to ^{255}{\rm{Rf}}$ 

${(11/2^-)\to(9/2^-)}$ 

0 $-0.40^{+0.06}_{-0.07}$ 

$9.77$ 

$-1.25$ 

$-1.24$ 

$9.80$ 

$-1.35$ 

$-1.34$ 

$9.76$ 

$-1.24$ 

$-1.22$ 

$^{259}{\rm{Sg}} \to ^{255}{\rm{Rf}}$ 

${(11/2^-)\to(9/2^-)}$ 

2 $-0.40^{+0.06}_{-0.07}$ 

$9.77$ 

$-0.80$ 

$-0.93$ 

$9.80$ 

$-0.90$ 

$-1.03$ 

$9.76$ 

$-0.78$ 

$-0.92$ 

$^{260}{\rm{Sg}} \to ^{256}{\rm{Rf}}$ 

${0^+\to0^+}$ 

0 $-1.77^{+0.03}_{-0.03}$ 

$9.90$ 

$-1.94$ 

$-1.99$ 

$9.89$ 

$-1.92$ 

$-1.97$ 

$9.93$ 

$-2.02$ 

$-2.07$ 

$^{261}{\rm{Sg}} \to ^{257}{\rm{Rf}}$ 

${(3/2^+)\to(1/2^+)}$ 

0 $-0.73^{+0.01}_{-0.01}$ 

$9.71$ 

$-1.13$ 

$-1.13$ 

$9.72$ 

$-1.15$ 

$-1.15$ 

$9.83$ 

$-1.44$ 

$-1.45$ 

$^{261}{\rm{Sg}} \to ^{257}{\rm{Rf}}$ 

${(3/2^+)\to(1/2^+)}$ 

2 $-0.73^{+0.01}_{-0.01}$ 

$9.71$ 

$-0.68$ 

$-0.83$ 

$9.72$ 

$-0.69$ 

$-0.84$ 

$9.83$ 

$-0.98$ 

$-1.14$ 

$^{263}{\rm{Sg}} \to ^{259}{\rm{Rf}}$ 

${3/2^+\#\to3/2^+\#}$ 

0 $0.03^{+0.06}_{-0.07}$ 

$9.40$ 

$-0.30$ 

$-0.28$ 

$9.19$ 

$0.31$ 

$0.36$ 

$9.49$ 

$-0.55$ 

$-0.53$ 

$^{265}{\rm{Sg}} \to ^{261}{\rm{Rf}}$ 

${11/2^-\#\to3/2^+\#}$ 

0 $<1.26^{}_{}$ 

$9.05\#$ 

$0.70$ 

$0.76$ 

$8.45$ 

$2.60$ 

$2.73$ 

$9.00$ 

$0.85$ 

$0.92$ 

$^{265}{\rm{Sg}} \to ^{261}{\rm{Rf}}$ 

${11/2^-\#\to3/2^+\#}$ 

5 $<1.26^{}_{}$ 

$9.05\#$ 

$2.37$ 

$2.30$ 

$8.45$ 

$4.29$ 

$4.27$ 

$9.00$ 

$2.52$ 

$2.45$ 

$^{261}{\rm{Bh}} \to ^{257}{\rm{Db}}$ 

${(5/2^-)\to9/2^+\#}$ 

0 $-1.89^{+0.1}_{-0.12}$ 

$10.50$ 

$-2.79$ 

$-2.94$ 

$10.33$ 

$-2.38$ 

$-2.51$ 

$10.36$ 

$-2.46$ 

$-2.60$ 

$^{261}{\rm{Bh}} \to ^{257}{\rm{Db}}$ 

${(5/2^-)\to9/2^+\#}$ 

3 $-1.89^{+0.10}_{-0.12}$ 

$10.50$ 

$-2.02$ 

$-2.33$ 

$10.33$ 

$-1.61$ 

$-1.89$ 

$10.36$ 

$-1.69$ 

$-1.98$ 

$^{267}{\rm{Bh}} \to ^{263}{\rm{Db}}$ 

${5/2^-\#\to9/2^+\#}$ 

0 $1.34^{+0.16}_{-0.26}$ 

$9.23\#$ 

$0.52$ 

$0.48$ 

$8.55$ 

$2.65$ 

$2.68$ 

$9.10$ 

$0.91$ 

$0.88$ 

$^{267}{\rm{Bh}} \to ^{263}{\rm{Db}}$ 

${5/2^-\#\to9/2^+\#}$ 

3 $1.34^{+0.16}_{-0.26}$ 

$9.23\#$ 

$1.30$ 

$1.09$ 

$8.55$ 

$3.44$ 

$3.30$ 

$9.10$ 

$1.69$ 

$1.49$ 

$^{264}{\rm{Hs}} \to ^{260}{\rm{Sg}}$ 

${0^+\to0^+}$ 

0 $-3.10^{+0.19}_{-0.13}$ 

$10.59$ 

$-3.04$ 

$-3.15$ 

$10.52$ 

$-2.87$ 

$-2.97$ 

$10.72$ 

$-3.35$ 

$-3.47$ 

$^{265}{\rm{Hs}} \to ^{261}{\rm{Sg}}$ 

${3/2^+\#\to(3/2^+)}$ 

0 $-2.71^{+0.03}_{-0.04}$ 

$10.47$ 

$-2.45$ 

$-2.50$ 

$10.15$ 

$-1.65$ 

$-1.66$ 

$10.50$ 

$-2.52$ 

$-2.58$ 

$^{266}{\rm{Hs}} \to ^{262}{\rm{Sg}}$ 

${0^+\to0^+}$ 

0 $-2.40^{+0.08}_{-0.10}$ 

$10.35$ 

$-2.47$ 

$-2.56$ 

$9.78$ 

$-0.99$ 

$-1.02$ 

$10.26$ 

$-2.26$ 

$-2.33$ 

$^{269}{\rm{Hs}} \to ^{265}{\rm{Sg}}$ 

${9/2^+\#\to11/2^-\#}$ 

0 $1.18^{+0.17}_{-0.27}$ 

$9.27\#$ 

$0.75$ 

$0.78$ 

$8.95$ 

$1.73$ 

$1.80$ 

$9.50$ 

$0.09$ 

$0.09$ 

Continued on next page Table 1. Calculations of the α decay half-lives of superheavy nuclei for which the spin and parity values of the parent and daughter nuclei are available, obtained from NUBASE 2020 (NUBASE) [61]. The experimental α decay half-lives and error uncertainties are obtained from the latest evaluated nuclear properties table NUBASE [61], except the experimental α decay half-life and error uncertainties of the nucleus
$^{264}{\rm{Hs}}$ , which are obtained from the NNDC [62]. The α decay energies are obtained from the evaluated atomic mass table AME 2020 (AME) [35], FRDM [32], and FRDM-NN. The symbol ''#'' of$Q_{\alpha}^{\text{AME}}$ indicates that the α decay energy is not derived from experimental data but from systematics, which are obtained from AME [35]. The α decay energies and half-lives are in units of ''MeV'' and ''s'', respectively. ''()'' denotes uncertain spin and/or parity. ''#'' of the spin and/or parity indicates values estimated from trends in neighboring nuclides with the same Z and N parities, which are obtained from NUBASE [61].α transition l $\text{lg}T^{\text{exp}}_{1/2}$ 

$Q_{\alpha}^{\text{AME}}$ 

$\text{lg}T^{\text{cal1}}_{1/2}$ 

$\text{lg}T^{\text{cal2}}_{1/2}$ 

$Q_{\alpha}^{\text{FRDM}}$ 

$\text{lg}T^{\text{cal3}}_{1/2}$ 

$\text{lg}T^{\text{cal4}}_{1/2}$ 

$Q_{\alpha}^{\text{FRDM-NN}}$ 

$\text{lg}T^{\text{cal5}}_{1/2}$ 

$\text{lg}T^{\text{cal6}}_{1/2}$ 

$^{260}{\rm{Db}} \to ^{256}{\rm{Lr}}$ 

0 $0.23^{+0.04}_{-0.04}$ 

$9.50\#$ 

$-0.36$ 

$-0.50$ 

$9.34$ 

$0.09$ 

$-0.03$ 

$9.43$ 

$-0.17$ 

$-0.31$ 

$^{260}{\rm{Bh}} \to ^{256}{\rm{Db}}$ 

0 $-1.39^{+0.13}_{-0.18}$ 

$10.40$ 

$-2.02$ 

$-2.20$ 

$10.25$ 

$-1.65$ 

$-1.81$ 

$10.20$ 

$-1.53$ 

$-1.69$ 

$^{262}{\rm{Bh}} \to ^{258}{\rm{Db}}$ 

0 $-1.08^{+0.05}_{-0.06}$ 

$10.32$ 

$-1.83$ 

$-2.03$ 

$10.11$ 

$-1.31$ 

$-1.48$ 

$10.23$ 

$-1.61$ 

$-1.79$ 

$^{264}{\rm{Bh}} \to ^{260}{\rm{Db}}$ 

0 $0.09^{+0.08}_{-0.09}$ 

$9.86\#$ 

$-0.68$ 

$-0.84$ 

$9.61$ 

$0.001$ 

$-0.13$ 

$9.94$ 

$-0.88$ 

$-1.05$ 

$^{266}{\rm{Bh}} \to ^{262}{\rm{Db}}$ 

0 $1.03^{+0.08}_{-0.10}$ 

$9.43\#$ 

$0.49$ 

$0.37$ 

$8.86$ 

$2.18$ 

$2.13$ 

$9.40$ 

$0.56$ 

$0.45$ 

$^{270}{\rm{Bh}} \to ^{266}{\rm{Db}}$ 

0 $2.36^{+0.25}_{-0.68}$ 

$9.06$ 

$1.53$ 

$1.40$ 

$8.33$ 

$3.90$ 

$3.87$ 

$8.91$ 

$2.00$ 

$1.89$ 

$^{266}{\rm{Mt}} \to ^{262}{\rm{Bh}}$ 

0 $-2.70^{+0.10}_{-0.12}$ 

$11.00$ 

$-2.83$ 

$-3.08$ 

$10.76$ 

$-2.29$ 

$-2.51$ 

$11.07$ 

$-3.01$ 

$-3.27$ 

$^{268}{\rm{Mt}} \to ^{264}{\rm{Bh}}$ 

0 $-1.64^{+0.12}_{-0.16}$ 

$10.77\#$ 

$-2.32$ 

$-2.56$ 

$10.03$ 

$-0.49$ 

$-0.64$ 

$10.55$ 

$-1.81$ 

$-2.00$ 

$^{270}{\rm{Mt}} \to ^{266}{\rm{Bh}}$ 

0 $-0.10^{+0.18}_{-0.30}$ 

$10.18\#$ 

$-0.89$ 

$-1.08$ 

$9.57$ 

$0.77$ 

$0.64$ 

$10.11$ 

$-0.71$ 

$-0.89$ 

$^{278}{\rm{Mt}} \to ^{274}{\rm{Bh}}$ 

0 $0.78^{+0.18}_{-0.30}$ 

$9.58$ 

$0.65$ 

$0.46$ 

$9.24$ 

$1.64$ 

$1.49$ 

$9.86$ 

$-0.14$ 

$-0.36$ 

$^{272}{\rm{Rg}} \to ^{268}{\rm{Mt}}$ 

0 $-2.38^{+0.10}_{-0.13}$ 

$11.20$ 

$-2.68$ 

$-2.98$ 

$11.00$ 

$-2.25$ 

$-2.51$ 

$11.29$ 

$-2.90$ 

$-3.21$ 

$^{282}{\rm{Rg}} \to ^{278}{\rm{Mt}}$ 

0 $2.11^{+0.14}_{-0.21}$ 

$9.55\#$ 

$1.41$ 

$1.25$ 

$8.79$ 

$3.77$ 

$3.69$ 

$9.42$ 

$1.81$ 

$1.66$ 

$^{282}{\rm{Nh}} \to ^{278}{\rm{Rg}}$ 

0 $-0.85^{+0.22}_{-0.45}$ 

$10.78$ 

$-1.21$ 

$-1.45$ 

$10.02$ 

$0.77$ 

$0.62$ 

$10.59$ 

$-0.75$ 

$-0.95$ 

$^{286}{\rm{Nh}} \to ^{282}{\rm{Rg}}$ 

0 $1.08^{+0.15}_{-0.23}$ 

$9.79$ 

$1.37$ 

$1.22$ 

$8.97$ 

$3.87$ 

$3.81$ 

$9.60$ 

$1.93$ 

$1.80$ 

$^{288}{\rm{Mc}} \to ^{284}{\rm{Nh}}$ 

0 $-0.75^{+0.05}_{-0.05}$ 

$10.65$ 

$-0.30$ 

$-0.50$ 

$10.14$ 

$1.06$ 

$0.91$ 

$10.45$ 

$0.21$ 

$0.04$ 

$^{290}{\rm{Mc}} \to ^{286}{\rm{Nh}}$ 

0 $-0.08^{+0.15}_{-0.24}$ 

$10.41$ 

$0.30$ 

$0.12$ 

$10.04$ 

$1.32$ 

$1.16$ 

$10.62$ 

$-0.24$ 

$-0.45$ 

$^{294}{\rm{Ts}} \to ^{290}{\rm{Mc}}$ 

0 $-1.15^{+0.15}_{-0.24}$ 

$11.18$ 

$-1.03$ 

$-1.27$ 

$11.30$ 

$-1.31$ 

$-1.57$ 

$11.36$ 

$-1.45$ 

$-1.72$ 

α transition ${j^{\pi}_{p}}\to{j^{\pi}_{d}}$ 

l $\text{lg}T^{\text{exp}}_{1/2}$ 

$Q_{\alpha}^{\text{AME}}$ 

$\text{lg}T^{\text{cal1}}_{1/2}$ 

$\text{lg}T^{\text{cal2}}_{1/2}$ 

$Q_{\alpha}^{\text{FRDM}}$ 

$\text{lg}T^{\text{cal3}}_{1/2}$ 

$\text{lg}T^{\text{cal4}}_{1/2}$ 

$Q_{\alpha}^{\text{FRDM-NN}}$ 

$\text{lg}T^{\text{cal5}}_{1/2}$ 

$\text{lg}T^{\text{cal6}}_{1/2}$ 

$^{267}{\rm{Sg}} \to ^{263}{\rm{Rf}}$ 

${3/2^+\to1/2^+}$ 

0 $2.80^{+0.14}_{-0.21}$ 

$8.63\#$ 

$2.02$ 

$2.10$ 

$7.93$ 

$4.41$ 

$4.59$ 

$8.50$ 

$2.42$ 

$2.52$ 

$^{267}{\rm{Sg}} \to ^{263}{\rm{Rf}}$ 

${3/2^+\to1/2^+}$ 

2 $2.80^{+0.14}_{-0.21}$ 

$8.63\#$ 

$2.47$ 

$2.41$ 

$7.93$ 

$4.87$ 

$4.89$ 

$8.50$ 

$2.88$ 

$2.83$ 

$^{269}{\rm{Sg}} \to ^{265}{\rm{Rf}}$ 

${13/2^-\to3/2^+}$ 

0 $2.48^{+0.15}_{-0.22}$ 

$8.58$ 

$2.16$ 

$2.22$ 

$7.86$ 

$4.66$ 

$4.82$ 

$8.45$ 

$2.57$ 

$2.65$ 

$^{269}{\rm{Sg}} \to ^{265}{\rm{Rf}}$ 

${13/2^-\to3/2^+}$ 

5 $2.48^{+0.15}_{-0.22}$ 

$8.58$ 

$3.84$ 

$3.76$ 

$7.86$ 

$6.36$ 

$6.36$ 

$8.45$ 

$4.25$ 

$4.19$ 

$^{271}{\rm{Sg}} \to ^{267}{\rm{Rf}}$ 

${3/2^+\to13/2^-}$ 

0 $2.50^{+0.18}_{-0.30}$ 

$8.75\#$ 

$1.60$ 

$1.62$ 

$8.48$ 

$2.47$ 

$2.52$ 

$9.09$ 

$0.54$ 

$0.51$ 

$^{271}{\rm{Sg}} \to ^{267}{\rm{Rf}}$ 

${3/2^+\to13/2^-}$ 

5 $2.50^{+0.18}_{-0.30}$ 

$8.75\#$ 

$3.28$ 

$3.16$ 

$8.48$ 

$4.15$ 

$4.06$ 

$9.09$ 

$2.21$ 

$2.05$ 

$^{271}{\rm{Bh}} \to ^{267}{\rm{Db}}$ 

${1/2^-\to1/2^-}$ 

0 $0.46^{+0.22}_{-0.46}$ 

$9.42$ 

$-0.05$ 

$-0.17$ 

$8.72$ 

$2.07$ 

$2.03$ 

$9.31$ 

$0.26$ 

$0.15$ 

$^{267}{\rm{Hs}} \to ^{263}{\rm{Sg}}$ 

${1/2+\to9/2+}$ 

0 $<-1.16^{}_{}$ 

$10.04$ 

$-1.37$ 

$-1.39$ 

$9.40$ 

$0.39$ 

$0.43$ 

$9.93$ 

$-1.08$ 

$-1.10$ 

$^{267}{\rm{Hs}} \to ^{263}{\rm{Sg}}$ 

${1/2+\to9/2+}$ 

4 $<-1.16^{}_{}$ 

$10.04$ 

$-0.21$ 

$-0.37$ 

$9.40$ 

$1.57$ 

$1.46$ 

$9.93$ 

$0.08$ 

$-0.07$ 

$^{273}{\rm{Hs}} \to ^{269}{\rm{Sg}}$ 

${3/2^+\to13/2^-}$ 

0 $0.03^{+0.17}_{-0.28}$ 

$9.65$ 

$-0.40$ 

$-0.42$ 

$9.48$ 

$0.08$ 

$0.08$ 

$10.07$ 

$-1.53$ 

$-1.60$ 

$^{273}{\rm{Hs}} \to ^{269}{\rm{Sg}}$ 

${3/2^+\to13/2^-}$ 

5 $0.03^{+0.17}_{-0.28}$ 

$9.65$ 

$1.24$ 

$1.12$ 

$9.48$ 

$1.72$ 

$1.62$ 

$10.07$ 

$0.09$ 

$-0.06$ 

$^{275}{\rm{Hs}} \to ^{271}{\rm{Sg}}$ 

${3/2^+\to3/2^+}$ 

0 $-0.55^{+0.17}_{-0.27}$ 

$9.45$ 

$0.15$ 

$0.13$ 

$9.35$ 

$0.44$ 

$0.44$ 

$9.96$ 

$-1.26$ 

$-1.34$ 

$^{275}{\rm{Mt}} \to ^{271}{\rm{Bh}}$ 

${11/2^+\to1/2^-}$ 

0 $-1.51^{+0.19}_{-0.35}$ 

$10.48$ 

$-2.25$ 

$-2.44$ 

$10.11$ 

$-1.31$ 

$-1.45$ 

$10.70$ 

$-2.79$ 

$-3.00$ 

$^{275}{\rm{Mt}} \to ^{271}{\rm{Bh}}$ 

${11/2^+\to1/2^-}$ 

5 $-1.51^{+0.19}_{-0.35}$ 

$10.48$ 

$-0.64$ 

$-0.90$ 

$10.11$ 

$0.32$ 

$0.09$ 

$10.70$ 

$-1.18$ 

$-1.46$ 

$^{269}{\rm{Ds}} \to ^{265}{\rm{Hs}}$ 

${1/2^+\to9/2^+}$ 

0 $-3.64^{+0.17}_{-0.28}$ 

$11.51$ 

$-4.17$ 

$-4.38$ 

$10.69$ 

$-2.35$ 

$-2.42$ 

$11.06$ 

$-3.22$ 

$-3.34$ 

$^{269}{\rm{Ds}} \to ^{265}{\rm{Hs}}$ 

${1/2^+\to9/2^+}$ 

4 $-3.64^{+0.17}_{-0.28}$ 

$11.51$ 

$-3.03$ 

$-3.35$ 

$10.69$ 

$-1.20$ 

$-1.39$ 

$11.06$ 

$-2.07$ 

$-2.31$ 

$^{277}{\rm{Ds}} \to ^{273}{\rm{Hs}}$ 

${11/2^+\to3/2^+}$ 

0 $-2.22^{+0.18}_{-0.30}$ 

$10.90\#$ 

$-2.94$ 

$-3.09$ 

$10.57$ 

$-2.15$ 

$-2.26$ 

$11.16$ 

$-3.53$ 

$-3.72$ 

$^{277}{\rm{Ds}} \to ^{273}{\rm{Hs}}$ 

${11/2^+\to3/2^+}$ 

4 $-2.22^{+0.18}_{-0.30}$ 

$10.90\#$ 

$-1.80$ 

$-2.06$ 

$10.57$ 

$-1.00$ 

$-1.24$ 

$11.16$ 

$-2.40$ 

$-2.70$ 

$^{281}{\rm{Ds}} \to ^{277}{\rm{Hs}}$ 

${3/2^+\to3/2^+}$ 

0 $2.15^{+0.08}_{-0.10}$ 

$9.47\#$ 

$0.76$ 

$0.73$ 

$8.35$ 

$4.36$ 

$4.46$ 

$8.99$ 

$2.24$ 

$2.26$ 

$^{281}{\rm{Rg}} \to ^{277}{\rm{Mt}}$ 

${13/2^+\to1/2^-}$ 

0 $2.16^{+0.10}_{-0.13}$ 

$9.90\#$ 

$-0.10$ 

$-0.23$ 

$9.22$ 

$1.88$ 

$1.82$ 

$9.83$ 

$0.08$ 

$-0.04$ 

$^{281}{\rm{Rg}} \to ^{277}{\rm{Mt}}$ 

${13/2^+\to1/2^-}$ 

7 $2.16^{+0.10}_{-0.13}$ 

$9.90\#$ 

$2.64$ 

$2.64$ 

$9.22$ 

$4.66$ 

$4.69$ 

$9.83$ 

$2.83$ 

$2.83$ 

$^{281}{\rm{Cn}} \to ^{277}{\rm{Ds}}$ 

${3/2^+\to11/2^+}$ 

0 $-0.74^{+0.16}_{-0.26}$ 

$10.43$ 

$-1.18$ 

$-1.25$ 

$10.25$ 

$-0.71$ 

$-0.76$ 

$10.84$ 

$-2.20$ 

$-2.32$ 

$^{281}{\rm{Cn}} \to ^{277}{\rm{Ds}}$ 

${3/2^+\to11/2^+}$ 

4 $-0.74^{+0.16}_{-0.26}$ 

$10.43$ 

$-0.04$ 

$-0.22$ 

$10.25$ 

$0.43$ 

$0.26$ 

$10.84$ 

$-1.07$ 

$-1.29$ 

$^{283}{\rm{Cn}} \to ^{279}{\rm{Ds}}$ 

${3/2^+\to15/2^-}$ 

0 $0.76^{+0.07}_{-0.08}$ 

$9.89\#$ 

$0.24$ 

$0.22$ 

$9.13$ 

$2.47$ 

$2.55$ 

$9.74$ 

$0.64$ 

$0.64$ 

$^{283}{\rm{Cn}} \to ^{279}{\rm{Ds}}$ 

${3/2^+\to15/2^-}$ 

7 $0.76^{+0.07}_{-0.08}$ 

$9.89\#$ 

$2.98$ 

$3.09$ 

$9.13$ 

$5.25$ 

$5.42$ 

$9.74$ 

$3.39$ 

$3.51$ 

$^{285}{\rm{Cn}} \to ^{281}{\rm{Ds}}$ 

${5/2^+\to3/2^+}$ 

0 $1.48^{+0.10}_{-0.13}$ 

$9.39\#$ 

$1.67$ 

$1.69$ 

$8.79$ 

$3.56$ 

$3.65$ 

$9.43$ 

$1.55$ 

$1.57$ 

Continued on next page Tables 1–3 show that the calculations of the α decay half-lives using the GLDM and Royer formula [47], adopting the α decay energy reported by AME [35], can reproduce the experimental data well, indicating that the models have been tested and are credible. However, the calculations of the GLDM and Royer formula using the α decay energy given by the FRDM [32] are less accurate and have significant deviations between the calculations and experimental data. This indicates that the the accurate α decay energy is important in studying the α decay half-life, and the α decay energy given by the FRDM should be optimized. The accuracy of the calculated α decay half-lives is improved in the reproduction of the experimental data by inputting the α decay energy given by the FRDM-NN. Thus, the α decay energy optimized using the neural network approach can be used to study α decay. In addition, for the nuclei
$ ^{269} {\rm{Hs}}$ ($ Z = 108 $ ,$ N = 161 $ ),$ ^{286} {\rm{Fl}}$ ($ Z = 114 $ ,$ N = 172 $ ), and$ ^{288} {\rm{Fl}}$ ($ Z = 114 $ ,$ N = 174 $ ) listed in Table 1, the α decay half-lives calculated using the GLDM and Royer formula [47] and adopting the α decay energy reported by AME [35] can reproduce the experimental data well. However, if the α decay energy obtained using the FRDM-NN is used, the calculated α decay half-lives deviate from the experimental data by about one order of magnitude. This is because the α decay energies obtained using the FRDM-NN for these three nuclei differ from the experimental data by about 0.3 MeV, possibly owing to the shell effects of proton number$ Z = 108 $ , neutron number$ N = 162 $ , and proton number$ Z = 114 $ . This suggests that the α decay half-life is very sensitive to the α decay energy.Furthermore, for the unfavored α decay listed in Tables 1 and 2, the zero angular moment transfer is also calculated to investigate the possibility of favoured α decay [60]. We observe that the calculated α decay half-life with non-zero l is longer than that with zero l. This is because for an unfavored α decay, the non-zero l causes an extra centrifugal potential. The centrifugal potential causes the total barrier to be higher, the penetration probability to be lower, and the α decay half-life to be longer. For some nuclei listed in Table 1, such as
$ ^{255} {\rm{Rf}}$ ,$ ^{257} {\rm{Rf}}$ ,$ ^{259} {\rm{Rf}}$ ,$ ^{257} {\rm{Db}}$ ,$ ^{259} {\rm{Db}}$ ,$ ^{263} {\rm{Db}}$ ,$ ^{259} {\rm{Sg}}$ ,$ ^{261} {\rm{Sg}}$ ,$ ^{261} {\rm{Bh}}$ ,$ ^{267} {\rm{Bh}}$ , and$ ^{269} {\rm{Hs}}$ , and nuclei listed in Table 2, such as$ ^{267} {\rm{Sg}}$ ,$ ^{271} {\rm{Sg}}$ ,$ ^{275} {\rm{Mt}}$ ,$ ^{277} {\rm{Ds}}$ ,$ ^{281} {\rm{Rg}}$ ,$ ^{281} {\rm{Cn}}$ , and$ ^{293} {\rm{Ts}}$ , calculations with a non-zero l input can better reproduce the experimental data than those with a zero l input. This indicates that these nuclei may undergo unfavored α decay. In addition, the calculations with a zero l input match the experimental data better than those with a non-zero l input for several nuclei listed in Table 1, such as$ ^{256} {\rm{Db}}$ ,$ ^{258} {\rm{Db}}$ , and$ ^{265} {\rm{Sg}}$ , and nuclei listed in Table 2, such as$ ^{269} {\rm{Sg}}$ ,$ ^{267} {\rm{Hs}}$ ,$ ^{273} {\rm{Hs}}$ ,$ ^{269} {\rm{Ds}}$ ,$ ^{283} {\rm{Cn}}$ ,$ ^{285} {\rm{Cn}}$ ,$ ^{285} {\rm{Nh}}$ ,$ ^{289} {\rm{Mc}}$ ,$ ^{291} {\rm{Lv}}$ , and$ ^{293} {\rm{Lv}}$ . This suggests that these nuclei tend to undergo favored α decay. Similarly, for the nuclei listed in Table 3, the calculated α decay half-lives with zero l can reproduce the experimental data well, indicating that these nuclei may undergo favoured α decay.The logarithmic differences between the calculated α decay half-lives and experimental data for 30 known superheavy nuclei with
$ {j^{\pi}_{p}} $ and$ {j^{\pi}_{d}} $ available in NUBASE [61], 20 known odd-A superheavy nuclei with$ {j^{\pi}_{p}} $ and/or$ {j^{\pi}_{d}} $ not available in NUBASE [61] but obtained using the FRDM [32], and 17 known doubly odd nuclei with$ {j^{\pi}_{p}} $ and/or$ {j^{\pi}_{d}} $ not available in NUBASE [61] with l assumed to be zero are shown in Figs. 3–5, respectively. Note that only the favored α decay and the unfavored α decay that have the minimum deviation with the corresponding angular momentum transfer are shown in Figs. 3–5. In Figs. 3–5, the subfigures (a), (b), and (c) represent the differences between the calculations of the α decay half-lives using the α decay energies obtained using AME [35], FRDM [32], and FRDM-NN and the experimental data, respectively. The solid (open) symbol represents the difference between the calculation by using the GLDM (Royer formula [47]) and the experimental data. To verify the precision of the calculated α decay half-lives, we determine the root mean square errors$ \sigma_{T_{1/2}} $ using Eq. (11) and show them in Figs. 3–5.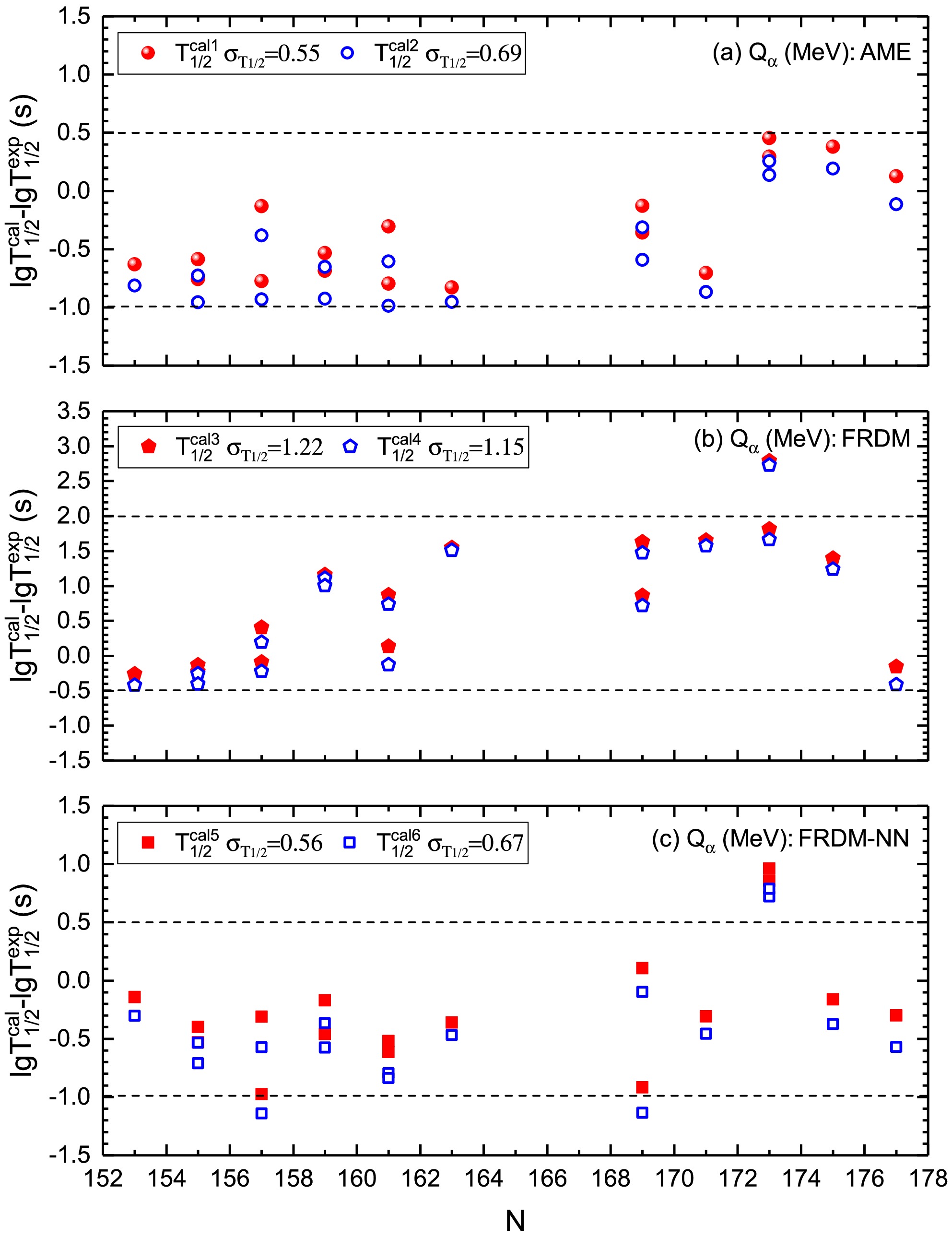
Figure 5. (color online) Same as Fig. 3, but depicting the logarithmic differences between the calculations of α decay half-lives using the GLDM and Royer formula [47] and the experimental data for 17 known doubly odd superheavy nuclei, where
${j^{\pi}_{p}}$ and/or${j^{\pi}_{d}}$ are not available in NUBASE [61], and the favored α decay is assumed with$l = 0$ .$ \sigma_{T_{1/2}} = \sqrt{\frac{1}{n}\sum ({\log_{10}T_{1/2}^{\text{cal}}-\log_{10}T_{1/2}^{\text{exp}}})^2} , $

(11) where the number of nuclei shown in Figs. 3–5 is
$ n = 30 $ for known superheavy nuclei with$ {j^{\pi}_{p}} $ and$ {j^{\pi}_{d}} $ available in NUBASE [61],$ n = 20 $ for known odd-A superheavy nuclei with$ {j^{\pi}_{p}} $ and/or$ {j^{\pi}_{d}} $ not available in NUBASE [61] but obtained using the FRDM [32], and$ n = 17 $ for known doubly odd nuclei with$ {j^{\pi}_{p}} $ and/or$ {j^{\pi}_{d}} $ not available in NUBASE [61] and l assumed to be zero, respectively. Fig. 3 (a) shows that the logarithmic deviations between the calculations obtained using the GLDM and Royer formula [47] and experimental data are approximately 0.5 for most nuclei. The deviation symbols of the GLDM are higher than those of the Royer formula for most nuclei, indicating that the GLDM yields longer α decay half-life results than those obtained using the Royer formula. This is because the GLDM considers the α preformation factors, whereas the Royer formula does not. Consequently, the α decay constants obtained using the GLDM are smaller than those calculated using the Royer formula, resulting in the α decay half-lives calculated using the GLDM being longer than those calculated using the Royer formula. The$ \sigma_{T_{1/2}} $ values of two types of calculations and experimental data are 0.40 and 0.40, respectively. This indicates that the calculations using the α decay energy of AME [35] can reproduce the experimental data well. Fig. 3(b) shows that, for a significant number of nuclei, the deviations between calculations and experimental data are approximately one order of magnitude, and for several nuclei, the deviations are over two orders of magnitude. This is caused by the α decay energy given by the FRDM [32]. Fig. 3(c) shows that the two types of calculated α decay half-lives can reproduce the experimental data well by using the optimized α decay energy obtained using the FRDM-NN. When adopting the α decay energy given by the FRDM-NN, the$ \sigma_{T_{1/2}} $ values of the calculated α decay half-lives are reduced from 1.26 to 0.51 using the GLDM and from 1.26 to 0.50 using the Royer formula, indicatingimprovements of$ \dfrac{1.26-0.51}{1.26} = $ 59.52% and$ \dfrac{1.26-0.50}{1.26} = 60.32 $ %, respectively. A similar scenario is observed in Figs. 4 and 5.Encouraged by the excellent precision of the calculated α decay half-lives for known nuclei, the α decay half-lives of superheavy nuclei, whose α decay mode is energetically allowed but not experimentally observed or whose α decay is observed but does not have an experimentally known intensity in NUBASE [61], are predicted using the GLDM and Royer formula [47] with the α decay energy obtained using the FRDM-NN. The predictions are listed in Table 4. The α decay half-lives of superheavy nuclei with
$ Z = 119 $ and 120 are also predicted using the GLDM and Royer formula [47] with the α decay energy obtained using the FRDM-NN and are listed in Table 5. In Tables 4 and 5, the first column lists the α decays including the parent and daughter nuclei. The second column represents the spin and parity transition of the parent and daughter nuclei obtained using the FRDM [32]. The third column denotes the minimum angular momentum taken away by the α particle, obtained based on the conservation laws of angular momentum and parity [52]. The fourth column shows the α decay energy given by the FRDM-NN. The fifth and sixth columns are the calculated α decay half-lives obtained using the GLDM and Royer formula [47] with the α decay energy given by the FRDM-NN. The last two columns show the relative error calculated using Eq. (12) and the average results of the two types of predictions. For the unfavored α decay listed in Tables 4 and 5, the zero angular moment transfer is also calculated for attesting the possibility of favored α decay. [60]α transition ${j^{\pi}_{p}}\to{j^{\pi}_{d}}$ 

l $Q_{\alpha}^{\text{FRDM-NN}}$ 

$\text{lg}T^{\text{pre1}}_{1/2}$ 

$\text{lg}T^{\text{pre2}}_{1/2}$ 

ε $\text{lg}T^{\text{pre-ave}}_{1/2}$ 

Part A: ${j^{\pi}_{p}}$ and

${j^{\pi}_{d}}$ are available and taken from NUBASE [61]

$^{253}{\rm{Rf}} \to ^{249}{\rm{No}}$ 

${(7/2)(^+\#)\to5/2^+\#}$ 

0 $9.49$ 

$-1.13$ 

$-1.10$ 

$2.81$ %

$-1.12$ 

$^{253}{\rm{Rf}} \to ^{249}{\rm{No}}$ 

${(7/2)(^+\#)\to5/2^+\#}$ 

2 $9.49$ 

$-0.67$ 

$-0.79$ 

$14.93$ %

$-0.73$ 

$^{260}{\rm{Rf}} \to ^{256}{\rm{No}}$ 

${0^+\to0^+}$ 

0 $9.03$ 

$-0.22$ 

$-0.23$ 

$5.41$ %

$-0.23$ 

$^{264}{\rm{Rf}} \to ^{260}{\rm{No}}$ 

${0^+\to0^+}$ 

0 $7.93$ 

$3.29$ 

$3.41$ 

$3.55$ %

$3.35$ 

$^{266}{\rm{Rf}} \to ^{262}{\rm{No}}$ 

${0^+\to0^+}$ 

0 $7.50$ 

$4.88$ 

$5.05$ 

$3.26$ %

$4.96$ 

$^{268}{\rm{Rf}} \to ^{264}{\rm{No}}$ 

${0^+\to0^+}$ 

0 $7.87$ 

$3.47$ 

$3.56$ 

$2.53$ %

$3.51$ 

$^{265}{\rm{Db}} \to ^{261}{\rm{Lr}}$ 

${9/2^+\#\to1/2^-\#}$ 

0 $8.27$ 

$2.81$ 

$2.86$ 

$1.75$ %

$2.84$ 

$^{265}{\rm{Db}} \to ^{261}{\rm{Lr}}$ 

${9/2^+\#\to1/2^-\#}$ 

5 $8.27$ 

$4.50$ 

$4.40$ 

$2.30$ %

$4.45$ 

$^{269}{\rm{Db}} \to ^{265}{\rm{Lr}}$ 

${9/2^+\#\to1/2^-\#}$ 

0 $8.28$ 

$2.75$ 

$2.75$ 

$0.03$ %

$2.75$ 

$^{269}{\rm{Db}} \to ^{265}{\rm{Lr}}$ 

${9/2^+\#\to1/2^-\#}$ 

5 $8.28$ 

$4.44$ 

$4.29$ 

$3.44$ %

$4.36$ 

$^{258}{\rm{Sg}} \to ^{254}{\rm{Rf}}$ 

${0^+\to0^+}$ 

0 $9.45$ 

$-0.69$ 

$-0.68$ 

$1.95$ %

$-0.68$ 

$^{262}{\rm{Sg}} \to ^{258}{\rm{Rf}}$ 

${0^+\to0^+}$ 

0 $9.73$ 

$-1.49$ 

$-1.55$ 

$3.65$ %

$-1.52$ 

$^{264}{\rm{Sg}} \to ^{260}{\rm{Rf}}$ 

${0^+\to0^+}$ 

0 $9.28$ 

$-0.28$ 

$-0.30$ 

$4.51$ %

$-0.29$ 

$^{266}{\rm{Sg}} \to ^{262}{\rm{Rf}}$ 

${0^+\to0^+}$ 

0 $8.68$ 

$1.52$ 

$1.57$ 

$3.21$ %

$1.54$ 

$^{268}{\rm{Sg}} \to ^{264}{\rm{Rf}}$ 

${0^+\to0^+}$ 

0 $8.33$ 

$2.66$ 

$2.73$ 

$2.59$ %

$2.69$ 

$^{270}{\rm{Sg}} \to ^{266}{\rm{Rf}}$ 

${0^+\to0^+}$ 

0 $8.83$ 

$1.01$ 

$1.00$ 

$1.82$ %

$1.01$ 

$^{272}{\rm{Sg}} \to ^{268}{\rm{Rf}}$ 

${0^+\to0^+}$ 

0 $9.10$ 

$0.18$ 

$0.10$ 

$42.41$ %

$0.14$ 

$^{263}{\rm{Bh}} \to ^{259}{\rm{Db}}$ 

${5/2^-\#\to9/2^+\#}$ 

0 $10.19$ 

$-2.07$ 

$-2.18$ 

$5.23$ %

$-2.12$ 

$^{263}{\rm{Bh}} \to ^{259}{\rm{Db}}$ 

${5/2^-\#\to9/2^+\#}$ 

3 $10.19$ 

$-1.29$ 

$-1.56$ 

$17.37$ %

$-1.43$ 

$^{265}{\rm{Bh}} \to ^{261}{\rm{Db}}$ 

${5/2^-\#\to9/2^+\#}$ 

0 $9.71$ 

$-0.82$ 

$-0.89$ 

$8.80$ %

$-0.85$ 

$^{265}{\rm{Bh}} \to ^{261}{\rm{Db}}$ 

${5/2^-\#\to9/2^+\#}$ 

3 $9.71$ 

$-0.04$ 

$-0.28$ 

$85.20$ %

$-0.16$ 

$^{269}{\rm{Bh}} \to ^{265}{\rm{Db}}$ 

${5/2^-\#\to9/2^+\#}$ 

0 $8.81$ 

$1.79$ 

$1.77$ 

$1.21$ %

$1.78$ 

$^{269}{\rm{Bh}} \to ^{265}{\rm{Db}}$ 

${5/2^-\#\to9/2^+\#}$ 

3 $8.81$ 

$2.57$ 

$2.38$ 

$7.37$ %

$2.48$ 

$^{272}{\rm{Hs}} \to ^{268}{\rm{Sg}}$ 

${0^+\to0^+}$ 

0 $9.80$ 

$-1.10$ 

$-1.20$ 

$8.09$ %

$-1.15$ 

$^{274}{\rm{Hs}} \to ^{270}{\rm{Sg}}$ 

${0^+\to0^+}$ 

0 $10.14$ 

$-2.05$ 

$-2.17$ 

$5.74$ %

$-2.11$ 

$^{276}{\rm{Hs}} \to ^{272}{\rm{Sg}}$ 

${0^+\to0^+}$ 

0 $9.81$ 

$-1.19$ 

$-1.30$ 

$8.54$ %

$-1.25$ 

$^{268}{\rm{Ds}} \to ^{264}{\rm{Hs}}$ 

${0^+\to0^+}$ 

0 $11.28$ 

$-3.99$ 

$-4.18$ 

$4.61$ %

$-4.09$ 

$^{272}{\rm{Ds}} \to ^{268}{\rm{Hs}}$ 

${0^+\to0^+}$ 

0 $10.60$ 

$-2.48$ 

$-2.61$ 

$4.96$ %

$-2.55$ 

$^{274}{\rm{Ds}} \to ^{270}{\rm{Hs}}$ 

${0^+\to0^+}$ 

0 $10.94$ 

$-3.34$ 

$-3.50$ 

$4.53$ %

$-3.42$ 

$^{276}{\rm{Ds}} \to ^{272}{\rm{Hs}}$ 

${0^+\to0^+}$ 

0 $11.37$ 

$-4.31$ 

$-4.56$ 

$5.44$ %

$-4.43$ 

$^{278}{\rm{Ds}} \to ^{274}{\rm{Hs}}$ 

${0^+\to0^+}$ 

0 $10.91$ 

$-3.30$ 

$-3.50$ 

$5.87$ %

$-3.40$ 

$^{284}{\rm{Ds}} \to ^{280}{\rm{Hs}}$ 

${0^+\to0^+}$ 

0 $8.51$ 

$3.42$ 

$3.48$ 

$1.81$ %

$3.45$ 

$^{276}{\rm{Cn}} \to ^{272}{\rm{Ds}}$ 

${0^+\to0^+}$ 

0 $12.23$ 

$-5.41$ 

$-5.78$ 

$6.43$ %

$-5.59$ 

$^{278}{\rm{Cn}} \to ^{274}{\rm{Ds}}$ 

${0^+\to0^+}$ 

0 $12.71$ 

$-6.29$ 

$-6.80$ 

$7.54$ %

$-6.54$ 

$^{280}{\rm{Cn}} \to ^{276}{\rm{Ds}}$ 

${0^+\to0^+}$ 

0 $11.67$ 

$-4.35$ 

$-4.64$ 

$6.19$ %

$-4.50$ 

$^{282}{\rm{Cn}} \to ^{278}{\rm{Ds}}$ 

${0^+\to0^+}$ 

0 $10.03$ 

$-0.46$ 

$-0.54$ 

$14.93$ %

$-0.50$ 

$^{288}{\rm{Cn}} \to ^{284}{\rm{Ds}}$ 

${0^+\to0^+}$ 

0 $9.26$ 

$1.71$ 

$1.69$ 

$1.65$ %

$1.70$ 

$^{284}{\rm{Fl}} \to ^{280}{\rm{Cn}}$ 

${0^+\to0^+}$ 

0 $9.85$ 

$0.72$ 

$0.71$ 

$1.45$ %

$0.71$ 

Continued on next page Table 4. Predictions of α decay half-lives of superheavy nuclei, whose α decay mode is energetically allowed but not experimentally observed or whose α decay is observed but does not have an experimentally known intensity in NUBASE [61]. The α decay energies are obtained using the FRDM-NN. The α decay energies and half-lives are in units of "MeV" and "s", respectively.
α transition ${j^{\pi}_{p}}\to{j^{\pi}_{d}}$ 

l $Q_{\alpha}^{\text{FRDM-NN}}$ 

$\text{lg}T^{\text{pre1}}_{1/2}$ 

$\text{lg}T^{\text{pre2}}_{1/2}$ 

ε $\text{lg}T^{\text{pre-ave}}_{1/2}$ 

$^{290}119 \to ^{286}{\rm{Ts}}$ 

0 $11.86$ 

$-1.88$ 

$-2.16$ 

$12.96$ %

$-2.02$ 

$^{291}119 \to ^{287}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

0 $11.90$ 

$-2.51$ 

$-2.76$ 

$8.85$ %

$-2.64$ 

$^{291}119 \to ^{287}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

2 $11.90$ 

$-2.09$ 

$-2.45$ 

$14.89$ %

$-2.27$ 

$^{292}119 \to ^{288}{\rm{Ts}}$ 

0 $11.87$ 

$-1.91$ 

$-2.22$ 

$13.98$ %

$-2.06$ 

$^{293}119 \to ^{289}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

0 $11.84$ 

$-2.38$ 

$-2.64$ 

$9.80$ %

$-2.51$ 

$^{293}119 \to ^{289}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

2 $11.84$ 

$-1.95$ 

$-2.33$ 

$16.26$ %

$-2.14$ 

$^{294}119 \to ^{290}{\rm{Ts}}$ 

0 $11.90$ 

$-2.04$ 

$-2.34$ 

$12.95$ %

$-2.19$ 

$^{295}119 \to ^{291}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

0 $12.13$ 

$-3.05$ 

$-3.34$ 

$8.90$ %

$-3.20$ 

$^{295}119 \to ^{291}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

2 $12.13$ 

$-2.62$ 

$-3.04$ 

$13.74$ %

$-2.83$ 

$^{296}119 \to ^{292}{\rm{Ts}}$ 

0 $12.31$ 

$-2.91$ 

$-3.29$ 

$11.59$ %

$-3.10$ 

$^{297}119 \to ^{293}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

0 $12.36$ 

$-3.55$ 

$-3.90$ 

$8.91$ %

$-3.72$ 

$^{297}119 \to ^{293}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

2 $12.36$ 

$-3.13$ 

$-3.59$ 

$12.91$ %

$-3.36$ 

$^{298}119 \to ^{294}{\rm{Ts}}$ 

0 $12.69$ 

$-3.66$ 

$-4.15$ 

$11.75$ %

$-3.91$ 

$^{299}119 \to ^{295}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

0 $12.81$ 

$-4.44$ 

$-4.90$ 

$9.42$ %

$-4.67$ 

$^{299}119 \to ^{295}{\rm{Ts}}$ 

${1/2^-\to3/2^-}$ 

2 $12.81$ 

$-4.01$ 

$-4.59$ 

$12.55$ %

$-4.30$ 

$^{300}119 \to ^{296}{\rm{Ts}}$ 

0 $12.90$ 

$-4.06$ 

$-4.63$ 

$12.19$ %

$-4.35$ 

$^{290}120 \to ^{286}{\rm{Og}}$ 

${0^+\to0^+}$ 

0 $11.92$ 

$-2.55$ 

$-2.71$ 

$6.03$ %

$-2.63$ 

$^{291}120 \to ^{287}{\rm{Og}}$ 

${3/2^+\to1/2^+}$ 

0 $12.13$ 

$-2.67$ 

$-2.86$ 

$6.53$ %

$-2.76$ 

$^{291}120 \to ^{287}{\rm{Og}}$ 

${3/2^+\to1/2^+}$ 

2 $12.13$ 

$-2.24$ 

$-2.55$ 

$11.98$ %

$-2.39$ 

$^{292}120 \to ^{288}{\rm{Og}}$ 

${0^+\to0^+}$ 

0 $12.14$ 

$-3.02$ 

$-3.26$ 

$7.38$ %

$-3.14$ 

$^{293}120 \to ^{289}{\rm{Og}}$ 

${5/2^+\to3/2^+}$ 

0 $12.11$ 

$-2.65$ 

$-2.86$ 

$7.33$ %

$-2.76$ 

$^{293}120 \to ^{289}{\rm{Og}}$ 

${5/2^+\to3/2^+}$ 

2 $12.11$ 

$-2.23$ 

$-2.56$ 

$12.86$ %

$-2.39$ 

$^{294}120 \to ^{290}{\rm{Og}}$ 

${0^+\to0^+}$ 

0 $12.07$ 

$-2.93$ 

$-3.13$ 

$6.53$ %

$-3.03$ 

$^{295}120 \to ^{291}{\rm{Og}}$ 

${1/2^+\to5/2^+}$ 

0 $12.16$ 

$-2.81$ 

$-3.00$ 

$6.43$ %

$-2.90$ 

$^{295}120 \to ^{291}{\rm{Og}}$ 

${1/2^+\to5/2^+}$ 

2 $12.16$ 

$-2.38$ 

$-2.69$ 

$11.58$ %

$-2.54$ 

$^{296}120 \to ^{292}{\rm{Og}}$ 

${0^+\to0^+}$ 

0 $12.41$ 

$-3.68$ 

$-3.96$ 

$7.03$ %

$-3.82$ 

$^{297}120 \to ^{293}{\rm{Og}}$ 

${1/2^+\to1/2^+}$ 

0 $12.61$ 

$-3.74$ 

$-4.03$ 

$7.22$ %

$-3.88$ 

$^{298}120 \to ^{294}{\rm{Og}}$ 

${0^+\to0^+}$ 

0 $12.33$ 

$-3.53$ 

$-3.81$ 

$7.41$ %

$-3.67$ 

$^{299}120 \to ^{295}{\rm{Og}}$ 

${1/2^+\to1/2^+}$ 

0 $12.96$ 

$-4.41$ 

$-4.81$ 

$8.16$ %

$-4.61$ 

$^{300}120 \to ^{296}{\rm{Og}}$ 

${0^+\to0^+}$ 

0 $13.06$ 

$-4.93$ 

$-5.40$ 

$8.75$ %

$-5.17$ 

Table 5. Predictions of α decay half-lives of superheavy nuclei with
$Z = 119$ and 120. The α decay energies are obtained using the FRDM-NN. The spin and parity values of the parent and daughter nuclei are obtained using the FRDM [32]. The α decay energies and half-lives are in units of "MeV" and "s", respectively.Tables 4 and 5 show that the predictions of α decay half-lives obtained using the GLDM agree with those obtained using the Royer formula [47], and the trends in half-lives change are consistent. Moreover, the calculated α decay half-life for non-zero l is longer than that for zero l owing to the contribution of the centrifugal potential. In addition, Tables 4 and 5 show that the predicted α decay half-lives using the GLDM
$ \text{lg}T^{\text{pre}1}_{1/2} $ are longer than those using the Royer formula$ \text{lg}T^{\text{pre}2}_{1/2} $ for most nuclei. This is because the GLDM considers the α preformation factors, whereas the Royer formula does not. Therefore, the α decay constants calculated using the GLDM are smaller than those given by the Royer formula, resulting in the α decay half-lives calculated using the GLDM being longer than those calculated using the Royer formula. Furthermore, to identify nuclei with reliable α decay half-life predictions, the relative error of the two types of predictions is analyzed by introducing the following quantity [63]:$ \varepsilon = \frac{{\rm Max}(\lvert{\text{lg}T^{\text{pre}i}_{1/2}}\rvert)-{\rm Min}(\lvert{\text{lg}T^{\text{pre}i}_{1/2}}\rvert)}{{\rm Max}(\lvert{\text{lg}T^{\text{pre}i}_{1/2}}\rvert)}, $

(12) where
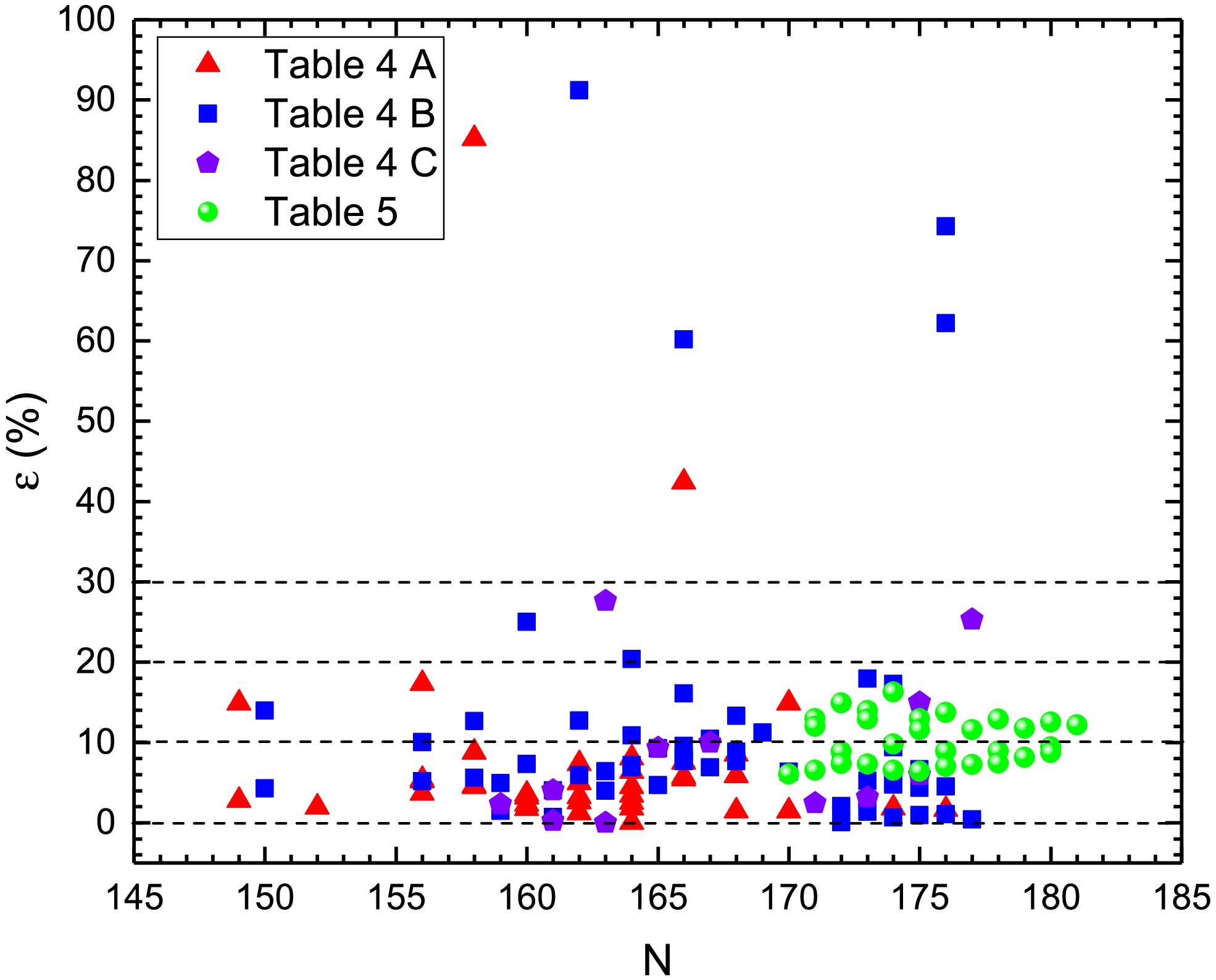
$ \text{lg}T^{\text{pre}i}_{1/2} $ presents the predicted α decay half-life given by the GLDM and Royer formula. This relative error assesses the quality of the predictions for each nucleus by relating the spread of the two types of predictions to the maximum predicted results [63]. The ε values of the predicted α decay half-lives for 138 superheavy nuclei presented in Table 4 A, B, C, and Table 5 are marked as red triangles, blue squares, purple pentagons, and green circles, respectively, and plotted in Fig. 6. This graphical representation facilitates the selection of nuclei with maximally superposing predictions [63]. For most nuclei,$ \varepsilon<30 $ % except for the nuclei listed in Table 4 such as$ ^{272} {\rm{Sg}}$ ($ l = 0 $ ,$ \varepsilon = 42.41 $ %),$ ^{265} {\rm{Bh}}$ ($ l = 3 $ ,$ \varepsilon = 85.20 $ %),$ ^{273} {\rm{Bh}}$ ($ l = 2 $ ,$ \varepsilon = 60.16 $ %),$ ^{271} {\rm{Mt}}$ ($ l = 3 $ ,$ \varepsilon = 91.18 $ %), and$ ^{291} {\rm{Mc}}$ ($ l = 2 $ ,$ \varepsilon = 74.27 $ %). However, when zero l is inputted in predicting the α decay half-lives,$ \varepsilon = 8.80 $ % for$ ^{265} {\rm{Bh}}$ ,$ \varepsilon = 16.11 $ % for$ ^{273} {\rm{Bh}}$ , and$ \varepsilon = 12.69 $ % for$ ^{271} {\rm{Mt}}$ , indicating that these nuclei may undergo favored α decay. For nuclei$ ^{272} {\rm{Sg}}$ ($ Z = 106 $ ,$ N = 166 $ ) and$ ^{291} {\rm{Mc}}$ ($ Z = 115 $ ,$ N = 176 $ ), the large ε may be caused by the shell effects of proton number$ Z = 108 $ , neutron number$ N = 162 $ , and proton number$ Z = 114 $ . Specifically,$ \varepsilon<20 $ % of the predicated α decay half-lives using the GLDM and Royer formula for superheavy nuclei with$ Z = 119 $ and 120. The α decay half-lives predicted using the GLDM model and Royer formula with the α decay energies predicted using the FRDM-NN can provide a reference for experimental and theoretical research, in particular, for the synthesis of new superheavy elements with$ Z = 119 $ and 120. -
We have examined the accuracy of the FRDM in describing the α decay energies of the 947 known heavy and superheavy nuclei. We observe important discrepancies between the α decay energies obtained using the FRDM and those reported by AME. In particular, the FRDM underestimates the experimental α decay energies of superheavy nuclei. We optimize the α decay energies of known nuclei obtained using FRDM using a neural network approach. The accuracy of the optimized α decay energies is significantly improved. The α decay energy systematics obtained using the FRDM and FRDM-NN reveal the evident shell effect at neutron number
$ N = 184 $ , implying that the next neutron magic number after$ N = 126 $ could be$ N = 184 $ . We study the α decay half-lives of known superheavy nuclei using the GLDM and Royer formula with the input of the optimized α decay energies. The calculations of the α decay half-lives reproduce the experimental data well. The α decay energies of superheavy nuclei, whose α decay mode is energetically allowed but not experimentally observed or whose α decay is observed but does not have an experimentally known intensity, are predicted using the FRDM-NN. The α decay half-lives of these superheavy nuclei are predicted using the GLDM and Royer formula. The α decay energies and half-lives of superheavy nuclei with$ Z = 119 $ and 120 are also predicted using the FRDM-NN, GLDM, and Royer formula. In addition, the relative error of predicted α decay half-lives and superposition are analyzed, and the average predictions are given. We hope that our research will provide a reference for experiments to synthesize new superheavy elements.
α decay properties of superheavy nuclei based on optimized α decay energies
- Received Date: 2024-10-21
- Available Online: 2025-05-15
Abstract: In this study, the accuracy of the Finite-Range Droplet Model 2012 (FRDM) in describing the α decay energies of the 947 known heavy and superheavy nuclei is investigated. We find evident discrepancies between the α decay energies obtained using the FRDM and those reported by the evaluated atomic mass table AME 2020 (AME). In particular, the FRDM underestimates the experimental α decay energies of superheavy nuclei. The α decay energies of known nuclei obtained using the FRDM are optimized using a neural network approach, i.e., FRDM-NN, and the accuracy improves significantly. The α decay energy systematics obtained using both the FRDM and FRDM-NN exhibit an evident shell effect at neutron number





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: