Three-nucleon correlations in light nuclei yield ratios from the AMPT model for QCD critical point investigations

Quantum chromodynamics (QCD), the bedrock theory of strong interactions between quarks and gluons, has motivated the exploration of QCD phase diagrams [1] to map the behavior of QCD matter under extreme conditions. One of the pivotal objectives of the Beam Energy Scan (BES) program at the Relativistic Heavy-Ion Collider (RHIC) is the search for the elusive QCD critical point [2−7]. This research is also a key motivation for future accelerators, such as the Facility for Anti-Proton and Ion Research (FAIR) in Darmstadt and the Nuclotron-based Ion Collider fAcility (NICA) in Dubna.

Close to the QCD critical point, fluctuations in conserved quantities, notably baryon number (B), charge (Q), and strangeness (S), are expected [8]. The production of light nuclei is predicted to be sensitive to baryon density fluctuations under the premise that the nuclei are formed by the coalescence of nucleons [9, 10]. The light nuclei yield ratio, expressed as $ N_pN_t/N_d^2 $, which encompasses the production of proton(p), deuteron(d), and triton(t), can be posited to be delineated by the relative neutron density fluctuation ($ \Delta\rho_n $) and the correlation between neutron and proton densities at the kinetic freeze-out point. Notably, the STAR collaboration has reported a non-monotonic energy dependence of the yield ratio that peaks around 20 − 30 GeV in the most central Au+Au collisions [11, 12]. If correlations between neutron and proton densities are disregarded, the light nuclei yield ratio has direct proportionality with relative neutron density fluctuations. Experimental observations have implied the existence of a large relative neutron density fluctuation at this energy range.

In our previous work [13], we used the AMPT model to investigate the impact of the two-body neutron-proton density correlation, $ C_{np} $, on the yield ratio of light nuclei. We arrived at the conclusion that the correlation $ C_{np} $ has a slight effect on the light nuclei yield ratio at central or mid-central Au+Au collisions. In other words, experimentalists can extract the relative neutron density fluctuation directly from the light nuclei yield ratio. In contrast, for peripheral collisions, the effect of $ C_{np} $ on the light nuclei yield ratio increases and related effects must be considered when extracting the density fluctuation. However, a critical aspect overlooked in that study concerned the three-nucleon correlation involving two neutrons and one proton, $ C_{n^2p} $, which directly influences triton yields and, consequently, the overall light nuclei yield ratio. Because tritons are products of coalescence processes involving multiple nucleons, the inclusion of $ C_{n^2p} $ is pivotal for a comprehensive understanding of light nuclei formation dynamics and the accurate extraction of relative neutron density fluctuations from experimental data.

Therefore, this study aims to build on our previous findings by delving into the influence of the three-nucleon correlation $ C_{n^2p} $ on the light nuclei yield ratio. Through this enhanced analysis, we expect to show the importance of $ C_{n^2p} $ on the extraction of relative neutron density fluctuations from the light nuclei yield ratio, thereby offering insights for the quest of identifying the QCD critical point. This paper is structured as follows: we commence with a review of the AMPT model. We then show the definition of the three-nucleon correlation and its connection to the light nuclei yield ratio. Subsequently, we present our results on the dependence of the three-nucleon correlation on rapidity coverage, collision centrality, and energy. Finally, we discuss the implications of the $ C_{n^2p} $ on the light nuclei yield ratio and its observed energy-dependent behavior in experiments.

AMPT, a multi-phase transport model, is a hybrid model consisting of four components: initial conditions, partonic interactions, partonic matter to hadronic matter conversion, and hadronic interactions [14]. The default version of the AMPT model involves only mini-jet partons in its parton cascade and uses the Lund string fragmentation for parton hadronization [15]. Conversly, the string melting version of the AMPT model involves the conversion of all excited strings into partons and the use of a quark coalescence model to describe parton hadronization. Typically, the default version gives a reasonable description of $\mathrm{d}N/\mathrm{d}\eta$, $\mathrm{d}N/ \mathrm{d}y$, and the $ p_T $ spectra, while the string melting version describes the magnitude of the elliptic flow but not the $ p_T $ spectra. The string melting version, with a modified set of parameters, can well reproduce the $ p_T $ spectra and elliptic flows at the RHIC top energy [16]. In this paper, all the results are studied using this set of parameters.

Based on Refs. [9, 11] and our preceding work [13], we commence with a review of the nucleon coalescence model and its consequent estimations of light nuclear yields. Ignoring the binding energy of light nuclei, their abundance can be formulated as follows:

Here, $ g_c =\dfrac{2S+1}{2^A} $ represents the coalescence factor for$ A=A_n+A_p $ nucleons of spin $ 1/2 $ forming a cluster with a total spin of S. The same nucleon mass $ m_0 $ is considered for both protons and neutrons. V denotes the system volum, and $ T_{\rm eff} $ is the effective temperature at kinetic freeze-out. $ \langle\rho_n\rangle $ and $ \langle\rho_p\rangle $ are the neutron and proton density. Combinations are represented by $ C_{A_p}^i $ and $ C_{A_n}^i $. $ C_{n^jp^i} $ is the corelation between $ j- $neutrons and $ i- $protons, defined as:

The relative neutron density fluctuation $ \Delta \rho_n =\sigma_n^2/ \langle\rho_n\rangle^2 $ is equivalent to $ C_{n^2p^0} $. The two-body neutron-proton density correlation, $ C_{np} $, is given by:

The three-nucleon correlation, $ C_{n^2p} $, can be expressed as

Employing these formulations, the yields of deuteron and triton are specified as:

Subsequently, the light nuclei yield ratio is compactly presented as:

The three-nucleon correlation $ C_{n^2p} $ exerts a significant influence on the light nuclei yield ratios, effectively enhancing them. Assuming the three-nucleon correlation $ C_{n^2p} $ is zero, Eq. (7) simplifies to:

Taking the analysis a step further, if the two-nucleon correlation $ C_{np} $ is also neglected, the light nuclei yield ratio is further simplified and can be expressed as:

In this highly simplified scenario, the yield ratio is directly proportional to the relative neutron density fluctuation $ \Delta\rho_n $, which forms the experimental basis for extracting the $ \Delta\rho_n $ from the yield ratios of light nuclei.

Following the procedure in our preceding work, the event-by-event multiplicity and fluctuation of the proton $ \langle N_p\rangle $, $ S_p $, neutron $ \langle N_n\rangle $, $ S_n $ and their mixed moments $ \langle N_pN_n\rangle,\langle N_pN_n^2\rangle $ can be extracted from the AMPT model. When calculating $ \Delta \rho_p, \Delta \rho_n $, the system volume effects are eliminated. In the AMPT model, nucleon production is analyzed across varying rapidity intervals and collision centralities. The definition of centrality is determined by the per-event charged particle multiplicity $ N_{\rm ch} $ for the pseudorapidity range $ \eta\leqslant $ 0.5.

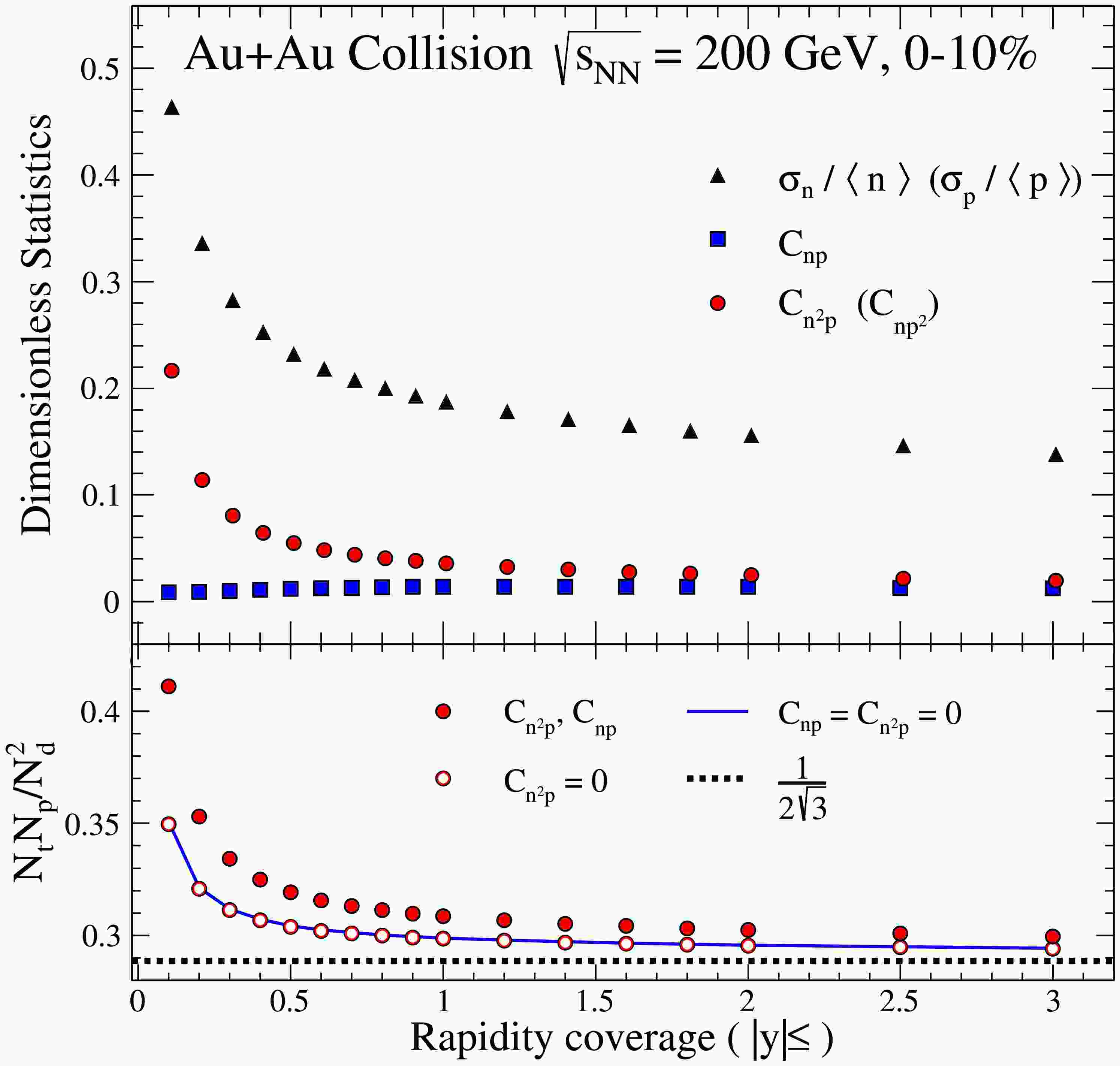
Figure 1 illustrates the rapidity coverage dependence of the dimensionless statistics $ \sigma_n/\langle n \rangle $, $ \sigma_p/\langle p \rangle $, $ C_{np} $, $ C_{n^2p} $, and $ C_{np^2} $ for $ 0-10 $% Au+Au collisions at $ \sqrt{s_{NN}}=200 $ GeV. $ \sigma_p/\langle\rho_p\rangle $ and $ \sigma_n/\langle\rho_n\rangle $, which can be regarded as relative nucleon density fluctuations, decrease with increasing rapidity coverage. It can be found that the relative density fluctuation for neutrons $ \sigma_n/\langle n \rangle $ and protons $ \sigma_p/\langle p \rangle $ are roughly equivalent and decrease with increasing rapidity coverage. In the smaller rapidity coverage region, especially at mid-rapidity, particle pair production dominates. Consequently, nucleon density fluctuations are relatively larger at mid-rapidity compared to a wider rapidity coverage. The correlation $ C_{np} $ is independent of rapidity coverage and almost vanishes for 0 − 10% Au+Au collisions at $ \sqrt{s_{NN}} = $ 200 GeV. Similar results are observed between the correlation $ C_{n^2p} $ for two neutrons and one proton and the correlation $ C_{np^2} $ for one neutron and two protons. The behavior of $ C_{n^2p} $ is similar to that of the relative neutron density fluctuations $ \sigma_n/\langle n \rangle $, with both decreasing with increasing rapidity coverage.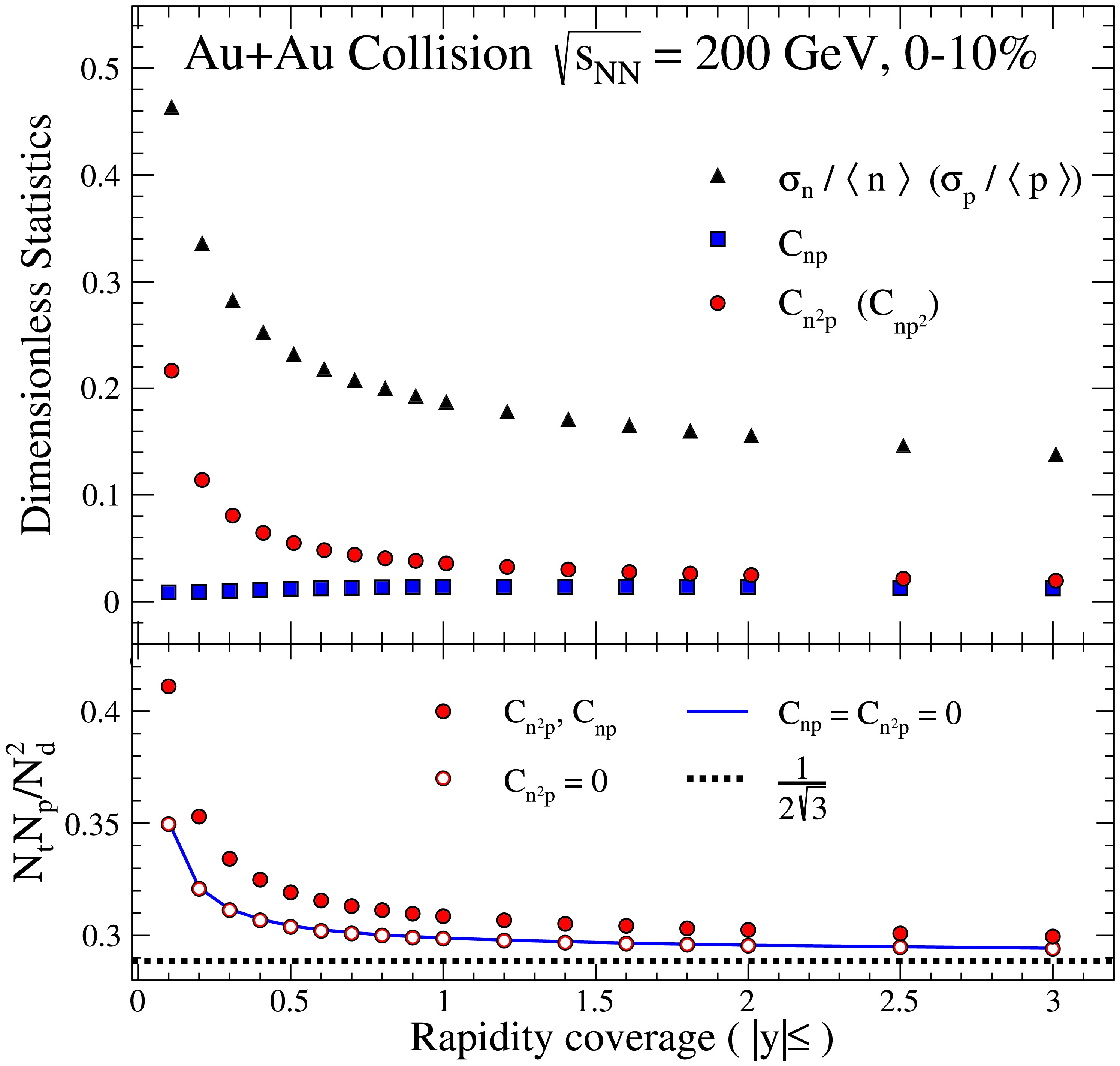

Figure 1.  (color online) Top panel: Dimensionless statistics $ \sigma_n/\langle n \rangle $, $ \sigma_p/\langle p \rangle $, $ C_{np} $, $ C_{n^2p} $, and $ C_{np^2} $ for 0 − 10% Au+Au collisions at $\sqrt{s_{NN}}= 200$ GeV. Bottom panel: The light nuclei yield ratio $ N_tN_p/N_d^2 $ calculated from the top panel shown as solid circles for Eq. (7), opened circles for Eq. (8), and a solid line for Eq. (9).

The lower panel in Fig. 1 presents the light nuclei yield ratios calculated using Eqs. (7), (8), and (9), demonstrating the comprehensive influence of both$ C_{np} $ and $ C_{n^2p} $, the effects of $ C_{np} $ without $ C_{n^2p} $, and the scenario without any nucleon correlation effects $ C_{np} $ and $ C_{n^2p} $. We also draw the line of $ 1/2\sqrt{3} $, which holds for scenarios without both relative neutron density fluctuation and nucleon correlations. It is observed that, due to the near-zero value of $ C_{np} $ for central collisions, its impact on the light nuclei yield ratios is insignificant. Moreover, since $ C_{n^2p} $ exhibits a similar dependence on the rapidity coverage as the relative neutron density fluctuation $ \sigma_n/\langle n \rangle $, including $ C_{n^2p} $ increases the calculated light nuclei yield ratios. Consequently, if $ C_{n^2p} $ is disregarded in the analysis, employing Eq. (8) to extract the relative neutron density fluctuation from the light nuclei yield ratios would yield an overestimated value compared compared to actual physical figure.

The top panel of Fig. 2 shows the rapidity coverage dependence of $ \sigma_n/\langle n \rangle $, $ \sigma_p/\langle p \rangle $, $ C_{np} $, $ C_{n^2p} $, and $ C_{np^2} $ for 60% − 80% Au+Au collisions at $\sqrt{s_{NN}}=39$ GeV. Consistent with the findings from central collisions, $ \sigma_p/\langle\rho_p\rangle $, $ \sigma_n/\langle\rho_n\rangle $, and $ C_{np^2} $ decrease with increasing rapidity coverage. At a given rapidity coverage, these quantities are greater in peripheral collisions compared to those in central collisions. For instance, the convergence value of $ \sigma_p/\langle\rho_p\rangle $ at larger rapidity coverages is approximately 0.7 for peripheral collisions, whereas it is roughly 0.14 for cental collisions at $ \sqrt{s_{NN}}=39 $ GeV.$ C_{np} $ is independent of rapidity coverage for a non-negligible value of 0.45 − 0.5 in peripheral collisions. Consequently, the influence of both $ C_{np} $ and $ C_{n^2p} $ on the related light nuclei yield ratio in peripheral collisions is evident in the bottom panel of Fig. 2. Specifically, the exclusion of $ C_{n^2p} $ yields a reduced light nuclei yield ratio, that is, a change from the solid circles to the open circles. Conversely, when $ C_{np} $ is not considered, the light nuclei yield ratio is increases, reflected by the shift from the open circles to the solid line. The impact of $ C_{np} $ and $ C_{n^2p} $ on the light nuclei yield ratio are contrasting. When both are considered, the deviation in the yield ratio from that obtained by neglecting both depends critically on the magnitude of their respective effects. Notably, the figure illustrates that for 60% − 80% Au+Au collisions at $\sqrt{s_{NN}}=39$ GeV, the effects of these two factors nearly offset each other. In other words, in this particular case, considering both $ C_{np} $ and $ C_{n^2p} $yields results similar to those derived when neither is considered. This highlights that, at least in this instance, the net effect of incorporating $ C_{np} $ and $ C_{n^2p} $ in the analysis does not significantly change the light nuclei yield ratio.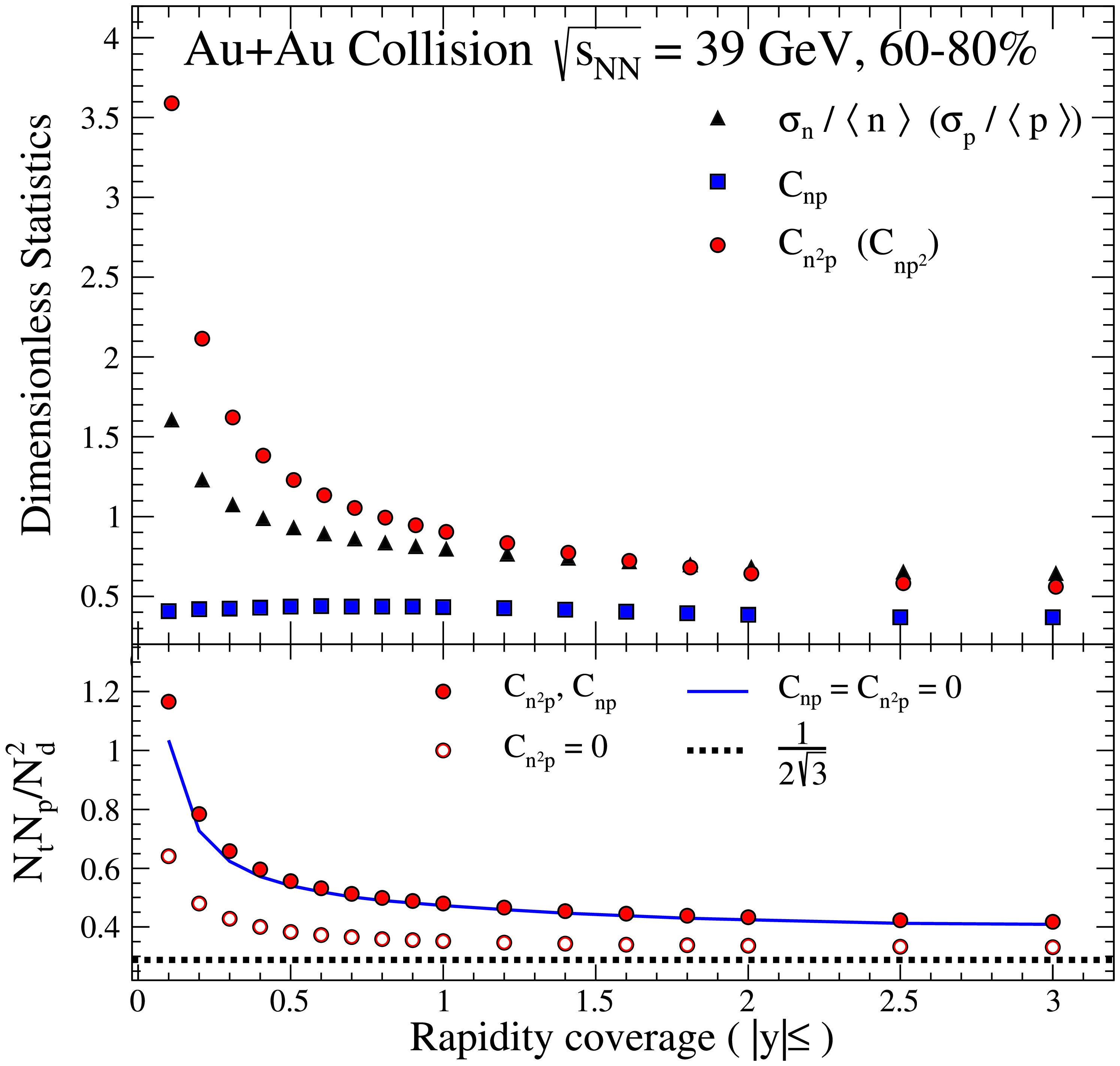

Figure 2.  (color online) Top panel: Dimensionless statistics $ \sigma_n/\langle n \rangle $, $ \sigma_p/\langle p \rangle $, $ C_{np} $, $ C_{n^2p} $, and $ C_{np^2} $ for 60% − 80% Au+Au collisions at $\sqrt{s_{NN}}= 39$ GeV. Bottom panel: The light nuclei yield ratio $ N_tN_p/N_d^2 $ calculated from the top panel are shown as solid circles for Eq. (7), open circles for Eq. (8), and solid lines for Eq. (9).

The top panel of Fig. 3 illustrates the centrality dependence of $ \sigma_n/\langle n \rangle $, $ \sigma_p/\langle p \rangle $, $ C_{np} $, $ C_{n^2p} $, and $ C_{np^2} $ for Au+Au collisions at $\sqrt{s_{NN}}=19.6$ GeV, confined to a rapidity coverage of $ |y|\leqslant 0.5 $. Notably, these quantities increase as the collisions transition from central to peripheral collisions. The corresponding light nuclei yield ratio calculated using Eqs. (7), (8), and (9) are presented at the bottom of Fig. (3). These illustrate the influence of $ C_{np} $ and $ C_{n^2p} $ on these yields. At central or mid-central collision, the variation between the yield ratios given by Eqs. (8) and (9) is very small, implying that the influence of $ C_{np} $ on the yield ratios can effectively be disregarded in these collisions. Conversely, in peripheral collisions, the effect of $ C_{np} $ on the yield ratios becomes significant and cannot be ignored. Furthermore, it is observed that $ C_{n^2p} $ exerts a positive effect on the yield ratios, increasing the light nuclei yield ratio. In contrast, $ C_{np} $ exerts a negative effect on the yield ratios. Consequently, when both $ C_{np} $ and $ C_{n^2p} $ are considered, in central and mid-central collisions, $ C_{n^2p} $is dominant, leading to an increase in the yield ratio. However, in peripheral collisions, the influences of these two factors may offset each other.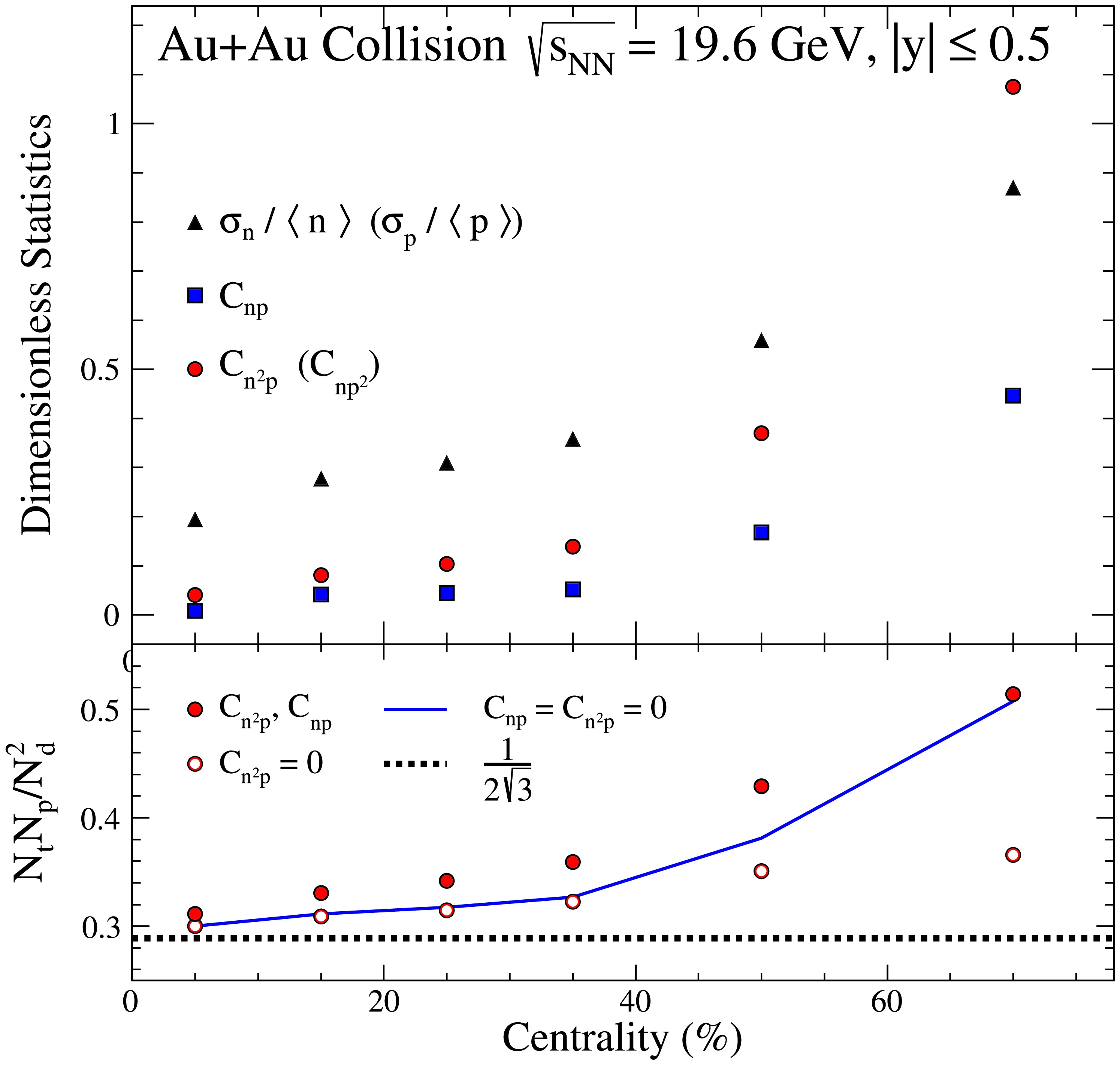

Figure 3.  (color online) Top panel: Dimensionless statistics $ \sigma_n/\langle n \rangle $, $ \sigma_p/\langle p \rangle $, $ C_{np} $, $ C_{n^2p} $, and $ C_{np^2} $ for Au+Au collisions at $\sqrt{s_{NN}}=19.6$ GeV with $ |y|\leqslant 0.5 $. Bottom panel: The light nuclei yield ratio $ N_tN_p/N_d^2 $ calculated from the top panel are shown as solid circles for Eq. (7), opened circles for Eq. (8), and solid line for Eq. (9).

Centrality bin width correction is important for any event-by-event fluctuation calculation. In Fig. 4, we present the light nuclei yield ratios obtained from different centrality bin widths centered around six centrality. The x-axis represents the centrality bin width. For example, for the red solid triangles, a centrality width of 2% corresponds to collisions within the centrality of 6% − 7%, while a centrality width of 5% corresponds to collisions within the centrality of 0 − 10%, representing the central collisions reported in this study. Similarly, for the opened circles, a centrality width of 6% indicates the centrality of 47% − 53%. To better illustrate the results, the data points corresponding to centrality centers of 50% and 70% are multiplied by factors of 0.85 and 0.45, respectively. As shown in the figure, except for the most peripheral collisions, for a given centrality center value, the light nuclei yield ratios increase slightly with increasing centrality width, with the increase being approximately between 2% and 4%. This suggests that the influence of the centrality bin width on the light nuclei yield ratios is relatively minor.

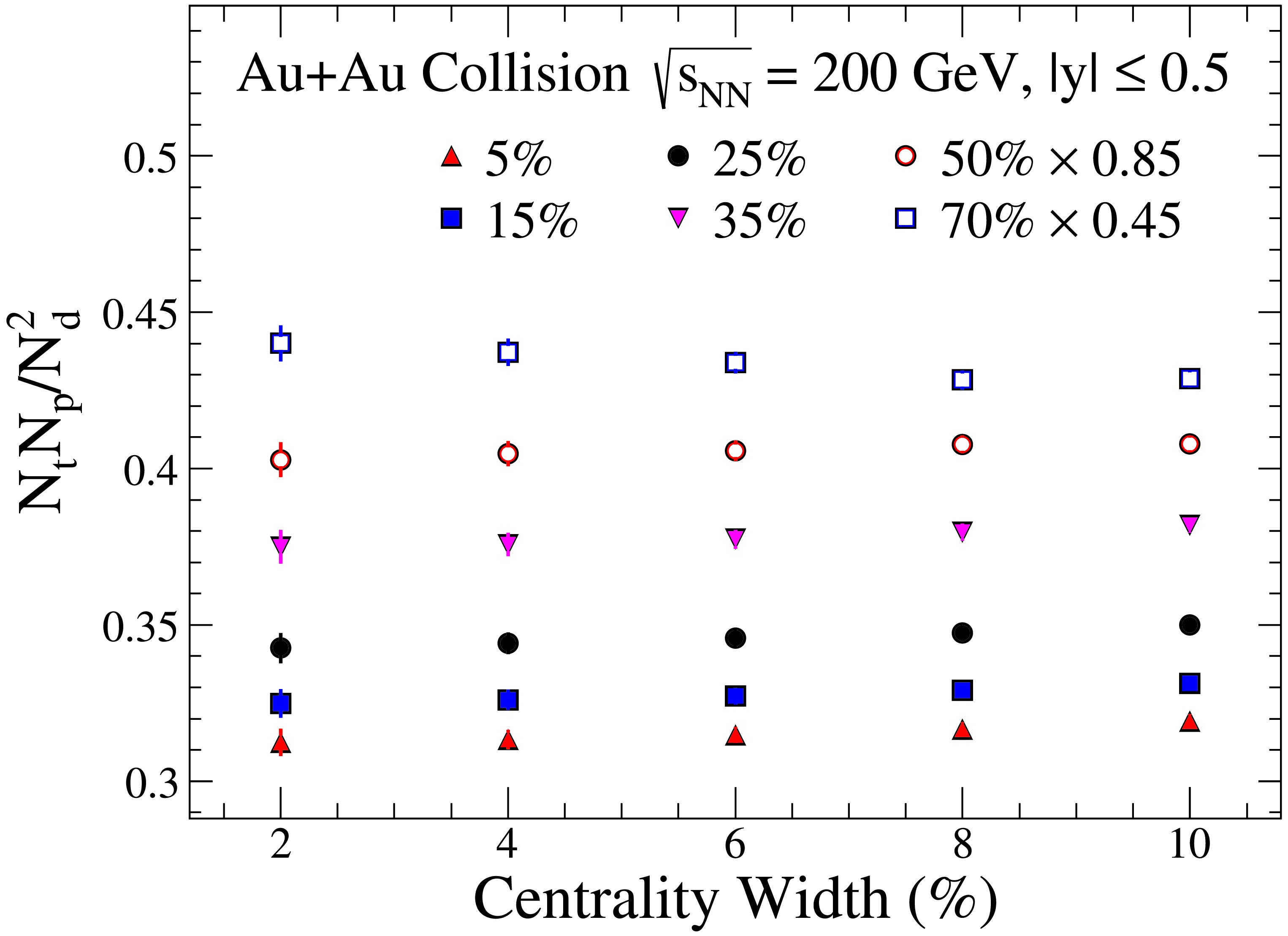
Figure 4.  (color online) Centrality bin width dependence of the light nuclei yield ratio $ N_tN_p/N_d^2 $ from the AMPT model for Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV with $ |y|\leqslant 0.5 $. The different symbols represent results obtained at different centrality centered around specific centrality values (5%, 15%, 25%, 35%, 50%, 70%). Data points for centrality centers of 50% and 70% are scaled by factors of 0.85 and 0.45, respectively, for clarity.

Figure 5 illustrates the collision energy dependence of the light nuclei yield ratio $ N_tN_p/N_d^2 $ extracted from 0 − 10% central and 60% − 80% peripheral Au+Au collisions within $ |y|\leqslant 0.5 $. The dash-dot lines represent cases where $ C_{np} $ and $ C_{n^2p} $ are disregarded. A slight increase in the light nuclei yield ratio with increasing collision energy is evident from the AMPT model. At 0 − 10% central collisions, the yield ratios are consistent with predictions from the coalescence model calculations, $ 1/2\sqrt{3} $. Peripheral collisions show larger yield ratios in comparison to central collisions. When $ C_{n^2p} $ is not considered, the yield ratio for both central and peripheral collisions is reduced, suggesting that neglecting $ C_{n^2p} $ would yield an overestimate of neutron density fluctuations from experimental data. Interestingly, the discrepancy between experimental and actual physical signals, induced by the omission of $ C_{n^2p} $, remains unaffected by the collision energy, except at lower energies, specifically at 7.7 GeV. At a lower energy regime, the influence of $ C_{n^2p} $ on the yield ratio becomes more important, whose underlying mechanisms are unclear and constitute a focal point for future research.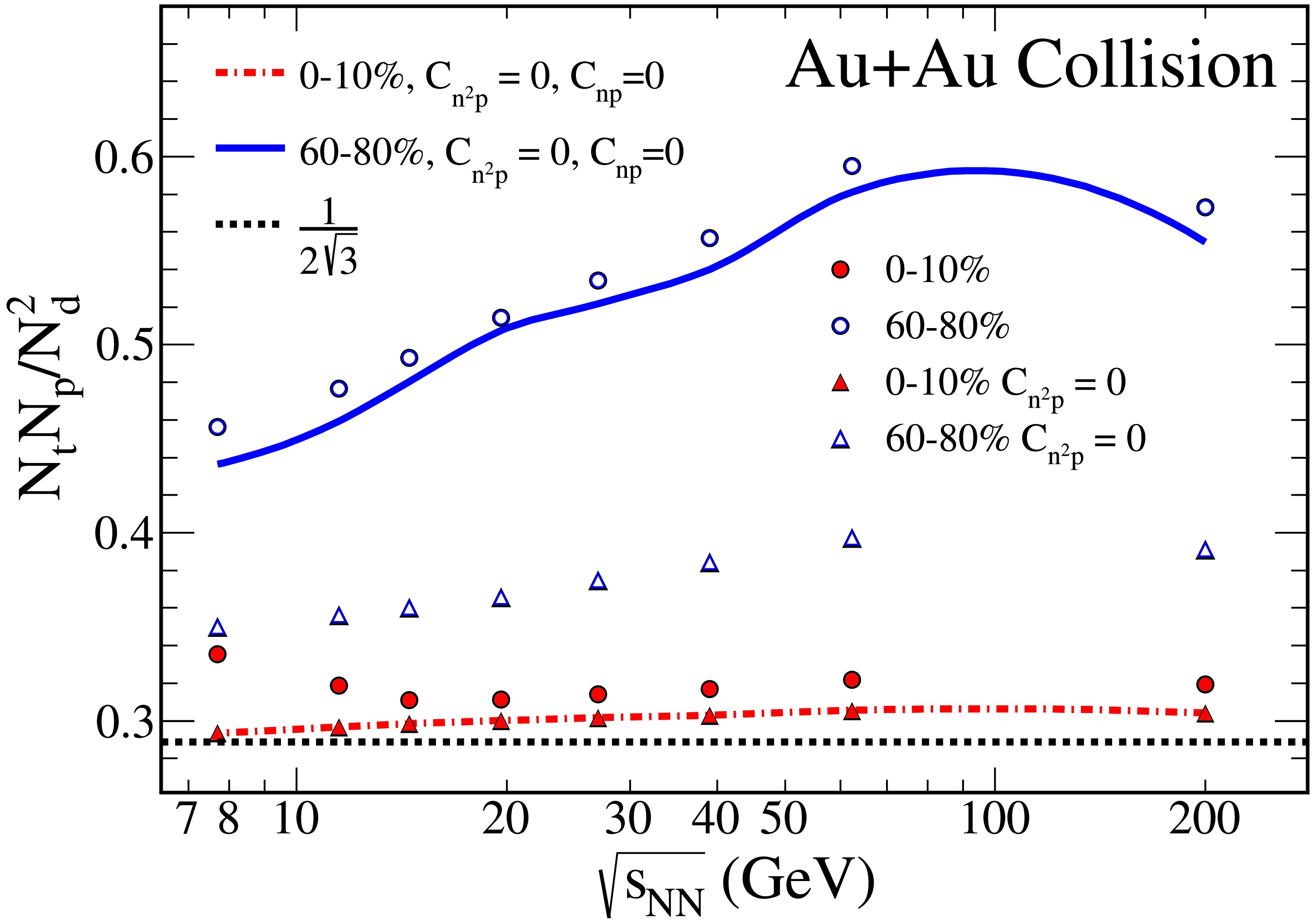

Figure 5.  (color online) Collision energy dependence of the light nuclei yield ratio $ N_tN_p/N_d^2 $ from the AMPT model for Au+Au collisions with $ |y|\leqslant 0.5 $. The results from 0 - 10% central Au+Au collision are shown as solid circles for Eq. (7), solid triangles for Eq. (8) and a red dashed line for Eq. (9). The results from 60% - 80% peripheral Au+Au collision are shown as open circles for Eq. (7), open triangles for Eq. (8), and a blue dashed line for Eq. (9).

Figure 6 compares the experimental results from STAR at 0 − 10% central Au+Au collisions [12] and NA49 at central Pb+Pb collisions [9, 17]. Since we compare the central collisions, the impact of $ C_{np} $ on the yield from the AMPT model is deemed negligible. The inclusion of $ C_{n^2p} $ enhances the light nuclei yield ratios, bringing the AMPT model estimates closer to the experimental results. However, the inclusion of $ C_{n^2p} $ does not change the collision energy dependence of the yield ratio, thereby failing to reproduce the non-monotonic behavior observed in experiments. Given the absence of critical phenomena in the AMPT, this result is reasonable. Using the AMPT model, we obtain a better baseline of the light nuclei yield ratio.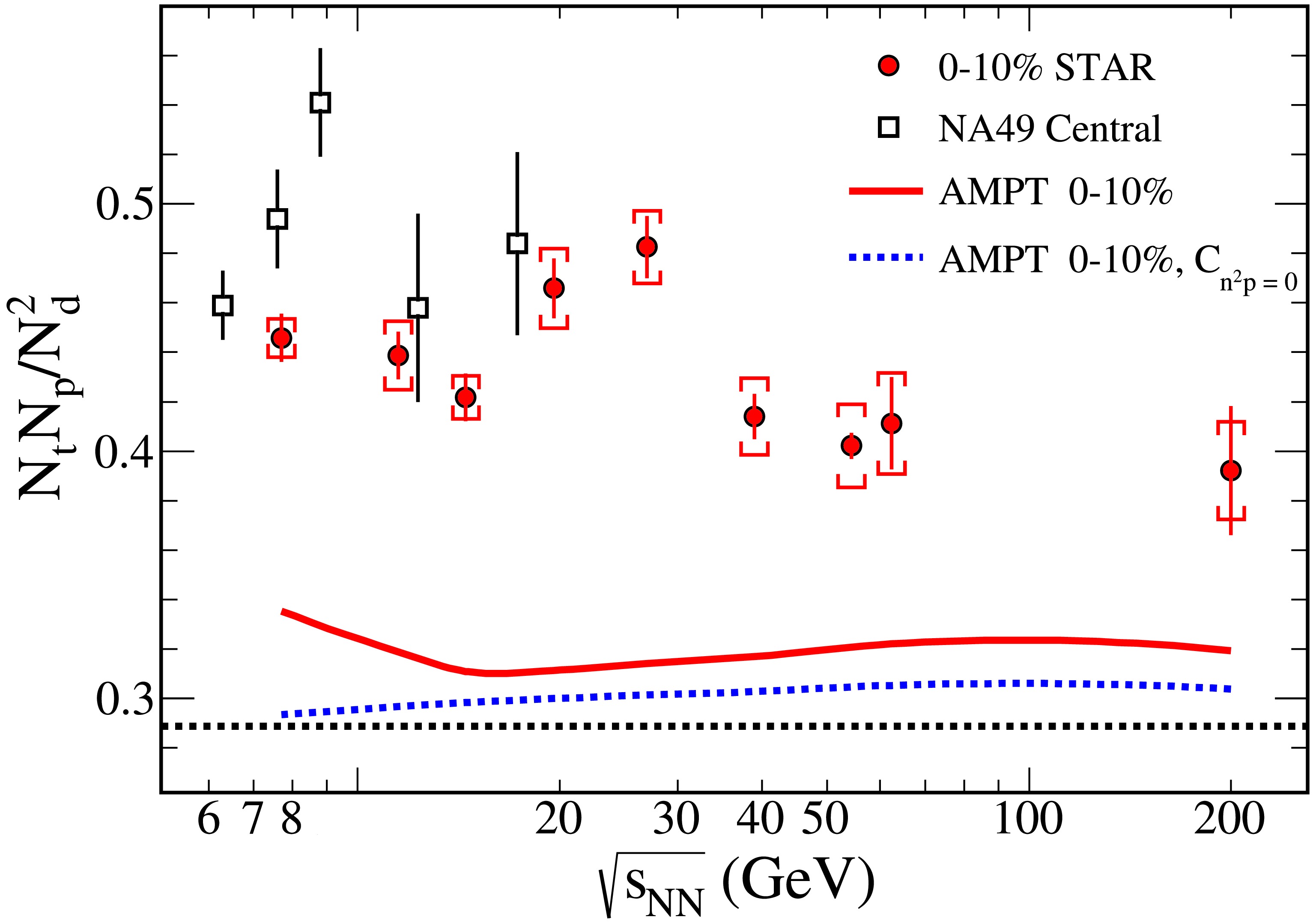

Figure 6.  (color online) Collision energy and centrality dependence of the light nuclei yield ratio $ N_tN_p/N_d^2 $ from the AMPT model with $ |y|\leqslant 0.5 $. Solid circles are the results from the STAR detector at 0 − 10% central Au+Au collision [12]. Open squares are the results from NA49 at central Pb+Pb collision [9, 17].

In summary, using the AMPT model for Au+Au collisions, we study the rapidity, collision energy, and centrality dependence of the relative neutron density fluctuation $ \sigma_n/\langle n \rangle $and the two nucleons and three nucleons correlations $ C_{np} $ and $ C_{n^2p} $. The related light nuclei yield ratios obtained using Eqs. (7), (8), and (9) are also investigated. At central or mid-central collisions, the influence of $ C_{np} $ on the light nuclei yield ratios is insignificant. However, in peripheral collisions, a non-zero $ C_{np} $ reduces the light nuclei yield ratio. Importantly, regardless of central or peripheral collisions, the $ C_{n^2p} $ leads to an overall enhancement in the light nuclei yield ratios. Owing to the absence of critical physics in the AMPT model, it fails to reproduce the experimental observations, particularly the peak observed in the light nuclei yield ratio around $ \sqrt{s_{NN}} = $20 − 30 GeV. Incorporating the three-nucleon correlation $ C_{n^2p} $, our model produces results that offer a more accurate baseline that is closer to the true experimental values.

The authors appreciate the referee for his/her careful reading of the paper and valuable comments.