Two texture zeros for Dirac neutrinos in a diagonal charged lepton basis

I. INTRODUCTION

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

Although the gauge boson sector of the Standard Model (SM) with $S U(3)_c\otimes S U(2)_L\otimes U(1)_Y$ local symmetry has been very successful [1−4], its Yukawa sector is still poorly understood. Questions related to this sector such as the total number of families in nature, the hierarchy of the charged fermion mass spectrum, the smallness of neutrino masses, the quark mixing angles, the neutrino oscillations, and the origin of CP violation, remain open questions to date in theoretical particle physics [5−10].

In the context of the SM, a neutrino flavor created by the weak interaction and associated with a charged lepton will maintain its flavor, which implies that the lepton flavor is conserved and neutrinos are massless. Moreover, recent experimental results confirm that neutrinos oscillate, and, consequently, at least two of them have non-zero masses [11−13].

Current neutrino experiments are measuring the neutrino mixing parameters with unprecedented accuracy. The next generation of neutrino experiments will be sensitive to subdominant neutrino oscillation effects that can, in principle, provide information on the yet-unknown neutrino parameters: the Dirac CP-violating phase in the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) mixing matrix $U_{\rm PMNS}$, the neutrino mass ordering, and the octant of the mixing angles [14−16].

To date, the solar and atmospheric neutrino oscillations have established the following values to 3 sigma of the deviation [17−19]:

which implies, among other things, that at least two neutrinos have very small but non-zero masses.

Masses of neutrinos require physics beyond the SM connected either to the existence of right-handed neutrinos and/or to the breaking of the baryon minus lepton number (B−L) symmetry [20]. If right-handed neutrinos exist, the Yukawa terms, after electroweak symmetry breaking, result in Dirac neutrino masses, requiring Yukawa coupling constants for neutrinos $h_\nu^\phi\leq 10^{-13}$. However, the right-handed neutrinos, singlets under the SM gauge group, can acquire large Majorana masses and render the Type I see-saw mechanism [8, 21−23] to be an appealing and natural scenery for neutrino mass generation. Another possibility is to generate neutrino masses via quantum loops [24, 25]

For Majorana fields, a process exists called neutrinoless double beta decay $(0\nu\beta\beta)$, which is strongly disfavored by current experimental results ([26−28]), the reason for which the alternative is to assume that massive neutrinos must be related to Dirac fields. Therefore, for the model analyzed, we assume that Majorana masses are forbidden by some type of physical mechanism.

In addition to the fact that no experiment has thus far excluded the possibility of Dirac neutrino masses, several theoretical motivations exist to assume them, for example, the generation of baryon asymmetry via leptogenesis [29], alternative approaches to the see-saw mechanism [30], and the generation of radiative neutrino masses via quantum loops [31−34]. Additionally, in models derived from string theories, the Majorana masses are strongly suppressed by selection rules related to the underlying symmetries [35].

Furthermore, the use of Dirac particle fields enables us to apply the polar decomposition theorem of algebra [36], which states that any complex matrix can be decomposed into the product of a Hermitian and a unitary matrix. This decomposition reduces the number of free parameters by half in this sector because the unitary matrix can be absorbed into the singlet representations of $S U(2)_L$, that is, in the right-handed sector (a simplification that is not possible for Majorana particles [37]).

Other theoretical motivations to study Dirac neutrinos include the conservation of global lepton number, a common mass generation mechanism for all Fermion fields, and a clearer distinction between matter and antimatter, which could aid in explaining CP violation in nature [38, 39].

To obtain Dirac neutrinos, three right-handed neutrinos are added to the SM of particles and fields (one for each family), enabling the most general possible Hermitian Dirac mass matrix in the neutral lepton sector in our study. Subsequently, after using a weak basis transformation (WBT) to eliminate nonphysical phases in the Hermitian neutral mass matrix, we aim to fit the mass-squared differences and the mixing angles in the $U_{\rm PMNS}$ matrix, values well measured in neutrino physics thus far, into the parameters.

In our analysis, we assume a diagonal charged lepton mass matrix in the weak basis, which implies that the mixing angles in $U_{\rm PMNS}$ are pure oscillation parameters with no relation with charged lepton mixing. Thus, the unitary matrix that diagonalizes the neutral mass matrix is the same $U_{\rm PMNS}$, and then, by introducing texture zeros in the neutral sector, we obtain physical predictions that can be tested numerically.

II. ZERO TEXTURES FOR DIRAC NEUTRINOS

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

For the analysis that follows, we adopt the following three hypotheses: 1) We extend the electroweak sector of the SM with three right-handed neutrino fields, $(\nu_{\alpha R};\;\alpha = e,\mu,\tau)$; 2) The charged lepton mass matrix is diagonal in the weak flavor basis; 3) Majorana masses are forbidden.

A Neutrino mass matrix

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

According to the previous hypothesis, for the charged lepton sector in the flavor basis, we have

which implies that the most general 3 × 3 mass matrix for the neutrinos, which, owing to the decomposition polar theorem of the matrix algebra [36] we assume to be Hermitian without loss of generality, can be expressed as

where the mixing matrix $U_{\rm PMNS}$ for Dirac neutrinos is parametrized in the usual form as [40]

where $Dg.(m_1,m_2,m_3)$ represents the neutrino mass eigenvalues, and $c_{ij}=\cos\theta_{ij}$ and $s_{ij}=\sin\theta_{ij}$ are the cosine and sine, respectively, of the mixing angle $\theta_{ij},\;\;i < j=1,2,3$.

Now, owing to the Hermiticity constraint, the elements of $M_\nu$ satisfy $m_{\nu_e\nu_e}=m_{\nu_e\nu_e}^*,\; m_{\nu_\mu\nu_\mu}=m_{\nu_\mu\nu_\mu}^*,\; m_{\nu_\tau\nu_\tau}= m_{\nu_\tau\nu_\tau}^*$, and $m_{\nu_\mu\nu_e}=m_{\nu_e\nu_\mu}^*$; $m_{\nu_\tau\nu_e}=m_{\nu_e\nu_\tau}^*$ and $m_{\nu_\mu\nu_\tau}=m_{\nu_\tau\nu_\mu}^*$.

For our analysis, it is convenient to use the following numerical values for the entries of $U_{\rm PMNS}$ evaluated at 3σ ranges, presented in Ref. [17]:

which include strong correlations between the allowed ranges owing to unitary constraints.

When the mass matrices for the lepton sector are given by (2) and (3), we observe that the Hermitian mass matrix $M_\nu$ has six real parameters and three phases that we can use to explain seven physical parameters: the three mixing angles $\theta_{12},\;\;\theta_{13}$, and $\theta_{23}$, one CP violating phase δ, and three neutrino masses $m_1,\; m_2$, and $m_3$. Therefore, in principle, we have a redundant number of parameters (two more phases).

Now, at this point, and contrary to the quark sector [41, 37], we cannot introduce texture zeros via the WBT [42−44] in the mass matrix $M_\nu$ because it will change the charged lepton diagonal mass matrix. However, as shown in the appendix, the WBT can be used to eliminate the two redundant phases.

When the redundant phases are removed via the WBT, the Hermitian matrix $M_\nu^\prime$ has six real parameters and one phase that can accommodate, in principle, the three mixing angles, three neutrino masses, and CP violation phase. Thus, one texture zero should imply a relationship between the mixing angles and physical masses.

However, we do not have six experimental entries to input in the analysis because the neutrinos masses are not known. Instead, we know the mass square differences $\Delta m_{32}^2=m_3^2-m_2^2$; $\Delta^2_{31}=m_3^2-m_1^2$, and $\Delta m_{21}^2=m_2^2-m_1^2$ in normal hierarchy, with the mathematical constraint $\Delta m_{21}^2+\Delta m^2_{32}-\Delta m^2_{31}=0$, which leaves us with only five experimental real constraints to be accommodated. Therefore, patterns with one texture zero should, in principle, be compatible with the experimental data at the 3σ level, although the parameter space for each of these zero textures should be strictly constrained (an analysis presented somewhere else). Therefore, real physical predictions should begin only when two texture zeros are considered.

B Texture zeros

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

The introduction of texture zeros in a general mass matrix has been an outstanding hypothesis that provides relationships between the mixing angles and mass values.

As discussed earlier, the six real mathematical parameters of the most general Hermitian mass matrix for Dirac neutrinos provides sufficient room to accommodate the five real experimental values with no prediction. Furthermore, one texture zero should not conduce to any prediction. Therefore, texture zeros become valuable when two of them are introduced, with two texture zeros providing one physical prediction.

In the following, for normal ordering, we study all the possible cases of two texture zeros in the Hermitian mass matrix of Dirac neutrinos and observe the prediction for the lightest Dirac neutrino mass, which consequently has the knowledge of the complete neutrino mass spectrum.

Three different cases must be analyzed: two texture zeros in the diagonal, one texture zero in the diagonal and the other outside the diagonal, and finally two off-diagonal texture zeros.

To set our mathematical notation, we begin studying the implications of one texture zero.

1   Diagonal texture zeros

Let us assume that $m_{\nu_e\nu_e}=0$ and observe its implications:

From (3), we obtain

dividing by $m_3$ and using the unitary constraint of matrix U, that is $|U_{e1}|^2 +|U_{e2}|^2 +|U_{e3}|^2=1$, we can express (6) as

which we can rearrange as

Similarly for $m_{\nu_\mu\nu_\mu}=0$, we have

and for $m_{\nu_\tau\nu_\tau}=0$, we have

The former three cases can be summarized as

for $\alpha=e$ if $m_{\nu_e\nu_e}=0$, $\alpha=\mu$ if $m_{\nu_\mu\nu_\mu}=0$, and $\alpha=\tau$ if $m_{\nu_\tau\nu_\tau}=0$. This shows the dependence between two of the $U_{\rm PMNS}$ matrix entries and the neutrino mass values.

2   Texture zeros outside the diagonal

Let us now consider a texture zero outside the diagonal. Let us begin with $m_{\nu_e\nu_\mu}=0$ (notice that $m_{\nu_\mu\nu_e}= m_{\nu_e\nu_\mu}^*=0$).

For this scenario, (3) implies that

which, dividing by $m_3$ and using the orthogonality condition $U_{e1}U_{\mu 1}^* +U_{e2}U_{\mu 2}^* +U_{e3}U_{\mu 3}^*=0$, can be expressed as

multiplying by $U_{e2}^*U_{\mu 2}$ and rearranging, we obtain

which we can finally expressed as

which, together with its complex conjugate, can be separated in two parts: a real part and an imaginary part both equal to zero (note that for a Hermitian matrix, its eigenvalues must be real but not necessarily positive).

As $m_{\nu_\mu\nu_e}$ must also be equal to zero, the two relations must also be equivalent to making the real and imaginary parts in (14) equal to zero. As the second term in (14) is real, making the imaginary part equal to zero produces

which means that this texture zero is associated with a Jarlskog invariant [45] equal to zero, and no CP violation is present for this texture zero.

Similarly for $m_{\nu_e\nu_\tau}=0$, we have

Dividing by $m_3$ and using the orthogonality relationship $U_{e1}U_{\tau 1}^* +U_{e2}U_{\tau 2}^* +U_{e3}U_{\tau 3}^*=0$, we can express (16) in the form

multiplying by $U_{e2}^*U_{\tau 2}$ and rearranging, we obtain

which implies

which again produces

The former means that this texture zero outside the diagonal is also associated with a Jarlskog invariant equal to zero and, again, there is no CP violation for this case.

Similarly, for $m_{\nu_\mu\nu_\tau}=0$ we obtain

which, divided by $m_3$ and using the appropriate orthogonality relationship, we obtain

which, multiplying by $U_{\mu 2}^*U_{\tau 2}$, we obtain

which again yields

Therefore, a texture zero in $M_\nu$ outside the main diagonal implies CP conservation, a result also obtained in a different manner in Appendix A.

III. NUMERICAL ANALYSIS

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

According to (4), the right-hand side of (3) depends only on the neutrino mixing angles, CP-violating phase, and neutrino masses. Therefore, each of the possible six texture zeros in the matrix $M_\nu$ in (3) implies an equation relating neutrino masses with the CP-phase and neutrino mixing angles. The equation must be confronted with the measured experimental values. Hence, we must place each equation in terms of physical parameters. Let us observe this:

A $m_{\nu_e\nu_e}$ = 0

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

The texture $m_{\nu_e\nu_e}=0$ produces the constraint in equation (7), which, when expressed in terms of physical parameters, becomes

This relationship that must be satisfied by experimentally measured values to obtain a realistic texture zero in the neutrino mass matrix.

The relationship (25) can be rearranged slightly by using the definitions $m=m_1+m_2+m_3$ and $\Delta m_{32}^2=m_3^2-m_2^2$

The parameter space can be studied through a $\chi^2$ analysis, which is defined as

where $\sin^2\tilde\theta_{12}$w is the value for this mixing angle obtained from Eq. (26), whereas $\sin^2\theta_{12}$ and $\sigma(\sin^{2}\theta_{12})$ are the current best fit value and its one sigma deviation, respectively. Experimental data in (1) and (5) are used to perform the analysis.

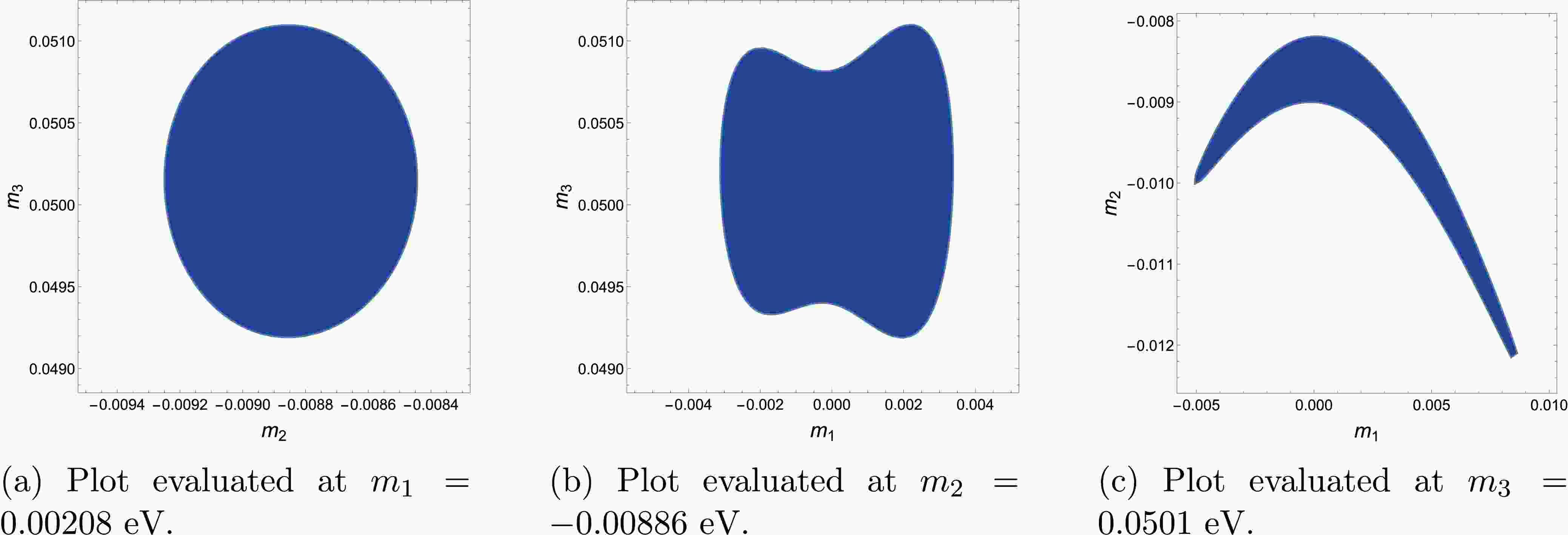
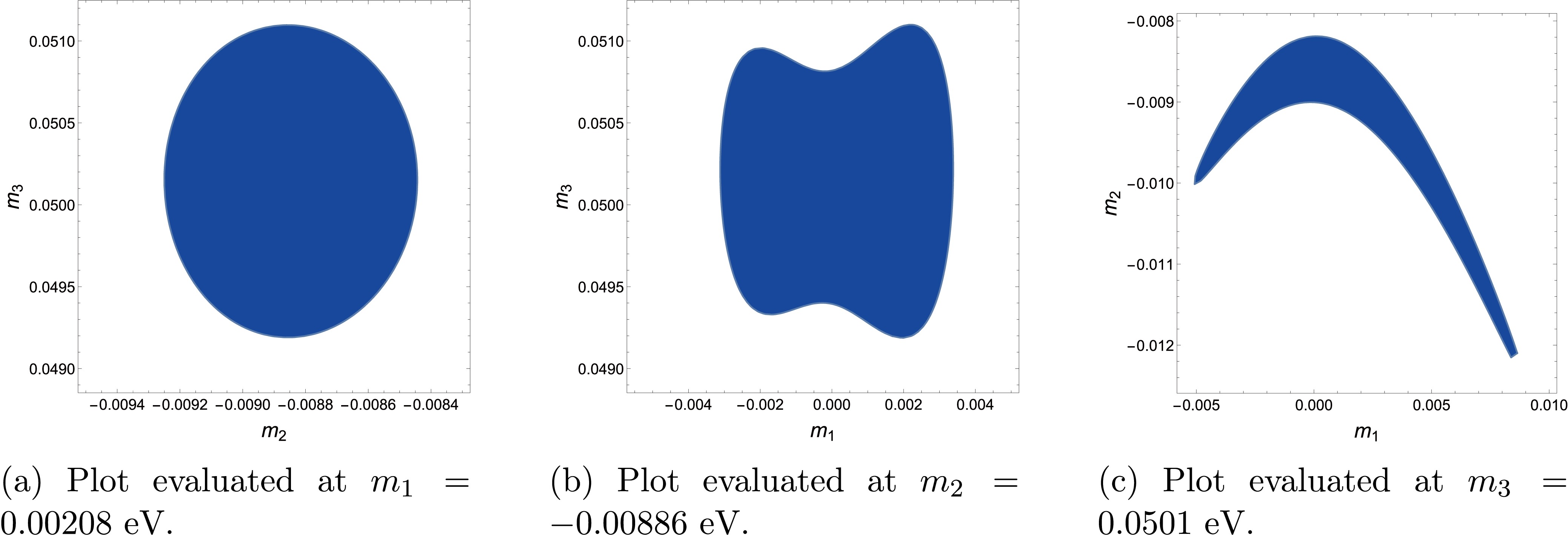
After defining the parameter space in terms of $\Delta m_{12}^{2}$, $\Delta m_{13}^{2}$ and the mixing angles $\theta_{12}$, $\theta_{13}$, we perform a minimization process for the $\chi^2$ function. The best fit points obtained around the minimum (about zero) for our analysis are

To study the $(m_1,\,m_2,\,m_3)$ parameter space, we first fix the $m_1$ value in its minimum and search for the allowed values of $m_2$ and $m_3$ at the 95% confidence level (CL); the results are presented in Fig. 1(a). Next, we fix $m_2$ in its minimum and search for the allowed values of $m_1$ and $m_3$ at the 95% CL, whose results are presented in 1(b). Finally, fixing $m_3$, we determine the parameter space allowed for $m_1$ and $m_2$, as presented in Fig. 1(c). The parameter spaces shown in the former three figures satisfy the experimental limits $|m_1|+|m_2|+|m_3|<0.12$ ${\mathrm{eV}}$ [46], the square mass differences, and the three mixing angles.

Figure 1

Figure 1.  (color online) Parameter space for the texture zero $M_{\nu_e \nu_e}=0$ at 95% CL.

DownLoad: Full-Size Img PowerPoint

Equation (25) shows that the CP violation phase is entirely unconstrained, but the plots in the figure show that the experimentally measured values can be well accommodated in the allowed parameter space, as anticipated above. The mixing angle $\theta _{23}$ is easily obtained from the (2,3) or (3,3) mixing matrix numerical entries.

A similar analysis can be performed for the other five one texture zero in the matrix $M_\nu$, that is, for $m_{\nu_\mu\nu_\mu}=0$, $m_{\nu_\tau\nu_\tau}=0$, $m_{\nu_e\nu_\mu}=$ $m_{\nu_\mu\nu_e}=0$, etc. The results for this analysis will be presented elsewhere.

B Two texture zeros

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

The next step is to study the different structures with two texture zeros in the neutrino mass matrix (with a diagonal charged lepton sector in the weak basis). We study three different cases: first, the two zeros are in the main diagonal (there are three CP violating patterns); next, one texture zero is in the main diagonal and the other one outside this diagonal (with nine CP conserving different patterns); finally, the two zeros are off the main diagonal (with three CP conserving different patterns). ¹

The following section presents, for one particular pattern, the detailed analytic and numerical analysis for all the different fifteen two texture zeros patterns. Our numerical results are presented in one appendix at the end of the paper.

1   Two zeros, one in the main diagonal

The number of different patterns in this category, all of them related to CP conservation, is nine. They are shown in Appendix B.B.1.

In our analysis, performed in two steps, we reconstruct first the neutrino mass matrix in terms of the three neutrino masses $m_1,\;\; m_2$, and $m_3$. This is achieved by using the invariant forms: tr[M], tr[M²], and det[M]. Thereafter, we derive the analytic orthogonal matrices that diagonalize the several 3×3 real neutrino mass matrices. The result is the $U_{PMNS}$ in analytic form as a function of the real mass eigenvalues and any other parameter required, this last one conveniently chosen.

To observe this, let us use as an example here with the texture in $A_7$:

Notice that the three eigenvalues of a general 3 × 3 Hermitian matrix are real but not necessarily positive. By taking the determinant of $A_7$, we obtain $|A_7|=-x_2|b|^2-x_1|c|^2 =m_1m_2m_3$, which by fixing $m_3>0$ by a global phase convention, we must have two classes of solutions: $m_1>0,\;\; m_2<0$ and $m_1<0,\;\;\; m_2>0$. Let us perform our example for the particular case of $m_1 > 0$ and $m_2<0$

After using the invariant forms for this $3\times 3$ mass matrix, and solving the equations, we obtain

where $m_1,\,m_2,\,m_3$, and $x_1$ are free parameters used to calculate the neutrino masses and mixing angles. After diagonalizing this texture, we obtain the $U_{\text{PMNS}}$ in terms of the free parameter.

After obtaining this expression, we conduct a $\chi^2$ minimization procedure:

where $\sin^2\tilde\theta_{ij}$ represents the angles mixing predicted by our forms, whereas $\sin^2\theta_{ij}$ and $\sigma(\sin^{2}\theta_{ij})$ are the current best-fit value and its one sigma deviation, respectively. To obtain the best values that fit the experimental data. Note that the analytical results contain some square root terms that imply several limits on the parameters, such that the results are real; that is, we must have

The minimization procedure produces the following phenomenological results: The neutrino masses $|m_1|= 0.0333\,\,\,$ eV, $|m_2|=0.0344$ eV, $|m_3|=0.0608$ eV, and the mixing angles $\sin^2{\theta_{12}}=0.315,\;\;\sin^2{\theta_{23}}=0.646,\;\; \sin^2{\theta_{13}}= 0.022.$

The numerical result agrees with the data reported experimentally by the Neutrino Global Fit [17].

The results of the other eight possibilities are shown in Appendix D.

2   Two zeros off the main diagonal

None of the three cases is viable because each one of them is associated with a vanishing oscillation parameter (for $A_{10}$, we have $\theta_{13}=0$, for $A_{11}$, we have $\theta_{23}=0$, and for $A_{12}$, we have $\theta_{12}=0$). The forms are shown in Appendix B.B.2.

3   Two zeros in the main diagonal

Three different patterns are given by the matrices $A_{13},\; A_{14}$, and $A_{15}$. Using the invariant forms as before, we obtain complicated analytic expressions for the $U_{\rm PMNS}$ matrix, whose tracking does not reveal much. Therefore, we proceed immediately with the numerical analysis.

Our result shows that none of the three different textures with two zeroes in the main diagonal can reproduce the three measured mixing angles in the $U_{\rm PMNS}$ oscillation matrix.

IV. SUMMARY

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

In the context of a model with right-handed neutrinos (one for each family) and global lepton number conservation, we perform an analytic and numerical systematic study of the Dirac neutrino Hermitian mass matrix $M_\nu$ with two independent texture zeros, under the assumption that the charged lepton sector is diagonal in the weak basis.

Analytic expressions for the entries of $M_\nu$ as functions of the the three neutrino masses are obtained using the mathematical invariant of a 3 × 3 matrix. Algebraic expressions are derived to obtain numerical values for the physical parameters via minimization with a $\chi^2$ statistical analysis.

According to our study, the cases compatible with the current experimental data at the 3σ level are $A_3$ and $A_7$ (in Appendix B), both of them associated to normal ordering an CP conservation. This is contrary to the results presented in Refs. [49, 50], where the analysis was performed for correlations between two of the three mixing angles. Now, performing our analysis but relaxing the correlation between the angle $\sin{\theta_{13}}$ with the other two mixing parameters at the 3σ level, the results in Table [3] are obtained, now in agreement with the results reported in the literature [49, 50].

A new feature in our analysis is the iterative use of WBTs [42−44], which provide the following results: first, the elimination of the two redundant phases in the most general Hermitian neutrino mass matrix ending up with only one physical phase connected with possible CP violation in the lepton sector; second, the demonstration the CP conservation in a novel manner in the context of our analysis when a texture zero outside the main diagonal is placed.

Note that in our analysis, based on the assumption of a diagonal charged lepton mass matrix in the weak basis, our $U_{\rm PMNS}$ matrix is a pure oscillation matrix and not a mixing one as it occurs in the quark sector. This is relevant because neutrino experiments have measured oscillations.

From our study, the mass for one of the three neutrinos can be predicted (we select the lightest one). Using this value, and the experimental mass squared differences, the entire neutrino mass spectrum can be inferred, as presented in the three tables at the end of the paper. Those values are exact predictions in our analysis. For example, for $A_3$ in Table D1, we obtain $m_1=0.021$, $m_2=0.087$, and $m_3=0.501$, whose values are predicted in eV.

Table D1

Table D1.  Results of the mixing angles and neutrino masses for the nine different textures obtained according to our analysis for $m_1>0$ and $m_2<0$.

Texture	$\sin^2{\theta_{12}}$	$\sin^2{\theta_{23}}$	$\sin^2{\theta_{13}}$	$|m_1|$/eV	$|m_2|$/eV	$|m_3|$/eV
1: $A_1$	0.298	0.250	0.022	0.0018	0.0091	0.0512
2: $A_2$	0.305	0.018	0.014	0.0044	0.0096	0.0503
3: $A_3$	0.334	0.007	0.022	0.0021	0.0087	0.0501
4: $A_4$	0.318	0.200	0.022	0.0046	0.0097	0.0512
5: $A_5$	0.465	0.010	0.032	0.0153	0.0175	0.0534
6: $A_6$	0.524	0.003	0.014	0.0209	0.0227	0.0546
7: $A_7$	0.315	0.646	0.022	0.0333	0.0344	0.0608
8: $A_8$	0.022	0.515	0.023	0.2685	0.2686	0.2731
9: $A_9$	0.023	0.516	0.023	0.2765	0.2767	0.2810

DownLoad: CSV

Show Table

Although we realized that all the six one zero textures are compatible with current neutrino oscillations, we have not obtained in detail the constraints in the parameter space coming from the experimentally measured values (results presented elsewhere).

Finally, whether neutrinos are Dirac or Majorana particles remains an open question.

APPENDIX A

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

In this appendix, we address two problems: first, we show how to use the weak basis transformation (WBT) to reduce the number of phases from three to one in a general 3 × 3 Hermitian neutrino mass matrix (for a diagonal mass matrix in the charged lepton sector). Second, we discuss the mathematical reason for CP conservation when an off-diagonal vanishing element exists in the neutrino sector.

In the context of the SM extended with right-handed neutrinos and lepton number conservation, the most general WBT that leaves the two 3 × 3 lepton mass matrices Hermitian and does not alter the physics implicit in the weak currents (does not alter the physical content in the $U_{\rm PMNS}$ mixing matrix) is an arbitrary unitary transformation U acting simultaneously in the charged lepton and in the neutrino mass matrices [43]. That is

Now, when the mass matrices for the charged lepton sector are diagonal, we have that the most general Hermitian mass matrix $M_\nu$ for the neutral sector has six real parameters and three phases that we can use to explain seven physical parameters: three neutrino masses $m_1, m_2$, and $m_3$, the three mixing angles $\theta_{12}, \theta_{13}$, and $\theta_{23}$, and one CP violating phase δ in the $U_{\rm PMNS}$ mixing matrix. Therefore, in principle, we obtain a redundant number of parameters (two more phases).

In contrast to the quark sector [41, 37], we cannot introduce texture zeros via WBTs in the mass matrix $M_\nu$ because it would change the charged lepton diagonal mass matrix. However, the WBTs can eliminate the redundant phases. Hence, we express the neutrino mass matrix as

and perform a WBT using the following diagonal unitary matrix:

which does not change the diagonal charged lepton mass matrix. After this, the matrix (32) has the following form:

where $M_\nu^\prime=M_\phi^\dagger M_\nu M_\phi$. Three cases are present in this expression:

Case A: $\phi_1=\phi_{e\mu}$ and $\phi_2=\phi_1-\phi_{e\tau}=\phi_{e\mu}-\phi_{e\tau}$, producing

with $\psi=\phi_{\mu\tau}+\phi_2=\phi_{\mu\tau}+\phi_{e\mu}-\phi_{e\tau}$.

Case B: $\phi_1=\phi_{e\mu}$ and $\phi_2=-\phi_{\mu\tau}$, producing

Case C: $\phi_2=-\phi_{\mu\tau}$ and $\phi_1=\phi_2+\phi_{e\tau}=\phi_{e\tau}-\phi_{\mu\tau}$, producing

From the former, we can conclude that using a WBT, we can eliminate two unwanted phases, obtaining a single phase responsible for the possible CP violation phenomena present in the $U_{\rm PMNS}$ mixing matrix.

Counting parameters once more, we find that in matrix (33) (or equivalently in (34) or (35)), the final number of parameters is six real numbers and one phase (ψ), just sufficient to accommodate the three mixing angles $\theta_{12},\theta_{13}$, and $\theta_{23}$ and the three neutrino masses $m_1, m_2$, and $m_3$, together with just one CP violating phase to consider the CP violation in the $U_{\rm PMNS}$ matrix via the parameter $(\delta_{\rm CP}$) for Dirac neutrinos. Further texture zeros will reveal relationships between neutrino masses and mixing parameters.

Thus, one texture zero would enable us to express one of the mixing angles $\theta_{ij}$ as a function of the neutrino masses; meanwhile, two texture zeros enable us to express two mixing angles as a function of the three neutrino masses. Three or more texture zeros are meaningless.

The most important consequence of the former analysis is that, because the phases $\phi_1$ and $\phi_2$ are arbitrary and they can take any value, the final phase ψ can be placed in any entry of the neutrino mass matrix, according to (33)−(35). In particular, if we impose an off-diagonal vanishing element, we can place the phase ψ in that entry, meaning that a phase will not be present in the mass matrix. That implies CP conservation for that case. This is a result obtained from the Jarlskog invariant analysis as shown in the main text.

APPENDIX B

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

As mentioned in the main text, the mass matrix $M_\nu$ for Dirac neutrinos, in the context of the SM enlarged with the right-handed neutrinos, can be transformed to be Hermitian without loss of generality, which means that three independent off-diagonal matrix elements are generally complex, whereas the three independent diagonal ones are real. If n of them are taken to vanish (n independent texture zeros), then a combinatorial analysis enables us to express the number of independent matrices as [50]

which means $C_1=6$, $C_2=15$, and $C_3=20$ (Textures with $n\geq 3$ are not realistic).

A One texture zero

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

Two different scenarios occur: texture zero in the main diagonal and texture zero off the main diagonal, with three different cases for each scenario:

1   Diagonal texture zero

Three different cases are given by the three matrices

with all three cases related to CP violation.

2   Off diagonal texture zero

Again, three different cases are given by the matrices

with all of them related to CP conservation.

B Two texture zeros

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

Fifteen different cases are grouped in three different categories:

1   One diagonal and other off-diagonal texture zeros

Nine different cases occur:

with all of them CP conserving.

2   Two texture zeros off the main diagonal

Three different cases occur:

All of them are related to CP conservation.

3   Two texture zeros in the main diagonal

Three different cases occur:

All of them related to CP violation.

APPENDIX C

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

In this appendix, we review the definition of the Jarlskog invariant.

The Swedish physicist Cecilia Jarlskog observed that the area of each of the six unitary triangles in a unitary matrix $3 \times 3$ (which is the same for all of them) is given by the relation:

where $-J$ is known as the Jarlskog invariant [45], which, in the parametrization that makes use of the Euler angles takes the form

which can also be expressed as

for any combination of $i,j,k,l$, where $i\neq k$ and $j\neq l$.

Thus, the Jarlskog invariant is an important information carrier for CP-violation [51].

APPENDIX D

• I. INTRODUCTION
• II. ZERO TEXTURES FOR DIRAC NEUTRINOS
•      A Neutrino mass matrix
•      B Texture zeros
• III. NUMERICAL ANALYSIS
•      A $m_{\nu_e\nu_e}$ = 0
•      B Two texture zeros
• IV. SUMMARY
• APPENDIX A
• APPENDIX B
•      A One texture zero
•      B Two texture zeros
• APPENDIX C
• APPENDIX D

In this appendix, we present the summary of the numerical results obtained from our analysis for the nine cases of two texture zeroes, one in the main diagonal and the other one outside of it. For the analysis, we use $\delta_{\rm CP}=0$. From the results, normal ordering is suggested. Three tables are presented:

The first one corresponds to the analysis for $m_1>0$ and $m_2< 0$. The second is for $m_1<0$ and $m_2>0$. The third table presents the results obtained when we relax the constraints imposed by the value $\theta_{13}$; that is, without having a correlation on the $\sin\theta_{13}$ mixing angle with the other parameters.

Table D1 shows that only the texture $A_7$ can accommodate the measured mixing angles, with the corresponding predictions for the neutrinos mass values.

Table D2 shows that only the texture $A_3$ can accommodate the measured mixing angles, with the corresponding predictions for the neutrinos mass values.

Table D2

Table D2.  Results of the mixing angles and the neutrino masses for the nine different textures obtained according to our analysis for $m_1<0$ and $m_2>0$.

Texture	$\sin^2{\theta_{12}}$	$\sin^2{\theta_{23}}$	$\sin^2{\theta_{13}}$	$|m_1|$/eV	$|m_2|$/eV	$|m_3|$/eV
1: $A_1$	0.255	0.104	0.022	0.0026	0.0093	0.0599
2: $A_2$	0.274	0.102	0.023	0.0040	0.0096	0.0513
3: $A_3$	0.379	0.548	0.022	0.0411	0.0420	0.0649
4: $A_4$	0.320	0.190	0.022	0.0041	0.0099	0.0508
5: $A_5$	0.296	0.325	0.020	0.0442	0.0450	0.0665
6: $A_6$	0.572	0.426	0.021	0.0315	0.0328	0.0600
7: $A_7$	0.002	0.542	0.021	0.0769	0.0774	0.0920
8: $A_8$	0.999	0.998	0.517	0.0237	0.0253	0.0557
9: $A_9$	0.010	0.986	0.511	0.0241	0.0256	0.0553

DownLoad: CSV

Show Table

To compare our results with previous published studies, we conducted an alternative analysis consisting in relaxing the constraint imposed by the value $\theta_{13}$, that is, without having a correlation of the $\sin{\theta_{13}}$ mixing angle with the other parameters. The results obtained are presented in Table D3. These values show that textures $A_1$, $A_4$, $A_7$, and $A_8$ are in fairly good agreement with the experimentally measured numbers at $3\sigma$, resulting in agreement with the analysis already presented in Refs. [49, 50]. Note that when the parameter $\sin{\theta_{13}}$ is smoothed, we cannot make predictions about all the entries in the $U_{\rm PMNS}$ mixing matrix.

Table D3

Table D3.  Values of the parameters obtained for the nine different two zero textures for the alternative analysis.

Texture	$\sin^2{\theta_{12}}$	$\sin^2{\theta_{23}}$	$|m_1|$/eV	$|m_2|$/eV	$|m_3|$/eV
1: $A_1$	0.320	0.522	0.0077	0.0114	0.0514
2: $A_2$	0.215	0.318	0.0089	0.0126	0.0508
3: $A_3$	0.334	0.0146	0	0.0089	0.0497
4: $A_4$	0.320	0.522	0.0355	0.0365	0.0611
5: $A_5$	0.230	0.430	0	0.0084	0.0512
6: $A_6$	0.540	0.020	0.0230	0.0245	0.0551
7: $A_7$	0.325	0.657	0.0283	0.0297	0.0569
8: $A_8$	0.318	0.512	0	0.0087	0.0511
9: $A_9$	0.364	0.909	0.0303	0.0585	0.0585

DownLoad: CSV

Show Table

1Other possibilities with two texture zeros in the neutral sector and three texture zeros in the charged sector with at least one of them in the diagonal are analyzed in Refs. [44, 47, 48]

References