Beauty-charm meson family with coupled channel effects and their strong decays

I. INTRODUCTION

• I. INTRODUCTION
• II. THEORETICAL FORMALISM
•      A Quenched quark model
•      B Gaussian expansion method
•      C Coupled channel framework
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

The understanding of hadron structures and their transitions at Fermi scale is a fundamental issue from both the theoretical and experimental aspects in particle physics. Given the meson spectrum, the beauty-charm meson family is relatively incomplete when compared with other systems. To date, only three beauty-charm mesons have been observed in experiments, i.e, the $B_c(1S)$, $B_c(2S)$ and $B^*_c(2S)$ [1].

The ground state $B_c(1^1S_0)$ of beauty-charm family was first discovered in 1998 by CDF at Fermilab [2]. The latest average mass for this state is determined as $6274.47\pm0.27\pm0.17$ MeV [1]. A new structure was first discovered in $B_c^+ \pi^+ \pi^-$ invariant mass spectrum with subprocess $B_c^+\to J/\psi\pi^+$ using the sample corresponding to 4.9 fb$^{-1}$ of 7 TeV and 19.2 fb$^{-1}$ of 8 TeV $pp$ collision data acquired by the ATLAS experiment at the LHC in 2014 [3]. Then, two radially excited beauty-charm states $B_c(2^1S_0)$ and $B^*_c(2^3S_1)$ as opposed to one peak are discovered in $B_c^+ \pi^+ \pi^-$ invariant mass spectrum in the same channels from both the CMS and LHCb experiments [4, 5]. The combined average mass for $B_c(2^1S_0)$ is determined as $6871.2\pm0.1$ MeV [1]. For the vector excited state, $B^*_c(2^3S_1)$ first decays via hadronic transition $B^{*+}_c(2^3S_1) \to B^{*+}_c(1^3S_1) \pi^+ \pi^-$ and then vector $B^{*+}_c(1^3S_1)$ decays via electromagnetic transition $B^{*+}_c(1^3S_1)\to B^{+}_c(1^1S_0)+\gamma$. However, the radiated photon is soft with energy of apprximately 60 MeV, which is not reconstructed among ATLAS, CMS, and LHCb experiments. Thus, the determination of the mass of $B^{*+}_c(2^3S_1)$ relies on the precise information of $B^{*+}_c(1^3S_1)$. Additionally, other beauty-charm meson states, including orbitally excited states, have not been observed in experiments to date. This requires precise theoretical predictions.

In theoretical aspects, the mass spectra of beauty-charm mesons have been examined in many studies. For example, quark potential models [6−15], QCD sum rule [16−20], heavy quark effective theory [21], and Dyson-Schwinger equation approach of QCD [22, 23]. Furthermore, the properties of low-lying $B_c$ mesons are also investigated in lattice QCD based on the first principles [24−26].

Up to now, the Godfrey-Isgur quenched approach in quark potential models [14] is usually considered to provide a good and systematical description for most of the meson spectra. However, the quenched quark models sometimes poorly explain higher excited states beyond the two-body threshold because they miss the generation of the light quark-antiquark pairs which enlarge the Fock space of the initial state [27]. These multiquark components will change the Hamiltonian of the conventional quark potential models and then lead to mass shift and mixing among states with the same quantum numbers. If the initial state exceeds two-body threshold, then the open channel strong decay will be allowed. This implies that the unquenched quark model includes virtual hadronic loops. The hadronic loop has turned out to be highly nontrivial and can lead to mass shifts to the bare hadron states and contribute continuum components to the physical hadron states [28].

The coupled-channel model as one of the unquenched quark model, which is usually neglected, will manifest as a coupling to meson-meson (meson-baryon) channels and lead to mass shifts. These effects are introduced explicitly into the constituent quark model via a QCD-inspired $^3P_0$ pair-creation mechanism. The pair-creation mechanism is inserted at the quark level and one-loop diagrams are calculated by summing over the possible intermediate states [29]. It has been shown that the coupled-channel effects play an important role for describing the mesons spectra, such as charmonium [30−33], bottomonium [27−29, 34], and charmed-strange mesons [35−46].

In this study, we will use this type of unquenched quark model to examine the beauty-charm mesons. We will sytematically investigate the mass spectrum of the beauty-charm mesons within the nonrelativistic quark model by consideirng the mass shifts from the coupled-channel effects. Additionally, the two-body hadronic decays are also examined. The paper is arranged as follows. The theoretical formalism in coupled channel framework is provided in Section II, where the nonrelativistic quenched quark model and ${}^3P_0$ model are introduced. The beauty-charm meson spectrum, including coupled channel effects, molecule and two quark components, and two body hadronic decay widths, are provided in Section III. Finally, we provide the summary in Section IV.

II. THEORETICAL FORMALISM

• I. INTRODUCTION
• II. THEORETICAL FORMALISM
•      A Quenched quark model
•      B Gaussian expansion method
•      C Coupled channel framework
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

A Quenched quark model

• I. INTRODUCTION
• II. THEORETICAL FORMALISM
•      A Quenched quark model
•      B Gaussian expansion method
•      C Coupled channel framework
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

First, we introduce a nonrelativistic quark model to denote the quenched quark interactions. Furthermore, Hamiltonian $H_Q$ can be expressed as:

where the reduced quark mass $m_r$ satisfies $m_r=m_b m_{\bar{c}}/ (m_b+m_{\bar{c}})$. Specifically, ${{\boldsymbol{S}}}_{i}$ denotes the heavy quark spin operator. The linear confining assumption is employed and parameters $m_{b}$, $m_c=m_{\bar{c}}$, $C_{b\bar{c}}$, $\sigma$, $b$, and $\alpha_s$ in the quenched quark model Hamiltonian will be refitted from the knowledge of the existing hadrons.

The left spin and orbital related term $H_{SL}$ has the expression:

where L denotes the orbital angular momentum between beauty charm quarks. ${\boldsymbol{S}}_{\pm}={{\boldsymbol{S}}}_b\pm{{\boldsymbol{S}}}_{\bar{c}}$. The expressions for each potential are as follows:

where $\gamma_E$ denots Euler constant. Furthermore, SU(3) color factors are $C_F=4/3$ and $C_A=3$. The renormalization scale $\mu=1$ GeV is adopted as in Refs. [47−52].

The spin operator ${\boldsymbol{S}}_{-}={{\boldsymbol{S}}}_b-{{\boldsymbol{S}}}_{\bar{c}}$ can lead to the mixing of the beauty-charm mesons with identical total angular momentum but with different total spins. For example, mixing between $B_c(n{}^3L_L)$ and $B_c(n{}^1L_L)$ states occurs, and this can be described by mixing matrix by introducing a mixing angle $\theta_{nL}$ [14, 53] as follows:

where the physical observed states are denoted as $B_{cL}(nL)$ and $B_{cL}^\prime(nL)$.

The mixing angle is determined by the spin-orbit term $H_{SL}$. The term include two parts, symmetric part $H_{\rm sym}$ and antisymmetric part $H_{\rm anti}$. These two parts can be expressed as [48]:

When the heavy-light mesons have different total spins but with same total angular momentum, the spin-orbit mixing will occur. The mixing angle can be estimated by the antisymmetric part $H_{\rm anti}$. Furthermore, $H_{\rm anti}$ provides the influence of non-diagonal terms, and the mixed angle can be extracted via diagonalization,

B Gaussian expansion method

• I. INTRODUCTION
• II. THEORETICAL FORMALISM
•      A Quenched quark model
•      B Gaussian expansion method
•      C Coupled channel framework
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

The Gaussian expansion method is a high-precision method for solving Schrodinger equation. The method was proposed by E. Hiyama [54]. By using Gaussian basis functions, it can describe accurately short-range correlations and long-range asymptotic behavior and highly oscillatory character of wave functions in bound and scattering states of the systems. The method is widely used to calculate hadron spectrum [27, 55, 56]. For a given two-body Schrodinger equation:

where μ denotes the reduced mass and $V(r)$ denotes a central potential. The equation can be solved by wave function $\psi_{l m}({\bf{r}})$ in terms of a set of Gaussian basis functions, $\phi_{n l m}^{\rm{G}}({\bf{r}})=\phi_{n l}^{{\rm{G}}}(r) Y_{l m}(\hat{{\bf{r}}})$. Furthermore, the functions can be expressed as follows:

The constant $N_{n l}$ is normalization constant, which can be determined by $\langle\phi_{n l m}^{{\rm{G}}} \mid \phi_{n l m}^{{\rm{G}}}\rangle=1$. Hence, set $\left\{\phi_{n l m}^{{\rm{G}}}; n=1-n_{\max }\right\}$ is a non-orthogonal set.

C Coupled channel framework

• I. INTRODUCTION
• II. THEORETICAL FORMALISM
•      A Quenched quark model
•      B Gaussian expansion method
•      C Coupled channel framework
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

The quenched quark potential model only includes the interaction between heavy quark pair. However, the hadronic loop interaction can also play a role via the generation of the light quark pair in $b\bar{c}\to (b\bar{q})(q\bar{c})$. Furthermore, the hadronic loop interaction becomes more important for the higher excited beauty-charm mesons. The coupled channel framework provides a good description for the hadronic loop interactions.

In this framework, the beauty-charm meson state can be expressed as:

where $c_0$ denotes the $b\bar{c}$ bare state probability amplitude, while $c_{BD}(p)$ denotes the beauty meson B and charm meson D molecular component probability amplitude with relative momentum p. To normalize the state, we impose the condition $|c_0|^2+\sum_{BD} \int {\rm d}^3p\, |c_{BD}(p)|^2=1$.

The total Hamiltonian in coupled channel framework can be expressed as:

where $H_{BD}$ denotes the Hamiltonian for beauty meson B and charm meson D system as:

$H_I$ leads to coupling between $b\bar{c}$ bare state and BD molecule component. In the following, the $^3P_0$ model, where the generated light quark pairs have identical quantum numbers $J^{PC} = 0^{++}$ in vacuum, is employed to analyze the mixing of $b\bar{c}$ bare state and BD molecule component [64−66].

Then, we solve the spectrum eigen equation as follows:

where $M$ denotes the final mass for the beauty-charm mesons in coupled channel framework. Practically, the eigenvalue $M$ can be rewritten as [29, 30, 32, 34]:

where $M_Q$ denotes the eigenvalue for the quenched Hamiltonian $H_Q$, while $\Delta M$ denotes the mass shift from the coupled channel effect. Operator ${T^{\text †} }$ in $^3P_0$ model can be expressed as [29, 32, 34]:

where operators $b_1^{{\text †}}(\vec{p}_1)$ and $d_2^{{\text †}}(\vec{p}_2)$ create a light quark pair. The light quark pair creation strength is denoted as $\gamma_0^{\rm eff}=\dfrac{m_u}{m_i}\gamma_0$ with $\gamma_0=0.4$ and $i=u, d, s$ [7]. The color, flavor, and spin wave functions for the light quark pair are $C_{34}$, $F_{34}$, and $\chi_{34}$, respectively. Furthermore, $r_q$ denotes a width parameter of Gaussian factor, whose value is determined by analyzing meson decays. The Gaussian factor reflects the effective scale of quark pairs via smearing. This parameter is an improvement of $^3P_0$ model. It is physically motivated and necessary to obtain a finite result when one sums over a complete set of virtual decay channels [67]. The value of $r_q$ is in the range of $0.25$ to $0.35$ fm [67−70]. We use the value $r_q = 0.3$ fm in the following calculation.

To weigh the importance of coupled channel effects, it is useful to investigate the probabilities of $b\bar{c}$ bare component and BD molecule component in the physical state. The probability of quenched $b\bar{c}$ bare component can be expressed as:

Then, the probability of BD molecule component can be naturally expressed as $P_{{\rm{molecule}}}=\sum_{BD}P_{BD}= 1- P_{b\bar{c}}$. Given that bare state mass is above the BD threshold, it is not possible to normalize the wave functions. Hence, we cannot estimate the proportion of the channel.

For highly excited beauty-charm mesons above the BD threshold, they undergo direct two-body decay into a beauty meson and charm meson. The strong decay width is related to the imaginary part in $\Delta M$ and can be expressed as:

III. RESULTS AND DISCUSSIONS

• I. INTRODUCTION
• II. THEORETICAL FORMALISM
•      A Quenched quark model
•      B Gaussian expansion method
•      C Coupled channel framework
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

Given that only$B_c$ mesons have experimental information, it is difficult to fit all parameters. Hence, we adopt a strategy similar to that in Ref. [7]. Although there are no experimental data for $B^*_c(1^3S_1)$ and $B^*_c(2^3S_1)$ masses, their values can be estimated as approximately $6334$ and $6900$ MeV, respectively. Furthermore, given that the hyperfine mass splitting in bottomonium family is measured as $\Delta M_{b\bar{b}(1S)}=62.3\pm 3.2$ MeV and $\Delta M_{b\bar{b}(2S)}=24\pm4$ MeV [1], the hyperfine mass splitting in beauty-charm meson family is considered as small as $m_{B_c^*}-m_{B_c}\geq \Delta M_{b\bar{b}(1S)}=62.3\pm 3.2$ MeV and $m_{B_c^*(2S)}-m_{B_c(2S)}\geq \Delta M_{b\bar{b}(2S)}= 24\pm4$ MeV because the hyperfine mass splitting is inversely proportional to the heavy quark mass. Based on experimental results and theoretical discussions, we have four data points $B_c(1^1S_0)$, $B_c^*(1^3S_1)$, $B_c(2^1S_0)$, and $B_c^*(2^3S_1)$ with masses 6274, 6334, 6871, and 6900 MeV, respectively. We use these values to fit the model parameters $\alpha_s$, $b$, $\sigma$. For the other parameters in the model, we use commonly used values, which can describe other mesons well [7, 47, 49]. It should be noted that we do not fit all parameters in the model due to the lack of sufficient experimental data for fitting. The final refitted parameters are listed in Table 1.

Table 1

Table 1.  Parameters refitted in this study.

Parameter	This work
$m_n$	$0.45$ GeV
$m_s$	$0.55$ GeV
$m_c$	$1.43$ GeV
$m_b$	$4.5$ GeV
$\alpha_s$	$0.51851$
b	$0.16178$ GeV2
σ	$1.3424$ GeV
$C_{b\bar{c}}$	$0.454$ GeV
$\gamma_0$	$0.4$

DownLoad: CSV

Show Table

With the parameters in Table 1, the mass spectrum and mass shifts of the $B_c$ mesons can be estimated. The results are shown in Fig. 1, with numbers listed in Table 2 and Table 3. The mixing angles of $1P$, $2P$, $1D$, and $2D$ states can be also calculated, which are $-35.0^\circ$, $-36.3^\circ$, $-42.8^\circ$ and $-43.9^\circ$, respectively. The mixing angles are close to $B$ mesons $\theta_{1P}=-34.6^\circ$, $\theta_{2P}=-36.1^\circ$, $\theta_{1D}= -39.6^\circ$, $\theta_{2D}=-39.7^\circ$ and $B_s$ mesons $\theta_{1P}= -34.9^\circ$, $\theta_{2P}=-36.1^\circ$, $\theta_{1D}=-39.8^\circ$, and $\theta_{2D}=-39.8^\circ$ [48].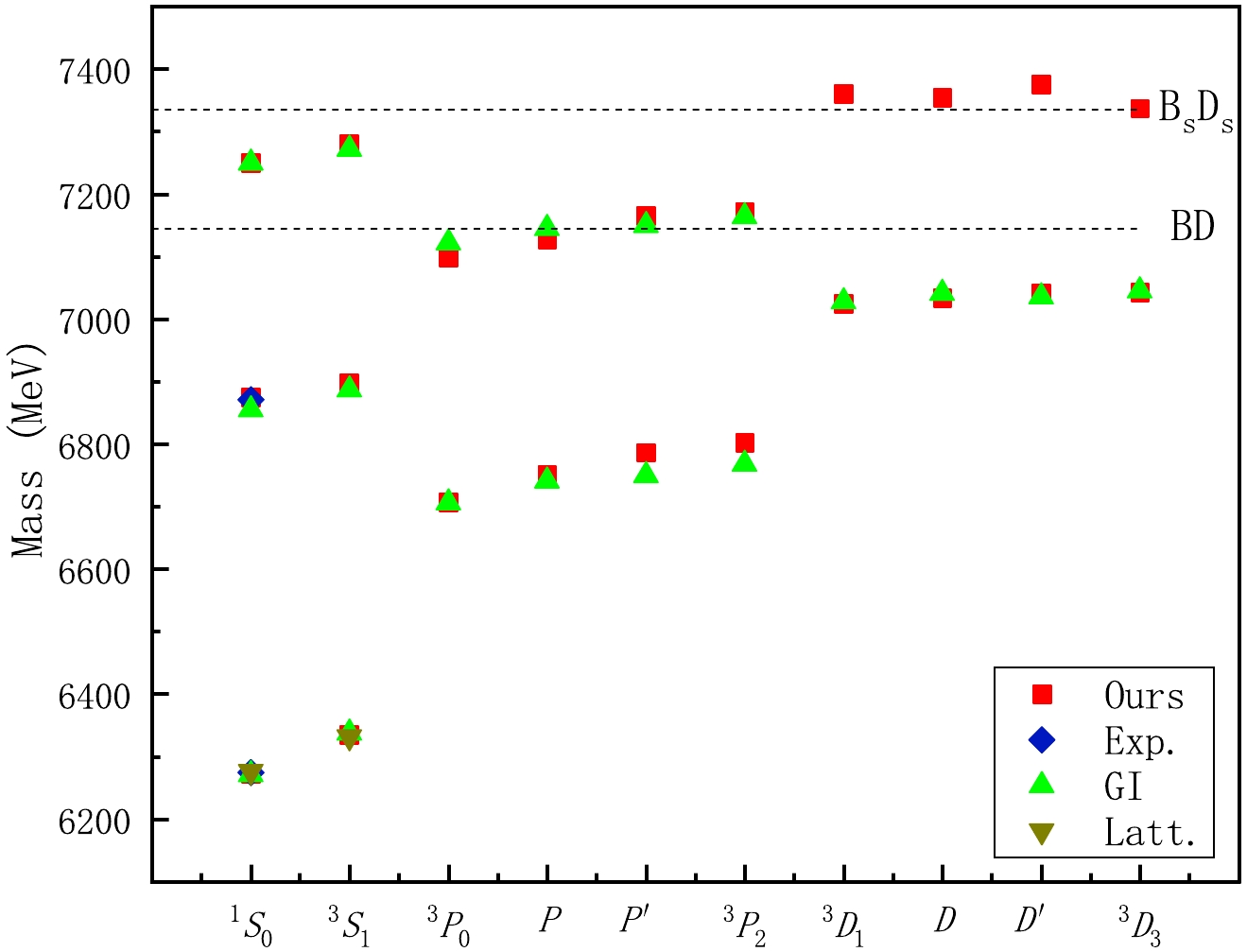

Figure 1

Figure 1.  (color online) Beauty-charm meson family spectrum. "Exp." denotes the current experimental values from the latest PDG [1] and our quenched quark model results are depicted as "Ours". The unquenched quark model results from Ref. [14] are shown as "GI". The Lattice results from Ref. [63] are shown as "Latt.". The dashed lines denote the threshold positions of BD and $B_sD_s$, respectively.

DownLoad: Full-Size Img PowerPoint

Table 2

Table 2.  Beauty charm meson family spectrum (in MeV). The third column denotes the naive mass in quenched quark model; the fourth column denotes the mass shift from coupled channel effects; the fifth column denotes the final results for the beauty charm meson family spectrum; the last column is the latest experimental data [1]. For comparison, other theoretical predictions from quenched quark models are also listed. The mixing angles of $1P$, $2P$, $1D$, and $2D$ are detemined as $-35.0^\circ$, $-36.3^\circ$, $-42.8^\circ$ and $-43.9^\circ$, respectively.

$n^{2S+1}L_J$	State	$M_0$	$\Delta M$	$M$	EPI [57]	EMK [58]	MAS [59]	RR [60]	QL [7]	GI [61]	XJL [12]	DE [62]	APM [10]	RPP [1]
$1^1S_0$	$B_c^+$	$6337$	$-65$	$6272$	6274	6277	6277	6277	6271	6271	6271	6270	6275	$6274.47\pm0.32$
$1^3S_1$	$-$	$6405$	$-70$	$6335$	$-$	$-$	$-$	$-$	6326	6338	6338	6332	6314	$6331\pm4\pm6$a
$2^1S_0$	$B_c(2S)^\pm$	$6989$	$-114$	$6874$	6845	7038	7383	6814	6871	6855	6855	6835	6838	$6871.2\pm1.0$
$2^3S_1$	$-$	$7013$	$-116$	$6897$	$-$	$-$	$-$	$-$	6890	6887	6886	6881	6850	$-$
$3^1S_0$	$-$	$7393$	$-141$	$7252$	7124	7798	7206	7351	7239	7250	7220	7193	$-$	$-$
$3^3S_1$	$-$	$7410$	$-129$	$7281$	$-$	$-$	$-$	$-$	7252	7272	7240	7235	$-$	$-$
$1^3P_0$	$-$	$6803$	$-98$	$6706$	6519	7799	7042	6340	6714	6706	6701	6699	6672	$-$
$1P$	$-$	$6852$	$-102$	$6750$	$-$	$-$	$-$	$-$	6757	6741	6745	6734	6766	$-$
$1P^\prime$	$-$	$6887$	$-102$	$6785$	$-$	$-$	$-$	$-$	6776	6750	6754	6749	6828	$-$
$1^3P_2$	$-$	$6906$	$-104$	$6802$	$-$	$-$	$-$	$-$	6787	6768	6773	6762	6776	$-$
$2^3P_0$	$-$	$7226$	$-127$	$7099$	6959	$-$	6663	6851	7107	7122	7097	7091	6914	$-$
$2P$	$-$	$7264$	$-136$	$7128$	$-$	$-$	$-$	$-$	7134	7145	7125	7126	7259	$-$
$2P^\prime$	$-$	$7300$	$-135$	$7165$	$-$	$-$	$-$	$-$	7150	7150	7133	7145	7322	$-$
$2^3P_2$	$-$	$7316$	$-144$	$7172$	$-$	$-$	$-$	$-$	7160	7164	7148	7156	7232	$-$
$1^3D_1$	$-$	$7147$	$-124$	$7023$	6813	$-$	$-$	$-$	7020	7041	7023	7072	7078	$-$
$1D$	$-$	$7154$	$-121$	$7033$	$-$	$-$	$-$	$-$	7024	7028	7032	7077	7009	$-$
$1D^\prime$	$-$	$7163$	$-122$	$7041$	$-$	$-$	$-$	$-$	7032	7036	7039	7079	7154	$-$
$1^3D_3$	$-$	$7163$	$-120$	$7043$	$-$	$-$	$-$	$-$	7030	7045	7042	7081	6980	$-$
$2^3D_1$	$-$	$7496$	$-136$	$7360$	$-$	$-$	$-$	$-$	7336	$-$	7327	$-$	$-$	$-$
$2D$	$-$	$7505$	$-150$	$7355$	$-$	$-$	$-$	$-$	7343	$-$	7335	$-$	$-$	$-$
$2D^\prime$	$-$	$7509$	$-130$	$7380$	$-$	$-$	$-$	$-$	7347	$-$	7340	$-$	$-$	$-$
$2^3D_3$	$-$	$7514$	$-175$	$7338$	$-$	$-$	$-$	$-$	7348	$-$	7344	$-$	$-$	$-$
aThis result is from Lattice QCD simulation [63]. Combing LHCb data and Lattice QCD result, the mass of $B_c^*(2^3S_1)$ is determined as $6897\pm 12$ MeV.

DownLoad: CSV

Show Table

The spectra of $B_c$ mesons have been examined in many studies [7, 10, 12, 57−62, 71]. We listed their results in Table 2. It can be observed that different theoretical models predict the mass of $B_c^+(1^1S_0)$ in accordance with experimental results. For state $B_c(2S)^{\pm}$, the predicted mass corresponds to 6845 MeV via exact quantization rule approach [57], 6814 MeV via asymptotic iteration method [60], 6871 MeV via nonrelativistic quark model [7], and 6855 MeV via relativistic quark model [61]. These values are consistent with experimental data value of $6871.2\pm1.0$ MeV. However, the given mass values of 7038 MeV via analytical exact iteration method [58], 7383 MeV via non-relativistic quark model using Nikiforov-Uvarov method [59], and 6814 MeV via asymptotic iteration method [60] deviate significantly from the experimental results. These theoretical studies have enriched our understanding of the properties of $B_c$ mesons. However, due to the limited experimental information on $B_c$ mesons, there are still significant differences in the theoretical research results. Further experimental data is required to enhance and optimize theoretical understanding.

We predicted that the masses of $B_c(1^1S_0)$ and $B_c(2^1S_0)$ are 6272 and 6874 MeV, respectively, which are close to the experimental values of $6274.47\pm0.32$ MeV and $6871.2\pm1.0$ MeV. Furthermore, we show the theoretical results of the other states in beauty-charm meson family. We expect that more experimental information can be found to support our results.

For states below BD threshold, the probabilities of each coupled channel can be estimated. The probabilities are listed in Table 4. Hence, all the states have coupled channel components. Specifically, when comparing $1S$, $2S$, $1P$, and the $1D$ states, the $2P$ states have larger non-$b\bar c$ components. For $1S$-wave states, we predicted they have 96% $b\bar c$ components. This implies that the coupled channel components is just 4%. For other states, we predicted $b\bar c$ component probabilities for $2S$, $1P$, $2P$, and $1D$ states, which are approximately 86%, 90%, 67%, and 84%, respectively.

Table 4

Table 4.  Two quark and molecule probabilities (in %) in the coupled channels framework.

State	BD	$BD^*$	$B^*D$	$B^*D^*$	$B_sD_s$	$B_sD_s^*$	$B_s^*D_s$	$B_s^*D_s^*$	$P_{\rm molecule}$	$P_{b\bar c}$
$1^1S_0$	$0$	$0.7$	$0.8$	$1.4$	$0$	$0.2$	$0.2$	$0.4$	$3.7$	$96.3$
$1^3S_1$	$0.3$	$0.5$	$0.6$	$1.8$	$0.1$	$0.1$	$0.2$	$0.5$	$4.3$	$95.7$
$2^1S_0$	$0$	$2.8$	$3.9$	$5.1$	$0$	$0.5$	$0.7$	$1.1$	$14.0$	$86.0$
$2^3S_1$	$1.6$	$1.9$	$2.7$	$6.2$	$0.2$	$0.4$	$0.5$	$1.3$	$14.8$	$85.2$
$1^3P_0$	$1.8$	$0$	$0$	$5.1$	$0.4$	$0$	$0$	$1.3$	$8.6$	$91.4$
$1^1P_1$	$0$	$1.8$	$2.4$	$3.5$	$0$	$0.4$	$0.5$	$0.9$	$9.6$	$90.4$
$1^3P_1$	$0$	$1.6$	$2.1$	$4.0$	$0$	$0.4$	$0.4$	$1.0$	$9.5$	$90.5$
$1^3P_2$	$1.2$	$1.3$	$1.7$	$4.1$	$0.3$	$0.3$	$0.4$	$1.0$	$10.2$	$89.8$
$2^3P_0$	$22.5$	$0$	$0$	$9.0$	$0.7$	$0$	$0$	$1.4$	$33.7$	$66.3$
$2^1P_1$	$0$	$5.3$	$16.7$	$8.4$	$0$	$0.6$	$0.8$	$1.1$	$32.9$	$67.1$
$2^3P_1$	$0$	$5.3$	$18.3$	$7.5$	$0$	$0.5$	$0.7$	$1.1$	$33.4$	$66.6$
$1^3D_1$	$4.3$	$0.9$	$1.5$	$8.0$	$0.4$	$0.1$	$0.2$	$1.7$	$17.1$	$82.9$
$1^1D_2$	$0$	$3.2$	$4.7$	$5.8$	$0$	$0.6$	$0.7$	$1.1$	$16.2$	$83.8$
$1^3D_2$	$0$	$3.1$	$4.8$	$6.1$	$0$	$0.5$	$0.7$	$1.2$	$16.4$	$83.6$
$1^3D_3$	$2.2$	$2.0$	$2.6$	$6.6$	$0.4$	$0.4$	$0.5$	$1.2$	$15.9$	$84.1$

DownLoad: CSV

Show Table

Table 3

Table 3.  Mass shift $\Delta M$ (in MeV) for beauty charm mesons from different channels.

State	BD	$BD^*$	$B^*D$	$B^*D^*$	$B_sD_s$	$B_sD_s^*$	$B_s^*D_s$	$B_s^*D_s^*$	Total
$1^1S_0$	$0$	$-13$	$-11$	$-25$	$0$	$-4$	$-4$	$-9$	$-65$
$1^3S_1$	$-4$	$-9$	$-8$	$-31$	$-1$	$-3$	$-3$	$-11$	$-70$
$2^1S_0$	$0$	$-23$	$-23$	$-44$	$0$	$-6$	$-6$	$-12$	$-114$
$2^3S_1$	$-8$	$-15$	$-16$	$-52$	$-2$	$-4$	$-4$	$-14$	$-116$
$3^1S_0$	$0$	$-36$	$-23$	$-60$	$0$	$-6$	$-6$	$-11$	$-142$
$3^3S_1$	$3$	$-32$	$1$	$-79$	$-2$	$-4$	$-4$	$-13$	$-130$
$1^3P_0$	$-12$	$0$	$0$	$-63$	$-3$	$0$	$0$	$-20$	$-98$
$1P$	$0$	$-20$	$-19$	$-39$	$0$	$-6$	$-6$	$-12$	$-102$
$1P^\prime$	$0$	$-16$	$-15$	$-47$	$0$	$-5$	$-4$	$-15$	$-102$
$1^3P_2$	$-10$	$-15$	$-14$	$-42$	$-3$	$-5$	$-4$	$-13$	$-104$
$2^3P_0$	$-33$	$0$	$0$	$-72$	$-4$	$0$	$0$	$-18$	$-127$
$2P$	$0$	$-27$	$-34$	$-51$	$0$	$-6$	$-6$	$-12$	$-136$
$2P^\prime$	$0$	$-24$	$-33$	$-54$	$0$	$-5$	$-5$	$-13$	$-135$
$2^3P_2$	$-19$	$-18$	$-21$	$-61$	$-3$	$-4$	$-4$	$-13$	$-143$
$1^3D_1$	$-13$	$-5$	$-6$	$-75$	$-3$	$-1$	$-1$	$-21$	$-124$
$1D$	$0$	$-24$	$-25$	$-47$	$0$	$-6$	$-6$	$-13$	$-121$
$1D^\prime$	$0$	$-21$	$-22$	$-54$	$0$	$-5$	$-5$	$-15$	$-122$
$1^3D_3$	$-13$	$-18$	$-17$	$-47$	$-3$	$-5$	$-4$	$-12$	$-120$
$2^3D_1$	$-7$	$0$	$1$	$-104$	$-6$	$-1$	$-2$	$-17$	$-136$
$2D$	$0$	$-28$	$-17$	$-83$	$0$	$-6$	$-6$	$-11$	$-150$
$2D^\prime$	$0$	$-13$	$-12$	$-79$	$0$	$-5$	$-7$	$-12$	$-130$
$2^3D_3$	$-10$	$-23$	$-20$	$-102$	$-3$	$-4$	$-4$	$-11$	$-175$

DownLoad: CSV

Show Table

For states, which have large masses, the strong decay channels will be open, and strong decay widths are shown in Table 5. For $1S$-wave, $2S$-wave, and $1P$-wave, most of $2P$-wave and $1D$-wave states, their masses are below the BD threshold and cannot undergo strong decay into BD states. Hence, we just discuss the strong decay of the $B_c(2^3P_2)$, $3S$-wave, and $2D$-wave $B_c$ mesons. For $B_c(2^3P_2)$, it can just decay to BD final states with decay width of approximately 3 MeV. For $3S$-wave states, $B_c(3^1S_0)$ can strong decay to $B^*D$ with predicted width of 109 MeV, while the $B_c(3^3S_1)$ can strong decay to BD and $B^*D$ with predicted width 10 and 57 MeV, whose total decay width becomes 67 MeV. For the $2D$-wave states, the total decay widths of the $B_c(2^3D_1)$, $B_c(2D)$, $B_c(2D^\prime)$, and $2^3D_3$ states are $60$, $57$, $201$, and $76$ MeV, respectively. The $B_c(2^3D_1)$ dominantly decay into $BD^*$ and $B^*D^*$ with predicted widths of $28$ and $22$ MeV. The $B_c(2D)$ can mainly decay into $BD^*$ and $B^*D^*$ with predicted widths of $15$ and $37$ MeV. Furthermore, the $B_c(2D^\prime)$ can mainly decay into $BD^*$, $B^*D$, and $B^*D^*$ with predicted widths of $64$, $69$, and $68$ MeV. The mixing angle of the two states is $-43.9^\circ$. Furthermore, $B_c(2^3D_3)$ have three major decay channels of BD, $B^*D$, and $B^*D^*$ with a decay width of $27$, $30$ and $15$ MeV, respectively. These differences in decays will aid in distinguishing these excited beauty-charm meson states.

Table 5

Table 5.  Hadronic decay widths (in MeV) of the beauty-charm mesons.

State	BD	$BD^*$	$B^*D$	$B^*D^*$	$B_sD_s$	$B_sD_s^*$	$B_s^*D_s$	$B_s^*D_s^*$	Total
$3^1S_0$	$0$	$0$	$109$	$0$	$0$	$0$	$0$	$0$	$109$
$3^3S_1$	$10$	$0$	$57$	$0$	$0$	$0$	$0$	$0$	$67$
$2^3P_2$	$3$	$0$	$0$	$0$	$0$	$0$	$0$	$0$	$3$
$2^3D_1$	$2$	$28$	$1$	$22$	$7$	$0$	$0$	$0$	$60$
$2D$	$0$	$15$	$4$	$37$	$0$	$0$	$0$	$0$	$57$
$2D^\prime$	$0$	$64$	$69$	$68$	$0$	$0$	$0$	$0$	$201$
$2^3D_3$	$27$	$4$	$30$	$15$	$0$	$0$	$0$	$0$	$76$

DownLoad: CSV

Show Table

IV. SUMMARY

• I. INTRODUCTION
• II. THEORETICAL FORMALISM
•      A Quenched quark model
•      B Gaussian expansion method
•      C Coupled channel framework
• III. RESULTS AND DISCUSSIONS
• IV. SUMMARY

We calculated the mass spectrum and two-body hadronic decays for beauty-charm mesons based on the coupled channel framework. The coupled channel effects are calculated from $^3P_0$ model. The wave functions in our calculations are obtained by solving the Hamiltonian of the potential model with Gaussian Expansion Method.

Our results indicate that all beauty-charm states have coupled channel components, with each state having a different composition. In general, the coupled channel effects are smaller for bound states compared to excited states. Furthermore, $1S$ states are approximately 3% – 5%, while the $1P$ states are approximately 8% – 11%. The $1D$ states are approximately 15% – 18%, and the $2S$ states are approximately 14% – 15%. Four $2P$ states have larger couple channel components of approximately 32% – 34%. The mixing angles of $1P$, $2P$, $1D$, and $2D$ states are determined as $-35.0^\circ$, $-36.3^\circ$, $-42.8^\circ$ and $-43.9^\circ$, respectively.

For the strong decays of excited states above BD threshold, the $B_c(3^1S_0)$ state mainly strongly decays to $B^*D$ channel and the $B_c(3^3S_1)$ mainly strongly decays to BD and $B^*D$. Furthermore, the $B_c(2^3P_2)$ mainly decays to BD. Additionally, $B_c(3S)$ and $B_c^*(3S)$ can be also detected in $B_c(3S)\to B_c(1S/2S)+\pi^++\pi^-$ and $B^*_c(3S)\to B_c(1S/2S) + \pi^++\pi^-+\gamma$ processes practically. For four $D$-wave states, the $B_c(2D^\prime)$ dominantly decays to $BD^*$, $B^*D$, and $B^*D^*$ final states with a total width of 201 MeV. However, $B_c(2^3D_1)$, $B_c(2D)$, and $B_c(2^3D_3)$ states have smaller decay widths of approximately $57 - 76$ MeV. For the electromagnetic and weak decays of beauty-charm mesons, including polarization analysis, one can refer to Refs. [72−77].

Only a few beauty-charm meson states have been observed in current experiments. Theoretical studies will be valuable in uncovering their nature and advancing experimental discoveries at the LHC and the future Tera-Z factory at CEPC.

References