-
General relativity (GR), proposed by Albert Einstein in 1915, is a theory of gravity described by the nature of space-time. The standard theory of gravity GR has been successfully tested in both weak and strong field regimes. In particular, GR has been successfully tested by solar system observations [1] using the effect of the bending of light around massive objects and other astrophysical observations, which can be treated as a weak field regime test. Just after the proposal of GR, the existence of gravitational waves was suggested, and it took a century to detect them experimentally: in 2015, the LIGO-Virgo collaboration [2] detected gravitational waves due to the merging of two stellar black holes. This experiment and observation of the shadow of supermassive black holes M87* [3] and SgrA* [4] by Event Horizon Telescope collaboration can be treated as a test of GR in the strong field regime.
GR is a very efficient instrument for explaining cosmological phenomena, offering a unique framework for models of the universe's evolution. It gives insights into the Big Bang theory and preliminary models for explaining the current epoch of the Expanding Universe. Although it is a well tested and consistent theory, GR is not free from its limitations and disadvantages. A major limitation of GR is its inconsistency with quantum mechanics, which is another essential aspect of modern physics. While GR explains gravity on a cosmological scale, quantum mechanics describes the behavior of particles on a microscopic scale. Efforts to combine these two theories into a single framework, called quantum gravity, have encountered significant obstacles and continue to be an area of ongoing research.
Moreover, the mathematical intricacies of GR intensify under extreme conditions, like near a black hole's singularity or at the universe's inception. In such situations, the GR equations fail, suggesting that unknown physics, potentially dictated by an undiscovered theory (e.g., quantum gravity), might be influential. This complexity hinders our capacity to forecast outcomes accurately in these intense settings, highlighting the need for a more all-encompassing gravitational theory. On the way to constructing quantum gravity theory, one may start with consideration of modifications to GR or alternative theories of gravity.
It is also worth noting that gravitational lensing is an interesting consequence of GR and other metric theories of gravity. Gravitational lensing was used to perform first test of GR during a solar eclipse [1]. Being the consequence of light deflection due to the spacetime curvature near the gravitating object, gravitational lensing can be used to test both the source of gravity and distance to the light source (e.g., see Refs. [5–16], where gravitational lensing in different gravity models is explored). Additionally we refer the reader to Refs. [17–40] for studies related to weak and strong gravitational lensing around compact objects within different models in a plasma medium.
Another consequence of the light deflection and absorption by the BH may lead to the phenomenon observed as BH shadow. Research on the shadows of compact objects has become a pivotal direction within astrophysics, providing valuable perspectives on the intrinsic characteristics of these objects and the properties of spacetime [41–45]. As mentioned earlier, observations of the shadow of Sgr A* and M87 have opened a window to test GR as well as modified and alternative gravity theories [3, 4]. Studies related to analysis of the shadow of compact gravitating objects in different gravity models can be found in Refs. [46–81].
Here, we plan to test the quantum-improved charged BH solutions using the analysis of shadow of such objects. The authors of Ref. [82] investigated the quantum effect in spherically symmetric charged BHs and proposed a solution. It has been shown that the horizons are stable except in extremal case. It has also been shown that the existence of a new extremal condition at the Planck scale could give clues about the final stage of the BH evaporation. The properties of this solution were investigated in Refs. [32, 83–88]. Particularly in Ref. [83], the authors explored the geodesic equation for time-like and null-like particles near an improved Schwarzschild black hole. The main motivation of this study is to propose an alternative way of testing quantum improved gravity through testing the photon motion in the presence of plasma. The large number of alternative and modified theories of gravity creates an additional problem related to degeneracy [89, 90]. One way to resolve the degeneracy issue is to consider several independent experiments/observations.
The remainder of this paper is organized as follows: In Sec. II, we start with analysis of the shadow of quantum-improved charged BHs in the presence/absence of a plasma environment. We also explore the weak gravitational lensing effect in the cases of different configuration of plasma environment in Sec. III. The magnification of image source due to gravitational lensing around a quantum-improved charged BH is investigated in Sec. IV. We summarize and conclude our results in Sec. V. Throughout the paper, we use the spacetime signature in the form
$ (-,+,+,+) $ . -
One can write the metric of the quantum-improved charged BH as
$ {\rm d}s^2=-f(r){\rm d}t^2+\frac{{\rm d}r^2}{f(r)}+r^2({\rm d}\theta^2+\sin{\theta}{\rm d}\phi^2), $

(1) where the lapse function is [82, 91]
$ f(r)=1-\frac{2G(r)M}{r}+\frac{G(r)Q^2}{r^2}, $

(2) where
$ M $ and$ Q $ are the BH's mass and electric charge, respectively. The running gravitational constant can be written in the limit of long distances related to the Planck length$ r\gg l_{\rm p}=\sqrt{\dfrac{\hbar G_0}{c^3}} $ as [82, 91]$ G(r)=\frac{G_0 r^2}{r^2+\Omega G_0}, $

(3) where
$ G_0 $ is Newton’s gravitational constant, and$ \Omega $ is a parameter arising from the non-perturbative renormalization group that measures the quantum effects. In fact, by taking$ \Omega \rightarrow 0 $ , the line element recovers the RN solution. Throughout this paper, we use the system of units$ G_0=c=1 $ . -
Now, to study photon motion around BH we explore the Hamilton-Jacobi equation. Thus, we can write the Hamiltonian of a photon around a BH surrounded by a plasma as [92]
$ \mathcal H(x^\alpha, p_\alpha)=\frac{1}{2}\left[ g^{\alpha \beta} p_\alpha p_\beta - (n^2-1)( p_\beta u^\beta )^2 \right] , $

(4) where
$ x^\alpha $ are the spacetime coordinates, and$ u^\beta $ and$ p_\alpha $ are the four-velocity and four-momentum of the photon, respectively. In Eq. (4),$ n $ represents the refractive index ($ n=\omega/k $ , where$ k $ is the wave number). The refractive index for plasma can be written as [93]$ n^2=1- \frac{\omega_{\rm p}^2}{\omega^2}\ , $

(5) with plasma frequency
$\omega^2_{\rm p}(x^\alpha)=4 \pi e^2 N(x^\alpha)/m_e$ ($ m_e $ and$ e $ are the electron mass and charge, respectively, whereas$ N $ is the number density of the electrons). Recall that a dynamic aspect of the plasma’s tendency towards neutralization shows as plasma oscillation. Plasma oscillations leads to one of the main characteristics referred to as plasma frequency. Plasma oscillations are the result of plasma trying to maintain charge neutrality. When one cosiders the collisions of ions in plasma, it may lead to Debye shielding, which is related to the plasma temperature. Astrophysical measurements of plasma temperature may give information about the plasma parameters, and consequently, one may extract information about plasma frequency (for more details, see Refs. [92, 94, 95]). One can define the frequency of the photon$ \omega $ using$\omega^2= ( p_\beta u^\beta )^2$ as$ \omega(r)=\frac{\omega_0}{\sqrt{f(r)}}\ ,\quad \omega_0=\text{const}\ . $

(6) The metric function is such that
$ f(r) \to 1 $ as$ r \to \infty $ and$ \omega(\infty)=\omega_0=-p_t, $ which shows the energy of the photon at spatial infinity [96]. Besides, the plasma frequency can be sufficiently small than the photon frequency$ \omega_{\text{p}}^2\ll \omega^2 $ , which allows the BH shadow to be differentiated from the vacuum case of$ \omega_{\text{p}}=0 $ . Now, we can write the Hamiltonian for the light rays in a plasma medium as [18, 92]$ \mathcal{H}=\frac{1}{2}\Big[g^{\alpha\beta}p_{\alpha}p_{\beta}+\omega^2_{\text{p}}]\ . $

(7) One can find the components of the four-velocity for the photons in the equatorial plane
$ (\theta=\pi/2,\; p_\theta=0) $ in the following form:$ \dot t\equiv\frac{{\rm d}t}{{\rm d}\lambda}= \frac{ {-p_t}}{f(r)} , $

(8) $ \dot r\equiv\frac{{\rm d}r}{{\rm d}\lambda}=p_r f(r) , $

(9) $ \dot\phi\equiv\frac{{\rm d} \phi}{{\rm d}\lambda}= \frac{p_{\phi}}{r^2}, $

(10) where we have used the relationship
$ \dot x^\alpha=\partial \mathcal{H}/\partial p_\alpha $ . Using Eqs. (9) and (10), the expression for the phase trajectory of light (or photon) can be obtained as$ \frac{{\rm d}r}{{\rm d}\phi}=\frac{g^{rr}p_r}{g^{\phi\phi}p_{\phi}}. $

(11) Using the constraint
$ \mathcal H=0 $ , we can rewrite the above expression as [96]$ \frac{{\rm d}r}{{\rm d}\phi}=\sqrt{\frac{g^{rr}}{g^{\phi\phi}}}\sqrt{\gamma^2(r)\frac{\omega^2_0}{p_\phi^2}-1}, $

(12) where
$ \gamma^2(r)\equiv-\frac{g^{tt}}{g^{\phi\phi}}-\frac{\omega^2_p}{g^{\phi\phi}\omega^2_0}\ . $

(13) The circular radius of light
$ r_{\text{ph}} $ can be determined as the solution of the following equation [96]:$ \frac{{\rm d}(\gamma^2(r))}{{\rm d}r}\bigg|_{r=r_{\text{ph}}}=0\ . $

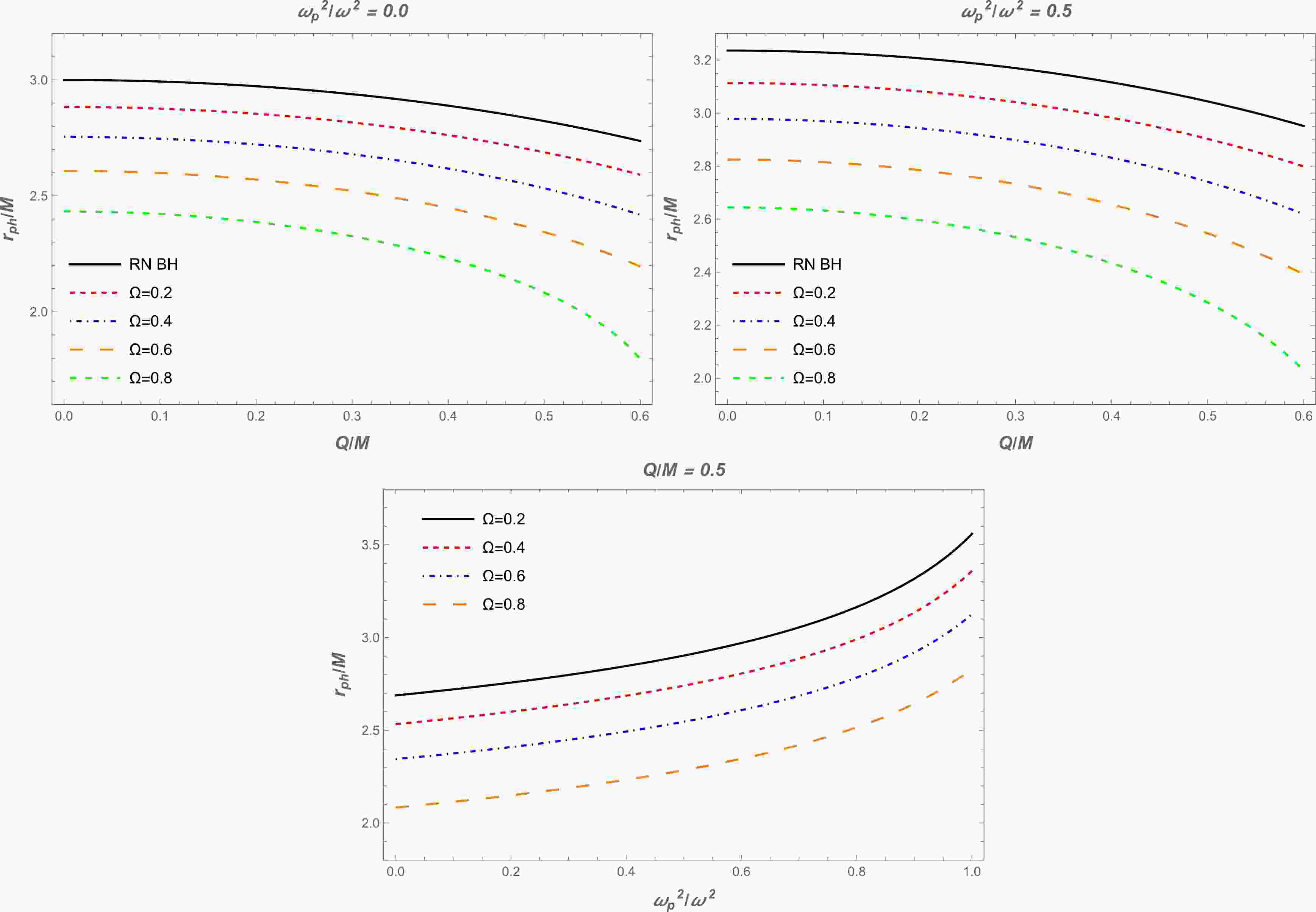
(14) We have solved Eq. (14) numerically instead of analytically. The results are demonstrated graphically in Fig. 1. It can be seen from this figure that the radius of the photon sphere decreased with increasing BH charge and parameter
$ \Omega $ . Also, there is a slight decrease with an increase in plasma frequency. It can also be seen that the plasma slightly increases the value of the photon sphere radius compared to the vacuum case.
Figure 1. (color online) Top panel: Radius of the photon sphere as a function of BH charge
$ Q $ for different values of parameter$ \Omega $ . The plasma frequencies are$ \omega^2_{\rm p}/\omega^2=0.0 $ (vacuum case) and$ \omega^2_{\rm p}/\omega^2=0.5 $ for the left and right plots, respectively. Bottom panel: Dependence of the radius of the photon sphere on the plasma frequency for different values of parameter$ \Omega $ . BH charge is$ Q/M=0.5 $ . -
Now we consider the radius of the shadow of the quantum-improved charged BH in the presence of plasma. The angular radius
$ \alpha_{\rm sh} $ of the BH can be defined as [96, 97]$ \begin{aligned}[b] \sin^2 \alpha_{\text{sh}}=\;&\frac{\gamma^2(r_{\text{ph}})}{\gamma^2(r_{\text{o}})}, \\=\;&\frac{r_{\text{ph}}^2\left[\dfrac{1}{f(r_{\text{ph}})}-\dfrac{\omega^2_{\rm p}(r_{\text{ph}})}{\omega^2_0}\right]}{r_{\text{o}}^2\left[\dfrac{1}{f(r_{\text{o}})}-\dfrac{\omega^2_{\rm p}(r_{\text{o}})}{\omega^2_0}\right]}, \end{aligned} $

(15) where
$ r_{\text{ph}} $ and$ r_{\text{o}} $ represent the locations of the photon sphere and observer, respectively. From Eq. (13), we can easily find$\gamma^2(r_{\rm ph})$ and$ \gamma^2(r_{\rm o}) $ . If the observer is located at a sufficiently large distance from the BH, then the radius of the BH shadow can be approximated using Eq. (15) as follows [96]:$ \begin{aligned}[b] R_{\text{sh}}\simeq\;& r_{\text{o}} \sin \alpha_{\text{sh}},\\ =\;&\sqrt{r_{\text{ph}}^2\bigg[\frac{1}{f(r_{\text{ph}})}-\frac{\omega^2_p(r_{\text{ph}})}{\omega^2_0}\bigg]}, \end{aligned} $

(16) where we have used the fact that
$ \gamma(r)\to r $ , which follows from Eq. (13), at spatial infinity for both models of plasma along with a constant magnetic field. The top panel of Fig. 2 shows the dependence of the radius of the BH shadow on the charge of BH for different values of parameter$ \Omega $ . From this panel, we can compare the cases of BH in vacuum and in plasma. Also, the radius of the BH shadow is depicted for different values of$ \Omega $ in the bottom panel of Fig. 2 for a homogeneous plasma with fixed BH charge. The radius of the BH shadow decreases under the influence of$ \Omega $ . In the top panel, the solid line corresponds to the Reissner-Nordström BH case. It can be seen from this figure that the size of the BH shadow radius decreases by increasing the plasma frequency. Accordingly, the BH shadow in the presence of a plasma medium would shrink further, as expected. Now, we consider the assumption that the compact objects Sgr A* and M87* are static, spherically symmetric objects, even though the observation obtained by the EHT collaboration does not support this assumption. However, we try to theoretically investigate the lower limits of the BH charge$ Q $ in the quantum-improved charged BH spacetime using the data provided by the EHT collaboration project. For constraints, we chose the BH charge$ Q $ and plasma frequency. One can use the observational data provided by the EHT collaboration regarding the shadows of the supermassive BHs Sgr A* and M87* to constrain these two quantities$ Q $ and$ \omega^2_{\rm p}/\omega^2 $ . The angular diameter$\theta_{\rm M87*}$ of the BH shadow, distance from Earth, and mass of the BH at the center of M87* are$\theta_{\rm M87*}=42 \pm 3 \,\; {{\rm \mu} {\rm as}}$ ,$D= 16.8 \pm 0.8\;\; {\rm M pc}$ , and$M_{\rm M87*} = 6.5 \pm 0.7 \times 10^9 M_{\odot}$ [3], respectively. For Sgr A*, the data provided by the EHT collaboration are$\theta_{\rm Sgr A*}=48.7 \pm 7 \;{\rm \mu {\rm as}} ,$ $D=8277 \pm 9 \pm 33 pc$ , and$M_{\rm Sgr A*} = 4.297 \pm 0.013 \times 10^6 M_{\odot}$ (VLTI) [4]. From this information, we can calculate the diameter of the shadow caused by the compact object per unit mass as follows: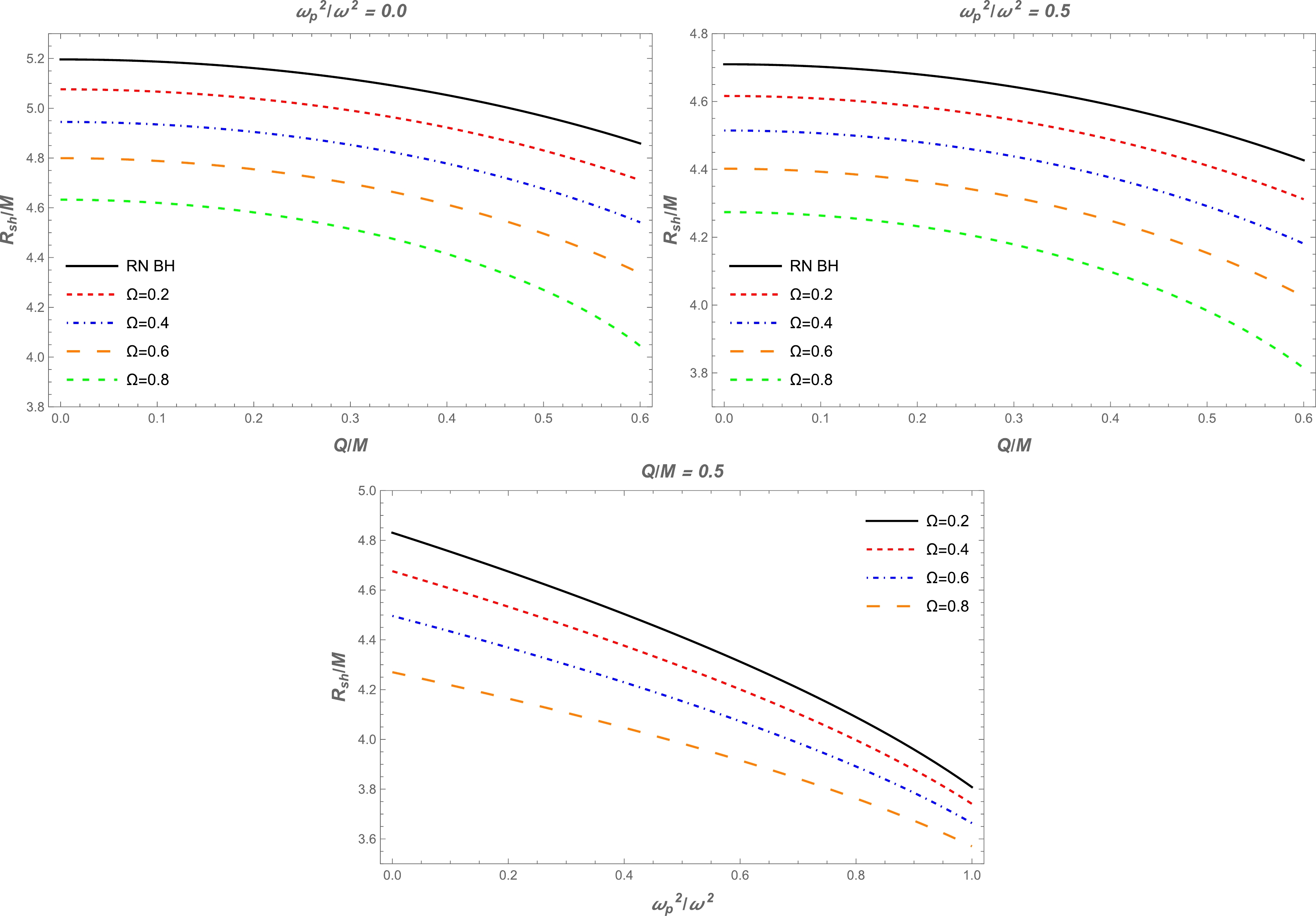
Figure 2. (color online) Top panel: Radius of the BH shadow as a function of BH charge
$ Q $ for different values of parameter$ \Omega $ . The plasma frequencies are$ \omega^2_{\rm p}/\omega^2=0.0 $ (vacuum case) and$ \omega^2_{\rm p}/\omega^2=0.5 $ for the left and right plots, respectively. Bottom panel: Fependence of the radius of the BH shadow from the plasma frequency for different values of parameter$ \Omega $ . The charge of the BH is$ Q/M=0.5 $ .$ d_{\rm sh}=\frac{D\theta}{M}\ . $

(17) From the expression
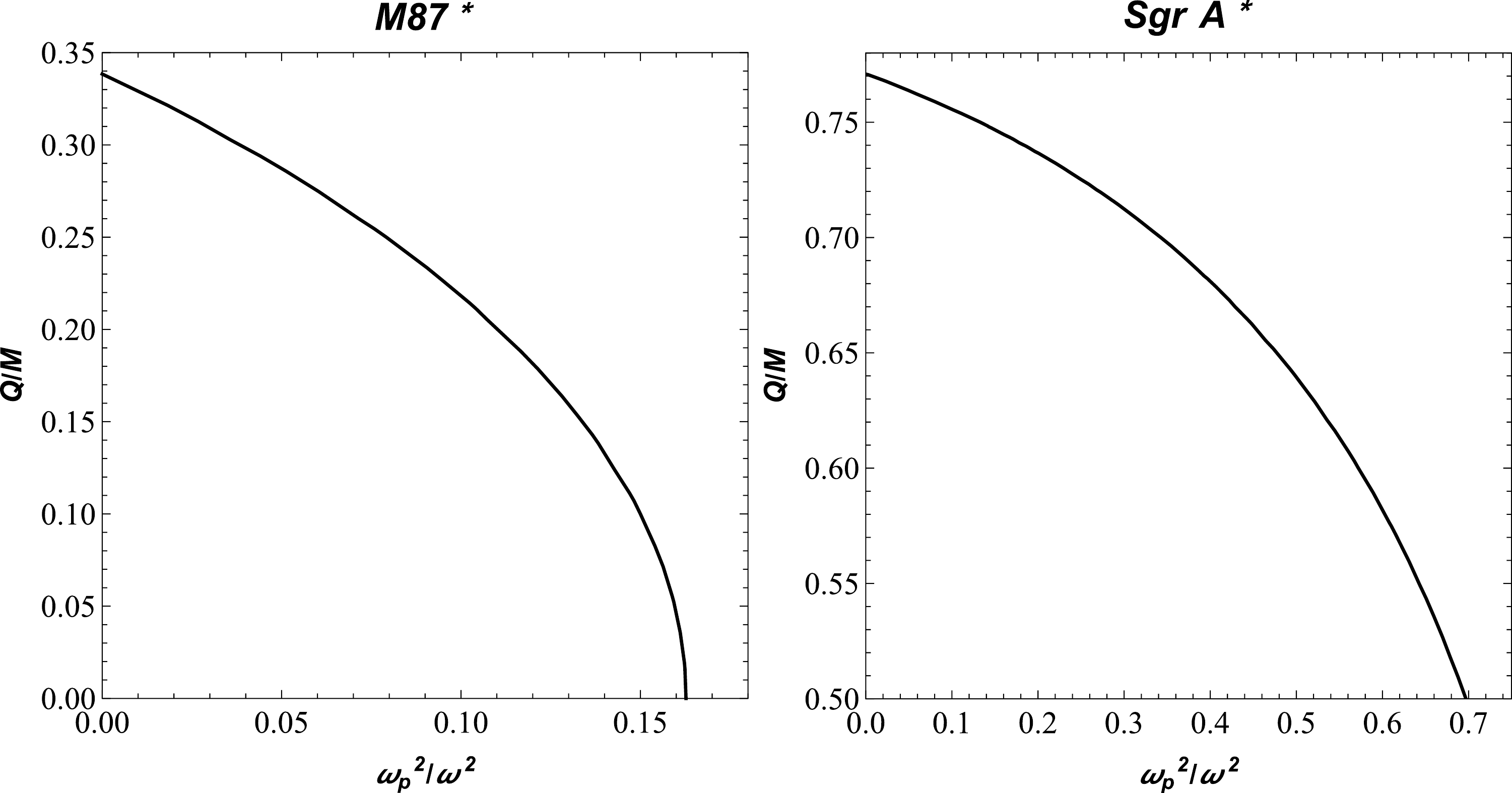
$d_{\rm sh}=2R_{\rm sh}$ , we can easily get the expression for the diameter of the BH shadow. Thus, the diameter of the BH shadow$d^{\rm M87*}_{\rm sh}=(11 \pm 1.5)M$ for M87* and$d^{\rm Sgr*}_{\rm sh}=(9.5 \pm 1.4)M$ for Sgr A*. From observational EHT data, we can find the lower limits on the quantities$ Q $ and$ \omega^2_{\rm p}/\omega^2 $ for the supermassive BHs at the centers of the galaxies Sgr A* and M87*. This is demonstrated numerically in Fig. 3. -
Here, we investigate the gravitational weak lensing around the quantum-improved charged BH. One can expand the metric (1) in the weak-field approximation as follows [17, 23]:
$ g_{\alpha \beta}=\eta_{\alpha \beta}+h_{\alpha \beta}\ , $

(18) where
$ \eta_{\alpha \beta} $ and$ h_{\alpha \beta} $ are the expressions for flat spacetime and perturbation due to gravity, respectively. The above expressions require the following properties:$ \begin{aligned}[b] & \eta_{\alpha \beta}= {\rm diag}(-1,~1,~1,~1)\ , \\ & h_{\alpha \beta} \ll 1, \quad h_{\alpha \beta} \rightarrow 0 \quad {\rm under} \quad x^{\alpha}\rightarrow \infty \ ,\\ & g^{\alpha \beta}=\eta^{\alpha \beta}-h^{\alpha \beta}, \quad h^{\alpha \beta}=h_{\alpha \beta}. \end{aligned} $

(19) Now, we will study the effect of plasma on the angle of deflection
$ \alpha_k $ in the gravitational field of the quantum-improved charged BH. In this work, we consider two types of plasma,$\omega_{\rm p}$ and$ \omega_c $ represent the frequencies for uniform and non-uniform plasma, respectively. The expression for the deflection angle around the BH can be written as [17]$ \hat{\alpha }_{\text{b}}=\frac{1}{2}\int_{-\infty}^{\infty}\frac{b}{r}\left(\frac{{\rm d}h_{33}}{{\rm d}r}+\frac{1}{1-\omega^2_{\rm p}/ \omega^2}\frac{{\rm d}h_{00}}{{\rm d}r}-\frac{K_e}{\omega^2-\omega^2_{\rm p}}\frac{{\rm d}N}{{\rm d}r} \right){\rm d}z\ , $

(20) where
$ \omega $ represents the frequency of a photon. We can write the line element (1) as follows:$ \begin{aligned}[b] {\rm d}s^2 \approx {\rm d}s^2_0+\left(\frac{2 M r}{r^2+\Omega }-\frac{Q^2}{r^2+\Omega }\right){\rm d}t^2 + \left(\frac{2 M r}{r^2+\Omega }-\frac{Q^2}{r^2+\Omega }\right){\rm d}r^2\ ,\end{aligned} $

(21) with
${\rm d}s^2_0=-{\rm d}t^2+{\rm d}r^2+(r^2+a^2)({\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2)$ . Now, one can easily find the components of$ h_{\alpha \beta} $ of metric tensor perturbations in Cartesian coordinates as$ h_{00}=\frac{2 M r}{r^2+\Omega }-\frac{Q^2}{r^2+\Omega }, $

(22) $ h_{ik}=\left(\frac{2 M r}{r^2+\Omega }-\frac{Q^2}{r^2+\Omega }\right)n_i n_k, $

(23) $ h_{33}=\left(\frac{2 M r}{r^2+\Omega }-\frac{Q^2}{r^2+\Omega }\right) \cos^2\chi \ , $

(24) with
$ \cos^2\chi=z^2/(b^2+z^2) $ and$ r^2=b^2+z^2 $ . Then, one may calculate the derivatives of$ h_{00} $ and$ h_{33} $ as$ \frac{{\rm d}h_{00}}{{\rm d}r}=-\frac{2 M r^2}{\left(r^2+\Omega \right)^2}+\frac{2 M \Omega }{\left(r^2+\Omega \right)^2}+\frac{2 Q^2 r}{\left(r^2+\Omega \right)^2}\ , $

(25) $ \begin{aligned}[b] \frac{{\rm d}h_{33}}{{\rm d}r}=\;&-\frac{6 M z^2}{\left(r^2+\Omega \right)^2}-\frac{2 M \Omega z^2}{r^2 \left(r^2+\Omega \right)^2}+\frac{4 Q^2 z^2}{r \left(r^2+\Omega \right)^2} \\ &+\frac{2 Q^2 \Omega z^2}{r^3 \left(r^2+\Omega \right)^2}\ . \end{aligned} $

(26) We can write the expression for deflection angle as [22]
$ \hat{\alpha_b}=\hat{\alpha_1}+\hat{\alpha_2}+\hat{\alpha_3}\ , $

(27) with
$ \begin{aligned}[b] \hat{\alpha_1}=\;&\frac{1}{2}\int_{-\infty}^{\infty} \frac{b}{r}\frac{{\rm d}h_{33}}{{\rm d}r}{\rm d}z\ ,\\ \hat{\alpha_2}=\;&\frac{1}{2}\int_{-\infty}^{\infty} \frac{b}{r}\frac{1}{1-\omega^2_{\rm p}/ \omega^2}\frac{{\rm d}h_{00}}{{\rm d}r}{\rm d}z\ ,\\ \hat{\alpha_3}=\;&\frac{1}{2}\int_{-\infty}^{\infty} \frac{b}{r}\left(-\frac{K_e}{\omega^2-\omega^2_{\rm p}}\frac{{\rm d}N}{{\rm d}r} \right){\rm d}z\ . \end{aligned} $

(28) In the next two subsections, we aim to examine and assess the angle of deflection for various plasma density distributions.
-
In this part. we consider the uniform plasma distribution, which can be expressed by the sum [22]
$ \hat{\alpha}_{\rm uni}=\hat{\alpha}_{\rm uni1}+\hat{\alpha}_{\rm uni2}+\hat{\alpha}_{\rm uni3}. $

(29) The expression for
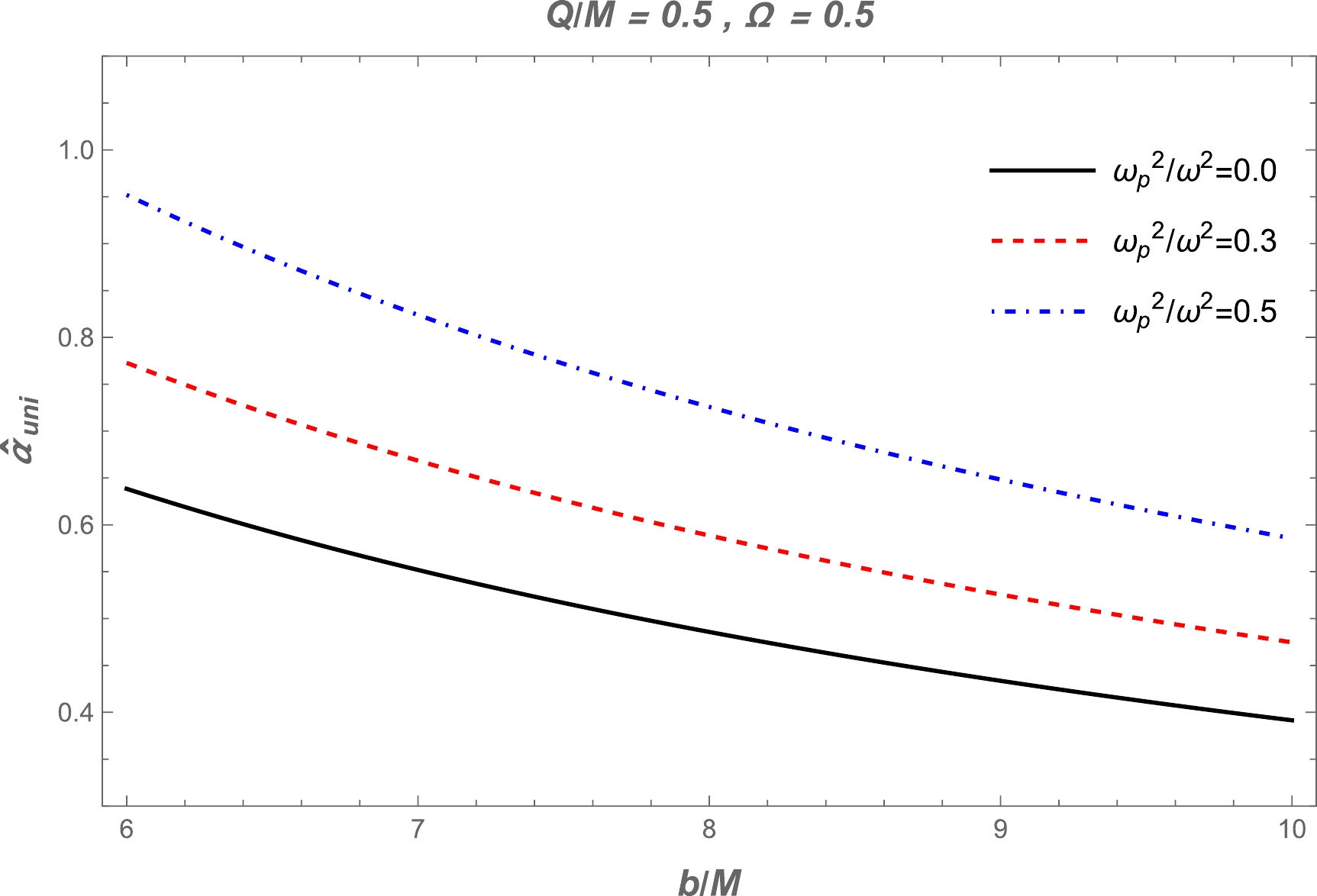
$\hat{\alpha}_{\rm uni}$ can be obtained from Eqs. (24), (27), and (28). This expression is very large; therefore, we use the numerical method. Fig. 4 demonstrates the dependence of the deflection angle on the impact parameter$ b $ for different values of BH charge and parameter$ \Omega $ . This figure also shows the angle of deflection around the BH in a vacuum. It can be seen from the graphs that the value of the deflection angle$\alpha_{\rm uni}$ decreases with increasing impact parameter. Also, there is a slight decrease under the influence of the BH charge and$ \Omega $ . Moreover, the dependence of the deflection angle$ \hat{\alpha}_{\text{uni}} $ on the impact parameter for different values of the plasma parameters is plotted in Fig. 5. One can easily see from this figure that the values of the deflection angle increase with increasing plasma parameter.
Figure 4. (color online) Top left panel: Dependence of the deflection angle
$\alpha_{\rm vac}$ on the impact parameter$ b $ for different values of parameter$ \Omega $ ; here,$ Q/M=0.5 $ and$ \omega^2_{\rm p} / \omega^2=0 $ . Dependence of the deflection angle$ \hat{\alpha}_{\text{uni}} $ on the impact parameter$ b $ for the different values of the parameter$ \Omega $ (top right panel) and BH charge (bottom panel). -
In this subsection, we consider the non-singular isothermal sphere (SIS), which represents the most favorable model for understanding the unique characteristics of gravitational weak lensing effects on photons around the BH. In general, the SIS is a spherical gas cloud characterized by a singularity located at its center, where the density tends to infinity. The density distribution of a SIS is described as follows [17]:
$ \rho(r)=\frac{\sigma^2_{\nu}}{2\pi r^2}\ , $

(30) where
$ \sigma^2_{\nu} $ denotes a one-dimensional velocity dispersion. The analytical expression for the plasma concentration is given by [17]$ N(r)=\frac{\rho(r)}{k m_{\rm p}}\ , $

(31) where
$m_{\rm p}$ represents the mass of a proton, and$ k $ is a dimensionless coefficient generally associated with the dark matter universe. The plasma frequency is$ \omega^2_e=K_e N(r)=\frac{K_e \sigma^2_{\nu}}{2\pi k m_{\rm p} r^2}\ . $

(32) Now, we investigate the non-uniform plasma (SIS) effect on the angle of deflection in the spacetime of the quantum-improved charged BH. We can express the deflection angle around the quantum-improved charged BH in the following form [22]:
$ \hat{\alpha}_{\rm SIS}=\hat{\alpha}_{\rm SIS1}+\hat{\alpha}_{\rm SIS2}+\hat{\alpha}_{\rm SIS3} \ . $

(33) For uniform plasma, we also use the numerical method. These calculations introduce a supplementary plasma constant
$ \omega^2_c $ , which has the following analytic expression [23]:$ \omega^2_c=\frac{K_e \sigma^2_{\nu}}{2\pi k m_{\rm p} R^2_S}\ . $

(34) We have demonstrated the dependence of the angle of deflection on the impact parameter
$ b $ for different values of$ \Omega $ and BH charge in the quantum-improved charged BH spacetime in Fig. 6. One can see from this figure that the value of the deflection angle$\alpha_{\rm sis}$ decreases with increasing impact parameter. Also, there is a slight increase under the influence of the BH charge and$ \Omega $ . Moreover, we demonstrate the dependence of the deflection angle of a light ray on the impact parameter$ b $ around a BH in the presence of a non-uniform plasma for different values of the plasma parameters in Fig. 7. It can be seen from this figure that the value of the deflection angle$\alpha_{\rm sis}$ decreases with increasing plasma frequency. In addition, we compared the different effects of plasma on the quantum-improved charged BH deflection angle with gravity, as shown in Fig. 8. By comparison, it can be seen that the value of the deflection angle of light for uniform plasma is greater than that for non-uniform plasma.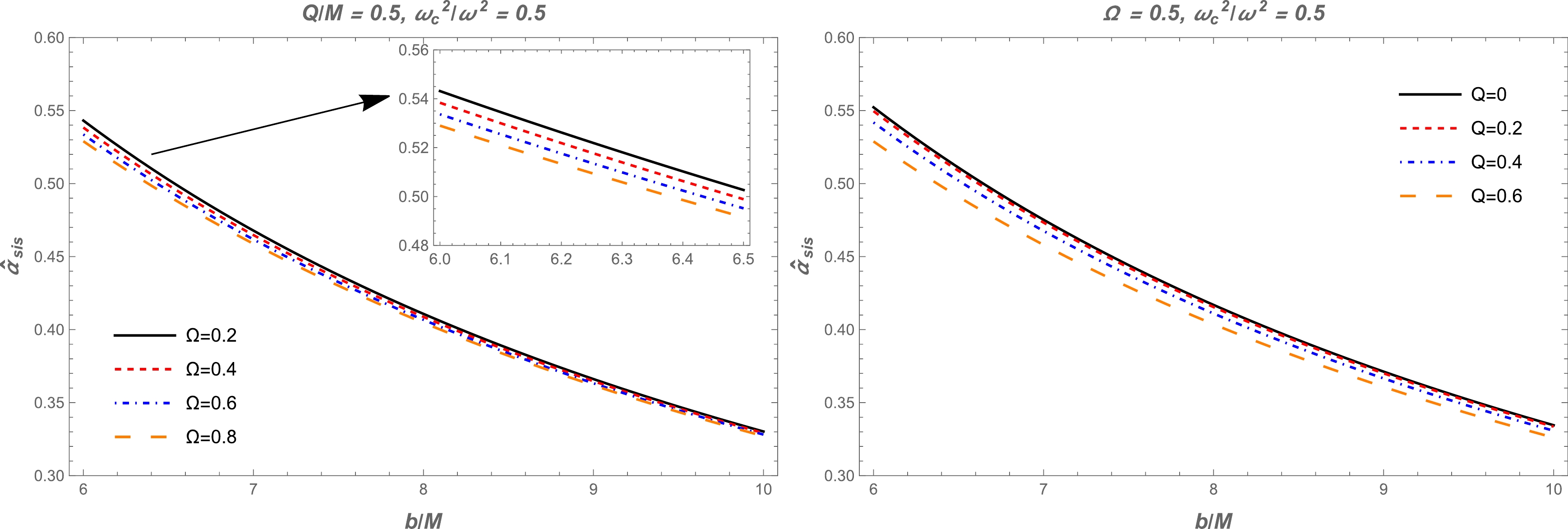
Figure 6. (color online) Dependence of the deflection angle
$ \hat{\alpha}_{\text{sis}} $ on the impact parameter$ b $ for different values of the parameter$ \Omega $ (left panel) and BH charge (right panel).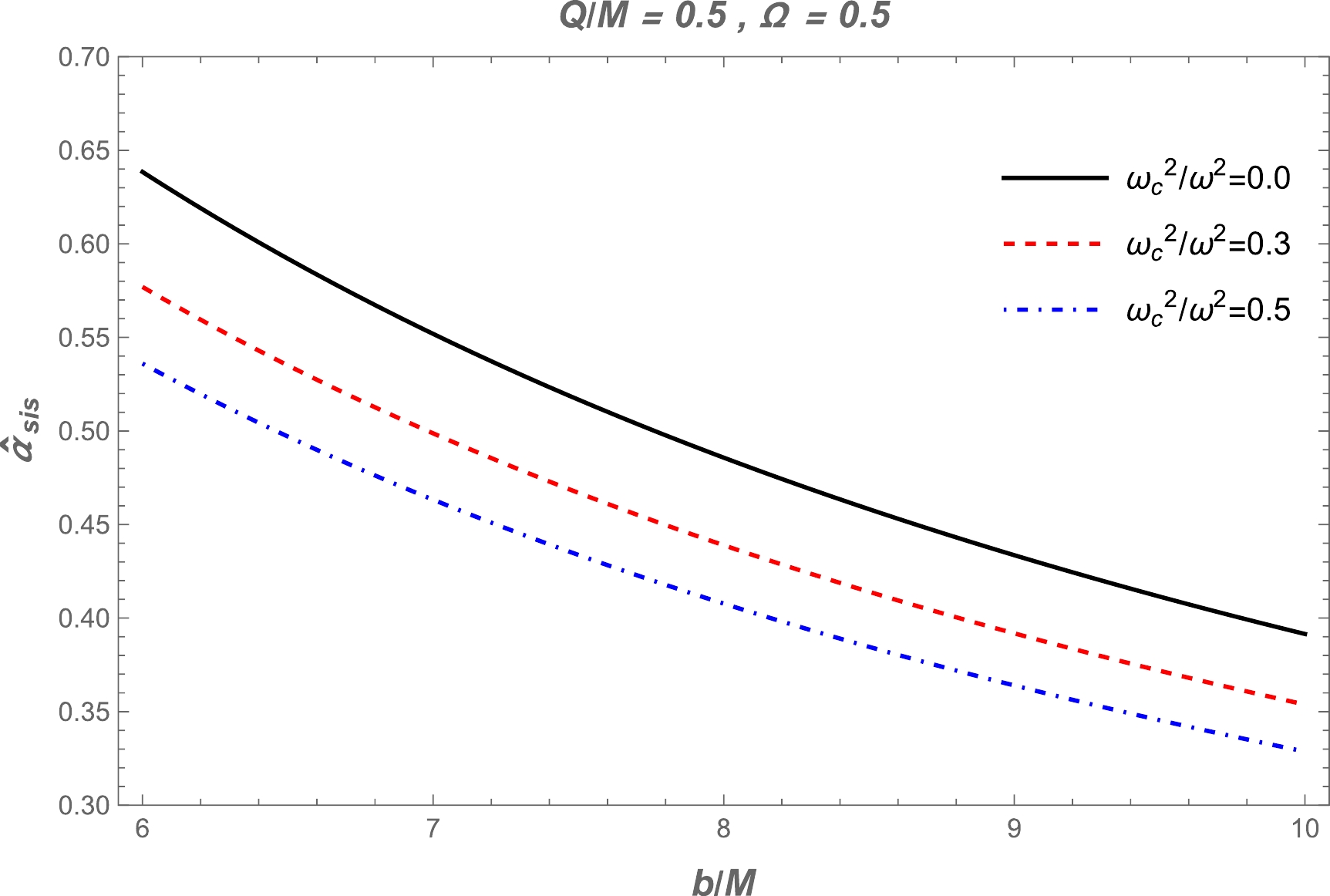
Figure 7. (color online) Deflection angle
$ \hat{\alpha}_{\text{sis}} $ as a function of the impact parameter$ b $ for different values of the plasma parameters. The other parameters are$ Q/M=0.5 $ and$ \Omega=0.5 $ .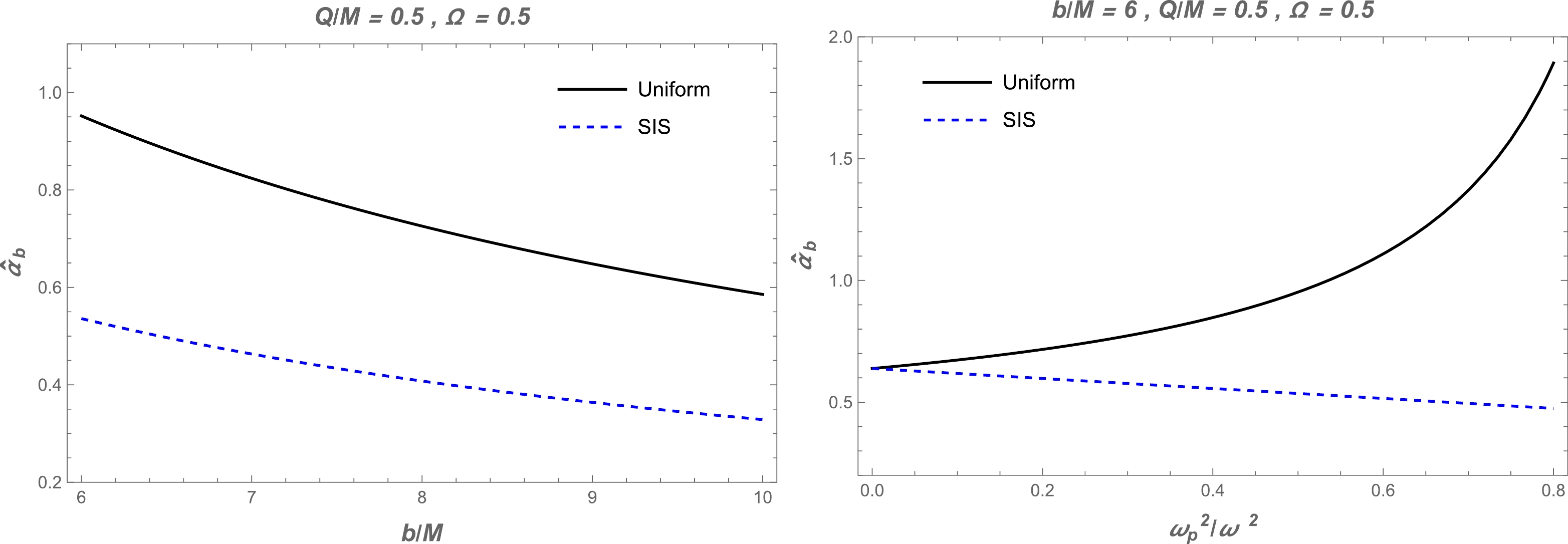
Figure 8. (color online) Left panel: Dependence of the deflection angle
$ \hat{\alpha }_{\text{b}} $ on the impact parameter$ b $ . The other parameters are$ Q/M=0.5 $ &$ \Omega=0.5 $ . Right panel: Deflection angle$ \hat{\alpha }_{b} $ as a function of the plasma parameters. The other parameters are$ b/M=6 $ ,$ Q/M=0.5 $ , and$ \Omega=0.5 $ . -
Now we explore the brightness of the image in the presence of plasma through the angle of deflection of light rays around the quantum-improved charged BH. By employing the lens equation, the combination of light angles around the quantum-improved charged BH can be written (
$ \hat{\alpha} $ ,$ \theta $ , and$ \beta $ ) [19, 23] as$ \theta D_\mathrm{s}=\beta D_\mathrm{s}+\hat{\alpha_b}D_\mathrm{ds}\ , $

(35) where
$ D_\mathrm{s} $ ,$ D_\mathrm{d} $ , and$ D_\mathrm{ds} $ are the distances from the source to the observer, lens to the observer, and source to the lens, respectively. In Eq. (35),$ \theta $ and$ \beta $ denote the angular positions of the image and source, respectively. Now, we can rewrite the above equation for$ \beta $ as$ \beta=\theta -\frac{D_\mathrm{ds}}{D_\mathrm{s}}\frac{\xi(\theta)}{D_\mathrm{d}}\frac{1}{\theta}\ , $

(36) with
$ \xi(\theta)=|\hat{\alpha}_b|b $ and$ b=D_\mathrm{d}\theta $ taken from Ref. [23]. When the image has a ring-like appearance, it is classified as Einstein's ring, with Einstein's ring radius defined as$R_{\rm s}=D_\mathrm{d}\theta_E$ . The angular part$ \theta_E $ , arising from the spacetime geometry between the source's images in a vacuum, can be expressed as [19]$ \theta_E=\sqrt{2R_\mathrm{s}\frac{D_\mathrm{ds}}{D_{\rm d}D_\mathrm{s}}}\ . $

(37) We investigate the equation of the magnification of brightness
$ \mu_{\Sigma}=\frac{I_\mathrm{tot}}{I_*}=\underset{k}\sum\bigg|\bigg(\frac{\theta_k}{\beta}\bigg)\bigg(\frac{\rm d\theta_k}{\rm d\beta}\bigg)\bigg|, \quad k=1,2, \cdot \cdot \cdot , j\ , $

(38) where
$ I_\mathrm{tot} $ and$ I_* $ are the the total brightness of all images and unlensed brightness of the source, respectively. The magnification of the source can be expressed as [17, 23]$ \mu^\mathrm{pl}_\mathrm+=\frac{1}{4}\bigg(\frac{x}{\sqrt{x^2+4}}+\frac{\sqrt{x^2+4}}{x}+2\bigg)\ , $

(39) $ \mu^\mathrm{pl}_\mathrm-=\frac{1}{4}\bigg(\frac{x}{\sqrt{x^2+4}}+\frac{\sqrt{x^2+4}}{x}-2\bigg)\ , $

(40) where
$ x={\beta}/{\theta_E} $ is a dimensionless quantity [23] and$ \mu_{+}^{\mathrm{pl}} $ and$ \mu_{-}^{\mathrm{pl}} $ are the magnifications of images. Using Eqs. (39) and (40), we can get the expression for the total magnification in the following form:$ \mu^\mathrm{pl}_\mathrm{tot}=\mu^\mathrm{pl}_++\mu^\mathrm{pl}_-=\frac{x^2+2}{x\sqrt{x^2+4}}\ . $

(41) The next two subsections explore magnification in the presence of plasma in the BH environment with different distributions of plasma: (ⅰ) uniform and (ⅱ) non-uniform.
-
Here, we study the effect of uniform plasma on the magnification image. The total magnification
$ \mu^{\rm pl}_{\rm tot} $ can be expressed as follows:$ \mu^\mathrm{pl}_\mathrm{tot}=\mu^\mathrm{pl}_++\mu^\mathrm{pl}_-=\dfrac{x^2_\mathrm{uni}+2}{x_\mathrm{uni}\sqrt{x^2_\mathrm{uni}+4}}\ , $

(42) The expression for
$(\theta^\mathrm{pl}_{E})_{\rm uni}$ is complicated; therefore, we use numerical calculations for it.$ x_{\rm uni} $ ,$(\mu^{\rm pl}_+)_{\rm uni}$ and$(\mu^{\rm pl}_-)_\mathrm{uni}$ are defined as$ x_\mathrm{uni}=\frac{\beta}{(\theta^\mathrm{pl}_E)_\mathrm{uni}} $

(43) Magnifications of the image can be written as
$ (\mu^\mathrm{pl}_+)_\mathrm{uni}=\frac{1}{4}\left(\dfrac{x_\mathrm{uni}}{\sqrt{x^2_\mathrm{uni}+4}}+\dfrac{\sqrt{x^2_\mathrm{uni}+4}}{x_\mathrm{uni}}+2\right) $

(44) $ (\mu^\mathrm{pl}_-)_\mathrm{uni}=\frac{1}{4}\left(\dfrac{x_\mathrm{uni}}{\sqrt{x^2_\mathrm{uni}+4}}+\dfrac{\sqrt{x^2_\mathrm{uni}+4}}{x_\mathrm{uni}}-2\right) $

(45) The total magnification of the image in the presence of a plasma
$ \mu^\mathrm{pl}_\mathrm{tot} $ for the quantum-improved charged BH is demonstrated in Fig. 9. One can see from this figure that the value of the total magnification of the image for uniform plasma increases with increasing plasma parameters. Also, there is a decrease with increasing$ \Omega $ . Fig. 10 illustrates the dependence of the total magnification on$ x_0 $ in the presence of uniform plasma for different values of the plasma parameters. -
In this subsection, we explore the effect of non-uniform plasma on the magnification of the image, and we can write the total magnification
$(\mu^\mathrm{pl}_\mathrm{tot})_\mathrm{SIS}$ as$ (\mu^\mathrm{pl}_\mathrm{tot})_\mathrm{SIS}=(\mu^\mathrm{pl}_+)_\mathrm{SIS}+(\mu^\mathrm{pl}_-)_\mathrm{SIS}=\dfrac{x^2_\mathrm{SIS}+2}{x_\mathrm{SIS}\sqrt{x^2_\mathrm{SIS}+4}}\ , $

(46) with
$ (\mu^\mathrm{pl}_+)_\mathrm{SIS}=\frac{1}{4}\left(\dfrac{x_\mathrm{SIS}}{\sqrt{x^2_\mathrm{SIS}+4}}+\dfrac{\sqrt{x^2_\mathrm{SIS}+4}}{x_\mathrm{SIS}}+2\right)\ , $

(47) $ (\mu^\mathrm{pl}_-)_\mathrm{SIS}=\frac{1}{4}\left(\dfrac{x_\mathrm{SIS}}{\sqrt{x^2_\mathrm{SIS}+4}}+\dfrac{\sqrt{x^2_\mathrm{SIS}+4}}{x_\mathrm{SIS}}-2\right)\ , $

(48) and
$ x_\mathrm{SIS}=\frac{\beta}{(\theta^\mathrm{pl}_E)_\mathrm{SIS}}\ . $

(49) As with
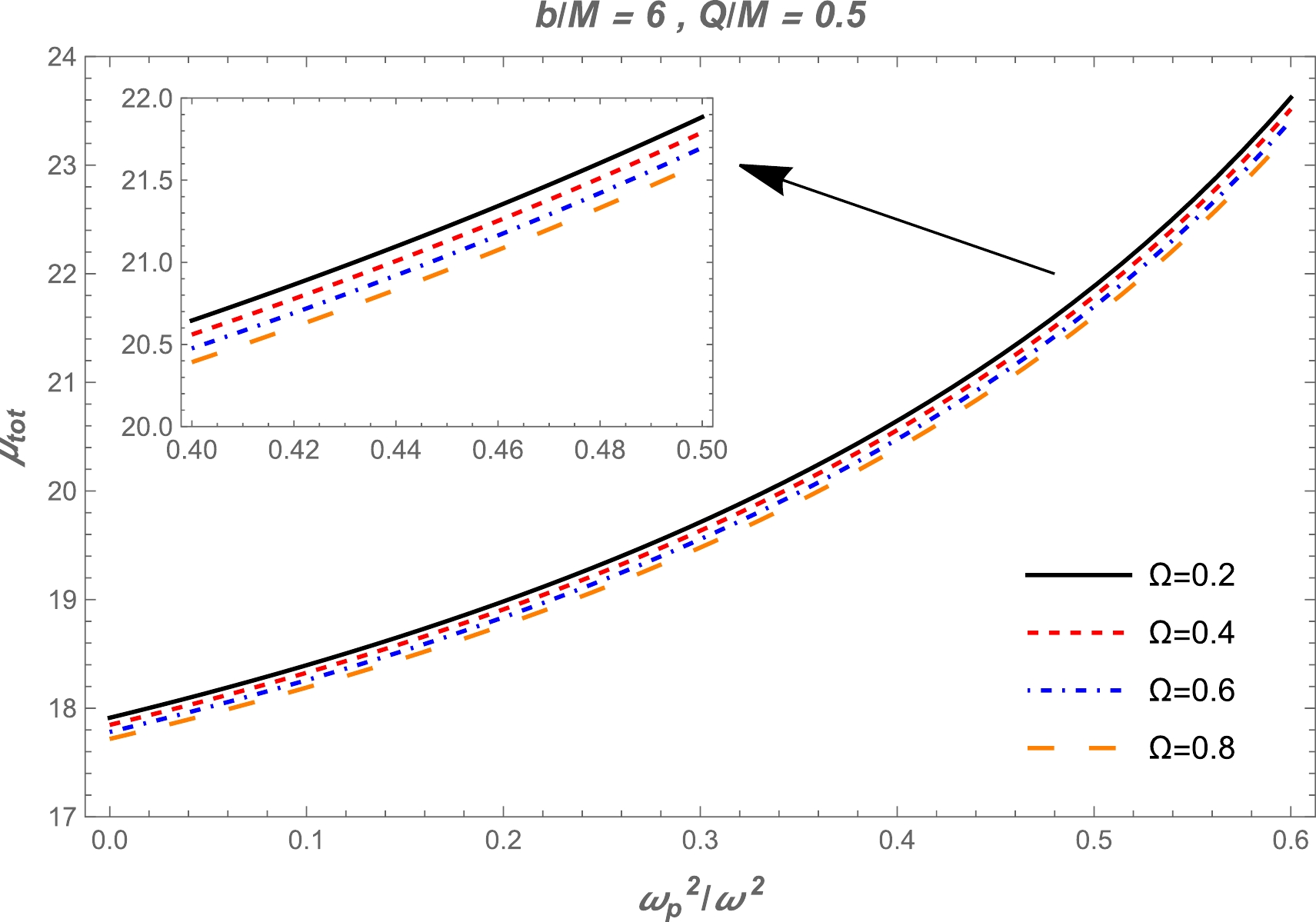
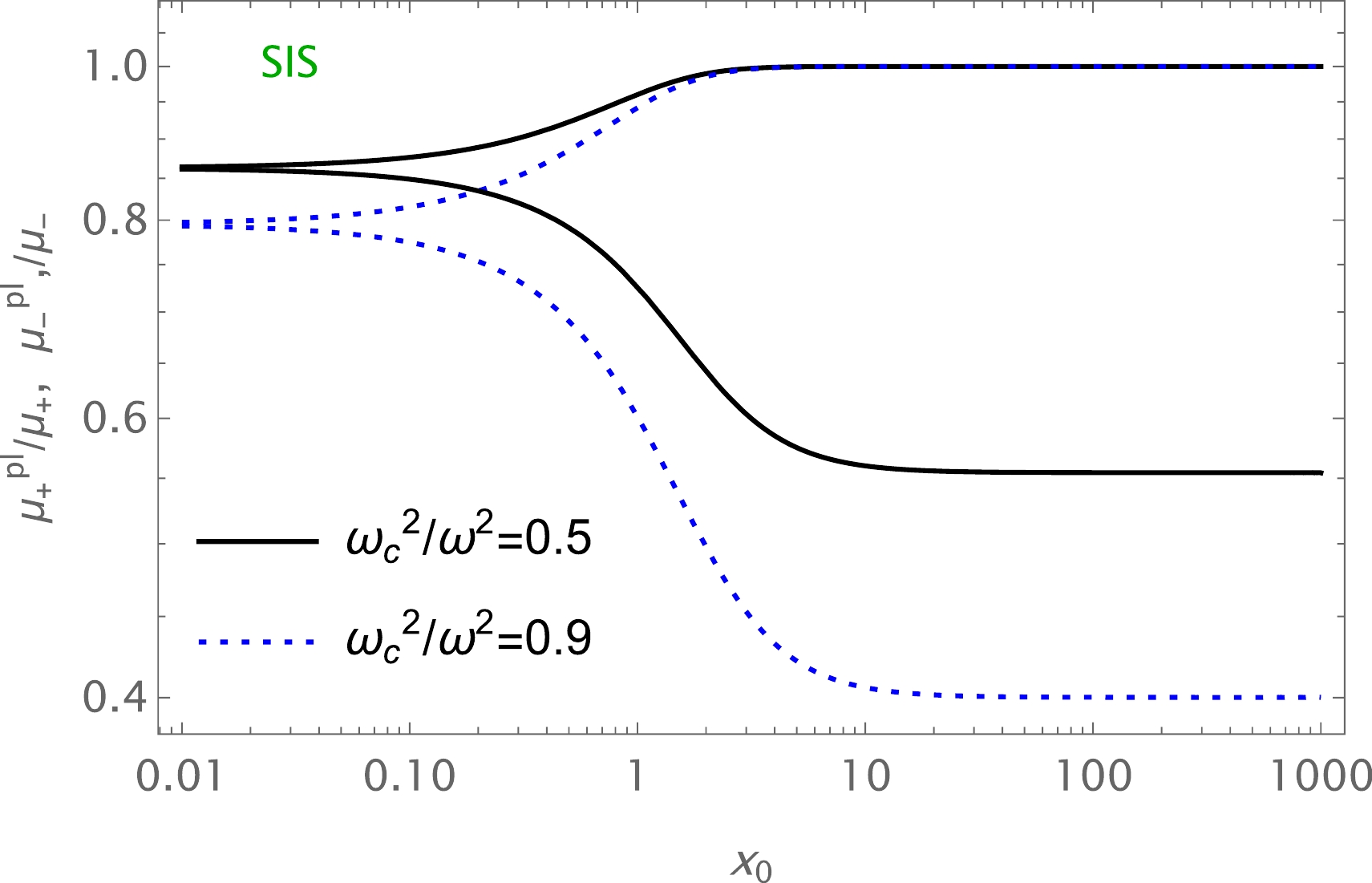
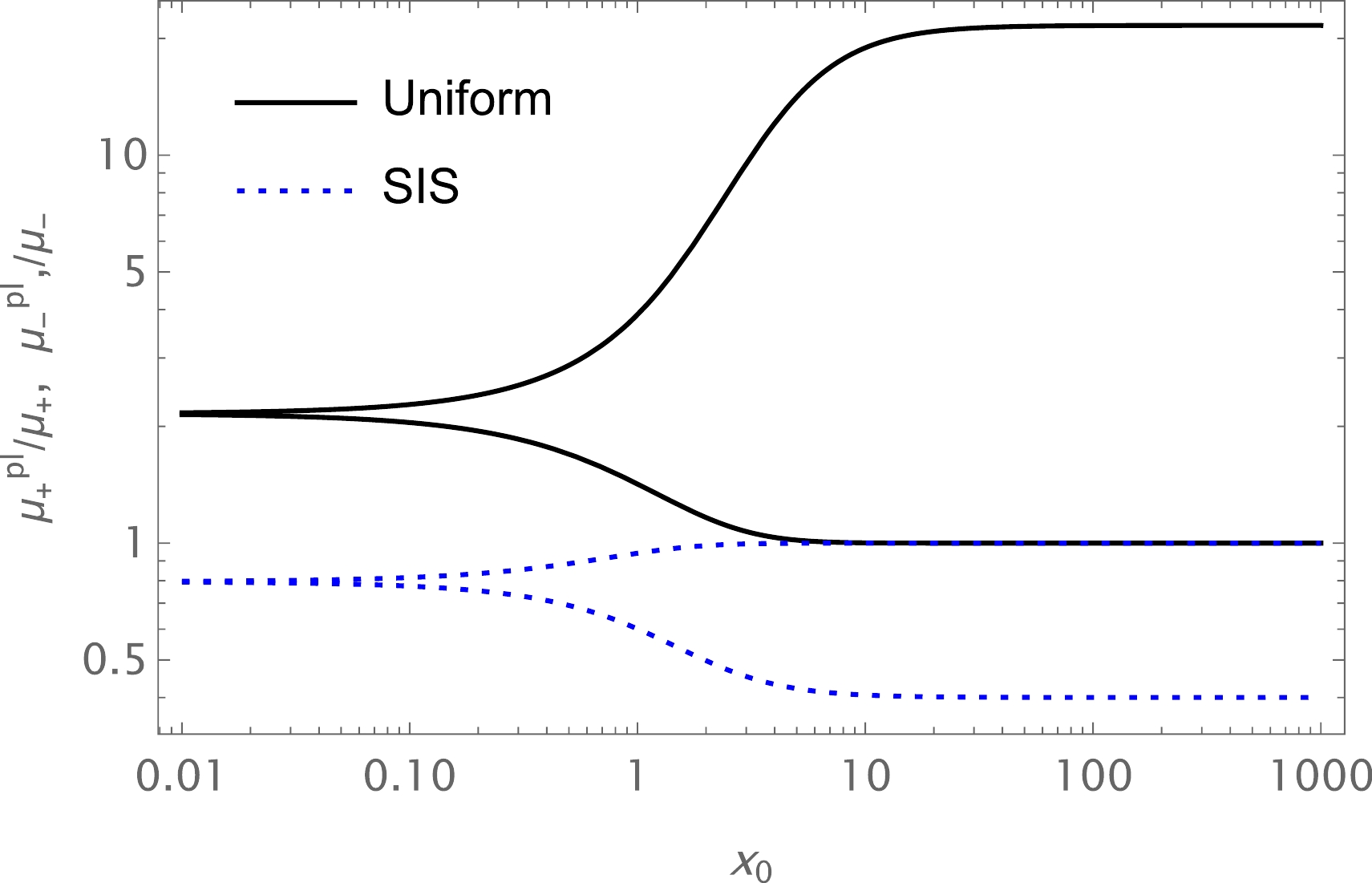
$(\theta^\mathrm{pl}_E)_\mathrm{uni}$ , we also use the numerical method for$(\theta^\mathrm{pl}_E)_\mathrm{SIS}$ . One can find the dependence of total magnification on the plasma parameter using Eq. (46). The value of the total magnification decreases with increasing plasma parameter. Also, there is a slight decrease under the influence of$ \Omega $ , as demonstrated in Fig. 11. Moreover, the plot of dependence of total magnification on$ x_{0} $ in the presence of plasma for the fixed values of the parameter$ \Omega $ and the impact parameter is demonstrated in Fig. 12. We can see from this figure that the value of the total magnification of the image for non-uniform plasma decreases with increasing plasma parameters. Finally, we compare the two cases of uniform and non-uniform plasma distributions in Fig. 13.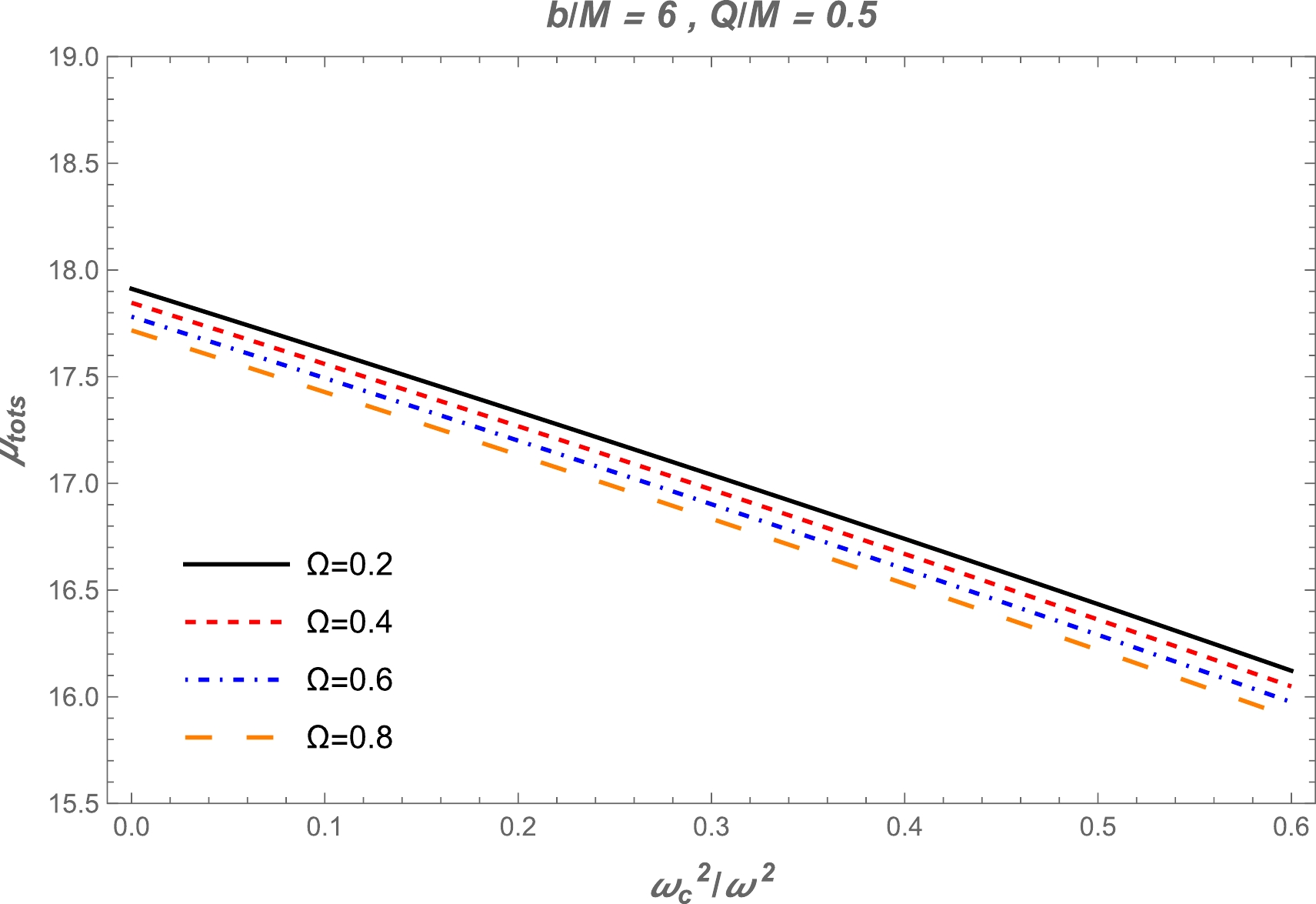
Figure 11. (color online) Total magnification of the images as a function of non-uniform plasma for different values of parameter
$ \Omega $ . The other parameters are$ b/M=6 $ and$ Q/M=0.5 $ . -
In this paper, we discussed the optical properties of the quantum-improved charged BH. From the performed research, we can summarize our main results as follows:
● We have investigated the photon motion around the BH surrounded by a plasma. We have obtained numerical results on the dependence of the radius of the photon sphere on the plasma frequency (see Fig. 1). It has been shown that the radius of the photon sphere decreases with increasing plasma frequency. Also, the value of the photon sphere radius decreases under the influence of the parameter
$ \Omega $ .● We have also studied the shadow of the quantum-improved charged BH in plasma. The radius of the BH shadow was calculated by numerical method. The dependencies of the radius of the BH shadow on the plasma frequency and BH parameter have been demonstrated in Fig. 2. One can see from this figure that the radius of the BH shadow decreases with increasing
$ \Omega $ and the plasma parameter. Similarly, there is a slight decrease with the rise of the BH charge.● Furthermore, weak gravitational lensing for the quantum-improved charged BH has been investigated. For this, we considered that the BH is surrounded by uniform and non-uniform plasma. We found the deflection angle for each case independently. Figs. 4 and 5 correspond to the uniform case. One can see from these figures that the value of the deflection angle is slightly decreased under the influence of the BH charge and
$ \Omega $ . On the contrary, the value of the deflection angle increases with increasing uniform plasma frequency. The obtained results for the non-uniform plasma case are illustrated in Figs. 6 and 7. These figures clearly demonstrate that the parameter$ \Omega $ and BH charge have the same impact in the case of non-uniform plasma as they do in the uniform plasma case.● In addition, we compared the deflection angle of light for uniform and non-uniform plasma in Fig. 8. We can easily see from this figure that the value of the deflection angle of light for uniform plasma is greater than that for non-uniform plasma.
● Finally, we have studied the total magnification of the images as a function of uniform and non-uniform plasma, and the dependencies are plotted in Figs. 9 and 11. It can be seen from these figures that the value of the total magnification of the image for uniform plasma increased with increasing plasma parameter, and vice versa for non-uniform plasma. Also, we have investigated the image magnification for both cases. The results are demonstrated in Figs. 10, 12, and 13.
Shadow and gravitational weak lensing for quantum improved charged black hole in plasma
- Received Date: 2024-06-24
- Available Online: 2024-11-15
Abstract: We investigated the shadow and weak gravitational lensing for the quantum-improved charged black hole (BH). First, the photon motion and BH shadow were studied in a plasma medium. It can be seen from our analysis that the radius of the photon sphere of the quantum-improved charged BH and size of the BH shadow decrease under the influence of the plasma parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: