-
The inflationary scenario [1] has become the standard paradigm for the early universe. It solves many of the theoretical problems of Big Bang cosmology and explains the observed cosmological perturbations [2]. However, the initial singularity problem [3] of the Big Bang cosmology remains unsolved under the inflationary paradigm [4, 5], i.e., ever expanding cosmologies must be past incomplete. This motivates us to explore alternatives to the inflationary cosmology.
A bouncing universe [6, 7] (for reviews, see [8−10]), an alternative to the inflationary cosmology, offers a potential solution to the initial singularity problem. However, the bounce scenario also faces several theoretically and phenomenologically challenging issues. Firstly, a cosmic nonsingular bounce can only occur when the null energy condition is violated, which typically gives rise to a ghost instability. This issue can be circumvented by introducing a new kind of matter field, such as ghost condensates [11, 12], Galileons [13], quintom fields [14], or Lee-Wick fields [15]. Secondly, a contracting phase of a bouncing cosmology is generally unstable under the growth of anisotropies, which is known as the BKL instability [16]. The solution to this problem is to introduce a scalar field with a steep and negative-valued potential that dominates over anisotropies during the contracting phase [17, 18]. During this ekpyrotic contracting phase, homogeneity, isotropy, and flatness can be achieved after the scale factor of the universe shrinks by just a few e-folds, even if the initial state is highly non-homogeneous and non-isotropic [19, 20].
Another important issue with bounce models is that it is relatively difficult to obtain them based on the low-energy effective field theory of string theory or quantum gravity. In [21], a nonsingular bounce model based on a ghost condensate and a Galileon field theory that includes a ekpyrotic phase was constructed within
$ \mathscr N=1 $ supergravity. In [22], this model was improved into a much simpler model where the nonsingular bounce is supported by a scalar field with a pure ghost condensate kinetic term and ekpyrotic potential.To generate nearly scale-invariant curvature perturbations with small non-Gaussianities, in [23], the model proposed in [22] was combined with the entropic mechanism [24] where the entropy field is coupled to the bounce field by a non-minimal kinetic coupling [25, 26]. In [27], the possibility of incorporating the late-time accelerated expansion was explored, and two phenomenological constraints were obtained by comparing the amplitude of curvature perturbations with the observed value [2]. In [28], the amount of generated particles up to the bounce phase was evaluated based on detailed investigation of the background evolution during the bounce phase.
All previous studies indicated that the models considered in [22, 23, 27] can be not only theoretically promising but also phenomenologically viable. However, it is unpreferable if the model suffers such severe constraints that the allowed parameter space has a much smaller volume than other models for the early universe.
In this paper, we aim to derive theoretical and phenomenological constraints on the nonsingular bounce scenario considered in [22, 23, 27] to investigate the allowed parameter space. Concretely, one constraint is obtained by requiring the model not to have a singularity at the background level, and the other is derived by using the relation between the energy density of the particles created by the classical backgrounds and the late-time accelerated expansion [27]. We then determine the allowed parameters of the model by combining these with the constraints obtained in [27].
Following [28], we use the Planck units with
$ \hbar=c= 8\pi G_N=1 $ (where$ G_N $ is Newton's gravitational constant) and take the sign of the metric to be$ (-,+,+,+) $ in this paper. -
The model that we consider consists of two kinetically-coupled scalar fields: a bounce field ϕ that violates the Null Energy Condition for a short period and induces the cosmic bounce and an entropic field χ that is responsible for generating nearly scale-invariant scalar perturbations. The corresponding Lagrangian is given by [22, 23, 27]
1 $ \begin{aligned}[b] \mathscr L=\;&\frac R2-\frac12 K(\phi)\partial_\mu\phi\partial^\mu\phi+\frac14Q(\phi)(\partial_\mu\phi \partial^\mu\phi)^2\\&-V(\phi)-\frac12 \Omega(\phi)^2\partial_\mu\chi\partial^\mu\chi, \end{aligned} $

(1) where R is the Ricci scalar, and
$ \begin{aligned} K(\phi)=1-\frac{2}{(1+\frac12\phi^2)^2},\quad Q(\phi)=\frac{q}{(1+\frac12\phi^2)^2}. \end{aligned} $

(2) The form of
$ \Omega(\phi) $ should be chosen such that nearly scale-invariant entropic perturbations are generated during the ekpyrotic contracting phase. A simple such form is [25, 30]$ \begin{aligned} \Omega(\phi)=\exp\left(\frac b2\phi\right), \end{aligned} $

(3) where the parameter b is slightly larger than λ (i.e.,
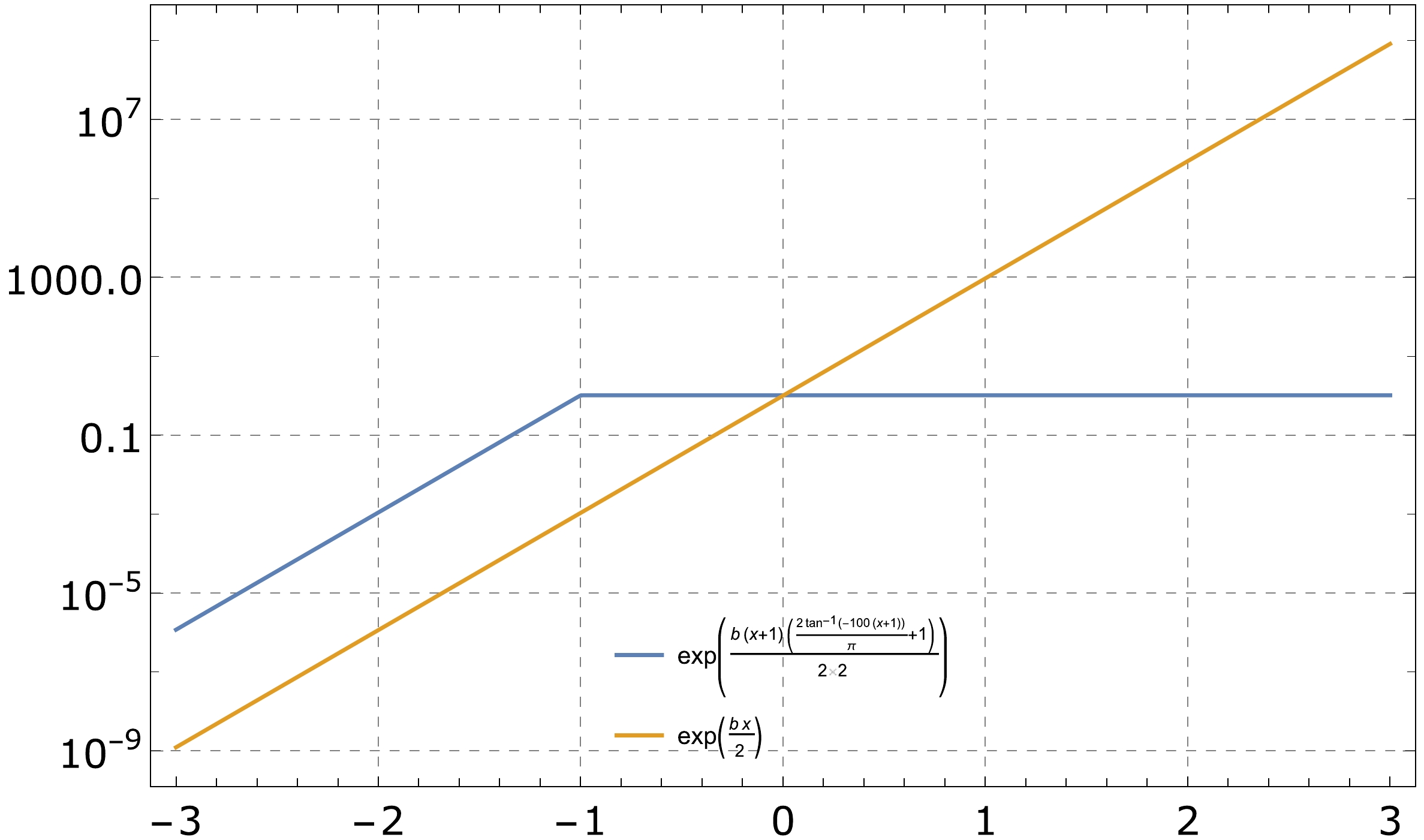
$ b\simeq 1.02\lambda $ ; see, e.g., [23]) so that the scalar spectral index$ n_s $ falls in the range of$ (0.95,0.97) $ . However, this simple form leads to an extremely inefficient conversion process from the entropic perturbation into the curvature fluctuation after the ekpyrotic contracting phase, due to the significant scalar curvature in the field space [31]. The curvature perturbation then has a small amplitude and large non-Gaussianities, which is clearly in contradiction with observations [31]. For this reason, it is necessary to flatten the field space metric after the ekpyrotic phase. As the ekpyrotic phase contracting ends at around$\phi= -\sqrt{2(\sqrt 2-1)}\simeq -0.9$ [28], we take the function$ \Omega(\phi) $ as$ \begin{aligned} \Omega(\phi)=\exp\left(\frac{b}{2}(x+1)\frac{\frac{2}{\pi}\arctan(-100(x+1))+1}{2}\right), \end{aligned} $

(4) see Fig. 1 for comparison of (3) and (4). As in [28], here, we assume that the scalar field ϕ evolves from
$ -\infty $ in the positive direction without loss of generality. In Section IV, we give results for particle creation significantly different from in [28], which is due to the change of the form of$ \Omega(\phi) $ .The scalar potential is given by [22, 23, 27, 32]
$ \begin{aligned} V(\phi)=V_{\rm DE}-V_0\cdot\text{sech}(\lambda\phi), \end{aligned} $

(5) where
$V_{\rm DE} > 0$ , which is almost equal to the dark energy density, is introduced to account for the late-time accelerated expansion [27, 32]. This parameter is so small that it can be neglected before the late-time accelerated expanding phase. As mentioned in the Introduction, the potential (5) should be so steep that the unwanted anisotropies are sufficiently diluted before the bounce. This is achieved by setting the parameter λ to be greater than$ \sqrt 6 $ [17, 33]. -
We take the background metric to be a flat Friedmann-Lemaître-Robertson-Walker (FLRW) universe with a scale factor
$ a(t) $ . The background equations of motion are then [23, 28]$ \begin{aligned} 3H^2 & =\frac12 K(\phi)\dot\phi^2+\frac34Q(\phi)\dot\phi^4+V(\phi), \end{aligned} $

(6) $ \begin{aligned} \dot H & =-\frac12 K(\phi)\dot\phi^2-\frac12 Q(\phi)\dot\phi^4, \end{aligned} $

(7) $ \begin{aligned}[b] 0 =\;& (K(\phi)+3Q(\phi)\dot\phi^2)\ddot{\phi}+3H\dot{\phi}(K(\phi)+Q(\phi)\dot{\phi}^2)\\ &+V_{,\phi}+\left(\frac12 K_{,\phi}+\frac34 Q_{,\phi}\dot{\phi}^2\right)\dot{\phi}^2-\frac 12\frac{\Omega_{,\phi}}{\Omega}\dot\chi^2, \end{aligned} $

(8) $ \begin{aligned} 0&=\ddot\chi+\left(3H+2\frac{\dot\Omega}{\Omega}\right)\dot\chi, \end{aligned} $

(9) where the Hubble parameter H is given by
$ H\equiv \dot a/a $ , and the over-dot refers to the derivative with respect to the cosmic time t; the subscript,$\phi$ denotes the derivative with respect to ϕ.One can readily see from (2) and (7) that violation of the null energy condition can occur only when
$ K(\phi) $ becomes negative, or$ |\phi|\leq \sqrt{2(\sqrt 2-1)}\simeq 0.9 $ . At this time,$ Q(\phi) $ that controls the magnitude of the higher derivative term becomes large so that the ghost condensation can occur [11, 21, 22, 28]. Here, we define the bounce phase by the period when$ K(\phi) $ has negative value.Outside of the bounce phase, the Lagrangian (1) is effectively reduced to the canonical form, and the background dynamics in this case were analysed in detail in [27]. In summary, the universe undergoes the ekpyrotic contracting phase, bounce phase, kinetic energy dominated expanding phase, and finally the standard Big Bang cosmology, which is a typical evolution of the nonsingular bounce scenario [22, 23, 27, 28], see Fig. 2.
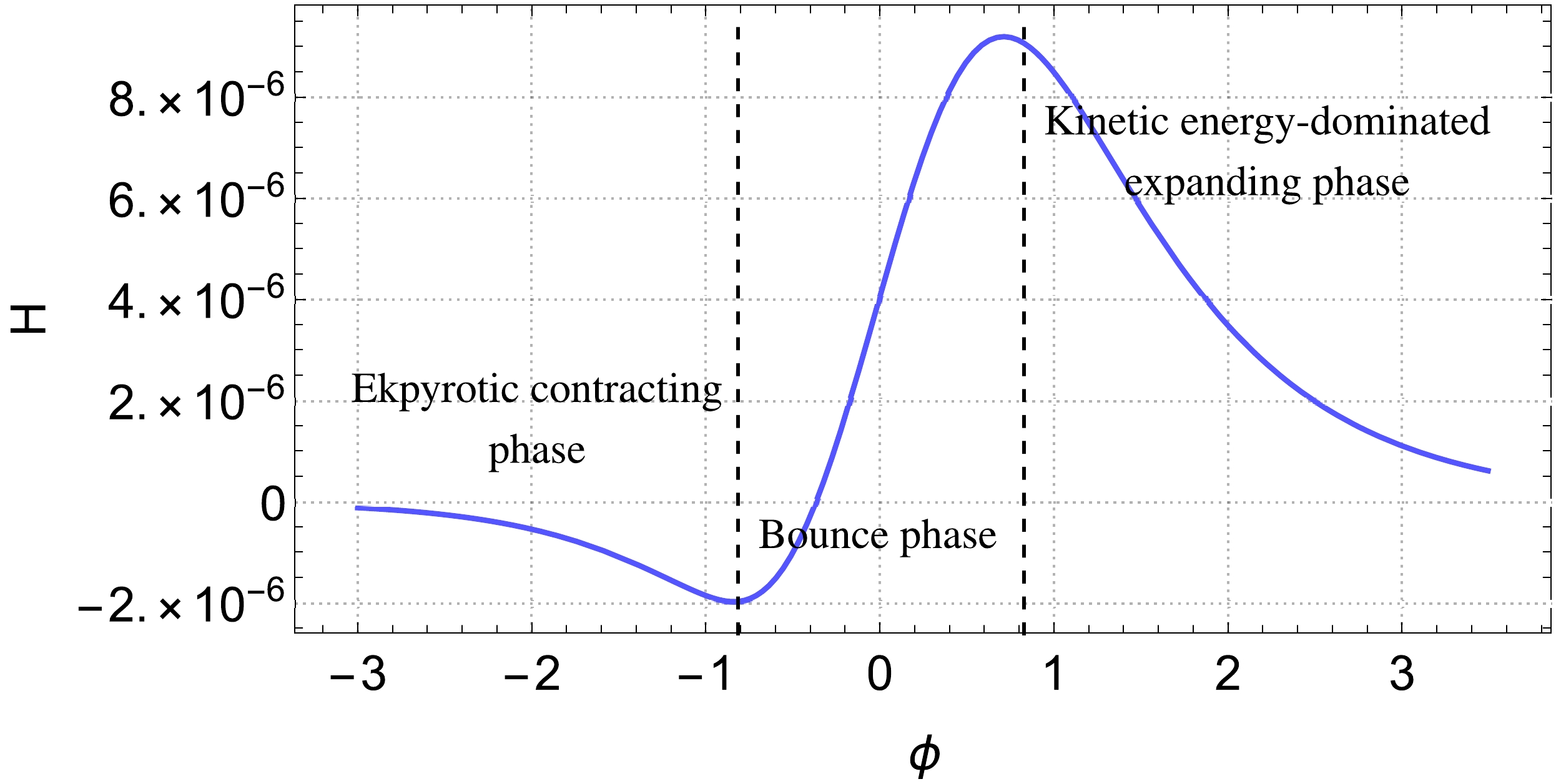
Figure 2. (color online) Plot of H for the model parameters given by
$ \lambda=\sqrt{10} $ ,$ q=10^8 $ , and$ V_0=2\times 10^{-10} $ . The horizontal axis denotes ϕ. The scalar field ϕ evolves in the positive direction. The universe undergoes ekpyrotic contracting phase, bounce phase, and kinetic energy-dominated expanding phase. The final Big Bang standard evolution is not depicted. The plot is insensitive to the initial condition due to the attractor nature of the ekpyrotic solution [34, 35].Note that it is not clear whether this means of evolution of the bouncing universe holds true for any values of the parameters in the model (1). It was indeed reported in [28] that when
$ qV_0 $ has a large value, the Hubble parameter decreases rapidly after the bounce phase so that it can become a negative infinity in a finite time, which leads to a new kind of classical singularity. Hence, we would like to derive a necessary condition for this sort of singularity not to occur.It is obvious that this classical singularity will certainly appear if the Hubble parameter takes a negative value at the end of the bounce phase. As the Hubble parameter is negative at the beginning of the bounce phase, one can immediately see that the necessary condition is
$ \begin{aligned} \int_{t_{B-}}^{t_{B+}} {\rm d} t\;\dot H>0, \end{aligned} $

(10) where
$ t_{B-} $ and$ t_{B+} $ refer to the cosmic time at the beginning and end of the bounce phase, respectively. In addition, it holds that during the bounce phase [28],$ \begin{aligned} \dot\phi^2\simeq \frac{-K(\phi)+\sqrt{K^2(\phi)-12Q(\phi)V(\phi)}}{3Q(\phi)}. \end{aligned} $

(11) Therefore, we find that the necessary condition becomes
$ \begin{aligned}[b]& \int_{\phi_{B-}}^{\phi_{B+}}{\rm d}\phi\;\sqrt{\frac{-K(\phi)+\sqrt{K^2(\phi)-12Q(\phi)V(\phi)}}{Q(\phi)}}\\&\quad \times \left(-2K(\phi)-\sqrt{K^2(\phi)-12Q(\phi)V(\phi)} \right) >0, \end{aligned} $

(12) where
$ \phi_{B-}= -\sqrt{2(\sqrt2-1)} $ and$ \phi_{B+}= +\sqrt{2(\sqrt2-1)} $ represent the values of ϕ at the beginning and end of the bounce phase, respectively. Using the fact that K, Q, and V are even functions and$ 1\leq Q(\phi)/q\leq 2 $ for$\phi_{B-}\leq \phi\leq\phi_{B+}$ , the above necessary condition is reduced into a simpler form, namely,$ \begin{aligned} \int_{0}^{\phi_{B+}}{\rm d}\phi\sqrt{|K(\phi)|+P(\phi)}\left(2\sqrt 2 |K(\phi)|-P(\phi)\right)>0, \end{aligned} $

(13) where
$ \begin{aligned} P(\phi)\equiv \sqrt{K^2(\phi)-12Q(\phi)V(\phi)}. \end{aligned} $

(14) We then proceed as follows:
$ \begin{aligned}[b] (13)&\Longrightarrow 2\sqrt2\int_{0}^{\phi_{B+}}{\rm d}\phi \;|K|\sqrt{|K|+P}>\int_{0}^{\phi_{B+}}{\rm d}\phi \;P\sqrt{|K|+P}\\ &\Longrightarrow 2\sqrt2\int_{0}^{\phi_{B+}}{\rm d}\phi \;\left(|K|^{3/2}+|K|\sqrt P\right)>\int_{0}^{\phi_{B+}}{\rm d}\phi \;P^{3/2}\\ & \Longrightarrow 4\sqrt 2\int_{0}^{\phi_{B+}}{\rm d}\phi\;|K|^{3/2}+2\sqrt2 (12qV_0)^{\frac14}\int_{0}^{\phi_{B+}}\frac{{\rm d}\phi}{\cosh^{\frac14}\lambda\phi}\\&>(12qV_0)^{\frac34}\int_{0}^{\phi_{B+}}\frac{{\rm d}\phi}{\cosh^{\frac34}\lambda\phi}\\ &\Longrightarrow 4\sqrt2\lambda+10\sqrt2 (12qV_0)^{\frac14}>\frac32(12qV_0)^{\frac34}, \end{aligned} $

(15) where in the last line, we used
$ \begin{aligned} \lambda\int_{0}^{\phi_{B+}}\frac{{\rm d}\phi}{\cosh^{\frac14}\lambda\phi}<5,\quad \lambda\int_{0}^{\phi_{B+}}\frac{{\rm d}\phi}{\cosh^{\frac34}\lambda\phi}>\frac32, \end{aligned} $

which can be verified numerically.
Equation (15) sets a λ-dependent upper bound on
$ qV_0 $ . For instance, one can find that$ qV_0\lesssim 16.2 $ when$ \lambda=\sqrt{20} $ ; otherwise, the divergence of the Hubble parameter will surely appear (see Fig. 3).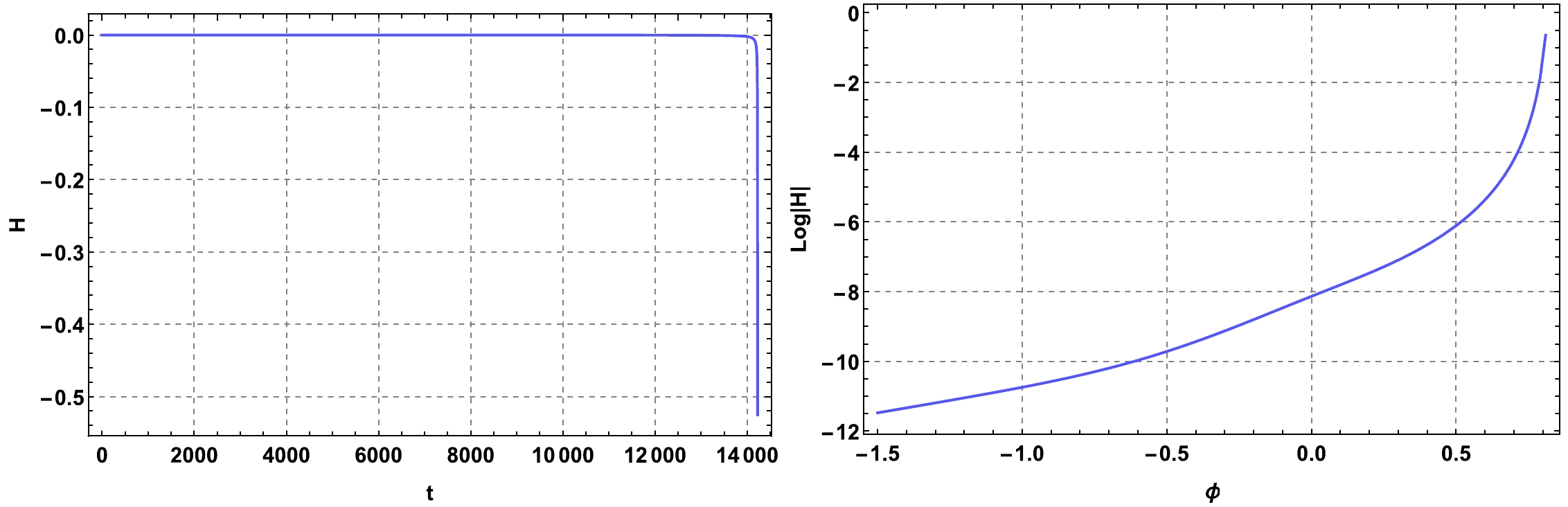
Figure 3. (color online) Plots showing divergence of the Hubble parameter H for the model parameters given by
$ \lambda=\sqrt{20} $ ,$ q=10^8 $ , and$ V_0=1.7\times 10^{-7} $ . The left panel shows the evolution of H according to the cosmic time t, while in the right panel, the horizontal axis denotes ϕ. As mentioned before, the form of these plots does not depend on the initial conditions. -
Particle production in nonsingular bounce scenarios has been discussed in [28, 36, 37], where it was shown that, during the ekpyrotic contracting and bounce phases, particles are generated enough to reheat the universe. Meanwhile, the amount of particle production up to the bounce phase should not exceed a certain bound for the nonsingular bounce scenario, such as that given by (1), to be consistent with the currently observed accelerated expansion of the universe, namely [27],
$ \begin{aligned} \frac{\sqrt{\dfrac{\rho_{m0}}{\rho_0}}}{1+\sqrt{1+\dfrac{\rho_{m0}}{\rho_0}}}< \left(\frac{\rho_{CC}}{2\lambda V_0}{\rm e}^{\lambda\phi_{B+}}\right)^{\frac{1-w_m}{\lambda}\sqrt{\frac 38}}, \end{aligned} $

(16) or
$ \begin{aligned} \frac{\lambda}{1-w_m}\sqrt{\frac32}\log\frac{\rho_{m0}}{\rho_0}<\phi_{B+}\lambda+\log\frac{\rho_{CC}}{2\lambda V_0}, \end{aligned} $

(17) where
$ \rho_{m0} $ and$ \rho_0 $ refer to the energy density of matter/radiation with equation of state$ w_m $ and background at the end of the bounce phase, respectively, and$ \rho_{CC} $ represents the observed dark energy density, which is of the order$ 10^{-120} $ in Planck units. Obviously, we can obtain a constraint on the bounce scenario from (17), once the lower bound of energy density of the generated particles is expressed in terms of the model parameters.Hence, we would like to estimate the lower bound of energy density of χ-particles generated up to the bounce phase. The whole procedure is similar to that in [28]. The first step is to solve the differential equation for the Fourier mode
$ v_k $ of$ v\equiv a\Omega(\phi)\chi $ , which is given by$ \begin{aligned} v_k''+\left(k^2-\mu^2(\eta)\right)v_k=0,\quad \mu^2(\eta)\equiv \mathscr H^2+\mathscr H'+\frac{\Omega''}{\Omega}+2\mathscr H\frac{\Omega'}{\Omega}, \end{aligned} $

(18) where the prime denotes the derivative with respect to the conformal time η defined by
${\rm d}\eta=a^{-1} {\rm d}t$ . Note that the contribution of$ \Omega(\phi) $ -related terms to$ \mu^2(\eta) $ becomes negligible from the bounce phase, which is in contrast to the case in [28], where$ \Omega(\phi) $ -related terms played a major role in particle creation during the bounce phase. As in [28, 36, 37], we assume the initial conditions for$ v_k $ corresponding to a Bunch-Davies vacuum state, i.e.,$ \begin{aligned} \lim_{\eta\to-\infty}v_k=\frac{{\rm e}^{-{\rm i} k\eta}}{\sqrt{2k}}. \end{aligned} $

(19) As can be seen in Fig. 4,
$ \mu^2(\eta) $ during the ekpyrotic and kinetic phase is much less than during the bounce phase. This implies that the solution of (18) during these phases is effectively given by a plane wave, namely,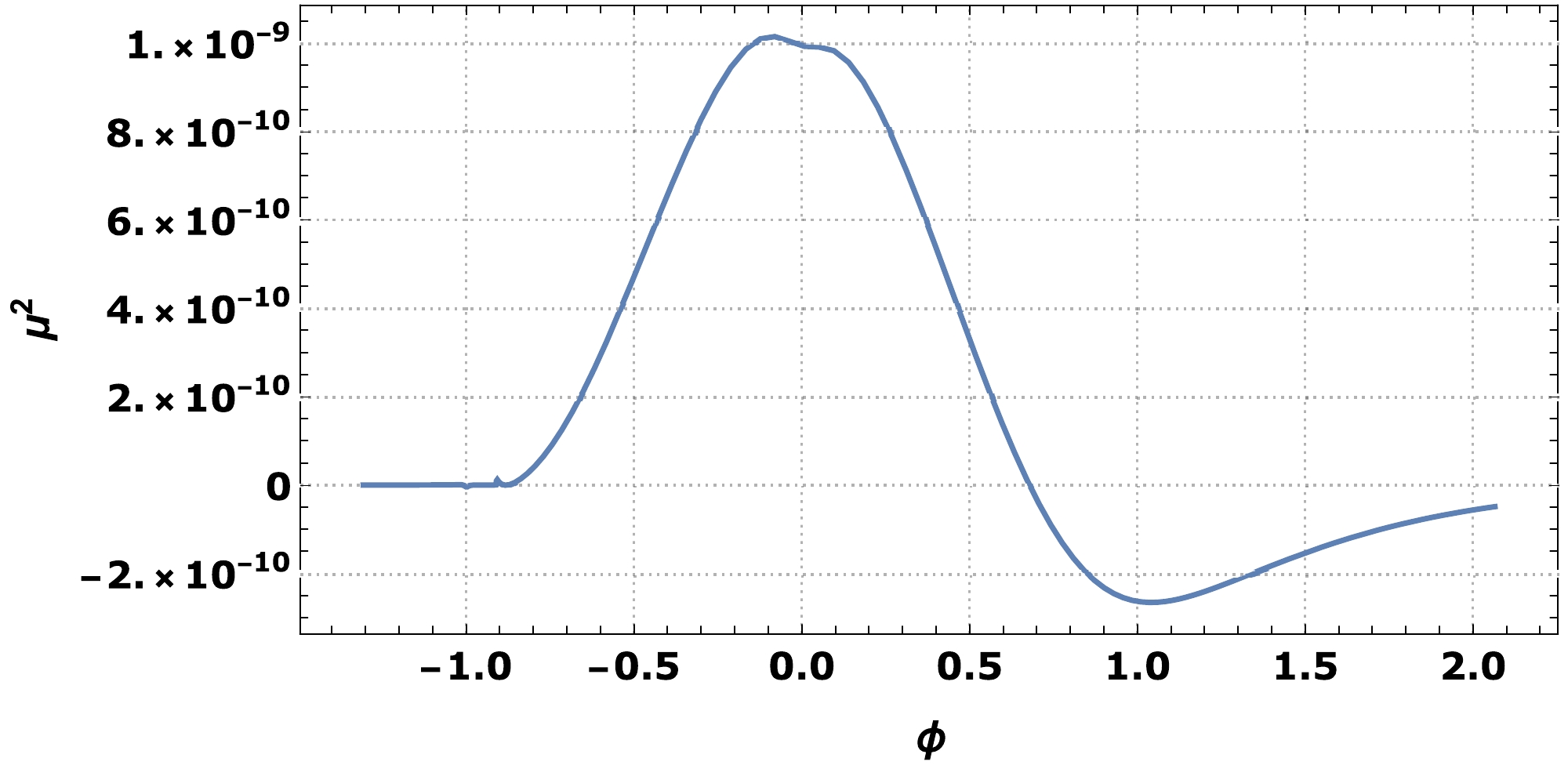
Figure 4. (color online) Plot of
$ \mu^2 $ for the model parameters given by$ \lambda=3\sqrt{20} $ ,$ q=10^8 $ , and$ V_0=2\times 10^{-10} $ . The horizontal axis denotes ϕ.$ \begin{aligned} v_k & \simeq \frac{{\rm e}^{-{\rm i}k(\eta-\eta_{B-})}}{\sqrt{2k}},& \eta\leq \eta_{B-}, \end{aligned} $

(20) $ \begin{aligned} v_k & \simeq \frac{1}{\sqrt{2k}}\left(\alpha_k {\rm e}^{-{\rm i}k(\eta-\eta_{B+})}+\beta_k {\rm e}^{+{\rm i}k(\eta-\eta_{B+})}\right), & \eta\geq \eta_{B+}, \end{aligned} $

(21) where
$ \eta_{B-} $ and$ \eta_{B+} $ denote the conformal time at the beginning and end of the bounce phase, respectively. Recall that$ \alpha_k $ and$ \beta_k $ are the so-called Bogolyubov coefficients, and$ n_k=|\beta_k|^2 $ gives the number density of generated particles with comoving wave number k. Once the Bogolyubov coefficient$ \beta_k $ is determined, we can compute the energy density of the generated particles via [36]$ \begin{aligned} \rho_{m0}=\frac{1}{2\pi^2}\int_{0}^{\infty}{\rm d} k\;k^3|\beta_k|^2. \end{aligned} $

(22) Determining
$ \beta_k $ requires us to solve (18) during the bounce phase as in [28], which is non-trivial because$ \mu^2(\eta) $ takes the complicated form in this phase (see, e.g., Fig. 4). As our aim is just to use the inequality (17), which contains only the logarithm of$ \rho_{m0} $ , we only need to estimate the order of$ \rho_{m0} $ . To this end,$ \mu^2(\eta) $ during the bounce phase can be approximated by a certain constant value, namely,$ \begin{aligned} \mu^2(\eta)\simeq \Lambda^2, \end{aligned} $

(23) where Λ is an order one fraction of
$ \mu_{\max}= $ $ \max_{\eta_{B-}\leq\eta\leq\eta_{B+}} |\mu(\eta)|$ . It is now simple to compute the Bogolyubov coefficient$ \beta_k $ , and hence, the energy density$ \rho_{m0} $ becomes$ \begin{aligned}[b] \rho_{m0}\simeq\; &\frac{1}{8\pi^2}\int_{0}^{\Lambda}{\rm d}k\;k^3 \left| \sqrt{\frac{\Lambda^2}{k^2}-1}-\frac{1}{\sqrt{\dfrac{\Lambda^2}{k^2}-1}}\right|^2 \sinh^2 (T\sqrt{\Lambda^2-k^2})\\ &+\frac{1}{8\pi^2}\int_{\Lambda}^{+\infty}{\rm d}k\;k^3\left|\sqrt{1-\frac{\Lambda^2}{k^2}}-\frac{1}{\sqrt{1-\dfrac{\Lambda^2}{k^2}}}\right|^2\\&\times\sin^2 (T\sqrt{k^2-\Lambda^2}), \end{aligned} $

(24) where
$ T \equiv\eta_{B+}-\eta_{B-} $ is the duration of the bounce phase. Obviously, the second integral in the above expression logarithmically diverges for large k, which has its origin in the approximation (23). Namely, this ultraviolet divergence disappears for smooth function$ \mu^2(\eta) $ [28, 38]. We therefore assume that there is an ultraviolet cutoff$ k_{\max} $ . In fact, as shown explicitly in [28], we can set$ k_{\max} $ to$ 3\mu_{\max} $ ; the produced particles with comoving wave number$ k\geq 3\mu_{\max} $ provide a minor contribution to$ \rho_{m0} $ . After a change in variables, we get$ \begin{aligned} \frac{8\pi^2}{\Lambda^4}\rho_{m0}\simeq&\int_{0}^{1}{\rm d}s\;s\left|2s-\frac 1s\right|^2\sinh^2(\Lambda Ts)+\int_{0}^{3}\frac{{\rm d}s}{s}\sin^2(\Lambda T s). \end{aligned} $

(25) One can readily see that the second integral is
$ \mathscr O(1) $ , while the first one has an exponential relationship with$ \Lambda T $ .Now, we only have to express
$\mu_{\max}$ and T in terms of the model parameters. It follows from (6) that we have$\dot\phi\sim{1}/{\sqrt q}$ up to an order one factor during the bounce phase; therefore, the duration T of the bounce phase is up to an order one constant (cf., Eq. (24) in [28])$ \begin{aligned} T\simeq \int_{\phi_{B-}}^{\phi_{B+}}\frac{{\rm d}\phi}{\dot\phi}\sim \sqrt q, \end{aligned} $

(26) where we have used the fact that the change of the scale factor a during the bounce phase is negligible. Meanwhile, as mentioned before, during the bounce phase, we have
$ \mu^2(\eta)\simeq \mathscr H'+\mathscr H^2 $ , which can be estimated by using$ \mathscr H^2\ll \mathscr H'\lesssim \dfrac{1}{9q} $ [28]. It follows that up to order one constants,$ \begin{aligned} \mu_{\max}\sim \Lambda\sim \frac{1}{\sqrt q}. \end{aligned} $

(27) Collecting the results above, we find that
$ \Lambda T $ is order one, and therefore,$ \begin{aligned} \rho_{m0} \sim \frac{1}{8\pi^2 q^2}, \end{aligned} $

(28) up to an order one factor (cf., Eq. (46) in [28], where
$ \rho_{m0} $ depends on both q and b). The dependence of$ \rho_{m0} $ only on q among the model parameters is obvious; most particle creation by classical backgrounds occurs during the bounce phase, whose background dynamics basically depend on q.Moreover,
$ \rho_0 $ is given by$ \rho_0=3H_{B+}^2 $ , where$ H_{B+} $ , the Hubble parameter at the end of the bounce phase, is an order one fraction of${1}/{\sqrt q}$ [28]. Combining this with (17) and (28), we get a constraint$ \begin{aligned} \frac{\lambda}{2}\log q+\lambda+\log\frac{\rho_{CC}}{2\lambda V_0}>0, \end{aligned} $

(29) where we consider the fact that most of the created particles have the equation of state
$ w_m=1/3 $ and ignore some order one factors. -
The two constraints we derived in the previous sections can be used in determining the parameter space for the nonsingular bounce scenario (1), in combination with other constraints already available in literature:
$ \begin{aligned} V_0\leq 10^{-4}, \end{aligned} $

(30a) $ \begin{aligned} \sqrt 6<\lambda\lesssim 38, \end{aligned} $

(30b) $ \begin{aligned} \frac{\left(\dfrac{\lambda^2}{2}-3\right)\cosh\left(\sqrt{2(\sqrt 2-1)}\lambda-2\right)}{\left(\dfrac{\lambda^2}{2}-1\right)^2}\lesssim 10^{7}\mathscr F^2 V_0, \end{aligned} $

(30c) where
$ \mathscr F $ , an amplification factor of the entropy perturbations across the bounce phase, is at most$ \mathscr O(10^4) $ [23]. The first constraint comes from the fact that we are using the low-energy effective field theory description and have to suppress any quantum gravity effect [22]. The second and last constraints are due to suppressing the anisotropic stresses during the ekpyrotic contracting phase [39] and having the amplitude of the curvature perturbations in agreement with the observations (see Eq. (4.26) and (4.27) in Ref. [27]). Note that all of these constraints are for the model parameters q,$ V_0 $ , and λ; the other ones, b and$V_{\rm DE}$ , are fixed in terms of λ and observations, as mentioned before.We plot the parameter space for the model (1) determined by the constraints (15), (29), and (30) (see Fig. 5). One can clearly see that the lower bound of λ is lifted from
$ \sqrt 6 $ to$ 7 $ ; for instance,$ \lambda=\sqrt{20} $ , which is typically used in the literature [22, 23, 27], is not allowed. In addition, it is evident that the greater the value of λ, the larger the allowed range of parameters q and$ V_0 $ . For instance, q and$ V_0 $ can vary by$ 12\sim 13 $ orders of magnitude for$ \lambda=32 $ . This is indeed a large space; for instance, under minimal warm inflation [40], the parameters can vary by$ 5\sim 7 $ orders of magnitude. This implies that the nonsingular bounce scenario (1) is preferable for the large values of λ.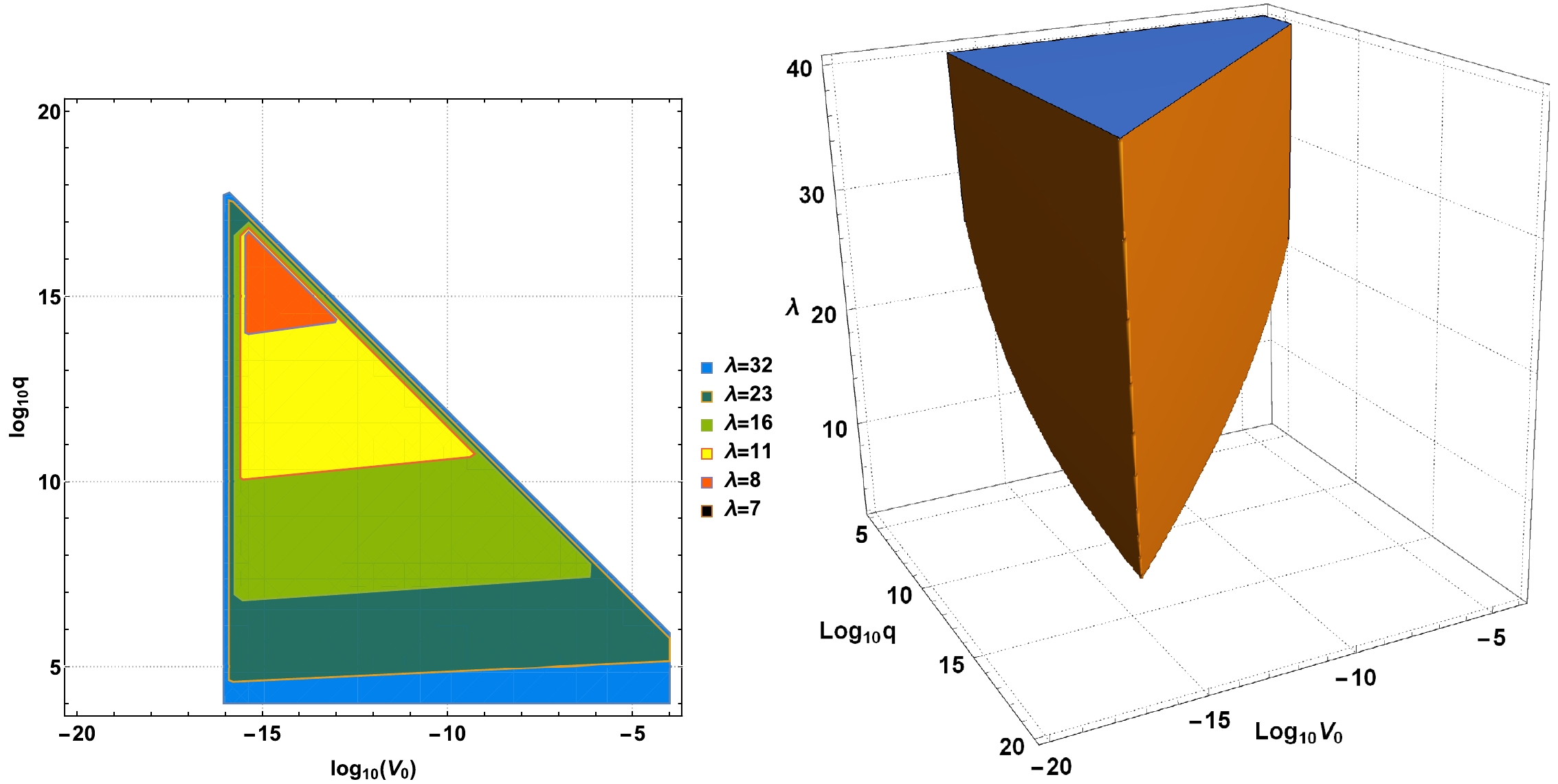
Figure 5. (color online) Allowed space for the model parameters q,
$ V_0 $ , and λ. Two dimensional space for q and$ V_0 $ is plotted for various values of λ in the left figure, while the total three dimensional space is plotted in the right figure. The left figure shows that$ \lambda\leq 7 $ is not allowed. -
In this study, we derived two constraints (15) and (29): one from the possible appearance of the singularity in background evolution and the other one from the relation between particle creation and late-time accelerated expansion. Combining these with the already known constraints, we determined the allowed parameter space for the nonsingular bounce scenario.
We emphasize that there can be other constraints; for instance, non-Gaussianity of the curvature perturbation may put a severe constraint on the model. For this, one must investigate the conversion of entropy perturbations into curvature perturbations in detail, which we plan to address in future work.
Cosmological constraints on the background dynamics of a two-field nonsingular bounce model
- Received Date: 2024-06-04
- Available Online: 2024-11-15
Abstract: In this study, we consider a nonsingular two-field bounce scenario with non-minimal kinetic coupling between two scalar fields. We derive constraints on the model parameters from the finiteness of the physical quantities at the classical level and from the relation between the late-time accelerated expansion and particle production up to the bounce phase. We then determine the allowed parameter space for the model.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: