-
All the experimental data collected until now indicate that the properties of the scalar particle discovered in 2012 at the LHC by the ATLAS and CMS collaborations [1, 2] are compatible with those of the long-sought Higgs boson, which is the remanent of the mechanism of spontaneous symmetry breaking of the
$S U(2)_L\times U(1)_Y$ gauge symmetry in the Glashow-Salam-Weinberg Standard Model (SM). Nonetheless, there are still several couplings of this particle that remain to be measured with enough accuracy, such as the$ H\bar{b}b $ and$ H\mu^-\mu^+ $ interactions, whereas other ones are not experimentally reachable yet. This is the case, for instance, of the couplings of the Higgs boson to light fermions, or even further, the self couplings of the Higgs boson. Therefore, the study of the phenomenology of the Higgs boson is expected to play an important role in probing the SM and searching for new-physics effects in present and future colliders. In these research lines, the couplings of the Higgs boson to the weak gauge bosons$ HZZ $ and$ HWW $ , which arise at the tree level in the SM, have long attracted considerable attention both theoretically and experimentally. Concerning the$ HZZ $ vertex, it has played a crucial role in the experimental study of the Higgs boson at the LHC via the$ H\to ZZ^*\to 4\ell $ decay, which provides a clear signal and allows for a precise resolution of the Higgs boson mass, despite the fact that its branching ratio is considerably smaller than that of other decay channels such as$ H\to WW^* $ ,$ H\to \tau^+\tau^- $ , and$ H\to\bar{b}b $ . A milestone was achieved in 2022 when the CMS collaboration reported the measurement of the off-shell$ H^*ZZ $ coupling via the$ pp\to H^*\to ZZ $ process for the first time [3]. This result was also confirmed by the ATLAS collaboration the following year [4].Although one-loop corrections to the
$ HZZ $ vertex were calculated long ago in the framework of the SM [5, 6], more recently, a new evaluation was presented [7] that could be more suitable for the recent progress on the theoretical and experimental study of this coupling.The most general
$ HZZ $ vertex can be parameterized by an effective Lagrangian expressed in terms of four coupling constants: as follows$ \begin{aligned}[b] \mathcal{L}^{HZZ}=\;&\frac{g }{c_W}m_Z \Bigg[\frac{(1+a_Z)}{2} H Z_\mu Z^\mu\\&+\frac{1}{2m^2_Z} \Big\{\hat{b}_Z HZ_{\mu\nu}Z^{\mu\nu}+\hat{c}_Z HZ_\mu\partial_\nu Z^{\mu\nu}+ \widetilde{b}_Z H Z_{\mu\nu}\widetilde{Z}^{\mu\nu}\Big\}\Bigg], \end{aligned} $

(1) where
$ a_Z $ denotes the corrections to the SM tree-level coupling via loop contributions or new-physics effects, whereas$ \hat{b}_Z $ ,$ \hat{c}_Z $ , and$ \widetilde{b}_Z $ are absent at the tree level in the SM and thus are termed anomalous couplings. The anomalous$\rm CP $ -conserving coupling$ \hat{b}_Z $ is induced at the one-loop level [5, 6] and can reach values of the order of$ 10^{-3} $ [7], while the$\rm CP$ -violating one$ \widetilde{b}_Z $ would arise up to the three-loop level and has been estimated to be of the order of$ 10^{-11} $ [8]. The$ \hat{c}_Z $ anomalous coupling is also expected to be generated at one-loop level; however, it has not been identified in SM calculations.The phenomenology of the
$ HZZ $ anomalous couplings has been extensively studied in both lepton [9−11] and hadron colliders [12]. These studies have shown that non-SM contributions to the$ HZZ $ coupling could be significantly constrained in the future, providing an opportunity to detect new-physics effects through$ HZZ $ -mediated processes. In particular, polarization observables in the$ Z^\ast\rightarrow HZ $ process at the LHC have been used to revisit the anomalous couplings, yielding limits of around$ 10^{-3}-10^{-4} $ for the real and absorptive parts of the$\rm CP$ -conserving$ \hat{b}_Z $ anomalous coupling and of the order of$ 10^{-3} $ for the$\rm CP$ -violating$ \widetilde{b}_Z $ coupling [13]. Furthermore, limits on the anomalous couplings have been established at$ e^-e^- $ ,$ ep $ , and$ \gamma e $ colliders [10, 14−24]. The CMS collaboration has also obtained bounds on effective ratios of the anomalous couplings [3, 25−27], which were combined with the theoretical SM contribution to$ \hat{b}_Z $ in a recent study [7]. It was found that the$ \hat{c}_Z $ and$ \widetilde{b}_Z $ anomalous couplings can be constrained to values as tight as$ 10^{-2}-10^{-4} $ depending on the energy region. Finally, other off-shell couplings such as trilinear neutral gauge boson couplings [28−31] and the coupling of the gluon with a quark-antiquark pair [32, 33] have also been investigated in recent studies.In this study, we aimed to analyze the effects of
$ HZZ $ anomalous couplings on the off-shell decay$H^*\to ZZ \to 4\ell$ via polarized$ Z $ gauge bosons. The polarizations of the$ Z $ boson are of great interest at the LHC because a longitudinally polarized$ Z $ boson pair has recently been reported by the ATLAS collaboration [34]. Moreover, the production of longitudinally$ W^\pm Z $ pairs is also being studied [35]. The polarization fractions of the$ Z $ boson have been measured by the CMS, ATLAS, and LHCb collaborations [36−39]. Previous analyses of the polarization of gauge bosons at the LHC include$ W^\pm Z $ production [40],$ W $ +Jets events [41, 42],$ W $ bosons produced in top decays [43−46], and$ W^\pm W^\pm $ production [47]. The$\mathrm{MadGraph5\_aMC@NLO} $ [48] and$\mathrm{SHERPA} $ [49] event generators have also included the possibility of generating polarized amplitudes. A method to identify polarizations of$ Z $ bosons has been discussed in Ref. [50], whereas a higher sensitivity to polarized$ Z $ bosons is also expected in the recent upgrade of the LHC [51]. We considered the most general scenario with both$ Z $ gauge bosons on-shell and complex anomalous$ HZZ $ couplings. Furthermore, we analyzed the behavior of some observables that can be sensitive to new-physics contributions. In particular, we studied the effects of the absorptive parts of the anomalous$ HZZ $ couplings, which have been overlooked in the past but can lead to interesting results. For the sake of completeness, we also studied the scenario with unpolarized$ Z $ gauge bosons.The rest of this paper is organized as follows. Section II is devoted to discuss the suitable theoretical framework for the study of the
$ H^*\to ZZ\to 4\ell $ decay width, with explicit analytical expressions for the polarized and unpolarized square amplitudes, out of which the respective$ H^*\to ZZ\to 4\ell $ differential decay widths were obtained. The numerical analysis conducted in this study is presented in Sec. III; we cross-checked our calculation method with an alternative evaluation performed via$ \mathrm{MadGraph5\_aMC@NLO}$ . The behavior of the differential decay, angular distributions, and left-right and forward-backward asymmetries were analyzed in some realistic scenarios for the values of the real and absorptive parts of the anomalous$ HZZ $ couplings. In Sec. IV, we present our concluding remarks and outlook. Finally, the kinematics of the$ H^*\to ZZ\to 4\ell $ decay and four-body phase space are discussed in Appendix A. -
We next present all the analytical formulas required for the calculation of the unpolarized and polarized
$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width. The most general form of the$ HZZ $ vertex functions with complex anomalous couplings is considered, whereas the contributions of the SM up to the one-loop level are also included [7]. -
The
$ S $ -matrix element obtained from the Lagrangian given by Eq. (1) can be expressed as$ {\rm i}\mathcal{M}={\rm i}\frac{g}{c_W}m_Z \Gamma^{ZZH}_{\mu\nu}(q^2) Z^\mu(p_1) Z^\nu(p_2) H(q), $

(2) where the vertex function
$ \Gamma^{ZZH}_{\mu\nu}(q^2) $ for on-shell$ Z $ gauge bosons and an off-shell Higgs boson can be as$ \begin{align} \Gamma_{\mu\nu}^{ZZH}(q^2)=h^H_1(q^2) g_{\mu\nu}+\frac{h_2^H(q^2)}{m_Z^2} p_{1\nu}p_{2\mu}+\frac{h_3^H(q^2) }{m_Z^2}\epsilon_{\mu\nu\alpha\beta}p_{1}^\alpha p_{2}^\beta, \end{align} $

(3) with
$ h_i^H $ ($ i= $ 1, 2, 3) denoting the form factors expressed in terms of the anomalous couplings of the Lagrangian in Eq. (1) as$ \begin{align} & h_1^H(q^2)=1+ a_Z- \hat{b}_Z \frac{q^2-2m_Z^2}{m_Z^2}+ \hat{c}_Z, \end{align} $

(4) $ \begin{align} &h_2^H(q^2)= 2 \hat{b}_Z, \end{align} $

(5) $ \begin{align} &h_3^H(q^2)= 2 \widetilde{b}_Z. \end{align} $

(6) These form factors are both explicit and implicit functions of
$ q^2 $ given that the anomalous couplings also depend on the off-shell Higgs boson four-momenta.The main objective of this study was the analysis of the anomalous contributions. Thus, we considered a vanishing
$ a_Z $ . For a study of the SM one-loop contributions to the$ a_Z $ coupling along with the renormalization procedure, we refer the reader to Ref. [5]. The$ \hat{b}_Z $ ,$ \hat{c}_Z $ , and$ \widetilde{b}_Z $ anomalous couplings are considered non-zero in the rest of this paper. This is feasible in the SM, and new-physics contributions from new particles can also arise under the context of the two-Higgs doublet and Higgs singlet models [52], minimal Higgs triplet model [53], and minimal supersymmetric SM [54]. Recently, the SMEFT contributions have also been revisited [24]. Additionally, the$\rm CP$ -violating$ \widetilde{b}_Z $ anomalous coupling may be induced through flavor changing neutral currents mediated by the$ Z $ or$ H $ bosons, as in the$ HZ\gamma $ vertex [55].Given that the anomalous couplings can be taken as complex in general [7, 56], the form factors in Eqs. (4)−(6) can be expressed as
$ h_i^H={\rm{Re}}\big[h_i^H\big]+{\rm i} {\rm{Im}}\big[h_i^H\big]. $

(7) Before moving forward, it is important to note some general limitations regarding the prescription used in the Lagrangian expressed by Eq. (1) and the absorptive parts of the form factors. It has been observed that the
$ HZZ $ Lagrangian requires real$ \hat{b}_Z $ ,$ \hat{c}_Z $ , and$ \widetilde{b}_Z $ anomalous couplings to be Hermitian. This seems to contradict our assumption in Eq. (7). However, the Lagrangian in Eq. (1) is only valid for the Born approximation because it exclusively describes the external particles in an effective approach [57]. Anomalous couplings are generated through quantum corrections by heavy or light particles at one-loop level or higher orders. The new operators that induce these loop effects are not accounted for in the Lagrangian expressed by Eq. (1) and do not necessarily require real anomalous couplings to form Hermitian amplitudes [9]. For instance, in the SM, the contributions arising at the one-loop level develop an absorptive part as long as the magnitude of the off-shell Higgs boson four-momenta is above the$ \|q\| = 2m_i $ threshold, where$ m_i $ is the mass of the particles coupled to$ H $ . Therefore, in the most general scenario, the$ \hat{b}_Z $ ,$ \hat{c}_Z $ , and$ \tilde{b}_Z $ anomalous couplings are no longer real constants but complex functions of$ q^2 $ .Although the absorptive parts have been neglected in experimental analyses at the LHC, their effects have been discussed in some theoretical studies [9, 13, 15] and more recently via a left-right asymmetry [7], which may be reconstructed in the final state of the
$ H^\ast\rightarrow ZZ\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay. Polarization effects of the$ Z $ gauge bosons on the$ H\to ZZ $ decay of the Higgs boson have already been studied [58, 59], though non-anomalous$ HZZ $ couplings and one on-shell$ Z $ gauge boson were considered. Similar calculations were also reported in [8, 60−62]. The scenario where both$ Z $ gauge bosons are on-shell and the$ HZZ $ couplings are purely real was studied in Refs. [6, 63, 64]. Finally, a restrictive scenario where not all the$ HZZ $ anomalous couplings were taken as complex was considered in Ref. [15].In this study, we analyzed the most general scenario where all the anomalous
$ HZZ $ couplings are complex and calculated the unpolarized and polarized off-shell$ H^\ast\rightarrow ZZ\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width. We also analyzed the implications of the absorptive parts of the$ HZZ $ anomalous couplings on some observables. -
Using the nomenclature shown in Fig. 1, the amplitude for the
$ H^\ast\rightarrow Z(p_1)Z(p_2)\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ process can be expressed as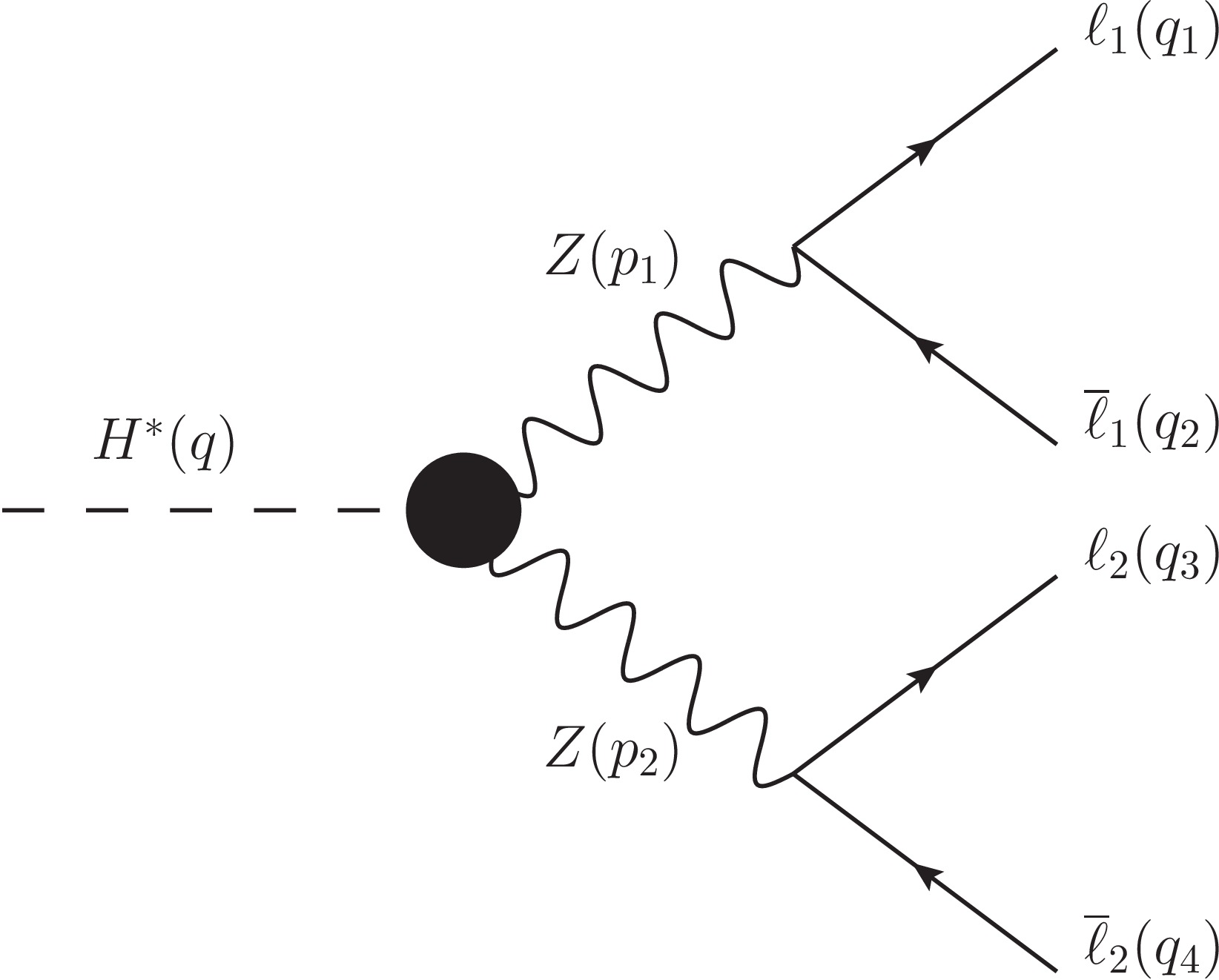
Figure 1. Nomenclature for the four-momenta of the particles involved in the Feynman diagram for the contribution of the
$ HZZ $ anomalous couplings to the Higgs boson decay$ H^\ast\rightarrow Z(p_1)Z(p_2)\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ .$ \begin{aligned}[b] \mathcal{M}_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}=\;&\mathcal{M}^{\mu\nu}_{H^\ast\rightarrow Z(p_1)Z(p_2)} \frac{{\rm i}\sum\epsilon_\eta(p_1,\lambda_1)\epsilon_\mu^{\ast}(p_1,\lambda_1)}{p_1^2-m_Z^2+{\rm i}\Gamma_Z m_Z} \\&\times\mathcal{M}^\eta_{Z(p_1)\rightarrow \overline{\ell}_1\ell_1} \frac{{\rm i}\sum\epsilon_\kappa(p_2,\lambda_2)\epsilon^{\ast}_\nu(p_2,\lambda_2)}{p_2^2-m_Z^2+{\rm i}\Gamma_Z m_Z} \\&\times\mathcal{M}^\kappa_{Z(p_2)\rightarrow \overline{\ell}_2\ell_2} , \end{aligned} $

(8) where
$ \Gamma_Z $ is the$ Z $ gauge boson decay width. According to the Lagrangian in Eq. (1), the amplitude for the process$ H^\ast\rightarrow ZZ $ is expressed in terms of the complex$ h_i^H $ form factors as$ \begin{aligned}[b] \mathcal{M}^{\mu\nu}_{H^\ast\rightarrow Z(p_1)Z(p_2)}=\;&{\rm i}\Big(\frac{g }{c_W}\Big)m_Z\Bigg\{g^{\mu \nu}\Big({\rm{Re}}\big[h_1^H\big]+{\rm i} {\rm{Im}}\big[h_1^H\big] \Big) \\&+\frac{p_2^{\mu }{p_1}^{\nu }}{m_Z^2} \Big( {\rm{Re}}\big[h_2^H\big]+{\rm i} {\rm{Im}}\big[h_2^H\big]\Big) \\ &+\frac{\epsilon^{\mu \nu \alpha \beta }p_{1\alpha} p_{2\beta} }{m_Z^2}\Big({\rm{Re}}\big[h_3^H\big] +{\rm i} {\rm{Im}}\big[h_3^H\big] \Big)\Bigg\}, \end{aligned} $

(9) whereas the amplitudes for the
$ Z\rightarrow \overline{\ell}_1\ell_1 $ and$ Z\rightarrow \overline{\ell}_2\ell_2 $ processes are$ \begin{align} & \mathcal{M}^\eta_{Z(p_1)\rightarrow \overline{\ell}_1\ell_1}={\rm i}\frac{g}{c_W}\overline{u}(q_2)\gamma^\eta \big( g_V-g_A \gamma^5\big)u(q_1), \end{align} $

(10) $ \begin{align} & \mathcal{M}^\kappa_{Z(p_2)\rightarrow \overline{\ell}_2\ell_2}={\rm i}\frac{g}{c_W}\overline{u}(q_4)\gamma^\kappa \big( g_V-g_A \gamma^5\big)u(q_3). \end{align} $

(11) For the
$ Z $ gauge boson propagators of Eq. (8), we used the completeness relation [49]$ -g^{\mu\nu}+\frac{k^\mu k^\nu}{m_Z^2}=\sum\limits^3_{\lambda=1}\epsilon^\mu_{\lambda}(k)\epsilon^{\ast\nu}_{\lambda}(k), $

(12) where we only considered three polarizations given that both
$ Z $ gauge bosons are on-shell.To study the polarization effects in the final state, it is convenient to rewrite Eq. (8) as a sum of the polarized amplitudes,
$ \begin{aligned}[b] &\mathcal{M}_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}(\lambda_1,\lambda_2)=\\&\sum_{\lambda_1}\sum_{\lambda_2}\frac{\mathcal{M}_{H^\ast\rightarrow Z(p_1)Z(p_2)}(\lambda_1,\lambda_2) \mathcal{M}_{Z(p_1)\rightarrow \overline{\ell}_1\ell_1}(\lambda_1)\mathcal{M}_{Z(p_2)\rightarrow \overline{\ell}_2\ell_2}(\lambda_2)}{\big(p_1^2-m_Z^2+{\rm i}\Gamma m_Z\big)\big(p_2^2-m_Z^2+{\rm i}\Gamma m_Z\big)} \end{aligned} $

(13) where
$ \mathcal{M}_{H^\ast\rightarrow Z(p_1)Z(p_2)}(\lambda_1,\lambda_2)=\mathcal{M}_{H^\ast\rightarrow Z(p_1)Z(p_2)}^{\mu\nu}\epsilon^\ast_\mu(p_1,\lambda_1)\epsilon_\nu^\ast(p_2,\lambda_2), $

(14) $ \begin{align} \mathcal{M}_{Z(p_i)\rightarrow \overline{\ell}_i\ell_i}(\lambda_i)&=\mathcal{M}_{Z(p_i)\rightarrow \overline{\ell}_i\ell_i}^\mu\epsilon_\mu(p_i,\lambda_i). \end{align} $

(15) Given that the
$ \mathcal{M}_{H^\ast\rightarrow Z(p_1)Z(p_2)}(\lambda_1,\lambda_2) $ polarized amplitude is non-vanishing only for$ \lambda_1=\lambda_2 $ [7, 64], the square amplitude can be expressed as$ \begin{align} \mathcal{M}^2_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}= &\frac{\sum_\lambda \mathcal{M}^2_{H^\ast\rightarrow Z(p_1)Z(p_2)}(\lambda,\lambda) \mathcal{M}^2_{Z(p_1)\rightarrow \overline{\ell}_1\ell_1}(\lambda)\mathcal{M}^2_{Z(p_2)\rightarrow \overline{\ell}_2\ell_2}(\lambda)+\mathcal{M}^2_{\rm{int}} }{\left((p_1^2-m_Z^2)^2+\Gamma^2 m_Z^2\right)\left((p_2^2-m_Z^2)^2+\Gamma^2 m_Z^2\right)}. \end{align} $

(16) where the interference term
$ \mathcal{M}^2_{\rm{int}} $ is given by$ \begin{aligned}[b] \mathcal{M}^2_{\rm{int}}=\;&\sum_{\lambda_1} \sum_{\lambda_2\neq \lambda_1 }\mathcal{M}_{H^\ast\rightarrow Z(p_1)Z(p_2)}(\lambda_1,\lambda_1) \mathcal{M}^\dagger_{H^\ast\rightarrow Z(p_1)Z(p_2)}(\lambda_2,\lambda_2)\mathcal{M}_{Z(p_1)\rightarrow \overline{\ell}_1\ell_1}(\lambda_1)\mathcal{M}^\dagger_{Z(p_1)\rightarrow \overline{\ell}_1\ell_1}(\lambda_2)\\ &\times\mathcal{M}_{Z(p_2)\rightarrow \overline{\ell}_2\ell_2}(\lambda_1)\mathcal{M}^\dagger_{Z(p_2)\rightarrow \overline{\ell}_2\ell_2}(\lambda_2). \end{aligned} $

(17) From the first term of the right-hand side in Eq. (16), we can extract the contributions of polarized
$ Z $ gauge bosons with polarizations$ \lambda=L $ ,$ R $ , and$ 0 $ , which enables the study of the polarized decay width and other observables of interest. As described below, to obtain the$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width, we followed the approach of Ref. [60] for the calculation of the$ H\rightarrow ZZ^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay. A similar procedure was followed in Refs. [65, 66] for the decay$ K^\pm\rightarrow \pi^\pm \pi^0 e^+ e^- $ , whereas an alternative method was implemented in Ref. [61] for the$ H\rightarrow ZZ^\ast\rightarrow \ell^+\ell^-\tau^+\tau^- $ and$ H\rightarrow WW^\ast\rightarrow \ell^-\overline{\nu}_\ell \tau^+\nu_\tau $ decays using transformation properties of the helicity amplitudes under the rotation group.The phase space for the
$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ process, along with the kinematics, is presented in Appendix A. The relevant angular variables which the square$ \mathcal{M}^2_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2} $ amplitude depends on$ \theta_1 $ ,$ \theta_2 $ , and$ \phi $ , described in Fig 2. Note that the square polarized amplitudes$\mathcal{M}^2_{H^\ast\to ZZ}(\lambda,\lambda)$ ,$\mathcal{M}^2_{Z(p_1)\to \bar{\ell}_1\ell_1}(\lambda)$ , and$\mathcal{M}^2_{Z(p_2)\to \bar{\ell}_2\ell_2}(\lambda)$ can be computed in the corresponding$ H^\ast $ ,$ Z(p_1) $ , and$ Z(p_2) $ rest frames because each one depends only on scalar products of four-momenta given in the same inertial frame. Furthermore, these square amplitudes are Lorentz invariant. Thus, it is not necessary to apply a boost to bring them into a common reference system. On the other hand, the interference term$ \mathcal{M}^2_{\rm{int}} $ is expressed in terms of partial amplitudes evaluated in distinct reference frames, so a boost from the$ Z(p_i)\rightarrow \overline{\ell}_i\ell_i $ reference frames into the rest frame of the Higgs boson is required to perform the sum in Eq. (17). The same is true for the calculation of the unpolarized case via standard techniques as scalar products of four-momenta given in distinct reference frames are also involved.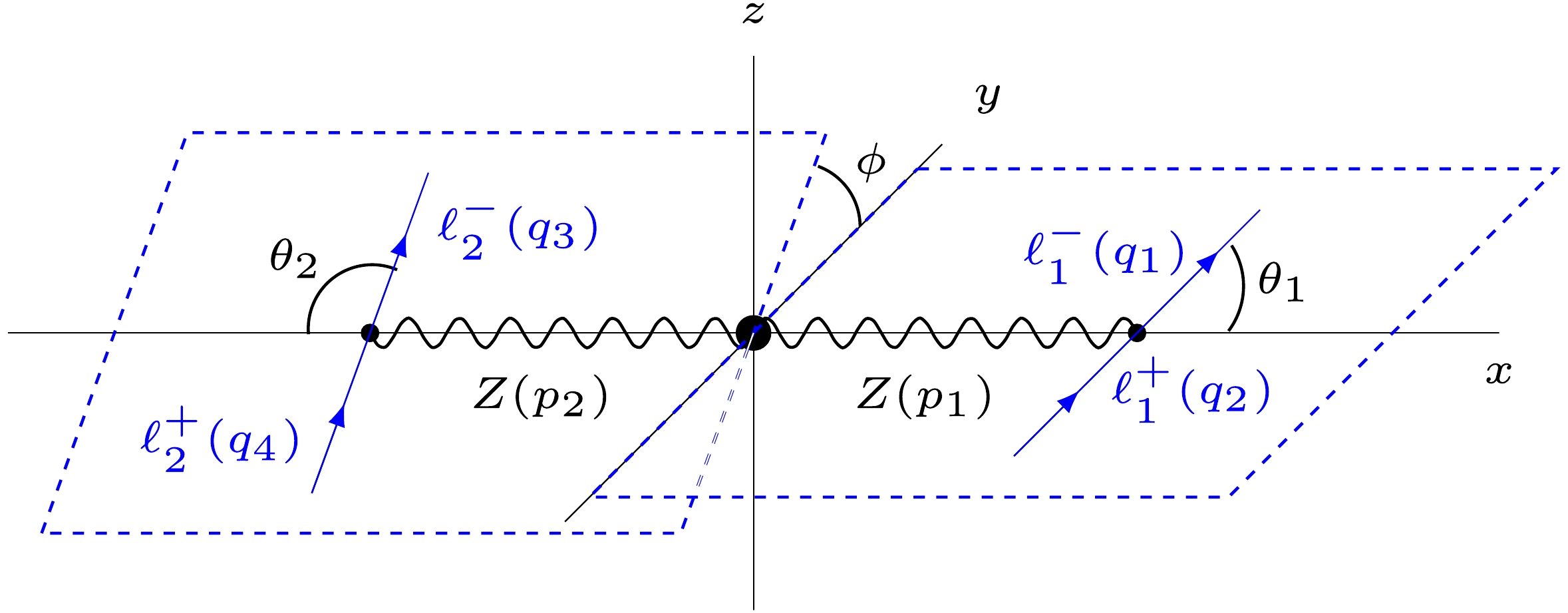
Figure 2. (color online) Nomenclature for the reference systems and angles used in the calculation of the
$ H\to ZZ\to \bar{\ell}_1\ell_1\bar{\ell}_2\ell_2 $ decay as described in Appendix A.We present below the analytical expressions for the polarized square amplitudes and the interference term in Eq. (16). They were obtained using the FeynCalc package [67−69]. The relation
$ p_i^2=m_Z^2 $ ($ i=1 $ , 2) was considered as both$ Z $ gauge bosons are on-shell. -
The polarized square amplitudes
$ \mathcal{M}^2_{H^\ast}(\lambda,\lambda) $ given in terms of the real and absorptive parts of the complex anomalous couplings$ h_i^H $ of the Lagrangian in Eq. (1) were presented by some of the authors in a previous study [7]. We considered a reference frame in which the motion of the$ Z(p_1) $ gauge boson is along the positive direction of the$ x $ axis and the off-shell Higgs boson is at rest. For further details, see Appendix A. In the energy region where both$ Z $ gauge bosons are on-shell, the transversally polarized$ H^\ast\rightarrow ZZ $ amplitudes read as$ \begin{aligned}[b] \mathcal{M}^2_{H^\ast\rightarrow Z(p_1)Z(p_2)}(L,L)= \left(\frac{g}{2c_W m_Z}\right)^2\Bigg(4 m_Z^2 Q\sqrt{Q^2-4 m_Z^2}\, {\rm{Im}}\left(h_3^H {h_1^H}^\dagger\right)+Q^2 \left(Q^2-4 m_Z^2\right) \big|h_3^H\big|^2+4 m_Z^4\big|h_1^H\big|^2\Bigg), \end{aligned} $

(18) and
$ \begin{align} \mathcal{M}^2_{H^\ast\rightarrow Z(p_1)Z(p_2)}(R,R)&=\left(\frac{g}{2c_W m_Z}\right)^2\left(-4 m_Z^2 Q\sqrt{Q^2-4 m_Z^2}\, {\rm{Im}}\left(h_3^H {h_1^H}^\dagger\right)+Q^2 \left(Q^2-4 m_Z^2\right) \big|h_3^H\big|^2+4 m_Z^4 \big|h_1^H\big|^2\right), \end{align} $

(19) whereas for the longitudinal polarization, we have
$ \begin{aligned}[b] \mathcal{M}^2_{H^\ast\rightarrow Z(p_1)Z(p_2)}(0,0)=\;&\left(\frac{g}{4c_W m^3_Z}\right)^2\Bigg(4 Q^6 m_Z^2 \left({\rm{Re}}\left(h_1^H {h_2^H}^\dagger\right)-2 \big|h_2^H\big|^2\right)+4 Q^4 m_Z^4 \left(\big|h_1^H\big|^2+4 \big|h_2^H\big|^2-6{\rm{Re}}\left(h_1^H {h_2^H}^\dagger\right)\right)\\ &-16 Q^2 m_Z^6 \left(\big|h_1^H\big|^2-2{\rm{Re}}\left(h_1^H {h_2^H}^\dagger\right)\right)+16 m_Z^8 \big|h_1^H\big|^2+Q^8 \big|h_2^H\big|^2\Bigg), \end{aligned} $

(20) where we have introduced the four-lepton invariant mass
$ Q^2=q^2 $ instead of the four-momenta of the off-shellHiggs boson. Moreover, we have used the expressions
${\rm{Re}}\left(h_i^H {h_j^H}^\dagger\right)= {\rm{Re}}\big[h_i^H\big] {\rm{Re}}\big[h_j^H\big]+ {\rm{Im}}\big[h_i^H\big]{\rm{Im}}\big[h_j^H\big]$ and${\rm{Im}}\left(h_i^H {h_j^H}^\dagger\right)= {\rm{Im}}\big[h_i^H\big]{\rm{Re}}\big[h_j^H\big]- {\rm{Re}}\big[h_i^H\big]{\rm{Im}}\big[h_j^H\big]$ . Our results reproduce those reported in Ref. [64] for the scenario with real anomalous couplings.Note that there is no dependence on the angular variables. Furthermore, the presence of a non-zero form factor
$ h_3^H $ could lead to a left-right asymmetry in the four-lepton final state, which vanishes at one-loop level in the SM. -
As already mentioned, the square amplitudes
$ \mathcal{M}^2_{Z(p_1)\rightarrow \overline{\ell}_1\ell_1}(\lambda) $ and$ \mathcal{M}^2_{Z(p_2)\rightarrow \overline{\ell}_2\ell_2}(\lambda) $ can be determined in the rest frame of the$ Z(p_i) $ gauge boson. According to the kinematics presented in Appendix A, the polarization vectors of the$ Z(p_1) $ ($ Z(p_2) $ ) gauge boson are oriented along the positive (negative) direction of the$ x $ axis; thus, the transversally and longitudinally polarized amplitudes are expressed as$ \begin{aligned}[b] \mathcal{M}^2_{Z(p_i)\rightarrow \overline{\ell}_i\ell_i}(R/L)=\;& \left(\frac{g}{c_W} \right)^2 \left( s^2_{\theta_i} \left(4 m_i^2-m_Z^2\right) \left(g_A^2+g_V^2\right)\pm4 g_A g_V c_{\theta_i} m_Z\sqrt{m_Z^2-4 m_i^2 }+2 m_Z^2 \left(g_A^2+g_V^2\right)-8 m_i^2 g_A^2 \right)\\\simeq\;& \left( \frac{g}{c_W}\right)^2m_Z^2 \left( \left(g_A^2+g_V^2\right) \left(1+ c^2_{\theta _i}\right)\pm4 g_A g_V c_{\theta _i} \right), \end{aligned} $

(21) and
$ \mathcal{M}^2_{Z(p_i)\rightarrow \overline{\ell}_i\ell_i}(0)= 2\left(\frac{g}{c_W} \right)^2 \left( c^2_{\theta_i} \left(4 m_i^2-m_Z^2\right) \left(g_A^2+g_V^2\right)+m_Z^2 \left(g_A^2+g_V^2\right)-4 m_i^2 g_A^2\right)\simeq 2\left( \frac{g}{ c_W}\right)^2 s^2_{\theta _i} m_Z^2 \left(g_A^2+g_V^2\right), \ $

(22) where
$ i=1,2 $ and we have introduced the short-hand notations$ c_\eta\equiv \cos\eta $ and$ s_\eta\equiv \sin\eta $ . The approximate results were obtained in the massless lepton limit, which is used in the phase space defined in Appendix A.To cross-check our calculations, we boosted Eqs. (21) and (22) into the rest frame of the Higgs boson via the Lorentz transformation given in Appendix A, which leaves them invariant, as expected. Note that the above square amplitudes are independent of the
$ \phi $ angle and the four-lepton invariant mass$Q$ . Moreover, although the$ g_Ag_V $ term in Eq. (21) seems to give rise to a left-right asymmetry, it vanishes after integration over the$ \theta_i $ angles. Therefore, the only observable effects of the left- and right-handed polarized$ Z(p_i)\rightarrow \overline{\ell}_i\ell_i $ amplitudes would appear via either angular distributions or forward-backward asymmetry. -
For the purpose of our study, it is enough to consider the massless lepton approximation, which yields
$ \begin{aligned}[b] \mathcal{M}^2_{\rm{int}}\equiv \;&\sum_{\lambda_1} \sum_{\lambda_2\neq \lambda_1 } \mathcal{M}^2_{H^\ast Z(p_1)Z(p_2)}(\lambda_1,\lambda_2) = \frac{s_{\theta_1} s_{\theta_2}}{2m_Z^2}\Big( s_{\theta_1} s_{\theta_2} m_Z^2\left(g_A^2+g_V^2\right){}^2 f_1\left(Q^2\right) +\big(2 g_A g_V+c_{\theta _1} \left(g_A^2+g_V^2\right)\big) \\&\times\big(2 g_A g_V+c_{\theta_2} \left(g_A^2+g_V^2\right)\big) f_2\left(Q^2\right) +\big(2 g_A g_V-c_{\theta _1} \left(g_A^2+g_V^2\right)\big) \big(2 g_A g_V-c_{\theta_2} \left(g_A^2+g_V^2\right)\big) f_3\left(Q^2\right)\Big), \end{aligned} $

(23) where
$ \begin{align} f_1\left(Q^2\right)&= 4 \sqrt{Q^2\left(Q^2-4 m_Z^2\right)}\, m_Z^2 {\rm{Re}}\left(h_1^H {h_3^H}^\dagger\right)s_{2 \phi}+\left(4m_Z^4\big|h_1^H\big|^2 -Q^2 \left(Q^2-4 m_Z^2\right)\big|h_3^H\big|^2\right) c_{2 \phi }, \end{align} $

(24) $ \begin{aligned}[b] f_2\left(Q^2\right)=\;&c_{\phi} \Bigg( \left(Q^2\left( Q^2-4 m_Z^2\right) \right){}^{3/2}{\rm{Im}}\left(h_3^H {h_2^H}^\dagger\right) +2 m_Z^2 \Bigg( \sqrt{ Q^2\left( Q^2-4 m_Z^2 \right)} \left(Q^2-2 m_Z^2\right){\rm{Im}}\left(h_3^H{h_1^H}^\dagger\right)\\ &+ \left(4 m_Z^2-Q^2\right)Q^2{\rm{Re}}\left(h_1^H{h_2^H}^\dagger\right)\Bigg)\Bigg)- s_{\phi} \Bigg( \left( Q^2\left( Q^2-4 m_Z^2\right)\right){}^{3/2}{\rm{Re}}\left(h_2^H{h_3^H}^\dagger\right) \\&+2m_Z^2 \left( \sqrt{Q^2-4 m_Z^2} \left(Q^2-2 m_Z^2\right){\rm{Re}}\left(h_1^H{h_3^H}^\dagger\right)+ \left(Q^2-4 m_Z^2\right)Q^2{\rm{Im}}\left(h_1^H{h_2^H}^\dagger\right)\right)\Bigg)+4c_{\phi}m_Z^4\left(2 m_Z^2- Q^2\right)\big|h_1^H\big|^2, \end{aligned} $

(25) and
$ \begin{aligned}[b] f_3\left(Q^2\right)=\;& c_{\phi } \Bigg(- \left(Q^2\left(Q^2-4 m_Z^2\right)\right){}^{3/2}{\rm{Im}}\left(h_3^H {h_2^H}^\dagger\right) +2 m_Z^2 \Big( \sqrt{Q^2\left(Q^2-4 m_Z^2\right)} \left(2 m_Z^2-Q^2\right){\rm{Im}}\left(h_3^H{h_1^H}^\dagger\right)\\ &+ \left(4 m_Z^2-Q^2\right)Q^2{\rm{Re}}\left(h_1^H{h_2^H}^\dagger\right)\Big)\Bigg)-s_{\phi} \Bigg( \left(Q^2\left(Q^2-4 m_Z^2\right)\right){}^{3/2}{\rm{Re}}\left(h_2^H{h_3^H}^\dagger\right)\\ &+2 m_Z^2 \left( \sqrt{Q^2-4 m_Z^2} \left(Q^2-2 m_Z^2\right){\rm{Re}}\left(h_1^H{h_3^H}^\dagger\right)+ \left(4 m_Z^2-Q^2\right)Q^2{\rm{Im}}\left(h_1^H{h_2^H}^\dagger\right)\right)\Bigg) +4c_{\phi }m_Z^4 \left(2 m_Z^2-4 Q^2\right)\big|h_1^H\big|^2. \end{aligned} $

(26) Although the terms dependent on the
$ \phi $ angle vanish after integration in the phase space, the study of observables related to$ \phi $ can lead to interesting results. -
Following the discussion of Appendix A, the differential
$ H^\ast\rightarrow Z(p_1)Z(p_2)\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width can be expressed as$ \frac{{\rm d}\Gamma_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}}{{\rm d}p^2_1{\rm d}p^2_2{\rm d}\cos{\theta_1}{\rm d}\cos{\theta_2}{\rm d}\phi}=\frac{\sqrt{Q^2-4 m_Z^2}}{ 512(2\pi)^6 Q^2 } \mathcal{M}^2_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}. $

(27) Given that we consider a scenario where both
$ Z $ gauge bosons are on-shell, we use the narrow-width approximation for their Breit-Wigner propagators,$ \lim_{m_Z \Gamma_Z\rightarrow 0}\frac{1}{(p_i^2-m_Z^2)^2+(m_Z\Gamma_Z)^2}=\delta(p_i^2-m_Z^2)\frac{\pi}{m_Z\Gamma_Z},\quad (i=1,2), $

(28) which enables the integration over
$p_1^2$ and$p_2^2$ . Introducing the polarized and interference amplitudes, the differential decay width can be expressed as$ \begin{aligned}[b] \frac{{\rm d}\Gamma_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}}{{\rm d}\cos{\theta_1}{\rm d}\cos{\theta_2}{\rm d}\phi}=\frac{\sqrt{Q^2-4 m_Z^2}}{(32\sqrt{2})^2 (2\pi)^4 Q^2 (m_Z\Gamma_Z)^2} \Big(\sum_\lambda \mathcal{M}^2_{H^\ast\rightarrow Z(p_1)Z(p_2)}(\lambda,\lambda) \mathcal{M}^2_{Z(p_1)\rightarrow \overline{\ell}_1\ell_1}(\lambda)\times\mathcal{M}^2_{Z(p_2)\rightarrow \overline{\ell}_2\ell_2}(\lambda)+ \mathcal{M}^2_{\rm{int}}\Big). \end{aligned} $

(29) All our results presented below were obtained from Eq. (29) along with Eqs. (18)–(22), whereas the interference term in Eq. (23) can be integrated out because we are mainly interested in the polarization effects.
Below we present the results for the
$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width in the scenario with polarized$ Z $ gauge bosons, though for completeness we also present the case of unpolarized$ Z $ gauge bosons, which can be obtained via standard calculation techniques and serve to cross-check our results obtained from Eq. (29). -
To obtain the polarized
$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width, we integrate Eq. (29) over the angular variables in the region given in Appendix A, which after some rearrangement yields$ \begin{align} \Gamma^\lambda_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}=&\frac{g^6 \left(g_A^2+g_V^2\right){}^2 \sqrt{Q^2-4 m_Z^2}}{ (48\sqrt{2})^2 (2\pi)^3 Q^2 c_W^6 m_Z^4 \Gamma _Z^2}F^\lambda\left(Q^2\right), \end{align} $

(30) with
$ \begin{aligned}[b] F^\lambda\left(Q^2\right)=\;& \left( \left(Q^2-2 m_Z^2\right){}^2 \left(4 m_Z^4\big|h_1^H\big|^2+Q^4 \big|h_2^H\big|^2\right) +4 Q^2 m_Z^2 \left(Q^4-6 Q^2 m_Z^2+8 m_Z^4\right){\rm{Re}}\left(h_1^H{h_2^H}^\dagger\right)\right)f_0\\&+ 4 m_Z^4 \left(4 m_Z^2 \sqrt{Q^2\left(Q^2-4 m_Z^2\right)}{\rm{Im}}\left(h_3^H{h_1^H}^\dagger\right)+Q^2 \left(Q^2-4 m_Z^2\right)\big|h_3^H\big|^2+ 4 m_Z^4\big|h_1^H\big|^2\right)f_L \\ &+ 4m_Z^2\left(-4 m_Z^2 \sqrt{Q^2\left(Q^2-4 m_Z^2\right)}{\rm{Im}}\left(h_3^H{h_1^H}^\dagger\right) +Q^2 \left(Q^2-4 m_Z^2\right) \big|h_3^H\big|^2+4 m_Z^4\big|h_1^H\big|^2\right)f_R, \end{aligned} $

(31) where the
$ f_L $ ,$ f_R $ , and$ f_0 $ coefficients must be set to$ 0 $ or$ 1 $ according to the polarization$ \lambda $ of the$ Z $ gauge bosons. For instance,$ f_L=1 $ and$ f_R=f_0=0 $ correspond to$ \lambda=L $ . As already pointed out, the interference term in Eq. (29) vanishes after$ \phi $ integration. Thus, it is possible to discriminate between the distinct contributions of polarized$ Z $ gauge bosons, which are functions of the four-lepton invariant mass only.The polarized
$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width can also be expressed in terms of the$ Z(p_i)\rightarrow \overline{\ell}_i\ell_i $ branching fractions as$ \begin{aligned}[b] \Gamma^\lambda_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}=\;&2\ \Gamma^\lambda_{H^\ast\rightarrow ZZ}\left(Q^2\right) \text{Br}(Z\rightarrow \ell_1\overline{\ell}_1)\text{Br}(Z\rightarrow \ell_2\overline{\ell}_2)\\=\;&0.00226418\times \Gamma^\lambda_{H^\ast\rightarrow Z_\lambda Z_\lambda}\left(Q^2\right), \end{aligned} $

(32) where an extra factor of 2 is included in Eq. (32); this factor emerges from the fact that the
$ Z $ bosons are not in the final state, and hence we have not considered the statical factor of 1/2 that corrects the double-counting of identical particles in the$ H^\ast\rightarrow ZZ $ amplitude. This factor has been overlooked in the past [6]. In Eq. (32), the polarized$ H^\ast\rightarrow Z_\lambda Z_\lambda $ decay width is given by$ \begin{align} \Gamma^\lambda_{H^\ast\rightarrow Z_\lambda Z_\lambda}&=\frac{g^2 \sqrt{Q^2-4 m_Z^2}}{ 128 \pi Q^2 c_W^2 m_Z^6 }F^\lambda\left(Q^2\right). \end{align} $

(33) We have used
$ \begin{align} \text{Br}(Z\rightarrow \ell_i\overline{\ell}_i)&\simeq\frac{g^2 m_Z }{12 \pi c_W^2\Gamma_Z}\left(g_A^2+g_V^2\right)\simeq 0.0336466, \end{align} $

(34) in the massless lepton approximation [70].
According to Eq. (32), it is clear that the four-lepton final state is sensitive to the polarization effects on the
$ HZZ $ vertex. Therefore, the left-right asymmetry in$ Z $ gauge boson pair production [7] has also effects on the decay of an off-shell Higgs boson into four-leptons. Such an asymmetry is a consequence of the$\rm CP$ violation due to complex anomalous couplings. Hence, new-physics effects may be detected via transversally polarized$ Z $ gauge bosons [71]. Moreover, they would provide an excellent probe of quantum field the violation and complex anomalous couplings. Hence, new-physics effects may be detected via transversally polarized nline-formula$h_i^V $ ($ i $ =1, 2, 3) form factors are complex [56]. By contrast, longitudinally polarized$ Z $ gauge bosons are not useful to observe$\rm CP$ -violating effects, though it is still possible to detect new-physics contributions through the$ \hat{c}_Z $ anomalous coupling, which becomes part of the definition of the$ h_1^H $ form factor. -
For the sake of completeness, we also analyzed unpolarized
$ Z $ gauge bosons. According to Eq. (30), we can obtain the unpolarized$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width by setting$f_L= f_R=f_0=1$ , which yields$ \begin{align} \Gamma_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}\left(Q^2\right)&= \frac{g^6 \left(g_A^2+g_V^2\right){}^2 \sqrt{Q^2-4 m_Z^2} }{(48\sqrt{2})^2 (2\pi)^3 Q^2 c_W^6 m_Z^4 \Gamma _Z^2}G\left(Q^2\right), \end{align} $

(35) where
$ \begin{aligned}[b] G^\lambda\left(Q^2\right)=\;& Q^2 \left(Q^2-4 m_Z^2\right) \left(Q^2 \left(Q^2-4 m_Z^2\right) \big|h_2^H\big|^2+8 m_Z^4 \big|h_3^H\big|^2\right) \\&+4 m_Z^4 \left(Q^4-4 Q^2 m_Z^2+12 m_Z^4\right) \big|h_1^H\big|^2\\&+4 Q^2 m_Z^2 \left(Q^4-6 Q^2 m_Z^2+8 m_Z^4\right) {\rm{Re}}\left(h_1^H {h_2^H}^\dagger\right). \end{aligned} $

(36) To cross-check this result, we inserted the left-hand side of Eq. (12) into Eq. (8) and used standard calculation techniques. In this case, the boosts defined in Appendix A are necessary because the square amplitude depends on scalar products of four-momenta given in their respective rest frame of the
$ Z(p_i) $ gauge boson.According to Eq. (35), the contribution of the
$\rm CP$ -violating form factor$ h_3^H $ to the four-lepton final state is suppressed as compared to the$\rm CP$ -conserving contributions, which are proportional to higher powers of the four-lepton invariant mass$ Q $ . Thus, the$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ unpolarized decay width is not really sensitive to$\rm CP$ -violating effects. Note also that one can extract the tree-level SM contribution from Eq. (35). This contribution is obtained for$ h_2^H=h_3^H=0 $ and$ h_1^H=1 $ . Concerning the one-loop level SM contribution, it is induced by setting$ h_3^H=0 $ , whereas the remaining form factors are expressed in terms of$ \hat{b}_Z $ only, given that$ \hat{c}_Z $ vanishes at this order. The one-loop level contribution to$ \hat b_Z $ was reported in Ref. [7].Eq. (35) can be expressed in the following short form:
$ \begin{aligned}[b] \Gamma_{H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2}=\;&2\ \Gamma_{H^\ast\rightarrow ZZ}\left(Q^2\right) \text{Br}(Z\rightarrow \ell_1\overline{\ell}_1)\text{Br}(Z\rightarrow \ell_2\overline{\ell}_2)\\=\;&0.00226418\times \Gamma_{H^\ast\rightarrow ZZ}\left(Q^2\right) ,\\[-10pt] \end{aligned} $

(37) where the unpolarized
$ H^\ast\rightarrow ZZ $ decay width for complex anomalous couplings is given by$ \begin{align} \Gamma_{H^\ast\rightarrow ZZ}\left(Q^2\right)=& \frac{g^2 \sqrt{Q^2-4 m_Z^2}}{512 \pi Q^2 c_W^2 m_Z^6}G\left(Q^2\right). \end{align} $

(38) The inclusion of a factor of
$ 2 $ in Eq. (37) has already been explained when obtaining the polarized decay width. The unpolarized$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ process was studied long ago, and both theoretical and numerical results can be found in the literature [72−77]. -
We now turn to the study of the polarized
$ H^\ast\rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width and some observables sensitive to new-physics effects. We first present a cross-check of our numerical evaluation method that relies on the analytical results presented in Section II along with the kinematics and four-body phase space discussed in Appendix A. -
Using our analytical results, we implemented a Mathematica code to perform a numerical evaluation; this code is available in a GitLab repository of ours [78]. For an alternative numerical evaluation, we also implemented the Lagrangian expressed by Eq. (1) into
$\mathrm{MadGraph5\_} \mathrm{aMC@NLO}$ [79] via the UFO format [80] using the FeynRules package [81]. We then compared the numerical results obtained via these two independent methods. The$ e^-e^+\mu^-\mu^+ $ final state was considered in our analysis; however, it is indistinguishable from other$ \bar{\ell}_1 \ell_1 \bar{\ell}_2 \ell_2 $ final states because we used the massless lepton approximation.Given that the anomalous
$ HZZ $ couplings have negligible effects on the unpolarized$ H^*\to \bar{\ell}_1 \ell_1 \bar{\ell}_2 \ell_2 $ decay width [7], we set$ h_1^H=1 $ and$ h^H_2=h_3^H=0 $ and calculated the tree-level SM contribution to the unpolarized$ H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+ $ and$ H^\ast\rightarrow ZZ $ decays. The results obtained by our own numerical evaluation method and$ \mathrm{MadGraph5\_aMC@NLO}$ are shown in Fig. 3 as functions of the four-lepton invariant mass. An excellent agreement between both results is observed, with a slight variation of the order of 2% in the decay widths. We also verified that the$ H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+ $ decay width obtained via Eq. (37) agrees with that obtained from$\mathrm{MadGraph5\_} \mathrm{aMC@NLO} $ and represented in the left plot of Fig. 3, which also shows the consistency of the extra factor of 2 inserted into Eq. (37). Furthermore, our numerical results agree with those reported in Ref. [72].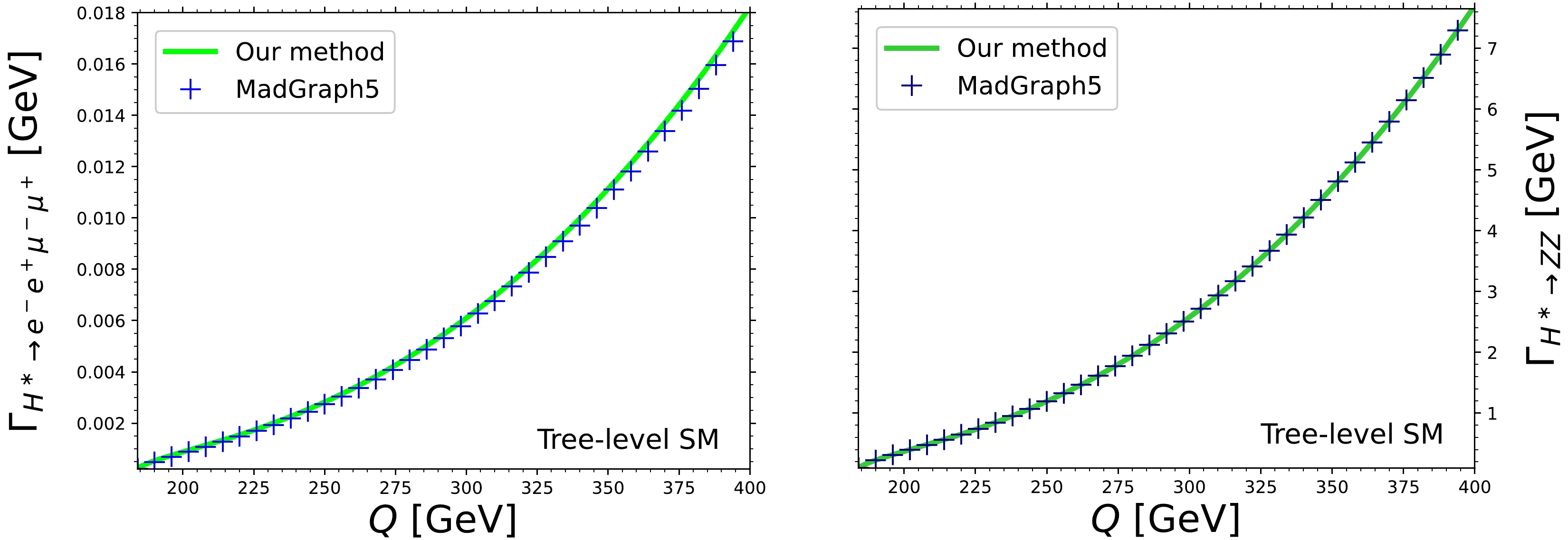
Figure 3. (color online) Tree-level SM contribution to the unpolarized
$ H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+ $ and$ H^\ast\rightarrow ZZ $ decay widths as functions of the four-lepton invariant mass$ Q $ obtained by both our own evaluation method and$ \mathrm{MadGraph5\_aMC@NLO}$ .We now turn to cross-check the numerical results for the polarized
$ H^\ast\rightarrow ZZ $ decay width, which is sensitive to the anomalous$ HZZ $ couplings and yields the polarized$ H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+ $ decay via Eq. (32). For our numerical evaluation method, we used the analytical result expressed in Eq. (33) for the polarized partial decay widths$\Gamma^\lambda_{H^\ast\rightarrow Z_\lambda Z_\lambda}$ . The left (right) plots in Fig. 4 show the behavior of the$ H^\ast\rightarrow Z_LZ_L $ ($ H^\ast\rightarrow Z_R Z_R $ ) decay width as a function of the four-lepton invariant mass for two sets of values of the anomalous$ HZZ $ couplings consistent with the most stringent bounds [7]. For comparison purposes, we also show the tree-level SM contributions.
Figure 4. (color online) Behavior of the polarized
$ H^\ast\rightarrow Z_LZ_L $ (left plot) and$ H^\ast\rightarrow Z_RZ_R $ (right plot) decay widths as functions of the four-lepton invariant mass for two sets of values of the anomalous couplings: scenario i)$\hat{b}_Z=0.001+{\rm i} 0.003$ ,$\hat{c}_Z=0.001+{\rm i}0.002$ , and$\widetilde{b}_Z=0.01+{\rm i}0.02$ ; scenario ii)$\hat{b}_Z=0.0001+{\rm i} 0.001$ ,$\hat{c}_Z=0.0001+{\rm i}0.001$ , and$\widetilde{b}_Z=0.001-{\rm i}0.01$ . We also show the SM tree-level contributions for comparison purposes. For the numerical evaluation, we used our own evaluation method and$\mathrm{MadGraph5\_aMC@NLO} $ .Again, we can conclude that the results obtained by our numerical evaluation method and
$\mathrm{MadGraph5\_} \mathrm{aMC@NLO} $ agree well. Note that the anomalous contributions yield a significant deviation from the tree-level SM contribution for large values of$ Q $ and that the$ H^\ast\rightarrow Z_\lambda Z_\lambda $ decay width exhibits a distinctive behavior for each polarization in both scenarios of new physics. As discussed below, this emerges from the$\rm CP$ -violating effects and complex form factors, which have already been studied through a left-right asymmetry in the decay$ H^\ast\rightarrow Z_\lambda Z_\lambda $ [7]. A more detailed analysis of the polarized$ H^*\to \bar{\ell}_1 \ell_1 \bar{\ell}_2 \ell_2 $ decay widths, including the SM contribution up to one-loop level, together with the analysis of other interesting observables sensitive to new physics will be presented below.In summary, there is an excellent agreement between the results obtained by our evaluation method and
$\mathrm{MadGraph5\_aMC@NLO} $ . We also corroborated the consistency of Eqs. (37) and (32), which enables the study of the four-lepton decay widths using the$ H^*\to ZZ $ decay width only. Note that, in our evaluation method, we consider a constant$ \Gamma_Z $ decay width in the narrow width approximation, whereas in$\mathrm{MadGraph5\_aMC@NLO} $ , the complex mass scheme is used. According to Ref. [82], both methods yield the same results for four-leptons in the final state. In the next sections, we present results from our evaluation method given that it is more suitable for our analysis. -
The physics of polarizations of weak bosons at the LHC has been discussed in Refs. [50, 58, 59], whereas that related to the
$ Z $ boson is of particular interest because they are being measured by the CMS, ATLAS, and LHCb collaborations [34−38]. To study the effects of the polarized$ Z $ boson, we considered the most general case with complex$ HZZ $ anomalous couplings and examined three realistic scenarios for their numerical values. For the$ \hat{b}_Z $ anomalous coupling, we considered the SM contribution up to the one-loop level. This result has been reported in Ref. [7] in terms of the Passarino-Veltman scalar functions and as a function of$ Q $ , the four-lepton invariant mass. The numerical evaluation of$ \hat{b}_Z $ was realized through the LoopTools package [83]. Meanwhile, for the$ \hat{c}_Z $ and$ \widetilde{b}_Z $ anomalous couplings, we used the stringent limits obtained through LHC data and theoretical results [3, 7]. They are shown in Table 1. Note that, although we considered a non-vanishing$ \hat{c}_Z $ , it yields a negligible contribution to the$ h_1^H $ form factor. Hence, the same values were considered for the three scenarios. Finally, the one-loop SM contribution was also studied for comparison with the new-physics scenarios.Scenario $ \widetilde{b}_Z $ 

$ \hat{c}_Z $ 

1 $0.01+{\rm i}0.02$ 

$ 0.0001+0.0003i $ 

2 $0.001-{\rm i}0.01$ 

$ 0.0001+0.0003i $ 

3 $0.0001+{\rm i}0.001$ 

$ 0.0001+0.0003i $ 

Table 1. Scenarios for the
$ HZZ $ anomalous couplings of the$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ decay used in our analysis. For the$ \hat{b}_Z $ coupling, we considered the SM contribution up to one-loop level [7], whereas for the remaining anomalous couplings, the stringent limits obtained through LHC data and theoretical results were used.We first analyzed the effects of the polarizations of the
$ Z $ gauge bosons on the$ H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+ $ decay, for which either Eq. (30) or Eq. (32) can be used as both yield the same results. Fig. 5 shows the results for the left- and right-handed polarized$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ decay widths as functions of$ Q $ . The longitudinally polarized$ Z $ gauge bosons were not considered because its decay width is not sensitive to the$C P$ -violating anomalous coupling$ \tilde b_Z $ .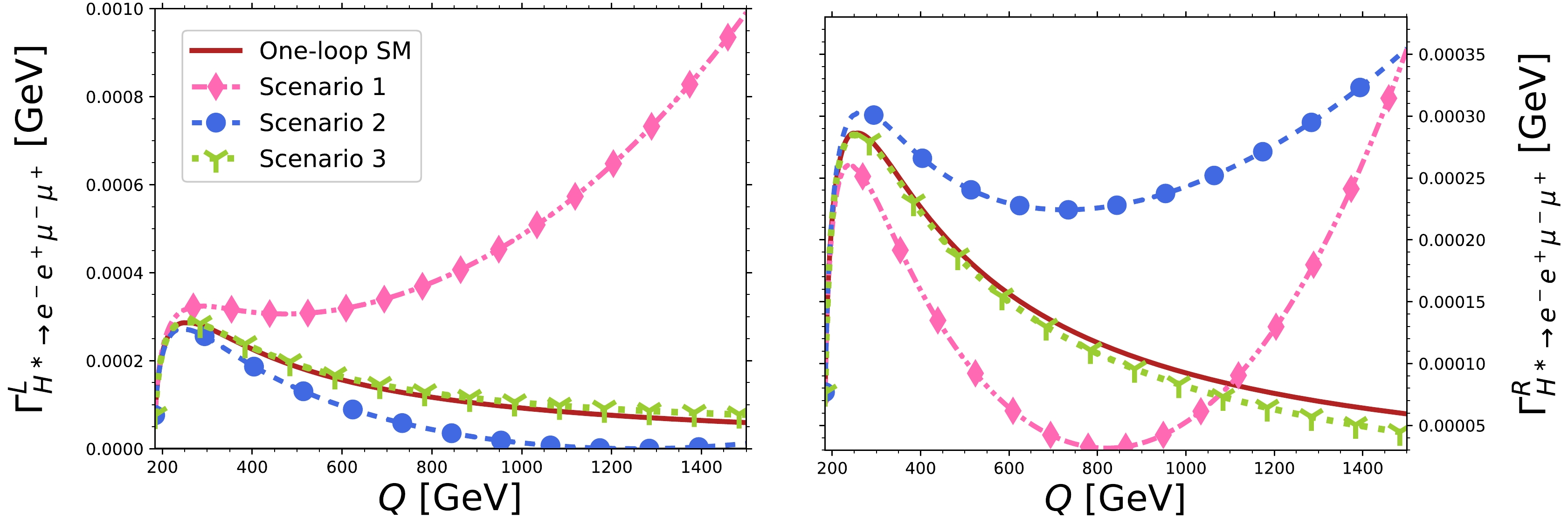
Figure 5. (color online) Behavior of the transversally polarized
$ \Gamma^\lambda_{H^\ast\rightarrow e^-e^+\mu^- \mu^+} $ decay widths ($ \lambda=L $ ,$ R $ ) for the SM contribution and the three scenarios of Table 1 for the anomalous$ HZZ $ couplings.Note in Fig. 5 that for small values of the real and absorptive parts of the
$\rm CP$ -violating anomalous coupling$ \tilde b_Z $ (scenario 3), the polarized$ \Gamma^\lambda_{H^\ast\rightarrow e^-e^+\mu^- \mu^+} $ decay widths exhibit little variation from the pure SM contribution, though such a deviation increases slightly as$ Q $ grows, being more appreciable in the case of right-handed polarization. By contrast, in scenarios 1 and 2, in which$ \tilde b_Z $ is assumed to be relatively large, a considerable deviation from the SM contribution develops around$ Q=250 $ GeV and becomes larger as$ Q $ increases. Therefore, the effects of the complex anomalous$ HZZ $ couplings in the four-lepton final state are more notable at high energies. Furthermore, in scenario 1,$ \Gamma_{H^\ast\rightarrow Z_LZ_L} $ is an increasing function of$ Q $ and is larger than the tree-level SM contribution, whereas$ \Gamma_{H^\ast\rightarrow Z_RZ_R} $ decreases around$ Q= 225 $ GeV and is smaller than the tree-level SM contribution. For scenario 2, the opposite is true. Thus, a distinct behavior between the left and right polarized widths is observed.Finally, note in Fig. 5 that the partial width increases significantly at high energies for some new physics scenarios because the non-SM contributions in Eqs. (18) and (19) are proportional to powers of
$ Q $ . A similar behavior has been observed in trilinear neutral gauge boson couplings [84, 85], where the unitarity can be preserved if we generalize the$ \widetilde{b}_Z $ and$ \hat{c}_Z $ anomalous couplings as$ \hat{c}_Z(Q^2)=\frac{\hat{c}_{Z0}}{\left(1+Q^2/\Lambda^2\right)^n}\text{,}\quad \widetilde{b}_Z(Q^2)=\frac{\widetilde{b}_{Z0}}{\left(1+Q^2/\Lambda^2\right)^n}, $

(39) where
$ \hat{c}_{Z0} $ and$ \widetilde{b}_{Z0} $ are constants that can be determined by considering unitarity conditions of the$ gg\rightarrow H^\ast\rightarrow ZZ $ process [86], whereas the parameter$ \Lambda $ is an energy scale introduced to avoid non-physical results as$ Q $ increases. Note that the$ \hat{c}_Z(Q^2) $ and$ \widetilde{b}_Z(Q^2) $ in Eq. (39) are approximately constant for$ Q\ll \Lambda $ . Therefore, our results in Fig. 5 are valid for an energy scale$ \Lambda\gg $ 1 TeV, given that we considered the values in Table 1 and there is no significant change in the one-loop SM contribution [7]. In general, the parameter$ \Lambda $ is fixed to the order of TeVs or$ \infty $ [70, 84]. For the latter case, the results obtained in this study remain unchanged. Nevertheless, for$ \Lambda\sim $ 1 TeV, the impact of our predicted effects reduces. The values of$ \Lambda $ and$ n $ must still be determined for the$ HZZ $ anomalous couplings; however, this lies beyond the scope of this study. -
The behavior of the
$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ polarized amplitudes give rise to a left-right asymmetry$ \mathcal{A}_{LR} $ $ \begin{align} \mathcal{A}_{LR}&=\frac{\Gamma^L_{H^\ast\rightarrow e^-e^+\mu^- \mu^+}-\Gamma^R_{H^\ast\rightarrow e^-e^+\mu^- \mu^+}}{\Gamma^L_{H^\ast\rightarrow e^-e^+\mu^- \mu^+}+\Gamma^R_{H^\ast\rightarrow e^-e^+\mu^- \mu^+}}, \end{align} $

(40) which is non-vanishing as long as complex anomalous couplings are present; thus, it can be expressed as
$ \begin{align} \mathcal{A}_{LR}&= \frac{4 m_Z^2 \sqrt{Q^2\left(Q^2-4 m_Z^2\right)} {\rm{Im}}\left(h_3^H{h_1^H}^\dagger \right)}{Q^2 \left(Q^2-4 m_Z^2\right) \big|h_3^H\big|^2+4 m_Z^4\big|h_1^H\big|^2}, \end{align} $

(41) thereby becoming suitable for detecting
$\rm CP$ -violating effects.Fig. 6 shows the behavior of
$ \mathcal{A}_{LR} $ as a function of the four-lepton invariant mass in the three scenarios of Table 1 for the anomalous$ HZZ $ couplings. The SM contribution is not shown because it vanishes at the one-loop level. Note that for scenario 2, in which the real and absorptive parts of$ h_3^H $ are of opposite sign, the$ \mathcal{A}_{LR} $ magnitude can be larger than for the other cases. Note also that in the three scenarios,$ \mathcal{A}_{LR} $ reaches its largest magnitude at a relatively high value of$ Q $ , and hence the$\rm CP$ -violating effects would be more significant beyond the$ 2m_Z $ threshold. Nevertheless, the asymmetry tends to decrease as$ Q $ grows, which arises from the fact that it behaves as a$ 1/Q^2 $ function at high energies.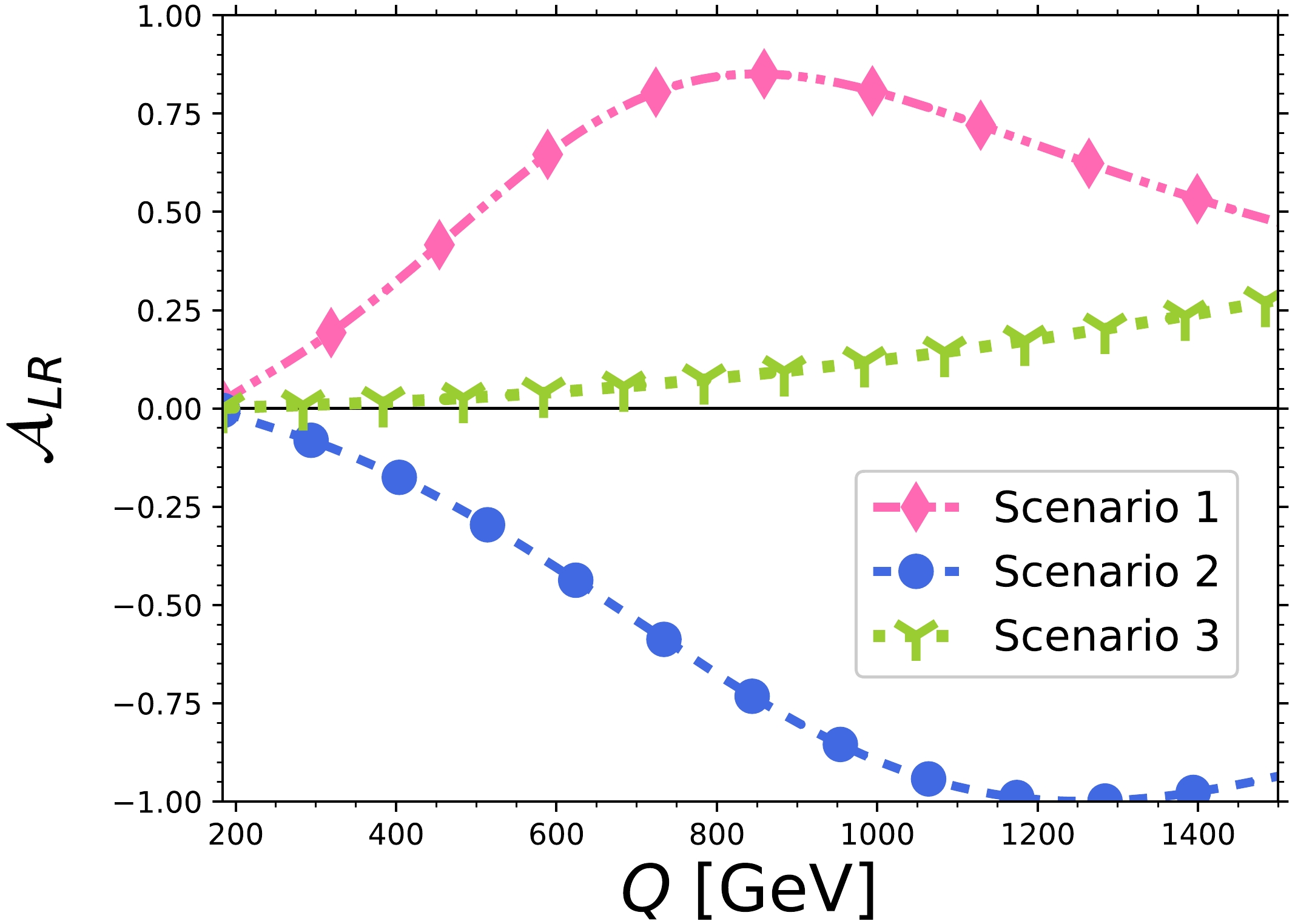
Figure 6. (color online) Left-right asymmetry
$ \mathcal{A}_{LR} $ as a function of the four-lepton invariant mass in the three scenarios of Table 1 for the anomalous$ HZZ $ couplings.The results presented in Figs. 5 and 6, together with Eq. (41), are in agreement with those reported in Ref. [7] for the
$ H^\ast\rightarrow Z_\lambda Z_\lambda $ process, which is a consequence of the fact that the four-lepton final state is a function of$ Q $ and independent of the$ Z\rightarrow \overline{\ell}\ell $ processes (see Eq. (32)). Note that the angular variables only appear in the production of lepton pairs and could also serve to detect new-physics effects from the$ HZZ $ anomalous couplings. -
The Higgs decay to four leptons is the cleanest channel to access the polarizations of the weak bosons, as they can be studied through the angular observables of the leptons produced by the
$ Z $ bosons decays [50, 59]. For this reason, we next analyze the role of the angular variables in the polarized$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ decay widths. Angular distributions together with the polarizations of the$ Z $ bosons are being measured at the LHC [36−39, 51]. As we pointed out, the results obtained in this study remain unchanged for an energy scale$ \Lambda\gg1 $ TeV. Usually, values of$ \Lambda $ of this order are considered to set limits on anomalous couplings similar to those considered in the$ HZZ $ interaction [70]. Given that the angle$ \phi $ only affects the interference term of the full square amplitude, its effects are not observable through polarized$ Z $ gauge bosons. After the integration of Eq. (29) over$ \phi $ , the differential$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ decay width becomes expressed in terms of the angles$ \theta_{1,2} $ . Therefore, it is still possible to study the polarization effects in the four lepton-final state through the angular variables. According to Eq. (21), we observe that the left- and right-handed square amplitudes are symmetric in both$ \theta_{1} $ and$ \theta_{2} $ angles, which is evident in Fig. 7, which shows the contours of the SM contribution to the transversally polarized$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ differential decay widths in the$ c_{\theta_1} $ vs$ c_{\theta_2} $ plane for$ Q=500 $ GeV. The left-handed polarized case reaches its higher values around$ \cos\theta_i=-1 $ , whereas for the right polarization, this occurs at$ \cos\theta_i=1 $ . In these regions, the partial widths can be of the order of$ 10^{-4} $ . Future experimental searches should focus on these specific angular regions to increase the sensitivity to potential deviations from the SM predictions. The smallest values are obtained around$ \cos\theta_i\approx0 $ in both scenarios. Furthermore, we found that the transversally polarized differential decay widths for$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ exhibit similar behavior for other values of$ Q $ and when non-zero anomalous couplings are considered.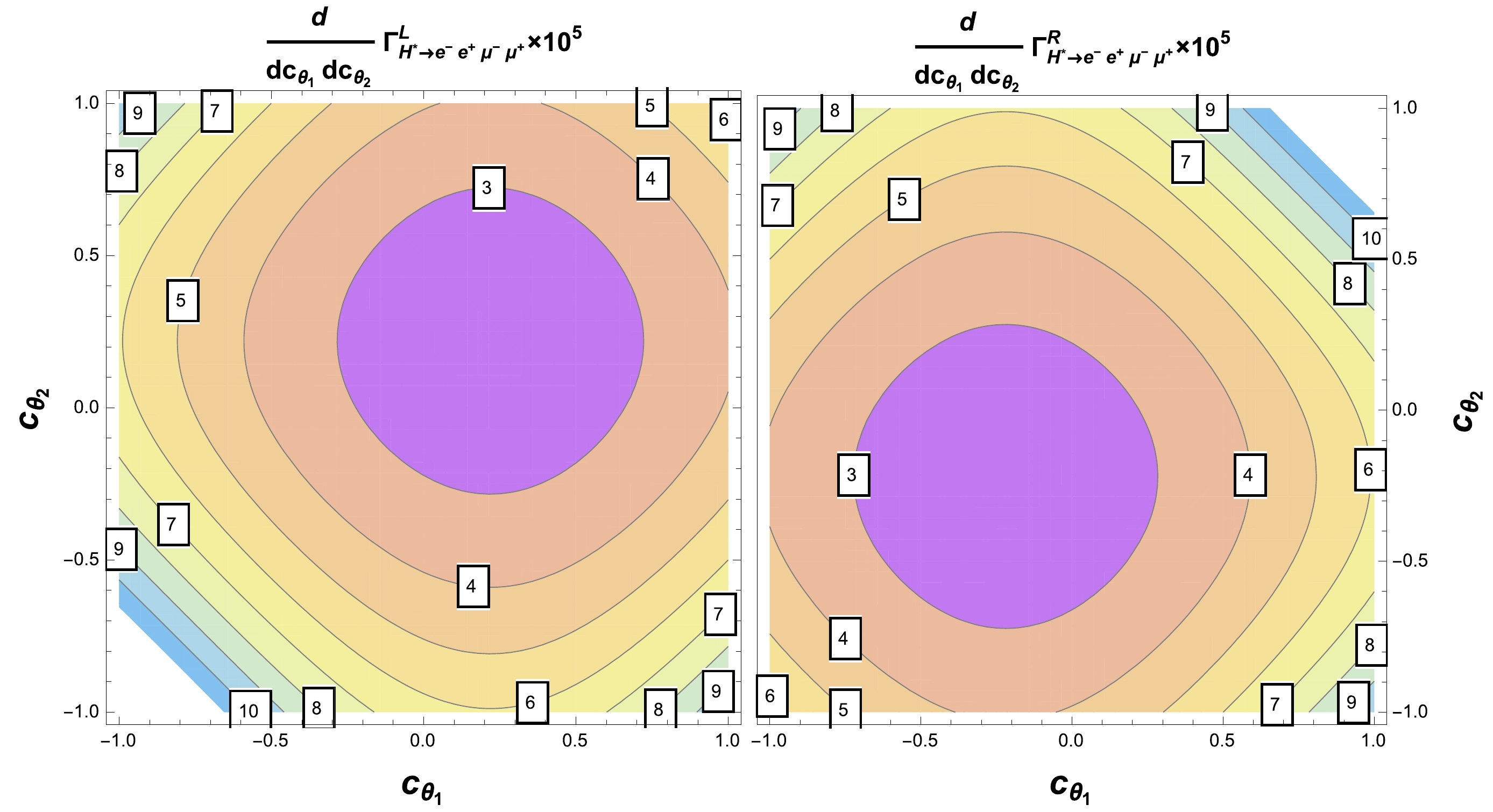
Figure 7. (color online) Contours of the transversally polarized
$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ differential decay widths in the$ c_{\theta_1} $ vs$ c_{\theta_2} $ plane for$ Q=500 $ GeV. Only the SM one-loop contribution is included.We next consider the three scenarios defined in Table 1 for the anomalous
$ HZZ $ couplings and study their effects on the polarized$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ angular distributions after integrating over$ \phi $ and one of the angles$ \theta_{1,2} $ . The results are presented in Figs. 8 and 9 as functions of the cosine of the remaining angle$ c_{\theta_i} $ . It is observed that the angular distributions show a significant deviation from the SM contribution in scenarios 1 and 2; this deviation becomes more pronounced at large values of$ Q $ . However, in scenario 3, where small values for the real and absorptive parts of the anomalous$ h_3^H $ coupling are considered, the deviation is hardly noticeable for small values of$ Q $ , though it becomes distinguishable as$ Q $ increases, particularly in the case of right-handed polarization. Note also that for left-handed polarization, the differential decay width is always above (below) the SM contribution in scenario 1 (scenario 2), whereas the opposite is true for right-handed polarization. Moreover, the left-handed (right-handed) polarized angular distributions reach their larger magnitude as$ c_{\theta_i}\to -1 $ $ (c_{\theta_i}\to 1) $ . This distinctive behavior emerges from the fact that the terms that give rise to the left-right asymmetry$ \mathcal{A}_{LR} $ in Eq. (41) and the terms proportional to$ c_{\theta_i} $ in Eq. (21), which have opposite signs, remain unchanged after$ \phi $ integration. This suggests new asymmetries associated with the angular variables. Note also that the results shown in Figs. 8 and 9 for the SM contributions agree with those reported in Ref. [58]. Some techniques to identify$ Z $ bosons polarizations through angular variables at the LHC have been addressed in Refs. [13, 59, 87], whereas the use of polarized beams in the future ILC or different$ e^+e^- $ colliders have also been studied in Refs. [22, 88, 89]. These approaches may be extended to observe the polarized angular distributions at high-energy colliders.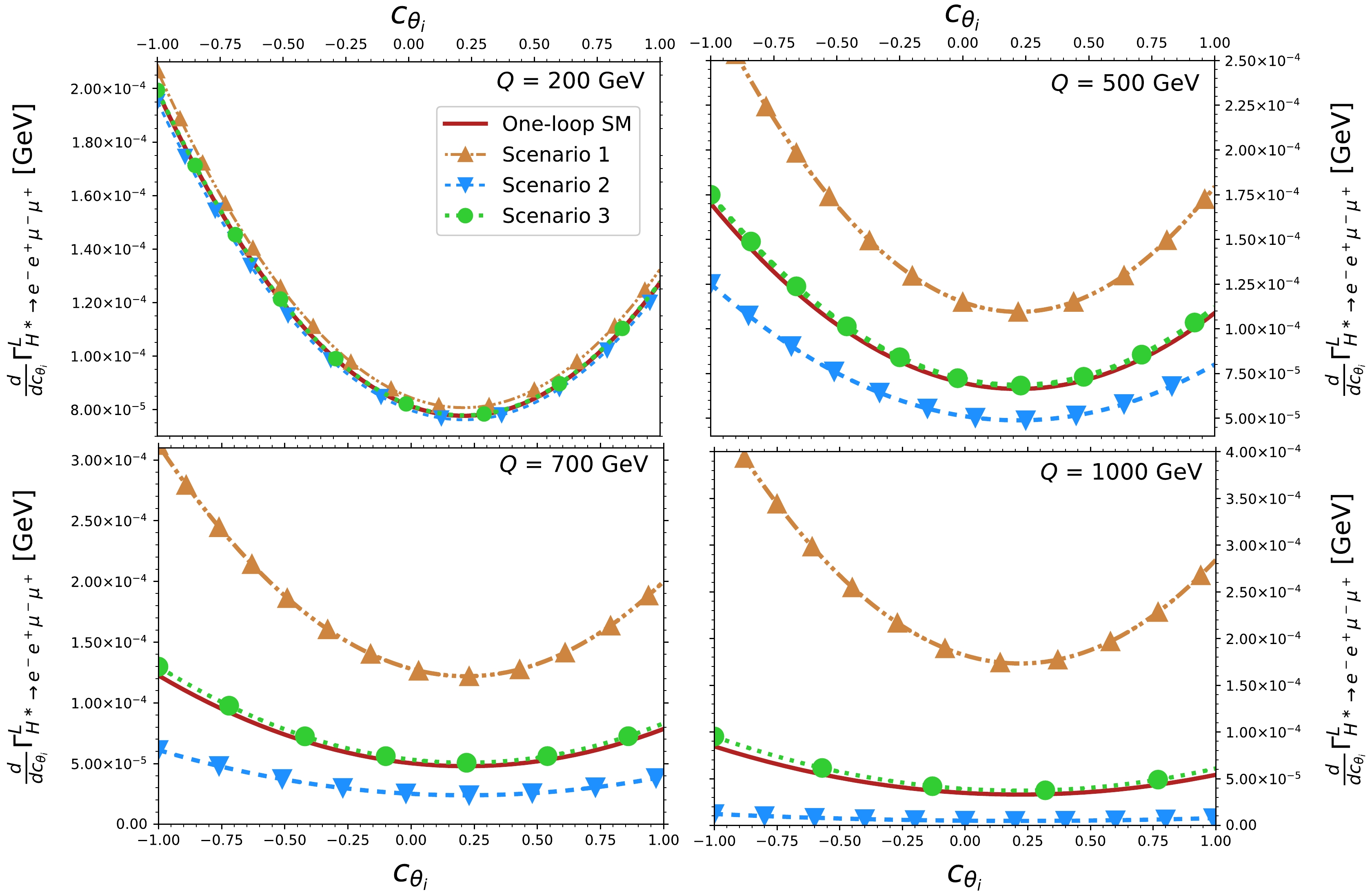
Figure 8. (color online) Differential
$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ decay width for left-handed polarization as a function of$ \cos\theta_i $ ($ i=1 $ , 2) for some values of the four-lepton invariant mass$ Q $ in the three scenarios shown in Table 1 for the anomalous$ HZZ $ couplings. The SM contribution up to the one-loop level is included. Integration over one of the two angles was already performed.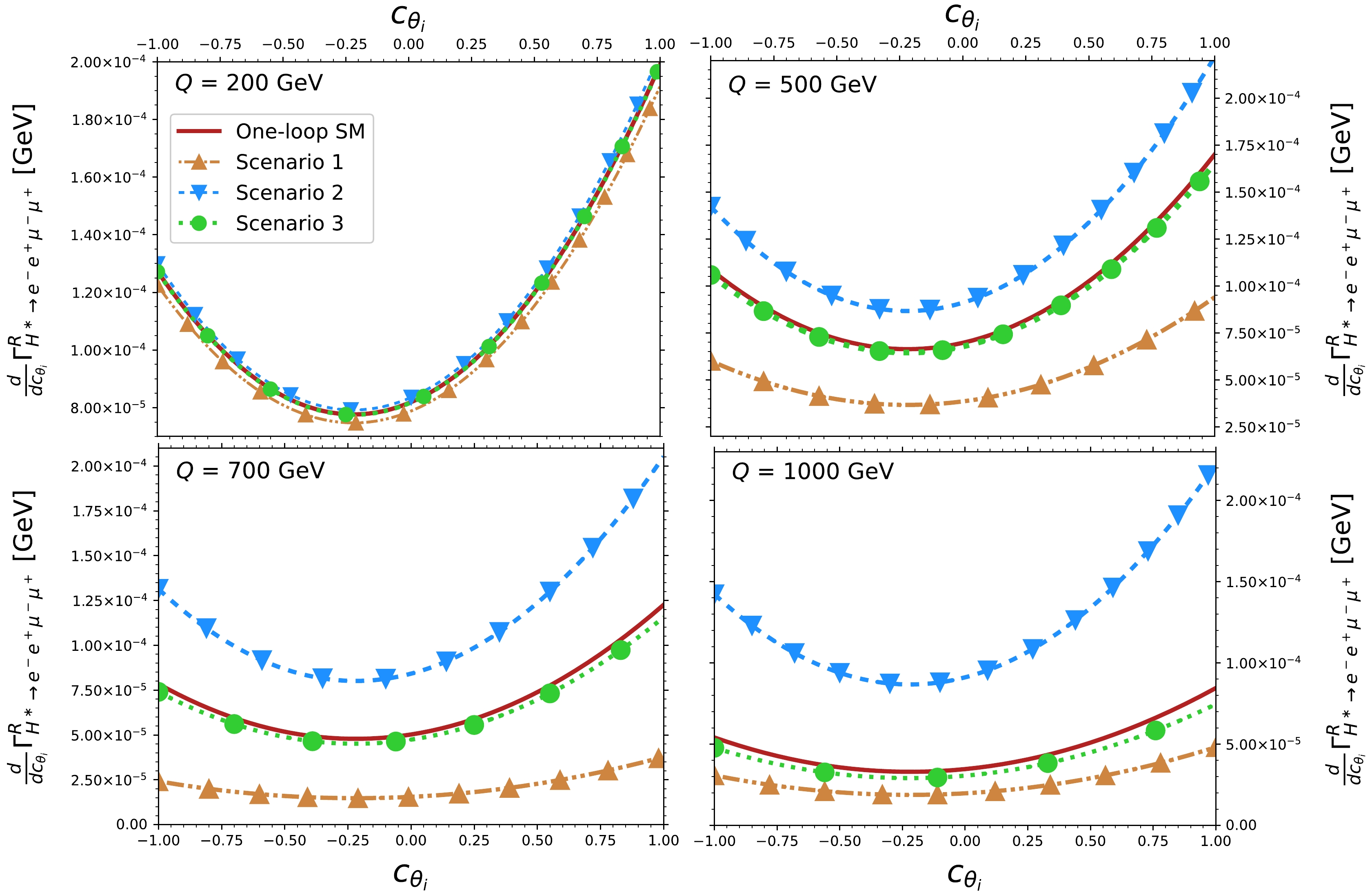
Figure 9. (color online) Same as in Fig. 8, but for right-handed polarizations.
-
Given that some asymmetries from the
$ HZZ $ coupling can be large enough to give evidence of new physics at the LHC [15], and motivated by the behavior of the$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ angular distributions for transverse polarizations, we define the following angular left-right asymmetry:$ \begin{align} \mathcal{A}_{LR\theta}&=\dfrac{\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma^L_{H^\ast\rightarrow e^-e^+\mu^- \mu^+}-\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma^R_{H^\ast\rightarrow e^-e^+\mu^- \mu^+}} {\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma^L_{H^\ast\rightarrow e^-e^+\mu^- \mu^+}+\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma^R_{H^\ast\rightarrow e^-e^+\mu^- \mu^+}}, \end{align} $

(42) where
$ i=1 $ (2) and the angle$ \theta_2 $ ($ \theta_1 $ ) was integrated over. Given that$ \Gamma_{H^\ast\rightarrow e^-e^+\mu^- \mu^+} $ is symmetric under$ \theta_i $ ($ i=1 $ , 2), the same expression holds for both angles. The analytical form, obtained from Eq. (29), can be expressed as$ \begin{align} \mathcal{A}_{LR\theta}&=- \frac{4}{m_Z^2}\frac{f(Q^2, c_{\theta_i} )}{h(Q^2, c_{\theta_i} )} , \end{align} $

(43) with the
$ f(Q^2, c_{\theta_i} ) $ and$ h(Q^2, c_{\theta_i}) $ functions are written as$ \begin{aligned}[b]& f(Q^2, c_{\theta_i} )=g_A g_V c_{\theta_i} m_Z^2 \left(Q^2 \left(Q^2-4 m_Z^2\right)\big|h_3^H\big|^2+4 m_Z^4\big|h_1^H\big|^2\right)\\&- \left(g_A^2 +g_V^2\right) \left(1+c^2_{\theta_i}\right)\left( m_Z^4 \sqrt{Q^2\left(Q^2-4 m_Z^2\right)}{\rm{Im}}\left(h_3^H{h_ 1^H}^\dagger\right)\right), \end{aligned} $

(44) $ \begin{aligned}[b] h(Q^2, c_{\theta_i} )=\;&-16 g_A g_V c_{\theta_i} m_Z^2 \sqrt{Q^2\left(Q^2-4 m_Z^2\right)} {\rm{Im}}\left(h_3^H{h_ 1^H}^\dagger\right)\\&+\Big(g_A^2+g_V^ 2\Big) \left(1+c^2_{\theta_i}\right)\Big(Q^2 \Big(Q^2-4 m_Z^2\Big) \big|h_3^H\big|^2\\&+4 m_Z^4 \big|h_1^H\big|^2\Big), \end{aligned} $

(45) where the terms proportional to
$ g_{V,A}^2 $ in$ f\left(Q^2, c_{\theta_i} \right) $ are identical to those in the$ \mathcal{A}_{LR} $ asymmetry given by Eq. (41), whereas the remaining terms arise from those proportional to$ c_{\theta_i} $ in the$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ amplitude, which have been not integrated out yet. Furthermore, note that if the numerator and denominator in Eq. (43) are integrated over$ c_{\theta_i} $ , we obtain the non-angular$ \mathcal{A}_{LR} $ asymmetry. Although the$ \mathcal{A}_{LR} $ and$ \mathcal{A}_{LR\theta} $ asymmetries are related, they have a distinct origin: the former is induced via the$ HZZ $ anomalous couplings, whereas the latter is a result of polarized$ Z $ gauge bosons decaying into leptons, where the angular variables appear. Note also that even for a vanishing$\rm CP$ -violating form factor$ h_3^H $ , the$ \mathcal{A}_{LR\theta} $ asymmetry is non-zero, thereby becoming non-vanishing in the SM at the one-loop level:$ \begin{align} \mathcal{A}^{\rm{SM}}_{LR\theta}=-\frac{4 g_A g_V c_{\theta _i}}{ \left( g_A^2+g_V^2\right) \left(1+c ^2_{\theta _i}\right)}. \end{align} $

(46) Next, we again consider the three scenarios shown in Table 1 for the anomalous
$ HZZ $ couplings and evaluate the effects on the$ \mathcal{A}_{LR\theta} $ asymmetry. The results are shown in Fig. 10, where the SM contribution is also included. Note that at low$ Q $ ,$ \mathcal{A}_{LR\theta} $ shows a slight deviation from the SM in scenarios 1 and 2, which becomes more significant as$ Q $ increases, whereas such a variation is negligible in scenario 3. Interestingly, the deviation of$ \mathcal{A}_{LR\theta} $ from the SM value is of the order of$ 10^{-1}-10^{-2} $ , whereas the corresponding difference in Figs. 8 and 9 is of the order of$ 10^{-4}-10^{-5} $ . Thus, there may be more possibilities to observe the effects of$\rm CP$ violation through the$ \mathcal{A}_{LR\theta} $ asymmetry than in the polarized differential widths.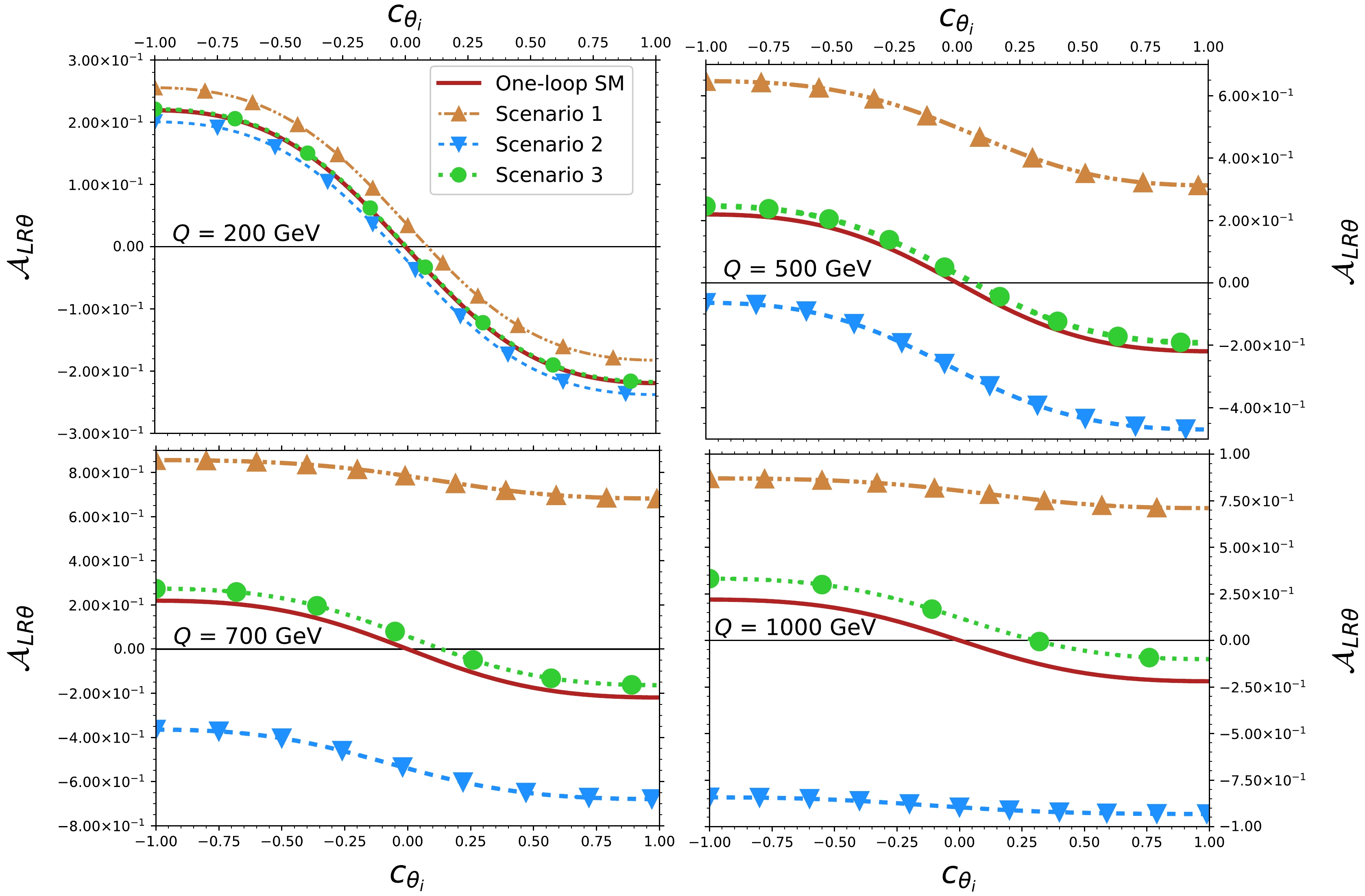
Figure 10. (color online) Behavior of the left-right asymmetry
$ \mathcal{A}_{LR\theta} $ as a function of$ \cos\theta_i $ for some values of the four-lepton invariant mass$ Q $ in the three scenarios described in Table 1 for the anomalous$ HZZ $ couplings. The SM contribution up to the one-loop level is included.Given the behavior observed in angular
$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ distributions, we also expect the presence of a polarized forward-backward asymmetry, which in general can be defined as$ \mathcal{A}_{FB}^\lambda=\dfrac{ \int_{0}^1{\rm d}c_{\theta_i}\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma^\lambda_{H^\ast\rightarrow \overline{f}_if_i \overline{f}_jf_j}-\int_{-1}^0{\rm d}c_{\theta_i}\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma^\lambda_{H^\ast\rightarrow \overline{f}_if_i \overline{f}_jf_j}} { \int_{0}^1{\rm d}c_{\theta_i}\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma^\lambda_{H^\ast\rightarrow \overline{f}_if_i \overline{f}_jf_j}+\int_{-1}^0{\rm d}c_{\theta_i}\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma^\lambda_{H^\ast\rightarrow \overline{f}_if_i \overline{f}_jf_j}}. $

(47) A straightforward calculation yields
$ \begin{align} \mathcal{A}_{FB}^{L/R}=\mp\frac{3 g_A g_V}{2 \left(g_A^2+g_V^2\right)}. \end{align} $

(48) Such a simple expression arises from the fact that
$ \mathcal{A}_{FB}^{L/R} $ is due to the$ Z\rightarrow \overline{\ell}\ell $ decay, thereby becoming independent of the anomalous$ HZZ $ couplings and the four-lepton invariant mass. Note that it is constant even in new-physics scenarios, but a difference in sign arises for left-handed and right-handed polarizations.Table 2 presents the values of the
$ \mathcal{A}_{FB}^\lambda $ asymmetry for all the combinations of light fermion flavors in the$ H^\ast\rightarrow \overline{f}_if_i \overline{f}_jf_j $ final state. We consider massless fermions and distinct fermion-antifermion pairs. Note that the result given by Eq. (48) is similar to the left-right$ Z $ gauge boson asymmetry in the SM [90, 91].$ f_i $ 

$ f_j $ 

$ \mathcal{A}_{FB}^{L/R} $ 

$ e $ ,

$ \mu $ ,

$ \tau $ 

$ e $ ,

$ \mu $ ,

$ \tau $ 

$ \mp $ 0.164

$ \nu_e $ ,

$ \nu_\mu $ ,

$ \nu_\tau $ 

$ \nu_e $ ,

$ \nu_\mu $ ,

$ \nu_\tau $ 

$ \mp $ 0.75

$ d $ ,

$ s $ ,

$ b $ 

$ d $ ,

$ s $ ,

$ b $ 

$ \mp $ 0.705

$ u $ ,

$ c $ 

$ u $ ,

$ c $ 

$ \mp $ 0.524

Table 2.
$ \mathcal{A}_{FB}^{L/R} $ asymmetry for all combinations of distinct pairs of light fermion-antifermion flavors in the$ H^\ast\rightarrow \overline{f}_if_i \overline{f}_jf_j $ decay. The fermion masses have been neglected. -
Up to now, we have focused only on the effects of the
$ Z $ gauge boson polarizations in the$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay. Nevertheless, the sign change in Eq. (48) suggests the presence of a forward-backward asymmetry$ \mathcal{A}_{FB} $ in the unpolarized case, which is defined as$ \mathcal{A}_{FB}=\dfrac{ \int_{0}^1{\rm d}c_{\theta_i}\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma_{H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+}-\int_{-1}^0{\rm d}c_{\theta_i}\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma_{H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+}} { \int_{0}^1{\rm d}c_{\theta_i}\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma_{H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+}+\int_{-1}^0{\rm d}c_{\theta_i}\dfrac{\rm d}{{\rm d}c_{\theta_i}}\Gamma_{H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+}}. $

(49) After inserting Eq. (29), we obtain
$ \begin{align} \mathcal{A}_{FB}=-\frac{48 g_A g_V m_Z^6 Q \sqrt{Q^2-4 m_Z^2}}{\left(g_A^2+g_V^2\right)} \frac{{\rm{Im}}\left(h_3^H{h_ 1^H}^\dagger\right)}{G\left(Q^2\right)}, \end{align} $

(50) where the
$ G\left(Q^2\right) $ function was given in Eq. (36). Note that$ \mathcal{A}_{FB} $ vanishes in the SM at the one-loop level given that$ h_3^H=0 $ . Our result reproduces the one reported in Ref. [15], where the absorptive part of$ h_1^H $ was dismissed.In contrast with the polarized forward-backward asymmetry, which is due only to the
$ Z \rightarrow \overline{\ell}_i\ell_i $ decay, the unpolarized one depends on the properties of both the$ H^\ast\rightarrow ZZ $ and$ Z \rightarrow \overline{\ell}_i\ell_i $ decays. The dependence on the complex anomalous couplings is a reflect of the former whereas the presence of the vector$ g_V $ and axial$ g_A $ couplings arises from the latter.Figure 11 shows the unpolarized forward-backward asymmetry
$ \mathcal{A}_{FB} $ as a function of the four-lepton invariant mass in the three scenarios considered in Table 1 . In addition to the anomalous contributions, we included the one-loop SM contribution to the real and absorptive parts of the$ h_1^H $ form factor. Similar to the above results for other observables,$ \mathcal{A}_{FB} $ can reach the largest values in scenarios 1 and 2, reaching the order of$ 10^{-3} $ at most, whereas it is one order of magnitude below in scenario 3. While$ \mathcal{A}_{FB} $ can be large at small energies, it tends to vanish at very large$ Q $ . An opposite behavior is observed for the$ \mathcal{A}_{LR} $ and$ \mathcal{A}_{LR\theta} $ asymmetries. To the best of our knowledge, the$ \mathcal{A}_{FB} $ asymmetry has not been analyzed in the literature yet.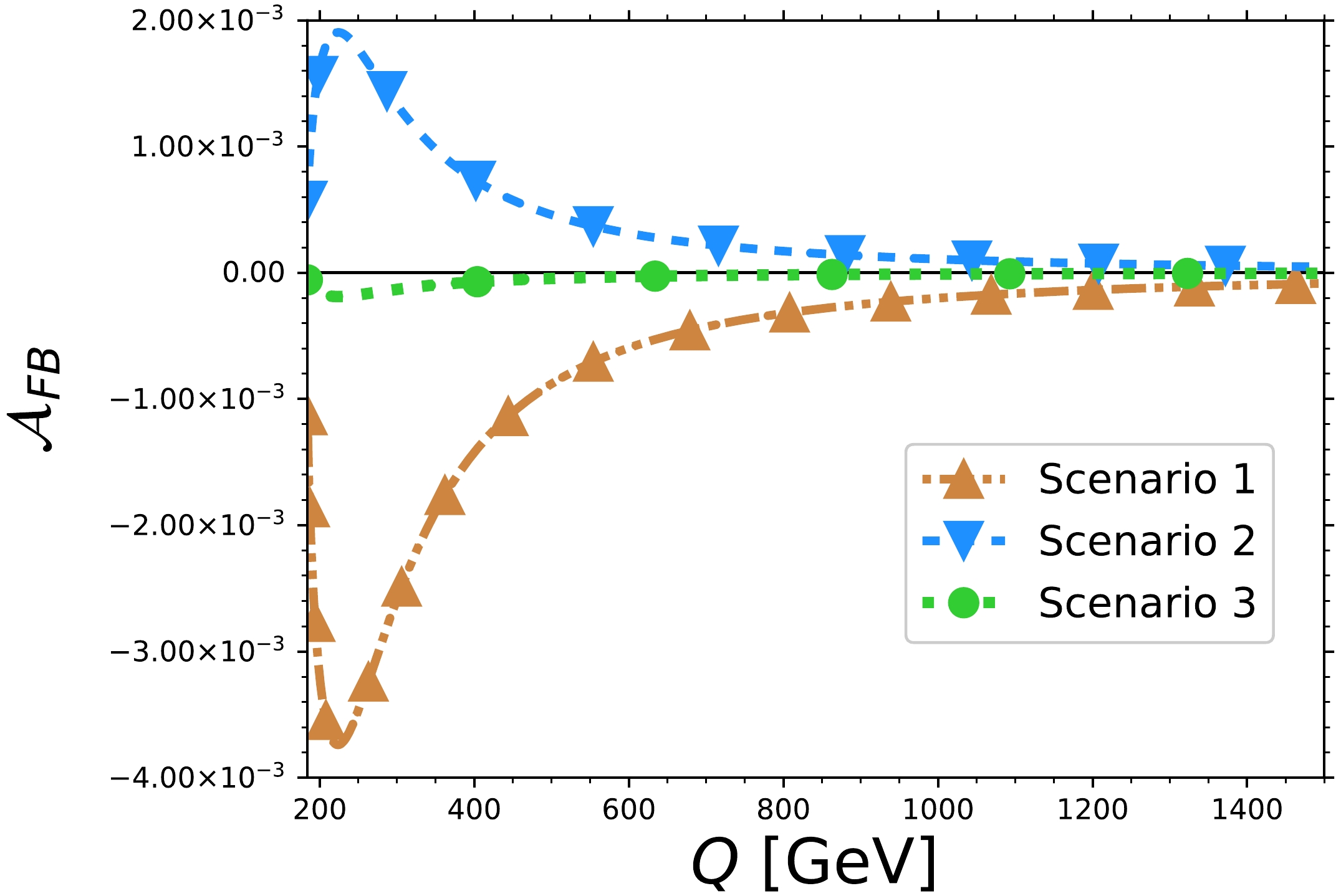
Figure 11. (color online) Behavior of the unpolarized forward-backward asymmetry
$ \mathcal{A}_{FB} $ as a function of the four-lepton invariant mass$ Q $ in the three scenarios described in Table 1 for the anomalous$ HZZ $ couplings. The one-loop SM contribution to the$ h_1^H $ form factor has been added to the new-physics contribution. -
The effects of the anomalous couplings on
$ \phi $ distributions have been neglected so far because they have been integrated out in previous sections. These effects can be studied through the interference term$ \mathcal{M}^2_{\text{int}} $ (Eq. (23)) after integrating Eq. (29) over$ c_{\theta_i} $ ($ i $ =1, 2). Fig. 12 shows the numerical results of the$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ partial width as a function of the azimuthal angle$ \phi $ for the SM at one-loop level and the three scenarios in Table 1. Note that larger values of$ \Gamma_{H^\ast\rightarrow e^-e^+\mu^- \mu^+} $ are obtained at high energies, where the new-physics effects are also notable given that significant deviations from the SM were found. Furthermore, a shift between the new-physics scenarios and the SM case is also observed. The consequences of the anomalous couplings are more pronounced for scenario 1, which considers the largest values of the$\rm CP$ -violating form factor.
Figure 12. (color online) Differential
$ H^\ast\rightarrow e^-e^+\mu^- \mu^+ $ decay width as a function of$ \phi $ for various values of the four-lepton invariant mass$ Q $ in the three scenarios considered in Table 1 for the anomalous$ HZZ $ couplings. The SM contribution up to the one-loop level is included.The shift observed in the
$ \phi $ distributions leads to the definition of the$ \mathcal{A}_\phi $ azimuthal asymmetry:$ \mathcal{A}_{\phi}=\dfrac{ \int_{\pi}^{2\pi}{\rm d}\phi\dfrac{\rm d}{{\rm d}\phi}\Gamma_{H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+}-\int_{0}^\pi {\rm d}\phi\dfrac{\rm d}{{\rm d}\phi}\Gamma_{H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+}} { \int_{\pi}^{2\pi}d\phi\dfrac{\rm d}{{\rm d}\phi}\Gamma_{H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+}+\int_{0}^\pi d\phi\dfrac{\rm d}{{\rm d}\phi}\Gamma_{H^\ast\rightarrow ZZ \rightarrow e^-e^+\mu^-\mu^+}}. $

(51) After integrating Eq. (29), we obtain
$ \begin{align} \mathcal{A}_{\phi}=-\frac{9\ \pi\ g^2_A g^2_V m_Z^2 Q \sqrt{Q^2-4 m_Z^2}}{2\left(g_A^2+g_V^2\right)^2} \frac{K\left(Q^2\right)}{G\left(Q^2\right)}, \end{align} $

(52) with
$ \begin{aligned}[b] K\left(Q^2\right)=\;&-2m_Z^2Q^2\Big[{\rm{Re}}\left(h_1^H{h_ 3^H}^\dagger\right)-2{\rm{Re}}\left(h_2^H{h_ 3^H}^\dagger\right)\Big]\\&+4m_Z^4 {\rm{Re}}\left(h_1^H{h_ 3^H}^\dagger\right)-Q^4 {\rm{Re}}\left(h_2^H{h_ 3^H}^\dagger\right), \end{aligned} $

(53) and the
$ G\left(Q^2\right) $ function defined in Eq. (36). According to Eq. (53), it is clear that the$ \mathcal{A}_\phi $ asymmetry is very sensitive to the$\rm CP$ -violating form factor$ h_3^H $ . Fig. 13 shows the$ \mathcal{A}_\phi $ asymmetry as a function of the four-lepton invariant mass for the three new-physics scenarios. The SM case is not considered as it is zero. Once again, the largest values, of the order of$ 10^{-4} $ , are reached for scenario 1. For scenario 3, results of the order of$ 10^{-6} $ are obtained. Unlike the behavior observed for the$ \mathcal{A}_{FB} $ asymmetry, we found that$ \mathcal{A}_\phi $ does not vanish at$ Q> 1000 $ GeV. Thus, the azimuthal asymmetry may be measured at super high energies.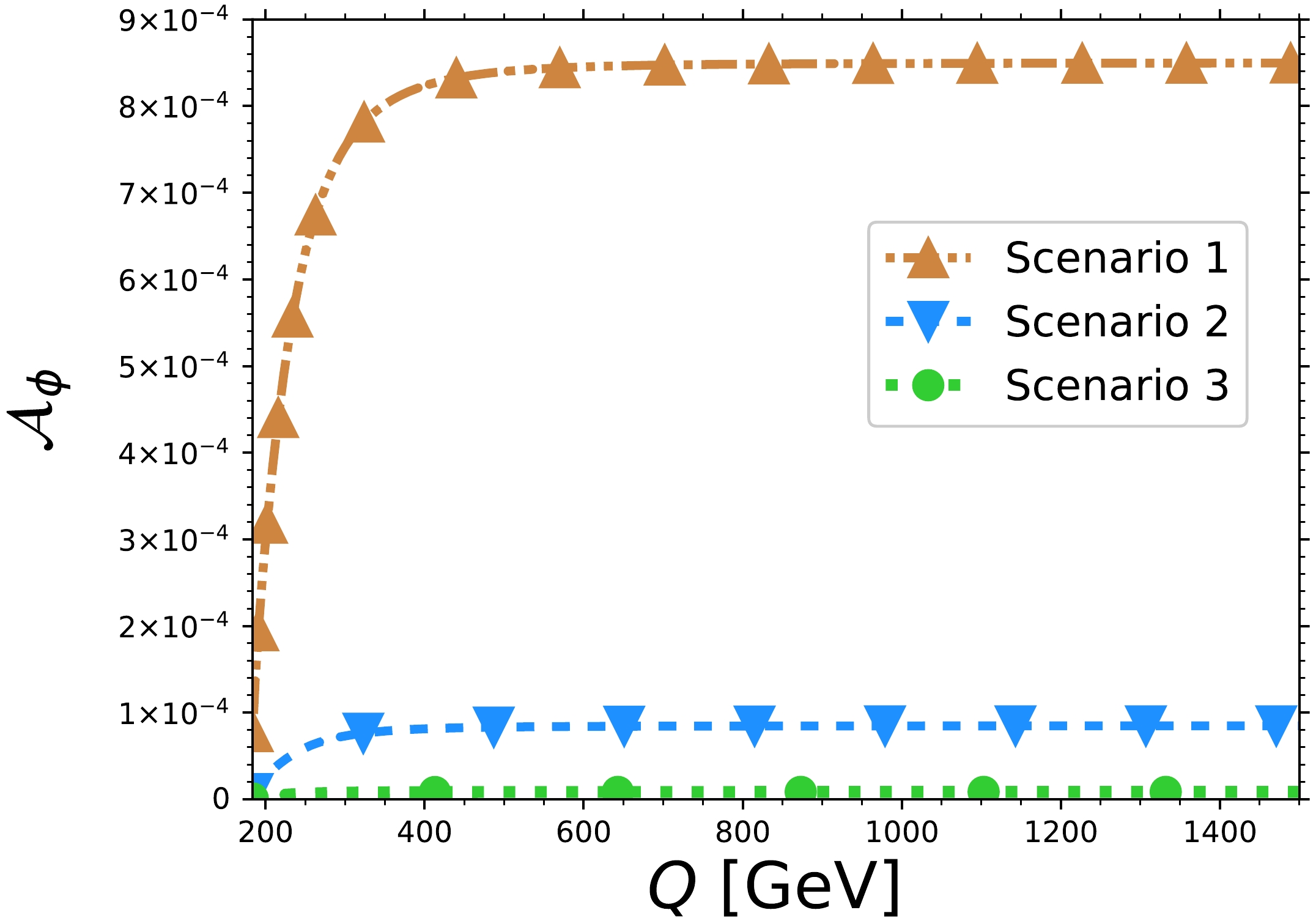
Figure 13. (color online) Behavior of the azimuthal asymmetry
$ \mathcal{A}_{\phi} $ as a function of the four-lepton invariant mass$ Q $ in the three scenarios described in Table 1 for the anomalous$ HZZ $ couplings. The one-loop SM contribution to the$ h_1^H $ form factor has been added to the new-physics contribution.The
$ \phi $ distributions are also good channels for observing the effects of anomalous couplings. Our SM results are in agreement with those reported in Ref. [15]. Nonetheless, the scenarios with anomalous cuplings are very different, as the shift in Fig. 12 was not observed. Therefore, the azimuthal asymmetry has not been examined in the form presented in this study.In summary, the azimuthal distributions are sensitive to new physics, particularly to
$\rm CP$ -violating effects. They can provide deeper insights into the potential impact on observables at high-energy colliders. -
We have presented a novel analysis of the
$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width for both unpolarized and polarized$ Z $ gauge bosons considering the most general$ H^*ZZ $ vertex function, which was parameterized by three form factors$ h^H_i $ ($ i $ =1, 2, 3), and where the SM contributions up to the one-loop level and anomalous contributions arising from new-physics were included. We then considered the scenario where all the$ h_i^H $ couplings are complex, which, to the best of our knowledge, has never been studied in the literature. We obtained analytical results for both the unpolarized and polarized$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ square amplitudes, out of which the decay widths, angular distributions, and left-right and forward-backward asymmetries were straightforwardly obtained. Our results reproduce previous ones obtained in more restrictive scenarios. We found that for the four-lepton invariant mass distributions, the polarized$H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2$ decay is mainly determined by the$ H^\ast\rightarrow ZZ $ process.To cross-check the consistency of our numerical evaluation method, we used
$ \mathrm{MadGraph5\_aMC@NLO}$ with the corresponding Feynman rules for our model obtained via the FeynRules package. For numerical analysis, we considered some realistic scenarios for the complex$ HZZ $ anomalous couplings, consistent with the current experimental and indirect constraints. We analyzed the role of the transversal (left-handed and right-handed) polarizations of the$ Z $ gauge bosons on the behavior of the$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width as a function of the four-lepton invariant mass$ Q $ , which turns out to be notably distinctive for each type of polarization. We found that for some specific values of the complex$ HZZ $ couplings, the polarized$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay width can deviate considerably from the SM contribution. This deviation is more pronounced at large values of$ Q $ . An opposite behavior between the left and right-handed polarizations was also observed. This leads to a left-right asymmetry$ \mathcal{A}_{LR} $ , which vanishes in the SM given that it requires the presence of$\rm CP$ -violating anomalous couplings. The angular distributions of the$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay were also analyzed. They exhibit similar behavior to that observed for the invariant mass distributions. Hence, we introduced an angular left-right asymmetry$ \mathcal{A}_{LR\theta} $ that has a non-vanishing SM one-loop level contribution. This asymmetry shows considerable deviations due to complex anomalous$ HZZ $ couplings. Furthermore, a polarized forward-backward asymmetry$ \mathcal{A}^\lambda_{FB} $ was studied. It was found to be constant, differing in a sign for left-handed and right-handed polarizations of the$ Z $ gauge bosons. Interestingly, the$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay is unsusceptible to new-physics effects in the case of longitudinally polarized$ Z $ gauge bosons. For completeness, we also studied the scenario with unpolarized$ Z $ gauge bosons, where the forward-backward$\mathcal{A}_{FB}$ and azimuthal$ \mathcal{A}_\phi $ asymmetries were examined as a function of the four-lepton invariant mass, and a different behavior compared with the polarized asymmetries was found.In summary, the study of the off-shell
$ H^\ast\rightarrow ZZ \rightarrow \overline{\ell}_1\ell_1\overline{\ell}_2\ell_2 $ decay, via the transverse polarizations of the$ Z $ gauge bosons, could be a useful tool to search for effects of new physics. The absorptive parts of the$ HZZ $ anomalous couplings could lead to significant deviations from the SM contributions in the decay widths as well as other observables such as angular distributions and new asymmetries. In particular, we put special emphasis on the study of the effects of the absorptive parts of the$ HZZ $ anomalous couplings because they have been largely overlooked in the past but can serve as a probe of the SM at the LHC and future colliders. Such absorptive parts constitute a unique prediction of quantum field theory. -
The phase space of an
$ n $ -body decay was studied by Cabibbo and Maksymowicz [92], Pais and Treiman [93], and Byckling and Kajanate [94−98]. In particular, the$ 1 \rightarrow 4 $ decay can be decomposed through a recursion relation into three partial$ 1\rightarrow 2 $ decays as follows [92, 96, 99]:$ 1\rightarrow 2 \longrightarrow 1\rightarrow 2 +1\rightarrow 2 $ . Following this approach, below we obtain the differential phase space for the$ H\to ZZ\to \bar{\ell}_1\ell_1\bar{\ell}_2\ell_2 $ decay.For the four-momenta, we used the nomenclature defined in Fig. 1, namely
$ H(q)\to Z(p_1)+Z(p_2) $ , followed by$ Z(p_1)\to \ell_1(q_1)+\bar{\ell}_1(q_2) $ and$ Z(p_2)\to\ell_2(q_3)+\bar{\ell}_2(q_4) $ . For our calculations, we considered the reference systems shown in Fig. 2. The differential decay width is expressed in terms of the angles$ \theta_1 $ ,$ \theta_2 $ , and$ \phi $ :●
$ \theta_1 $ is the angle between$ \vec{p}_1 $ and$ \vec{q}_1 $ in the rest frame of the$ Z(p_1) $ gauge boson.●
$ \theta_2 $ is the angle between$ \vec{p}_2 $ and$ \vec{q}_3 $ in the rest frame of the$ Z(p_2) $ gauge boson.●
$ \phi $ is the relative angle between the$ Z(p_1)\rightarrow 2\ell_1 $ and$ Z(p_2)\rightarrow 2\ell_2 $ decay planes, taken as positive from the$ Z(p_1) $ to the$ Z(p_2) $ planes, with$ \phi=0 $ in the case in which both planes coincide and both$ \vec{q_1} $ and$ \vec{q_3} $ are in the same direction.We next discuss the kinematics for the distinct reference frames introduced above.
-
The kinematics of the
$ H^\ast\rightarrow ZZ $ decay in the rest frame of the Higgs boson can be described as$ \begin{aligned} q^\mu=\big(Q,\ 0 \big), \end{aligned} $

(A1) $ p_{1,2}^\mu=\big(Q/2,\pm \vec{p}\big), $

(A2) where the magnitude of the three-momentum
$ \vec{p} $ is$ \|\vec{p}\|=\frac{\sqrt{Q^2-4 m_Z^2}}{2}. $

(A3) We consider that in this frame, the
$ Z $ gauge bosons move along the$ x $ axis, so their polarization vectors can be expressed as$ \epsilon^\mu_{1,2}(0)=\frac{1}{m_Z}\Big( \| \vec{p} \|, \pm \frac{\sqrt{Q^2}}{2} ,0 , 0 \Big), $

(A4) $ \epsilon^\mu_{1}(R/L)=\frac{1}{\sqrt{2}}\Big(0 , 0 , - i , \pm1 \Big). $

(A5) -
In our calculations, we also used the rest frame of a
$ Z(p_i) $ gauge boson decaying into a lepton-antilepton pair, which obeys the following kinematics:$ p_i^\mu=\big(m_Z,\ 0 \big), $

(A6) $ q_1^\mu=\big(m_Z/2,\ \vec{k}_1\big), \quad q_2^\mu=\big(m_Z/2,\ -\vec{k}_1\big), $

(A7) $ q_3^\mu=\big(m_Z/2,\ \vec{k}_2\big), \quad q_4^\mu=\big(m_Z/2,\ -\vec{k}_2\big), $

(A8) where, according to Fig. 2, the three-momenta
$ \vec{k}_i $ are expressed as$ \vec{k}_1=\frac{\sqrt{m_Z^2-4 m_{\ell_i}^2}}{2}\big(\cos{\theta_1} , \sin{\theta_1}, 0\big), $

(A9) $ \vec{k}_2=\frac{\sqrt{m_Z^2-4 m_{\ell_i}^2}}{2} \big(-\cos{\theta_2},\sin{\theta_2}\cos{\phi} , \sin{\theta_2}\sin{\phi}\big), $

(A10) whereas the form of the transverse polarization vectors in Eq. (A5) still holds; for longitudinal polarizations, we have
$ \epsilon^\mu_{1,2}(0)=\Big(0, \pm 1 ,0 , 0 \Big). $

(A11) Given that the interference term of the
$H\to ZZ \to \bar{\ell}_1\ell_1\bar{\ell}_2\ell_2$ square amplitude has to be calculated in the frame of the Higgs boson, we need to boost the four-momenta and polarization vectors defined in the$ Z(p_i) $ rest frames into the rest frame of the Higgs boson, which is achieved via the following Lorentz matrix:$ \Lambda^\mu_\nu=\left(\begin{array}{cccc}\gamma & \gamma v & 0 & 0 \\\gamma v & \gamma & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{array}\right), $

(A12) with
$ v=\frac{\vec{p}_i}{E_i}=\pm \frac{\sqrt{Q^2-4m_Z^2}}{Q}. $

(A13) -
The
$ H\to ZZ\to \bar{\ell}_1\ell_1\bar{\ell}_2\ell_2 $ phase space${\rm d}\left(R_4\right)$ can be expressed as$ \begin{aligned}[b] {\rm d}\left(R_4\right)=\;& \frac{{\rm d}^3q_1}{(2\pi)^3 2E_{q_1}}\frac{{\rm d}^3q_2}{(2\pi)^3 2E_{q_2}}\frac{{\rm d}^3q_3}{(2\pi)^3 2E_{q_3}}\frac{{\rm d}^3q_4}{(2\pi)^3 2E_{q_4}}\\&\times(2\pi)^4\delta^4\big(q-q_1-q_2-q_3-q_4\big), \end{aligned} $

(A14) where the lepton energies are
$E_{q_i}=\sqrt{m_i^2+ \vec{p}_i ^2}$ ($ i= $ 1, 2, 3, 4). We followed the approach described in Ref. [99], which is analogous to that used in [92d]. We thus introduce the relations$ \int \frac{{\rm d}^3 p_1}{2E_{p_1}} {\rm d}S_1 \delta^4\big(p_1-q_1-q_2\big)=1, $

(A15) and
$ \int \frac{{\rm d}^3 p_2}{2E_{p_2}} {\rm d}S_2 \delta^4\big(p_2-q_3-q_4\big)=1, $

(A16) where
$ E_{p_i}=\sqrt{{\vec{p}_i}^{\ 2}+S_i} $ , with$ S_i=p_i^2 $ ($ i=1,2 $ ).The
$ d\left(R_4\right) $ phase space can thus be expressed as$ {\rm d}\left(R_4\right)= \frac{{\rm d}S_1 {\rm d}S_2 }{(2\pi)^8}I_{p_1}I_{p_2}I_{q}, $

(A17) where, in the rest frames of the
$ Z $ gauge bosons and Higgs boson, the$ I_{p_i} $ and$ I_{q} $ integrals are expressed for massless leptons as$ I_{p_1}=\int \frac{{\rm d}^3q_1}{2E_{q_1}} \frac{{\rm d}^3q_2}{2E_{q_2}}\delta^4\big(p_1-q_1-q_2\big)=\frac{\pi}{4}{\rm d}\cos{\theta_1}, $

(A18) $ I_{p_2}=\int \frac{{\rm d}^3q_3}{2E_{q_3}} \frac{{\rm d}^3q_4}{2E_{q_4}}\delta^4\big(p_2-q_3-q_4\big)=\frac{1}{8}{\rm d}\cos{\theta_2}{\rm d}\phi, $

(A19) and
$ I_{q}=\int \frac{{\rm d}^3p_1}{2E_{p_1}} \frac{{\rm d}^3p_2}{2E_{p_2}}\delta^4\big(q-p_1-p_2\big)=\frac{\pi}{2 Q}\sqrt{Q^2-4 m_Z^2}. $

(A20) Therefore, the
${\rm d}\left(R_4\right)$ phase space reads$ {\rm d}\left(R_4\right)= \frac{\sqrt{Q^2-4 m_Z^2}}{256 Q (2\pi)^6} {\rm d}S_1 {\rm d}S_2 {\rm d}\cos{\theta_1} {\rm d}\cos{\theta_2}{\rm d}\phi, $

(A21) For massless leptons, the integration region reads
$ 0< \ S_2<\left(Q-\sqrt{S_1}\right)^2, $

(A22) $ 0< \ S_1<Q^2, $

(A23) $ 0<\ \theta_1,\ \theta_2 < \pi, $

(A24) $ 0<\ \phi<2\pi, $

(A25) where
$ Q^2=q^2 $ is the invariant mass of the four final leptons, which is the same in all frames of reference and is usually employed for LHC analyses. For the purpose of our calculations, we use$ Q=\|q\| $ .
Polarized and unpolarized off-shell ${ \boldsymbol H^\ast{\bf\to} \boldsymbol Z\boldsymbol Z{\bf\rightarrow 4}\boldsymbol\ell}$ decay above the ${{\bf 2}\boldsymbol m_Z} $ threshold
- Received Date: 2024-05-23
- Available Online: 2024-11-15
Abstract: An analysis of the off-shell








 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF








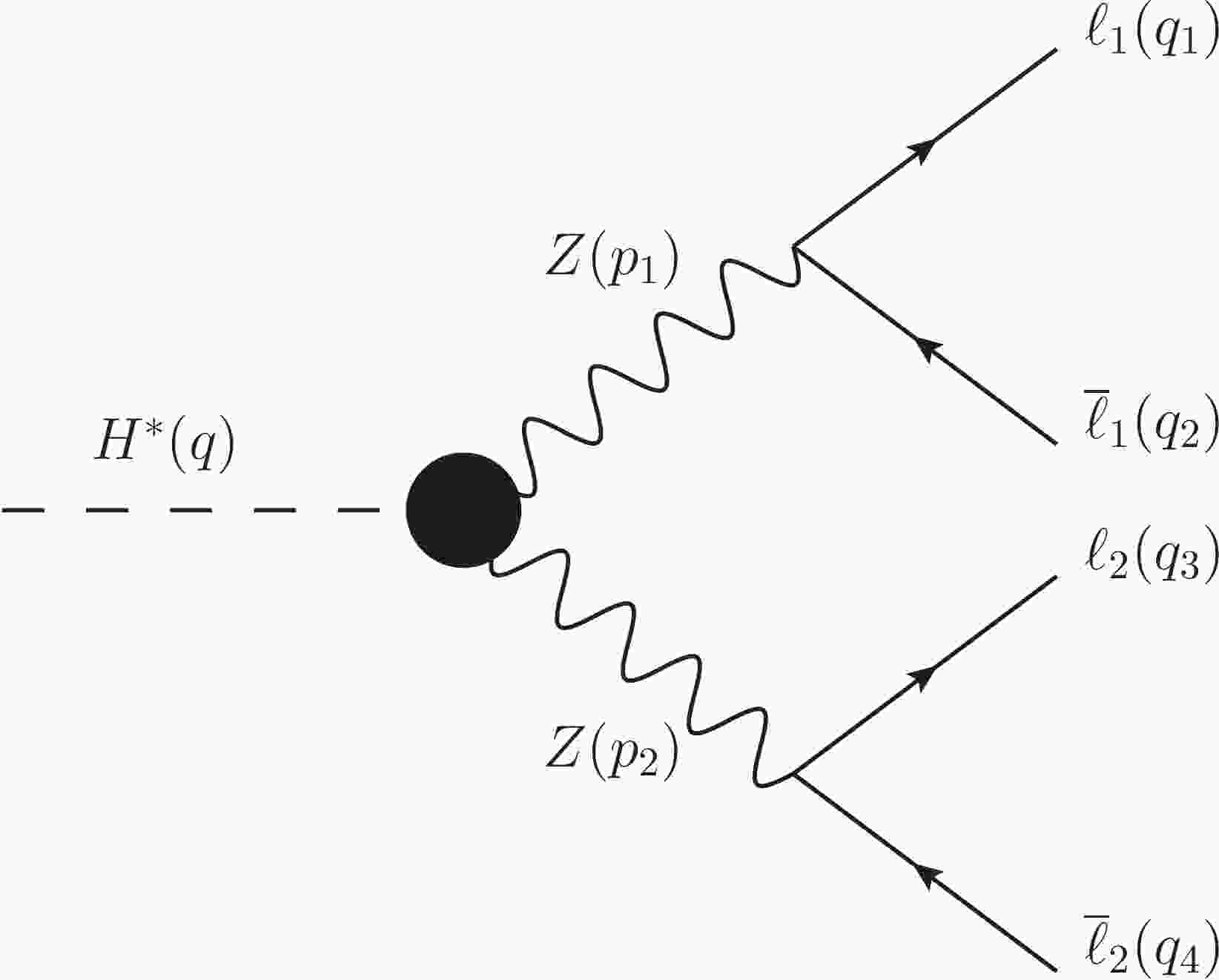













 DownLoad:
DownLoad: