-
Black holes are among the strangest objects in the universe, and they primarily reside at the heart of the galaxies. A well-defined boundary called the event horizon specifies them, separates the black hole's interior and exterior regions and is causally disconnected [1, 2]. The event horizon is also a null hypersurface. The thermodynamics of any generic black holes are studied in terms of the event horizon radius [3]. The thermodynamics of black holes connect several interdisciplinary branches of theoretical physics, e.g., general relativity, quantum mechanics, statistical mechanics, and information theory. The first study that revolutionized black hole thermodynamics was that of Bardeen et al. [4]. They formulated the laws of black hole mechanics in analogy with the ordinary thermodynamic system in their pioneering work. The continued interest led Bekenstein to propose that the entropy of the black holes must have a direct correspondence to the horizon area itself [5, 6]. Hawking and Page [7] proposed that the black holes in anti-de Sitter (AdS) spacetime must exhibit a phase transition between the pure thermal AdS bath and the Schwarzschild-AdS spacetimes, which is familiarly known as the Hawking-Page phase transition. This placed the study of black hole thermodynamics in AdS spacetimes at the forefront of modern scientific research because of its relevance to AdS/CFT correspondence [8–10]. The AdS/CFT correspondence tremendously affects the thermodynamics and phase structure of various AdS black holes. The Reissner-Nordstr
${\rm \ddot{o}}$ m-AdS black holes exhibit a van der Waals-like phase transition [11–13]. When we model the charged-AdS black holes as a canonical ensemble, we find a first-order phase transition that terminates at the second order where critical parameters are determined through the$ P-v $ criticality [13]. Such black holes also show a Hawking-Page-like phase transition when considered a grand canonical ensemble. A zeroth-order phase transition, the reentrant one, also seems to exist for specific AdS black hole systems, e.g., the Born-Infeld-AdS black holes [14, 15]. In all such analyses, one considers the cosmological constant as a thermodynamic pressure$ P=(-\Lambda/8\pi) $ and its conjugate quantity as a thermodynamic volume. We have also observed multiple exotic phenomena, including the coexistence lines in the$ P-T $ diagrams, terminating at the finite critical points and the$ P-v $ criticality mimicking the van der Waals type phase transition [16]. Despite such vivid descriptions, the thermodynamics of AdS black holes remains puzzling. We expose the phase structure from various perspectives. For example, some researchers have probed the microstructure of the black holes by investigating the related Ruppeiner geometry [15–18]. We can construct the repulsive or attractive nature of the micro-molecules through the formalism reported in [19–24]. The thermodynamic phase structure of the black holes in AdS spacetimes has been exposed to probe some of the observational signatures, such as the geodesics structure of the circular photon orbits [25, 26], the black hole shadow radius [27–29], and the quasinormal modes [30–34]. The discontinuous changes in the phase transition behavior between the small black hole (SBH) and large black hole (LBH) may help determine the order parameter of various thermodynamic quantities of physical interest.Motivated by the correlation of dynamics and thermodynamics, in the context of the AdS black hole geometry, a well-posed attempt was recently made in the analysis related to gravity and thermodynamics. The phase transition behavior between the SBH-LBH stable phases was probed through the unstable photon orbit radius. The phase transition behavior of the unstable photon orbit radius and the minimum impact parameter have an oscillatory behavior similar to that of the
$ T-r_h $ and$ T-S $ diagrams of the usual vdW-like fluids. Another motivation comes from the discontinuous changes in the photon orbit radius and the minimum impact parameter between the SBH-LBH phases, with a critical exponent of$ 1/2 $ . Therefore, the phase transition behavior was scrutinized for many AdS black hole spacetimes. The connection of the unstable photon circular orbits in several other contexts has also been significantly studied. Maintaining the utility of the phase transition behavior, we probed them through the photon orbit radius and the minimum impact parameter. In the present paper, we propose a possible correlation connecting the unstable circular null geodesics and the minimum impact parameter for the Letelier black holes in the AdS spacetime in the presence of perfect fluid dark matter (PFDM). The PFDM spacetime in the AdS background has been studied in different contexts in order to investigate, e.g., the topological classes of thermodynamic phase transitions and the justification of the weak censorship conjecture [35–37]. The criticality and thermal phase transition behavior was explored in the string cloud background in the presence of an additional field [38]. Another study was also devoted to the shadow analysis for the Letelier spacetime [39, 40], whereas the others were studied in another contexts [41–53]. The Letelier spacetime in a spherically symmetric case is obtained with a gauge invariant model of an array of a cloud of strings coupled to gravity in the framework of Einstein's general relativity. The enigmatic phenomenon of Letelier AdS black holes in PFDM may find its origin in the presence of a surrounding fluid-like dark matter, a pivotal and unanswered inquiry within the realm of physics. Dark matter is 25% of the universe's energy density. Our investigation might offer illuminating glimpses into the elusive properties of dark matter.After obtaining the exact solution, we investigate the Hawking temperature,
$ P-v $ criticality, Gibbs free energy, and other thermodynamic quantities of physical interest for the Letelier black holes in AdS spacetime surrounded by PFDM. We also explicitly show the effects of the cloud of strings parameter and the parameter characterizing the PFDM on the photon orbits and related quantities by plotting them numerically.We organized the paper as follows. In Section I, we briefly review the Letelier black holes in the AdS spacetimes surrounded by PFDM. Section II discusses the black holes' usual phase transition phenomena, compares them with the typical van der Waals-like fluid, and distinguishes the SBH and LBH phases. In the next section, we investigate the unstable photon orbit radius and the minimum impact parameter using the effective potential. We also examine the discontinuous changes in photon orbits and the impact parameter at the point where SBH-LBH phase transitions occur, acting as an order parameter, in Section IV. Section V deals with the null geodesics and phase transition behavior near the critical points. Finally, we conclude the paper in Sec. VI.
-
The action for (
$ 3+1 $ ) dimensional gravity with cosmological constant is$ \frac{1}{16\pi} \int {\rm d}^{4}x \sqrt{-g}\left[R +6l^{-2}+{\cal{L}}_{\cal{DM}}\right]+I_{S}, $

(1) where R is the Ricci scalar, g is the determinant of the metric tensor
$ g_{\mu\nu} $ ,$ {\cal{L}}_{\cal{DM}} $ gives the Lagrangian density of PFDM, and [54]$ {\cal{I}}_{S} = \int_{\Sigma} {\cal{L}} {\rm d}\lambda^{0}{\rm d}\lambda^{1} $

is the Nambu-Gotu action of a string characterized by timelike and spacelike parameters (
$ \lambda^{0},\lambda^{1} $ ), respectively. The Lagrangian density of a string cloud is$ {\cal{L}}=m(\gamma)^{-1/2} $ , where m is a dimensionless positive constant representing each string. The worldsheet of the string has an induced metric [55, 56]$ \gamma_{ab}=g_{\mu\nu}\frac{{\rm d}x^{\mu}}{{\rm d}x^{a}}\frac{{\rm d}x^{\nu}}{{\rm d}x^{b}} $

with
$ |\gamma|= $ det$ \gamma_{ab} $ . The bivector associated with the string worldsheet has the form$ \sigma^{ab}=\epsilon^{ab}\frac{{\rm d}x^{\mu}}{{\rm d}\lambda^{a}}\frac{{\rm d}x^{\nu}}{{\rm d}\lambda^{b}}, $

where
$ \epsilon^{0\; 1}=-\epsilon^{1\; 0}=1 $ is the two dimensional Levi-Civita tensor. Hence, the Lagrangian density becomes$L= m\left[-1/2\sigma^{\mu\nu}\sigma_{\mu\nu}\right]$ . Since$ T^{\mu\nu}=\partial{\cal{L}}/\partial g^{\mu\nu} $ , the energy momentum tensor for clouds of strings is$T^{\mu\nu}= \rho\sigma^{\mu\Sigma}\sigma^{\nu}_{\Sigma}/(-\gamma^{1/2})$ , where ρ is the proper density of the string cloud.Extremizing the action leads to the Einstein field equation [57]
$ G_{ab}-\frac{3}{l^{2}}g_{ab}=8\pi(T^{S}_{ab}+T^{DM}_{ab}), $

(2) where
$ T^{S}_{ab} $ and$ T^{DM}_{ab} $ , respectively, are the energy-momentum tensors of the cloud of strings and PFDM. In the rest frame associated with the observer,$ \rho=a/r^2 $ and the components of the energy-momentum tensor for clouds of strings are [58, 59]$ (T^{a}_{b})^{S}={\rm{diag}}\left(-\frac{a}{r^2},\frac{a}{r^2},0,0\right), $

(3) where a is some real constant. The energy-momentum of PFDM [60] reads
$ (T^{a}_{b})^{DM}={\rm{diag}}\left(-\epsilon,P_{r},P_{\theta},P_{\phi}\right), $

(4) with
$ \epsilon = -P_{r} = -\frac{\beta}{8\pi r^3},\quad\quad P_{\theta} = P_{\phi} = -\frac{\beta}{16\pi r^3}, $

(5) where ϵ is the energy density and
$ P_{r} $ is the radial and$ P_{\theta} $ ,$ P_{\phi} $ are the tangential pressures of the PFDM. Using Eq. (2) with Eqs. (3) and (4), and the static spherically symmetric metric [59]$ {\rm d}s^{2}=-f(r){\rm d}t^2+\frac{1}{f(r)}{\rm d}r^2+r^2 \left({\rm d}\theta^2\,+\,{\rm sin}^2\,\theta\, {\rm d}\phi^2\right), $

(6) For this system, the Letelier black hole immersed in PFDM with a negative cosmological constant for the metric (6) reads
$ f(r)=1-\frac{2M}{r}-a+\frac{\beta}{r}\ln\left(\frac{r}{|\beta|}\right)+\frac{r^2}{l^2}. $

(7) Here, M arising from integration is related to black hole mass, and β is the PFDM parameter. Henceforth, we shall refer to our solution (7) as a Letelier AdS black hole in PFDM. Our solution extends the Letelier black holes in AdS spacetime (
$ \beta=0 $ ) to include PFDM. When$ \beta=a=0 $ , we obtain Schwarzchild AdS black holes.a. Energy Conditions: We examine the status of the energy conditions [61–63] and assess their applicability to our solution (6). The components of the stress-energy tensor
$ T_{ab} $ , calculated using Eq. (2), are then$ \begin{aligned}[b] \rho & =\frac{ar-\beta }{r^{3}} = -P_{r},\\ & P_{\theta}=P_{\phi}=-\frac{\beta}{2r^3}. \end{aligned} $

(8) ● The weak energy condition (WEC) requires that for any timelike vector
$ t^{a} $ ,$ T_{ab}t^{a}t^{b}\geq 0 $ everywhere, that is$ \rho \geq 0 $ and$ \rho + P_{\theta}\geq 0 $ . It turns out that$ \rho+P_{\theta}=\frac{2ar-3\beta}{2r^2}, $

(9) which implies that
$ \rho+P_{\theta} $ is always positive for$ r>0 $ and$ 0<a<1 $ . The WEC is satisfied when$ {(ar-\beta)}/{r^3}\geq 0 $ for$ 0<a<1 $ .● The null energy condition (NEC) requires that
$ T_{ab}t^{a}t^{b}\geq 0 $ holds throughout the entire space-time for any null vector$ t^{a} $ . Consequently, note that$ \rho+P_{r}\geq 0 $ is inherently zero. Additionally,$ \rho+P_{\theta} $ ($ P_{\phi} $ )$ \geq 0 $ is consistently satisfied for$ 0<a<1 $ and$ r>0 $ .● The strong energy condition (SEC) states that
$ T_{ab}t^{a}t^{b}\geq 1/2T^{a}_{a}t^{b}t_{b} $ globally, for any timelike vector$ t^{a} $ , that is$ \rho+P{r}+2P_{\theta}=\frac{(2ar-5\beta)}{2r^3}. $

(10) Thus, it can be observed from Eq. (10) that the SEC is satisfied.
b. Extremal Black Holes: The horizons are determined by the points where the metric's singularity occurs, characterized by
$f(r) = 0,$ indicating coordinate singularities. As illustrated in Fig. 2, solving the equation$ f(x) = 0 $ numerically reveals the possible existence of two roots. Corresponding to specific values of a and$ \gamma=\beta/l $ , we identify the mass parameter's critical point ($ M_{c} $ ). Consequently, for mass values ($ M>M_{c} $ ), we encounter two zeros representing the Cauchy and event horizons (refer to Fig. 2). The plot in Fig. 2 illustrates the Cauchy and event horizons for$ a=0.4 $ and$ \gamma=-0.02 $ ($ -0.04 $ ). Additionally, the plot indicates the absence of a horizon (naked singularity) for$ M<M_{c} $ . However, when$ M=M_{c} $ , an extremal black hole with a degenerate horizon emerges. The expression for extremal black holes is derived from the equation
Figure 2. (color online) Plot of the metric function
$ f(x) $ vs$ x=r/l $ . In the degenerate cases, we obtain an extremal black hole for$ m=M_c=0.004910 $ (left) and$ M=M_c=0.009926 $ (right). A naked singularity is evident for$ M < M_c $ .$ f(r)=0=\frac{\partial f(r)}{\partial r}, $

(11) which yields the values of
$ r_{o} $ and$ M_{c} $ as$ r_{o}=\frac{1}{3}\left[\frac{-2(1-a) l^2 +(2\; {\cal{U}}^{2})^{\frac{1}{3}}}{(2^2\; {\cal{U}})^{\frac{1}{3}}}\right] $

(12) and
$\begin{aligned}[b] M_{c}=\;&\frac{1}{18\; {\cal{U}}^{\frac{1}{3}}}\Bigg[-2^{\frac{4}{3}}(a-1)^2-3\beta\; {\cal{U}}^{\frac{1}{3}} + {2\; {\cal{U}}}^{\frac{2}{3}}\\&-{2\; {\cal{U}}}^\frac{2}{3}a+9\beta\; {\cal{U}}^\frac{1}{3}\ln{(\frac{2^\frac{1}{3}\; {\cal{U}}^\frac{2}{3}-2(a-1)l^2}{2^\frac{2}{3}\; {\cal{U}}^\frac{1}{3}\; 3|\beta|})}\Bigg]\end{aligned} $

(13) where
$ {\cal{U}}=-9\; l^2\; \beta+\sqrt{-4(-1+a)^3 l^6 +81 l^4 \beta^2} $

(14) In Fig. 1, we present the parametric space for the values of a and γ while keeping the mass constant. The solid black curve in the figure signifies the extremal black hole, and the blue region denotes the presence of black holes with two horizons. Conversely, the white region represents the absence of a black hole. The thermodynamic analysis of the Letelier spacetime immersed in PFDM pertains to values of the CS and PFDM parameters, a and γ, falling within the region associated with a black hole.
-
Next, we try to connect the Letelier black holes in PFDM with the concept of black hole chemistry [60], which requires the study of the thermodynamic properties of Letelier in PFDM in AdS background. To investigate chemical aspects, we must discuss all thermodynamic variables [64]. The relation
$ f(r_+)=0 $ gives the ADM mass of the black hole solution and reads$ M_+=\frac{1}{2}\left[(1-a)r_++\beta \ln{\frac{r_+}{|\beta|}}+\frac{r_+^3}{l^2}\right]. $

(15) The identification of mass as chemical enthalpy, which is also the system's total energy, originates from consideration of the cosmological constant (Λ) as the system's pressure. The temperature of the black hole is viewed as radiation emitted by a black body satisfying the relation [65]
$ T={\kappa}/{2\pi} $ , where κ is the surface gravity of the black hole. The expression for the temperature is obtained as$ T_+ = \frac{1}{4\pi} {\left[\,\frac{3}{l^2}-\frac{(1-a)r_++2\beta}{r_+^{3}}\,\right]}. $

(16) The local extrema of Hawking temperature are identified from the expression
$ Z(r_{+})=\partial T_{+}/\partial r_{+} $ . Numerically,$ Z(r_{+}) $ yields a pair of complex roots and one real root as the solution of$ Z(r_{+})=0 $ , which corresponds to the extrema of the Hawking temperature. Figure 3 shows the plot of temperature vs horizon radius varying the values of the dark parameter$ \gamma =\beta/l $ . For decreasing values of the ratio$ \beta/l $ the extremal values of the temperature curve gradually merge to become monotonically increasing. In addition, the temperature becomes zero (cf. Fig. 3) at horizon radius$ r_{+}=0.09562 $ for$ a=0.4 $ and$ \gamma=-0.06 $ . Further, the plot also indicates a positive slope for large and small black holes and a negative slope for intermediate black holes (IBHs). This behavior of the Hawking temperature is indicative of van der Waals-like first-order phase transition [10, 64, 66–70]. The entropy of the black hole is calculated from the Bekenstein area law [60]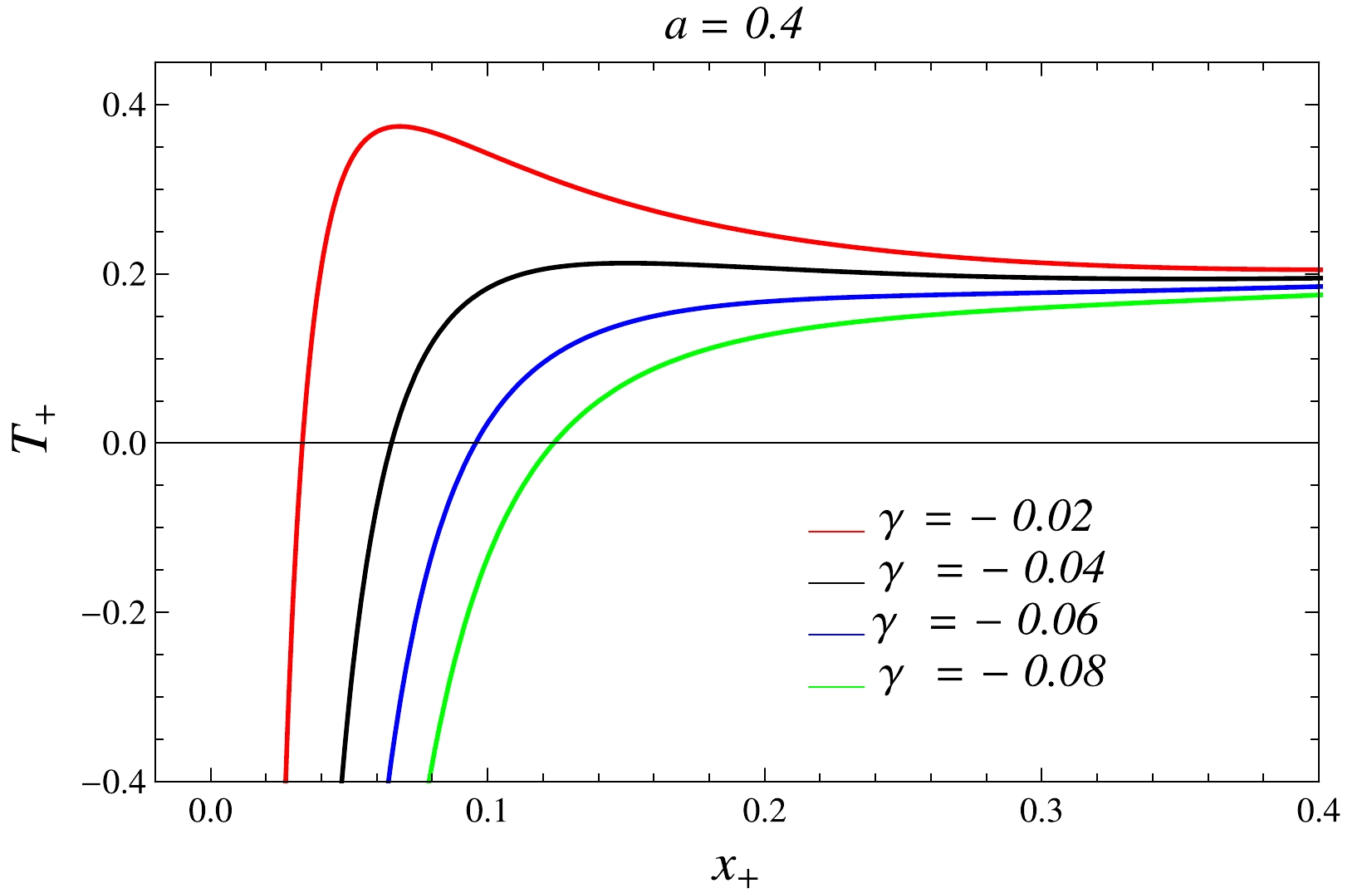
Figure 3. (color online) Hawking temperature
$ T_{+} $ vs horizon$ x_+ = r_+/l $ for$ a=0.4 $ and different values of$ \gamma=\beta/l $ .$ S_+=\frac{A}{4}=\int^{2\pi}_{0}\int^{2\pi}_{0}\sqrt{g_{\theta\theta}\,g_{\phi\phi}}\,{\rm d}\theta \,{\rm d}\phi=\pi r_+^2, $

(17) for Letelier AdS black holes in PFDM. The mass may be a function of three thermodynamic variables, e.g., the entropy S, pressure P, and PFDM parameter β. Considering pressure in terms of the cosmological constant Λ, the first law of black hole thermodynamics is derived as the total derivative of the mass
$ M_{+} $ [64, 65]$ {\rm d}M_+=\left(\frac{\partial M_+}{\partial S_+}\right)_{\beta, P}\,{\rm d}S{_+}\,+\,\left(\frac{\partial M_+}{\partial P}\right)_{\beta, S_+}\,{\rm d}P\, +\,\left(\frac{\partial M_+}{\partial \beta}\right)_{S_+, P}\,{\rm d}\beta $

(18) This identification of the black hole first law with that of the classical thermodynamics is possible after mass is viewed as enthalpy and a pressure term is accounted with the relation [71]
$ P=-\Lambda/8\pi $ . The conjugate quantities are defined as$ T_+=\left(\frac{\partial M_+}{\partial S_+}\right),\; \; \; V_+=\left(\frac{\partial M_+}{\partial P}\right),\; \; \; \pi=\left(\frac{\partial M_+}{\partial \beta}\right), $

(19) giving the expression for the first law as [72]
$ {\rm d}M_+\,=\,T_+{\rm d}S_+-P\,{\rm d}V_++\pi\,{\rm d}\beta. $

(20) The Smarr formula can be realized from the first law with the help of a small scaling argument and Euler's theorem. In the asymptotically flat case, the first law and Smarr relation are found out by geometrical means [8, 73]. Scaling of the cosmological constant by (length)
$ ^{-2} $ , mass$ M_{+} $ by (length)$ ^1 $ , and area A by (length)$ ^{2} $ in conjunction with Euler's theorem give the following expression for the Smarr relation [10]$ M_+=2\left(\frac{\partial M_+}{\partial A}\right)\; A-2\left(\frac{\partial M_+}{\partial \Lambda}\right)\; \Lambda $

(21) where Area A is perceived as entropy and Λ as pressure in black hole thermodynamics. The presence of the PFDM parameter in our black hole configuration modifies the Smarr relation to [10, 74]
$ M_+=2T_+S_+-2PV_+ +\Pi \beta $

(22) The analytical expressions for the conjugate quantities Π and volume of the black hole system are [60]
$ \Pi=\frac{1}{2}\left[-1+\ln\frac{r_+}{|\beta|}\right],\qquad V_+=\frac{4}{3} \pi r_+^3,\qquad P=\frac{3}{8 \pi l^2}. $

(23) In the limit
$ \beta \to 0 $ , the above quantities reduce to the corresponding expressions for the Letelier AdS black holes [58].The local stability is determined by the specific heat
$ C_V{_{+}} $ and$ C_P{_{+}} $ computed from the expressions$ C_{V}{_{+}}= T{_{+}}(\partial S_{+}/\partial T_{+})_{V_+,\,\beta} $ and$ C_{P}{_{+}}=T_{+}(\partial S_{+}/\partial T_{+})_{P,\,\beta} $ [33, 55]. It is well known that a positive value of the heat capacity signifies a locally stable black hole spacetime. In contrast, a negative value means a locally unstable black hole solution. The specific heat at constant volume,$ C_{V}{_{+}} $ , comes out to be zero since entropy$ S_{+} $ is interdependent on the volume$ V_{+} $ [64] for the solution under investigation. The specific heat at constant pressure,$ C_{P}{_{+}} $ , is$ C_{P}{_+}=\frac{2\pi r_+^2\,(\,3r_+^3\,+\,(1-a)\,r_+\,+\beta)}{3r_+^3\,-l^2(r_+\,(1-a)\,-2\beta)}. $

(24) Figure 4 (left) shows the behavior of
$ C_{P}{_{+}} $ for various values of the PFDM parameter$ \gamma=\beta/l $ . The plot in Fig. 4 shows that a second order phase transition is obtained at two critical points,$ r_{c1} $ and$ r_{c2} $ , for$ \gamma=-0.02 $ ($ -0.04 $ ). The critical points indicate the divergence of the specific heat as the values of$ \gamma=\beta/l $ decrease. These points of inflexion are the points of extrema for the temperature. For$ \gamma=-0.06 $ ($ -0.08 $ ), the plot positively increases, signifying a stable black hole region. The global stability of the black hole system is measured by Gibbs free energy [57]. The expression for free energy is computed from$ G_{+}\,=\,M_{+}-T_{+}S_{+} $ , which is
Figure 4. (color online) Plot of specific heat (a)
$ C_{P+} $ vs horizon$ x_+=r_{+}/l $ (left) and (b) Gibbs free energy$ G_{+} $ vs horizon$ x_+=r_{+}/l $ (right) for decreasing values of γ.$ G_+=\frac{1}{4}\left[r_+\,(1-a)-\frac{r_+^2}{l^2}-\beta+2\,\beta\, \ln\,\frac{r_+}{|\beta|}\right]. $

(25) Figures 4 (right) and 6 determine the behavior of the free energy G in the
$ G-x $ plane as the ratio$ \beta/l $ decreases. The right panel in Fig. 4 shows that the free energy becomes negative, which signifies the presence of a Hawking-Page phase transition. The free energy curve becomes “0”, transitioning from pure radiation to a stable black hole configuration. Next, we show the plot of the Gibbs free energy vs temperature to highlight the small-to-large black hole transition. Figure 6 shows a swallowtail-like structure for pressures below the critical pressure. The plot shows the existence of three states, i.e., SBH, LBH, and IBH, and the transitions between them. The red curve in the plot represents two first-order phase transitions, from a stable SBH to a less stable IBH and from an IBH to a stable LBH, which can be observed where the Gibbs free energy intersects with itself. The figure indicates a swallowtail for values of pressure below the critical pressure$ P_{c} $ , and the behavior of the free energy at the critical pressure is denoted by the green curve, which shows a cusp, meaning a second-order phase transition. Further, for$ P>P_{c} $ , the plot indicates monotonic behavior.
Figure 6. (color online) Plot of Gibbs free energy
$ \tilde{G} $ vs temperature$ \tilde{T} $ showing a swallowtail for$ P<P_{c} $ . The curve attains a cusp at$ P=P_{c} $ , which is also a point of second-order phase transition, and further becomes monotonically increasing for$ P>P_{c} $ .In the limit
$ \gamma \to 0 $ , the specific heat and free energy reduce to those of nonsingular AdS black holes endowed with clouds of strings [58] and for$ a=0 $ , we retrieve the heat capacity and Gibbs free energy for Schwarzschild AdS black holes [64]. Next, we investigate the$ P-V $ criticality of our solution via the equation of state$ P=\frac{T_+}{2r_+}-\frac{(1-a)}{r_+^2}-\frac{\beta}{8\pi r_+^3}. $

(26) The various isotherms of Eq. (26) are shown in Fig. 5, which is indicative of a liquid-to-gas-like phase transition for values of temperature below the critical temperature (
$ T_{c} $ ). The plot shows ideal gas behavior for isotherms with temperature values above the critical temperature$ T_{c} $ . The isotherms with high pressures correspond to an LBH, and low-pressure isotherms show the SBH. The first-order phase transition corresponding to the Van der Waals theory is represented by the oscillating branch between the SBH and LBH [64]. The point of inflection is a solution of the equation
Figure 5. (color online) Pressure P vs volume
$ V_{+} $ plot for$ a=0.4 $ ,$ \beta=-0.2 $ (left) and$ \beta=-0.4 $ (right), showing the isotherms for the Letelier spacetime immersed in perfect fluid dark matter.$ \left.{\frac{\partial P}{\partial r_+}}\right\vert_{T_+}\,=\,0\,=\,\left.\frac{\partial^{2} P}{\partial r_+^{2}}\right\vert_{T_+}. $

(27) The expression for critical temperature and pressure can be computed using Eq. (27)
$ T_{c} = \frac{3\beta+2r_+(1-a)}{4\pi r_+^2} $

(28) $ P_{c}=\frac{3\beta\left[r_+(1-a)+\beta\right]\,+\,r_+^2\left(1-a\right)^2}{12\pi r_+^3 \beta} $

(29) Inserting the expression for critical radius, we obtain the expressions for temperature, pressure, and volume
$\begin{aligned}[b]& r_{c}=-\frac{3\,\beta}{1-a}, \quad T_{c}=-\frac{(1-a)^2}{12 \pi \beta}, \\& P_{c}=\frac{(1-a)^3}{216 \pi \beta^2},\quad V_{c}=-\frac{36 \pi \beta^3}{(1-a)^3}, \end{aligned}$

(30) and the universal constant
$ \epsilon= P_{c}V_{c}^{1/3}/T_{c} $ for Letelier AdS black holes in PFDM is 0.28. In comparison to the value of ϵ for van der Waals gas, which is$ 0.375 $ [59], the value of the universal constant is corrected for the solution under investigation. The critical value of the horizon radius$ r_c $ depends on the cloud of strings parameter and the PFDM parameter, and so do the other critical values. -
In this section, we study the phase structure of the Letelier AdS black hole endowed with PFDM during the first-order phase transition between the SBH and LBH. The entire study will be in the reduced parameter space. The coexistence curve in the
$ \tilde{P}-\tilde{T} $ plane may be parametrized in the dimensionless way$ \begin{aligned}[b] \tilde{P}\;\; =\;&-28.2377 \tilde{T}^{10}+159.835 \tilde{T}^9-392.309 \tilde{T}^8+549.059 \tilde{T}^7\\&-483.738 \tilde{T}^6+279.524 \tilde{T}^5-106.737 \tilde{T}^4 + 26.7808 \tilde{T}^3\\&-3.51489 \tilde{T}^2+0.349711 \tilde{T}-0.0126105 \end{aligned} $

(31) where we define the dimensionless variables as
$ \tilde{T}=\frac{T}{T_c} \qquad \tilde{G}=\frac{G}{G_c} \quad\tilde{P}=\frac{P}{P_c} \quad \tilde{V}=\frac{V}{V_c}. $

(32) The reduced forms of these variables, along with the other variables, determine the phase transition behavior. As is evident from the first law itself (20), the mass of the black hole in AdS spacetime has a unique prescription, namely, the enthalpy designated as H. This prescription leads us to define the Gibbs free energy,
$ \tilde{G}=\tilde{M}_+-\tilde{T}_+\tilde{S}_+ $ , which is defined in Eq. (25).We have the critical horizon radius at the critical point,
$ r_{+c} $ . Then, the reduced horizon radius is expressed as$ \tilde{r}_+=r_+/r_{+c} $ . The reduced horizon radius$\tilde{r}_+ $ is plotted as a function of the reduced temperature (left of Fig. 7) , reflecting two phases of the black holes, the green dotted line corresponds to the LBH while the red solid line to that of the SBH phases. The differences of the reduced horizon radius as function of the reduced Hawking temperature (right of Fig. 7) is plotted to show the concavity of the graph.$ \tilde{r}_+ $ is a function of$ (\tilde{P},\tilde{T}) $ as can be observed from the equation of state itself. We show the phase diagram in the$ (\tilde{P}-\tilde{T}) $ plane in Fig. 8. The black dot in the figure denotes the critical point [18]. In Fig. 8, in the$ \tilde{P}-\tilde{T} $ plane, the metastable curve (the blue dotted line) is depicted for the small and large black hole phases. Such a scenario dictates the fact that the phase transition terminates at the critical point, and just above it the phases are supercritical. In particular, for the coexistence curves, we have$ \left(\Delta{G}\right)_{\tilde{P},\tilde{T}}=0 $ , whereas for the metastable curves we have the following conditions:
Figure 7. (color online) Plot showing the variation of the reduced horizon radius
$\tilde{r}_+$ vs the Hawking temperature$\tilde{T}$ (left) and the differences of the reduced horizon radius$\Delta\tilde{r}$ vs the Hawking temperature (right). We can observe that the plot at the right has the value$\Delta\tilde{r}=0$ exactly at$\tilde{T=1}$ , mimicking the critical point, and beyond it, there is a second-order phase transition.
Figure 8. (color online) Phase structure of Letelier AdS black holes in PFDM. In the
$ \tilde{P}-\tilde{T} $ and$ \tilde{T}-\tilde{V} $ diagrams, the coexistence curve is shown in a solid line and the spinodal curves are shown in a dashed line.$ ( \partial _V P)_T=0, \qquad (\partial _V T)_P=0. $

(33) Therefore, the metastable curves are the locus of the extremal points. The region between the coexistence and metastable curves is the metastable phase as is depicted in the
$ (\tilde{T}-\tilde{S}) $ or$ (\tilde{P}-\tilde{V}) $ diagrams [18]. In the above analysis of the phase transition diagrams, we find that a connection should exist between the black hole horizon geometries and the phase transition behavior of the black holes. Such distinction hints us to link the behavior of the null geodesics or the photon orbits to the thermodynamic phase transition behavior of the black holes. It can be observed from Fig. 8 that the coexistence of small and large black holes shows the same behavior in the$ (\tilde{P}-\tilde{T}) $ diagram, which for the metastable curves acts differently. Therefore, the thermodynamic notion for the metastable and coexistence curves is not the same. -
This section considers a free photon orbiting a black hole in the equatorial plane (
$ \theta=\pi/2 $ ). The Lagrangian takes the form$ 2 {\cal{L}}=-f(r)\dot{t}^2+\frac{\dot{r}^2}{f(r)}+r^2\dot{\phi}^2, $

(34) where the dots over the coordinates are meant for differentiation with respect to the proper time. For the Letelier AdS black holes endowed with PFDM, there are two killing vectors
$ \partial_{t} $ and$ \partial_{\phi} $ such that$ p_t=-f(r)\dot{t}\equiv E, $

(35) $ p_\phi= r^2\dot{\phi} \equiv L, $

(36) $ p_r=\dot{r}/f(r). $

(37) which correspond to the conserved quantities E and L along the geodesics. The quantities E and L are the photon's energy and orbital angular momentum, respectively, denoting the constants of motion. The equations of motion for the t and ϕ coordinates read
$ \dot{t}=\frac{E}{f(r)}, $

(38) $ \dot{\phi}=\frac{L}{r^2 \sin ^2\theta}. $

(39) The Hamiltonian for the black holes is
$ 2{\cal{H}}=-E\dot{t}+L\dot{\phi}+\dot{r}^2/f(r)=0. $

(40) We are interested only in the radial motion. The radial equation of motion is obtained as
$ \dot{r}^2+V_{eff}=0, $

(41) where
$V_{\rm eff}$ is the effective potential. We define the dimensionless effective potential$\tilde{V}_{\rm eff}=V_{\rm eff}/E^2$ , which has the following explicit form:$ \tilde{V}_{\rm eff}=\frac{u^2}{r^2}f(r)-1. $

(42) The quantity
$ u=L/E $ in the above equation is called the impact parameter. We plotted the behavior of the effective potential$ \tilde{V}_{\rm eff} $ with the radial coordinate, as shown in Fig. 9, for different values of the impact parameter u, for three different cases:$ {\bf{a.}}\;u>u_c,\; {\rm{the\; unbounded\; motion}} $

$ {\bf{b.}}\;u=u_c,\;{\rm{the\; critically\; bounded}} $

and
$ {c.}\;u<u_c,\;{\rm{for\; the\; impinging one}} $

The only accessible region for the photon is
$ V_{eff}<0 $ because$ \dot{r}^2>0 $ there. As is evident from Fig. 9, the photon falls into the black hole for$ u<u_c $ , whereas for$ u>u_c $ , it is reflected off the black hole. Between these two cases, there is a critical case$ u=u_{c}=5.78298 $ , which is shown by a red thick line (see Fig. 9). The condition c is meant for the unstable photon orbits, and they are circular. The angular momentum of the photon becomes critical at the point where$ \tilde{V}_{\rm eff}=0 $ (red solid curve) as is shown in Fig. 9. Because the effective potential is zero, the radial velocity of the photon also vanishes there. The value of the radial coordinate at the point where the radial velocity is zero is called the photon orbit radius. The unstable circular orbits are determined through the following relations:$ V_{\rm eff}=0\quad , \quad V^{\prime}_{\rm eff}=0 \quad , \quad V^{\prime\prime}_{\rm eff}<0, $

(43) where the prime denotes the differentiation with respect to the radial coordinate r. From the second equation
$ V^{\prime}_{\rm eff}=0 $ , we find that the photon orbit radius$ r_{ps} $ satisfies$ 2f(r_{ps})-r_{ps}\partial _r f(r_{ps})=0, $

(44) which gives the radius of photon sphere
$ r_{ps} $ as$ r_{ps}=-\frac{3 \beta W\left(\frac{2}{3} (a-1) {\rm e}^{\frac{2 M}{q}+\frac{1}{3}}\right)}{2 (a-1)}, $

(45) whose peak approaches zero where the radial velocity of the photon vanishes and "W" is the Lambert W function. Given the parametric values
$ a>0 $ and$ \beta<0 $ , we must restrict ourselves to the output of the Lambert W function to be negative as$ r_{ps}>0 $ always.The above photon orbit radius is used to calculate the minimum impact parameter. Solving
$ (\tilde{V}_{\rm eff}=0) $ , we obtain$ u_{ps}=\frac{L_c}{E}=\left. \frac{r}{\sqrt{f(r)}} \right| _{r_{ps}}. $

(46) The explicit form of this can be obtained as
$ u_{ps}=\frac{\left(3\beta{\cal{Y}}\right)^{3/2}}{(1-a)^3\left[-4M+3\beta{\cal{Y}}+2\beta\log\left(\frac{3{\cal{Y}}}{2}\frac{|\beta|}{(1-a)}\right)+18P\pi \beta^3{\cal{Y}}^3\right]} $

with
$ {\cal{Y}}=W\left(\frac{2}{3} (a-1) {\rm e}^{\frac{2 M}{\beta}+\frac{1}{3}}\right). $

(47) For a photon coming from a distant source, it encounters strong gravity effects while passing by the black holes. The photon would experience a maximum deflection as
$ u\to u_{ps} $ , where the deflection angle is infinitely large. Such a phenomenon is described by the black hole lensing observables. Therefore, for the photon with a large u, the deflection angle is smaller, but it will become more deflected as u decreases, and the deflection becomes maximum at$ u=u_{ps} $ , where the photons are unbounded. Therefore, the quantities$ r_{ps} $ and$ u_{ps} $ play essential roles in describing the photon spheres. In the subsequent discussion, we investigate the behavior using the photon sphere parameters$ r_{ps} $ and$ u_{ps} $ and find that there should exist a correlation to the small-large black hole phase transition. The critical quantity that plays a vital role in such a connection is the mass parameter M. We determine the mass in terms of the lensing variables$ r_{ps} $ and$ u_{ps} $ and use them to express it in terms of the reduced pressure$ \tilde{P} $ and reduced horizon radius$ \tilde{S} $ . In this way, we can find the correlation of the lensing observables to the thermodynamic variables, as shown in Fig. 10. -
Our main concern is to study the behavior of the
$ r_{ps} $ and$ u_{ps} $ along the isobars and isotherms. A straightforward analysis leads us to study the reduced temperature$ \tilde{T} $ numerically, as a function of the reduced photon orbit radius$ r_{ps} $ and the reduced minimum factor$ u_{ps} $ . Figures 10 and 11 show that for smaller values of the temperatures, we have smaller values of both the quantities$ r_{ps} $ and$ u_{ps} $ , which at larger temperatures become larger. However, the behavior for the reduced pressure$ \tilde{P}<1 $ has interesting features. In such cases, we have similar behaviors of the isobaric curves as in the usual vdW-like fields in the$ \tilde{T}-\tilde{S} $ plane in the ordinary thermodynamic systems. If one continues increasing the$ \tilde{P} $ values and reaches$ \tilde{P}=1 $ , the extrema of the curves in the$ \tilde{T}-\tilde{r}_{ps} $ plane coincide. As an obvious conclusion, for$ \tilde{P}>1 $ , the isobars increase monotonically. Similar phenomena are observed in the numerical analysis of the$ \tilde{T}-\tilde{u}_{ps} $ diagrams. We also plotted the diagrams in the$ \tilde{P}-\tilde{r}_{ps} $ and$ \tilde{P}-\tilde{u}_{ps} $ planes. All such plots for$ \tilde{T}<1 $ correspond to the thermal phase transition of the first order, whereas at$ \tilde{T}=1 $ , we have the critical points, thereby representing a second-order phase transition. We have no phase transitions for$ \tilde{T}>1 $ . However, whether such phase transitions would emerge from Maxwell's equal area law is not clear in the case of photon orbits or minimum impact parameters. One should not forget to mention that such curves depict the isothermal curves in the$ \tilde{P}-\tilde{V} $ plane of the ordinary thermodynamic system, which is certainly a case study. Having experienced such features of the usual vdW-like fields, the mimickers of the isothermal or isobaric curves in the$ \tilde{T}-\tilde{r}_{ps}(\tilde{u}_{ps}) $ or$ \tilde{P}-\tilde{r}_{ps}(\tilde{u}_{ps}) $ planes must have some connections to the thermodynamic phase transitions via the small-large black hole phases.
Figure 11. (color online) Reduced Hawking temperature (
$ \tilde{T} $ ) : (a)$ \tilde{T} $ vs$\tilde{r}_{ps}$ (left), (b)$ \tilde{T} $ vs$ \tilde{u}_{ps} $ (right).We show the plot for
$ \tilde{r}_{ps} $ or$ \tilde{u}_{ps} $ as a function of phase transition temperature$ \tilde{T} $ (for reference, see Fig. 11). As we increase the temperature$ \tilde{T} $ , the value in the photon orbit radius$ \tilde{r}_{ps} $ decreases for the coexistence of LBHs. On the contrary, for the increase in the values of the quantity$ \tilde{T} $ , the radius$ \tilde{r}_{ps} $ increases for the coexistence of SBHs. For the phase transition temperature,$ \tilde{T}=1 $ , the radius$ \tilde{r}_{ps} $ approaches the same value for the coexistence of small and large black holes. We plot the reduced Hawking temperature reduced as a function photon orbit radius (left of Fig. 12) and as a function of reduced minimum impact parameter (right of Fig. 12) for different values of the reduced Hawking temperatures.
Figure 12. (color online) Reduced pressure (
$\tilde{P}$ ) : (a)$\tilde{P}$ vs$\tilde{r}_{ps}$ (left), (b)$\tilde{P}$ vs$\tilde{u}_{ps}$ (right).We also plot the relative differences
$ \Delta\tilde{r}_{ps}/\tilde{r}_{ps} $ or$ \Delta\tilde{u}_{ps}/\tilde{u}_{ps} $ with respect to the phase transition temperature (see Fig. 13, for your reference ) in the left and right figures, resepctively. As expected, the differences decrease with increasing values of the phase transition temperature, and ultimately they vanish at the critical point. The interesting thing that may be a consequence of such results is that the quantity$ \Delta\tilde{r}_{ps}/\tilde{r}_{ps} $ or$ \Delta\tilde{u}_{ps}/\tilde{u}_{ps} $ behaves as the order parameters. They correspond to the non-vanishing contribution for the first-order phase transition and become zero at the critical point, and the phase transition is second order. The critical exponent around the critical points will simply follow the relation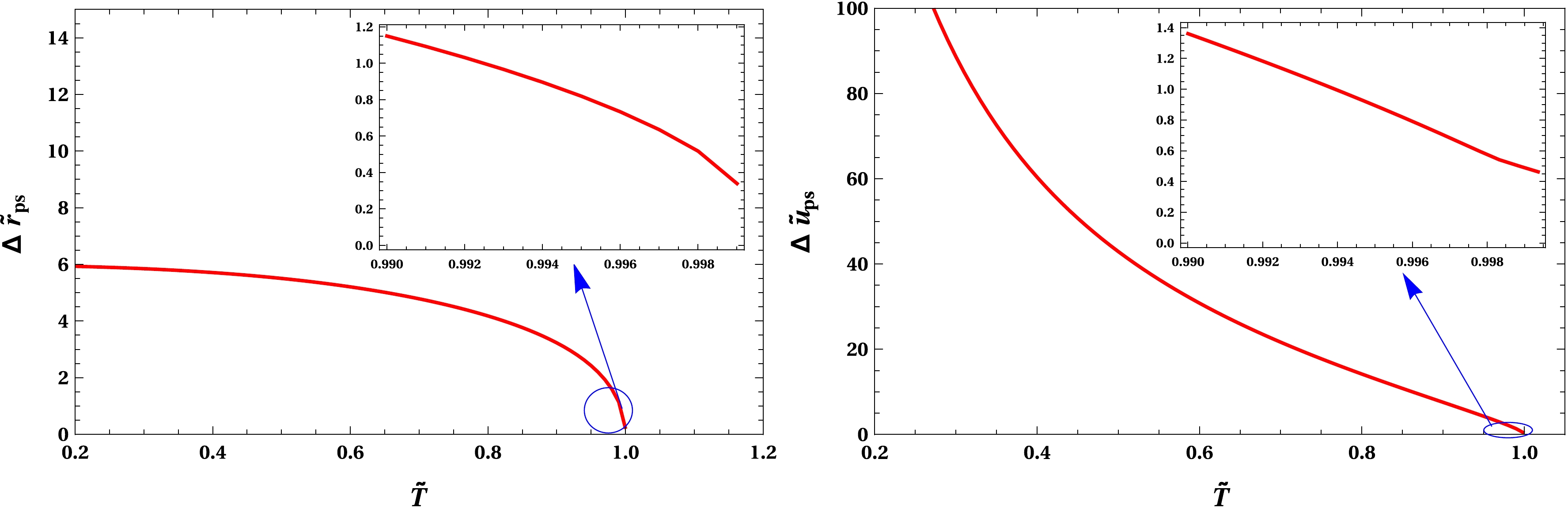
Figure 13. (color online) Variation in reduced photon orbit radius
$\tilde{r}_{ps}$ (left) and minimum impact factor$\tilde{u}_{ps}$ (right) vs the Hawking temperature$\tilde{T}$ .$ \Delta\tilde{r}_{ps}/\tilde{r}_{ps},\;\; \Delta\tilde{u}_{ps}/\tilde{u}_{ps}\sim a \left({1-\tilde{T}}\right)^{\delta} $

(48) which is also written as
$ \ln\left({\Delta\tilde{r}_{ps}/\tilde{r}_{ps}}\right),\;\; \ln\left({\Delta\tilde{u}_{ps}/\tilde{u}_{ps}}\right)\sim \ln a+\delta \ln\left({1-\tilde{T}}\right). $

(49) The logarithmic variation of
$ \Delta{\tilde{r}_{ps}}/\tilde{r}_{ps} $ or$ \Delta{\tilde{r}_{ps}}/\tilde{r}_{ps} $ is linear with respect to$ 1-\tilde{T} $ (see Fig. 14, for your renference), in the left and right figures, respectively, which helps us in determining the critical exponents. A numerical fit to the logarithmic variation yields that the output δ for$ \Delta{\tilde{r}_{ps}}/\tilde{r}_{ps} $ is$ \delta=0.500918203 $ , or for$ \Delta{\tilde{r}_{ps}}/\tilde{r}_{ps} $ $ \delta=0.490567809 $ . As for a wide class of black holes in the asymptotically AdS spacetime in four as well as in higher dimensions, for our black hole the approximate value of the critical exponent also turns out to be$ \delta\sim 1/2 $ at the critical points. -
We examined the thermodynamics
$ P-V $ criticality and the relationship between the photon orbit radius and thermodynamic phase transition for Letelier AdS black holes in PFDM, which may be useful to link the gravity and thermodynamics of black holes. First, we obtained an exact Letelier AdS black hole solution in PFDM with additional clouds of strings parameter (a) and PFDM parameter (β) and discussed the energy conditions. Next, we analyzed the extended phase space thermodynamics of Letelier AdS black holes in PFDM, showing an interesting phase transition. We showed that the thermodynamic$ ansatz $ viz, ADM mass, Hawking temperature, specific heat, and free energy are corrected overall by the additional parameters a and β. The behavior of Letelier AdS black holes with PFDM is consistent with that of the van der Waals fluid. The$ \tilde{G} $ vs$ \tilde{T} $ analysis confers first-order phase transition. The analysis of heat capacity dictates a second-order phase transition. We also used the mass term as a function of the thermodynamic variables in the reduced parameter space.We examined the relationship between the photon sphere radius and thermodynamic phase transition for the Letelier AdS black hole immersed in PFDM. This will provide a new way to realize the link between the gravity and thermodynamics of black holes. We found that the isobaric and isothermal curves concerning the photon orbit radius
$ \tilde{r}_{ps} $ , and also with the minimum impact parameter$ \tilde{u}_{ps} $ , in the reduced parameter space, signify the same thermal phase transition behavior of the usual van der Waals like fluids. This means that the curves in the$ \tilde{T}-\tilde{r}_{ps}(\tilde{u}_{ps}) $ or in the$ \tilde{P}-\tilde{r}_{ps}(\tilde{u}_{ps}) $ planes show the oscillatory behaviors confirming the first order phase transition of the van der Waals fluids. The oscillatory behavior confirms that two extrema should exist. When the two extrema coincide, we have the second-order phase transition. For other parameters above the second-order phase transition values, we do not have any such curves with a higher-order phase. We also plotted the relative differences$ \Delta{r_{ps}}/r_{ps} $ and$ \Delta{u_{ps}}/u_{ps} $ to show that they may serve as the order parameters near the critical points. We have the critical exponent$ \delta\sim 1/2 $ at the critical points. This value of the critical exponent is the universal feature of many black hole systems in four and higher dimensional spacetimes in asymptotically AdS spaces.A groundbreaking development has emerged wherein the AdS black hole is depicted dually as a thermal system, specifically through the holographic counterpart of the extended phase space thermodynamics. This breakthrough stems from the perturbation of the conformal factor within the dual CFT metric, as outlined in [75]. Our aspiration is to expand our research within the realm of holographic thermodynamics. It holds substantial promise to explore analogous analyses within different spacetime geometries, including but not limited to the de Sitter black hole, the black hole solution within alternative gravitational frameworks, or those arising from higher curvature theories.
Photon orbits and phase transition for Letelier AdS black holes immersed in perfect fluid dark matter
- Received Date: 2024-01-19
- Available Online: 2024-06-15
Abstract: We obtain an exact solution for spherically symmetric Letelier AdS black holes immersed in perfect fluid dark matter (PFDM). Considering the cosmological constant as the positive pressure of the system and volume as its conjugate variable, we analyze the thermodynamics of our black holes in the extended phase space. Owing to the background clouds of strings parameter (a) and the parameter endowed with PFDM (β), we analyze the Hawking temperature, entropy, and specific heat. Furthermore, we investigate the relationship between the photon sphere radius and phase transition for the Letelier AdS black holes immersed in PFDM. Through the analysis, with a particular condition, non-monotonic behaviors are found between the photon sphere radius, impact parameter, PFDM parameter, temperature, and pressure. We can regard the changes in both the photon sphere radius and impact parameter before and after phase transition as the order parameter; their critical exponents near the critical point are equal to the same value, 1/2, similar to that in ordinary thermal systems. This indicates that a universal relation of gravity may exist near the critical point for a black hole thermodynamic system.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: