-
The mass hierarchy problem is one of the most exciting issues in particle physics that requires the extension of the Standard Model (SM). Some experimental data are related to the flavour problem, including the origin of the quark mass hierarchy [1]
$ m_u \ll m_c \ll m_t $ and$m_d \ll m_s \ll m_b$ , the hierarchy of the charged lepton mass$m_e \ll m_\mu \ll m_\tau_\tau$ , and the origin of the three extremely small quark mixing angles as well as the neutrino mass spectrum and mixings.Because of the mentioned issues, various SM extensions have been proposed, such as symmetry extensions with scalars and/or fermion fields. The
$ B-L $ model [2–8] is relevant because it constitutes the simplest approach to add three right-handed neutrinos to generate neutrino masses. Although this model solves many interesting problems, such as dark matter [3], the muon anomalous magnetic moment [4, 8], leptogenesis [5, 6], and gravitational wave radiation [7], it cannot provide a satisfactory explanation for fermion masses and mixing observables. Non-Abelian discrete symmetries are considered the most powerful tool for reproducing the observed mass and mixing patterns of leptona and quarks (see, for example, Ref. [9]). In particular, the$ D_4 $ symmetry received much attention because it provides a predictive depiction of the mentioned patterns [10–23]. These previous studies are essentially different from the present study in the following basic points:$ (1) $ Ref. [16] is based on symmetries1 $ G_{BL}\times D_4\times Z_4 $ in which, for the quark sector, up to four$ SU(2)_L $ doublets and three singlets are introduced, and the obtained quark mixing matrix, whose "13", "23", "31", and "32" entries are zero, is not natural because all the elements of the quark mixing matrix must be non-zero [1].$ (2) $ Ref. [17] is based on symmetries2 $ G_{SM}\times D_4\times Z_2 $ in which the realistic quark mixing pattern is not considered and the quark mass hierarchy is not satisfied.$ (3) $ Ref. [18] is based on symmetries$G_{331}\times U(1)_{{\cal{L}}}\times D_4$ in which five$S U(3)_L$ triplets are used, and the$ 1-2 $ mixing of the ordinary quarks is obtained if the$ D_4 $ symmetry is violated with$ 1^{\prime} $ symmetry instead of$ \underline{1} $ , as usual.$ (4) $ Ref. [19] is based on symmetries$G_{331}\times U(1)_{{\cal{L}}}\times D_4$ in which a realistic quark mixing matrix is achieved; however, the quark mass hierarchy is not satisfied.$ (5) $ In Ref. [20], the obtained quark mixing matrix, whose "13", "23", "31", and "32" entries are zero, is not natural because all the elements of the quark mixing matrix must be non-zero [1], and the quark mass hierarchy is not satisfied.$ (6) $ In Ref. [21], the obtained quark mixing matrix, whose "13", "23", "31" and "32" entries are zero, is not natural because all the elements of the quark mixing matrix must be non-zero [1], and the quark mass hierarchy is not satisfied.$ (7) $ Ref. [22] is based on symmetries$G_{331}\times D_{4}\times Z_{4}\times Z_{3}^{(1) } \times Z_{3}^{(2)} \times Z_{16}$ in which two$S U(3)_L$ triplets and six$S U(3)_L$ singlets are used.$ (8) $ In Ref. [23], the quark mass hierarchy is slightly unnatural given that the Yukawa couplings spread over the region from$ {\cal{O}} (10^{-3}) $ to$ {\cal{O}} (1) $ (difference of three orders of magnitude).Hence, it is desirable to develop another
$ D_4 $ flavor model to overcome the aforementioned limitations of previous studies, especially the quark mass hierarchy, the extremely small quark mixing angles, the neutrino mass spectrum, and the mixing pattern.In this paper, we propose an alternative
$ D_4 $ model that differs from those of Refs. [13, 16]. We additionally introduce one doublet ($ H^{\prime} $ ) put in$ \underline{1}^{\prime} $ under$ D_4 $ [13] and use one singlet instead of one doublet in the quark sector [16]. The properties under$ D_4 $ of the right-handed charged lepton ($ l_{1R} $ ) and right-handed neutrino ($ \nu_{1R} $ ), as well as the properties under$ Z_4 $ of right-handed leptons$l_{1R},\, l_{\alpha R}, \nu_{1R}, \, \nu_{\alpha R}$ and singlet scalars$ \chi,\, \varphi, \, \phi $ in the present study are completely different from those of Ref. [13, 16]. As a consequence, the charged leptons, neutrinos, and quark mass hierarchies can be naturally achieved.The rest of this paper is organized as follows. We describe the model in Section II. Sections III and IV are devoted to the quark and lepton masses and mixings, respectively. Section V presents a numerical analysis. Some conclusions are drawn in Sec. VI.
-
The total symmetry of the model is
$\Gamma=S U(2)_L\times U(1)_Y \times U(1)_{B-L}\times D_4\times Z_4{\times Z_2}$ , where the lepton, quark, and scalar fields under$ D_4 $ and$ Z_4 $ are essentially different from those of Refs. [13, 16]. In particular, in this study, the first families of the left-handed quark and right-handed up-and down quarks are assigned in$ {\bf{1}}_{+-} $ ; the two other families of quarks are assigned in$ {\bf{2}} $ . To explain the hierarchies of quark masses, one$ S U(2)_L $ doublet$ H^{\prime} $ with$ B-L=0 $ put in$ {\bf{1}}_{-+} $ under$ D_4 $ together with three flavons$ \rho, \varphi $ and ϕ with$ B-L=0 $ respectively put in$ {\bf{2}} $ and$ {\bf{1}}_{+-} $ under$ D_4 $ are additional introduced, i.e., the considered model contains two$S U(2)_L$ doublets3 . The particle and scalar contents of the model are shown in Table 1.Fields $ Q_{1 L} $ 

$ Q_{ \alpha L} $ 

$ u_{1 R} $ 

$ u_{ \alpha R} $ 

$ d_{1R} $ 

$ d_{ \alpha R} $ 

$ \psi_{1 L} $ 

$ \psi_{\alpha L} $ 

$ l_{1 R} $ 

$ l_{\alpha R} $ 

$ \nu_{1 R} $ 

$ \nu_{ \alpha R} $ 

H $ H^{\prime} $ 

ρ ϕ φ χ U(1) $ _{B-L} $ 

$ \frac{1}{3} $ 

$ \frac{1}{3} $ 

$ \frac{1}{3} $ 

$ \frac{1}{3} $ 

$ \frac{1}{3} $ 

$ \frac{1}{3} $ 

–1 –1 –1 –1 –1 –1 0 0 0 0 0 2 $ D_4 $ 

$ {\bf{1}}_{+-} $ 

$ {\bf{2}} $ 

$ {\bf{1}}_{+-} $ 

$ {\bf{2}} $ 

$ {\bf{1}}_{+-} $ 

$ {\bf{2}} $ 

$ {\bf{1}}_{-+} $ 

$ {\bf{2}} $ 

$ {\bf{1}}_{-+} $ 

$ {\bf{2}} $ 

$ {\bf{1}}_{-+} $ 

$ {\bf{2}} $ 

$ {\bf{1}}_{+-} $ 

$ {\bf{1}}_{-+} $ 

$ {\bf{2}} $ 

$ {\bf{1}}_{+-} $ 

$ {\bf{1}}_{--} $ 

$ {\bf{1}}_{+-} $ 

$ Z_4 $ 

1 i -1 $-{\rm i}$ 

-1 $-{\rm i}$ 

1 i –1 $-{\rm i}$ 

i i –1 –1 $-{\rm i}$ 

1 –1 –1 $ Z_2 $ 

– + – + – + + + + + – – + + – + – + Table 1. Particle and scalar contents of the model (
$ \alpha=2,3 $ ).With the given particle content,
$ \bar{Q}_{1 L} u_{1 R} $ transforms as$ ({\bf{2}}, \frac{1}{2}, 0, {\bf{1}}_{++}, -1) $ and can couple to$ (\widetilde{H}\phi)_{{\bf{1}}_{++}} $ ;$\overline{Q}_{ \alpha L} u_{ \alpha R}\sim ({\bf{2}}, \frac{1}{2}, 0, {\bf{1}}_{+-}+{\bf{1}}_{-+}+{\bf{1}}_{++}+{\bf{1}}_{-}, 1)$ can couple to$ \widetilde{H}, \widetilde{H^{\prime}}, (\widetilde{H} \phi)_{{\bf{1}}_{++}} $ and$ (\widetilde{H^{\prime}}\phi)_{{\bf{1}}_{-}} $ , respectively;$ \overline{Q}_{1 L} u_{ \alpha R} \sim ({\bf{2}}, \frac{1}{2}, 0, {\bf{2}}, i) $ can couple to$ (\widetilde{H}\rho)_{{\bf{2}}} $ and$ (\widetilde{H^{\prime}}\rho)_{{\bf{2}}} $ ; and$ \overline{Q}_{ \alpha L} u_{1 R} \sim ({\bf{2}}, \frac{1}{2}, 0, {\bf{2}}, -i) $ can couple to$ (\widetilde{H}\rho^*)_{{\bf{2}}} $ and$ (\widetilde{H^{\prime}}\rho^*)_{{\bf{2}}} $ to form invariant terms that generate an up-quark mass matrix. The situation is similar for the down quark sector. The Yukawa terms in the quark and lepton sectors are$ \begin{aligned}[b] -{\cal{L}}_Y^{q } =\;&\frac{x_{1}^{u}}{\Lambda} (\overline{Q}_{1 L}u_{1 R})_{{\bf{1}}_{++}} (\widetilde{H}\phi)_{{\bf{1}}_{++}} + x_{2}^{u} (\overline{Q}_{ \alpha L}u_{ \alpha R})_{{\bf{1}}_{+-}} \widetilde{H} + x_{3}^{u}(\overline{Q}_{ \alpha L}u_{ \alpha R})_{{\bf{1}}_{-+}} \widetilde{H^{\prime}} +\frac{y_{1}^{u}}{\Lambda}(\overline{Q}_{ \alpha L}u_{ \alpha R})_{{\bf{1}}_{++}} (\widetilde{H}\phi)_{{\bf{1}}_{++}} + \frac{y_{2}^{u}}{\Lambda}(\overline{Q}_{ \alpha L}u_{ \alpha R})_{{\bf{1}}_{--}} (\widetilde{H^{\prime}}\phi)_{{\bf{1}}_{--}} \\ &+ \frac{z_{1}^{u }}{\Lambda} (\overline{Q}_{1L} u_{ \alpha R})_{\underline{2}}(\widetilde{H}\rho)_{\underline{2}} +\frac{z_{2}^{u }}{\Lambda} (\overline{Q}_{ \alpha L} u_{1 R})_{\underline{2}}(\widetilde{H}\rho^*)_{\underline{2}} +\frac{z_{3}^{u }}{\Lambda} (\overline{Q}_{1L} u_{ \alpha R})_{\underline{2}}(\widetilde{H}^{\prime}\rho)_{\underline{2}} +\frac{z_{4}^{u }}{\Lambda} (\overline{Q}_{ \alpha L} u_{1 R})_{\underline{2}}(\widetilde{H}^{\prime}\rho^*)_{\underline{2}} \\ &+\frac{x_{1}^{d}}{\Lambda} (\overline{Q}_{1 L}d_{1 R})_{{\bf{1}}_{++}} (H\phi)_{{\bf{1}}_{++}} + x_{2}^{d}(\overline{Q}_{ \alpha L}d_{ \alpha R})_{{\bf{1}}_{+-}} H + x_{3}^{d}(\overline{Q}_{ \alpha L}d_{ \alpha R})_{{\bf{1}}_{-+}} H^{\prime} \\ &+\frac{y_{1}^{d}}{\Lambda}(\overline{Q}_{ \alpha L}d_{ \alpha R})_{{\bf{1}}_{++}} (H \phi)_{{\bf{1}}_{++}} + \frac{y_{2}^{d}}{\Lambda}(\overline{Q}_{ \alpha L}d_{ \alpha R})_{{\bf{1}}_{--}} (H^{\prime} \phi)_{{\bf{1}}_{--}} + \frac{z_{1}^{d}}{\Lambda}(\overline{Q}_{1L} d_{ \alpha R})_{\underline{2}}(H \rho)_{\underline{2}} \\ &+ \frac{z_{2}^{d}}{\Lambda} (\overline{Q}_{ \alpha L} d_{1 R})_{\underline{2}}(H\rho^*)_{\underline{2}} +\frac{z_{3}^{d}}{\Lambda}(\overline{Q}_{1L} d_{ \alpha R})_{\underline{2}}(H^{\prime} \rho)_{\underline{2}} + \frac{z_{4}^{d}}{\Lambda} (\overline{Q}_{ \alpha L} d_{1 R})_{\underline{2}}(H^{\prime}\rho^*)_{\underline{2}} + {\rm{H.c,}} \end{aligned} $ 
(1) $ \begin{aligned}[b] -{\cal{L}}^{Y}_{lep}=\;&\frac{h_1}{\Lambda}(\overline{\psi}_{1L} l_{1R})_{{\bf{1}}_{++}} (H \phi)_{{\bf{1}}_{++}} +h_2(\overline{\psi}_{\alpha L} l_{\alpha R})_{{\bf{1}}_{+-}} H +h_3(\overline{\psi}_{\alpha L} l_{\alpha R})_{{\bf{1}}_{-+}} H^{\prime} + \frac{h_4}{\Lambda}(\overline{\psi}_{\alpha L} l_{\alpha R})_{{\bf{1}}_{++}} (H \phi)_{{\bf{1}}_{++}} +\frac{h_5}{\Lambda}\big(\overline{\psi}_{\alpha L} l_{\alpha R}\big)_{{\bf{1}}_{--}} (H^{\prime} \phi)_{{\bf{1}}_{--}} \\ &+\frac{x_1}{\Lambda} \left(\bar{\psi}_{1 L}\nu_{ \alpha R}\right)_{{\bf{2}}} \big(\widetilde{H} \rho^*\big)_{{\bf{2}}} +\frac{x_2}{\Lambda} \left(\bar{\psi}_{1 L}\nu_{ \alpha R}\right)_{{\bf{2}}} \big(\widetilde{H^{\prime}} \rho^*\big)_{{\bf{2}}} +\frac{x_3}{\Lambda} \left(\bar{\psi}_{ \alpha L}\nu_{ \alpha R}\right)_{{\bf{1}}_{-+}} \big(\widetilde{H} \varphi\big)_{{\bf{1}}_{-+}} \\&+\frac{x_4}{\Lambda} \left(\bar{\psi}_{ \alpha L}\nu_{ \alpha R}\right)_{{\bf{1}}_{+-}} \big(\widetilde{H^{\prime}} \varphi\big)_{{\bf{1}}_{+-}} + \frac{y_1}{2\Lambda} \left(\bar{\nu}^c_{1 R}\nu_{1 R}\right)_{{\bf{1}}_{++}}\big(\phi\chi)_{{\bf{1}}_{++}} + y_2 (\bar{\nu}^c_{ \alpha R} \nu_{ \alpha R})_{{\bf{1}}_{+-}} \chi\\ & +\frac{y_3}{2\Lambda} (\bar{\nu}^c_{ \alpha R}\nu_{ \alpha R})_{{\bf{1}}_{++}} (\phi\chi)_{{\bf{1}}_{++}} +{\rm{H.c}}, \end{aligned} $

(2) where
$ x^{u,d}_{1,2,3}, y^{u,d}_{1,2} $ and$ z^{u,d}_{1,2,3,4} $ are the Yukawa-like couplings in the quark sector,$ h_{1,2,3,4,5}; x_{1,2,3,4} $ and$ y_{1,2,3} $ are the Yukawa-like couplings in the lepton sector, and Λ is the cut-off scale of the theory.Note that the additional discrete symmetries
$ D_4 $ ,$ Z_4 $ and$ Z_2 $ play crucial roles in forbidding undesired terms to obtain the expected quark and lepton mass matrices listed in Table A1. For instance, in the absence of$ Z_2 $ , there will be additional invariant terms,$(\overline{\psi}_{1L} l_{ \alpha R})_{{\bf{2}}} (H\rho)_{{\bf{2}}},\; (\overline{\psi}_{1L} l_{ \alpha R})_{{\bf{2}}} (H^{\prime}\rho)_{{\bf{2}}},\; (\overline{\psi}_{ \alpha L} l_{1 R})_{{\bf{2}}} (H\rho)_{{\bf{2}}}$ , and$ (\overline{\psi}_{ \alpha L} l_{1 R})_{{\bf{2}}} (H^{\prime}\rho)_{{\bf{2}}} $ , which contribute to the entries "12", "13", "21", and "31" of the charged lepton matrix. As a result, we cannot obtain the mass of charged leptons as expected because the charged lepton matrix cannot be diagonalized.Yukawa terms Forbidden by $ (\overline{\psi}_{ \alpha L} l_{ \alpha R})_{1_{+-}}\widetilde{H}, (\overline{\psi}_{ \alpha L} l_{ \alpha R})_{1_{-+}}\widetilde{H^{\prime}}; (\overline{\psi}_{1L} \nu_{ \alpha R})_{2}(H\rho^*)_{2}, (\overline{\psi}_{1L} \nu_{ \alpha R})_{2}(H^{\prime}\rho^*)_{2}; $ 

$ U(1)_Y $ 

$ (\overline{\psi}_{ \alpha L} \nu_{ \alpha R})_{1_{-+}}(\widetilde{H}\varphi)_{1_{-+}}, (\overline{\psi}_{ \alpha L} \nu_{ \alpha R})_{1_{+-}}(\widetilde{H^{\prime}}\varphi)_{1_{+-}}; (Q_{1L}u_{1R})_{1_{++}}(H\phi)_{1_{++}}, $ 

$ (Q_{ \alpha L}u_{ \alpha R})_{1_{++}}(H\phi)_{1_{++}}, $ 

$(Q_{ \alpha L}u_{ \alpha R})_{1_{+-} } H, (Q_{ \alpha L}u_{ \alpha R})_{1_{-+} } H^{\prime}, (Q_{ \alpha L}u_{ \alpha R})_{1_{--} } (H^{\prime}\phi)_{1_{--} };$ 

$ (Q_{1 L}u_{ \alpha R})_{2} (H\rho)_{2}, (Q_{1 L}u_{ \alpha R})_{2} (H^{\prime}\rho)_{2}, (Q_{ \alpha L}u_{1 R})_{2} (H\rho^*)_{2}, (Q_{ \alpha L}u_{1 R})_{2} (H^{\prime}\rho^*)_{2}, $ 

$ (Q_{1L}d_{1R})_{1_{++}}(\widetilde{H}\phi)_{1_{++}}, (Q_{ \alpha L}d_{ \alpha R})_{1_{++}}(\widetilde{H}\phi)_{1_{++}}, (Q_{ \alpha L}d_{ \alpha R})_{1_{+-}} \widetilde{H}, (Q_{ \alpha L} d_{ \alpha R})_{1_{-+}} \widetilde{H^{\prime}}, $ 

$(Q_{ \alpha L}d_{ \alpha R})_{1_{--} } (\widetilde{H^{\prime} }\phi)_{1_{--} }; (Q_{1 L}d_{ \alpha R})_{2} (\widetilde{H}\rho)_{2}, (Q_{1 L}d_{ \alpha R})_{2} (\widetilde{H^{\prime} }\rho)_{2},$ 

$ (Q_{ \alpha L}d_{1 R})_{2} (\widetilde{H}\rho^*)_{2}, (Q_{ \alpha L}d_{1 R})_{2} (\widetilde{H^{\prime}}\rho^*)_{2} $ 

$ (\overline{\nu}^C_{1 R} \nu_{1 R})_{1_{++}} (\phi \chi^*)_{1_{++}}, (\overline{\nu}^C_{1 R} \nu_{1 R})_{1_{++}} (\rho^2)_{1_{++}}, (\overline{\nu}^C_{1 R} \nu_{1 R})_{1_{++}} (\rho^{*2})_{1_{++}}; $ 

$ U(1)_{B-L} $ 

$ (\overline{\nu}^C_{ \alpha R} \nu_{ \alpha R})_{1_{++}} (\phi \chi^*)_{1_{++}}, (\overline{\nu}^C_{ \alpha R} \nu_{ \alpha R})_{1_{++}} (\rho^2)_{1_{++}}, (\overline{\nu}^C_{ \alpha R} \nu_{ \alpha R})_{1_{++}} (\rho^{*2})_{1_{++}}; $ 

$ (\overline{\nu}^C_{ \alpha R} \nu_{ \alpha R})_{1_{+-}} \chi^*; (\overline{\psi}_{1 L} \psi^C_{1 L})_{1_{++}} \widetilde{H^2}, (\overline{\psi}_{1 L} \psi^C_{1 L})_{1_{++}} \widetilde{H^{'2}}. $ 

$(\overline{\psi}_{1L} l_{1R})_{1_{++} }H, (\overline{\psi}_{1L} l_{1R})_{1_{++} }H^{\prime}, (\overline{\psi}_{1L} l_{1R})_{1_{++} }(H^{\prime}\phi)_{1_{--} }; (\overline{\psi}_{1L} \nu_{1R})_{1_{+-} }(H\rho^*)_{2},$ 

$ D_4 $ 

$ (\overline{\psi}_{1L} \nu_{1R})_{1_{+-}}(H^{\prime}\rho^*)_{2}; (\overline{\psi}_{ \alpha L} \nu_{1 R})_{2}(\widetilde{H}\varphi)_{1_{-+}}, (\overline{\psi}_{ \alpha L} \nu_{1 R})_{2}(\widetilde{H^{\prime}}\varphi)_{1_{+-}}; (\overline{\nu}^C_{1 R} \nu_{1 R})_{1_{++}} \chi; $ 

$ (\overline{\nu}^C_{1 R} \nu_{ \alpha R})_{2} \chi, (\overline{\nu}^C_{1 R} \nu_{ \alpha R})_{2} (\phi\chi)_{1_{++}}; (Q_{1L}u_{1R})_{1_{++}}\widetilde{H}, (Q_{1L}u_{1R})_{1_{++}}\widetilde{H^{\prime}}, $ 

$(Q_{1L}u_{1R})_{1_{++} }(\widetilde{H^{\prime} }\phi)_{1_{--} }, (Q_{ \alpha L}u_{ \alpha R})_{1_{++} }\widetilde{H}, (Q_{ \alpha L}u_{ \alpha R})_{1_{++} }\widetilde{H^{\prime} }, (Q_{ \alpha L}u_{ \alpha R})_{1_{++} }(\widetilde{H^{\prime} }\phi)_{1_{--} },$ 

$(Q_{1L}d_{1R})_{1_{++} }H, (Q_{1L}d_{1R})_{1_{++} }H^{\prime},(Q_{1L}d_{1R})_{1_{++} }(H^{\prime}\phi)_{1_{--} },$ 

$(Q_{ \alpha L}d_{ \alpha R})_{1_{++} } H, (Q_{ \alpha L} d_{ \alpha R})_{1_{++} } H^{\prime}, (Q_{ \alpha L}d_{ \alpha R})_{1_{++} }(H^{\prime}\phi)_{1_{--} }$ 

$ (\overline{\psi}_{1L} \nu_{ \alpha R})_{2}(\widetilde{H}\rho)_{2}, (\overline{\psi}_{1L} \nu_{ \alpha R})_{2}(\widetilde{H^{\prime}}\rho)_{2}, (\overline{\psi}_{ \alpha L} \nu_{1 R})_{2}(\widetilde{H}\rho)_{2}, (\overline{\psi}_{ \alpha L} \nu_{1 R})_{2}(\widetilde{H}\rho^*)_{2}, $ 

$ Z_4 $ 

$ (\overline{\psi}_{ \alpha L} \nu_{1 R})_{2}(\widetilde{H^{\prime}}\rho)_{2}, (\overline{\psi}_{ \alpha L} \nu_{1 R})_{2}(\widetilde{H^{\prime}}\rho^*)_{2}, (Q_{1 L}u_{ \alpha R})_{2} (H\rho^*)_{2}, (Q_{1 L}u_{ \alpha R})_{2} (H^{\prime}\rho^*)_{2}, $ 

$ (Q_{ \alpha L}u_{1 R})_{2} (H\rho)_{2}, (Q_{ \alpha L}u_{1 R})_{2} (H^{\prime}\rho)_{2}; (Q_{1 L}d_{ \alpha R})_{2} (\widetilde{H}\rho^*)_{2}, (Q_{1 L}d_{ \alpha R})_{2} (\widetilde{H^{\prime}}\rho^*)_{2},\;(Q_{ \alpha L}d_{1 R})_{2} (\widetilde{H}\rho)_{2}, (Q_{ \alpha L}d_{1 R})_{2} (\widetilde{H^{\prime}}\rho)_{2} $ 

$ (\overline{\psi}_{1L} l_{ \alpha R})_{2}(H\rho)_{2}, (\overline{\psi}_{1L} l_{ \alpha R})_{2}(H^{\prime}\rho)_{2}, (\overline{\psi}_{ \alpha L} l_{1 R})_{2}(H\rho^*)_{2}, (\overline{\psi}_{ \alpha L} l_{1 R})_{2}(H^{\prime}\rho^*)_{2} $ 

$ Z_2 $ 

Table A1. Yukawa terms forbidden by the symmetries of the model.
The vacuum expectation value (VEV) of the scalar fields takes the form
$ \begin{align} &\langle H \rangle = (0 v)^T,~~ \langle H^{\prime} \rangle = (0 v^{\prime})^T,~~ \langle \varphi \rangle = v_\varphi,~~ \langle \phi \rangle = v_\phi, \\ & \langle \rho \rangle =\left(\langle \rho_1 \rangle,~~ \langle \rho_1 \rangle \right)\equiv \left(v_\rho, v_\rho\right). \end{align} $

(3) In fact, the electroweak symmetry breaking scale is approximately in the order of one hundred GeV,
$v^2+v^{'2} = (174 \,\; {\rm{GeV}})^2$ . Furthermore, in the 2HDM, the limits of the parameter$t_\beta ={v^{\prime}}/{v}$ are given by [26]$t_\beta ={v^{\prime}}/{v}\in $ [1.0, 10.0] or [27]$t_\beta ={v^{\prime}}/{v}\in [1.0, 3.0]$ . For the purpose of determining the scale of the Yukawa couplings, we consider the case of$ t_\beta=1.424 $ , i.e.,$ v=100 ~{\rm{GeV}},\;\; v^{\prime}=142.40~ {\rm{GeV}}. $

(4) In addition, to satisfy the quark mass hierarchy, the VEV of the singlets and cut-off scale are assumed to be
$ v_\rho =5\times 10^{11} ~ {\rm{GeV}},\; v_\phi=10^{11}~ {\rm{GeV}}, \;\Lambda \simeq 10^{13}~ {\rm{GeV}}. $

(5) For models with more than one
$S U(2)_L$ scalar doublet, as the one proposed in this study, Flavor Changing Neutral Current (FCNC) processes such as$ b\rightarrow s \gamma $ exist in the Higgs sector. However, they are suppressed by non-Abelian discrete symmetries [28, 29]. For these processes to be below current experimental limits, some restrictions on the model parameters, such as the Yukawa couplings and large masses for non SM scalars, need to be imposed. The considered model contains many free parameters, which enables assuming that the remaining scalars are sufficiently heavy to fullfil current experimental limits. Furthermore, the first two lines in Eq. (2) imply that the off-diagonal Yukawa couplings in the charged-lepton sector are proportional to$ \dfrac{v_{\phi}}{ \Lambda}\sim 10^{-2} $ . Therefore, lepton flavor violation (LFV) processes, such as$ l_j\rightarrow l_i \gamma $ , are suppressed by the extremely small factor$ \dfrac{v_{\phi}}{ \Lambda} \dfrac{1}{m_H^2} $ associated with the mentioned small Yukawa couplings and large mass scale of the heavy scalars$ m_H $ [30–33]. A detailed analysis of FCNC and LFV processes are beyond the scope of this study. -
Using the Clebsch-Gordan coefficients of the
$ D_4 $ symmetry [34] and Eq. (1), when the scalar fields take the VEVs as in Eq. (3), the up- and down-quark mass matrices take the following forms:$ M_{q} =M^{(0)}_{q} + \delta M_{q} \,\, (q=u, d), $

(6) where
$ \begin{aligned}[b]&M^{(0)}_{q}=\left( \begin{array}{*{20}{c}} {a_{1q} } & {0 } & {0} \\ {0} & {a_{2q}+a_{3q}} & { 0 }\\ {0 } & {0} & { a_{2q}- a_{3q}} \end{array} \right), \\&\delta M_{q}=\left( \begin{array}{*{20}{c}} {0 } & { c_{1q}+c_{3q}} & { c_{1q}-c_{3q} }\\ {c_{2q}+c_{4q} } & {0} & { b_{1q}+b_{2q} }\\ {c_{2q}-c_{4q}} & {b_{1q}- b_{2q} } & { 0} \end{array} \right), \end{aligned}$

(7) with
$ \begin{aligned}[b]& a_{1q}=x_{1}^{q} v \frac{v_\varphi}{\Lambda},\quad a_{2q}=x_{2}^{q} v,\quad a_{3q}=x_{3}^{q} v^{\prime},\\& b_{1q}=y_{1}^{q} v\frac{v_\phi}{\Lambda}, \quad b_{2q}=y_{2}^{q} v^{\prime}\frac{v_\phi}{\Lambda}, \quad c_{1q}=z_{1}^{q} v\frac{v_\rho}{\Lambda},\\& c_{2q}=z_{2}^{q} v\frac{v_\rho}{\Lambda},\quad c_{3q}=z_{3}^{q} v^{\prime}\frac{v_\rho}{\Lambda},\quad c_{4q}=z_{4}^{q} v^{\prime}\frac{v_\rho}{\Lambda} \, (q=u, d). \end{aligned} $

(8) Equations (6)−(8) show that, besides the two doublets H and
$ H^{\prime} $ , one singlet φ contributes to$ M^{(0)}_{q} $ while$ \delta M_{q} $ is due to the contribution of two singlets ρ and ϕ. Without the contributions of ρ and ϕ,$ \delta M_{q} $ will vanish, and the quark mass matrices$ M_{q} $ in Eq. (6) reduce to the diagonal matrices$ M^{(0)}_{q} $ , i.e., the corresponding quark mixing matrix$V_{\rm CKM}=\mathbb{I}_{3\times 3}$ , which was ruled out by recent data. The realistic quark mixing angles are extremely small [1], which implies that the quark mixing matrix is very close to the identity matrix; thus, the second term$ \delta M_{q} $ in Eq. (7) can be considered as a perturbed parameter for generating the quark mixing pattern. As a consequence, a realistic quark mixing pattern can be achieved at the first order of the perturbation theory. Indeed, at this first order, the matrices$ \delta M_{q} $ contribute to the eigenvectors but they do not contribute at all to the eigenvalues of the quark mass matrices$ M_q $ . The quark masses are determined as$ \begin{aligned}[b] m_{u} &= a_{1u},~~ m_{c}=a_{2u} + a_{3u},~~ m_t=a_{2u} - a_{3u}, \\ m_{d} &= a_{1d},~~ m_{s}=a_{2d} + a_{3d},~~ m_b=a_{2d} - a_{3d}, \end{aligned} $

(9) and the corresponding perturbed quark mixing matrices are
$\begin{aligned}[b]& U^{u}_{L}=U^{u}_{R}=\left( \begin{array}{*{20}{c}} {1 } & {\dfrac{c_{1u}+c_{3u}}{m_c-m_{u}} } & {\dfrac{c_{1u}-c_{3u}}{m_t-m_{u}} }\\ { \dfrac{c_{4u}+c_{2u}}{m_{u}-m_c} } & {1 } & {\dfrac{b_{2u}+b_{1u}}{m_{t}-m_c} }\\ { \dfrac{c_{4u}-c_{2u}}{m_{t}-m_u} } & {\dfrac{b_{2u}-b_{1u}}{m_{t}-m_c} } & {1} \end{array} \right),\,\,\, \\&U^{d}_{L}=U^{d}_{R}=\left( \begin{array}{*{20}{c}} { 1 } & {\dfrac{c_{1d}+c_{3d}}{m_s-m_{b}} } & {\dfrac{c_{1d}-c_{3d}}{m_b-m_{d}}} \\ { \dfrac{c_{4d}+c_{2d}}{m_{d}-m_s} } & {1 } & {\dfrac{b_{2d}+b_{1d}}{m_{b}-m_s} }\\ { \dfrac{c_{4d}-c_{2d}}{m_{b}-m_d} } & {\dfrac{b_{2d}-b_{1d}}{m_{b}-m_s} } & {1 } \end{array} \right),\end{aligned} $

(10) with
$ b_{1,2 q} $ and$ c_{1,2,3,4 q}\, (q=u,d) $ given in Eq. (8). For simplicity, we consider tha case of$y_{1q}=y_{2q}=y_{q} \, (q=u,d), z_{3d}=z_{1d}=z_{d}$ , i.e.,$ b_{2d} = b_{1d} = b_d,\quad b_{2u} = b_{1u} = b_u, \quad c_{3d} = c_{1d}. $

(11) The quark mixing matrix,
$ V_{\rm{CKM}}= V^u_L V^{d \dagger}_L $ , includes the following entries:$ \begin{aligned}[b] & V_{\rm{CKM}}^{11}=1+\frac{2 c^*_{1d} (c_{1u}+c_{3u})}{(m_{u}-m_{c}) (m_{d}-m_{s})}, \\ & V_{\rm{CKM}}^{12}=\frac{2 b^*_{d} (c_{1u}-c_{3u})}{(m_{b}-m_{s}) (m_{t}-m_{u})}+\frac{c_{1u}+c_{3u}}{m_{c}-m_{u}}+\frac{c^*_{2d}+c^*_{4d}}{m_{d}-m_{s}}, \\ & V_{\rm{CKM}}^{13}=\frac{c_{1u}-c_{3u}}{m_{t}-m_{u}}+\frac{c^*_{4d}-c^*_{2d}}{m_{b}-m_{d}}, V_{\rm{CKM}}^{21}=\frac{c_{2u}+c_{4u}}{m_{u}-m_{c}}+\frac{2 c^*_{1d}}{m_{s}-m_{d}}, \\ & V_{\rm{CKM}}^{22}=1+\frac{4 b^*_{d} b_{u}}{(m_{b}-m_{s}) (m_{t}-m_{c})}+\frac{(c_{2u}+c_{4u}) (c^*_{2d}+c^*_{4d})}{(m_{u}-m_{c}) (m_{d}-m_{s})}, \\ & V_{\rm{CKM}}^{23}=\frac{2 b_{u}}{m_{t}-m_{c}}+\frac{(c_{2u}+c_{4u}) (c^*_{2d}-c^*_{4d})}{(m_{b}-m_{d}) (m_{c}-m_{u})}, V_{\rm{CKM}}^{31}=\frac{c_{4u}-c_{2u}}{m_{t}-m_{u}}, \\ & V_{\rm{CKM}}^{32}=\frac{2 b^*_{d}}{m_{b}-m_{s}}+\frac{(c_{2u}-c_{4u}) (c^*_{2d}+c^*_{4d})}{(m_{d}-m_{s}) (m_{u}-m_{t})},\\& V_{\rm{CKM}}^{33}=1 + \frac{(c_{2u}-c_{4u}) (c^*_{2d}-c^*_{4d})}{(m_{b}-m_{d}) (m_{t}-m_{u})}. \end{aligned} $

(12) Comparing the model results on the quark masses and quark mixing matrix in Eqs. (9) and (12) with their corresponding experimental constraints on
$ {\rm{V}}^{{\rm{exp}}}_{ij} $ shown in Table 2 (second column), we obtain explicit expressions for$a_{1u,d},\; a_{2u,d},\; a_{3u,d},\; b_{u,d}, c_{1u, d}$ ,$ c_{2u,d} $ ,$ c_{3u} $ , and$ c_{4u,d} $ as functions of quark masses and quark mixing matrix elements as presented in Eqs. (B1) and (B2) of Appendix B.Observable Best-fit point [1] Model prediction Percentage error (%) $m_u /{\rm{MeV} }$ 

2.16 2.16 0 $ m_c /{\rm{GeV}} $ 

1.27 1.27 0 $ m_t /{\rm{GeV}} $ 

172.69 172.69 0 $ m_d /{\rm{MeV}} $ 

4.67 4.67 0 $ m_s /{\rm{MeV}} $ 

93.4 93.4 0 $ m_b /{\rm{GeV}} $ 

4.18 4.18 0 $ V_{{\rm{CKM}}}^{11} $ 

0.974352 0.974352 0 $ V_{{\rm{CKM}}}^{12} $ 

0.224998 0.224998 0 $ V_{{\rm{CKM}}}^{13} $ 

$0.0015275 - 0.003359 {\rm i}$ 

$0.0015275 - 0.003359 {\rm i}$ 

0 $ V_{{\rm{CKM}}}^{21} $ 

$-0.224865 - 0.000136871 {\rm i}$ 

$-0.224865 - 0.000136871 {\rm i}$ 

0 $ V_{{\rm{CKM}}}^{22} $ 

0.973492 0.973492 0 $ V_{{\rm{CKM}}}^{23} $ 

0.0418197 0.0418197 0 $ V_{{\rm{CKM}}}^{31} $ 

$0.00792247 - 0.00327 {\rm i}$ 

$0.00792247 - 0.00327 {\rm i}$ 

0 $ V_{{\rm{CKM}}}^{32} $ 

$-0.0410911 - 0.000755113 {\rm i}$ 

$-0.0410911 - 0.000755113 {\rm i}$ 

0 $ V_{{\rm{CKM}}}^{33} $ 

0.999118 0.999118 0 Table 2. Best-fit points for quark parameters taken from Ref. [1] and model prediction.
Equations (8), (11), (B1), and (B2) imply that the model parameters
$a_{1u,d},\; a_{2u,d},\; a_{3u,d},\; b_{u,d},\; c_{1u, d}$ ,$ c_{2u,d} $ ,$ c_{3u} $ , and$ c_{4u,d} $ depend on the observed parameters in the quark sector, including quark masses$m_u,\; m_c,\; m_t,\;m_d,\;m_s,\;m_b$ and quark mixing matrix elements$V^{{\rm{exp}}}_{ij}\, (i,j=1,\,2,\,3)$ , which have been determined accurately [1]. At the best-fit points of the mentioned parameters4 given in Refs.[1], we obtain a prediction for the quark mixing matrix as well as the parameters of the model in the quark sector, as shown in Table 2 and Eq. (13), respectively.$ \begin{aligned}[b]& a_{1u}=2.160\times 10^{-3} \,{\rm{GeV}},\quad a_{2u}=86.980\; {\rm{GeV}},\\& a_{3u}=-85.710 \;\,{\rm{GeV}}, \quad b_u=(2.308+0.5413 {\rm i}) \;\,{\rm{GeV}}, \\& c_{1u}=8.414+3.028 {\rm i}\,\; {\rm{GeV}}, \quad c_{2u}=(-0.614+0.211 {\rm i})\,\; {\rm{GeV}},\\& c_{3u}=(-8.269-3.170 {\rm i})\,\; {\rm{GeV}}, \quad c_{4u}=(0.754-0.353{\rm i})\,\; {\rm{GeV}}, \\& a_{1d}=4.670\times 10^{-3} \,\;{\rm{GeV}},\quad a_{2d}=2.140\, \; {\rm{GeV}}, \\& a_{3d}=-2.040 \;\,{\rm{GeV}},\quad b_d=(-8.658+0.262 {\rm i})10^{-2} \;\,{\rm{GeV}}, \\& c_{1d}=(-5.080+4.973 {\rm i}) 10^{-3}\,\; {\rm{GeV}},\\& c_{2d}=(0.193-0.077 {\rm i})\,\; {\rm{GeV}}, \\& c_{4d}=(-0.204+0.087 {\rm i})\,\; {\rm{GeV}}. \end{aligned} $

(13) The Jarlskog invariant in the quark sector,
$J_{CP}^{q}= {\rm{Im}}\big[V_{us} V_{cb} V_{cs}^* V_{ub}^*\big]$ , is calculated from Eq. (12) with the model results listed in Table 2 (third column), obtaining$ J_{CP}^{q}=3.08\times 10^{-5} $ , which coincides with the value reported in Ref. [1].Then, comparing Eqs. (8) and (13) with the aid of Eqs. (4)−(5), we obtain
$ \begin{aligned}[b] & |x_{1u}|=2.16\times 10^{-3},\; |x_{2u}| =0.87, \;|x_{3u}| =0.60, \;|y_{1u}|=2.37, \\ & |y_{2u}|=1.67, \;|z_{1u}|=1.79,\; |z_{2u}|=0.13,\; |z_{3u}|=1.24, \;|z_{4u}|=0.12, \\ & |x_{1d}|=4.67\times 10^{-3},\; |x_{2d}| =2.14\times 10^{-2},\; |x_{3d}| =1.43\times 10^{-2}, \\ & |y_{1d}|=8.66\times 10^{-2},\; |y_{2d}|=6.08\times 10^{-2},\; |z_{1d}|=1.42\times 10^{-3}, \\ & |z_{2d}|=4.16\times 10^{-2}, \;|z_{3d}|=10^{-2},\; |z_{4d}|=3.11\times 10^{-2}, \end{aligned} $

(14) which differ by approximately three orders of magnitude.
-
Using the Clebsch-Gordan coefficients of
$ D_4 $ [34] and Eq. (2), when the scalar fields take the VEVs, as in Eq. (3), we obtain the charged leptons ($ M_l $ ) and neutrino (Dirac and right-handed Majorana) mass matrices$ (M_D, M_R) $ as follows:$ M_l= \left( \begin{array}{*{20}{c}} { a_1 } & { 0 } & { 0 }\\{ 0 } & { a_2+a_3} & { a_4+a_5}\\{ 0 } & { a_4-a_5 } & { a_2-a_3} \end{array} \right), $

$\begin{aligned}[b]&M_D=\left( \begin{array}{*{20}{c}} {0} & { -a_{D}+b_{D}} & { a_{D}+b_{D} }\\{ 0} & { c_{D}+d_{D} } & { 0 } \\{ 0} & { 0 } & { -c_{D}+d_{D} } \end{array} \right),\\& M_R= \left( \begin{array}{*{20}{c}} {a_R} & { 0 } & { 0} \\{ 0 } & { b_R } & { c_R }\\{ 0 } & { c_R } & { b_R } \end{array} \right),\end{aligned} $

(15) where
$\begin{aligned}[b]& a_1 = \left(\frac{v_\phi }{\Lambda}\right) v h_1,\quad a_2=h_2 v,\quad a_3=h_3 v^{\prime},\\& a_4= \left(\frac{v_\phi }{\Lambda}\right) v h_4,\quad a_5= \left(\frac{v_\phi }{\Lambda}\right) v^{\prime} h_5.\end{aligned} $

(16) $ \begin{aligned}[b]& a_D=\left(\frac{v_{\rho}}{\Lambda}\right) x_1 v,\quad b_D = \left(\frac{v_{\rho}}{\Lambda}\right) x_2 v^{\prime},\quad c_D = \left(\frac{v_{\varphi}}{\Lambda}\right) x_3 v,\\& d_D = \left(\frac{v_{\varphi}}{\Lambda}\right) x_4 v^{\prime}, \quad a_R = \frac{y_1}{\Lambda} v_\chi v_{\phi}, \quad b_R=y_2 v_\chi, \\& c_R=\frac{y_3}{\Lambda} v_\chi v_{\phi}. \end{aligned} $

(17) $ \bullet $ Charged-lepton sector: For simplicity, we consider the case of$ \arg h_3=(\arg h_2+\pi) $ and$ \arg h_5=\arg h_4 $ , i.e.,$ \arg a_3=(\arg a_2+\pi) $ and$ \arg a_5=\arg a_4 $ . Yukawa couplings$ h_i \, (i=1\div 5) $ are complex in general; therefore, the matrix$ M_l $ and its eigenvalues are complex. Let us first define a Hermitian matrix$ m^2_l=M_l M^{+}_l $ as$ m^2_l = M_l M^+_l =\left( \begin{array}{*{20}{c}} {A_{0} } & { 0 } & { 0} \\{ 0 } & { B_{0} } & { {\cal{D}}_0. {\rm e}^{-{\rm i}\theta}} \\ { 0 } & { {\cal{D}}_0. {\rm e}^{{\rm i}\theta} } & { C_{0} } \end{array} \right),$

(18) where
5 $ \begin{aligned}[b] & A_0 = |a_{1}|^2,\quad B_0 = \big(|a_{2}| - |a_{3}|\big)^2 + \big(|a_{4}| + |a_{5}|\big)^2,\\& C_0 = \big(|a_{2}| + |a_{3}|\big)^2 + \big(|a_{4}| -|a_{5}|\big)^2, \\ & D_0 = 2 \big(|a_{2}| |a_{4}| + |a_{3}| |a_{5}|\big) c_\alpha, \\&G_0 = -2 \big(|a_{3}| |a_{4}| + |a_{2}| |a_{5}|\big)s_\alpha,\quad {\cal{D}}_0=\sqrt{D^2_0+G^2_0}, \end{aligned} $

(19) $ \theta=\arccos \left(\frac{D_0}{{\cal{D}}_0}\right),\quad \alpha=\arg a_2 - \arg a_4. $

(20) The matrix
$ m^2_l $ in Eq. (18) is diagonalized by two mixing matrices$ V_{l(L, R)} $ with$ V^+_{lL} m^2_l V_{lR}={\rm{diag}} (m^2_e, m^2_\mu, m^2_\tau) $ , where$ m^2_e =A_{0}, \,\, m^2_{\mu, \tau}= \frac{1}{2} \left(B_0+C_0\mp \sqrt{(B_0-C_0)^2+4 {\cal{D}}_0^2}\right), $

(21) $ V_{lL}=V_{lR}=\left( \begin{array}{*{20}{c}} { 1 } & { 0 } & { 0 }\\ { 0 } & { c_\psi } & { -s_\psi . {\rm e}^{-{\rm i} \theta}}\\ { 0 } & { s_\psi . {\rm e}^{{\rm i} \theta} } & { c_\psi } \end{array} \right), $

(22) where
$ s_\psi = \frac{1}{\sqrt{2}\sqrt{1-\dfrac{B_0-C_0}{B_0-C_0+\sqrt{(B_0-C_0)^2+4 {\cal{D}}^2_0}}}}. $

(23) Equations (19)−(21) and (23) yield the following relations:
$ \begin{aligned}[b] & |a_{1}|=m_e, \quad |a_{2}|=\frac{|a_{4}| D_0 s_\alpha+|a_{5}| c_\alpha G_0}{\big(|a_{4}|^2 - |a_{5}|^2\big) s_{2\alpha}}, \\& |a_{3}| =\frac{|a_{4}| c_\alpha G_0 + |a_{5}| D_0 s_\alpha}{(|a_{5}|^2-|a_{4}|^2)s_{2\alpha}}, \\ &|a_{4}| = \frac{a + b}{2},\quad |a_{5}| = \frac{a - b}{2}, \end{aligned} $

(24) where
$ \begin{aligned}[b] & a=\sqrt{\frac{\sqrt{(B_0 C_0-x_0+y_0)^2-4 B_0 C_0 y_0}+B_0 C_0-x_0+y_0}{2C_0}}, \\ & b=\sqrt{\frac{\sqrt{(B_0 C_0-x_0+y_0)^2-4 B_0 C_0 y_0}+B_0 C_0+x_0-y_0}{2 B_0}}, \end{aligned} $

(25) $ x_0=\frac{\big(c_\alpha G_0+D_0 s_\alpha\big)^2}{s^2_{2\alpha}},\quad y_0=\frac{\big(c_\alpha G_0-D_0 s_\alpha\big)^2}{s^2_{2\alpha}}, $

(26) $ \begin{aligned}[b] & B_0=\left(m_\mu^2-m_\tau^2\right) s_\psi^2 +m_\tau^2,\quad C_0=\left(m_\mu^2-m_\tau^2\right)s_\psi^2 +m_\mu^2, \\ & D_0=\left(m_\tau^2-m_\mu^2\right)c_\theta s_\psi c_\psi ,\quad G_0=\left(m_\mu^2-m_\tau^2\right)s_\theta s_\psi c_\psi . \end{aligned} $

(27) Equations (16) and (24)−(27) imply that
$ h_{1} $ depends on$ m_e, \Lambda, v_\phi $ and v;$ h_{2} $ depends on$ v, m_\mu, m_\tau, \psi, \theta $ and α;$ h_{3} $ depends on$v^{\prime},\; m_\mu,\; m_\tau,\; \psi, \; \theta$ and α; and$ h_{4} $ and$ h_5 $ depend on$ v, \Lambda, v_\phi, m_\mu, m_\tau $ ,$ \psi, \theta $ , and α. We show in Sec. V that, according to the observed charged leptons$ m_{e,\mu,\tau} $ [1] and cut-off scale, and the VEV scales of scalar fields defined by Eqs. (4) and (5), there exist possible ranges of the model parameters such that the Yukawa couplings in the charged lepton sector,$ h_{i}\, (i=1\div5) $ , differ by approximately two orders of magnitude, i.e., the charged lepton mass hierarchy is satisfied.$ \bullet $ Neutrino sector: The effective neutrino mass matrix arises from the type-I seesaw mechanism, that is, according to Eq. (15),$ M_{\nu}=-M_D M_R^{-1} M^T_D $ :$ M_{\nu} = \left( \begin{array}{*{20}{c}} { A } & { -B_1 } & { -B_2 }\\ { -B_1 } & { C_1 } & { C_3} \\ { -B_2 } & { C_3 } & { C_2 } \end{array} \right), $

(28) where
$ \begin{aligned}[b] & A=\frac{2 b_{D}^2}{b_{R}+c_{R}}+\frac{2 a_{D}^2}{b_{R}-c_{R}},\\& B_{1}=\frac{(c_{D}+d_{D}) \big[a_{D} (b_{R}+c_{R})-b_{D} (b_{R}-c_{R})\big]}{b_R^2-c_R^2}, \\ & B_{2}=\frac{(c_{D}-d_{D}) \big[a_{D} (b_{R}+c_{R})+b_{D} (b_{R}-c_{R})\big]}{b_{R}^2-c_{R}^2},\\& C_{1}=\frac{b_{R} (c_{D}+d_{D})^2}{b_{R}^2-c_{R}^2}, \quad C_{2}=\frac{b_{R} (c_{D}-d_{D})^2}{b_{R}^2-c_{R}^2},\\& C_{3}=\frac{c_{R} \left(c_{D}^2-d_{D}^2\right)}{b_{R}^2-c_{R}^2}. \end{aligned} $

(29) The mass matrix
$ M_{\nu} $ in Eq. (28) presents the following three eigenvalues and corresponding mixing matrix:$ \begin{aligned}[b] & \lambda_1=0, \lambda_{2}=\frac{C_2 - 2 B_2 n_1 + A n_1^2 + n_2 (2 C_3 - 2 B_1 n_1 + C_1 n_2)}{n_{1}^2+n_{2}^2+1}, \\ &\lambda_{3}=\frac{C_2 - 2 B_2 t_1 + A t_1^2 + t_2 (2 C_3 - 2 B_1 t_1 + C_1 t_2)}{t_{1}^2+t_{2}^2+1}, \end{aligned} $

(30) $ {\rm{R}}=\left( \begin{array}{*{20}{c}}{ \dfrac{k_1}{\sqrt{1 + k_1^2 (1 + k_2^2)}} } & {\dfrac{n_1}{\sqrt{n^2_1+n^2_2+1}}} & {\dfrac{t_1}{\sqrt{t^2_1+t^2_2+1}}}\\ { \dfrac{k_1 k_2}{\sqrt{1 + k_1^2 (1 + k_2^2)}}} & {\dfrac{n_2}{\sqrt{n^2_1+n^2_2+1}}} & {\dfrac{t_2}{\sqrt{t^2_1+t^2_2+1}}}\\{ \dfrac{1}{\sqrt{1 + k_1^2 (1 + k_2^2)}} } & {\dfrac{1}{\sqrt{n^2_1+n^2_2+1}} } & {\dfrac{1}{\sqrt{t^2_1+t^2_2+1}} }\end{array}\right), $

(31) where the expressions of parameters
$ k_{1,2}, n_{1,2} $ and$ t_{1,2} $ are provided in Appendix C, satisfy the following relations:$\begin{aligned}[b]& k_1 (n_1 + k_2 n_2)+1=0,\,\,\quad k_1 (t_1 + k_2 t_2)+1=0, \\& n_1 t_1 + n_2 t_2+1=0,\end{aligned} $

(32) $\begin{aligned}[b]& C_2 - B_2 (k_1 + n_1) + C_3 (k_1 k_2 + n_2) \\&\quad+ k_1 \big[A n_1 + C_1 k_2 n_2 - B_1 (k_2 n_1 + n_2)\big]=0,\end{aligned} $

(33) $ \begin{aligned}[b]&C_2 - B_2 (k_1 + t_1) + C_3 (k_1 k_2 + t_2)\\&\quad + k_1 \big[A t_1 + C_1 k_2 t_2 - B_1 (k_2 t_1 + t_2)\big]=0,\end{aligned} $

(34) $\begin{aligned}[b]& C_2 + C_3 n_2 + A n_1 t_1 - B_1 n_2 t_1 \\&\quad- B_2 (n_1 + t_1) + (C_3 - B_1 n_1 + C_1 n_2) t_2=0, \end{aligned}$

(35) $ C_2 + k_1 \big[2 C_3 k_2 -2 B_2+ k_1 (A - 2 B_1 k_2 + C_1 k_2^2)\big]=0. $

(36) Depending on the sign of
$ \Delta m^2_{31} $ , the neutrino mass spectrum can exhibit a normal or inverted hierarchy [1]. In the considered model,$ 0=m_1\equiv \lambda_1< m_{2}\equiv \lambda_2< m_{3}\equiv \lambda_3 $ for NH and$ 0=m_3\equiv \lambda_1< m_1\equiv \lambda_2< m_2\equiv \lambda_3 $ for IH. Given that the lightest neutrino mass is equal to zero, other neutrino masses and their sum are given by$ \left\{ \begin{array}{l} m_1=0,\quad m_2=\sqrt{\Delta m^2_{21}},\quad m_3=\sqrt{\Delta m^2_{31}} \quad {\rm{for}}\; {\rm{NH}},\ \ \\ m_1=\sqrt{-\Delta m^2_{31}},\;\; m_2=\sqrt{\Delta m^2_{21}-\Delta m^2_{31}},\;\; m_3=0 \quad \rm{for IH.} \end{array} \right. $

(37) $ \sum m_\nu=\left\{ \begin{array}{l} \sqrt{\Delta m^2_{21}}+\sqrt{\Delta m^2_{31}} \;\;{\rm{for}}\;\; {\rm{NH}}, \\ \sqrt{\Delta m^2_{21}-\Delta m^2_{31}} +\sqrt{-\Delta m^2_{31}} \quad {\rm{for}}\;\; {\rm{IH}}. \end{array} \right. $

(38) The neutrino mass matrix
$ M_{\nu} $ in Eq. (28) is diagonalized as$ {\rm{U}}_{\nu }^T M_{\nu} {\rm{U}}_{\nu }=\left\{ \begin{array}{*{20}{l}} {\left( \begin{array}{*{20}{c}} {0 } & { 0 } & { 0} \\ {0 } & { m_{2} } & { 0} \\ {0 } & { 0 } & { m_{3} }\end{array} \right) ,} & {{\rm{U}}_{\nu }=\left( \begin{array}{*{20}{c}} {\dfrac{k_1}{\sqrt{1 + k_1^2 (1 + k_2^2)}} } & {\dfrac{n_1}{\sqrt{n^2_1+n^2_2+1}}} & {\dfrac{t_1}{\sqrt{t^2_1+t^2_2+1}}}\\ {\dfrac{k_1 k_2}{\sqrt{1 + k_1^2 (1 + k_2^2)}}} & {\dfrac{n_2}{\sqrt{n^2_1+n^2_2+1}}} & {\dfrac{t_2}{\sqrt{t^2_1+t^2_2+1}}}\\ {\dfrac{1}{\sqrt{1 + k_1^2 (1 + k_2^2)}} } & {\dfrac{1}{\sqrt{n^2_1+n^2_2+1}} } & {\dfrac{1}{\sqrt{t^2_1+t^2_2+1}}} \end{array}\right) }&{ {\rm{for}}\; {\rm{NH}},} \\ {\left( \begin{array}{*{20}{c}} {m_{1} } & { 0 } & { 0 }\\ {0 } & { m_{2} } & { 0}\\ {0 } & { 0 } & { 0 }\end{array} \right) ,} & {{\rm{U}}_{\nu }=\left(\begin{array}{*{20}{c}} {\dfrac{n_1}{\sqrt{n^2_1+n^2_2+1}}} & {\dfrac{t_1}{\sqrt{t^2_1+t^2_2+1}}} & {\dfrac{k_1}{\sqrt{1 + k_1^2 (1 + k_2^2)}}}\\ {\dfrac{n_2}{\sqrt{n^2_1+n^2_2+1}}} & {\dfrac{t_2}{\sqrt{t^2_1+t^2_2+1}}} & {\dfrac{k_1 k_2}{\sqrt{1 + k_1^2 (1 + k_2^2)}}}\\ {\dfrac{1}{\sqrt{n^2_1+n^2_2+1}} } & {\dfrac{1}{\sqrt{t^2_1+t^2_2+1}}} & { \dfrac{1}{\sqrt{1 + k_1^2 (1 + k_2^2)}} }\end{array}\right) } & { {\rm{for}}\; {\rm{IH}}, }\end{array} \right. $ 
(39) where
$ \lambda_{2}, \lambda_3 $ ,$ k_{1,2}, n_{1,2} $ and$ t_{1,2} $ are given in Appendix C.Equations (30) and (32)−(36) yield
$ \left\{ \begin{array}{*{20}{l}} {k_{1}=\dfrac{n_{1} t_{1}+n_{2}^2+1}{t_{1} \left(n_{1}^2+n_{2}^2\right)+n_{1}},\quad k_{2}=\dfrac{n_{2} (t_{1}-n_{1})}{n_{1} t_{1}+n_{2}^2+1},\quad t_{2}=-\dfrac{n_{1} t_{1}+1}{n_{2}}} & {{\rm{for}}\; {\rm{NH}},} \\ {n_2 = \dfrac{1 - k_1 n_1}{k_1 k_2}, \,\,\quad t_1 = \dfrac{k_1 (n_1-k_1 k_2^2)-1}{k_1 \left[k_1 (1 + k_2^2) n_1-1\right]}, \quad t_2 = \dfrac{k_2 (k_1 + n_1)}{-1 + k_1 (1 + k_2^2) n_1} } & { {\rm{for}}\; {\rm{IH}}, }\end{array} \right. $

(40) $ A=-\frac{C_2 - B_2 (k_1 + n_1) + C_1 k_1 k_2 n_2 + C_3 (k_1 k_2 + n_2) - B_1 k_1 (k_2 n_1 + n_2)}{k_1 n_1} \quad \rm{(NH and IH),} \quad $

(41) $ B_1=\frac{C_3 + C_1 k_1 k_2}{k_1}+\frac{(C_2 - B_2 k_1 + C_3 k_1 k_2) (n_1 - t_1)}{(n_1 t_2-n_2 t_1) k_1} \quad \rm{(NH and IH),} $

(42) $ B_2=\frac{C_2}{k_1} + C_3 k_2 \quad \rm{(NH and IH),} $

(43) $ C_1=\dfrac{C_3 (k_1 - n_1)+\dfrac{(C_2 - B_2 n_1 + C_3 n_2) (k_1 - t_1)}{t_2-k_2 t_1}+\dfrac{(C_2 - B_2 k_1 + C_3 k_1 k_2)(n_1 - t_1)n_1}{n_2 t_1-n_1 t_2}}{k_1 (k_2 n_1 - n_2)} \quad \rm{(NH and IH),} $

(44) $ C_2=\left\{ \begin{array}{l} \dfrac{\sqrt{\Delta m^2_{21}}}{1 + n_1^2 + n_2^2}+\dfrac{\sqrt{\Delta m^2_{31}} n_2^2}{(1 + n_1 t_1)^2 + n_2^2 (1 + t_1^2)} \quad {\rm{for}}\; {\rm{NH}},\ \ \\ k^2_1\left(\dfrac{k_2^2 \left(\sqrt{-\Delta m^2_{31}}-\sqrt{\Delta m^2_{21}-\Delta m^2_{31}}\right)}{1 + 2 k_1 n_1 + k_1^2 \big[n_1^2 + k_2^2 (1 + n_1^2)\big]}+\dfrac{(1 + k_2^2) \sqrt{\Delta m^2_{21}-\Delta m^2_{31}}}{1 + k_1^2 (1 + k_2^2)}\right) \quad {\rm{for}}\; {\rm{IH}}, \end{array} \right. $

(45) $ C_3=\left\{ \begin{array}{l} \dfrac{\sqrt{\Delta m^2_{21}} n_2}{1 + n_1^2 + n_2^2}-\dfrac{\sqrt{\Delta m^2_{31}}(1+n_1 t_1) n_2}{(1 + n_1 t_1)^2 + n_2^2 (1 + t_1^2)} \quad {\rm{for}}\; {\rm{NH}},\ \ \\ k_1 k_2\left(\dfrac{\left(\sqrt{\Delta m^2_{21}-\Delta m^2_{31}}-\sqrt{-\Delta m^2_{31}}\right) (k_1 n_1+1)}{1 + 2 k_1 n_1 + k_1^2 \big[n_1^2 + k_2^2 (1 + n_1^2)\big]}-\dfrac{\sqrt{\Delta m^2_{21}-\Delta m^2_{31}}}{1 + k_1^2 (1 + k_2^2)}\right) \quad \rm{for IH.} \end{array} \right. $

(46) The corresponding leptonic mixing matrix is
$ {\rm{U}}={\rm{U}}_{L}^{\dagger} {\rm{U}}_{\nu }=\left\{ \begin{array}{*{20}{l}} {\left( \begin{array}{*{20}{c}} { \dfrac{k_{1}}{\sqrt{\left(k_{2}^2+1\right) k_{1}^2+1}} } & { \dfrac{n_{1}}{\sqrt{n_{1}^2+n_{2}^2+1}}} & {\dfrac{t_{1}}{\sqrt{t_{1}^2+t_{2}^2+1}} } \\ { \dfrac{c_\psi k_{1} k_{2}+ {\rm e}^{-{\rm i} \theta} s_\psi}{\sqrt{\left(k_{2}^2+1\right) k_{1}^2+1}} } & { \dfrac{{\rm e}^{-{\rm i} \theta} \left(c_\psi {\rm e}^{{\rm i} \theta} n_{2}+s_\psi\right)}{\sqrt{n_{1}^2+n_{2}^2+1}} } & { \dfrac{{\rm e}^{-{\rm i} \theta} \left(s_\psi+ {\rm e}^{{\rm i} \theta} c_\psi t_{2}\right)}{\sqrt{t_{1}^2+t_{2}^2+1}}} \\ { \dfrac{c_\psi-{\rm e}^{{\rm i} \theta} k_{1} k_{2} s_\psi}{\sqrt{\left(k_{2}^2+1\right) k_{1}^2+1}} } & { \dfrac{c_\psi-{\rm e}^{{\rm i} \theta} n_{2} s_\psi}{\sqrt{n_{1}^2+n_{2}^2+1}} } & { \dfrac{c_\psi-{\rm e}^{{\rm i} \theta} s_\psi t_{2}}{\sqrt{t_{1}^2+t_{2}^2+1}} } \end{array} \right)} & { {\rm{for}}\; {\rm{NH}},} \\ {\left( \begin{array}{*{20}{c}} {\dfrac{n_{1}}{\sqrt{n_{1}^2+n_{2}^2+1}}} & {\dfrac{t_{1}}{\sqrt{t_{1}^2+t_{2}^2+1}}} & {\dfrac{k_{1}}{\sqrt{\left(k_{2}^2+1\right) k_{1}^2+1}}} \\ {\dfrac{{\rm e}^{-{\rm i} \theta} \left(c_\psi {\rm e}^{{\rm i} \theta} n_{2}+s_\psi\right)}{\sqrt{n_{1}^2+n_{2}^2+1}} } & { \dfrac{{\rm e}^{-{\rm i} \theta} \left(s_\psi+ {\rm e}^{{\rm i} \theta} c_\psi t_{2}\right)}{\sqrt{t_{1}^2+t_{2}^2+1}}} & {\dfrac{c_\psi k_{1} k_{2}+{\rm e}^{-{\rm i} \theta} s_\psi}{\sqrt{\left(k_{2}^2+1\right) k_{1}^2+1}}} \\ { \dfrac{c_\psi-{\rm e}^{{\rm i} \theta} n_{2} s_\psi}{\sqrt{n_{1}^2+n_{2}^2+1}} } & { \dfrac{c_\psi-{\rm e}^{{\rm i} \theta} s_\psi t_{2}}{\sqrt{t_{1}^2+t_{2}^2+1}}} & {\dfrac{c_\psi-{\rm e}^{{\rm i} \theta} k_{1} k_{2} s_\psi}{\sqrt{\left(k_{2}^2+1\right) k_{1}^2+1}} } \end{array} \right)} & {{\rm{for}}\; {\rm{IH}}.} \end{array} \right. $

(47) The lepton mixing matrix
$ {\rm{U}}_{{\rm{PMNS}}} $ , according to the standard parametrization, takes the form${\rm{U}}_{{\rm{MPNS}}}=\left( \begin{array}{*{20}{c}} { c_{13} c_{12} } & { s_{12} c_{13} } & { s_{13} {\rm e}^{-{\rm i} \delta}} \\ {-c_{23} s_{12}-{\rm e}^{{\rm i} \delta} c_{12} s_{13} s_{23} } & { c_{12} c_{23}-{\rm e}^{{\rm i} \delta} s_{12} s_{13} s_{23} } & { c_{13} s_{23}} \\ {s_{12} s_{23}-{\rm e}^{{\rm i} \delta} c_{12} c_{23} s_{13} } & { -c_{12} s_{23}-{\rm e}^{{\rm i} \delta} c_{23} s_{12} s_{13} } & { c_{13} c_{23}} \end{array} \right)\left( \begin{array}{*{20}{c}} {1 } & { 0} & {0 } \\ { 0}&{{\rm e}^{{\rm i} \eta_1} } & { 0 } \\ { 0} & { 0 } & { {\rm e}^{{\rm i} \eta_2} } \end{array} \right), $

(48) where
$ s_{ij} = \sin \theta_{ij} $ and$ c_{ij} = \cos \theta_{ij} $ with$ \theta_{13}, \theta_{12} $ and$ \theta_{23} $ are the reactor, solar, and atmospheric mixing angles, respectively;$ \delta_{CP} $ is the Dirac CP violation phase and$ \eta_{1,2} $ are the two Majorana CP violating phases. Comparing the entries "12" and "13" of the two mixing matrices in Eqs. (47) and (48), we obtain$ \eta_1=0, \, \eta_2=\delta \rm{(both NH and IH)}. $

(49) The lepton mixing angles, obtained from Eqs. (47) and (48), are
$ s_{13}^2=\left| {\rm{U}}_{e 3}\right|^2=\left\{ \begin{array}{*{20}{l}} {\dfrac{t_{1}^2}{t_{1}^2+t_{2}^2+1}} & {\rm{for}}\; {\rm{NH}}, \\ \dfrac{k^2_1}{1 + k_1^2 \big(1 + k_2^2\big)} & {{\rm{for}}\; {\rm{IH}}, }\end{array} \right. $

(50) $ s_{12}^2 =\frac{\left|{\rm{U}}_{e 2}\right|^2}{1-\left|{\rm{U}}_{e 3}\right|^2}=\left\{ \begin{array}{*{20}{l}} {\dfrac{n_{1}^2 \left(t_{1}^2+t_{2}^2+1\right)}{\left(t_{2}^2+1\right) \left(n_{1}^2+n_{2}^2+1\right)}} & {{\rm{for}}\; {\rm{NH}},} \\ {\dfrac{\left[1 + k_1^2 (1 + k_2^2)\right] t_1^2}{(1 + k_1^2 k_2^2) (1 + t_1^2 + t_2^2)} } & {{\rm{for}}\; {\rm{IH}}, }\end{array} \right. $

(51) $ s_{23}^2=\frac{\left| {\rm{U}}_{\mu 3}\right|^2}{1-\left| {\rm{U}}_{e 3}\right|^2}= \left\{ \begin{array}{*{20}{l}} {\dfrac{c_\psi^2 t_{2}^2+ s_{2\psi} c_\theta t_{2} +s_\psi^2}{t_{2}^2+1}}& {{\rm{for}}\; {\rm{NH}},} \\{ \dfrac{c_\psi^2 k_1^2 k_2^2 + s_\psi^2 + k_1 k_2 s_{2\psi} c_\theta}{1 + k_1^2 k_2^2}}& {{\rm{for}}\; {\rm{IH}}, }\end{array} \right. $

(52) The Jarlskog invariant in the active sector, determined from Eq. (47), takes the form [1, 35]
$ J^{(l)}_{CP} = \frac{ n_1 t_1 (t_2-n_2) s_\psi c_\psi s_\theta}{\left(n_{1}^2+n_{2}^2+1\right) \left(1 + t_1^2 + t_2^2\right)} \quad {\rm{NH}}\; {\rm{and}}\; {\rm{IH}}. $

(53) Comparing
$ J^{(l)}_{CP} $ in Eq. (53) and that of the standard parametrization,$ J^{(l)}_{CP} = c_{12} c_{13}^2 c_{23} s_{12} s_{13} s_{23} s_\delta $ , we obtain$ s_\delta=\frac{ n_1 t_1 (t_2-n_2) s_\psi c_\psi s_\theta}{\left(n_{1}^2+n_{2}^2+1\right) \left(1 + t_1^2 + t_2^2\right) c_{12} c_{13}^2 c_{23} s_{12} s_{13} s_{23} } \quad {\rm{NH}}\; {\rm{and}}\; {\rm{IH}}. $

(54) The effective neutrino masses [36], obtained from Eqs. (37), (39), and (47), exhibit the following forms:
$ \langle m_{ee}\rangle = \left| \sum^3_{i=1} U_{ei}^2 m_i \right|=\left\{ \begin{array}{*{20}{l}} {\dfrac{\sqrt{\Delta m^2_{21}} n_1^2}{1 + n_1^2 + n_2^2} +\dfrac{\sqrt{\Delta m^2_{31}} t_1^2}{1 + t_1^2 + t_2^2}} & {{\rm{for}}\; {\rm{NH}},} \\{ \dfrac{\sqrt{-\Delta m^2_{31}} n_1^2}{1 + n_1^2 + n_2^2} + \dfrac{\sqrt{\Delta m^2_{21}-\Delta m^2_{31}} t_1^2}{1 + t_1^2 + t_2^2} } & {{\rm{for}}\; {\rm{IH}}, }\end{array} \right. $ 
(55) $ m_{\beta }= \sqrt{\sum^3_{i=1} \left|U_{ei}\right|^2 m_i^2}=\left\{ \begin{array}{*{20}{l}} {\sqrt{\dfrac{\Delta m^2_{21} n_1^2}{1 + n_1^2 + n_2^2} +\dfrac{\Delta m^2_{31} t_1^2}{1 + t_1^2 + t_2^2}}} & {{\rm{for}}\; {\rm{NH}}, }\\ {\sqrt{\dfrac{\left(\Delta m^2_{21}-\Delta m^2_{31}\right) t_1^2}{1 + t_1^2 + t_2^2}-\dfrac{\Delta m^2_{31} n_1^2}{1 + n_1^2 + n_2^2}} } & {{\rm{for}}\; {\rm{IH}}, }\end{array} \right. $

(56) According to Eqs. (50)−(52), we can express
$ n_{1,2}, t_{1} $ and$ s_{\delta} $ in terms of two constrained parameters$ c_\theta, s_\psi $ and five observable parameters$\Delta m^2_{21},\; \Delta m^2_{31}$ ,$ s^2_{12}, s^2_{23} $ ,$ s^2_{13} $ as follows:$ \bullet $ For NH:$ n_1=\frac{s_{12}^2 c_{13}^4 t_1^2}{\sqrt{\big(c_{13}^2 t_1^2-s_{13}^2\big) s_{12}^2 c_{12}^2 c_{13}^4 t_1^2 }-s_{12}^2 s_{13}^2 c_{13}^2 t_1},\quad n_2=\frac{(1 + n_1 t_1) s_{13}}{\sqrt{c_{13}^2 t_1^2-s_{13}^2}}, $

(57) $ t_1=t_{13}\sqrt{\frac{s_\psi^2 (s_{23}^2 - c_\psi^2) +c_\psi^2 (c_{23}^2 + c_{2\theta} s_\psi^2)+ 2 \sqrt{c_\theta^2 c_\psi^2 s_\psi^2 (s_{23}^2 c_{23}^2 - s_\psi^2 c_\psi^2 s_\theta^2 )}}{ \big(c_\psi^2-s_{23}^2\big)^2}}. $

(58) $ \bullet $ For IH:$ k_1=-t_{13}\sqrt{\frac{s_\psi^2 (s_{23}^2 - c_\psi^2) +c_\psi^2 (c_{23}^2 + c_{2\theta} s_\psi^2)- 2 \sqrt{c_\theta^2 c_\psi^2 s_\psi^2 (s_{23}^2 c_{23}^2 - s_\psi^2 c_\psi^2 s_\theta^2 )}}{\left(c_{\psi}^2-s_{23}^2\right)^2}}, $

(59) $ k_2=\frac{\sqrt{k_1^2 c_{13}^2- s_{13}^2}}{k_1 s_{13}}, \quad n_1=\frac{s_{12} c_{12} c_{13}^2\sqrt{k_1^2\left(k_1^2 c_{13}^2-s_{13}^2\right)}-k_1 c_{12}^2 s_{13}^2 c_{13}^2}{s_{13}^4 + s_{12}^2 c_{13}^2 \left(s_{13}^2- k_1^2\right)}. $

(60) Equations (40)−(46) and (54)−(60) show that the model parameters
$s_\delta,\; k_{1,2},\; n_{1,2}$ and$ t_{1,2} $ depend on two constrained parameters$ c_\theta, s_\psi $ and three observable parameters$ s^2_{12}, s^2_{23} $ ,$ s^2_{13} $ while$ A, B_{1,2}, C_{1,2, 3}, \langle m_{ee}\rangle $ and$ m_{\beta} $ depend on two constrained parameters$ c_\theta, s_\psi $ and five observable parameters$ \Delta m^2_{21}, \Delta m^2_{31} $ ,$ s^2_{12}, s^2_{23} $ ,$ s^2_{13} $ . -
$ \bullet $ Concerning the charged lepton sector, using the values of Λ, the observed values of the charged lepton masses [1], that is,$m_e=0.51099 ~{\rm{MeV}},~ m_\mu = 105.65837 {\rm{MeV}}, ~m_\tau = 1776.86 ~{\rm{MeV}}$ , and the VEV of scalar fields in Eqs. (4) and (5), and with the help of Eqs. (16) and (24)−(27), we obtain$ |h_1|\simeq 10^{-2} $ , and$ h_{2,3,4,5} $ still depend on three parameters: α, θ, and ψ. In the case of$s_\alpha= -0.95\, (\alpha=288.2^\circ)$ , the Yukawa-like couplings$ h_{2,3,4,5} $ depend on two parameters, namely θ and ψ, which are plotted in Figs. 1 and 2.
Figure 1. (color online)
$10^3|h_2|$ (left panel) and$10^3|h_3|$ (right panel) versus$c_\theta$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ .
Figure 2. (color online)
$|h_4|$ (left panel) and$|h_5|$ (right panel) versus$c_\theta$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ .$ |h_2|\simeq |h_3| \sim 10^{-2},\quad |h_4|\simeq |h_5| \sim 10^{-1}, $

(61) which in turn implies that the Yukawa couplings in the charged lepton sector differ from each other by one order of magnitude for a natural explanation of the charged lepton mass hierarchy.
$ \bullet $ Regarding the neutrino sector, Equation (37) shows that the neutrino masses ($ m_{2,3} $ for NH and$ m_{1,2} $ for IH) depend on two experimental parameters,$ \Delta m^2_{31} $ and$ \Delta m^2_{21} $ , which have been measured with high accuracy. In the case of$ \Delta m^2_{21} $ and$ \Delta m^2_{31} $ , their values lie in the 3σ range [37], i.e.,$\Delta m^2_{21}\in (69.40, 81.40)~ {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 3.63) \times 10^3 {\rm{meV}}^2$ . The allowed regions are$ m_{1,2,3} $ ,$m_1=0, m_2\in (8.33, 9.02)~ {\rm{meV}}$ ,$m_3= (49.70, 51.30)$ meV for NH, and$m_1\in (48.70, 50.30)~ {\rm{meV}}, m_2= (49.4,51.0)~ {\rm{meV}},~ m_3=0$ for IH. The sum of neutrino masses is predicted to be$ \sum m_{\nu} \, ({\rm{meV}}) \in \left\{ \begin{array}{*{20}{l}} {(58.25, 60.25)} & {{\rm{for}}\; {\rm{NH}},} \\ {(98.50,101.0) } & { {\rm{for}}\; {\rm{IH}},} \end{array} \right. $

(62) which is consistent with the limits [38]
$ \sum m_{\nu} $ < 0.15 eV (NH) and$ \sum m_{\nu} $ < 0.17 eV (IH),$ \sum m_{\nu} $ < 0.14 eV [39],$ \sum m_{\nu} $ < 0.152 eV [40] (minimal$ \Lambda {\rm{CDM}} + \sum m_{\nu} $ ),$ \sum m_{\nu} $ < 0.118 eV (high-l polarization),$ \sum m_{\nu} $ < 0.101 eV (NPDDE model),$ \sum m_{\nu} $ < 0.093 eV (NPDDE+r model); the most aggressive bound is$ \sum m_{\nu} $ < 0.078 eV (NPDDE+r with the R16 prior) [40, 41],$ \sum m_{\nu} $ < 0.183 eV for IH [42],$ \sum m_{\nu} $ < 0.13 eV (the base dataset) and$ \sum m_{\nu} $ < 0.11 eV (pol dataset) [43],$ \sum m_{\nu} $ < 0.19 eV [44].To determine the possible ranges of the parameters
$ k_{1,2}, n_{1,2}, t_{1,2} $ and obtain predictive values for the Dirac CP viloation phase δ, we use the observables$ \Delta m^2_{21} $ ,$ \Delta m^2_{31} $ ,$ \sin^2 \theta_{12} $ ,$ \sin^2\theta_{23} $ and$ \sin^2 \theta_{13} $ as input parameters; these observables are given in Table 3.Best-fit point
(3σ range) (NH)Best-fit point
(3σ range) (IH)$ \Delta m^2_{21} \left[{\rm{meV}}^2\right] $ 

$ 75.0\, (69.4\rightarrow 81.4) $ 

$ 75.0\, (69.4\rightarrow 81.4) $ 

${|\Delta m^2_{31}|/{10^{3} } \,\left[{\rm{meV} }^2\right]}$ 

$ 2.55 \, (2.47\rightarrow 2.63) $ 

$ 2.45 \, (2.37 \rightarrow 2.53) $ 

$ \sin^2\theta_{12} $ 

$ 0.318\, (0.271\rightarrow 0.369) $ 

$ 0.318\, (0.271\rightarrow 0.369) $ 

$ \sin^2\theta_{23} $ 

$ 0.574 \, (0.434\rightarrow 0.610) $ 

$ 0.578\, (0.433\rightarrow 0.608) $ 

${\sin^2\theta_{13} }/{10^{-2} }$ 

$ 2.200\, (2.00\rightarrow 2.405) $ 

$ 2.225\, (2.018\rightarrow 2.424) $ 

$ \delta_{CP}/\pi $ 

$ 1.08\, (0.71\rightarrow 1.99) $ 

$ 1.58\, (1.11\rightarrow 1.96) $ 

Table 3. Global analysis of neutrino oscillation data [37].
At the best-fit values of the lepton mixing angles [37],
$ \sin^2\theta_{12}=0.318 $ and$ \sin^2\theta_{13}=2.200\times 10^{-2} $ for NH while$ \sin^2\theta_{12}=0.318 $ and$ \sin^2\theta_{13}=2.225\times 10^{-2} $ for IH;$s_\delta,\; k_{1,2}, n_{1,2}$ and$ t_{1,2} $ depend on two parameters:$ c_\theta $ and$ s_\psi $ . The Dirac CP violating phase δ (more precisely,$ s_\delta $ ) is a function of two parameters,$ c_{\theta} $ and$ s_{\psi} $ , with$ c_\theta\in(0.29, 0.31) $ and$ s_\psi\in (0.25, 0.65) $ for both IH and NH; it is plotted in Fig. 3. According to this figure, we have that
Figure 3. (color online)
$s_\delta$ versus$c_{\theta}$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ for both NH and IH.$ s_\delta\in (-0.95, \, -0.50),\,\, {\rm{i.e.}},\,\, \delta^\circ\in (288.20, \, 330.00)\, \quad ({\rm{NH}}\; {\rm{and}}\; {\rm{IH}}). $

(63) The dependences of
$ k_{1,2}, n_{1,2} $ and$ t_{1,2} $ on the parameters$ c_{\theta} $ and$ s_{\psi} $ , with$ c_\theta\in(0.29, 0.31) $ and$ s_\psi\in (0.25, 0.65) $ for both IH and NH, are respectively plotted in Figs. 4, 5, 6, 7, 8, and 9.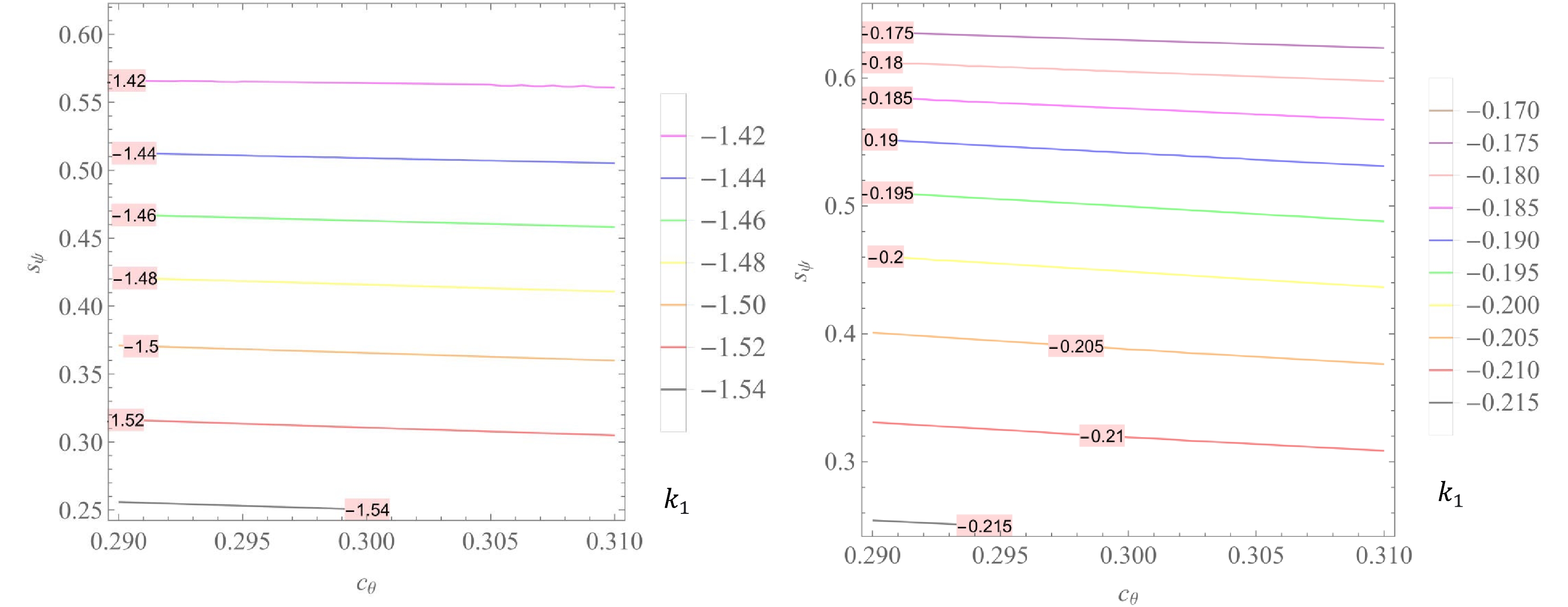
Figure 4. (color online)
$k_1$ versus$c_{\theta}$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ for NH (left panel) and IH (right panel).
Figure 5. (color online)
$k_2$ versus$c_{\theta}$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ for NH (left panel) and IH (right panel).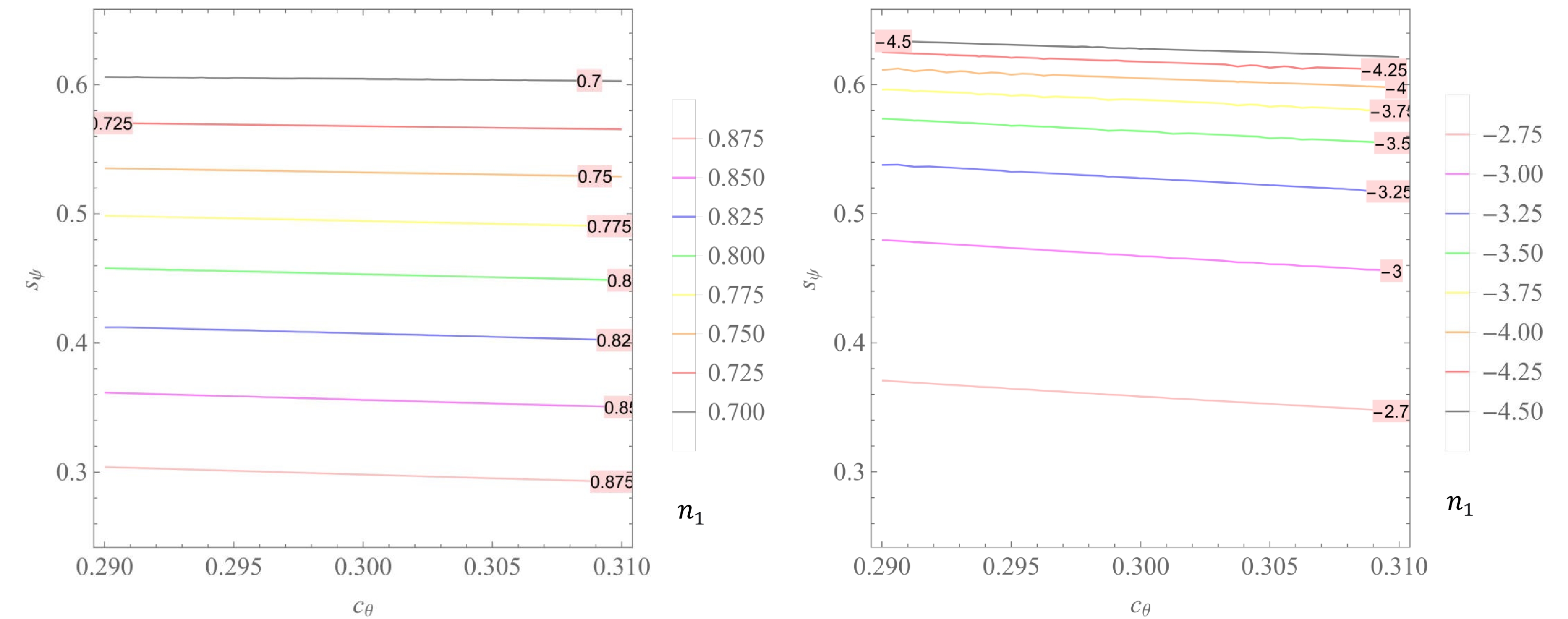
Figure 6. (color online)
$n_1$ versus$c_{\theta}$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ for NH (left panel) and IH (right panel).
Figure 7. (color online)
$n_2$ versus$c_{\theta}$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ for NH (left panel) and IH (right panel).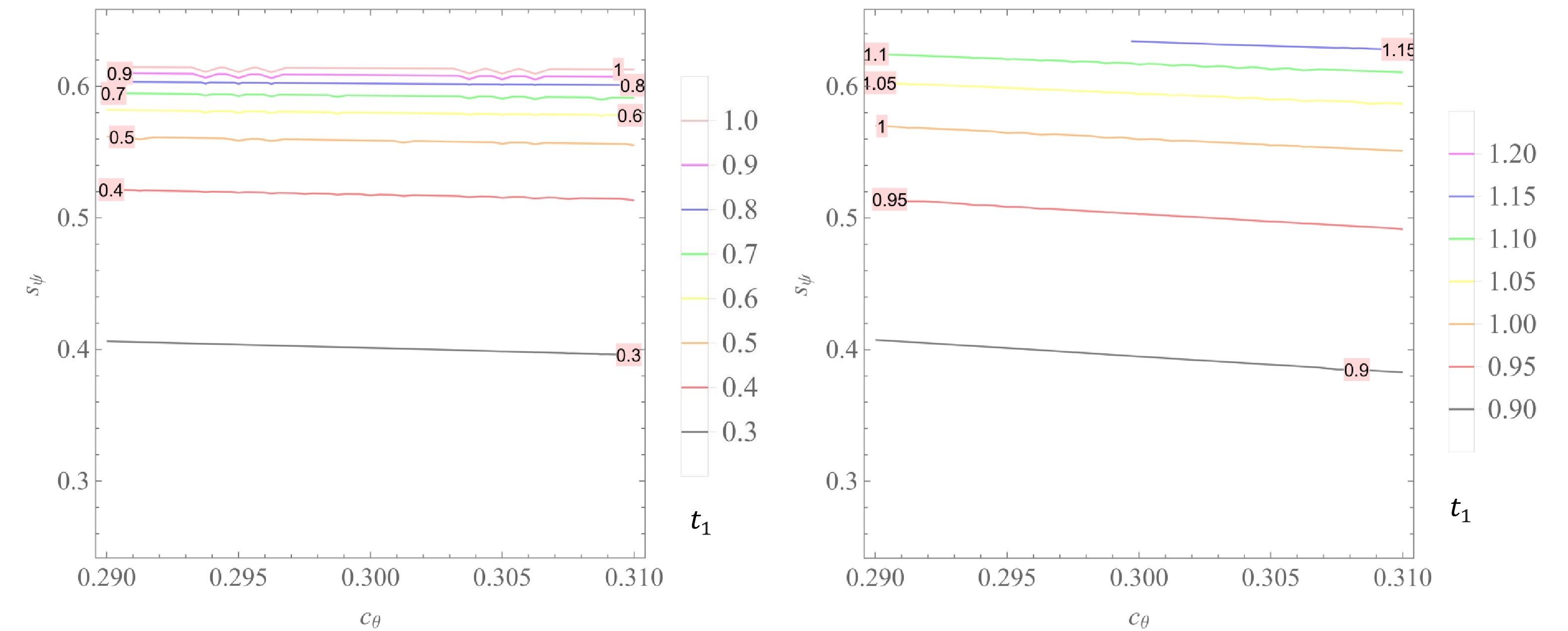
Figure 8. (color online)
$t_1$ versus$c_{\theta}$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ for NH (left panel) and IH (right panel).
Figure 9. (color online)
$t_2$ versus$c_{\theta}$ and$s_{\psi}$ with$c_\theta\in(0.29, 0.31)$ and$s_\psi\in (0.25, 0.65)$ for NH (left panel) and IH (right panel).These figures imply that
$\begin{aligned}[b]& k_{1}\in \left\{ \begin{array}{*{20}{l}} {(-1.54, -1.42) }&{{\rm{for}}\; {\rm{NH}}, }\\ {(-0.215, -0.170) }&{ {\rm{for}}\; {\rm{IH}},} \end{array} \right. \\& k_{2}\in \left\{ \begin{array}{*{20}{l}} {(-0.25, 0.10) }&{{\rm{for}}\; {\rm{NH}}, }\\ {(-4.60, -3.20)}&{ {\rm{for}}\; {\rm{IH}},} \end{array} \right. \end{aligned}$

(64) $\begin{aligned}[b] n_{1}\in \left\{ \begin{array}{*{20}{l}} {(0.70, 0.875) }&{{\rm{for}}\; {\rm{NH}},} \\ {(-4.50, -2.75)}&{ {\rm{for}}\; {\rm{IH}},} \end{array} \right.\end{aligned} $

$\begin{aligned}[b] n_{2}\in \left\{ \begin{array}{*{20}{l}} {(0.20, 0.80)}&{{\rm{for}}\; {\rm{NH}}, }\\ {(-3.00, -1.60) }&{ {\rm{for}}\; {\rm{IH}}, }\end{array} \right.\end{aligned} $

(65) $\begin{aligned}[b]& t_{1}\in \left\{ \begin{array}{*{20}{l}} {(0.30,1.00)}&{ {\rm{for}}\; {\rm{NH}}, }\\ {(0.90, 1.20)}&{{\rm{for}}\; {\rm{IH}}, }\end{array} \right. \\& t_{2}\in \left\{ \begin{array}{*{20}{l}} {(-5.00,-1.50)}&{ {\rm{for}}\; {\rm{NH}}, }\\{(-1.50, -0.90) }&{ {\rm{for}}\; {\rm{IH}}. }\end{array} \right.\end{aligned} $

(66) Similarly, to determine the possible ranges of the parameters
$A,\; B_{1,2},\; C_{1,2, 3},\; \langle m_{ee}\rangle$ , and$ m_{\beta} $ , we fix$ \sin^2 \theta_{12} $ ,$ \sin^2\theta_{23} $ , and$ \sin^2 \theta_{13} $ at their best-fit points [37],$ c_\theta=0.30\, (\theta=72.54^\circ) $ and$ s_\psi=0.40\, (\psi=23.58^\circ) $ for both IH and NH, and$ \Delta m^2_{21} $ and$ \Delta m^2_{31} $ take their values in their corresponding 3 σ ranges [37]:$ \Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2 $ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ (NH) while$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ (IH). The dependence of$A, B_{1,2}, C_{1,2, 3}, \langle m_{ee}\rangle$ , and$ m_{\beta} $ on the parameters$ \Delta m^2_{21} $ and$ \Delta m^2_{31} $ are presented in Figs. 10, 11,12, 13,14, 15, 16, and 17, respectively.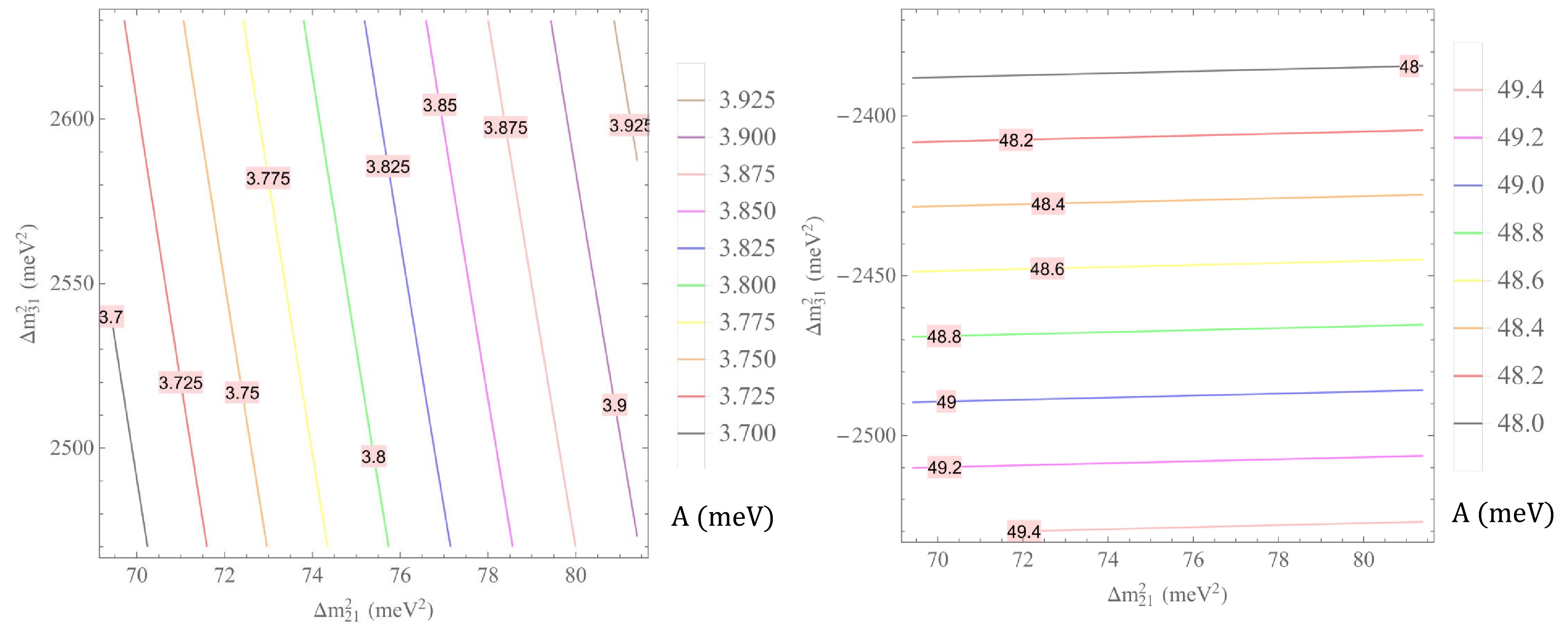
Figure 10. (color online) A (
${\rm{meV}}$ ) versus$\Delta m^2_{21}$ and$\Delta m^2_{31}$ with$\Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ for NH (left panel) and$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ for IH (right panel).
Figure 11. (color online)
$B_1$ (${\rm{meV}}$ ) versus$\Delta m^2_{21}$ and$\Delta m^2_{31}$ with$\Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ for NH (left panel) and$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ for IH (right panel).
Figure 12. (color online)
$B_2$ (${\rm{meV}}$ ) versus$\Delta m^2_{21}$ and$\Delta m^2_{31}$ with$\Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ for NH (left panel) and$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ for IH (right panel).
Figure 13. (color online)
$C_1$ (${\rm{meV}}$ ) versus$\Delta m^2_{21}$ and$\Delta m^2_{31}$ with$\Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ for NH (left panel) and$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ for IH (right panel).
Figure 14. (color online)
$C_2$ (${\rm{meV}}$ ) versus$\Delta m^2_{21}$ and$\Delta m^2_{31}$ with$\Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ for NH (left panel) and$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ for IH (right panel).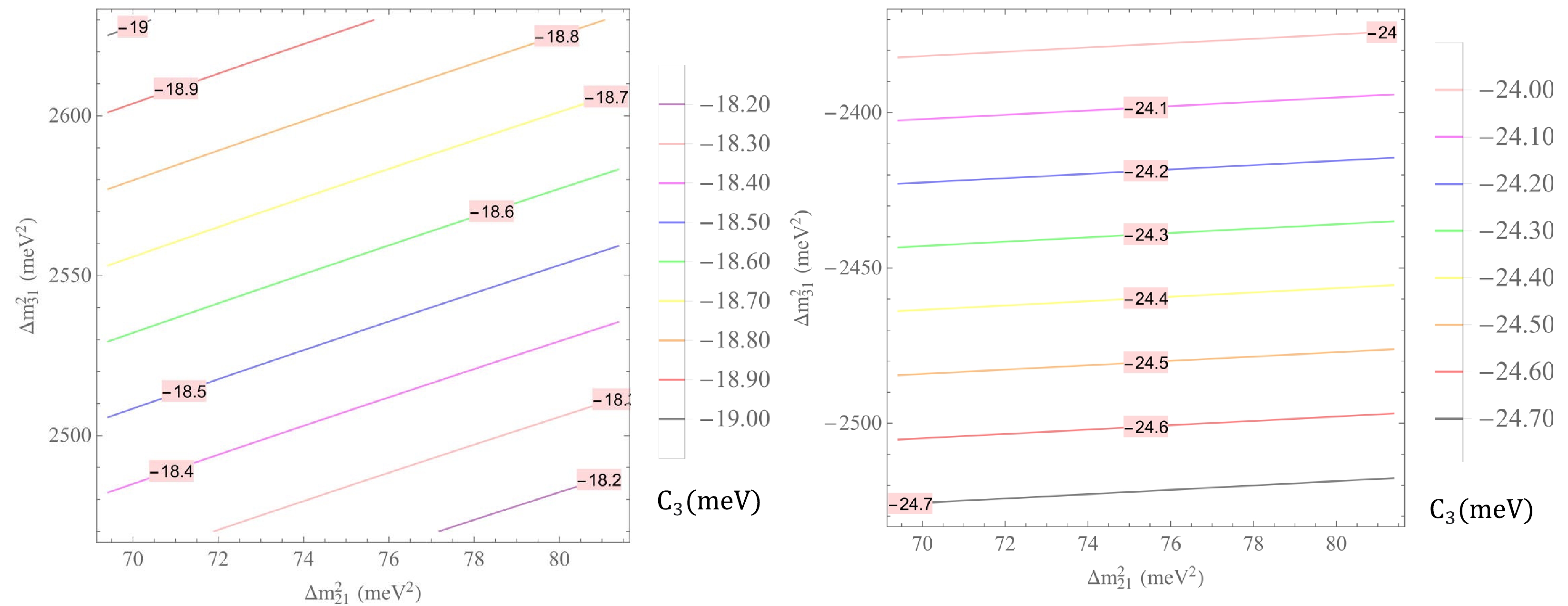
Figure 15. (color online)
$C_3$ (${\rm{meV}}$ ) versus$\Delta m^2_{21}$ and$\Delta m^2_{31}$ with$\Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ for NH (left panel) and$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ for IH (right panel).
Figure 16. (color online)
$\langle m_{ee}\rangle$ (${\rm{meV}}$ ) versus$\Delta m^2_{21}$ and$\Delta m^2_{31}$ with$\Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ for NH (left panel) and$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ for IH (right panel).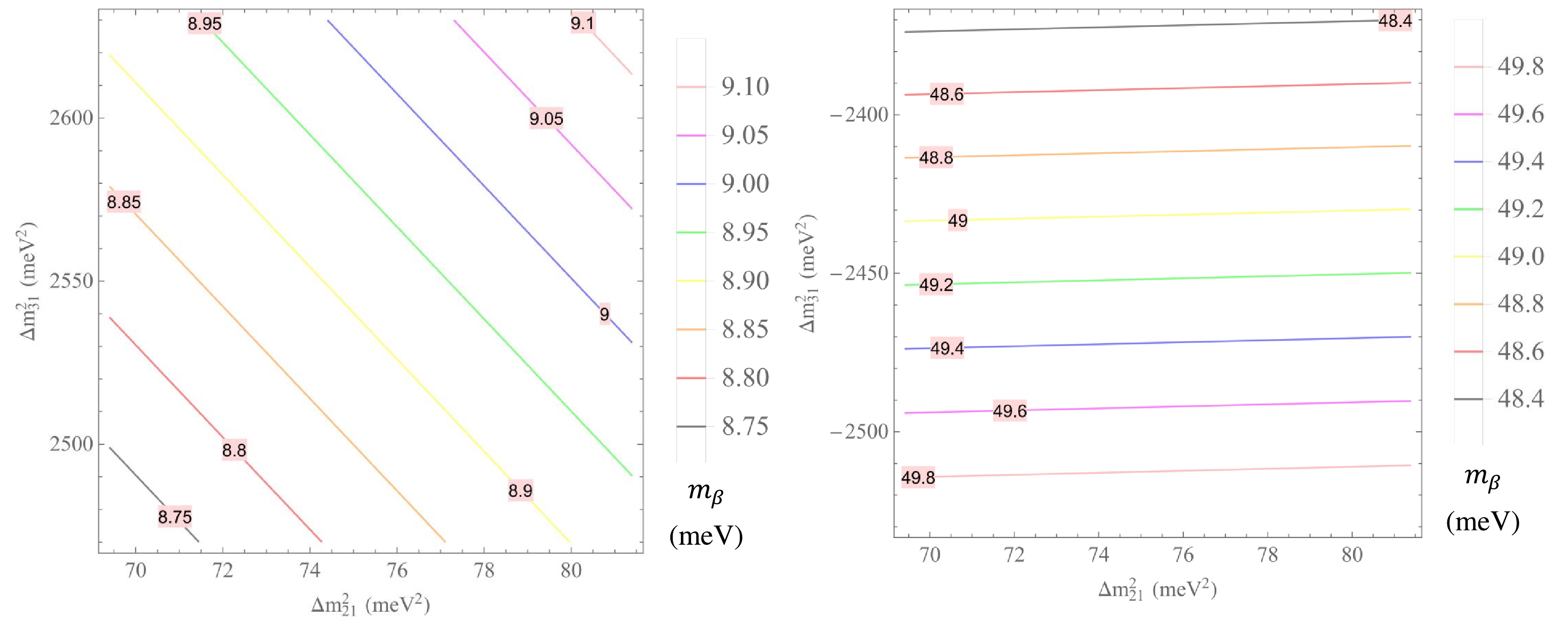
Figure 17. (color online)
$m_{\beta}$ (${\rm{meV}}$ ) versus$\Delta m^2_{21}$ and$\Delta m^2_{31}$ with$\Delta m^2_{21}\in (69.4, 81.4)\, {\rm{meV}}^2$ and$\Delta m^2_{31}\in (2.47, 2.63) 10^3\, {\rm{meV}}^2$ for NH (left panel) and$\Delta m^2_{31}\in (-2.53, -2.37) 10^3\, {\rm{meV}}^2$ for IH (right panel).Figures 10 and 15 imply that
$\begin{aligned}[b]& A \in \left\{ \begin{array}{*{20}{l}} {(3.700, 3.925) \, {\rm{meV}} }&{{\rm{for}}\; {\rm{NH}},} \\ {(48.00, 49.40)\, {\rm{meV}}}&{ {\rm{for}}\; {\rm{IH}}, }\end{array} \right. \\& B_1\in \left\{ \begin{array}{*{20}{l}} {(3.90, 4.25)\, {\rm{meV}} }&{{\rm{for}}\; {\rm{NH}}, }\\ {(-4.775,-4.60)\, {\rm{meV}} }&{{\rm{for}}\; {\rm{IH}}, }\end{array}\right.\end{aligned} $

(67) $\begin{aligned}[b]& B_2\in \left\{ \begin{array}{*{20}{l}} {(-7.15, -6.80)\, {\rm{meV}} }&{{\rm{for}}\; {\rm{NH}},} \\ {(-5.75, -5.575)\, {\rm{meV}} }&{{\rm{for}}\; {\rm{IH}}, }\end{array} \right. \\& C_{1}\in \left\{ \begin{array}{*{20}{l}} {(38.40, 39.60)\, {\rm{meV}} }&{{\rm{for}}\; {\rm{NH}},} \\ {(27.40, 28.20)\, {\rm{meV}} }&{ {\rm{for}}\; {\rm{IH}}. }\end{array} \right. \end{aligned}$

(68) $\begin{aligned}[b]& C_2\in \left\{ \begin{array}{*{20}{l}} {(16.00, 16.60)\, {\rm{meV}}}&{ {\rm{for}}\; {\rm{NH}},} \\ {(23.00, 23.70)\, {\rm{meV}}}&{ {\rm{for}}\; {\rm{IH}},} \end{array} \right. \\& C_{3}\in \left\{ \begin{array}{*{20}{l}} {(-19.00, -18.20)\, {\rm{meV}} }&{{\rm{for}}\; {\rm{NH}}, }\\ {(-24.70, -24.00)\, {\rm{meV}} }&{{\rm{for}}\; {\rm{IH}}. }\end{array} \right. \end{aligned}$

(69) Figures 16 and 17 show the predictive regions of the effective neutrino masses:
$\begin{aligned}[b]& \langle m_{ee}\rangle \in \left\{ \begin{array}{*{20}{l}} {(3.700, 3.925) \, {\rm{meV}}}&{ {\rm{for}}\; {\rm{NH}},} \\ {(48.00, 49.40)\, {\rm{meV}} }&{ {\rm{for}}\; {\rm{IH}}, }\end{array} \right. \\& m_\beta\in \left\{ \begin{array}{*{20}{l}} {(8.75, 9.10)\, {\rm{meV}}}&{ {\rm{for}}\; {\rm{NH}}, }\\ {(48.40, 49.80)\, {\rm{meV}} }&{{\rm{for}}\; {\rm{IH}},} \end{array} \right. \end{aligned}$

(70) which are values below the upper limits for
$ \langle m_{ee}\rangle $ from KamLAND-Zen [45]$ \langle m_{ee} \rangle <61 \div 165\, {\rm{meV}} $ , GERDA [46]$ \langle m_{ee} \rangle < 104\div 228\; {\rm{meV}} $ , and CUORE [47]$ \langle m_{ee} \rangle < 75 \div 350 {\rm{meV}} $ ; the constraints for$ m_{\beta} $ are expressed as$ 8.5 \;{\rm{meV}} < m_{\beta} < 1.1\; {\rm{eV}} $ for NH and$ 48 \; {\rm{meV}} < m_{\beta} < 1.1\; {\rm{eV}} $ for IH [1],$ m_{\beta} \in (8.90\div 12.60)\, {\rm{eV}} $ [48], and$ m_{\beta} < 0.8\, {\rm{eV}} $ [49]. -
We propose a gauge
$ B-L $ model with$ D_4\times Z_4\times Z_2 $ symmetry to explain the quark and lepton mass hierarchies and their mixing patterns with realistic CP phases via the type-I seesaw mechanism. Six quark mases, three quark mixing angles, and a CP phase in the quark sector take the central values whereas Yukawa couplings in the quark sector are diluted in a range of difference of three orders of magnitude by the perturbation theory at the first order. Concerning the neutrino sector, a small neutrino mass is achieved by the type-I seesaw mechanism. Both inverted and normal neutrino mass hierarchies are consistent with the experimental data. The predicted sum of neutrino masses is$ 58. 25\; {\rm{meV}} \leq $ $ \sum m_\nu \leq 60.25 $ meV for normal hierarchy and$ 98.50\; {\rm{meV}}\leq$ $ \sum m_\nu \leq 101.00 $ meV for inverted hierarchy; these results are consistent with all the recently reported limits. In addition, the Dirac CP phase is predicted to be$ 288.20\leq \delta (^\circ) \leq 330.00 $ within the 3σ range of experimental constraints. The effective neutrino masses are predicted to be$ 3.700\; {\rm{meV}} \leq \langle m_{ee}\rangle \leq 3.925 $ meV,$ 8.75\; {\rm{meV}} \leq m_{\beta} \leq 9.10\; {\rm{meV}} $ for normal hierarchy and$ 48.00\; {\rm{meV}} \leq \langle m_{ee}\rangle \leq 49.40 $ meV and$ 48.40\; {\rm{meV}} \leq m_{\beta} \leq 49.80\; {\rm{meV}} $ for inverted hierarchy. These values are also consistent with recently reported constraints. -
The explicit expressions of
$ a_{1u,d}, a_{2u,d}, a_{3u,d}, b_{u,d}, c_{1u, d} $ ,$ c_{2u,d} $ ,$ c_{3u} $ , and$ c_{4u,d} $ are$ \begin{aligned}[b] a_{1u} =\;& m_u, a_{2u} = \frac{m_c + m_t}{2}, a_{3u} =\frac{m_c - m_t}{2}, \\ a_{1d} = \;&m_d, a_{2d} = \frac{m_s+m_b}{2}, a_{3d} = \frac{m_s-m_b}{2}, \\ c_{1u} =\;& -c_{3u}+\frac{(m_d - m_s) (m_c - m_u) \big(1- {\rm{V}}^{{\rm{exp}}}_{11}\big)}{2 c^*_{1d}}, \\c_{2u}=\; &\frac{(m_{u}-m_{c}) (m_{d}-m_{s})}{c^*_{2d}+c^*_{4d}} \left[\frac{4 b^*_{d} b_{u}}{(m_{b}-m_{s}) (m_{c}-m_{t})}+\frac{c_{4u} (c^*_{2d}+c^*_{4d})}{(m_c-m_u) (m_d-m_s)}+{\rm{V}}^{{\rm{exp}}}_{22}-1\right], \\ c_{3u}=\;&\frac{m_{u}-m_{t}}{2} \left[\frac{({\rm{V}}^{{\rm{exp}}}_{11}-1) (m_{c}-m_{u}) (m_{d}-m_{s})}{2 c^*_{1d} (m_{t}-m_{u})}+\frac{c^*_{2d}-c^*_{4d}}{m_{b}-m_{d}}+{\rm{V}}^{{\rm{exp}}}_{13}\right], \\ 2c_{4u}=\;&\frac{4 b^*_{d} b_{u} (m_{c}-m_{u}) (m_{s}-m_{d})}{(c^*_{2d}+c^*_{4d}) (m_{b}-m_{s}) (m_{c}-m_{t})}-\frac{{\rm{V}}^{{\rm{exp}}}_{33} (m_{b}-m_{d}) (m_{t}-m_{u})}{c^*_{2d}-c^*_{4d}} \\ & +\frac{(m_{b}-m_{d}) (m_{t}-m_{u})}{c^*_{2d}-c^*_{4d}}+\frac{{\rm{V}}^{{\rm{exp}}}_{22} (m_{u}-m_{c}) (m_{d}-m_{s})}{c^*_{2d}+c^*_{4d}}+\frac{(m_{c}-m_{u}) (m_{d}-m_{s})}{c^*_{2d}+c^*_{4d}}, \\ b_u=\;&\frac{(m_{b}-m_{s}) (m_{c}-m_{t}) \big\{(c^*_{2d} + c^*_{4d}) \big[2 c^*_{1d} +(m_d - m_s) {\rm{V}}^{{\rm{exp}}}_{21}\big] +(m_d - m_s)^2 \big(1-{\rm{V}}^{{\rm{exp}}}_{22}\big)\big\}}{4 b^*_{d} (m_{d}-m_{s})^2}, \\ b^*_{d} =\;& \frac{(m_{b}-m_{d}) (m_{b}-m_{s}) \left\{(1-{\rm{V}}^{{\rm{exp}}}_{11}) (m_{d}-m_{s})^2+2 c^*_{1d} \big[c^*_{2d}+c^*_{4d}+(m_{s}-m_{d}) {\rm{V}}^{{\rm{exp}}}_{12}\big]\right\}}{4 c^*_{1d} (m_{d}-m_{s}) \big[c^*_{4d}-c^*_{2d}+{\rm{V}}^{{\rm{exp}}}_{13} (m_{d}-m_{b})\big]}, \\ c^*_{2d}=\;&\frac{c^*_{4d} {\rm{V}}^{{\rm{exp}}}_{31}+\big({\rm{V}}^{{\rm{exp}}}_{33}-1\big) (m_{d}-m_{b})}{{\rm{V}}^{{\rm{exp}}}_{31}}, c^*_{4d}=\big\{2 c^*_{1d} (m_{d}-m_{s})\big[m_{b} {\bf{F}}_q+m_{d} {\bf{G}}_q+m_{s} {\bf{H}}_q\big] \\ &+(m_{d}-m_{s})^3 {\bf{T}}_q +4 c^{*2}_{1d} ({\rm{V}}^{{\rm{exp}}}_{33}-1) \big[{\rm{V}}^{{\rm{exp}}}_{13} (m_{b}-m_{d})+{\rm{V}}^{{\rm{exp}}}_{12} (m_{d}-m_{s})\big]\big\}/\big\{4 c^*_{1d} {\rm{V}}^{{\rm{exp}}}_{31} \big[2 c^*_{1d} {\rm{V}}^{{\rm{exp}}}_{13} \\ &+(m_{d}-m_{s}) ({\rm{V}}^{{\rm{exp}}}_{13} {\rm{V}}^{{\rm{exp}}}_{21}-{\rm{V}}^{{\rm{exp}}}_{23})\big]\big\}, \\ c^*_{1d}=\;&\frac{(m_{s}-m_{d})\sqrt{{\bf{K}}_{1q}}+(m_{s}-m_{d}) {\bf{P}}_{1q}+{\rm{V}}^{{\rm{exp}}}_{13} (m_{d}-m_{s}) \big[({\rm{V}}^{{\rm{exp}}}_{22}-1) {\rm{V}}^{{\rm{exp}}}_{31}-{\rm{V}}^{{\rm{exp}}}_{21} {\rm{V}}^{{\rm{exp}}}_{32}\big]}{4 {\rm{V}}^{{\rm{exp}}}_{13} {\rm{V}}^{{\rm{exp}}}_{32}-4 {\rm{V}}^{{\rm{exp}}}_{12} {\rm{V}}^{{\rm{exp}}}_{33}}, \end{aligned}\tag{B1} $

where
$ \begin{aligned}[b] {\bf{F}}_q = &({\rm{V}}^{{\rm{exp}}}_{33}-1) ({\rm{V}}^{{\rm{exp}}}_{13} {\rm{V}}^{{\rm{exp}}}_{21}-{\rm{V}}^{{\rm{exp}}}_{23}), {\bf{G}}_q={\rm{V}}^{{\rm{exp}}}_{33} \big[{\rm{V}}^{{\rm{exp}}}_{11}+\big({\rm{V}}^{{\rm{exp}}}_{12}-{\rm{V}}^{{\rm{exp}}}_{13}\big) {\rm{V}}^{{\rm{exp}}}_{21}-{\rm{V}}^{{\rm{exp}}}_{22}+{\rm{V}}^{{\rm{exp}}}_{23}\big] \\ & +{\rm{V}}^{{\rm{exp}}}_{22}-{\rm{V}}^{{\rm{exp}}}_{23}-{\rm{V}}^{{\rm{exp}}}_{11}-{\rm{V}}^{{\rm{exp}}}_{12} ({\rm{V}}^{{\rm{exp}}}_{21}+{\rm{V}}^{{\rm{exp}}}_{23} {\rm{V}}^{{\rm{exp}}}_{31})+{\rm{V}}^{{\rm{exp}}}_{13} [{\rm{V}}^{{\rm{exp}}}_{21}+({\rm{V}}^{{\rm{exp}}}_{22}-1) {\rm{V}}^{{\rm{exp}}}_{31}], \\ {\bf{H}}_q=\;&\big({\rm{V}}^{{\rm{exp}}}_{11}+{\rm{V}}^{{\rm{exp}}}_{22}\big) (1-{\rm{V}}^{{\rm{exp}}}_{33})+{\rm{V}}^{{\rm{exp}}}_{12} ({\rm{V}}^{{\rm{exp}}}_{21}-{\rm{V}}^{{\rm{exp}}}_{21} {\rm{V}}^{{\rm{exp}}}_{33}+{\rm{V}}^{{\rm{exp}}}_{23} {\rm{V}}^{{\rm{exp}}}_{31})+{\rm{V}}^{{\rm{exp}}}_{13} {\rm{V}}^{{\rm{exp}}}_{31}(1-{\rm{V}}^{{\rm{exp}}}_{22}), \\ {\bf{T}}_q=\;&(1-{\rm{V}}^{{\rm{exp}}}_{11})\big[{\rm{V}}^{{\rm{exp}}}_{21}(1-{\rm{V}}^{{\rm{exp}}}_{33})+{\rm{V}}^{{\rm{exp}}}_{23} {\rm{V}}^{{\rm{exp}}}_{31}\big], \\ {\bf{K}}_{1q}=\;&\big[\big({\rm{V}}^{{\rm{exp}}}_{11}+{\rm{V}}^{{\rm{exp}}}_{12} {\rm{V}}^{{\rm{exp}}}_{21}\big) {\rm{V}}^{{\rm{exp}}}_{33}-{\rm{V}}^{{\rm{exp}}}_{12} {\rm{V}}^{{\rm{exp}}}_{23} {\rm{V}}^{{\rm{exp}}}_{31}-{\rm{V}}^{{\rm{exp}}}_{13} {\rm{V}}^{{\rm{exp}}}_{21} {\rm{V}}^{{\rm{exp}}}_{32}+\big({\rm{V}}^{{\rm{exp}}}_{22}-1\big) {\rm{V}}^{{\rm{exp}}}_{13} {\rm{V}}^{{\rm{exp}}}_{31} \\ & -{\rm{V}}^{{\rm{exp}}}_{22} {\rm{V}}^{{\rm{exp}}}_{33}+{\rm{V}}^{{\rm{exp}}}_{23} {\rm{V}}^{{\rm{exp}}}_{32}\big]^2+4 \big({\rm{V}}^{{\rm{exp}}}_{11}-1\big) \big({\rm{V}}^{{\rm{exp}}}_{13} {\rm{V}}^{{\rm{exp}}}_{32}-{\rm{V}}^{{\rm{exp}}}_{12} {\rm{V}}^{{\rm{exp}}}_{33}\big) \big({\rm{V}}^{{\rm{exp}}}_{21} {\rm{V}}^{{\rm{exp}}}_{33}-{\rm{V}}^{{\rm{exp}}}_{23} {\rm{V}}^{{\rm{exp}}}_{31}\big), \\ {\bf{P}}_{1q}=\;&({\rm{V}}^{{\rm{exp}}}_{22}-{\rm{V}}^{{\rm{exp}}}_{11} -{\rm{V}}^{{\rm{exp}}}_{12} {\rm{V}}^{{\rm{exp}}}_{21}) {\rm{V}}^{{\rm{exp}}}_{33} +({\rm{V}}^{{\rm{exp}}}_{12} {\rm{V}}^{{\rm{exp}}}_{31} - {\rm{V}}^{{\rm{exp}}}_{32}){\rm{V}}^{{\rm{exp}}}_{23}. \end{aligned}\tag{B2} $

-
The explicit expressions of
$ k_{1,2}, n_{1,2} $ and$ t_{1,2} $ are$ k_1=\frac{c_D - d_D}{a_D + b_D},\quad k_2=\frac{a_D - b_D}{c_D + d_D},\tag{C1} $

$ \begin{aligned}[b] n_1 =\;&\Big\{a_D^2(b_D-a_D)(b_R + c_R) - b_D \big[(c_R-b_R)(b_D^2 + 2 c_D d_D) + (c_D^2 + d_D^2)c_R\big] \\ & -a_D \big[b_D^2 (b_R - c_R) + 2 c_D d_D (b_R + c_R) + (c_D^2 + d_D^2)c_R\big] + (a_D -b_D) \sqrt{\Delta}\Big\} \\ & \ /\Big\{(c_D - d_D) \big\{ b_D^2 (c_R-b_R) + a_D^2 (b_R + c_R) + \big[(c_D + d_D)^2-2 a_D b_D\big]c_R\big\}\Big\},\end{aligned}\tag{C2} $

$ \begin{aligned}[b] n_2 =\;&\Big\{(c_D + d_D) \big\{\big[(a_D+b_D)^2+(c_D-d_D)^2\big] c_R^2 + (a_D^2-b_D^2) c_R b_R+ 2 (c_D d_D -a_D b_D) b_R^2 \\ & - b_R \sqrt{\Delta}\big\}\Big\}/\Big\{(c_D - d_D) \big[b_D^2 b_R (c_R-b_R) + a_D^2 b_R (b_R + c_R) + b_R c_R (c_D^2 + d_D^2) - c_R \sqrt{\Delta}\big]\Big\}, \end{aligned}\tag{C3} $

$ \begin{aligned}[b] t_1 =\;&\Big\{a_D^2 (b_D-a_D) (b_R + c_R) + b_D \big[(b_D^2 + 2 c_D d_D)(b_R - c_R) - (c_D^2+ d_D^2)c_R \big] \\ & - a_D \big[b_D^2 (b_R - c_R) + c_D^2 c_R + 2 c_D d_D (b_R + c_R) + c_R d_D^2\big] + (b_D -a_D) \sqrt{\Delta}\Big\} \\ & \ /\Big\{(c_D - d_D) \big[b_D^2 (c_R-b_R) -2 a_D b_D c_R+ a_D^2 (b_R + c_R) + c_R (c_D + d_D)^2\big]\Big\} ,\end{aligned}\tag{C4} $

$\begin{aligned}[b] t_2 =\;&\Big\{(c_D + d_D) \big\{\big[(a_D+ b_D)^2+(c_D-d_D)^2\big]c_R^2 + (a_D^2 -b_D^2) c_R b_R +2 (c_D d_D - a_D b_D) b_R^2 \\ & +b_R \sqrt{\Delta}\big]\big\}\Big\}/\Big\{(c_D - d_D) \big[b_D^2 b_R (c_R-b_R) + a_D^2 b_R (b_R + c_R) + b_R c_R (c_D^2 + d_D^2) + c_R\sqrt{\Delta}\big]\Big\}, \end{aligned}\tag{C5} $

where
$\begin{aligned}[b] \Delta =\;&a_D^4 (b_R + c_R)^2 + \big[b_D^2 b_R - (b_D^2 + c_D^2) c_R\big]^2 + 8 a_D b_D c_D d_D (c_R^2-b_R^2)+ c_R^2 d_D^4 \\ & + 2 \big[2 b_R^2 c_D^2 - b_D^2 b_R c_R + (b_D ^2- c_D^2) c_R^2\big] d_D^2 + 2 a_D^2 (b_R + c_R) \big[b_D^2 (b_R - c_R) + c_R (c_D^2 + d_D^2)\big].\end{aligned}\tag{C6} $

B − L model with D4 × Z4 × Z2 symmetry for fermion mass hierarchies and mixings
- Received Date: 2023-11-16
- Available Online: 2024-06-15
Abstract: We constructed a gauge





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: