-
Given that it contains the key information of EWSB, precision measurement of W boson mass can provide a stringent test of the SM and constrain various new physics models. Recently, CDF II collaborators at the Fermilab Tevatron collider [1] utilized data corresponding to an integrated luminosity of
$8.8~\rm fb^{-1}$ , acquired in proton-antiproton collisions at a 1.96 TeV center-of-mass energy, to obtain the new value of W boson mass as$ \begin{aligned}[b] M_W=&80,433.5 \pm 6.4({\rm stat}) \pm 6.9 ({\rm syst})\\=&80,433.5\pm 9.4 {\rm MeV}/c^2\; , \end{aligned} $

(1) This finding presents a considerable discrepancy with the predictions of the Standard Model (SM), which suggests that [2]
$ \begin{array}{*{20}{l}} M_W=80,357\pm 4({\rm inputs})\pm 4 ({\rm theory}) {\rm MeV}/c^2\; , \end{array} $

(2) $ \begin{array}{*{20}{l}} \Delta M_W= 70 \pm 11 {\rm MeV}/c^2. \end{array} $

(3) If these deviations are corroborated by further experiments, they would strongly suggest the presence of new physics beyond the SM [5, 6]. Therefore, it is intriguing to examine the additional constraints that the recent CDF II data can place on new physics models, particularly in the context of the 125-GeV Higgs.
The significant increase in the W mass compared to the SM prediction could suggest the presence of new physics beyond the SM. Various efforts within new physics frameworks have been undertaken, where the anomaly is commonly attributed to deviations in oblique parameters, especially
$ \Delta T $ [7, 8].In contrast, with the current world-averaged result reported by [8], the precision measurement of
$ a_\mu=(g-2)/2 $ has been performed by the E821 experiment at Brookhaven National Laboratory [10],$ \begin{array}{*{20}{l}} a_\mu^{\rm exp}= 116592091(\pm54)(\pm33)\times 10^{-11}. \end{array} $

(4) Although the SM prediction from the Particle Data Group leads to [9]
$ \begin{array}{*{20}{l}} a_\mu^{\rm SM}= 116591803(\pm1)(\pm42)(\pm26)\times 10^{-11}, \end{array} $

(5) the difference between theory and experiment shows a discrepancy of
$ 4.2\sigma $ , hinting at tantalizing new physics beyond the SM.In models beyond the SM, there may exist a new confining unbroken non-abelian gauge interaction [11−17], similar to quantum chromodynamics (QCD) in the realm of strong interactions. In general, it can be assumed that the new color group confinement scale
$ \Lambda_X $ is smaller than the QCD scale$\Lambda_{\rm QCD}$ such that the new color degree of freedom bears the name infracolor (IC). We term these infracolor gluon fields as igluons and fermions as quirks2 . It is termed as the quirk model, which is also regarded as a certain limit of QCD with some heavy quarks referred to as quirks3 . Furthermore, when QCD becomes strong, scale$ \Lambda_X $ becomes much smaller than the quirk masses [13, 14] with the light quarks removed from the particle list. In contrast to the real world scenario with light quarks, where spontaneous chiral symmetry breaking is a concern, this hypothetical version of QCD could exhibit significantly different phenomenological characteristics.Following the discovery of the SM Higgs boson, the Large Hadron Collider (LHC) has conducted extensive searches for various potential new physics phenomena beyond the SM. Solutions addressing the SM's gauge hierarchy problem, such as supersymmetry and composite Higgs models, typically anticipate a colored top partner with a mass around the TeV scale. However, these theories have faced challenges due to the absence of confirmatory results in LHC searches to date. Theories of neutral naturalness [18] aim to address the gauge hierarchy problem without introducing colored states and thereby relieve the tension with the LHC searches. This class of models includes folded supersymmetry [19, 20], quirky little Higgs [21], twin Higgs [22−24], and minimal neutral naturalness models [25]. In these models, some new
$S U(N)$ gauge symmetries are introduced in addition to the SM gauge group. Within the framework of supersymmetry, quirk particles, new vector-like fermions, and their scalar counterparts are part of the same supermultiplet. Therefore, we will explore the low-energy effects of quirks in this model.The quirk particle is charged under both the SM electroweak gauge group and new confining
$ G_X $ gauge group, and its mass is much larger than the confinement scale ($ \Lambda_X $ ) of the$ G_X $ . At colliders, the quirk can only be produced in pairs due to the conserved$ G_X $ symmetry. The interaction between two quirks induced by the$ G_X $ gauge bosons, the infracolor force$ F_s $ , will lead to non-conventional signals in the detector. The manifestation of the quirk signal is strongly dependent on$ \Lambda_X $ given that$ F_s \propto \Lambda_X^2 $ [15, 26].The quirk particle, due to its substantial electroweak couplings with gauge bosons and interactions with leptons, may have a significant impact. Hence, we consider the quirk contributions to the W mass increment and the
$ g-2 $ anomaly in this study. The rest of this paper is organized as follows. In Sec. II, we introduce the supersymmetric quirk particles and relevant couplings. In Sec. III, we discuss the constraints of the CDF II W boson mass data on the parameters within the quirk models. In Sec. IV, the quirk contribution to the$ g-2 $ anomaly will be calculated. Sec. V lists our conclusions. -
The dynamics of infracolor interactions can enable
$ Q\bar Q $ bound states to remain stable over distances on the order of centimeters, thus preventing their annihilation. In some cases, production of the "squirk-antisquirk" pair at the LHC can quickly lose their excitation energy via bremsstrahlung and can relax to the ground state of the scalar quirkonium [19, 20, 27].To maintain perturbative gauge coupling unification, the new gauge non-Abelian group should be
$G_X=S U(2)_X$ or$S O(3)_X$ or$S U(3)_X$ , and the new vector-like fermions and their scalar partners in the same supermultiplets under the framework of supersymmetry can all be quirk particles [27]. With the new color group$ G_X $ , the new fields are taken to transform in$ N=2 $ ,$ 3 $ , or$ 3 $ dimensional representations, respectively, for these three cases. Thus, the new quirk chiral supermultiplets containing fermion multiplet$ D,\; L,\; S $ and their partners$ \tilde D,\; \tilde L,\; \tilde S $ transform under$G_X \times S U(3)_c \times S U(2)_L \times U(1)_Y$ [27].When
$G_X=S U(2)_X$ ,$ D, \overline D= ({\bf 2}, {\bf 3}, {\bf 1}, -\frac{1}{3}) + ({\bf 2}, {\bf \overline 3}, {\bf 1}, \frac{1}{3}), $

(6) $ \overline L, L = ({\bf 2}, {\bf 1}, {\bf 2}, \frac{1}{2}) + ({\bf 2}, {\bf 1}, {\bf 2}, -\frac{1}{2}), $

(7) $ S, \overline S = ({\bf 2}, {\bf 1}, {\bf 1}, 0) \times 2 n_S, $

(8) and
$G_X=S U(3)_X$ ,$ D, \overline D = ({\bf 3}, {\bf 3}, {\bf 1}, -\frac{1}{3}) + ({\bf \overline 3}, {\bf \overline 3}, {\bf 1}, \frac{1}{3}), $

(9) $ \overline L, L = ({\bf 3}, {\bf 1}, {\bf 2}, \frac{1}{2}) + ({\bf \overline 3}, {\bf 1}, {\bf 2}, -\frac{1}{2}), $

(10) $ S, \overline S =[({\bf 3}, {\bf 1}, {\bf 1}, 0) + ({\bf \overline 3}, {\bf 1}, {\bf 1}, 0)] \times n_S, $

(11) and
$G_X=S O(3)_X$ ,$ D, \overline D = ({\bf 3}, {\bf 3}, {\bf 1}, -\frac{1}{3}) + ({\bf 3}, {\bf \overline 3}, {\bf 1}, \frac{1}{3}), $

(12) $ \overline L, L = ({\bf 3}, {\bf 1}, {\bf 2}, \frac{1}{2}) + ({\bf 3}, {\bf 1}, {\bf 2}, -\frac{1}{2}), $

(13) $ S \equiv \overline S = ({\bf 3}, {\bf 1}, {\bf 1}, 0) \times n_S. $

(14) $ D,\; L,\; S $ and their partners$ \tilde D,\; \tilde L,\; \tilde S $ can be assumed to obtain the masses, which are similar to the superpotential term of the minimum SUSY models (MSSM),$ \mu H_uH_d $ , where$ H_u $ and$ H_d $ denote vector-like Higgs chiral supermultiplets in SUSY models, with VEVs$ v_u, v_d $ ratio$ \tan\beta = v_u/v_d $ and$ v = \sqrt{v_u^2 + v_d^2} \approx 175 $ GeV. If it is assumed that the mass terms$ H_uH_d $ and$ D\bar D $ and$ L\bar L $ and$ S\bar S $ are forbidden at tree-level, the non-renormalizable superpotential terms may appear as [27−29]$ W = \frac{1}{M_P^2} X \overline X \left ( \lambda_\mu H_u H_d + \lambda_D D \overline D + \lambda_L L \overline L + \lambda_{S_i} S_i \overline S_i \right ), $

(15) where
$ i=1,\ldots, n_S $ with$ n_S $ SM group singlets in the same representations of$ G_X $ , and the reduced Planck mass$ M_P = 2.4 \times 10^{18} $ GeV. Fields$ X, \overline X $ will obtain VEVs approximately in the order of$ 10^{11} $ GeV, which are at intermediate-scale. These VEVs are natural because terms such as a superpotential W and soft terms$ -{\cal L}_{\rm soft} $ [29] exist:$ W = \frac{\lambda_X}{4 M_P^2} X^3 \overline X, $

(16) $ -{\cal L}_{\rm soft} = m_X^2 |X|^2 + m_{\overline X}^2 |\overline X|^2 + \left (\frac{a_X}{4 M_P^2} X^3 \overline X + {\rm c.c.} \right ). $

(17) Given that there may exist a minimum value of the potential, the vector-like mass terms in the low-energy effective superpotential can be expressed as [27]
$ \begin{array}{*{20}{l}} W = \mu H_u H_d + \mu_D D \overline D + \mu_L L \overline L + \mu_{S_i} S_i \overline S_i . \end{array} $

(18) where
$ \mu, \mu_D, \mu_L, \mu_S $ can be in the order of 100 GeV to 1 TeV only if the corresponding couplings$ \lambda_\mu, \lambda_D, \lambda_L, \lambda_S $ , which are respectively absorbed into$ \mu, \mu_D, \mu_L, \mu_S $ factors, are not too small.For
$ n_S > 0 $ , the new chiral supermultiplets can have Yukawa couplings in addition to their mass terms in Eq. (18):$ \begin{array}{*{20}{l}} W = k_i H_u L \overline S_i + k'_i H_d \overline L S_i. \end{array} $

(19) Furthermore, if there exists a superpotential term such as
$ \begin{array}{*{20}{l}} W = \lambda_\ell \overline {\tilde S} \overline L \ell \end{array} $

(20) with
$ \ell $ being an MSSM$S U(2)_L$ doublet lepton, we can that expect it can influence the muon$ g-2 $ discrepancy between the experiments and theoretical calculation. -
The corrections to various electroweak precision observables can be obtained from the corresponding oblique parameters. The new physics contributions to the W-boson mass increment can embody in the Peskin's
$ S,T,U $ oblique parameters [7, 8, 30−32] as follows [7, 8, 33−35]:$ \Delta m_W= \frac{ \alpha m_W}{2(c_W^2-s_W^2)}\left(- \frac{1}{2}S+c_W^2 T+ \frac{c_W^2-s_W^2}{4s_W^2} U\right)\; , $

(21) with
$ \begin{aligned}[b] \alpha S & =4 s_w^2 c_w^2\left[\Pi_{{ZZ}}^{\prime}(0)-\frac{c_w^2-s_w^2}{s_w c_w} \Pi_{{Z} \gamma}^{\prime}(0)-\Pi_{\gamma \gamma}^{\prime}(0)\right], \\ \alpha T & =\frac{\Pi_{{WW}}(0)}{m_w^2}-\frac{\Pi_{{ZZ}}(0)}{m_Z^2}, \\ \alpha U & =4 s_w^2\left[\Pi_{{WW}}^{\prime}(0)-c_w^2 \Pi_{{ZZ}}^{\prime}(0)-2 s_w c_w \Pi_{{Z} \gamma}^{\prime}(0)-s_w^2 \Pi_{\gamma \gamma}^{\prime}(0)\right], \end{aligned} $

(22) and
$ \alpha^{-1}(0)=137.035999084\;,s_W^2=0.23126 $ .The oblique parameters
$ (S,\; T,\; U) $ [7, 8], which represent radiative corrections to the two-point functions of gauge bosons, can describe most effects on precision measurements. As we know, the total size of the new physics sector can be measured by the oblique parameter S, while the weakisospin breaking can be measured by T parameter. The new results of$ S,\; T,\; U $ can be expressed as [36]$ \begin{array}{*{20}{l}} S = 0.14\pm 0.08,\; \; T = 0.26 \pm 0.06, \; \; U = 0. \end{array} $

(23) The most important electroweak precision constraints on quirk models comes from the electroweak oblique parameters S and T [7, 8, 30−32]. Hence, we will proceed to study the connection between the electroweak precision data with the W mass. The model can produce main corrections to the masses of gauge bosons via the self-energy diagrams exchanging the vector-like extra fermions.
With the Yukawa couplings
$ k,\; k' $ , the new contributions to Peskin-Takeuchi$ S,T $ observables from the new fermions can be expressed as [27]$ \begin{aligned}[b] \Delta T =& \frac{N v^4}{480 \pi s_W^2 M_W^2 M_F^2} [13 (\hat k^4 + \hat k^{\prime 4}) + 2 (\hat k^3 \hat k^{\prime} + \hat k \hat k^{\prime 3})\\& + 18 \hat k^2 \hat k^{\prime 2} ], \end{aligned} $

(24) $ \Delta S = \frac{N v^2}{30 \pi M_F^2} [4 \hat k^2 + 4 \hat k^{\prime 2} -7 \hat k \hat k^{\prime} ], $

(25) where
$ \hat k = k \sin\beta $ and$ \hat k' = k' \cos\beta $ and$ v \approx 175 $ GeV,In our analysis, we will perform a global fit to the predictions of
$ S,\; T $ parameters in profiled$ 1\sigma $ favoured regions. We scan$ m_F $ ,$\tan\beta$ , k, and$ k' $ parameters in the following ranges:$ \begin{align} 100 {\rm \; GeV} \leq m_F \leq 1100 {\rm \; GeV},\; 1\leq \tan\beta \leq 50, \; 0.01 < k,k' < 1. \end{align} $

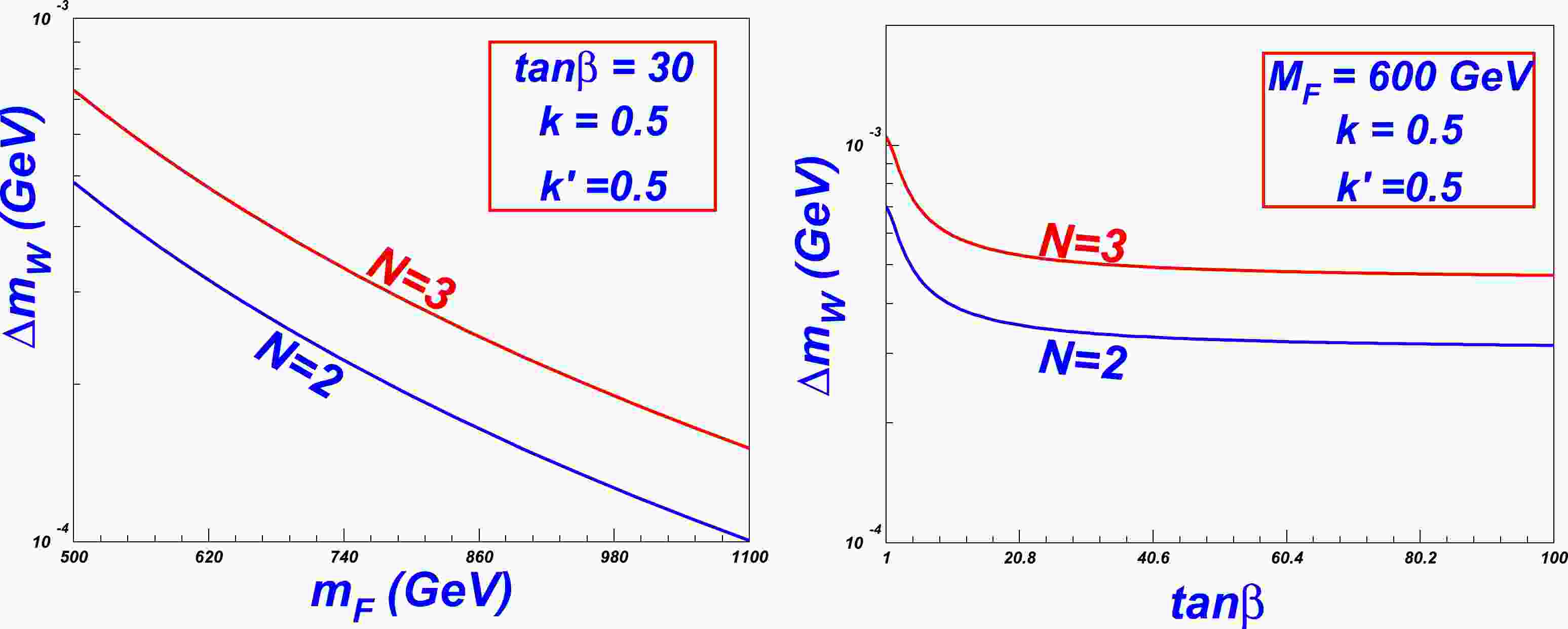
(26) In Fig. 1 and Fig. 2, we show that the W mass increment varies with ratio
$ \tan\beta $ , Fermion masses$ m_F $ , and$ k,\; k' $ , which are in the range of (1−50), ($ 100-1100 $ GeV), and$ (0.01-1 $ ), respectively, with the fixed parameters shown in the figures. Based on the two figures, we can observe that the W mass increment decreases monotonously as$m_F,\; \tan\beta$ increase, while it increases monotonously as$ N,\; k,\; k' $ increase. The dependence of N and$ m_F $ of the W mass increment is obvious.
Figure 2. (color online) Same as Fig. 1, but with varying k and
$ k' $ .However, when
$\tan\beta$ increases, the influence will consistently decrease. This is because, from Eq. (24) and (25), the ratio of$\tan\beta$ appears in$ \Delta S $ and$ \Delta T $ in the form of$ \sin\beta $ and$ \cos\beta $ . Specifically, the former approaches the maximum value of$ 1 $ , and latter approaches the minimum value of 0 as the value of$ \tan\beta $ increases.We can also observe that the effect from the couplings k and
$ k' $ is not equivalent in Fig. 2 and the contribution range from k can span from negative to positive$ 10^{-2} $ GeV, while that from$ k' $ can be within$ 10^{-3} $ GeV. The insensitivity of$ k' $ is due to oblique parameters in Eq. (24) and (25). Furthermore,$ k' $ is always multiplied by$ \cos\beta $ , which is too small when$ \tan\beta=30 $ , as shown inFig. 1 and Fig. 2. Hence, it is necessary to consider the contributions in the whole parameter space.Additionally, in most parameter space, the W mass increment is in the experimental limit. Hence, we can try to constrain the parameters according to the bound of the W mass discrepancy between the experiments and SM prediction in Eq. (3).
The aforementioned constraints on the W increment mass from parameters
$N,\; m_F,\; \tan\beta,\; k,\; k'$ are obtained independently. In Fig. 3, we consider the joint effect by scanning the allowed points, which potentially exist for the mass increment in the$ 1\sigma $ range of the experimental bound. We set$ 10000 $ scanned random points, and$ 6149 $ points meet the constraints in the scanning. It should be noted that we fixed$ N=2 $ in Fig. 3 to ensure that it does not exert much influence on the results.
Figure 3. (color online) Allowed points in the parameter space to explain the CDF II results of the W-mass within
$ 1\sigma $ range.Based on the first diagram in Fig. 3, we can observe that there are almost no constraints on
$ m_F $ , and it can be any value selected in the scanning. This is due to the fact that in our parameter spaces, within all the potential values of the fermion mass$ m_F $ , it can be observed from Eqs. (24) and (25) that the coefficient of$ \Delta T $ is much larger than that of$ \Delta S $ . Furthermore, the contributions of the following terms of the twos are of the same size. Hence, the contribution of$ \Delta T $ is primary. On the other hand, the coefficient is much smaller than the subsequent terms. Then, from Eq. (21), we can observe that the coefficient of$ \Delta T $ is larger than that of$ \Delta S $ . This ensures that they together contribute positively to$ \Delta m_W $ and the coefficients are smaller than the subsequent terms, while$ m_F $ is a part of the coefficients. Therefore, as long as the result is positive,$ m_F $ hardly affects$ \Delta m_W $ . This implies that$ m_F $ is not restrained by the CDF data.Based on the first diagram in Fig. 3, we can also observe that the contributions from k and
$ k' $ are not the same as discussed above and k is bound as$ k>0.4 $ , while the range of$ k' $ is the whole space. The insensitivity of$ k' $ is due to the fact that$ k' $ is always multiplied by the factor$\cos\beta$ , which is small for large values of$ \tan\beta $ which start at$ 1 $ .The third diagram of Fig. 2 shows that the constraints on
$ \tan\beta $ are also quite weak, which can also be observed in the right diagram of Fig. 1. Given k and$ \sin\beta $ ,$ k' $ and$ \cos\beta $ appear together, and the relation$ \sin^2\beta+ \cos^2\beta=1 $ will finally decrease the contribution as$ \tan\beta $ increases.Thus, we can conclude that in most of the parameter space, the parameters in supersymmetric quirk models can account for the CDF data of the W mass increment, and only the constraints on k is evident,
$ k\gtrsim 0.4 $ . -
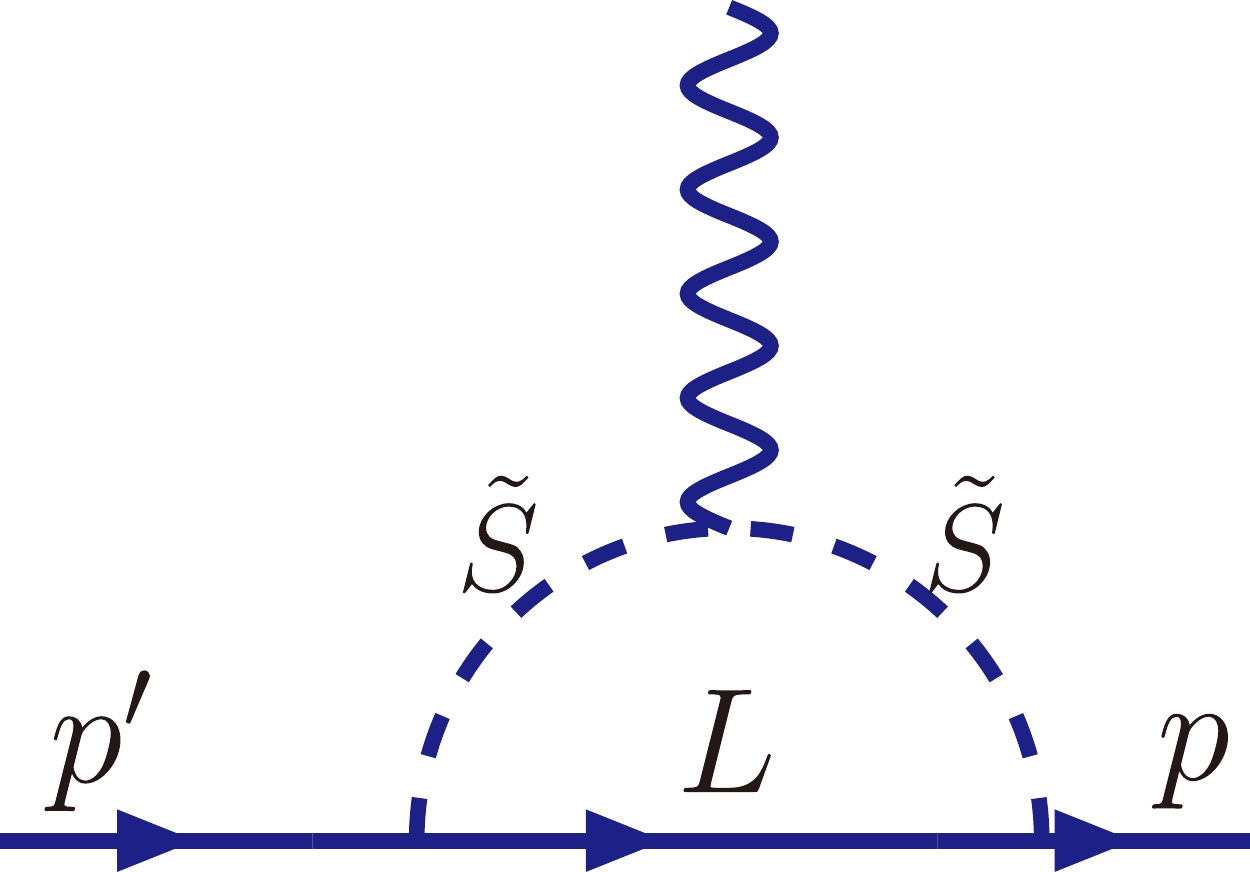
In quirk models, the muon
$ g-2 $ contributions are mainly obtained via the one-loop diagrams induced by the couplings shown in Eq. (20) as shown in Fig. 4. It should be noted that two-loop Barr-Zee diagrams disappear because there is no mixing between SM gauge bosons of the new quirk particles [27] and$ m_\mu^2/m_S^2 $ suppression of the diagram containing such two couplings [37].The one-loop contribution can be expressed as [38−41]
$ \Delta a_\mu^{qm}({\rm 1-loop})_H^{(b)} = \lambda_\ell^2 \frac{m_\mu^2}{16\pi^2 } \int_0^1 {\rm d} x \frac{x^3-x^2}{m_S^2 x+ m_L^2(1-x)}, $

(27) where
$ \lambda_\ell^2 $ denotes the coupling shown in Eq. (20), where the one-loop moment magnetic can be realized as shown in Fig. 4.Given that
$ \tilde S $ (L) is the scalar (fermion) component of the supermultiplet, its mass should be in the same level as that of the fermion F; therefore, we consider it to vary also in the range of$ 100-1100 $ GeV. We scan coupling$ \lambda_\ell^2 $ from$ 0 $ to$ 1 $ .Figure 5 indicates that the contributions from the scalar and fermion within the supermultiplet at the one-loop level are negative, and their absolute values are relatively small, approximately
$ \sim 10^{-10} $ , which can not possibly explain the the discrepancy between the experiments and the theoretical prediction. The situation is not surprising, since it has been pointed out that the contribution may be large only if the scalar masses are very small, such as several GeV [42, 43]. However, our choice for the new particle masses is larger than$ 100 $ GeV.
Figure 5. (color online) One-loop muon anomalous magnetic moment varying with
$ m_S $ for$ \lambda_\ell^2=1 $ and$ m_L= $ 100, 400, 1100 GeV, respectively. The green shadow area is the discrepancy between the SM and measurement for the anomalous magnetic moment$ \Delta a_\mu $ .Hence, at the one-loop level, it is difficult to fill the gap between the experiments and theoretical prediction in the supersymmetric quirk models. Therefore, with the missing two-loop Barr-Zee diagram, we can conclude that the supersymmetric quirk models cannot account for the muon
$ g-2 $ anomaly. -
In this study, we first show that the W mass increment varies with the parameters
$ \tan\beta $ ,$ m_F $ , and$ k,\; k' $ with respect to different new color group representations N. Furthermore, we determine that the dependence on parameters of the W mass increment is obvious. Then, we scan the allowed points that can potentially exist for the mass increment in the$ 1\sigma $ range of the experimental bound and determine that there are almost no constraints on$ m_F $ . Hence, we determine that the contributions from k and$ k' $ are not the same, with$ k>0.4 $ , while the range of$ k' $ is the whole space. Moreover, the constraints on$ \tan\beta $ are quite weak. This implies that, in most of the parameter space, supersymmetric quirk models can account for the CDF data of the W mass increment, and only the constraints on k are obvious,$ k\gtrsim 0.4 $ .Additionally, we calculate the contribution from the vector-like fermions and scalars in the supermultiplet to the muon
$ g-2 $ anomaly at the one-loop level. We determine that it is difficult to account for the gap between the experiments and theoretical prediction in the supersymmetric quirk models.Thus, we conclude that, in the parameter space of supersymmetric quirk models, the W mass increment of the CDF data can be accounted for. However, the contribution from the vector-like fermions and scalars in the supermultiplet to the muon
$ g-2 $ anomaly at the one-loop level is not sufficient to remedy the discrepancy between experiment and theory.
Influence of low-energy supersymmetric vector-like quirk particles on W mass increment and muon g–2 anomaly
- Received Date: 2023-11-22
- Available Online: 2024-03-15
Abstract: In the low energy realization of the quirk assisted Standard Model, the couplings between the exotic particles "quirks" and gauge bosons may contribute to the W mass and muon





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: