-
Over the past few decades, incresingly more new hadrons have been reported in experiments, which can not be well explained in the frame of the conventional quark model [1]. There are a number of explanations for such exotic hadrons, which include the molecular state picture, compact multiquark picture, and kinetic mechanisms. With the experimental observations of increasigly more exotic states close to thresholds of two hadrons, the molecular state picture is widely applied to understand the exotic states.
The dibaryons are important exotic states, which attract significant attention from hadron physics community since about sixty years ago. The idea of dibaryons was theoretically proposed by Dyson and Xuong in 1964 [2]. The concept of the dibaryon gained significant attention after Jaffe suggested the possibility of the H-dibaryon in 1977 [3]. After a long history of ups and downs in experiments [4], resonance
$ d^*(2380) $ with a mass of approximately 2370 MeV and width of approximately 70 MeV was observed at WASA-at-COSY [5]. The resonant structure was examined in many pictures [6−11], including a molecular state from the$ \Delta\Delta $ interaction [8]. Some authors also suggested that it may be not a genuine particle, but only a triangle singularity in the last step of the reaction [12−14]. Even if$ d^*(2380) $ is a genuine particle, it is challenging to categorize it as a molecular state because this assumption results in a binding energy of approximately 80 MeV. This energy suggests it might be a compact hexaquark rather than a bound state of two Δ baryons. Therefore, exploring molecular states composed of two baryons beyond the well-established deuteron remains an intriguing subject. Over the past two decades, numerous potential molecular states in the charmed sector have been observed, including the hidden- charm pentaquarks$ P_c $ [15−17],$ X(3872) ,$ and$ Z_c(3900) $ [18−21], which are pretty close to the thresholds of two charmed hadrons. Hence, a natural direction involves examining dibaryon molecular states with heavy quarks, such as molecular$ N\Omega_{c} $ and$ N\Lambda_c $ states proposed in the literature [22, 23].The molecular states were widely examined in the past two decades. Nevertheless, experimental observations of molecular states consisting of two charmed/anticharmed baryons remain limited. In the literature, several theoretical studies address hidden-charm molecular states composed of a charmed baryon and its anticharmed counterpart, particularly
$ \Lambda_c\bar{\Lambda}_c $ molecular states inspired by the observation of$ Y(4630) $ [24−28]. The double-charm dibaryons also attract significant attention from hadron physics community [29−35]. In our previous study, possible molecular states from hidden-charm systems$ \Lambda_c\bar{\Lambda}_c $ ,$ \Sigma_c^{(*)}\bar{\Sigma}_c^{(*)} $ , and$ \Lambda_c \bar{\Sigma}_c^{(*)} $ and corresponding double-charm systems$ \Lambda_c{\Lambda}_c $ ,$ \Sigma_c^{(*)}{\Sigma}_c^{(*)} $ , and$ \Lambda_c {\Sigma}_c^{(*)} $ have already been studied, and strong attractions were found in these systems [35]. In Ref. [25], it was concluded that there may exist four loosely deuteron-like bound states$ \Xi_c{\Xi}_c $ ($ \Xi_c\bar{\Xi}_c $ ) and$ \Xi_c^{'}{\Xi}_c^{'} $ ($ \Xi_c^{'}\bar{\Xi}_c^{'} $ ). In the current study, we will examine the possible molecular states composed of two charmed strange baryons from$ \Xi_c^{(',*)}{\Xi}_c^{(',*)} $ interaction, and their hidden-charm hidden-strange partners from the$ \Xi_c^{(',*)}\bar{\Xi}_c^{(',*)} $ interaction in a quasipotential Bethe–Salpeter equation (qBSE) approach.This article is organized as follows. After introduction, the Lagrangians depicting the couplings of light mesons and baryons will be presented, and the potentials are constructed. Additionally, the qBSE approach will also be introduced briefly in Section II. The numerical results on the binding energies will be presented in Section III. Finally, a brief summary is provided in Section IV.
-
In the current research, to study interactions
$ \Xi_c^{(',*)}{\Xi}_c^{(',*)} $ and$ \Xi_c^{(',*)}\bar{\Xi}_c^{(',*)} $ , potential kernel will be constructed within the one-boson exchange model. The exchanges are intermediated by pseudoscalar$ \mathbb{P} $ (π and η), vector$ \mathbb{V} $ (ρ, ω, and ϕ), and scalar σ mesons. The Lagrangians that depict the couplings of light mesons and charmed strange baryons are required and presented in the below. -
The vertices between charmed baryon and light π, ρ, η, ω, ϕ, σ mesons are described by the Lagrangians with SU(3), heavy quark and chiral symmetry as [23, 36, 37]:
$ \begin{aligned}[b] {\cal L}_{S}=&- \frac{3}{2}g_1(v_\kappa)\epsilon^{\mu\nu\lambda\kappa}{\rm tr}[\bar{S}_\mu {\cal A}_\nu S_\lambda]+ {\rm i}\beta_S{\rm tr}[\bar{S}_\mu v_\alpha (\mathcal{V}^\alpha- \rho^\alpha) S^\mu]\\ & + \lambda_S{\rm tr}[\bar{S}_\mu F^{\mu\nu}S_\nu] +\ell_S{\rm tr}[\bar{S}_\mu \sigma S^\mu],\\ {\cal L}_{B_{\bar{3}}}&= {\rm i}\beta_B{\rm tr}[\bar{B}_{\bar{3}}v_\mu(\mathcal{V}^\mu-\rho^\mu) B_{\bar{3}}] +\ell_B{\rm tr}[\bar{B}_{\bar{3}}{\sigma} B_{\bar{3}}], \\ {\cal L}_{\rm int}&={\rm i} g_4 {\rm tr}[\bar{S}^\mu {\cal A}_\mu B_{\bar{3}}]+ {\rm i} \lambda_I \epsilon^{\mu\nu\lambda\kappa}v_\mu{\rm tr}[\bar{S}_\nu F_{\lambda\kappa} B_{\bar{3}}]+{\rm h.c.}, \end{aligned} $

(1) where
$ S^{\mu}_{ab} $ is composed of Dirac spinor operators,$ \begin{aligned}[b] S^{ab}_{\mu}&=-\sqrt{\frac{1}{3}}(\gamma_{\mu}+v_{\mu}) \gamma^{5}B^{ab}+B^{*ab}_{\mu}\equiv{ B}^{ab}_{0\mu}+B^{ab}_{1\mu},\\ \bar{S}^{ab}_{\mu}&=\sqrt{\frac{1}{3}}\bar{B}^{ab} \gamma^{5}(\gamma_{\mu}+v_{\mu})+\bar{B}^{*ab}_{\mu}\equiv{\bar{B}}^{ab}_{0\mu}+\bar{B}^{ab}_{1\mu}. \end{aligned} $

(2) Substituting Dirac spinor operators into the Lagrangians, we can realize explicit forms as:
$ \begin{aligned}[b] {\cal L}_{BB\mathbb{P}}=&-{\rm i}\frac{3g_1}{4f_\pi\sqrt{m_{\bar{B}}m_{B}}}\; \epsilon^{\mu\nu\lambda\kappa}\partial^\nu \mathbb{P}\; \sum_{i=0,1}\bar{B}_{i\mu} \overleftrightarrow{\partial}_\kappa B_{j\lambda},\\ {\cal L}_{BB\mathbb{V}}=&-\frac{\beta_S g_V}{2\sqrt{2m_{\bar{B}}m_{B}}}\mathbb{V}^\nu \sum_{i=0,1}\bar{B}_i^\mu \overleftrightarrow{\partial}_\nu B_{j\mu}\\ &-\frac{\lambda_S g_V}{\sqrt{2}}(\partial_\mu \mathbb{V}_\nu-\partial_\nu \mathbb{V}_\mu) \sum_{i=0,1}\bar{B}_i^\mu B_j^\nu,\\ {\cal L}_{BB\sigma}=&\ell_S\sigma\sum_{i=0,1}\bar{B}_i^\mu B_{j\mu},\\ {\cal L}_{B_{\bar{3}}B_{\bar{3}}\mathbb{V}}=&-\frac{g_V\beta_B}{2\sqrt{2m_{\bar{B}_{\bar{3}}}m_{B_{\bar{3}}}} }\mathbb{V}^\mu\bar{B}_{\bar{3}}\overleftrightarrow{\partial}_\mu B_{\bar{3}},\\ {\cal L}_{B_{\bar{3}}B_{\bar{3}}\sigma}=& {\rm i} \ell_B \sigma \bar{B}_{\bar{3}}B_{\bar{3}},\\ {\cal L}_{BB_{\bar{3}}\mathbb{P}} =&-{\rm i}\frac{g_4}{f_\pi} \sum_i\bar{B}_i^\mu \partial_\mu \mathbb{P} B_{\bar{3}}+{\rm H.c.},\\ {\cal L}_{BB_{\bar{3}}\mathbb{V}} =&\frac{g_\mathbb{V}\lambda_I}{\sqrt{2m_{\bar{B}}m_{B_{\bar{3}}}}} \epsilon^{\mu\nu\lambda\kappa} \partial_\lambda \mathbb{V}_\kappa\sum_i\bar{B}_{i\nu} \overleftrightarrow{\partial}_\mu B_{\bar{3}}+{\rm H.c.}. \end{aligned} $

(3) The charmed baryon matrices are defined as
$ \begin{aligned}[b] B_{\bar{3}}&=\left(\begin{array}{ccc} 0&\Lambda^+_c&\Xi_c^+\\ -\Lambda_c^+&0&\Xi_c^0\\ -\Xi^+_c&-\Xi_c^0&0 \end{array}\right),\\ B&=\left(\begin{array}{ccc} \Sigma_c^{++}&\dfrac{1}{\sqrt{2}}\Sigma^+_c&\dfrac{1}{\sqrt{2}}\Xi'^+_c\\ \dfrac{1}{\sqrt{2}}\Sigma^+_c&\Sigma_c^0&\dfrac{1}{\sqrt{2}}\Xi'^0_c\\ \dfrac{1}{\sqrt{2}}\Xi'^+_c&\dfrac{1}{\sqrt{2}}\Xi'^0_c&\Omega^0_c \end{array}\right). \\ B^*&=\left(\begin{array}{ccc} \Sigma_c^{*++}&\dfrac{1}{\sqrt{2}}\Sigma^{*+}_c&\dfrac{1}{\sqrt{2}}\Xi^{*+}_c\\ \dfrac{1}{\sqrt{2}}\Sigma^{*+}_c&\Sigma_c^{*0}&\dfrac{1}{\sqrt{2}}\Xi^{*0}_c\\ \dfrac{1}{\sqrt{2}}\Xi^{*+}_c&\dfrac{1}{\sqrt{2}}\Xi^{*0}_c&\Omega^{*0}_c \end{array}\right). \end{aligned} $

(4) Specifically,
$ \mathbb{V} $ and$ \mathbb{P} $ are denote vector and pseudoscalar matrices, respectively, as:$ \begin{aligned}[b] {\mathbb P}=\left(\begin{array}{ccc} \dfrac{\sqrt{3}\pi^0+\eta}{\sqrt{6}}&\pi^+&K^+\\ \pi^-&\dfrac{-\sqrt{3}\pi^0+\eta}{\sqrt{6}}&K^0\\ K^-&\bar{K}^0&\dfrac{-2\eta}{\sqrt{6}} \end{array}\right),\end{aligned} $

$ \begin{aligned}[b] \mathbb{V}=\left(\begin{array}{ccc} \dfrac{\rho^{0}+\omega}{\sqrt{2}}&\rho^+&K^{*+}\\ \rho^-&\dfrac{-\rho^{0}+\omega}{\sqrt{2}}&K^{*0}\\ K^{*-}&\bar{K}^{*0}&\phi \end{array}\right). \end{aligned} $

We choose the central values suggested in the Review of Particle Physics (PDG) [1] as the masses of particles involved in the calculation. The values for different charges will be averaged. The coupling constants involved are listed in Table 1.
β g $ g_V $ 

λ $ g_{s} $ 

0.9 0.59 5.9 0.56 0.76 $ \beta_S $ 

$ \ell_S $ 

$ g_1 $ 

$ \lambda_S $ 

$ \beta_B $ 

$ \ell_B $ 

$ g_4 $ 

$ \lambda_I $ 

−1.74 6.2 −0.94 −3.31 $ -\beta_S/2 $ 

$ -\ell_S/2 $ 

$ 3g_1/{(2\sqrt{2})} $ 

$ -\lambda_S/\sqrt{8} $ 

The flavor wave functions for the double-charm double-strange system
$ \Xi_c^{(',*)}{\Xi}_c^{(',*)} $ can be expressed as:$ \begin{aligned}[b] |\Xi_c^{(',*)}{\Xi}_c^{(',*)}\rangle|_{I=0}&=\frac{1}{\sqrt{2}}\left(|\Xi_c^{(',*)+}{\Xi}_c^{(',*)0}\rangle-|\Xi_c^{(',*)0}{\Xi}_c^{(',*)+}\rangle\right),\\ |\Xi_c^{(',*)}{\Xi}_c^{(',*)}\rangle|_{I=1}&=|\Xi_c^{(',*)+}{\Xi}_c^{(',*)+}\rangle. \end{aligned} $

(5) Following the method in Ref. [42], we input vertices Γ and propagators P into the code directly. The explicit forms of a potential can be expressed with the Lagrangians and flavor wave functions as:
$ \begin{equation} {\cal V}_{\mathbb{P},\sigma}=f_I\Gamma_1\Gamma_2 P_{\mathbb{P},\sigma}f(q^2),\ \ {\cal V}_{\mathbb{V}}=f_I\Gamma_{1\mu}\Gamma_{2\nu} P^{\mu\nu}_{\mathbb{V}}f(q^2). \end{equation} $

(6) The propagators are defined as usual as
$ \begin{equation} P_{\mathbb{P},\sigma}= \frac{{\rm i}}{q^2-m_{\mathbb{P},\sigma}^2},\ \ P^{\mu\nu}_\mathbb{V}={\rm i}\frac{-g^{\mu\nu}+q^\mu q^\nu/m^2_{\mathbb{V}}}{q^2-m_\mathbb{V}^2}, \end{equation} $

(7) where
$ f(q^2) $ denotes a form factor adopted to compensate the off-shell effect of exchanged meson. The form factor is shown as$f(q^2)={\rm e}^{-(m_e^2-q^2)^2/\Lambda_e^2}$ , where$ m_e $ and q denote the mass and momentum of the exchanged meson, respectively. Furthermore,$ f_I $ denotes the flavor factor for a specific meson exchange in a given interaction, and the detailed values can be found inTable 2.$ I_i^d $ 

I π η ρ ω ϕ σ $ \Xi_c \bar{\Xi}_c $ 

$ 0 $ 

$ \dfrac{3}{2}[-\dfrac{3}{2}] $ 

$ -\dfrac{1}{2}[\dfrac{1}{2}] $ 

$ -1[1] $ 

$ 4[4] $ 

$ 1 $ 

$ -\dfrac{1}{2}[\dfrac{1}{2}] $ 

$ -\dfrac{1}{2}[\dfrac{1}{2}] $ 

$ -1[1] $ 

$ 4[4] $ 

$ \Xi_c^{(',*)} \bar{\Xi}_c^{(',*)} $ 

$ 0 $ 

$ -\dfrac{3}{8}[-\dfrac{3}{8}] $ 

$ \dfrac{1}{24}[\dfrac{1}{24}] $ 

$ \dfrac{3}{8}[-\dfrac{3}{8}] $ 

$ -\dfrac{1}{8}[\dfrac{1}{8}] $ 

$ -\dfrac{1}{4}[\dfrac{1}{4}] $ 

$ 1[1] $ 

$ 1 $ 

$ \dfrac{1}{8}[\dfrac{1}{8}] $ 

$ \dfrac{1}{24}[\dfrac{1}{24}] $ 

$ -\dfrac{1}{8}[\dfrac{1}{8}] $ 

$ -\dfrac{1}{8}[\dfrac{1}{8}] $ 

$ -\dfrac{1}{4}[\dfrac{1}{4}] $ 

$ 1[1] $ 

$ \Xi_c \bar{\Xi}_c^{(',*)} $ 

$ 0 $ 

$ \dfrac{3}{4}[-\dfrac{3}{4}] $ 

$ -\dfrac{1}{4}[\dfrac{1}{4}] $ 

$ -\dfrac{1}{2}[\dfrac{1}{2}] $ 

$ 2[2] $ 

$ 1 $ 

$ -\dfrac{1}{4}[\dfrac{1}{4}] $ 

$ -\dfrac{1}{4}[\dfrac{1}{4}] $ 

$ -\dfrac{1}{2}[\dfrac{1}{2}] $ 

$ 2[2] $ 

$ (-1)^{(J+1)} I_i^c $ 

I π η ρ ω ϕ $ \Xi_c \bar{\Xi}_c^{'} $ 

$ 0 $ 

$ \dfrac{3c}{4}[-\dfrac{3}{4}] $ 

$ -\dfrac{3c}{4}[\dfrac{3}{4}] $ 

$ -\dfrac{3c}{4}[-\dfrac{3}{4}] $ 

$ \dfrac{c}{4}[\dfrac{1}{4}] $ 

$ \dfrac{c}{2}[\dfrac{1}{2}] $ 

$ 1 $ 

$ \dfrac{c}{4}[\dfrac{1}{4}] $ 

$ \dfrac{3c}{4}[\dfrac{3}{4}] $ 

$ -\dfrac{c}{4}[\dfrac{1}{4}] $ 

$ -\dfrac{c}{4}[\dfrac{1}{4}] $ 

$ -\dfrac{c}{2}[\dfrac{1}{2}] $ 

$ \Xi_c \bar{\Xi}_c^* $ 

$ 0 $ 

$ -\dfrac{3c}{4}[-\dfrac{3}{4}] $ 

$ \dfrac{3c}{4}[\dfrac{3}{4}] $ 

$ \dfrac{3c}{4}[-\dfrac{3}{4}] $ 

$ -\dfrac{c}{4}[\dfrac{1}{4}] $ 

$ -\dfrac{c}{2}[\dfrac{1}{2}] $ 

$ 1 $ 

$ \dfrac{c}{4}[\dfrac{1}{4}] $ 

$ \dfrac{3c}{4}[\dfrac{3}{4}] $ 

$ -\dfrac{c}{4}[\dfrac{1}{4}] $ 

$ -\dfrac{c}{4}[\dfrac{1}{4}] $ 

$ -\dfrac{c}{2}[\dfrac{1}{2}] $ 

$ \Xi_c^{'} \bar{\Xi}_c^* $ 

$ 0 $ 

$ -\dfrac{3c}{8}[-\dfrac{3}{8}] $ 

$ \dfrac{c}{24}[\dfrac{1}{24}] $ 

$ \dfrac{3c}{8}[-\dfrac{3}{8}] $ 

$ -\dfrac{c}{8}[\dfrac{1}{8}] $ 

$ -\dfrac{c}{4}[\dfrac{1}{4}] $ 

$ 1 $ 

$ -\dfrac{c}{8}[\dfrac{1}{8}] $ 

$ -\dfrac{c}{24}[\dfrac{1}{24}] $ 

$ \dfrac{c}{8}[\dfrac{1}{8}] $ 

$ \dfrac{c}{8}[-\dfrac{1}{8}] $ 

$ -\dfrac{c}{4}[\dfrac{1}{4}] $ 

Table 2. Isospin factors
$ I_i^d $ and$ (-1)^{(J+1)} I_i^c $ of exchange i for direct diagrams and cross diagrams, respectively. The values in bracket are for the case double-charm baryons.The potential kernels of a charmed strange and an anticharmed antistrange baryon differ from those of the double-charm double-strange systems. However, the former potential kernel
$ \bar{\cal V} $ can be expressed from the latter one$ {\cal V} $ , which has been calculated above with the aid of well-known G-parity rule. However, before applying this type of treatment, the C or G parity should be introduced for the system$ \Xi_c^{(')}\bar{\Xi}_c^{*} $ . We consider the following charge conjugation convention as in Ref. [41]:$ \begin{equation} |B_1B_2\rangle_c=\frac{1}{\sqrt{2}}|B_1\bar{B}_2\rangle-(-1)^{J-J_1-J_2}cc_1c_2|B_2\bar{B}_1\rangle, \end{equation} $

(8) where
$ J_1 $ and$ J_2 $ denote the spins of baryons$ |B_1\rangle $ and$ |B_2\rangle $ , respectively. J denotes the total angular momentum of the coupling of$ J_1 $ and$ J_2 $ , and$ c_i $ is defined by$ \mathcal{C}|B_i\rangle = c_i\bar{B}_i\rangle $ . For the isovector states, the C parity can not be defined. Hence, we will use the G parity instead as$ G=(-1)^{I}C $ . By inserting$ G^{-1}G $ operator into the potential, the G-parity rule can be easily obtained as [25, 43−45]:$ \begin{eqnarray} \bar{\cal V}&=&\sum_{i}{\zeta_{i}{\cal V}_{i}}. \end{eqnarray} $

(9) The G parity of the exchanged meson is left as a
$ \zeta_{i} $ factor for meson i.To solve the scattering amplitude, the potential kernel obtained above is adopted to solve the qBSE [38, 46−52]. The 4-dimensional integral equation in the Minkowski space can be reduced to a 1-dimensional integral equation with fixed spin-parity
$ J^P $ , as reported in [51], via partial-wave decomposition and spectator quasipotential approximation. The 1-dimensional Bethe–Saltpeter equation is further converted to a matrix equation, and the scattering amplitude can be obtained as [38, 46−52]:$ \begin{aligned}[b] {\rm i}{\cal M}^{J^P}_{\lambda'\lambda}({\rm p}',{\rm p}) =&{\rm i}{\cal V}^{J^P}_{\lambda',\lambda}({\rm p}',{\rm p})+\sum_{\lambda''}\int\frac{{\rm p}''^2d{\rm p}''}{(2\pi)^3}\\ &\times {\rm i}{\cal V}^{J^P}_{\lambda'\lambda''}({\rm p}',{\rm p}'') G_0({\rm p}''){\rm i}{\cal M}^{J^P}_{\lambda''\lambda}({\rm p}'',{\rm p}), \end{aligned} $

(10) where the sum extends only over nonnegative helicity
$ \lambda'' $ . Furthermore,$ G_0({\rm p}'') $ is reduced from the 4-dimensional propagator under quasipotential approximation as$G_0({\rm p}'')= \delta^+(p''^{\; 2}_h- m_h^{2})/(p''^{\; 2}_l-m_l^{2})$ with$ p''_{h,l} $ and$ m_{h,l} $ being the momentum and mass of heavy or light constituent particle. The partial wave potentials are obtained with the potentials obtained above in Eq. (6) as:$ \begin{align} {\cal V}_{\lambda'\lambda}^{J^P}({\rm p}',{\rm p}) &=2\pi\int {\rm d} \cos\theta \; [d^{J}_{\lambda\lambda'}(\theta) {\cal V}_{\lambda'\lambda}(\boldsymbol{p}',\boldsymbol{p})\\ &+\eta d^{J}_{-\lambda\lambda'}(\theta) {\cal V}_{\lambda'-\lambda}(\boldsymbol{p}',\boldsymbol{p})], \end{align} $

(11) where
$ \eta=PP_1P_2(-1)^{J-J_1-J_2} $ , where P and J denote parity and spin for system, respectively. The initial relative momentum is chosen as$ \boldsymbol{p}=(0,0,{\rm p}) ,$ and the final momentum is chosen as$ \boldsymbol{p}'=({\rm p}'\sin\theta,0,{\rm p}'\cos\theta) $ . Furthermore,$ d^J_{\lambda\lambda'}(\theta) $ is the Wigner d-matrix. We also adopt an exponential regularization by introducing a form factor into the propagator as$G_0({\rm p}'')\to G_0({\rm p}'')\left[{\rm e}^{-(p''^2_l-m_l^2)^2/\Lambda_r^4}\right]^2$ with$ \Lambda_r $ being a cutoff [51]. -
With previous preparation, the numerical calculation can be performed on the systems mentioned above, which involves studying the molecular states from interactions
$ \Xi_c^{(',*)}\bar{\Xi}_c^{(',*)} $ and$ \Xi_c^{(',*)}\Xi_c^{(',*)} $ . Molecular states can be identified by searching for poles of the scattering amplitude in the complex energy plane. The parameters of the Lagrangians used in this study are consistent with those from our earlier research on hidden-charm pentaquarks [42, 53], and they are listed in Table 1. The only free parameters are cutoff$ \Lambda_e $ and$ \Lambda_r $ , which are rewritten as a form of$ \Lambda_e=\Lambda_r=m_e+\alpha\; 0.22 $ GeV with the$ m_e $ being the mass of exchanged meson between two constituent baryons. Hence, in the current study, only one free parameter α is involved in explicit calculation, which is constrained in a reasonable range from 0 to 2. In the current study, only S-wave bound states will be considered. -
Given that isospin and spin of the
$ \Xi_c $ baryon are the same as those of the$ \Xi'_c $ baryon, the same number of channels will be involved in interactions$ \Xi_c^{(')} \bar{\Xi}^{(')}_c $ and$ \Xi^{(')}_c\Xi^{(')}_c $ . The$ \Xi_c^{(')} $ baryon carries spin 1/2 and isospin 1/2. Hence, the total angular momentum of the systems can be$J=0 $ or$ 1 $ in S-wave channel, and the total isospin can be 0 and 1. According to the Pauli exclusion principle, the isoscalar axial-vector$ \Xi^{(')}_c\Xi^{(')}_c $ state, as well as isovector scalar$ \Xi^{(')}_c\Xi^{(')}_c $ state, do not exist.For interactions
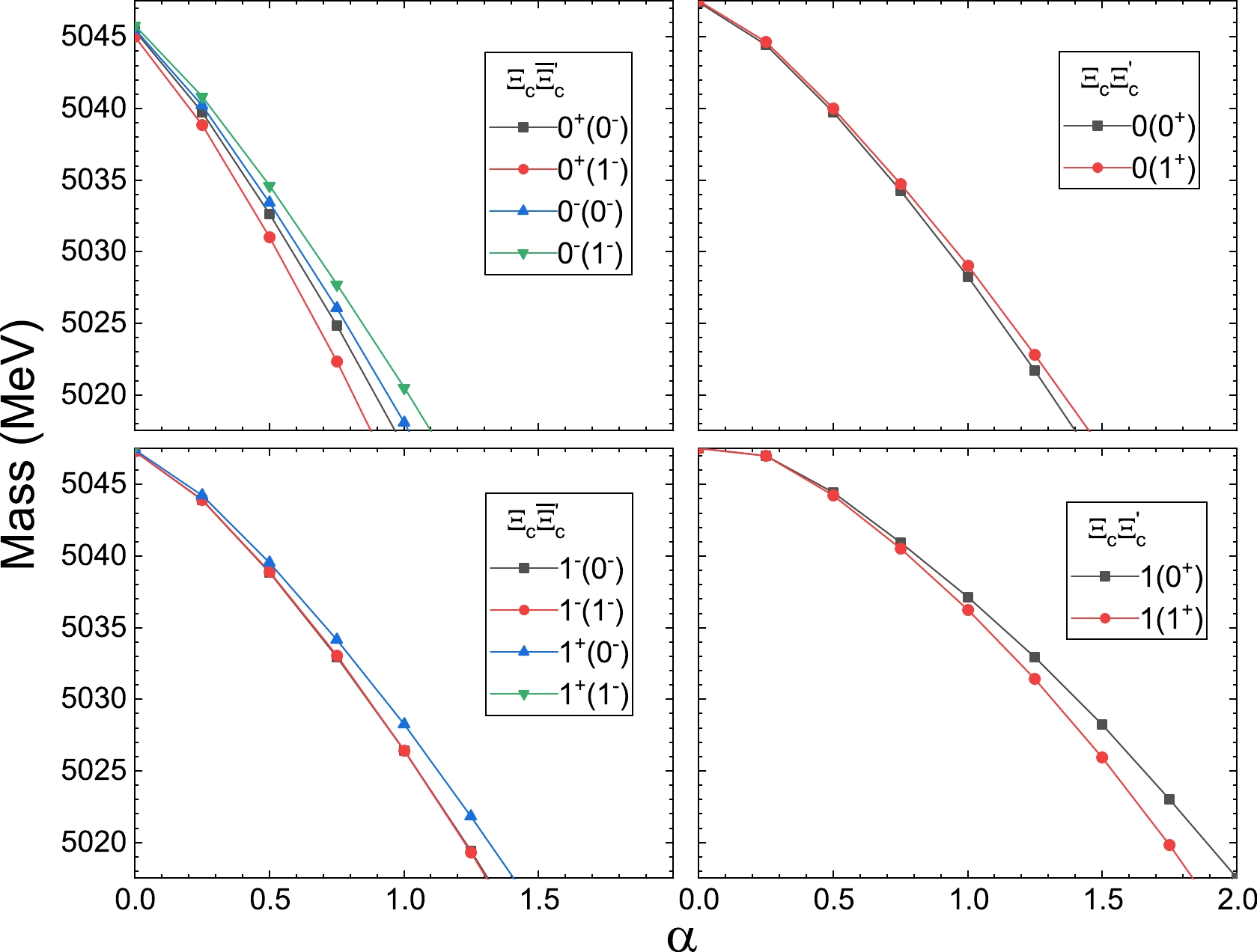
$ \Xi_c \bar{\Xi}_c $ and$ \Xi_c \Xi_c $ considered, the masses of produced bound states with the variation in parameter α are shown in Fig. 1. The results suggest that isoscalar bound states are produced from the$ \Xi_c \bar{\Xi}_c $ interaction with total angular momenta$J=1 $ and 0. The masses of these two states are almost the same at the same α values. The states appear even at α values below 0, and the masses decrease rapidly with an increase in α value. This implies a potent attraction between the two baryons. A bound state can also be observed in the double-charm system. The bound state emerges when α values are approximately 0, and its mass decreases more gradually than that of hidden-charm states. For isovector interactions, bound states manifest at α values close to 0 for both hidden-charm and double-charm interactions. Their masses exhibit a more gradual decline when compared to the isoscalar interactions.
Figure 1. (color online) Masses of the bound states from the interactions
$ \Xi_c \bar{\Xi}_c $ (left) and$ \Xi_c\Xi_c $ (right) with threshold of 4938.15 MeV with respect to the variation in parameter α.In Fig. 2, the bound states from
$ \Xi_c^{'} \bar{\Xi}_c^{'} $ interaction and their double-charm partners are presented. Given that the flavor factors are the same as those for interactions$ \Xi_c \bar{\Xi}_c $ and$ \Xi_c\Xi_c $ , bound states are also produced in all channels, and the masses exhibit similar behaviors as the results in Fig. 1. For the isoscalar hidden-charm$ \Xi_c^{'}\bar{\Xi}_c^{'} $ system, the bound states are produced at α values below 0, which are smaller than those for the double-charm$ \Xi_c^{'}\Xi_c^{'} $ interaction. This indicates that$ \Xi_c^{'}\bar{\Xi}_c^{'} $ interaction is more attractive than$ \Xi_c^{'}\Xi_c^{'} $ interaction due to different contributions from the meson exchanges. As in the case of$ \Xi_c\bar{\Xi}_c $ interaction, the masses for corresponding hidden-charm systems increase faster than the double-charm system.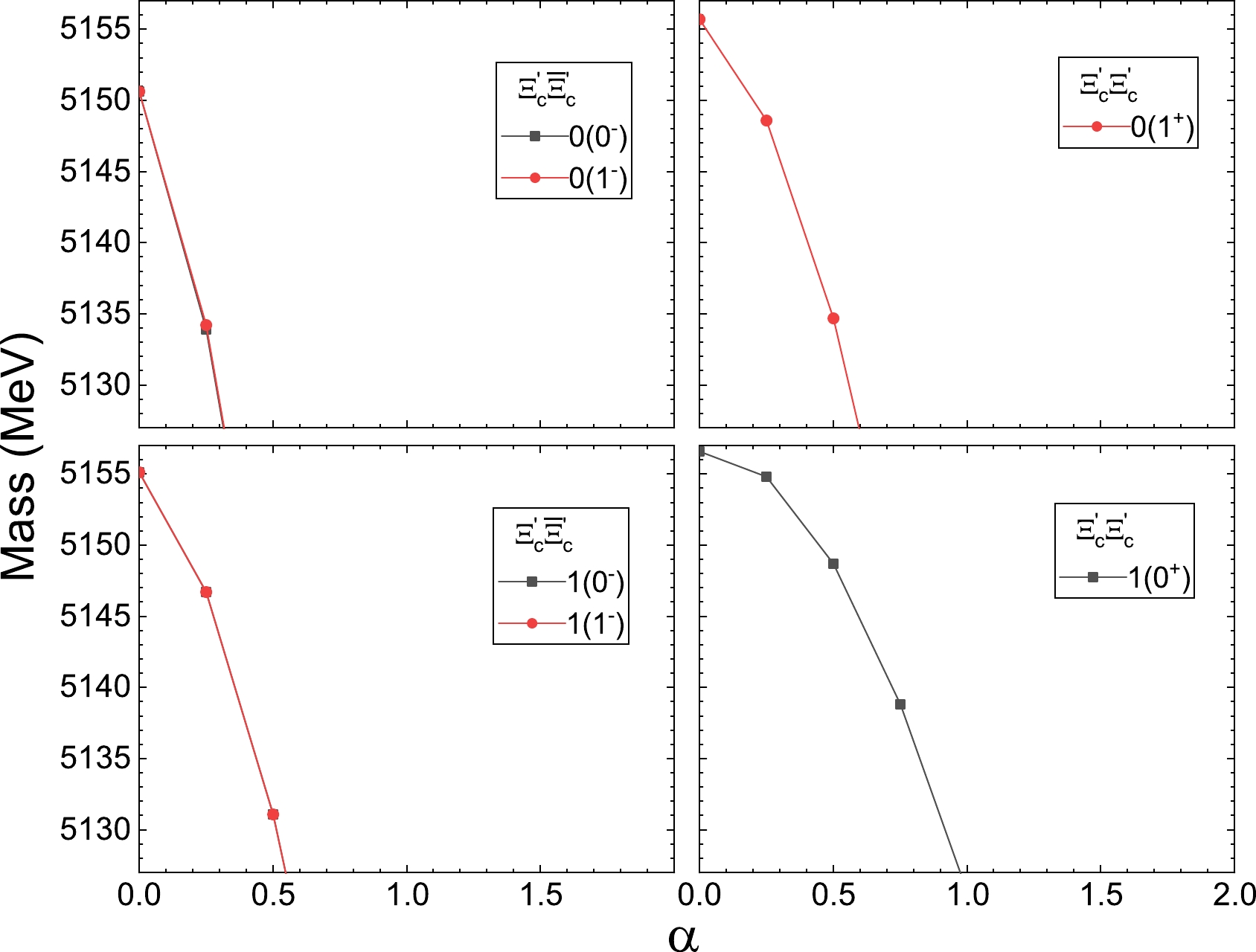
Figure 2. (color online) Masses of the bound states from interactions
$ \Xi'_c \bar{\Xi}'_c $ (left) and$ \Xi'_c\Xi'_c $ (right) with threshold of 5156.9 MeV with variation in parameter α.The masses of the states produced from
$ \Xi_c\bar{\Xi}_c' $ interaction and their double-charm partners are shown in Fig. 3. Given that the two constituent baryons are differ, the C parity is involved in the hidden-charm sector, whereas it is not involved in the double-charm sector. For the hidden-charm system with$I=0 $ , the bound states are produced at α values below 0. The corresponding double-charm partners appear at larger α values. The hidden-charm bound states with$I=1 $ appear at α values below 0, whereas their double-charm partner appears at α values about 0 and their masses increase at a much slower rate than those of hidden-charm states. -
Now, we consider systems with a
$ \Xi/\Xi' $ and$ \Xi^{*} $ baryon. Given that these baryons carry spins of 1/2 and 3/2, respectively, the S-wave states exhibit total angular momenta$J=1 $ and 2, and they will be considered in the calculation. The isospins of$ \Xi_c^{(')}\bar{\Xi}_c^{*} $ and$ \Xi_c^{(')}\Xi_c^{*} $ systems are the same as those of$ \Xi_c^{(')} \bar{\Xi}^{(')}_c $ and$ \Xi^{(')}_c\Xi^{(')}_c $ systems. In these systems, two constituent baryons are differ. Hence, the C parity will involve the hidden-charm sector. The masses of$ \Xi_c\bar{\Xi}_c^{(*)} $ states and their double-charm partners are shown in Fig. 4. The hidden-charm states with$I=0 $ emerge when α values are approximately 0, and the binding energies increase to 30 GeV when α values approach 1.25. Their double-charm counterparts also appear around α values of 0 but achieve a binding energy of approximately 30 MeV at higher α values, approximately 2. Both double-charm states with$J=1 $ and 0 possess nearly identical masses. The isovector states also emerge around α values of 0. The double-charm states manifest at slightly larger α values, and their binding energies escalate gradually, reaching 30 MeV for α values greater than 2, consistent with the isoscalar scenario.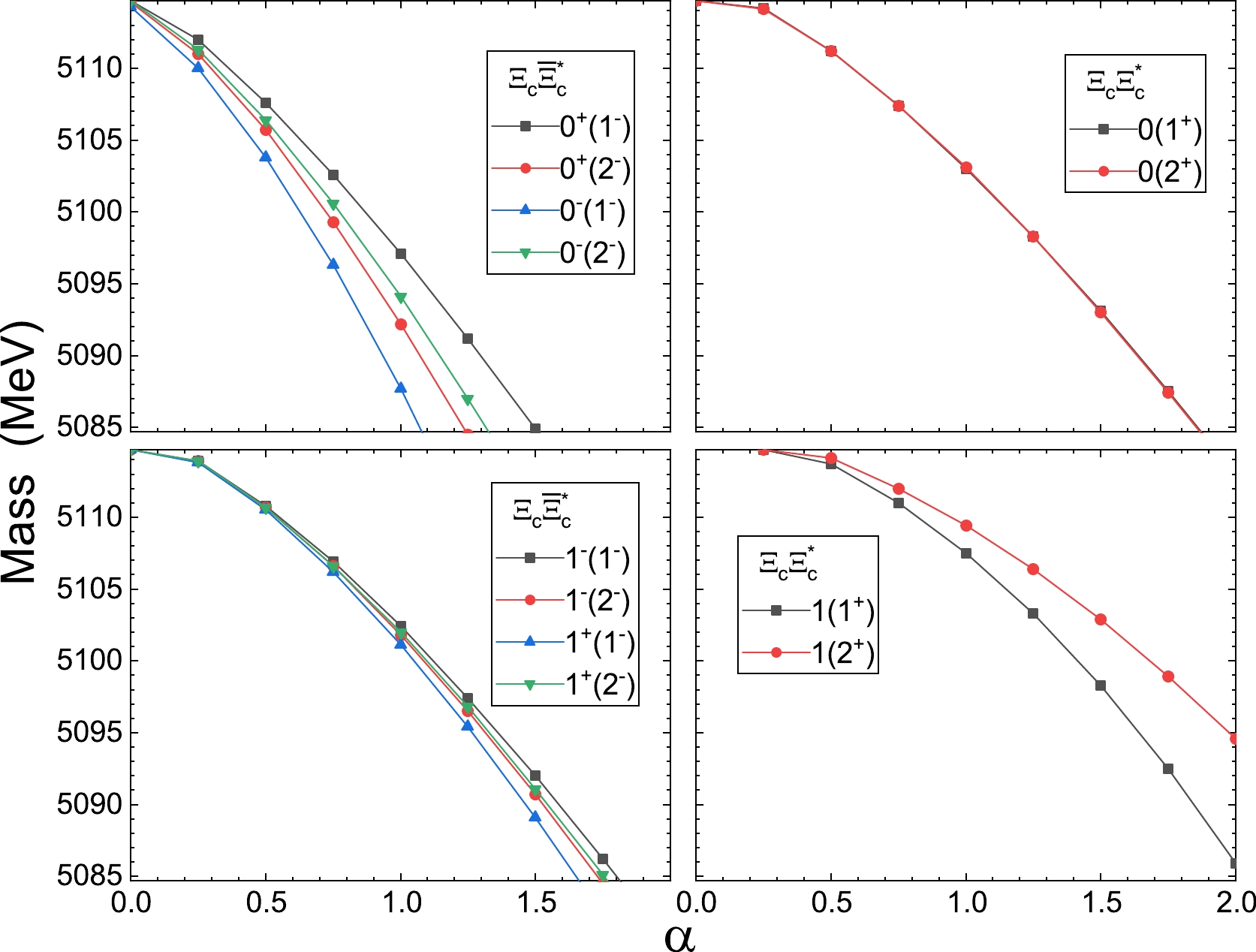
Figure 4. (color online) Masses of the bound states from interactions
$ \Xi_c\bar{\Xi}_c^* $ (left) and$ \Xi_c\Xi_c^* $ (right) with a threshold of 5114.7 MeV with respect to variation in parameter α.The results for interactions
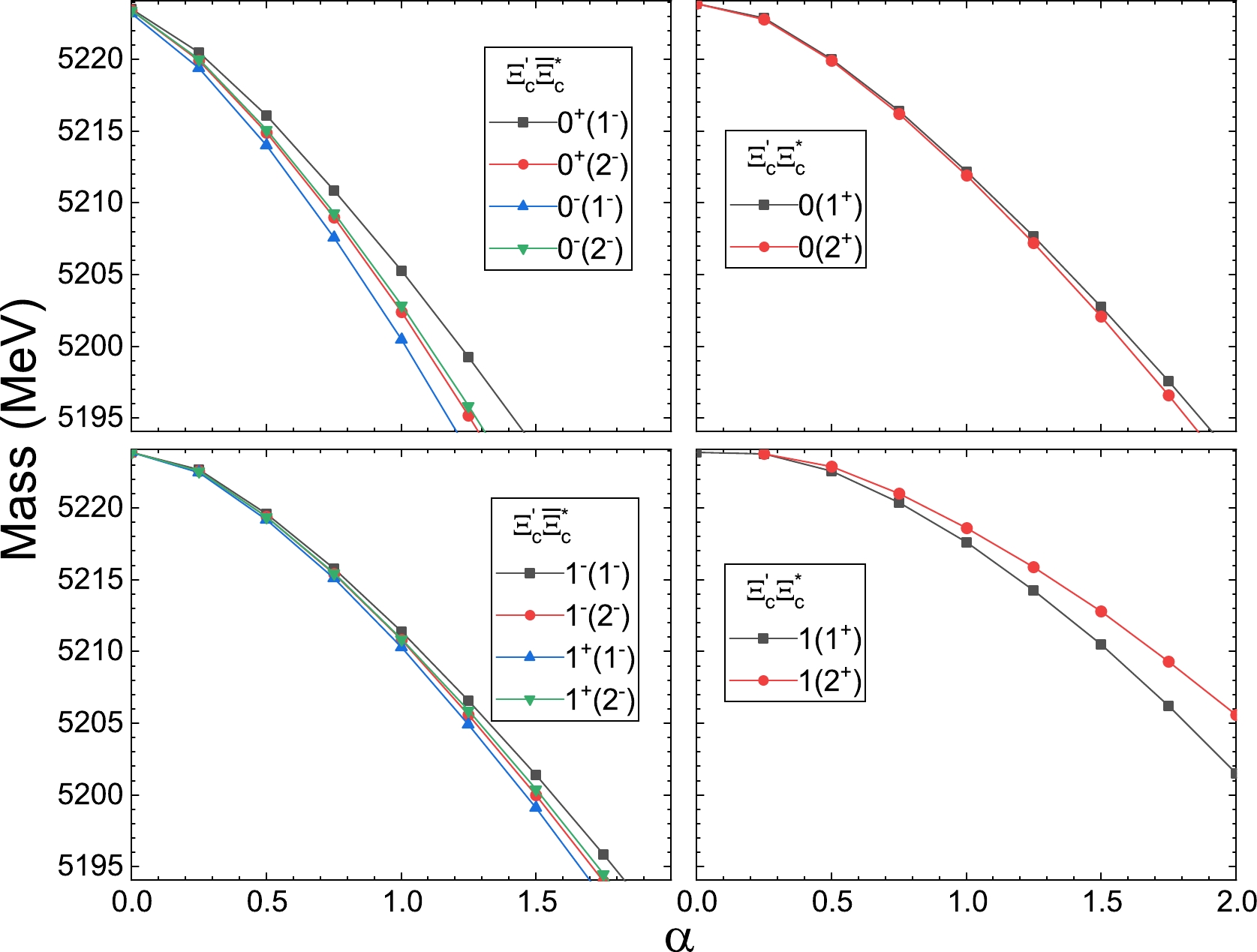
$ \Xi'_c \bar{\Xi}_c^* $ and$ \Xi'_c\Xi_c^* $ are presented in Fig 5. The C parity also involves the hidden-charm systems. For the hidden-charm systems with$ I=0 $ , the bound states appear at α values about 0 and the binding energies increase to 30 MeV at α values about 1.25. Their double-charm partners appear at α values greater than 0, and the binding energies increase to 30 MeV at α values of approximately 1.9. In the isovector case, the states appear at α values about 0, and the binding energies increase to 30 MeV at α values about 1.75. For their double-charm partners, the bound states appear at α values larger than 0, and the binding energies increase more slowly than those of hidden charm states. -
The masses of the states produced from interactions
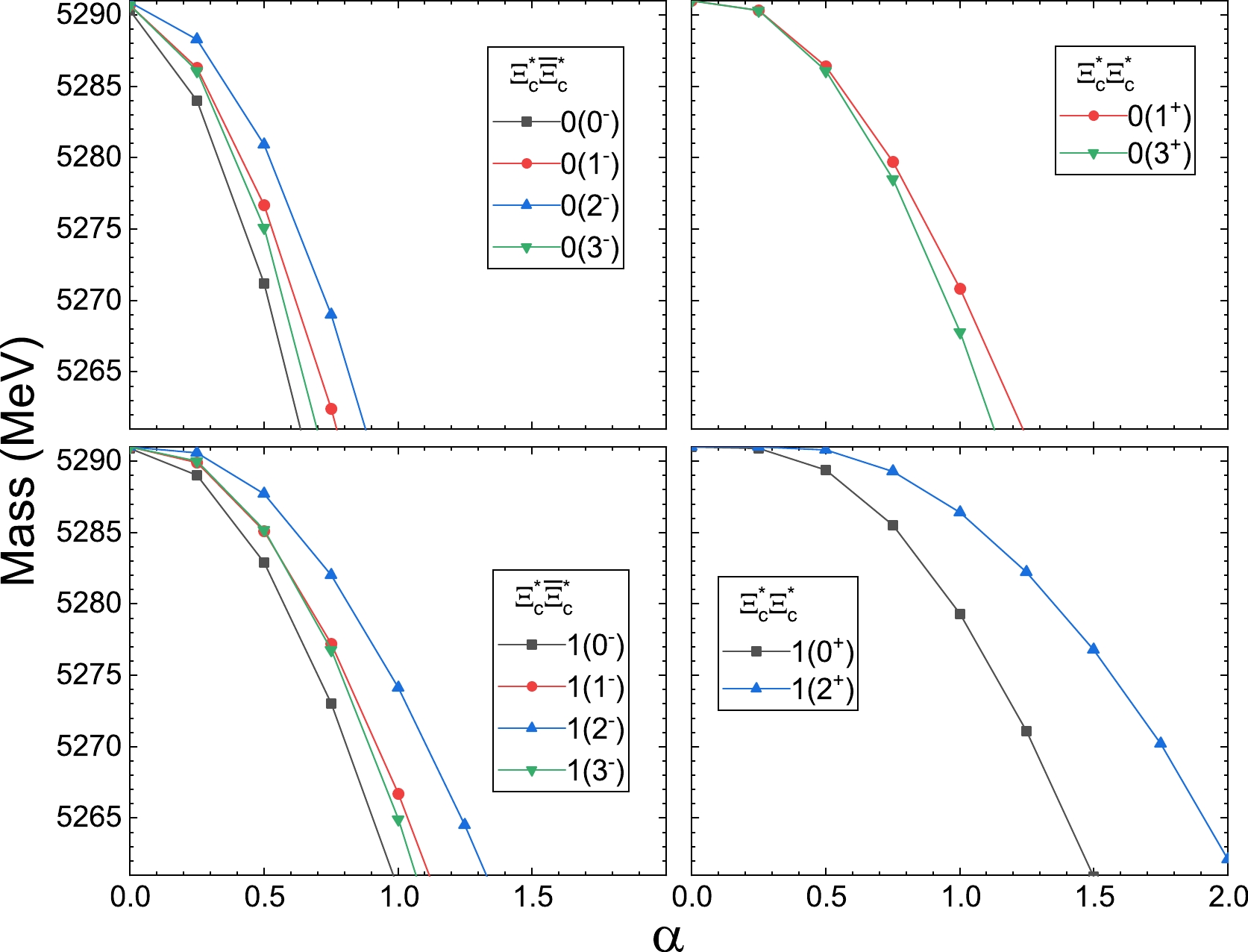
$ \Xi_c^* \bar{\Xi}_c^* $ and$ \Xi^*_c \Xi_c^{*} $ are presented in Fig. 6. Given that both baryons carry spin 3/2, four total angular momenta$J=0 $ , 1, 2, and 3 are possible. According to the Pauli exclusion principle, the isoscalar$ \Xi^{(')}_c\Xi^{(')}_c $ states with$ J= $ 2, 4 as well as isovector$ \Xi^{(')}_c\Xi^{(')}_c $ states with$ J= $ 1, 3 do not exist. For the hidden-charm system with$I=0 $ , there are four states produced at α values about 0. For the double-charm system with$I=0 $ , the binding energies increase to 30 MeV at α values about 1.25. The hidden-charm states with$I=1 $ appear at α values about 0 while their double-charm partners appear at α values about 0.25 or larger. For the hidden-charm system with$I=1 $ , the binding energies increase to 30 MeV at α values about 0.75. However, for the$ \Xi_c^*\Xi_c^* $ states, their binding energies increase to 30 MeV at α values of approximately 1.75 or larger. -
In this study, we systematically examined the molecular states resulting from interactions of charmed strange baryons, which include hidden-charm hidden-strange systems
$ \Xi_c^{(',*)}\bar{\Xi}_c^{(',*)} $ as well as their double-charm double-strange partners$ \Xi_c^{(',*)}\Xi_c^{(',*)} $ . The calculation indicates that attractions exist widely in systems composed of two charmed strange baryons. For$ \Xi_c\bar{\Xi}_c $ interaction, the bound states are produced at α values about 0, and the binding energies of their double-charm partner increase to 30 MeV at slightly higher α values. The situations for interactions$ \Xi_c^{'}\Xi_c^{'} $ and$ \Xi_c\Xi_c $ are quite similar, and the attractions in the hidden-charm systems$ \Xi_c^{'}\bar{\Xi}_c^{'} $ are stronger than those in the double-charm systems. For the states with the same angular momenta, the masses for states with different isospins behave in almost the same manner as the variations in parameter α. However, for interactions$ \Xi_c^{*}\Xi_c^{*} $ and$ \Xi_c^{'}\Xi_c^{*} $ , the masses of states with different isospins exhibit different behaviors with respect to the variation in parameter α.Generally, many interactions of the two charmed strange baryons are found attractive, and many bound states are predicted [24−28, 35]. However, to date, the candidates for hidden-charm molecular states consisting of two baryons have been rarely observed experimentally, and there have been no reports of candidates for double-charm molecular states composed of two baryons. This is understandable, as two baryons, comprising six quarks including two heavy quarks, need to be produced simultaneously with minimal relative momentum to establish a bound state. This makes their experimental production more challenging than states made up of two mesons. However, as experimental techniques advance and data accumulates at facilities, such as LHCb, we can anticipate potential observations of these states in the future. Consequently, experimental searches for such molecular states are recommended for upcoming high-precision experiments.
Possible molecular states from interactions of charmed strange baryons
- Received Date: 2023-07-24
- Accepted Date: 2023-07-25
- Available Online: 2023-11-15
Abstract: In this study, we investigate possible molecular states composed of two charmed strange baryons from the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: