-
The effect of a curved spacetime on wave propagation is an important subject in modern relativistic astrophysics. The first ever observation of gravitational waves by the LIGO-Virgo collaboration [1, 2] was the starting point for a new era of gravitational wave observation. Later, the observation of images of M87 [3, 4] and SgrA* [5] motivated specialists to use these observations to test gravity theories in the strong field regime.
Although well tested in the weak [6] and strong field regimes [2, 3], Einstein's general relativity still encounters several fundamental problems. One is the existence of the physical (curvature) singularity at the origin of most solutions within the theory. There is a belief that an undiscovered new quantum gravity theory will resolve this issue. One of the main aims of introducing alternative theories of gravity and modified versions of general relativity is to move in the direction of constructing a quantum gravity theory.
Owing to the strong gravitational field, the spacetime around massive objects is curved. The propagation of an electromagnetic wave is affected by this curvature, and an observer at infinity can detect light deflection due to gravity. However, because of the strong gravitational field around black holes, the part of the light rays propagating near a black hole will be captured by the central object. Consequently, the observer at infinity will detect a black spot on the celestial plane near the position of the black hole. The original idea of the possible observation of this black spot, usually referred to as a black hole shadow, was proposed by Synge [7] and later developed by Luminet [8] and Bardeen [9]. The shadow of a black hole for different solutions within general relativity and/or modified/alternative theories of gravity has subsequently been investigated by the various authors [10−38].
The deflection of light, also known as gravitational lensing, around a gravitating object can be used to either study the light source or test the gravitational field around the lensing object. The effect of gravitational lensing was first used to test general relativity by Eddington in 1919 during the solar eclipse. Later, the gravitational lensing around compact objects within different gravity models was investigated by various authors (see, for example, [39−49]). The existence of a plasma environment is one of the main markers of most black holes and compact objects. The light propagating through the plasma is also affected by the latter. The effects of both uniform and nonuniform plasma on the optical properties of black holes were investigated in Refs. [50−58]). Moreover, using gravitational lensing, one may study the effects of different plasma configurations on the light deflection angle (see, for example, [59−80]).
A regularization method was proposed by Simpson and Visser [81], in which the expression
$ 1/r $ in the Schwarzschild metric is replaced with$ 1/\sqrt{r^2+a^2} $ . As a result, one may obtain a globally regular family of metrics, including black-bounce geometry and a traversable wormhole. A particularly interesting feature of these solutions is that they may be considered a one-parameter extension of the Schwarzschild solution. The generalization of Reissner-Nordström spacetime using this technique has been reported in Ref. [82]. Later, the authors of Ref. [83] extended them and proposed a number of new solutions for black-bounce spacetime. Recently, the effect of retrolensing by two-photon spheres within black-bounce spacetime was studied in detail in Ref. [84]. In this paper, we extend the analysis of this spacetime by studying massless test particle motion around a black-bounce compact object. Moreover, we also study the effect of the gravitational lensing and shadow of the compact object described by black-bounce spacetime.The paper is arranged as follows. First, we review the spacetime metric in Sec. II. We study the photon motion around the black bounce compact object in Sec. III. Then, the shadow of the black-bounce object is studied in Sec. IV in the presence of plasma. Gravitational lensing in the presence of plasma in black bounce spacetime is then investigated in Sec. V. We conclude our study in Sec. VI. Throughout, we use the unit system
$ G=c=1 $ . -
Non-rotating spacetime in black bounce gravity has the following linear element in spherical coordinates [83, 84]:
$ {\rm d}s^2=-f(r){\rm d}t^2+\frac{{\rm d}r^2}{f(r)}+\gamma(r)({\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2)\ , $

(1) where the metric functions
$ f(r) $ and$ \gamma(r) $ are defined as$ f(r)=1-\frac{2 M r^2}{\left(a^2+r^2\right)^{3/2}}\ , $

(2) $ \gamma(r)=r^2+a^2\ , $

(3) where M is the mass of the compact object, and a is a nonnegative constant [83]. To understand the nature of the gravitational potential of the source, we may introduce the effective mass as
$M_{\rm eff}=M\Big({r}/{\sqrt{r^2+a^2}}\Big)^3$ .Spacetime metric (1) describes a regular black hole when the condition
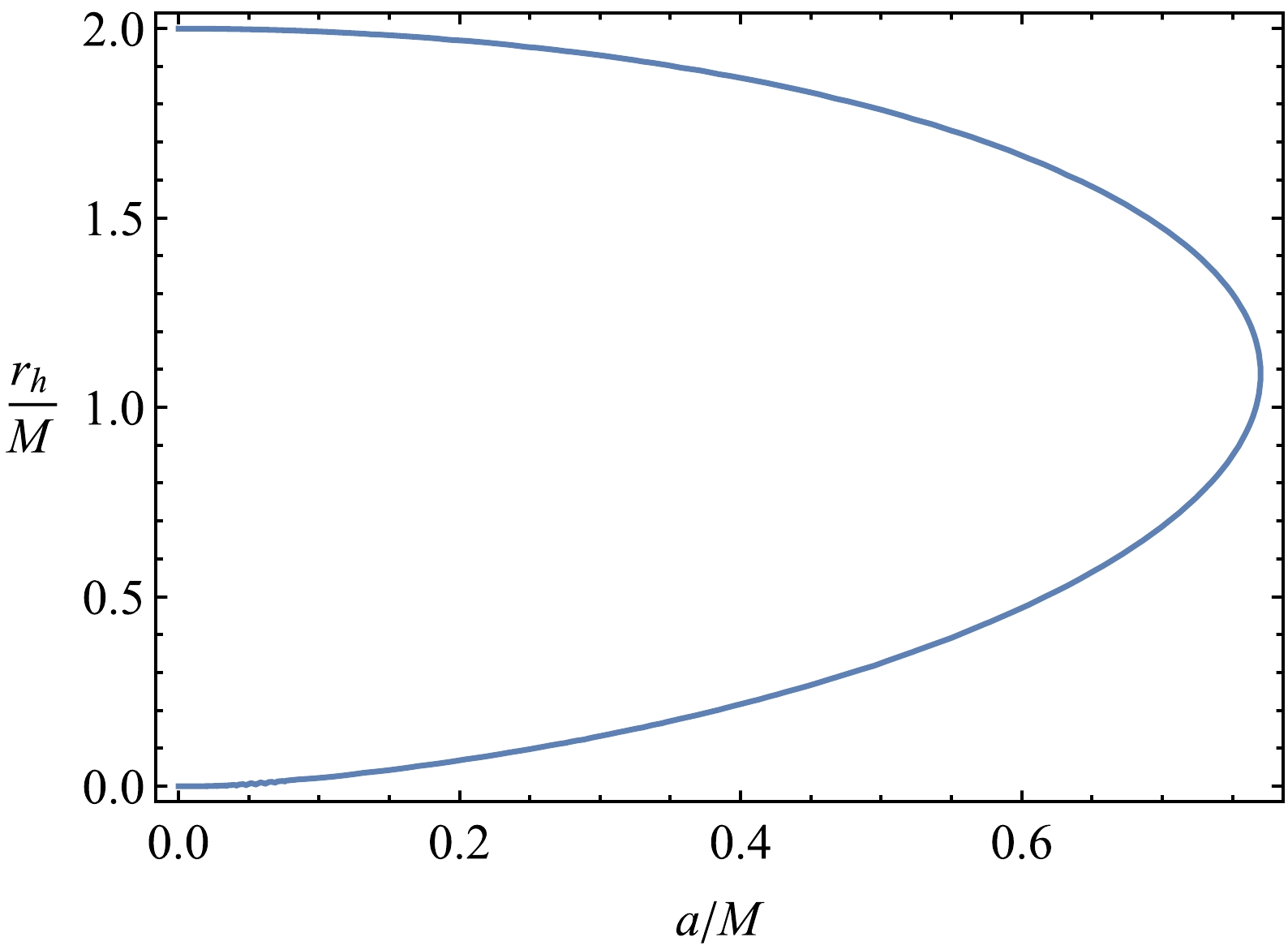
$ 0<a/m<4\sqrt{3}/9 $ is satisfied. To obtain more information about the spacetime structure, we can analyze the function$ f(r) $ . The dependence of$ f(r) $ on radial coordinates is shown in Fig. 1. From the plot, we can easily see that there is an extreme value of$ a/M $ when the graph has one$ r/M $ -intercept. The extreme value of the parameter$ a_{\rm ext}=4\sqrt{3}/9 $ . The values of parameter a that are less than its extreme value correspond to a black hole with two horizons (Fig. 2 shows the existence of two roots for a set of parameters a values, which corresponds to the Cauchy horizon (smaller root) and event horizon (larger root)), whereas the values of parameter a that are greater than its extreme value correspond to a naked singularity. The dependence of the radius of the horizon corresponding to the condition$ f(r)=0 $ is represented in Fig. 2. From the plot, we can see that with an increase in parameter a in black-bounce spacetime, the outer horizon decreases until the value M is reached. -
Consider the motion of photons around a gravitational object in the framework of black-bounce gravity. To describe the dynamics, we can use the Hamilton-Jacobi equation in the following form [85]:
$ g^{\mu\nu} \frac{{\rm d}S}{{\rm d}x^\mu}\frac{{\rm d}S}{{\rm d}x^\nu} = 0, $

(4) where
$ g^{\mu\nu} $ is the metric tensor of spacetime metric (1), and S is the action. Using the separation of variables method and the symmetry of spacetime metric (1), the action S can be expressed as the following form:$ \begin{array}{*{20}{l}} S = - Et +L\varphi + S_r(r) + S_\theta(\theta), \end{array} $

(5) where E and L can be described as the energy and angular momentum of a massless particle, respectively. The dynamics of particles with zero rest mass are defined by null geodesics of spacetime. Using Eqs. (4) and (5), we can obtain the equations of motion of massless particles at the equatorial plane (
$ \theta=0.5\pi $ ,$ \dot{\theta}=0 $ ) as$ \frac{{\rm d}t}{{\rm d}\lambda}= \frac{E}{f(r)}, $

(6) $ \frac{{\rm d}r}{{\rm d}\lambda}= \pm \sqrt{R(r)}, $

(7) $ \frac{{\rm d}\phi}{{\rm d}\lambda}=\frac{L}{\gamma(r)} , $

(8) with
$ R(r) = E^2-\frac{f(r)}{\gamma(r)} L^2, $

(9) where λ is the affine parameter, and we consider
$ \theta = 0.5\pi $ . Accordingly, the effective potential for the radial motion of photons takes the following form:$ V_{\rm eff} = f(r) \frac{{{L}^2}}{\gamma(r)}. $

(10) The study of circular orbits r reflects significant interest while considering the photon (massless particle) motion. Photon circular orbits
$ r_{\rm ph} $ are determined using the following conditions:$ \begin{array}{*{20}{l}} \qquad V'_{\rm eff} = 0. \end{array} $

(11) Using the above conditions, we can obtain the equation to determine the radius of circular photon orbits
$r_{\rm ph}$ as$ \begin{array}{*{20}{l}} \left(a^2+r^2\right)^{3/2}+2 M a^2-3 M r^2 = 0. \end{array} $

(12) We can obtain the radius of the photon sphere (
$r_{\rm ph})$ by solving Eq. (12) with respect to the radial coordinate,$ r_{\rm ph} = \sqrt{-a^2 \left(\frac{10 M^2}{D}+1\right)+D+\frac{9 M^4}{D}+3 M^2}\ , $

(13) where D is defined as
$ \begin{aligned}[b] D =& \Bigg(\frac{25 a^4 M^2}{2}-45 a^2 M^4 \\&+\frac{5\sqrt{5}}{2} a^3 M^2\sqrt{5 a^2-4 M^2}+27 M^6\Bigg)^{1/3}. \end{aligned} $

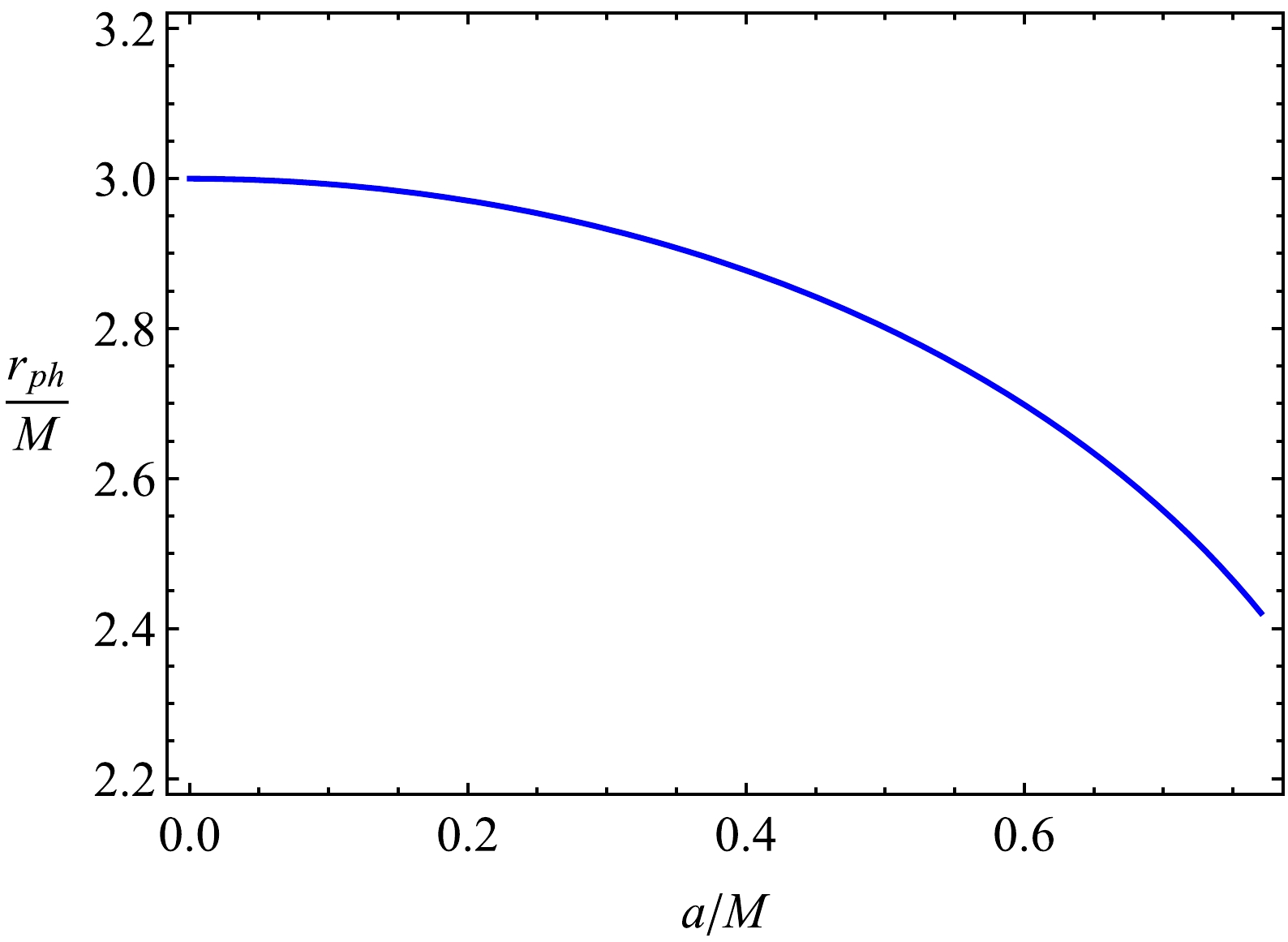
(14) The dependence of the photon orbit
$r_{\rm ph}$ on the parameter a is shown in Fig. 3. From the plot, we can conclude that with an increase in parameter a, the radius of the photon orbit$r_{\rm ph}$ decreases. -
The detailed study of photon motion around a black hole leads to a phenomenon known as a black hole shadow [16]. The shadow cast by a black hole is a result of photon capture by the central object, and the observer will see a black spot on the bright background [16]. In this section, we explore the radius (
$R_{\rm sh}$ ) of the shadow of a black hole in the presence of a plasma medium [55]. The boundary of the shadow is fully defined by the photon (massless particle) trajectory governed by the equation of motion in the plasma medium. To analyze the shadow of the black hole in black-bounce spacetime in a plasma medium, we should first study the photon equation in a plasma environment. -
The Hamiltonian for photons around a black hole in the presence of an electron plasma medium can be expressed as [55, 85]
$ {\cal H} = \frac{1}{2}\left[ g^{\mu\nu} p_\mu p_\nu - (n^2-1) \frac{p_t^2}{f(r)} \right]= 0, $

(15) with
$ n^2 = 1-\frac{\omega_e^2}{\omega^2(x^i)}, $

(16) where
$ \omega(x^i) $ and$ \omega_e $ are the photon and plasma frequencies, respectively, and n is the refractive index of the medium. We denote the value of the photon frequency observed at infinity as$ \omega_0 $ :$ \begin{array}{*{20}{l}} \omega(\infty)=\omega_0=-p_t. \end{array} $

(17) The components of the four-velocity (
$ \dot t $ ,$ \dot \phi $ ,$ \dot r $ ) for the photons (massless particle) in the equatorial plane ($ \theta=0.5\pi $ ,$ p_\theta=0 $ ) are given by$ \frac{{\rm d}t}{{\rm d}\lambda} = -\frac{p_t}{f(r)}, $

(18) $ \frac{{\rm d}r}{{\rm d}\lambda} = p_r f(r), $

(19) $ \frac{{\rm d}\phi}{{\rm d}\lambda} = \frac{p_\phi}{r^2+a^2}, $

(20) where we consider the relationship
${\rm d}x^\mu/{\rm d}\lambda = \partial {\cal H}/ \partial p_\mu$ . From Eqs. (19) and (20), we can obtain an expression for the phase trajectory of light (photon) rays,$ \frac{{\rm d}r}{{\rm d}\phi} = \frac{g^{rr}p^r}{g^{\phi\phi}p^\phi} $

(21) Using the constraint
$ {\cal H} = 0 $ , we can define the above equation as [50]$ \frac{{\rm d}r}{{\rm d}\phi} = \sqrt{\frac{g^{rr}}{g^{\phi\phi}}} \sqrt{h^2(r) \frac{\omega_0^2}{p_\phi^2}-1}, $

(22) where the following definition is introduced:
$ h^2(r) \equiv -\frac{g^{tt}}{g^{\phi\phi}} - \frac{1}{g^{\phi\phi}}\frac{\omega_e^2(r)}{\omega_0^2}. $

(23) The radius of a circular orbit of photons
$r_{\rm ph}$ , particularly the one that forms the photon sphere of radius$r_{\rm ph}$ , is determined by the following equation [50]:$ \left.\frac{{\rm d}(h^2(r))}{{\rm d}r}\right\vert_{r=r_{\rm ph}} = 0. $

(24) Substituting Eq. (24) into Eq. (23), we can define an algebraic expression for
$r_{\rm ph}$ in the plasma environment as$ \frac{\left(a^2+r^2\right) f'(r)}{f(r)}+\frac{2 f(r) \omega_e (r) }{\omega_0^2} \left[\left(a^2+r^2\right) \omega_e '(r)+r \omega_e (r)\right] = 2 r, $

(25) where the prime stands for the derivative with respect to r. In the case of homogeneous plasma (
$\omega_e^2(r)={\rm const.}$ ), Eq. (25) can be simplified to$ \frac{\left(a^2+r^2\right) f'(r)}{f(r)}+2 r f(r)\frac{\omega_e^2}{\omega_0^2}=2 r. $

(26) As mentioned above, the solution to this equation with respect to r leads to the radius of the photon sphere
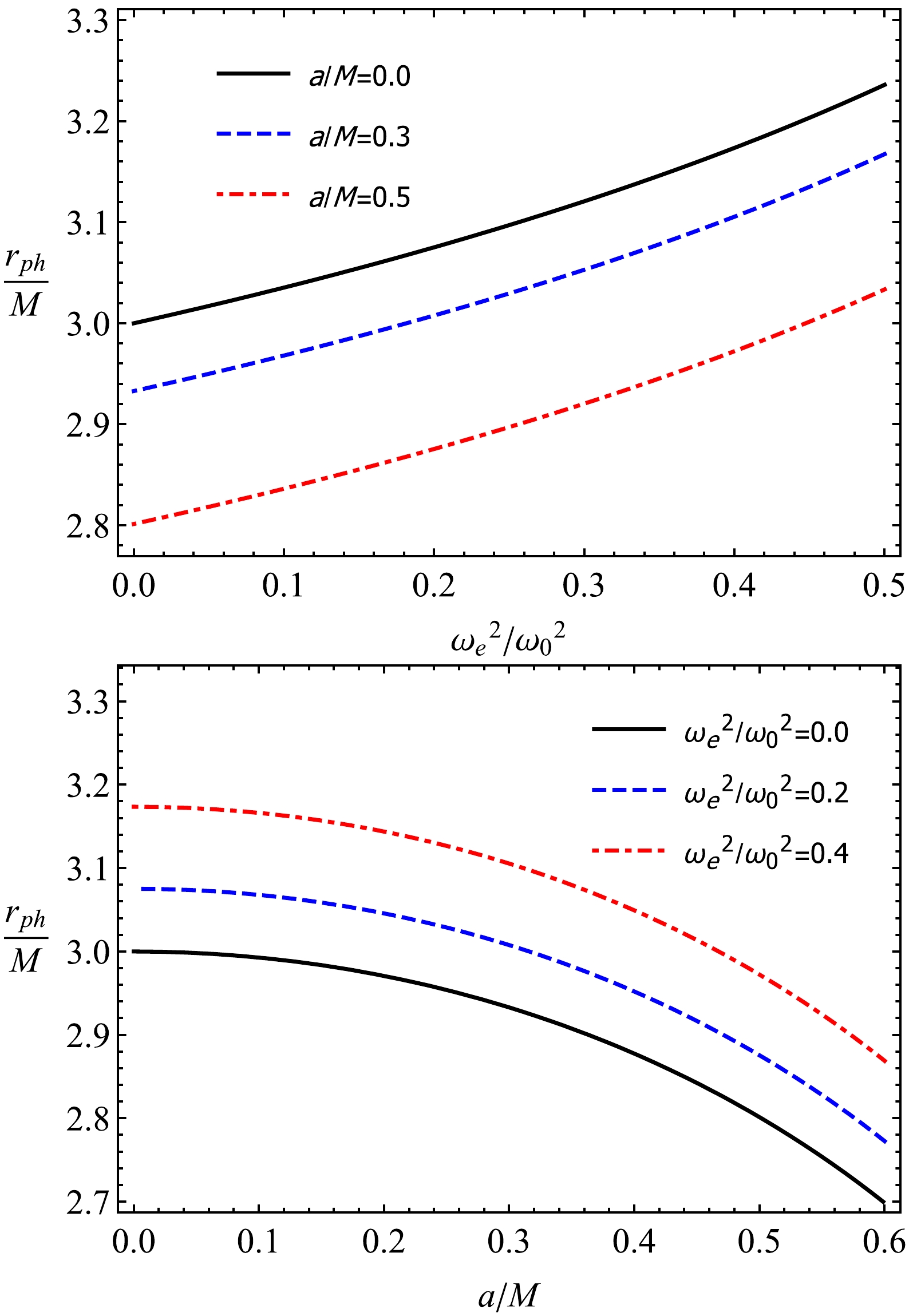
$ r_{\rm ph} $ of the black hole in a uniform plasma environment.Figure 4 gives information on the dependence of the radius of the photon sphere
$r_{\rm ph}$ on the black-bounce parameter a and plasma parameters. It is clear from the plots that the radius of the photon sphere$r_{\rm ph}$ decreases with an increase in parameter a. Note that the presence of plasma causes an increase in the value of the photon sphere radius, as shown in Fig. 4. -
In this section, we study the radius (
$R_{\rm sh}$ ) of the shadow of the black hole in the presence of uniform plasma. The angular radius$\alpha_{\rm sh}$ of the black hole shadow is defined by [7, 50]$ \sin^2{\alpha_{\rm sh}} = \frac{h^2(r_{\rm sh})}{h^2(r_o)} = \frac{\left(a^2+r_{\rm ph}^2\right) \left(\dfrac{1}{f(r_{\rm ph})}-\dfrac{\omega _e^2(r_{\rm ph})}{\omega _0^2}\right)}{\left(a^2+r_o^2\right) \left(\dfrac{1}{f(r_o)}-\dfrac{\omega _e^2(r_o)}{\omega _0^2}\right)}, $

(27) where
$ r_o $ and$r_{\rm ph}$ are the radial positions of the observer and photon sphere (introduced in the previous section), respectively. If the observer is located at a sufficiently large distance from the black hole, we can approximate the radius of the black hole shadow (for the case of uniform plasma) using Eq. (27) [50]:$ R_{\rm sh} \simeq r_o \sin{\alpha_{\rm sh}} = \sqrt{\left(a^2+r_{\rm ph}^2\right) \left(\frac{1}{f(r_{\rm ph})}-\frac{\omega _e^2}{\omega _0^2}\right)}. $

(28) For the case of no plasma in the vicinity of the black-bounce black hole, the shadow radius can be represented by
$ R_{\rm sh} \simeq r_o \sin{\alpha_{\rm sh}} = \sqrt{\frac{a^2+r_{\rm ph}^2}{f(r_{\rm ph})}}. $

(29) Figure 5 describes the dependence of the radius of black hole shadow on parameter a and plasma parameters. In the plots, we define
$R_{\rm sh}$ in terms of$M_{\rm eff}$ because it is known from EHT data that the masses of M87* and Sgr A* are given by the gravitational potential. Based on these data, we can conclude that the shadow radius is diminished due to the influence of both plasma and the black-bounce parameter a.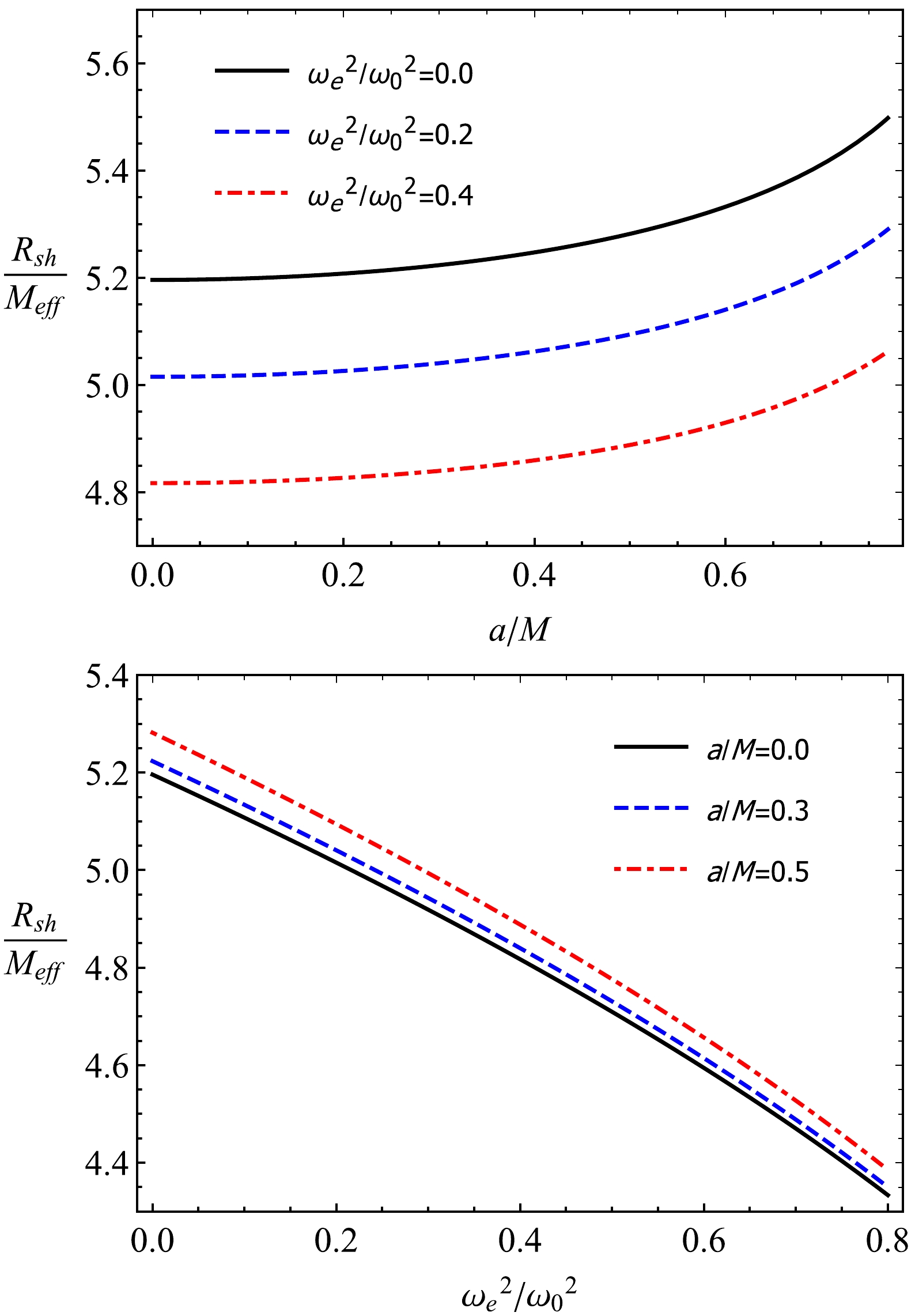
Figure 5. (color online) Dependence of the radius of the black hole shadow on parameter a (top) and plasma frequency (bottom).
Now, we consider the rough assumption that the supermassive black holes M87* and Sgr A* are the black-bounce black holes that we are studying. Then, we can theoretically obtain the constraints from the EHT observation results.
The angular diameter of the image of the supermassive black hole M87* is
$\theta=42\pm3~{\rm \mu as}$ at the$ 1\sigma $ confidence level, and the mass of M87* and the distance from the solar system are$ M=6.5\times10^9M_\odot $ and$D=$ 16.8 Mpc, respectively [3, 4]. The same data for Sgr A* are as follows:$\theta=48.7\pm7~{\rm \mu as}$ ,$ M\simeq4\times10^6M_\odot $ , and$ D\simeq 8 $ kpc [5]. The shadow radius caused by the black hole per unit mass can be expressed as the following equation:$ d_{\rm sh} = \frac{D \theta}{M_{\rm eff}} , $

(30) where
$M_{\rm eff}=M\Big({r}/{\sqrt{r^2+a^2}}\Big)^3$ from black-bounce spacetime. Here, we must use the effective mass because the masses of M87 and Sgr A* are given by the gravitational potential.Using Eq. (30), we can easily calculate the diameter of the shadow images. The diameter of the black hole shadow is
$d_{\rm sh}=(11\pm1.5)M_{\rm eff}$ for M87* and$d_{\rm sh}=(9.5\pm 1.4)M_{\rm eff}$ for Sgr A*. From these data, we can now obtain the constraints on the black-bounce and plasma parameters for the supermassive black holes Sgr A* and M87*. The results are presented in Fig. 6 for the case of no plasma around the black hole and in Fig. 7 for the black hole in plasma.
Figure 6. (color online) Constraints on the black-bounce parameter a with no plasma around the black hole. The brown and black dashed lines describe the limits of the measured shadow radii of M87* and Sgr A*, respectively.
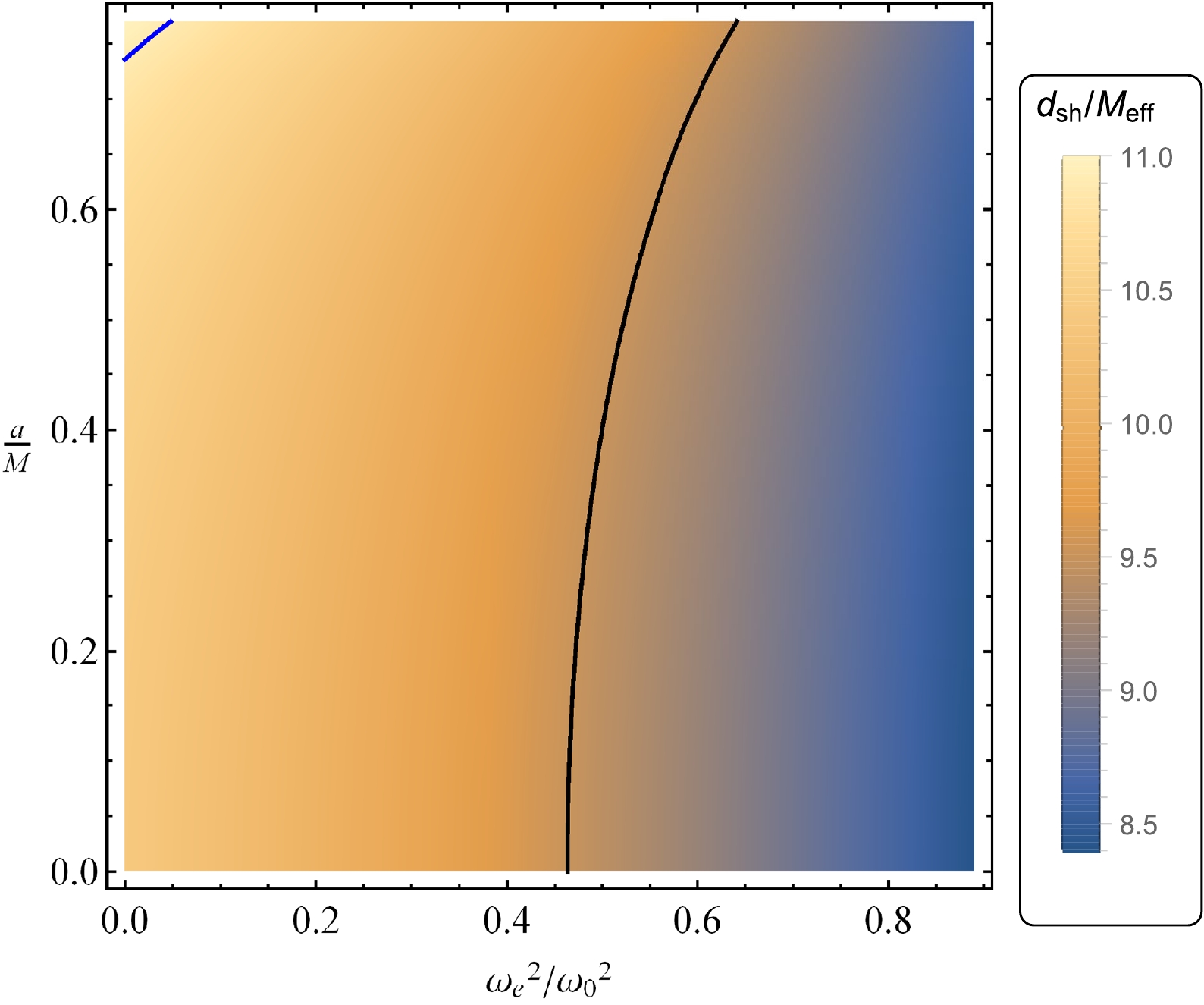
Figure 7. (color online) Shadow diameter of the black-bounce black hole as a function of the parameter a and plasma parameter. The black curve corresponds to
$d_{\rm sh}=9.5M_{\rm eff}$ , which is the lower limit for M87*. The blue curve corresponds to$d_{\rm sh}=10.9 M_{\rm eff}$ , which is the upper limit for Sgr A*. -
Now, we can move on to another part of our study: gravitaional lensing in spacetime metric (1) in a weak-field case explicated via [59]
$ \begin{array}{*{20}{l}} g_{\alpha\beta} = \eta_{\alpha\beta} + \xi_{\alpha\beta}\ , \end{array} $

(31) where
$ \eta_{\alpha\beta} $ is the general metric of Minkowski spacetime, and$ \xi_{\alpha\beta} $ is a perturbation of the flat spacetime metric, which can be described by the spacetime metric theory of gravity and is written as [59]$ \begin{array}{*{20}{l}} &&\eta_{\alpha\beta} = {\rm diag} (-1, 1, 1, 1),\\ && \xi_{\alpha\beta} \ll 1, \quad \xi_{\alpha\beta} \rightarrow 0 \quad {\rm under } \quad x^i\rightarrow \infty\ , \\ && g^{\alpha\beta}=\eta^{\alpha\beta}-\xi^{\alpha\beta},\ \ \ \xi^{\alpha\beta}=\xi_{\alpha\beta}\ . \end{array} $

(32) Here, we can study the effects of the plasma medium on the deflection angle
$ \hat{\alpha}_k $ in the gravitational weak field of the black hole. The general expression for the deflection angle in plasma is [59, 64]$ \hat{\alpha}_i= \frac{1}{2} \int_{-\infty}^\infty \left(\xi_{33} +\frac{\xi_{00} \omega^2-K_e N(x^i)}{\omega^2-\omega_e^2}\right)_{,i} {\rm d}z, \ \ i=1,2 $

(33) where
$ N(x^i) $ is the number density of particles in a plasma medium around a compact object,$ K_{e}=4\pi e^2/m_{e} $ is constant (e and$ m_e $ are the electron charge and mass), and ω and$ \omega_e $ are the photon (massless particle) and plasma frequencies, respectively [59]. Using Eqs. (32) and (33), we can rewrite Eq. (33) for the deflection angle in the following form [59]:$ \begin{aligned}[b] \hat{\alpha}_b=& \frac{1}{2} \int_{-\infty}^\infty \frac{b}{r}\Big(\frac{{\rm d}\xi_{33}}{{\rm d}r}+\frac{1}{1-\omega_e^2/\omega^2}\frac{{\rm d}\xi_{00}}{{\rm d}r} \\&-\frac{K_{e}}{\omega^2-\omega_e^2}\ \frac{{\rm d}N}{{\rm d}r}\Big) {\rm d}z, \end{aligned} $

(34) where b is the impact parameter of light rays. It is useful to note that the values of
$ \hat{\alpha}_b $ can be both negative and positive [59].In the weak-field case for far distances from the black hole, the black-bounce spacetime metric (1) can be written as
$ \begin{aligned}[b] {\rm d}s^2 =& {\rm d}s^2_{0} + \frac{2 M r^2}{(a^2+r^2)^{3/2}} {\rm d}t^2 + \frac{2 M r^2}{(a^2+r^2)^{3/2}} {\rm d}r^2 \\& + a^2({\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2), \end{aligned} $

(35) where
${\rm d}s^2_{0}=-{\rm d}t^2+{\rm d}r^2+r^2({\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2)$ is the metric element in the Minkowski spacetime metric, and we can use the notation$ R_s=2M $ for further calculations.To analyze the deflection angle (
$ \hat{\alpha}_b $ ) of light rays around the black hole in the plasma medium using Eq. (34), we can rewrite the required components ($ \xi_{00} $ and$ \xi_{33} $ ) in Cartesian coordinates as$ \begin{aligned}[b] \xi_{00}=&\frac{R_s r^2}{(a^2+r^2)^{3/2}}, \\ \xi_{33}=&\frac{R_s r^2}{(a^2+r^2)^{3/2}}\cos^2\chi + \frac{a^2}{r^2}\sin^4\chi \ , \end{aligned} $

(36) where
$ \cos^2\chi=z^2/(b^2+z^2) $ and$ r^2=b^2+z^2 $ are introduced, for example, in [64]. Here, z is the coordinate aligned with the optical axis. We can obtain the derivative of$ \xi_{00} $ and$ \xi_{33} $ with respect to the radial coordinate as$ \begin{aligned}[b] \frac{{\rm d}\xi_{33}}{{\rm d}r}=& -\frac{3 r R_s z^2}{\left(a^2+r^2\right)^{5/2}}-\frac{2 a^2 \left(r^4-4 r^2 z^2+3 z^4\right)}{r^7}, \\ \frac{{\rm d}\xi_{00}}{{\rm d}r}=& \frac{R_s \left(2 a^2 r-r^3\right)}{\left(a^2+r^2\right)^{5/2}}. \end{aligned} $

(37) For simplicity, the expression for the deflection angle
$ \hat{\alpha}_b $ can be expanded as [63]$ \begin{array}{*{20}{l}} &&\hat{\alpha}_b=\hat{\alpha}_1+\hat{\alpha}_2+\hat{\alpha}_3, \end{array} $

(38) with
$ \begin{aligned}[b] \hat{\alpha}_1=&\frac{1}{2} \int_{-\infty}^\infty \frac{b}{r}\frac{{\rm d}\xi_{33}}{{\rm d}r} {\rm d}z, \\ \hat{\alpha}_2=&\frac{1}{2} \int_{-\infty}^\infty \frac{b}{r}\Bigg(\frac{1}{1-\omega_e^2/\omega^2}\frac{{\rm d}\xi_{00}}{{\rm d}r}\Bigg) {\rm d}z, \\ \hat{\alpha}_3=&\frac{1}{2} \int_{-\infty}^\infty \frac{b}{r}\Bigg(-\frac{K_{e}}{\omega^2-\omega_e^2}\ \frac{{\rm d}N}{{\rm d}r}\Bigg) {\rm d}z, \\ \end{aligned} $

(39) where the notations
$ \hat{\alpha}_1 $ ,$ \hat{\alpha}_2 $ , and$ \hat{\alpha}_3 $ represent the contributions to the deflection angle due to gravity, uniform plasma, and non-uniform plasma, respectively. In this study, we use Eqs. (38) and (39) to investigate the effect of plasma on the deflection angle in gravitational weak lensing. In the following sections, we consider each case in detail. -
Here, we can test the deflection angle of photons (light rays) around the black hole in the presence of a uniform plasma environment using expression (38) written in the following form:
$ \begin{array}{*{20}{l}} &&\hat{\alpha}_{\rm uni}=\hat{\alpha}_{\rm uni1}+\hat{\alpha}_{{\rm uni}2}+\hat{\alpha}_{{\rm uni}3}, \end{array} $

(40) We can claim that the third term of this equation will vanish due to the uniform distribution of the plasma environment. Using Eqs. (38), (37), and (40), we can obtain an equation for the deflection angle of light rays (photon) around the black hole in black-bounce spacetime surrounded by uniform plasma:
$ \hat\alpha_{\rm uni} = \frac{b R_s}{a^2+b^2}+\frac{3 \pi a^2}{16 b^2} - \frac{b R_s \left(a^2-b^2\right)}{ \left(a^2+b^2\right)^2} \frac{\omega^2}{\omega^2-\omega_{e}^2}. $

(41) In this equation, the second term appears owing to the property of black-bounce spacetime itself.
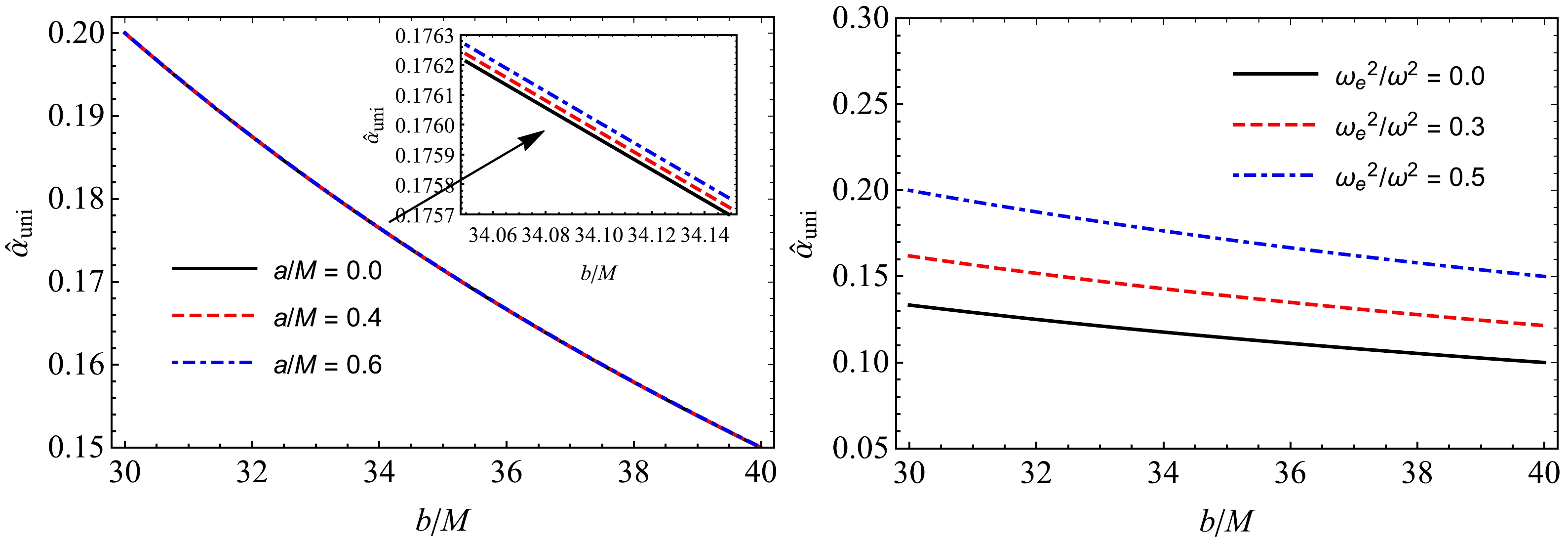
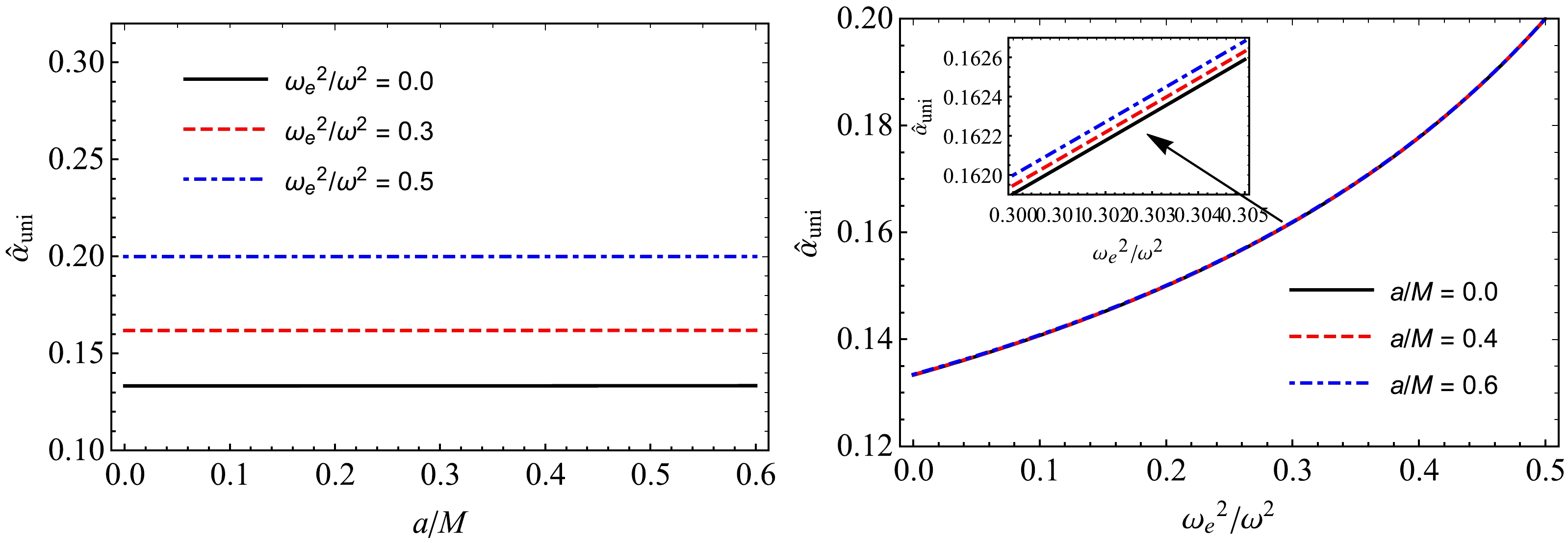
Using expression (41), we can plot the deflection angle against the impact b, plasma frequency, and a. Fig. 8 shows the dependence of the deflection angle
$\hat \alpha_{\rm uni}$ of light rays (photon) around the black hole on the impact parameter b for different values of the parameter a and plasma parameter$ \omega_{e}^2/\omega^2 $ . The dependence of the deflection angle$\hat \alpha_{\rm uni}$ plasma frequency and parameter a for fixed values of the impact parameter is shown in Fig. 9. The graphs of the defection angle$\hat \alpha_{\rm uni}$ on the impact parameter b and plasma parameter are reliable, as expected. The presence of uniform plasma leads to an increase in the value of the deflection angle of light rays, whereas the angle of deflection decreases dramatically with increasing impact parameter b. However, interestingly, the deflection angle remains almost unchanged with the influence of the black-bounce parameter a. There is only a slight increase in the value of the deflection angle with an increase in parameter a, as shown in Figs. 8 and 9. -
Here, we investigate the deflection angle
$\hat \alpha_{\rm uni}$ of light rays (photons) around the black hole in the presence of non-uniform plasma and in the framework of black-bounce spacetime with a nonzero parameter a. We can consider the singular isothermal sphere (SIS) medium as the non-uniform plasma distribution [59, 64]. The plasma number density of the SIS environment is written in the following form [59, 63]:$ N(r)=\frac{\rho(r)}{k m_p}\ , $

(42) where
$ m_p $ is the proton mass, and k is a non-dimensional coefficient responsible for the dark matter contribution in the SIS model and with$ \rho(r)=\frac{\sigma^2_{\nu}}{2 \pi r^2}\ , $

(43) where
$ \sigma_\nu $ and$ \rho(r) $ are the velocity of dispersion and the density of plasma around the compact object, respectively [59]. Here, Eq. (38) can be written in the non-uniform plasma case as [63]$ \begin{array}{*{20}{l}} &&\hat{\alpha}_{\rm SIS}=\hat{\alpha}_{\rm SIS1}+\hat{\alpha}_{\rm SIS2}+\hat{\alpha}_{\rm SIS3}\ , \end{array} $

(44) where
$\hat{\alpha}_{\rm SIS1}$ ,$\hat{\alpha}_{\rm SIS2}$ , and$\hat{\alpha}_{\rm SIS3}$ represent the deflection angle due to the gravity of the black hole, due to plasma, and due to the density of the non-uniform plasma medium around the compact object in black-bounce spacetime, respectively. From Eqs. (38), (37), and (44), we can obtain an equation for the deflection angle of light rays (photons) around the black hole in black-bounce surrounded by non-uniform plasma:$ \hat\alpha_{\rm SIS} = \frac{3 \pi a^2}{16 b^2}+\frac{2 b^3 R_s}{\left(a^2+b^2\right)^2} +\frac{R_s^2 \omega_c^2}{2 b^2 \omega^2} + \frac{2 b R_s^3 \omega_c^2 \left(5 b^2-7 a^2\right)}{15 \pi \omega^2 \left(a^2+b^2\right)^3}, $

(45) where the new notation for the non-uniform case is
$ \omega_c^2= \frac{\sigma^2_{\nu} K_e}{2 k m_p R^2_{s}}. $

(46) In Fig. 10, we show the plasma effect of non-uniform plasma and the parameter a on the deflection angle of photons around the black hole in black-bounce spacetime. The dependence of the deflection angle
$\hat{\alpha}_{\rm SIS}$ on non-uniform plasma and the parameter a for fixed values of the impact parameter b and the non-uniform plasma parameter is clearly shown in Fig. 11. The plots reveal that the deflection angle increases gradually with increasing plasma parameter, whereas there is a small change in the value of the deflection angle due to the influence of parameter a.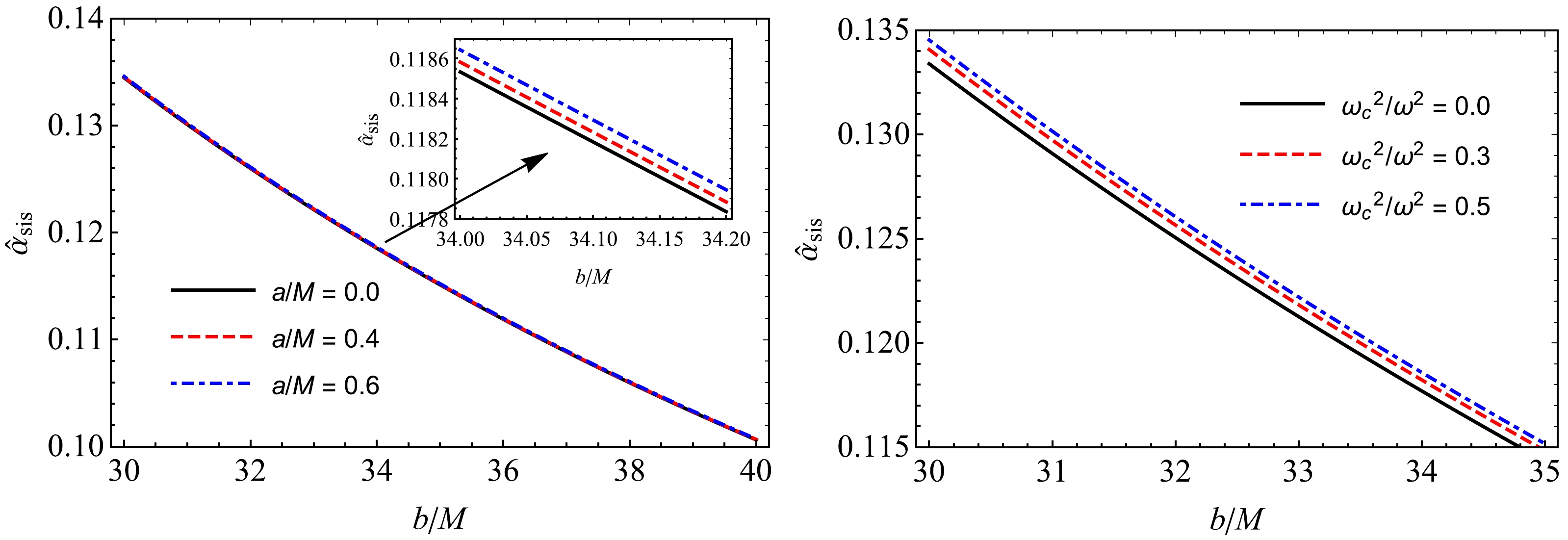
Figure 10. (color online) Dependence of the deflection angle
$\hat \alpha_{\rm SIS}$ on the impact parameter b for different values of the parameter$ a/M $ (left panel) and non-uniform plasma parameter (right panel).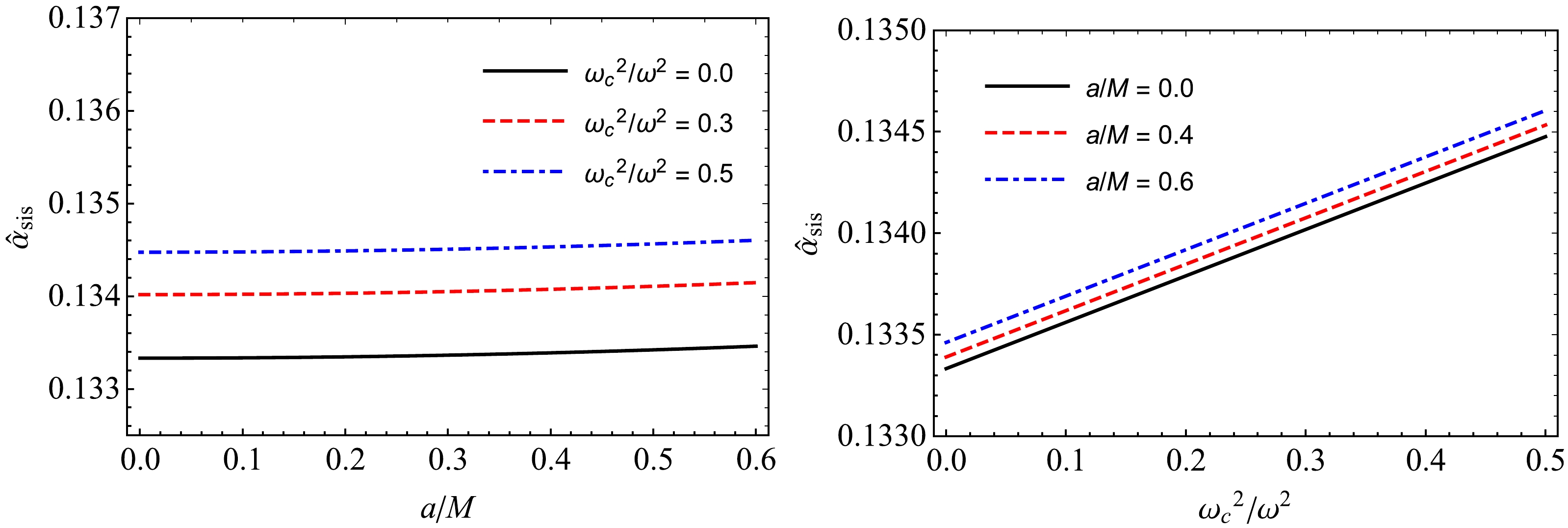
Figure 11. (color online) Dependence of the deflection angle
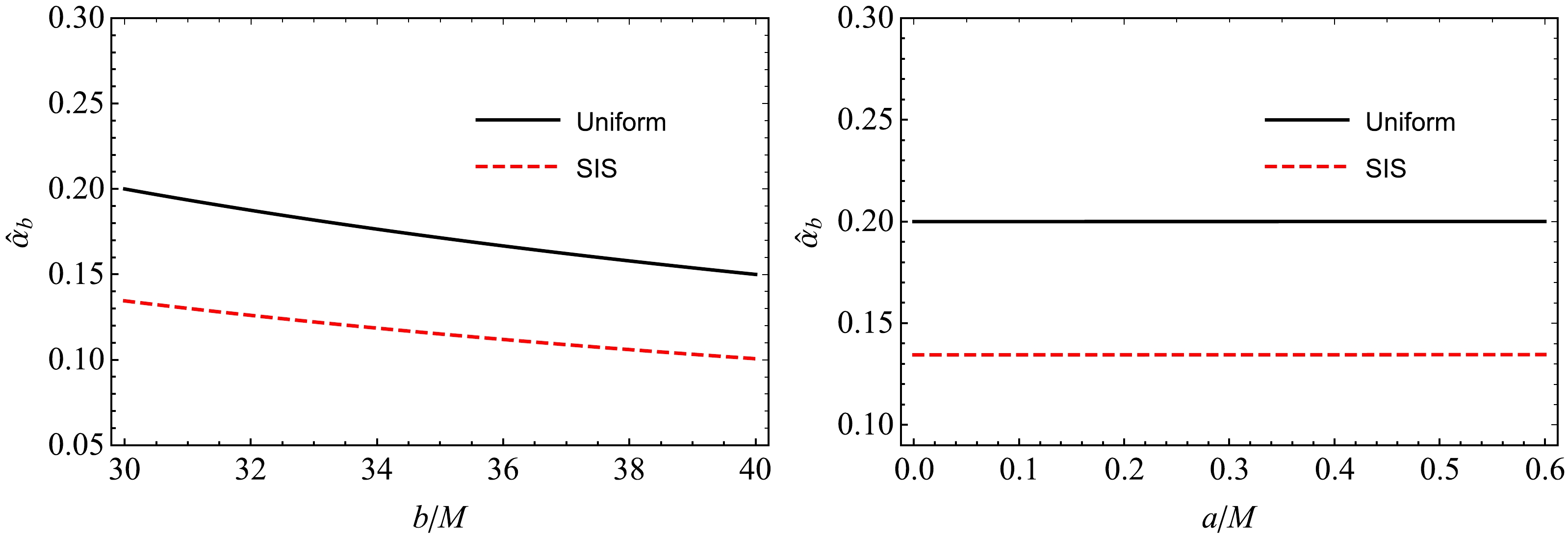
$\hat\alpha_{\rm SIS}$ on the parameter$ a/M $ (left panel) and non-uniform plasma parameter (right panel) for a fixed value of the impact parameter$ b/M=30 $ .We can easily compare the two cases for analysis (uniform and non-uniform) with the help of Fig. 12. It is evident that the deflection angle of light rays (photons) in the presence of a uniform plasma medium is larger than that of the non-uniform plasma case.
-
Now, we can study the brightness of an image source as a consequence of gravitational lensing in the presence of uniform plasma using a lens equation in the form [64, 76]
$ \begin{array}{*{20}{l}} \theta D_s=\beta D_s +\hat{\alpha}_{b} D_{ds}\ , \end{array} $

(47) where
$ D_s $ and$ D_{ds} $ are the distances from the distant source to the observer and the lens object, respectively, and θ and β represent the angular positions of the image and source, respectively. We use the following relation between the impact parameter b and angle θ:$ \begin{array}{*{20}{l}} b=D_d\theta, \end{array} $

(48) where
$ D_d $ is the distance from the observer to the lens object. Using these expressions, we can rewrite Eq. (47) as [64, 76]$ \beta = \theta - \frac{D_{ds}}{D_s}\frac{F(\theta)}{D_d} \frac{1}{\theta} \ , $

(49) with
$ F(\theta)=|\alpha_b| b=|\alpha_b (\theta)| D_d \theta. $

We can write the expression for Einstein's angle
$ \theta_E^{pl} $ in the presence of uniform plasma around a black-bounce black hole using Eq. (41),$ \theta_E^{\rm pl}=\frac{D_{ds}}{D_{s}}\hat\alpha_{\rm uni}(b). $

(50) We numerically determine the angle by solving this equation to analyze the dependence of the magnification on the black hole parameter.
It is well-known that the general equation to compute the magnification of an image source can be expressed in the following form [59]:
$ \mu_\Sigma=\frac{I_{\rm tot}}{I_{*}}=\sum\limits_k \left| \left(\frac{\theta_k}{\beta}\right) \left(\frac{{\rm d}\theta_k}{{\rm d}\beta}\right) \right| \ , \quad k=1,2, ..., s\ , $

(51) where s denotes the total number of images of the source, and
$ I_{\rm tot} $ can be explained as the value of the total increased brightness due to multiple images of the source with brightness$ I_{*} $ .From Eq. (51), we can obtain the expression for the magnification of the image source as
$ \mu_{\rm tot}^{\rm pl}=\mu_+^{\rm pl}+\mu_-^{\rm pl}=\frac{x_{\rm uni}^2+2}{x_{\rm uni}\sqrt{x_{\rm uni}^2+4}}\ , $

(52) where
$ x_{\rm uni}=\frac{\beta}{(\theta_E^{\rm pl})_{\rm uni}} . $

(53) The magnification of the image source is written as
$ \left(\mu_+^{\rm pl}\right)_{\rm uni}=\frac{1}{4}\Bigg(\frac{x_{\rm uni}}{\sqrt{x_{\rm uni}^2+4}}+\frac{\sqrt{x_{\rm uni}^2+4}}{x_{\rm uni}}+2\Bigg)\ , $

(54) $ \left(\mu_-^{\rm pl}\right)_{\rm uni}=\frac{1}{4}\Bigg(\frac{x_{\rm uni}}{\sqrt{x_{\rm uni}^2+4}}+\frac{\sqrt{x_{\rm uni}^2+4}}{x_{\rm uni}}-2\Bigg)\ . $

(55) Using Eq. (52), we present the dependence of the total magnification on the plasma parameter for different values of parameter a in Fig. 13. From these plots, we can conclude that the total magnification of the images increases owing to the influence of uniform plasma, and there is a slight change in the total magnification with an increase in the parameter a.
-
In this study, particle orbits around black holes in black bounce gravity are studied in detail. The results obtained can be summarized as follows:
● We calculate the horizon radius for various values of the black bounce parameter a. The results show that the radius of the horizon
$ r_{h} $ decreases in the presence of the parameter a in black-bounce spacetime.● We analyze the photon orbits around a black-bounce compact object. It is shown that orbits shift toward the central object because of black bounce gravity.
● We obtain and discuss the observable shadow of the black hole described by the black-bounce spacetime metric in plasma. We reveal that the shadow radius (
$R_{\rm sh}$ ) of the black hole decreases with an increase in both the black-bounce parameter a and plasma frequency (Fig. 5). The tendency of the black hole shadow size to decrease with an increase in parameter a can be explained in a similar way to that of photon deflection. The effect of parameter a decreases the gravitational effect of the central object on photons, and we may observe a decrease in the size of the shadow in the black-bounce spacetime metric. The negative effect of parameter a on photon orbits may be useful in obtaining constraints using current and future observation of the black hole shadow with event horizon telescopes.● We also study the effect of weak gravitational lensing around the black hole in black bounce spacetime in the presence of a plasma medium around a compact object. Here, uniform and non-uniform cases are considered and discussed in detail (see. Figs. 8−12).
● For the non-uniform case, we find that the plasma frequency depends on
$ 1/r $ . The deflection angle around compact objects increases with increasing value of the parameter a. We also compare the uniform and non-uniform cases and find that the deflection angle is larger in uniform plasma than in non-uniform plasma.● Additionally, we consider the magnification of the image using the deflection angle of light rays, which is clearly represented in Fig. 13.
Photon motion and weak gravitational lensing in black-bounce spacetime
- Received Date: 2023-05-10
- Available Online: 2023-11-15
Abstract: The effect of spacetime curvature on photon motion may offer an opportunity to propose new tests on gravity theories. In this study, we investigate and focus on the massless (photon) particle motion around black-bounce gravity. We analyze the horizon structure around a gravitational compact object described by black-bounce spacetime. The photon motion and the effect of gravitational weak lensing in vacuum and plasma are discussed, and the shadow radius of the compact object is also studied in black-bounce spacetime. Additionally, the magnification of the image is studied using the deflection angle of light rays.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: