-
Since enhanced ϕ yield was first suggested as a signature for the formation of quark-gluon plasmas [1, 2], many measurements on ϕ mesons have been made in relativistic heavy-ion collisions, such as Au-Au collisions at the BNL Relativistic Heavy Ion Collider [3−11] and Pb-Pb collisions at the CERN Large Hadron Collider [12−15]. Measured ratios such as
$ \phi/\pi $ ,$ \phi/K $ , and$ \Omega/\phi $ exhibit enhancement in ϕ mesons produced in relativistic heavy-ion collisions relative to p+p collisions. This indicates that strange quarks and strange antiquarks are produced in parton-parton scattering in initial nucleus-nucleus collisions and deconfined matter. The combination of a strange quark and strange antiquark forms a ϕ meson at the hadronization of quark-gluon plasma. The ϕ meson in collisions with hadrons in hadronic matter may be broken, and this changes the ϕ yield. For example, the ϕ nuclear modification factor as a function of transverse momentum is smaller than 1 for central and midcentral Au-Au collisions at the center-of-mass energy per nucleon-nucleon pair$ \sqrt{s_{NN}}=200 $ GeV [3, 6] and for central and midcentral Pb-Pb collisions at$ \sqrt{s_{NN}}=2.76 $ TeV [13]. Therefore, studying inelastic hadron-ϕ scattering is fundamental in relativistic heavy-ion collisions.Hadron-ϕ reactions can be studied in hadron degrees of freedom [16−22] or quark degrees of freedom [23, 24]. Starting from an effective meson Lagrangian, Feynman diagrams with one-kaon exchange have been considered, and squared invariant amplitudes for
$ \pi \phi \to K\bar{K}^* +K^*\bar{K} $ ,$ \rho \phi \to K\bar K $ , and$ \phi \phi \to K\bar K $ were provided in Ref. [17]. By using a Lagrangian based on an effective theory in which vector mesons are identified as the dynamical gauge bosons of the hidden$ U(3)_V $ local symmetry in the$ U(3)_L \times U(3)_R/U(3)_V $ nonlinear sigma model, large cross sections for$ K^* \phi \to \pi K $ and$ K\phi \to \pi K^* $ were obtained in Ref. [22]. With$ \pi \phi \rho $ coupling, cross sections for$ \phi N \to \pi N $ ,$ \phi N \to \rho N $ , and$ \phi N \to \pi \Delta $ were obtained in Ref. [20]. With$ N\Lambda K $ coupling, cross sections for$ \phi N \to K\Lambda $ were shown to be considerably larger than those for$ \phi N \to \pi N $ ,$ \phi N \to \rho N $ , and$ \phi N \to \pi \Delta $ . Experimental efforts to extract the$ \phi +N $ total cross section from$ d(\gamma,pK^+K^-)n $ have been made by the CLAS Collaboration [25]. The$ \phi +N $ cross section may lead to a difference in ϕ production between$ \pi^- $ -induced reactions on C and W targets [26]. Inelastic$ \pi+\phi $ scattering and inelastic$ \rho+\phi $ scattering were studied in Ref. [23] in the quark interchange mechanism [27, 28]. By adopting temperature dependence in a quark potential, mesonic quark-antiquark wave functions, and meson masses, prominent temperature-dependent cross sections were obtained for inelastic$ \pi+\phi $ and$ \rho+\phi $ scattering in hadronic matter [23]. Besides pions and rho mesons, kaons in hadronic matter also interact with ϕ mesons. However, the quark-level study of inelastic$ K+\phi $ scattering has not yet been conducted. Moreover, the temperature dependence of inelastic$ K+\phi $ scattering is unexplored both experimentally and theoretically. Therefore, this study aims to investigate inelastic$ K+\phi $ scattering and its temperature dependence.Some meson-meson reactions may be dominated by the process of a quark and an antiquark annihilating into a gluon, followed by the gluon creating another quark-antiquark pair. Such quark-antiquark annihilation and creation has been used in Refs. [29, 30] to obtain unpolarized cross sections for the reactions
$ \pi \pi \to \rho \rho $ ,$ K \bar {K} \to K^* \bar {K}^\ast $ ,$ K \bar{K}^\ast \to K^* \bar{K}^\ast $ ,$ K^\ast \bar{K} \to K^* \bar{K}^\ast $ ,$ \pi \pi \to K \bar K $ ,$ \pi \rho \to K \bar {K}^\ast $ ,$ \pi \rho \to K^* \bar{K} $ ,$ K \bar {K} \to \rho \rho $ ,$ K \bar {K} \to K \bar {K}^\ast,\; K \bar{K} \to K^* \bar{K}, \; \pi K \to \pi K^\ast,\; \pi K \to \rho K, \; \pi \pi \to K \bar{K}^\ast,\; \pi \pi \to K^\ast \bar{K}, \; \pi \pi \to K^\ast \bar{K}^\ast, \; \pi \rho \to K \bar{K}, \; \pi \rho \to K^\ast \bar{K}^\ast, \, \rho \rho \to K^\ast \bar{K}^\ast, \; K \bar{K}^\ast \to \rho \rho $ ,and$ K^* \bar{K} \to \rho \rho $ . The s quark (or$ \bar s $ antiquark) of a kaon may annihilate with the$ \bar s $ antiquark (or s quark) of a ϕ meson to produce a gluon, and subsequently, the gluon splits into a$ u\bar u $ or$ d\bar d $ pair. The$ u\bar u $ or$ d\bar d $ pair combines with spectator constituents of the K and ϕ mesons to form two mesons that are not ϕ mesons. Thus, quark-antiquark annihilation and creation leads to inelastic$ K+\phi $ scattering. By contrast, quark interchange does not cause inelastic$ K+\phi $ scattering. The mechanism that governs inelastic$ K+\phi $ scattering completely differs from the mechanism that governs inelastic$ \pi+\phi $ and$ \rho+\phi $ scattering. Therefore, with quark-antiquark annihilation and creation in the first Born approximation, we study the reactions$ K\phi\to\pi K $ ,$ K\phi\to\rho K $ ,$ K\phi\to\pi K^* $ , and$ K\phi\to\rho K^* $ .The remainder of this paper is organized as follows. In the next section, we derive transition-amplitude formulas for 2-to-2 meson-meson scattering driven by quark-antiquark annihilation and creation. Numerical results and relevant discussions are given in Sec. III. A summary is presented in the final section.
-
The reaction
$A(q_1\bar{q}_1)+B(q_2\bar{q}_2) \to C(q_{3}\bar{q}_{1})+D(q_{2}\bar{q}_{4})$ ($ A(q_1\bar{q}_1)+B(q_2\bar{q}_2) \to C(q_{1}\bar{q}_{4})+D(q_{3}\bar{q}_{2}) $ ) takes place when a quark$ q_1 $ ($ q_2 $ ) and antiquark$ \bar{q}_2 $ ($ \bar{q}_1 $ ) in the initial mesons annihilate into a gluon, and the gluon subsequently creates a quark$ q_3 $ and antiquark$ \bar{q}_4 $ . The two processes$ q_1+\bar{q}_2 \to q_{3} +\bar{q}_4 $ and$ \bar{q}_1+q_2 \to q_{3}+\bar{q}_4 $ give rise to the two transition potentials$ V_{{\rm a}q_1\bar{q}_2} $ and$ V_{{\rm a}\bar{q}_1q_2} $ , respectively.$ E_{\rm i} $ and$ \vec{P}_{\rm i} $ ($ E_{\rm f} $ and$ \vec{P}_{\rm f} $ ) denote the total energy and total momentum of the two initial (final) mesons, respectively. Let$ E_A $ ($ E_B $ ,$ E_C $ ,$ E_D $ ) be the energy of meson A (B, C, D), and V the volume where every meson wave function is normalized. The S-matrix element for$ A+B \to C+D $ is$ \begin{array}{*{20}{l}} S_{\rm fi} = \delta_{\rm fi} -(2\pi)^4 i \delta (E_{\rm f} - E_{\rm i}) \delta^3 (\vec{P}_{\rm f} - \vec{P}_{\rm i}) \dfrac {{\cal M}_{{\rm a}q_1\bar{q}_2}+{\cal M}_{{\rm a}\bar{q}_1q_2}} {{V^2}\sqrt{2E_A2E_B2E_C2E_D}}, \end{array} $

(1) where
$ {\cal M}_{{\rm a}q_1\bar{q}_2} $ and$ {\cal M}_{{\rm a}\bar{q}_1q_2} $ are the transition amplitudes given by$ \begin{aligned}[b] {\cal M}_{{\rm a}q_1 {\bar q}_2}=&\frac {{(m_{q_3}+m_{\bar{q}_1})}^3}{{m^{3}_{\bar{q}_1}}}\sqrt {2E_A2E_B2E_C2E_D} \\ & \times \int {\rm d} \vec{r}_{q_1\bar{q}_1} {\rm d} \vec{r}_{q_2\bar{q}_4} {\rm d} \vec{r}_{q_3\bar{q}_1, q_2\bar{q}_4} \psi_{CD}^+ V_{{\rm a}q_1\bar{q}_2} \\ & \times \psi_{AB} {\rm e}^{{\rm i}\vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2}\cdot \vec{r}_{q_1\bar{q}_1,q_2\bar{q}_2}-{\rm i}\vec{p}_{q_3\bar{q}_1, q_2\bar{q}_4}\cdot \vec{r}_{q_3\bar{q}_1,q_2\bar{q}_4}}, \end{aligned} $

(2) $ \begin{aligned}[b] {\cal M}_{{\rm a}\bar{q}_1q_2}=&\frac {{(m_{q_1}+m_{\bar{q}_4})}^3}{m_{q_1}^3}\sqrt {2E_A2E_B2E_C2E_D} \\ & \times \int {\rm d}\vec{r}_{q_1\bar{q}_1} {\rm d}\vec{r}_{q_3\bar{q}_2} {\rm d}\vec{r}_{q_1\bar{q}_4, q_3\bar{q}_2} \psi_{CD}^+ V_{{\rm a}\bar{q}_1q_2} \\ & \times \psi_{AB} {\rm e}^{{\rm i}\vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2}\cdot \vec{r}_{q_1\bar{q}_1,q_2\bar{q}_2}-{\rm i}\vec{p}_{q_1\bar{q}_4, q_3\bar{q}_2}\cdot \vec{r}_{q_1\bar{q}_4,q_3\bar{q}_2}}, \end{aligned} $

(3) where
$ m_{q_{1}} $ ($ m_{\bar{q}_{1}} $ ,$ m_{q_{3}} $ ,$ m_{\bar{q}_{4}} $ ) is the mass of$ q_{1} $ ($ \bar{q}_{1} $ ,$ q_{3} $ ,$ \bar{q}_{4} $ ),$ \vec {r}_{ab} $ is the relative coordinate of constituents a and b,$ \vec{r}_{q_1\bar {q}_1,q_2\bar {q}_2} $ ($ \vec {r}_{q_3\bar {q}_1,q_2\bar {q}_4} $ ,$ \vec {r}_{q_1\bar {q}_4, q_3\bar {q}_2} $ ) is the relative coordinate of$ q_1\bar {q}_1 $ and$ q_2\bar {q}_2 $ ($ q_3\bar {q}_1 $ and$ q_2\bar {q}_4 $ ,$ q_1\bar {q}_4 $ and$ q_3\bar {q}_2 $ ),$ \vec {p}_{q_1\bar {q}_1,q_2\bar {q}_2} $ ($ \vec {p}_{q_3\bar {q}_1, q_2\bar {q}_4} $ ,$ \vec {p}_{q_1\bar {q}_4, q_3\bar {q}_2} $ ) is the relative momentum of$ q_1\bar {q}_1 $ and$ q_2\bar {q}_2 $ ($ q_3\bar {q}_1 $ and$ q_2\bar {q}_4 $ ,$ q_1\bar {q}_4 $ and$ q_3\bar {q}_2 $ ),$ \psi_{AB} $ ($ \psi_{CD} $ ) is the wave function of mesons A and B (C and D), and$ \psi_{AB}^+ $ ($ \psi_{CD}^+ $ ) is the Hermitian conjugate of$ \psi_{AB} $ ($ \psi_{CD} $ ). The wave function of mesons A and B is$ \begin{array}{*{20}{l}} \psi_{AB} =\phi_{A\rm color} \phi_{B\rm color} \phi_{A\rm rel} \phi_{B\rm rel} \chi_{S_A S_{Az}} \chi_{S_B S_{Bz}} \varphi_{AB\rm flavor}, \end{array} $

(4) and the wave function of mesons C and D is
$ \begin{array}{*{20}{l}} \psi_{CD} =\phi_{C\rm color} \phi_{D\rm color} \phi_{C\rm rel} \phi_{D\rm rel} \chi_{S_C S_{Cz}} \chi_{S_D S_{Dz}} \varphi_{CD\rm flavor}, \end{array} $

(5) where
$ S_A $ ($ S_B $ ,$ S_C $ ,$ S_D $ ) is the spin of meson A (B, C, D) with its magnetic projection quantum number$ S_{Az} $ ($ S_{Bz} $ ,$ S_{Cz} $ ,$ S_{Dz} $ ),$ \phi_{A\rm color} $ ($ \phi_{B\rm color} $ ,$ \phi_{C\rm color} $ ,$ \phi_{D\rm color} $ ),$ \phi_{A\rm rel} $ ($ \phi_{B\rm rel} $ ,$ \phi_{C\rm rel} $ ,$ \phi_{D\rm rel} $ ), and$ \chi_{S_A S_{Az}} $ ($ \chi_{S_B S_{Bz}} $ ,$ \chi_{S_C S_{Cz}} $ ,$ \chi_{S_D S_{Dz}} $ ) are the color wave function, quark-antiquark relative-motion wave function, and spin wave function of meson A (B, C, D), respectively, and$ \varphi_{AB\rm flavor} $ ($ \varphi_{CD\rm flavor} $ ) is the flavor wave function of mesons A and B (C and D).The development in the spherical harmonics of the relative-motion wave function of mesons A and B (aside from a normalization constant) is given by
$ \begin{aligned}[b] {\rm e}^{{\rm i}\vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2} \cdot \vec{r}_{q_1\bar{q}_1,q_2\bar{q}_2}} = & 4\pi \sum\limits_{L_{\rm i}=0}^{\infty} \sum\limits_{M_{\rm i}=-L_{\rm i}}^{L_{\rm i}} i^{L_{\rm i}} j_{L_{\rm i}} (\mid \vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2} \mid r_{q_1\bar{q}_1,q_2\bar{q}_2}) \\ & \times Y_{L_{\rm i}M_{\rm i}}^\ast (\hat{p}_{q_1\bar{q}_1,q_2\bar{q}_2}) Y_{L_{\rm i}M_{\rm i}} (\hat{r}_{q_1\bar{q}_1,q_2\bar{q}_2}), \end{aligned} $

(6) and the development in the spherical harmonics of the relative-motion wave function of mesons C and D leads to
$ \begin{aligned}[b] {\rm e}^{-{\rm i}\vec{p}_{q_3\bar{q}_1,q_2\bar{q}_4} \cdot \vec{r}_{q_3\bar{q}_1,q_2\bar{q}_4}} = & 4\pi \sum\limits_{L_{\rm f}=0}^{\infty} \sum\limits_{M_{\rm f}=-L_{\rm f}}^{L_{\rm f}} i^{L_{\rm f}} (-1)^{L_{\rm f}} j_{L_{\rm f}} (\mid \vec{p}_{q_3\bar{q}_1,q_2\bar{q}_4} \mid r_{q_3\bar{q}_1,q_2\bar{q}_4}) \\ & \times Y_{L_{\rm f}M_{\rm f}}^\ast (\hat{p}_{q_3\bar{q}_1,q_2\bar{q}_4}) Y_{L_{\rm f}M_{\rm f}} (\hat{r}_{q_3\bar{q}_1,q_2\bar{q}_4}), \end{aligned} $

(7) in
${\cal{M}}_{{\rm a}q_{1}\bar{q}_{2}}$ , and$ \begin{aligned}[b] {\rm e}^{-{\rm i}\vec{p}_{q_1\bar{q}_4,q_3\bar{q}_2} \cdot \vec{r}_{q_1\bar{q}_4,q_3\bar{q}_2}} = & 4\pi \sum\limits_{L_{\rm f}=0}^{\infty} \sum\limits_{M_{\rm f}=-L_{\rm f}}^{L_{\rm f}} i^{L_{\rm f}} (-1)^{L_{\rm f}} j_{L_{\rm f}} (\mid \vec{p}_{q_1\bar{q}_4,q_3\bar{q}_2} \mid r_{q_1\bar{q}_4,q_3\bar{q}_2}) \\ & \times Y_{L_{\rm f}M_{\rm f}}^\ast (\hat{p}_{q_1\bar{q}_4,q_3\bar{q}_2}) Y_{L_{\rm f}M_{\rm f}} (\hat{r}_{q_1\bar{q}_4,q_3\bar{q}_2}), \end{aligned} $

(8) in
${\cal{M}}_{{\rm a}\bar{q}_{1}q_{2}}$ , where$ Y_{L_{\rm i}M_{\rm i}} $ ($ Y_{L_{\rm f}M_{\rm f}} $ ) are the spherical harmonics with the orbital-angular-momentum quantum number$ L_{\rm i} $ ($ L_{\rm f} $ ) and the magnetic projection quantum number$ M_{\rm i} $ ($ M_{\rm f} $ ),$ j_{L_{\rm i}} $ and$ j_{L_{\rm f}} $ are the spherical Bessel functions, and$ \hat{p}_{q_1\bar{q}_1,q_2\bar{q}_2} $ ($ \hat{p}_{q_3\bar{q}_1,q_2\bar{q}_4} $ ,$ \hat{p}_{q_1\bar{q}_4,q_3\bar{q}_2} $ ,$ \hat{r}_{q_1\bar{q}_1,q_2\bar{q}_2} $ ,$ \hat{r}_{q_3\bar{q}_1,q_2\bar{q}_4} $ ,$ \hat{r}_{q_1\bar{q}_4,q_3\bar{q}_2} $ ) denotes the polar angles of$ \vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2} $ ($ \vec{p}_{q_3\bar{q}_1,q_2\bar{q}_4} $ ,$ \vec{p}_{q_1\bar{q}_4,q_3\bar{q}_2} $ ,$ \vec{r}_{q_1\bar{q}_1,q_2\bar{q}_2} $ ,$ \vec{r}_{q_3\bar{q}_1,q_2\bar{q}_4} $ ,$ \vec{r}_{q_1\bar{q}_4,q_3\bar{q}_2} $ ).Let
$ \chi_{SS_{z}} $ ($ \chi_{S^{\prime}S^{\prime}_{z}} $ ) denote the spin wave function of mesons A and B (C and D), which has the total spin S ($ S^{\prime} $ ) and its z component$ S_z $ ($ S^{\prime}_{z} $ ). The Clebsch-Gordan coefficients$ (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z}) $ relate$ \chi_{SS_z} $ to$ \chi_{S_AS_{Az}}\chi_{S_BS_{Bz}} $ , and$ (S_{C}S_{Cz}S_{D}S_{Dz}|S^{\prime}S^{\prime}_{z}) $ relate$ \chi_{S^{\prime}S^{\prime}_{z}} $ to$ \chi_{S_CS_{Cz}}\chi_{S_DS_{Dz}} $ :$ \chi_{S_{A}S_{A_{z}}}\chi_{S_{B}S_{B_{z}}}= \sum\limits^{S_{\rm max}}_{S=S_{\rm min}}\sum\limits^{S}_{S_{z}=-S} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z})\chi_{SS_{z}}, $

(9) $ \chi_{S_{C}S_{C_{z}}} \chi_{S_{D}S_{D_{z}}} = \sum\limits^{S^{\prime}_{\rm max}}_{S^{\prime}=S^{\prime}_{\rm min}} \sum\limits^{S^{\prime}}_{S^{\prime}_z=-S^{\prime}} (S_{C}S_{Cz}S_{D}S_{Dz}|S^{\prime}S^{\prime}_z) \chi_{S^{\prime}S^{\prime}_z}, $

(10) where
$ S_{\rm min}=\mid S_A-S_B \mid $ ,$ S_{\rm max}=S_A+S_B $ ,$ S^{\prime}_{\rm min}=\mid S_C-S_D \mid $ , and$ S^{\prime}_{\rm max}=S_C+S_D $ .$ Y_{L_{\rm i}M_{\rm i}} $ and$ \chi_{SS_{z}} $ ($ Y_{L_{\rm f}M_{\rm f}} $ and$ \chi_{S^{\prime}S^{\prime}_z} $ ) are coupled to the wave function$ \varphi^{\rm in}_{JJ_z} $ ($ \varphi^{\rm final}_{J^\prime J_z^\prime} $ ), which has the total angular momentum J ($ J^{\prime} $ ) of mesons A and B (C and D) and its z component$ J_z $ ($ J^{\prime}_z $ ),$ Y_{L_{\rm{i}}M_{\rm{i}}}\chi_{SS_{z}}= \sum\limits^{J_{\rm max}}_{J=J_{\rm min}}\sum\limits^J_{J_z=-J} (L_{\rm{i}}M_{\rm{i}}SS_{z}|JJ_{z})\varphi^{\rm{in}}_{JJ_{z}}, $

(11) $ Y_{L_{\rm f}M_{\rm f}}\chi_{S^{\prime}S^{\prime}_z} = \sum\limits^{J^{\prime}_{\rm max}}_{J^{\prime}=J^{\prime}_{\rm min}} \sum\limits^{J^{\prime}}_{J^{\prime}_z=-J^{\prime}} (L_{\rm f}M_{\rm f}S^{\prime}S^{\prime}_z|J^{\prime}J^{\prime}_z) {\varphi}^{\rm final}_{J^{\prime}J^{\prime}_z}, $

(12) where
$ J_{\rm min}=\mid L_{\rm i}-S \mid $ ,$ J_{\rm max}=L_{\rm i}+S $ ,$ J^{\prime}_{\rm min}=\mid L_{\rm f}-S^{\prime} \mid $ , and$ J^{\prime}_{\rm max}=L_{\rm f}+S^{\prime} $ .$ (L_{\rm{i}}M_{\rm{i}}SS_{z}|JJ_{z}) $ and$ (L_{\rm{f}}M_{\rm{f}}S^{\prime}S^{\prime}_{z}|J^{\prime}J^{\prime}_{z}) $ are the Clebsch-Gordan coefficients. It follows from Eqs. (6)−(12) that the transition amplitude given in Eq. (3) becomes$ \begin{aligned}[b] {\cal M}_{{\rm a}\bar{q}_{1}q_{2}}=& \frac{(m_{q_1}+m_{\bar{q}_4})^3}{{m^3_{q_1}}} \sqrt{2E_{A}2E_{B}2E_{C}2E_{D}} (4\pi)^2 \sum\limits^{\infty}_{L_{\rm i}=0} \sum\limits^{L_{\rm i}}_{M_{\rm i}=-L_{\rm i}} i^{L_{\rm i}} Y^*_{L_{\rm i}M_{\rm i}}(\hat{p}_{q_{1}\bar{q}_{1},q_{2}\bar{q}_{2}}) \\ & \times \sum\limits^{\infty}_{L_{\rm f}=0} \sum\limits^{L_{\rm f}}_{M_{\rm f}=-L_{\rm f}} i^{L_{\rm f}} (-1)^{L_{\rm f}} Y^*_{L_{\rm f}M_{\rm f}}(\hat{p}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}) {\phi}^+_{C{\rm color}} {\phi}^+_{D{\rm color}} {\varphi}^+_{CD{\rm flavor}} \int{{\rm d}\vec{r}_{q_{1}\bar{q}_{1}} {\rm d}\vec{r}_{q_{3}\bar{q}_{2}} {\rm d}\vec{r}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}} {\phi}^+_{C{\rm rel}} {\phi}^+_{D{\rm rel}} \sum\limits_{S^{\prime}S^{\prime}_{z}} (S_{C}S_{Cz}S_{D}S_{Dz}|S^{\prime}S^{\prime}_{z}) \\ & \times \sum\limits_{J^{\prime}J^{\prime}_{z}} (L_{\rm f}M_{\rm f}S^{\prime}S^{\prime}_{z}|J^{\prime}J^{\prime}_{z}) \varphi^{\rm final}_{J^{\prime}J^{\prime}_{z}} V_{{\rm a}q_{1}\bar{q}_{2}} \sum\limits_{SS_{z}} (S_{A}S_{Az}S_{B}S_{Bz}|SS_{z}) \sum\limits_{JJ_{z}}(L_{\rm i}M_{\rm i}SS_{z}|JJ_{z}) \varphi^{\rm in}_{JJ_{z}} {\phi}_{A{\rm rel}} {\phi}_{B{\rm rel}} {\varphi}_{AB{\rm flavor}} \phi_{A{\rm color}}\phi_{B{\rm color}} \\ & \times j_{L_{\rm i}}(\mid \vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2} \mid r_{q_1\bar{q}_1,q_2\bar{q}_2}) j_{L_{\rm f}} (\mid \vec{p}_{q_1\bar{q}_4,q_3\bar{q}_2} \mid r_{q_1\bar{q}_4,q_3\bar{q}_2}). \end{aligned} $ 
(13) Conservation of the total angular momentum implies that J equals
$ J^{\prime} $ and$ J_z $ equals$ J^{\prime}_{z} $ . This leads to$ \begin{aligned}[b] {\cal M}_{{\rm a}\bar{q}_{1}q_{2}}=& \frac{(m_{q_1}+m_{\bar{q}_4})^3}{{m^3_{q_1}}} \sqrt{2E_{A}2E_{B}2E_{C}2E_{D}} (4\pi)^2 \sum\limits^{\infty}_{L_{\rm i}=0} \sum\limits^{L_{\rm i}}_{M_{\rm i}=-L_{\rm i}} i^{L_{\rm i}} Y^*_{L_{\rm i}M_{\rm i}}(\hat{p}_{q_{1}\bar{q}_{1},q_{2}\bar{q}_{2}})\\& \times \sum\limits^{\infty}_{L_{\rm f}=0} \sum\limits^{L_{\rm f}}_{M_{\rm f}=-L_{\rm f}} i^{L_{\rm f}} (-1)^{L_{\rm f}} Y^*_{L_{\rm f}M_{\rm f}}(\hat{p}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}) {\phi}^+_{C{\rm color}} {\phi}^+_{D{\rm color}} {\varphi}^+_{CD{\rm flavor}} \int{{\rm d}\vec{r}_{q_{1}\bar{q}_{1}} {\rm d}\vec{r}_{q_{3}\bar{q}_{2}} {\rm d}\vec{r}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}} {\phi}^+_{C{\rm rel}} {\phi}^+_{D{\rm rel}} \sum\limits_{S^{\prime}S^{\prime}_{z}} (S_{C}S_{Cz}S_{D}S_{Dz}|S^{\prime}S^{\prime}_{z}) \\ & \times \sum\limits_{JJ_{z}}(L_{\rm f}M_{\rm f}S^{\prime}S^{\prime}_{z}|JJ_{z}) \varphi^{\rm final}_{JJ_{z}} V_{{\rm a}\bar{q}_{1}q_{2}} \sum\limits_{SS_{z}}(S_{A}S_{Az}S_{B}S_{Bz}|SS_{z}) (L_{\rm i}M_{\rm i}SS_{z}|JJ_{z}) \varphi^{\rm in}_{JJ_{z}} {\phi}_{A{\rm rel}} {\phi}_{B{\rm rel}} {\varphi}_{AB{\rm flavor}} \phi_{A{\rm color}}\phi_{B{\rm color}} \\ & \times j_{L_{\rm i}}(\mid \vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2} \mid r_{q_1\bar{q}_1,q_2\bar{q}_2}) j_{L_{\rm f}} (\mid \vec{p}_{q_1\bar{q}_4,q_3\bar{q}_2} \mid r_{q_1\bar{q}_4,q_3\bar{q}_2}). \\[-8pt]\end{aligned} $

(14) Using the relation
$ \varphi^{\rm{in}}_{JJ_{z}} = \sum\limits_{\bar{M}_{\rm i}\bar{S}_{z}} (L_{\rm{i}}\bar{M}_{\rm{i}}S\bar{S}_{z}|JJ_{z}) Y_{L_{\rm{i}}\bar{M}_{\rm{i}}}\chi_{S\bar{S}_{z}}, $

(15) $ \varphi^{\rm final}_{JJ_{z}} = \sum\limits_{\bar{M}_{\rm f}\bar{S}^{\prime}_{z}} (L_{\rm f}\bar{M}_{\rm f}S^{\prime}\bar{S}^{\prime}_{z}|JJ_{z}) Y_{L_{\rm f}\bar{M}_{\rm f}} \chi_{S^{\prime}S^{\prime}_{z}}, $

(16) where
$ (L_{\rm{i}}\bar{M}_{\rm{i}}S\bar{S}_{z}|JJ_{z}) $ and$ (L_{\rm{f}}\bar{M}_{\rm{f}}S^{\prime}\bar{S}^{\prime}_{z}|J_{}J_{z}) $ are the Clebsch-Gordan coefficients, we get$ \begin{aligned}[b] {\cal M}_{{\rm a}\bar{q}_{1}q_{2}}=& \frac{(m_{q_1}+m_{\bar{q}_4})^3}{{m^3_{q_1}}} \sqrt{2E_{A}2E_{B}2E_{C}2E_{D}} (4\pi)^2 \sum\limits^{\infty}_{L_{\rm i}=0} \sum\limits^{L_{\rm i}}_{M_{\rm i}=-L_{\rm i}} i^{L_{\rm i}} Y^*_{L_{\rm i}M_{\rm i}}(\hat{p}_{q_{1}\bar{q}_{1},q_{2}\bar{q}_{2}}) \\ & \times \sum\limits^{\infty}_{L_{\rm f}=0} \sum\limits^{L_{\rm f}}_{M_{\rm f}=-L_{\rm f}} i^{L_{\rm f}} (-1)^{L_{\rm f}} Y^*_{L_{\rm f}M_{\rm f}}(\hat{p}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}) \sum\limits_{S^{\prime}S^{\prime}_{z}} (S_{C}S_{Cz}S_{D}S_{Dz}|S^{\prime}S^{\prime}_{z}) \\ & \times \sum\limits_{JJ_{z}}(L_{\rm f}M_{\rm f}S^{\prime}S^{\prime}_{z}|JJ_{z}) \sum\limits_{\bar{M}_{\rm f}\bar{S}^{\prime}_{z}} (L_{\rm f}\bar{M}_{\rm f}S^{\prime}\bar{S}^{\prime}_{z}|JJ_{z}) \sum\limits_{SS_{z}}(S_{A}S_{Az}S_{B}S_{Bz}|SS_{z}) \\ & \times (L_{\rm i}M_{\rm i}SS_{z}|JJ_{z}) \sum\limits_{\bar{M}_{\rm i}\bar{S}_{z}}(L_{\rm i}\bar{M}_{\rm i}S\bar{S}_{z}|JJ_{z}) {\phi}^+_{C{\rm color}} {\phi}^+_{D{\rm color}} {\varphi}^+_{CD{\rm flavor}} \chi^+_{S^{\prime}\bar{S}^{\prime}_{z}} \\ & \times \int{{\rm d}\vec{r}_{q_{1}\bar{q}_{1}} {\rm d}\vec{r}_{q_{3}\bar{q}_{2}} {\rm d}\vec{r}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}} j_{L_{\rm f}}(\mid \vec{p}_{q_1\bar{q}_4,q_3\bar{q}_2} \mid r_{q_1\bar{q}_4,q_3\bar{q}_2}) Y_{L_{\rm f}\bar{M}_{\rm f}}(\hat{r}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}) \\ & \times {\phi}^+_{C{\rm rel}} {\phi}^+_{D{\rm rel}} V_{{\rm a}\bar{q}_{1}q_{2}}\phi_{A{\rm rel}}\phi_{B{\rm rel}} j_{L_{\rm i}}(\mid \vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2} \mid r_{q_1\bar{q}_1,q_2\bar{q}_2}) Y_{L_{\rm i}\bar{M}_{\rm i}}(\hat{r}_{q_{1}\bar{q}_{1},q_{2}\bar{q}_{2}}) \\&\times \chi_{S\bar{S}_{z}} {\varphi}_{AB{\rm flavor}} \phi_{A{\rm color}}\phi_{B{\rm color}}. \end{aligned} $

(17) Furthermore, we need the identity
$ j_l(pr)Y_{lm}(\hat{r})=\int \frac{{\rm d}^3p^\prime}{(2\pi)^3}\frac{2\pi^2}{p^2} \delta (p-p^\prime) i^l (-1)^l Y_{lm}(\hat{p}^\prime) {\rm e}^{{\rm i}\vec{p}^{\; \prime} \cdot \vec{r}} , $

(18) which is obtained with the help of
$\int_0^\infty j_l(pr)j_l(p^\prime r)r^2{\rm d}r=\dfrac{\pi}{2p^2} \delta (p-p^\prime)$ [31, 32], and where$ \hat{r} $ ($ \hat{p}^\prime $ ) denotes the polar angles of$ \vec r $ ($ \vec{p}^{\; \prime} $ ). Substituting Eq. (18) in Eq. (17), we get$ \begin{aligned}[b] {\cal M}_{{\rm a}\bar{q}_{1}q_{2}}=& \frac{(m_{q_1}+m_{\bar{q}_4})^3}{{m^3_{q_1}}} \sqrt{2E_{A}2E_{B}2E_{C}2E_{D}} (4\pi)^2 \sum\limits^{\infty}_{L_{\rm i}=0} \sum\limits^{L_{\rm i}}_{M_{\rm i}=-L_{\rm i}} i^{L_{\rm i}} Y^*_{L_{\rm i}M_{\rm i}}(\hat{p}_{q_{1}\bar{q}_{1},q_{2}\bar{q}_{2}}) \\ & \times \sum\limits^{\infty}_{L_{\rm f}=0} \sum\limits^{L_{\rm f}}_{M_{\rm f}=-L_{\rm f}} i^{L_{\rm f}} (-1)^{L_{\rm f}} Y^*_{L_{\rm f}M_{\rm f}}(\hat{p}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}) \sum\limits_{S^{\prime}S^{\prime}_{z}} (S_{C}S_{Cz}S_{D}S_{Dz}|S^{\prime}S^{\prime}_{z}) \\ & \times \sum\limits_{JJ_{z}}(L_{\rm f}M_{\rm f}S^{\prime}S^{\prime}_{z}|JJ_{z}) \sum\limits_{\bar{M}_{\rm f}\bar{S}^{\prime}_{z}} (L_{\rm f}\bar{M}_{\rm f}S^{\prime}\bar{S}^{\prime}_{z}|JJ_{z}) \sum\limits_{SS_{z}}(S_{A}S_{Az}S_{B}S_{Bz}|SS_{z}) \\ &\times (L_{\rm i}M_{\rm i}SS_{z}|JJ_{z}) \sum\limits_{\bar{M}_{\rm i}\bar{S}_{z}}(L_{\rm i}\bar{M}_{\rm i}S\bar{S}_{z}|JJ_{z}) {\phi}^+_{C{\rm color}} {\phi}^+_{D{\rm color}} {\varphi}^+_{CD{\rm flavor}} \chi^+_{S^{\prime}\bar{S}^{\prime}_{z}} \\ & \times \int{\frac{{\rm d}^{3}p_{\rm frm}}{(2\pi)^{3}}} \frac{2\pi^{2}}{\vec{p}^{2}_{{q_{1}}\bar{q}_{4},q_{3}\bar{q}_{2}}} \delta(\mid \vec{p}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}} \mid-\mid \vec{p}_{\rm frm} \mid) i^{L_{\rm f}} (-1)^{L_{\rm f}} Y_{L_{\rm f}\bar{M}_{\rm f}} (\hat{p}_{\rm frm}) \end{aligned} $

$ \begin{aligned}[b]& \times \int{\frac{{\rm d}^{3}p_{\rm irm}}{(2\pi)^{3}}} \frac{2\pi^{2}}{\vec{p}^{2}_{{q_{1}}\bar{q}_1,q_{2}\bar{q}_{2}}} \delta(\mid \vec{p}_{q_{1}\bar{q}_1,q_{2}\bar{q}_{2}} \mid-\mid \vec{p}_{\rm irm} \mid) i^{L_{\rm i}} (-1)^{L_{\rm i}} Y_{L_{\rm i}\bar{M}_{\rm i}} (\hat{p}_{\rm irm}) \\ & \times \int{{\rm d}\vec{r}_{q_{1}\bar{q}_{1}} {\rm d}\vec{r}_{q_{3}\bar{q}_{2}} {\rm d}\vec{r}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}} {\phi}^+_{C{\rm rel}} {\phi}^+_{D{\rm rel}} V_{{\rm a}\bar{q}_{1}q_{2}}\phi_{A{\rm rel}}\phi_{B{\rm rel}}\\& \times {\rm e}^{{\rm i}\vec{p}_{\rm frm}\cdot\vec{r}_{q_{1}\bar{q}_4,q_{3}\bar{q}_2}} {\rm e}^{{\rm i}\vec{p}_{\rm irm}\cdot\vec{r}_{q_{1}\bar{q}_1,q_{2}\bar{q}_2}} \chi_{S\bar{S}_{z}} \varphi_{AB{\rm flavor}} \phi_{A{\rm color}}\phi_{B{\rm color}}. \end{aligned} $

(19) Let
$ \vec{r}_c $ be the position vector of constituent c.$ \phi_{A\rm{rel}} $ and$ \phi_{B\rm{rel}} $ are functions of the relative coordinate of the quark and antiquark inside mesons A and B, respectively. We take the Fourier transform of$ V_{{\rm a}q_1\bar{q}_2} $ ,$ V_{{\rm a}\bar{q}_1q_2} $ ,$ \phi_{A\rm{rel}} $ , and$ \phi_{B\rm{rel}} $ :$ V_{{\rm a}q_1\bar{q}_2}(\vec{r}_{q_3}-\vec{r}_{q_1}) = \int \frac {{\rm d}^3k}{(2\pi)^3} V_{{\rm a}q_1\bar{q}_2} (\vec {k}) {\rm e}^{{\rm i} \vec {k} \cdot (\vec{r}_{q_3}-\vec{r}_{q_1})}, $

(20) $ V_{{\rm a}\bar{q}_1q_2}(\vec{r}_{q_3}-\vec{r}_{q_2}) = \int \frac {{\rm d}^3k}{(2\pi)^3} V_{{\rm a}\bar{q}_1q_2} (\vec {k}) {\rm e}^{{\rm i}\vec {k} \cdot (\vec{r}_{q_3}-\vec{r}_{q_2})}, $

(21) $ \phi_{A\rm rel}(\vec{r}_{q_1\bar{q}_1}) = \int \frac {{\rm d}^3p_{q_1\bar{q}_1}}{(2\pi)^3} \phi_{A\rm rel} (\vec {p}_{q_1\bar{q}_1}) {\rm e}^{{\rm i}\vec {p}_{q_1\bar{q}_1} \cdot \vec {r}_{q_1\bar{q}_1}}, $

(22) $ \phi_{B\rm rel}(\vec{r}_{q_2\bar{q}_2}) = \int \frac {{\rm d}^3p_{q_2\bar{q}_2}}{(2\pi)^3} \phi_{B\rm rel} (\vec {p}_{q_2\bar{q}_2}) {\rm e}^{{\rm i}\vec {p}_{q_2\bar{q}_2} \cdot \vec {r}_{q_2\bar{q}_2}}. $

(23) In Eqs. (20)−(21),
$ \vec k $ is the gluon momentum, and in Eqs. (22)−(23),$ \vec{p}_{ab} $ is the relative momentum of constituents a and b. In momentum space, the normalizations are$ \int \frac{{\rm d}^3p_{q_1\bar{q}_1}}{(2\pi)^3} \phi_{A\rm rel}^+(\vec{p}_{q_1\bar{q}_1}) \phi_{A\rm rel}(\vec{p}_{q_1\bar{q}_1})=1, $

$ \int \frac{{\rm d}^3p_{q_2\bar{q}_2}}{(2\pi)^3} \phi_{B\rm rel}^+(\vec{p}_{q_2\bar{q}_2}) \phi_{B\rm rel}(\vec{p}_{q_2\bar{q}_2})=1. $

The spherical polar coordinates of
$ \vec{p}_{\rm irm} $ and$ \vec{p}_{\rm frm} $ are expressed as$ (\mid \vec{p}_{\rm irm} \mid, \theta_{\rm irm}, \phi_{\rm irm}) $ and$ (\mid \vec{p}_{\rm frm} \mid, \theta_{\rm frm}, \phi_{\rm frm}) $ , respectively. Integration over$ \mid \vec{p}_{\rm irm} \mid $ ,$ \mid \vec{p}_{\rm frm} \mid $ ,$ \vec{r}_{q_1\bar{q}_1} $ ,$ \vec{r}_{q_3\bar{q}_2} $ , and$ \vec{r}_{q_1\bar{q}_4,q_3\bar{q}_2} $ in Eq. (19) yields$ \begin{aligned}[b] {\cal M}_{{\rm a}\bar{q}_{1}q_{2}}=& \sqrt{2E_{A}2E_{B}2E_{C}2E_{D}} \sum\limits^{\infty}_{L_{\rm i}=0} \sum\limits^{L_{\rm i}}_{M_{\rm i}=-L_{\rm i}} Y^*_{L_{\rm i}M_{\rm i}}(\hat{p}_{q_{1}\bar{q}_{1},q_{2}\bar{q}_{2}}) \\ & \times \sum\limits^{\infty}_{L_{\rm f}=0} \sum\limits^{L_{\rm f}}_{M_{\rm f}=-L_{\rm f}} (-1)^{L_{\rm f}} Y^*_{L_{\rm f}M_{\rm f}}(\hat{p}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}}) \sum\limits_{S^{\prime}S^{\prime}_{z}} (S_{C}S_{Cz}S_{D}S_{Dz}|S^{\prime}S^{\prime}_{z}) \\ & \times \sum\limits_{JJ_{z}}(L_{\rm f}M_{\rm f}S^{\prime}S^{\prime}_{z}|JJ_{z}) \sum\limits_{\bar{M}_{\rm f}\bar{S}^{\prime}_{z}} (L_{\rm f}\bar{M}_{\rm f}S^{\prime}\bar{S}^{\prime}_{z}|JJ_{z}) \sum\limits_{SS_{z}}(S_{A}S_{Az}S_{B}S_{Bz}|SS_{z}) \\ & \times (L_{\rm i}M_{\rm i}SS_{z}|JJ_{z}) \sum\limits_{\bar{M}_{\rm i}\bar{S}_{z}}(L_{\rm i}\bar{M}_{\rm i}S\bar{S}_{z}|JJ_{z}) {\phi}^+_{C{\rm color}} {\phi}^+_{D{\rm color}} {\varphi}^+_{CD{\rm flavor}} \chi^+_{S^{\prime}\bar{S}^{\prime}_{z}} \\ & \times \int{{\rm d}\theta_{\rm frm}{\rm d}\phi_{\rm frm}} \sin{\theta}_{\rm frm} Y_{L_{\rm f}\bar{M}_{\rm f}}(\hat{p}_{\rm frm}) \int{{\rm d}\theta_{\rm irm}{\rm d}\phi_{\rm irm}} \sin{\theta}_{\rm irm} Y_{L_{\rm i}\bar{M}_{\rm i}}(\hat{p}_{\rm irm}) \\ &\times \int{\frac{{\rm d}^{3}p_{q_{1}\bar{q}_{1}}}{(2\pi)^3}} \int{\frac{{\rm d}^{3}p_{q_{2}\bar{q}_{2}}}{(2\pi)^3}} {\phi}^+_{C{\rm rel}} (\vec{p}_{q_{1}\bar{q}_{1}} +\frac{m_{q_1}}{m_{q_{1}}+m_{\bar{q}_{1}}}\vec{p}_{\rm irm} +\frac{m_{q_1}}{m_{q_{1}}+m_{\bar{q}_{4}}}\vec{p}_{\rm frm}) \\ & \times {\phi}^+_{D{\rm rel}} (\vec{p}_{q_{2}\bar{q}_{2}} +\frac{m_{\bar{q}_{2}}}{m_{q_{2}}+m_{\bar{q}_{2}}}\vec{p}_{\rm irm} +\frac{m_{\bar{q}_{2}}}{m_{q_{3}}+m_{\bar{q}_{2}}}\vec{p}_{\rm frm}) \\ & \times V_{{\rm a}\bar{q}_{1}q_{2}} [\vec{p}_{q_{2}\bar{q}_{2}}-\vec{p}_{q_{1}\bar{q}_{1}} -(\frac{m_{q_2}}{m_{q_{2}}+m_{\bar{q}_{2}}} -\frac{m_{\bar{q}_{1}}}{m_{q_{1}}+m_{\bar{q}_{1}}})\vec{p}_{\rm irm}] \\ & \times \phi_{A{\rm rel}}(\vec{p}_{q_{1}\bar{q}_{1}}) \phi_{B{\rm rel}}(\vec{p}_{q_{2}\bar{q}_{2}}) \chi_{S\bar{S}_{z}} \varphi_{AB{\rm flavor}} \phi_{A{\rm color}}\phi_{B{\rm color}}, \end{aligned} $ 
(24) in which
$ \mid \vec{p}_{\rm irm} \mid = \mid \vec{p}_{q_1\bar{q}_1,q_2\bar{q}_2} \mid $ and$ \mid \vec{p}_{\rm frm} \mid = \mid \vec{p}_{q_1\bar{q}_4,q_3\bar{q}_2} \mid $ ,$ \hat{p}_{\rm irm} $ ($ \hat{p}_{\rm frm} $ ) denotes the polar angles of$ \vec{p}_{\rm irm} $ ($ \vec{p}_{\rm frm} $ ), and$ m_{q_2} $ and$ m_{\bar{q}_2} $ are the$ q_2 $ and$ \bar{q}_2 $ masses, respectively. The expression for the other transition amplitude$ {\cal M}_{{\rm a}q_1\bar{q}_2} $ is similar to the right-hand side in Eq. (24) and is thus given from$ {\cal M}_{{\rm a}\bar{q}_1q_2} $ by replacing$ \hat{p}_{q_{1}\bar{q}_{4},q_{3}\bar{q}_{2}} $ ($\vec{p}_{q_{1}\bar{q}_{1}} +\frac{m_{q_1}}{m_{q_{1}} +m_{\bar{q}_{1}}}\vec{p}_{\rm irm} + \frac{m_{q_1}}{m_{q_{1}}+m_{\bar{q}_{4}}}\vec{p}_{\rm frm}$ ,$ \vec{p}_{q_{2}\bar{q}_{2}} +\frac{m_{\bar{q}_{2}}}{m_{q_{2}}+m_{\bar{q}_{2}}}\vec{p}_{\rm irm} + \frac{m_{\bar{q}_{2}}}{m_{q_{3}}+m_{\bar{q}_{2}}}\vec{p}_{\rm frm} $ ,$\vec{p}_{q_{2}\bar{q}_{2}}-\vec{p}_{q_{1}\bar{q}_{1}} - (\frac{m_{q_2}}{m_{q_{2}}+m_{\bar{q}_{2}}} - \frac{m_{\bar{q}_{1}}}{m_{q_{1}}+m_{\bar{q}_{1}}})\vec{p}_{\rm irm}$ ) with$ \hat{p}_{q_{3}\bar{q}_{1},q_{2}\bar{q}_{4}} $ ($ \vec{p}_{q_{1}\bar{q}_{1}} - \frac{m_{\bar{q}_1}}{m_{q_{1}}+m_{\bar{q}_{1}}}\vec{p}_{\rm irm} - \frac{m_{\bar{q}_1}}{m_{q_{3}}+m_{\bar{q}_{1}}}\vec{p}_{\rm frm} $ ,$ \vec{p}_{q_{2}\bar{q}_{2}} -\frac{m_{q_{2}}}{m_{q_{2}}+m_{\bar{q}_{2}}}\vec{p}_{\rm irm} -\frac{m_{q_{2}}}{m_{q_{2}}+m_{\bar{q}_{4}}}\vec{p}_{\rm frm} $ ,$ \vec{p}_{q_{1}\bar{q}_{1}}-\vec{p}_{q_{2}\bar{q}_{2}} + (\frac{m_{q_1}}{m_{q_{1}}+m_{\bar{q}_{1}}} - \frac{m_{\bar{q}_{2}}}{m_{q_{2}}+m_{\bar{q}_{2}}})\vec{p}_{\rm irm} $ ). Thus far, we have obtained new expressions for the transition amplitudes from Eqs. (2) and (3).With the transition amplitudes, the unpolarized cross section for
$ A+B \to C+D $ is$ \begin{aligned}[b] \sigma^{\rm unpol}(\sqrt{s},T) =& \frac{1}{(2J_{A}+1)(2J_{B}+1)}\frac{1}{32\pi s} \frac{\mid \vec{P}^{\; \prime}(\sqrt{s}) \mid}{\mid \vec{P}(\sqrt{s}) \mid} \\ & \times{\int^{\pi}_{0} {\rm d}\theta \sum\limits_{J_{A_{z}}J_{B_{z}}J_{C_{z}}J_{D_{z}}} {\mid {\cal M}_{{\rm a}q_1\bar{q}_2} +{\cal M}_{{\rm a}\bar{q}_1q_2} \mid}^{2} \sin{\theta}}, \end{aligned} $

(25) where s is the Mandelstam variable obtained from the four-momenta
$ P_A $ and$ P_B $ of mesons A and B using$ s=(P_A+P_B)^2 $ , T is the temperature,$ J_A $ ($ J_B $ ,$ J_C $ ,$ J_D $ ) and$ J_{Az} $ ($ J_{Bz} $ ,$ J_{Cz} $ ,$ J_{Dz} $ ) of meson A (B, C, D) are the total angular momentum and its z component, respectively, θ is the angle between$ \vec{P} $ and$ \vec{P}' $ , which are the three-dimensional momenta of mesons A and C in the center-of-mass frame, respectively. Let$ m_A $ ,$ m_B $ ,$ m_C $ , and$ m_D $ be the masses of mesons A, B, C, and D, respectively.$ \vec P $ and$ \vec{P}^\prime $ are given by$ {\vec{P}}^2(\sqrt{s})=\frac{1}{4s} \left[ \left(s-m^2_A-m^2_B \right) ^2 -4m^2_Am^2_B \right], $

(26) $ {\vec{P}}^{\prime 2}(\sqrt{s})=\frac{1}{4s}\left[ \left(s-m^2_C-m^2_D \right) ^2-4m^2_Cm^2_D \right]. $

(27) Based on the relativistic energy-momentum relation, we have
$ E_A=\sqrt{\vec{P}^2+m_A^2}=\frac{1}{2\sqrt s}(s+m_A^2-m_B^2), $

(28) $ E_B=\sqrt{\vec{P}^2+m_B^2}=\frac{1}{2\sqrt s}(s-m_A^2+m_B^2), $

(29) $ E_C=\sqrt{\vec{P}^{\prime 2}+m_C^2}=\frac{1}{2\sqrt s}(s+m_C^2-m_D^2), $

(30) $ E_D=\sqrt{\vec{P}^{\prime 2}+m_D^2}=\frac{1}{2\sqrt s}(s-m_C^2+m_D^2). $

(31) We calculate the cross section in the center-of-mass frame of the two initial mesons. According to the Feynman rules, the two processes
$ q_1+\bar{q}_2 \to q_{3} +\bar{q}_4 $ and$ \bar{q}_1+q_2 \to q_{3}+\bar{q}_4 $ contribute to meson-meson scattering on an equal footing, and the sum$ {\cal M}_{{\rm a}q_1\bar{q}_2}+{\cal M}_{{\rm a}\bar{q}_1q_2} $ appears in Eq. (25) if$ {\cal M}_{{\rm a}q_1\bar{q}_2} \neq 0 $ and$ {\cal M}_{{\rm a}\bar{q}_1q_2} \neq 0 $ . -
The quark-antiquark relative-motion wave functions
$ \phi_{A\rm rel} $ and$ \phi_{B\rm rel} $ in Eq. (4) as well as$ \phi_{C\rm rel} $ and$ \phi_{D\rm rel} $ in Eq. (5) are solutions of the Schrödinger equation with a temperature-dependent quark potential. The potential between constituents a and b in coordinate space is [29]$ \begin{aligned}[b] V_{ab}(\vec{r}_{ab}) = & - \frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \xi_1 \left[ 1.3- \left( \frac {T}{T_{\rm c}} \right)^4 \right] \tanh (\xi_2 r_{ab})\\& + \frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \frac {6\pi}{25} \frac {v(\lambda r_{ab})}{r_{ab}} \exp (-\xi_3 r_{ab})\; \; \; \; \\ & -\frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2} \frac {16\pi^2}{25}\frac{{\rm d}^3}{\pi^{3/2}}\exp(-{\rm d}^2r^2_{ab}) \frac {\vec {s}_a \cdot \vec {s}_b} {m_am_b} \\&+\frac {\vec{\lambda}_a}{2} \cdot \frac {\vec{\lambda}_b}{2}\frac {4\pi}{25} \frac {1} {r_{ab}} \frac {{\rm d}^2v(\lambda r_{ab})}{{\rm d}r_{ab}^2} \frac {\vec {s}_a \cdot \vec {s}_b}{m_am_b}, \end{aligned} $

(32) where
$ \xi_1=0.525 $ GeV,$ \xi_2=1.5[0.75+0.25 (T/{T_{\rm c}})^{10}]^6 $ GeV,$ \xi_3=0.6 $ GeV, and$ \lambda=\sqrt{25/16\pi^2 \alpha'} $ with$ \alpha'=1.04 $ GeV$ ^{-2} $ ,$ T_{\rm c}=0.175 $ GeV is the critical temperature at which the phase transition between quark-gluon plasma and hadronic matter takes place [33−35],$ m_a $ ,$ \vec{s}_a $ , and$ \vec{\lambda}_a $ are the mass, spin, and Gell-Mann matrices for the color generators of constituent a, respectively, the dimensionless function v is given by Buchmüller and Tye in Ref. [36], and the quantity d is related to constituent quark masses via$ { d}^2={d}_1^2\left[\frac{1}{2}+\frac{1}{2}\left(\frac{4m_a m_b}{(m_a+m_b)^2} \right)^4\right]+{d}_2^2\left(\frac{2m_am_b}{m_a+m_b}\right)^2, $

(33) where
$ d_1=0.15 $ GeV and$ d_2=0.705 $ . The potential originates from perturbative quantum chromodynamics (QCD) at short distances and lattice QCD at intermediate and long distances. The first and second terms are the central spin-independent potential of which the short-distance part arises from one-gluon exchange plus perturbative one- and two-loop corrections in vacuum [36] and the intermediate-distance and long-distance part effectively fits the numerical potential, which was obtained in lattice gauge calculations [33]. The third term is the smeared spin-spin interaction that originates from one-gluon exchange between constituents a and b [37], and the fourth term is the spin-spin interaction that arises from perturbative one- and two-loop corrections to one-gluon exchange [38]. The temperature dependence of the potential is given by the first term and originates from the lattice gauge calculations [33]. At long distances, the spin-independent potential is independent of$ r_{ab} $ and obviously exhibits a plateau at$ T/T_{\rm c}>0.55 $ . The plateau height decreases with increasing temperature. Thus, confinement becomes progressively weaker.The Schrödinger equation with the potential yields energy eigenvalues and quark-antiquark relative-motion wave functions in the coordinate space. The sum of the quark mass, antiquark mass, and an energy eigenvalue gives the meson mass. In this study, we use the constituent quark masses 0.32 GeV for the up and down quarks and 0.5 GeV for the strange quark. The quark masses are independent of temperature. The experimental masses of the π, ρ, K,
$ K^* $ , η, ω, and ϕ mesons are reproduced from the Schrödinger equation with the potential at$ T=0 $ . Furthermore, the temperature dependence of the potential leads to the temperature dependence of meson masses and mesonic quark-antiquark relative-motion wave functions. The temperature dependence of the π, ρ, K, and$ K^* $ masses is shown in Ref. [39], where the temperature covers the temperature region of hadronic matter, and the parameterizations of these meson masses are given. The temperature dependence of the ϕ mass is shown in Ref. [40], which is parameterized as$ m_{\phi}=0.931\left[ 1-\left( \frac{T}{1.12T_{\rm c}} \right)^{5.46} \right]^{1.32}. $

(34) Because confinement becomes progressively weaker with increasing temperature, the spatial extension of the mesonic quark-antiquark relative-motion wave functions becomes progressively larger. Because the orbital-angular-momentum quantum numbers of the π, ρ, K,
$ K^* $ , η, ω, and ϕ mesons are zero, the wave functions are not zero at$ r_{ab}=0 $ . When the temperature increases, the absolute values of the wave functions at$ r_{ab}=0 $ decrease.The transition potentials
$ V_{{\rm a}q_1\bar{q}_2} $ and$ V_{{\rm a}\bar{q}_1q_2} $ are derived from the perturbative QCD in Ref. [29]. From the wave functions and transition potentials, we get the transition amplitudes$ {\cal M}_{{\rm a}q_{1}\bar{q}_{2}} $ and$ {\cal M}_{{\rm a}\bar{q}_{1}q_{2}} $ . In practical calculations, the summations over$ L_{\rm i} $ and$ L_{\rm f} $ in the transition amplitudes are from 0 to 3. The orbital-angular-momentum quantum numbers$ L_{\rm i} $ and$ L_{\rm f} $ are selected such that parity is conserved and that the total angular momentum of the two final mesons equals the total angular momentum of the two initial mesons. The values of$ L_{\rm i} $ and$ L_{\rm f} $ are listed in Table 1.Reaction S $ S^\prime $ 

$ L_{\rm i} $ 

$ L_{\rm f} $ 

$ K\phi \to \pi K $ 

1 0 1 1 1 0 2 2 1 0 3 3 $ K\phi \to \rho K $ 

1 1 0 0,2 1 1 1 1,3 1 1 2 0,2 1 1 3 1,3 $ K\phi \to \pi K^* $ 

1 1 0 0,2 1 1 1 1,3 1 1 2 0,2 1 1 3 1,3 $ K\phi \to \rho K^* $ 

1 0 1 1 1 0 2 2 1 0 3 3 1 1 0 0,2 1 1 1 1,3 1 1 2 0,2 1 1 3 1,3 1 2 0 2 1 2 1 1,3 1 2 2 0,2 1 2 3 1,3 Table 1. Total spin and orbital-angular-momentum quantum number.
We consider the four K+ϕ reactions
$ K\phi\to\pi K $ ,$ K\phi\to\rho K $ ,$ K\phi\to\pi K^* $ , and$ K\phi\to\rho K^* $ .$ {\cal M}_{{\rm a}q_1\bar{q}_2} $ and$ {\cal M}_{{\rm a}\bar{q}_1q_2} $ are proportional to flavor matrix elements. Because the flavor matrix elements for the K+ϕ reactions with total isospin$I = \dfrac{1}{2}$ are zero for$ {\cal M}_{{\rm a}q_1\bar{q}_2} $ and$-\dfrac{\sqrt{6}}{2}$ for$ {\cal M}_{{\rm a}\bar{q}_1q_2} $ , only the process$ \bar{q}_1+q_2 \to q_{3}+\bar{q}_4 $ contributes to these reactions. The unpolarized cross section for the four K+ϕ reactions is$ \begin{aligned}[b] \sigma^{\rm unpol}(\sqrt{s},T) =&\frac{1}{(2J_{A}+1)(2J_{B}+1)}\frac{1}{32\pi s} \frac{\mid \vec{P}^{\; \prime}(\sqrt{s}) \mid}{\mid \vec{P}(\sqrt{s}) \mid} \\& \times{\int^{\pi}_{0}{\rm d}\theta \sum\limits_{J_{A_{z}}J_{B_{z}}J_{C_{z}}J_{D_{z}}} {\mid {\cal M}_{{\rm a}\bar{q}_1q_2} \mid}^{2} \sin{\theta}}. \end{aligned} $

(35) If the sum of the masses of the two initial mesons of a reaction is larger than that of the two final mesons, the reaction is exothermic. Even slowly-moving initial mesons may start the reaction, and a certain amount of the initial meson masses are converted into the kinetic energies of the final mesons. If the sum of the masses of the two initial mesons is smaller than that of the two final mesons, the reaction is endothermic. The initial mesons need kinetic energies to satisfy energy conservation and to start the reaction, and a certain amount of the kinetic energies are converted into the masses of the final mesons.
The reaction
$ K\phi\to\rho K^* $ is endothermic at$ T/T_c=0 $ and exothermic at$ T/T_c=0.65 $ , 0.75, 0.85, 0.9, and 0.95. The other three reactions are exothermic. The cross sections for exothermic reactions are infinite at threshold energies. Thus, we begin cross section calculations for exothermic reactions at$ \sqrt{s}=m_K+m_\phi+10^{-4} $ GeV, where$ m_K $ and$ m_\phi $ are the masses of the kaon and ϕ meson, respectively. Numerical unpolarized cross sections for$ K\phi\to\pi K $ ,$ K\phi\to\rho K $ ,$ K\phi\to\pi K^* $ , and$ K\phi\to\rho K^* $ are plotted as red solid curves in Figs. 1 to 4. Because the quark potential, meson masses, and mesonic quark-antiquark relative-motion wave functions depend on the temperature,$ \mid \vec{P} \mid $ ,$ \mid \vec{P}^{\prime} \mid $ ,$ E_A $ ,$ E_B $ ,$ E_C $ ,$ E_D $ , and$ {\cal M}_{{\rm a}\bar{q}_1q_2} $ , which are given in Eq. (24) and Eqs. (26)−(31), depend on the temperature. This leads to the temperature dependence of the unpolarized cross sections.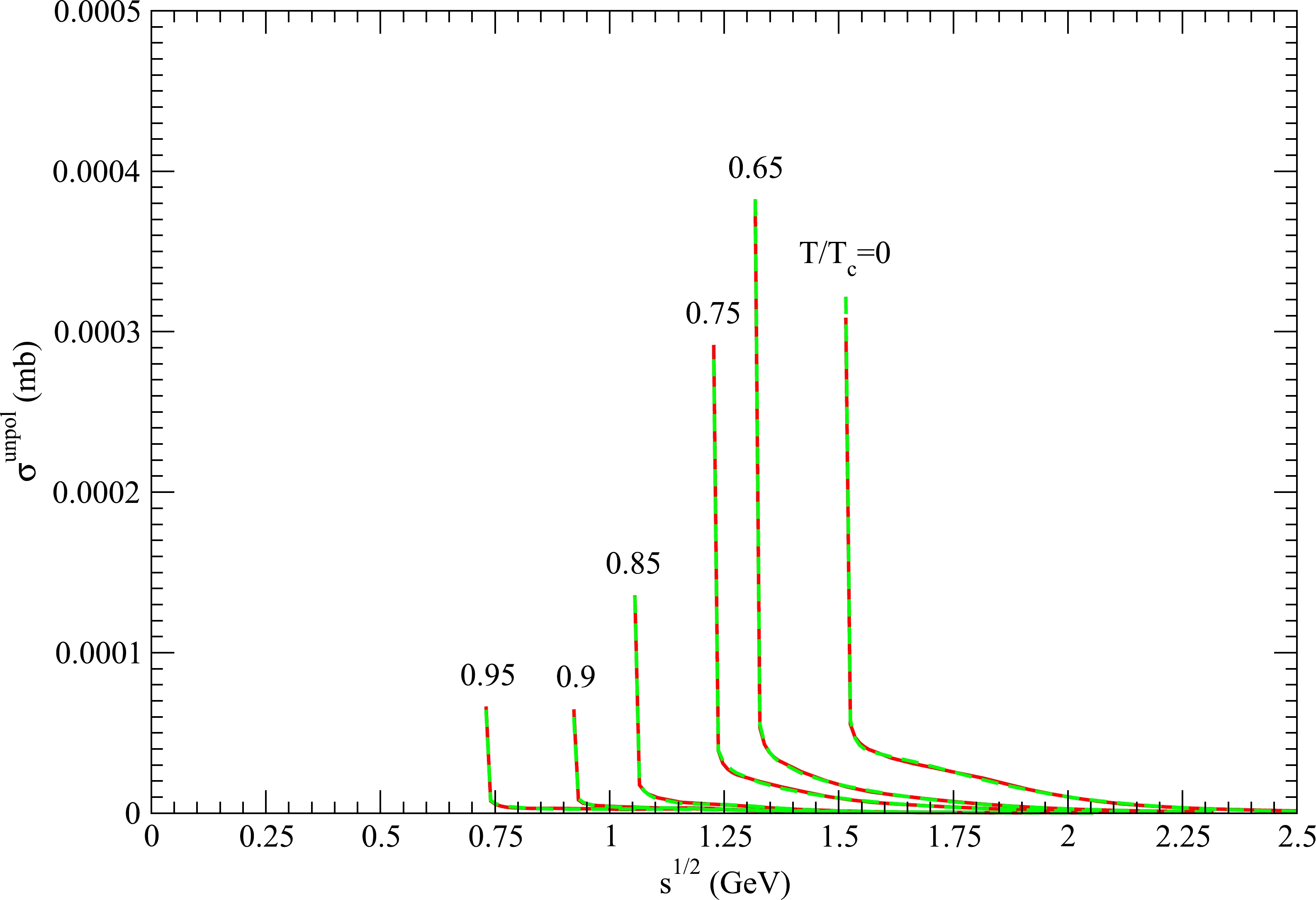
Figure 1. (color online) Cross sections for
$ K \phi \to \pi K $ at various temperatures. The red solid curves and green dashed curves are obtained from Eqs. (35) and (37), respectively.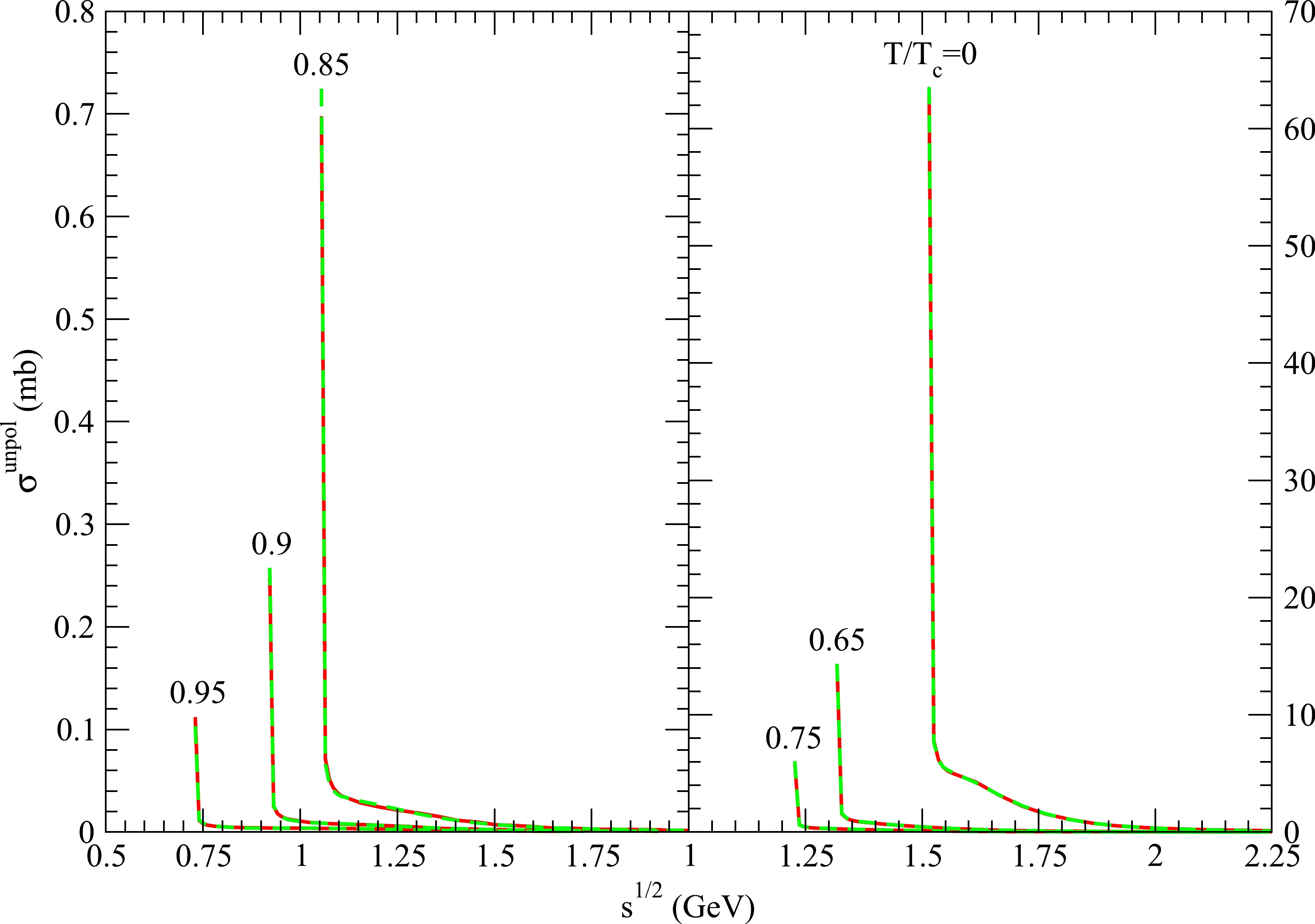
Figure 2. (color online) Same as Fig. 1 except for
$ K \phi \to \rho K $ .
Figure 3. (color online) Same as Fig. 1 except for
$ K \phi \to \pi K^* $ .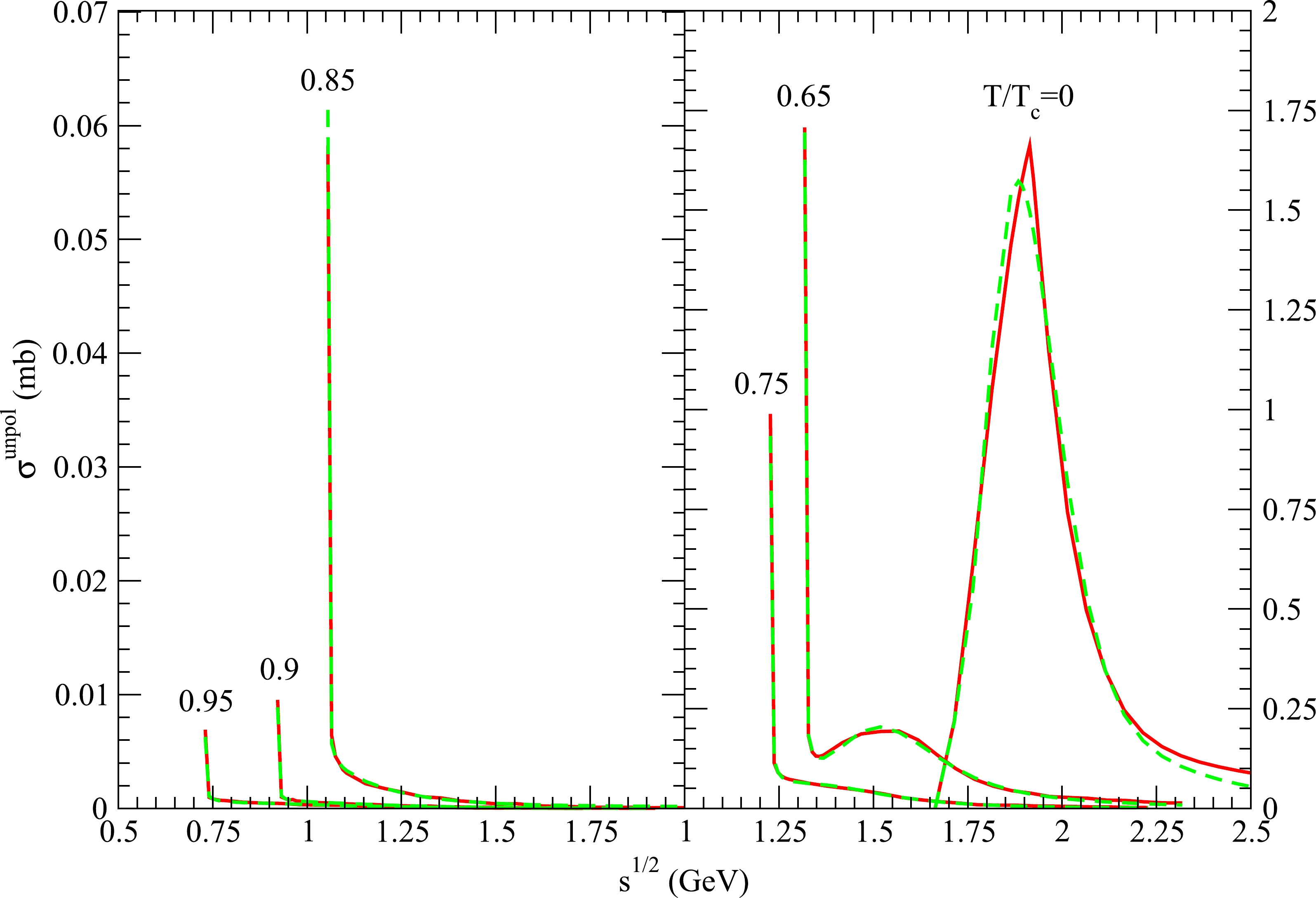
Figure 4. (color online) Cross sections for
$ K \phi \to \rho K^* $ at various temperatures. The red solid curves and green dashed curves are obtained from Eq. (35) and Eqs. (36)−(37), respectively.The numerical cross sections for endothermic reactions are parameterized as
$ \begin{aligned}[b] \sigma^{\rm unpol}(\sqrt {s},T) =&a_1 \left( \frac {\sqrt {s} -\sqrt {s_0}} {b_1} \right)^{c_1} \\& \times \exp \left[ c_1 \left( 1-\frac {\sqrt {s} -\sqrt {s_0}} {b_1} \right) \right] \\ &+ a_2 \left( \frac {\sqrt {s} -\sqrt {s_0}} {b_2} \right)^{c_2} \\& \times \exp \left[ c_2 \left( 1-\frac {\sqrt {s} -\sqrt {s_0}} {b_2} \right) \right], \end{aligned} $

(36) where
$ \sqrt{s_0} $ is the threshold energy, and$ a_1 $ ,$ b_1 $ ,$ c_1 $ ,$ a_2 $ ,$ b_2 $ , and$ c_2 $ are parameters. The numerical cross sections for exothermic reactions are parameterized as$ \begin{aligned}[b] \sigma^{\rm unpol}(\sqrt {s},T) =&\frac{\vec{P}^{\prime 2}}{\vec{P}^2} \left\{a_1 \left( \frac {\sqrt {s} -\sqrt {s_0}} {b_1} \right)^{c_1} \right.\\& \times \exp \left[ c_1 \left( 1-\frac {\sqrt {s} -\sqrt {s_0}} {b_1} \right) \right] \\ &+ a_2 \left( \frac {\sqrt {s} -\sqrt {s_0}} {b_2} \right)^{c_2} \\&\left. \times \exp \left[ c_2 \left( 1-\frac {\sqrt {s} -\sqrt {s_0}} {b_2} \right) \right] \right\}. \end{aligned} $

(37) The parameter values are listed in Table 2.
$ d_0 $ is the separation between the peak's location on the$ \sqrt s $ -axis and the threshold energy, and$ \sqrt{s_z} $ is the square root of the Mandelstam variable at which the cross section is 1/100 of the peak cross section. For the endothermic reaction$ K\phi \to \rho K^* $ at$ T=0 $ , a peak is displayed in Fig. 4, and$ d_0=0.25 $ GeV and$ \sqrt{s_z}=3.04 $ GeV are obtained from the numerical cross section for$ K\phi \to \rho K^* $ . Peak cross sections may not be observed for exothermic reactions; however,$ \vec{P}^2/\vec{P}^{\; \prime 2} $ times numerical cross sections must reveal peak cross sections for exothermic reactions. Hence, for exothermic reactions,$ d_0 $ and$ \sqrt{s_z} $ are obtained from$ \vec{P}^2/\vec{P}^{\; \prime 2} $ times the numerical cross sections.Reaction $ T/T_{c} $ 

$ a_{1} $ 

$ b_{1} $ 

$ c_{1} $ 

$ a_{2} $ 

$ b_{2} $ 

$ c_{2} $ 

$ d_{0} $ 

$ \sqrt{s_{z}} $ 

$ K\phi\to\pi K $ 

0 0.0000026 0.17 0.62 0.0000046 0.27 1.95 0.3 2.83 0.65 0.000002 0.13 0.54 0.000003 0.24 1.2 0.15 2.57 0.75 0.0000002 0.1 0.25 0.0000037 0.19 0.86 0.2 2.46 0.85 0.00000076 0.239 8.37 0.00000124 0.136 0.58 0.2 2.15 0.9 0.00000042 0.271 4.7 0.00000094 0.237 0.59 0.3 1.97 0.95 0.0000008 0.43 5.9 0.0000009 0.23 0.55 0.45 2.17 $ K\phi\to\rho K $ 

0 0.64 0.125 2.21 0.6 0.107 0.53 0.1 2.87 0.65 0.11 0.12 0.52 0.07 0.14 2.15 0.15 2.65 0.75 0.04 0.137 0.49 0.03 0.148 1.93 0.15 1.4 0.85 0.004 0.183 2.54 0.005 0.167 0.48 0.25 2.81 0.9 0.00233 0.202 0.5 0.00115 0.2582 4.2 0.25 2.2 0.95 0.0009 0.371 6.63 0.0014 0.258 0.53 0.4 3.52 $ K\phi\to\pi K^* $ 

0 0.1 0.153 0.34 0.33 0.096 0.95 0.1 2.94 0.65 0.121 0.132 0.51 0.068 0.121 1.84 0.15 2.69 0.75 0.05 0.147 0.5 0.027 0.127 1.65 0.15 2.52 0.85 0.0025 0.2 3.4 0.0044 0.18 0.55 0.2 2.14 0.9 0.00089 0.211 0.54 0.00145 0.256 2.24 0.35 2.27 0.95 0.0014 0.358 3.9 0.0016 0.153 0.55 0.3 1.86 $ K\phi\to\rho K^* $ 

0 0.29 0.17 0.72 1.29 0.22 6.18 0.25 3.04 0.65 0.062 0.14 0.49 0.096 0.226 3.9 0.25 4.19 0.75 0.013 0.202 3.04 0.019 0.123 0.55 0.2 2.48 0.85 0.00018 0.34 0.28 0.00059 0.11 0.91 0.15 2.16 0.9 0.000087 0.199 1.86 0.000105 0.153 0.54 0.25 1.48 0.95 0.00007 0.26 2.7 0.00013 0.17 0.62 0.2 18.02 Table 2. Values of the parameters.
$ a_1 $ and$ a_2 $ are in units of millibarns,$ b_1 $ ,$ b_2 $ ,$ d_0 $ , and$ \sqrt{s_{z}} $ are in units of GeV,$ c_1 $ and$ c_2 $ are dimensionless.The cross sections given by the parameterizations are plotted as green dashed curves in Figs. 1 to 4. For the exothermic reactions, the solid and dashed curves appear to coincide. For the endothermic reaction
$ K\phi \to \rho K^* $ at$ T=0 $ , a difference between the solid and dashed curves exists around the two peak cross sections and at$ \sqrt {s}>2.2 $ GeV.The threshold energy for each of the exothermic reactions
$ K\phi\to\pi K $ ,$ K\phi\to\rho K $ , and$ K\phi\to\pi K^* $ is the sum of the K and ϕ masses. When the temperature increases, the decreases in the masses lead to a decrease in the threshold energy, as shown in Figs. 1−3. As$ \sqrt s $ increases near the threshold energy, the cross sections for these reactions decrease rapidly owing to the factor$ \mid \vec{P}^{\; \prime} \mid / \mid \vec{P} \mid $ in Eq. (35). The threshold energy of the endothermic reaction$ K\phi\to\rho K^* $ at$ T=0 $ is the sum of the ρ and$ K^* $ masses. As$ \sqrt s $ increases from the threshold energy, the cross section for$ K\phi\to\rho K^* $ at$ T=0 $ increases rapidly from zero, reaches a peak value of approximately 1.66 mb, and then decreases.Because the reactions
$ K\phi\to\pi K $ ,$ K\phi\to\rho K $ , and$ K\phi\to\pi K^* $ are exothermic, the exclusive final states$ \pi K $ ,$ \rho K $ , and$ \pi K^* $ can always be found in a$ K+ \phi $ reaction. However, the exclusive final state$ \rho K^* $ may not be found in a$ K+ \phi $ reaction in vacuum because the reaction$ K\phi\to\rho K^* $ is endothermic at$ T=0 $ . If the total energy$ \sqrt s $ of the K and ϕ mesons in the center-of-mass frame is smaller than the threshold energy of$ K\phi\to\rho K^* $ , the reaction does not occur. If$ \sqrt s $ is larger than the threshold energy,$ \rho K^* $ production can be observed.In hadronic matter with high temperatures, the four reactions considered in this study are exothermic and always take place. The K and ϕ mesons satisfy the Bose-Einstein distribution functions. The reactions and distribution reduce the ϕ number and affect the ϕ momentum spectra and ϕ nuclear modification factor, which are observed in ultrarelativistic heavy-ion collisions [3, 6, 13].
The total spin of the two initial mesons in the reaction
$ K\phi\to\pi K $ is 1, and the total spin of the two final mesons is 0. Because the two total spins are unequal, the cross section for$ K\phi\to\pi K $ is small. For$ K\phi\to\rho K $ ,$ K\phi\to\pi K^* $ , and$ K\phi\to\rho K^* $ , the total spin of the two initial mesons may equal that of the two final mesons, and the cross sections may be a few millibarns when$ \sqrt s $ is not at the threshold energy. -
With the development in the spherical harmonics of the relative-motion wave functions of the two initial mesons and two final mesons, new expressions are obtained for the transition amplitudes. With the transition amplitudes, we calculate unpolarized cross sections for
$ K\phi\to\pi K $ ,$ K\phi\to\rho K $ ,$ K\phi\to\pi K^* $ , and$ K\phi\to\rho K^* $ , which are governed by quark-antiquark annihilation and creation. Both parity conservation and total-angular-momentum conservation are maintained. To use the numerical cross sections conveniently, we parameterize the cross sections. Each of the exothermic reactions$ K\phi\to\pi K $ ,$ K\phi\to\rho K $ , and$ K\phi\to\pi K^* $ first exhibits a rapid decrease and then a slow decrease in cross section with increasing$ \sqrt{s} $ from the threshold energy. Whether the reaction$ K\phi\to\rho K^* $ is endothermic or exothermic depends on temperature. The temperature-dependent cross sections are related to the temperature dependence of the quark potential, quark-antiquark relative-motion wave functions, and meson masses.
Cross sections for inelastic K+ϕ scattering
- Received Date: 2023-03-11
- Available Online: 2023-08-15
Abstract: In the first Born approximation, we study the reactions





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: