-
The analysis of neutron-rich isotopes near the doubly magic nucleus
$ ^{132} $ Sn can provide fascinating findings related to nuclear physics and nuclear astrophysics. The abundance peak appears at$ A\sim130 $ , which is formed through the rapid neutron capture process [1, 2]. The properties of doubly magic$ ^{132} $ Sn have been explored and confirmed in both experiments and theories [3−8]. In this nuclei region, tellurium isotopes have attracted experimental and theoretical research interest [5, 9−13]. For example, the g-factor of$ ^{134} $ Te in the 4$ ^+ $ state was measured, which provides direct insight into the single particle structure [9]. The state (17$ ^+ $ ) of$ ^{132} $ Te was observed to be 6.166 MeV using the reaction$ ^{9} $ Be($ ^{238} $ U, f ) with a beam energy of 6.2 MeV/u at GANIL [14]. A significant energy difference exists in this state between experiments and shell-model calculations, which should conceal unknown information about the nuclear structure.In theory, the extended pairing plus multipole-multipole force and monopole correction terms model (EPQQM) provides a suitable method to describe both the low-lying states and core excitations [15−18]. For example, the ordering and energies of the low-lying isomers in
$ ^{129} $ Cd are predicted and determined by using the implemented phase-imaging ion-cyclotron-resonance method [18, 19]. The 16$ ^+ $ level in$ ^{128} $ Cd is predicted as a spin-trap isomer feeding the known 16$ ^+ $ of$ ^{128} $ In through$ \beta^- $ decay [20]. In addition to monopole interactions, it is necessary to consider the cross-shell excitations to study the properties of these neutron-rich nuclei in this region. For example, identifying the isomer state of level 19/2$ ^+ $ at 1942 keV in$ ^{133} $ Ba requires the cross-shell orbits lying above the energy gap$ N = 82 $ . As reported in Ref. [21], the interactions without core excitations cannot provide the B(E1) value for the transition from$ J^{\pi} = 19/2^+ $ to$ J^{\pi} = 19/2^- $ .This model has an advantage for studying monopole effects by employing monopole correction (Mc) terms. For example, in the southwest quadrant (
$ Z \leq 50, N \leq 82 $ ) of$ ^{132} $ Sn, the level spectra and the energy gap across$ N = 82 $ can be modified by monopole correction between neutron orbit$ h_{11/2} $ and$ f_{7/2} $ [15]. In the northeast quadrant ($ Z \geq 50, N \geq 82 $ ), five monopole terms are used to describe core excitations and high-spin levels, and the states 2$ ^- $ and 9$ ^- $ in$ ^{136,138} $ Te are predicted as a spin-trap structure coupled by the neutron intruder orbit$ i_{13/2} $ [22]. Different effects of tensor forces are also discussed together with the monopole-driven shell evolutions [23], as well as other ones in the nucleon-nucleon interaction [24−27]. For the particle-hole nuclei in the northwest region of$ ^{132} $ Sn, a suitable interaction has been found, and the spectra of Sb and Te isotopes are well described as single-orbital couplings and cross-shell excitations [18, 28]. The transition probabilities in these nuclei are also calculated and reproduced well through comparisons with the known data.In this study, we investigate high-spin levels and monopole effects in particle-hole nuclei near
$ ^{132} $ Sn by employing the interaction in Ref. [18]. The shell-model code NUSHELLX@MSU is used for the calculations [29]. -
In this work, we use the Hamiltonian in the proton-neutron (
$ pn $ ) representation [18]:$ \begin{aligned}[b] H = & H_{\rm sp} + H_{P_0} + H_{P_2} + H_{QQ} + H_{OO} + H_{HH} + H_{\rm mc} \\ = & \sum\limits_{\alpha,i} \varepsilon_a^i c_{\alpha,i}^\dagger c_{\alpha,i} - \frac{1}{2} \sum\limits_{J=0,2} \sum\limits_{ii'} g_{J,ii'} \sum\limits_{M} P^\dagger_{JM,ii'} P_{JM,ii'} \\ & - \frac{1}{2} \sum\limits_{ii'} \frac{\chi_{2,ii'}}{b^4} \sum\limits_M :Q^\dagger_{2M,ii'} Q_{2M,ii'}: \\ & - \frac{1}{2} \sum\limits_{ii'} \frac{\chi_{3,ii'}}{b^6} \sum\limits_M :O^\dagger_{3M,ii'} O_{3M,ii'}: \\ & - \frac{1}{2} \sum\limits_{ii'} \frac{\chi_{4,ii'}}{b^8} \sum\limits_M :H^\dagger_{4M,ii'} H_{4M,ii'}: \\ & + \sum\limits_{a \leq c,ii'} k_{\rm mc}(ia,i'c) \sum\limits_{JM}A^\dagger_{JM}(ia,i'c) A_{JM}(ia,i'c). \end{aligned} $

(1) Equation (1) includes the single-particle Hamiltonian (
$ H_{\rm sp} $ ); the$ J=0 $ and$ J=2 $ pairings ($ P_{0}^{\dagger}P_{0} $ and$ P_{2}^{\dagger}P_{2} $ ); the quadrupole-quadrupole ($ Q^{\dagger}Q $ ), octupole-octupole ($ O^{\dagger}O $ ), and hexadecapole-hexadecapole ($ H^{\dagger}H $ ) terms; and the monopole corrections ($ H_{\rm mc} $ ). In the$ pn $ -representation,$ P^\dagger_{JM,ii'} $ and$ A^\dagger_{JM}(ia,i'c) $ are the pair operators, while$ Q^\dagger_{2M,ii'} $ ,$ O^\dagger_{3M,ii'} $ , and$ H^\dagger_{4M,ii'} $ are the quadrupole, octupole, and hexadecapole operators, respectively, in which i ($ i' $ ) is an index for protons (neutrons). The parameters$ g_{J,ii'} $ ,$ \chi_{2,ii'} $ ,$ \chi_{3,ii'} $ ,$ \chi_{4,ii'} $ , and$ k_{\rm mc}(ia,i'c) $ are the corresponding force strengths, and b is the harmonic-oscillator range parameter.The model space includes five orbits
$ (0g_{7/2}, 1d_{5/2}, 1d_{3/2}, 2s_{1/2}, 0h_{11/2}) $ for both protons and neutrons. Two extra neutron orbits above the$ N=82 $ shell, i.e.,$ (1f_{7/2} $ and$ 2p_{3/2}) $ , are added to allow neutron cross-shell excitations. We keep the same parameters of single-particle energies and the two-body force strengths used in Ref. [18]. The monopole interactions were found to be crucial for describing nuclear properties, which are entirely responsible for global saturation properties and single-particle behavior. The neutron-rich nuclei near$ ^{132} $ Sn can be divided into four quadrants by the crossing of$ Z = 50 $ and$ N = 82 $ . According to nuclei studied previously [15, 22, 30], the monopole corrections are necessary for the hole (particle) nuclei in the southwest (northeast) quadrant of$ ^{132} $ Sn.In southwest quadrant (
$ Z \leq 50, N \leq 82 $ ), the ground state inversion in$ ^{129} $ Cd can be well described by the monopole correction between proton orbit$ 0g_{9/2} $ and neutron orbit$ 0h_{11/2} $ with a strength of –0.40 MeV [17], and it was verified using the recently implemented phase-imaging ion-cyclotron-resonance method [19]. Recently, the ground-state inversions from$ N = 81 $ to$ N = 79 $ were explained for the first time by monopole correction between neutron orbits$ h_{11/2} $ and$ d_{3/2} $ . Furthermore, this monopole correction has been found in different isotonic chains of$ N = 79,80,81 $ , as all being hole nuclei near$ ^{132} $ Sn.In the northeast quadrant (
$ Z \geq 50, N \geq 82 $ ), five monopole terms are used to describe core excitations and high-spin levels [22]. For particle-pole nuclei in the northwest quadrant of$ ^{132} $ Sn ($ Z \geq 50, N \leq 82 $ ), the protons and neutrons occupy the same major shell. The properties of particle-hole nuclei can be well described without additional monopole correlations [28]. Such a situation is confirmed by the electromagnetic transitions of Sb and Te isotopes in the northwest quadrant of$ ^{132} $ Sn [28, 31], which is a strict test for shell model calculations. However, in level 17$ ^+ $ of$ ^{132} $ Te, the large difference between experiment and theory motivates us to investigate monopole interactions in the particle-hole nuclei region near$ ^{132} $ Sn. -
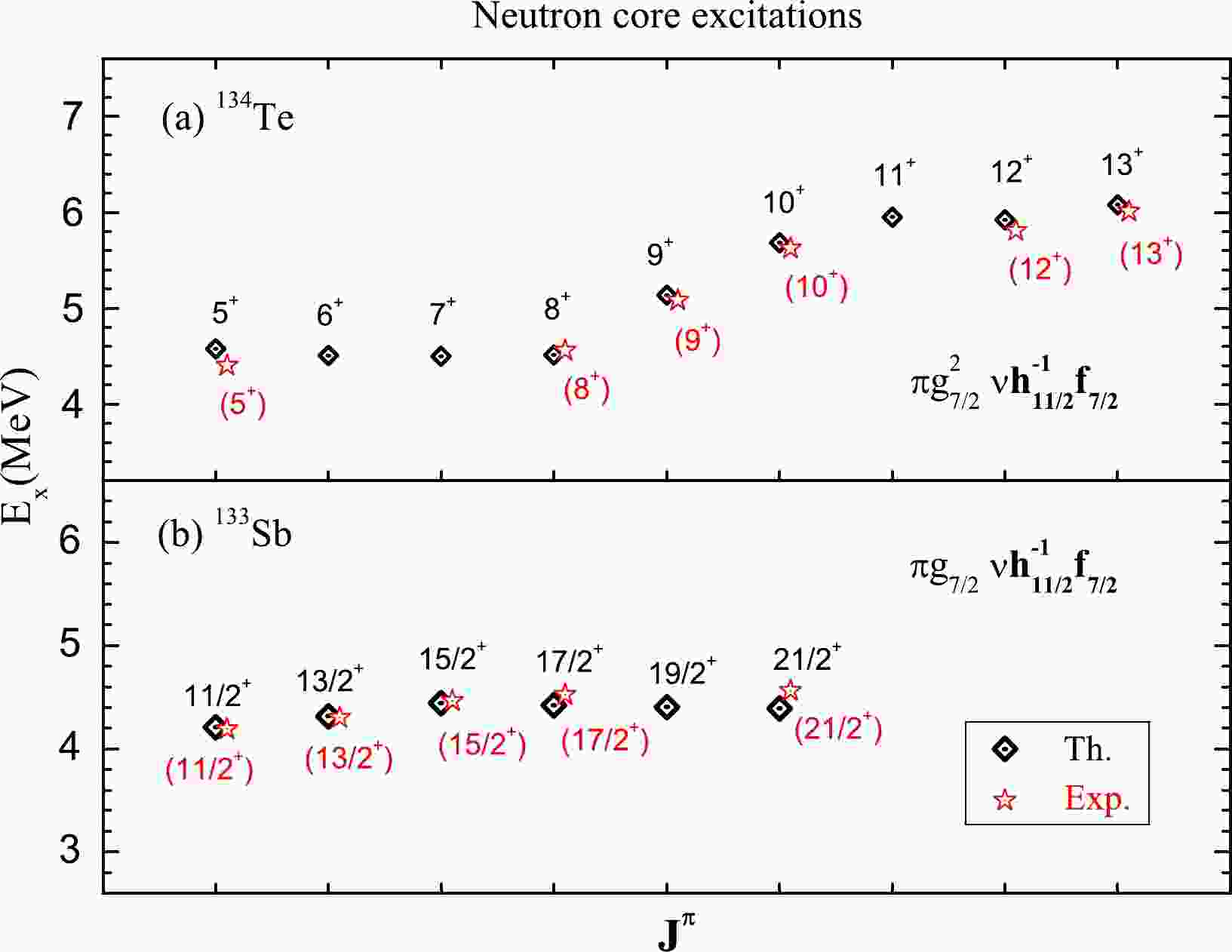
In this part, high-spin levels are investigated with the monopole effects and quadruple-quadruple force in
$ ^{132-134} $ Te,$ ^{131-133} $ Sb, and$ ^{130} $ Sn. The monopole correction alone cannot solve the puzzle of level 17+; it should be combined with quadrupole correction. As shown in Table 1, there are four different types of level 17$ ^+ $ under 10 MeV according to the EPQQM model, i.e., Nos. 1 to 4. The possibility of neutron core excitation (config.1 in Table 1) at 8.189 MeV can be excluded to explain the high-spin level 17$ ^+ $ of$ ^{132} $ Te [28]. The given experimental data of$ ^{134} $ Te and$ ^{133} $ Sb have been reproduced very well as core excitations with a common neutron configuration of$ \nu h^{-1}_{11/2} f_{7/2} $ (Fig. 1). If we modify the monopole term of Mc($ \nu h^{-1}_{11/2}, \nu f_{7/2} $ ) to explain the level 17$ ^+ $ of$ ^{132} $ Te, the 17 states of neutron core excitations would catastrophically depart from their corresponding data.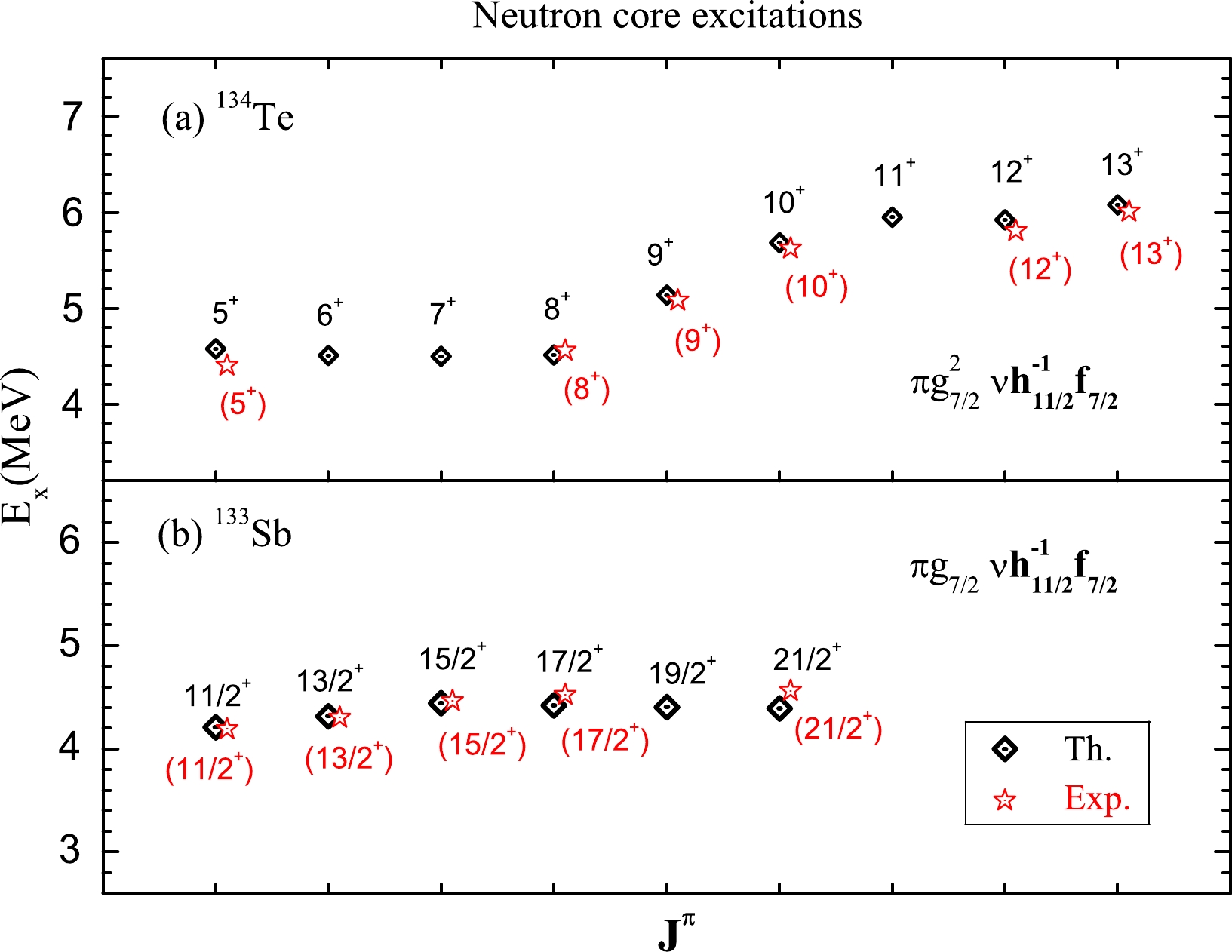
Figure 1. (color online) Neutron core excitations in
$^{134}$ Te and$^{133}$ Sb nuclei. Corresponding data are from Ref. [32].$^{132}$ Te

$E_x$ 

(MeV) Config. $J^{\pi}$ 

Th. Exp. No. P(\%) (17 $^+$ )

8.189 6.166 1. $\pi g^2_{7/2}\nu h^{-3}_{11/2} f_{7/2}$ 

88 8.779 2. $\pi g_{7/2} h_{11/2} \nu g^{-1}_{7/2} h^{-1}_{11/2}$ 

76 9.125 3. $\pi g_{7/2} h_{11/2} \nu d^{-1}_{5/2} h^{-1}_{11/2}$ 

72 9.314 4. $\pi h^2_{11/2} \nu h^{-2}_{11/2}$ 

93 Table 1. 17
$^+$ states in$^{132}$ Te with main configurations. The data are from Ref. [14].After excluding neutron core excitation, we focus on the level at 8.779 MeV coupled by config.2
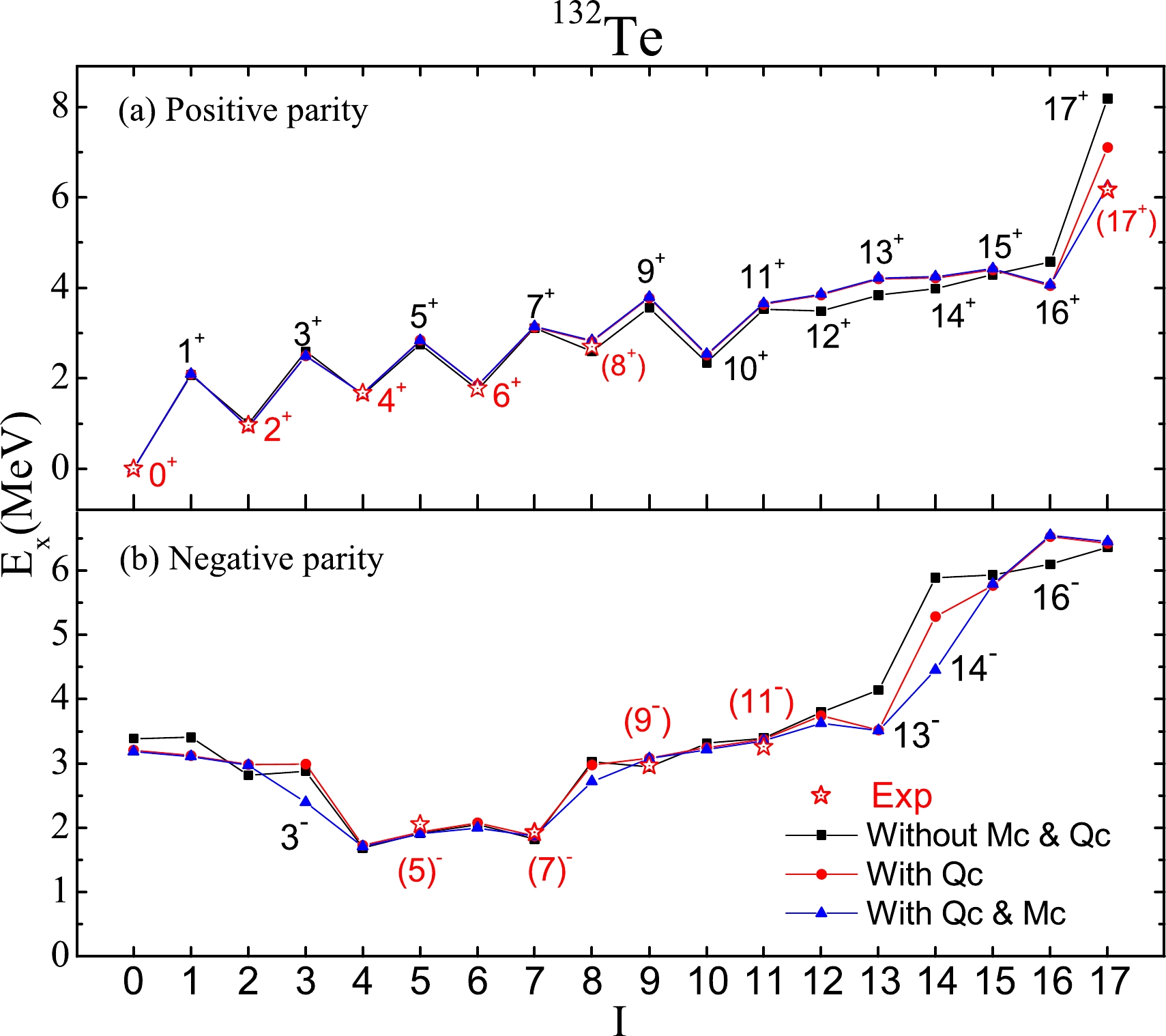
$ \pi g_{7/2} h_{11/2} \nu g^{-1}_{7/2} h^{-1}_{11/2} $ . This level can be affected by these monopole terms from this configuration, i.e., Mc($ \pi g_{7/2} $ ,$ \pi h_{11/2} $ ), Mc($ \nu g_{7/2} $ ,$ \nu h_{11/2} $ ), and Mc($ \pi g_{7/2} $ ,$ \nu h_{11/2} $ ). The level at 8.779 MeV is abandoned, since the biggest difference is only 0.227 MeV in level 3$ ^- $ of$ ^{132} $ Sb (Fig. 2). For the 17$ ^+ $ level at 9.314 MeV, it has a new monopole term of Mc($ \pi h_{11/2} \nu h_{11/2} $ ). This monopole term has almost no effects in levels 17$ ^+ $ coupled by config.1, 2, and 3.$(\kappa = 0.1 \sim 0.9~\rm MeV)$ , while the level 17$ ^+ $ at 9.314 MeV drops to 8.3 MeV (Fig. 3). The level at 9.134 MeV is excluded too, because all 17$ ^+ $ levels are increased sharply when the strength is$\kappa > 0.9~\rm MeV$ . For the last one coupled by config.3, the suitable monopole term$ Mc(\nu d_{5/2},\nu h_{11/2}) $ is turned up from this configuration. Its monopole effects are investigated in the states of$ ^{132} $ Te from 0$ ^+ $ to 17$ ^+ $ by adding$ Mc(\nu d_{5/2},\nu h_{11/2}) $ = –2.6 MeV. As shown in Fig. 4, the level 17$ ^+ $ is reduced to 6.311 MeV, but the values of the 5$ ^- $ and 7$ ^- $ levels become far from the corresponding data.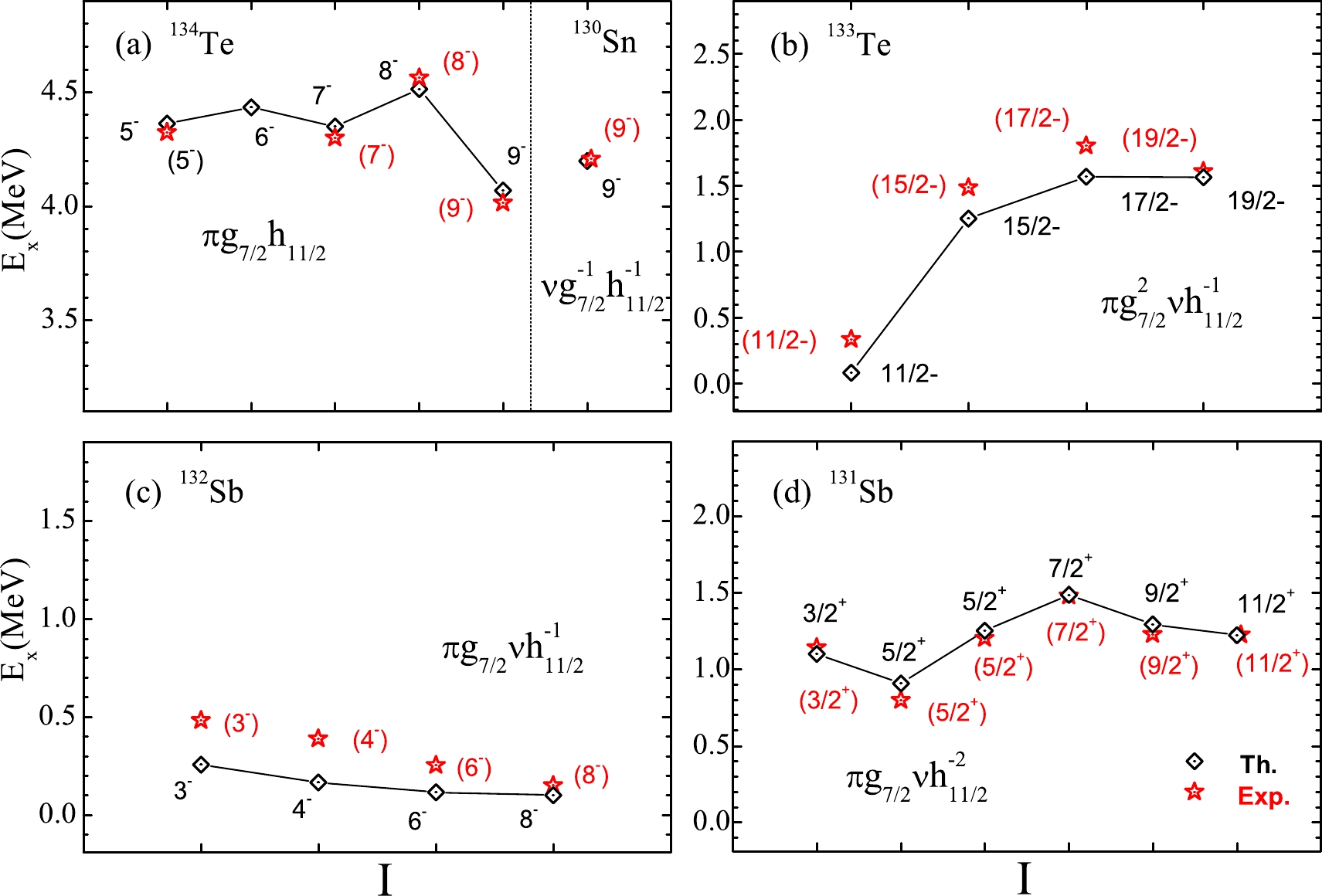
Figure 2. (color online) Levels produced by particular configurations in
$^{134}$ Te,$^{133}$ Te,$^{132}$ Sb,$^{131}$ Sb, and$^{130}$ Sn nuclei, in comparison with given data [32].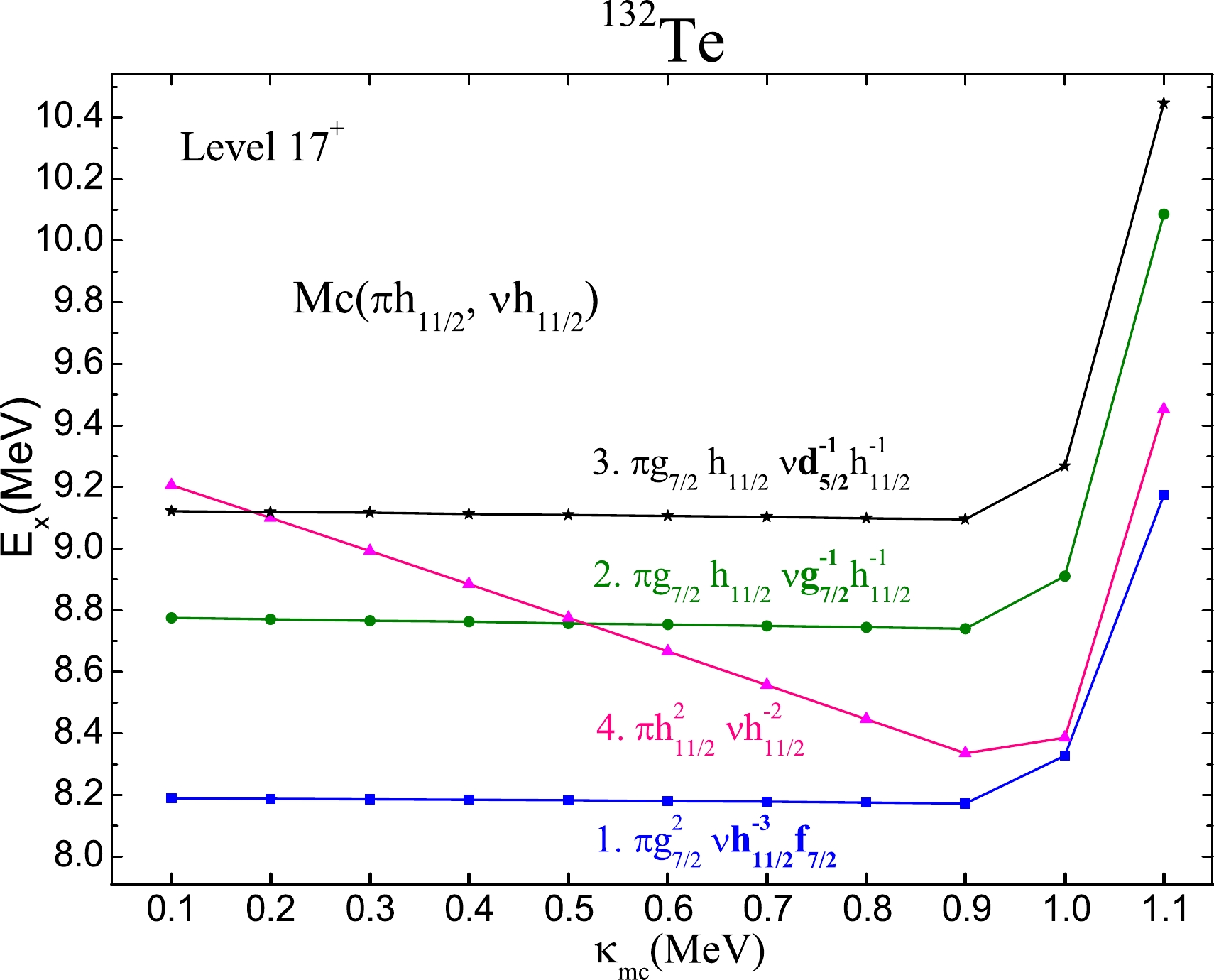
Figure 3. (color online) Monopole effects of Mc(
$\pi h_{11/2} \nu h_{11/2}$ ) in level$17^+$ of$^{132}$ Te.
Figure 4. (color online) Monopole effects of
$Mc(\nu d_{5/2},\nu h_{11/2})$ in$^{132}$ Te. Data marked with stars are from Ref. [32].As shown above, the monopole interaction alone cannot solve the present puzzle, and we focus on the quadrupole-quadrupole force between the proton and neutron (
$ QQ_{\pi,\nu} $ ).As shown in Fig. 5, the value of the
$ QQ_{\pi,\nu} $ force equals the quadruple-quadruple force strength divided by$ [1/A(^{132}Sn)]^{5/3} $ . The level 17$ ^+ $ coupled by configuration$ \pi g_{7/2}h_{11/2} \nu h^{-1}_{11/2} d^{-1}_{5/2} $ is reduced by 2.121 MeV when the QQ force changes from 300 to –450. The lowest value is 7.107 MeV, which occurs when$ QQ_{\pi \nu} $ = –350. It seems the$ QQ_{\pi,\nu} $ force provides a new method to explain the large difference in level 17$ ^+ $ . As shown in Fig. 6, the datum (17$ ^+ $ ) is reproduced very well with$ QQ_{\pi \nu} $ = –350 and$Mc(\nu d_{5/2}, \nu h_{11/2}) = -0.8~\rm MeV$ . Furthermore, the values of 5$ ^- $ and 7$ ^- $ levels are close to data (5)$ ^- $ and (7)$ ^- $ . The levels 13$ ^- $ and 14$ ^- $ drop by approximately 1 MeV with$ QQ_{\pi,\nu} $ correction$(Q_c) $ . The levels 3$ ^- $ and 14$ ^- $ are sensitive to the monopole effects of$ Mc(\nu d_{5/2},\nu h_{11/2}) $ . These levels are connected with datum 17$ ^+ $ by the$ QQ_{\pi,\nu} $ force and monopole effects of$ Mc(\nu d_{5/2},\nu h_{11/2}) $ . If they could be observed experimentally, this would be evidence confirming the datum (17$ ^+ $ ).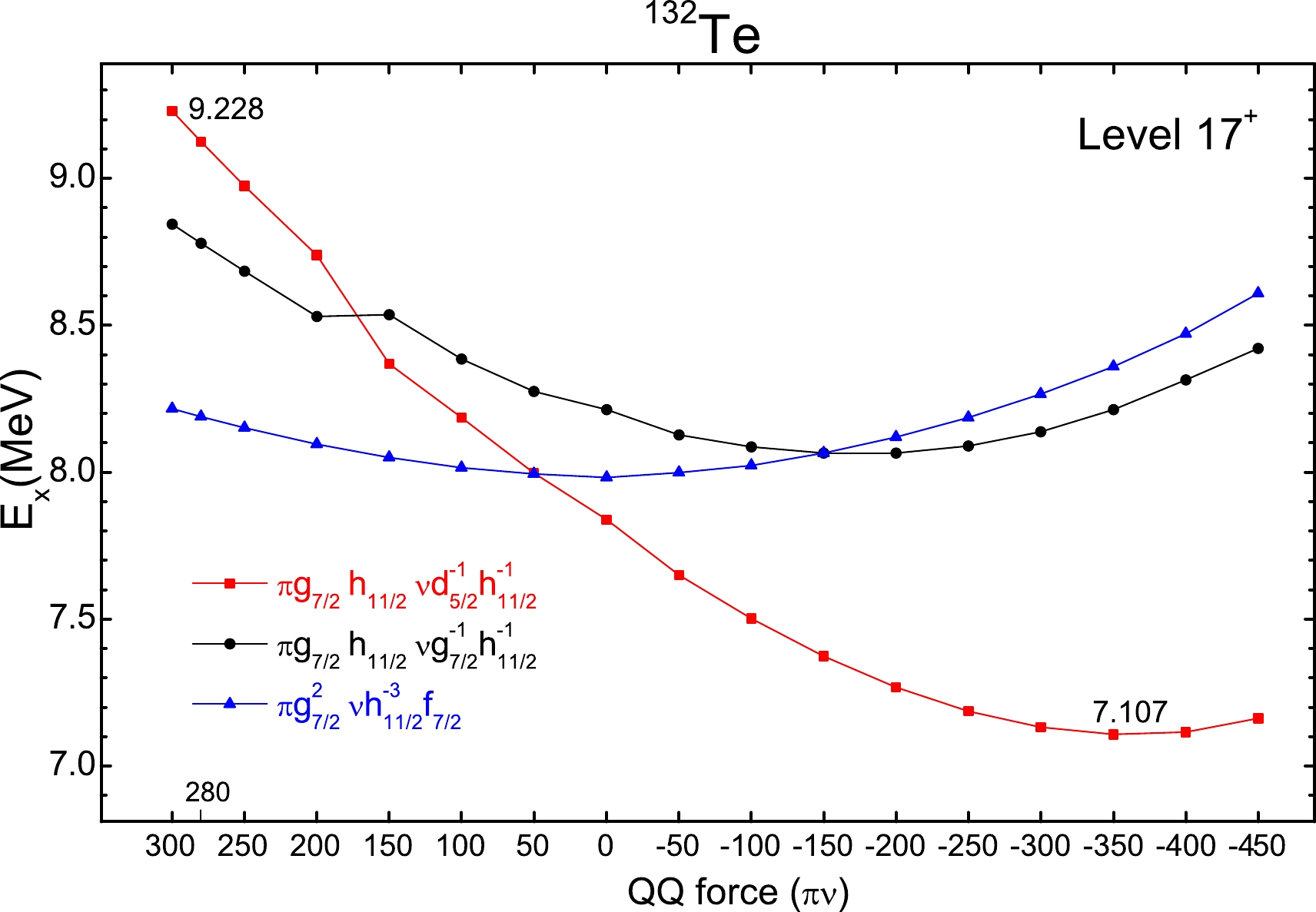
Figure 5. (color online) Effects of the quadruple-quadruple force between the proton and neutron in level 17
$^+$ of$^{132}$ Te.For determining the
$ QQ_{\pi,\nu} $ correction and monopole term$ Mc(\nu d_{5/2},\nu h_{11/2}) $ , an alternative of lack data in$ ^{132} $ Te is to study the$ QQ_{\pi,\nu} $ correction and monopole effects in other nuclei nearby. The monopole effects of$ Mc(\nu d_{5/2},\nu h_{11/2}) $ also exist in$ ^{130} $ Sn and$ ^{131} $ Sb. In$ ^{130} $ Sn, the configuration$ \nu h^{-1}_{11/2} d^{-1}_{5/2} $ produces levels from 3$ ^- $ to 8$ ^- $ . With the$ Mc(\nu d_{5/2},\nu h_{11/2}) $ , the configuration percentages have almost no change in levels 3$ ^- $ , 7$ ^- $ , and 8$ ^- $ , while the percentage of level 5$ ^- $ (6$ ^- $ ) drops from 57$ \% $ (49$ \% $ ) to 52$ \% $ (39$ \% $ ). Level 3$ ^- $ is the first state of$ J^{\pi} = 3^- $ , and its energy decreases by 1.01 MeV when Mc is added. Here, the$ QQ_{\pi,\nu} $ force has no effect on one-shell closed nuclei. If this state could be observed near 2.199 MeV, this would be evidence for considering monopole correction in particle-hole nuclei near$ ^{132} $ Sn. The same applies to level 8$ ^- $ as the first state of$ J^{\pi} = 8^- $ .In
$ ^{131} $ Sb, levels from 1/2$ ^- $ to 21/2$ ^- $ have a main configuration of$ \pi g_{7/2} \nu h^{-1}_{11/2} $ . As shown in Fig. 7(b), the$ QQ_{\pi,\nu} $ correction has obvious effects on levels 1/2$ ^- $ , 3/2$ ^- $ , 5/2$ ^- $ , 21/2$ ^- $ , and 23/2$ ^- $ , while monopole correction Mc has almost no effects except in the case of level 23/2$ ^- $ . The lowest energy level of$ J^{\pi} = 23/2^- $ drops to 2.570 MeV with Qc and Mc. We are very interested in whether the high-spin state 23/2$ ^- $ can be observed experimentally. This 23/2$ ^- $ level can be used to determine the necessity of$ QQ_{\pi,\nu} $ correction in the particle-hole nuclei region and finally explain the large difference in level (17$ ^+ $ ) of$ ^{132} $ Te.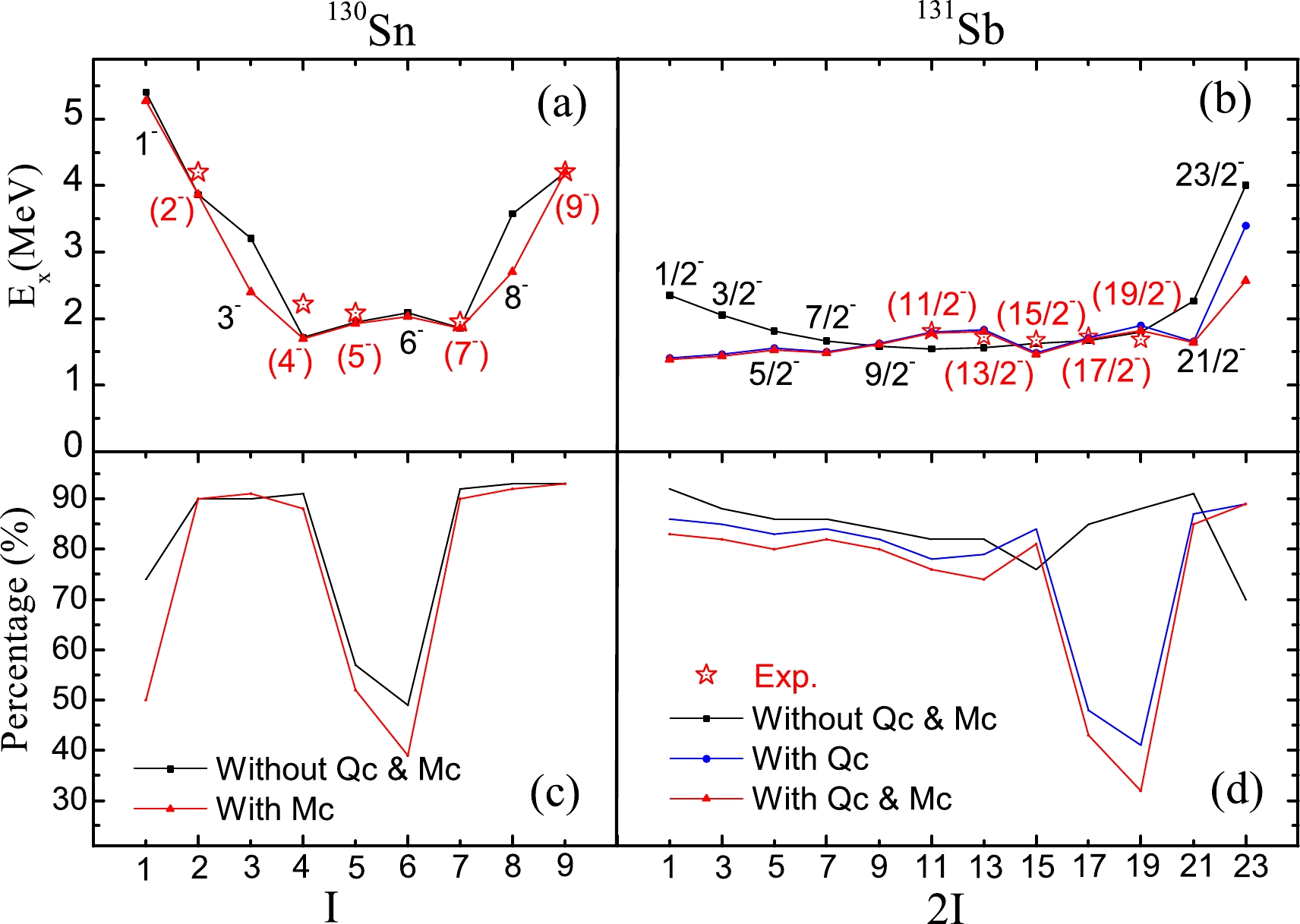
Figure 7. (color online)
$QQ_{\pi,\nu}$ force and monopole effects of$Mc(\nu d_{5/2},\nu h_{11/2})$ in$^{130}$ Sn and$^{131}$ Sb. Data marked with stars are from Ref. [32]. -
The monopole effects and high-spin levels in
$ ^{132-134} $ Te,$ ^{131-133} $ Sb, and$ ^{130} $ Sn are investigated. The datum 6.166 MeV of level 17$ ^+ $ in$ ^{132} $ Te is excluded from configurations$ \pi g_{7/2} h_{11/2} \nu g^{-1}_{7/2} h^{-1}_{11/2} $ or$ \pi h^2_{11/2} \nu h^{-2}_{11/2} $ . The present work suggests the datum (17$ ^+ $ ) coupled by configuration$ \pi g_{7/2} h_{11/2} \nu d^{-1}_{5/2} h^{-1}_{11/2} $ . Several levels are connected with state (17$ ^+ $ ) by monopole effects of$ Mc(\nu d_{5/2},\nu h_{11/2}) $ and the quadruple-quadruple force between the proton and neutron, i.e., 3$ ^- $ (8$ ^- $ ) in$ ^{130} $ Sn, 14$ ^- $ in$ ^{132} $ Te, and 23/2$ ^- $ in$ ^{131} $ Sb. If these states could be observed at lower energies, the lower state (17$ ^+ $ ) of$ ^{132} $ Te would be explained with quadruple-quadruple correction between the proton and neutron and the increasing strength of the monopole interaction between neutron orbits$ d_{5/2} $ and$ h_{11/2} $ .
Monopole effects and high-spin levels in neutron-rich 132Te
- Received Date: 2023-02-15
- Available Online: 2023-07-15
Abstract: The neutron-rich nuclei near doubly magic





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: