-
The dependence of nuclear temperature on emitting source neutron-proton (
$ N/Z $ ) asymmetry, also called the isotopic dependence of nuclear temperature, is closely related to studies on the$ N/Z $ asymmetry dependence of the nuclear force, the nuclear equation of state, and the postulated nuclear liquid-gas phase transition [1–5]. For instance, the assumption of the$ N/Z $ asymmetry independence of nuclear temperature is of great importance in symmetry energy extraction using an isoscaling approach [6, 7].Recently, we studied the source
$ N/Z $ asymmetry dependence of nuclear temperature using light charged particles (LCPs) and intermediate mass fragments (IMFs) from thirteen reaction systems with different$ N/Z $ asymmetries,$ ^{64} \rm{Zn} $ on$ ^{112} \rm{Sn} $ , and$ ^{70} \rm{Zn} $ ,$ ^{64} \rm{Ni} $ on$ ^{112,124} \rm{Sn} $ ,$ ^{58,64} \rm{Ni} $ ,$ ^{197} \rm{Au} $ , and$ ^{232} \rm{Th} $ at 40 MeV/nucleon [8, 9]. In these works, the double isotope ratio thermometers of Albergo et al. [10] with different LCP and IMF yield ratio pairs were used to deduce the temperature values. Because the fragments produced in heavy-ion collisions are generally highly excited, the measured isotope yields are significantly perturbed by their sequential decays, leading to a serious inaccuracy in the temperature determination. Typically, the temperature deduced from experimentally measured isotope yields is referred to as the "apparent temperature", whereas that before the sequential decays is referred to as the "real temperature." To consider the sequential decay effect on the experimentally obtained apparent temperature values, the "indirect" correction method of Sfienti et al. [11] was adopted. That is, instead of using the double isotope ratio thermometer as an absolute thermometer, we used it as a relative thermometer [8, 9]. Following this strategy, a weak$ N/Z $ asymmetry dependence of the real temperature for LCPs and IMFs was inferred from the deduced weak$ N/Z $ asymmetry dependence of the apparent temperature using the experimentally measured isotope yields and the deduced weak$ N/Z $ asymmetry dependence of the relative temperature change by the sequential decay effects with the aid of the statistical multifragmentation model [12] and antisymmetrized molecular dynamics (AMD) model [13], incorporating the statistical decay code GEMINI [14] as an afterburner. One may notice that in such an indirect method, the quantitative deduction of the real temperature values is absent, making the deduction for temperature$ N/Z $ asymmetry dependence using the indirect method qualitative. Therefore, to gain quantitative insights into the temperature$ N/Z $ asymmetry dependence, further efforts are still required.This article aims to investigate the
$ N/Z $ asymmetry dependence of nuclear temperature by introducing a "direct" method, further improving upon our previous studies [8, 9]. In the present study, sequential decay corrections from the apparent temperature to the real temperature are performed quantitatively so that the$ N/Z $ asymmetry dependence of the real temperature after the corrections can be quantitatively deduced. For this purpose, a theoretical model, the quantum statistical model (QSM) of Hahn and Stöcker [15], is used to achieve the sequential decay corrections. For consistency, the same neutron, LCP, and IMF yield data from thirteen reaction systems,$ ^{64} \rm{Zn} $ on$ ^{112} \rm{Sn} $ , and$ ^{70} \rm{Zn} $ ,$ ^{64} \rm{Ni} $ on$ ^{112,124} \rm{Sn} $ ,$ ^{58,64} \rm{Ni} $ ,$ ^{197} \rm{Au} $ , and$ ^{232} \rm{Th} $ at 40 MeV/nucleon and the same double isotope ratio thermometers constructed with two helium-related isotope ratios for LCPs and eight carbon-related isotope ratios for IMFs are used as in our previous studies [8, 9].Although detailed descriptions about the experiment and data analyses have been presented in Refs. [8, 9], we highlight here details closely related to the analysis and results presented in the subsequent sections. The experiment was performed at the K-500 superconducting cyclotron facility at Texas A
$ \& $ M University. During the experiment on the thirteen reaction systems, IMFs were detected by a detector telescope placed at$ 20^\circ $ . The LCPs in coincidence with the IMFs were measured using 16 single-crystal CsI(Tl) detectors with a length of 3 cm set around the target at angles between$ 27^{\circ} $ and$ 155^{\circ} $ . Sixteen detectors of the Belgian-French neutron detector array DEMON (Detecteur Modulaire de Neutrons) [16] outside the target chamber were used to measure neutrons. It is worthy emphasizing that a moving source fit technique [17] was employed to characterize the fragmenting sources, that is, projectile-like (PLF), intermediate-velocity (IV), and target-like (TLF) sources. In the present analyses, only the neutron, LCP, and IMF yields from the IV sources for each given reaction system are considered to allow for the elimination of interference from source property (such as isospin, temperature, and density) deviations [6, 18]. Using the yields from the IV sources also ensures, to some extent, the equilibrium of emitting sources.This article is organized as follows: In Sec. II, a brief description of the sequential decay corrections from the apparent temperature to the real temperature within the framework of the QSM is given. In Sec. III, the
$ N/Z $ asymmetry dependence of nuclear temperature is quantitatively deduced from the corrected temperature values and discussed. Finally, a summary is given in Sec. IV. -
Using the double isotope ratio thermometer of Albergo [10], the temperature for the given reaction system can be deduced as
$ \begin{eqnarray} T = \frac{\Delta B}{\ln(aR)}, \end{eqnarray} $

(1) where
$ R = (Y_1/Y_2)/ (Y_3/Y_4) $ is the experimentally measured isotope yield ratio for isotope pairs$ (1,2) $ and$ (3,4) $ , B is the binding energy difference,$ \Delta B = (BE_1 -BE_2) - (BE_3 -BE_4) $ , and a is the statistical weight factor, defined as$ \begin{eqnarray} a = \frac{(2S_3+1)/(2S_4+1)}{(2S_1+1)/(2S_2+1)}\left[\frac{A_3/A_4}{A_1/A_2} \right]^{3/2}, \end{eqnarray} $

(2) where
$ S_i $ and$ A_i $ are the ground state spin and mass number of the ith isotope, respectively. The ratios used to construct the thermometers for this study and their associated$ \Delta B $ and a values are summarized in the second to fourth columns of Table 1. The selection of these thermometers maintains consistency with our previous studies [8, 9]. Note again that because the experimental yields are perturbed by the sequential decays, the temperature deduced from the experimentally measured isotope yields using Eq. (1) is called the "apparent temperature ($ T_{\rm app} $ )", whereas that before the sequential decay is called the "real temperature (T)", and similarly hereinafter.ID Isotope ratio $ \Delta B $ /MeV

a $ \ln \kappa/B $ /MeV

$ ^{-1} $ 

1 $ ^{1,2} $ H

$ / $ 

$ ^{3,4} $ He

18.40 5.60 0.0671 2 $ ^{2,3} $ H

$ / $ 

$ ^{3,4} $ He

14.29 1.59 0.0472 3 $ ^{6,7} $ Li

$ / $ 

$ ^{11,12} $ C

11.47 5.90 0.033 4 $ ^{7,8} $ Li

$ / $ 

$ ^{11,12} $ C

16.69 5.36 0.114 5 $ ^{9,10} $ Be

$ / $ 

$ ^{11,12} $ C

11.91 1.03 -0.031 6 $ ^{11,12} $ B

$ / $ 

$ ^{11,12} $ C

15.35 3.00 0.093 7 $ ^{12,13} $ B

$ / $ 

$ ^{11,12} $ C

13.84 5.28 0.123 8 $ ^{12,13} $ C

$ / $ 

$ ^{11,12} $ C

13.77 7.92 0.0743 9 $ ^{13,14} $ C

$ / $ 

$ ^{11,12} $ C

10.54 1.96 0.097 10 $ ^{15,16} $ N

$ / $ 

$ ^{11,12} $ C

16.23 9.67 0.161 Table 1. Parameters of the helium- and carbon-related thermometers used in this study. The binding energy difference
$ \Delta B $ and statistical weight factor a are taken from Refs. [8, 9]. The$ \ln \kappa/B $ values are evaluated with the experimentally deduced source temperature of$ 5.2 $ MeV from the reconstructed hot isotope yields of the reaction system$ ^{64} $ Zn+$ ^{112} $ Sn at 40 MeV/nucleon [19, 20].To achieve the quantitative sequential decay corrections from
$T_{\rm app}$ to T, the QSM of Hahn and Stöcker [15] is utilized. The QSM has been applied to study the characteristic natures of sources produced in heavy-ion collisions in the energy range from several tens of MeV/nucleon to approximately ten GeV/nucleon [21–25]. In the QSM, fragmentation is characterized at a given fragmenting volume under thermal and chemical equilibrium. Therefore, both the temperature and density of the given fragmenting source are required. Here, the temperature of the given source is treated as a free input parameter (see below). In our previous study [19], an IV source fragmentation density was determined as$ \rho/\rho_0 = 0.56\pm0.02 $ with the reconstructed hot isotope yields from one of the presently used systems,$ ^{64} $ Zn+$ ^{112} $ Sn at 40 MeV/nucleon, using a self-consistent approach. However, this obtained fragmentation density cannot be arbitrarily applied for other sources with different$ N/Z $ asymmetries because the source density dependence on source$ N/Z $ asymmetry has not yet been addressed.To pursue this issue, AMD simulations are performed. The central collision events of
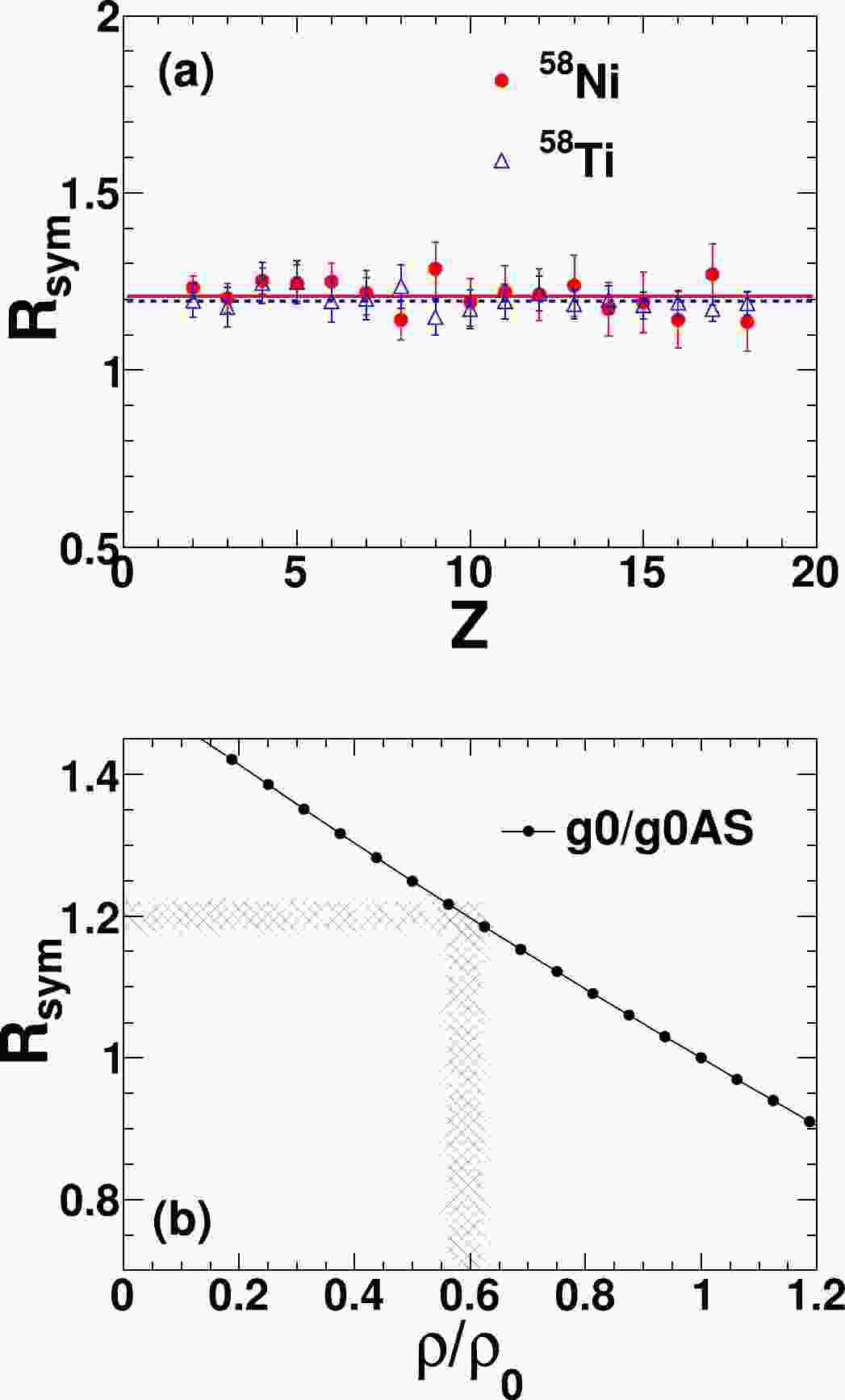
$ ^{58} \rm{Ni} $ +$ ^{58} \rm{Ni} $ and$ ^{58} \rm{Ti} $ +$ ^{58} \rm{Ti} $ are generated using two interactions with different density dependencies of the symmetry energy term, that is, the standard Gogny interaction with an asymptotic soft symmetry energy (g0) and the Gogny interaction with an asymptotic stiff symmetry energy (g0AS). The system size selection allows for the average source sizes from the central collisions of$ ^{58} \rm{Ni} $ +$ ^{58} \rm{Ni} $ and$ ^{58} \rm{Ti} $ +$ ^{58} \rm{Ti} $ to be similar to those of the IV sources measured in the present thirteen systems. The fragments are identified at a time of 300 fm/c using a coalescence technique with a coalescence radius of$ R_c =5 $ fm in the coordinate space to eliminate the sequential decay effect.Following the self-consistent approach [20], the ratios of the deduced symmetry energies with the g0 and g0AS interactions,
$ R_{\rm sym} $ , are first deduced for both systems. The results are shown in Fig. 1(a). The deduced$ R_{\rm sym} $ values are further compared with the$ R_{\rm sym} $ density dependence determined from the input g0 and g0AS density dependent symmetry energies in the AMD simulations in Fig. 1(b). The fragment formation densities for the two systems are then obtained as$(\rho/\rho_0)_{^{58} \rm{Ni}} = 0.58\pm 0.04$ and$ (\rho/\rho_0)_{^{58} \rm{Ti}} = 0.60\pm 0.04 $ , respectively [see Fig. 1(b)]. One can find that despite the large system$ N/Z $ asymmetry difference between$ ^{58} \rm{Ti} $ +$ ^{58} \rm{Ti} $ and$ ^{58} \rm{Ni} $ +$ ^{58} \rm{Ni} $ , that is,$\delta_{^{58} \rm{Ni}} =(N_{^{58} \rm{Ni}}- Z_{^{58} \rm{Ni}})/A_{^{58} \rm{Ni}}= 0.03$ and$\delta_{^{58} \rm{Ti}}=(N_{^{58} \rm{Ti}}- Z_{^{58} \rm{Ti}})/A_{^{58} \rm{Ti}} = 0.24$ , the deduced densities for both systems are in good agreement within errors, demonstrating a negligible$ N/Z $ asymmetry dependence of nuclear density in such reactions. Therefore, the experimentally deduced fragmentation density of$ \rho/\rho_0 = 0.56 $ [19] can be utilized as a common input density when initializing the fragmenting sources with different asymmetries in QSM simulations.
Figure 1. (color online) (a)
$R_{\rm sym}$ as a function of Z from the AMD central collision events of$ ^{58} \rm{Ni} $ +$ ^{58} \rm{Ni} $ and$ ^{58} \rm{Ti} $ +$ ^{58} \rm{Ti} $ . The lines are the constant fit of the data points. (b) Horizontal shaded areas are the ratios deduced in (a), and the vertical shaded areas are the density regions corresponding to the ratios. The two different shadings correspond to the two systems. The solid line is the ratio between the g0 and g0AS density dependent symmetry energies in the AMD simulations.The input fragmentation temperature, namely, the real temperature T, is varied from 2 to 10 MeV in the QSM simulations. The input source sizes and
$ N/Z $ asymmetries are taken according to those of the IV sources from the thirteen systems. Using the helium- and carbon-related thermometers, the$T_{\rm app}$ values are deduced from the isotope yields after the sequential decays within the QSM framework. The resultant correlations between T and$T_{\rm app}$ for all ten thermometers are shown in Fig. 2, where the different colored lines in each panel correspond to those from the sources with different$ N/Z $ asymmetries. Using the obtained T versus$T_{\rm app}$ correlations in the figure, the point-to-point sequential decay corrections from$T_{\rm app}$ to T can be performed by mapping out the T value for the given$T_{\rm app}$ value using an interpolation technique. For clarification, the deduced real temperature with the QSM is denoted by$T_{\rm QSM}$ hereinafter.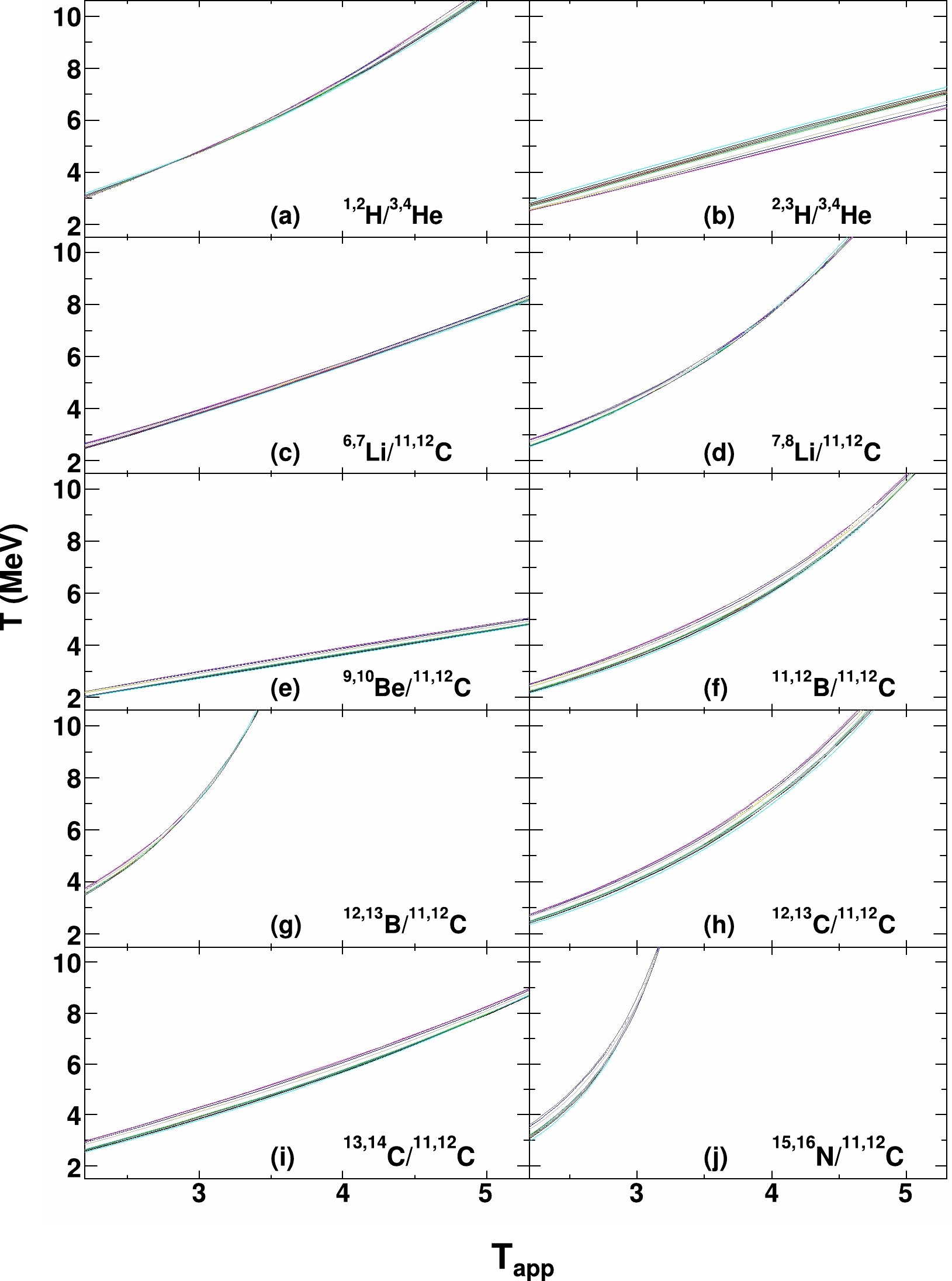
Figure 2. (color online) T versus
$T_{\rm app}$ correlations from the QSM simulations. The different panels correspond to the thermometers with different isotope pairs, and the different lines in each panel correspond to different emitting source asymmetries.To crosscheck the performance of the temperature corrections within the framework of the QSM, the obtained
$ T_{\rm QSM} $ values from the reaction system of$ ^{64} $ Zn+$ ^{112} $ Sn (squares) are plotted in Fig. 3 as an example, where the "ID of thermometers" along the x-axis corresponds to the values indicated in the left column of Table 1. For comparison, the temperature of$ 5.2\pm0.6 $ MeV deduced from our previous self-consistent analysis of the reconstructed hot isotope yields for the$ ^{64} $ Zn+$ ^{112} $ Sn system [19] is also plotted in the shaded area of the figure. As shown in the figure, the$T_{\rm QSM}$ values deduced with the double isotope ratios$ ^{2,3} $ H$ / $ $ ^{3,4} $ He,$ ^{7,8} $ Li$ / $ $ ^{11,12} $ C,$ ^{9,10} $ Be$ / $ $ ^{11,12} $ C,$ ^{11,12} $ B$ / $ $ ^{11,12} $ C, and$ ^{13,14} $ C$ / $ $ ^{11,12} $ C are consistent with that obtained from the self-consistent approach within errors, whereas the others exhibit an$ \sim $ 0.5– 2 MeV discrepancy beyond the shaded area.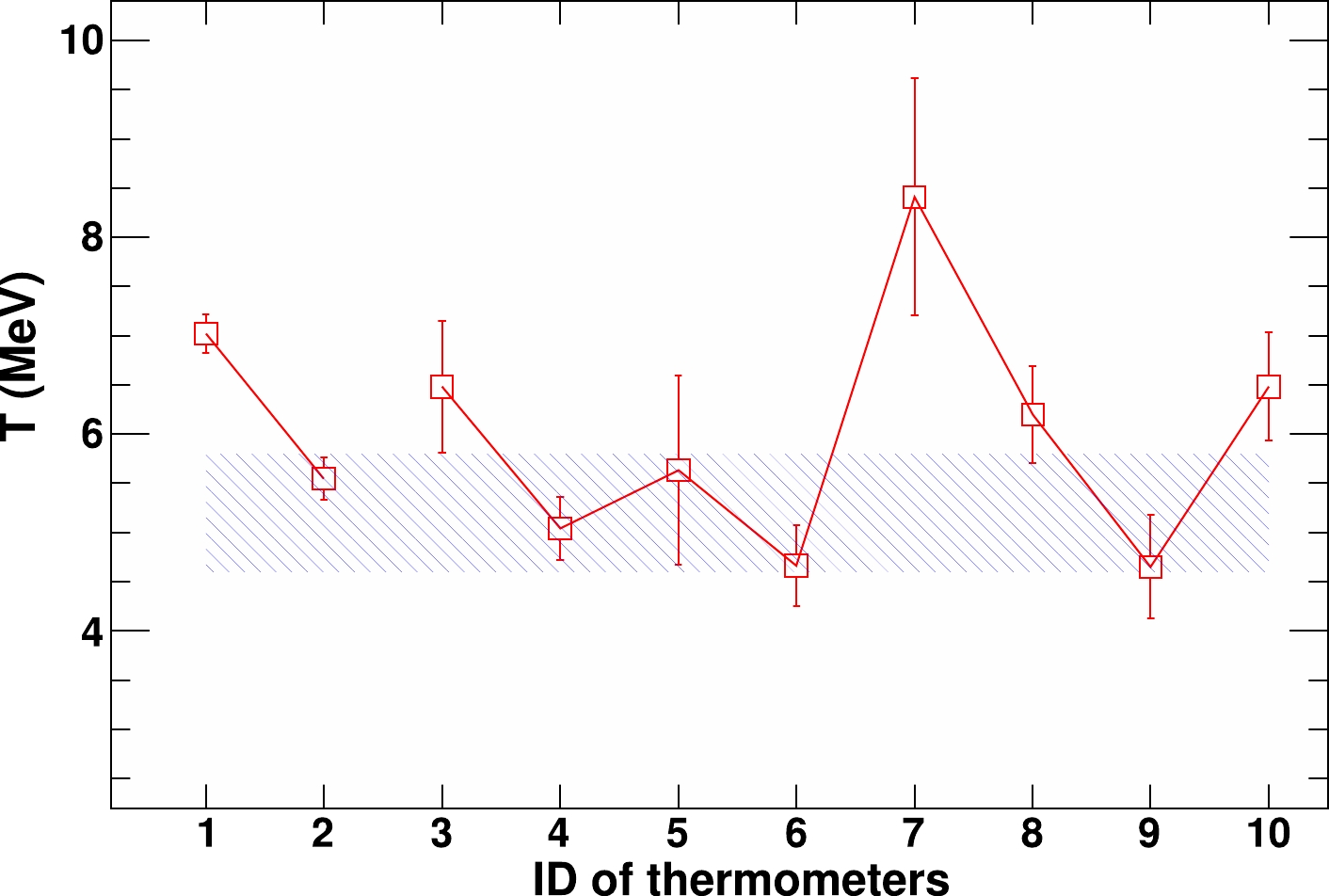
Figure 3. (color online) Corrected real temperature values after feedings using the QSM (squares) and that deduced using the self-consistent method (shaded area) from the reaction system of
$ ^{64} $ Zn+$ ^{112} $ Sn.This significant temperature fluctuation of the
$T_{\rm QSM}$ values is highly surprising because for the given emitting source, the temperature values determined using different thermometers are presumed to be similar. We conjecture that the$T_{\rm QSM}$ fluctuation may arise from the inaccurate descriptions of the role of nuclear structure effects for the isotopes of interest in the QSM. As is well known, the inclusion of nuclear spectral information into the calculations when simulating the effects of secondary decays has not been fully successful because the task is not only computationally difficult but also hampered by the lack of complete information on nuclear resonances from experiments [26, 27]. One may find support from the relatively more significant temperature overestimation for the$ ^{12,13} $ B$ / $ $ ^{11,12} $ C thermometer, for which isotopes with larger isospins, that is,$ ^{12} $ B and$ ^{13} $ B, are included, and the influence of the absence of complicated structure information appears more significant. However, for completeness, the point-to-point corrections for all ten considered thermometers are performed in a preliminary trial using the correlations obtained in Fig. 2, despite possibly involving the incomplete inclusion problem of nuclear structure characteristics in the QSM. As demonstrated in the following section, this effect only weakly jeopardizes the final conclusion. -
Figure 4 first shows the resultant
$T_{\rm app}$ values from the helium- and carbon-related thermometers as a function of IV source$ N/Z $ asymmetry,$\delta_{\rm IV} = (N_{\rm IV}-Z_{\rm IV})/A_{\rm IV}$ , where$N_{\rm IV}$ ,$Z_{\rm IV}$ , and$A_{\rm IV}$ are the neutron, proton, and mass of the fragmenting source calculated by summing over the experimentally measured IV component yields of neutrons, LCPs, and IMFs with Z up to 18. The errors shown in the figure are evaluated from the isotope yield errors. In the figure, the$T_{\rm app}$ values show a rather negligible$ N/Z $ asymmetry dependence on$\delta_{\rm IV}$ for all ten thermometers within the error bars. One may notice an exception for the LCP temperature from the$ ^{70} $ Zn+$ ^{64} $ Ni system; however, this data point does not significantly disturb the overall trend of$T_{\rm app}$ versus$\delta_{\rm IV}$ . Global fits are performed for the helium- and carbon-related$T_{\rm app}$ versus$\delta_{\rm IV}$ plots using linear functions with one common slope$k_{\rm app}$ and individual intercepts, where$k_{\rm app}$ indicates the average trend of$T_{\rm app}$ as a function of$ \delta_{\rm IV} $ , and the individual intercepts indicate the sensitivity of the$T_{\rm app}$ values to the applied thermometers.$k_{\rm app} = -0.1\pm 0.5$ MeV for the helium-related thermometers and$k_{\rm app} = -0.5\pm 0.9$ MeV for the carbon-related thermometers are obtained from the fits [28], where the$k_{\rm app}$ errors are the fitting errors. The$k_{\rm app}$ values from both types of thermometers are small and in good agreement within the error bars.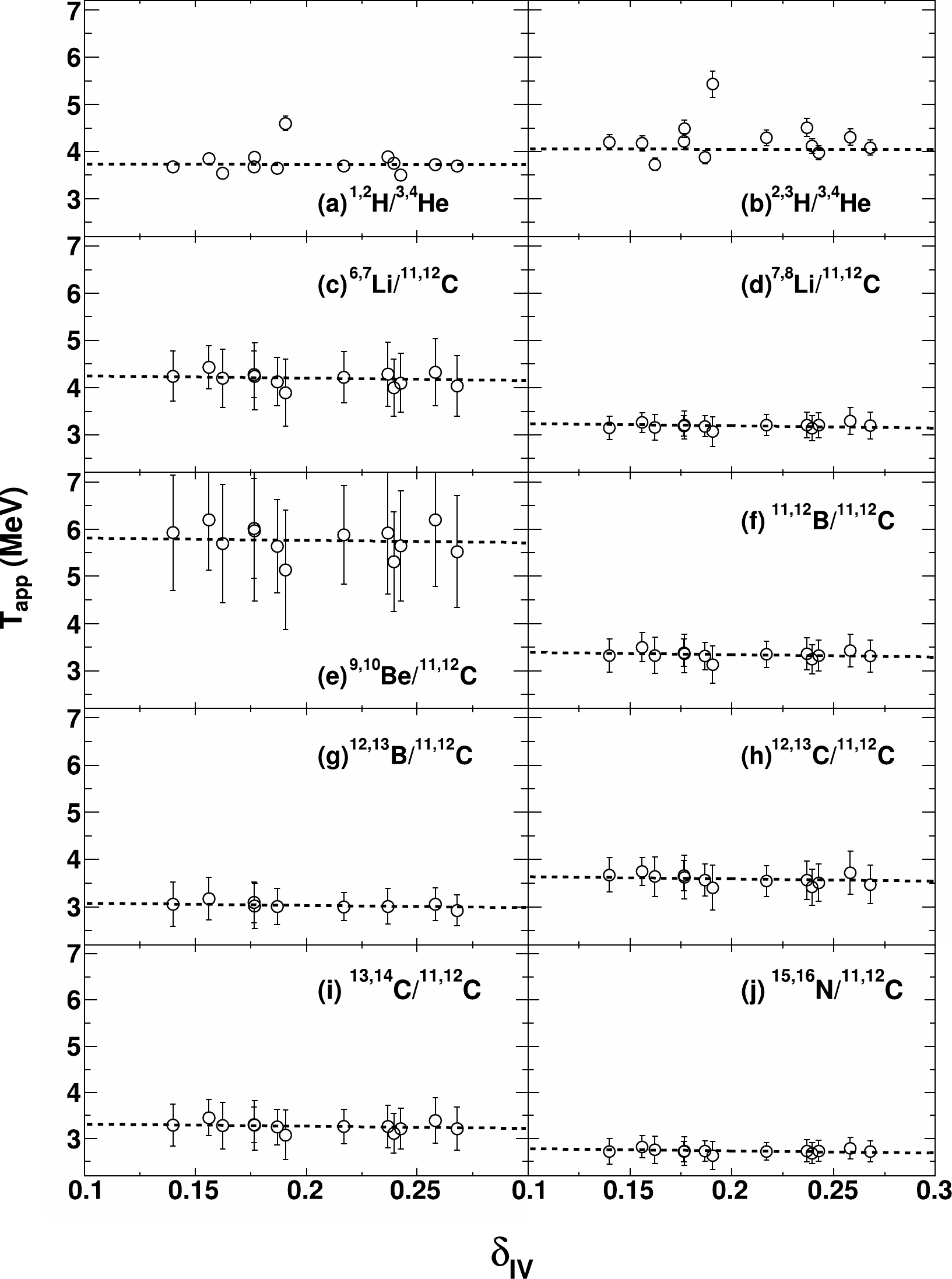
Figure 4.
$T_{\rm app}$ obtained from the experimental isotope yields using the helium- and carbon-related double isotope ratio thermometers as a function of the source$ N/Z $ asymmetry$\delta_{\rm IV}$ . The dashed lines are the global fits for the helium- and carbon-related$T_{\rm app}$ versus$\delta_{\rm IV}$ plots (see the text).Using the T versus
$T_{\rm app}$ correlations in Fig. 2, the sequential decay corrections are performed via point-to-point mapping out of the$T_{\rm QSM}$ value corresponding to a given$T_{\rm app}$ value in Fig. 4. Figure 5 shows the resultant$T_{\rm QSM}$ values as a function of$\delta_{\rm IV}$ . The data points from the helium- and carbon-related thermometers are also fitted similar to those in Fig. 4. The slope ($k_{\rm QSM}$ ) values for the helium- and carbon-related thermometers are obtained as$ -1.4\pm1.0 $ MeV and$ 1.8\pm1.5 $ MeV, respectively. Although different signs are obtained for$ k_{\rm QSM} $ for both types of thermometers, the values of$k_{\rm QSM}$ are small and similar. The similarity in the magnitude of$k_{\rm QSM}$ with the application of the LCP and IMF double isotope ratio thermometers is an indication of an early chemical freeze-out in the heavy-ion collisions at the present intermediate energies, and after the early chemical freeze-out, the partitioning into particles and fragments is completed, and mutual scatterings are no longer sufficiently energetic to significantly modify the channel composition. Moreover, comparing Figs. 4 and 5, one may find an average temperature increase of$ \sim $ 1 MeV owing to the sequential decay corrections from$T_{\rm app}$ to$T_{\rm QSM}$ . This result can be considered representative of a reducing effect of sequential decay on the real temperature from the double isotope ratio thermometers in general. A significant intercept fluctuation of$ \sim $ 4–7 MeV among the different thermometers is also observed for$T_{\rm QSM}$ , which is directly linked to the imperfect performance of the corrections for the sequential decays with the QSM, similar to the case of Fig. 3.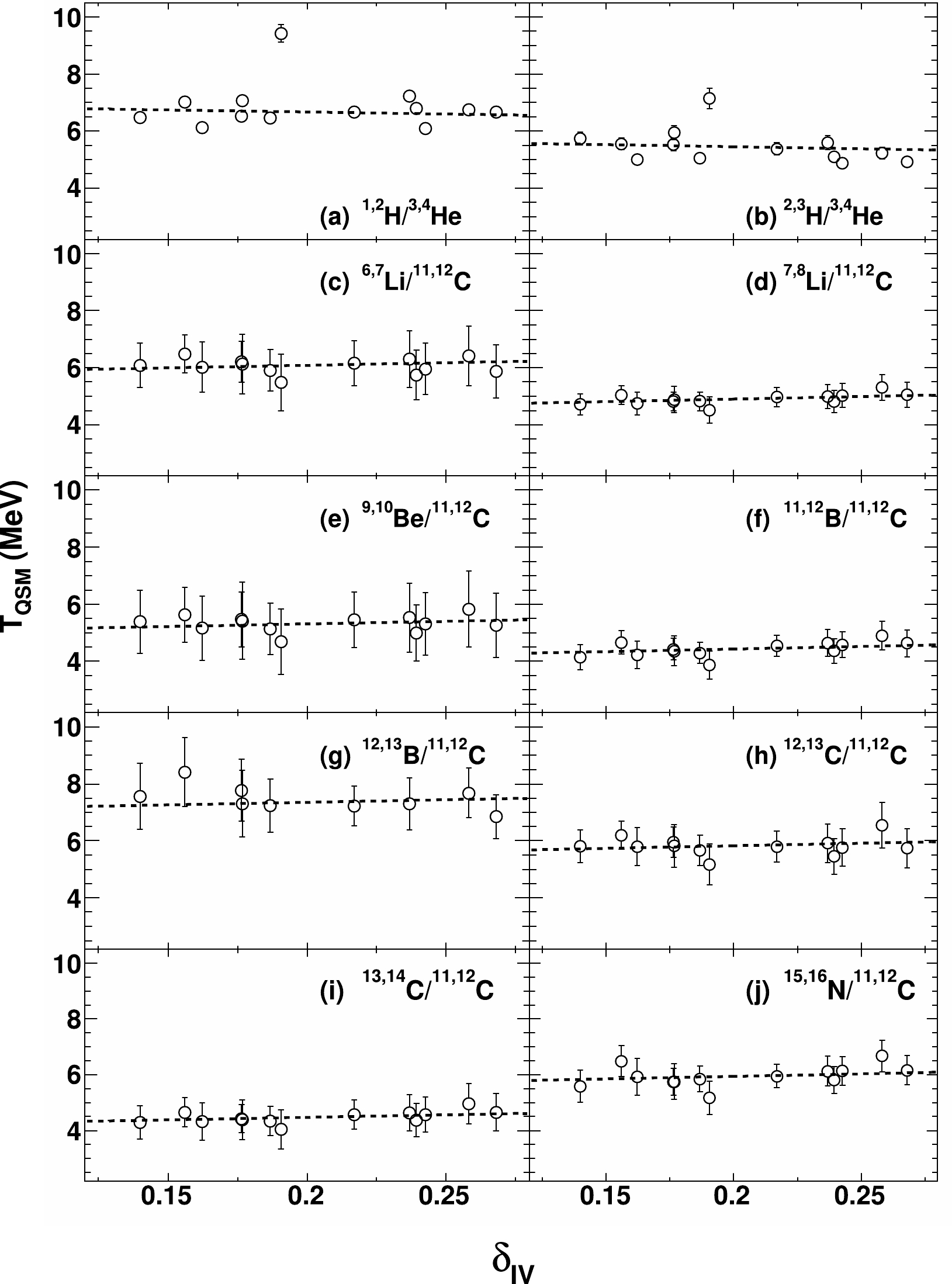
Figure 5. Same as Fig. 4, but for the real temperature values obtained after sequential feedings with the QSM.
It should be mentioned that the present sequential decay corrections from
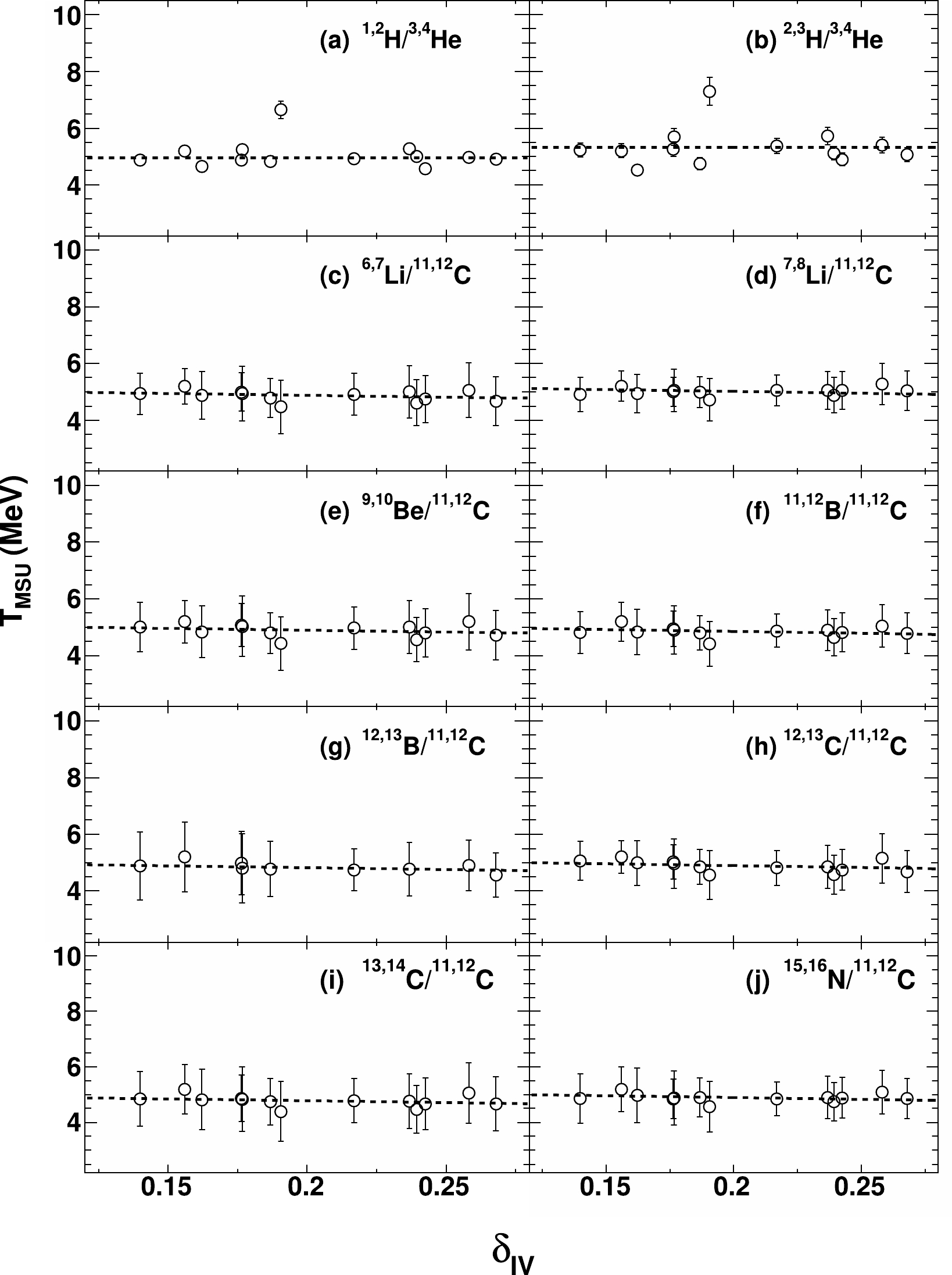
$T_{\rm app}$ to$T_{\rm QSM}$ are in the framework of the QSM only, and therefore the model-dependent effect is inevitable, potentially leading to uncertainties in the determination of the real temperature$ N/Z $ asymmetry dependence. Because of this issue, a model-independent empirical method proposed by Tsang et al. [29] is applied to correct the apparent temperature for comparison. In the method of Tsang et al., an empirical factor κ is defined, and the relation between the real temperature and the apparent temperature can be written as$ \begin{eqnarray} \frac{1}{T_{\rm MSU}}= \frac{1}{T_{\rm app}} - \frac{\ln\kappa}{B}. \end{eqnarray} $

(3) To distinguish it from the QSM corrections, the corrected real temperature using Eq. (3) is referred to as
$T_{\rm MSU}$ hereinafter. Knowing the experimentally determined real source temperature of$ 5.2 $ MeV from the system of$ ^{64} $ Zn+$ ^{112} $ Sn in our previous study [19], the$ \ln \kappa/B $ values for the ten thermometers are evaluated and listed in the fifth column of Table 1. In Ref. [30], Xi et al. found that at temperatures of approximately 4.5 MeV, the$ \ln \kappa/B $ value for a given double isotope ratio thermometer is independent of the projectile-target combination of reactions. This supports the application of the$ \ln \kappa/B $ values obtained from one single system of$ ^{64} $ Zn+$ ^{112} $ Sn to the other twelve systems with different$ N/Z $ asymmetries. The sequential decay feedings for$ T_{\rm app} $ in Fig. 4 are then performed using the obtained$ \ln \kappa/B $ in Table 1. The resultant$T_{\rm MSU}$ values as a function of$\delta_{\rm IV}$ for all ten thermometers are presented in Fig. 6. The same global fits are also performed as those in Figs. 4 and 5.$ k_{\rm MSU}=0.1\pm1.0 $ MeV and$ -1.3\pm2.0 $ MeV are obtained for the helium- and carbon-related thermometers, respectively.For comparison, we summarize the slopes deduced from the fittings for the corrected real temperatures using the QSM (
$k_{\rm QSM}$ ) and empirical correction factor ($k_{\rm MSU}$ ) in Table 2. From the above analyses, one may find that the sequential decay corrections with the QSM and empirical correction factor are within completely different scenarios. However, the application of both methods for the temperature corrections does not disturb the consistency between$k_{\rm QSM}$ and$k_{\rm MSU}$ , as shown in Table 2. This reveals that the underlying differences originating from the internal specific assumptions in the given method are canceled out in the sequential decay corrections from$T_{\rm app}$ to T among the sources with different$ N/Z $ asymmetries. Based on this finding, it is reasonable to conclude that even if an incomplete inclusion of the nuclear structure characteristics is involved in the QSM simulations, the "imperfect" point-to-point temperature corrections with the QSM leads to little influence on our present "dependence" study of nuclear temperature.$k_{\rm QSM}$ /MeV

$k_{\rm MSU}$ /MeV

He-related $ -1.4\pm 1.0 $ 

$ 0.1\pm 1.0 $ 

C-related $ 1.8\pm 1.5 $ 

$ -1.3\pm 2.0 $ 

The
$ N/Z $ asymmetry dependence of T with the QSM can be obtained quantitatively as$k^{\rm avg.}_{\rm QSM}=1.6\pm1.3$ MeV by averaging the absolute values of$k_{\rm QSM}$ from the helium- and carbon-related double isotope ratio thermometers, where a change of 0.1 units in source$ N/Z $ asymmetry leads to an absolute change in temperature of the order of 0.03 to 0.29 MeV on average for LCPs and IMFs. Therefore, a negligible dependence of nuclear temperature on source$ N/Z $ asymmetry can be quantitatively addressed in heavy-ion collisions in the present intermediate energy range. This conclusion agrees well with that of our previous studies [8, 9], in which a negligible$ N/Z $ asymmetry dependence of nuclear temperature was qualitatively inferred, using the indirect method of Sfienti et al. [11] to qualitatively consider the sequential decay effect.Recently, McIntosh et al. studied the temperature
$ N/Z $ dependence with LCPs from compound nuclei produced in$ ^{78,86} $ Kr+C fusion reactions using both a double isotope ratio thermometer and classical momentum quadrupole fluctuation thermometer [31]. They found that neutron-rich compound nuclei exhibit higher temperatures compared to less neutron-rich compound nuclei, independent of the thermometer selection [32]. This result contrasts with not only our present result but also their previous result [33]. A difference can be noticed in the type of reaction system studied, that is, a multi-fragmentation system in this study and Ref. [31], and a fusion-evaporation system in Ref. [33]. The inconsistent conclusions may be related to the different reaction mechanisms in the multi-fragmentation and fusion-evaporation processes [33]. However, to date, our understanding of such inconsistency is still far from complete, and further studies are required.As a final remark, the highlight of this study is that we consider the sequential decay effect on the experimentally obtained
$T_{\rm app}$ values by quantitatively correcting them with the aid of theory prior to investigating the dependence properties of nuclear temperature. However, ambiguities still exist in the corrections from$T_{\rm app}$ to T themselves owing to the incomplete theoretical description for the fragmentation of nuclear systems, although it has been proven that they weakly jeopardize the present dependence study of nuclear temperature on source$ N/Z $ asymmetry. To obtain valuable information from heavy-ion collisions, the search for an "ideal" transport model or establishing a novel one based on existing transport codes is an important long-standing goal in transport theory. For the first step, the transport model comparison project has proceeded worldwide to establish a theoretical systematic error that quantifies the model dependence of transport predictions and further minimize it. Great progress has recently been achieved [34]. The perspective of solving this open problem in the real temperature determination via experiment may become accessible with the aid of the ideal transport model in future. -
In this study, the dependence of nuclear temperature on emitting source
$ N/Z $ asymmetry is investigated with LCPs and IMFs generated from intermediate-velocity sources in thirteen reaction systems with different$ N/Z $ asymmetries,$ ^{64} \rm{Zn}+^{112} \rm{Sn} $ ,$ ^{70} \rm{Zn} $ , and$ ^{64} \rm{Ni} $ on$ ^{112,124} \rm{Sn} $ ,$ ^{58,64} \rm{Ni} $ ,$ ^{197} \rm{Au} $ , and$ ^{232} \rm{Th} $ at 40 MeV/nucleon. First, the apparent temperature ($T_{\rm app}$ ) values of LCPs and IMFs from different systems are determined using two helium-related and eight carbon-related double isotope ratio thermometers, respectively. Quantitative sequential decay corrections from the deduced$T_{\rm app}$ values to the real temperature (T) values are then performed with the aid of the QSM of Hahn and Stöcker to improve upon our previous work. For comparison, the empirical method of Tsang et al. is also used for the sequential decay corrections. The T values deduced from the two sequential decay correction methods are found to show a negligible dependence on source$ N/Z $ asymmetry, revealing a negligible impact originating from the internal specific assumptions in the given method on the sequential decay corrections from$T_{\rm app}$ to T. Based on this finding, the$ N/Z $ asymmetry dependence of T from the QSM corrections is deduced, where a change of 0.1 units in source$ N/Z $ asymmetry corresponds to an absolute change in temperature of the order of 0.03 to 0.29 MeV on average for LCPs and IMFs. Therefore, a negligible dependence of nuclear temperature on the source$ N/Z $ asymmetry range is quantitatively addressed in heavy-ion collisions in the present intermediate energy region, indicating high consistency with the conclusion drawn in our previous studies. -
The authors thank colleagues in the Natowitz group at the Cyclotron Institute, Texas A & M University, for their great support in accessing experimental data and for useful discussions.
Determining the nuclear temperature dependence on source neutron-proton asymmetry in heavy-ion reactions at intermediate energy
- Received Date: 2022-10-19
- Available Online: 2023-05-15
Abstract: In this article, we investigate the dependence of nuclear temperature on emitting source neutron-proton (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: