-
Einstein's theory of general relativity (GR) is an effective gravitational theory applicable to physical scales much greater than the Planck scale but smaller than the Hubble scale. However, near the Planck scale, the GR theory is ammended in terms of the action by certain averaging effects such as those resulting from the renormalization group [1]. The renormalization group improved (RGI) approach is based on the UV complete and non-perturbative renormalization to quantum gravity, which is manifested in the asymptotically safe gravity as well [2, 3]. Consequently, quantum gravity effects are manifested in the quantum Schwarzschild black hole (BH) spacetime as various correction terms of the form
$ r^{-n} $ , where n denotes a positive real number [4].The gravitational effects attributed to these quantum corrections are experienced by test particles located near the BHs. The RGI Schwarzschild BH has 2, 1, or 0 horizons, provided the ADM mass of the BH is greater, equal to, or less than a critical mass, respectively. Within the semi-classical approach to quantum gravity, the Hawking evaporation of a BH leads to the formation of a naked singularity, whereas RGI effects prevent the complete evaporation of a BH when the ADM mass of the BH reaches the critical mass, thus leaving behind a cold remnant. It should be noted that the free parameters of the RGI BH have been constrained recently using data from various astronomical sources involving gravitational lensing by the BHs at the centers of the M87 and Milky Way galaxies [5, 6]. The bound orbits and epicyclic frequencies of massive particles around RGI BHs have been recently reported in Ref. [7].
Astrophysical BHs are surrounded by plasma and magnetic fields. This has been recently confirmed based on astronomical observations of the M87 galactic center by the Event Horizon Telescope (EHT) collaboration using polarized synchrotron radiation probes [8, 9]. In particular, the observations reveal the presence of hot plasma with a temperature on the order of ten billion kelvin, along with a magnetic field with a strength on the order of 30 G. The M87 central BH is also an active BH candidate surrounded by an accretion disk, and the mass accretion rate is approximately
$ (3-20) \times 10^{-4} $ solar mass per year. Theoretical models depicting the dynamics of non-magnetized plasma near BHs with a spherical or axial symmetry have been developed by Perlick et al. [10–14]. These authors not only studied gravitational lensing and BH shadows in the presence of plasma but also investigated plasma accretion in the radial infall of the BH. In the literature, plasma effects on the shadows of diverse modified gravity BHs have been vigorously investigated for phenomenological reasons [15–23], along with gravitational weak lensing in the presence of plasma [24–34]. Previously, gravitational lensing in the weak and strong field regimes in the vacuum surrounding BHs has been reported by some authors in Refs. [35–48]. More recently, new observations made by the EHT team on the shadow of the Sgr A$ ^* $ BH [49] have also spurred interest in further analytical studies on BH and wormhole shadow models [50–56].In this study, we aim to extend the previous phenomenological studies on RGI BHs by analyzing the impact of the presence of plasma, along with the effects of quantum corrections, on the motion of photons near a BH. The outline of this article is as follows: In Sec. II, we outline the equations of motion in a plasma medium. In Sec. III, we investigate the shadow images of an RGI BH. In Sec. IV, we compute the deflection angle of light within the weak limit. In Sec. V, we evaluate the shadow images casted by the infalling gas on the BH. Finally, in Sec. VI, we comment on our results. Note that throughout the paper, we use a system of geometric units wherein
$ G = 1 = c $ . -
The spacetime metric describing a static and spherically symmetric RGI BH is given as follows [4]:
$ {\rm d} s^2=-f(r){\rm d}t^2+\frac{1}{f(r)}{\rm d}r^2+r^2({\rm d}\theta^2+\sin^2{\theta}{\rm d}\phi^2), $

(1) where
$ f(r)=1-\frac{2M}{r}\Big(1+\frac{\Omega M^2}{r^2}+\frac{\Omega \gamma M^3}{r^3}\Big)^{-1}. $

(2) Both the Ω and γ parameters denote the quantum effect and are completely free based on the RGI theory. As mentioned earlier in the Introduction, these parameters have been recently constrained, i.e.,
$ 0.02\leq\gamma\leq 0.22 $ and$ 0.165\leq\Omega\leq9.804 $ , and the constraints can be further refined using future astronomical observations acquired from closer inspections of BHs. However, from a theoretical point of view, Ω should be an extremely small quantity. In the astrophysical observations of supermassive BHs with$ M\gg \Omega $ , quantum effects are therefore extremely small, i.e.,$ \Omega\ll 1 $ . However, to identify some interesting effects, in the present study, we assume Ω as a free parameter to extrapolate a stronger quantum effect. In our view, current astronomical observations are not precise enough; for example, a huge uncertainty exists in the BH mass, which is why we cannot constrain such quantum effects to a satisfactory level. The Hamiltonian representing the propagation of photons in the plasma medium has the form [57]$ \mathcal H(x^\alpha, p_\alpha)=\frac{1}{2}\left[ g^{\alpha \beta} p_\alpha p_\beta - (n^2-1)( p_\beta u^\beta )^2 \right], $

(3) where
$ x^\alpha $ denote the spacetime coordinates,$ p_\alpha $ and$ u^\beta $ denote the four-momentum and four-velocity vectors of the photon, respectively, and n is the refractive index ($n= \omega/k$ , where k is the wave number). The refractive index is expressed as follows [58]:$ n^2=1- \frac{\omega_{p}^2}{\omega^2}, $

(4) in terms of the plasma frequency
$ \omega^2_{p}(x^\alpha)=4 \pi e^2 N(x^\alpha)/m_e $ (e and$ m_e $ are the electron charge and mass, respectively, and N is the number density of the electrons); the photon frequency$ \omega(x^\alpha) $ is defined by$ \omega^2=(p_\beta u^\beta)^2 $ with$ \omega(r)=\frac{\omega_0}{\sqrt{f(r)}},\qquad \omega_0=\text{const}. $

(5) The lapse function is defined such that
$ f(r) \to 1 $ as$ r \to \infty $ and$ \omega(\infty)=\omega_0=-p_t, $ which represents the energy of the photon at spatial infinity [13]. Moreover, the plasma frequency must be sufficiently smaller than the photon frequency$ (\omega_{p}^2\ll \omega^2) $ , thereby allowing the BH shadow to be differentiated from that in the vacuum case. In other words, the natural frequency of oscillation of electrons within the plasma is much smaller than the frequency of light passing through the medium. Using Eqs. (3) and (4), the Hamiltonian for light rays in the plasma medium has the following form:$ \mathcal{H}=\frac{1}{2}\Big[g^{\alpha\beta}p_{\alpha}p_{\beta}+\omega^2_{p}\Big]. $

(6) The components of the four-velocity vector for photons in the equatorial plane
$ (\theta=\pi/2,\; p_\theta=0) $ are given by$ \dot t\equiv\frac{{\rm d}t}{{\rm d}\lambda}= \frac{ {-p_t}}{f(r)} , $

(7) $ \dot r\equiv\frac{{\rm d}r}{{\rm d}\lambda}=p_rf(r) , $

(8) $ \dot\phi\equiv\frac{{\rm d} \phi}{{\rm d}\lambda}= \frac{p_{\phi}}{r^2}, $

(9) where we use the following relationship:
$ \dot x^\alpha=\partial \mathcal{H}/\partial p_\alpha $ . From Eqs. (8) and (9), we obtain a governing equation for the phase trajectory of light$ \frac{{\rm d}r}{{\rm d}\phi}=\frac{f(r) r^2 p_r}{p_{\phi}}. $

(10) Using the constraint
$ \mathcal H=0 $ , we can rewrite the above equation as [13]$ \frac{{\rm d}r}{{\rm d}\phi}=\sqrt{r^2 f(r)}\sqrt{h^2(r)\frac{\omega^2_0}{p_\phi^2}-1}, $

(11) where we define [13]
$ h^2(r)=r^2\Bigg[\frac{1}{f(r)}-\frac{\omega^2_{ {p}}(r)}{\omega^2_0}\Bigg]. $

(12) The radius of a circular orbit of light, particularly the one that forms a photon sphere of radius
$r_{p}$ , is determined by solving the following equation [13]:$ \frac{{\rm d}(h^2(r))}{{\rm d}r}\bigg|_{r=r_{p}}=0. $

(13) After substituting Eq. (12) into (13), one can write the algebraic equation for
$r_{p}$ in the presence of a plasma medium as$ \begin{aligned}[b]& \frac{r_{p}^2-3 r_{p} M}{(r_{p}-2 M)^2}-\frac{\Omega(2\gamma M^4+2M^4+M^3 r_{p})}{r_{p}(2M-r_{p})^3} \\=&\Bigg[\frac{\omega^2_{p}(r_{p})}{\omega^2_0}+\frac{r\omega'_{p}(r_{p}) \omega_{p}(r_{p})}{\omega^2_0}\Bigg], \end{aligned} $

(14) where prime denotes the derivative with respect to radial coordinate r. Evidently, the roots of Eq. (14) cannot be obtained analytically for most choices of
$\omega_{p}(r)$ ; however, we will consider a few simplified cases below. -
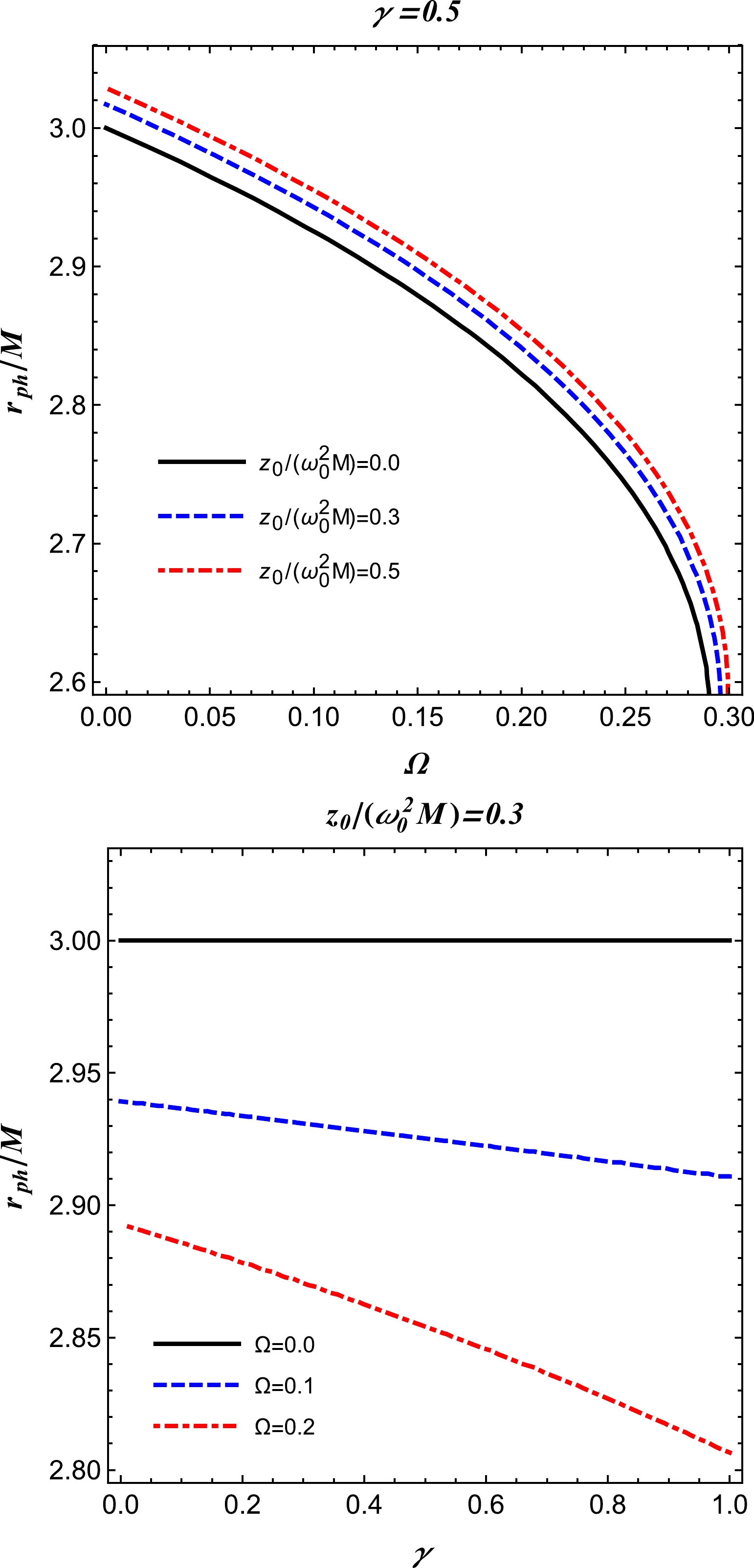
For the special case of a homogeneous plasma medium with a constant plasma frequency throughout the medium, i.e.
$ \omega _p^2= \text{const.} $ , Eq. (14) can be solved numerically and is depicted in Fig. 1. The displayed figures indicate that the photon radius decreases with increasing parameters γ and Ω. -
Further, we explore photon spheres in the presence of an inhomogeneous plasma medium, where the plasma frequency must satisfy a simple power-law of the form [59, 60]
$ \omega^2_{p}(r)=\frac{z_0}{r^q}, $

(15) where
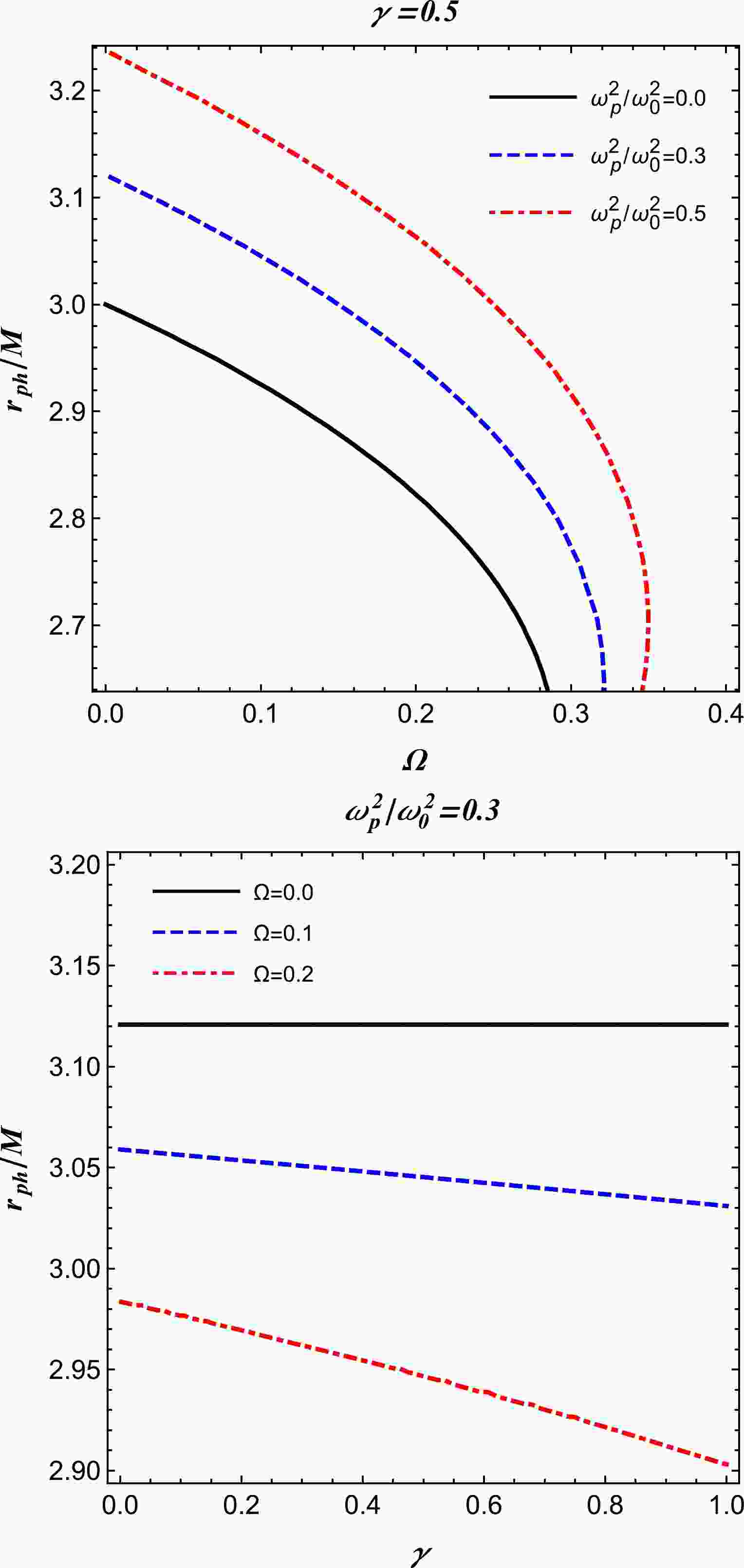
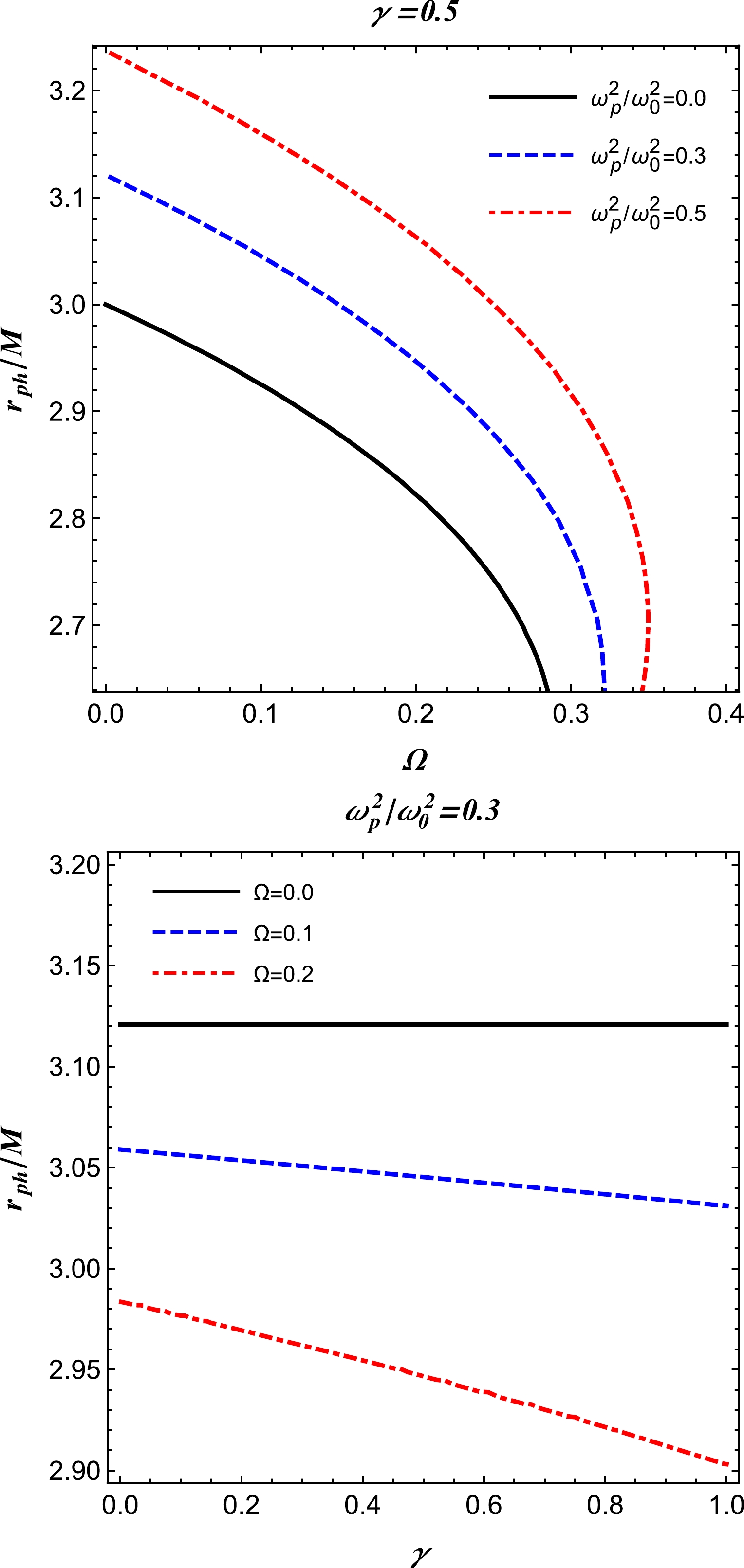
$ z_0 $ and q are free parameters. To analyze the primary features of the power-law model, we restrict ourselves to the following case:$ q=1 $ and$ z_0 $ as a constant [59]. Using Eqs. (14) and (15), we obtain the radius of the photon sphere based on a numerical scheme for the inhomogeneous plasma medium, as illustrated in Fig. 2. One can observe that this profile of the photon radius is approximately similar to that displayed in Fig. 1. This suggests that testing and distinguishing the homogeneous plasma from inhomogeneous plasma around BHs based on their shadows may be quite challenging. -
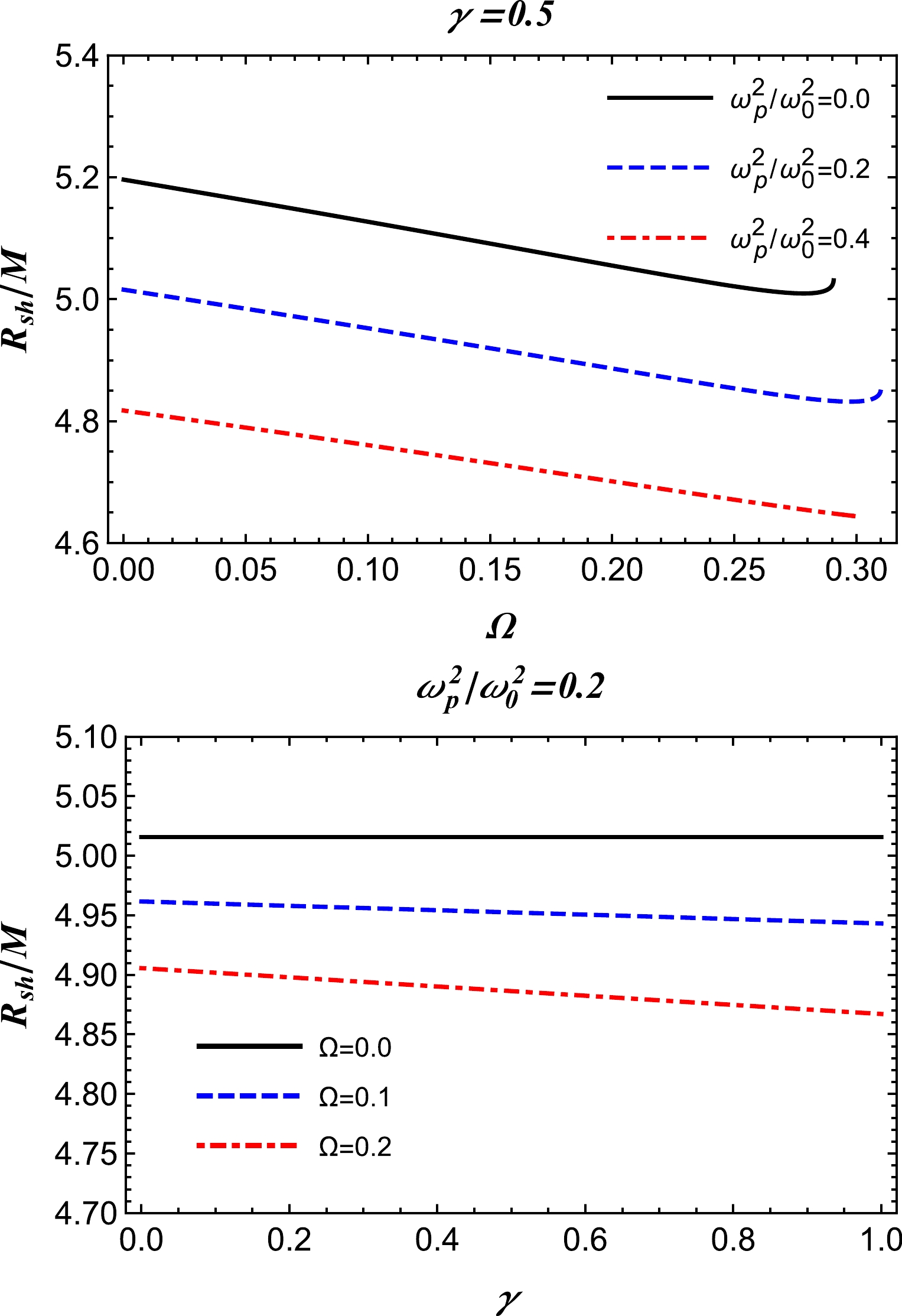
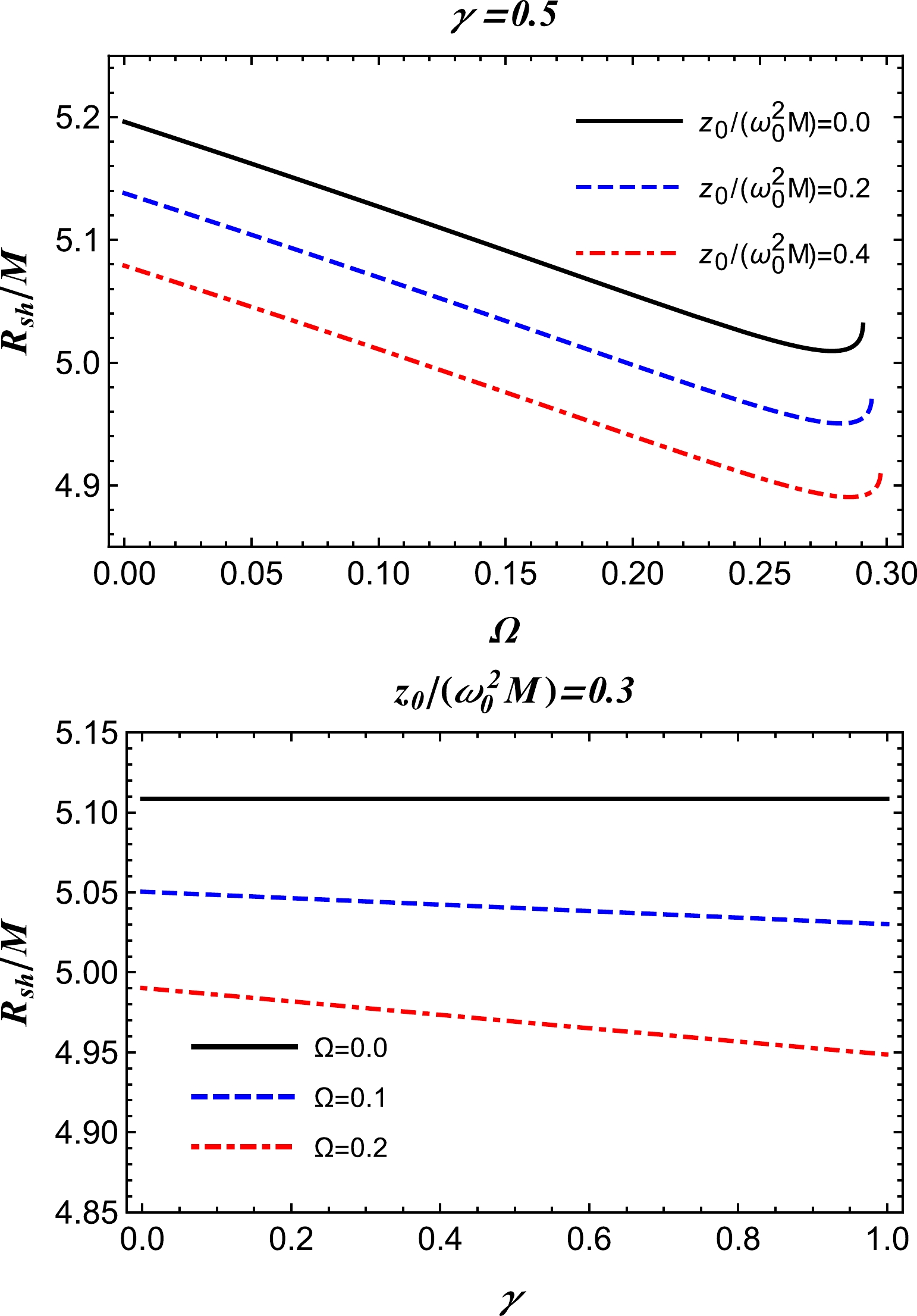
In this section, we investigate the radius of the shadow of an RGI Schwarzschild spacetime metric in a plasma medium. The angular radius,
$ \alpha_{\text{sh}} $ , of the BH shadow is defined by a geometric approach, which results in the following [13, 61]:$ \sin^2 \alpha_{\text{sh}}=\frac{h^2(r_{p})}{h^2(r_{o})}=\frac{r_{p}^2\left[\dfrac{1}{f(r_{p})}-\dfrac{\omega^2_p(r_{p})}{\omega^2_0}\right]}{r_{o}^2\left[\dfrac{1}{f(r_{o)}}-\dfrac{\omega^2_p(r_{o})}{\omega^2_0}\right]}, $

(16) where
$r_{o}$ and$r_{p}$ represent the locations of the observer and the photon sphere, respectively. Notably, if the observer is located at a sufficiently large distance from the BH, one can approximate the radius of the BH shadow using Eq. (16), as follows [13]:$ R_{\text{sh}}\simeq r_{o} \sin \alpha_{\text{sh}}=\sqrt{r_{p}^2\bigg[\frac{1}{f(r_{p})}-\frac{\omega^2_p(r_{p})}{\omega^2_0}\bigg]};$

this is based on the fact that
$ h(r)\to r $ , which follows from Eq. (12), at spatial infinity for both the models of plasma. For vacuum$\omega_{p}(r)\equiv0$ , we recover the radius of the Schwarzschild BH shadow,$ R_{\text{sh}}=3\sqrt{3} M $ , when$r_{p}=3M$ . The radius of the BH shadow is depicted for different parameters in Fig. 3 for a homogeneous plasma medium with a fixed plasma frequency, and Fig. 4 presents the case for a power-law model with a plasma frequency of$ \omega^2_{p}(r)=z_0/r $ . Both sets of figures illustrate that the shadow radius decreases much more steeply with Ω but remains almost constant with the variation in γ. -
For simplicty, to perform weak lensing, we focus on a weak-field approximation given by
$ \begin{array}{*{20}{l}} g_{\alpha\beta} = \eta_{\alpha\beta} + h_{\alpha\beta}\ , \end{array} $

(17) where
$ \eta_{\alpha\beta} $ and$ h_{\alpha\beta} $ represent a Minkowski spacetime geometry and a minute perturbation in the background of the Minkowski spacetime, respectively. For the foregoing, the general properties are given as follows [62]:$ \begin{aligned}[b] &\eta_{\alpha\beta} = {\rm diag} (-1, 1, 1, 1),\\ & h_{\alpha\beta} \ll 1, \quad h_{\alpha\beta} \rightarrow 0 \quad {\rm under } \quad x^i\rightarrow \infty\ , \\ & g^{\alpha\beta}=\eta^{\alpha\beta}-h^{\alpha\beta},\ \ \ h^{\alpha\beta}=h_{\alpha\beta}\, . \end{aligned} $

(18) We now explore the effect of the plasma in the environment surrounding the BH on the gravitational deflection angle. For the plasma medium, the basic equation for the deflection angle is written as [24, 62]
$ \hat{\alpha}_k= \frac{1}{2} \int_{-\infty}^\infty \left(h_{33} +\frac{h_{00} \omega^2-K_e N(x^i)}{\omega^2-\omega_e^2}\right)_{,k} {\rm d}z \ , $

(19) with
$ N(x^i) $ representing the concentration of charged particles in the plasma medium and ω and$ \omega_e $ respectively referring to the photon and plasma frequencies. Note that$ K_{e}=4\pi e^2/m_{e} $ defines the constant value of a plasma particle. The above equation [62] can be rewritten as follows:$ \begin{aligned}[b] \hat{\alpha}_b= \frac{1}{2} \int_{-\infty}^\infty \frac{b}{r}\Bigg(\frac{{\rm d}h_{33}}{{\rm d}r}+\frac{1}{1-\omega_e^2/\omega^2}\frac{{\rm d}h_{00}}{{\rm d}r} -\frac{K_{e}}{\omega^2-\omega_e^2}\ \frac{{\rm d}N}{{\rm d}r}\Bigg) {\rm d}z\, . \end{aligned} $

(20) Note that in further calculations,
$ \hat{a}_b $ can assume both negative and positive values, depending on the light position and on its motion toward the compact object or away from the compact object.On expanding, for greater r, the BH metric can be expressed as
$ \begin{aligned}[b] {\rm d}s^2 =& {\rm d}s^2_{0} + \left(\frac{2M}{r}-\frac{2M^4\gamma\Omega}{r^4}-\frac{2M^3\Omega}{r^3} \right){\rm d}t^2 \\&+\left(\frac{2M}{r}-\frac{2M^4\gamma\Omega}{r^4}-\frac{2M^3\Omega}{r^3} \right){\rm d}r^2\, , \end{aligned} $

(21) where
${\rm d}s^2_{0}$ describes the line element for the Minkowski spacetime, which is defined by$ \begin{array}{*{20}{l}} {\rm d}s^2_{0}=-{\rm d}t^2+{\rm d}r^2+r^2({\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2)\, . \end{array} $

(22) For further calculations associated with Eq. (20), we rewrite the
$ h_{a\beta} $ components in Cartesian coordinates for simplicity:$ \begin{aligned}[b] h_{00}=&\left(\frac{2M}{r}-\frac{2M^4\gamma\Omega}{r^4}-\frac{2M^3\Omega}{r^3} \right), \\ h_{ik}=&\left(\frac{2M}{r}-\frac{2M^4\gamma\Omega}{r^4}-\frac{2M^3\Omega}{r^3} \right)n_{i}n_{k}, \\ h_{33}=&\left(\frac{2M}{r}-\frac{2M^4\gamma\Omega}{r^4}-\frac{2M^3\Omega}{r^3} \right)\cos^2\chi \, . \end{aligned} $

(23) Here,
$ \cos^2\chi=z^2/(b^2+z^2) $ and$ r^2=b^2+z^2 $ are new notations. In creating these notations, we write the first derivatives of$ h_{00} $ and$ h_{33} $ as follows:$ \begin{aligned}[b] \frac{{\rm d}h_{33}}{{\rm d}r}=& \frac{2z^2(6\gamma M^4 \Omega+5M^5 r \Omega-3M r^3)}{r^7}, \\ \frac{{\rm d}h_{00}}{{\rm d}r}=& \frac{8\gamma M^4 \Omega}{r^5}+\frac{6M^3 \Omega}{r^4}-\frac{2M}{r^2}. \end{aligned} $

(24) Further, the deflection angle considered can be obtained based on the following parts [34]:
$ \begin{array}{*{20}{l}} &&\hat{\alpha}_b=\hat{\alpha}_1+\hat{\alpha}_2+\hat{\alpha}_3, \end{array} $

(25) with
$ \begin{aligned}[b] \hat{\alpha}_1=&\frac{1}{2} \int_{-\infty}^\infty \frac{b}{r}\frac{{\rm d}h_{33}}{{\rm d}r} {\rm d}z\, , \\ \hat{\alpha}_2=&\frac{1}{2} \int_{-\infty}^\infty \frac{b}{r}\Big(\frac{1}{1-\omega_e^2/\omega^2}\frac{{\rm d}h_{00}}{{\rm d}r}\Big) {\rm d}z\, , \\ \hat{\alpha}_3=&\frac{1}{2} \int_{-\infty}^\infty \frac{b}{r}\Big(-\frac{K_{e}}{\omega^2-\omega_e^2}\ \frac{{\rm d}N}{{\rm d}r}\Big) {\rm d}z\ . \\ \end{aligned} $

(26) From the above equations,
$ \hat{\alpha}_1 $ ,$ \hat{\alpha}_2 $ , and$ \hat{\alpha}_3 $ respectively refer to the contributions of gravity and the homogeneous and inhomogeneous plasma medium to the deflection angle. To consider the impact of the plasma medium on the deflection angle, we exploit Eq. (25). -
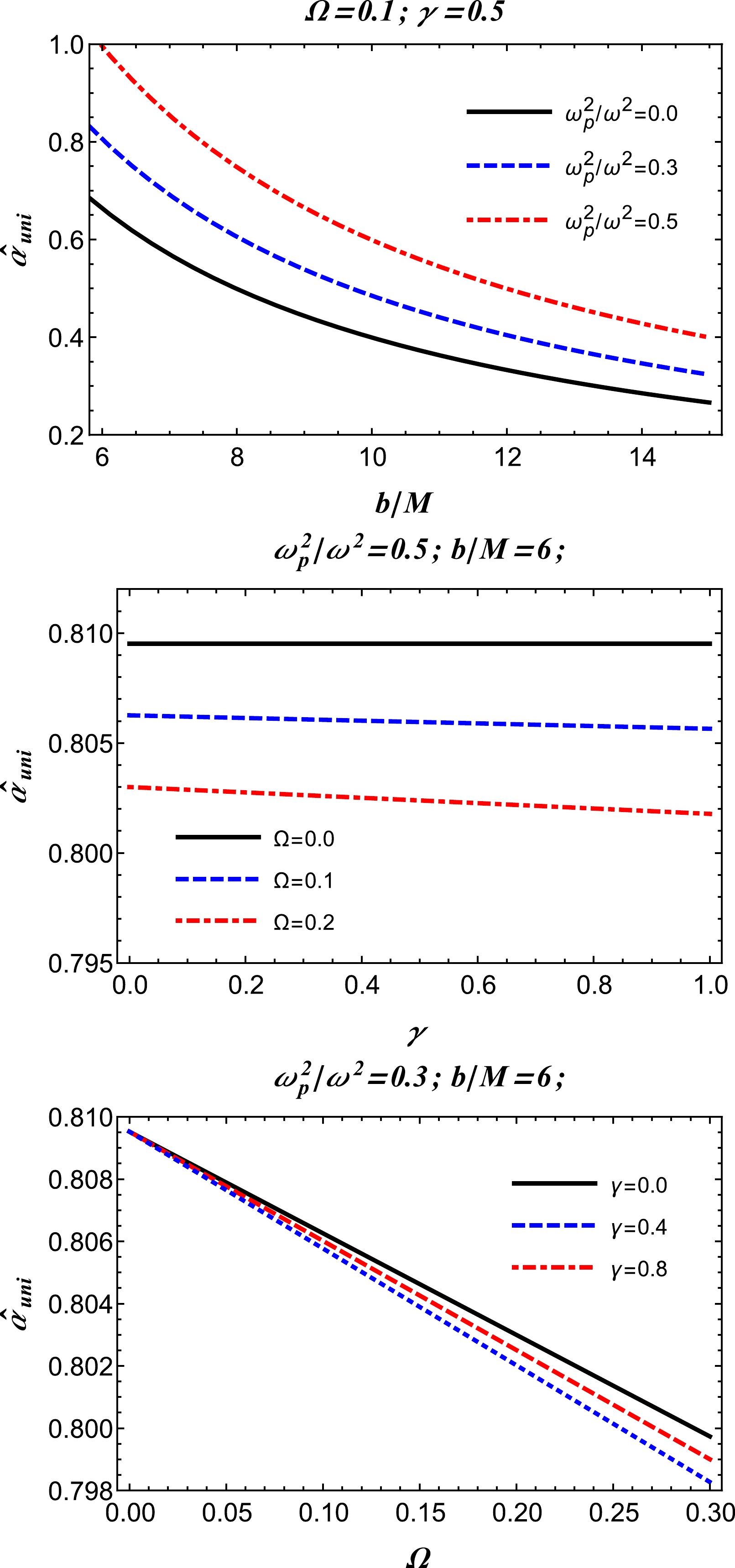
Let us consider the impact of a uniform plasma medium on the deflection angle given by Eq. (25) [26]:
$ \begin{array}{*{20}{l}} &&\hat{\alpha}_{\rm uni}=\hat{\alpha}_{\rm uni1}+\hat{\alpha}_{\rm uni2}+\hat{\alpha}_{\rm uni3}\, , \end{array} $

(27) where
$\hat{a}_{\rm uni1}$ and$\hat{a}_{\rm uni2}$ respectively refer to the contributions of uniform plasma, and$\hat{a}_{\rm uni3}=0$ represents the contribution of the uniform plasma distribution. Following Eqs. (24), (25), and (27), the deflection angles of photons around static BHs with spherical symmetry in the presence of RGI gravity and uniform plasma can be defined by$ \begin{aligned}[b] \hat \alpha_{\rm uni}=&\frac{2 M}{b}-\frac{3 \pi \gamma M^4 \Omega }{8 b^4}-\frac{4 M^3 \Omega }{3 b^3} \\&+\Big(\frac{2 M}{b}-\frac{3 \pi \gamma M^4 \Omega }{2 b^4}-\frac{4 M^3 \Omega }{b^3}\Big)\frac{1}{1-(w_p^2/w^2)}. \end{aligned} $

(28) In Fig 5, the deflection angle of light travelling in a uniform density plasma medium about an RGI BH is plotted against the impact parameter and RGI theory parameters. The figures demonstrate that to achieve a large deflection angle of light in the presence of strong gravity, the RGI parameters must be extremely small.
-
Further, we investigate the impact of non-uniform plasma on the deflection angle of photons around a BH in RGI gravity. Note that in a previous study, a Singular Isothermal Sphere (SIS) has been proposed to describe the non-uniform plasma medium distribution (see for example [62]). Thus, the plasma concentration in the SIS medium is defined by [24, 62]
$ N(r)=\frac{\rho(r)}{k m_p}\, , $

(29) with the following plasma density
$ \rho(r)=\dfrac{\sigma^2_{\nu}}{2 \pi r^2} $ , where$ \sigma_\nu $ refers to the dispersion velocity. Thus, Eq. (25) can be written as$ \begin{array}{*{20}{l}} &&\hat{\alpha}_{\rm SIS}=\hat{\alpha}^1_{\rm SIS}+\hat{\alpha}^2_{\rm SIS}+\hat{\alpha}^3_{\rm SIS}\, , \end{array} $

(30) where the first two terms
$\hat{a}^1_{\rm SIS}$ and$\hat{a}^2_{\rm SIS}$ reflect the contributions of the gravity and plasma effects to the deflection angle, respectively, whereas the last term$\hat{a}^3_{\rm SIS}$ reflects the contribution of the density gradient of the plasma medium. Relying on Eqs. (24), (25), and (30), the deflection angles of the photons in non-uniform plasma assume the following form:$ \begin{aligned}[b] \hat \alpha_{\rm SIS}=&\frac{4 M}{b}-\frac{5 \gamma M^6 \Omega w_c^2}{b^6 w^2}-\frac{64 M^5 \Omega w_c^2}{5 \pi b^5 w^2}-\frac{15 \pi \gamma M^4 \Omega }{8 b^4} \\ &+\frac{16 M^3 w_c^2}{3 \pi b^3 w^2}-\frac{16 M^3 \Omega }{3 b^3}+\frac{2 M^2 w_c^2}{b^2 w^2}, \end{aligned} $

(31) where we define
$ w_c^2= \frac{\sigma^2_{\nu} K_e}{2 k m_p R^2_{s}}\ . $

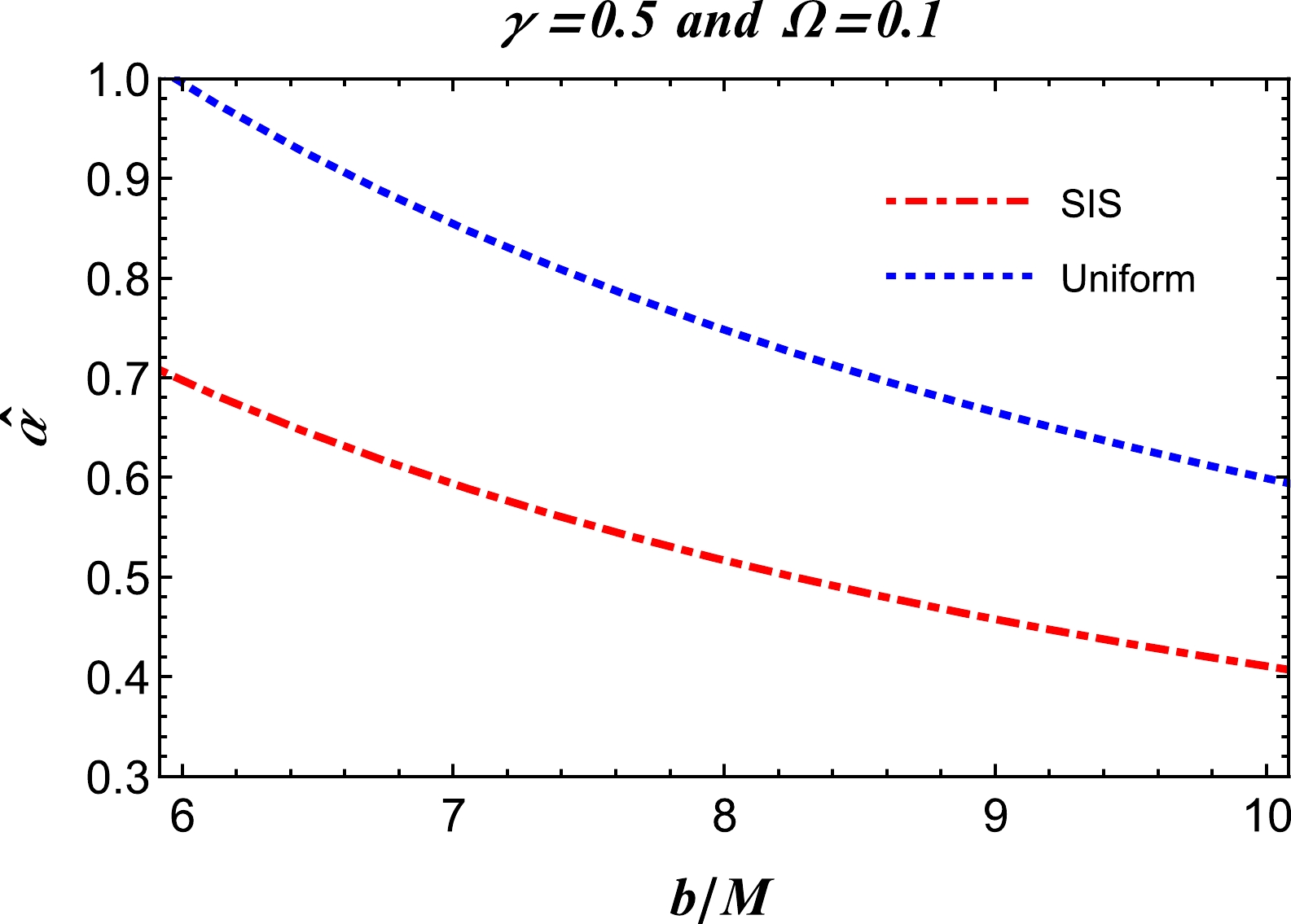
(32) In Fig. 6, the deflection angle of light in an SIS with inhomogeneous density plasma about an RGI BH is plotted against the impact parameter and RGI theory parameters. The figures demonstrate that to achieve a large deflection angle of light in the presence of strong gravity, the RGI parameters must be extremely small.
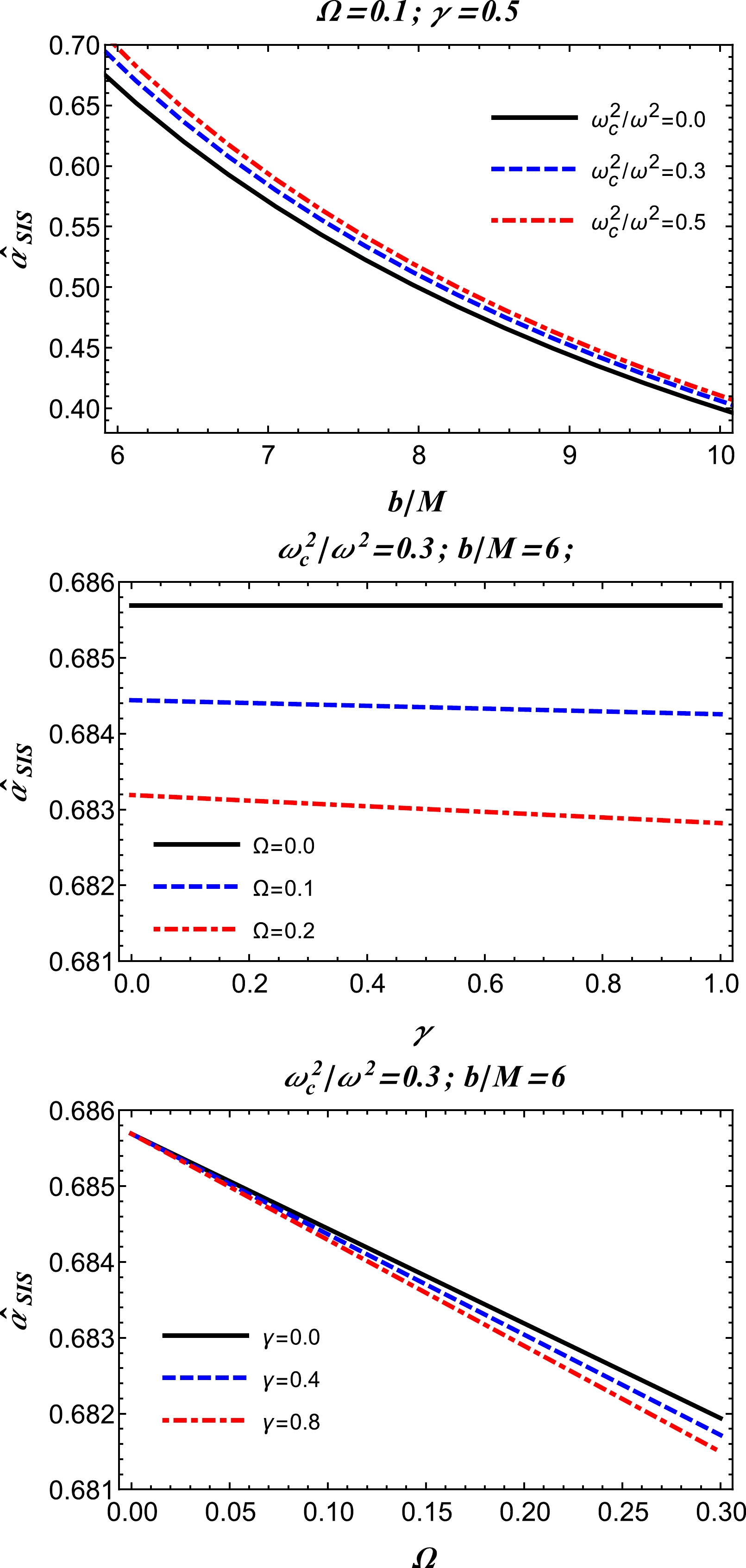
Figure 6. (color online) SIS: dependence of the deflection angle on the impact parameter b and RGI theory parameters
$ \{\gamma,\Omega\} $ .We now consider a comparison of the deflection angles between uniform and non-uniform plasma media. The behavior of the deflection angle for both the uniform and non-uniform plasma medium cases is depicted in Fig. 7. As can be observed from Fig. 7, the behavior evidently indicates that the deflection angle of the photon beam around the BH has larger values compared to that in the non-uniform case. This is because the photon beam is scattered under the influence of the non-uniform plasma. Thus, the deflection angle in the uniform plasma medium is greater than that in the non-uniform plasma medium.
-
Further, we aim to evalute the effect of the plasma medium on the optical images of the RGI BH. To achieve this goal, we use the backward raytracing technique [50, 63–68]. In this technique, for the given image, one has to compute the specific intensity,
$ I_{\nu 0} $ , observed at some distance from the BH [64]$ I_{\rm obs}(\nu_{\rm obs},X,Y) = \int_{\gamma}\mathrm{g}^3 j(\nu_{e}) {\rm d} l_{\text{prop}},\, $

(33) where
$g=\nu_{\rm obs}/\nu_e$ is the redshift factor, and$ \nu_e $ denotes the photon frequency measured in the rest-frame of the emitter. For the total flux, we have [64, 69]$ F_{\rm obs}(X,Y) =\int_{\gamma} I_{\rm obs}(\nu_{\rm obs},X,Y) {\rm d} \nu_{\rm obs}. $

(34) Notably, for radiating gas (in free fall), one has to use the four-velocity components [64]
$ u^t_{e} = \frac{1}{f(r)},\, u^r_{e} = -\sqrt{1-f(r)},\, u^{\theta}_{e} =u^{\phi}_{e}= 0. $

(35) In addition, we must consider the relation between the radial and time components of the photon four-velocity vector, given by
$ k_r= \pm k_t \sqrt{\frac{1}{f(r)}\bigg(\frac{1}{f(r)}-\frac{b^2}{r^2}-\frac{\omega_p^2}{\omega_0^2}\bigg)}, $

(36) which is derived from
$ \mathcal{H}=0 $ . Thus, we determine the presence of an extra term owing to the plasma medium compared to the corresponding form in [64]. The signs$ +(-) $ indicate cases when the photon approaches or recedes from the BH. Furthermore, the impact parameter b is also modified in the plasma medium:$ b = r\sqrt{ \frac{1}{f(r)} - \frac{\omega_{\text{p}}^2(r)}{\omega_0^2}} \,. $

(37) For the redshift function
${ g}$ , we use [64]$ {g} = \frac{k_{\alpha}u^{\alpha}_o}{k_{\beta}u^{\beta}_e}. $

(38) A radial profile is assumed with the
$ 1/r^2 $ law and the specific emissivity$ j(\nu_{e}) \propto \frac{\delta(\nu_{e}-\nu_{\star})}{r^2}, $

(39) where δ is the Dirac delta function. For the proper length, we have
$ {\rm d} l_{\text{prop}} = k_{\alpha}u^{\alpha}_{e}{\rm d}\lambda = -\frac{k_t}{\mathrm{g}|k^r|}{\rm d} r. $

(40) For the total flux, we can therefore write [64]
$ F_{\rm obs}(X,Y) \propto -\int_{\gamma} \frac{\mathrm{g}^3 k_t}{r^2k^r}{\rm d}r. $

(41) Let us finally consider one additional model consisting of radiating gas at rest (static gas model). In this case, for the redshift factor, we have
${g}=f(r)^{1/2}$ . Assuming a radial profile with$ 1/r^2 $ , the proper length can be written as follows:$ \begin{array}{*{20}{l}} {\rm d} l_{\text{prop}} =\sqrt{f(r)^{-1}{\rm d}r^2+r^2{\rm d} \phi^2}. \end{array} $

(42) For the specific intensity observed, we have
$ I_{\rm obs}(\nu_{\rm obs}) = \int_{\gamma} \frac{f(r)^{3/2}}{r^2} \sqrt{f(r)^{-1}+r^2 \left(\frac{{\rm d}\phi}{{\rm d}r}\right)^2} {\rm d} r,$

(43) where
$ \frac{{\rm d}r}{{\rm d}\phi}=\pm r \sqrt{f(r)\left(\frac{h(r)^2}{b^2}-1\right)}$

(44) is determined based on the equation of motion obtained for the light ray moving along the equatorial plane. As the function
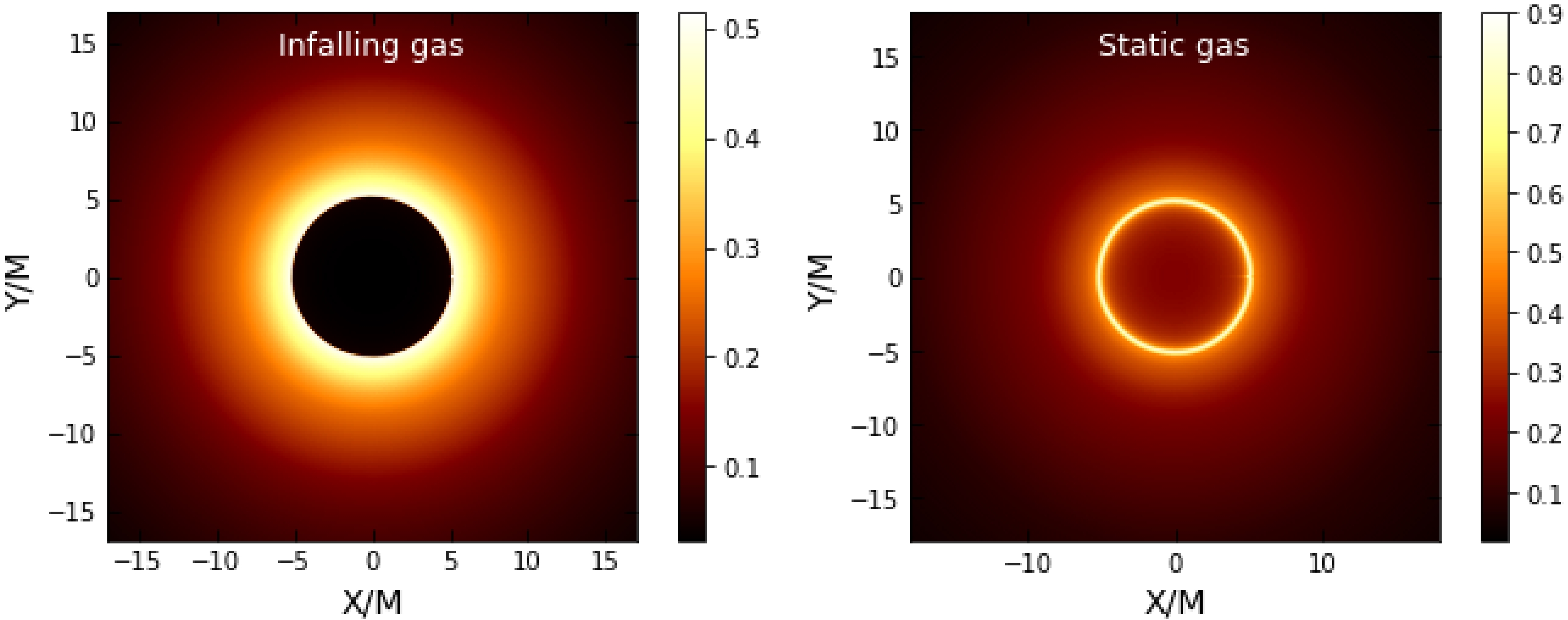
$ h(r) $ and the impact parameter encode the plasma effect, the intensity should change. In addition to this, the RGI parameters γ and Ω also exert some effects. In Figs. 8, 9, and 10, we illustrate the shadow images of the BH with/without a plasma medium.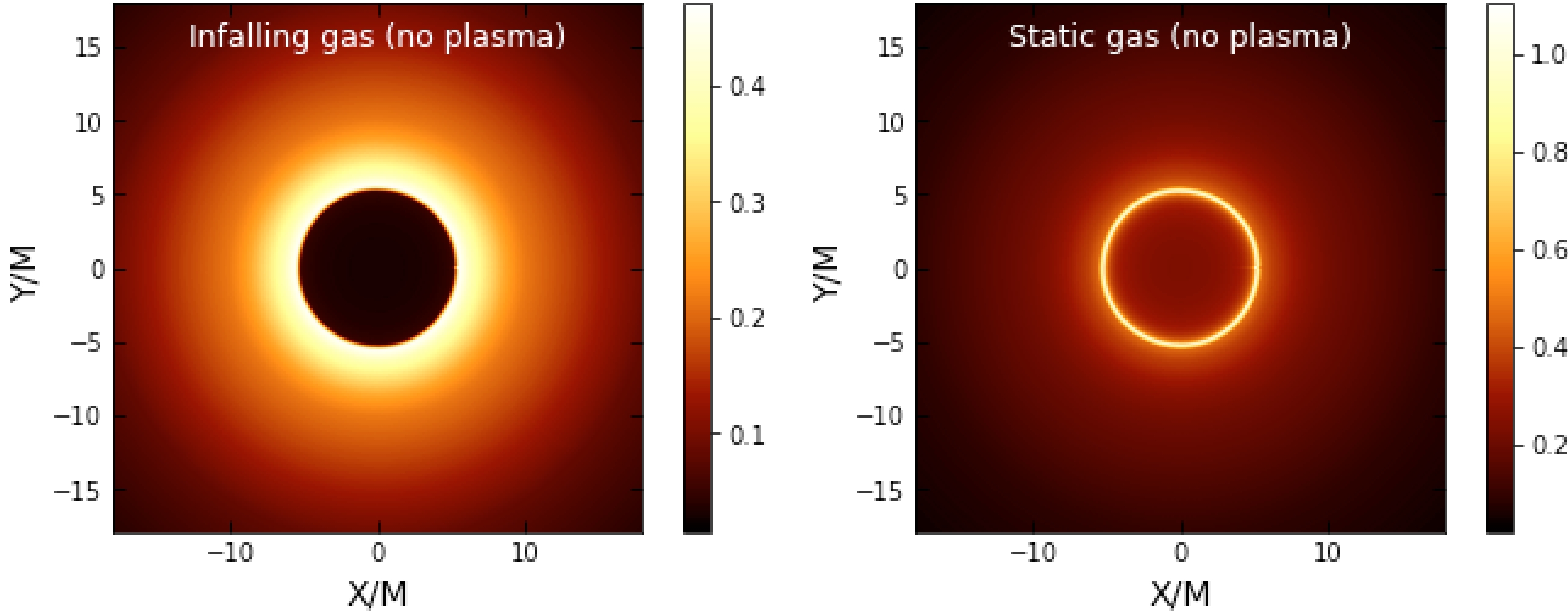
Figure 8. (color online) Shadow images with an infalling and static gas model in the RGI BH without a plasma medium with
$ \Omega=0.1 $ and$ \gamma=0.5 $ . -
In this study, we investigate the effect of plasma on the optical properties of an RGI Schwarzschild BH and discover the presence of relevant significant effects on the photon sphere radius of the BH shadow and gravitational weak lensing. Here, the orbits of photons are obtained using the general method and are presented in Figs. 1 and 2. The plots indicate that the photon orbits come closer to the central object with an increase in γ or Ω. We also discuss the shadow cast by the BH in the presence of RGI gravity and notice the effects of the model parameters γ and Ω on the BH shadow. The results reveal that with increasing values of the parameters γ and Ω, the radius of the shadow of the BH decreases, and this can be visually confirmed from Figs. 3 and 4. Additionally, we consider the deflection angle of light rays around a BH in RGI gravity in the presence of plasma (different distributions: uniform and non-uniform cases) and analytically obtain an equation for the deflection angle in the weak-field regime. In this part of our results, we discuss and analyze the effect of the uniform and non-uniform plasma on the deflection angle for different values of the parameters γ and Ω.
We also demonstrate the effect mechanism of the plasma medium on the motion of light owing to infalling gas or gas at rest and obtain corresponding optical images. Although the final image is found to depend on the specific model, the photon ring is a universal characteristic and therefore interesting from an observational point of view. From Figs. 8–10,it can be observed that the intensity of the photon ring predicted by these models is significantly higher for the static gas model compared to the infalling model. As another observation, one can infer that in the plasma medium, the intensity is lower compared to that in the absence of plasma.
-
F.A. acknowledges support from the Inha University, Tashkent.
Quantum effects on the black hole shadow and deflection angle in the presence of plasma
- Received Date: 2022-11-26
- Available Online: 2023-03-15
Abstract: In this study, the optical properties of a renormalization group improved (RGI) Schwarzschild black hole (BH) are investigated in a plasma medium. Beginning with the equations of motion in a plasma medium, we aim to present the modifications in the shadow radius of the RGI BH. To this end, we compute the deflection angle of light in the weak gravity regime for uniform and non-uniform plasma media. Importantly, owing to the plasma media, we discover that the equations of motion for light obtained from the radiating and infalling/rest gas have to be modified. This, in turn, changes and modifies the expression for the intensity observed far away from the BH. Finally, we obtain the shadow images for the RGI BH for different plasma models. Although quantum effects change the background geometry, such effects are minimal, and practically detecting these effects using the current technology based on supermassive BH shadows is impossible. The parameter Ω encodes the quantum effects, and in principle, one expects such quantum effects to play significant roles only for very small BHs. However, the effects of plasma media can play an important role in the optical appearance of BHs, as they affect and modify the equations of motion.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: