-
The weakness of their interactions with matter renders neutrinos ideal messengers to their sources. They are mostly produced from the decay of secondary pions and kaons, which originate from hadronic interactions of cosmic-rays with surrounding matters in cosmic accelerators. The detection of high-energy astrophysical neutrinos therefore enables us to address the sources of high-energy cosmic-rays. The IceCube Neutrino Observatory is capable of detecting high-energy neutrinos with a unique instrumental volume of 1 km3 within the Antarctic ice sheet. Recently, blazars, as candidate sources of the high-energy neutrino flux, have been reported by the IceCube collaboration [1, 2], and other searches are in progress [3, 4]. In addition to the search for sources of high-energy cosmic-rays, optimization for neutrinos with energy in the TeV to PeV range allows IceCube to probe into fundamental physics beyond the current laboratory scale [5–9]. In the multi-TeV region, inelasticity distributions of neutrino charged-current (CC) scattering are measured using IceCube data of five years [10]. The energy-dependence of neutrino-nucleon cross sections above 10 TeV is also extracted from IceCube high energy cascade data [11, 12]. These measurements allow testing quantum chromodynamics (QCD) through neutrino interactions at a very high energy scale, which is associated with the future FASERν experiment [13]. Besides studies on QCD, new physics searches at high energy scales are performed. Potential decays of high-energy neutrinos from distant astrophysical sources can significantly alter the neutrino flavor composition, and this phenomenon can be constrained by measurements of neutrino fluxes [14]. These measurements also allow us to test CPT invariance at high-energy scales [15]. More phenomenological studies probing into new physics with neutrino telescopes can be found in [16–30].
Apart from the basic single-track topology, there is widespread interest in double-track events [31–47]. In most beyond standard models (BSMs), a
$ \mathbb{Z}_2 $ symmetry is assumed to ensure the stability of the lightest particle, which results in the pair production of new physics particles. This scenario has been investigated in supersymmetric models with breaking scale below 10$ ^{10} $ GeV [48]. Below that scale, the typical pair products are charged sleptons. Owing to their heavy masses, charged sleptons suffer much smaller energy losses in media. Meanwhile, their weak coupling to the lightest supersymmetric particle entails long lifetimes. These two reasons provide them a vast production volume, which compensates for their low production rate and results in double-track signals with hundreds of meters in lateral separation. Double-track signal with lateral distance of hundreds of meters is extremely rare in the standard model (SM). The main background comes from two neutrinos produced in the same air shower, which only contributes to approximately 0.07 events per year [49]. In the SM scenario, the more general source of double-track events generally arises from CC deep inelastic scattering (DIS) interactions of neutrinos with nucleons. The nucleons are broken apart and produce a charm quark, which later fragments into charmed hadrons. These hadrons then decay into the second muons$ \begin{array}{*{20}{l}} \nu_{\mu} N \rightarrow \mu^- c(D)X \rightarrow \mu^- \mu^+ \nu_{\mu} X. \end{array} $

(1) This so-called dimuon process is essential in the determination of strange-quark PDF [50, 51], and has been measured for decades in various DIS experiments [52–54]. On the contrary, no signals for such events have been observed in current neutrino telescopes mainly due to their small dimuon lateral distances. The lateral distance of this process is typically distributed much below 100 m.
In this study, a simulation framework down to detector-level is constructed to estimate the sensitivities for such dimuon events. To meet the experimental cut for lateral distance, only dimuon productions outside the detector volume are considered. The dominating background of dimuon events is the misconstruction of single muon to dimuon. Therefore, an analysis based on reconstruction algorithms is employed to obtain acceptance rates of dimuons as well as fake rates of single muons. The results indicate that, even though fake rates to misconstruction of percent level can be achieved, the large background from single muon events can substantially lower the experimental significance. However, this difficulty is surmountable for denser configurations, for instance, KM3NET/ORCA [55]. The recent work [56] studied a similar scenario without detector-level simulation. We thus compare the predictions on energy distributions of muons in both works. Furthermore, we discuss the distinctions arsing from different calculations of energy losses.
The rest of this paper is organized as follows. In Sec. II, we discuss the simulation framework. We elaborate on aspects of neutrino flux and provide descriptions of the detector model as well as the event generation method in use. Simulation results are presented at the end of this section. We then compare our results with those of a recent work[56] in Sec. III. Cuts and other conditions are set similar to those in that work. In Sec. IV, the detector simulation is fully described. Several detector-level settings are selected to estimate the significances of the dimuon signal over the single-muon background. Finally, we present the conclusions in Sec. V.
-
The generation of dimuon events involves the following steps. First, event rates are computed in the interaction volume. These rates are taken from the convolution of the neutrino flux with relevant cross-sections, multiplied by the exposure time and target number. Dimuon events are then generated according to differential distributions and normalized to these event rates. These dimuons are subsequently steered to the detector. If any one in the muon pair loses its whole energy before reaching the detector surface, this event is discarded. The final sample of dimuon events is the set of dimuons where both can reach the detector boundaries. More details are presented as follows.
-
The high-energy neutrino flux can be roughly divided into astrophysical and atmospheric components. The former has a harder spectrum than the latter and dominates at high-energy region. Below 100 TeV, however, the atmospheric flux is three to four orders larger than the astrophysical flux [57]. Given the approximate linear relation of neutrino-nucleon cross-section to neutrino energy in the range of tens of GeV to a few TeV, with spectral indices 3.7 and 2 for the atmospheric and astrophysical flux, respectively, the DIS event rate of atmospheric neutrinos in this energy range is three orders of magnitude larger than their astrophysical counterpart. This estimation matches the simulation of DIS muon events in Ref. [58]. Consequently, as a subset of DIS muon events, dimuon events from atmospheric sources are also expected to have higher order of magnitude.
For energy above 100 TeV, the astrophysical flux becomes dominant because of the softer decreasing behavior in event number of
$ E^{-1} $ compared with$ E^{-2.7} $ for the atmospheric flux. However, the absolute strength of the flux is negligible in this region, and the neutrino-nucleon cross-section practically drops from the linear increment [59–61]. The suppression becomes stronger when the neutrino absorption resulting from the propagation through Earth is taken into account. Such phenomenon becomes sizable for neutrinos with energies higher than several hundreds TeV [62].We therefore consider only the neutrino flux from the atmospheric component in this work. A posterior estimation shows that dimuon events are mainly induced by neutrinos with energies below 10 TeV, in which flux attenuation due to the Earth absorption can also be safely neglected. Further, neutrino oscillation leads to the disappearance of muon neutrinos. This effect, however, only impacts neutrinos with energies below 100 GeV [63], and the energy cut allows us to exclude this region from our analysis.
The atmospheric neutrino flux below 10 TeV is taken from HKKM15 [64], and is extrapolated up to 1 PeV by fitting a standard parameterization in Ref. [57]. To reduce atmospheric muon background, only up-going neutrinos (zenith angle larger than
$ 90^\circ $ ) are maintained. Specially, the detailed treatment of very high energy neutrino induced dimuon events would be more complicated. In such scenario, the contribution from astrophysical neutrinos, prompt atmospheric neutrinos, and flux attenuation due to absorption of the Earth play essential roles. For ultra-high energy, subtle treatments of calculation of cross-sections are also necessary [61]. -
The detector is modeled as a cylinder with height of 1 km and radius of 0.5 km. For the convenience of description, we set a cylindrical coordinate, displayed in Fig. 1, in which the origin is at the center of the top surface of the detector and the unit of length is given in kilometers. The detector volume then covers
$ \{r < 0.5, ~ 0 < h < 1\} $ and consists of ice. Because the interaction volume is outside the detector volume, it is either in region$ \{r < 5, ~ 1 < h < 2\} $ filled with rock, or$ \{0.5 < r < 5, ~ 0 < h < 1\} $ filled with ice. The densities of ice and rock are taken to be 0.92$ {\rm{g}}/{\rm{cm}}^3 $ and 2.70$ {\rm{g}}/{\rm{cm}}^3 $ , respectively. The chemical composition of ice is$ {\rm{H_2O}} $ , and rock is composed of the same elements as those in the Earth crust.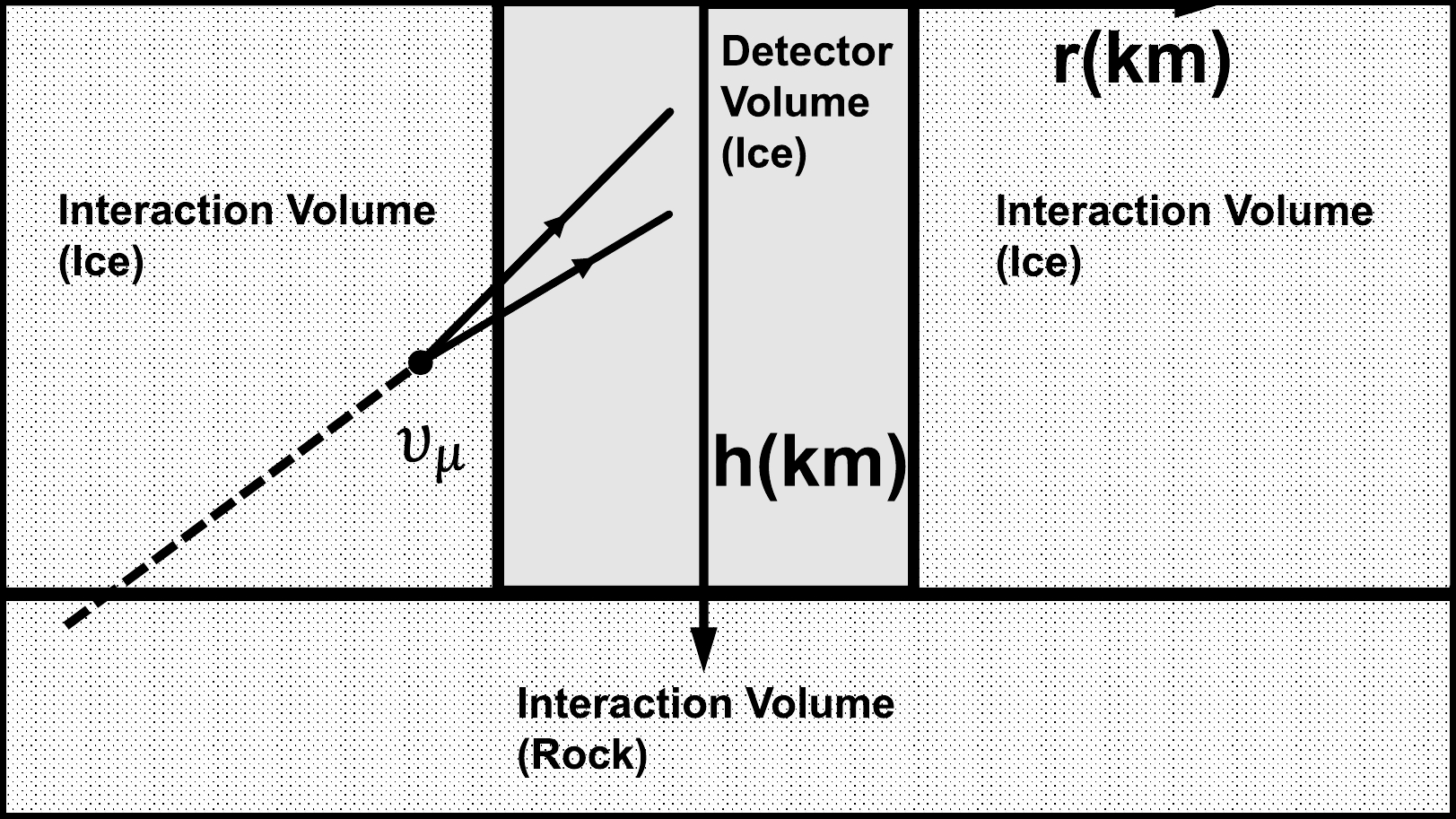
Figure 1. Schematic of the simulation framework. The primary muon neutrino interacts outside the detector and produces a pair of muons. The detector locates above rock media, padded with ice in the horizontal direction.
The first step is to calculate the total event rates from
$ \frac{{\rm d}^2N_{{\rm{tot}}}}{{\rm d}E_\nu {\rm d}\theta} = N T \times 2\pi \frac{{\rm d}^2F_\nu}{{\rm d} E_\nu {\rm d}\theta} \times \sigma_{{\rm{tot}}}(E_\nu), $

(2) where N is the number of nucleons in the interaction volume, T is the exposure time, and
${\rm d}^2F_\nu/{\rm d} E_\nu {\rm d}\theta$ is the differential neutrino flux over neutrino energy and zenith angle.$ \sigma_{{\rm{tot}}} $ is the total cross-section per nucleon for neutrino CC DIS taken from the integration of$ \begin{aligned}[b] \frac{{\rm d}^2 \sigma ^{\nu(\bar{\nu})} _{{\rm{cc}}}}{{\rm d} Q^2 {\rm d} W^2} =& \frac{G_F^2 m_W^4}{2 \pi} \frac{1}{(Q^2+W^2)(Q^2+m_W^2)^2} \\ & \times \bigg[(1-y)F_2(x,Q^2) + y^2 xF_1(x, Q^2) \\ & \pm y \left(1-\frac{y}{2}\right) xF_3(x, Q^2) \bigg], \end{aligned}$

(3) for either charm-quark production or inclusive production in hadronic final states, and the plus (minus) sign accounts for ν (
$ \bar{\nu} $ ). Q2 is the transferred momentum square and W is the invariant mass of the final hadronic system. x and y denote the Bjorken-x and inelasticity of the DIS process, respectively. In our calculation, the structure function$ F_i(x, Q^2) $ is adopted at next-to-leading order in QCD [51] to reduce the perturbative uncertainties. Additionally, distinctions between the ice and rock targets are taken into account and the CT14NNLO PDF set [65] is used. Neutrino scattering events are generated according to the aforementioned differential distribution. Their production positions are distributed uniformly because the mean free path of the neutrino is much larger than the length scale of the interaction volume, and the azimuthal angles of incident neutrinos are also distributed evenly by the definition of the flux model. These DIS events are then fed into${\tt Pythia v8}$ [66] for parton showering, hadronization, and hadron decays, from which dimuon events are generated and their energies along with separation angles are extracted. The primary muon comes from the DIS primary vertex and is, most of the time, more energetic, whereas the second muon is the decay product of charmed hadrons. The displacement between two production vertices is much smaller than the lateral distance of dimuons at the detector boundary and is, therefore, neglected. Hence, we take the starting position of dimuons as the neutrino interaction point. Another approximation is in the direction of two muons. Due to the large boost, dimuons follow the direction of primary neutrinos to a good approximation. Their separation angles$ \theta_{\nu\mu} $ obey the relation$ \tan\theta_{\nu\mu} \approx \langle P_\perp \rangle / E_\nu $ , where$ \langle P_\perp \rangle $ is the average transverse momentum of the primary muon [67]. For$ E_\nu = 1 \text{ TeV} $ , we have$ \langle P_\perp \rangle \sim 30 \text{ GeV} $ , and$ \theta_{\nu\mu} $ reaches a value$ 0.03 \ll 1 $ . This is also true for the separation angle$ \theta_{\mu\mu} $ of two muons. For$ E_\nu \gg \text{a few GeV} $ ,$ \theta_{\mu\mu} $ is of order$ p_{\rm CM}/p_{\rm LAB} \approx \sqrt{\text{GeV}/E_\nu} \ll 1 $ . The lateral distance of dimuons is then simplified as$ D_{\mu\mu} \approx \theta_{\mu\mu} l $ , where l is the distance traversed by the dimuon. Finally, the dimuon is steered to the boundary of the detector. The energy loss is simulated with${\tt MMC v1.6.0}$ [68]. The dimuon events where either of the two muons cannot reach the detector boundary are discarded. The dimuon lateral distance at the boundary, denoted as dimuon separation, along with further kinematic information of the two muons, is recorded.It is noted that there is not much ambiguity from the choice of interaction volume. In fact, the interaction volume should be taken large enough to encapsulate as many as possible detectable dimuon events. For an ideal and exact simulation, the interaction volume can be taken to cover the whole Earth. The distribution of production positions in this case is then impossibly uniform. However, this simulation would be very time-consuming and a very large part of the interaction volume would be useless because the events generated there cannot reach the detectable region. It is therefore useful to adopt the concept of flux attenuation for the events that clearly cannot reach the detector. In our consideration, the view of attenuation continues until the flux reaches the interaction volume, and the losses from this attenuation are small and ignored. Meanwhile, the interaction volume must not be taken so small as to lose potential dimuon events that can reach the detector. It can be observed from Fig. 2 and Fig. 3 that only a small portion of survived events are generated at the far-end of the interaction volume. This convinces us that our choice of the interaction volume is indeed sufficiently large to include most if not all detectable dimuon events.
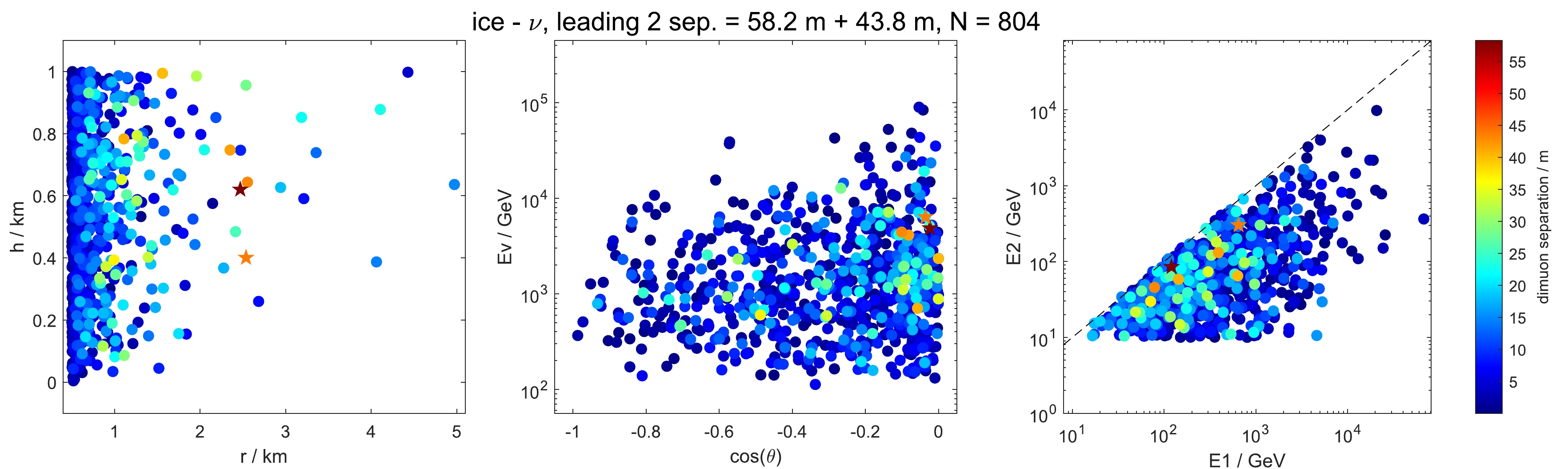
Figure 2. (color online) Statistics for dimuon events induced by atmospheric muon neutrino in ice. The exposure time is ten years. The energy cut for the primary neutrino is set at 100 GeV, and energy cut for muons at the detector boundary is set at 10 GeV. Every colored point represents one dimuon event, and the relevant color stands for the lateral distance of dimuons at the detector boundary. Two events with the first and second largest lateral distance are marked with stars. Left: h and r coordinates of starting positions of dimuon events. Middle: energy and zenith angle of the primary neutrino that induces the dimuon event. Right: energies of dimuons when entering the detector. E1 and E2 represent the energies of the leading and sub-leading muons, respectively.
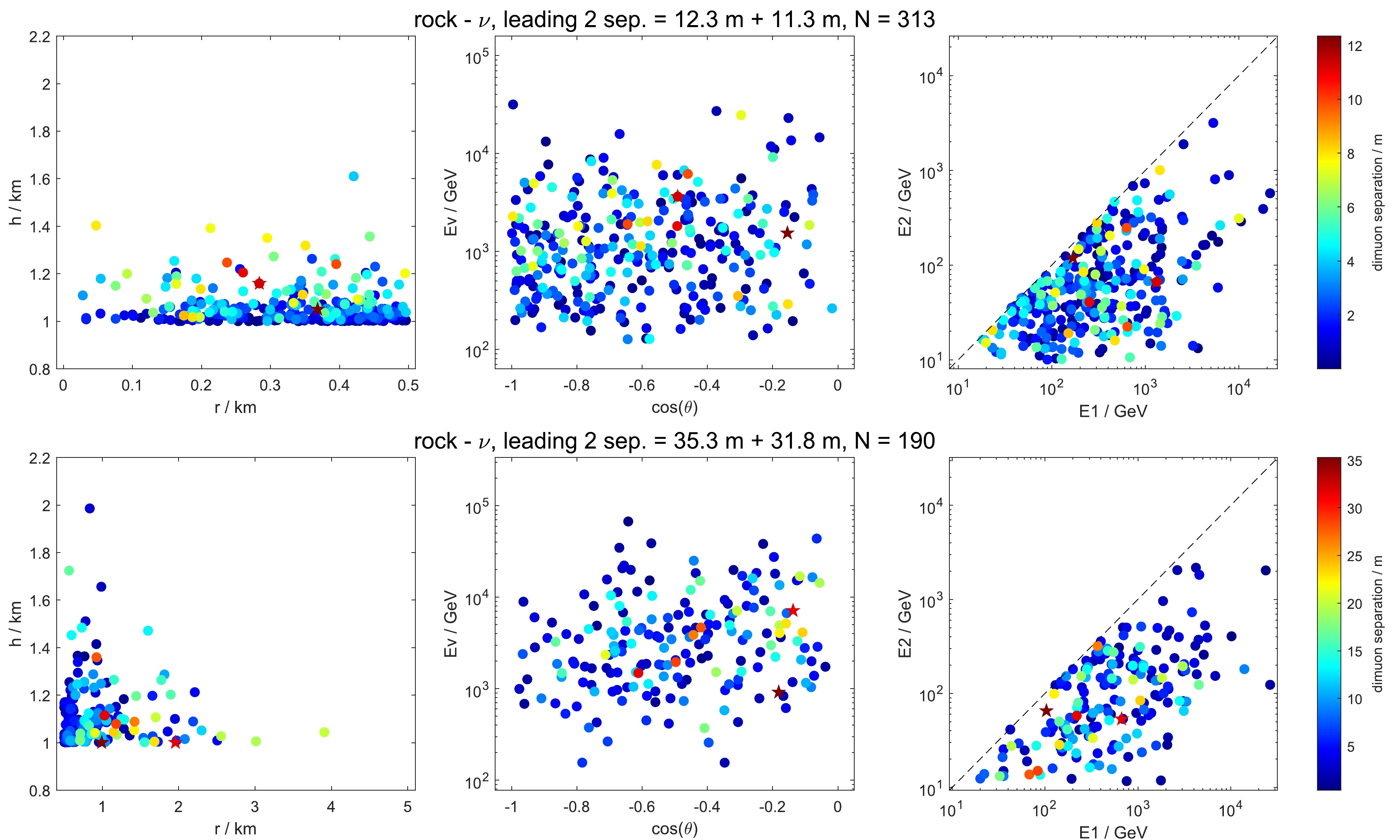
Figure 3. (color online) The same as Fig. 2, but for muon neutrino in rock. Due to the different behaviors of energy losses, this interaction volume is divided into two sub-regions with
${r} < 0.5\rm{\ km}$ (upper) and$ 0.5 {\rm\ km}< {r}<5 {\rm\ km} $ (lower). -
One sample in our simulation framework for the muon neutrino is demonstrated in Fig. 2 and Fig. 3. Results for the muon anti-neutrino are similar and not shown here. The exposure time is ten years. Cuts on primary neutrino energies and muon entering-detector energies are set to be 100 GeV and 10 GeV, respectively.
Statistics for dimuon events induced by muon neutrinos in the interaction volume filled with ice are shown in Fig. 2. Each colored dot represents one dimuon event, and the kinematic information is given by relevant coordinates. The dot color denotes the lateral distance at the time of dimuon entering the detector, or say, the dimuon separation. Most dimuon events have separations below 30 m, and the two largest separation are marked with stars. A total number of 804 events are collected, with the two largest dimuon separations being 58.4 m and 43.8 m. The left panel shows the starting positions of dimuon events. Almost all events occur near the detector and in the region
$ 0.5 < r < 2.5 $ . This is because the lower-energy muons at starting positions are mostly distributed below several hundred GeV and on average a 500 GeV muon exhausts its energy in ice when travelling approximately 2 km. The right panel of Fig. 2 shows the energy distributions of two muons when they enter the detector. E1 and E2 represent the energies of the leading and sub-leading muons, respectively. In spite of the energy losses before reaching the detector, a significant number of sub-leading muons have energy smaller than a few hundred GeV. In the middle panel, the energies and zenith angles of the primary neutrinos inducing the dimuon events are shown. The preference of$ \cos(\theta) = 0 $ is a reflection of the fact that the neutrino flux peaks at the horizon.The same information for interactions in rock is displayed in Fig. 3. Because muons can lose energies both in the ice and in the rock for
$ 0.5< r <5 $ , while they only lose energies in rock for$ r <0.5 $ , we divide the interaction volume of rock into two sub-regions, and the statistics are shown in the lower and the upper panels, respectively. For$ r <0.5 $ in the upper panel, the events have rather small separations and prefer directions close to up-warding. The contributions from this region are, then, negligibly small. For$ 0.5< r <5 $ in the lower panel, some events reach the detector with slightly larger dimuon separations. However, the total number of events turns out to be small. Thus, the interaction volume of rock only gives sub-leading contributions. -
Both the recent work [56] (labelled as ZB21) and this paper discuss a similar situation. It is therefore worth comparing results from both works. In this section, a comparison of dimuon events for 10-year exposure of IceCube is performed. We also discuss the difference between the two calculation methods of muon energy losses.
-
Except for the simulation framework, the differences in some setups between ZB21 and this study are listed as follows:
$ \bullet $ The zenith angle in ZB21 covers the whole sky, while only up-going neutrinos are considered in this study.$ \bullet $ In ZB21, a cross-sectional area of 1 km2 is used in the analytical calculation, which has no direct correspondence in our simulation framework. We estimate an effective area of 0.85 km2, which is calculated from the two-thirds power of our detector volume.$ \bullet $ The average energy loss formula is used in ZB21, but in this study, the muon energy loss is simulated with the Monte Carlo (MC) program${\tt MMC}$ .$ \bullet $ In ZB21, the atmospheric neutrino flux above 10 TeV and the astrophysical neutrino flux are both taken from IceCube's measurement. However, we only take into account the atmospheric part and use a standard parameterization to extrapolate it. The flux attenuation due to Earth absorption is treated in ZB21 but not in this work.The first distinction is eliminated by doubling the events in each bin because an approximate reflection symmetry exists. We do not rescale our binned events number by
$ 1/0.85 $ to eliminate the second one, but this can be done if only the total number of events matters. The influence on normalization from the last distinction is expected to be small since both works predict a small contribution from neutrino energy higher than 10 TeV. However, the differences in differential energy distribution at the high energy tail can be marked, especially that for the leading muon. We completely remove the third difference by using the average energy loss formula${\rm d}E/{\rm d}X=-\alpha - \beta E$ from the starting position of the dimuon in this comparison. The energies of the two muons at the detector boundary are then calculated based on that formula, as well as the distance the muon can traverse.The comparison is performed for 10-year exposure of IceCube. Our result is shown in Fig. 4, and the counterpart is the right panel of Fig. 5 in ZB21. The lateral distance cut is set to be the same as that of ZB21, i.e.,
$ R_{\mu2}\theta_{\mu\mu} > 34 \text{ m} $ . Here,$ \theta_{\mu\mu} $ is the separation angle of dimuons, and$ R_{\mu2} $ is the range of the sub-leading muon between the dimuon starting position and where it exits the detector or stops in it. The cut on muon energy when entering the detector is also set to be the same as that in ZB21, namely, 100 GeV. The total number of dimuon events passing the cut is 80. After rescaling by ratio of cross-sectional area$ 1/0.85 $ , we obtain a value of 94, which is approximately 110% of that in ZB21. However, such a rescaling is rather informative than exact owing to the ambiguity in definition of the effective area on the detector geometries. The energy distributions for leading and sub-leading muons follow similar patterns in both works, whereas differences can be observed for muon energy greater than approximately 1 TeV. Apart from the fluctuation of Monte Carlo computation, this difference may come from different treatments in the high energy flux. One noteworthy feature is that lateral distances of dimuons can be markedly amplified inside the detector, which manifests in the fact that$ R_{\mu2}\theta_{\mu\mu} $ is larger than the dimuon separation at the detector boundary by a factor of 2 to 5 or more. This implies that the approximation of the parallel dimuon is crude at the level of tens of meters, and it is therefore conservative to use the dimuon separation at the detector boundary as a criterion for experimental lateral distance cut in dimuon searches.
Figure 4. (color online) Predictions of energy distribution of two muons when entering the detector. Exposure time is ten years.
$ \mu1$ is defined to be the more energetic muon. The same cut as that in [56] Eq. (7) is set. After considering the difference between cross-sectional area, this figure can be directly compared with the right panel of Fig. 5 in [56].
Figure 5. (color online) Comparison of number of events passing cuts for two different approaches. The MMC simulation (the average energy loss formula using parameters in ZB21) is used to calculate the energy loss for the red (blue) curve. The curve using the average energy loss formula based on parameters by
${\tt MMC}$ stochastic fitting is also plot in magenta. The x axis represents the energy cut for the muon at the detector boundary, whereas the y axis indicates the number of events passing the cut as well as the lateral distance cut, which is set to 34 m. -
Besides the complete removal of the third difference by the employment of the average energy loss formula, we also count dimuon events passing the energy cut at the detector boundary with the
${\tt MMC}$ simulation. The lateral distance cut is still conducted in the same way as in ZB21. The results are illustrated in Fig. 5.In that figure, the x-axis indicates the muon energy cut at the entering-detector point, and the y-axis is the number of dimuon events passing both the energy and the lateral distance cuts. The blue curve (adapted ZB21) is for the method used in the previous subsection. We also consider whether the dimuon can pass the energy cut with the
${\tt MMC}$ simulation, which is shown in the red curve. Note that the${\tt MMC}$ simulation is only used for predicting whether the dimuon can pass the energy cut, whereas the final energy losses that decide the lateral distance are still consistently calculated with the average energy loss formula with the same parameters as those used in the previous subsection. From this comparison, it is observed that the adapted ZB21 leads to enhancement of dimuon events in comparison with the${\tt MMC}$ simulation. For low energy thresholds, the relative decrements are 10% at most, and the discrepancy in absolute number becomes smaller as the energy cut increases. One reason for this behavior is that the fitted parameters α and β in the${\tt MMC}$ are different from those taken in ZB21. In their work, α and β are taken to be 3.0$ \times $ 10$ ^{-3} $ GeV cm2/g and 3.0$ \times $ 10$ ^{-6} $ cm2/g, respectively①. Furthermore, the stochastic process makes muons travel shorter distances in general [67]. To explain this point more clearly, a similar curve based on α and β from the${\tt MMC}$ stochastic fitting is plot in magenta, in which α = 2.68$ \times $ 10$ ^{-3} $ GeV cm2/g and β = 4.70$ \times $ 10$ ^{-6} $ cm2/g. This curve is very close to that from the Monte Carlo simulations. The uncertainties from the modeling of processes such as pair production, photonuclear interactions, and bremsstrahlung in${\tt MMC}$ are small [67]. -
In this section, a phenomenological study on the experimental potential probing dimuon events is performed. A framework of simplified detector response modeling is constructed. Based on it, multiple simulation settings are applied to estimate dimuon acceptance efficiencies. Considering that a large fraction of the background comprises mis-reconstructed single-muon events, single-muon fake rates are also calculated in the corresponding situation. Multiplied by the detector-level evaluation, the significances are estimated for several theoretical benchmarks. We simply assume that the detector-level settings and theoretical benchmarks can be factorized in the calculation of significance. In addition to an IceCube-like detector configuration, an ORCA-like configuration [55], as the prototype of a denser but smaller detector, is modeled as well. The estimated results imply that ORCA shows a larger potential to observe dimuon signals with lower energies and shorter lateral distances than IceCube.
-
To investigate the effect of detector response on the dimuon identification, detector simulation and reconstruction of dimuon events are performed. The simulation set up used in this section is modified based on the development in Ref. [69]. The benchmark detector configuration is composed of 5000 DOMs arranged on 100 strings with 100 m horizontal and 20 m vertical spacings, respectively. Each DOM is a 17-inch glass sphere housing 31 3-inch PMTs. Note that, such mDOM design differs from the one in IceCube. However, to perform a fast detector response modeling, this distinction is inevitable. In this simulation, parallel muons are injected horizontally to the detector with fixed separation (30
$ \,\text{m} $ ) but different energies and propagated in sea water instead of ice as for IceCube. The simulation settings of two sets are described below:$ \bullet $ Set 1. The two muons in the dimuon event have identical energies of 200 GeV with fixed separation$d=30$ m, while the single muon background is 400 GeV.$ \bullet $ Set 2. The two muons in the dimuon event have identical energy of 400 GeV with fixed separation$d=30$ m, while the single muon background is 800 GeV.The single-muon event reconstruction chain starts with a simple line-fit and m-estimator to obtain a better seed for further reconstruction and selection. The m-estimator result is then applied in the first single-photon-electron (SPE) maximum-likelihood reconstruction that only uses the first photon hit on each DOM. The first photon SPE fit is then followed by a more comprehensive multiple-photon-electron (MPE) maximum-likelihood reconstruction.
The dimuon reconstruction algorithm is essentially the same as the single-muon reconstruction, but has two additional parameters. The single-muon reconstruction is based on five parameters. Three of them represent the track starting position
$ (x, y, z) $ , and the other two represent the track direction$ (\theta, \phi) $ . In addition to the aforementioned five parameters, dimuon events have two extra parameters, the track separation d and the displacement angle γ of the second track. To construct the dimuon reconstruction algorithm, hit splitting into two groups is necessary. A schematic is displayed in Fig. 6. The hit splitting starts with a simple least square plane fit that is similar to the line-fit. Then, a perpendicular plane that contains the line-fit result is constructed and thereby, all photon hits are divided into two sides of this perpendicular plane.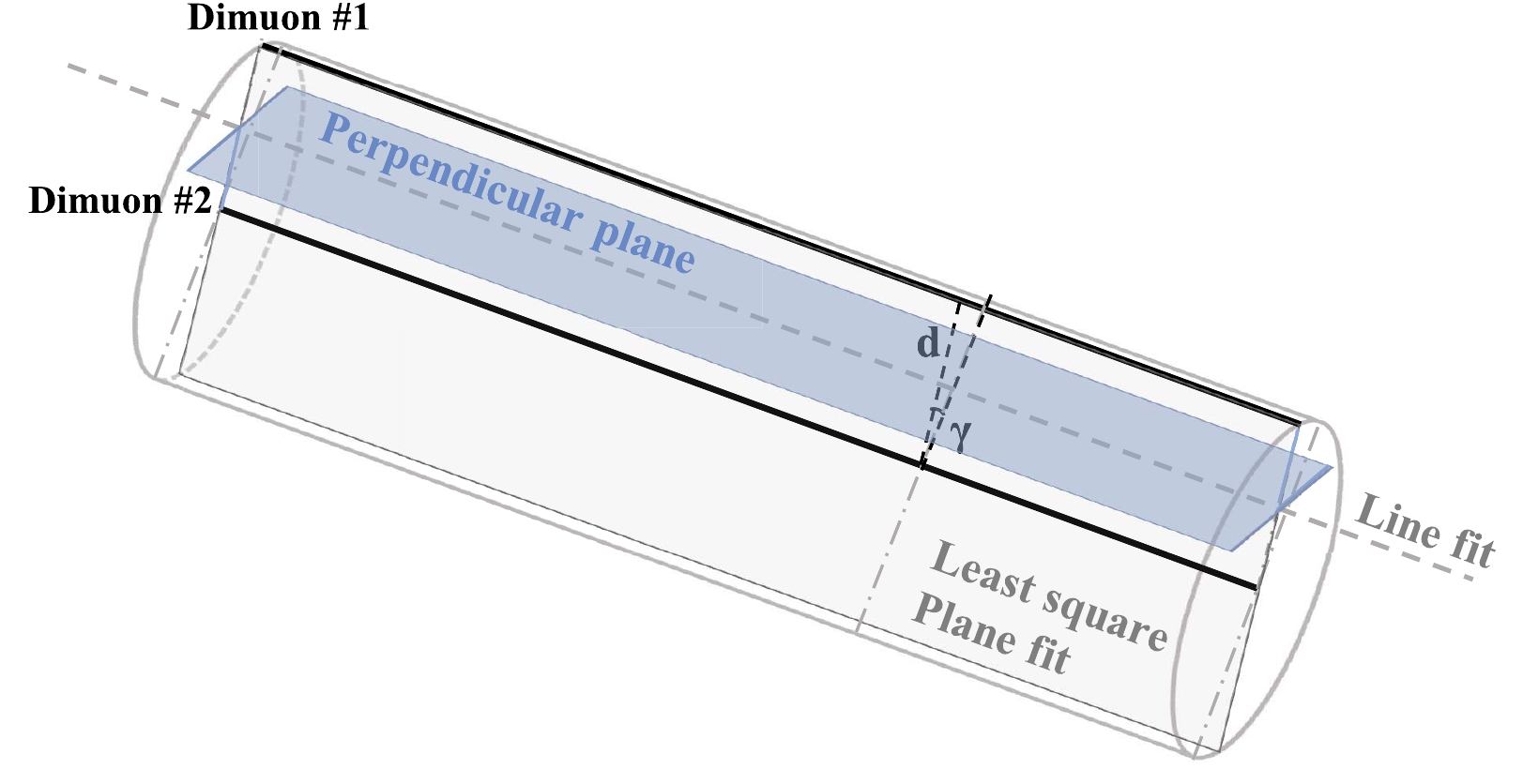
Figure 6. (color online) Schematic of dimuon hit splitting. Two parallel muon tracks, indicated as black solid lines, propagate horizontally in the detector. Two additional reconstructed parameters of the dimuon hypothesis, track separation d and displacement angle γ, are marked in the figure. All hits are split into two groups by the perpendicular plane (blue shaded).
All Monte Carlo events comprising of true single- and di-muon samples are reconstructed with dimuon hypothesis. Depending on the basic reconstruction quality and results, the pre-level selection requires that the reconstruction fit converges. The reconstructed separation distributions of the true single- and di-muon samples are shown in Fig. 7, in which the blue and purple lines represent Set 1 and Set 2, respectively. It can be clearly seen that a large number of single muon events are misclassified as dimuons with reconstructed separation below approximately 10 m. As the separation increases, the dimuon events dominate the distribution. Therefore, the events are further selected by their reconstructed separations and this is referred to as level-1. We define a test statistics for events that pass the level-1 selection:
$ TS: = -2\ln{(L_{d=0}/L_{bf})} $ , where$ L_{d=0} $ indicates the likelihood that the separation d is fixed to be zero and$ L_{bf} $ indicates the best fit dimuon hypothesis. The event is classified as a dimuon event if its$ TS>10 $ ; otherwise, the event goes into the single-muon sample (level-2).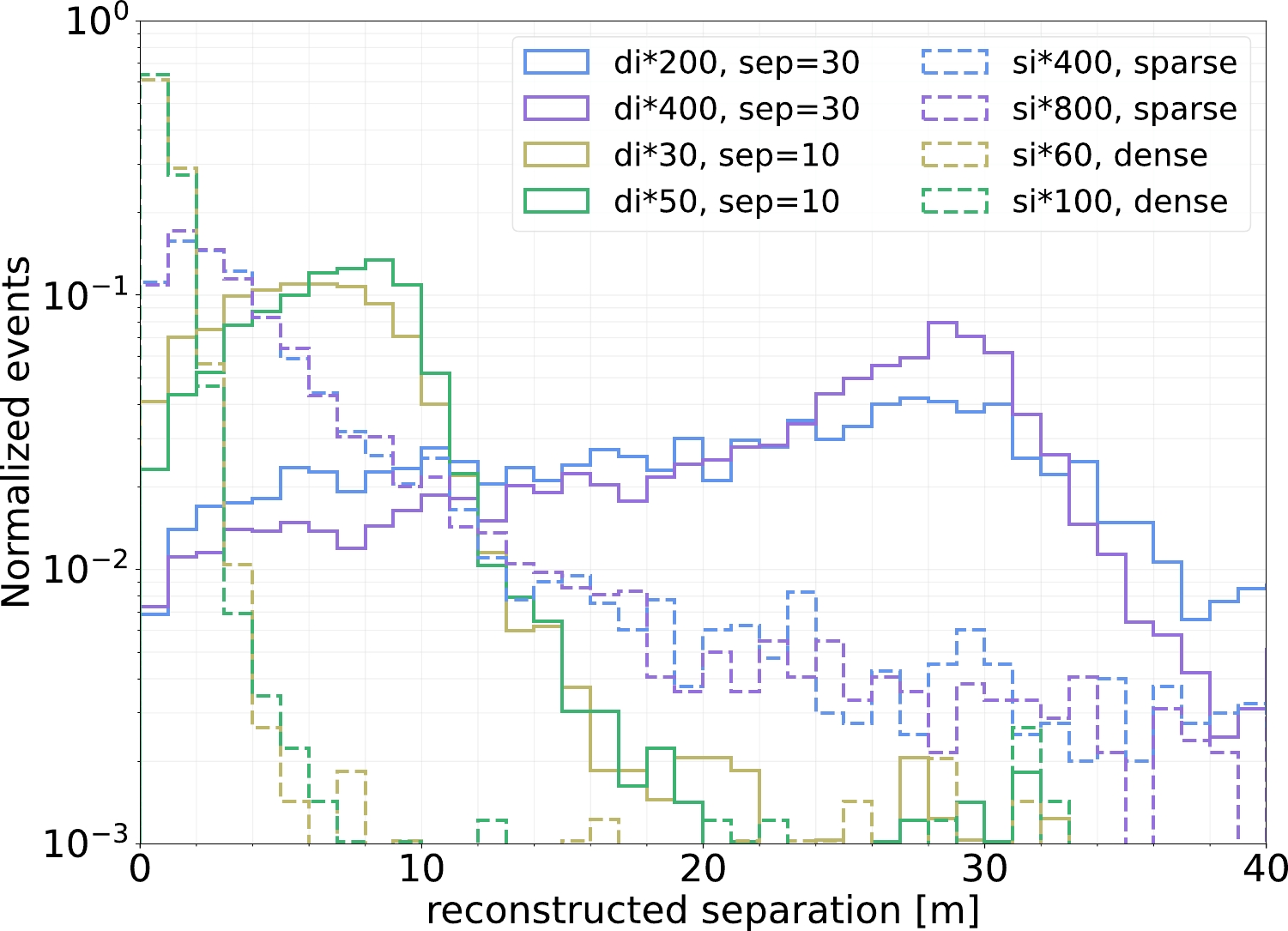
Figure 7. (color online) Distributions of reconstructed separations of true single- and di-muon samples, shown by dashed and solid lines, respectively. Samples with 30-m separation are reconstructed in the sparse detector configuration. Samples with 10-m separation are reconstructed in the dense detector configuration. In each set labeled with the same color, di denotes dimuons, and si denotes single muons.
The dimuon acceptance rate is defined as the number of dimuon events that pass the final selection divided by the total injected MC events, while mis-identified single muons are background events. The reconstructed separation cut is selected to optimize the dimuon acceptance rate
$ \epsilon_{\mu\mu} $ and single muon fake rate$ \epsilon_{\mu} $ . The resultant optimized values are listed in Table 1 with the corresponding separation cuts. As a comparison, a denser but smaller detector configuration similar to that of KM3NeT/ORCA is additionally investigated, as the medium and DOM design used in this work are the same as those of ORCA. In this dense configuration, 20 and 10 DOMs are separated by 10 and 20 m vertically and horizontally, respectively. In addition to the detector geometry, the energies of the true dimuon samples are reduced to$ 30\,$ GeV and$ 50\,$ GeV with 10-m true separation, whereas the corresponding single muon backgrounds are$ 60\,$ GeV and$ 100\,$ GeV. They are referred to as Set 3 and Set 4. The reconstructed separation distributions for these two sets are shown in yellow and green lines in Fig. 7, and the optimized dimuon acceptance rate and single muon fake rate are also listed in Table 1. By contrast with the sparse detector, the dense detector shows a significant improvement in dimuon classification in spite of reduced track separation, along with reduced single muon fake rates.Sparse Configuration (IceCube-like) Set 1 Set 2 sep. cut 2*200 GeV 400 GeV sep. cut 2*400 GeV 800 GeV 18 m $ 19.0\% $ 

$ 2.9\% $ 

17 m $ 45.5\% $ 

$ 2.5\% $ 

Dense Configuration (ORCA-like) Set 3 Set 4 sep. cut 2*30 GeV 60 GeV sep. cut 2*50 GeV 100 GeV 4 m $ 57.12\% $ 

$ 0.74\% $ 

4 m $ 69.32\% $ 

$ 0.78\% $ 

Table 1. Optimal dimuon acceptances
$ \epsilon_{\mu\mu} $ and single-muon fake rates$ \epsilon_{\mu} $ with the corresponding separation cuts are listed for two type detector configurations. In each configuration, two sets of muon samples with the same fixed track separation ($ 30\,\text{m} $ for sparse,$ 10\,\text{m} $ for dense) but different energies are reconstructed. In each set, the dimuon sample is indicated by a prefactor 2.In addition to the dimuon samples listed in Table 1, two muons with unequal energies are explored as well. However, the acceptance rates of dimuons and fakes rates of single muons in this case tend to be closer. This is because, so far, the energy reconstruction is not included in the algorithm. To enhance the track separation, the energy reconstruction, along with the optimization of hit splitting will be taken into account in the near future. Moreover, an optimized design of the optical sensor, for instance, a hybrid DOM consisting of not only PMTs but also silicon photomultipliers (SiPMs) with better timing performance, would potentially improve the track separation resolution.
-
Based on the dimuon acceptances and single-muon fake rates computed in Sec. IV.A, experimental significances for several theoretical benchmarks are calculated. Under background-only hypothesis, the significance is calculated from
$ \text{sig} = \epsilon_{\mu\mu} N_{\mu\mu} / \sqrt{\epsilon_{\mu} N_{\mu}} $ . Here,$ N_{\mu\mu} $ and$ N_{\mu} $ are the numbers of events of dimuons and single-muons that pass cuts, respectively.This formula can be approximately factorized into two independent components:
$ \epsilon_{\mu\mu} / \sqrt{\epsilon_{\mu}} $ and$ N_{\mu\mu} / \sqrt{N_{\mu}} $ . The former factor only relies on the detector-level simulation results listed in Table 1, which are categorized into four detector-level sets. The latter one is dependent on theoretical predictions. By applying different cuts on muon energy and dimuon separation at the detector boundary, different numbers of events of dimuons and single-muons are obtained and they constitute the theoretical benchmarks. In our estimation, the single-muon background is generated using the same flux and flux cut as that for dimuon events. Under consideration of the energy information that can be used in a real experiment to enhance the power of classification, the energy cut at the detector boundary for a single-muon is twice the value for a dimuon. In Sec. III, it is shown that the lateral distance of dimuons increases as they propagate inside the detector. Hence, it is conservative to use dimuon separation as the counterpart of the track separation mentioned in Sec. IVA. In that subsection, dimuons in detector-level modeling are simulated with fixed separations, namely,$ 30\,\text{m} $ and$ 10\,\text{m} $ for the sparse and dense configurations, respectively. In contrast, dimuon events in theoretical benchmarks are considered with smaller separations. For example, we consider dimuon separation cuts of either 30 m or 20 m in IceCube-like configurations. In addition, for an ORCA-like configuration,$ N_{\mu\mu} / \sqrt{N_{\mu}} $ is rescaled by a factor of 0.205 to account for the distinction of cross-sectional areas. The results of our estimations are shown in the left panels of Fig. 8. The exposure time is taken as either 10 years or 20 years. Note that, for the IceCube-like configuration, no marked significances are achieved even for an exposure of 20 years. To enhance the significance, it is essential to lower the energy threshold and improve the separation resolution. This makes ORCA more promising for searching dimuon events. In the lower-left panel, the experimental sensitivities of ORCA are displayed. The significances achieved in ORCA are approximately one order higher than those in the IceCube configuration. For a dimuon energy cut of 50 GeV and a separation cut of 5 m with an exposure time of 20 years, the sensitivity reaches its most optimistic value and surpasses a significance of one sigma.
Figure 8. (color online) Upper-left: Significances of dimuon signal over single muon background are calculated with different detector-level classification (mis-)efficiencies (line and dashed line) for each theoretical benchmark (shown in x labels, e.g., (100, 20) represents dimuon energy cut of 100 GeV and dimuon separation cut of 20 m). Detector-level settings are based on the IceCube configuration. Exposures of 10 years (red) and 20 years (blue) are taken. Upper-right: Critical dimuon acceptance and single-muon fake rate for achieving one sigma significance for different theoretical benchmarks (shown in legends, e.g., (50, 5, 10) represents dimuon energy cut of 50 GeV, dimuon separation cut of 5 m, and exposure time of 10 years) in IceCube. Lower-left: The same as the upper-left panel, but the detector-level settings are for ORCA. Lower-right: The same as the upper-right panel but modified for ORCA.
For these theoretical benchmarks, critical dimuon efficiencies and single-muon fake rates for achieving significance of one sigma are also shown in the right panels of Fig. 8. In contrast with the simulation results in Table 1, the critical boundary lines are far-to-reach for IceCube. Even for a 100% acceptance rate of dimuon signals, background rejections better than per-mille are required. In comparison, the boundary lines for ORCA are lifted by orders, which is another manifestation of the advantages of ORCA for the search of dimuon events.
We have not considered the effects of various systematic uncertainties so far. For instance, the flux uncertainties are approximately 20% in the bulk region of neutrino energies from theoretical models [64]. This can reduce the significance by a order of magnitude if added directly to the uncertainties on predictions of background yields for the configuration of either IceCube or ORCA. However, one can use data driven methods to directly estimate the background yields from measurements on normal single muon events [70] without relying much on the theoretical inputs of neutrino fluxes. This can also help reduce the impact of other experimental systematic uncertainties. Besides, it must be emphasized that our phenomenological study is based on a preliminary reconstruction algorithm and simplified detector modeling. This is a starting point for future development. The optimization of hit splitting and the development of other sensitive selection criteria can improve the detecting potential significantly. Furthermore, machine learning might be efficient to distinguish dimuon signals from the single muon background.
-
Dimuon events induced by charm-quark production in charged-current DIS merit investigation in neutrino telescopes. For those with lateral separation of hundreds of meters, their discovery would strongly imply physics beyond the SM. In the context of the SM, dimuon events are still of great interests for the test of QCD. However, short dimuon lateral distances make it challenging to find such signals in current neutrino telescopes. In this study, we set up a framework to simulate DIS dimuon events in two neutrino telescope models. Only dimuon events produced outside the detector are considered. Energy losses of muon traversing media are simulated with
${\tt MMC}$ . The resultant event sample from our simulation is exemplified in Fig. 2 and Fig. 3. Most events that can reach the detector occur near detector boundaries.Further, even though developed independently, an earlier work and our work discuss a similar scenario. For a comparison of results, in Sec. III, the simulation conditions are modified to match the baseline in the previous work. In the first part of that section, the normalization of muons in a 10-year exposure is compared, and a further comparison of muon energy distributions shows consistency in patterns. Furthermore, the difference from calculation methods of muon energy losses is discussed.
To investigate the detection prospects in a real experiment, we set up a detection framework in Sec. IV. The efficiencies of four sets in two experimental configurations, namely IceCube-like and ORCA-like, are evaluated. With the help of these efficiencies, several theoretical benchmarks are selected to estimate the significance of the dimuon signal over the single-muon background. In this phenomenological study with over-simplified detector-level modeling, even the most optimistic significance achieved in IceCube is far less than one. To achieve one sigma significance, the required dimuon acceptance rates and single-muon fake rates are also shown. These critical lines are far-to-reach in the current simplified IceCube detection simulation. It is therefore a big challenge to observe DIS dimuon signals in sparse km3 scale neutrino telescopes. By contrast, a denser but smaller configuration similar to that of ORCA shows a better performance on dimuon searches. In the case of a 50 GeV cut for energy and a 5 m cut for dimuon separation, a significance level higher than one sigma is expected to be achieved under an exposure of 20 years. However, denser configurations are favored when the surrounding media can be used as targets. For detectors such as Hyper-K, dimuon events can only be produced inside the detector; thus, they continue to face challenges.
In spite of limited sensitivities in this study, the dimuon search is still prospective. On the one hand, the detector-level simulation and reconstruction in this study are simplified. By extending the detector response with PMT response modeling, time-correlated double pulse waveforms are expected on a series of DOMs. Moreover, an optimization of the double-track reconstruction with an additional small separation angle, instead of the parallel tracks assumed in the current algorithm, is helpful to improve the ability of classification. On the other hand, the detector design optimization would largely enhance the dimuon searches. In particular, an optimized optical sensors with much better timing resolution, for instance, a hybid-DOM consisting of multiple PMTs and SiPMs, would significantly improve the direction resolution. This is potentially beneficial to the search of dimuons with short lateral distances. At present, such optimization is ongoing.
-
The authors would like to thank John Beacom and Bei Zhou for useful comments.
Search for charm-quark production via dimuons in neutrino telescopes
- Received Date: 2022-09-15
- Available Online: 2023-02-15
Abstract: Dimuon events induced by charm-quark productions from neutrino deep inelastic scattering (DIS) processes have been studied in traditional DIS experiments for decades. The recent progress in neutrino telescopes makes it possible to search for such dimuon events at energies far beyond the laboratory scale. In this study, we construct a simulation framework to calculate yields and distributions of dimuon signals in an IceCube-like km3 scale neutrino telescope. Owing to the experimental limitation in the resolution of double-track lateral distance, only dimuons produced outside the detector volume are considered. Detailed information about simulation results for a 10-year exposure is presented. As an earlier paper[Physical Review D 105, 093005 (2022)] and ours report on a similar situation, we use that paper as a baseline to conduct comparisons. We then estimate the impacts of different calculation methods of muon energy losses. Finally, we study the experimental potential of dimuon searches under the hypothesis of single-muon background only. Our results based on a simplified double-track reconstruction indicate a moderate sensitivity, especially with the ORCA configuration. Further developments on both the reconstruction algorithm and possible detector designs are thus required and are under investigation.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: