-
In the universe, there exists an extremely interesting and bizarre object: the black hole. After intense research in the past few years, it is believed that supermassive black holes exist at the core of most galaxies. We can study at least two types of black holes: those of the Milky Way and neighboring elliptical
$ M87^* $ galaxies [1, 2]. The Event Horizon Telescope (EHT) Collaboration provided a breakthrough in the study of black holes with the first two images of supermassive black holes, namely$ M87^* $ [3–5] and$ SgrA^* $ [6, 7]. It is well known that the gravitational attraction around a black hole is so intense that nearby objects fall into it when they reach a critical radius. This phenomenon is known as gravitational lensing. We expect that the properties of black holes can be better understood from the gravitational lensing effect. This means that much more attention must be devoted to gravitational lensing in the strong gravity regime of black holes. Some lensing observables of Kerr black holes were evaluated in [8–10], and further discussions can be found in [11–16].In addition, when nearby objects are photons emitted by an illuminated source located behind the black hole, a shadow is created that can be seen by an observer located at infinity. The shadow concept was first studied by Bardeen [17]. Specifically, photons that escape from the spherical orbits form the boundary of the dark silhouette of the black hole. This dark silhouette is seen as a black hole shadow from the outside observer. Interestingly, shadows of spherically symmetric black holes are circular [18–22], but those of spinning black holes are deformed [23–28]. Moreover, the photon region of gravitational lensing also provides key properties of the black hole shadow. Besides, the unstable photon regions outside the black hole event horizon can enable the direct observation of the black hole. The first black hole image of
$ M87^* $ published by EHT collaborations in 2019 established certain constraints on some shadow observables. The angular shadow radius of$ M87^* $ was studied later in [29]. Recently, the angular shadow radius of$ SgrA^* $ in the second black hole image has been presented [6, 7]. These constraints on the shadow radius were obtained with the Kerr geometry in GR as a premise, but they do not exclude other black holes in GR or some exotic black holes in the modified gravity theory. EHT observations of shadows can be applied as a tool to constrain the parameters of various black holes in various theories of gravity, and in the future, more precise observational results can allow distinguishing different black holes. Therefore, theoretically possible results for various black holes should be obtained for future testing of observational data from EHT.Black hole thermodynamics has attracted much attention because of the remarkable and non-trivial results corresponding to criticality and stability behaviors. A crucial issue is the investigation on black holes in AdS/dS geometry [30–39]. Since the cosmological constant was regarded as thermodynamical pressure by Kastor in 2009 [40], researchers have focused on the thermodynamics of AdS black holes in the expanded phase space [30, 31, 34–39]. Concerning black holes in the dS spacetime, i.e., dS black holes, the thermodynamical phase transition of a dS spacetime with black hole was analyzed in terms of the interplay between the black hole horizon and cosmological horizon [32, 33, 41–46]. For various AdS/dS black holes, their corresponding thermodynamical quantities have been presented in various gravity theories. Certain black holes show similarities with van der Waals fluid systems, such as the phase transition. Furthermore, for black hole systems, there exists an interesting phase transition, namely the Hawking-Page phase transition, proposed in [47]. Another simply charged AdS black hole is Reissner Nordstrom-AdS (RN-AdS), which has been studied under different backgrounds including Dark Energy and Dark Matter [22, 48, 49]. The corresponding shadows and deflection angle of the light rays in a d-dimensional spacetime were studied in [22, 25, 48, 50]. The authors [26, 28] also reported on the influence of Dark Matter on the shadows and photon rings of a stringy black hole illuminated by certain accretions. Therefore, motivated by the investigations on these spacetimes, interplays between black hole thermodynamics and optical properties should be established. In addition, the phase transition and microstructure states of AdS black holes in [51–53] were analyzed through their shadow. Moreover, the specific relation between shadow and thermodynamics of black holes was derived for regular space-times [54]. However, there are few works about the specific relation between two coexistent black hole phases and their shadows for a black hole undergoing the first-order phase transition. In this work, we will investigate this issue for non-linear charged AdS black holes.
Linear charged black holes in AdS spacetime [55] within a second-order phase transition show a scaling symmetry: at the critical point, the state parameters scale with respect to charge q, i.e.,
$ S\sim q^2,\; P\sim q^{-2},\; T\sim q^{-1} $ [56]. It is natural to gauge whether there exists scaling symmetry in non-linear charged AdS black holes. As a generalization of charged AdS Einstein-Maxwell black holes, it is interesting to explore new non-linear charged systems. Owing to infinite self-energy points such as charges in Maxwell's theory [57–61], Born and Infeld proposed a generalization when the field is strong, leading to non-linearities [62, 63]. Power-law Maxwell electrodynamics is a famous non-linear electrodynamics model. It involves a Yang-Mill field exponentially coupled to Einstein gravity and has the Lagrangian density for the electromagnetic part expressed as$ Tr[F_{\mu\nu}^{(a)}F^{\mu\nu(a)}]^\gamma $ with positive parameter γ [64]. This non-linear theory features conformal invariance and enables a simple construction of the analogs of the four-dimensional Reissner-Nordström black hole solutions. Additionally, several features of the Einstein-power-Yang-Mills (EPYM) gravity in extended thermodynamics have been recently studied [64–66].Inspired by this research context, herein, we mainly investigate the relation between the shadow radius and phase transitions of charged EPYM AdS black holes. The paper is organized as follows. In Sec. II, we briefly review thermodynamic quantities and present the relationship between an observable quantity (i.e., shadow radius) and the horizon radius of charged EPYM AdS black holes. In Sec. II, the behavior of the shadow radius with respect to the horizon radius and temperature close to the phase transition point is investigated. The effect of the non-linear Yang-Mills (YM) charge parameter on these behaviors is also addressed. For a more intuitive explanation of the relationship between the EPYM AdS black hole phase structure and its shadow, we show the thermal profiles of two coexistent large and small black hole phases in a two-dimensional plane in Sec. IV. Finally, a discussion and conclusions are provided in Sec. V.
-
The solution of a four-dimensional Einstein-power-Yang-Mills (EPYM) AdS black hole with non-linear Yang-Mills (YM) charge was presented in [67]:
$ \begin{eqnarray} {\rm d} s^{2}=-f(r) {\rm d} t^{2}+f^{-1} {\rm d} r^{2}+r^{2} {\rm d} \Omega_{2}^{2}, \end{eqnarray} $

(1) $ \begin{eqnarray} f(r)=1-\frac{2 M}{r}-\frac{\Lambda}{3} r^{2}+\frac{\left(2 q^{2}\right)^{\gamma}}{2(4 \gamma-3) r^{4 \gamma-2}}, \end{eqnarray} $

(2) where
${\rm d}\Omega_{2}^{2}$ is the metric on the unit$ 2 $ -dimensional sphere. Letters q and M stand for the YM charge and mass parameter of the black hole, respectively. In this system, the condition of the non-linear YM charge parameter satisfies$ \gamma\neq0.75 $ , and the power YM term holds the weak energy condition for$ \gamma>0 $ [68]. The cosmological constant Λ is interpreted as the thermodynamic pressure$ P=-\frac{\Lambda}{8\pi} $ in the extended phase space, and the black hole event horizon is located at$ f(r_+)=0 $ .The thermodynamical quantities of this system were expressed in [66] as follows:
$ \begin{aligned}[b] M=\frac{1}{6}\left[8 \pi Pr_+^{3 / 2}+3r_+^{\frac{3-4 \gamma}{2}} \frac{\left(2 q^{2}\right)^{\gamma}}{8 \gamma-6}+3 r_+\right],\quad \Psi=\frac{r_+^{3-4 \gamma} 2^{\gamma-2}}{4\gamma-3}, \end{aligned} $

(3) $ \begin{aligned}[b] T =&\frac{1}{4 \pi r_+}\left(1+8 \pi P r_+^{2}-\frac{\left(2 q^{2}\right)^{\gamma}}{2 r_+^{(4 \gamma-2)}}\right),\\ S=&\pi r_+^{2},\; \; \; \; V=\frac{4\pi r_+^3}{3}, \end{aligned} $

(4) $ \begin{eqnarray} P = r_+\left[\frac{T}{2}-\frac{1}{8 \pi}r_++\frac{\left(2 q^{2}\right)^{\gamma}}{16 \pi}r_+^{1-4\gamma}\right]. \end{eqnarray} $

(5) It is easy to check that these thermodynamical quantities satisfy the first law of thermodynamics in the expanded phase space:
${\rm d} M=T{\rm d} S+V{\rm d} P+\Psi {\rm d} q$ [64, 67]. Based on the classification of phase transitions for a thermodynamical system by Ehrenfest, the critical point satisfies the following expressions [34, 35, 64]:$ \begin{eqnarray} \left(\frac{\partial P}{\partial V}\right)_T=0,\; \; \left(\frac{\partial^2 P}{\partial V^2}\right)_T=0. \end{eqnarray} $

(6) As shown in [66, 69], this non-linear AdS black hole exhibits a vdW's-like phase transition and the corresponding critical thermodynamical quantities read as follows:
$ \begin{aligned}[b] r_{c}^{4 \gamma-2}=\left(2 q^{2}\right)^{\gamma} f(1, \gamma), \quad S_c=\pi \left(2 q^{2}\right)^{\frac{\gamma}{2\gamma-1}} f^{1/(2\gamma-1)}(1, \gamma), \end{aligned} $

(7) $ \begin{eqnarray} T_{c}=\frac{2 \gamma-1}{\pi\left(2 q^{2}\right)^{\gamma /(4 \gamma-2)} f^{1 /(4 \gamma-2)}(1, \gamma)(4 \gamma-1)} , \end{eqnarray} $

(8) $ \begin{eqnarray} P_{c}=\frac{2 \gamma-1}{16 \pi \gamma\left(2 q^{2}\right)^{\gamma /(2 \gamma-1)} f^{1 /(2 \gamma-1)}(1, \gamma)}. \end{eqnarray} $

(9) where
$ f(1, \gamma)=\gamma(4 \gamma-1) $ and$ \dfrac{1}{2}<\gamma $ . It is evident that at the critical point, the thermodynamical quantities are only determined by the YM charge information carried by system. From the above quantities, we can obtain an interesting relation that only involves γ:$ \begin{eqnarray} S_c^2T_c^2P_c=\frac{(2\gamma-1)^3}{16\pi\gamma(4\gamma-1)^2}. \end{eqnarray} $

(10) In the following, we will focus on a free photon orbit of the EPYM black hole. There are two methods to address this issue: null geodesics and the Hamiltonian approach. Generally, we can solve the null geodesics to obtain the photon sphere radius. Given that the geodesics are expressed through four second-order coupled equations, it is difficult to solve them directly. Hence, we adopt the Hamiltonian approach, which takes the following form:
$ \begin{eqnarray} H=\frac{1}{2}g^{\mu\nu}p_\mu p_\nu=\frac{1}{2}\left(-f^{-1}p_t^2+fp_r^2+r^{-2}p_\phi^2\right) \end{eqnarray} $

(11) with the equatorial hyperplane defined by
$ \theta=\pi/2 $ and$ p_\theta=0 $ . Here,$p_\mu=\dfrac{{\rm d} x_{\mu}}{{\rm d}\lambda}$ denote the generalized momenta, and λ is the affine parameter. For a black hole background, there are two conserved quantities for the Killing fields$ \partial_t $ and$ \partial_\phi $ , i.e., the particle energy E and orbital angular momentum L along each geodesics:$ \begin{eqnarray} -E=p_t=-f(r)\dot{t},\; \; \; \; \; \; L=p_\phi=r^2\dot{\phi}, \end{eqnarray} $

(12) and the dot represents the derivative with respect to λ. The prime stands for the derivative with respect to the radial coordinate. The light rays are the solutions to Hamilton's equations:
$ \begin{eqnarray} \dot{p}_\mu=-\frac{\partial H}{\partial x^\mu},\; \; \; \; \dot{x}^\mu=\frac{\partial H}{\partial p_\mu}, \end{eqnarray} $

(13) which read as follows:
$ \begin{aligned}[b] \dot{p}_t=&0,\; \; \dot{p}_\phi=0,\; \; \dot{p}_\theta=0,\\ \dot{p}_r=&-\frac{1}{2}\left(\frac{f'(r)p _t^2}{f^2(r)}+f'(r)p_r^2+2f(r)p_rp_r'-\frac{2p_\phi^2}{r^3}\right),\\ \dot{t}=&-\frac{p_t}{f(r)},\; \; \dot{r}=f(r)p_r,\; \; \dot{\phi}=\frac{p_\phi}{r^2}. \end{aligned} $

(14) With
$ H=0 $ , we have$ \begin{eqnarray} \dot{r}^2+V_{\rm eff}=0,\; \; \; V_{\rm eff}=\frac{L^2f(r)}{r^2}-E^2. \end{eqnarray} $

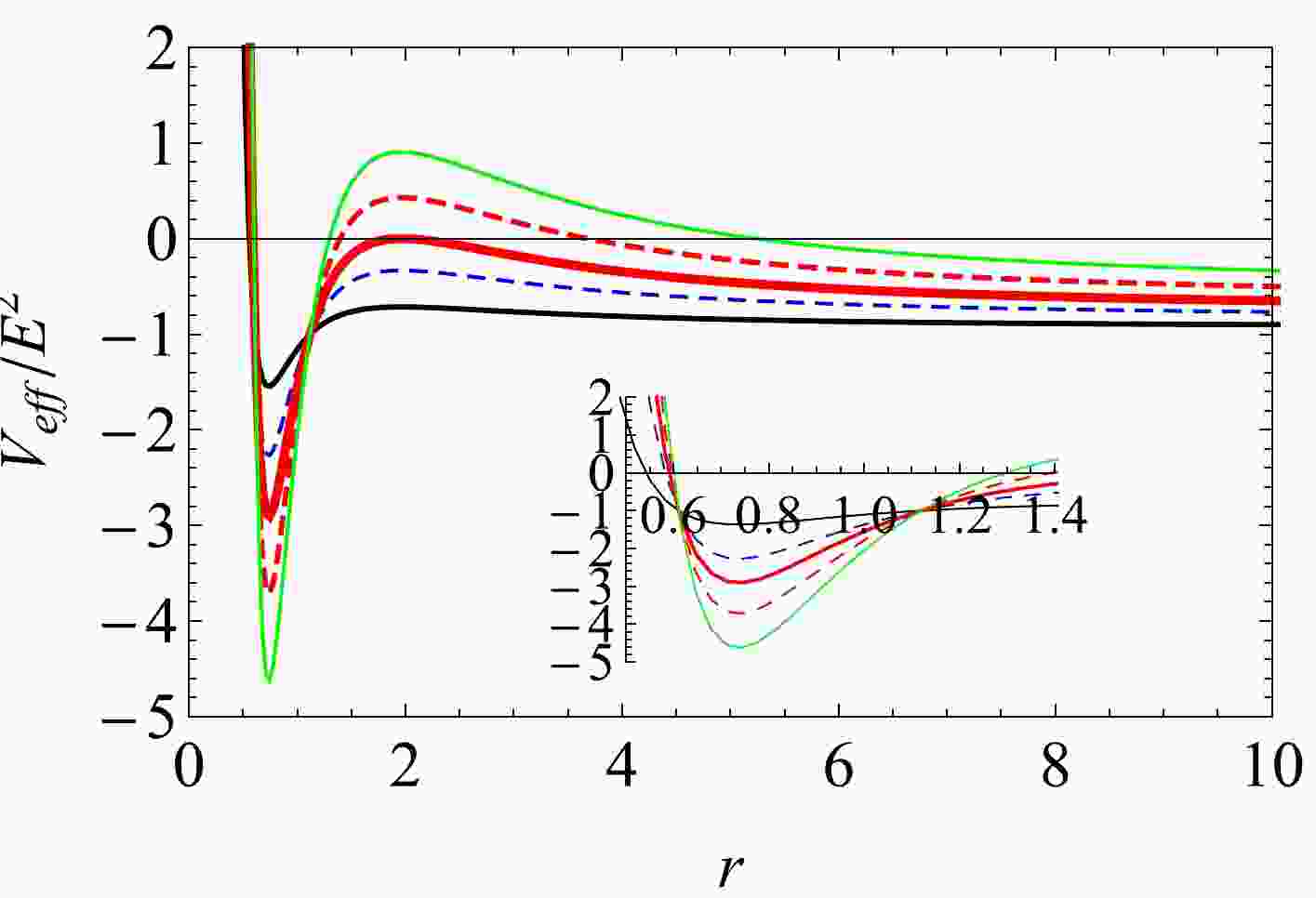
(15) We present the effective potential as a function of the radial radius in Fig. 1 for an EPYM AdS black hole with parameters
$ \gamma=1,\; P=0.003,\; q=0.85,\; M=0.9 $ and different angular momenta$ L/E $ . For a given angular momentum, there exists a special point in the$T_{\rm eff}/E^2-r$ diagram, namely the local unstable maximum, which will increase with increasing angular momentum.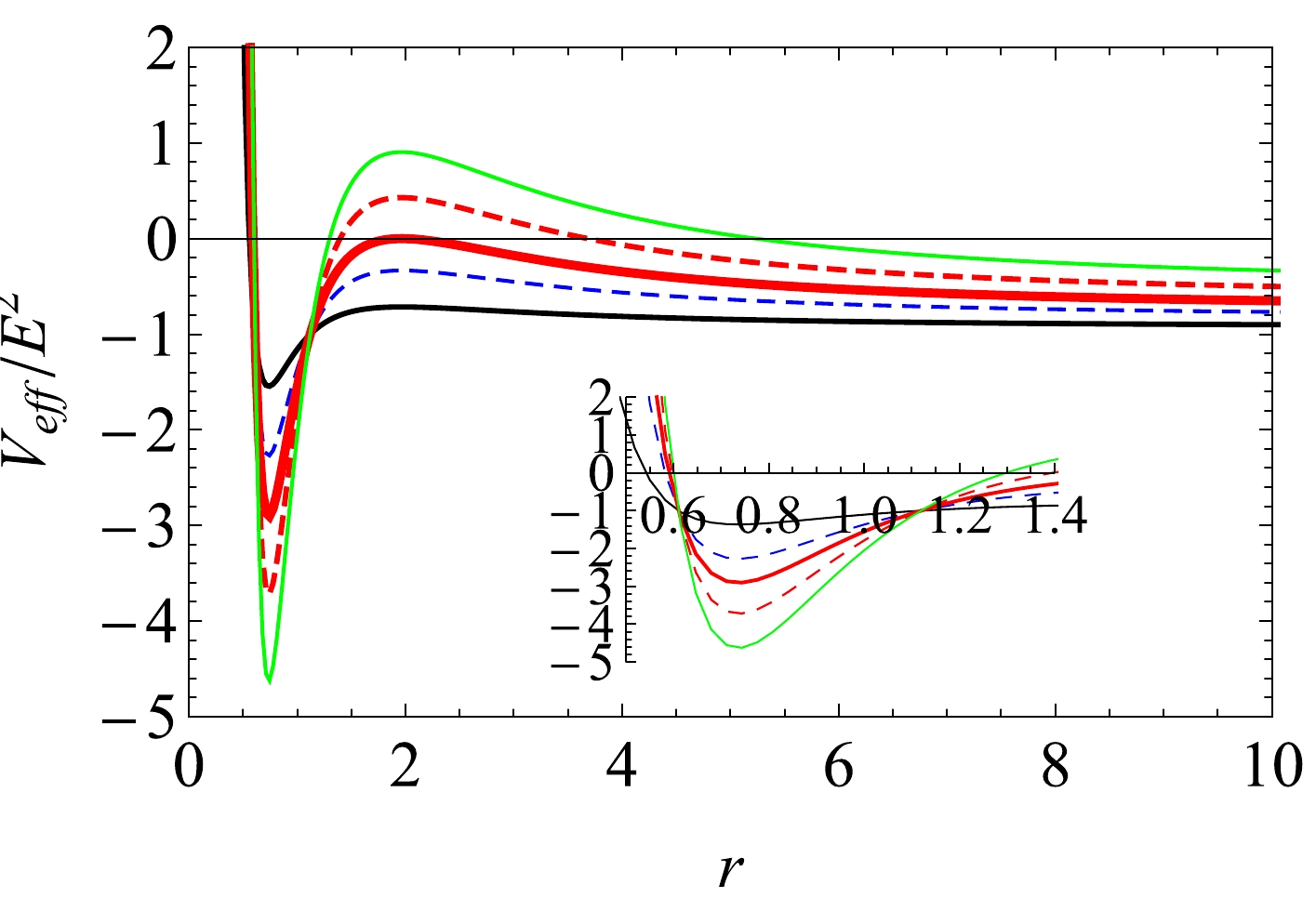
Figure 1. (color online) Effective potential for the EPYM AdS black hole with parameters
$ \gamma=1,\; P=0.003, $ $ \; q=0.85,\; M=0.9 $ . The angular momenta$ L/E $ of the photon vary from$ 2 $ to$ 20 $ .Because of the positive sign of
$ \dot{r}^2 $ in Eq. (15), the effective potential must be negative. Thus, the photon can only survive in the range of negative effective potential. For a small angular momentum, the photon will fall into the black hole from a location with a larger value of r. The local unstable maximum of the effective potential will increase with large angular momenta, and photon reflection will occur before it falls into the black hole. Between these two cases, there exists the critical case represented by the thickness red line in Fig. 1, whose peak approaches zero, and simultaneously, the radial photon velocity vanishes. This point corresponds to the photon sphere radius because of the spherically symmetric static nature of the black hole. In the following, we will study the relation between a spatially static observer and the photon sphere radius.According to Fig. 1, the local unstable circular photon sphere satisfies the following expressions:
$ \begin{eqnarray} V_{\rm eff}=0,\quad \frac{{\rm d}V_{\rm eff}}{{\rm d}r}=0,\quad \frac{{\rm d}^2V_{\rm eff}}{{\rm d}r^2}<0. \end{eqnarray} $

(16) Here, we denote the photon sphere radius as
$ r_{ph} $ . According to the second expression in Eq. (16), the radius$ r_{ph} $ satisfies$ \begin{eqnarray} 2f(r)\mid_{r_{ph}}=rf'(r)\mid_{r_{ph}}, \end{eqnarray} $

(17) where the prime represents the derivative with respect to the radial coordinate r. By solving the first equation in Eq. (16), the impact parameter or the angular momentum of the photon can be written as follows:
$ \begin{eqnarray} \mu_{ph}\equiv\frac{L}{E}=\frac{r}{\sqrt{f(r)}}\bigg|_{r_{ph}}. \end{eqnarray} $

(18) Let us consider light rays sent from an observer at radius coordinate
$ r_0 $ into the past. These light rays can be divided into two classes: Light rays belonging to the first class travel to infinity after being deflected by the black hole. Light rays belonging to the second class travel towards the horizon of the black hole. If there are no light sources between the observer and the black hole, the initial directions of the second class correspond to darkness in the observer's sky. This dark circular disk on the observer's sky is called the shadow of the black hole. The boundary of the shadow is determined by the initial directions of light rays that asymptotically spiral towards the outermost photon sphere. The light ray sent from a static observer at position$ r_0 $ travels into the past with an angle α relative to the radial direction, which reads$ \begin{eqnarray} \cot{\alpha}=\sqrt{\frac{1}{r^2 f(r)}}\frac{{\rm d}r}{{\rm d}\phi}\bigg|_{r_0}. \end{eqnarray} $

(19) If the light ray goes out again after reaching
$ r_{ph} $ , according to Eqs. (14) and (18), the orbit equation can be expressed as follows:$ \begin{eqnarray} \frac{{\rm d}r}{{\rm d}\phi}=\pm r\sqrt{\frac{r^2}{\mu_{ph}^2}-f(r)}. \end{eqnarray} $

(20) Thus, the angular radius of the shadow becomes
$ \begin{eqnarray} \cot{\alpha}^2=\frac{r_0^2}{\mu_{ph}^2 f(r_0)}-1, \end{eqnarray} $

(21) and by using a trigonometric identity, namely
$ 1+\cot{\alpha}^2= \dfrac{1}{\sin^2{\alpha}} $ , it can be rewritten as follows:$ \begin{eqnarray} \sin{\alpha}=\frac{\mu_{ph}\sqrt{f(r_0)}}{r_0}. \end{eqnarray} $

(22) The shadow radius of the black hole observed by a static observer at
$ r_0 $ can be expressed as follows:$ \begin{eqnarray} r_s =\frac{r_{ph}}{\sqrt{f(r_{ph})}}\sqrt{f(r_0)}. \end{eqnarray} $

(23) -
When this system is undergoing the first-order phase transition (HPBH/LPBH phase transition) with temperature T (
$ T=\chi T_c,\; \chi<1 $ ), we denote the horizon radius of two coexistence black hole phases as$ r_1 $ and$ r_2 $ , respectively. Using the Maxwell's equal area law, the condition of the first-order phase transition for this system with given temperature T derived in previous works [66, 69] reads as follows:$ \begin{eqnarray} \chi\frac{2\gamma-1}{\gamma^{1/(4\gamma-2)}(4\gamma-1)^{(4\gamma-1)/(4\gamma-2)}} =\frac{1}{f^{1/(4\gamma-2)}(x,\gamma)}\left(1+x- \frac{1-x^{4\gamma}}{2f(x,\gamma)(1-x)x^{4\gamma-2}}\right),\; \; \frac{(2q^2)^\gamma}{r_2^{4\gamma-2}}=\frac{1}{f(x,\gamma)} \end{eqnarray} $ 
(24) with
$ \begin{eqnarray} f(x,\gamma)=\frac{(3-4\gamma)(1+x)(1-x^{4\gamma})+8\gamma x^2(1-x^{4\gamma-3})}{2x^{4\gamma-2}(3-4\gamma)(1-x)^3},\; \; x=\frac{r_{1}}{r_{2}}. \end{eqnarray} $

(25) Given that
$ q=1.9 $ , by numerically fitting the data, the horizon radii of the coexistent large and small black hole phases close to the critical point as a function of temperature are expressed as follows:$ \begin{eqnarray} r_1&\approx& \begin{cases} 2.65\times10^7T^4-8.16\times10^5T^3+8.77\times10^3T^2+1.9, & \; \; \; \; \; \; \; \; \; \; \gamma=1\\ 2.39\times10^6T^4-1.2\times10^5T^3+2.16\times10^3T^2+1.77, & \; \; \; \; \; \; \; \; \; \; \gamma=1.5 \end{cases} \end{eqnarray} $

(26) $ \begin{eqnarray} r_2&\approx& \begin{cases} -7.11+3.81\times10^{-10}/T^3-2.52\times10^{-6}/T^2+0.32/T, & \; \; \; \; \; \; \gamma=1 \\ -4.12+8.1\times10^{-10}/T^3-3.27\times10^{-6}/T^2+0.32/T. & \; \; \; \; \; \; \gamma=1.5 \end{cases} \end{eqnarray} $

(27) The coexistent curves read as follows:
$ \begin{eqnarray} P\approx \begin{cases} -6.42\times10^5T^8+6.33\times10^3T^7-1.49\times10^3T^6+7.27T^5+1.13\times10^3T^4-5.58T^3+1.3T^2, & \gamma=1 \\ 250T^8+17.5T^7-116.9T^6-16.4T^5-0.57T^4+15.32T^3+1.01T^2. & \gamma=1.5 \end{cases} \end{eqnarray} $

(28) The radii of two coexistent black hole phases as a function of temperature close to the critical point are depicted in Fig. 2. It is evident that the horizon radius for the small coexistent phase increases with temperature, while for the large coexistent phase, it increases with temperature as well.

Figure 2. (color online) Plots of horizon radii for two coexistent black hole phases as a function of temperature. The YM charge is set to
$ q=1.9 $ .Next, we will investigate the phase transition information of this system from the viewpoint of the shadow radius. We first set the non-linear YM charge parameter equal to one, i.e.,
$ \gamma=1 $ . The photon sphere radius becomes$ \begin{eqnarray} r_{ph}=\frac{1}{2}\left(3M+\sqrt{9M^2-8q^2}\right). \end{eqnarray} $

(29) It is clear that this result is exactly equal to that of an asymptotically flat charged black hole, in which the photon sphere radius depends on pressure. Note that the mass in Eq. (3) is related to pressure. Substituting it into Eq. (29), we obtain the photon sphere radius:
$ \begin{aligned}[b]\\[-5pt] r_{ph} =\frac{3q^2+r_+^2(3+8\pi Pr_+^2)+\sqrt{[3q^2+r_+^2(3+8\pi Pr_+^2)]^2-32 q^2r_+^2}}{4r_+}. \end{aligned} $ 
(30) At the critical point (
$ r_+=r_c $ and$ P=P_c $ ), the critical photon sphere radius reads$ r_{phc}=(2+\sqrt{6})q $ for$ \gamma=1 $ . Therefore, the shadow radius as a function of the black hole horizon radius becomes$ \begin{eqnarray} r_s=\frac{r_{ph}(r_+)}{\sqrt{f(r_{ph}(r_+))}}\sqrt{f(r_0)}. \end{eqnarray} $

(31) Substituting the critical photon sphere radius and pressure into Eq. (31), we can obtain the critical shadow radius
$ r_{sc} $ , which is related to the YM charge q.Based on this constraint, a static observer at spatial infinity has
$ f(r_0)=1 $ [51]. Using Eqs. (30) and (31), the behavior of the shadow radius as a function of the black hole horizon radius for different values of pressure can be analyzed, as shown in Fig. 3(a). It is evident that there exists a minimum value of the shadow radius for this system with given pressure (regardless of whether it is greater or less than the critical pressure). The shadow radius decreases with increasing horizon radius for small black holes, while for large ones, it increases with the horizon radius until reaching a constant,$ \sqrt{3/(8\pi P)} $ . This indicates that at the minimum point, the system will undergo a phase transition that is different from that of the HPBH/LPBH one. Furthermore, for small EPYM black holes, the shadow radius decreases with increasing pressure.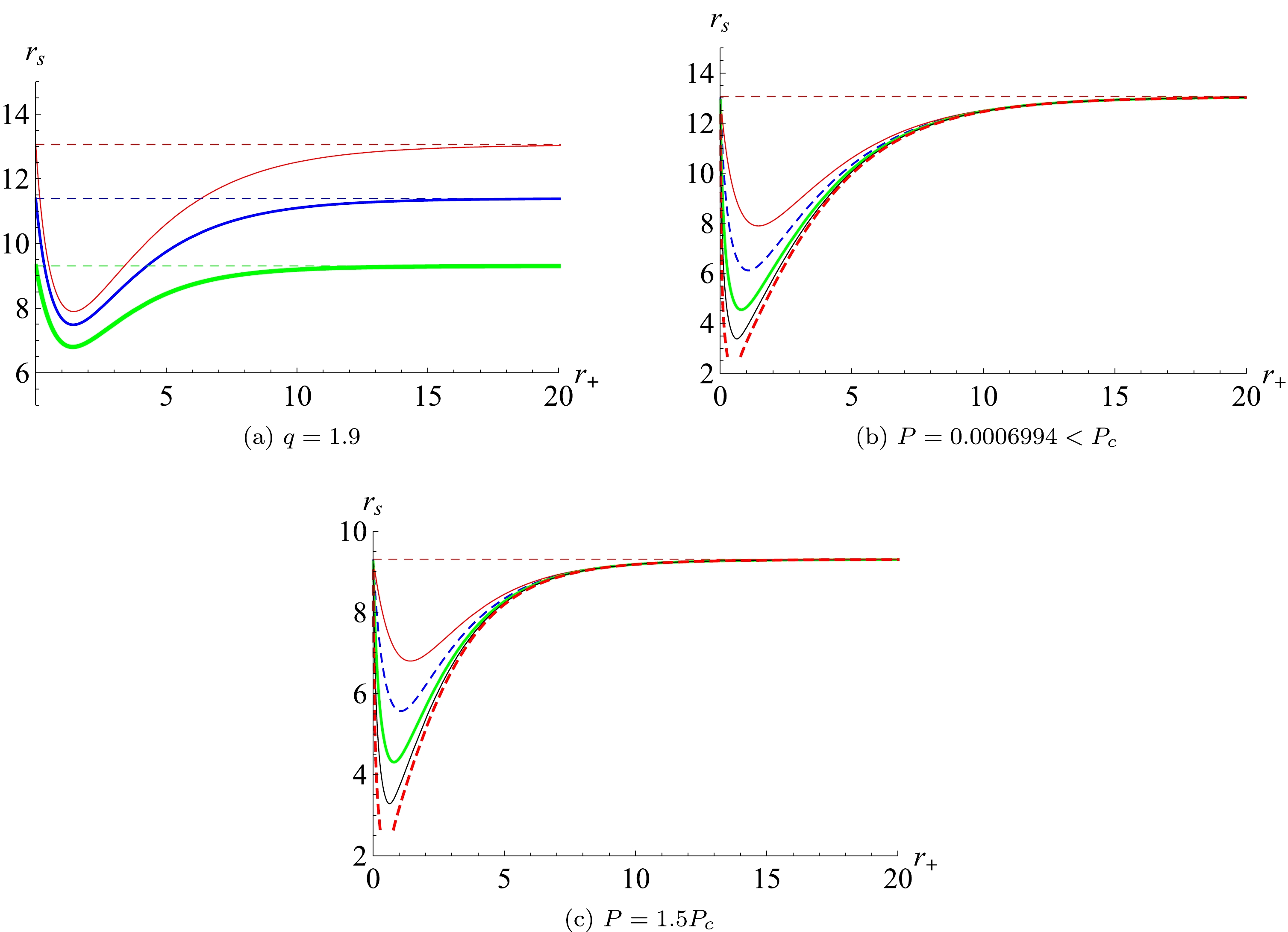
Figure 3. (color online) Non-linear YM charge parameter set to
$ \gamma=1 $ . Left plot: pressure set to$ P_c-0.00022,\; P_c, $ and$ 1.5P_c $ from bottom to top. Middle and right plots: the YM charge varies from$ 1.9 $ to$ 0.8 $ from top to bottom. The horizontal thin dashed lines represent the limited value of the shadow radius.There is an interesting phenomenon: the values of the shadow radius under the limitations
$ r_+\rightarrow0 $ and$ r_+\rightarrow \infty $ are the same. This is related to pressure P, but not to YM charge q (shown in Figs. 3(b) and 3(c)). The limited forms of the shadow radius for two values of γ are as follows:$ \begin{eqnarray} r_s|_{r_+\rightarrow0,\infty}= \begin{cases} \sqrt{-\dfrac{3}{\Lambda}}=\sqrt{\dfrac{3}{8\pi P}}, & \gamma=1 \\ \dfrac{4.3416}{4\pi\sqrt{P}}, & \gamma=1.5 \end{cases} \end{eqnarray} $

(32) Note that for both values of the non-linear YM charge parameter, the inverse square coefficient between
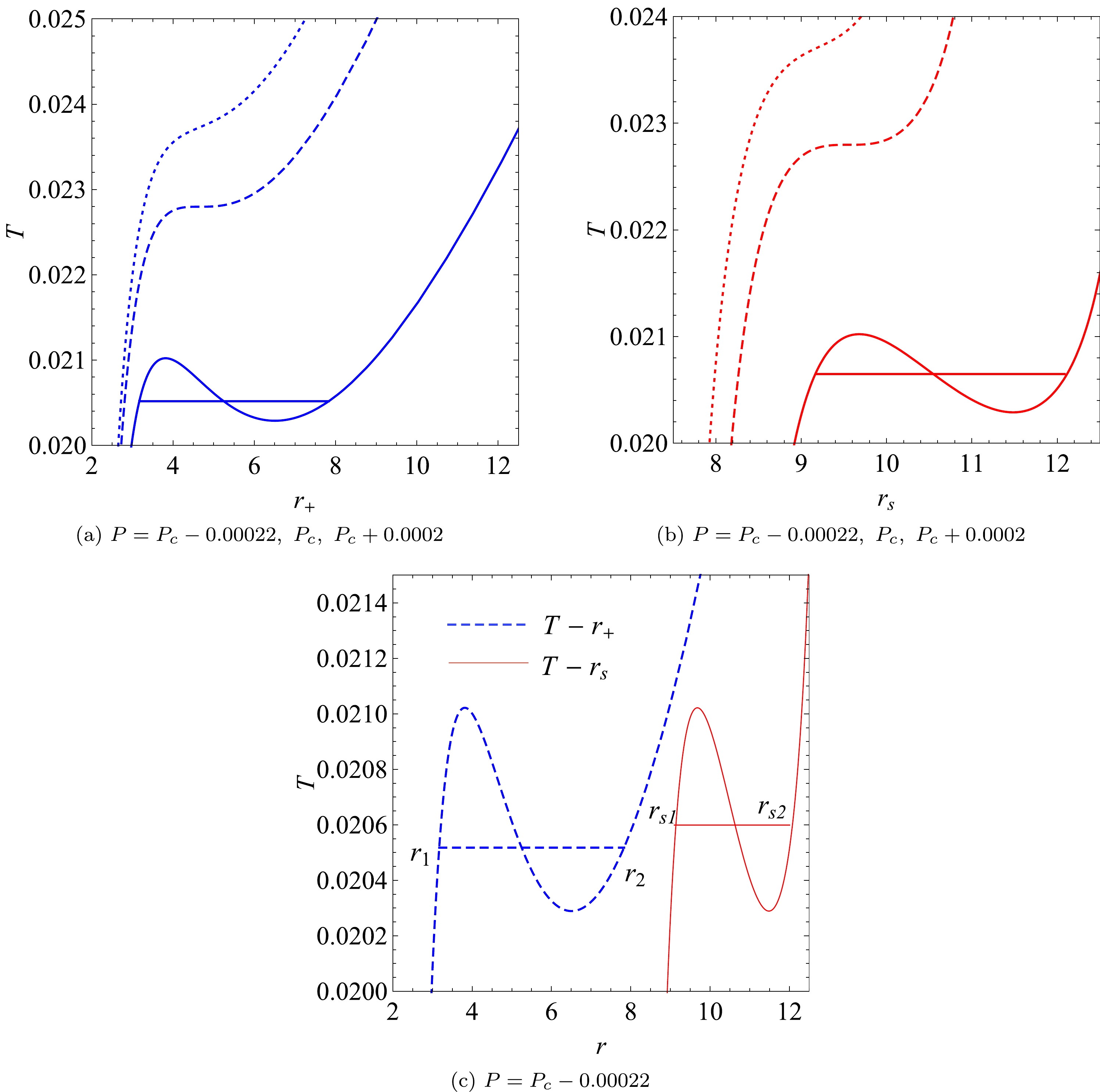
$ r_s|_{r_+\rightarrow0,\infty} $ and pressure is the same:$ 0.345494 $ . This means that for EPYM AdS black holes, the limited value of the shadow radius does not depend on the charge information (q and γ) carried by the system; it only depends on the pressure.Considering different values of pressure and combining the first-order phase transition condition expressed in Eq. (24) and Eqs. (2), (4), (9), (30), and (31) gives rise to the
$ T-r_{+,s} $ phase diagrams shown in Figs. 4(a) and 4(b). It is evident that for$ P<P_c $ , there exists non-monotonic behavior in both the$ T-r_+ $ and$ T-r_s $ planes. However, the temperature becomes a monotonically increasing function of the shadow radius and horizon radius when the pressure is greater than the critical one. At the critical pressure, there exist deflection points at$ r_+=r_{c} $ and$ r_s=r_{sc} $ , respectively. These behaviors are notably similar to the isobar process of a VdW's system in the$ T-S $ plane, which means that there exists a first-order phase transition from the viewpoint of both the horizon radius and shadow radius. By constructing the Maxwell's equal-area law in the$ T-r_+ $ and$ T-r_s $ planes, we also obtain the phase transition points. The corresponding shadow radii are denoted by$ r_{s_1} $ and$ r_{s_2} $ .It should be noted that a peculiar phenomenon emerges: for a given pressure
$ P<P_c $ , the phase transition temperature from the viewpoint of the horizon radius is slightly lower than that from the viewpoint of the shadow radius for$ \gamma=1 $ , as shown in Fig. 4(c). This situation may be caused by the gravitational effect and non-linear YM charge term. So far, we have converted the phase transition information of the EPYM AdS black hole phase transition into a measurable physical quantity, i.e., the shadow radius. This means that we can detect whether there is a phase transition by measuring the shadow radius of the black hole, so as to obtain the microscopic structure of the black hole.In addition, the non-monotonic behavior of
$ T-r_s $ simply indicates the existence of the first-order phase transition, but it is not the first-order transition between high potential and low potential black holes. Although the black hole horizon radius cannot be directly obtained from experiments, its shadow can be observed. Therefore, the shadow radius may serve as a probe for the phase structure of EPYM AdS black holes. For$ \gamma=1.5 $ , we also present numerical results of the shadow radius along with the black hole horizon radius for different pressures and YM charges in Fig. 5(a); their behaviors are similar to those for$ \gamma=1 $ . In this case, the limited form of the shadow radius is provided in Eq. (32). The behaviors of temperature as a function of horizon and shadow radii are shown in Fig. 6; they are similar to those for$ \gamma=1 $ .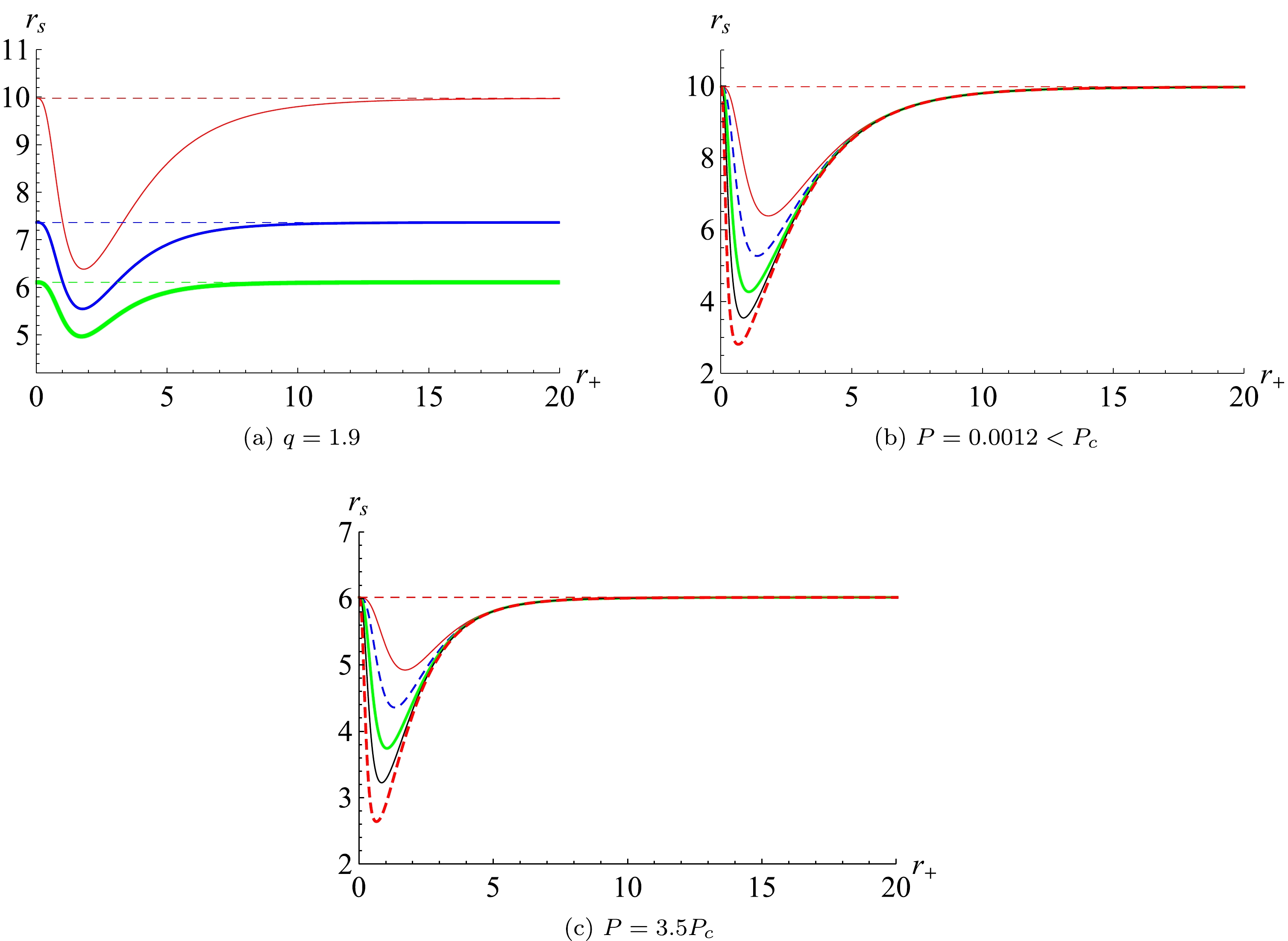
Figure 5. (color online) Non-linear YM charge parameter set to
$ \gamma=1.5 $ . Left plot: pressure set to$ P_c-0.0001,\; P_c, $ and$ 1.5P_c $ from bottom to top. Middle and right plots: YM charge varies from$ 1.9 $ to$ 1 $ from bottom to top. The horizontal thin dashed lines stand for the limited value of the shadow radius.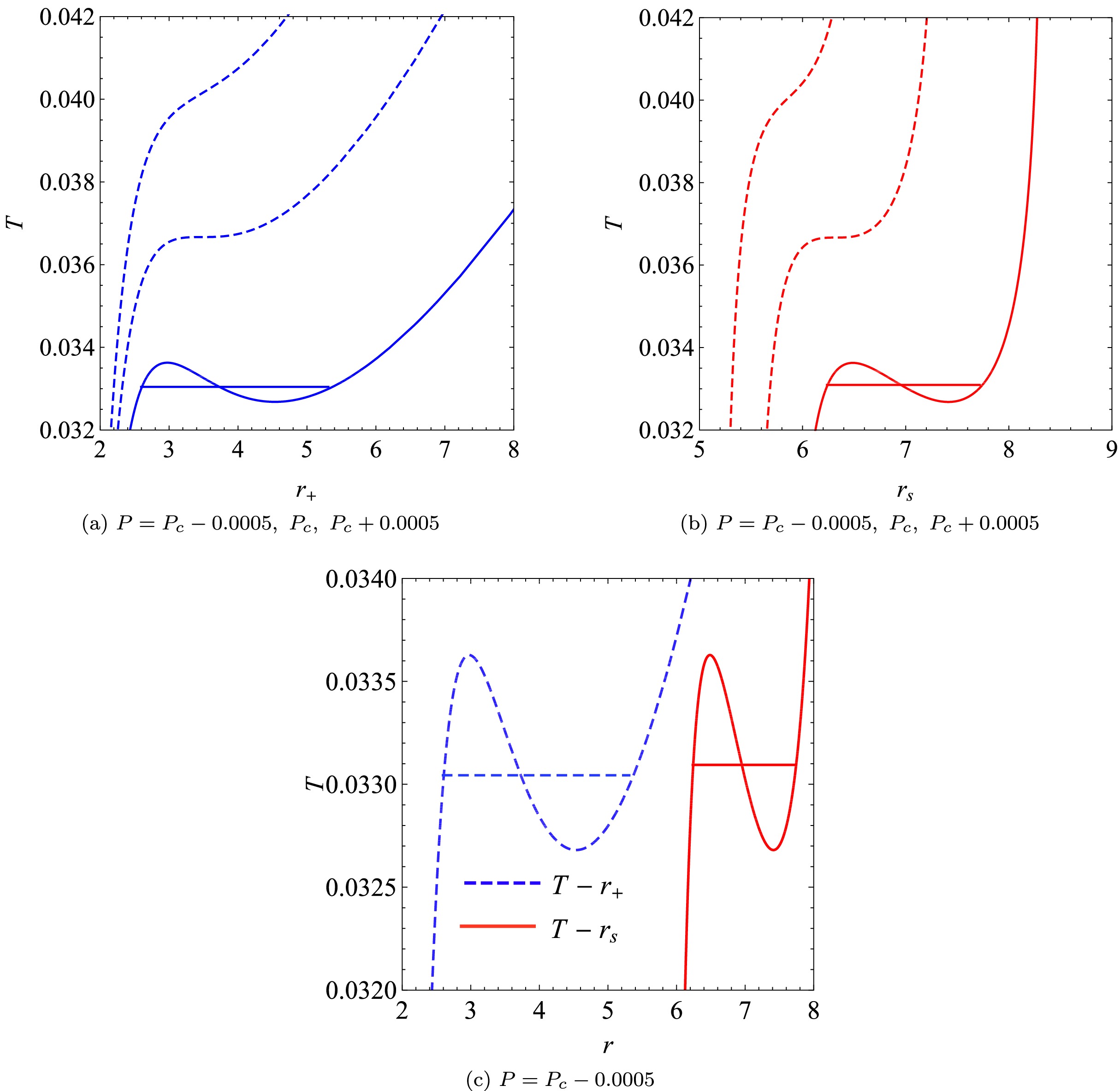
Figure 6. (color online) Parameters set to
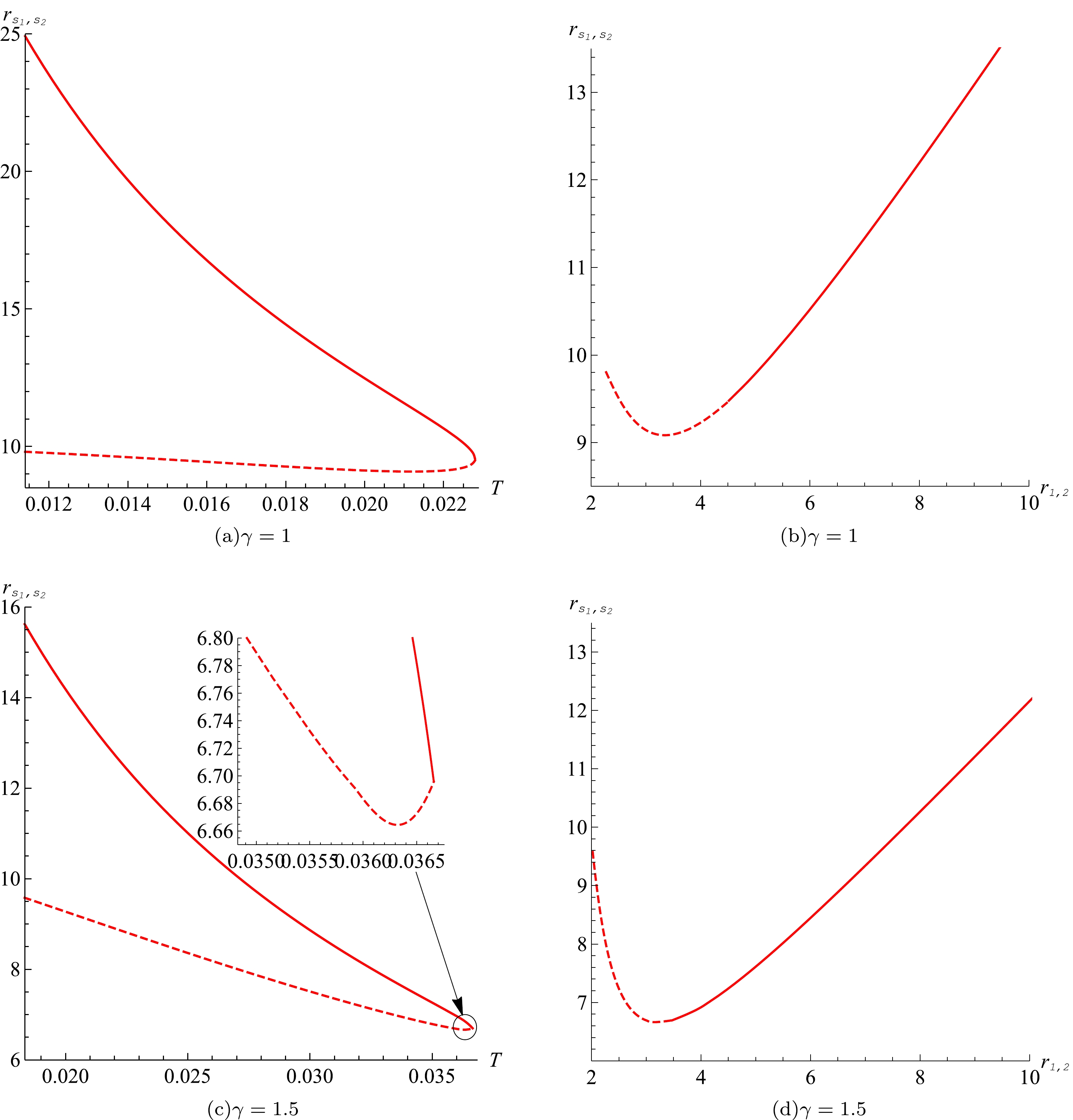
$ \gamma=1.5,\; q=1.9 $ . A static observer is assumed at$ r_0=100 $ .To illustrate the relationship between the black hole phase transition and shadow radius in both cases, i.e.,
$ \gamma=1,1.5 $ , plots of the shadow radii for two coexistent black hole phases as functions of temperature and horizon radius are shown in Fig. 7. For the large coexistent phase, its shadow radius decreases with increasing temperature, while it increases with the horizon radius. However, for the small coexistent phase, its shadow radii as functions of temperature and horizon radius have a local minimum value. A new phase transition may exist at this local minimum point. -
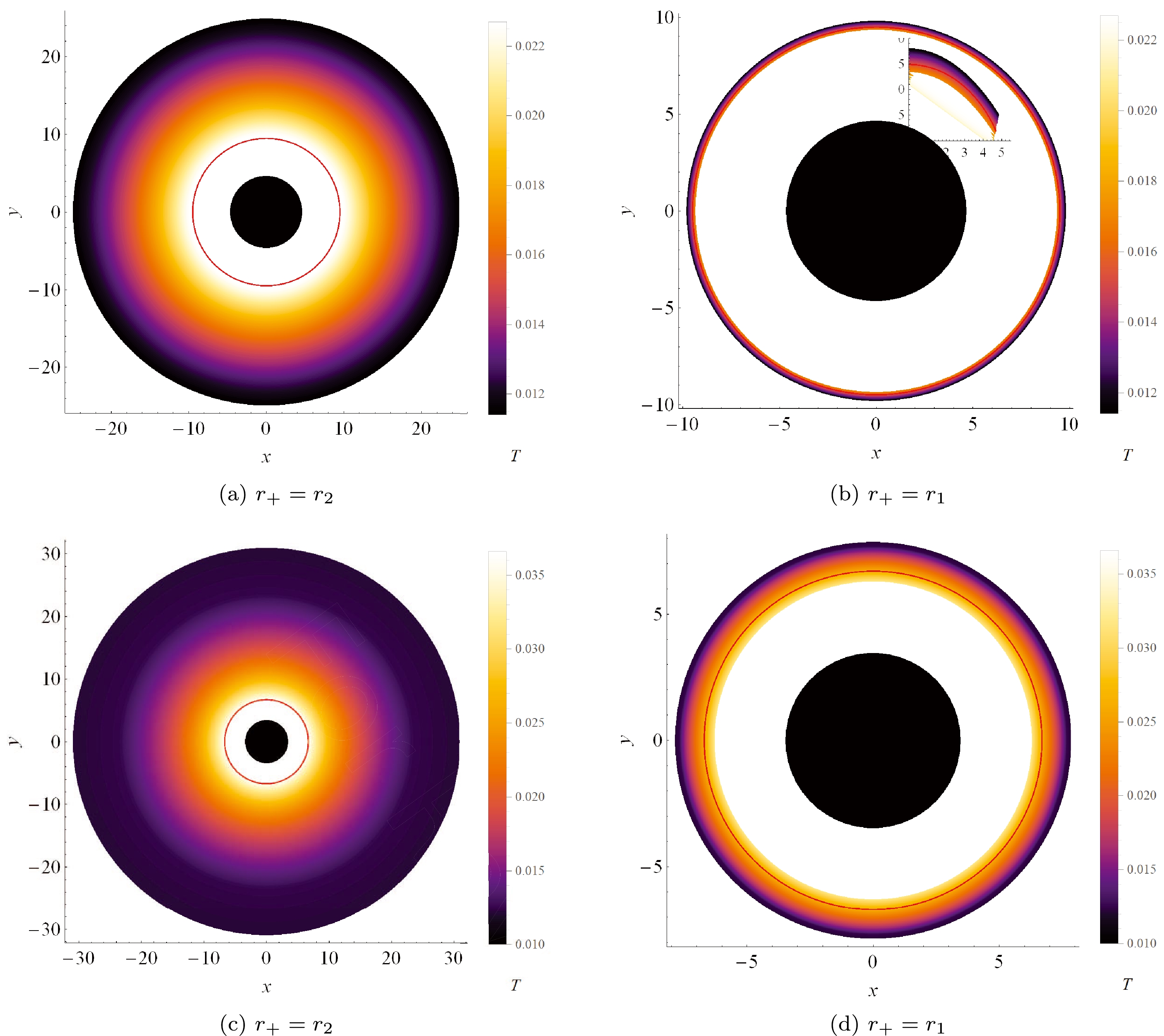
Given that the shape of a spherically symmetric black hole shadow is circular for any observer [70], we consider a thermal profile in a two-dimensional plane to more intuitively present the relationship between the BH phase structure and its shadow for EPYM AdS black holes. According to a previous study [20], the shadow boundary curve at the celestial coordinate reads as follows:
$ \begin{aligned}[b] x=&\lim_{r\rightarrow \infty}\left(-r^2\sin\theta_0\frac{{\rm d}\phi}{{\rm d}r}\right)_{\theta_0\rightarrow \pi/2},\; \;\\ y=&\lim_{r\rightarrow \infty}\left(r^2\frac{{\rm d}\theta}{{\rm d}r}\right)_{\theta_0\rightarrow \pi/2}. \end{aligned} $

(33) For
$ \gamma=1 $ and$ 1.5 $ , the shadow contours of coexistent large and small black hole phases as a function of temperature for a static spatial infinity observer are depicted in Fig. 8.These results show that the size of the BH shadow depends on the temperature. When
$ T<T_c $ , the shadow radius for the coexistent large black hole phase decreases monotonically with temperature until reaching the critical shadow, which is in the large radius region corresponding to supercritical black hole phases; the red thick curves represent the critical shadow; for small black hole phases, the shadow radii find support in the small radius region; the inner black disks represent the coexistent large and small black hole phases for different temperatures. It is evident that for coexistent small phases, the shadow radius slightly decreases with temperature until reaching its minimum value and then increases abruptly with higher temperatures. These behaviors are consistent with those presented in Fig. 7. -
In the present work, we examined the relationship between the thermodynamic phase transition of the four-dimensional charge Einstein-power-Yang-Mills (EPYM) AdS black hole and its shadow. This provides a new approach to link gravity and thermodynamics of black holes.
First, we presented the characteristics of EPYM AdS black hole phase transitions: the critical point depends on the YM charge and non-linear YM charge parameter under the conditions
$ \gamma>1/2 $ and$ \gamma\neq3/4 $ . Given that the critical point represents the boundary of the coexistent phases, it is key to probe the black hole phase structure. Then, we investigated the null geodesics of a photon in the equatorial plane of EPYM AdS black hole background. By analyzing the effective potential of photon orbits with certain parameters, we obtained the photon sphere radius and impact parameter (angular momentum of the photon sphere). For a static observer at infinity, the corresponding black hole shadow can be directly expressed as a function of the photon sphere radius, that is, the shadow is related to the black hole horizon. The results show that non-monotonic behaviors appear in$ T-r_s $ and$ r_s-r_{+} $ diagrams. This indicates that there exists a certain relationship between the shadow and phase transition of this system. In addition, we presented the influence of the non-linear YM charge parameter γ on the shadow.Finally, we further explored the relationship between shadow, temperature, and two-existent black hole phases. Relevant conclusions can be summarized as follows:
● For an isobar process of this system, the shadow radius as a function of the black hole horizon exhibits a non-monotonic behavior with certain parameters. In the
$ r_s-r_+ $ plane, the local stable minimum might indicate a new phase transition different from the black hole phase transition. Furthermore, for a given pressure, the limitations of the shadow radius with$ r_+\rightarrow0,\infty $ are the same. This means that for$ r_+\rightarrow0,\infty $ the limitation of the shadow radius does not depend on the charge information (q and γ) carried by the system; it only depends on the pressure.● For a given pressure below the critical value, there exist two extreme points in the
$ T-r_s $ plane. Both extreme points coincide with each other. When the pressure is larger than the critical one, there is no extreme point. These behaviors of the shadow radius are consistent with that of black hole phase transitions. Therefore, the behavior of the photon sphere can be regarded as a probe to reveal the thermodynamic phase transition information of black holes.● For the same set of parameters, the phase transition temperature from the viewpoint of the shadow radius is slightly higher than that from the viewpoint of the black hole horizon; this may be caused by the gravitational effect and non-linear YM charge term.
● At the coexistent curve of
$ T-P $ , the shadow radius for the coexistent large black hole phase decreases monotonically with temperature until reaching the critical shadow, which corresponds to the supercritical black hole phases; for the coexistent small black hole phases, the shadow radius slightly decreases with temperature until reaching a minimum value and then increases abruptly with temperature. These behaviors are consistent regardless of the$ r_{s_1,s_2}-r_{1,2} $ planes and thermal profiles.This analysis strongly supports our conjecture that there exists a relationship between the null geometry and thermodynamic phase transition for EPYM AdS black holes. It further supports the link between gravity and thermodynamics of black holes and provides a possible approach to describe the strong gravitational effect from a thermodynamic viewpoint.
Currently, EHT observations are providing certain information about spinning black holes; however, no data related to shadows of static black holes are available yet. In this work, we have theoretically presented the corresponding information of static black holes from their shadow. In future studies, we expect to have more precise observational results to distinguish different black holes, including static black holes. We will also explore theoretically possible results of various black holes from their thermal properties that can be tested using future observational data from EHT.
-
We would like to thank Prof. Ren Zhao, Meng-Sen Ma, and Yu-Peng Zhang for their indispensable discussions and comments.
Shadow thermodynamics of non-linear charged Anti-de Sitter black holes
- Received Date: 2022-07-05
- Available Online: 2022-12-15
Abstract: It is well known that when vacuum polarization emerges in quantum electrodynamics, the non-linear interaction between electromagnetic fields should be considered. Moreover, the corresponding field of non-linear electrodynamics can have important effects on black hole physics. In this work, we focus on the relationship between an observable quantity, that is, the shadow radius, and the first-order phase transition of non-linear charged AdS black holes in the framework of Einstein-power-Yang-Mills gravity. The results show that, under a certain condition, there exists a first-order phase transition from the viewpoint of both the shadow radius and horizon radius, which depend on temperature (or pressure). From the viewpoint of the shadow radius, the phase transition temperature is higher than that from the viewpoint of the horizon radius under the same condition. This may be due to the non-linear Yang Mills charge and the gravitational effect. This indicates that the shadow radius can be regarded as a probe to reveal the thermodynamic phase transition information of black holes. The thermal profiles of coexistent large and small black hole phases when the system is undergoing the phase transition are presented for two different values of the non-linear Yang Mills charge parameter:






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: