-
The images of Sagittarius A* in our galaxy provide new opportunities for testing the validity of gravity theories and proving the existence of the thermodynamic phase transition (PT) of a black hole (BH) [1–7]. BH thermodynamics has been researched since the 1970s [8–11], and the Hawking-Page PT was first found in 1983 [12]. In the current century, owing to the AdS/CFT correspondence [13–15], the thermodynamics of AdS BHs has been a widely researched topic in physics [16–21]. In extended phase space, the cosmological constant can be regarded as the pressure of a BH thermal system, i.e.,
$ P=-\Lambda / 8 \pi $ [13, 17, 18]. The research shows that there could exist some special PTs associated with AdS BHs [22–40]. The$ P-V $ criticality of charged AdS BHs was studied by Kubiznak et al., and the results showed that there exists a van der Waals (vdW)-like PT and that the charged AdS BH system bears a resemblance to the liquid-gas system [22]. At present, more different types of AdS BH PTs are being studied, such as the reentrant PT (RPT) and the triple point PT [24, 25, 27]. For an exhaustive overview of the thermodynamic PT of AdS BHs, one can refer to Ref. [41].For AdS BHs, an interesting question is how to understand the underlying kinetics of BH PTs. Recently, Li et al. used the Gibbs free landscape to investigate the dynamical properties of the Hawking-Page PT for Schwarzschild AdS BHs and the vdW-like PT for Reissner-Nordström (RN) AdS BHs [42, 43]. In the case of the Hawking-Page PT, the thermal AdS space phase can transit to the large Schwarzschild AdS BH phase due to thermal fluctuations, and the probability evolution can be researched by applying the Fokker-Planck equation with the reflecting boundary condition [42]. For the vdW-like PT, Li et al. calculated the Fokker-Planck equation with the reflecting and absorbing boundary conditions to study the switching dynamics of the BH state [43].
Following the works of Li et al., this method was generalized to rotating BHs and beyond-GR BHs [44–48]. In the case of a Kerr AdS BH, Yang et al. found that the BH microstructure can be understood via the dynamical properties of BH PTs [44]. For RN AdS BH surrounded by quintessence, Lan et al. studied the impact of the quintessence dark energy on the dynamical properties of BH PTs [47]. The results show that the mean first passage time is not a simple monotonic relationship with respect to the state parameter quintessence dark energy, and that there exists a local maximum value.
Inspired by these pioneering works, we extend the works of Li et al. to a charged AdS BH with a global monopole. During a PT in the early universe, a global monopole could be generated from the breaking of a global
$ O(3) $ symmetry to$ U(1) $ [49]. Barriola and Vilenkin studied a BH with a global monopole and found that the monopole can generate a deficit solid angle in space [50]. Recently, Soroushfar and Upadhyay used geometrical thermodynamics to study the thermodynamic PT of charged AdS BH with a global monopole and found that the monopole parameter η can affect the thermodynamic PT [51]. In this study, we inspect the effects of a global monopole on the thermodynamic PT of a charged AdS BH by studying the probability evolution and the first passage process of the BH state.This paper is organized as follows: In Sec. II, the thermodynamics of a charged AdS BH with a global monopole is briefly reviewed. In Sec. III, we study the thermodynamic PT of a charged AdS BH with a global monopole, focusing on the probability evolution and the first passage process of the BH state. The conclusions are given in Sec. IV. In this paper, we employ the units
$ G_{\mathrm{N}}=\hbar=\kappa_{\mathrm{b}}=c=1 $ . -
In this section, we present a brief overview of a charged AdS BH with a global monopole and its thermodynamics. The Lagrangian density of a charged AdS BH with a global monopole is [50]
$ \begin{equation} \mathcal{L}=R-2 \Lambda+\frac{1}{2} \partial_{\mu} \phi^{a} \partial^{\mu} \phi^{* a}-\frac{\gamma}{4}\left(\phi^{a} \phi^{* a}-\eta_{0}^{2}\right)^{2}, \end{equation} $

(1) where γ is a constant and
$ \eta_{0} $ is the energy scale of symmetry breaking. The parameter$ \phi^{a} $ represents a triplet of the scalar field as$ \begin{equation} \phi^{a}=\eta_{0} h(\tilde{r}) \frac{\tilde{x}^{a}}{\tilde{r}} \end{equation} $

(2) with the boundary conditions [52, 53]
$ \begin{equation} \eta_{0} h(0)=0, \quad \lim \limits_{\tilde{r} \rightarrow \infty} \eta_{0} h(\tilde{r})=\pm \eta_{0}. \end{equation} $

(3) Here,
$ {x}^{a} $ is the Cartesian coordinate and r is the spherical coordinate, which satisfy$ \tilde{x}^{a} \tilde{x}^{a}=\tilde{r}^{2} $ . The metric of a charged AdS BH with a global monopole is given by [50]$ \begin{equation} \mathrm{d} s^{2}=-f(\tilde{r}) \mathrm{d} \tilde{t}^{2}+\frac{1}{f(\tilde{r})} \mathrm{d} \tilde{r}^{2}+\tilde{r}^{2}\left(\mathrm{d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right), \end{equation} $

(4) where the metric function
$ f(\tilde{r}) $ is$ \begin{equation} f(\tilde{r})=1-8 \pi \eta_{0}^{2}-\frac{2 \tilde{m}}{\tilde{r}}+\frac{\tilde{q}^{2}}{\tilde{r}^{2}}+\frac{\tilde{r}^{2}}{l^{2}}. \end{equation} $

(5) Here,
$ \tilde{m} $ is the BH mass,$ \tilde{q} $ is the BH charge, and$ l(=\sqrt{-\frac{\Lambda}{3}}) $ is the AdS curvature radius. For convenience, we introduce the following coordinate transformation:$ \begin{equation} \tilde{t}=\left(1-8 \pi \eta_{0}^{2}\right)^{-1 / 2} t,\; \; \; \; \tilde{r}=\left(1-8 \pi \eta_{0}^{2}\right)^{1 / 2} r, \end{equation} $

(6) and new parameters
$ \begin{equation} m=\left(1-8 \pi \eta_{0}^{2}\right)^{-3 / 2} \tilde{m}, \; \; q=\left(1-8 \pi \eta_{0}^{2}\right)^{-1} \tilde{q}, \; \; \eta^{2}=8 \pi \eta_{0}^{2}. \end{equation} $

(7) Therefore, metric (4) can be rewritten as
$ \begin{equation} \mathrm{d} s^{2}=-f(r) \mathrm{d} t^{2}+\frac{1}{f(r)} \mathrm{d} r^{2}+\left(1-\eta^{2}\right) r^{2}\left(\mathrm{\; d} \theta^{2}+\sin ^{2} \theta \mathrm{d} \phi^{2}\right), \end{equation} $

(8) where
$ \begin{equation} f(r)=1-\frac{2 m}{r}+\frac{q^{2}}{r^{2}}+\frac{r^{2}}{l^{2}}. \end{equation} $

(9) It is noteworthy that the non-vanishing monopole parameter η will result in a solid angle deficit in Eq. (8). Therefore, the ADM mass and the electric charge of the BH are modulated by the monopole parameter η:
$ \begin{equation} M=\left(1-\eta^{2}\right) m, \quad\; \; \; \; \; \; \; Q=\left(1-\eta^{2}\right) q. \end{equation} $

(10) The event horizon
$ r_{h} $ can be obtained by solving$ f\left(r\right)=0 $ , and then the ADM mass M can be rewritten as$ \begin{equation} M=\frac{Q^{2}}{2 r_{h}-2 \eta^{2} r_{h}}-\frac{1}{2}\left(\eta^{2}-1\right) r_{h}\left(1+ l^{-2} r_{h}^{2}\right). \end{equation} $

(11) The temperature and entropy of the BH can be expressed as
$ \begin{equation} T=\frac{1}{4 \pi r_{h}}\left(1+\frac{3 r_{h}^{2}}{l^{2}}-\frac{Q^{2}}{\left(1-\eta^{2}\right)^{2} r_{h}^{2}}\right),\; \; \; \; \; \; S=\pi\left(1-\eta^{2}\right) r_{h}^{2}. \end{equation} $

(12) Furthermore, in the extended phase space (i.e.,
$P= 3/8 \pi l^{2}$ ), we get$ \begin{equation} \mathrm{d} M= T\mathrm{d}S+\Phi\mathrm{d}Q+V\mathrm{d}P, \end{equation} $

(13) where
$ \begin{equation} \begin{aligned} \Phi=\frac{q}{r_{h}}, \; \; \; \; \; \; \; \; \; V=\frac{4}{3} \pi\left(1-\eta^{2}\right) r_{h}^{3}. \end{aligned} \end{equation} $

(14) The Smarr relation still holds, as follows:
$ \begin{equation} M=2(T S-V P)+\Phi Q. \end{equation} $

(15) Note that M in Eq. (15) is now regarded as the enthalpy of the BH.
Therefore, for a charged AdS BH with a global monopole, the equation of state is given by
$ \begin{equation} P=\frac{T}{2 r_{h}}-\frac{1}{8 \pi r_{h}{ }^{2}}+\frac{Q^{2}}{8 \pi\left(1-\eta^{2}\right) r_{h}{ }^{4}}. \end{equation} $

(16) By solving the equations
$ \left(\partial_{r_{\mathrm{h}}} P\right)_{T}=0 $ and$ \left(\partial_{r_{\mathrm{h}}, r_{\mathrm{h}}} P\right)_{T}=0 $ , one can obtain the critical point$ \begin{equation} P_{c}=\frac{\left(1-\eta^{2}\right)^{2}}{96 \pi Q^{2}},\; \; r_{c}=\frac{\sqrt{6} Q}{\sqrt{1-2 \eta^{2}+\eta^{4}}}, \; \; T_{c}=\frac{\sqrt{\left(1-\eta^{2}\right)^{2}}}{3 \sqrt{6} \pi Q}. \end{equation} $

(17) In this paper, we set
$ Q=1 $ for convenience.As shown in Fig. 1, the evolution of the BH temperature over the BH radius
$ r_{h} $ is closely related to the value of the pressure P. When$ P\geq P_{c} $ , T is a monotonic function of the radius$ r_{h} $ ; however, for$ P<P_{c} $ , there is a local minimum temperature and a local maximum temperature. The local minimum and maximum of the BH temperature T are determined by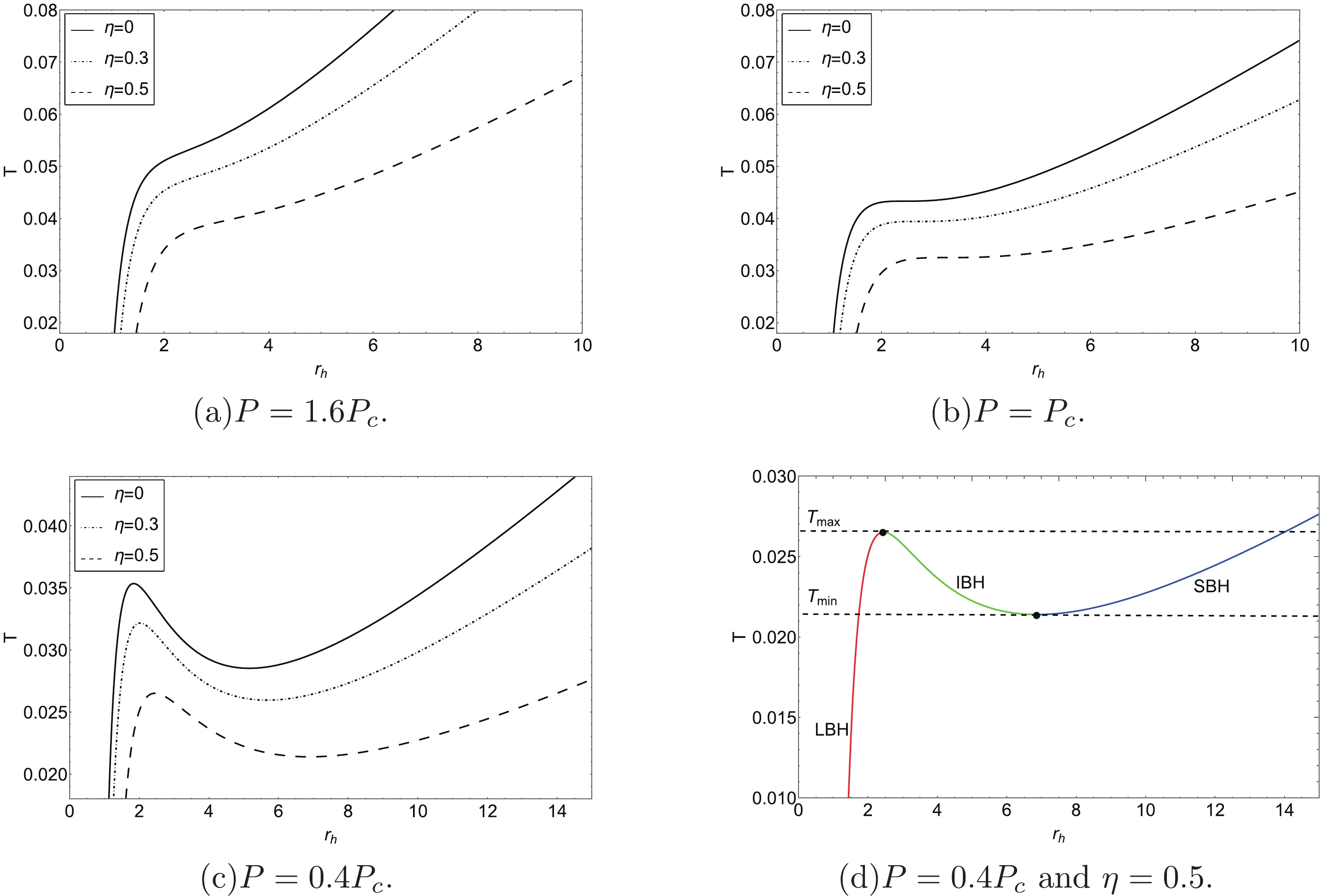
Figure 1. (color online) The temperature T as a function of the BH radius
$ r_{h} $ . The pressures in the first three panels are selected as (a)$ P=1.6P_c $ ; (b)$ P=P_c $ ; (c)$ P=0.4P_c $ . There are three sets of monopole parameters ($ \eta=0,\; 0.3,\; 0.5 $ ) for comparison. The last panel corresponds to the dashed line in (c).$ \begin{equation} \frac{\partial T}{\partial r_{h}}=0, \end{equation} $

(18) which yields
$ \begin{equation} r_{\min / \max }=\frac{1}{4} \sqrt{\frac{1-\eta^{2} \pm \sqrt{1-96 P \pi Q^{2}-2 \eta^{2}+\eta^{4}}}{P \pi-P \pi \eta^{2}}}. \end{equation} $

(19) The positive (negative) sign in Eq. (19) corresponds to the BH radius
$ r_{\min} $ ($ r_{\max} $ ). By substituting Eq. (19) into Eq. (16), we get the local minimum and maximum of the BH temperature:$ \begin{equation} T_{\min / \max }=\frac{-64 P \pi Q^{2} \pm 2\left(-1+\eta^{2}\right)\left(1-\eta^{2}+\sqrt{-96 P \pi Q^{2}+\left(-1+\eta^{2}\right)^{2}}\right)}{P \sqrt{\pi}\left(-1+\eta^{2}\right)^{2}\left(\dfrac{1-\eta^{2}+\sqrt{-96 P \pi Q^{2}+\left(-1+\eta^{2}\right)^{2}}}{P-P \eta^{2}}\right)^{3 / 2}}, \end{equation} $ 
(20) where the positive (negative) sign in Eq. (20) corresponds to the local minimum
$ T_{\min} $ (the local maximum$ T_{\max} $ ). When$ T_{\min }<T<T_{\max} $ , there are three branches: small BH (SBH) state, intermediate BH (IBH) state, and large BH (LBH) state (see Figs. 1(c) and 1(d)). It is worth noting that the IBH state is not stable, and there exists a first-order SBH/LBH PT. -
In the study of BH thermodynamics, Gibbs free energy is usually used to investigate the thermodynamic PT of BHs [22–27, 29–32, 34, 38]. For a charged AdS BH with a global monopole, the Gibbs free energy is given by
$ \begin{equation} G=H-T S=\frac{1}{6} r_{h}\left(3+8 P \pi r_{h}^{2}-6 \pi r_{h} T\right)\left(1-\eta^{2}\right)+\frac{Q^{2}}{2 r_{h}\left(1-\eta^{2}\right)}. \end{equation} $

(21) The
$ G-T $ diagram of a charged AdS BH with a global monopole is plotted in Fig. 2(a) with$ \eta=0.5 $ and$ P=0.4P_{c} $ , from which we can see that there exist three branches of the BH state and a swallowtail behavior. The blue, green, and red lines represent the SBH, IBH, and LBH branches, respectively. The temperature corresponding to the intersection (see point A(C) in Fig. 2(a)) of the SBH branch and the LBH branch is about$T_{\rm A}=T_{\rm C}=$ 0.022355. Point B is in the state of IBH, and points A and C are in the states of SBH and LBH, respectively.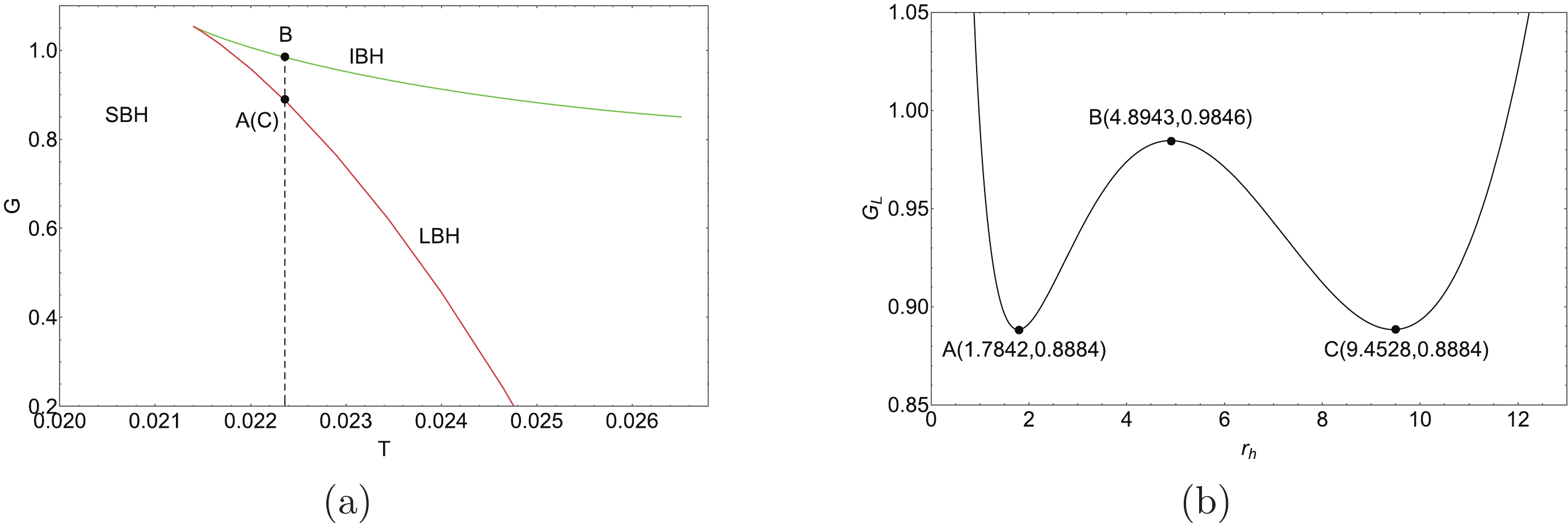
Figure 2. (color online) Gibbs free energy of a charged AdS BH with a global monopole. For all plots, we set
$ \eta=0.5 $ and$ P=0.4P_{c} $ . The left panel is the$ G-T $ diagram, and the right panel is the$ G_{L}-r_{h} $ diagram with$ T_{E}=0.022355 $ .Recently, the concept of the Gibbs free energy landscape was introduced to study the dynamical properties of the thermodynamic PH of BHs [42, 43]. In the Gibbs free energy landscape, the Hawking temperature of a BH is replaced by the temperature of the ensemble. Therefore, for a charged AdS BH with a global monopole, the Gibbs free energy
$ G_{L} $ can be expressed as$ \begin{aligned}[b] G_{L}=&H-T_{E} S=-\frac{1}{2} r_{h}\left(-1+\eta^{2}\right)-\frac{4}{3} P \pi r_{h}^{3}\left(-1+\eta^{2}\right)\\&+\pi r_{h}^{2} T_{E} \left(-1+\eta^{2}\right)+\frac{Q^{2}}{2 r_{h}-2 r_{h} \eta^{2}}, \end{aligned} $

(22) where
$ T_{E} $ is the temperature of the ensemble. The$ G_L-r_h $ diagram is plotted in Fig. 2(b) with$ \eta=0.5 $ ,$ P=0.4P_{c} $ , and$ T_{E}=0.022355 $ . As can be seen, the$ G_{L}-r_{h} $ diagram has a double-well shape and there exist two equivalent local minimums and a local maximum. As the SBH and LBH correspond to the local minimums of the Gibbs free energy, they are stable. The IBH, which has the local maximum of the Gibbs free energy, is unstable. -
Recently, the Fokker-Planck equation was proposed for studying the probability evolution of a BH phase transition, which is given by [42, 43, 54–58]
$ \begin{equation} \frac{\partial \rho(r_{h}, t)}{\partial t}=D \frac{\partial}{\partial r_{h}}\left\{{\rm e}^{-\beta G_{L}(r_{h})} \frac{\partial}{\partial r_{h}}\left[{\rm e}^{\beta G_{L}(r_{h})} \rho(r_{h}, t)\right]\right\}, \end{equation} $

(23) where
$ G_{L} $ is a function of the radius$ r_{h} $ modulated by the BH temperature,$ \rho(r_{h}, t) $ is the probability distribution of the BH state in the ensemble,$ \beta=\dfrac{1}{k_{\mathrm{B}} T} $ represents the inverse temperature, and$ D=\dfrac{k_{\mathrm{B}} T}{\zeta} $ is the diffusion coefficient. As usual, the Boltzman constant$ k_{\mathrm{B}} $ and the dissipation coefficient ζ are set to$ 1 $ .Mathematically, the Fokker-Planck equation can be calculated by choosing specific boundary conditions. To study the probability evolution of the BH phase transition, we use the reflecting and absorbing boundary conditions at
$ r_{h}=r_{0} $ for calculating the Fokker-Planck equation, which can be given as$ \begin{equation} \begin{aligned} \beta G_{\mathrm{L}}^{\prime}\left(T, P, r_{0}\right) \rho\left(r_{0}, t\right)+\rho^{\prime}\left(r_{0}, t\right) =0, \\ \rho\left(r_{0}, t\right)=0. \end{aligned} \end{equation} $

(24) Here, the prime indicates the time derivative.
We first consider the reflecting boundary condition, for which there are two boundaries at
$ r_{h}=0 $ and$ r_{h}=\infty $ . The reflecting boundary condition preserves the normalization of the probability distribution. The Gaussian wave packet is selected as the initial wave packet, which is given by$ \begin{equation} \rho(r_{h}, 0)=\frac{1}{\sqrt{\pi} a} {\rm e}^{-\frac{\left(r_{h}-r_{s/m/l}\right)^{2}}{a^{2}}}, \end{equation} $

(25) where the parameter a is set to
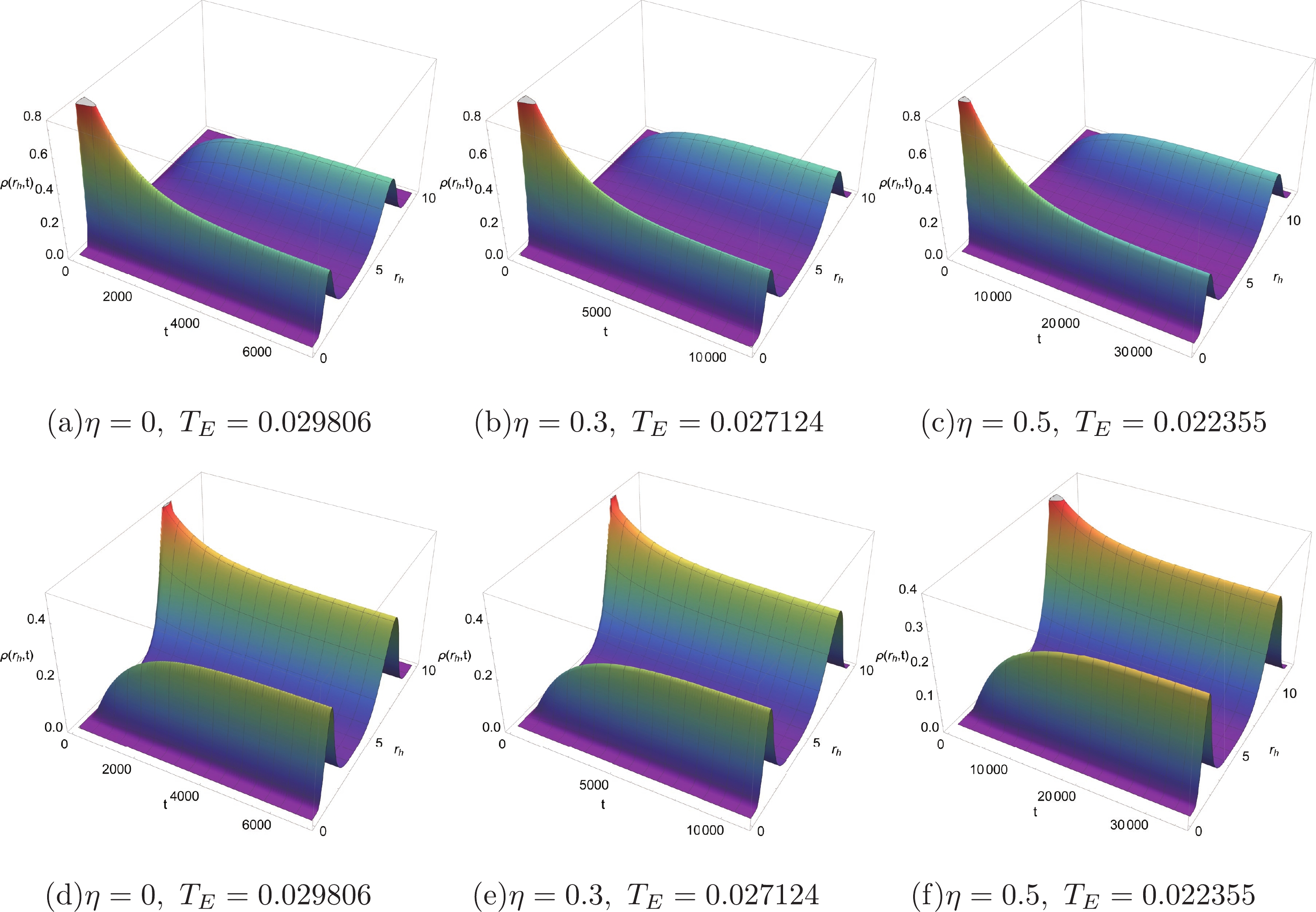
$ 1 $ and the Gaussian wave packet is located at the SBH/IBH/LBH radius$ r_{s/m/l} $ .In Fig. 3, we plot the probability distribution diagrams of a charged AdS BH with a global monopole via numerical calculation. Note that in order to avoid numerical instability, we replaced the boundaries at
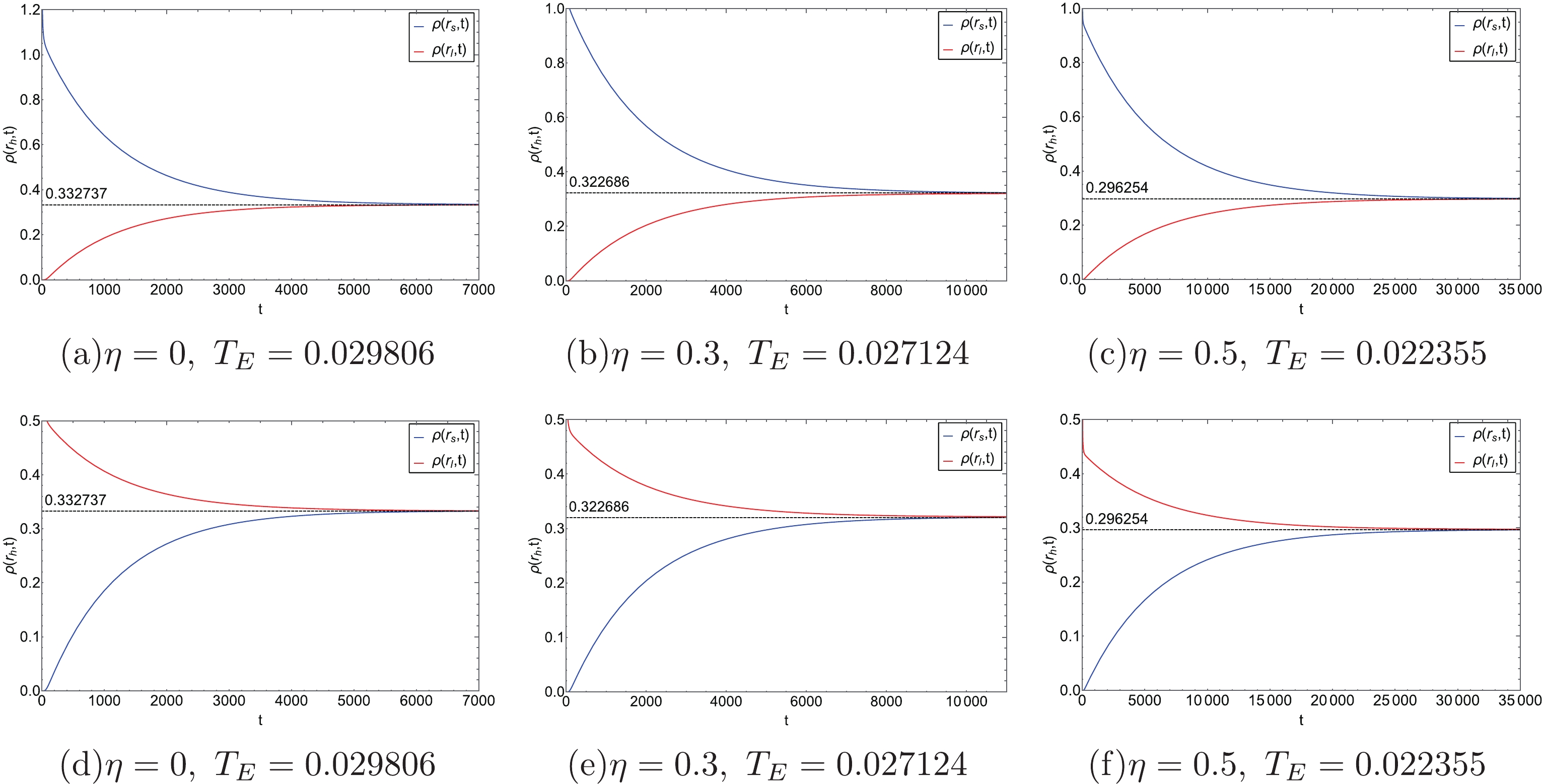
$ r_{h}=0 $ and$ r_{h}=\infty $ with$ r_{h}=0.1 $ and$ r_{h}=12 $ , respectively. From Figs. 3(a), 3(b), and 3(c), it can be seen that when the probability distribution evolves from the SBH state, the probability distribution of the SBH state decreases gradually, while the probability distribution of the LBH state increases from$ \rho\left(r_{l}, t\right)=0 $ . In Figs. 3(d), 3(e), and 3(f), we can observe a similar phenomenon for the case where the probability distribution evolves from the LBH state. More intuitive descriptions of the time evolution of the probability distribution for the SBH and LBH states are shown in Fig. 4. When the Gibbs free energy of the SBH state is equal to that of the SBH state, the probability distribution of the black hole states is a steady-state distribution. In this case, the probability distributions of the SBH and LBH states are exactly equal. No matter what the value of the monopole parameter η is, the system will always reach a steady-state distribution after a period of time. Moreover, according to Fig. 4, it is also clear that the global monopole influences the thermodynamic PT of BHs. On comparing Figs. 4(a), 4(b), and 4(c), it can be seen that an initial SBH state with a global monopole (such as$ \eta=0.5 $ and$ \eta=0.3 $ ) evolves more slowly than the one without a global monopole ($ \eta=0 $ ). For the initial LBH state with a global monopole, the same conclusion can be obtained (see Figs. 4(d), 4(e), and 4(f)). Besides, as the monopole parameter η increases, it takes longer for the system to reach equilibrium. -
In the BH PT, the process of the initial SBH (LBH) state reaching the IBH state for the first time is called the first passage process, and the time it takes is called the first passage time. In order to study the first passage process, we need to solve the Fokker-Planck equation not only with the reflecting boundary condition but also with the absorbing boundary condition
$ \rho\left(r_{m}, t\right)=0 $ . Note that$ r_{m} $ represents the radius of the IBH, which satisfies$ \begin{equation} G_{L}^{\prime}\left(T,P,r\right)|_{r_{h}=r_{m}}=0, \quad G_{L}^{\prime \prime}\left(T,P,r\right)|_{r_{h}=r_{m}}>0. \end{equation} $

(26) One can suppose that there exits a perfect absorber placed at the coordinate
$ r_{h}=r_{m} $ . When$ t \rightarrow +\infty $ , the probability$ \Sigma(t) $ decreases and tends to zero.Taking the reflecting and absorbing boundary conditions into the Fokker-Planck equation, we can solve the probability distribution
$ \rho(r_{s/l}, t) $ numerically. In the case of a transition from the LBH state to the SBH state, the reflecting and absorbing boundary conditions are located at$ r_{h}=0 $ and$ r_{h}=r_{m} $ , respectively. For the transition from the SBH state to the LBH state, the reflecting boundary condition should be located at$ r_{h}=\infty $ instead of$ r_{h}=0 $ . In Fig. 5, we plot the time evolution of the probability distribution of the first passage process for a charged AdS BH with a global monopole. It is clear from Fig. 5 that the probability distributions of both the SBH and LBH states decay quickly. Moreover, by comparing Figs. 5(a), 5(b), and 5(c), we can conclude that the probability distribution of the SBH state with a global monopole evolves more slowly than that of the one without a global monopole. In addition, as the monopole parameter η increases, it also takes longer for the system to reach equilibrium. These effects of the global monopole on the probability distribution of the BH state are consistent with the ones in Sec. III. B where we only consider the reflecting boundary condition.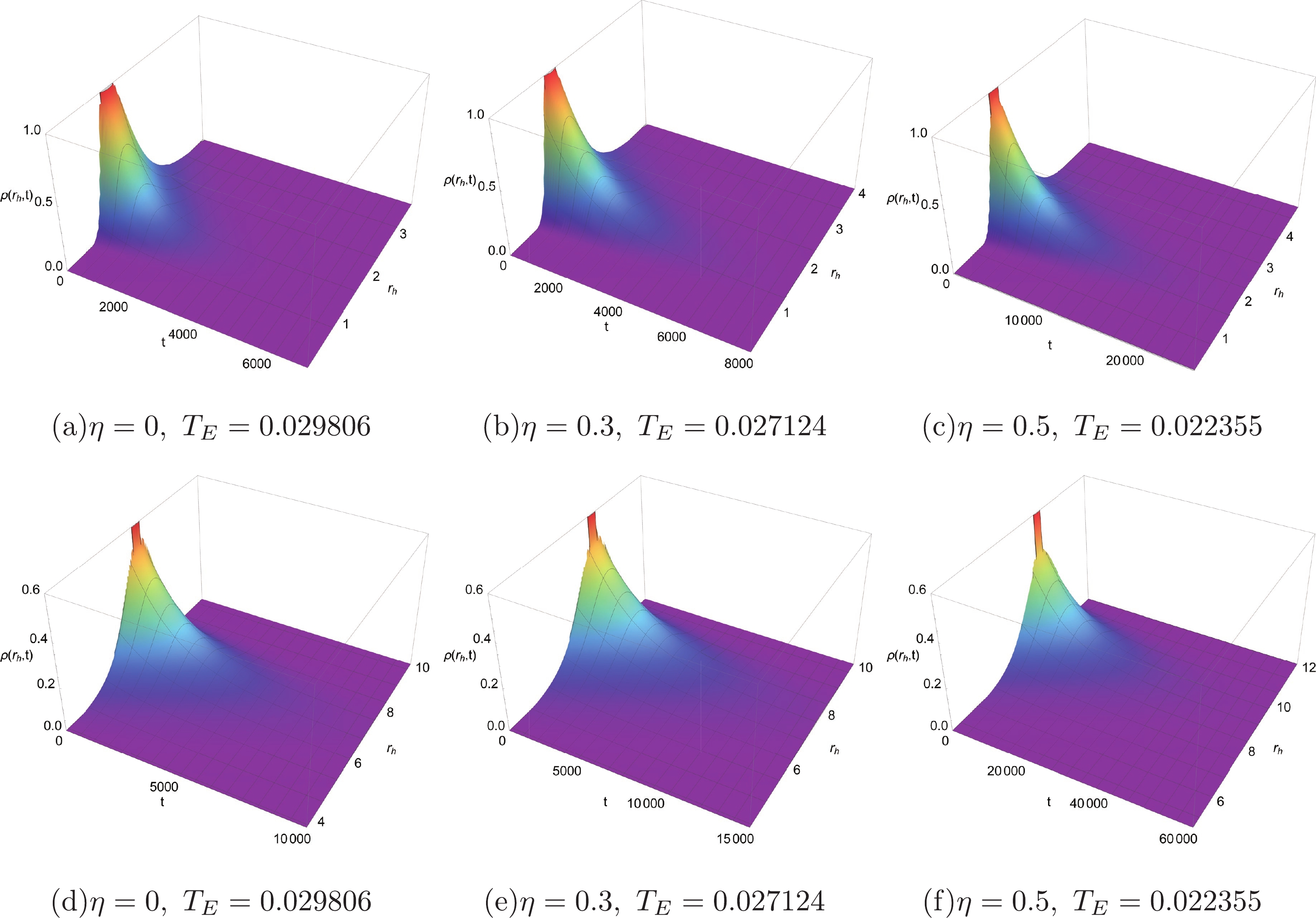
Figure 5. (color online) The distributions of probability
$ \rho(r_{h}, t) $ of the first passage process for a charged AdS BH with a global monopole. For the upper panels, the Gaussian wave packet is located at the SBH state. For the lower panels, the Gaussian wave packet is located at the LBH state.Now, we define the probability that the present state of the BH is still in the system at time t as follows:
$ \begin{equation} \Sigma(t)=\int_{0}^{r_{m}} \rho(r_{h}, t) {\rm d} r, \end{equation} $

(27) which can also be interpreted that the BH at time t has not made the first passage process.
For a charged AdS BH with a global monopole, we plot the
$ \Sigma(t)-t $ diagrams for a charged AdS BH with a global monopole are plotted in Fig. 6. One can see that$ \Sigma(t) $ vanishes after a period of time, which means that the BH has made the first passage process. It is clear that in the presence of the global monopole, the time evolution of the probability$ \Sigma(t) $ is longer. As the global monopole parameter increases, the effect is more prominent.
Figure 6. (color online) Time evolution of the probability
$ \Sigma(t) $ . In (a), the Gaussian wave packet is located at the SBH state, and (b) denotes the LBH state.Moreover, the distribution of the first passage time can be defined as [43]
$ \begin{equation} F_{p}(t)=-\left.D \frac{\partial}{\partial r_{h}} \rho(r_{h}, t)\right|_{r_{h}=r_{m}}. \end{equation} $

(28) We plot the
$ F_{p}(t)-t $ diagrams in Fig. 7. It can be seen that for each η, there is a single peak near the beginning time, which indicates that most of the first passage events are completed within a short time. It is easy to see that the impact of the global monopole on the first passage time is similar to that in the previous cases.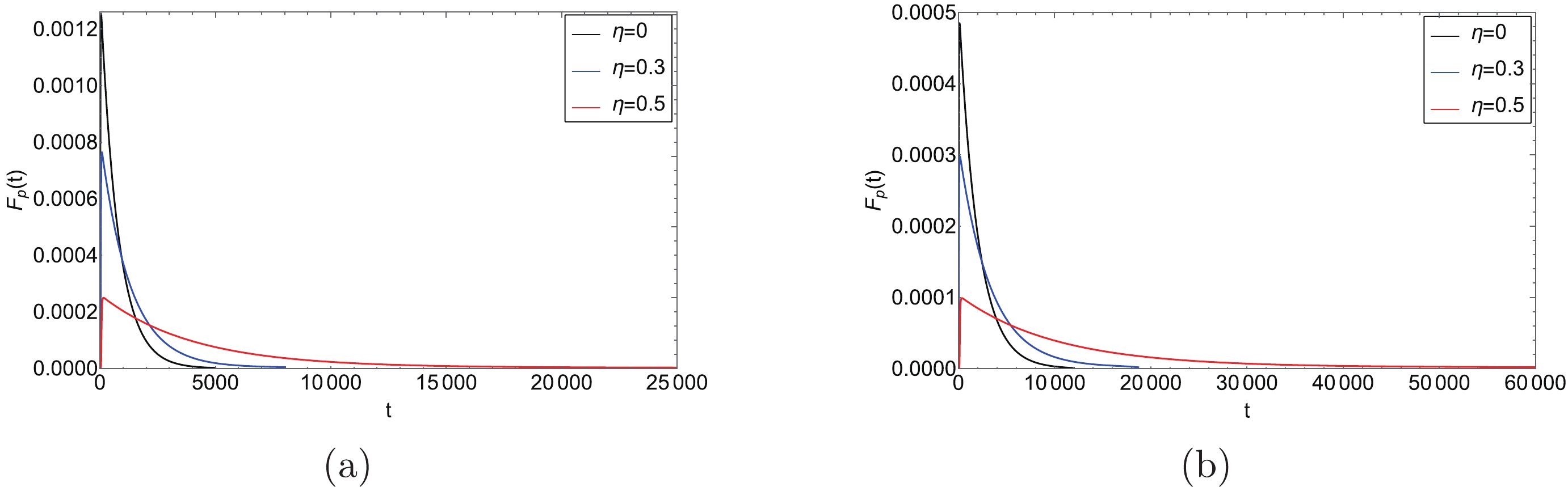
Figure 7. (color online) First passage time
$ F_{p}(t) $ . In (a), the Gaussian wave packet is located at the SBH state, and (b) denotes the LBH state.To further study the effects of the global monopole on the thermodynamic PT of the BH, we calculate the mean first passage time, which is defined as [ 43]
$ \begin{equation} \langle t\rangle=\int_{0}^{\infty} t F_{p}(t) {\rm d} t. \end{equation} $

(29) The values of the mean first passage time for different monopole parameters are listed in Table 1 . We have calculated seven sets of values for the mean first passage time and the results show that the mean first passage time increases with the monopole parameter.
η 0 0.1 0.2 0.3 0.4 0.5 0.6 $ \left.\langle t\rangle\right|_{\mathrm{SBH}\rightarrow \mathrm{LBH}} $ 

774 845 958 1278 1937 3962 11290 $ \left.\langle t\rangle\right|_{\mathrm{LBH}\rightarrow \mathrm{SBH}} $ 

1922 2086 2429 3108 5053 9933 24857 Table 1. The mean first passage time for different monopole parameters
-
The aim of this paper was to research the effects of a global monopole on the thermodynamic PT of a charged AdS BH. First, we briefly reviewed the thermodynamics of a charged AdS BH with a global monopole. Then, we studied the Gibbs free energy of the BH and the dynamical properties of the thermodynamic PH of the BH in the context of the Gibbs free energy landscape. It is found that a AdS BH with a global monopole has similar thermodynamic and dynamical characteristics to ordinary AdS BHs [42–48].
The influence of the global monopole on the BH can be analyzed by solving the Fokker-Planck equation. Therefore, we first obtained the solution of the Fokker-Planck equation with the reflecting boundary condition. The probability distribution diagrams signify that the system will eventually reach a steady state, at which the probability distributions of the SBH and LBH states are equal. Interestingly, it is found that the global monopole could slow down the decay rate of the initial BH state. Moreover, the larger the monopole parameter is, the more obvious the effect will be. In order to investigate further the impact of the global monopole on the thermodynamic PT of the AdS BH, we studied the first passage process of the dynamical PT of the BH. We resolved the Fokker-Planck equation with the reflecting and absorbing boundary conditions. The time evolution of the probability distribution with the varying monopole parameter shows that the probability distribution always decays rapidly, but that the decay rate decreases with an increase in the monopole parameter. Finally, we calculated the mean first passage time for different monopole parameters. The result shows that the mean first passage time increases monotonically as the monopole parameter increases, which means that the effect of the monopole parameter on the mean first passage time is similar to its effect on the probability distribution.
For a charged AdS BH with a global monopole, the monopole parameter has significant influence on the mean first passage time. Therefore, if we can figure out the observational effect of the mean first passage time of the thermodynamic PT in the future, we may further constrain the monopole parameter in related astronomical observations. Recently, there has been some new theoretical and observational progress on the relationship between BH thermodynamics and the BH shadow [1–6, 59–68]. The thermodynamic PT of a charged AdS BH with a global monopole might be reflected in the shadow radius, which can give an upper limit to the monopole parameter of the BH.
Effects of a global monopole on the thermodynamic phase transition of a charged AdS black hole
- Received Date: 2022-06-30
- Available Online: 2022-12-15
Abstract: We study the dynamical properties of the thermodynamic phase transition (PT) of a charged AdS black hole (BH) with a global monopole via the Gibbs free energy landscape and reveal the effects of the global monopole on the kinetics of thermodynamic PTs. First, we briefly review the thermodynamics of a charged AdS BH with a global monopole. Then, we introduce the Gibbs free energy landscape to investigate the thermodynamic stability of the BH states. Because of thermal fluctuations, the small black hole (SBH) state can transit to a large black hole (LBH) state, and vice versa. Further, we use the Fokker-Planck equation with the reflecting boundary condition to study the probability evolution of the BH state with and without a global monopole separately. It is found that for both the SBH and LBH states, the global monopole could slow down the evolution of the BH state. In addition, we obtain the relationship between the first passage time and the monopole parameter η. The result shows that as the monopole parameter η increases, the mean first passage time becomes longer for both the SBH and LBH states.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: