-
In 1983, the Hawking–Page (HP) phase transition of an AdS spacetime was proposed by Hawking and Page, which describes the evolution of spacetime in different phases [1]. Namely, with increasing temperature the dominant configuration starts from the pure thermal radiation phase, then transitions to the coexistent phase with an AdS black hole and thermal radiation, and finally to a stable black hole. Witten explained it as a confinement/deconfinement phase transition in gauge theory in Ref. [2]. It could also be understood as a solid/liquid phase transition [3] by regarding the cosmological constant as pressure
$ P = -\dfrac{\Lambda}{8\pi} = \dfrac{(n-1)(n-2)}{16\pi l^2} $ , whose conjugate variable is the thermodynamic volume. Subsequently the phase transition in the extended AdS/dS phase space has been widely considered [4–42].The phase transition of an ordinary thermodynamic system is a result of the competition between micro-components. Since black holes have similar thermal behavior to an ordinary thermodynamic system, the microstructure of black hole becomes a hot issue. The authors in Ref. [30] investigated the AdS black hole microstructure by the Ruppeiner scalar curvature following the Ruppeiner geometry [43]. The number density of the speculative black hole molecules was introduced to examine its phase transition and microstructure. This way of indicating different kinds of interaction between black hole molecules by the different values of the Ruppeiner scalar curvature was quickly generalized to other black holes [44–49].
With the development of theories of phase transitions and microstructure for various AdS black holes, people attempt to probe the dynamic process of black hole phase transitions. Recently from the viewpoint of the Gibbs free energy landscape (
$ G_{\rm L} $ ), the authors in Ref. [50] probed the dynamics of switching between the coexistent black hole phases by solving the Fokker–Planck equation with different reflection/aborption boundary conditions and initial conditions, and calculating the mean first passage time. In this approach, the phase transition is due to the thermal fluctuation and$ G_{\rm L} $ is regarded a function of black hole horizon and which is the order parameter of phase transition. Subsequently, this method was applied to the HP phase transition in Einstein gravity [51] and in massive gravity [52], and the large/small black hole phase transition in Gauss–Bonnet gravity [53, 54], in Einstein gravity [55] minimally coupled to nonlinear electrodynamics [56], and in dilaton gravity [57].The linear charged black holes in AdS spacetime [58, 59] with a second-order phase transition show a scaling symmetry: at the critical point the state parameters scale with respect to charge q, i.e.,
$ S\sim q^2,\; P\sim q^{-2}, $ $ T\sim q^{-1} $ [60, 61]. It is natural to guess whether a scaling symmetry exists in non-linear charged AdS black holes. As a generalization of the charged AdS Einstein–Maxwell black holes, it is interesting to explore new non-linear charged systems. Due to the infinite self-energy of point-like charges in Maxwell's theory [62–66], Born and Infeld proposed a generalization when the field is strong, bringing in non-linearities [67, 68]. An interesting non-linear generalization of charged black holes involves a Yang–Mills field exponentially coupled to Einstein gravity, which possesses conformal invariance and makes it easy to construct the analogues of the four-dimensional Reissner–Nordström black hole solutions in higher dimensions. Additionally several features of the Einstein-power–Yang–Mills (EPYM) gravity in extended thermodynamics have recently been studied [40, 69, 70].Inspired by these studies, we will probe the behaviour of the Gibbs free energy landscape for charged AdS black holes and explore the dynamic process of the high-/low-potential black hole phase transition in four-dimensional EPYM gravity. This work is organized as follows. In Sec. II, we briefly review the thermodynamic quantities and high-/low-potential black hole (HPBH/LPBL) phase transition of the charged EPYM AdS black hole by Maxwell's equal-area law. In Sec. III, we present the behaviour of the Gibbs free energy landscape at the phase transition point and explore the probability evolution by solving the Fokker–Planck equation with different reflection/aborption boundary conditions and initial conditions. Then we probe the dynamics of switching between the coexistent high-/low-potential black hole states by calculating the mean first passage time. Furthermore, we also investigate the effect of temperature on the dynamic properties of the phase transition. A brief summary is given in Sec. IV.
-
In this section, we will give a brief review of the thermodynamics and phase transitions of the non-linear charged AdS black hole.
-
The action for four-dimensional Einstein-power–Yang–Mills (EPYM) gravity with a cosmological constant Λ is given by [70–73]
$ I = \frac{1}{2}\int {\rm d}^4x\sqrt{g} \left(R-2\Lambda-[{\rm Tr}(F^{(a)}_{{\mu\nu}}F^{{(a)\mu\nu}})]^\gamma\right) $

(1) with the Yang–Mills (YM) field
$ F_{\mu \nu}^{(a)} = \partial_{\mu} A_{\nu}^{(a)}-\partial_{\nu} A_{\mu}^{(a)}+\frac{1}{2 \xi} C_{(b)(c)}^{(a)} A_{\mu}^{b} A_{\nu}^{c}, $

(2) where
$ {\rm Tr}(F^{(a)}_{\mu\nu}F^{(a)\mu\nu}) = \sum^3_{a = 1}F^{(a)}_{\mu\nu}F^{(a)\mu\nu} $ , R is the scalar curvature, γ is a positive real parameter,$ C_{(b)(c)}^{(a)} $ represents the structure constants of three-parameter Lie group G, ξ is the coupling constant, and$ A_{\mu}^{(a)} $ are the$ SO(3) $ gauge group YM potentials.For this system, the black hole solution of the corresponding field equation with the negative cosmological constant Λ is [74]:
$ {\rm d} s^{2} = -f(r) {\rm d} t^{2}+f^{-1} {\rm d} r^{2}+r^{2} {\rm d} \Omega_{2}^{2}, $

(3) $ f(r) = 1-\frac{2 M}{r}-\frac{\Lambda}{3} r^{2}+\frac{\left(2 q^{2}\right)^{\gamma}}{2(4 \gamma-3) r^{4 \gamma-2}}, $

(4) where
$ {\rm d}\Omega_{2}^{2} $ is the metric on unit$ 2 $ -sphere with volume$ 4\pi $ , and q is the YM charge. Note that this solution is valid for the condition where the non-linear YM charge parameter$ \gamma\neq0.75 $ and the power YM term holds the weak energy condition (WEC) for$ \gamma>0 $ [71]. In the extended phase space, Λ was interpreted as the thermodynamic pressure$ P = -\dfrac{\Lambda}{8\pi} $ . The black hole event horizon locates at$ f(r_+) = 0 $ . The parameter M represents the ADM mass of the black hole and reads [10]$\begin{aligned}[b] H =& M(S, q, P) = \frac{1}{6}\left[8 \pi P\left(\frac{S}{\pi}\right)^{3 / 2}\right.\\&\left.+3\left(\frac{S}{\pi}\right)^{({3-4 \gamma})/{2}} \frac{\left(2 q^{2}\right)^{\gamma}}{8 \gamma-6}+3 \sqrt{\frac{S}{\pi}}\right]. \end{aligned}$

(5) In our set up, this parameter is associated with the enthalpy of the system. The black hole temperature, entropy, and volume are given by [70]
$\begin{aligned}[b] T =& \frac{1}{4 \pi r_+}\left(1+8 \pi P r_+^{2}-\frac{\left(2 q^{2}\right)^{\gamma}}{2 r_+^{(4 \gamma-2)}}\right),\\ S =& \pi r_+^{2},\; \; \; \; V = \frac{4\pi r_+^3}{3}. \end{aligned} $

(6) The YM potential Ψ is given by [64]
$ \Psi = \frac{\partial M}{\partial q^{2 \gamma}} = \frac{r_+^{3-4 \gamma} 2^{\gamma-2}}{4\gamma-3}. $

(7) The above thermodynamic quantities satisfy the first law
$ {\rm d} M = T {\rm d} S+\Psi {\rm d} q^{2 \gamma}+V {\rm d} P. $

(8) The equation of state
$ P(V,T) $ for the canonical ensemble (fixed YM charge q) can be obtained from the expression of temperature as$ P = \left(\frac{4 \pi}{3 V}\right)^{1 / 3}\left[\frac{T}{2}-\frac{1}{8 \pi}\left(\frac{4 \pi}{3 V}\right)^{1 / 3}+\frac{\left(2 q^{2}\right)^{\gamma}}{16 \pi}\left(\frac{4 \pi}{3 V}\right)^{({1-4\gamma})/{3}}\right]. $

(9) -
From Eq. (9), we know the state equation of the EPYM black hole with fixed YM charge corresponds to the one of an ordinary thermodynamic system and can be written as
$ f(T,P,V) = 0 $ . Furthermore, the number of particles in the system is unchanged. Through Maxwell's equal-area law, we can construct the phase transition of the EPYM black hole in$ P-V $ ,$ T-S $ , and$ q^{2\gamma}-\Psi $ , respectively. For the same parameters, the phase transition points in$ P-V $ ,$ T-S $ , and$ q^{2\gamma}-\Psi $ should be the same. In the following we will present the phase diagram in$ T-S $ and label the phase transition point with$ T_0 $ and$ P_0 $ .For the EPYM black hole with a given YM charge q and pressure
$ P_0<P_{\rm c} $ , the entropy values at the boundary of the two-phase coexistence area are$ S_1 $ and$ S_2 $ , respectively. The corresponding temperature is$ T_0 $ , which is less than the critical temperature$ T_{\rm c} $ and is determined by the horizon radius$ r_+ $ . Therefore, from the Maxwell's equal-area law$ T_0(S_2-S_1) = \int^{S_2}_{S_1}T{\rm d}S $ and Eq. (6), we have$ \begin{aligned}[b] 2 \pi T_{0} =& \frac{1}{r_{2}(1+x)}+\frac{8 \pi P_0 r_{2}}{3(1+x)}\left(1+x+x^{2}\right)\\&-\frac{\left(2 q^{2}\right)^{\gamma} r_{2}^{1-4 \gamma}}{2(3-4 \gamma)} \frac{\left(1-x^{3-4 \gamma}\right)}{\left(1-x^{2}\right)} \end{aligned} $

(10) with
$ x = \dfrac{r_1}{r_2} $ . In addition, from the state equation we have$ T_{0} = \frac{1}{4 \pi r_{2}}\left(1+8 \pi P_0 r_{2}^{2}-\frac{\left(2 q^{2}\right)^{\gamma}}{2 r_{2}^{(4 \gamma-2)}}\right),\; \; \; \; $

(11) $ T_{0} = \frac{1}{4 \pi r_{1}}\left(1+8 \pi P_0 r_{1}^{2}-\frac{\left(2 q^{2}\right)^{\gamma}}{2 r_{1}^{(4 \gamma-2)}}\right). $

(12) From Eq. (10), we have
$ 0 = -\frac{1-x}{r_{2} x}+8 \pi P_0r_{2}(1-x)+\frac{\left(2 q^{2}\right)^{\gamma}}{2 r_{2}^{4 \gamma-1} x^{4 \gamma-1}}\left(1-x^{4 \gamma-1}\right), \; \; \; \; $

(13) $ 8 \pi T_{0} = \frac{1+x}{r_{2} x}+8 \pi P_0r_{2}(1+x)-\frac{\left(2 q^{2}\right)^{\gamma}}{2 r_{2}^{4 \gamma-1} x^{4 \gamma-1}}\left(1+x^{4 \gamma-1}\right). $

(14) Considering Eqs. (10), (13), and (14), we find the larger horizon has the following form:
$ \begin{aligned}[b] r_{2}^{4 \gamma-2} =& \frac{\left(2 q^{2}\right)^{\gamma}\left[(3-4 \gamma)(1+x)\left(1-x^{4 \gamma}\right)+8 \gamma x^{2}\left(1-x^{4 \gamma-3}\right)\right]}{2 x^{4 \gamma-2}(3-4 \gamma)(1-x)^{3}} \\=& \left(2 q^{2}\right)^{\gamma} f(x,\gamma). \end{aligned} $

(15) Since the above state parameters must be positive, the non-linear YM charge parameter satisfies the condition
$ \dfrac{1}{2}<\gamma $ . For the critical point ($ x = 1 $ ), the state parameters are$ r_{\rm c}^{4 \gamma-2} = \left(2 q^{2}\right)^{\gamma} f(1, \gamma), \quad f(1, \gamma) = \gamma(4 \gamma-1), $

(16) $ T_{\rm c} = \frac{1}{\pi\left(2 q^{2}\right)^{\gamma /(4 \gamma-2)} f^{1 /(4 \gamma-2)}(1, \gamma)} \frac{2 \gamma-1}{4 \gamma-1}, $

(17) $ P_{\rm c} = \frac{2 \gamma-1}{16 \pi \gamma\left(2 q^{2}\right)^{\gamma /(2 \gamma-1)} f^{1 /(2 \gamma-1)}(1, \gamma)}. $

(18) Substituting Eq. (15) into Eq. (13), we have the following expression:
$ \begin{aligned}[b] \frac{1-x}{x} =& 8\pi P_0 \left(2 q^{2}\right)^{{\gamma}/({2 \gamma-1})}f^{{1}/({2 \gamma-1})}(x,\gamma)\\&+\frac{1-x^{4 \gamma-1}}{2x^{4 \gamma-1}f(x,\gamma)}f^{({4 \gamma-3})/({4 \gamma-2})}(x,\gamma).\end{aligned} $

(19) For a given parameter γ and pressure
$ P_0 $ , we can obtain the value of x from the above equation. Then from Eq. (15), we know that for a given pressure$ P_0 $ ($ P_0<P_{\rm c} $ ), i.e., for a fixed value of x, the phase transition condition reads$ \frac{\left(2 q^{2}\right)^{\gamma}}{r_{2}^{4 \gamma-2}} = \frac{1}{f(x, \gamma)}. $

(20) Therefore, the phase transition of the EPYM black hole with a given temperature
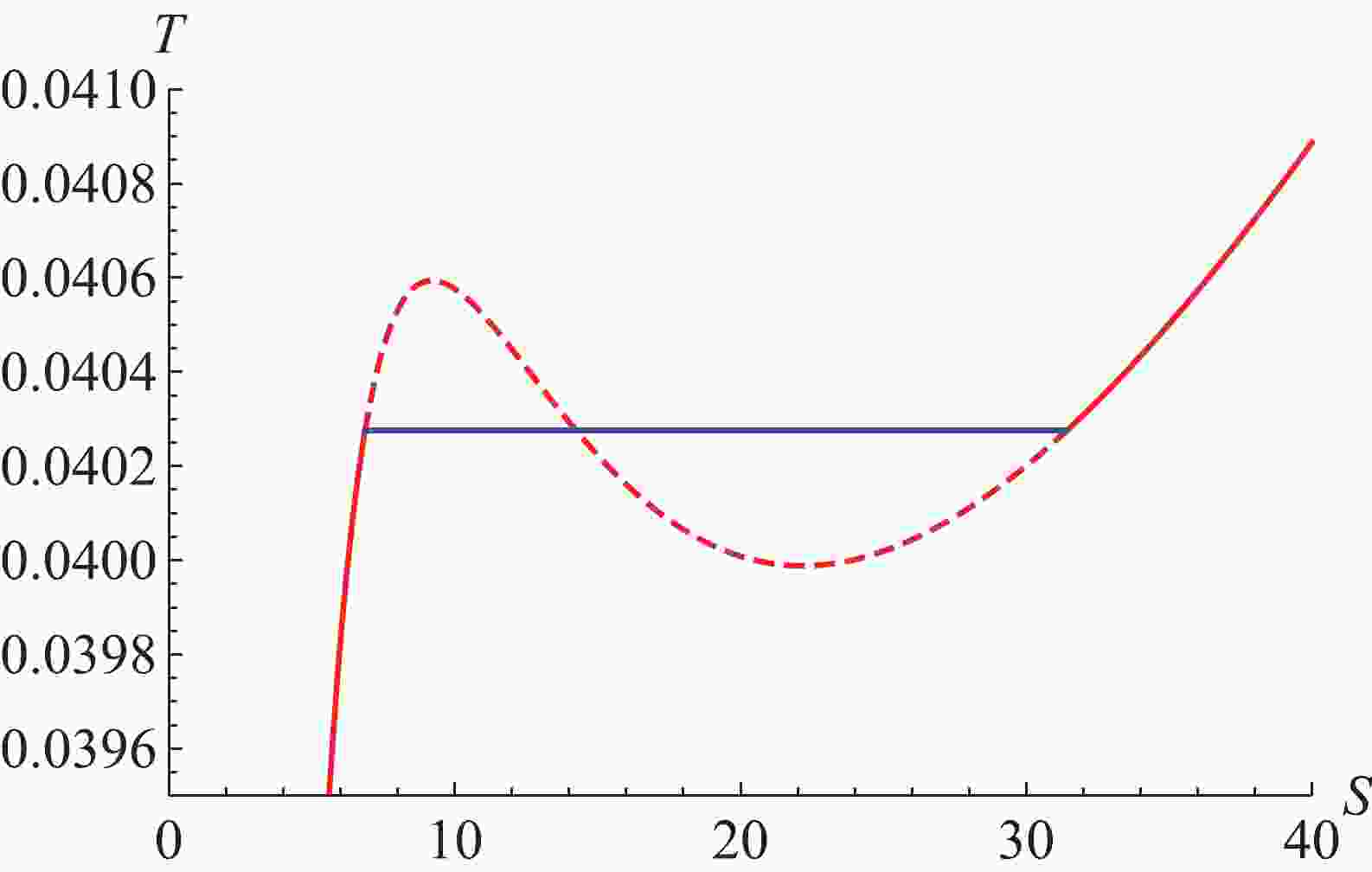
$ P_0 $ ($ P_0<P_{\rm c} $ ) is determined by the ratio between the YM charge$ (2q^2)^\gamma $ and$ r_{2}^{4 \gamma-2} $ , not only the value of the horizon. Note that we call this ratio the YM electric potential with the horizon radius$ r_2 $ . Therefore, the phase transition of this thermodynamic system is the high-/low-potential black hole (HPBH/LPBL) phase transition. The plot of the phase transition in the$ T-S $ diagram with fixed pressure$ P_0 = 0.85955P_{\rm c} $ is shown in Fig. 1. The effects of the non-linear parameter γ and YM charge q on phase transition were exhibited in our last work [40] -
As well as the equal-area law, the Gibbs free energy is an important thermodynamic quantity for investigating the phase transition. It exhibits swallow-tail behavior at a first-order phase transition point. While it is continuous, it is not smooth at a second-order phase transition. These two methods are thermodynamically equivalent. Therefore, we do not present the swallow-tail behavior in this section.
Recently, authors in Ref. [50] proposed that the Gibbs free energy landscape should also correspond to the thermal dynamic phase transition of a black hole. In this section, we will investigate the thermal dynamic phase transition of the EPYM AdS black hole from the view of the Gibbs free energy landscape.
-
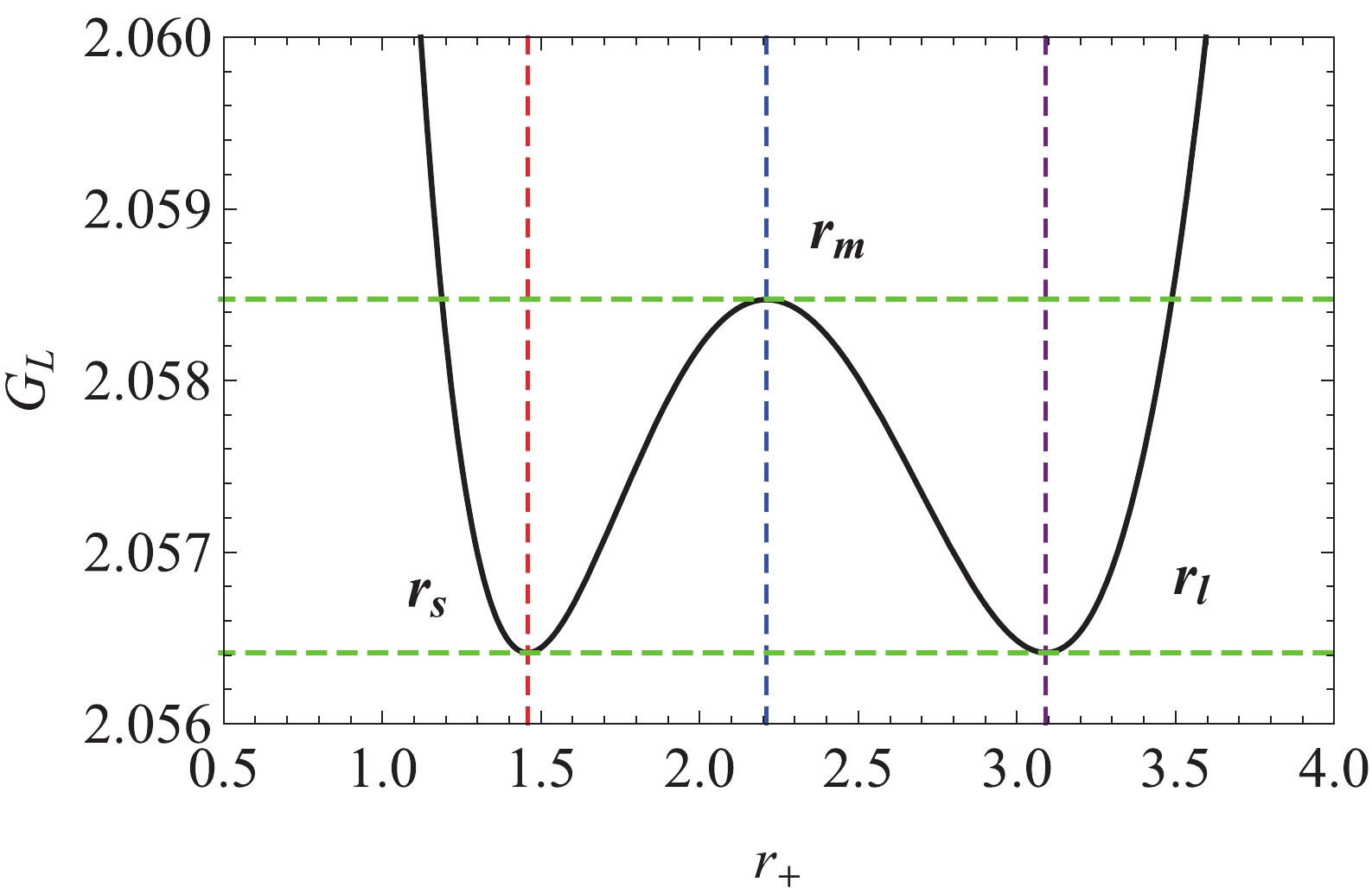
For the EPYM charged AdS black hole with non-linear charge, we proposed the existence of the HPBH/LPHB phase transitions in Ref. [40], not only the large/small black holes transition. In the following we present the thermal dynamic phase transition at the phase transition point (
$ T_0 = 0.0402 $ and$ P_0 = 0.85955P_{\rm c} $ ) with the parameters$ q = 0.85,\; \gamma = 0.8 $ .The Gibbs free energy landscape of the charged EPYM AdS black hole reads
$ G_{\rm L} = M-T_{E}S, $

(21) where
$ T_E $ is a temperature parameter and equals$ T_0 $ , which is not the Hawking temperature. The picture of the Gibbs free energy landscape at the phase transition point of$ P_0 = 0.85955P_{\rm c} $ and$ T_E = T_0 = 0.0402 $ is shown in Fig. 2. From this picture, we can see that, at the phase transition point, the Gibbs free energy landscape displays double-well behavior. Namely there are two local minima (located at$ r_l = 1.4577,\; r_s = 3.0904 $ ) which correspond to the stable high-/low-potential black hole states with positive heat capacity. The local maximum located at$ r_m = 2.2107 $ represents the unstable intermediate-potential black hole state with negative heat capacity, and acts as a barrier between the stable HPBH and LPBH states. Furthermore, the depths of two local minima are the same. This indicates that the HPBH/LPBH phase transition will occur at the same depth for the two wells from the view of Gibbs free energy landscape. At this point, we expect that the reentrant phase transition or triple point will maybe correspond to more wells of the Gibbs free energy landscape. -
As shown in the previous section, we find that the HPBH/LPBH phase transition of the charged EPYM AdS black hole emerges when the double wells of
$ G_{\rm L} $ have the same depth. Next we will investigate the dynamic process of the HPBH/LPBH phase transition for the charged EPYM AdS black hole.Recently, authors proposed that the stochastic dynamic process of black hole phase transition can be studied by the associated probabilistic Fokker–Planck equation on the Gibbs free energy landscape [50], which is an equation of motion governing the distribution function of flucturating macroscopic variables. For a black hole thermodynamic system, the horizon
$ r_+ $ is the order parameter and can be regarded as a stochastic fluctuating variable during the phase transition. Based on this, we will exhibit the dynamical process of the HPBH/LPBH phase transition in the canonical ensemble under thermal fluctuations. Note that the canonical ensemble consists of a series of black holes with arbitrary horizons. The probability distribution of these black hole states$ \rho(t,r_+) $ satisfies the Fokker–Planck equation on the Gibbs free energy landscape:$ \frac{\partial\rho(t,r_+)}{\partial t} = D\frac{\partial}{\partial r_+}\left({\rm e}^{-\beta G_{\rm L}(r_+)}\frac{\partial}{\partial r_+}\left[{\rm e}^{\beta G_{\rm L}(r_+)}\rho(t,r_+)\right]\right), $

(22) where
$ \beta = 1/kT_E $ ,$ D = kT_E/\xi $ is the diffusion coefficient with k being the Boltzman constant and ξ being the dissipation coefficient. Without loss of generality, we set$ k = \xi = 1 $ . In order to solve the above equation, two types of boundary ($ r_+ = r_{0} $ ) condition should be imposed. One is the reflection boundary condition, which preserves the normalization of the probability distribution. The other is the absorption boundary condition.In this system the location of the left boundary should be smaller than
$ r_s $ , and the right boundary is larger than$ r_l $ . Since the temperature of the charged EPYM AdS black hole with pressure$ P_0 = 0.85955P_{\rm c} $ and parameters$ q = 0.85,\; \gamma = 0.8 $ should be not negative, there exists a minimum value$ r_{\rm min} = 0.695808 $ . We can regard$ r_{\rm min} $ as the left boundary$ r_{\rm lb} $ , and set the right boundary$ r_{\rm rb} $ as$ 6 $ . The reflection boundary condition means the probability current vanishes at the left and right boundaries:$ j(t,r_0) = -T_E{\rm e}^{-G_{\rm L}/T_E}\frac{\partial}{\partial r_+}\left({\rm e}^{G_{\rm L}/T_E}\rho(t,r_+)\right)\mid_{r_+ = r_0} = 0 . $

(23) The absorption condition means the probability distribution function vanishes at the boundary:
$ \rho(t,r_0) = 0 $ . The adoption of this boundary condition is determined by considering the physical problem.The initial condition is chosen as a Gaussian wave packet located at
$ r_i $ :$ \rho(0,r_+) = \frac{1}{\sqrt{\pi}}{\rm e}^{-{(r_+-r_i)^2}/{a^2}}. $

(24) Here a is a constant which determines the initial width of the Gaussian wave packet, and its value does not influence the final result. Since we mainly consider the thermal dynamic phase transition between HPBH/LPBH states,
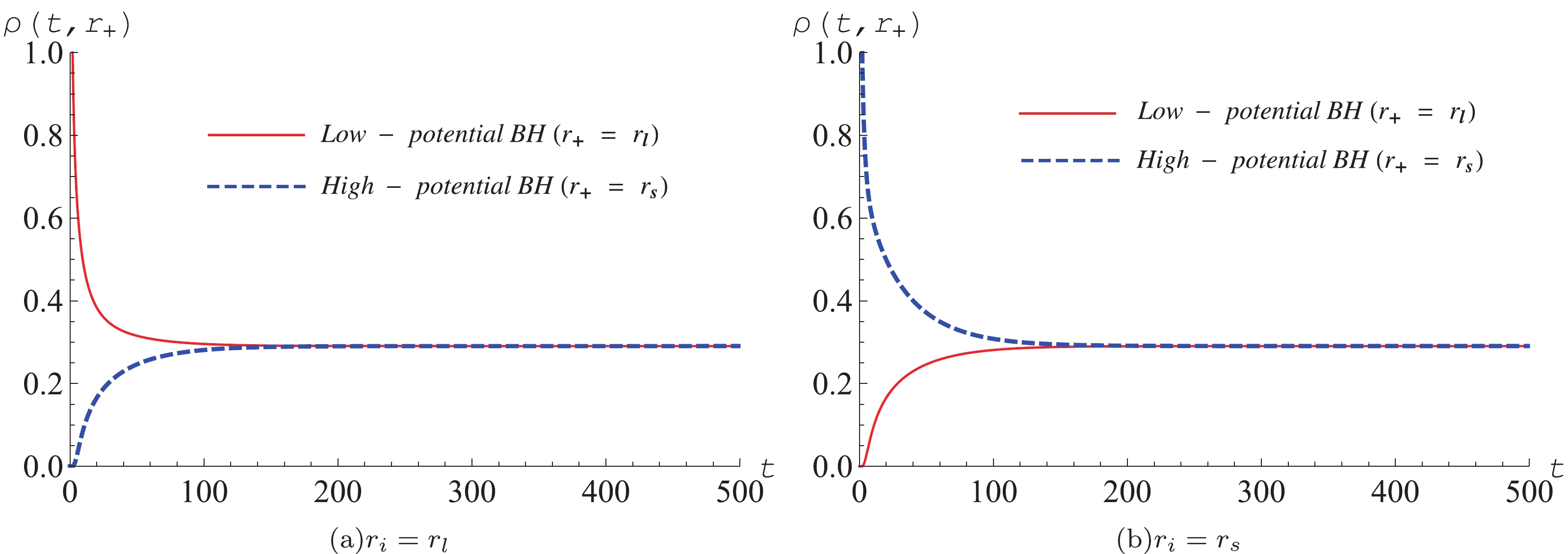
$ r_i $ can be set to$ r_s $ or$ r_l $ . This means this thermal system is initially in the high- or low-potential black hole state.The time evolution of the probability distribution is shown in Fig. 3. At
$ t = 0 $ the Gaussian wave packets locate at LPBH (Fig. 3(a)) and HPBH (Fig. 3(b)) with$ T_E = T_0 $ and$ a = 0.1 $ , respectively. They both decrease with increasing time t until tending to a certain constant. However, at the same time the peaks of$ \rho(t,r) $ at$ r = r_{s} $ (Fig. 3(a)) and$ r = r_{s} $ (Fig. 3(b)) are increasing from zero to the same constant. This indicates that the black hole system in the LPBH phase tends to the HPBH phase as shown Fig. 3(a), while in the HPBH phase tends to the low phase as shown Fig. 3(b). Finally the system reaches a LPBH/HPBH coexistence stationary state after a short time. In order to further clarify the dynamical process of the HPBH/LPBH phase transition, we show the probability distributions of$ \rho(t,r_l) $ and$ \rho(t,r_s) $ in Fig. 4. The probability distribution of the initial LPBH (or HPBH) is at its maximum, whereas the corresponding HPBH (or LPBH) state is at zero. With increasing time, both approach to the same value. This is consistent with what was shown in$ G_{\rm L}-r_+ $ , i.e., the LPBH and HPBH states have the same depth in the double well of the Gibbs free energy landscape. -
In general, an important quantity in the dynamical process of the HPBH/LPBH phase transition is the first passage time, which is defined as the mean value of the first passage time that a stable HPBH or LPBH scape to the unstable intermediate-potential black hole state (i.e., from the one well to the barrier of Gibbs free energy landscape).
Suppose there is a perfect absorber in the stable HPBH or LPBH state. If the system makes the first passage under thermal fluctuation, then the system will leave this state. We can define Σ to be the summed probability of the dynamical process within the first passage time as
$ \Sigma = \int^{r_{\rm m}}_{r_{\rm min}}\rho(t,r_+){\rm d}r_+, \; \; \; \; \; \; {\rm{or}}\; \; \; \; \; \Sigma = -\int^{r_{\rm m}}_{r_{\rm rb}}\rho(t,r_+){\rm d}r_+, $

(25) where
$ r_{\rm m} $ ,$ r_{\rm min} $ ,$ r_{\rm rb} $ are the intermediate, minimum, and right boundary of charged EPYM AdS black hole horizons. After a long time, the probability of the stable HPBH or LPBH state still in this system becomes zero, i.e.,$ \Sigma(t,r_l)\mid_{t\rightarrow \infty} = 0 $ or$ \Sigma(t,r_s)\mid_{t\rightarrow \infty} = 0 $ . As claimed, the first passage time is a random variable because the dynamical process of phase transition is caused by thermal fluctuation. Hence, we denote the distribution of the first passage time by$ F_p $ , which reads$ F_p = -\frac{{\rm d}\Sigma}{{\rm d}t}. $

(26) It is obviously that
$ F_p{\rm d}t $ indicates the probability of the system passing through the intermediate-potential black hole state for the first passage in the time interval ($ t,\; t+{\rm d}t $ ). Considering Eqs. (22) and (25), the distribution of the first passage time$ F_p $ becomes [52]$ F_p = -D\frac{\partial\rho(t,r_+)}{\partial r}{\bigg|}_{r_{\rm m}}, \; \; \; \; \; {\rm or}\; \; \; \; F_p = D\frac{\partial\rho(t,r_+)}{\partial r}{\bigg|}_{r_{\rm m}}. $

(27) Here the absorbing and reflecting boundary conditions of the Fokker–Planck equation are imposed at
$ r_{\rm m} $ and the other limit ($ r_{\rm min} $ or$ r_{\rm rb} $ ). Note that the normalisation of the probability distribution is not preserved.By solving the Fokker–Planck Eq. (22) with different phase transition temperatures (
$ T_0 = 0.0402 $ and$ T_0 = $ $ 0.038 $ ) and substituting these into Eqs. (25) and (26), numerical results are obtained, as displayed in Figs. 5 and 6 for different initial conditions. It is clear that in Fig. 5, no matter what kind of initial condition has been considered, Σ decays very quickly. Furthermore, the increase of temperature makes the probability of Σ drop faster. An important point is that the probability is not conserved. From the corresponding probability distribution picture in Fig. 6, the behavior of$ F_p $ is similar for both initial conditions. A single peak emerges near$ t = 0 $ in the curve of$ F_p $ with fixed temperature. This can be understood as a large number of first passage events occurring in a short interval of time, and then the probability distribution decays exponentially with time. The effect of temperature at phase transition points on$ F_p $ is consistent with that of Σ and$ G_{\rm L} $ . That means that the higher the temperature, the faster the probability decreases, the easier the phase transition occurs, and the lower the depth of the barrier. Conversely, the lower the temperature, the slower the probability decreases, the harder the phase transition, and the higher the depth of the barrier.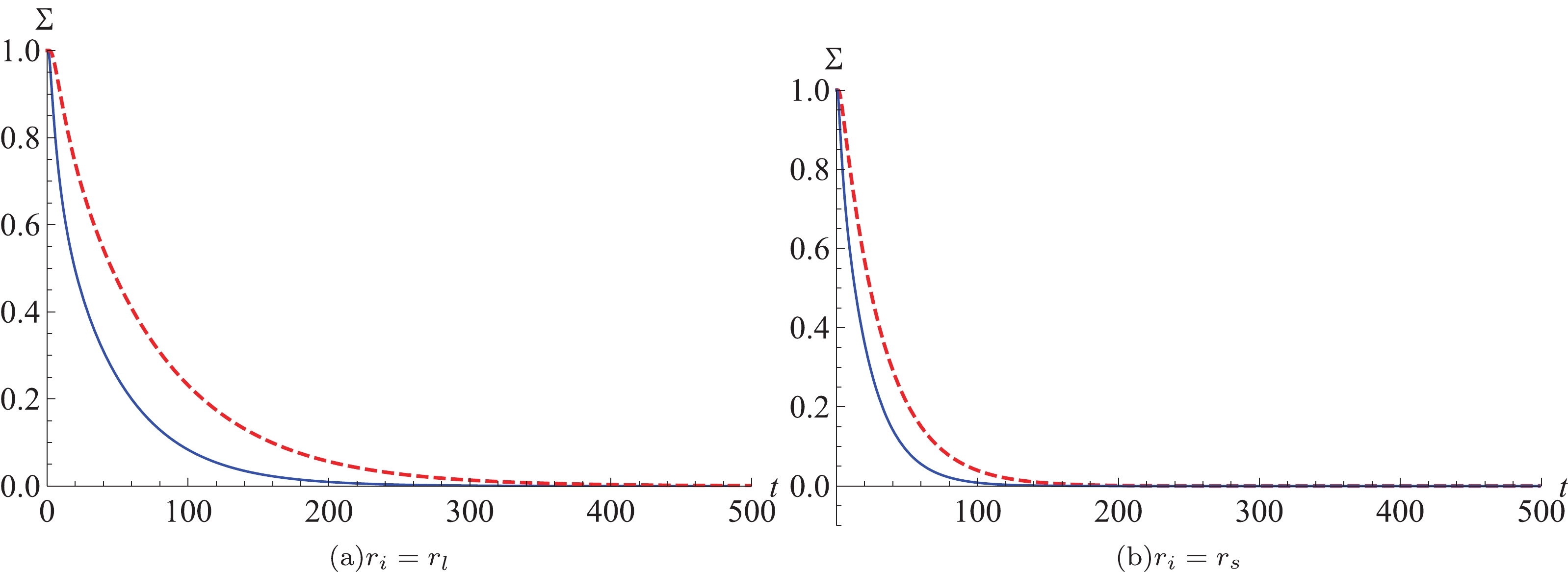
Figure 5. (color online)
$ \Sigma$ for different temperatures:$ T_0 = 0.0402 $ (thin blue lines) and$ T_0 = 0.038 $ (dashed thick red lines) for the charged EPYM AdS black holes with different initial conditions, with parameters$ q = 0.85,\; \gamma = 0.8.$ 
Figure 6. (color online) Time evolution of the distribution of first passage time
$ F_p$ for different temperatures:$ T_0 = 0.0402 $ (thin blue lines) and$ T_0 = 0.038 $ (dashed thick red lines) for the charged EPYM AdS black holes with different initial conditions, with parameters$ q = 0.85,\; \gamma = 0.8.$ -
Since the precise statistical description of the corresponding thermodynamic states of black holes is still unclear, the investigation of the thermodynamic phase transition of black holes becomes an issue of concern. In this manuscript, we investigated the dynamical property of the HPBH/LPBH phase transition for the four-dimensional charged Einstein-power–Yang–Mills (EPYM) AdS black hole from the view point of the Gibbs free energy landscape.
Firstly we reviewed the thermodynamic properties of the charged EPYM AdS black hole. From the phase transition condition (20), we suggested that the phase transition is between HPBH and LPBH states, not only the pure transition between a small/large black hole. The HPBH/LPBH phase transition in the
$ T-S $ diagram can be constructed using Maxwell's equal-area law when$ P_0<P_{\rm c} $ . Since the results are the same no matter whether derived from Maxwell's equal-area law or the Gibbs free energy, the swallow-tail behavior of G was not presented in this manuscript.At the phase point we have given, we found there is a double-well in the Gibbs free energy landscape (
$ G_{\rm L} $ ). The two local minima of$ G_{\rm L} $ correspond to the stable HPBH and LPBH states. The local maximum stands for the unstable intermediate-potential black hole state and acts as a barrier between the stable HPBH and LPBH states. Furthermore, the depths of the two wells are the same. This indicates that the HPBH/LPBH phase transition will occur when the two wells have the same depth from the point view of$ G_{\rm L} $ . Next we studied the dynamical process of the HPBH/LPBH phase transition governed by the Fokker–Planck equation. By imposing reflection boundary conditions on the minimum black hole horizon and a larger value than the LPBH, and considering a Gaussian wave packet in the HPBH or LPBH state as the initial condition, we obtained the numerical result of the Fokker–Planck equation: the initial Gaussian wave packet at the HPBH or LPBH state decreases with increasing time, however at the same time the other peak of$ \rho(t,r_+) $ at the LPBH or HPBH state increases from zero to the same constant. That indicates that with increasing time the system will leave the initial state towards another state, until it becomes a two-state coexistent state, which is consistent with the fact that the depths of two wells in$ G_L $ (standing for the LPBH and HPBH states) have the same value.Finally we considered the first passage time. By imposing the absorption boundary condition on the intermediate-potential black hole state and considering a Gaussian wave packet at the HPBH or LPBH state as the initial condition, we obtained another numerical result of the Fokker–Planck equation: no matter what kind initial condition had been considered, Σ decays very quickly, and it drops faster with increasing temperature. The behavior of
$ F_p $ is similar for both initial conditions. A single peak exists near$ t = 0 $ in$ F_p $ . This can be understood as a large number of first passage events occurring in a short interval of time, and then the probability distribution decays exponentially with time. From the effect of temperature at phase transition points on$ F_p $ , Σ, and$ G_{\rm L} $ , we found that the higher the temperature, the faster the probability decreases, the easier the phase transition occurs, and the lower the depth of the barrier. Conversely, the lower the temperature, the slower the probability decreases, the harder the phase transition, and the higher the depth of the barrier. -
We would like to thank Prof. Ren Zhao, Meng-Sen Ma, and Si-Jiang Yang for their indispensable discussions and comments.
Dynamic property of phase transition for non-linear charged anti-de Sitter black holes
- Received Date: 2021-12-23
- Available Online: 2022-05-15
Abstract: Understanding the thermodynamic phase transition of black holes can provide deep insights into the fundamental properties of black hole gravity and help to establish quantum gravity. In this work, we investigate the phase transition and its dynamics for the charged EPYM AdS black hole. Through reconstructing Maxwell's equal-area law, we find there exists a high-/low-potential black hole (HPBH/LPBL) phase transition, not only the pure large/small black hole phase transition. The Gibbs free energy landscape (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: