-
Recently, with the development of radioactive beam facilities, the study of exotic nuclei far from the
$ \beta $ -stability line has became an interesting topic in nuclear physics [1-7]. Two-proton ($ 2p $ ) radioactivity, an important exotic decay mode, provides a new opportunity to obtain the nuclear structure information of rich-proton nuclei [8-10]. In the 1960s, this decay mode was first predicted independently by Zel’dovich [11] and Goldansky [12, 13]. However owing to the limitations in experiments, it was not until 2002 that true$ 2p $ radioactivity ($ Q_{2p} $ $ > $ 0 and$ Q_p $ $ < $ 0, where$ Q_p $ and$ Q_{2p} $ are the released energies of the proton and two-proton radioactivity, respectively) was observed from the$ ^{45} $ Fe ground state was observed at the Grand Acc$ \acute{\rm{e}} $ $ \rm{l} $ $ \acute{\rm{e}} $ rateur National d'lons Lourds (GANIL) [14] and Gesellschaft F$ \ddot{\rm{u}} $ r Schwerionenforschung (GSI) [15], respectively. Later, the$ 2p $ radioactivity of$ ^{54} $ Zn,$ ^{48} $ Ni,$ ^{19} $ Mg, and$ ^{67} $ Kr were consecutively identified at different radioactive beam facilities [16-19].The
$ 2p $ radioactivity process is considered as an isotropic emission with no angular correlation or a correlated emission forming a$ ^2 $ He-like cluster with a strong correlation from the even-Z nuclei either in the vicinity of or beyond the proton drip line [14, 20-22]. Based on these physical mechanisms, many theoretical models have been proposed to study$ 2p $ radioactivity, such as the direct decay model [23-29], simultaneous versus sequential decay model [30], diproton model [31, 32], and three-body model [33-36]. Moreover, some empirical formulas can successfully reproduce the half-lives of$ 2p $ radioactive nuclei, such as the four-parameter empirical formula proposed by Sreeja$ et $ $al.$ [37] and the new Geiger-Nuttall law for two-proton radioactivity proposed by Liu$ et $ $ al $ [38]. The two-potential approach (TPA) [39, 40] proposed by Gurvitz, was initially used to address quasi-stationary problems and has been extended to studying$ \alpha $ decay, cluster radioactivity, and proton radioactivity [41-55]. In our previous studies, we systematically investiagted proton radioactivity using the TPA approach, and the nuclear potential was calculated using the Skyrme-Hartree-Fock (SHF) approach [56, 57], and this is denoted as TPA-SHF. The calculated results can closely reproduce experimental data. Since$ 2p $ radioactivity process may share a similar theory of barrier penetration with proton radioactivity [58-61], whether TPA-SHF can be extended to study$ 2p $ radioactivity is an interesting question. Therefore, in this paper, considering the spectroscopic factor ($ S_{2p} $ ), we extend TPA-SHF to systematically study$ 2p $ radioactivity half-lives of nuclei with 4$ < $ Z$ < $ 36. For comparison, the generalized liquid drop model (GLDM) [62], effective liquid drop model (ELDM) [20] and Gamow-like model [63] are also used.The remainder of this article is organized as follows. In Section II, the theoretical framework for the TPA-SHF is described in detail. The calculated results and discussion are given in Section III. In Section IV, a brief summary is provided.
-
The
$ 2p $ radioactivity half-life ($ T_\frac{1}{2} $ ) is an important indicator of nuclear stability, and it can be calculated using$ T_\frac{1}{2} = \frac{\ln 2}{\lambda} = \frac{\hbar \ln 2}{\Gamma}. $

(1) Here
$ \lambda $ ,$ \Gamma $ , and$ \hbar $ are the two-proton radioactivity constant, decay width, and reduced Planck constant, respectively. In the TPA framework [39, 40],$ \Gamma $ can be represented by the normalized factor (F) and the penetration probability (P). It is expressed as$ \Gamma = \frac{\hbar^2 S_{2p}F P }{4\mu}, $

(2) where
$ S_{2p} = G^2[A/ (A -2)]^{2n}\chi ^2 $ denotes the spectroscopic factor of the$ 2p $ radioactivity. It can be obtained using cluster overlap approximation [64]. Here,$G^2 = $ $ (2n)! / [2^{2n}(n!)^2]$ where$ n \approx(3Z)^{1/3} - 1 $ [65] is the average principal proton oscillator quantum number [66],$ \chi ^2 $ is set as 0.0143 according to the study by Cui$ et\ al. $ [62], A and Z are the mass and proton number of parent nucleus, respectively, and F is the normalized factor, which can be calculated as$ F \int_{r_1}^{r_2}\frac{1}{2 k(r)}\, {\rm d}r = 1,$

(3) where
$ k(r) = \sqrt{\dfrac{2\mu}{\hbar^2}\left|Q_{2p}-V(r)\right|} $ is the wave number;$ \mu = m_{2p}m_{d}/(m_{2p}+m_{d}) $ is the reduced mass, where$ m_{2p} $ and$ m_{d} $ are the masses of the two emitted protons and residual daughter nucleus, respectively;$ Q_{2p} $ is the released energy of the two-proton radioactivity;$ V(r) $ is the total interaction potential between the two emitted protons and daughter nucleus, which are described in more detail in the following;$ r_1 $ ,$ r_2 $ , and the subsequent$ r_3 $ are the classical turning points. They satisfy the condition$ V(r_{1}) = V(r_2) = V(r_3) = Q_{2p} $ . Penetration probability P can be formulated as$ P = \exp \left[-2 \int_{r_2}^{r_3} k(r)\, {\rm d}r\right]. $

(4) The total interaction potential (
$ V(r) $ ) is composed of the nuclear potential ($ V_N(r) $ ), Coulomb potential ($ V_C(r) $ ), and centrifugal potential ($ V_l(r) $ ), and it can be expressed as$ V(r) = V_N(r)+V_{\rm C}(r)+V_l(r). $

(5) In this work, based on the assumption that the two protons spontaneously emitted from parent nuclear share a momentum (
$ \boldsymbol{p} $ ) on average, and the nuclear interaction potential between the two-proton emission and daughter nucleus is twice that between an emitted proton and daughter nucleus, we can obtain the nuclear potential of the two-proton emission$ V_N(r) = 2U_q(\rho, \rho_q, \dfrac{\boldsymbol{p}}{2}) $ using the SHF approach. In this model, the nuclear effective interaction is expressed as the standard Skyrme form [67]$ \begin{aligned}[b] V_{12}(\boldsymbol{r}_1, \boldsymbol{r}_2) =& t_0(1+x_0P_\sigma)\delta(\boldsymbol{r}_1-\boldsymbol{r}_2)\\& + \frac{1}{2}t_1(1+x_1P_\sigma)[\boldsymbol{P}'^2\delta(\boldsymbol{r}_1-\boldsymbol{r}_2)+\delta(\boldsymbol{r}_1-\boldsymbol{r}_2)\boldsymbol{P}^2] \\& + t_2(1+x_2P_\sigma)\boldsymbol{P}'\cdot\delta(\boldsymbol{r}_1-\boldsymbol{r}_2)\boldsymbol{P} \\& + \frac{1}{6}t_3(1+x_3P_\sigma)\left[\rho\left({\frac{\boldsymbol{r}_1+\boldsymbol{r}_2}{2}}\right)\right]^{\alpha}\delta(\boldsymbol{r}_1-\boldsymbol{r}_2) \\& + {\rm i} {W_0} \mathit{\boldsymbol{\sigma}}\cdot[\boldsymbol{P}'\times\delta(\boldsymbol{r}_1-\boldsymbol{r}_2)\boldsymbol{P}], \end{aligned} $

(6) where
$ t_0 $ –$ t_3 $ ,$ x_0 $ –$ x_3 $ ,$ W_0 $ , and$ \alpha $ are the Skyrme parameters;$ \boldsymbol{r}_i $ (i = 1, 2) is the coordinate vector of i-th nucleon;$ \boldsymbol{P}' $ and$ \boldsymbol{P} $ are the relative momentum operators acting on the left and right, respectively; and$ P_\sigma $ and$ \mathit{\boldsymbol{\sigma}} $ are the spin exchange and Pauli spin operators, respectively. In the SHF model, the single-nucleon potential that depends on the momentum of the nucleon ($ \boldsymbol{p } $ ) can be calculated using [68]$ U_q\left(\rho, \rho_q, \frac{\boldsymbol{p}}{2}\right) = a\left(\frac{\boldsymbol{p}}{2}\right)^2+b, $

(7) where subscript q is the proton/neutron ratio (q = p/n). The total nucleonic density (
$ \rho $ ) is the sum of the proton density ($ \rho_p $ ) and neutron density ($ \rho_n $ ). Coefficients a and b can be expressed as$ \begin{aligned}[b] a =& \frac{1}{8}[t_1(x_1+2)+t_2(x_2+2)]\rho\\& + \frac{1}{8}[-t_1(2x_1+1)+t_2(2x_2+1)]\rho_q, \end{aligned} $

(8) $ \begin{aligned}[b] b =& \frac{1}{8}[t_1(x_1+2)+t_2(x_2+2)]\frac{k^5_{f, n}+k^5_{f, p}}{5\pi^2}\\& +\frac{1}{8}[t_2(2x_2+1)-t_1(2x_1+1)]\frac{k^5_{f, q}}{5\pi^2} \\& + \frac{1}{2}t_0(x_0+2)\rho-\frac{1}{2}t_0(2x_0+1)\rho_q \\& + \frac{1}{24}t_3(x_3+2)(\alpha+2)\rho^{(\alpha+1)} \\ &-\frac{1}{24}t_3(2x_3+1)\alpha\rho^{(\alpha-1)}(\rho^2_n+\rho^2_p) \\ &-\frac{1}{12}t_3(2x_3+1)\rho^\alpha\rho_q. \end{aligned}$

(9) Here,
$ k_{f, q} = (3\pi\rho_q)^{1/3} $ represents the Fermi momentum. The relationship among the total energy (E) of$ 2p $ emission in a nuclear medium, nuclear potential, and Coulomb potential can be expressed as$ E = 2U_q\left(\rho, \rho_q, \frac{\boldsymbol{p}}{2}\right)+\frac{\boldsymbol{p}^2}{2m_{2p}}+V_{\rm C}(r). $

(10) In this paper, E is obtained using the corresponding
$ Q_{2p} $ as E = [($ A- $ 2)/A]$ Q_{2p} $ . Based on the premise that the total energy remains constant when$ 2p $ emits from parent nuclei, using Eqs. (7) and (10), we can obtain the momentum of the two emitted protons$ \left|\boldsymbol{p}\right| $ , expressed as$ \left|\boldsymbol{p}\right| = \sqrt{\frac{2(E-2b-V_c(r))}{a+\dfrac{1}{m_{2p}}}}.$

(11) The Coulomb potential
$V_{\rm C}(r)$ can be obtained from a uniformly charged sphere with radius R:$ V_{\rm C}(r) = \begin{cases} \dfrac{Z_d Z_{2p} e^2}{2R}\left[3-\left(\dfrac{r}{R}\right)^2\right],\quad r<R, \\ \dfrac{Z_d Z_{2p} e^2}{r},\quad r>R, \end{cases} $

(12) where
$ Z_{2p} = 2 $ is the proton number of the two emitted protons in$ 2p $ radioactivity. The radius R is given by [69]$ R = 1.28A^{1/3}-0.76+0.8A^{-1/3}. $

(13) For the last part of Eq. (5), centrifugal potential
$ V_l(r) $ , we select the Langer modified form since$ l(l + 1) \rightarrow $ $ (l + 1/2)^2 $ is necessary in one-dimensional problems [70]. It can be expressed as$ {V_{l}(r) = \frac{\hbar^2\left(l+\dfrac{1}{2}\right)^2}{2{\mu}r^2},}{} $

(14) where l is the orbital angular momentum of the two emitted protons in
$ 2p $ radioactivity. -
In this work, we first calculated the
$ 2p $ radioactivity half-lives of nuclei with 4$ < $ Z$ < $ 36 using the TPA, obtained the nuclear potential using the SHF apparoach, and compared our calculated results with the experimental data and theoretical results calculated usisng the GLDM [62], ELDM [20], and Gamow-like model [63]. The Skyrme effective interaction currently has approximately 120 sets of Skyrme parameters. The SLy series parameters have been widely used to describe the different nuclear reactions in various studies, and the$ \alpha $ decay since spin-gradient term or a more refined two-body cent of mass correction is considered [29, 71-74]. These parameters are listed in Table 1. As an example, we select the Skyrme parameters of SLy8 in this paper. The detailed calculation results are listed in Table 2, in which the first two columns represent the two-proton emitter and texperimental released energy of$ 2p $ radioactivity ($ Q_{2p} $ ), respectively. The experimental data of$ 2p $ radioactivity half-lives and the theoretical ones obtained using the GLDM, ELDM, Gamow-like model, and our model are provided in logarithmic form in columns 3-7, respectively. As shown in Table 2, the theoretical$ 2p $ radioactivity half-lives calculated using our model can closely reproduce the experimental data. To intuitively survey their deviations, we plot the difference of$ 2p $ radioactivity logarithmic half-lives of the experimental data and the ones calculated busing the four models (our model, GLDM, ELDM, and Gamow-like) in Fig. 1. The figure clearly shows that all the points representing the difference are basically within$ \pm $ 1. For$ ^{48} $ Ni of$ Q_{2p} $ = 1.350 MeV and$ ^{54} $ Zn of$ Q_{2p} $ = 1.280 MeV in particualr, our calculated results can better reproduce the experimental data compared with the other models.model $ t_0 $ 

$ t_1 $ 

$ t_2 $ 

$ t_3 $ 

$ x_0 $ 

$ x_1 $ 

$ x_2 $ 

$ x_3 $ 

$ W_0 $ 

$ \alpha $ 

Sly0 [72] −2486.40 485.20 −440.50 13783.0 0.790 −0.500 −0.930 1.290 123.0 1/6 Sly1 [72] −2487.60 488.30 −568.90 13791.0 0.800 −0.310 −1.000 1.290 125.0 1/6 Sly2 [72] −2484.20 482.20 −290.00 13763.0 0.790 −0.730 −0.780 1.280 125.0 1/6 Sly3 [72] −2481.10 481.00 −540.80 13731.0 0.840 −0.340 −1.000 1.360 125.0 1/6 Sly4 [71] −2488.91 486.82 −546.39 13777.0 0.834 −0.344 −1.000 1.354 123.0 1/6 Sly5 [71] −2484.88 483.13 −549.40 13763.0 0.778 −0.328 −1.000 1.267 126.0 1/6 Sly6 [71] −2479.50 462.18 −448.61 13673.0 0.825 −0.465 −1.000 1.355 122.0 1/6 Sly7 [71] −2482.41 457.97 −419.85 13677.0 0.846 −0.511 −1.000 1.391 126.0 1/6 Sly8 [72] −2481.40 480.80 −538.30 13731.0 0.800 −0.340 −1.000 1.310 125.0 1/6 Sly9 [72] −2511.10 510.60 −429.80 13716.0 0.800 −0.620 −1.000 1.370 125.0 1/6 Table 1. Skyrme parameters of SLy series.
Nucleus $Q_{2p}/ {\rm{MeV} }$ 

${\log_{10}}{T}_{1/2}^{\rm exp}/{\rm{s}} $ 

$ {\log_{10}}{T}_{1/2}^{\rm GLDM}/{\rm{ s}}\;[62]$ 

$ {\log_{10}}{T}_{1/2}^{\rm ELDM}/{\rm{ s}}\;[20]$ 

$ {\log_{10}}{T}_{1/2}^{\rm Gamow-like}/{\rm{s}}\;[63] $ 

$ {\log_{10}}{T}_{1/2}^{\rm our\;model}/{\rm{ s}}$ 

$ ^{19}\;{\rm{ Mg}} $ 

0.750 [18] $ -11.40 $ [18]

$ -11.79 $ 

$ -11.72 $ 

$ -11.46 $ 

$ -11.00 $ 

$ ^{45} $ Fe

1.100 [15] $ -2.40 $ [15]

$ -2.23 $ 

– $ -2.09 $ 

$ -2.31 $ 

1.140 [14] $ -2.07 $ [14]

$ -2.71 $ 

– $ -2.58 $ 

$ -2.87 $ 

1.210 [75] $ -2.42 $ [75]

$ -3.50 $ 

– $ -3.37 $ 

$ -3.53 $ 

1.154 [17] $ -2.55 $ [17]

$ -2.87 $ 

$ -2.43 $ 

$ -2.74 $ 

$ -2.88 $ 

$ ^{48} $ Ni

1.350 [17] $ -2.08 $ [17]

$ -3.24 $ 

– $ -3.21 $ 

$ -2.27 $ 

1.290 [76] $ -2.52 $ [76]

$ -2.62 $ 

– $ -2.59 $ 

$ -2.23 $ 

$ ^{54} $ Zn

1.480 [16] $ -2.43 $ [16]

$ -2.95 $ 

$ -1.32 $ 

$ -3.01 $ 

$ -2.08 $ 

1.280 [77] $ -2.76 $ [77]

$ -0.87 $ 

– $ -0.93 $ 

$ -1.32 $ 

$ ^{67} $ Kr

1.690 [19] $ -1.70 $ [19]

$ -1.25 $ 

$ -0.06 $ 

$ -0.76 $ 

$ -1.05 $ 

Table 2. Experimental and theoretical data of
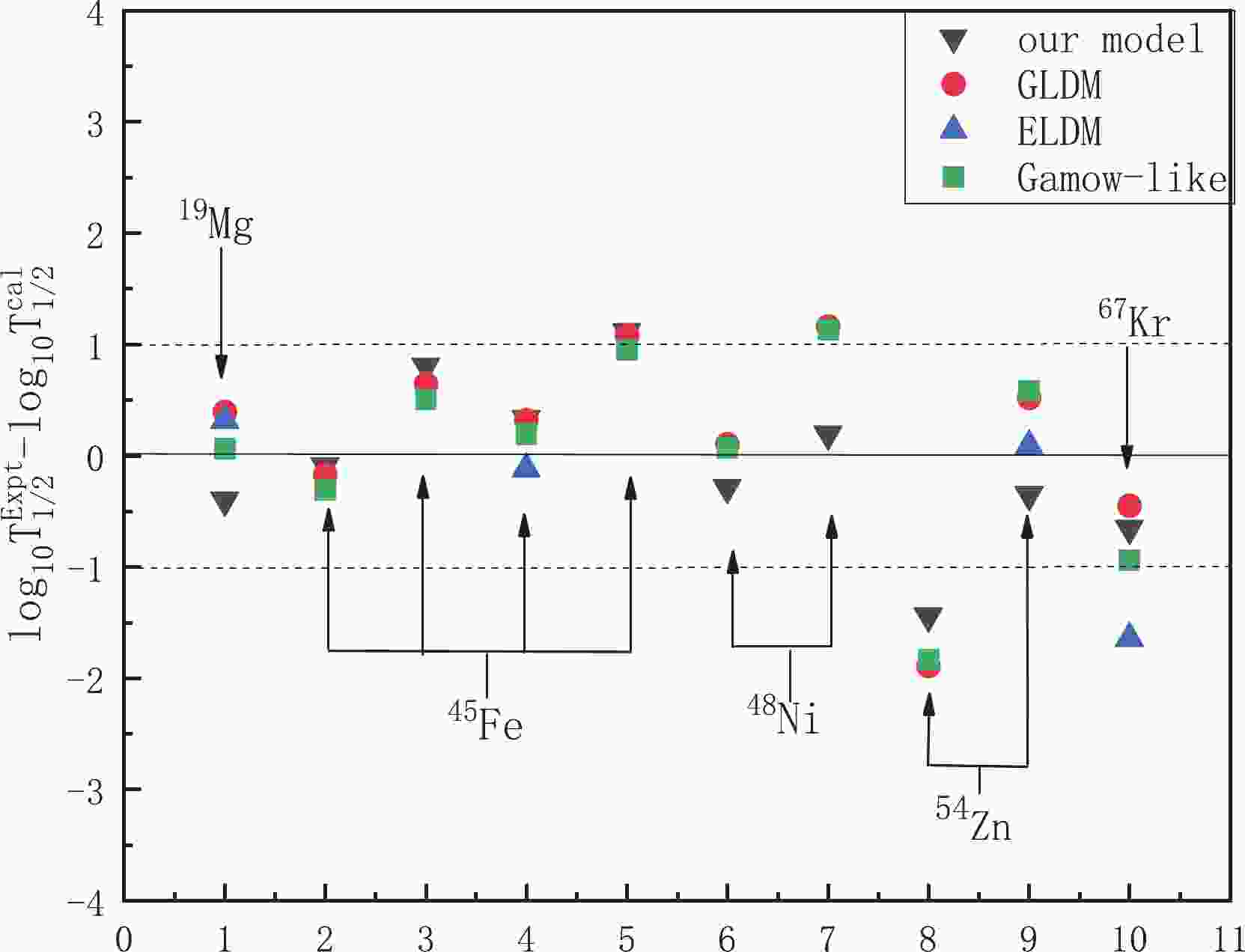
$ 2p $ radioactivity half-lives calculated using GLDM, ELDM, Gamow-like, and our model.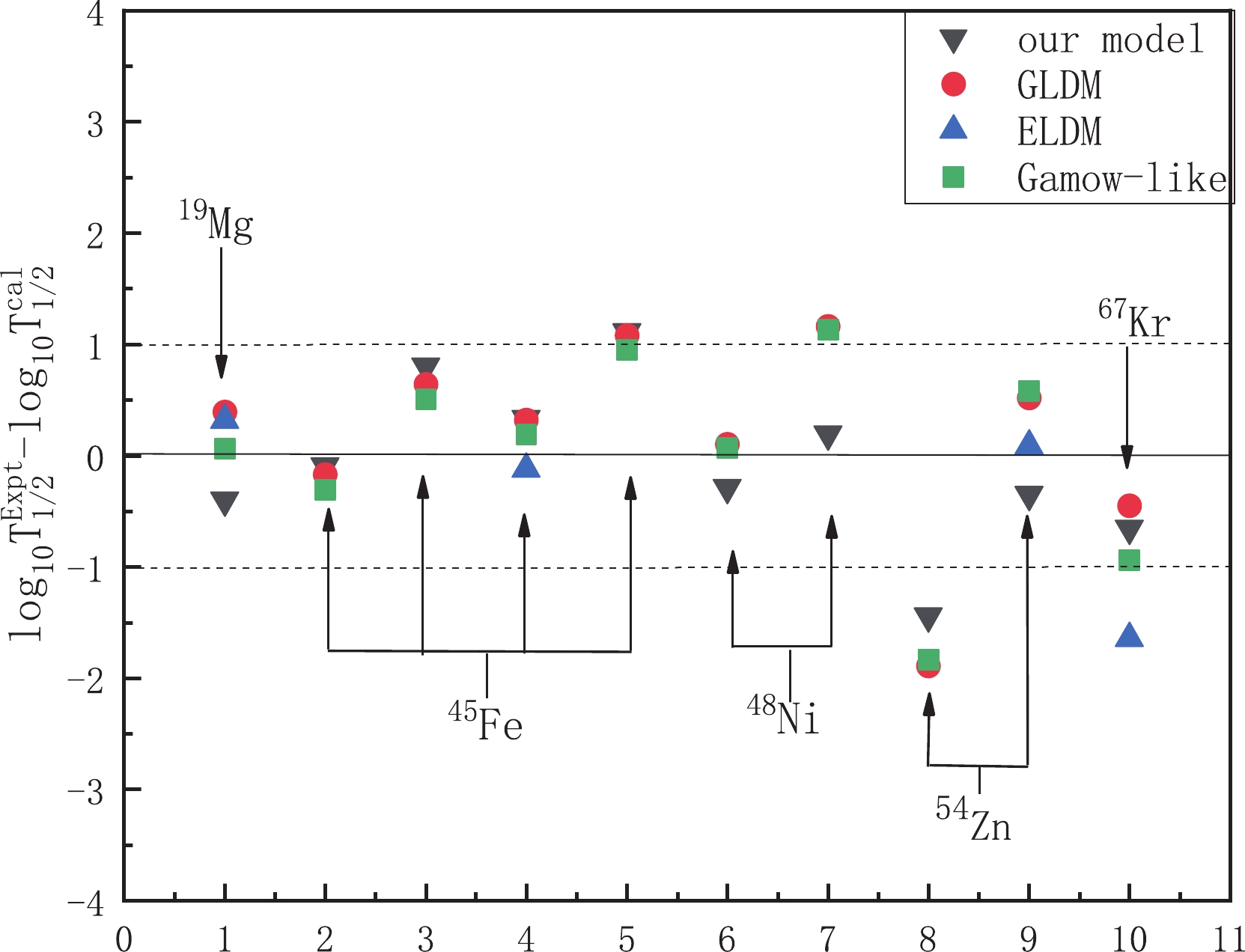
Figure 1. (color online) Difference between the experimental data of
$2p$ radioactivity half-lives and theoretical data calculated using GLDM, ELDM, Gamow-like, and our model in logarithmic form.To obtain further insight into the agreement and systematics of the results, the standard deviation (
$ \sigma $ ) between the theoretical and experimental values is used to quantify the calculated capabilities of the above four models for$ 2p $ radioactivity half-lives. In this paper, it is defined as follows:$ \sigma = \left[\sum_{i = 1}^{n} \,[{\log_{10}T^{i}_{1/2}}({\rm expt.}) -\log_{10}T^{i}_{1/2}({\rm cal.})]^2\, / \,n\right]^{1/2}. $

(15) Here,
${\log_{10}T^{i}_{1/2}}({\rm expt.})$ and${\log_{10}T^{i}_{1/2}}({\rm cal.})$ are the logarithmic forms of the experimental and calculated$ 2p $ radioactivity half-lives for the$ i $ -th nucleus, respectively. For comparison, the$ \sigma $ values of these four models are listed in Table 3, which clearly shows that the$ \sigma = {0.701} $ of this paper is better than that of the GLDM and Gamow-like model with the same data. This indicates that our mode is suitable to studying$ 2p $ radioactivity half-lives.Model Our model GLDM ELDM Gamow-like $\sigma$ 

0.701(10) $0.852(10)$ 

$0.531(4)$ 

$0.844(10)$ 

Table 3. Standard deviation (
$\sigma$ ) between the experimental and theoretical data calculated using our model, GLDM, ELDM, and Gamow-like model.In addition, as an application, we extend our model to predicting the half-lives of 15 possible
$ 2p $ radioactivity candidates with$ Q_{2p} $ $ > $ 0 obtained from the evaluated atomic mass table AME2016 [78, 79]. For comparison, the GLDM, ELDM, and Gamow-like models are also used. The detailed results are shown in Table 4, where the first three columns represent the$ 2p $ radioactivity candidates, experimental$ 2p $ radioactivity released energy ($ Q_{2p} $ ) and orbital angular momentum (l), respectively. The last four columns are the theoretical values of$ 2p $ radioactivity half-lives calculated using GLDM, ELDM, Gamow-like model, and our model in logarithmic form, respectively. The table clearly shows that for short-lived$ 2p $ radioactivity nuclei, the orders of magnitude of most predicted results calculated using our model are consistent with the ones obtained using the other three models. However, for long-lived$ 2p $ radioactivity nuclei, such as$ ^{49} $ Ni and$ ^{60} $ Ge, the magnitude of our model is less than 2-3 orders of the other three models. To further clearly compare the evaluation capabilities of those four models, the relationship between the predicted results of those four models listed in Table 4 and coulomb parameters considering orbital angular momentum (($ Z_{d}^{0.8} $ +$ l^{\,0.25} $ )$ Q_{2p}^{-1/2} $ ) i.e., new Geiger-Nuttall law for two-proton radioactivity proposed by Liu$ et $ $al.$ [38] is plotted in Fig. 2. The figure shows that the predicted results of those four models are all linearly dependent on ($ Z_{d}^{0.8} $ +$ l^{\,0.25} $ )$ Q_{2p}^{-1/2} $ and our model can better conform to the linear relationship.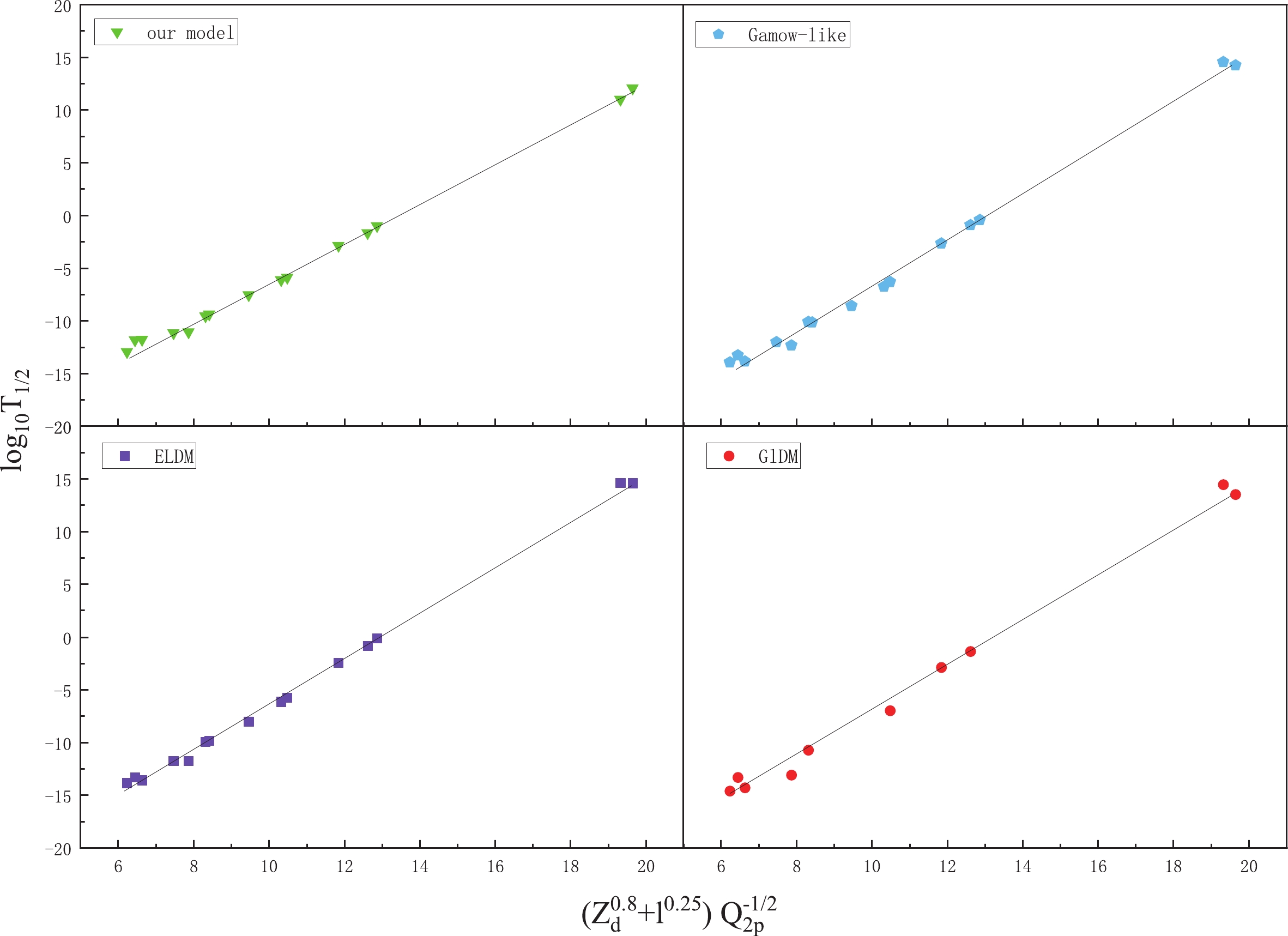
Figure 2. (color online) Relationship between the predicted results of these four models listed in Table 3 and coulomb parameters ((
$Z_{d}^{0.8}$ +$l^{\,0.25}$ )$Q_{2p}^{-1/2}$ ) considering the effect of the orbital angular momentum, i.e., new Geiger-Nuttall law for two-proton radioactivity proposed by Liu$et$ $al$ .Nucleus $Q_{2p}/{\text{MeV} }$ 

l ${\log_{10} }{T}_{1/2}^{\rm GLDM}/{\text{s} }\;[62]$ 

${\log_{10} }{T}_{1/2}^{\rm ELDM}/{\text{s} }\;[20]$ 

${\log_{10} }{T}_{1/2}^{\rm Gamow-like}/{\text{s} }\;[63]$ 

${\log_{10} }{T}_{1/2}^{\rm our\;model}/{\text{s} }$ 

$ ^{22} $ Si

1.283 0 $ -13.30 $ 

$ -13.32 $ 

$ -13.25 $ 

$ -11.78 $ 

$ ^{26} $ S

1.755 0 $ -14.59 $ 

$ -13.86 $ 

$ -13.92 $ 

$ -12.93 $ 

$ ^{34} $ Ca

1.474 0 $ -10.71 $ 

$ -9.91 $ 

$ -10.10 $ 

$ -9.51 $ 

$ ^{36} $ Sc

1.993 0 $ -11.74 $ 

$ -12.00 $ 

$ -11.12 $ 

$ ^{38} $ Ti

2.743 0 $ -14.27 $ 

$ -13.56 $ 

$ -13.84 $ 

$ -11.77 $ 

$ ^{39} $ Ti

0.758 0 $ -1.34 $ 

$ -0.81 $ 

$ -0.91 $ 

$ -1.62 $ 

$ ^{40} $ V

1.842 0 $ -9.85 $ 

$ -10.15 $ 

$ -9.34 $ 

$ ^{42} $ Cr

1.002 0 $ -2.88 $ 

$ -2.43 $ 

$ -2.65 $ 

$ -2.83 $ 

$ ^{47} $ Co

1.042 0 $ -0.11 $ 

$ -0.42 $ 

$ -0.97 $ 

$ ^{49} $ Ni

0.492 0 $ 14.46 $ 

$ 14.64 $ 

$ 14.54 $ 

$ 11.05 $ 

$ ^{56} $ Ga

2.443 0 $ -8.00 $ 

$ -8.57 $ 

$ -7.51 $ 

$ ^{58} $ Ge

3.732 0 $ -13.10 $ 

$ -11.74 $ 

$ -12.32 $ 

$ -11.06 $ 

$ ^{59} $ Ge

2.102 0 $ -6.97 $ 

$ -5.71 $ 

$ -6.31 $ 

$ -5.88 $ 

$ ^{60} $ Ge

0.631 0 $ 13.55 $ 

$ 14.62 $ 

$ 14.24 $ 

$ 12.09 $ 

$ ^{61} $ As

2.282 0 $ -6.12 $ 

$ -6.76 $ 

$ -6.07 $ 

Table 4. Comparison of the predicted
$ 2p $ radioactivity half-lives using GLDM, ELDM, Gamow-like model, and our model. The$ 2p $ radioactivity released energy ($ Q_{2p} $ ) and orbital angular momentum ($ l $ ) of the two emitted protons were obtained from Ref. [20]. -
In this paper, using the two-potential approach comprising the Skyrme-Hartree-Fock to calculate the nuclear potential and the Skyrme effective interaction of SLy8, we systematically studied the
$ 2p $ radioactivity half-lives of nuclei with 4$ < $ Z$ < $ 36. The calculated results can closely reproduce experimental data. In addition, we extended our model to predict the half-lives of 15 possible$ 2p $ radioactivity candidates with$ Q_{2p} $ $ > $ 0 obtained from the evaluated atomic mass table AME2016 and compared our calculated results with the theoretical ones calculated using the GLDM, ELDM, and Gamow-like model. The predicted results of these four models are all linearly dependent on ($ Z_{d}^{0.8} $ +$ l^{\,0.25} $ )$ Q_{2p}^{-1/2} $ , i.e., the new Geiger-Nuttall law for two-proton radioactivity proposed by Liu$ et $ $ al $ . -
We would like to thank X. -D. Sun, J. -G. Deng, J. -L. Chen and J. -H. Cheng for useful discussion.
Systematic study of two-proton radioactivity half-lives using the two-potential and Skyrme-Hartree-Fock approaches
- Received Date: 2021-05-31
- Available Online: 2021-12-15
Abstract: In this work, we systematically study the two-proton (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
























 DownLoad:
DownLoad: