-
Since the discovery of the
$ X(3872) $ state [1], many charmonium-like structures have been observed with properties beyond the expectations of conventional quark models. In the baryon sector, the LHCb Collaboration announced the observation of hidden-charm pentaquark states in the$ J/\psi p $ invariant mass distribution in the$ \Lambda_b^0\to J/\psi K^- p $ decay in 2015 [2], and the measurement results were updated in 2019 [3]. These new hidden-charm structures are widely regarded as candidate exotic hadrons, and have been extensively studied (see recent reviews [4-16] for more information).So far most of the observations of these new structures were made at electron-positron colliders and hadron colliders (including the B factories). Nevertheless, there have been attempts to search for them in photoproduction processes, which is useful not only for confirming their existence but also for gaining more insights into their nature. In particular, photoproduction processes are free of triangle singularities that sometimes induce ambiguities in interpreting the observed peaks as resonances [3, 17-25] (see Ref. [16] for a review). Hence, the photo-induced production of pentaquarks has been proposed to discriminate their nature [26-30]. The COMPASS Collaboration searched for exclusive photoproduction of the
$ Z_c(3900)^\pm\to J/\psi\pi^\pm $ transition, but found no signal [31]. Subsequently, a search was conducted for the muoproduction of the$ X(3872)\to J/\psi\pi^+\pi^- $ transition, and the observation of a structure with a mass of approximately 3.86 GeV was reported [32]. The C-parity was, however, negative, opposite to that of the$ X(3872) $ state [33, 34]. Its relation to the$ h_c(2P) $ and other$ PC = ++ $ states around 3.9 GeV through heavy quark spin symmetry deserves to be explored. In Ref. [35], this negative C-parity state was suggested to be an isoscalar$ D\bar D^* $ molecule with$ J^{PC} = 1^{+-} $ as the spin partner of the$ X(3872) $ state. In this regard, the recently reported narrow structure$ X(4014) $ with a mass of$ (4014.4\pm4.1\pm0.5) $ MeV and a width of$ (6\pm16\pm6) $ MeV [36] is an excellent candidate for the$ 2^{++} $ spin partner of the$ X(3872) $ that is generally predicted in hadronic molecular models [35, 37-44]. Its mass and width nicely agree with the predictions in Ref. [42].The GlueX Collaboration searched for the$ P_c $ pentaquark states through the near-threshold$ J/\psi $ exclusive photoproduction off the proton in Hall D at Jefferson Lab (JLab), and no evidence was found [45], implying a small branching fraction for the decay into$ J/\psi p $ [46, 47]. There is also a proposal to search for the$ P_c $ state in Hall C at JLab [48].There have been many estimates of the photoproduction cross sections of hidden-charm states for exclusive processes [26-31, 47, 49-61]. The analysis of the exclusive productions of pentaquarks at both JLab and the Electron-ion collider in China (EicC) [60] suggests that the colliding mode is more useful than the fixed-target mode at JLab, for extracting the feeble exclusive pentaquark signal. For the three experiments of interest here, i.e., EicC, COMPASS and the Electron-Ion Collider in US (US-EIC), the c.m. energies were much higher than the hidden-charm hadron masses, thus allowing for their production together with many other light hadrons. Although semi-inclusive productions have larger backgrounds compared with exclusive processes, the production rates could exceed those of the exclusive processes by a few orders of magnitude, which makes them promising for studying exotic hadrons.
In this paper, we will estimate the semi-inclusive lepto-production rates of the
$ X(3872) $ [1],$ Z_c(3900) $ [62, 63],$ Z_c(4020) $ [64],$ Z_{cs}(3985) $ [65], and$ P_c $ states [2, 3] together with their spin partners predicted by the hadronic molecular model [68-74] (We regard the$ Z_{cs}(4000) $ reported by LHCb as due to the same origin following the suggestion of Refs. [66, 67]). The results will be presented for three experiments: the proposed US-EIC with the ep c.m. energy covering 30–140 GeV and a luminosity of$ 10^{34}\;\text{cm}^{-2}\;\text{s}^{-1} $ or higher [75], EicC at lower energies ($15 - 25$ GeV) [76, 77], and the COMPASS experiment with muon beams at CERN [78].Notably, almost all of the existing literature [26-31, 47, 49-61] estimated the photoproduction cross sections of hidden-charm or hidden-bottom resonances using the vector-meson dominance model, where a photon is assumed to convert to a highly virtual vector heavy quarkonium, such as the
$ J/\psi $ , and is assumed to interact with a proton. However, Ref. [79] pointed out the importance of open-charm channels in the$ J/\psi $ near-threshold photoproduction, and the estimated total cross section considering only the intermediate$ \Lambda_c\bar D^{(*)} $ channels quantitatively agrees with the GlueX measurement in the near-threshold region [45]. The reliability of the vector-meson dominance model in the photoproduction of vector heavy quarkonia has also been questioned recently based on the Dyson–Schwinger equation calculations in Ref. [80]. Here, we considered the mechanism of open-charm channels—the charmed-hadron pairs are produced first and the hadronic molecular candidates are produced through their final state interactions.This paper is organized as follows. We first introduce the formalism of the semi-inclusive production of hadronic molecules in Sec. II. Then we present the production rates of some typical exotic hadrons, including
$ X(3872) $ ,$ Z_c(3900) $ ,$ Z_c(4020) $ ,$ Z_{cs}(3985) $ , and seven$ P_c $ states, which are considered as hadronic molecules of$ D\bar D^*+c.c. $ ,$ D\bar D^*+c.c. $ ,$ D^*\bar D^* $ ,$ D_s\bar D^*+ D_s^*\bar D $ , and$ \Sigma_c^{(*)}\bar D^{(*)} $ , respectively, at the proposed EicC, US-EIC and the currently running COMPASS discussed in Sec. III. The last section summarizes the study. -
A resonance corresponds to a pole of the S-matrix. For the S-matrix element between the initial state, which, in this study, was a lepton-proton pair, and the final state containing the exotic hadron of interest, a complete set of states that can couple to the exotic hadron can be inserted. All of them can contribute to the production. Yet, it is natural to expect that the ones that couple most strongly to the exotic hadron have the most significant contributions. For hadronic molecules, such states correspond to the particles that are bound together to give the dominant part of the wave function at large distances.
The lepto-production of an exotic hadron X in the molecular picture is shown in Fig. 1; this mechanism assumes that the formation of a hadronic molecule occurs after the production of its constituents. A detailed description of the mechanism can be found in Refs. [81-83]. The mechanism can be applied to the
$ X(3872) $ and$ Z_c(3900) $ states, which are known to couple strongly to the$ D\bar D^* $ pair (and their antiparticles) [34, 84-88] as well as to the$ P_c $ hidden-charm pentaquarks. It has been used for estimating the prompt production cross sections of the$ X(3872) $ state [89, 90] and its partners [83], the$ Z_c $ and$ Z_b $ states [91], the charm-strange hadronic molecules [82], and the$ P_c $ states [92] at hadron colliders. As for the production of the$ X(3872) $ state, despite the debates [11, 83, 89, 90, 93-101], the estimated total cross sections [83, 90] are consistent with the CDF [102] and CMS [103] measurements.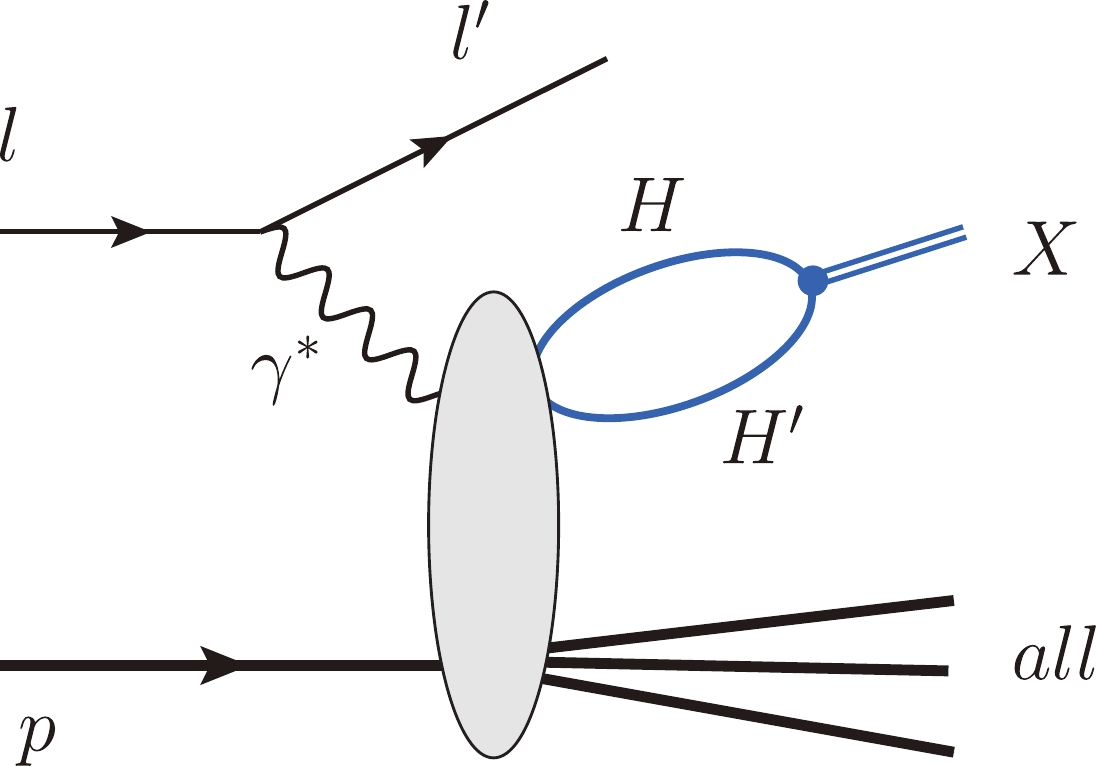
Figure 1. (color online) Mechanism of the hadronic molecule production, where X denotes the
$ HH^{\prime} $ molecular state, in the lepton-proton semi-inclusive reaction. Here all represents all the produced particles other than the final lepton and X.The prompt production of hadronic molecules can be factorized into short-distance and long-distance contributions [81, 89]. The hadron pairs, denoted as
$ HH' $ , are produced at short distances, and then form loosely bound hadronic molecules at long distances. The production cross section may be written as [83]$ \sigma[X] = \frac{1}{4m_Hm_{H'}} g^2 |G(E)|^2 \frac{{\rm d}\sigma[HH^{\prime}(k)]}{{\rm d}k}\frac{4\pi^{2}\mu}{k^{2}}, $

(1) where μ is the reduced mass of the
$ HH^{\prime} $ pair and${\rm d}\sigma[HH^{\prime}(k)]/ {\rm d}k$ is the differential cross section of the$ HH^{\prime} $ production with k the three-momentum magnitude in the center-of-mass frame of the$ HH^{\prime} $ system. Without considering the final state interaction, its behavior follows the phase space,$ \frac{{\rm d}\sigma[HH^{\prime}(k)]}{{\rm d}k} \propto k^2. $

(2) The exact behavior may be approximated by Monte Carlo (MC) event generators [81]. The ultraviolet divergent loop function
$ G(k) $ can be regularized by employing a Gaussian regulator, and yields [40]$ G(E) = -\frac{\mu}{(2\pi)^2}\left\{\sqrt{2\pi}\,\Lambda + 2k\,\pi\,{\rm e}^{-2\,k^2/\Lambda^2}\left[i-\text{erfi}\left(\frac{\sqrt{2}k}{\Lambda}\right)\right]\right\}, $

(3) where
$ k^2 = 2\mu(E-m_H-m_{H'}) $ with E the invariant mass of the$ HH' $ pair,$\text{erfi}(z) = (2/\sqrt{\pi})\int_0^z e^{t^2} {\rm d}t$ is the imaginary error function, and Λ is the cut-off momentum in the Gaussian regulator. A reasonable choice of Λ is$ 0.5-1 $ GeV, which is used in the literature on hadronic molecular models for the states of interest here [41, 66, 69]. The long-distance contribution is contained in the effective coupling of the hadronic molecule to its constituents g, whose square is given by the residue of the transition matrix element for the scattering$ HH'\to HH' $ at the pole,$ g^2 = \lim\limits_{E\to E_\text{pole} } \left(E^2-E^2_\text{pole} \right)\, T(E), $

(4) where
$ E_\text{pole} = M $ for a bound or a virtual state pole, and$E_\text{pole} = M-{\rm i}\,\Gamma/2$ for a resonance pole, with M and Γ being the mass and the width of the hadronic molecule, respectively. In the above equation,$ T(E) $ should take its value on the specific Riemann sheet where the pole is located.For the T-matrix element, we consider the Lippmann-Schwinger equation,
$ T(E) = V + V G(E) T(E), $

(5) with constant contact terms for the
$ HH'\to HH' $ scattering collected as the V matrix, which is the leading order nonrelativistic approximation for molecular states close to thresholds. The molecular states correspond to the poles of the T-matrix at the solutions of$ {\rm{det}}[1- $ $ V\,G(E_\text{pole})] = 0 $ .The values of the constant contact terms for the
$ Z_c $ and$ Z_{cs} $ states are given by Eq. (16) in Ref. [66]. For the$ X(3872) $ state, we take the V-matrix as given in Ref. [104],$ V = \frac{1}{2}\left( {\begin{array}{*{20}{c}} {{C_0} + {C_1}}&{{C_0} - {C_1}}\\ {{C_0} - {C_1}}&{{C_0} + {C_1}} \end{array}} \right), $

(6) where the two channels correspond to the neutral and charged
$ D\bar D^*+c.c. $ pairs. The two low-energy parameters$ C_0 $ and$ C_1 $ can be solved by using as inputs the$ X(3872) $ mass and the isospin violation ratio of the amplitudes for the$ X(3872) $ decays to$ J/\psi\pi\pi $ and$ J/\psi\pi\pi\pi $ [104, 105]. While for the$ P_c $ states, the relevant hadron pairs are$ \Sigma_c^{(*)}\bar D^{(*)} $ that can form seven S-wave combinations. Heavy quark spin symmetry (HQSS) imposes a constraint of two low-energy parameters in the leading order of the nonrelativistic expansion. The linear combinations of the two parameters for all seven$ \Sigma_c^{(*)}\bar D^{(*)} $ can be found in Refs. [71, 72]. They can be fixed from reproducing the masses of two states among the$ P_c(4312) $ (as the$ \Sigma_c\bar D $ bound state with$ J^P = 1/2^- $ ),$ P_c(4440) $ and$ P_c(4457) $ (as$ \Sigma_c\bar D^* $ bound states with one of them being$ J^P = 1/2^- $ and the other being$ 3/2^- $ ) [69]. Recently, it was shown in Refs. [72, 74] that the$ J/\psi p $ line shape measured by LHCb can be well described in the hadronic molecular picture with HQSS built in. In this study, we used the seven$ P_c $ masses from the preferred scheme II in the analysis of Ref. [72] as inputs for determining the two low-energy parameters in the contact terms. -
With the assumed production mechanism, as discussed in Sec. II, the hadronic constituents were first produced and moved with a small relative momentum such that they were in the kinematic region of molecular formation. We first generated events of the semi-inclusive lepton-proton scattering process using the Monte Carlo generator Pythia [106] at the three platforms (COMPASS, EicC and US-EIC) according to the energy configurations in Table 1. The pair of constituent hadrons with a small relative momentum were picked out from the final states generated by Pythia③. Their differential cross sections with respect to the relative momenta are shown in Fig. 2. Here, we consider the
$ D^0\bar{D}^{*0} $ and$ \Sigma_c^{*+}\bar{D}^0 $ pairs as examples; it is shown that the distributions behave exactly as prescribed by Eq. (2), proportional to$ k^2 $ .COMPASS EicC US-EIC Lepton energy/GeV 200 3.5 20 Proton energy/GeV 0 20 250 Luminosity/( $\text{cm}^{-2}\text{s}^{-1}$ )

$2\times10^{32}$ 

$2\times10^{33}$ 

$10^{34}$ 

Table 1. Energy configurations and luminosities of the three machines studied in this work. The lepton is muon for COMPASS and electron for EicC and US-EIC. Note that COMPASS is a fixed-target experiment, and a dilution factor needs to be considered for the luminosity in estimating event numbers.
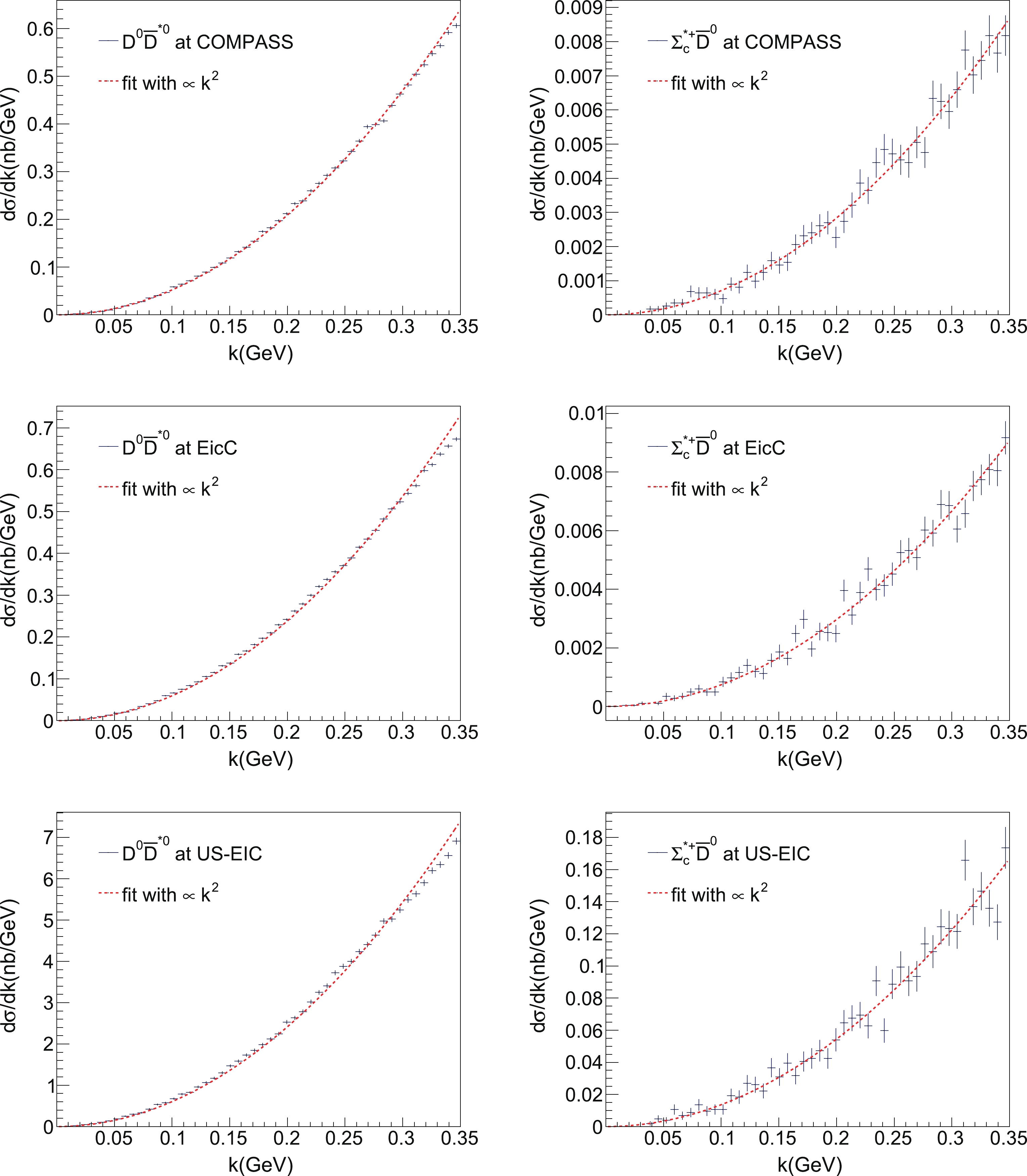
Figure 2. (color online) Differential cross sections
${{\rm d}\sigma}/{{\rm d}k}$ (in units of nb/GeV) for the semi-inclusive production$D^{0}\bar{D}^{*0}$ and$\Sigma_c^{*+}\bar{D}^0$ at COMPASS, EicC, and EIC, by lepton-proton scattering. The histograms were obtained from the Pythia event generator while the curves were fitted according to the momentum dependence$k^2$ .From Eq. (1), we could estimate the cross sections, which depend on the cut-off parameter Λ in the loop function. In principle the cut-off dependence should be absorbed by that of the short-distance production of the hadron pairs. As an order-of-magnitude estimate of the cross sections, we simply used the hadron pair productions from Pythia and chose the cut-off parameter to be
$ \Lambda \in [0.5,1.0] $ GeV, as that used in the calculation of the spectrum in hadronic molecular models. The estimated cross sections with the uncertainty caused by the cut-off range are shown in Table 2 for the$ X(3872) $ ,$ Z_c(3900) $ ,$ Z_c(4020) $ , two$ Z_{cs} $ states and seven$ P_c $ states at COMPASS, EicC and US-EIC. Evidently, COMPASS and EicC have similar cross sections, while US-EIC has one order of magnitude larger cross sections, owing to its higher center-of-mass energy.Constituents $J^{P(C)}$ 

COMPASS EicC US-EIC $X(3872)$ 

$D\bar{D}^{*}$ 

$1^{++}$ 

19(78) 21(89) 216(904) $Z_c(3900)^0$ 

$D\bar{D}^{*}$ 

$1^{+-}$ 

$0.3\times10^3$ (

$1.2\times10^3$ )

$0.4\times10^3$ (

$1.3\times10^3$ )

$3.8\times10^3$ (

$14\times10^3$ )

$Z_c(3900)^+$ 

$D^{*+}\bar{D}^0$ 

$1^{+}$ 

$0.2\times10^3$ (

$0.9\times10^3$ )

$0.3\times10^3$ (

$1.0\times10^3$ )

$2.7\times10^3$ (

$9.9\times10^3$ )

$Z_c(4020)^0$ 

$D^{*}\bar{D}^{*}$ 

$1^{+-}$ 

$0.1\times10^3$ (

$0.5\times10^3$ )

$0.2\times10^3$ (

$0.6\times10^3$ )

$1.7\times10^3$ (

$6.3\times10^3$ )

$Z^-_{cs}$ 

$D^{*0}D_s^{-}$ 

$1^{+}$ 

8.3(29) 19(69) 253(901) $Z_{cs}^{*-}$ 

$D^{*0}D_s^{*-}$ 

$1^{+}$ 

6.2(22) 14(51) 192(679) $P_c(4312)$ 

$\Sigma_c\bar{D}$ 

$\frac12^{-}$ 

0.8(4.1) 0.8(4.1) 15(73) $P_c(4440)$ 

$\Sigma_c\bar{D}^{*}$ 

$\frac32^{-}$ 

0.6(4.3) 0.7(4.7) 11(79) $P_c(4457)$ 

$\Sigma_c\bar{D}^{*}$ 

$\frac12^{-}$ 

0.5(2.0) 0.6(2.2) 9.9(36) $P_c(4380)$ 

$\Sigma_c^{*}\bar{D}$ 

$\frac32^{-}$ 

1.6(8.0) 1.6(8.4) 30(155) $P_c(4524)$ 

$\Sigma_c^{*}\bar{D}^{*}$ 

$\frac12^{-}$ 

0.8(3.6) 0.8(3.9) 14(67) $P_c(4518)$ 

$\Sigma_c^{*}\bar{D}^{*}$ 

$\frac32^{-}$ 

1.2(6.6) 1.2(6.9) 22(123) $P_c(4498)$ 

$\Sigma_c^{*}\bar{D}^{*}$ 

$\frac52^{-}$ 

1.1(9.3) 1.2(9.8) 21(173) Table 2. Integrated cross sections (in units of pb) for
$l+p\to \text{HM}$ +all, where$\text{HM}=X(3872), \;Z_c(3900)^{0/+}, \;Z_c(4020) $ , and seven Pc states. The listed quantum numbers for these states are those in the considered hadronic molecular model. The lepton l is muon for COMPASS, and is electron for EicC and US-EIC. Results outside (inside) brackets were obtained using cutoff$\Lambda=0.5 \;\text{GeV}\;(1\;\text{GeV})$ , respectively.The COMPASS Collaboration already searched for the exclusive muoproduction of
$ {X(3872)} $ with the reaction$ \mu^+ N \to \mu^+ (J/\psi\pi^+\pi^-)\pi^\pm N' $ using data with incoming muons of 160 GeV and 200 GeV momenta [32]. Although no signal of the$ {X(3872)} $ state was seen, a negative C-parity$ \tilde{X}(3872) $ with a mass of$ (3860.0\pm10.4) $ MeV and width$ <51 $ MeV (CL = 90%) was reported with a statistical significance of$ 4.1\sigma $ . The measured cross section was$ \sigma_{\gamma N\to \tilde X(3872) N'}\times $ $ {\cal{B}}_{\tilde X(3872)\to J/\psi\pi^+\pi^-} = (71\pm 28_\text{stat}\pm $ $ 39_\text{syst}) $ pb. The upper limit for the$ X(3872) $ production at COMPASS was also given as$\sigma_{\gamma N\to X(3872) N'}\times $ $ {\cal{B}}_{X(3872)\to J/\psi\pi^+\pi^-}< 2.9 $ pb (CL = 90%). The measured upper limit for the exclusive production of the$ Z_c(3900)^\pm $ at COMPASS was$ \sigma_{\gamma N\to Z_c(3900)^\pm N'}\times {\cal{B}}_{Z_c(3900)^\pm\to J/\psi\pi^\pm}<52 $ pb (CL = 90%) [31]. Although the photoproduction rates should be higher than the leptoproduction ones by roughly two orders of magnitude, the estimates for the$ X(3872) $ and$ Z_c(3900)^\pm $ states at COMPASS, listed in Table 2 , are not inconsistent with these upper limits—the semi-inclusive rates should be much higher than the exclusive ones, and$ J/\psi \pi^+\pi^- $ and$ J/\psi\pi^\pm $ contribute only a small part of the decay fractions of the$ X(3872) $ [34] and$ Z_c(3900) $ [87] states, respectively. It is of interest to investigate the exotic states at COMPASS through the semi-inclusive processes considered here.However, for
$ P_c $ , the GlueX measurements [45] were performed with energies just above the threshold, and far below the energies considered here. Thus, a direct comparison is not possible. Still, our result for the semi-inclusive cross sections of the$ P_c $ states at EicC are on the order of a few pb, implying a few hundreds of pb for the corresponding photoproduction cross sections. Assuming the$ P_c \to J/\psi p $ branching fractions to be on the per cent level, we expect$ \sigma(\gamma p \to P_c)\times{\cal{B}}(P_c\to J/\psi p) $ to be on the order of pb at EicC, and the cross sections at GlueX would not be larger. One the one hand, this is compatible with the GlueX upper limits (a few nb [45]); on the other hand, this means that it is difficult to observe the$ P_c $ states at GlueX.The exclusive photoproduction cross sections of
$ Z_{cs}^{(*)-} $ were estimated to be around 500 pb at the c.m. energy of EicC, using the vector meson dominant model [107], where the results are independent on their inner structure. The exclusive leptoproduction would be roughly two orders of magnitude smaller, making it around 5 pb. It is not in conflict with our result under the molecular assumption through the semi-inclusive process in Table 2.Considering the luminosities in Table 1, these exotic states can be copiously produced at EicC and US-EIC. Taking the
$ {X(3872)} $ state as an example, there will be approximately$ 8\times10^3 $ and$ 4\times10^5 $ events produced per day at EicC and US-EIC, respectively. If we set the branching fractions$ {\cal{B}}( {X(3872)}\to J/\psi\pi\pi) = (3.8\pm1.2) $ %,$ {\cal{B}}(J/\psi\to l^+l^-) = 12 $ % [34] and assume the detection efficiency of 50%, the reconstructed event numbers will be approximately 20 and 1000 a day for EicC and US-EIC, respectively. In contrast, owing to the much higher c.m. energies, the produced exotic states at US-EIC are distributed in the large rapidity range, which complicates the detector design. Therefore, further simulations of the final particle distribution at US-EIC are necessary. -
We presented order-of-magnitude estimates of the semi-inclusive production rates of hidden-charm exotic hadrons through lepton-proton scattering processes. The present calculation was based on the hadronic molecular picture with the factorization assumption, where the hadron constituents are produced first and subsequently bound together through the final state interaction. Three machines were considered, including COMPASS, EicC and US-EIC. The cross sections for the
$ X(3872) $ and$ Z_c(3900)^\pm $ states production at COMPASS were not inconsistent with the reported upper limits for exclusive photoproduction reactions. According to our estimates, the proposed electron-ion colliders EicC and US-EIC can produce a large number of events for the near-threshold hidden-charm molecular states. Moreover, regarding the current COMPASS experiment, it is also promising to search for these exotics through the semi-inclusive process. -
Z.Y. gratefully acknowledges the insightful discussions with Meng-Lin Du and Xu Cao.
Semi-inclusive lepto-production of hidden-charm exotic hadrons
- Received Date: 2021-07-29
- Available Online: 2021-12-15
Abstract: We investigate the semi-inclusive production of hidden-charm exotic states, including the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: