-
Doubly-heavy tetraquarks including
$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ ,$ T^{\{bc\}}_{[\bar{q}\bar{q}']} $ , and$ T^{\{bb\}}_{[\bar{q}\bar{q}']} $ have drawn considerable attention from theorists after the discovery of the first double-charm hadron$ \Xi_{cc}^{++} $ [1]. The doubly-heavy tetraquarks can shed light on strong dynamics and greatly help us identify the nature of the exotic$ XYZ $ states or structures, e.g., cusps or true resonances. In addition, several studies of both heavy quark symmetry and lattice [2-8] suggest that some of them have masses below the threshold and thus can only decay weakly. If such weakly-decaying tetraquarks are found, they will provide evidence of compact diquarks as building blocks of hadronic matter. Among these doubly-heavy tetraquarks,$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ is the most promising one to be observed in experiments in the near future, because both its production rate and detection efficiency are the highest at the LHCb. In this work, we analyze the potential of finding$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ at the LHCb and also future Z-factories [9, 10], evaluating their production cross sections at the two kinds of facilities and proposing possible golden channels according to their decay properties.Decay properties of the doubly-heavy tetraquarks
$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ rely on whether their masses are above or below the thresholds$ D^0D^{*+} $ and$ D^*D_s^+ $ . If they are stable particles below the threshold, they will mainly decay radiatively (or even weakly according to [11]) and thus have a relatively long lifetime, which will considerably suppress the background and make the experimental search easier. In contrast, if they are unstable particles above the thresholds①, they will decay strongly and still have a good chance to be found at the LHCb using a method similar to that in [12]. Their masses have been calculated in many different procedures, such as QCD sum rule [13-17], lattice [18], Bethe-Salpeter equation approach [11], heavy quark symmetry [3, 19], and several QCD inspired models [2, 20-32]. The results are listed in Table 1 in the form of the mass differences of$ T^{\{cc\}}_{\bar{n}\bar{n}'} $ and$ T^{\{cc\}}_{\bar{n}\bar{s}} $ ($ n^{(\prime)} = u $ or d) from their thresholds$ D^0D^{*+} $ and$ D^*D_s^+ $ , respectively. These results are far from conclusive because some of the calculations suggest they lie above the thresholds while the others are against it. As a result, the decay channels of$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ are analyzed case by case.Reference [21] [22] [23] [24] [25] [26] [13] [18] [3] [19] [15] $ T^{\{cc\}}_{\bar{n}\bar{n}'} $ 

−79 −96 +53 −150 +166 +60 − AT +102 +88 +25 $ T^{\{cc\}}_{\bar{n}\bar{s}} $ 

−9 −56 +128 +94 +255 +166 +143 AT +179 +181 −15 Reference [11] [27] [28] [29] [2] [30] [14] [31] [20] [32] $ T^{\{cc\}}_{\bar{n}\bar{n}'} $ 

−215 BT −149 −182 +7 +98 +91 +125 AT AT Table 1. Theoretical predictions on the mass differences of
$ T^{\{cc\}}_{\bar{n}\bar{n}'} $ and$ T^{\{cc\}}_{\bar{n}\bar{s}} $ from their thresholds$ D^0D^{*+} $ and$ D^*D_s^+ $ , respectively, in units of MeV. The quarks$ n,n' $ = u or d. For some works without explicit numerical results, we use "AT" and "BT" denoting "above threshold" and "below threshold," respectively.The rest of the paper is organized as follows. In section II, we study the production of
$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ at both the LHCb and future Z-factories. According to our estimation of the production cross sections, the LHCb has produced$ \mathcal{O}(10^8) $ double-charm tetraquarks to date, and this number will increase by almost one order of magnitude by the end of Run 4 [33, 34]. It is also shown that a Tera-Z factory will produce$ \mathcal{O}(10^6) $ double-charm tetraquarks in a very clean environment. In section III, possible decay channels of$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ are discussed, in three cases with the double-charm tetraquarks either above or below the$ DD^* $ and$ DD\gamma $ thresholds. For the LHCb, we propose some decay channels to search for the double-charm tetraquarks, because they have relatively large branching ratios, and more importantly, all of their final-state particles have high detection efficiencies, e.g.,$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^0D^{*+}\to $ $ D^0D^0\pi^+ $ and$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^+K^-\pi^+ $ . In contrast, future Z-factories have an advantage over the LHCb in searching for other decay channels containing a photon, e.g.,$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to $ $ D^0D^+\gamma $ . We conclude our study in section IV. -
Following the approach proposed in [35-37], we estimate the production rate of double-charm hadrons
$ H_{cc} $ at the LHCb and future Z-factories. The basic idea is as follows. First, the underlying processes for their production at the quark level are$ pp\to cc\bar{c}\bar{c} +X $ and$ e^+e^-\to Z\to $ $ cc\bar{c}\bar{c} $ at these two kinds of facilities, respectively. The two charm quarks must stay close enough to form a$ cc $ diquark jet, which further fragments into different kinds of double-charm hadrons. The invariant mass of the two heavy quarks$ m_{QQ'} $ is used to parameterize their collinear level, and if$ m_{QQ'} $ is smaller than some cut-off value$ M_{QQ'}(\Delta M)\equiv m_Q+m_{Q'}+\Delta M $ , we regard the two heavy quarks as a$ QQ' $ diquark that will eventually produce a doubly-heavy hadron. In contrast, if$ m_{QQ'} $ exceeds$ M_{QQ'}(\Delta M) $ , the two heavy quarks fragment separately. The parameter$ \Delta M $ can be determined by matching the partonic$ b\bar{c} $ production simulation to the experimental measurements of the$ B_c $ meson production cross sections [38], and it has been found by [35, 37] that$ \Delta M = \left\{ {\begin{array}{*{20}{l}} {\left( {2.0_{ - 0.4}^{ + 0.5}} \right)\;{{\rm{GeV}}},\;{\rm{for}}\;{\rm{LHCb}},}\\ {\left( {2.7_{ - 0.5}^{ + 1.3}} \right)\;{{\rm{GeV}}},\;{\rm{for}}\;{{Z}}\;{\rm{factories}}.} \end{array}} \right.$

(1) Next, we will discuss the production of the doubly-heavy hadrons at the LHCb and future Z-factories separately.
LHCb: For the analysis of
$ H_{cc} $ production at the LHC with$ \sqrt{s} = 13 $ TeV, we generate$ 10^5 $ $ pp\to cc\bar{c}\bar{c} +X $ events via the Monte Carlo generator MadGraph5_aMC@NLO [39] at the next-to-leading-order level showered by Pythia8 [40, 41]. It is found that the total cross section$ \sigma(pp\to cc\bar{c}\bar{c} +X) \approx 4.9\times 10^7 $ pb, and after applying the invariant mass cut in (1), we obtain$ \sigma(p+p\to H_{cc} + X) = \left(3.1^{+1.7}_{-0.7}\right) \times 10^5\ {\rm{pb}} \; , $

(2) in the transverse momentum range
$ 4<p_{\rm{T}}<15 $ GeV and the pseudorapidity range$ 2< \eta <4.5 $ .The double-charm hadrons
$ H_{cc} $ include both the double-charm baryons$ \Xi_{cc}^{++} (ccu) $ ,$ \Xi_{cc}^+ (ccd) $ , and$ \Omega_{cc}^- (ccs) $ and the double-charm tetraquarks$ T^{\{cc\}}_{[\bar q \bar q^\prime]} $ and their excited states. Therefore, we still need to know the relative fractions of$ H_{cc} $ to these hadrons. It is difficult to calculate these non-perturbative fragmentation ratios, while we can approximately borrow the corresponding ratios of a b-quark jet under the heavy quark - heavy diquark symmetry. Such ratios have been measured by the LHCb [42, 43] as$ \begin{aligned}[b] \left[ {\frac{{{f_{\Lambda _b^0}}}}{{{f_d}}}} \right]({p_{\rm{T}}}) = &\;(0.151 \pm 0.030) + \exp \left[ ( - 0.57 \pm 0.11) \right.\\ &-\left. (0.095 \pm 0.016){p_{\rm{T}}}({{\rm{GeV}}}) \right]\;,\\ \left[ {\frac{{{f_s}}}{{{f_d}}}} \right]({p_{\rm{T}}}) = &\;(0.263 \pm 0.008) \\ &+ (( - 17.6 \pm 2.1) \times {10^{ - 4}}) \cdot {p_{\rm{T}}}({{\rm{GeV}}})\;, \end{aligned}$

(3) which are
$ p_{\rm{T}} $ dependent. In addition, we assume that for states containing the same valence quarks, the ground state fraction is approximately$ r_g = 0.48\pm 0.08 $ [44]. Then, convoluting the$ p_{\rm{T}} $ -distribution of the$ cc $ -diquark jets fetched from the simulated events with the$ p_{\rm{T}} $ -dependent fragmentation functions (3), we estimate the direct production cross sections of the double-charm tetraquarks to be$ \begin{aligned}[b]& \sigma\left(pp\!\to\! T^{\{cc\}}_{[\bar u\bar d]} \!+\!X\right) \!=\! \left(24^{+14}_{-7}\right) \ {\rm{nb}}\; , \\ &\sigma\left(pp\!\to\! T^{\{cc\}}_{[\bar u\bar s]} \!+\!X\right) \!=\! \sigma\left(pp\!\to\! T^{\{cc\}}_{[\bar d\bar s]} \!+\!X\right) \!=\! \left(6.0^{+3.5}_{-1.7}\right) \ {\rm{nb}}\; . \end{aligned} $

(4) The
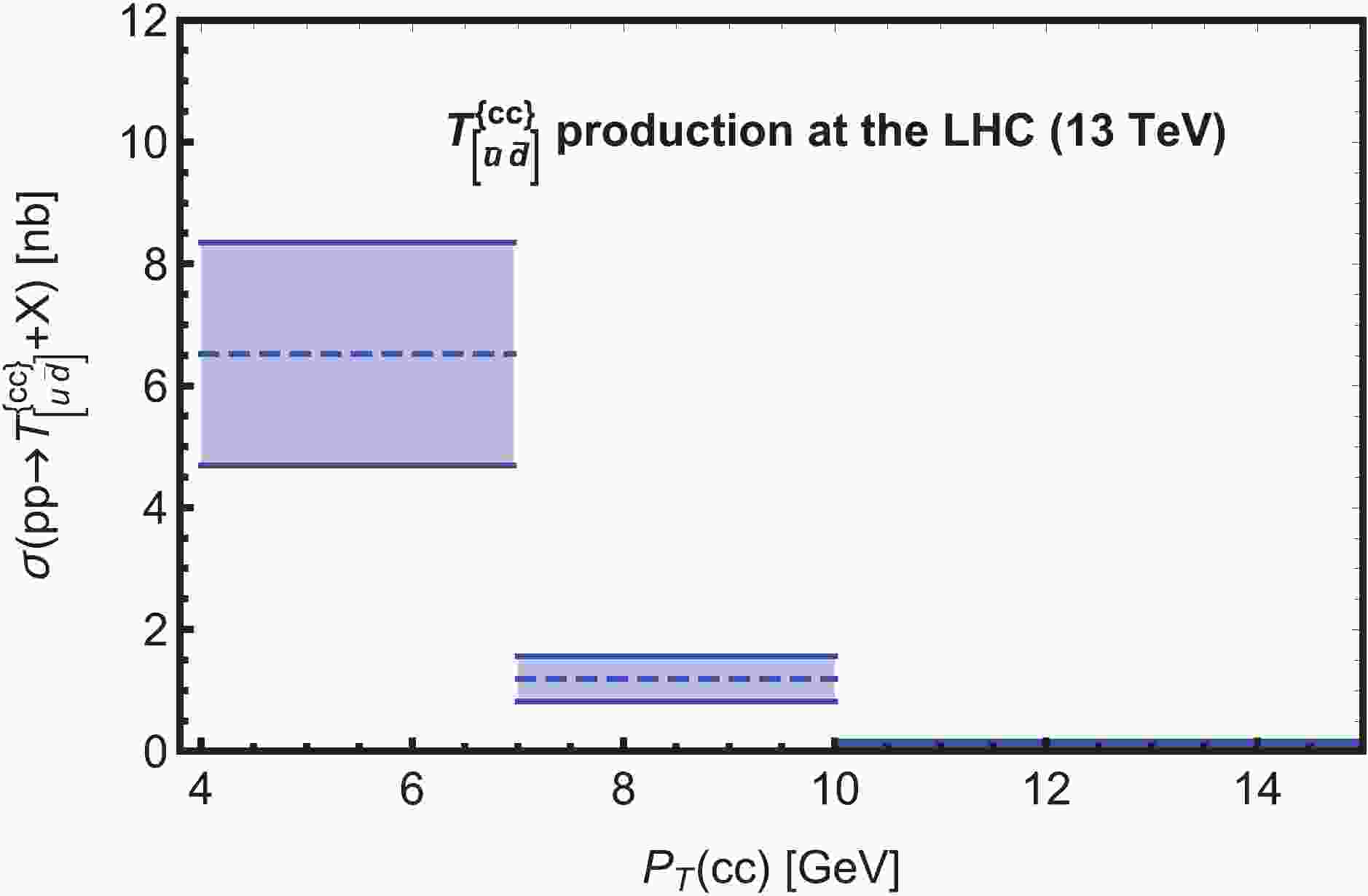
$ p_{\rm{T}} $ distribution of the$ pp\to T^{\{cc\}}_{[\bar u\bar d]} +X $ events from the simulation is displayed in Fig. 1. In contrast, because almost all the excited states of$ \Xi_{cc} $ and$ \Omega_{cc} $ decay into their ground states, we do not need to multiply the$ r_g $ ratio for their production cross section, which reads
Figure 1. (color online) Projected
$ p_{\rm{T}} $ -dependence of the tetraquark production cross section in$ pp \to T^{\{cc\}}_{[\bar u\bar d]} +X $ at the LHC for$ \sqrt{s} = 13 $ TeV with$ 2<\eta<4.5 $ .$ \begin{aligned}[b] & \sigma\left(pp\to \Xi_{cc}^{++} +X\right) = \sigma\left(pp\to \Xi_{cc}^+ +X\right) = \left(103^{+56}_{-22}\right)\ {\rm{nb}}\; , \\ &\sigma\left(pp\to \Omega_{cc}^+ +X\right) = \left(26^{+14}_{-6}\right) \ {\rm{nb}}\; . \end{aligned} $

(5) The
$ \Xi_{cc} $ production cross section has been calculated in the framework of non-relativistic QCD as$ \sigma(\Xi_{cc}^{++}) = $ $ \sigma(\Xi_{cc}^+) \approx 62 $ nb [45], with the experimental cuts$ p_{\rm{T}}> $ 4 GeV and$ |\eta|\leq1.5 $ . To compare with this result, we reset the same cuts and find$ \sigma(\Xi_{cc}^{++}) = \sigma(\Xi_{cc}^+) \approx 100 $ nb. Taking into account the large uncertainties, they agree with each other. In addition, the$ \Xi_{cc}^{++} $ production has been studied by the LHCb, with a relative production rate given as [46]$ {\sigma(\Xi_{cc}^{++})\!\times\! \mathcal{B}(\Xi_{cc}^{++}\! \to\! \Lambda_c^+K^-\pi^+\pi^+)\over \sigma(\Lambda_c^+)} \!=\! (2.22 \pm 0.27 \pm 0.29) \times 10^{-4} \; , $

(6) choosing the cuts
$ 4<p_{\rm{T}}<15 $ GeV and$ 2<\eta<4.5 $ . From an LHCb measurement with$ \sqrt{s} = 7 $ TeV [47], it can be extracted that$\sigma(\Lambda_c^+ + \Lambda_c^-) \approx 38$ μb with$ 4<p_{\rm{T}}< 8\ {\rm{GeV}}, 2.0< \eta<4.5 $ (the$ p_{\rm{T}}>8 $ GeV contributions are negligible). By comparing the D meson production at 13 TeV [48] and 7 TeV [47], one expects that the$ \Lambda_c $ production rate with$ \sqrt{s} = 13 $ TeV should exhibit an enhancement of approximately 50%, i.e.,$ \sigma(\Lambda_c^+ + \Lambda_c^-) \approx 57 $ μb. Assuming$ \mathcal{B}(\Xi_{cc}^{++} \to \Lambda_c^+K^-\pi^+\pi^+)\in $ $ [5,20]\% $ as suggested in [49], one can solve from (6) that$ \sigma(\Xi_{cc}^{++})\in [30,130] $ nb, which is also consistent with our result (5).The LHCb collaboration has collected approximately 9 fb
$ ^{-1} $ of data up to now, which indicates$ {\cal O}(10^8) $ $ T^{\{cc\}}_{[\bar q\bar q']} $ particles. If reconstructed by proper decay channels, as we analyze in the next section, they have a good chance to be discovered in the near future.Z-factories: For future Z-factories which are designed to produce
$ 10^{12} $ or more Z bosons, we also generate$ 10^5 $ $ e^+e^-\to Z \to cc\bar{c}\bar{c} $ events via MadGraph5 [39] and Pythia8 [40, 41]. We find that the total cross section$ \sigma(e^+e^-\to cc\bar{c}\bar{c} ) \approx 120 $ pb, and after the diquark jet condition$ m_{cc}<M_{cc}(\Delta M) $ is applied, the decay branching ratio of the Z boson into double-charm hadrons is found to be$ \mathcal{B}(Z\to H_{cc} +X ) = \left(10.1 ^{+7.9}_{-2.7}\right)\times 10^{-5} \; . $

(7) Analogous to the analysis of the LHCb, we assume that the fragmentation fraction
$ f ((cc)_{\rm{jet}} \to T^{\{cc\}}_{[\bar u \bar d]} + X)/ $ $ f ((cc)_{\rm{jet}} \to \Xi_{cc} + X) $ is close to two times$ f_{\Lambda_b}/(f_{B_u} + f_{B_d}) = $ $ 0.11 \pm 0.02 $ [50],$ f_s/f_d\approx 0.25 $ , and the ground-state fraction is still$ r_g = 0.48\pm 0.08 $ [44]. With these approximations, the branching ratios of the Z boson decays into double-charm tetraquarks are estimated to be$ \begin{aligned}[b] & \mathcal{B} \left(Z \to T^{\{cc\}}_{[\bar u \bar d]} + X\right) \!=\! \left(4.1^{+3.4}_{-1.5}\right) \times 10^{-6}\; , \\ &\mathcal{B} \left(Z\to T^{\{cc\}}_{[\bar u\bar s]} +X\right) \!=\! \mathcal{B} \left(Z\to T^{\{cc\}}_{[\bar d\bar s]} +X\right) \!=\! \left(1.0^{+0.8}_{-0.4}\right) \!\times\! 10^{-6}\; . \end{aligned} $

(8) We also give the Z decay branching ratios to the ground-state double-charm baryons, including those secondarily decaying from their excited states,
$ \begin{aligned}[b] & \mathcal{B} (Z\to \Xi_{cc}^{++} +X) = \mathcal{B} (Z\to \Xi_{cc}^+ +X) = (3.9^{+3.1}_{-1.1}) \times 10^{-5}\; , \\ &\mathcal{B} (Z\to \Omega_{cc}^+ +X) = (1.0^{+0.8}_{-0.3}) \times 10^{-5}\; . \end{aligned} $

(9) It can be seen that our estimation for the
$ \Xi_{cc} $ production rate at Z-factories is consistent with the NRQCD calculation$ \mathcal{B} (Z\to \Xi_{cc} +X)\approx (1.7^{+1.3}_{-0.6}) \times 10^{-5} $ [51]. Therefore, it is expected that future Tera-Z factories will produce$ \mathcal{O}(10^6) $ $ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ particles. Owing to the clean background of electron-positron collisions, future Z-factories have the advantage of measuring some of the decay channels of$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ containing neutral particles such as photons in their final states, while it is difficult for hadron colliders. More details are given in the next section. -
In addition to the production rates, the decaying processes are another important issue in the experimental searches for the double-charm tetraquarks. An example of the importance of decaying processes is the discovery of the first doubly charmed baryon. With the prediction of the most favorable decay channels of
$ \Xi_{cc}^{++}\to \Lambda_c^+K^-\pi^+\pi^+ $ and$ \Xi_c^+\pi^+ $ [49], the LHCb collaboration observed$ \Xi_{cc}^{++} $ via the above two modes [1, 52].The decaying properties depend on the masses of
$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ . Above the$ DD^* $ thresholds, they will decay strongly. In contrast, between the$ DD^* $ and$ DD\gamma $ thresholds, they will decay radiatively; below the$ DD\gamma $ thresholds, they will decay weakly. Since the theoretical predictions on the masses are very different from each other, as shown in Table 1, we will discuss the decay processes separately according to the above cases.In the case that the masses of double-charm tetraquarks are above the thresholds of
$ DD^* $ , they are unstable and will decay strongly. The decaying processes include$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^0D^{*+}\; {\rm{or}}\; D^+D^{*0} $ ,$ T^{\{cc\}}_{[\bar{u}\bar{s}]}\to D^0D_s^{*+}\; {\rm{or}}\; D_s^+D^{*0} $ , and$ T^{\{cc\}}_{[\bar{d}\bar{s}]}\to D^+D_s^{*+}\; {\rm{or}}\; D_s^+D^{*+} $ . The reconstructions of$ D^{*0} $ and$ D_s^{*+} $ require the reconstructions of neutral particles$ \pi^0 $ or$ \gamma $ , which will reduce the detection efficiencies significantly. Then, the favorable decay processes of the LHCb are$T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^0D^{*+} \to D^0 D^0 \pi^+,\; \; \; \; \; \; T^{\{cc\}}_{[\bar{d}\bar{s}]}\to D_s^+D^{*+}\to D_s^+D^0\pi^+. $

(10) If their masses are above the
$ DD\gamma $ thresholds but below the$ DD^{*} $ thresholds, they will decay radiatively, such as$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^0D^{+}\gamma $ ,$ T^{\{cc\}}_{[\bar{u}\bar{s}]}\to D^0D_s^{+}\gamma $ , and$ T^{\{cc\}}_{[\bar{d}\bar{s}]}\to D^+D_s^{+}\gamma $ . These channels are expected to be better measured at future Z-factories.In the case of
$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ below the$ DD\gamma $ thresholds, they can only decay weakly and are thus stable particles. This is different from the exotic states discovered in experiments so far, which decay strongly. The scales of heavy quark weak decays, at$ \mathcal{O} $ (GeV), are different from the ones of strong decays at the scale of hundreds of MeV. Thus, it will provide another way to distinguish the nature of hadrons to study the weak decays of such particles. Since they can only weakly decay, they must be long-lived particles and cannot be kinematical effects or coupled-channel effects. Due to large non-perturbative contributions, it is difficult to precisely predict the branching fractions of weak decays of charmed hadrons. Considering the Cabibbo-favored processes with charged particles in the final states, the most favorable processes of weak decays at the LHCb are$ \begin{aligned}[b] &T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^+K^-\pi^+,\\ &T^{\{cc\}}_{[\bar{u}\bar{s}]}\to D_{s}^+K^-\pi^+,\quad {\rm{or}}\quad D^{0}\pi^+,\quad {\rm{or}}\quad D^+K^+ K^-,\\ &T^{\{cc\}}_{[\bar{d}\bar{s}]}\to D^+K^+K^-\pi^+,\quad {\rm{or}}\quad D^+\pi^+. \end{aligned} $

(11) Considering a more abundant production of
$ T^{\{cc\}}_{[\bar{u}\bar{d}]} $ compared to the ones containg a strange quark, we will discuss the possible signal events of$ T^{\{cc\}}_{[\bar{u}\bar{d}]} $ in experiments. If it decays strongly, it decays into$ D^0D^{*+} $ with$ D^{*+}\to $ $ D^0\pi^+ $ ,$ D^0\to K^-\pi^+ $ , and$ K^-\pi^+\pi^+\pi^- $ . The total branching fraction would be$ \mathcal{O}(10^{-2}) $ . In case it is a stable particle, the branching fraction of$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^{+}K^{-}\pi^{+} $ would be of the order of 10%. Considering the further decay$ D^+\to K^-\pi^+\pi^+ $ , the total branching fraction of the weak decay of$ T^{\{cc\}}_{[\bar{u}\bar{d}]} $ would be$ \mathcal{O}(10^{-2}) $ as well. The order of the branching fractions of$ T^{\{cc\}}_{[\bar{u}\bar{d}]} $ decays is thus the same as that of the observed$ \Xi_{cc}^{++} $ . Comparing with the production rates between double-charm tetraquarks and baryons and considering approximately$ 2\times10^3 $ events of$ \Xi_{cc}^{++} $ with the current LHCb data, the signal yields of$ T^{\{cc\}}_{[\bar{u}\bar{d}]} $ would be$ \mathcal{O}(10^{2}) $ at LHCb, either for a strongly or weakly decaying$ T^{\{cc\}}_{[\bar{u}\bar{d}]} $ . This number will reach$ \mathcal{O}(10^{3}) $ at LHCb Run III. Therefore, it is expected that the double-charm tetraquark will be observed at the LHCb in the near future. Although the production rates are smaller at the future Z factories, it is also expected to be observed at the Tera-Z factories due to smaller backgrounds. -
To search for double-charm tetraquarks
$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ , we study their productions and decay channels at the LHCb and also future Z-factories. It is found that the LHCb has already collected plenty of events for the discovery of$ T^{\{cc\}}_{[\bar{u}\bar{d}]} $ . In case$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ are above the$ DD^* $ thresholds, we propose that the decay channel$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^0D^{*+}\to D^0D^0\pi^+ $ should be analyzed at the LHCb. In contrast, in case$ T^{\{cc\}}_{[\bar{q}\bar{q}']} $ are below the$ DD\gamma $ thresholds, the decay channel$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^{+}K^{-}\pi^{+} $ should be analyzed at the LHCb. Although these double-charm tetraquarks will probably be discovered at the LHCb, there are still some decay channels containing neutral particles in their final states, e.g.,$ D^0D^+\gamma $ , which are better to be studied at future Z-factories. -
The authors are grateful to Ji-Bo He and Xiao-Rui Lyu for useful discussions.
-
After the first version of this paper appeared on arxiv.org, with e-Print No. 2008.08026 [hep-ph], and during the preparation of its submission to Chinese Physics C, the observation of the first double-charm tetraquark, a
$ T^{\{cc\}}_{[\bar{u}\bar{d}]} $ -like particle, was reported in the talks "Highlights from the LHCb Experiment" given by Franz Muheim and "Recent LHCb results on exotic meson candidates" given by Ivan Polyakov at the European Physical Society Conference on high energy physics 2021. For details, see https://indico.desy.de/event/28202/contributions/102717/ and https://indico.desy.de/event/28202/contributions/105627/. It turns out that the observed double-charm tetraquark is an unstable particle dominated by strong decays, and indeed, it was discovered through the channel$ T^{\{cc\}}_{[\bar{u}\bar{d}]}\to D^0D^{*+}\to D^0D^0\pi^+ $ , as we suggested in this paper. Moreover, the signal yield at the LHCb was reported to be$ N = 117\pm16 $ , which is very consistent with our prediction,$ \mathcal{O}(10^2) $ , using the current LHCb data.
Discovery potentials of double-charm tetraquarks
- Received Date: 2021-07-29
- Available Online: 2021-10-15
Abstract: In this study, we investigate the discovery potential of double-charm tetraquarks






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: