-
Isoscaling indicates the ratio of isotope yields from two systems, h and l, which have same charge number but different neutron numbers. The ratio exhibits an exponential relationship [1-9], i.e.,
$ R_{hl}(n,z) = \frac{Y_h(n,z)}{Y_l(n,z)}\propto \exp(\alpha n+\beta z), $

(1) where Y
$ _h(n,z) $ and Y$ _l(n,z) $ denote the yields of the fragment with the neutron number n and charge number z.$ \alpha $ and$ \beta $ are referred to as the isoscaling parameters. The parameter$ \alpha $ is extracted from the isotopic yield ratios at the given z, and$ \beta $ is extracted from the isotone yield ratios at a given neutron number n.Isoscaling behavior has been observed and discussed in a variety of nuclear reactions, including deep-inelastic collisions [2], evaporation following excitation [3], multifragmentation [4-6], and fission [10]. For the fissioning system, Friedman examined the isotope yields of the fission fragments from binary fission with a simple statistical model [10]. When the symmetry energy plays a dominant role in the isotopic distributions, the isoscaling parameter
$ \alpha $ increases with the charge number of the fragment, i.e., z. However, the shell corrections are also important for describing the fissioning system, and it leads the deviation from a smooth linear n dependence of$ \ln R_{hl} $ appears [10, 11]. Thus, the$ \alpha $ values exhibit significant uncertainties in certain region. The isoscaling behaviors of the Kr and Xe isotopes from the photofission of actinides were also investigated in Ref. [12], and the isoscaling of Xe was found to be affected by$ N = 82 $ and 88 neutron shells. Veselsky$ et \;al $ . examined the isoscaling parameter$ \alpha $ of the independent fission fragment yields from the evaluated nuclear data file ENDF-349 for the binary fission of$ ^{238,233} $ U targets induced by 14 MeV neutrons and the spontaneous fission of$ ^{248,244} $ Cm to understand the fission dynamics around the scission point [11]. The importance of the shell closure is verified again, but the behaviors of the intrinsic temperature of the fission fragment are less discussed.In this work, we only explore the isoscaling parameter
$ \alpha $ from the evaluated data, i.e., ENDF/B-VIII.0 [13] and JEFF-3.3 [14]. The isoscaling parameter$ \alpha $ extracted from the evaluated fission yield data is referred to as$ \alpha_{\rm eval} $ in the following description. The systems are n+$ ^{238,235,233} $ U and the induced neutron energy is 14 MeV. To understand the physics behind the z dependence of$ \alpha_{\rm eval} $ , we analyze it within the framework of the statistic scission-point model. Our results illustrate that symmetry energy is crucial for describing the$ \alpha_{\rm eval} $ ; however, the shell correction, nuclear shape deformation and intrinsic temperature of the fission fragments cannot be ignored in the description of the isoscaling parameter even away from the shell closure. Additionally, the isoscaling analysis also provides an alternative method to extract the intrinsic temperature of the fission fragments. The finding is that the intrinsic temperature of the light fission fragment is higher than that of the heavy fission fragment, which is consistent with the conclusion in Ref. [15]. -
The evaluated data from the ENDF/B-VIII.0 and JEFF-3.3 database are wildly used in nuclear engineering and technology and can be regarded as ''experiment-like data'' to a certain extent. Thus, in this study, we only present the isoscaling parameter
$ \alpha $ obtained from the evaluated data, i.e.,$ \alpha_{\rm eval} $ , for neutron induced fission at 14 MeV. The isoscaling parameter$ \alpha_{\rm eval} $ of the binary fission of n (14 MeV)+$ ^{238,233} $ U systems, which were obtained from the evaluated independent fragment yields, has been reported in Ref. [11]. Their studies show that the isoscaling parameter$ \alpha_{\rm eval} $ increases with the fission fragment proton number z, except in the region of$ z = 38-43 $ where the$ \alpha_{\rm eval} $ decreases with z. Is this true and is the behavior of$ \alpha_{\rm eval} $ as a function of z also valid for n+$ ^{235,233} $ U?To understand it, we investigated two sets of fission systems, one set is n+
$ ^{235} $ U and n+$ ^{233} $ U, and the other is n+$ ^{238} $ U and n+$ ^{233} $ U. The evaluated fission yields in the ENDF/B-VIII.0 [13] and JEFF-3.3 databases [14] are adopted to estimate the model dependence. Figure 1 presents the$ \ln R_{hl}(n,z)+(65-z) $ for n+$ ^{235} $ U/n+$ ^{233} $ U (left panels) and n+$ ^{238} $ U/n+$ ^{233} $ U (right panels), in which,$ \ln R_{hl}(n,z) = {\rm ln}(Y_{h}(n,z)/Y_{l}(n,z)) $ . To clearly show the results of$ \ln R_{hl}(n,z) $ at different z, we shift them by a factor of$ (65-z) $ . The upper panels are the results obtained with JEFF-3.3, whereas the bottom panels are for ENDF/B-VIII.0. A linear behavior of$ \ln R_{hl}(n,z) $ is observed for both sets, and isoscaling behavior for fission fragments is observed from the evaluated data.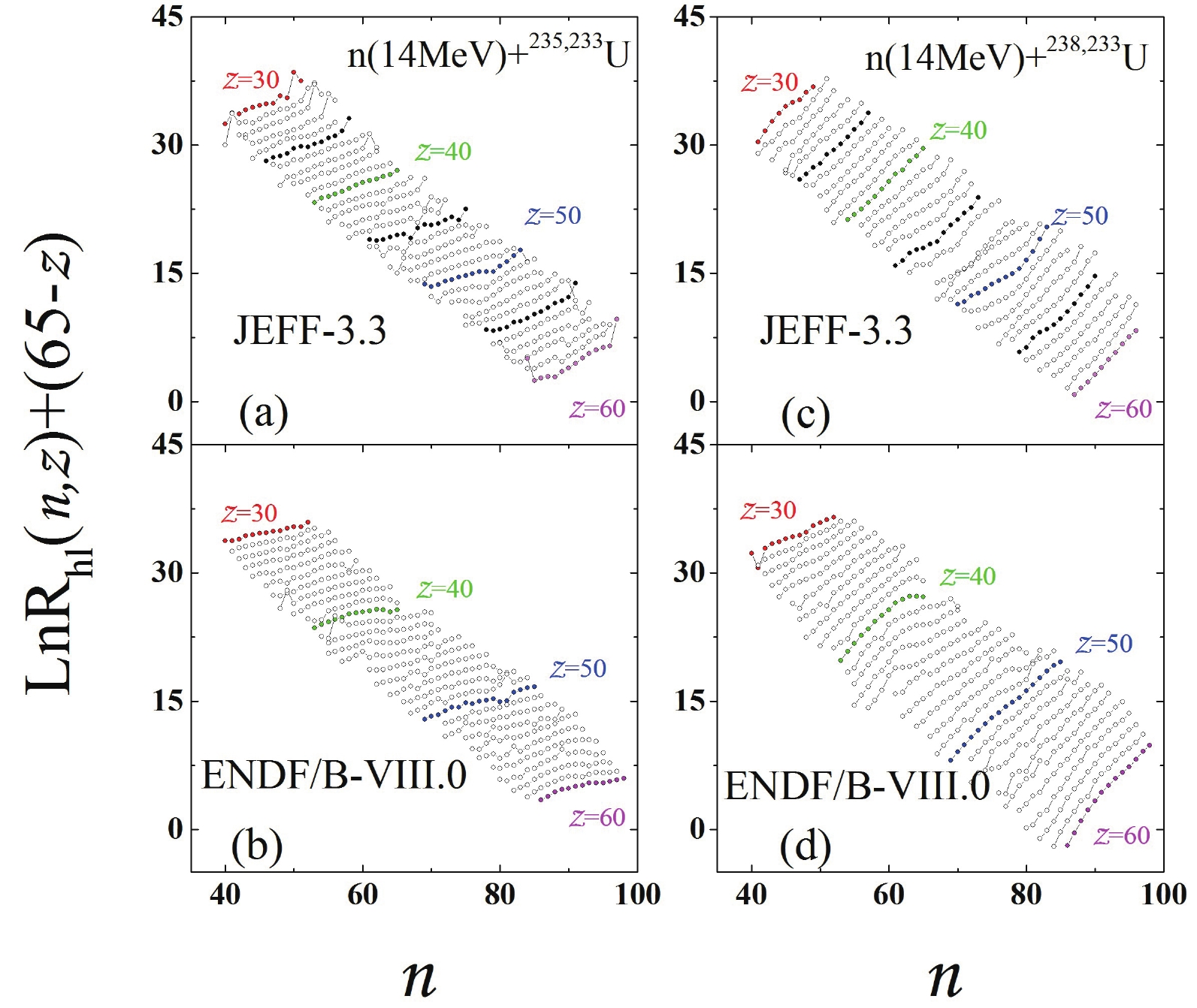
Figure 1. (color online)
$\ln R_{hl}(n,z)+(65-z)$ from two evaluated database. Left panels are the results for n+$^{235}$ U/n+$^{233}$ U, and right panels are for n+$^{238}$ U/n+$^{233}$ U. Upper panels are the results from JEFF-3.3, and bottom panels are from ENDF/B-VIII.0.Figure 2 presents the extracted
$ \alpha_{\rm eval} $ values as a function of z. The left panel is the$ \alpha_{\rm eval} $ for n+$ ^{235} $ U and n+$ ^{233} $ U, and the right panel is$ \alpha_{\rm eval} $ for n+$ ^{238} $ U and n+$ ^{233} $ U. The values of$ \alpha_{\rm eval} $ for n+$ ^{238} $ U and n+$ ^{235} $ U are similar to those of n+$ ^{238} $ U and n+$ ^{233} $ U, which is not shown here. The red square symbols are from the evaluated fission yields in ENDF/B-VIII.0. The blue circle symbols are from JEFF-3.3. It should be noted that the evaluated fission yields in the ENDF/B-VIII.0 file are based on the Wahl systematics [16], and its accuracy heavily depends on the measured data. The JEFF-3.3 database includes a more extensive experimental database and the use of the GEF code, which is mainly based on the fundamental laws of physics and general properties of microscopic systems [17]. As shown in Fig. 2, the general trends of$ \alpha_{\rm eval} $ as a function of z obtained from the ENDF/B-VIII.0 and JEFF-3.3 are different.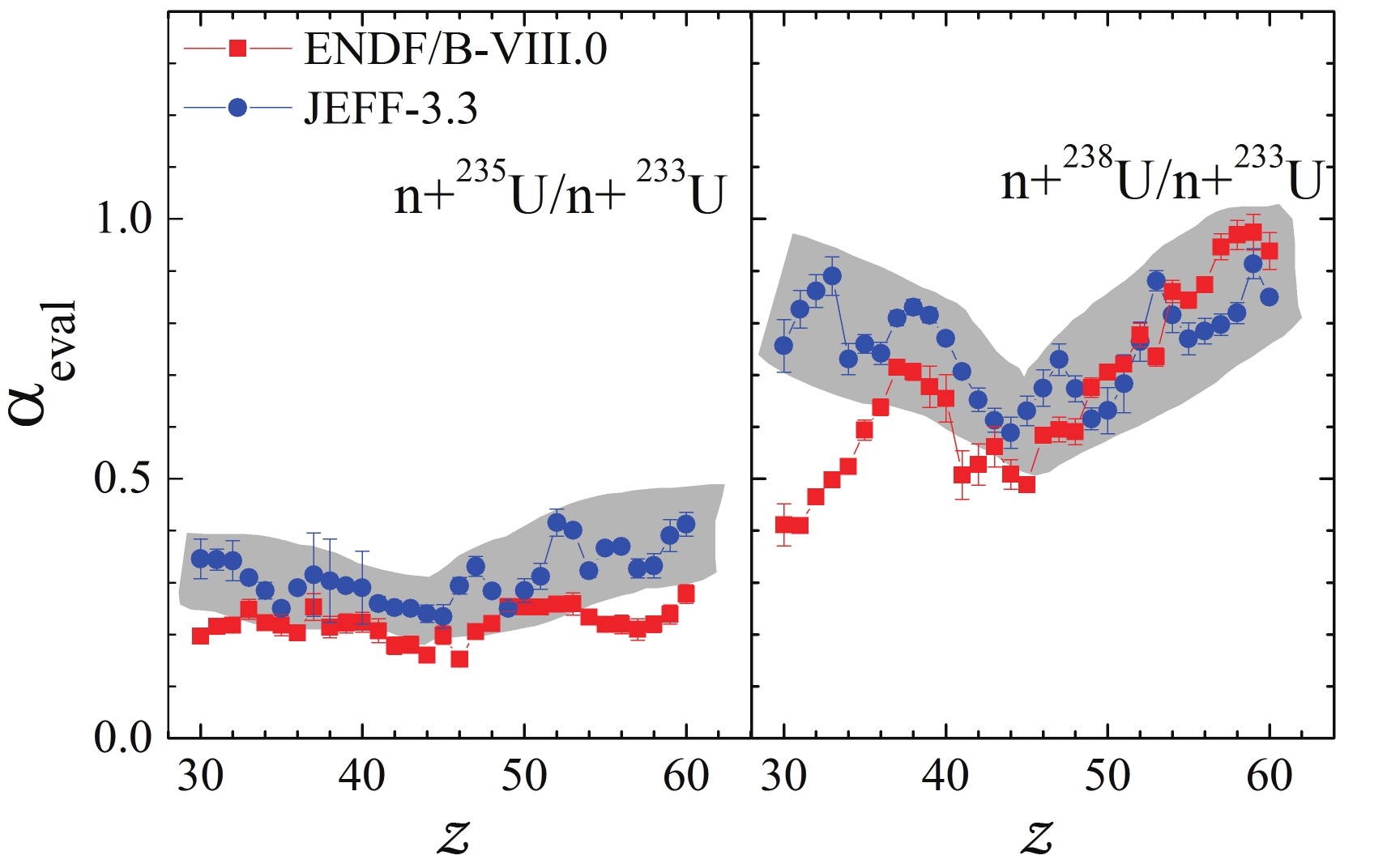
Figure 2. (color online) Extracted isoscaling parameter
$\alpha_{\rm eval}$ as a function of proton number of fission fragment for n+$^{235}$ U/n+$^{233}$ U (left) and n+$^{238}$ U/n+$^{233}$ U (right) at 14 MeV. Blue circle symbols are the results from JEFF-3.3, and red square symbols are from ENDF/B-VIII.0.In the cases of
$ \alpha_{\rm eval} $ extracted from ENDF/B-VIII.0, the$ \alpha_{\rm eval} $ as a function of z is relatively flat for n+$ ^{235} $ U/n+$ ^{233} $ U, where$ \alpha_{\rm eval}\approx 0.25 $ . For n+$ ^{238} $ U/n+$ ^{233} $ U, our results confirm again that$ \alpha_{\rm eval} $ increases with z, except in$ z = 38-43 $ , as in Ref. [11]. In more detail, the$ \alpha_{\rm eval} $ values monotonically increase from 0.41 to 0.7 with z increasing from 30 to 38, and from 0.5 to 0.94 in the range of$ z = 44-60 $ .In the cases of
$ \alpha_{\rm eval} $ extracted from JEFF-3.3, the general trend of$ \alpha_{\rm eval} $ as a function of z is that$ \alpha_{\rm eval} $ decreases with z until$ z\sim 46 $ and then increase with z. These trends are highlighted with the shaded region. For n+$ ^{235} $ U/n+$ ^{233} $ U,$ \alpha_{\rm eval} = 0.25-0.40 $ . For n+$ ^{238} $ U/n+$ ^{233} $ U, the$ \alpha_{\rm eval} $ values increase from 0.74 to 0.9 with z increasing from 30 to 33, and then,$ \alpha_{\rm eval} $ decreases from 0.9 to 0.72 from$ z = 33 $ to 34, and then increases from 0.72 to 0.83 with z increasing from 34 to 38. In the range of$ z<38 $ , there are large discrepancies of$ \alpha_{\rm eval} $ as a function of z between JEFF-3.3 and ENDF/B-VIII.0, which should be understood in the future. -
The previous analysis show that
$ \alpha_{\rm eval} $ as a function of z has a structure. Ideally, it must be understood from the fission dynamics [18-26], but the theoretical predictions of the fission isotope distributions based on the microscopic many-body theory is still a big challenge [27-30]. In this work, we will understand the structure of$ \alpha_{\rm eval}(z) $ in the view point of the statistic scission-point model. -
For the fissioning system, one can assume an intermediate coupling between the collective and single-particle levels populated when the system moves along the fission path toward scission [31, 32]. This situation can be described by introducing a collective temperature parameter, i.e.,
$ T_{\rm coll} $ , which characterizes the quasi-statistical equilibrium of the collective degrees of freedom and is different from an effective intrinsic temperature of the fission fragments, i.e.,$ \tau $ . In the following analysis, we assume a quasi-equilibrium among collective degrees of freedom near the scission point, which is fundamental for the calculation of the relative probabilities of the complementary fission fragment pairs.In the statistic scission-point model, the relative probability of the formation of any fission fragment pair is given by [31, 32]
$ \begin{aligned}[b]& Y(n,z,\tau_{1},N-n,Z-z,\tau_{2})\\ \propto&\exp \Big[-E(n,z,\tau_{1},N-n,Z-z,\tau_{2})/T_{\rm coll}\Big]. \end{aligned} $

(2) Here, N and Z are the neutron number and proton number of the fissioning systems
$ n+^{233,235,238} $ U. n and z are the neutron and proton numbers of the fission fragment 1, and$ N-n $ and$ Z-z $ are the neutron and proton numbers of the complementary fission fragment 2. The free energy E of the system around the scission configuration can be approximately expressed as,$ \begin{aligned}[b] E(n,z,\tau_{1},N-n,Z-z,\tau_{2}) =& E_{1}(n,z,\tau_{1})+E_{2}(N-n,Z-z,\tau_{2}) \\&+V_{N,12}+V_{{\rm C},12}, \end{aligned} $

(3) where
$ E_1(n,z,\tau_{1}) $ is the free energy of fragment 1 at intrinsic temperature$ \tau_{1} $ and$ E_2(N-n,Z-z,\tau_{2}) $ is the free energy of complementary fragment 2 at intrinsic temperature$ \tau_{2} $ .$ V_{N,12} $ and$ V_{{\rm C},12} $ are the nucleonic interaction and Coulomb interaction energy between fission fragment 1 and fission fragment 2, respectively. After scission, the short-ranged nucleus interaction$ V_{N,12} $ can be ignored when the two fragments are separated sufficiently but not the long-ranged Coulomb interaction$ V_{{\rm C},12} $ .Thus, the yield ratio of fission fragment with charge number z and neutron number n between the heavy and light systems can be expressed as
$ \begin{aligned}[b] \ln R_{hl}(n,z) =& \ln \left(\frac{Y_h(n,z)}{Y_l(n,z)} \right) \\ \; \propto \,& \Big[-E_{h,1}(n,z)-E_{h,2}(N_h-n,Z-z)-V^h_{{\rm C},12} \\& +E_{l,1}(n,z)+E_{l,2}(N_l-n,Z-z)+V^l_{{\rm C},12}\Big]/T_{\rm coll}\\ \approx & -(E_{h,2}(N_h-n, Z-z)-E_{l,2}(N_l-n,Z-z))/T_{\rm coll}. \end{aligned} $

(4) Because the heavy and light systems have the same charge number Z,
$ V^h_{{\rm C},12} = V^{l}_{{\rm C},12} $ and the Coulomb contributions to the yield ratios are canceled out.In our analysis, a simple prescription for the free energy of the fragment with mass
$ A = N+Z $ and charge Z,$ E(A,Z)\approx -BE(A,Z)+f^\ast(\tau(A,Z)), $

(5) is used. The binding energy
$ BE(A,Z) $ of a nucleus is calculated based on the method proposed in Ref. [33]. The rms deviation between the AME2003 data and the prediction with this method is only 0.516 MeV, which is better than the results from FRDM [34], HFB-14 [35], and HFB-17 [36]. Briefly, the binding energy of the nucleus with mass A, charge Z and deformation$ \beta $ is calculated as a sum of the liquid-drop energy term and the Strutinsky shell correction energy term as in Ref. [33]:$ BE(A,Z,\beta) = -E_{LD}(A,Z)\Pi_{k\geqslant 2}(1+b_k\beta_k^2)-E_{\rm shell}. $

(6) Here,
$ \beta_k $ is the deformation parameter, and$ E_{\rm shell} $ is the shell correction energy. The$ E_{LD}(A,Z) $ is described by a modified Bethe-Weizsäcker mass formula [33, 37], where the pairing contribution is involved in,$ \begin{aligned}[b] E_{LD}(A,Z) =& a_v A + a_s A^{2/3} + a_c\frac{Z(Z-1)}{A^{1/3}}(1-Z^{-2/3})\\ &+a_{\rm sym}(N-Z)^2/A + a_{\rm pair}A^{-\frac{1}{3}}\delta_{np}. \end{aligned} $

(7) The shell correction is obtained by the traditional Strutinsky procedure [33]. The intrinsic temperature related energy term
$ f^\ast(\tau(A,Z)) $ can be approximately written as$ f^\ast(\tau(A,Z)) = \frac{A}{\epsilon_0}\Big[\tau(A,Z)\Big]^2, $

(8) based on the form of free energy in the Fermi gas model.
$ \tau(A,Z) $ is the intrinsic temperature of the fragment with mass A and charge Z, and$ \epsilon_0 = A/a_0 $ .$ a_0 $ is taken as the usual level density parameter in Refs. [38, 39]. In our studies, the exact value of$ \epsilon_0 $ is not used, because we are only interested in which temperature is higher between the heavy and light fission fragments.By inserting Eq. (5) into Eq. (4), we obtain
$ \begin{aligned}[b] \ln R_{hl}(n,z) \propto =& -(E_{h,2}(N_h-n,Z-z)\\&-E_{l,2}(N_l-n,Z-z))/T_{\rm coll}\\ =& \Big[\Delta BE(Z-z)-\Delta f^*(\tau)(Z-z)\Big]/T_{\rm coll}, \end{aligned} $

(9) with
$ \Delta BE(Z-z) = BE_{h,2}(N_h-n,Z-z)-BE_{l,2}(N_l-n,Z-z) $ , and$\Delta f^*(\tau) = \Big[f^*(\tau(A_h-a,Z-z))-f^*(\tau(A_l-a, Z-z))\Big]$ . It leads,$ \begin{aligned}[b] \alpha(z)\approx&\frac{1}{T_{\rm coll}}\frac{\partial \big[\Delta BE(Z-z)-\Delta f^*(\tau)(Z-z)\big]}{\partial n}\bigg|_{z}\\ =& \alpha_{BE}(z)-\alpha_{f^*}(z), \end{aligned} $

(10) with
$ \alpha_{BE}(z) = \dfrac{1}{T_{\rm coll}}\dfrac{\partial \Delta BE(Z-z)}{\partial n}\bigg|_{z} $ and$ \alpha_{f^*}(z) = \dfrac{1}{T_{\rm coll}} $ $ \dfrac{\partial \Delta f^*(\tau(Z-z))}{\partial n}\bigg|_{z} $ . -
Because the symmetry energy, shell correction energy, and nuclear deformation energy have been included in the binding energy of the nucleus, their effects on
$ \alpha $ should be understood. In this section, we discuss the influences of the binding energy on the isoscaling parameter$ \alpha $ .According to Eq. (10), the difference in the binding energy
$ \Delta BE $ between the heavy and light systems determines the main behavior of$ \alpha $ as a function of z. In the expression of$ \Delta BE $ , the terms related to the difference of the volume symmetry energy$ \Delta BE_{\rm sym} $ , shell correction energy$ \Delta BE_{\rm shell} $ , and nuclear deformation energy$ \Delta BE_{\rm def} $ are defined as,$ \begin{aligned}[b] \Delta BE_{\rm sym}(Z-z) = &(BE_{\rm sym}^{h,2}-BE_{\rm sym}^{l,2})\\ =& -a_{\rm sym}\left[\frac{(N_h-n-Z+z)^2}{N_h-n+Z-z}\right.\\&\left.-\frac{(N_l-n-Z+z)^2}{N_l-n+Z-z}\right], \end{aligned} $

(11) $ \Delta BE_{\rm shell}(Z-z) = BE^{h,2}_{\rm shell}-BE^{l,2}_{\rm shell}, $

(12) and
$ \begin{aligned}[b]\Delta BE_{\rm def}(Z-z) =& BE^{h,2}_{\rm def}-BE^{l,2}_{\rm def} \\ =& -\Big[(E_{LD}\Pi_k b_k\beta_k^2)^{h,2}-(E_{LD}^{l,2}\Pi_k b_k\beta_k^2)^{l,2}\Big]. \end{aligned} $

(13) For the systems of n+
$ ^{235} $ U/n+$ ^{233} $ U and n+$ ^{238} $ U/n+$ ^{233} $ U, the magnitudes of$ \Delta BE_{\rm sym} $ are in the range of$ 35-43 $ MeV and$ 90-106 $ MeV, respectively. In Fig. 3 (a), (b), (c), and (d), we present the difference of the shell correction energy ($ \Delta BE_{\rm shell} $ ) and deformation energy ($ \Delta BE_{\rm def} $ ). The left panels show the results from n+$ ^{235} $ U/n+$ ^{233} $ U, and the right panels show those from n+$ ^{238} $ U/n+$ ^{233} $ U. The displayed regions correspond to the isotopes for extracting the isoscaling parameter$ \alpha $ .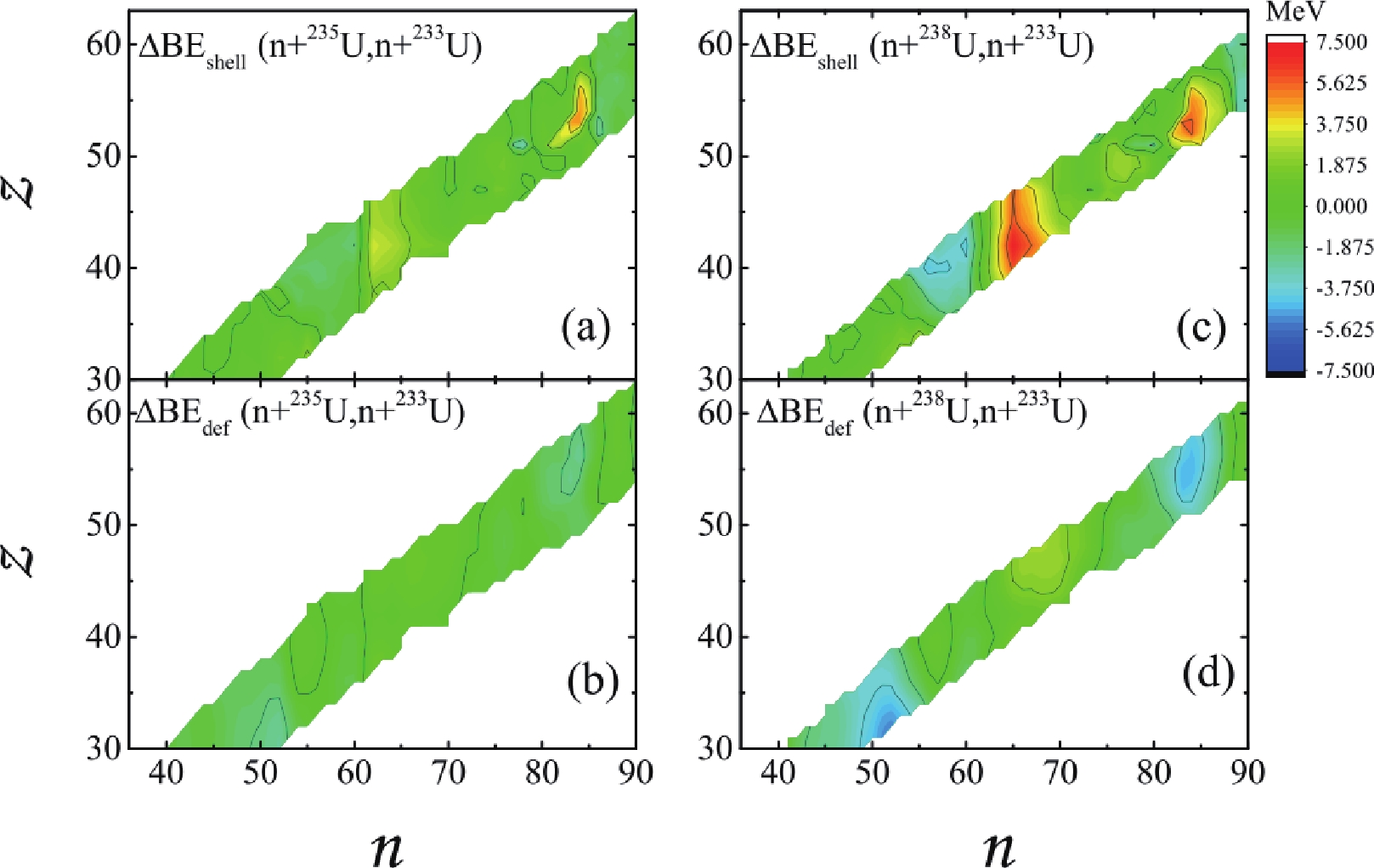
Figure 3. (color online) The upper panels (a) and (c) show the
$\Delta BE_{\rm shell}$ , and the bottom panels (b) and (d) show$\Delta BE_{\rm def}$ . The left panels show n+$^{235}$ U/n+$^{233}$ U, whereas the right panels show n+$^{238}$ U/n+$^{235}$ U.The
$ |\Delta BE_{\rm shell}| $ and$ |\Delta BE_{\rm def}| $ for n+$ ^{235} $ U/n+$ ^{233} $ U are shown in panels (a) and (b), and their values are less than 2 MeV in most areas, except in the region of ($ z\sim42 $ ,$ n\sim62 $ ) and ($ z\sim52 $ ,$ n\sim82 $ ), where the$ |\Delta BE_{\rm shell}| $ reaches up to 4 MeV.$ |\Delta BE_{\rm sym}| $ in this region is approximately 38 MeV. Thus, one can expect that$ \alpha $ mainly depends on the symmetry energy, but could be modified in a certain region.The results of
$ |\Delta BE_{\rm shell}| $ and$ |\Delta BE_{\rm def}| $ for n+$ ^{238} $ U/n+$ ^{233} $ U are presented in panels (c) and (d). The maxima of$ |\Delta BE_{\rm shell}|\approx 6 $ MeV is located at approximately$ z = 42 $ and 52, and the corresponding$|\Delta BE_{\rm sym}|$ is approximately 95-99 MeV. In detail, there is a valley at approximately$ z = 40 $ and two peaks around ($ z\sim 42, n\sim 63) $ and$ (z\sim 52, n\sim 82) $ . For the$ |\Delta BE_{\rm def}| $ , a valley in the region of ($ z\sim32 $ ,$ n\sim 52 $ ) is also observed. Thus, it is expected that$ \alpha $ as a function of z for n+$ ^{238} $ U/n+$ ^{233} $ U should have two peaks around$ z\sim 32 $ and 40. This behavior is well visible in Fig. 2 for the JEFF-3.3, but obscure for the ENDF/B-VIII.0. In the region of$ 38<z<45 $ ,$ \Delta BE_{\rm shell} $ increases with n, and it may significantly influence$ \alpha $ in this region.To quantitatively understand the total effect from the symmetry energy, shell correction, nuclear deformation, and others on the
$ \alpha $ , we present$ \Delta BE $ as a function of n for z from 30 to 60 in Fig. 4 (a) and (b). The left panel shows n+$ ^{235} $ U/n+$ ^{233} $ U, whereas the right panel shows n+$ ^{238} $ U/n+$ ^{233} $ U. Roughly, we can observe that the slope of$ \Delta BE $ with respect to n, i.e.,$ \dfrac{\partial \Delta BE}{\partial n} $ , first decreases with z in$ z<35 $ , and then increases with z in$ z>48 $ . For n+$ ^{238} $ U/n+$ ^{233} $ U,$ \Delta BE $ exhibits staggering behavior, which is caused by the odd-even effect in$ \Delta BE $ . The staggering behaviors are not observed for n+$ ^{235} $ U/n+$ ^{233} $ U, as both systems of n+$ ^{235} $ U and n+$ ^{233} $ U are even-A systems and the odd-even effects are canceled out. It should be noted that the simple linear relationship of$ \Delta BE $ as a function of n cannot be used in the region of$ 38<z<45 $ owing to the shell correction effects.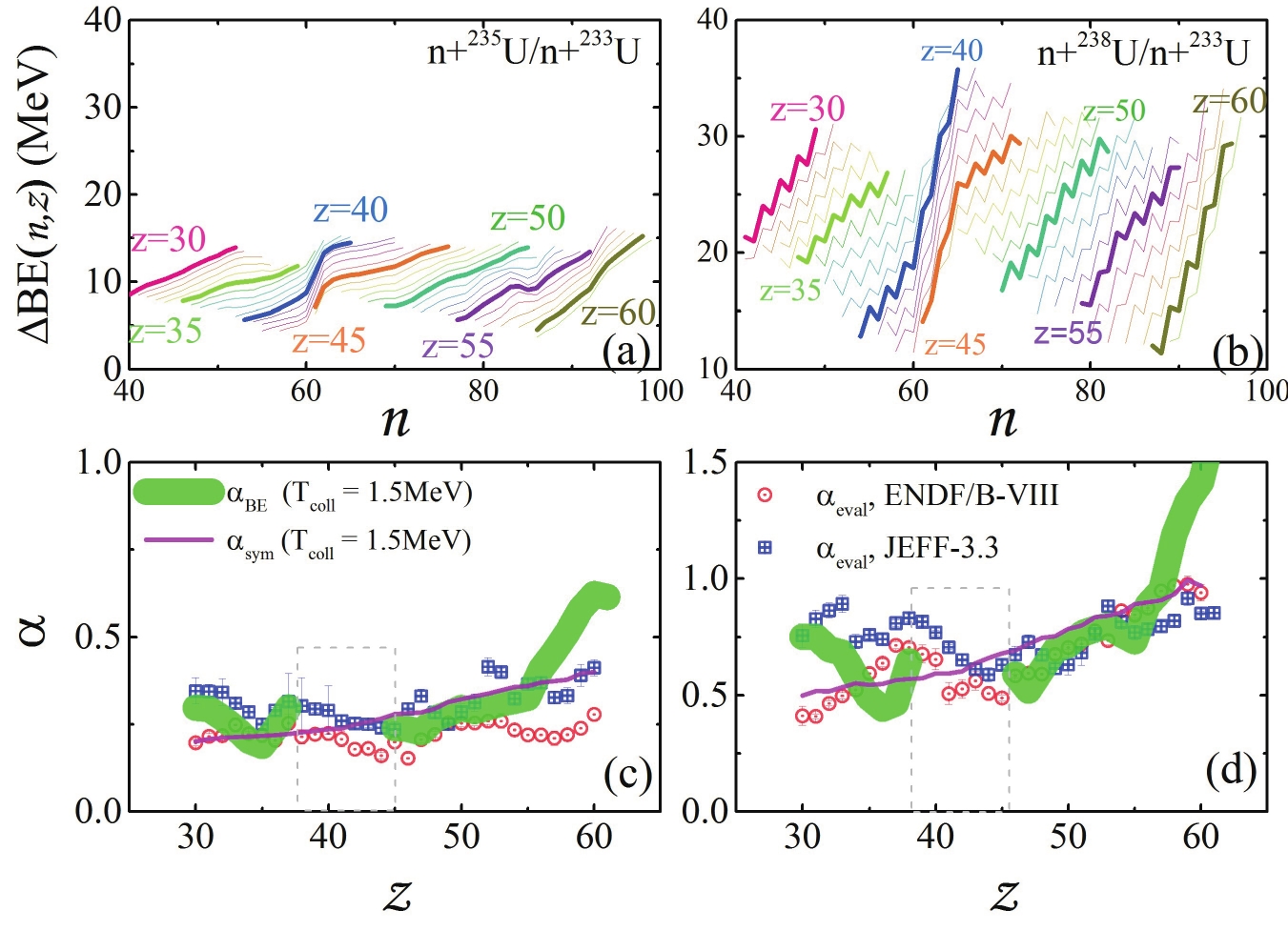
Figure 4. (color online) Upper panels:
$\Delta BE$ of n+$^{235}$ U/n+$^{233}$ U (a), and of n+$^{238}$ U/n+$^{233}$ U (b). Bottom panels: extracted$\alpha_{BE}$ compared with$\alpha_{\rm eval}$ obtained with ENDF/B-VIII.0 and JEFF-3.3 and extracted$\alpha_{\rm sym}. $ (c) is for n+$^{235}$ U/n+$^{233}$ U and (d) is for n+$^{238}$ U/n+$^{233}$ U.In Fig. 4 (c) and (d), we present the
$ \alpha $ values extracted from the symmetry energy, i.e.,$ \alpha_{\rm sym}(z) $ , and binding energy, i.e.,$ \alpha_{BE}(z) $ for n+$ ^{235} $ U/n+$ ^{233} $ U and n+$ ^{238} $ U/n+$ ^{233} $ U, respectively. The collective temperature$ T_{\rm coll} $ is approximately taken as 1.5 MeV for describing the$ \alpha_{\rm eval} $ from JEFF-3.3 in the region of$ 46<Z<55 $ . The pink lines are the$ \alpha_{\rm sym} $ obtained only with the symmetry energy term based on Eq. (6) in Ref. [10], the green bold lines are the$ \alpha $ values obtained from the binding energy, i.e.,$ \alpha_{BE} $ . In the region of$ 38<z<45 $ , we do not calculate the$ \alpha_{BE} $ values because there is no good linear relationship of$ \Delta BE $ as a function of n. For n+$ ^{235} $ U/n+$ ^{233} $ U, the values of$ \alpha_{BE} $ are roughly close to$ \alpha_{\rm eval} $ obtained with JEFF-3.3 but different from the results from ENDF/B-VIII.0. For n+$ ^{238} $ U/n+$ ^{233} $ U, a clear difference between$ \alpha_{BE} $ and$ \alpha_{\rm eval} $ can be observed. In the region of$ z<38 $ , our analysis shows that$ \alpha_{BE} $ decreases until$ z\sim 36 $ and then increases with z. The values of$ \alpha_{BE} $ are smaller than$ \alpha_{\rm eval} $ obtained with the JEFF-3.3 in the region of$ z<38 $ . For the heavy fragments of$ z>58 $ , the extracted values of$ \alpha_{BE} $ are larger than$ \alpha_{\rm eval} $ obtained with ENDF/B-VIII.0 or JEFF-3.3. The underestimation in$ 35<z\le38 $ and overestimation in$ z>55 $ indicate the significance of the intrinsic temperature$ \tau $ of the fission fragments. -
Using Eq. (8) and the Taylor expansion of
$ \tau(A_h-a,Z-z) $ at$ A_l-a $ as in appendix A,$ \Delta f^*(\tau) $ is rewritten as$ \Delta f^*(\tau(Z-z))\approx c_0+c_1*a+c_2*a*\tau(A_l-a,Z-z), $

(14) with parameters
$ c_0 $ ,$ c_1 $ , and$ c_2 $ . Here, a and z are the mass and charge of the fission fragment, respectively, and$ A_{h/l}-a $ and$ Z-z $ are the mass and charge of the complementary fission fragment. If the$ \alpha_{\rm eval} $ are considered as the "experiment-like data" of$ \alpha $ ,$ \begin{aligned}[b] \alpha_{f^*} (z) =& \alpha_{BE}(z)-\alpha_{\rm eval}(z) = \frac{1}{T_{\rm coll}}\frac{\partial \Delta f^*(\tau)}{\partial n} \\ =& \frac{c_1}{T_{\rm coll}}+\frac{c_2}{T_{\rm coll}}\tau(A_l-a,Z-z), \end{aligned} $

(15) according to Eq. (10). Therefore, one can qualitatively understand the intrinsic temperature of fission fragment 2 from the isoscaling parameter
$ \alpha $ of fission fragment 1 according to the relationship,$ \tau(Z_l-z) = \frac{T_{\rm coll}}{c_2}\Big[\alpha_{BE}(z)-\alpha_{\rm eval}(z)\Big]-\frac{c_1}{c_2}. $

(16) In Fig. 5 (a), the lines are the
$ \alpha $ values obtained with the consideration of the intrinsic temperature according to Eq. (16). This means that all the effects, such as the symmetry energy, shell correction, nuclear shape deformation, and intrinsic temperature have been included. Owing to the complication of the fission mechanism, it is difficult to extract the exact values of the intrinsic temperature. Thus, in Fig. 5 (b), we present the normalized intrinsic temperature$ \tau^0 $ , i.e.,$ \tau^0 = \tau(Z-z)/{\rm max}(\tau(Z-z)) $ , to estimate which temperature is higher between the two fission fragments. The shaded region represents the uncertainties of$ \tau^0 $ which are obtained by fitting two sets of reaction systems, i.e. n+$ ^{238} $ U/n+$ ^{233} $ U and n+$ ^{235} $ U/n+$ ^{233} $ U. Even there is a complicated structure on the charge number dependence of$ \tau_0 $ , it is clear that the intrinsic temperature of the light fission fragments is higher than that of the heavy fission fragments. In addition, the normalized intrinsic temperature$ \tau^0 $ does not depend on the choice of$ c_2 $ , which is connected to the$ \epsilon_0 $ in Eq. (8). The value of$ c_1 $ may change the exact value of$ \tau_0 $ but cannot change the conclusion on which temperature is higher between the light and heavy fission fragments.
Figure 5. (color online) (a):
$\alpha$ values considering the temperature effect in the statistic scission-point model. The red dashed line represents n+$^{235}$ U/n+$^{233}$ U, whereas the green solid line represents n+$^{238}$ U/n+$^{233}$ U; symbols are the$\alpha_{\rm eval}$ values obtained with JEFF-3.3. (b) normalized$\tau$ as a function of the proton number of fission fragment 2. -
In summary, the evaluated data of the fission fragment yields of the systems of n+
$ ^{238} $ U and n+$ ^{233} $ U as well as n+$ ^{235} $ U and n+$ ^{233} $ U at 14 MeV neutron energy were analyzed to calculate the isoscaling parameter$ \alpha_{\rm eval} $ . The isoscaling parameters$ \alpha_{\rm eval} $ extracted from the ENDF/B-VIII.0 and JEFF-3.3 databases show an obvious difference from the simple statistic model prediction where only the symmetry energy plays the dominant role.To explain the
$ \alpha_{\rm eval} $ as a function of z of the fission fragment within the framework of the statistic scission-point model, the effects of the shell correction, nuclear shape deformation, and intrinsic temperature of fission fragments are indispensable. Our results show that the isoscaling parameter$ \alpha $ can be used to learn the intrinsic temperature of the complementary fission fragment, and the intrinsic temperatures of the light fission fragments are higher than those of heavy fission fragments.Additionally, different behaviors of the isoscaling parameter
$ \alpha $ as a function of the fragment proton number are observed in the ENDF/B-VIII.0 and JEFF-3.3 files, especially for n+$ ^{238} $ U/n+$ ^{233} $ U in$ z<38 $ . The values of$ \alpha_{\rm eval} $ obtained from JEFF-3.3 are larger than those from ENDF/B-VIII.0. The difference in the isotope distributions of$ z<38 $ from the ENDF/B-VIII.0 and JEFF-3.3 evaluated data could cause the difference in predictions on the production of neutron-rich nuclei, energy release, and the neutrino emission in the utility of the evaluated data. Thus, it will be interesting and important to measure the fission fragments at the$ z<38 $ region. It will also be helpful for us to understand the fission mechanism more deeply. Furthermore, a systematic study on the isoscaling parameter$ \beta $ will also be helpful to completely understand the isotope distribution of the fissioning system and should be conducted in future. -
The authors thank Prof. Ning Wang for providing the binding energy results and are grateful for the comments and suggestions from Profs. Zhuxia Li, Xizhen Wu, and K. Pomorski.
-
Based on the form of free energy in the Fermi gas model, the intrinsic temperature related term
$ f^\ast(\tau(A,Z)) $ can be approximately written as$ f^\ast(\tau(A,Z)) = \dfrac{A}{\epsilon_0}\Big[\tau(A,Z)\Big]^2 $ , where$ \epsilon_0 = A/a_0 $ and$ a_0 $ is the usual level density parameter [38, 39] and$ \tau(A,Z) $ is the intrinsic temperature of the fragment with mass A and charge Z. The$ \Delta f^*(\tau) $ defined in Eq. (10) can be written as$\tag{A1} \begin{aligned}[b] \Delta f^*(\tau) =& \frac{A_h-a}{\epsilon_0}[\tau_{h2}]^2-\frac{A_l-a}{\epsilon_0}[\tau_{l2}]^2\\ =& \frac{A_h\tau_{h2}^2-A_{l}\tau_{l2}^2}{\epsilon_0}-\frac{a(\tau_{h2}^2-\tau_{l2}^2)}{\epsilon_0}, \end{aligned} $

(A1) where
$ \tau_{h2} = \tau(A_h-a,Z-z) $ , and$ \tau_{l2} = \tau(A_l-a,Z-z) $ . Using Taylor expansion for$ \tau_h(A_h-a,Z-z) $ at$ A_l-a $ , we obtain$ \tag{A2} (\tau_h^2-\tau_l^2)\approx b_0+b_1\tau_l(A_l-a,Z-z), $

(A2) here,
$ b_0 $ and$ b_1 $ are the Taylor expansion parameters. Inserting Eq. (A2) into Eq. (A1),$\tag{A3} \Delta f^*(\tau)\approx c_0+c_1*a+c_2*a*\tau(A_l-a,Z-z), $

(A3) with parameters
$ c_0 $ ,$ c_1 $ , and$ c_2 $ .
Understanding the isoscaling relationship in the fissioning system with evaluated data
- Received Date: 2021-02-02
- Available Online: 2021-08-15
Abstract: The isoscaling parameters





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: