-
At low temperature and low baryon chemical potential, a strongly interacting system is in the hadronic phase, and as temperature and/or baryon chemical potential increases the system will transition to a quark-gluon plasma (QGP) phase, in which the quarks and gluons are deconfined and chiral symmetry is partially restored. This new state of matter can be created from a hot and dense fireball, which is able to reach the transition temperature, in high energy nucleus-nucleus collisions [1]. The early Universe should have been in this phase for the first few microseconds after the Big Bang. QGP is also expected in the interior of quark stars or hybrid stars [2]. In the last twenty years, the study of the quantum chromodynamics (QCD) phase diagram has been extended to finite isospin chemical potential [3-5]. The physical motivation to study QCD at finite isospin chemical potential is related to the investigation of neutron stars, isospin asymmetric nuclear matter, and heavy ion collisions using neutron-rich heavy-ion beams. The phenomenon in which quark-antiquark condensation can be rotated by the isospin chemical potential is called the pion condensate, which means the direction of the broken symmetry of
$ U_I(1) $ is related to the conservation of the pion number. A superfluid of charged pions will appear in the zero momentum state, once the isospin chemical potential exceeds the pion mass ($ \mu_I>m_\pi $ ) [6, 7]. Unlike the normal phase ($ \mu_I \leqslant m_\pi $ ) with zero pion condensate, the occurence of the pion condensate can affect the low-energy nature of hadronic matter, like the lifetimes and the masses of mesons [8-10], as well as many other phenomena [11, 12]. Therefore, it is meaningful for us to investigate the phase transitions of strongly interacting systems in a baryon and isospin medium.Generally, QCD is recognized as the basic theory of strong interactions. Theoretically, QCD has rich phase structures at finite temperatures and densities. Perturbative QCD works well for the properties of the phase structures in the regions of high temperatures and/or high densities. In a finite temperature region with vanishing baryon chemical potential, lattice simulations give a valuable understanding of QCD phase diagrams. Although lattice simulations are hindered when dealing with finite chemical potential, due to the "sign" problem, this can in principle be handled with the situation of finite isospin chemical potential [13, 14]. Furthermore, the phase structure has also been investigated in many low-energy effective models, such as ladder QCD [15], the random matrix method [16, 17], the quark-meson model [18, 19] and the Nambu-Jona-Lasinio (NJL) model [20-27].
The phase diagram of QCD matter in three dimensions, i.e., the temperature, the isospin chemical potential
$ \mu_I $ and the baryon chemical potential$ \mu_B $ , is the holy grail of nuclear physics. In this paper, we study the three-dimensional QCD matter phase diagram at finite isospin and baryon chemical potentials in the NJL-type model with the self-consistent mean field approximation [28]. The standard Lagrangian density of the NJL model contains scalar$ \left(\bar{\psi}\psi\right)^2 $ and pseudoscalar-isovector$ \left(\bar{\psi}i\gamma_5{{\tau}}\psi\right)^2 $ channels [27], which is insufficient for describing the physics in the case of finite density. Because of this, people often use the Fierz transformation to generate other interaction channels. These interaction terms play an important role in the case of finite density. For example, the vector-isoscalar channel becomes vital when a finite chemical potential is discussed [29, 30]. Similarly, if the axial chemical potential is involved, the isovector-isoscalar channel is important [31-34], and we cannot ignore the contributions of the axial-vector channel in a chirally imbalanced system [35]. At this point, if the system in the case of finite isospin and baryon densities is studied, we should consider the effects of the vector-isoscalar channels and the pseudoscalar-isovector channels [36]. In previous discussions of the NJL model, people usually neglect the contributions of various terms from the Fierz transformation or add the relevant channels by hand [37]. This leads to the realization that the above approach of mean field approximation is not self-consistent. In our work, the self-consistent mean field approximation [28] of the NJL model will be employed to study the phase structure of a strongly interacting system at nonzero isospin and baryon chemical potentials. A free parameter$ \alpha $ is introduced in this model to reflect the competition of the different channels through the Fierz transformation.The rest of this paper is organized as follows. In Sec. II, the two-flavor NJL model and the self-consistent mean field approximation in the finite isospin and baryon chemical potentials are introduced, and the self-consistent gap equations are obtained. In Sec. III we will discuss QCD phase structures, and analyze our numerical results with different
$ \alpha $ 's. We summarize in the last section. -
In the present study, two flavors of light quarks are involved. The standard Lagrangian density of the two-flavor NJL model is defined as [27]
$ {\cal{L}}_{\rm NJL} = \bar{\psi}\left({\rm i}{\not\!\!{\partial}}-m_0\right)\psi +G\left[\left(\bar{\psi}\psi\right)^2+\left(\bar{\psi}{\rm i}\gamma_5{{{{\tau}}}}\psi\right)^2 \right] $

(1) with the interaction channels of the scalar and pseudoscalar corresponding to the excitations of
$ \sigma $ and$ {\bf \pi} $ respectively, where$ m_0 = {\rm{diag}}(m_{0u},m_{0d}) $ is the current quark mass matrix and the coupling is G.The four-fermion interaction channel is calculated by the Fierz transformation [27], giving
$ \begin{aligned}[b] {\cal{L}}_{IF} =& \frac{G}{8N_c} \left[2\left(\bar{\psi}\psi\right)^2+2\left(\bar{\psi}{\rm i}\gamma_5{{\tau}}\psi\right)^2 -2\left(\bar{\psi}{{\tau}}\psi\right)^2 \right. \\ & -2\left(\bar{\psi}{\rm i}\gamma_5\psi\right)^2-4\left(\bar{\psi}\gamma^{\mu}\psi\right)^2-4\left(\bar{\psi}{\rm i}\gamma^{\mu}\gamma_5\psi\right)^2 \\& \left.+\left(\bar{\psi}\sigma^{\mu\nu}\psi\right)^2 -\left(\bar{\psi}\sigma^{\mu\nu}{{\tau}}\psi\right)^2 \right], \end{aligned} $

(2) where the contributions of the color octet have been omitted, and
$ N_c = 3 $ is the number of colors. Next, the Lagrangian density is found to be$ {\cal{L}}_F = \bar{\psi}\left({\rm i}{\not\!\!{\partial}}-m_0\right)\psi+{\cal{L}}_{IF}. $

(3) Because of the Fierz transformation, the Lagrangian
$ {\cal{L}}_{\rm NJL} $ and the transformed Lagrangian$ {\cal{L}}_{F} $ are equivalent. In view of the mathematical equivalence of$ {\cal{L}}_{\rm NJL} $ and$ {\cal{L}}_{F} $ , the general effective Lagrangian density is introduced [28]:$ {\cal{L}}_R = (1-\alpha) {\cal{L}}_{\rm NJL} + \alpha {\cal{L}}_F $ , where the parameter$ \alpha $ is a weighting factor (a real number from 0 to 1) used to reflect the competition between the "direct" channel ($ {\cal{L}}_{\rm NJL} $ ) and the "exchange" channel ($ {\cal{L}}_{F} $ ). In this way, we can get more interaction channels through the Fierz transformation. This helps us to recognize and handle the strong interaction system with finite density. As mentioned in the last section, the contributions of the various channels are not negligible if we research the system in the case of finite density.Nevertheless, the contributions of
$ {\cal{L}}_{\rm NJL} $ and$ {\cal{L}}_{F} $ are no longer identical once the mean field approximation is used, because of the noncommutability between the Fierz transformation and the mean field approximation. Especially for a system at finite density, the results given by the two Lagrangians are quite different [27]. This indicates that it is vital for us to acknowledge the contributions of each interaction channel once the mean field approximation is applied. In fact, just as shown by Refs. [28, 35, 36, 38-43], there is currently no physical requirement to determine the value of$ \alpha $ . In principle,$ \alpha $ needs to be constrained by experiments but not the self-consistent mean field approximation itself. The Lagrangian density with the self-consistent mean field approximation is adopted as$ \langle{\cal{L}}_R\rangle_m = \left(1-\alpha\right) \langle{\cal{L}}_{\rm NJL}\rangle_m + \alpha \langle{\cal{L}}_F\rangle_m $ [28], where$ \langle \rangle_m $ marks the mean field approximation. What needs to be emphasized here is that the mean field approximation that does not consider the contribution of the "exchange" channel ($ {\cal{L}}_{F} $ ) is theoretically not self-consistent [37, 44].For the sake of the investigation of the system in isospin and baryon matter, we can introduce the isospin chemical potential
$ \mu_I $ and the baryon chemical potential$ \mu_B $ , which connect to the isospin number density$ n_I = (n_u-n_d)/2 $ and the baryon number density$ n_B = (n_u+n_d)/3 $ respectively. In finite temperature field theory [45], the partition function for a system with finite isospin and baryon chemical potentials is expressed as$ Z\left(T,\mu_I,\mu_B,V\right) = \int \left[{\rm d}\bar{\psi}\right]\left[{\rm d}\psi\right] {\rm e}^{\int_{0}^{\beta} {\rm d}{{\tau}} \int {\rm d}^3\vec{x} \left({\cal{L}} + \bar{\psi}\mu\gamma_0\psi\right)}\ , $

(4) where
$ \beta = 1/T $ is the inverse temperature of the system, the volume is V, and$ \mu_I $ and$ \mu_B $ are the isospin and baryon chemical potentials respectively. The quark chemical potential matrix in flavor space is$ \mu = {\rm{diag}}(\mu_u,\mu_d) $ with$ u$ - and$ d $ -quark chemical potentials$ \mu_u = \frac{\mu_B}{3}+\frac{\mu_I}{2}\ ,\quad \mu_d = \frac{\mu_B}{3}-\frac{\mu_I}{2}\ . $

(5) The factors
$ \dfrac{1}{2} $ and$ \dfrac{1}{3} $ reflect the fact that$ \dfrac{1}{2} $ is the isospin quantum number of quark and one baryon is made up of 3 quarks.Then the equivalent Lagrangian density is rewritten as
$ {\cal{L}}_r = (1-\alpha) {\cal{L}}_{\rm NJL} + \alpha {\cal{L}}_F + \bar{\psi}\mu\gamma_0\psi. $

(6) In our work, only the contributions from the vector, scalar and pseudoscalar-isovector channels are considered. At the level of the mean field approximation, no other terms affect our calculation. Using the mean field approximation to this Lagrangian, and dropping the irrelevant channels, one can obtain the effective Lagrangian density,
$ \begin{aligned}[b] {\cal{L}}_{\rm eff} = & \bar{\psi}\left({\rm i}{\not\!\!{\partial}}-M+\mu^{\prime} \gamma_0 +2G\pi {\rm i}\gamma_5\tau_1\right)\psi \\&- G\left(\sigma^2 + \pi^2\right) +\beta n^2\ , \end{aligned} $

(7) where
$ \sigma $ is the quark condensate and$ \pi $ is the pion condensate, and the constituent quark mass is$ M = m_0-2G\sigma, $

(8) with
$ \mu^{\prime} = \mu - 2 \beta n. $

(9) Employing Eqs. (5) and (9), we get the following relations:
$ \mu^{\prime}_I = \mu_I - 8 \beta n_I, $

(10) and
$ \mu^{\prime}_B = \mu_B - 18 \beta n_B, $

(11) where for convenience we redefine the parameter in the formalism
$ \beta = \frac{-2 G \alpha}{11 \alpha-12}. $

The quark condensate
$ \sigma = \langle\bar{\psi}\psi\rangle $ , the pion condensate$ \pi = \langle\bar{u} i\gamma_5 d\rangle+\langle\bar{d} i\gamma_5 u\rangle $ , the quark number density$ n = \langle\bar{u}\gamma_0u\rangle+ $ $ \langle\bar{d}\gamma_0d\rangle $ , the isospin number density$ n_I = \dfrac{1}{2}(\langle\bar{u}\gamma_0u\rangle- $ $ \langle\bar{d}\gamma_0d\rangle) $ , and the baryon number density$ n_B = \dfrac{1}{3}(\langle\bar{u}\gamma_0u\rangle+ $ $ \langle\bar{d}\gamma_0d\rangle) $ are solved in a thermodynamically self-consistent way. By inserting the effective Lagrangian density (7) into the partition function (4), one can get the mean-field thermodynamic potential,$ \Omega = -\frac{T}{V} \ln{Z} = G\left(\sigma^2 + \pi^2\right) - \beta n^2 + \Omega_M , $

(12) where
$ \Omega_M $ can be represented as$ \begin{aligned}[b] \Omega_M =& -N_c \int_{0}^{\Lambda} {{\rm d}^3\vec{p}\over (2\pi)^3} \left[E_-^- - E_+^- + E_-^+ - E_+^+ + 2T\right.\\ &\times \left(\ln\left(1+\exp{(-E_-^-/T)}\right) + \ln\left(1+\exp{(E_+^-/T)}\right) \right. \\&+ \left.\left. \ln\left(1+\exp{(-E_-^+/T)}\right) +\ln\left(1+\exp{(E_+^+/T)}\right)\right)\right], \end{aligned} $

(13) and the energies of the effective quark
$ E^\pm_\mp $ are given by:$ E^\pm_\mp = E^\pm_p \mp {\mu^{\prime}_B \over 3}, $

(14) $ E^\pm_p = \sqrt{\left(E_p \pm \mu^{\prime}_I/2\right)^2 + 4G^2\pi^2} , $

(15) $ E_p = \sqrt{|{{p}}|^2 + M^2}\ . $

(16) Given the extremum condition of thermodynamic potential
$ \dfrac{\partial{\Omega}}{\partial{\sigma}} = 0,\dfrac{\partial{\Omega}}{\partial{\pi}} = 0 $ , one has the quark condensation,$ \begin{aligned}[b] \sigma =& \int_{0}^{\Lambda} {{\rm d}^3\vec{p}\over (2\pi)^3} \frac{2N_cM}{E_p} \left[\frac{E_p-\mu^{\prime}_I/2}{E_p^-}(f(E_-^-)-f(-E_+^-)) \right.\ \\&+ \left. \frac{E_p+\mu^{\prime}_I/2}{E_p^+}(f(E_-^+)-f(-E_+^+))\right]\ , \end{aligned} $

(17) and the pion condensation,
$ \begin{aligned}[b] \pi =& -4N_cG\pi \int_{0}^{\Lambda} {{\rm d}^3\vec{p}\over (2\pi)^3} \left[\frac{1}{E_p^-} \left(f(E_-^-)-f(-E_+^-)\right) \right.\ \\ &+ \left. \frac{1}{E_p^+} \left(f(E_-^+)-f(-E_+^+)\right)\right]\ . \end{aligned}$

(18) From the derivatives of the thermodynamic potential with respect to their respective chemical potential
$ n = \dfrac{\partial{\Omega}}{\partial{\mu}} ,n_I = \dfrac{\partial{\Omega}}{\partial{\mu_I}},n_B = \dfrac{\partial{\Omega}}{\partial{\mu_B}} $ , one has the density of quark number,$ \begin{aligned}[b] n = 2 N_c\int_{0}^{\Lambda} {{\rm d}^3\vec{p}\over (2\pi)^3} \left[f(E_-^-)+f(-E_+^-)+f(E_-^+) \right.+ \left. f(-E_+^+)-2\right]\ , \end{aligned} $

(19) the isospin number density,
$ \begin{aligned}[b] n_I =& N_c\int_{0}^{\Lambda} {{\rm d}^3\vec{p}\over (2\pi)^3} \left[ \frac{E_p-\mu^{\prime}_I/2}{E_p^-}(f(E_-^-)-f(-E_+^-)) \right.\ \\ &- \left. \frac{E_p+\mu^{\prime}_I/2}{E_p^+}(f(E_-^+)-f(-E_+^+))\right]\ , \end{aligned} $

(20) and the baryon number density,
$ \begin{aligned}[b] n_B = & {2 \over 3} N_c\int_{0}^{\Lambda} {{\rm d}^3\vec{p}\over (2\pi)^3} \left[f(E_-^-)+f(-E_+^-)+f(E_-^+) \right.\ \\& + \left. f(-E_+^+)-2\right] \end{aligned}$

(21) with the Fermi-Dirac distribution function
$ f(x) = {1\over {\rm e}^{x/T}+1}. $

(22) Eventually, we insert Eqs. (17)-(21) into Eqs. (8)-(11), and obtain a set of integral equations in the case of finite isospin and baryon chemical potentials. By numerically solving this set of equations we can get the relevant phase diagram.
The parameters used in the present work are the mass of the current quark
$ m_{0u} = m_{0d} = m_0 = 4.76 $ $ {\rm{MeV}} $ , the cutoff$ \Lambda = 659 $ $ {\rm{MeV}} $ , and the coupling$ G = 4.78\times $ $ 10^{-6} \;{\rm{MeV}}^{-2} $ , which are fixed by fitting the mass of the pion$ m_{\pi} = 131.7 $ $ {\rm{MeV}} $ from lattice QCD calculation [46] at$ T = \mu_I = \mu_B = 0 $ . The other parameters are the quark condensation per flavor$ \langle\bar{\psi}\psi\rangle = -(250\; {\rm{MeV}})^3 $ and the decay constant$ f_{\pi} = 92.4 $ $ {\rm{MeV}} $ . -
As mentioned above, Refs. [28, 35, 36, 38-41] point out that the parameter
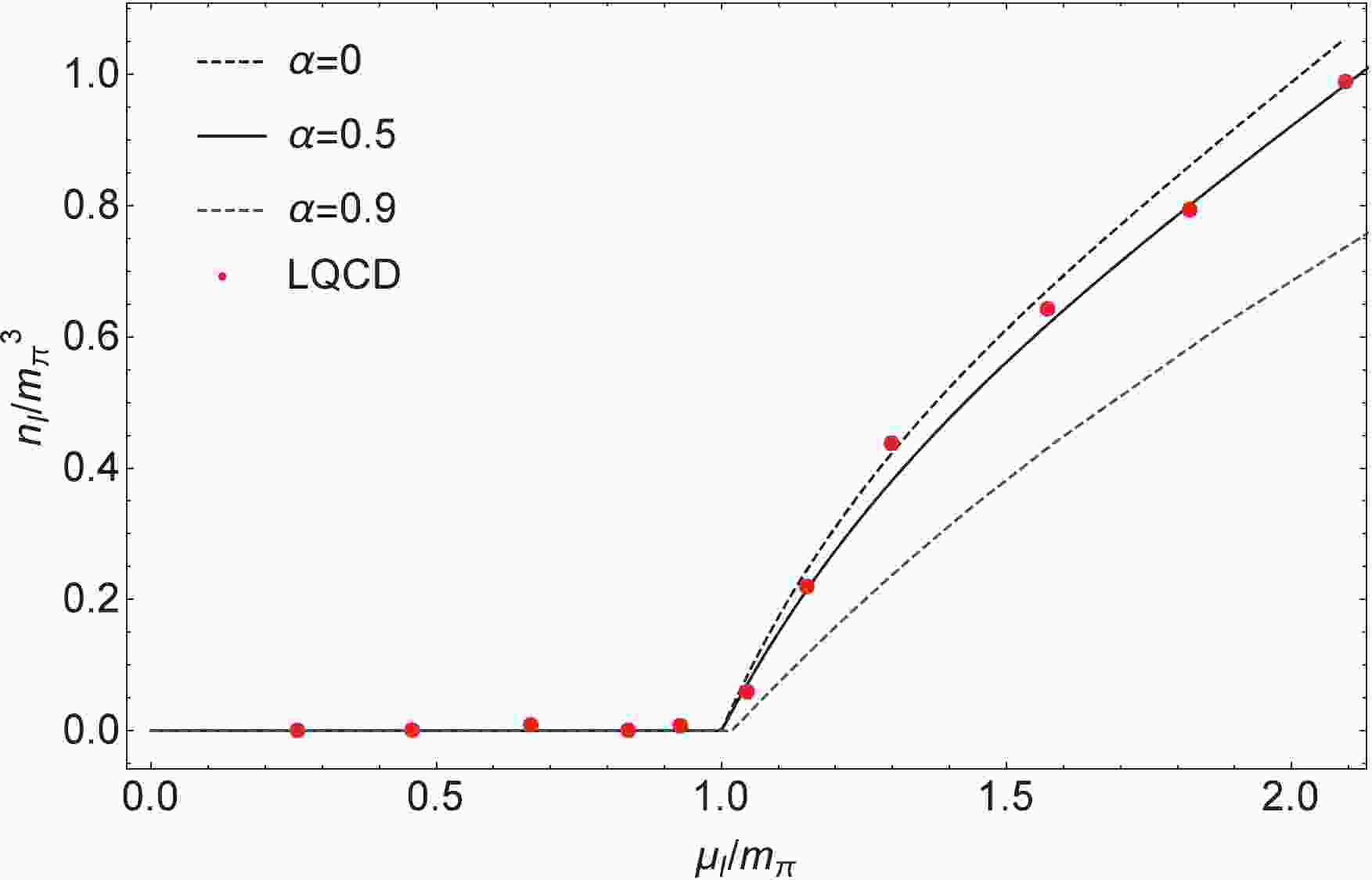
$ \alpha $ needs to be determined experimentally. A possible choice, for instance in Refs. [38, 39], is that$ \alpha $ can be constrained by astronomical observation data of a recent binary neutron star merger. Nevertheless, there is a lack of reliable experimental data for strongly interacting matter at finite densities so far, so in our work$ \alpha $ is considered to be a free parameter. In this paper, our results are shown with different$ \alpha $ 's.$ \alpha $ = 0 represents the standard NJL model [26, 27];$ \alpha $ = 0.5, which is in good agreement with lattice data, is taken from Ref. [36]; and$ \alpha $ = 0.9 is adopted from Ref. [38].Figures 1 and 2 show the variation of the normalized isospin density and energy density with
$ \alpha = 0,0.5,0.9 $ versus$ \mu_I $ , scaled by$ m_{\pi} $ , compared with the corresponding lattice results from Ref. [47] and Ref. [48] respectively. The lattice QCD data are described well by the calculation with$ \alpha = 0.5 $ . Only some data are situated on the$ \alpha = 0 $ curve (i.e. the standard NJL model results) around$ \mu_I \sim 1.5m_{\pi} $ [11]. Our results show that in order to better match the corresponding lattice results, the contributions of the "exchange" channel need to be considered in the framework of the NJL model, and a weighting factor$ \alpha = 0.5 $ should be taken. This is consistent with the finding of Refs. [37, 44] in the mid-1980s. We remark that finite isospin density experiment confirmation is still lacking. The lattice data calculation, combined with our calculation, provides some support for Refs. [37, 44]. The solutions of Eq. (18) for a$ \pi $ condensate with different$ \alpha $ 's, delimiting the regions of the pion superfluidity phase ($ \pi\ne 0 $ ) and the normal phase ($ \pi = 0 $ ), are given in Fig. 3 in the$ T-\mu_I $ plane for$ \mu_B = 0 $ . It can be seen that the phase transition line of these two regions becomes lower as$ \alpha $ increases (the$ \alpha = 0 $ corresponding to the result of Ref. [26]), except that in the beginning they always remain at zero, and the largest differences among them appear at$ \mu_I \sim 1.5m_{\pi} $ . Especially at zero temperature, the critical isospin chemical potential$ \mu_I^{\rm C} $ of the phase transition is at$ \mu_I^{\rm C} = m_{\pi} $ .
Figure 1. (color online) Normalized isospin density
$ n_I/m_{\pi}^3 $ with different$ \alpha $ 's as a function of the normalized isospin chemical potential$ \mu_I/m_{\pi} $ at$ T = $ $ \mu_B $ $ = 0 $ compared with lattice data [47].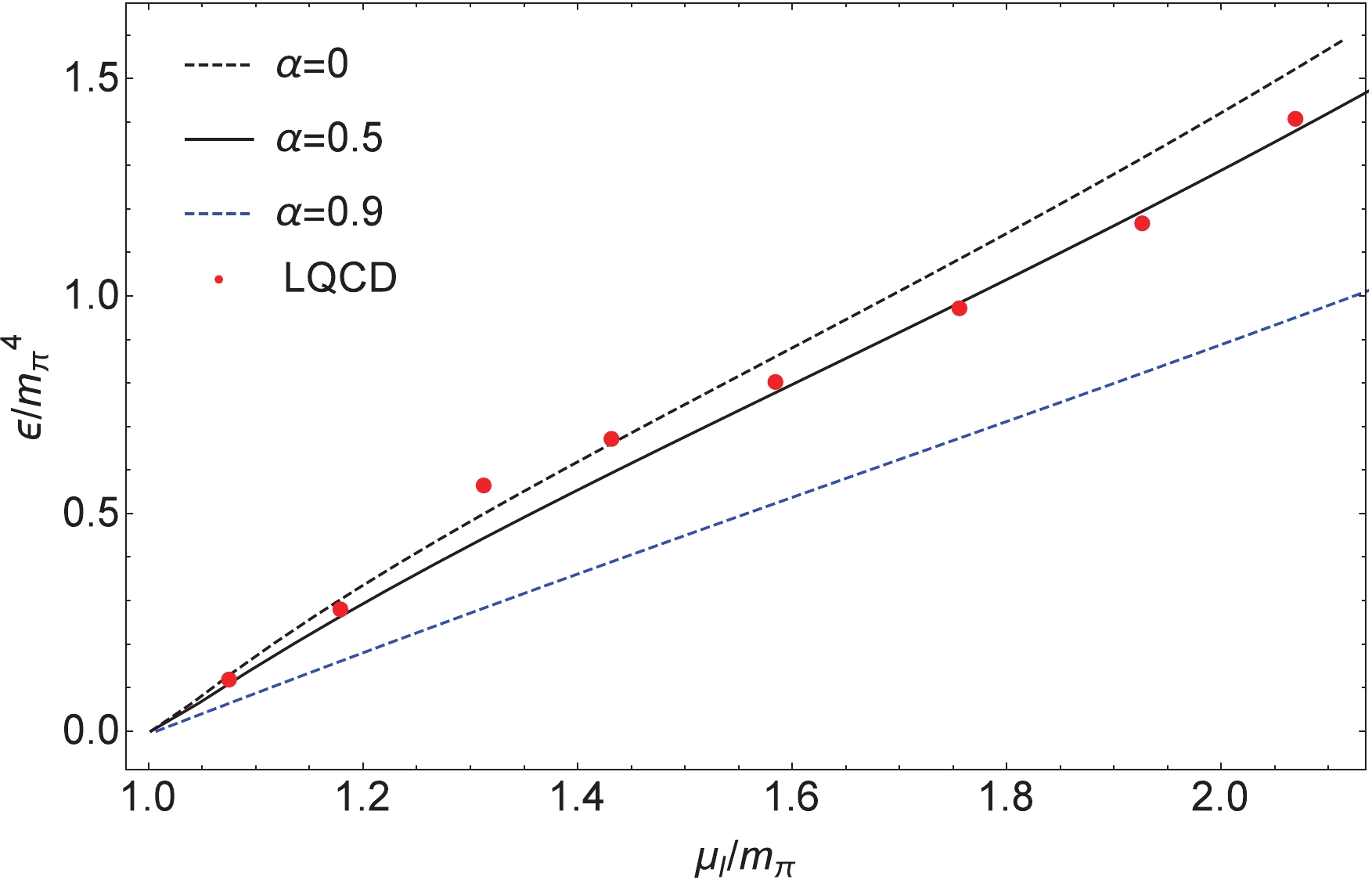
Figure 2. (color online) Normalized energy density
$ \epsilon/m_{\pi}^4 $ with different$ \alpha $ 's as a function of the normalized isospin chemical potential$ \mu_I/m_{\pi} $ at$ T = $ $ \mu_B $ $ = 0 $ , compared with lattice data [48].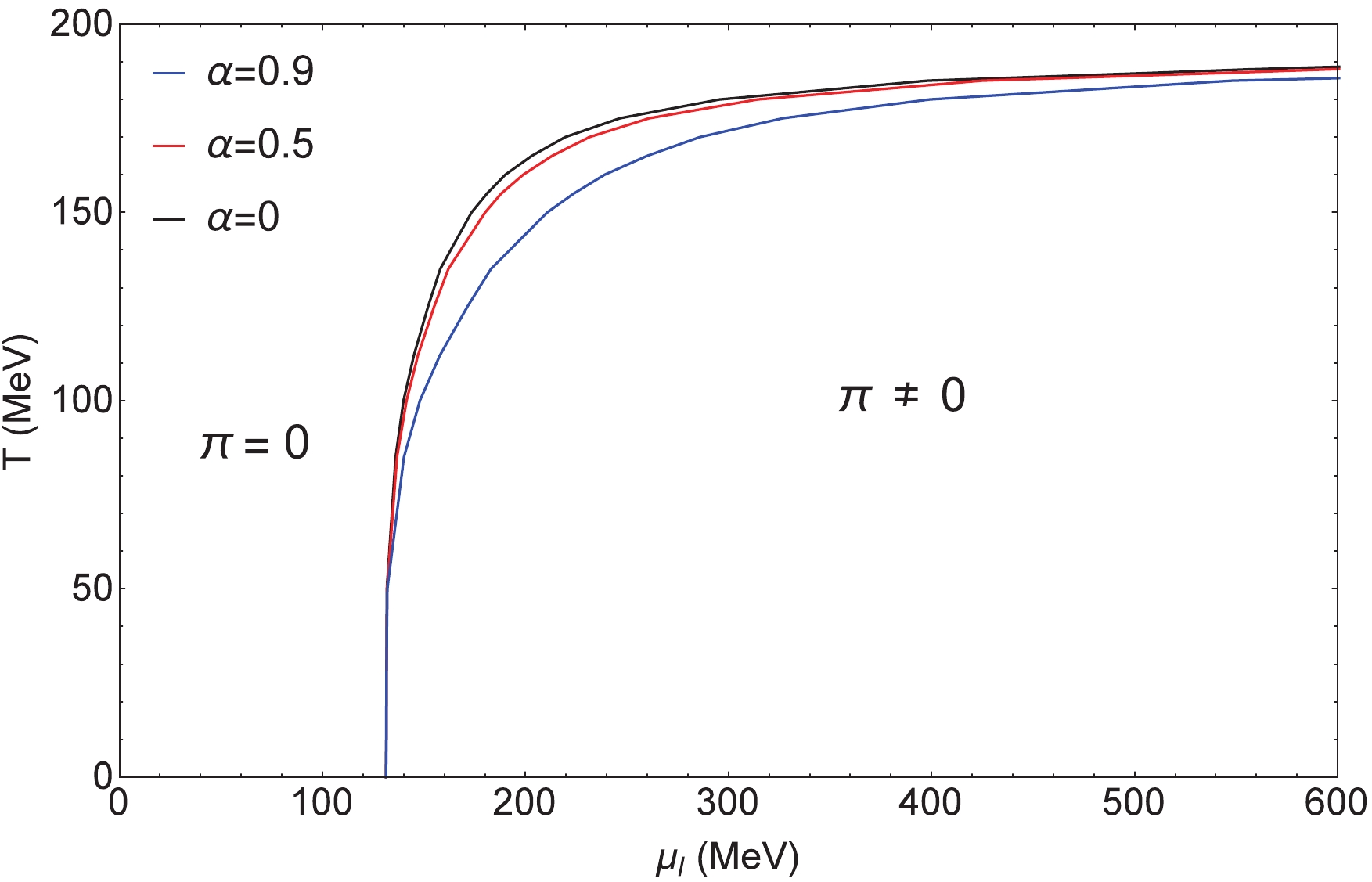
Figure 3. (color online) Phase diagram of pion superfluidity in the
$ T-\mu_I $ plane$ (\mu_B = 0) $ .In the following, we will discuss the phase diagram at finite baryon chemical potential for different fixed isospin chemical potentials. By solving Eqs. (8)-(11) numerically, we can obtain the phase diagrams (Figs. 4 and 5) in
$ T-\mu_B $ plane at$ \mu_I = 0 $ and$ \mu_I = 200 $ $ {\rm{MeV}} $ (without considering pion condensation). The chiral phase transition lines with different$ \alpha $ 's in the diagram represent the phase transition from the chiral symmetry broken phase to the symmetric one, with the solid lines denoting the crossover and the dashed lines the first-order phase transition. At$ \mu_I = 0 $ , for the same temperature the critical baryon chemical potential of the phase transition gets larger with increasing$ \alpha $ , which means that at a fixed temperature, for the larger$ \alpha $ the occurrence of the phase transition will be postponed as the baryon chemical potential increases. At$ \mu_I = 200 $ $ {\rm{MeV}} $ , the phase transition lines with different$ \alpha $ 's intersect at medium T and medium$ \mu_B $ . For higher fixed$ \mu_I $ ($ \mu_I>400 $ $ {\rm{MeV}} $ ), the value of the chiral condensate with different temperatures and baryon chemical potentials tends to zero.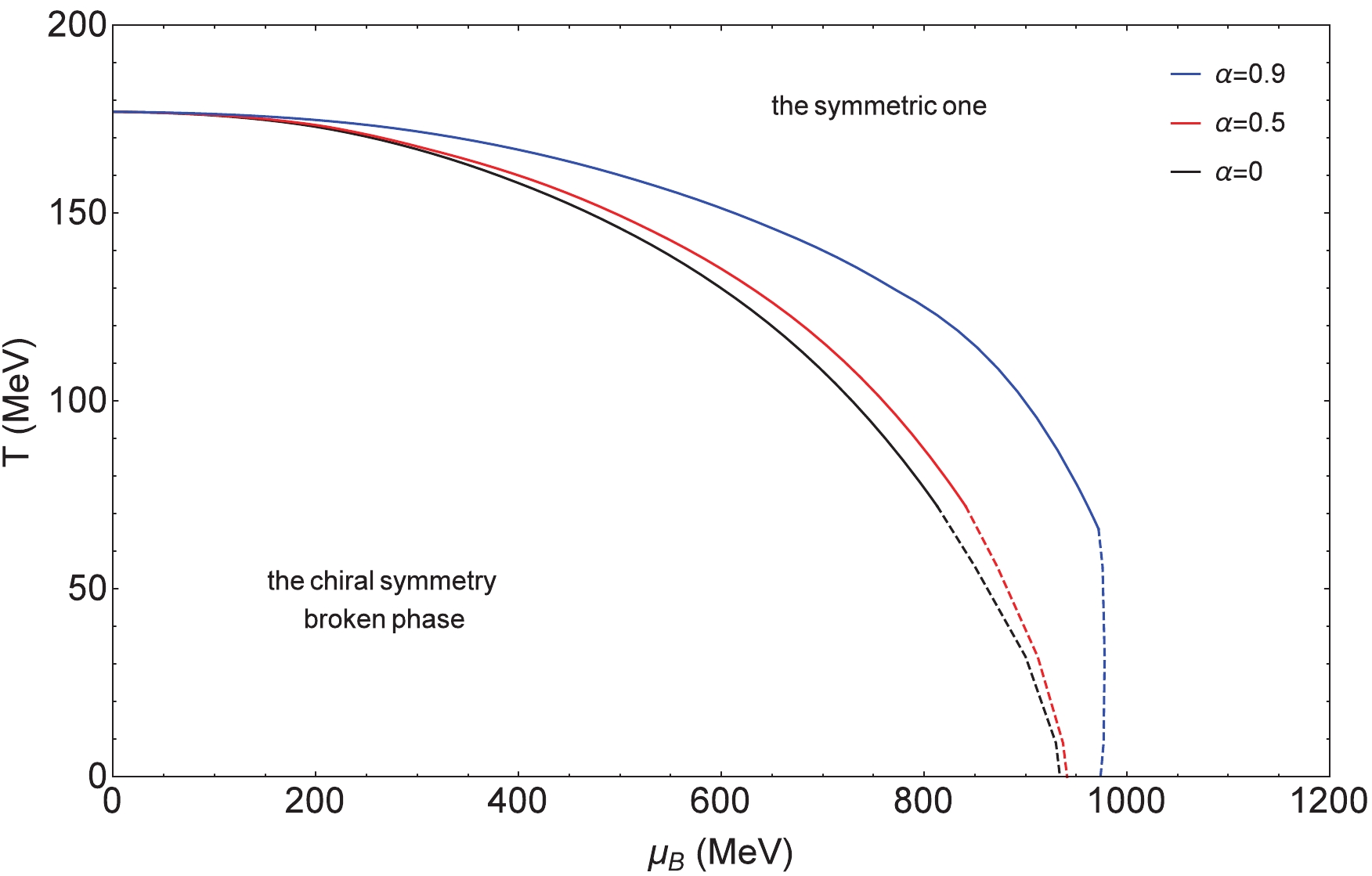
Figure 4. (color online) Phase diagram of chiral condensate in the
$ T-\mu_B $ plane$ (\mu_I = 0) $ (without considering pion condensation).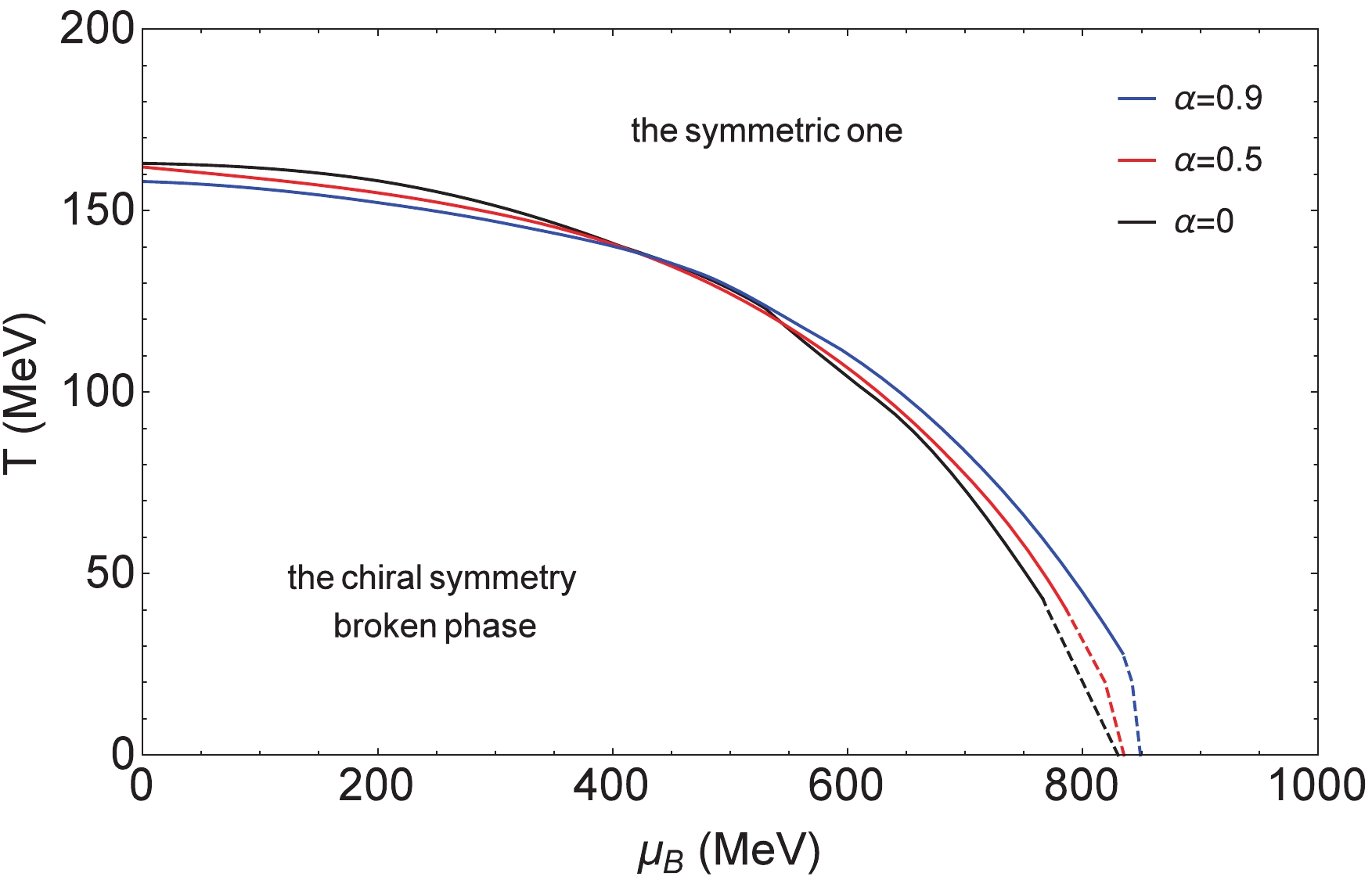
Figure 5. (color online) Phase diagram of chiral condensate in the
$ T-\mu_B $ plane ($ \mu_I = 200 $ $ {\rm{MeV}} $ ) (without considering pion condensation).We solve Eqs. (17) and (18) simultaneously and obtain the phase diagrams (Figs. 6 and 7) in the
$ T-\mu_B $ plane at$ \mu_I = 200 $ $ {\rm{MeV}} $ and$ \mu_I = 500 $ $ {\rm{MeV}} $ . There is an onset of pion condensation (i.e.$ \pi\neq 0 $ corresponding to the system in the pion superfluidity phase) at$ \mu_I^{\rm C} = m_{\pi} $ and$ T = \mu_B = 0 $ [7]. From the figures, we can see that at low temperatures the system transitioning from the pion superfluidity phase to the normal phase ($ \pi = 0 $ ) needs a much larger$ \mu_B $ . In Figs. 6 and 7, the solid lines indicate the second-order phase transition, the dashed lines indicate the first-order phase transition, and for the lower$ \mu_I = 200 $ MeV the phase transition lines with different$ \alpha $ 's ($ \alpha = 0 $ corresponding to the result of Ref. [26]) intersect at low T and high$ \mu_B $ , while for the higher$ \mu_I = 500 $ MeV they intersect at high T and low$ \mu_B $ .
Figure 6. (color online) Phase diagram of pion superfluidity in the
$ T-\mu_B $ plane ($ \mu_I = 200 $ $ {\rm{MeV}} $ ).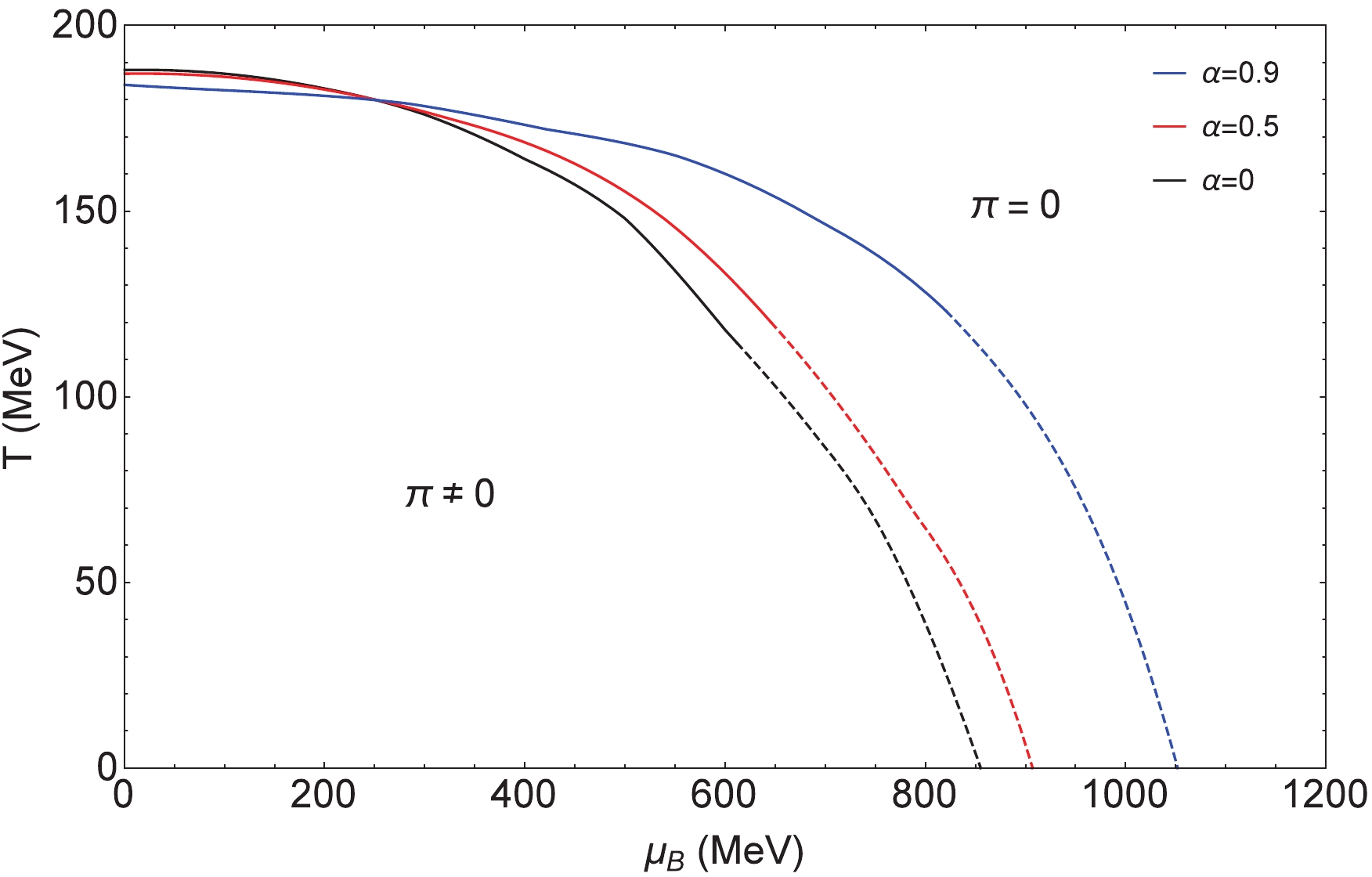
Figure 7. (color online) Phase diagram of pion superfluidity in the
$ T-\mu_B $ plane ($ \mu_I = 500 $ $ {\rm{MeV}} $ ).Mapping the phase diagram and testing the existence of the critical endpoint (CEP) or tricritical point (TCP) is one of the most active fields in high energy physics [49]. The existence of the CEP (or TCP) is shown, and its probable position is also estimated below. At
$ \mu_I = 0 $ and$ \mu_I = 200 $ $ {\rm{MeV}} $ , the phase diagrams, Figs. 4 and 5, of the chiral condensate give the CEP with different$ \alpha $ 's. This is the terminal point of the first-order phase transition curve. In the cases of$ \mu_I = 200,\;500 $ $ {\rm{MeV}} $ , the phase diagrams, Fig. 6 and Fig. 7, of pion superfluidity give the TCP with different$ \alpha $ 's separately. This is the intersection of the first-order phase transition curve and the second-order phase transition curve. In Table 1, the critical points of the phase transitions are presented. For CEPs with fixed$ \mu_I $ , the larger the value of$ \alpha $ , the larger the critical baryon chemical potential but the smaller the critical temperature. For TCPs at the lower fixed isospin chemical potential$ \mu_I = 200 $ $ {\rm{MeV}} $ the variation of the critical baryon chemical potential and the critical temperature versus$ \alpha $ is similar to the case of CEPs, but at the higher fixed isospin chemical potential$ \mu_I = 500 $ $ {\rm{MeV}} $ the larger the value of$ \alpha $ the larger the critical temperature. Our calculations indicate that as the weighting factor$ \alpha $ increases, the critical baryon chemical potential of the CEP gets larger.$\alpha=0$ 

$\alpha=0.5$ 

$\alpha=0.9$ 

CEP ( $\mu_I= 0$ )

$(T=72 \;{\rm{MeV}}$ ,

$\mu_B=813 \;{\rm{MeV}})$ 

$(T=72 \;{\rm{MeV}}$ ,

$\mu_B=841 \;{\rm{MeV}})$ 

$(T=69 \;{\rm{MeV}}$ ,

$\mu_B=971 \;{\rm{MeV}})$ 

CEP ( $\mu_I= 200$ 

${\rm{MeV}}$ )

$(T=43 \;{\rm{MeV}}$ ,

$\mu_B=766 \;{\rm{MeV}})$ 

$(T=40 \;{\rm{MeV}}$ ,

$\mu_B=786 \;{\rm{MeV}})$ 

$(T=28 \;{\rm{MeV}}$ ,

$\mu_B=834 \;{\rm{MeV}})$ 

TCP ( $\mu_I= 200$ 

${\rm{MeV}}$ )

$(T=49 \;{\rm{MeV}}$ ,

$\mu_B=761 \;{\rm{MeV}})$ 

$(T=49 \;{\rm{MeV}}$ ,

$\mu_B=769 \;{\rm{MeV}})$ 

$(T=30 \;{\rm{MeV}}$ ,

$\mu_B=823 \;{\rm{MeV}})$ 

TCP ( $\mu_I= 500$ 

${\rm{MeV}}$ )

$(T=111 \;{\rm{MeV}}$ ,

$\mu_B=612 \;{\rm{MeV}})$ 

$(T=120 \;{\rm{MeV}}$ ,

$\mu_B=646 \;{\rm{MeV}})$ 

$(T=123 \;{\rm{MeV}}$ ,

$\mu_B=821 \;{\rm{MeV}})$ 

Table 1. The critical endpoint (CEP) and the tricritical point (TCP) with different
$\alpha$ 's for different fixed isospin chemical potentials.In Fig. 8, we compare the results with
$ \alpha = 0.5 $ and the results with$ \alpha = 0 $ (the standard NJL model results) for different fixed nonzero isospin chemical potentials. The figure shows that for the same$ \alpha $ , increasing$ \mu_I $ moves the phase transition line to its upper right in the$ T-\mu_B $ plane, and for the$ \alpha = 0 $ case the part of the first-order phase transition line moves less. This indicates that a higher$ \mu_I $ gives a larger critical baryon chemical potential (or temperature) with the same$ \alpha $ for a fixed temperature (or baryon chemical potential).
Figure 8. (color online) Phase diagram of pion superfluidity in the
$ T-\mu_B $ plane ($\mu_I = 200,\;500$ $ {\rm{MeV}} $ ).We show the critical temperature
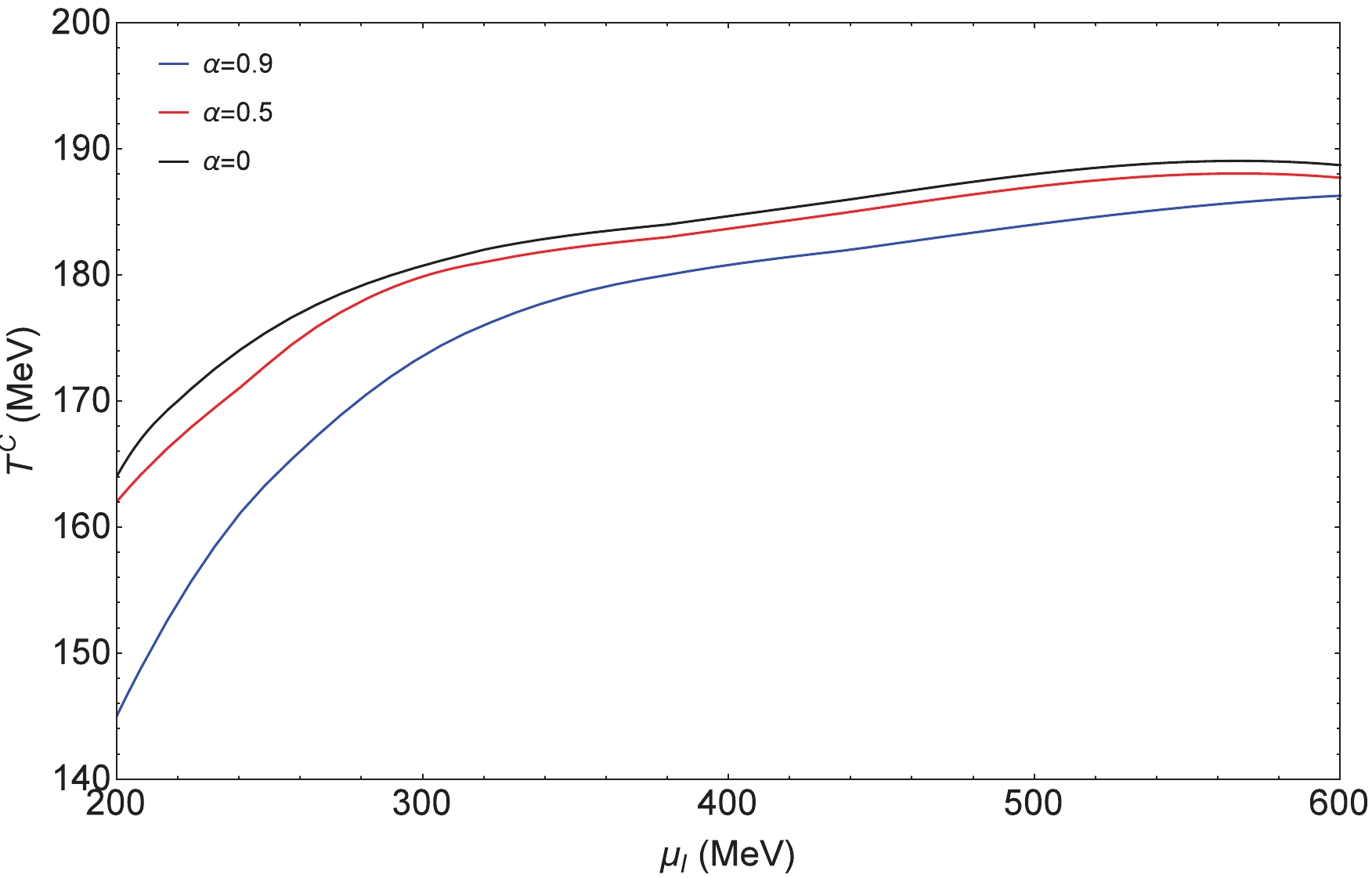
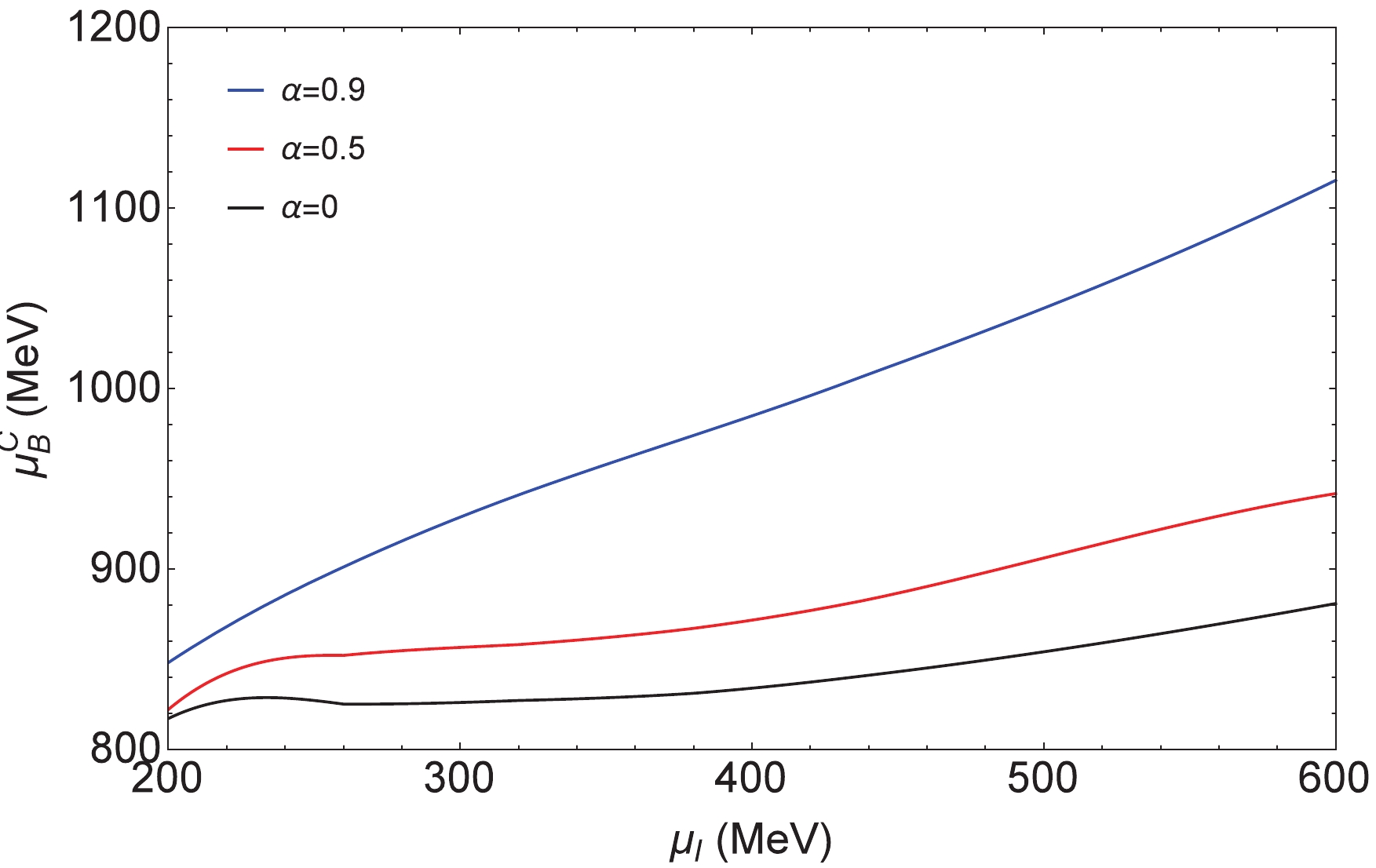
$ T^{\rm C} $ of phase transition with different$ \alpha $ 's at$ \mu_B = 0 $ as a function of$ \mu_I $ in Fig. 9. It shows that the critical temperature$ T^{\rm C} $ of phase transition with different$ \alpha $ increases quickly at the beginning as the isospin chemical potential increases, and when$ \mu_I > 300 $ MeV the critical temperature$ T^{\rm C} $ increases slowly to a constant value. On the whole, the$ T^{\rm C} $ values are closer between$ \alpha = 0 $ and$ \alpha = 0.5 $ compared with$ \alpha = 0.9 $ . The critical baryon chemical potential$ \mu_B^{\rm C} $ of phase transition with different$ \alpha $ 's at$ T = 0 $ as a function of$ \mu_I $ is plotted in Fig. 10. For small$ \mu_I $ , the values of$ \mu_B^{\rm C} $ with different$ \alpha $ are closer, and as the isospin chemical potential increases,$ \mu_B^{\rm C} $ with$ \alpha = 0, 0.5 $ increases slowly and synchronously, while$ \mu_B^{\rm C} $ with$ \alpha = 0.9 $ increases almost linearly. -
The behavior of a system in both vacuum and dense and hot medium depends on its physical symmetries. The symmetries change as temperature and density vary. In this paper, we have employed the self-consistent mean field approximation of the NJL model to study the changes of isospin symmetry and chiral symmetry, and the QCD phase structure at finite densities and finite temperature. In our calculation, we have considered the contributions of different interaction channels (the introduced parameter
$ \alpha $ reflects the weight) with different cases of$ \alpha = 0 $ ,$ \alpha = 0.5 $ , and$ \alpha = 0.9 $ [36]. The results with$ \alpha = 0.5 $ are in good agreement with lattice data, and the contributions of the "exchange" channel need to be considered in the framework of the NJL model. We find that the phase transition line of the$ T-\mu_I $ plane with$ \alpha = 0.5 $ is located in the middle, in the three cases of$ \alpha = 0,\,0.5,\,0.9 $ , and the difference of these three lines is largest at$ \mu_I \sim 1.5m_{\pi} $ .We have plotted the phase transition lines in the
$ T-\mu_B $ plane for different fixed isospin chemical potentials. At$ \mu_I = 0 $ and$ \mu_I = 200 $ $ {\rm{MeV}} $ , the chiral phase diagrams Figs. 4 and 5 give the CEPs with different$ \alpha $ 's. It can be seen that the critical baryon chemical potential of the CEP increases with increasing$ \alpha $ , and a smaller critical baryon chemical potential of the CEP with the same$ \alpha $ is given for higher fixed$ \mu_I $ . At$ \mu_I = 200 $ $ {\rm{MeV}} $ and$ 500 $ $ {\rm{MeV}} $ ($ > $ $ m_\pi $ ), the corresponding phase diagrams, Figs. 6 and 7, of pion condensate give the TCPs with different$ \alpha $ 's. We can see that at low temperatures the system is in the pion superfluidity phase at first. It transitions to the normal phase with increasing$ \mu_B $ , and a smaller critical baryon chemical potential of the TCP is obtained for higher fixed$ \mu_I $ .Finally, the critical temperature
$ T^{\rm C} $ and the critical baryon chemical potential$ \mu_B^{\rm C} $ of the phase transition, varying with$ \mu_I $ , were discussed. It was found that for$ \mu_I > 300 $ MeV, the variation rate of the critical temperature$ T^{\rm C} $ of the phase transition with different$ \alpha $ 's decreases as$ \mu_I $ increases, and the critical baryon chemical potential$ \mu_B^{\rm C} $ of phase transition with$ \alpha = 0, 0.5 $ rises more slowly with$ \mu_I $ , compared with$ \alpha = 0.9 $ . In general, through investigating the QCD phase structure and the location of the critical points, we can further understand the properties of phase transitions at finite densities and finite temperatures. This also provides some information about the phase transitions for experimental measurements.
QCD phase diagram at finite isospin and baryon chemical potentials with the self-consistent mean field approximation
- Received Date: 2020-12-09
- Available Online: 2021-06-15
Abstract: The self-consistent mean field approximation of the two-flavor NJL model, with a free parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






















 DownLoad:
DownLoad: