-
In recent decades, with the continuous progress of high energy physics experiments, more and more exotic hadron states have been discovered [1-3]. The study of the production and properties of exotic hadron states is not only important for the improvement and development of the hadron spectrum and hadron classification, but is also of great significance for an in-depth understanding of non-perturbative quantum chromodynamics (QCD). The candidate particles of the exotic states that have been discovered are mostly concentrated in the charm energy region, and the exotic states discovered in the bottom quark energy region are still very limited [1-3]. In 2011, two bottomonium-like states,
$ Z_{b}(10610) $ and$ Z_{b}(10650) $ , were observed by the Belle Collaboration [4], and a series of subsequent experiments also discovered these two states from different decay channels [4-7]. Since the quantum numbers and decay properties of$ Z_{b}(10610) $ and$ Z_{b}(10650) $ are very similar [1], for convenience$ Z_{b}(10610) $ and$ Z_{b}(10650) $ will be abbreviated as$ Z_{b} $ in the following. These two states are considered to be different from traditional hadron states and are likely to contain at least four quarks [2,3].Observations of the
$ Z_b $ states have inspired extensive studies on the underlying properties, including interpretations as tetraquark states [8-11] and hadronic molecules [12-17]. More discussions can be found in Refs. [2,18]. In Ref. [3], the authors pointed out that since these two states were discovered through the decay reaction of bottomonium, the contribution of triangular singularities during the reaction cannot be neglected, which means that one cannot yet determine whether these two states are genuine particles. At present, investigating$ Z_b $ is still an interesting research topic.Besides the analysis of the mass spectrum and the decay behavior, studying the production of
$ Z_b $ by different mechanisms is very helpful to obtain definite evidence for their nature as genuine states. The meson photoproduction process has been proposed to be an effective way to search for exotic states [19-27]. We take notice of the$ Z_b \to \Upsilon(nS)\pi^+ $ decay modes, which indicate that there exists a strong coupling between$ Z_b $ and$ \Upsilon(nS)\pi^+ $ . Since$ \Upsilon(nS) $ is a vector meson, we suppose that we can produce the$ Z_b $ states through meson photoproduction. In the current work, the photoproduction of$ Z_{b} $ is studied within the framework of the effective Lagrangian approach and the vector-meson-dominance (VMD) model [28-30]. The calculations provide crucial information on a suitable process and the best energy window for searching for the$ Z_b $ states in related photoproduction experiments.In hadron-hadron collisions, when the impact parameter between the two nuclei is larger than the sum of the radii of the two nuclei, the direct strong interaction between the nuclei is suppressed since the strong interaction is short range. However, the electromagnetic interaction cannot be neglected, since it is a long-range interaction. These collisions are called ultraperipheral collisions (UPCs) [31,32]. In UPCs, the photon is almost a real photon when the mass number of an atomic nucleus is larger than 16. Hence, UPCs are a good platform to study photoproduction with small photon virtuality.
Electron-ion colliders (EICs) are an important future platform to investigate nucleon structure. In an EIC, the electron scatters off a nucleon or nucleus via a virtual photon. Then, vector mesons and exotic states can be produced. Thus, the photoproduction of exotic states can be studied at EICs in the future. There are several proposed EIC plans, including the EicC, EIC-US, LHeC and FCC [33-36]. In EICs, the photon emitted from the electron beam has large virtuality. This is different from the photon in UPCs. Hence, EICs can be applied to investigate the photoproduction in a large
$ Q^2 $ region.STARlight and eSTARlight are two important Monte Carlo packages to simulate the photoproduction of vector mesons and exotic states in UPCs and EICs [37-39]. The cross-sections of vector mesons and exotic states produced in photon-proton scattering are needed in the simulation process. Information about the four-momenta of final states is produced in the simulation processes. The total cross-sections of vector mesons or exotic states in UPCs and EICs are also calculated in STARlight and eSTARlight. In this work, the total cross-sections of
$ Z_b $ at UPCs and the proposed EICs will be performed, using the STARlight and eSTARlight packages. The rapidity and transverse momentum distributions of$ Z_b $ will be presented. These distributions will be useful for the detector systems in future experiments.This paper is organized as follows. We present the formalism for the production of
$ Z_{b} $ in Section II. The numerical results for the$ Z_{b} $ production follow in Section III. Finally, the paper ends with a summary. -
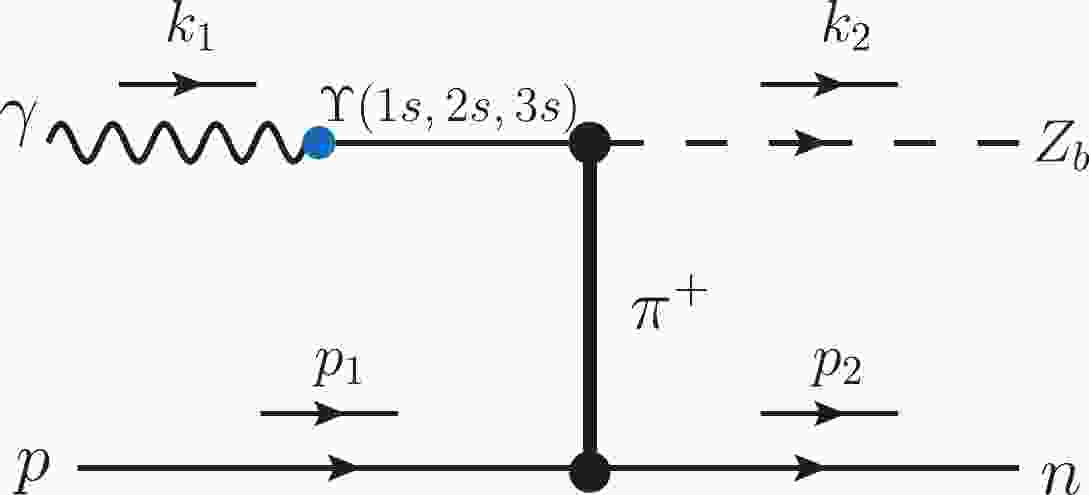
In this work, the production of the hidden-bottom
$ Z_{b}(10610) $ and$ Z_{b}(10650) $ states via the$ \gamma p\rightarrow Z_{b}n $ reaction is studied with an effective Lagrangian approach. In the PDG book [1], one finds that$ Z_{b}(10610) $ or$ Z_{b}(10650) $ can decay to a bottomonium plus$ \pi $ meson with a branching ratio of a few percent. Since$ Z_{b} $ states are not directly coupled to photons, the VMD model can be used to calculate the photoproduction of$ Z_{b} $ states through the t channel with$ \pi $ exchange. The Feynman diagram of the$ \gamma p\rightarrow Z_{b}n $ reaction via t channel$ \pi $ exchange is depicted in Fig. 1. It is noted from Fig. 1 that we only consider the coupling of$ \Upsilon (1s,2s,3s) $ and photons. Also, although$ Z_{b} $ can also decay to$ h_{b}(1p,2p)\pi $ , since the parity of the$ h_{b} $ state is opposite to that of the photon, the direct coupling of$ h_{b} $ to the photon can be neglected. -
In the PDG [1], the spin-parity quantum numbers of
$ Z_{b}(10610) $ and$ Z_{b}(10650) $ are both$ 1^{+} $ , and thus the Lagrangian densities for the vertices of$ Z_{b}\Upsilon \pi $ and$ \pi NN $ are written as [19,40],$ {\cal{L}}_{Z_{b}\Upsilon \pi } = \frac{g_{Z_{b}\Upsilon \pi }}{M_{Z_{b}}} (\partial ^{\mu }\Upsilon ^{\nu }\partial _{\mu }\pi Z_{b\nu }-\partial ^{\mu }\Upsilon ^{\nu }\partial _{\nu }\pi Z_{b\mu }), $

(1) $ \begin{array}{l} {\cal{L}}_{\pi NN} = -{\rm i}g_{_{\pi NN}}\bar{N}\gamma _{5}\vec{\tau}\cdot \vec{\pi}N, \end{array} $

(2) where
$ Z_{b} $ ,$ \Upsilon $ ,$ \pi $ and N denote the fields of$ Z_{b}(10610)/ $ $ Z_{b}(10650) $ ,$ \Upsilon $ , pion and nucleon meson, respectively. Here,$ g_{_{\pi NN}}^{2}/4\pi = 12.96 $ is adopted [41].The coupling constant
$ g_{Z_{b}\Upsilon \pi } $ can be derived from the corresponding decay width,$ \begin{aligned}[b] \Gamma _{Z_{b}\rightarrow \Upsilon \pi } =& \left( \frac{g_{Z_{b}\Upsilon \pi }}{M_{Z_{b}}}\right) ^{2}\frac{|\vec{p}_{\pi }^{\; \mathrm{c.m.}}|}{24\pi M_{Z_{b}}^{2}} \\& \times \left[ \frac{(M_{Z_{b}}^{2}-m_{\Upsilon }^{2}-m_{\pi }^{2})^{2}}{2} +m_{\Upsilon }^{2}E_{\pi }^{2}\right] , \end{aligned} $

(3) with
$ |\vec{p}_{\pi }^{\; \mathrm{c.m.}}| = \frac{\lambda ^{1/2}(M_{Z_{b}}^{2},m_{\Upsilon }^{2},m_{\pi }^{2})}{2M_{Z_{b}}}, $

(4) $ E_{\pi } = \sqrt{|\vec{p}_{\pi }^{\; \mathrm{c.m.}}|^{2}+m_{\pi }^{2}}, $

(5) where
$ \lambda $ is the Källen function with$\lambda (x,y,z)\equiv $ $ \sqrt{(x-y-z)^{2}-4yz} $ , and$ M_{Z_{b}} $ ,$ m_{\Upsilon } $ , and$ m_{\pi } $ are the masses of$ Z_{b} $ ,$ \Upsilon $ , and the pion meson, respectively. The partial decay widths and coupling constants for$ Z_{b}\rightarrow \Upsilon \pi $ are listed in Table 1.state $ \Gamma _{Z_{b}\rightarrow \Upsilon (1S)\pi } $ 

$ g_{Z_{b}\Upsilon (1S)\pi } $ 

$ \Gamma _{Z_{b}\rightarrow \Upsilon (2S)\pi } $ 

$ g_{Z_{b}\Upsilon (2S)\pi } $ 

$ \Gamma _{Z_{b}\rightarrow \Upsilon (3S)\pi } $ 

$ g_{Z_{b}\Upsilon (3S)\pi } $ 

$ Z_{b}(10610) $ 

0.099 0.487 0.662 3.299 0.386 9.292 $ Z_{b}(10650) $ 

0.019 0.206 0.161 1.468 0.184 4.916 Table 1. The values of coupling constants
$ g_{Z_{b}\Upsilon \pi } $ by taking the corresponding decay width of$ \Gamma _{Z_{b}\rightarrow \Upsilon \pi } $ in the PDG book [1]. The unit of width is MeV.The coupling of
$ Z_{b} $ to the photon can be derived using the VMD mechanism [28-30]. In the VMD mechanism, a real photon can fluctuate into a virtual vector meson, which subsequently scatters off the target proton.The Lagrangian for the coupling of the meson
$ \Upsilon $ with a photon reads as [24,25]$ {\cal{L}}_{\Upsilon \gamma } = -\frac{em_{\Upsilon}^{2}}{f_{\Upsilon}}\Upsilon _{\mu }A^{\mu }, $

(6) where
$ f_{\Upsilon} $ is the$ \Upsilon $ decay constant. Thus one gets the expression for the$ \Upsilon \rightarrow e^{+}e^{-} $ decay width,$ \Gamma _{\Upsilon \rightarrow e^+e^-} = \left( \frac{e}{f_{\Upsilon }}\right) ^{2}\frac{8\alpha \left\vert \vec{p}_{e}^{\; \mathrm{c.m.}}\right\vert ^{3}}{3m_{\Upsilon}^{2}}, $

(7) where
$ \vec{p}_{e}^{\; \mathrm{c.m.}} $ denotes the three-momentum of an electron in the rest frame of the$ \Upsilon $ meson.$ \alpha = e^{2}/4\pi = 1/137 $ is the electromagnetic fine structure constant. With the partial decay width of$ \Upsilon (1s,2s,3s)\rightarrow e^{+}e^{-} $ [1], one gets$ e/f_{\Upsilon (1s)}\simeq 0.008 $ ,$ e/f_{\Upsilon (2s)}\simeq 0.005 $ and$ e/f_{\Upsilon (3s)}\simeq 0.004 $ . -
Since the energy corresponding to the
$ \gamma p\rightarrow Z_{b}n $ reaction is above 10 GeV, the Reggeized treatment will be applied to the t channel process. Usually, one just needs to replace the Feynman propagator with the Regge propagator as$ \frac{1}{t-m_{\pi }^{2}}\rightarrow \left(\frac{s}{s_{\rm scale}}\right)^{\alpha _{\pi }(t)}\frac{\pi \alpha _{\pi }^{\prime }}{\Gamma \lbrack 1+\alpha _{\pi }(t)]\sin [\pi \alpha _{\pi }(t)]}, $

(8) where the scale factor
$s_{\rm scale}$ is fixed at 1 GeV. In addition, the Regge trajectory of$ \alpha _{\pi }(t) $ is written as [40]$ \begin{array}{l} \alpha _{\pi }(t) = 0.7(t-m_{\pi }^{2}).\quad \ \ \end{array} $

(9) It can be seen that no free parameters have been added after introducing the Regge model.
-
Based on the Lagrangians above, the scattering amplitude for the reaction
$ \gamma p\rightarrow Z_{b}n $ can be constructed as$ \begin{array}{l} -{\rm i}{\cal{M}}_{\gamma p\rightarrow Z_{b}n} = \epsilon _{Z_{b}}^{\mu }(k_{2}) \bar{u}(p_{2}){\cal{A}}_{\mu \nu }u(p_{1})\epsilon _{\gamma }^{\nu }(k_{1}), \end{array} $

(10) where u is the Dirac spinor of the nucleon, and
$ \epsilon _{Z_{b}} $ and$ \epsilon _{\gamma } $ are the polarization vectors of the$ Z_{b} $ meson and photon, respectively.The reduced amplitude
$ {\cal{A}}_{\mu \nu } $ for t-channel$ Z_{b} $ photoproduction reads$ \begin{aligned}[b] {\cal{A}}_{\mu \nu } =& -{\rm i}\left(\sqrt{2}g_{\pi NN}\frac{g_{Z_{b}\Upsilon \pi }}{M_{Z_{b}}}\frac{e}{f_{\Upsilon }}\right)\gamma _{5}[k_{1}\cdot (k_{2}-k_{1})g_{\mu \nu }\\&-k_{1\mu }(k_{2}-k_{1})_{\nu }] \frac{1}{q^{2}-m_{\pi }^{2}}{\cal{F}}_{\pi NN}(q^{2}){\cal{F}}_{Z_{b}\Upsilon \pi }(q^{2}). \end{aligned} $

(11) For the t-channel meson exchanges [19,20,23,40], the general form factor
$ {\cal{F}}_{t}(q_{t}^{2}) $ consisting of$ {\cal{F}}_{Z_{b}\Upsilon \pi } = (m_{\Upsilon }^{2}-m_{\pi }^{2})/ $ $ (m_{\Upsilon }^{2}-q_{\pi }^{2}) $ and$ {\cal{F}}_{\pi NN} = (\Lambda _{t}^{2}-m_{\pi }^{2})/(\Lambda _{t}^{2}-q_{\pi }^{2}) $ is taken into account. Here,$ q_{\pi } $ and$ m_{\pi } $ are the 4-momentum and mass of the$ \pi $ meson, respectively. The cutoff$ \Lambda _{t} $ will be taken as 0.7 GeV, which is the same as that in Ref. [19,21-23].With the preparation in the previous sections, the differential cross section in the center of mass (c.m.) frame is written as
$ \frac{{\rm d}\sigma }{{\rm d}\cos \theta } = \frac{1}{32\pi s}\frac{\left\vert \vec{k}_{2}^{{\; \mathrm{c.m.}}}\right\vert }{\left\vert \vec{k}_{1}^{{\; \mathrm{c.m.}}}\right\vert }\left( \frac{1}{4}\sum\limits_{\lambda }\left\vert {\cal{M}}\right\vert ^{2}\right) . $

(12) Here,
$ s = (k_{1}+p_{1})^{2} $ , and$ \theta $ denotes the angle of the outgoing$ Z_{b} $ meson relative to the$ \gamma $ beam direction in the c.m. frame.$ \vec{k}_{1}^{{\; \mathrm{c.m.}}} $ and$ \vec{k}_{2}^{{\; \mathrm{c.m.}}} $ are the three-momenta of the initial photon beam and final$ Z_{b} $ meson, respectively. -
In the electron-proton scattering, the cross-section of
$ Z_{b} $ is given by [38,39]$ \sigma (ep\rightarrow eZ_{b}n) = \int {\rm d}k{\rm d}Q^{2}\frac{{\rm d}N^{2}(k,Q^{2})}{{\rm d}k{\rm d}Q^{2}}\sigma _{\gamma ^{\ast }p\rightarrow Z_{b}n}(W,Q^{2}), $

(13) where k is the momentum of the photon emitted from the electron in the target rest frame, W is the c.m. energy of the photon and proton system, and
$ Q^{2} $ is the virtuality of the photon. The photon flux reads as [42]$ \frac{{\rm d}^{2}N(k,Q^{2})}{{\rm d}k{\rm d}Q^{2}} = \frac{\alpha }{\pi kQ^{2}}\bigg[1-\frac{k}{E_{e}}+\frac{k^{2}}{2E_{e}^{2}}-\bigg(1-\frac{k}{E_{e}}\bigg)\bigg|\frac{Q_{min}^{2}}{Q^{2}}\bigg|\bigg]. $

(14) The
$ Q^{2} $ dependence of$ \sigma _{\gamma ^{\ast }p\rightarrow Z_{b}n}(W,Q^{2}) $ is factorized as$ \sigma _{\gamma ^{\ast }p\rightarrow Z_{b}n}(W,Q^{2}) = \sigma _{\gamma p\rightarrow Z_{b}n}(W,Q^{2} = 0)\bigg(\frac{M_{V}^{2}}{M_{V}^{2}+Q^{2}}\bigg)^{\eta }, $

(15) where
$ M_V $ is the mass of the vector meson. Since there is no parameter for the$ Z_{b} $ state, we apply the same$ \eta $ from$ J/\psi $ as Ref. [38]. This assumption has very little impact on the projection for$ Z_{b} $ because we consider$ 0<Q^{2}<1{\mathrm{GeV}}^{2} $ , which gives quasi-real events [43].The cross-section of an exotic charged particle in UPCs is computed in integrating the photon flux and photon-proton cross-section. The photon flux represents the number as a function of momentum of the photon emitted from a nucleus. In
$ p\rm{-}A $ UPCs, the cross-section of$ pA\rightarrow nAZ_{b} $ reads [37]$ \sigma (pA\rightarrow AZ_{b}n) = \int {\rm d}k\frac{{\rm d}N_{\gamma }(k)}{{\rm d}k}\sigma _{\gamma p\rightarrow Z_{b}n}(W) , $

(16) where k is the momentum of the real photon emitted from the nucleus, and W is the c.m. energy of the photon and proton system. The photon flux of the photon emitted from the nucleus is given as [44]
$ \frac{{\rm d}N_{\gamma }(k)}{{\rm d}k} = \frac{2Z^{2}\alpha }{\pi k}\big(XK_{0}(X)K_{1}(X)- \frac{X^{2}}{2}[K_{1}^{2}(X)-K_{0}^{2}(X)]\big), $

(17) where
$X = b_{\rm min}k/\gamma _{L}$ , and$b_{\rm min} = R_{A}+R_{p}$ is the sum of the radii of the proton and nucleus.$ \gamma _{L} = \sqrt{s}/2m_p $ is the Lorentz boost factor.$ K_{0}(x) $ and$ K_{1}(x) $ are modified Bessel functions. Z denotes the charge number of the nucleus.Adopting the cross-sections of
$ Z_b $ in the photon-proton interaction, we can obtain the$ Z_b $ cross-sections in e-p scattering in EIC and$ p\rm{-}A $ UPCs. With the help of the eSTARlight and STARlight packages, we can simulate the$ Z_{b} $ production processes and get the four-momenta of the final states. Then, we will further obtain$ Z_{b} $ in rapidity distributions and transverse momentum distributions, where the rapidity is defined as$y = \dfrac{1}{2}\ln[(E+p_z)/(E-p_z)]$ . -
In Fig. 2 we present the total cross-sections for the reaction
$ \gamma p\rightarrow Z_{b}n $ , from threshold to 50 GeV of the c.m. energy. One finds that the total cross-section of the$ \gamma p\rightarrow Z_{b}(10610)n $ scattering process reaches a maximum at the center-of-mass energy$ W\simeq 22 $ GeV, which is about 0.09 nb. Also, when the cutoff parameter is changed from 0.5 to 0.9 GeV, the total cross-section of$ \gamma p\rightarrow Z_{b}(10610)n $ at$ W\simeq 22 $ GeV is approximately between 0.06 and 0.12 nb.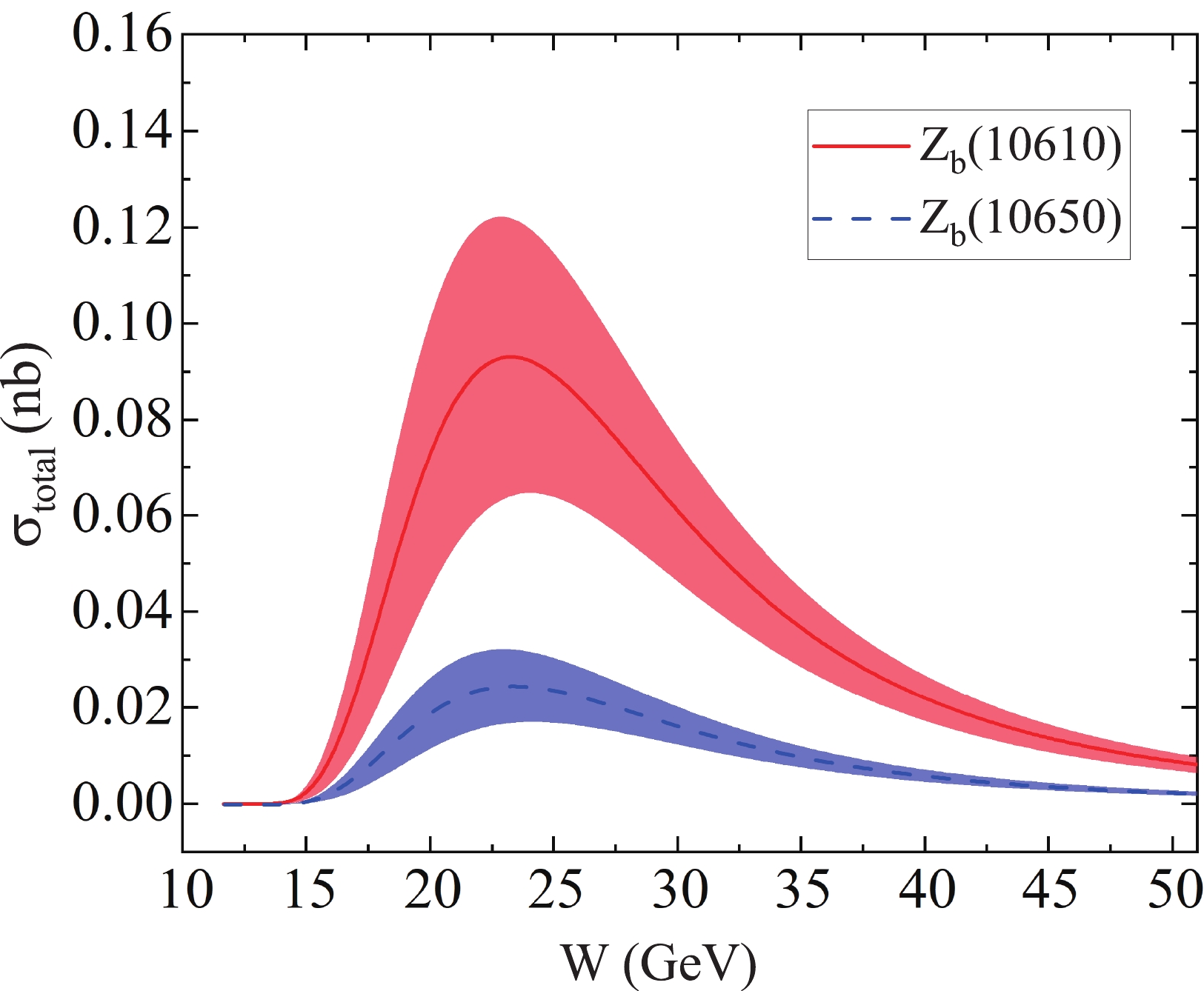
Figure 2. (color online) Total cross-section for the
$ \gamma p\rightarrow Z_{b}n $ reaction via pionic Regge trajectory exchange. The solid red and dashed blue lines are for$ Z_{b}(10610) $ and$ Z_{b}(10650) $ respectively. The value of cutoff$ \Lambda _{t} $ is taken as$ 0.7\pm 0.2 $ GeV. The bands stand for the error bar of the cutoff$ \Lambda _{t}. $ -
Photoproduction measurement is an important test of the structure of exotic states. Since the energy span of EIC and UPC facilities is large, it is advantageous to find the exotic states in the bottom quark energy region. Based on the previous
$ Z_{b} $ photoproduction results, with the help of the eSTARlight and STARlight programs, we have obtained the cross-sections and numbers of events for$ Z_{b}(10610) $ production in EICs and UPCs. As presented in Table 2, the results were calculated based on several different accelerators. The cross-sections of$ Z_{b}(10610) $ in UPCs are larger than in EICs, since the photon flux of the nucleus is larger than the electron beam. However, the number of$ Z_{b}(10610) $ events in EICs is larger than that in UPCs, especially the FCC.$e$ -

$p$ EIC-US

$e$ -

$p$ LHeC

$e$ -

$p$ FCC

$p$ -

${\rm Au}$ RHIC

$p$ -

${\rm Pb}$ LHC

Beam energy, GeV 18 (e) vs. 275 (p) 60 (e) vs. $7\times 10^3$ (p)

60 (e) vs. $50\times 10^3$ (p)

100 (p) vs. 100 (Au) $7 \times 10^3$ (p) vs.

$2.778\times 10^3$ (Pb)

Integrated luminosity 10 $\mathrm{fb}^{-1}$ 

10 $\mathrm{fb}^{-1}$ 

150 $\mathrm{fb}^{-1}$ 

4.5 $\mathrm{pb}^{-1}$ 

2 $\mathrm{pb}^{-1}$ 

$Z_b(10610) $ Cross sections

6.2 pb 8.5 pb 9.8 pb 2.0 nb 30 nb Expected statistics, $10^6$ events

0.062 0.085 1.5 0.0090 0.060 It can be seen from Table 2 that the differences between the total cross-sections in EICs are small, since the cross-section of EICs is not very sensitive to the collision energy. However, the cross-section of
$ Z_{b} $ in EICs depends heavily on the value of the cross-section of$ Z_{b} $ photoproduction. It can be seen from Fig. 2 that if the c.m. energy is too small, the photoproduced cross-sections of$ Z_{b} $ will also be small, which indirectly leads to small cross-sections of$ Z_{b} $ in EICs. For the EicC [33], the present designation of collision energies is 5 GeV vs 20 GeV, so the c.m energy is about 16.7 GeV. Thus, the cross-sections of$ Z_b(10610) $ in EicC will be very small. Table 3 shows the cross-sections of$ Z_{b} $ in EicC and the numbers of events when the beam energy is up to 10 GeV vs 100 GeV. These results will provide theoretical references for future experimental measurements and upgrades.Beam energy 5 (e) vs. 20 (p) 5 (e) vs. 30 (p) 10 (e) vs. 50 (p) 10 (e) vs. 100 (p) $ Z_b(10610) $ cross sections

0.52 pb 1.3 pb 3.4 pb 4.4 pb Expected statistics, $ 10^3 $ events

5.2 13 34 44 Table 3. Cross-sections and numbers of events for
$ Z_{b}(10610) $ in e-p collisions. Here, the integrated luminosity is taken as 10$ \mathrm{fb}^{-1} $ , which is the current design value of the EicC [33].For
$ Z_{b}(10610) $ production in EIC and UPC processes, we also present the rapidity distributions of$ Z_{b}(10610) $ in e-p and p-A processes, as shown in Fig. 3. These two distributions are relatively wide, which is related to the production mechanism of$ Z_{b} $ through the t-channel with pionic Regge trajectory exchange [23]. This indicates that the distribution shape of the rapidity and transverse momentum reflects the shape of the cross-section in Fig. 2. From the left-hand graph in Fig. 3, it can be seen that photoproduction at the EIC-US is near mid-rapidity and it is easy to identify in the detector system. From the right-hand graph of Fig. 3, we can also conclude that it is easier to observe$ Z_b(10610) $ in p-${\rm Au}$ UPCs than in p-${\rm Pb}$ UPCs, since the$ Z_b(10610) $ will be produced near mid-rapidity.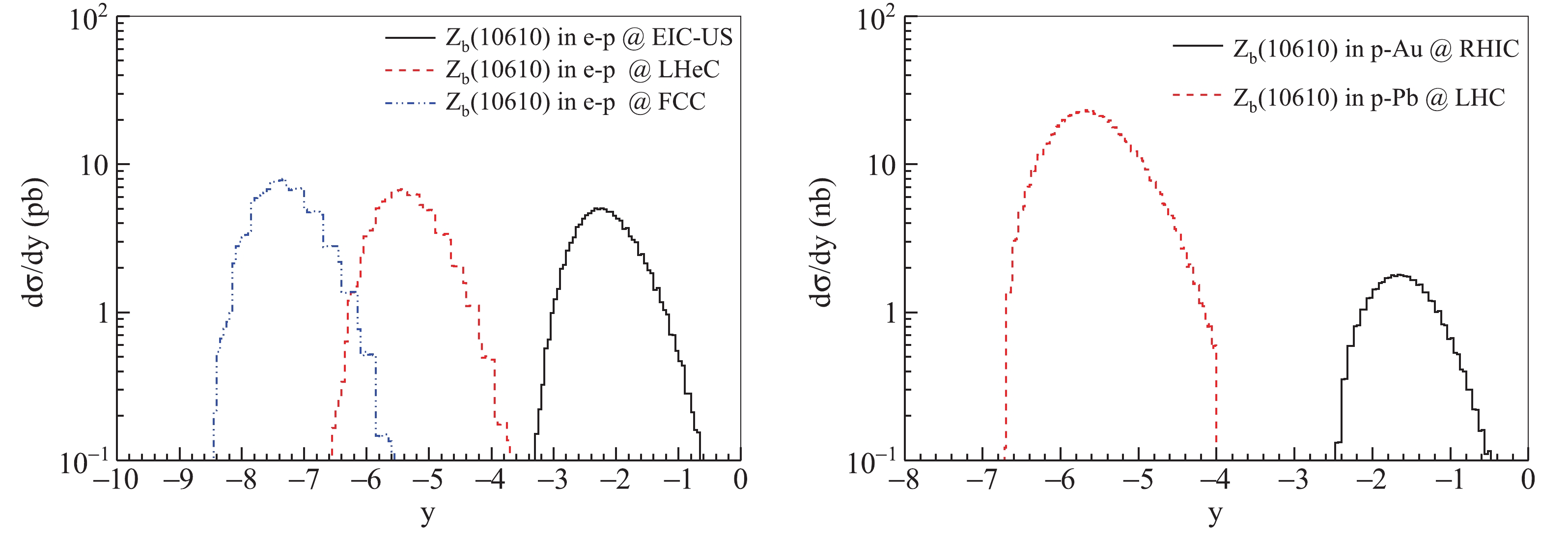
Figure 3. (color online) Rapidity distributions of
$Z_{b}(10610)$ in (left) e-p at EIC-US, LHeC and FCC with$0<Q^{2}<1 \;\mathrm{GeV}^{2}$ and (right)$p$ -${\rm Au}$ and$p$ -${\rm Pb}$ UPCs at RHIC and LHC.In addition, the transverse momentum distributions in e-p scattering and p-A UPCs are shown in Fig. 4. These results can be used as predictions for experiments. We notice that the three transverse momenta of the EICs are close to each other, since the total cross-sections are close to each other. These distributions can be employed to identify the exotic states. In p-A UPCs, the difference between the two distributions is large because the total cross-section in p-
${\rm Pb}$ is larger than the cross-section in p-${\rm Au}$ . It can be found that the largest value of transverse momentum is about 0.2 - 0.4 GeV in both EICs and UPCs.
Figure 4. (color online) Transverse momentum distributions of
$Z_{b}(10610)$ in (left) e-p at EIC-US, LHeC and FCC with$0<Q^{2}<1\;\mathrm{GeV}^{2}$ and$p$ -${\rm Au}$ and$p$ -${\rm Pb}$ UPCs at RHIC and LHCWe also give the t-distribution for
$ Z_{b}(10610) $ production in e-$ p $ and p-A UPCs in Fig. 5. The t-distributions are close to each other in the three EICs and are different in the two UPCs. These conclusions are the same as for the transverse momentum distributions. Due to the adoption of the Regge propagator, it can be seen from Fig. 5 that the shape of the curves of the differential cross-sections of the t-distribution is relatively steep. This will be an important theoretical basis for us to clarify the role and contribution of the Regge propagator through EIC or UPC experiments. -
In this work, based on effective field theory and the VMD mechanism, the photoproduction of the two bottomonium-like
$ Z_{b}(10610) $ and$ Z_{b}(10650) $ states has been investigated for the first time. The numerical results show that the total cross-sections of the$ \gamma p\rightarrow Z_{b}n $ reaction reach a maximum at the center-of-mass energy$ W\simeq 22 $ GeV, which indicates that the center-of-mass energy 22 GeV is the best energy window for searching for the$ Z_{b} $ states via$ \gamma p $ scattering. Hence, an experimental study of the bottomonium-like states$ Z_{b} $ via the$ \gamma p $ reaction is suggested.With the help of the eSTARlight and STARlight packages, the cross-sections and numbers of events for
$ Z_{b}(10610) $ production in EICs and UPCs have been presented. As shown in Table 2, EIC experiments may collect more events due to their larger luminosity. Moreover, we have also simulated the rapidity and transverse momentum distributions of$ Z_{b}(10610) $ in e-p scattering and p-A UPC processes. These results will provide an important basis for estimating the production and studying the properties of$ Z_{b} $ in the RHIC, LHC, EIC-US, LHeC, and FCC in the future.Since Reggeons are composed mostly of quarks, using Reggeons to prove the distributions of sea quarks and anti-quarks in nuclei may be a feasible method [39]. In this work, the photoproduction of
$ Z_{b} $ is calculated by introducing the Regge exchange model. Thus, the numerical results will be beneficial for experimental studies of the Reggeon model. Also, the cross-sections of t distributions of$ Z_{b} $ in different scattering processes have been obtained, which will provide an important theoretical reference for clarifying the role and contribution of Reggeons.
Production of bottomonium-like Zb states in e-h and ultraperipheral h-h collisions
- Received Date: 2020-09-18
- Available Online: 2021-05-15
Abstract: The photoproduction of the bottomonium-like states






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF























 DownLoad:
DownLoad: