-
Properties of neutron matter play a crucial role in determining the structures of not only neutron stars [1-7] but also extremely isospin-asymmetric nuclear systems [8-11]. Though finite nuclei have provided much information about nuclear matter at sub- and around saturation densities [12-19], it is difficult to extrapolate the properties to a higher-density region. To obtain a reliable equation of state (EOS) of nuclear matter in the overall density region, microscopic many-body calculations can be conducted based on bare nucleon–nucleon (
$ NN $ ) interactions. In a short-distance region, the central force of the$ NN $ interaction has a strong repulsion core, while in intermediate- and long-distance regions, there is a strong tensor force [20-22]. The high-momentum components in the nuclear system are mainly induced by the aforementioned two types of forces. The short-range repulsion can decrease the wave function amplitude of the relative motion at short-range distances for the two nucleons in a nucleon pair, while the tensor force can introduce the D-wave state because there can exist strong S–D couplings.Different approaches have been proposed to treat the
$ NN $ correlations originating from the$ NN $ interaction, such as the utilization of correlation functions introducing the Jastrow factor and the renormalization of the$ NN $ interaction using unitary transformation. In our recent variational approach proposed for finite nuclei, namely tensor-optimized antisymmetrized molecular dynamics (TOAMD) [23-27], the central- and tensor-operator-type correlation functions are employed to treat the short-range and tensor correlations, respectively. Within this method, the antisymmetrized-molecular-dynamics (AMD) [28] bases are used as the basis wave functions. With bare$ NN $ interactions, the two aforementioned correlations in s-shell nuclei, as well as their structure and properties, have been successfully investigated [24-27]. Recently, Yamada proposed another variational theory to study the properties of nuclear matter, namely, the tensor-optimized Fermi sphere (TOFS) method [29, 30]. In this method, the nuclear matter is described within a Fermi sphere, and the correlation functions multiplied with the Fermi-sphere state are used to treat the$ NN $ correlations in nuclear matter. The minimal energy of nuclear matter is searched to determine the parameters in the functions. With Argonne V4' (AV4') central$ NN $ potential [22], which can induce short-range correlation, the obtained EOS of symmetric nuclear matter within TOFS agrees with the benchmark results calculated with other theories [29, 30].The short-range correlation can be also treated by the unitary correlation operator method (UCOM) by employing the unitary correlation operator [31-33]. The short-range repulsion results in decreasing the wave function amplitudes for the two nucleons in a nucleon pair for the relative motion at short-range distances. It has been shown that UCOM can effectively describe the short-range correlation in finite nuclei [31-35]. Under the relativistic and nonrelativistic frameworks within the Hartree-Fock (HF) approximation for a Fermi sphere [36, 37], Hu et al. employed UCOM to further describe the short-range correlation in neutron matter. The obtained EOS of neutron matter agrees well with those calculated by the Relativistic Brueckner–Hartree–Fock theory, which indicates that the short-range correlation in neutron matter can also be treated by UCOM [36, 37].
To describe the tensor correlation, besides employing correlation functions, other approaches have also been successfully proposed in our previous studies on finite nuclei. As is well known that the two-particle two-hole (2p2h) excitations can describe the strong tensor correlation originating from the tensor force in nucleon pairs, the tensor correlation can be described by optimizing the 2p2h configurations, as introduced in the tensor-optimized shell model (TOSM) [33-35]. In the TOSM, the total wave function is superposed by the standard shell-model state and sufficient 2p2h states. By optimizing the 2p2h configurations without truncation of the particle states, the tensor correlation can be treated based on the framework of the shell model. Within the extension of HF theory [38], the 2p2h configurations are employed to describe the high-momentum components of nuclear matter. The obtained results are similar to those of Brueckner–Hartree–Fock (BHF) theory, and the corresponding momentum distribution is found to have high-momentum components because of the 2p2h excitations. In our recently developed approach, namely high-momentum AMD (HM-AMD) [39-43], a high-momentum (HM) nucleon pair is introduced, in which both nucleons for a 2p2h excitation involve a large transfer momentum in an opposite direction [44]. Similar to the TOAMD approach, the AMD bases [28] are used as basis wave functions. However, the 2p2h excitations are employed in HM-AMD to treat the
$ NN $ correlations instead of the correlation functions used in TOAMD. This new approach clearly describes the HM components in finite nuclei [39-43].In the study of nuclear matter, there are several other microscopic theories treating the
$ NN $ correlations, starting from the bare$ NN $ interactions, such as BHF and Brueckner-Bethe-Goldstone (BBG) [45-47], self-consistent Green's function (SCGF) [48-51], Fermi hypernetted chain (FHNC) [52-55], auxiliary field diffusion Monte Carlo (AFDMC) [56-58], Green's function Monte Carlo (GFMC) [59, 60], and coupled cluster theory (CC) [61-63]. The BHF approach can be interpreted as the lowest order under the framework of the BBG theory. The ground-state energy of the latter is calculated by employing the linked cluster expansion by means of the G-matrix, which is ordered based on the number of independent hole lines. The diagram corresponding to the hole line with a number n describes the n-body correlations. In the BHF approach, the total energy is calculated within the truncation of two hole-line approximation, which only includes the two-body correlations. In the SCGF approach, the total energy is calculated from the in-medium one-body propagator, which is obtained from the Dyson equation by using the ladder diagram expansion. The FHNC approach is one of the variational methods different from the above nonperturbative ones. With a given trial wave function multiplied by correlation operators, the total energy can be evaluated within the cluster expansion by using the FHNC integral equations [52]. Besides, both the AFDMC and GFMC approaches are extended for nuclear systems under the framework of the quantum Monte Carlo (QMC) method, which has successfully described the ground state of infinite atomic systems [64, 65]. The difference between AFDMC and GFMC mainly exists in their treatments of the spin and isospin channels. The AFDMC samples the spin-isospin states according to the Hubbard-Stratonovich auxiliary fields, while the GFMC sums all the states. Compared to AFDMC, GFMC can treat nuclear systems with more accuracy but smaller mass number. The comparison of benchmark results obtained by Baldo et al. by applying the different above-mentioned theories for nuclear matter with several types of Argonne bare$ NN $ interactions [45] results in similar density dependence of the total energy per particle of nuclear matter. In detail, if only the central potential, including the short-range repulsion, is considered, the calculated results agree with each other. However, when the tensor and spin-orbit forces are additionally included in the$ NN $ potentials, there will be large differences among the density dependences, especially for the symmetric nuclear matter [45], which mainly result from the different treatments of the tensor force as tensor correlations. The intermediate- and long-range properties of the tensor correlation derived from the$ NN $ interaction can induce many-body correlations, which is important for nuclear matter studies. In particular, the saturation property of symmetric nuclear matter has a close relation to tensor correlation. Besides the bare two-body$ NN $ force, there are also studies discussing the effects of many-body forces on the properties of nuclear matter, especially three-body force (TBF) [66-71]. A detailed analysis with several different forms for TBF in Ref. [70] showed that the TBF can have a large impact on the EOS of nuclear matter at high densities. Considering the several uncertainties in many-body forces, we mainly concentrate on the bare two-body$ NN $ interaction to investigate the properties of neutron matter in this study.In our recent paper, we proposed a new variational approach for nuclear matter description starting from the bare
$ NN $ interaction [72]. Under a periodic boundary condition, the nuclear matter is described in a cubic box with finite size. This finite particle number approach has been successfully used in AFDMC, GFMC, CC, and electron systems [73]. Allowing for the different correlations originating from the$ NN $ interaction, UCOM is employed in the new variational method to treat the central short-range correlation induced by the short-range repulsion. In addition, the 2p2h excitations of nucleon pairs are further included to describe the HM components in nuclear matter. The 2p2h configurations are added into the total wave function in the same manner for finite nuclei [33-35]. Both nucleons in the nucleon pair for a 2p2h excitation obtain a transfer momentum with opposite directions, which results in a large relative momentum for the two nucleons of a 2p2h excitation. The aforementioned new framework for nuclear matter is named UCOM+HM [72].We have previously validated the present UCOM+HM framework to study the neutron and symmetric nuclear matters [72]. From the calculation for nuclear matter with AV4' central potential involving the short-range repulsion, we confirm the applicability of UCOM to treat the central short-range correlation. Besides, the additional 2p2h excitations are found to contribute to the total energy around the normal nuclear density in nuclear matter by several MeVs per particle. The EOSs provided by the present method for the neutron and symmetric nuclear matters are consistent with those of other theories from low- to high-density regions [72], which indicates the reliability of this new variational approach.
In the present study, we concentrate on the effects of tensor correlation and spin-orbit coupling on the properties of neutron matter. The tensor correlation is well known to be important for the symmetric nuclear matter, especially the saturation property. It is also interesting to investigate the tensor correlation in neutron matter. With Argonne V6' (AV6') and V8' (AV8')
$ NN $ interactions [22], the effects of not only tensor correlation but also spin-orbit coupling on the EOS of neutron matter are studied, and their respective contributions to the total energy of neutron matter are obtained. In addition, the corresponding EOSs of neutron matter calculated with different$ NN $ interactions are compared with those of several other microscopic many-body theories. In Section 2, a detailed formulism of this new variational framework is presented. In Section 3, the calculated results of neutron matter are discussed. A summary is provided in Section 4. -
The Argonne V18 (AV18) potential is, currently, one of the most accurate bare
$ NN $ interactions [20-22]. Because of its sophisticated operatorial structure for some many-body schemes, several simplified versions of AV18 potential have been devised for benchmark purposes, such as AV4', AV6', and AV8'$ NN $ interactions [22]. The AV8' potential can be written as the summation of the first eight components of AV18 potential:$ V_{ij} = \sum\limits_{k = 1,...,8}v_k(r_{ij})O^k_{ij}. $

(1) The other six quadratic spin-orbit and four charge-dependent components of AV18 potential are removed for the AV8' version, and the radial functions
$ v_k(r_{ij}) $ are readjusted to preserve experimental data on the phase shifts and properties of deuterons. The eight operators$ O^k_{ij} $ in Eq. (1) include the spin, isospin, tensor, and spin-orbit coupling components of nuclear force [22]:$ \begin{aligned}[b] O^{k = 1,...,8}_{ij} = &1,\ { \sigma}_i\cdot{ \sigma}_j,\ { \tau}_i\cdot{ \tau}_j,\ ({ \sigma}_i\cdot{ \sigma}_j)({ \tau}_i\cdot{ \tau}_j),\\ &S_{ij},\ S_{ij}({ \tau}_i\cdot{ \tau}_j),\\ &{ L}\cdot{ S},\ { L}\cdot{ S}({ \tau}_i\cdot{ \tau}_j). \end{aligned} $

(2) By removing the last two spin-orbit coupling components and refitting the radial functions, the first six components in Eq. (2) constitute the AV6' potential. Similarly, without considering the tensor and spin-orbit coupling components, the AV4' central potential only includes the first four components of Eq. (2), but the radial functions have been refitted by the deuteron binding energy. With these simplified
$ NN $ interactions, namely AV4', AV6', and AV8', the EOSs of neutron matter will be microscopically calculated in the present study and the effects of the tensor correlation and spin-orbit coupling on the results will be discussed. -
As introduced in our recent study [72], the 0p0h state of neutron matter is defined by the Slater determinant as
$ |{0p0h}\rangle = \frac{1}{\sqrt{N!}}\mathrm{det}\left\{\mathop \prod \limits_{i = 1}^N \phi_{\alpha_i}({ r}_i)\right\}, $

(3) $ \phi_{\alpha}({ r}) = \frac{1}{\sqrt{L^3}}{\rm e}^{{\rm i}{ k}_{\alpha}\cdot{ r}}\chi^{\sigma}_{\alpha}, $

(4) $ \langle\phi_{\alpha}|\phi_{\alpha'}\rangle = \delta_{\alpha,\alpha'},$

(5) where N is the neutron number of neutron matter,
$ \phi_{\alpha}({ r}) $ is the plane wave function of a neutron,$ { k}_{\alpha} $ is the momentum, and$ \chi^{\sigma}_{\alpha} $ is the spin component, which can be up or down. The index$ \alpha $ represents the quantum number for both momentum and spin. The neutron matter is described in a cubic box with finite size L, as given in Eq. (4), which is determined by wave function normalization. With the periodic boundary condition$ \phi_{\alpha}({ r}+L\hat{{ x}}) = \phi_{\alpha}({ r}) $ employed in the description of neutron matter, the neutron momentum is discretized by the gap$ \Delta k = \dfrac{2\pi}{L} $ . By using an integer vector$ { n} = (n_x, n_y, n_z) $ , the momentum of each neutron can be calculated by$ { k} = \dfrac{2\pi}{L}{ n} $ . Within a lattice in momentum space corresponding to the cubic box in coordinate space, as shown in our previous study [72], the momentum eigenstate of each neutron can be represented by the grid point.On account of the periodic boundary condition and symmetry of the wave function in Eq. (3), there exist magic particle numbers corresponding to the shell closures, where the corresponding grid points are
$ N_g = 1, 7, 19, 27, 33, 57, ... $ . For each grid number$ N_g $ , besides the single neutron wave function with momentum$ { k}_i $ ($ i = 1, ..., N_g $ ) in the 0p0h state, the total particle number becomes$ N = 2N_g $ because of the spin.For the 2p2h excitations of neutron matter, the 2p2h configurations can be written as
$ |{2p2h}\rangle = |mn;i^{-1}j^{-1}\rangle = a^{\dagger}_ma^{\dagger}_na_ia_j|{0p0h}\rangle, $

(6) where the indices i and j (
$ i, j = 1, ..., N $ ) represent hole states from lower magnitude of momenta, and the indices m and n ($ m, n>N $ ) are particle states in 2p2h configurations. The total momentum between two holes and two particles is conserved under the following condition:${ k}_i+{ k}_j = { k}_m+{ k}_n, $

(7) ${ k}_m = { k}_i+{ q},\quad { k}_n = { k}_j-{ q}. $

(8) The quantity
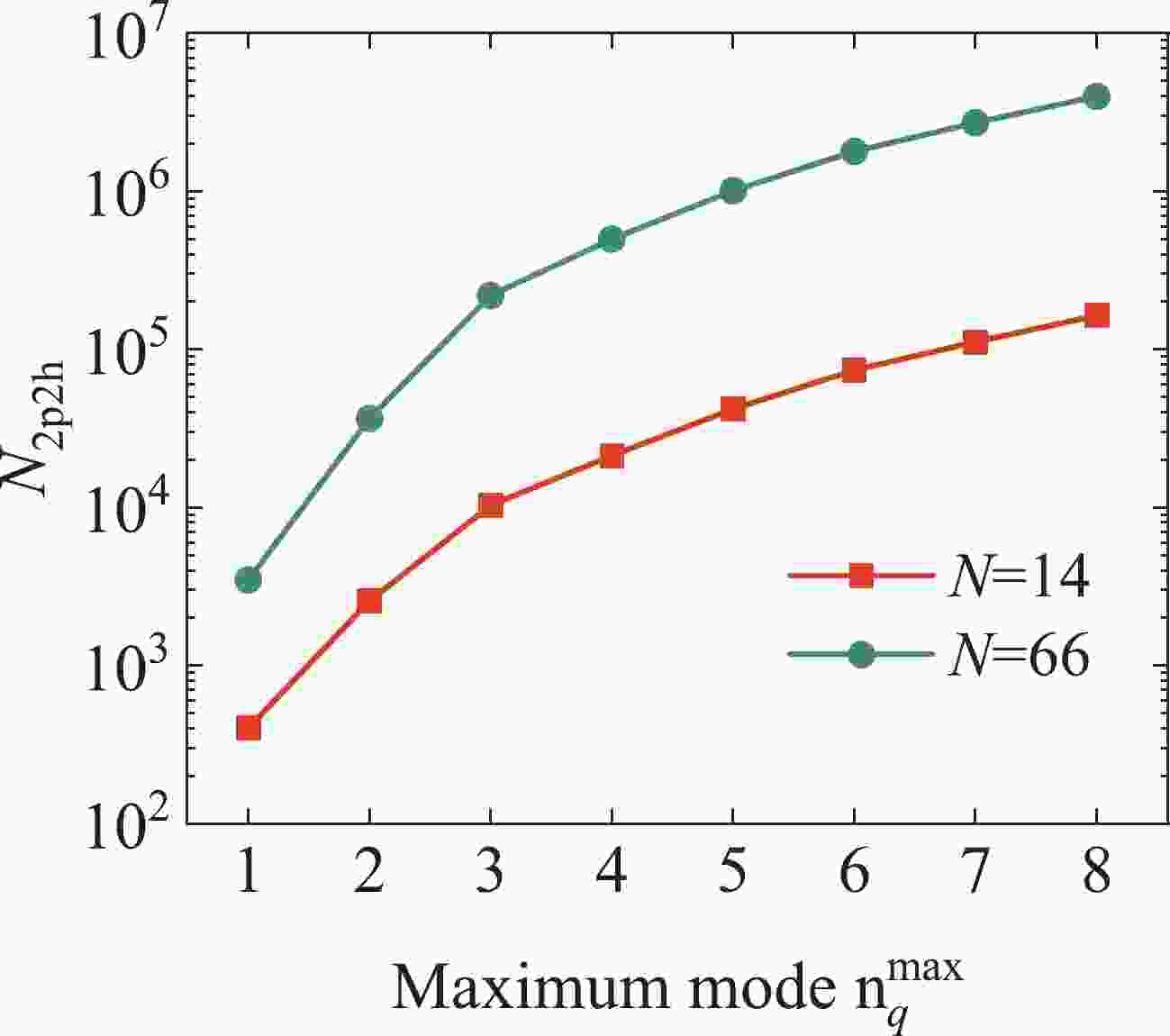
$ { q} = \dfrac{2\pi}{L}{ n}_q $ is the transfer momentum to link the two particles and two holes in a 2p2h configuration, which are correlated with the relative momentum of the two particle states. Besides, the periodic boundary condition leads to the transfer momentum also being discretized with the mode$ { n}_q = (n_{qx}, n_{qy}, n_{qz}) $ . If the transfer momentum is large enough, the HM components in neutron matter can be naturally induced by 2p2h excitations. For example, if the neutron number$ N = 66 $ and normal density$ \rho = 0.17\; \mathrm{fm}^{-3} $ , the magnitude of the transfer momentum is approximately$ |{ q}| = \dfrac{2\pi}{L}|{ n}_q| = 5.2\; \mathrm{fm}^{-1} $ with the integer mode$ |{ n}_q| = 6 $ . Compared to the empirical Fermi momentum$ k_F = 1.4\; \mathrm{fm}^{-1} $ , it is large enough to excite nucleons to HM regions. The HM component is closely related to the descriptions of both short-range and tensor correlations [40-43]. In the present study, a maximum integer for the magnitude of the transfer mode$ { n}_q $ as$ n^{\mathrm{max}}_q $ is employed under the condition$ n^{\mathrm{max}}_q\geqslant|{ n}_q| $ . The total number of 2p2h configurations is determined by the quantity$ n^{\mathrm{max}}_q $ , which affects the basis space for the present calculation. By increasing this parameter, we first check the energy convergence of neutron matter at normal density.By superposing the 0p0h and 2p2h configurations, the total wave function
$ \Phi $ of neutron matter can be written as [72]$\Phi = {C_0}|{{0p0h}}\rangle + \sum\limits_{p = 1}^{{N_{{{2p2h}}}}} {{C_p}} |{{2p2h}},p\rangle , $

(9) where
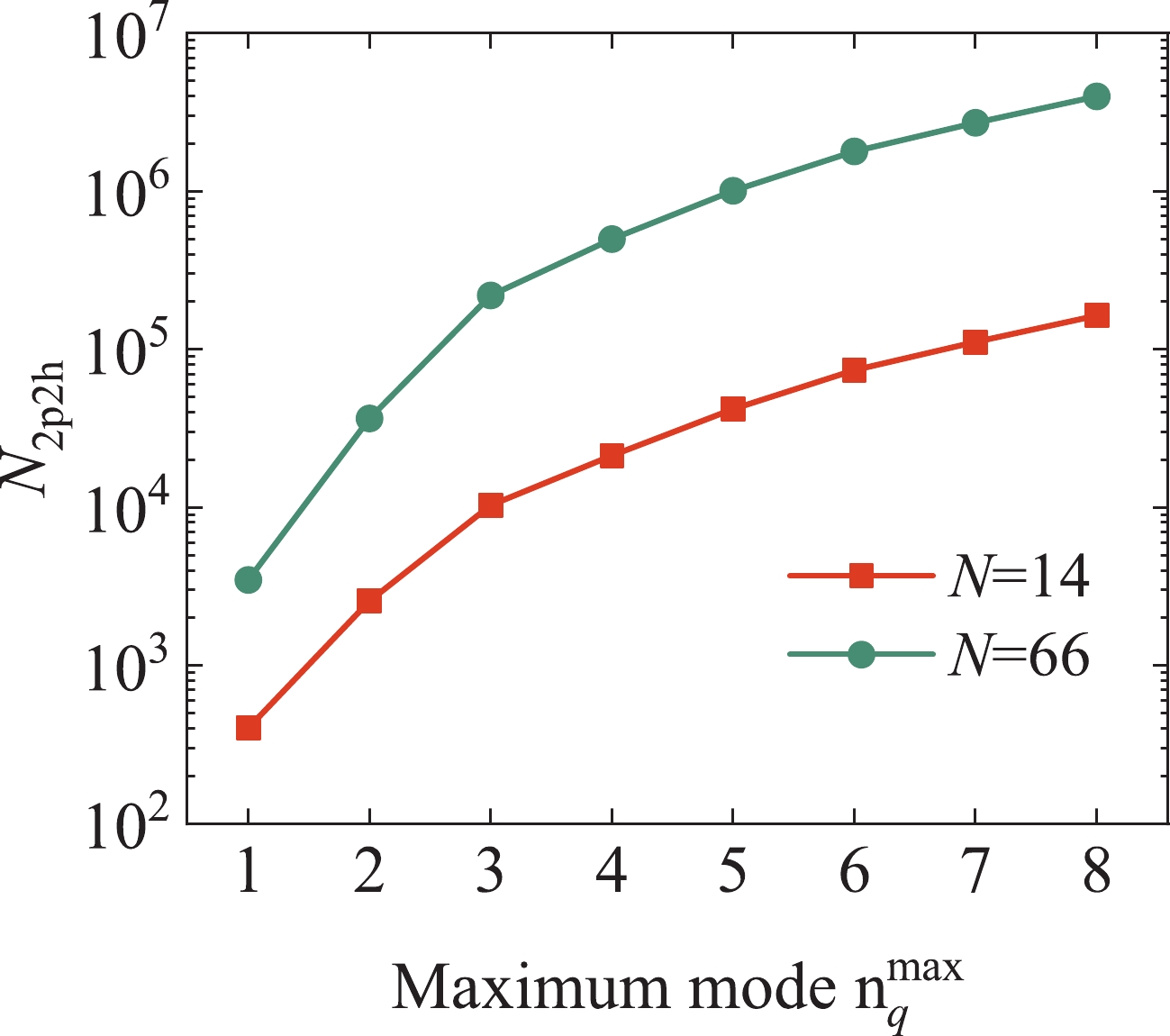
$ N_{{2p2h}} $ is the total number of 2p2h configurations and$ \{C_p\} $ are the configuration amplitudes, which can be variationally determined. The index p represents each configuration, where$ p = 0 $ corresponds to the 0p0h state. In Fig. 1, by taking the neutron magic numbers$ N = 14 $ and$ N = 66 $ as examples, we show the variation in the number$ N_{{2p2h}} $ with the maximum transfer mode$ n^{\mathrm{max}}_q $ . As shown in Fig. 1, the total number of 2p2h configurations approximately exponentially increases with the maximum transfer mode. That is, the mode space of the present calculation will increase sharply with the maximum transfer mode. -
For the short-range repulsion in
$ NN $ interaction, UCOM is further used to treat the corresponding central short-range correlation in neutron matter. Within UCOM, the correlated wave function$ \Psi $ considering the short-range correlation in the nuclear system can be obtained by multiplying a unitary correlation operator$ C_r $ with the uncorrelated one$ \Phi $ :$ \Psi = C_r\Phi $ , where the unitary correlation operator$ C_r $ is defined as [31, 32]$ C_r = \exp\left(-{\rm i}\sum\limits_{i<j}g_{ij}\right) = \mathop \prod \limits^N_{i<j}c_{r,ij}, $

(10) where g is a pair-type Hermite generator and
$ c_{r,ij} $ is a nucleon pair. The specific form of operator g can be written as$ g = \frac{1}{2}\{p_rs(r)+s(r)p_r\}, $

(11) where
$ p_r $ is the parallel relative momentum between the nucleons and$ s(r) $ is the variation in the relative wave function. By using the transformation$ \Psi = C_r\Phi $ under UCOM, the transformed Schrödinger equation for$ \Phi $ can be written as$ \tilde{H}\Phi = E\Phi $ , where$ \tilde{H} $ is the Hamiltonian transformed from the original,$ H = T+V $ as$ \tilde{H}= C^{\dagger}_rHC_r = C^{\dagger}_rTC_r+C^{\dagger}_rVC_r = \tilde{T}+\tilde{V}, $

(12) $ \tilde{T}= \mathop \sum \limits^N_{i = 1}t_i+\mathop \sum \limits^N_{i<j}u_{ij},\quad \tilde{V} = \mathop \sum \limits^N_{i<j}\tilde{v}_{ij}. $

(13) With the unitary correlation operator
$ C_r $ , we first derive the transformed Hamiltonian$ \tilde{H} $ within UCOM. Then, by using the total wave function$ \Phi $ given in Eq. (9), the Hamiltonian matrix$ {\cal H} $ can be calculated for different Hamiltonian components as$ \begin{align} {\cal H} = \left( \begin{array}{ccc} \langle0|\tilde{H}|0\rangle & \langle0|\tilde{H}|2,p = 1\rangle & ... \\ \langle2,p' = 1|\tilde{H}|0\rangle & \langle2,p' = 1|\tilde{H}|2,p = 1\rangle & ... \\ ... & ... & ... \end{array} \right), \end{align} $

(14) where
$ |0\rangle $ and$ |2,p\rangle $ denote the configurations$ |{0p0h}\rangle $ and$ |{2p2h},p\rangle $ , respectively. Within the power method [74-76], we can solve the energy eigenvalue problem for the Hamiltonian matrix with$ N_{{2p2h}}+1 $ dimensions. Then, the configuration amplitudes$ \{C_p\} $ in Eq. (9) can be variationally determined by minimizing the total energy as well as each Hamiltonian component energy. In fact, Eq. (10) shows that as the operator$ C_r $ is a many-body operator, we also confront a many-body problem regarding the transformed Hamiltonian$ \tilde{H} $ . However, it is reasonable to take the two-body operator truncation for the short-range correlation case, as discussed in previous studies [31-35]. For the transformed kinetic part$ \tilde{T} $ in Eq. (13), there are two terms, the uncorrelated one-body term$ t_i $ and the correlated two-body term$ u_{ij} $ , where the latter originates from the short-range correlation between nucleons and is closely related to both the momentum and angular momentum of relative motion:$ u(r) = w(r)+\frac{1}{2}\left[p^2_r\frac{1}{2\mu_r(r)}+\frac{1}{2\mu_r(r)}p^2_r\right]+\frac{{ L}^2}{2\mu_{\Omega}(r)r^2}, $

(15) where the forms for the functions
$ w(r) $ ,$ \mu_r(r) $ , and$ \mu_{\Omega}(r) $ are, respectively, [32]$ w(r) = \frac{\hbar^2}{m}\left(\frac{7}{4}\frac{R^{''2}_{+}(r)}{R^{'4}_{+}(r)}-\frac{1}{2}\frac{R^{'''}_{+}(r)}{R^{'3}_{+}(r)}\right), $

(16) $ \frac{1}{2\mu_r(r)} = \frac{1}{m}\left(\frac{1}{R^{'2}_{+}(r)}-1\right), $

(17) $ \frac{1}{2\mu_{\Omega}(r)} = \frac{1}{m}\left(\frac{r^2}{R^{2}_{+}(r)}-1\right), $

(18) where the function
$ R_+(r) $ is usually employed to replace the previous function$ s(r) $ for UCOM calculations. For the two-body potential part$ \tilde{V} $ in Eq. (13), the potential energy$ \tilde{v} $ is also related to the function$ R_+(r) $ and is usually calculated by$ v(R_+(r)) $ . The function$ R_+(r) $ indicates the transformed relative distance from the original one r [31, 32]. The relation between the two functions$ R_+(r) $ and$ s(r) $ is$ \frac{{\rm d}R_+(r)}{{\rm d}r} = \frac{s[R_+(r)]}{s(r)}, $

(19) $ c^{\dagger}_rrc_r = R_+(r).$

(20) The function
$ R_+(r) $ can decrease the wave function amplitude of the relative motion of the two nucleons in a nucleon pair at short-range distances, which can simulate the effect of the short-range correlation. The specific forms of$ R_+(r) $ for the even (odd) channel with positive (negative) parity are given as [31, 32]$ R^{\mathrm{even}}_+(r) = r+\alpha\left(\frac{r}{\beta}\right)^{\gamma}\exp\left[-\exp\left(\frac{r}{\beta}\right)\right], $

(21) $ R^{\mathrm{odd}}_+(r) = r+\alpha\left[1-\exp\left(-\frac{r}{\delta}\right)\right]\exp\left[-\exp\left(\frac{r}{\beta}\right)\right],$

(22) where
$ \alpha $ ,$ \beta $ ,$ \gamma $ , and$ \delta $ are the parameters variationally determined by minimizing the total energy per particle of the 0p0h state within UCOM for neutron matter, which corresponds to the 0p0h+UCOM calculation. The values of the parameters$ \alpha $ ,$ \beta $ ,$ \gamma $ , and$ \delta $ are listed in Table 1. For neutron matter, the parameters of$ R_+(r) $ are naturally determined to be the same for AV4', AV6', and AV8'$ NN $ interactions. This is because, for the three aforementioned$ NN $ interactions, the differences among them exist in the isospin-singlet channels$ ^3E $ and$ ^1O $ , which are absent in neutron matter. For the two active channels$ ^1E $ and$ ^3O $ in neutron matter, the corresponding central parts are identical. In addition, the tensor and spin-orbit forces are not included in the process of determining the values of the three parameters, i.e., only the 0p0h+UCOM calculation is involved. As the number of 2p2h configurations increases very sharply with the maximum transfer mode, as shown in Fig. 1, it is difficult to determine the parameters with UCOM+HM calculation. Besides, we find that the small changes in the parameters slightly affect the total energy. Hence, we determine the values of the parameters at the 0p0h+UCOM level without much loss of accuracy.$\alpha$ /fm

$\beta$ /fm

$\gamma$ 

$\delta$ /fm

$^1E$ 

1.33 1.00 0.31 $^3O$ 

0.65 1.39 0.24 Table 1. Values of the parameters
$\alpha$ ,$\beta$ ,$\gamma$ , and$\delta$ in the function$R_+(r)$ for UCOM with$^1E$ and$^3O$ channels in neutron matter.For the UCOM transformation, the wave function contains two-body correlations. In addition, as shown in Eq. (9), the 2p2h configurations with HM components are included in the total wave function. Physically, there are up to 4p4h correlations involved in the present approach. This new method is called UCOM+HM hereafter.
-
First, we validate the present finite particle number approach for neutron matter. We calculate the HF energies for infinite neutron matter and the energies of the finite neutron matter system with the finite particle number approach. In Fig. 2, we show the absolute values of the relative error of the Hamiltonian component energy changing with the neutron magic number for both the 0p0h and 0p0h+UCOM wave functions. The calculations with the AV4' potential and normal density
$ \rho = 0.17\; \mathrm{fm}^{-3} $ are demonstrated as an example. The quantities$ T_{N} $ and$ V_{N} $ are the kinetic and potential energies for a finite neutron matter system, while$ T_{\infty} $ and$ V_{\infty} $ are those for infinite neutron matter, which can be directly calculated using the Fermi sphere wave function with the infinite-space integral from the Hamiltonian matrix elements.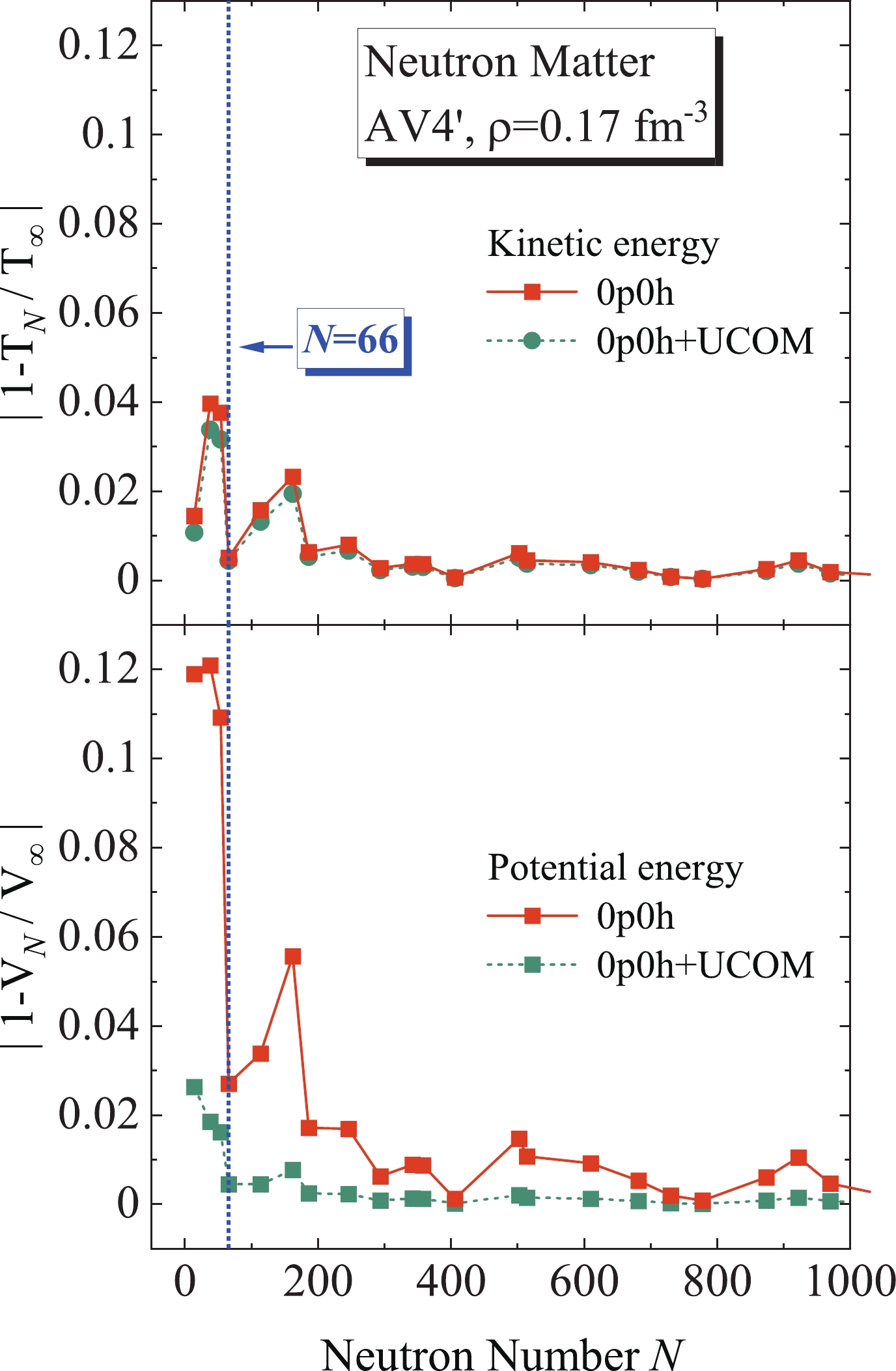
Figure 2. (colour online) Relative errors of the Hamiltonian component energy for both 0p0h and 0p0h+UCOM wave functions calculated with AV4' potential.
As shown in Fig. 2, the relative errors for both the kinetic and potential energies roughly decrease with the increasing neutron number N. In a small-neutron-number region, regardless of the kinetic or potential energy, the relative energy errors between the finite particle number approach and infinite neutron matter are the smallest with the neutron magic number
$ N = 2N_g = 66 $ . In our recent study [72], the relation between the total energy of nuclear matter and the particle magic numbers was investigated. The results confirmed that, with the grid number$ N_g = 33 $ , i.e., neutron magic number$ N = 66 $ , the numerical results of the kinetic and potential energies per particle for the 0p0h state within the present approach can provide the best simulation for those of the infinite nuclear matter at the HF level for smaller magic particle numbers [72]. The same conclusion has also been obtained by other microscopic calculations for nuclear matter with this finite particle number approach, such as AFDMC [56-58], GFMC [59], and CC [62]. As a result, in the present study, the neutron number$ N = 2N_g = 66 $ is chosen throughout the calculations for neutron matter.In addition, Fig. 2 shows that, for the kinetic energy, the difference in the relative error between the 0p0h and 0p0h+UCOM calculations is relatively small. With neutron magic number
$ N = 66 $ , the values are approximately 0.5% and 0.4% for the 0p0h and 0p0h+UCOM cases, respectively. However, the relative errors for the potential energy calculated with the 0p0h+UCOM wave function are generally much smaller than those calculated with the 0p0h wave function, especially in a small-neutron-number region. With the neutron magic number$ N = 66 $ , the relative error decreases from 2.7% for the 0p0h case to 0.4% for the 0p0h+UCOM case. This indicates that the UCOM can effectively treat the short-range correlation resulting from the$ NN $ interaction in neutron matter.As mentioned before, the maximum mode of transfer momentum
$ n^{\mathrm{max}}_q $ is introduced to control the model space of the present calculation. Thus, we first check whether the total energy per particle can converge with the increasing value of the integer mode$ n^{\mathrm{max}}_q $ . Fig. 3 shows the dependencies of energies per particle on the maximum mode$ n^{\mathrm{max}}_q $ within UCOM+HM by including 2p2h excitations to describe the high-momentum components in neutron matter. The mass number of neutron matter is set as$ N = 66 $ and the neutron density is the normal value$ \rho = 0.17\; \mathrm{fm}^{-3} $ .
Figure 3. (color online) Convergence of the Hamiltonian components as well as the total energy per particle for neutron matter with the increasing maximum mode of transfer momentum
$n^{\mathrm{max}}_q$ in UCOM+HM. The energies at$n_q = 0$ correspond to the 0p0h+UCOM calculation. Panels (a), (b), and (c) correspond to the results obtained with AV4', AV6', and AV8'$NN$ interactions, respectively. The term E is the total energy, T is the total kinetic energy,$T_{\mathrm{uncorr.}}$ is the uncorrelated one-body kinetic energy, and$V_{\mathrm{c}}$ ,$V_{\mathrm{T}}$ , and$V_{\mathrm{so}}$ are the potential energies corresponding to the central, tensor, and spin-orbit forces of the$NN$ interactions, respectively. The total energy per particle E converging with the maximum mode of transfer momentum$n^{\mathrm{max}}_q$ for the above three potentials is shown in panel (d) .The Hamiltonian components per particle varying with the maximum mode
$ n^{\mathrm{max}}_q $ corresponding to AV4', AV6', and AV8'$ NN $ interactions are shown in panels (a), (b), and (c) of Fig. 3, respectively. The energies at$ n_q = 0 $ correspond to the 0p0h+UCOM calculation. Our previous study [72] clearly showed that the finite particle number approach with the 0p0h and 0p0h+UCOM wave functions by using the neutron number$ N = 66 $ can successfully reproduce the EOSs with a Fermi sphere at the HF and HF+UCOM levels for neutron matter, respectively, which validates the present calculations. By comparing the results obtained with the 0p0h and 0p0h+UCOM wave functions, it can be seen in Fig. 3 that, for each$ NN $ interaction case, there exists a large rise in the kinetic energy and a larger fall in the central potential, leading to a smaller total energy. This is because of the short-range correlation induced by the short-range repulsion in the central force, which has been successfully treated by UCOM. Because of the amplitude decrease in nucleon pairs induced by the short-range correlation at short-range distances, there is a more attractive central force and an additional correlated two-body part of the kinetic energy, as shown in Eq. (13). We can obtain the effect of the short-range correlation from the correlated two-body part of the kinetic energy as a result of the difference between the total one T and the uncorrelated one$ T_{\mathrm{uncorr.}} $ , where the latter corresponds the one-body operator$ \sum^N_{i = 1}t_i $ in Eq. (13) without UCOM. All contributions of the short-range correlation to the kinetic energy for neutron matter amount to approximately 9 MeV per particle for the AV4', AV6', and AV8' potentials. Furthermore, with the 0p0h+UCOM+HM wave function, by including the 2p2h configurations, the convergences of the Hamiltonian components per particle for the AV4', AV6', and AV8' potentials are clearly confirmed for each component, as shown in Fig. 3. Similar behavior for the three aforementioned potentials is also obtained under the consideration of 2p2h excitations as HM pairs, where both the kinetic energy and potential energy slightly increase.The variation in the total energy per particle with the maximum mode of transfer momentum
$ n^{\mathrm{max}}_q $ for the three aforenoted$ NN $ interactions is shown in panel (d) of Fig. 3. It is apparent in panel (d) that the total energies per particle converge well with the increasing maximum mode$ n^{\mathrm{max}}_q $ for the three potentials. Though the number of 2p2h configurations$ N_{{2p2h}} $ increases by more than two times from$ 1.8\times10^6 $ with$ n^{\mathrm{max}}_q = 6 $ to$ 4.0\times10^6 $ with$ n^{\mathrm{max}}_q = 8 $ , the energy differences between the two maximum modes for the three potentials are only tens of keV. Compared to the values calculated with$ n^{\mathrm{max}}_q = 6 $ , the energies with$ n^{\mathrm{max}}_q = 8 $ only decrease by approximately 0.3%, 0.3%, and 0.4% for the AV4', AV6', and AV8'$ NN $ interactions, respectively. Allowing for a sharp increase in the model space and a small energy decrease, it is reasonable to take the maximum mode of transfer momentum$ n^{\mathrm{max}}_q = 6 $ to perform all the following calculations.Table 2 shows the values of the total energy per particle calculated with the 0p0h, 0p0h+UCOM, and 0p0h+UCOM+HM wave functions. The neutron density considers the normal value
$ \rho = 0.17\; \mathrm{fm}^{-3} $ as an example. The results with neutron numbers$ N = 14 $ and$ N = 66 $ are both listed here. In the last two lines, the quantities$ \Delta_{\mathrm{UCOM}} $ and$ \Delta_{\mathrm{HM}} $ denote the calculated total energy differences between the 0p0h and 0p0h+UCOM wave functions and between the 0p0h+UCOM and 0p0h+UCOM+HM ($ n^{\mathrm{max}}_q = 6 $ ) wave functions, respectively. The former denotes the contribution of short-range correlation, while the latter corresponds to the contribution of HM pairs. Table 2 thus clearly shows that, for the same neutron number, the short-range correlation contributes the same amount for the three$ NN $ potentials. As mentioned above, the differences among the three potentials exist in channels$ ^3E $ and$ ^1O $ , which are absent in neutron matter. However, for the two active channels$ ^1E $ and$ ^3O $ in neutron matter, the corresponding central parts are identical, which results in the same contribution of the short-range repulsion. Compared to the effect of short-range correlation, the high-momentum pairs make a relatively smaller contribution to the total energy per particle of neutron matter. For example, with neutron number$ N = 66 $ , the short-range repulsion contributes to a total energy of approximately 23.995 MeV per particle for AV4', AV6', and AV8'$ NN $ interactions, while the corresponding attractive effects of HM pairs for the three potentials are only 0.682, 0.831, and 1.585 MeV per particle, respectively. This indicates that, for neutron matter, the majority correlations originating from the AV4', AV6', and AV8'$ NN $ interactions can be treated by UCOM and the residual part is described by the high-momentum pairs, including tensor correlation and spin-orbit effect. This is consistent with our previous study [72]. Besides, from the above-mentioned values for the HM pairs, the effect of high-momentum pairs is successively increased for AV4', AV6', and AV8'$ NN $ interactions. This is because of the existence of the additional tensor and spin-orbit forces included in AV6' and AV8' potentials, which will induce more excited high-momentum pairs than those with AV4' potential.$n^{\mathrm{max}}_q$ 

$E(N=14)$ /MeV

$E(N=66)$ /MeV

AV4' AV6' AV8' AV4' AV6' AV8' 0p0h 42.064 42.064 42.064 41.873 41.873 41.873 0p0h+UCOM 0 17.963 17.963 17.963 17.878 17.878 17.878 0p0h+UCOM+HM 1 17.629 17.505 17.311 17.766 17.759 17.749 2 17.473 17.298 16.691 17.579 17.542 17.455 3 17.274 17.062 16.109 17.432 17.332 16.933 4 17.212 16.988 15.980 17.323 17.196 16.600 5 17.162 16.932 15.914 17.241 17.100 16.388 6 17.136 16.903 15.884 17.196 17.047 16.293 7 17.124 16.890 15.871 17.168 17.015 16.250 8 17.118 16.884 15.865 17.145 16.988 16.221 $\Delta_{\mathrm{UCOM}}$ 

24.101 24.101 24.101 23.995 23.995 23.995 $\Delta_{\mathrm{HM}}$ 

0.827 1.060 2.079 0.682 0.831 1.585 Table 2. Values of the total energy per particle at the normal density
$\rho = 0.17\; \mathrm{fm}^{-3}$ calculated with 0p0h, 0p0h+UCOM, and UCOM+HM wave functions for AV4', AV6', and AV8'$NN$ interactions, respectively. The results obtained for both neutron numbers$N = 14$ and$N = 66$ are given here. The quantity$\Delta_{\mathrm{UCOM}}$ denotes the difference in the total energy calculated by 0p0h and 0p0h+UCOM wave functions, which corresponds to the contribution of the short-range correlation. Similarly, the one$\Delta_{\mathrm{HM}}$ denotes the difference in the total energy calculated by 0p0h+UCOM and 0p0h+UCOM+HM (with$n^{\mathrm{max}}_q = 6$ ) wave functions, which represents the contribution of HM pairs.Compared to the results for neutron number
$ N = 14 $ in Table 2, the results for$ N = 66 $ obtained with the 0p0h and 0p0h+UCOM wave functions are both slightly smaller. By including the HM pairs into the total wave function, i.e., 0p0h+UCOM+HM wave function, the converged total energies with$ N = 66 $ are generally larger than those with$ N = 14 $ at each maximum transfer mode$ n^{\mathrm{max}}_q $ for the three$ NN $ potentials. This trend$ E(N = 66)>E(N = 14) $ is in good agreement with the results given in Ref. [57].Fig. 4 shows the density dependence of the total energy per particle of neutron matter calculated with the 0p0h, 0p0h+UCOM, and 0p0h+UCOM+HM wave functions for AV4', AV6', and AV8'
$ NN $ interactions, respectively. The figureclearly shows that, for the three$ NN $ interactions, the behaviors of the calculated results are similar by successively using the 0p0h, 0p0h+UCOM, and 0p0h+UCOM+HM wave functions. Under only the 0p0h wave function, the EOS of neutron matter is rather stiff. After considering the short-range correlation treated by UCOM, i.e., by using the 0p0h+UCOM wave function to calculate the EOS, the total energy per particle decreases considerably at all densities. That is, the short-range correlation described by UCOM leads to a significantly more attractive EOS compared to that of the 0p0h state without involving any$ NN $ correlation. With the 0p0h+UCOM+HM wave function, including the 2p2h configurations, to describe the HM components in neutron matter, the EOS can be further softened, as shown in Fig. 4.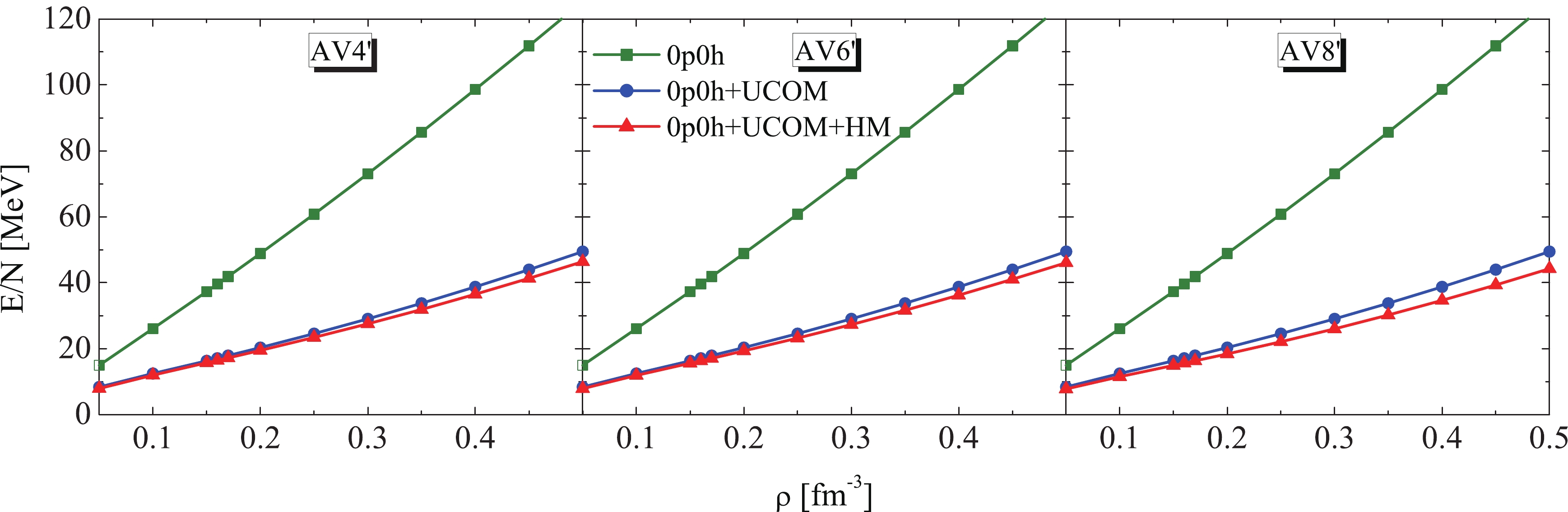
Figure 4. (color online) Comparison of the EOS for neutron matter calculated with AV4', AV6', and AV8' potentials by using 0p0h, 0p0h+UCOM, and 0p0h+UCOM+HM wave functions.
Fig. 5 shows all Hamiltonian components as well as the total energy per particle dependent on the neutron matter density calculated under UCOM+HM with the AV4', AV6', and AV8'
$ NN $ interactions. The figure shows that, for the three aforementioned potentials, for neutron matter, the kinetic and central parts of potential energies mainly contribute to the total energy per particle (absolutely for AV4' potential), while the tensor and spin-orbit parts of potential energy are both relatively small. As a result of the difference between the total and uncorrelated kinetic energies, the effect of short-range correlation on the kinetic energy$ T-T_{\mathrm{uncorr.}} $ increases with the density of neutron matter for three types of$ NN $ interactions, which can be as large as 32 MeV per particle with$ \rho = 0.5\; \mathrm{fm}^{-3} $ . Besides, the results obtained with the AV8' potential indicate that the effects of both tensor force and spin-orbit force are definitely small throughout the densities for neutron matter. Though the tensor force is considered to substantially contribute to symmetric nuclear matter, it is weak for neutron matter because of the absence of the isospin-singlet channels$ ^3E $ and$ ^1O $ in neutron matter [36-38, 45]. The values of the Hamiltonian components, as well as the total energy per particle of neutron matter, at some densities calculated under UCOM+HM are summarized in Table 3.$\rho$ /

$\mathrm{fm}^{-3}$ 

AV4'/MeV AV6'/MeV AV8'/MeV E T $V_{\mathrm{c}}$ 

E T $V_{\mathrm{c}}$ 

$V_{\mathrm{T}}$ 

E T $V_{\mathrm{c}}$ 

$V_{\mathrm{T}}$ 

$V_{\mathrm{so}}$ 

0.03 5.93 13.42 −7.49 5.91 13.42 −7.47 −0.04 5.87 13.43 −7.43 −0.05 −0.09 0.05 7.91 19.14 −11.23 7.87 19.13 −11.19 −0.08 7.74 19.15 −11.07 −0.09 −0.25 0.10 11.97 31.23 −19.26 11.88 31.23 −19.17 −0.18 11.49 31.28 −18.84 −0.18 −0.77 0.17 17.20 46.07 −28.87 17.05 46.09 −28.75 −0.30 16.29 46.22 −28.20 −0.28 −1.45 0.20 19.47 52.08 −32.62 19.30 52.12 −32.48 −0.34 18.40 52.27 −31.85 −0.31 −1.70 0.30 27.52 71.35 −43.82 27.30 71.41 −43.66 −0.45 26.01 71.63 −42.81 −0.40 −2.41 0.40 36.48 89.86 −53.38 36.21 89.94 −53.19 −0.54 34.62 90.23 −52.19 −0.46 −2.96 0.50 46.38 107.98 −61.60 46.07 108.08 −61.39 −0.61 44.24 108.44 −60.27 −0.52 −3.41 Table 3. Values of the Hamiltonian components, as well as the total energy per particle for neutron matter, at some densities calculated under UCOM+HM with AV4', AV6', and AV8'
$NN$ interactions. Total, kinetic, central part, tensor part, and spin-orbit part of potential energies are given as E, T,$V_{\mathrm{c}}$ ,$V_{\mathrm{T}}$ , and$V_{\mathrm{so}}$ , respectively.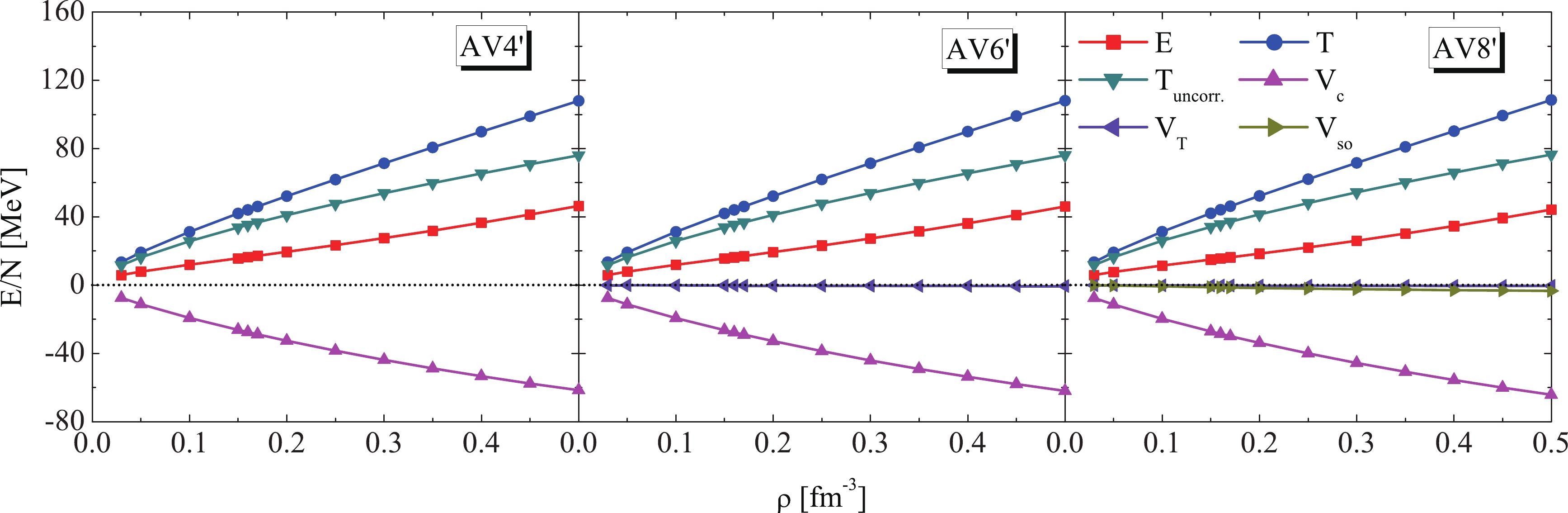
Figure 5. (color online) Density dependence of all Hamiltonian components, as well as the total energy per particle for neutron matter, calculated under UCOM+HM with AV4', AV6', and AV8'
$NN$ interactions. The term E is the total energy, T is the total kinetic energy,$T_{\mathrm{uncorr.}}$ is the uncorrelated one-body kinetic energy, and$V_{\mathrm{c}}$ ,$V_{\mathrm{T}}$ , and$V_{\mathrm{so}}$ are the potential energies corresponding to the central, tensor, and spin-orbit forces of the$NN$ interactions, respectively.Under the present UCOM+HM framework, we calculate the EOSs of neutron matter by using the AV4', AV6', and AV8'
$ NN $ interactions. In Fig. 6, we compare the EOSs provided by UCOM+HM with those calculated under six different microscopic many-body approaches, namely BHF, BBG, SCGF, FHNC, AFDMC, and GFMC. The results corresponding to AFDMC_CP and AFDMC_UC given in Ref. [58] are, respectively, calculated with constrained- and unconstrained-path approximations for the complex wave functions and propagators to alleviate the sign problem in AFDMC approach [77-79]. It can be clearly seen from Fig. 6 that the present results agree with the corresponding ones obtained with the six aforementioned theories for three$ NN $ interactions. In detail, at lower densities, the energies calculated by the present UCOM+HM are similar to those of other six theories, while at higher densities, there exist differences that increase with the density of neutron matter. In particular, the present results provided by UCOM+HM for the three$ NN $ interactions are all close to those calculated with AFDMC in Refs. [45] and [70], as well as in Ref. [58], with the constrained-path approximation. The results corresponding to the unconstrained-path approximation in Ref. [58] are much smaller than the above four calculations, especially at larger densities, which indicates the importance of the treatment of the sign problem in the AFDMC approach. Besides, by comparing the results under UCOM+HM calculated with the AV4' and AV6' potentials, it is found that when the tensor force is included in the$ NN $ interaction, the difference in the EOS is small. This is because of the absence of channels$ ^3E $ and$ ^1O $ in neutron matter, with especially the former providing a strong tensor correlation. Hence, the tensor force makes little contribution to the total energy per particle of neutron matter, as shown in Table 3. When the spin-orbit force is considered, the present UCOM+HM provides a more attractive EOS in the overall density by comparing the results of the AV8' potential with those of the AV4' and AV6' potentials. In the present study, we focus on the nuclear EOSs of neutron matter calculated with the AV4', AV6', and AV8'$ NN $ interactions and study the tensor correlation and spin-orbit effect in neutron matter. In the future, we will employ the AV6' and AV8' potentials to further investigate the properties of the symmetric nuclear matter, in which the tensor correlation can play a significant role.
Figure 6. (color online) Comparison of the EOSs of neutron matter between the UCOM+HM and six other many-body approaches, namely Brueckner-Hartree-Fock (BHF), Brueckner-Bethe-Goldstone (BBG), self-consistent Green's function (SCGF), Fermi hypernetted chain (FHNC), auxiliary field diffusion Monte Carlo (AFDMC), and the Green's function Monte Carlo (GFMC). The results corresponding to AFDMC_CP and AFDMC_UC are, respectively, calculated with constrained- and unconstrained-path approximations for the complex wave functions and propagators to alleviate the sign problem in AFDMC approach [77-79].
-
With our recently proposed variational approach, UCOM+HM, for describing nuclear matter, we calculate the EOS of neutron matter with the AV4', AV6', and AV8'
$ NN $ interactions. The neutron matter is described under a finite particle number approach with neutron magic number$ N = 66 $ under a periodic boundary condition. UCOM is used to treat the short-range correlation induced by the short-range repulsion in the$ NN $ interaction. In addition, the 2p2h excitations as HM nucleon pairs are included to describe the high-momentum components of neutron matter, where the two nucleons in a 2p2h configuration involve a large relative momentum. The 2p2h excitations contribute toward treating the non-central tensor and spin-orbit forces in neutron matter.Under the present UCOM+HM framework, the total energies per particle of neutron matter for the three aforementioned potentials are all well-converged with the increasing 2p2h configurations. By comparing the total energies for neutron matter calculated with the 0p0h, 0p0h+UCOM, and 0p0h+UCOM+HM wave functions, the same conclusion is found, where for neutron matter, the majority correlations originating from the
$ NN $ interaction can be treated by UCOM and the residual part is described by the HM pairs, such as tensor correlation and the spin-orbit effect. Besides, as the tensor and spin-orbit forces can induce additional excited HM pairs, the effect of HM pairs is successively increased for the AV4', AV6', and AV8' potentials.We also obtain the density dependence of all Hamiltonian components as well as the total energy per particle for the three aforementioned potentials. The results indicate that the kinetic and central parts of potential energies mainly contribute to the total energy per particle for neutron matter, while both the tensor and spin-orbit parts of potential energy are relatively small. Besides, the effect of short-range correlation is found to increase with the density of neutron matter.
The obtained EOSs of neutron matter calculated under the present UCOM+HM framework are also compared with those of other microscopic many-body theories with the same bare interactions. The comparison shows that the calculated total energy per particle of neutron matter is similar to those of other approaches, and it is especially consistent with that concerning AFMDC. The absence of the isospin-singlet channels
$ ^3E $ and$ ^1O $ in neutron matter leads to the effect of the tensor correlation being small. When the spin-orbit effect is included in the calculations, a more attractive EOS of neutron matter is obtained.In the future, we will extend the investigations to the properties of symmetric nuclear matter to study both the tensor correlation and spin-orbit effect, because of the significance of the tensor correlation. In addition, it will be interesting to study the effect of a three-body force on EOSs of both neutron and symmetric nuclear matters.
Finite particle number description of neutron matter using the unitary correlation operator and high-momentum pair methods
- Received Date: 2020-02-25
- Accepted Date: 2020-06-15
- Available Online: 2020-12-01
Abstract: Using bare Argonne V4' (AV4'), V6' (AV6'), and V8' (AV8') nucleon–nucleon (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: