-
Charge-Parity (
$ CP $ ) violation is one of the most fundamental and important properties of a weak interaction. Nonleptonic decays of hadrons containing a heavy quark play an important role in testing the standard model (SM) picture for the$ CP $ violation mechanism in flavor physics, improving our understanding of nonperturbative and perturbative QCD and exploring new physics beyond the SM.$ CP $ violation is related to the weak complex phase in the Cabibbo-Kobayashi-Maskawa (CKM) matrix, which describes the mixing of different generations of quarks [1, 2]. In additino to the weak phase, a large strong phase is usually needed for a large$ CP $ violation. Generally, this strong phase is provided by QCD loop corrections and some phenomenological models.Recently, theoretical and experimental studies on two- or three-body heavy meson decays have attracted more attention [3-12], while studies on four-body nonleptonic decays of these heavy mesons have been limited [13-15]. Because of the complicated phase spaces and relatively smaller branching fractions, four-body decays of heavy mesons are difficult to be investigated. However, in regard to studying the intermediate resonances, four-body decays of heavy mesons can provide rich information, especially for the unclear compositions of scalar mesons such as
$ f_0(500) $ ($ \sigma $ ),$ K^*(700) $ ($ \kappa $ ),$ a_0(980) $ and$ f_0(980) $ . The descriptions of inner structures of light scalar states are still unclear and even controversial, which could be, for example,$ q\bar{q} $ ,$ \bar{q}\bar{q}qq $ , meson-meson bound states or even those supplemented with a scalar glueball [16-19]. Studying four-body decays of heavy mesons, in addition to two- or three- body decays, can provide useful information for clarifying configurations of light scalar mesons. In fact, with the considerable development of the large hadron collider beauty (LHCb) and Belle-II experiments, more four-body decay modes involving one or two scalar states in the$ B $ and$ D $ meson decays are expected to be measured with good precision in the future.As mentioned above, four-body meson decays are generally dominated by intermediate resonances, which means that they proceed through quasi-two-body or quasi-three-body decays. In our work, we will adopt the quasi-two-body decay mechanism to study the four-body decay
$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ , i.e.,$ \bar{B}^0\rightarrow \bar{K}_0^*(700)\rho^0(770)\rightarrow K^-\pi^+\pi^-\pi^+ $ and$ \bar{B}^0\rightarrow \bar{K}^*(892)f_0(500)\rightarrow K^-\pi^+\pi^-\pi^+ $ , where the light scalars$ f_0(500) $ and$ K^*(700) $ will be considered as lowest-lying and first excited$ q\bar{q} $ states [20], respectively. We can then explore whether the localized CP violation of the four-body decay$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ can be induced by the interference of these two channels.Theoretically, to calculate the hadronic matrix elements of
$ B $ or$ D $ weak decays, some approaches, such as QCD factorization (QCDF) [6, 21], the perturbative QCD (pQCD) [22], and the soft-collinear effective theory (SCET) [23], have been fully developed and extensively employed in recent years. Unfortunately, in collinear factorization approximation, the calculation of annihilation corrections always suffers from end-point divergence. In the QCDF approach, such divergence is usually parameterized in a model-independent manner [6, 21] and will be explicitly expressed in Sec. 2.The remainder of this paper is organized as follows. In Sec. 2, we present our theoretical framework. The numerical results are given in Sec. 3, and we summarize our work in Sec. 4. Appendix A recapitulates explicit expressions of hard spectator-scattering and weak annihilation amplitudes. The factorizable amplitudes of two-body decays are summarized in Appendix B. Related theoretical parameters are listed in Appendix C.
-
The kinematics of the process
$ \bar{B}^0\rightarrow K^-(p_1)\pi^+ (p_2) \pi^-(p_3)\pi^+(p_4) $ is described in terms of the five variables displayed in Fig. 1 [24, 25] in which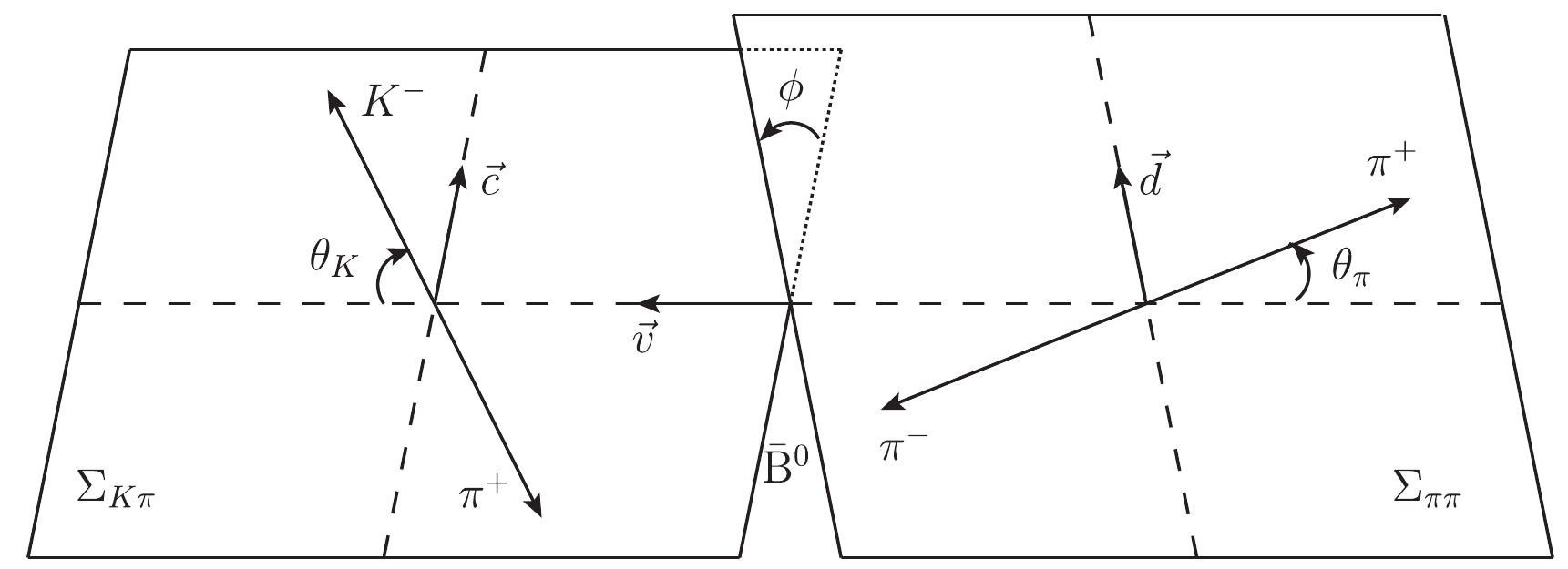
Figure 1. The reference frames and the kinematic variables in the
$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ decay.(i) the invariant mass squared of the
$ K\pi $ system is$ s_{K\pi} = (p_1+p_2)^2 = m_{K\pi}^2 $ ;(ii) the invariant mass squared of the
$ \pi\pi $ system is$ s_{\pi\pi} = (p_3+p_4)^2 = m_{\pi\pi}^2 $ ;(iii)
$ \theta_\pi $ is the angle of the$ \pi^+ $ in the$ \pi^-\pi^+ $ center-of-mass frame$ \Sigma_{\pi\pi} $ with respect to the$ \pi s $ ' line of flight in the$ \bar{B}^0 $ rest frame$ \Sigma_{\bar{B}^0} $ ;(iv)
$ \theta_K $ is the angle of the$ K^- $ in the$ K\pi $ center-of-mass system$ \Sigma_{K\pi} $ with respect to the$ K\pi $ line of flight in$ \Sigma_{\bar{B}^0} $ ;(v)
$ \phi $ is the angle between the$ K\pi $ and$ \pi\pi $ planes.The physical ranges are
$ \begin{split} \ 4m_{\pi\pi}^2\leqslant & s_{\pi\pi}\leqslant (m_{\bar{B}^0}-m_{K\pi})^2,\\ (m_K+m_\pi)^2\leqslant & s_{K\pi}\leqslant(m_{\bar{B}^0}-\sqrt{s_{\pi\pi}})^2,\\ 0\leqslant &\theta_\pi,\theta_K\leqslant \pi,\quad 0\leqslant\phi\leqslant 2\pi. \end{split} $

(1) We consider the localization of
$ CP $ violation of the$ \bar{B}^0\rightarrow K^-(p_1)\pi^+(p_2)\pi^-(p_3)\pi^+(p_4) $ decay when the invariant mass of$ \pi\pi $ is near the masses of$ f_0(500) $ (including$ \rho^0(770) $ ), and the invariant mass of$ K\pi $ is near the masses of$ \bar{K}_0^*(700) $ (including$ \bar{K}^*(892) $ ). We adopt$ \begin{split}& \ \bigg(m_{f_0(500)}-\frac{\Gamma_{f_0(500)}}{2}\bigg)^2\leqslant s_{\pi\pi}\leqslant\bigg(m_{f_0(500)}+\frac{\Gamma_{f_0(500)}}{2}\bigg)^2,\\& \bigg(m_{\bar{K}_0^*(700)}-\frac{\Gamma_{\bar{K}_0^*(700)}}{2}\bigg)^2\leqslant s_{K\pi}\leqslant\bigg( m_{\bar{K}_0^*(700)}+\frac{\Gamma_{\bar{K}_0^*(700)}}{2}\bigg)^2. \end{split} $

(2) In Eq. (2),
$ m_{f_0(500)} $ and$ m_{\bar{K}_0^*(700)} $ are the masses of$ f_0(500) $ and$ \bar{K}_0^*(700) $ mesons, respectively;$ \Gamma_{f_0(500)} $ and$ \Gamma_{\bar{K}_0^*(700)} $ are the widths of the corresponding mesons.Instead of the individual momenta
$ p_1 $ ,$ p_2 $ ,$ p_3 $ ,$ p_4 $ , it is more convenient to use the following kinematic variables$ \begin{split} & P = p_1+p_2,\quad Q = p_1-p_2,\\ & L = p_3+p_4,\quad N = p_3-p_4. \end{split} $

(3) It follows that
$ \begin{split} P^2 =& s_{K\pi},\quad Q^2 = 2(p_K^2+p_\pi^2)-s_{K\pi},\quad L^2 = s_{\pi\pi},\\ P\cdot L =& \frac{1}{2}(m_{\bar{B}^0}^2-s_{K\pi}-s_{\pi\pi}),\quad P\cdot N = X\cos\theta_1, \end{split} $

(4) where the function
$ X $ is defined as$ \begin{split} \ X(s_{K\pi},s_{\pi\pi}) =& \bigg[(P\cdot L)^2-s_{K\pi}s_{\pi\pi}\bigg]^{1/2} \\=& \frac{1}{2}\lambda^{1/2}(m_{\bar{B}^0}^2,s_{K\pi},s_{\pi\pi}),\\ \lambda(x,y,z) =& (x-y-z)^2-4yz. \end{split} $

(5) -
The effective weak Hamiltonian for nonleptonic
$ B $ weak decays is [6]$ \begin{split} {\cal{H}}_{\rm eff} =& \frac{G_F}{\sqrt{2}}\bigg[\sum\limits_{p = u,c}\sum\limits_{D = d,s}\lambda_{p}^{(D)}(c_1O_1^p+c_2O_2^p\\&+\sum\limits_{i = 3}^{10}c_iO_i+c_{7\gamma}O_{7\gamma}+c_{8g}O_{8g})\bigg]+{\rm h.c.}, \end{split} $

(6) where
$ G_F $ represents the Fermi constant,$ \lambda_p^{(D)} = V_{pb}V_{pD}^* $ ,$ V_{pb} $ and$ V_{pD} $ are the CKM matrix elements,$ c_i (i = 1 -10,7\gamma,8g) $ are Wilson coefficients,$ O_{1,2}^p $ are the tree level operators,$ O_{3-6} $ are the QCD penguin operators,$ O_{7-8} $ arise from electroweak penguin diagrams, and$ O_{7\gamma} $ and$ O_{8g} $ are the electromagnetic and chromomagnetic dipole operators, respectively.With the effective Hamiltonian in Eq. (6), the QCDF method has been fully developed and extensively employed to calculate the hadronic two-body B decays. The spectator scattering and annihilation amplitudes are expressed with the convolution of scattering functions and the light-cone wave functions of the participating mesons [6]. The explicit expressions for the basic building blocks of the spectator scattering and annihilation amplitudes have been given in Ref. [6] and are also listed in Appendix A for convenience. The annihilation contributions
$ A_n^{i,f} $ ($ n = 1,2,3 $ ) can be simplified as [26]$ \begin{split} A_1^i(VS)\approx & 6\pi\alpha_s\bigg\{3\mu_S\bigg[B_1(3X_A+4-\pi^2)+B_3\bigg(10X_A\\&+\frac{23}{18}-\frac{10}{3}\pi^2\bigg)\bigg]-r_\chi^Sr_\chi^VX_A(X_A-2)\bigg\},\\ A_2^i(VS)\approx & 6\pi\alpha_s\bigg\{3\mu_S\bigg[B_1(X_A+29-3\pi^2)+B_3\bigg(X_A\\&+\frac{2956}{9}-\frac{100}{3}\pi^2\bigg)\bigg]-r_\chi^Sr_\chi^VX_A(X_A-2)\bigg\},\\ A_3^i(VS) \approx & 6\pi\alpha_s\bigg\{-r^V_\chi\mu_S\bigg[9B_1(X_A^2-4X_A-4+\pi^2)\\&+10B_3\bigg(3X_A^2-19X_A+\frac{61}{6}+3\pi^2\bigg)\bigg]\\& -r_\chi^S\bigg(X_A^2-2X_A+\frac{\pi^2}{3}\bigg)\bigg\},\\ A_3^f(VS) \approx & 6\pi\alpha_s\bigg\{-3r^V_\chi\mu_S(X_A-2)\bigg[B_1(6X_A-11)\\&+B_3\bigg(20X_A-\frac{187}{3}\bigg)\bigg]+r_\chi^SX_A(2X_A-1)\bigg\},\\ A_1^f(VS) =& A_2^f(VS) = 0, \end{split} $

(7) for
$ M_1M_2 = VS $ , and$ \begin{split} A_1^i(SV) =& -A_2^i(SV),\quad A_2^i(SV) = -A_1^i(SV),\\ A_3^i(SV) =& A_3^i(VS),\quad A_3^f(SV) = -A_3^f(VS), \end{split} $

(8) for
$ M_1M_2 = SV $ , where the superscripts$ i $ and$ f $ refer to gluon emission from the initial and final state quarks, respectively. The model-dependent parameter$ X_A $ is used to estimate the end-point contributions and expressed as$ \begin{array}{l} X_A = (1+\rho_A {\rm e}^{{\rm i}\phi_A})\ln\dfrac{m_B}{\Lambda_h}, \end{array} $

(9) with
$ \Lambda_h $ being a typical scale of order 500$ \mathrm{MeV} $ ,$ \rho_A $ an unknown real parameter, and$ \phi_A $ the free strong phase in the range$ [0,2\pi] $ . For the spectator scattering contributions, the calculation of twist-3 distribution amplitudes also suffers from the end-point divergence, which is usually dealt with in the same manner as in Eq. (9) and labeled by$ X_H $ . In our work, when dealing with the end-point divergences from the hard spectator scattering and weak annihilation contributions, we will follow the assumption$ X_H = X_A $ for the$ B $ two-body decays [20]. -
For the
$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ decay, we consider the contributions from$ \bar{B}^0\rightarrow \bar{K}_0^*(700)\rho^0(770)\rightarrow K^-\pi^+\pi^-\pi^+ $ and$ \bar{B}^0\rightarrow \bar{K}^*(892)f_0(500)\rightarrow K^-\pi^+\pi^-\pi^+ $ channels. For convenience,$ f_0(500) $ ,$ \rho^0(770) $ ,$ \bar{K}_0^*(700) $ and$ \bar{K}^*(892) $ mesons will be denoted as$ \sigma $ ,$ \rho $ ,$ \bar{\kappa} $ and$ \bar{K}^* $ , respectively. The amplitudes of these two channels are$ \begin{split} & {\cal{M}}(\bar{B}^0\rightarrow \bar{\kappa}\rho\rightarrow K^-\pi^+\pi^+\pi^- ) \\=& \frac{\langle \bar{\kappa}\rho|{\cal{H}}_{\rm eff}|\bar{B}^0\rangle \langle K^-\pi^+|{\cal{H}}_{\bar{\kappa}\pi^+\pi^-}|\bar{\kappa}\rangle \langle \pi^-\pi^+|{\cal{H}}_{\rho \pi^-\pi^+}|\rho\rangle}{S_{\bar{\kappa}}S_{\rho}}, \end{split} $

(10) and
$ \begin{split} & {\cal{M}}(\bar{B}^0\rightarrow \bar{K}^*\sigma\rightarrow K^-\pi^+\pi^+\pi^-) \\=& \frac{\langle \bar{K}^*\sigma|{\cal{H}}_{\rm eff}|\bar{B}^0\rangle \langle K^-\pi^+|{\cal{H}}_{\bar{K}^*\pi^+\pi^-}|\bar{K}^*\rangle \langle \pi^-\pi^+|{\cal{H}}_{\sigma \pi^-\pi^+}|\sigma\rangle}{S_{\bar{K}^*}S_{\sigma}}, \end{split} $

(11) respectively, where
$ {\cal{H}}_{\rho\pi^+\pi^-} $ ,$ {\cal{H}}_{\sigma\pi^+\pi^-} $ ,$ {\cal{H}}_{\bar{\kappa}K^-\pi^+} $ and$ {\cal{H}}_{\bar{K}^*K^-\pi^+} $ are strong Hamiltonians for$ \rho\rightarrow\pi^-\pi^+ $ ,$ \sigma\rightarrow\pi^-\pi^+ $ ,$ \bar{\kappa}\rightarrow K^-\pi^+ $ , and$ \bar{K}^*\rightarrow K^-\pi^+ $ decays, respectively.$ S_{\bar{\kappa}} $ ,$ S_{\rho} $ ,$ S_{\bar{K}^*} $ , and$ S_{\sigma} $ are the reciprocals of the dynamical functions of the corresponding mesons. Since the width of$ \sigma $ is larger than the other three mesons, we shall adopt the Breit-Wigner function and the Bugg model [27, 28] to deal with the distributions of the first three mesons ($ \bar{\kappa} $ ,$ \rho $ and$ \bar{K}^* $ ) and$ \sigma $ meson, respectively.In the Breit-Wigner model,
$ S_{k} $ takes the form$ S-m_k^2+im_k\Gamma_k $ ,$ k = 1,2,3 $ corresponding to$ {\bar{\kappa}} $ ,$ \rho $ and$ \bar{K}^* $ mesons.$ S = s_{\pi\pi} $ or$ S = s_{K\pi} $ when dealing with$ \pi\pi $ or$ K\pi $ systems.The Bugg model is used to parameterize the distribution of
$ \sigma $ [27, 28],$ \begin{array}{l} \ S_{\sigma}(s) = \bigg[M^2-s-g_1^2(s)\dfrac{s-s_A}{M^2-s_A}z(s)-{\rm i}M\Gamma_{\mathrm{tot}}(s)\bigg]/M\Gamma_1(s), \end{array} $

(12) where
$ z(s) = j_1(s)-j_1(M^2) $ with$j_1(s) = \dfrac{1}{\pi}\left[2+\rho_1\ln \left(\dfrac{1-\rho_1}{1+\rho_1}\right)\right]$ ,$ \Gamma_{\mathrm{tot}}(s) = \displaystyle\sum\limits_{i = 1}^4 \Gamma_i(s) $ and$ \begin{split} M\Gamma_1(s) =& g_1^2(s)\frac{s-s_A}{M^2-s_A}\rho_1(s),\\ M\Gamma_2(s) =& 0.6g_1^2(s)(s/M^2)\mathrm{exp}(-\alpha|s-4m_K^2|)\rho_2(s),\\ M\Gamma_3(s) = &0.2g_1^2(s)(s/M^2)\mathrm{exp}(-\alpha|s-4m_\eta^2|)\rho_3(s),\\ M\Gamma_4(s) =& Mg_{4\pi}\rho_{4\pi}(s)/\rho_{4\pi}(M^2),\\ g_1^2(s) =& M(c_1+c_2s)\mathrm{exp}[-(s-M^2)/A],\\ \rho_{4\pi}(s) =& 1.0/[1+\mathrm{exp}(7.082-2.845s)], \end{split} $

(13) where we abbreviate
$ s_{\pi\pi} $ as$ s $ , related parameters are fixed to be$ M = 0.953\; \mathrm{GeV} $ ,$ s_A = 0.14m_\pi^2 $ ,$ c_1 = 1.302\;\mathrm{GeV}^2 $ ,$ c_2 = 0.340 $ ,$ A = 2.426\;\mathrm{GeV}^2 $ and$ g_{4\pi} = 0.011\;\mathrm{GeV} $ , as given in the fourth column of Table I in Ref. [27]. The parameters$ \rho_{1,2,3} $ are the phase-space factors of the decay channels$ \pi\pi $ ,$ KK $ and$ \eta\eta $ , respectively, which are defined as [27]$ \begin{array}{l} \rho_i(s) = \sqrt{1-4\dfrac{m_i^2}{s}}, \end{array} $

(14) with
$ m_1 = m_\pi $ ,$ m_2 = m_K $ and$ m_3 = m_\eta $ .When dealing with the final state interactions, unitarized chiral perturbation theory is an effective method; they have been studied in Refs. [29-32]. Now we will adopt the method in Refs. [7, 28]
$ \begin{array}{l} \ \langle M_1M_2|{\cal{H}}_s|V\rangle = g_{VM_1M_2}\epsilon_V\cdot(p_{M_1}-p_{M_2}), \end{array} $

(15) and
$ \begin{array}{l} \langle M_1M_2|{\cal{H}}_s|S\rangle = g_{SM_1M_2}, \end{array} $

(16) respectively, where
$ g_{VM_1M_2} $ and$ g_{SM_1M_2} $ are the strong coupling constants of the corresponding vector and scalar meson decays, respectively. Generally, these coupling constants can be derived from experiments, which have been listed in Eq. (C4).Within the QCDF framework in Ref. [6], we can get the decay amplitudes of
$ \bar{B}^0\rightarrow \bar{\kappa}\rho, \bar{K}^*\sigma $ , which have been listed in Appendix B. Combining Eqs. (35), (15) and (10), (B2), (16) and (11), respectively, the amplitudes of$ \bar{B}^0\rightarrow \bar{\kappa}\rho\rightarrow K^-\pi^+\pi^-\pi^+ $ and$ \bar{B}^0\rightarrow \bar{K}^*\sigma\rightarrow K^-\pi^+\pi^-\pi^+ $ channels can be written as$ \begin{split} {\cal{M}}(\bar{B}^0\rightarrow \bar{\kappa}\rho\rightarrow K^-\pi^+\pi^+\pi^- ) =& \frac{{\rm i}G_Fg_{\bar{\kappa}K\pi}g_{\rho\pi\pi}\varepsilon_{\rho}\cdot(p_{\pi^-}-p_{\pi^+})}{S_{\bar{\kappa}}S_\rho }\sum_{p = u,c}\lambda_p^{(s)}\\& \times\bigg\{2f_\rho m_\rho \varepsilon_\rho^*\cdot p_BF_1^{\bar{B}^0 \bar{\kappa}}(m_{\rho}^2)\bigg[\delta_{pu}\alpha_2(\bar{\kappa}\rho) +\frac{3}{2}\alpha_{3,EW}^p(\bar{\kappa}\rho)\bigg]\\& +2\bar{f}_{\bar{\kappa}}m_\rho \varepsilon_\rho^*\cdot p_BA_0^{\bar{B}^0\rho}(m_{\bar{\kappa}}^2)\bigg[\alpha_4^p(\rho\bar{\kappa})-\frac{1}{2}\alpha_{4,EW}^p(\rho\bar{\kappa})\bigg]\\& +2m_{\rho}f_{\bar{B}^0}f_\rho \bar{f}_{\bar{\kappa}}\bigg[b_3^p(\rho\bar{\kappa})-\frac{1}{2}b_{3,EW}^p(\rho\bar{\kappa})\bigg]\bigg\}, \end{split} $

(17) and
$ \begin{split} {\cal{M}}(\bar{B}^0\rightarrow \bar{K}^*\sigma\rightarrow K^-\pi^+\pi^+\pi^-) =& -\frac{{\rm i}G_Fg_{\bar{K}^*K\pi}g_{\sigma\pi\pi}}{S_{\bar{K}^*}S_\sigma }\sum_{p = u,c}\lambda_p^{(s)}\bigg\{2\bar{f}_{\sigma^s}A_0^{\bar{B}^0\bar{K}^*}(m_\sigma^2) \bigg[\frac{1}{\sqrt{2}}\delta_{pu}\alpha_2(\bar{K}^*\sigma)\\& +\sqrt{2}\alpha_3^p(\bar{K}^*\sigma)+\frac{1}{2\sqrt{2}}\alpha_{3,EW}^p(\bar{K}^*\sigma)\bigg] +2\bar{f}_{\sigma^s}A_0^{\bar{B}^0\bar{K}^*}(m_\sigma^2)\bigg[\alpha_3^p(\bar{K}^*\sigma)\\& +\alpha_4^p(\bar{K}^*\sigma)-\frac{1}{2}\alpha_{3,EW}^p(\bar{K}^*\sigma)-\frac{1}{2}\alpha_{4,EW}^p(\bar{K}^*\sigma)\bigg]+2f_{\bar{K}^*} F_1^{\bar{B}^0\sigma}(m_{\bar{K}^*}^2)\\& \times\bigg[\frac{1}{2\sqrt{2}}\alpha_{4,EW}^p(\sigma\bar{K}^*)-\frac{1}{\sqrt{2}}\alpha_4^p(\sigma\bar{K}^*)\bigg]-\frac{m_{\bar{K}^*}f_{\bar{B}^0}f_{\bar{K}^*}\bar{f}_\sigma^s}{(m_{\bar{B}^0}p_c)}\bigg[b_3^p(\bar{K}^*\sigma)\\& +b_{3,EW}^p(\bar{K}^*\sigma)\bigg] +\frac{m_{\bar{K}^*}f_{\bar{B}^0}f_{\bar{K}^*}\bar{f}_\sigma^n}{(m_{\bar{B}^0}p_c)}\bigg[\frac{1}{\sqrt{2}}b_3^p(\sigma\bar{K}^*)-\frac{1}{2\sqrt{2}}b_{3,EW}^p(\sigma\bar{K}^*)\bigg]\bigg\}, \end{split} $

(18) respectively, where
$ g_{\bar{\kappa}K\pi} $ ,$ g_{\rho\pi\pi} $ ,$ g_{\bar{K}^*K\pi} $ ,$ g_{\sigma \pi\pi} $ are the strong coupling constants of the corresponding decays, which are listed in Eq. (C4);$ F_1^{\bar{B}^0 \bar{\kappa}}(m_{\rho}^2) $ ,$ A_0^{\bar{B}^0\rho}(m_{\bar{\kappa}}^2) $ ,$ A_0^{\bar{B}^0 \bar{K}^*}(m_\sigma^2) $ and$ F_1^{\bar{B}^0\sigma}(m_{\bar{K}^*}^2) $ are form factors for$ \bar{B}^0 $ to$ \bar{\kappa} $ ,$ \rho $ ,$ \bar{K}^* $ and$ \sigma $ transitions, respectively;$ f_\rho $ ,$ \bar{f}_{\bar{\kappa}} $ ,$ f_{\bar{B}^0} $ and$ f_{\bar{K}^*} $ are decay constants of$ \rho $ ,$ \bar{\kappa} $ ,$ \bar{B}^0 $ and$\bar{K}^*$ mesons, respectively;$ \bar{f}_{\sigma^s} $ and$ \bar{f}_\sigma^n $ are decay constants of$ \sigma $ coming from the up and strange quark components, respectively.There can be a relative strong phase
$ \delta $ between the two interference amplitudes, the value of which depends on experimental data and theoretical models. Since little information about$ \delta $ can be provided by experiments, we choose to adopt the same method as that in Refs. [7, 33, 34], i.e., setting$ \delta = 0 $ . The total decay amplitude of the$ \bar{B}^0\rightarrow K^-\pi^+\pi^+\pi^- $ including both$ \bar{B}^0\rightarrow \bar{\kappa}\rho\rightarrow K^-\pi^+\pi^+\pi^- $ and$ \bar{B}^0\rightarrow \bar{K}^*\sigma\rightarrow K^-\pi^+\pi^+\pi^- $ channels can be written as$ \begin{split} {\cal{M}} =& {\cal{M}}(\bar{B}^0\rightarrow \bar{\kappa}\rho\rightarrow K^-\pi^+\pi^+\pi^- )\\&+{\cal{M}}(\bar{B}^0\rightarrow \bar{K}^*\sigma\rightarrow K^-\pi^+\pi^+\pi^-). \end{split} $

(19) The differential CP asymmetry parameter can be defined as
$ \mathcal{A_{CP}} = \frac{|{\cal{M}}|^2-|\bar{{\cal{M}}}|^2}{|{\cal{M}}|^2+|\bar{{\cal{M}}}|^2}. $

(20) The localized integration
$ CP $ asymmetry can be measured by experiments and takes the following form:$ \mathcal{A_{CP}} = \frac{\displaystyle\int {\rm d}\Omega(|{\cal{M}}|^2-|\bar{{\cal{M}}}|^2)}{\displaystyle\int {\rm d}\Omega(|{\cal{M}}|^2+|\bar{{\cal{M}}}|^2)}, $

(21) where
$ \Omega $ represents the phase space given in Eq. (2) with${\rm d}\Omega = {\rm d}s_{\pi\pi}{\rm d}s_{K\pi}{\rm d}\cos\theta_\pi {\rm d}\cos\theta_K {\rm d}\phi$ .As for the decay rate, one has [13]
$ {\rm d}^5\Gamma = \frac{1}{4(4\pi)^6m_{\bar{B}^0}^3}\sigma(s_{\pi\pi})X(s_{\pi\pi},s_{K\pi})\sum_{\mathrm{spins}}|{\cal{M}}|^2{\rm d}\Omega, $

(22) with
$ \sigma(s_{\pi\pi}) = \sqrt{1-4m_\pi^2/s_{\pi\pi}}. $

(23) This leads to the branching fraction
$ {\cal{B}} = \frac{1}{\Gamma_{\bar{B}^0}}\int {\rm d}^5\Gamma, $

(24) where
$ \Gamma_{\bar{B}^0} $ is the decay width of the$ \bar{B}^0 $ meson. -
Within the QCDF approach, we get the amplitudes of the two-body decays
$ \bar{B}^0\rightarrow \bar{\kappa}\rho $ and$ \bar{B}^0\rightarrow \bar{K}^*\sigma $ , where the light scalar$ \sigma $ and$ \bar{\kappa} $ mesons are considered as the lowest-lying and first excisted$ q\bar{q} $ states [20], respectively. As for the parameters for the end-point divergences, we take$ \rho_{H(A)}\leqslant 0.5 $ and arbitrary strong phases$ \phi_{A(H)} $ . All the form factors are evaluated at$ q^2 = 0 $ due to the smallness of$ m_{\rho}^2 $ ,$ m_{\bar{\kappa}}^2 $ ,$ m_\sigma^2 $ and$ m_{\bar{K}^*}^2 $ compared with$ m_{\bar{B}^0}^2 $ . We also simply set$ F^{\bar{B}^0\rightarrow\kappa}(0) = 0.3 $ and assign its uncertainty as$ \pm0.1 $ . With the given parameters, we obtain the$ CP $ violations and branching fractions of the$ \bar{B}^0\rightarrow \bar{\kappa}\rho $ and$ \bar{B}^0\rightarrow \bar{K}^*\sigma $ decays by substituting Eqs. (B1) and (B2) into (20), respectively. The results are$ \mathcal{A_{CP}}(\bar{B}^0\rightarrow \bar{\kappa}\rho) \in [0.20, 0.36] $ ,$ \mathcal{A_{CP}}(\bar{B}^0 \rightarrow \bar{K}^*\sigma)\in [0.08, 0.12] $ ,$ {\cal{B}} (\bar{B}^0\rightarrow \bar{\kappa}\rho)\in [6.76, 18.93]\times10^{-8} $ and$ {\cal{B}} (\bar{B}^0\rightarrow \bar{K}^*\sigma)\in [2.66, 4.80]\times10^{-6} $ , respectively. Obviously, the$ CP $ violations of these two-body decays are both positive, with the$ CP $ violation in$ \bar{B}^0\rightarrow \bar{K}^*\sigma $ decay being smaller than that in$ \bar{B}^0\rightarrow \bar{\kappa}\rho $ . The magnitudes of the branching fractions in these two-body decays are different with the former being about two orders smaller than the latter. When dealing with the the four-body decay$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ , we adopt$ {\cal{B}}(\rho\rightarrow \pi^-\pi^+)\approx 1 $ ,$ {\cal{B}}(\sigma\rightarrow \pi^-\pi^+)\approx \frac{2}{3} $ ,$ {\cal{B}}(\bar{K}^*\rightarrow K^-\pi^+)\approx 1 $ ,$ {\cal{B}}(\bar{\kappa}\rightarrow K^-\pi^+)\approx \frac{2}{3} $ . Then, substituting Eq. (19) into (21) and (24), we respectively get the localized$ CP $ violation and branching fraction of the four-body decay$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ , with the results$ \mathcal{A_{CP}}(\bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+)\in[0.15,0.28] $ and$ {\cal{B}}(\bar{B}^0\rightarrow K^-\pi^+ \pi^-\pi^+)\in[1.73,5.10]\times10^{-7} $ . Compared with the uncertainties from the Gegenbauer moments, we find that those from the divergence parameters are much larger. It is clear that the sign of the localized$ CP $ violation of$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ is positive when the invariant masses of$ \pi\pi $ and$ K\pi $ are near the masses of$ \rho $ ($ \sigma $ ) and$ \bar{\kappa} $ ($ \bar{K}^* $ ), respectively. This indicates that the interference of$ \bar{B}^0\rightarrow \bar{\kappa}\rho\rightarrow K^-\pi^+\pi^-\pi^+ $ and$ \bar{B}^0\rightarrow \bar{K}^*\sigma\rightarrow K^-\pi^+\pi^-\pi^+ $ channels can induce the localized$ CP $ violation to the four-body decay$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ . Our theoretical results shown herein are predictions for ongoing experiments at LHCb and Belle-II. If our predictions are confirmed by experiments in the future, the viewpoint that$ \bar{K}_0^*(700) $ and$ f_0(500) $ have the$ q\bar{q} $ composition should be well supported. However, to exclude other possible structures, more investigations will be needed due to uncertainties from both theory and experiments. -
By studying the quasi-two-body decays within the QCDF approach, we predicted the localized
$ CP $ violation and branching fraction of the four-body decay$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ due to the interference of the two channels$ \bar{B}^0\rightarrow \bar{K}_0^*(700)\rho^0(770)(\rightarrow\bar{\kappa}\rho)\rightarrow K^-\pi^+\pi^-\pi^+ $ and$ \bar{B}^0\rightarrow \bar{K}^*(892)f_0(500)(\rightarrow\bar{K}^*\sigma)\rightarrow K^-\pi^+\pi^-\pi^+ $ , with the results$ \mathcal{A_{CP}}(\bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+)\in[0.15,0.28] $ and$ {\cal{B}}(\bar{B}^0\rightarrow K^-\pi^+ \pi^-\pi^+)\in[1.73,5.10]\times10^{-7} $ . It is clear that the sign of the localized$ CP $ violation of$ \bar{B}^0\rightarrow K^-\pi^+\pi^-\pi^+ $ is positive. In the two quark model for the scalar mesons, we also obtained the$ CP $ violations and branching fractions of the two-body decays$ \bar{B}^0\rightarrow \bar{K}_0^*(700)\rho^0(770) $ and$ \bar{B}^0\rightarrow \bar{K}^* (892)f_0(500) $ as$ \mathcal{A_{CP}}(\bar{B}^0\rightarrow \bar{K}_0^*(700)\rho^0(770)) \in [0.20, 0.36] $ ,$ \mathcal{A_{CP}}(\bar{B}^0\rightarrow \bar{K}^*(892)f_0(500))\in [0.08, 0.12] $ ,$ {\cal{B}} (\bar{B}^0\rightarrow \bar{K}_0^*(700) \rho^0 (770)\in [6.76, 18.93]\times10^{-8} $ and$ {\cal{B}} (\bar{B}^0\rightarrow \bar{K}^*(892) f_0(500)) \in [2.66, 4.80]\times10^{-6} $ , respectively. Obviously, the$ CP $ violations of these two-body decays are both positive, and the$ CP $ violation in$ \bar{B}^0\rightarrow \bar{K}^*(892)f_0(500) $ is smaller than that in$ \bar{B}^0\rightarrow \bar{K}_0^*(700)\rho^0(770) $ . Furthermore, the branching fractions in these two body decays are quite different, with the former being two orders smaller than the latter. Our results will be tested by the precise data from future LHCb and Belle-II experiments. In the present work, we assumed that$ f_0(500) $ and$ \bar{K}_0^*(700) $ are dominated by the$ q\bar{q} $ configuration. Other possible structures of$ f_0(500) $ and$ \bar{K}_0^*(700) $ could affect the results in our interference model, which will need further investigation. If predictions of CP violation and branch ratio in our work are both confirmed by a future experiment, we agree and support the view that scalar mesons have the$ q\bar{q} $ composition. However, there is still a long way ahead to study the structure of scalar mesons. -
For the hard spectator terms, we obtain [26]
$ \begin{split} H_i(M_1M_2) =& -\frac{f_{\bar{B}^0}f_{M_1}}{D(M_1M_2)}\int_0^1\frac{{\rm d}\rho}{\rho}\Phi_{\bar{B}^0}(\rho)\int_0^1\frac{{\rm d}\xi}{\bar{\xi}}\Phi_{M_2}(\xi) \\&\times \int_0^1\frac{{\rm d}\eta}{\bar{\eta}}\left[\pm\Phi_{M_1}(\eta)+r_\chi^{M_1}\frac{\bar{\xi}}{\xi}\Phi_{m_1}(\eta)\right], \end{split}\tag{A1} $

(A1) for
$ i = 1-4,9,10 $ , where the upper sign is for$ M_1 = V $ and the lower sign for$ M_1 = S $ ,$ \begin{split} H_i(M_1M_2) =& -\frac{f_{\bar{B}^0}f_{M_1}}{D(M_1M_2)}\int_0^1\frac{{\rm d}\rho}{\rho}\Phi_{\bar{B}^0}(\rho)\int_0^1\frac{{\rm d}\xi}{\xi}\Phi_{M_2}(\xi) \\&\times \int_0^1\frac{{\rm d}\eta}{\bar{\eta}}\left[\pm\Phi_{M_1}(\eta)+r_\chi^{M_1}\frac{\xi}{\bar{\xi}}\Phi_{m_1}(\eta)\right], \end{split} \tag{A2}$

(A2) for
$ i = 5,7 $ and$ H_i = 0 $ for$ i = 6,8 $ ,$ \bar{\xi} = 1-\xi $ and$ \bar{\eta} = 1-\eta $ ,$ \Phi_M(\Phi_m) $ is the twist-2 (twist-3) light-cone distribution amplitude of the meson$ M $ , and$ \begin{array}{l} D(SV) = F_1^{\bar{B}^0S}(0)m_{\bar{B}^0}^2, \quad D(VS) = A_0^{\bar{B}^0V}(0)m_{\bar{B}^0}^2, \end{array} \tag{A3}$

(A3) and
$ r_\chi^{M_i} $ (i = 1,2) are "chirally-enhanced" terms defined as$ \begin{split} r_\chi^V(\mu) =& \frac{2m_V}{m_b(\mu)}\frac{f_V^\perp(\mu)}{f_V},\\ \bar{r}_\chi^S(\mu) =& \frac{2m_S}{m_b(\mu)}. \end{split} \tag{A4}$

(A4) The twist-2 light-cone distribution amplitudes (LCDA) for the pseudoscalar and vector mesons are respectively [6, 35]
$ \Phi_{M}(x,\mu) = 6x(1-x)\bigg[\sum\limits_{m = 0}^\infty \alpha_m^{M}(\mu)C_m^{3/2}(2x-1)\bigg], \quad M = P,V \tag{A5}$

(A5) and the twist-3 ones are respectively
$ \begin{array}{l} \ \Phi_m(x) = \begin{cases} 1& \quad m = p, \\ 3\bigg[2x-1+\displaystyle\sum\limits_{m = 1}^\infty \alpha_{m,\perp}^V(\mu)P_{m+1}(2x-1)\bigg]& \quad m = v, \\ \end{cases} \end{array}\tag{A6} $

(A6) where
$ C_m^{3/2} $ and$ P_m $ are the Gegenbauer and Legendre polynomials in Eq. (A5) and Eq. (A6), respectively,$ \alpha_m(\mu) $ are Gegenbauer moments, which depend on the scale$ \mu $ .The twist-2 light-cone distribution amplitude for a scalar meson is [20, 26]
$ \begin{array}{l} \Phi_S(x,\mu)^{(n,s)} = \bar{f}^{n,s}_S6x(x-1)\displaystyle\sum_{m = 1,3,5}^\infty B_m(\mu)C_m^{3/2}(2x-1), \end{array}\tag{A7} $

(A7) where
$ B_m $ are Gegenbauer moments,$ \bar{f}_S $ is the decay constant of the scalar meson,$ n $ denotes the$ u $ ,$ d $ quark component of the scalar meson,$ n = \frac{1}{\sqrt{2}}(u\bar{u}+d\bar{d}) $ , and$ s $ denotes the component$ s\bar{s} $ . As for the twist-3 ones, we shall take the asymptotic forms [20, 26]$ \begin{array}{l} \Phi_s(x)^{(n,s)} = \bar{f}^{n,s}_S. \end{array}\tag{A8} $

(A8) Moreover, a quantity
$ \lambda_{\bar{B}^0} $ is introduced to parametrize the integral over the$ \bar{B}^0 $ meson distribution amplitude through [6]$ \begin{array}{l} \displaystyle\int_0^1\frac{{\rm d}\rho}{\rho}\Phi_{\bar{B}^0}(\rho)\equiv\frac{m_{\bar{B}^0}}{\lambda_{\bar{B}^0}}.\\ \end{array} \tag{A9}$

(A9) With the asymptotic light-cone distribution amplitudes, the building blocks for the annihilation amplitudes are given by [26]
$ \begin{split} \ A_1^i =& \pi\alpha_s\int_0^1 {\rm d}x {\rm d}y\begin{cases} \bigg(\Phi_{V}(x)\Phi_{S}(y)\bigg[\dfrac{1}{x(1-\bar{x}y)}+\dfrac{1}{x\bar{y}^2}\bigg]+r_\chi^{V}r_\chi^{S} \Phi_{v}(x)\Phi_{S}^s(y)\dfrac{2}{x\bar{y}}\bigg),\quad \text{for $M_1M_2 = VS,$}\\ \bigg(\Phi_{S}(x)\Phi_{V}(y)\bigg[\dfrac{1}{x(1-\bar{x}y)}+\dfrac{1}{x\bar{y}^2}\bigg]+r_\chi^{V}r_\chi^{S} \Phi_{S}^s(x)\Phi_{v}(y)\dfrac{2}{x\bar{y}}\bigg),\quad \text{for $M_1M_2 = SV,$}\\ \end{cases}\\ A_2^i =& \pi\alpha_s\int_0^1 {\rm d}x {\rm d}y\begin{cases} \bigg(\Phi_{V}(x)\Phi_{S}(y)\bigg[\dfrac{1}{\bar{y}(1-\bar{x}y)}+\dfrac{1}{x^2\bar{y}}\bigg]+r_\chi^{V}r_\chi^{S} \Phi_{v}(x)\Phi_{S}^s(y)\dfrac{2}{x\bar{y}}\bigg),\quad \text{for $M_1M_2 = VS,$}\\ \bigg(\Phi_{S}(x)\Phi_{V}(y)\bigg[\dfrac{1}{\bar{y}(1-\bar{x}y)}+\dfrac{1}{x^2\bar{y}}\bigg]+r_\chi^{V}r_\chi^{S} \Phi_{S}^s(x)\Phi_{v}(y)\dfrac{2}{x\bar{y}}\bigg),\quad \text{for $M_1M_2 = SV,$}\\ \end{cases}\\ A_3^i =& \pi\alpha_s\int_0^1 {\rm d}x {\rm d}y\begin{cases} \bigg(r_\chi^{V}\Phi_{v}(x)\Phi_{S}(y)\dfrac{2\bar{x}}{x\bar{y}(1-\bar{x}y)}-r_\chi^{S} \Phi_{V}(x)\Phi_S^s(y)\dfrac{2y}{x\bar{y}(1-\bar{x}y)}\bigg),\quad \text{for $M_1M_2 = VS,$}\\ \bigg(-r_\chi^{S}\Phi_{S}^s(x)\Phi_{V}(y)\dfrac{2\bar{x}}{x\bar{y}(1-\bar{x}y)}+r_\chi^{V} \Phi_{S}(x)\Phi_v(y)\dfrac{2y}{x\bar{y}(1-\bar{x}y)}\bigg),\quad \text{for $M_1M_2 = SV,$}\\ \end{cases}\\ A_3^f =& \pi\alpha_s\int_0^1 {\rm d}x {\rm d}y\begin{cases} \bigg(r_\chi^{V}\Phi_{v}(x)\Phi_{S}(y)\dfrac{2(1+\bar{y})}{x\bar{y}^2}+r_\chi^{S} \Phi_{V}(x)\Phi_S^s(y)\dfrac{2(1+x)}{x^2\bar{y}}\bigg),\quad \text{for $M_1M_2 = VS,$}\\ \bigg(-r_\chi^{V}\Phi_{S}^s(x)\Phi_{V}(y)\dfrac{2(1+\bar{y})}{x\bar{y}^2}-r_\chi^{V} \Phi_{S}(x)\Phi_v(y)\dfrac{2(1+x)}{x^2\bar{y}}\bigg),\quad \text{for $M_1M_2 = SV,$}\\ \end{cases}\\ A_1^f =& A_2^f = 0. \end{split} \tag{A10}$

(A10) -
With the conventions in Ref. [11], we obtain the amplitudes for
$ \bar{B}^0\rightarrow \bar{K}_0^*\rho^0, \bar{K}^*\sigma $ decays within the QCDF framework, which have the following forms:$ \begin{split} {\cal{M}}(\bar{B}^0\rightarrow \bar{\kappa}\rho) =& \frac{{\rm i}G_F}{2}\sum_{p = u,c}\lambda_p^{(s)}\bigg\{2f_\rho F_1^{\bar{B}^0 \bar{\kappa}}(m_{\rho}^2)m_{\bar{B}^0}p_c\bigg[\delta_{pu}\alpha_2(\bar{\kappa}\rho) +\alpha_{3,EW}^p(\bar{\kappa}\rho)\bigg]+2\bar{f}_{\bar{\kappa}}A_0^{\bar{B}^0\rho}(m_{\bar{\kappa}}^2)m_{\bar{B}^0}p_c\\& \times\bigg[\alpha_4^p(\rho\bar{\kappa})-\frac{1}{2}\alpha_{4,EW}^p(\rho\bar{\kappa})\bigg] +f_{\bar{B}^0}f_\rho f_{\bar{\kappa}}\bigg[b_3^p(\rho\bar{\kappa})-\frac{1}{2}b_{3,EW}^p(\rho\bar{\kappa})\bigg]\bigg\}, \end{split} \tag{B1}$

(B1) $ \begin{split} {\cal{M}}(\bar{B}^0\rightarrow \bar{K}^*\sigma) =& -\frac{{\rm i}G_F}{2}\sum_{p = u,c}\lambda_p^{(s)}\bigg\{2\bar{f}_{\sigma^s}A_0^{\bar{B}^0 \bar{K}^*}(m_\sigma^2)m_{\bar{B}^0}p_c\bigg[\frac{1}{\sqrt{2}}\delta_{pu}\alpha_2(\bar{K}^*\sigma)+\sqrt{2}\alpha_3^p(\bar{K}^*\sigma) \\ &+\frac{1}{2\sqrt{2}}\alpha_{3,EW}^p(\bar{K}^*\sigma)\bigg]+2\bar{f}_{\sigma^s}A_0^{\bar{B}^0\bar{K}^*}(m_\sigma^2)m_{\bar{B}^0}p_c\bigg[\alpha_3^p(\bar{K}^*\sigma)-\frac{1}{2} \alpha_{3,EW}^p(\bar{K}^*\sigma)\\& +\alpha_4^p(\bar{K}^*\sigma)-\frac{1}{2}\alpha_{4,EW}^p(\bar{K}^*\sigma)\bigg]+2f_{\bar{K}^*} F_1^{\bar{B}^0\sigma}(m_{\bar{K}^*}^2)m_{\bar{B}^0}p_c\bigg[\frac{1}{2\sqrt{2}}\alpha_{4,EW}^p(\sigma\bar{K}^*)\\& -\frac{1}{\sqrt{2}}\alpha_4^p(\sigma\bar{K}^*)\bigg]-f_{\bar{B}^0}f_{\bar{K}^*}\bar{f}_\sigma^s\bigg[b_3^p(\bar{K}^*\sigma)+b_{3,EW}^p(\bar{K}^*\sigma)\bigg]+ f_{\bar{B}^0}f_{\bar{K}^*}\bar{f}_\sigma^n\bigg[\frac{1}{\sqrt{2}}b_3^p(\sigma\bar{K}^*)\\& -\frac{1}{2\sqrt{2}}b_{3,EW}^p(\sigma\bar{K}^*)\bigg]\bigg\}. \end{split}\tag{B2} $

(B2) -
The predictions obtained in the QCDF approach depend on many input parameters. The values of the Wolfenstein parameters are taken from Ref. [36]:
$ \bar{\rho} = 0.117\pm0.021 $ ,$ \bar{\eta} = 0.353\pm0.013 $ .The effective Wilson coefficients used in our calculations are taken from Ref. [28]:
$ \begin{split} C'_1 =& -0.3125, \quad C'_2 = -1.1502, \\ C'_3 =& 2.120\times10^{-2}+5.174\times10^{-3}i,\quad C'_4 = -4.869\times10^{-2}-1.552\times10^{-2}i, \\ C'_5 =& 1.420\times10^{-2}+5.174\times10^{-3}i,\quad C'_6 = -5.792\times10^{-2}-1.552\times10^{-2}i, \\ C'_7 =& -8.340\times10^{-5}-9.938\times10^{-5}i,\quad C'_8 = 3.839\times10^{-4}, \\ C'_9 =& -1.017\times10^{-2}-9.938\times10^{-5}i,\quad C'_{10} = 1.959\times10^{-3}. \end{split}\tag{C1} $

(C1) For the masses used in
$ \bar{B}^0 $ decays, we use the following values (in$ \mathrm{GeV} $ ) [36]:$ \begin{split} m_u =& m_d = 0.0035,\quad m_s = 0.119, \quad m_b = 4.2,\quad m_{\pi^\pm} = 0.14,\\ m_{K^+} =& 0.494,\quad m_{f_0(500)} = 0.50,\quad m_{{\bar{K}_0^*}(700)} = 0.824, \\ m_{\rho^0(770)} =& 0.775,\quad m_{\bar{K}^*(892)} = 0.895,\quad m_{\bar{B}^0} = 5.28, \end{split}\tag{C2}$

(C2) and widths are (in
$ \mathrm{GeV} $ ) [36]$ \begin{split} \ \Gamma_{\rho^0(770)} =& 0.149,\\\Gamma_{f_0(500)} =& 0.5,\\ \Gamma_{\bar{K}_0^*(700)} =& 0.047,\\\Gamma_{\bar{K}^*(892)} =& 0.047. \end{split} \tag{C3}$

(C3) The strong coupling constants are determined from the measured partial widths through the relations [7, 37]
$ \begin{split} g_{S M_1M_2} =& \sqrt{\frac{8\pi m_S^2}{p_c(S)}\Gamma_{S\rightarrow M_1M_2}},\\ g_{V M_1M_2} =& \sqrt{\frac{6\pi m_V^2}{p_c(V)^3}\Gamma_{V\rightarrow M_1M_2}},\end{split} \tag{C4}$

(C4) where
$ p_c(S,V) $ are the magnitudes of the three momenta of the final state mesons in the rest frame of S and V mesons, respectively.The following related decay constants (in
$ \mathrm{GeV} $ ) are used [20, 35]:$ \begin{split}f_{\pi^\pm} =& 0.131,\quad f_{\bar{B}^0} = 0.21\pm0.02, \quad f_{K^-} = 0.156\pm0.007, \\ \bar{f}^s_{f_0(500)} =& -0.21\pm0.093,\quad \bar{f}_{f_0(500)}^u = 0.4829\pm0.076,\\ \bar{f}_{\bar{K}_0^*(700)} =& 0.34\pm0.02,\quad f_{\rho^0(770)} = 0.216\pm0.003,\\ f_{\rho^0(770)}^\perp =& 0.165\pm0.009,\quad f_{\bar{K}^*(892)} = 0.22\pm0.005,\\ f_{\bar{K}^*(892)}^\perp =& 0.185\pm0.010. \end{split} \tag{C5}$

(C5) As for the form factors, we use [20, 35]:
$ \begin{split} F_0^{\bar{B}^0\rightarrow K}(0) =& 0.35\pm0.04,\\ F_0^{\bar{B}^0\rightarrow f_0(500)}(m_K^2) =& 0.45\pm0.15,\\ A_0^{\bar{B}^0\rightarrow \rho^0(770)}(0) =& 0.303\pm0.029,\\ A_0^{\bar{B}^0\rightarrow \bar{K}^*(892)}(0) =& 0.374\pm0.034, \\ F_0^{\bar{B}^0\rightarrow \pi}(0) =& 0.25\pm0.03. \end{split} \tag{C6}$

(C6) The values of Gegenbauer moments at
$ \mu = 1 \mathrm{GeV} $ are taken from [20, 35],$ \begin{split} \alpha_1^\rho =& 0,\quad \alpha_2^\rho = 0.15\pm0.07, \quad \alpha_{1,\perp}^\rho = 0,\quad \alpha_{2,\perp}^\rho = 0.14\pm0.06, \\ \alpha_1^{K^*(892)} =& 0.03\pm0.02,\quad \alpha_{1,\perp}^{K^*(892)} = 0.04\pm0.03,\\ \alpha_2^{K^*(892)} =& 0.11\pm0.09,\quad \alpha_{2,\perp}^{K^*(892)} = 0.10\pm0.08,\\ B_{1,f_0(500)}^u =& -0.42\pm0.02,\quad B_{3,f_0(500)}^u = -0.58\pm0.19,\\ B_{1,f_0(500)}^s =& -0.35\pm0.003,\quad B_{3,f_0(500)}^s = -0.43\pm0.013,\\ B_{1,\bar{K}_0^*(700)} =& -0.92\pm0.11,\quad B_{3,\bar{K}_0^*(700)} = 0.15\pm0.09. \end{split} \tag{C7}$

(C7)
Studying the localized CP violation and the branching fraction of the ${\bar{B}^0\rightarrow K^-\pi^+\pi^+\pi^-}$ decay
- Received Date: 2020-04-24
- Available Online: 2020-10-01
Abstract: In this work, we study the localized







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




























 DownLoad:
DownLoad: