-
The basic constituents of nuclear matter are quarks and gluons. Their interactions are governed by the rules of quantum chromodynamics (QCD). QCD matter, normally confined into hadrons, is deconfined into a state of matter known as the quark-gluon plasma (QGP) under extreme conditions of high energy/matter densities [1]. A QGP phase existed in the early universe and is also created in heavy-ion collisions at the relativistic heavy-ion collider (RHIC) [2-5] and the large hadron collider (LHC) [6]. One important piece of evidence for the discovery of the QGP is jet quenching, i.e. parton (jet) energy loss in the QGP medium, which in relativistic heavy-ion collisions suppresses high transverse momentum (
$ p_T $ ) particle and jet production [7-16]. The suppression is so strong that a density at least 30-fold the normal nuclear density is required for describing data in model calculations [17].The partonic energy loss mechanisms are, however, less clear. Some models focus on collisional and radiative energy losses [17]. Others propose more exotic mechanisms, such as collective excitation modes [18-23]. While single-particle measurements are not sufficiently sensitive to energy loss mechanisms, measurements of the lost energy's redistribution at low to modest
$ p_T $ are expected to be more sensitive. One approach is to reconstruct jets and study$ p_T $ and angular distributions of jet fragments [24-26]. Distributions of the lost energy can also be measured via dihadron angular correlations with respect to high-$ p_T $ trigger particles and jets. Previous measurements of two- and multi-particle correlations, after subtracting elliptic flow background, have revealed novel correlation structures [27-31]. However, owing to initial collision geometry fluctuations, all orders of harmonics (not just elliptic) flow anisotropies are possible [32, 33]. Full subtraction of anisotropic backgrounds is challenging and suffers from large uncertainties [24, 31, 34-43].Here, we devise a data-driven method with an "automatic" subtraction of anisotropic flow backgrounds. The method was first tested with toy model and PYTHIA simulations [44]. Although the correlated jetlike yield cannot be readily determined using this method, the correlation shape can be obtained without the large uncertainty associated with the flow subtraction. We study the correlation shape as a function of the collision centrality and associated particle
$ p_T $ . The correlation shape should be sensitive to the nature of jet-medium interactions, and therefore offers new opportunities to investigate energy loss mechanisms and medium properties. -
The data reported here were collected in 2011 in the STAR experiment using a minimum bias (MB) trigger in Au+Au collisions at the nucleon-nucleon center-of-mass energy of
$ \sqrt{s_{{NN}}} = 200 $ GeV. The MB trigger is defined by a coincidence signal between the east and west vertex position detectors (VPDs) [45] located at the pseudorapidity range of$ 4.4<|\eta|<4.9 $ . Overall,$ 3.2\times10^8 $ MB trigger events are used. The event centrality is defined by the measured charged particle multiplicity within$ |\eta|<0.5 $ . Data are reported in four centrality bins, corresponding to 0-10%, 10%-30%, 30%-50%, and 50%-80% of the total hadronic cross-section [46].The main detector used for this analysis is the time projection chamber (TPC) [47, 48], residing in a 0.5 T magnetic field along the beam direction (
$ z $ ). Particle tracks are reconstructed in the TPC and are required to have at least 20 out of 45 maximally possible hits. The ratio of the number of hits used in the track reconstruction to the number of possible hits is required to be above 0.51, for eliminating multiple track segments being reconstructed from a single particle trajectory. The primary vertex (PV) is reconstructed using tracks. Events with the PV position ($ z_{\rm vtx} $ ) within 30 cm of the TPC center along$ z $ are used. To remove secondaries from particle decays, only tracks with the distance of closest approach DCA <2 cm to the PV are used. -
Jetlike correlations are studied with respect to high-
$ p_T $ trigger particles, which serve as proxies for jets [17, 31]. High-$ p_T $ particles measured at RHIC are strongly biased toward the surface of the collision zone [17, 49, 50]. The away-side jet partner, which is preferentially directed inward, is therefore very likely to traverse the entire volume, suffering maximal interactions with the medium. Because of the broad distribution of the underlying parton kinematics, the away-side jet direction is mostly uncorrelated in$ \eta $ relative to the trigger particle [31]. It is therefore difficult to distinguish the jet signal from the underlying background; the large, azimuthally anisotropic background has to be specifically subtracted, with large uncertainties, traditionally using measured anisotropy parameters [31]. The away-side jet direction can be localized by requiring a second high-$ p_T $ particle back-to-back in the azimuthal angle ($ \phi $ ) with respect to the first one. However, by doing so, the back-to-back dijets are biased towards being tangential to the collision zone [41, 51], substantially weakening the purpose of studying jet-medium interactions.In this analysis, we impose a less biasing requirement of a large recoil transverse momentum (
$ P_x $ ) azimuthally opposite to the high-$ p_T $ trigger particle, within a given$ \eta $ range, to enhance the away-side jet population in the acceptance. The schematic diagram in Fig. 1 shows the away-side$ \eta - \phi $ space and illustrates by the fading gray area the away-side jet population enhanced in a particular$ \eta $ regoin.$ P_x $ is given by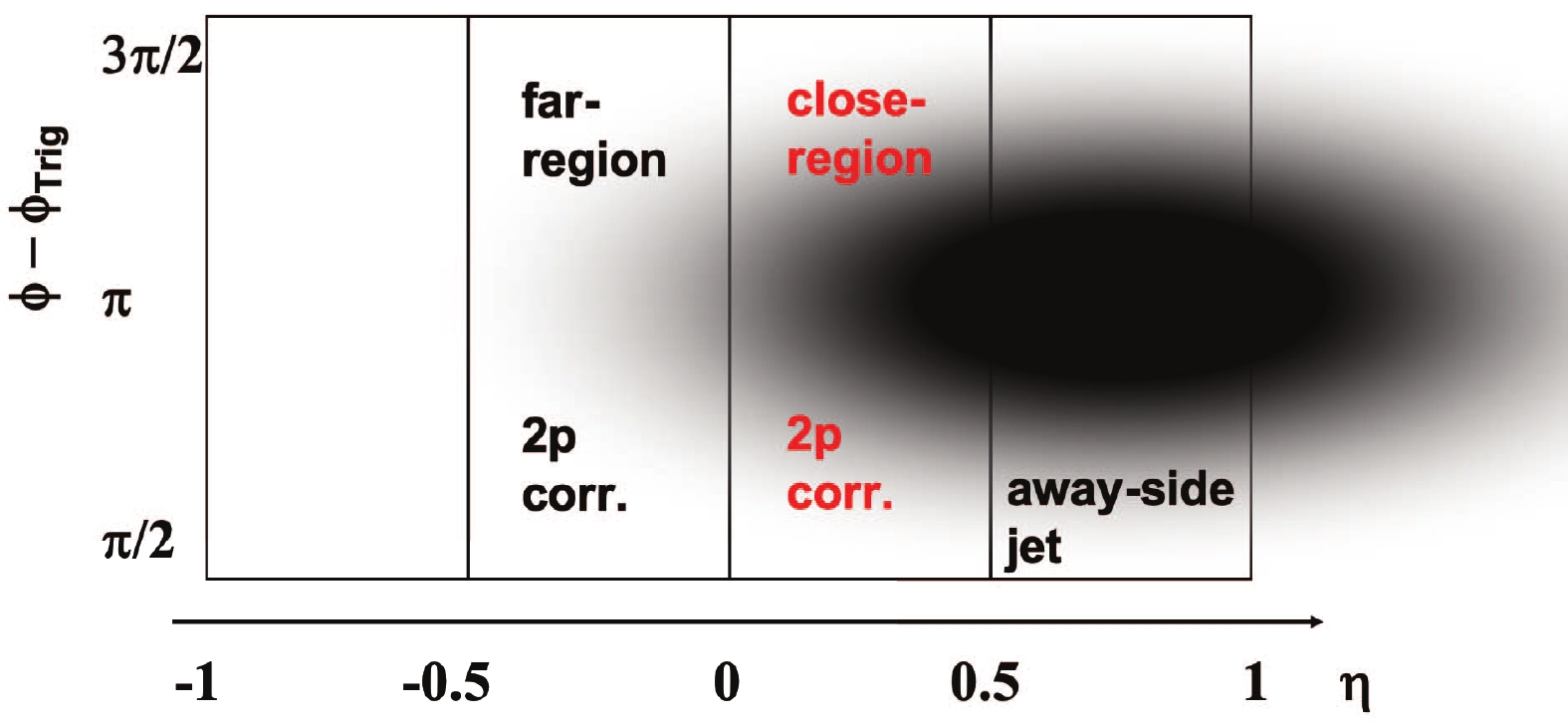
Figure 1. (color online) Schematic of the analysis method. The requirement of a large recoil
$ P_x $ [Eq. (1)] in a particular$ \eta $ region ($ 0.5<\eta<1 $ shown here) selects events with enhanced population of jets close to the$ \eta $ region. Jetlike correlations in the close-region and far-region, symmetric with respect to midrapidity, contain different contributions from the jet but the same contribution from the flow background. Their difference measures the jetlike correlation shape.$ P_x|_{\eta_1}^{\eta_2} = \sum\limits_{\eta_1<\eta<\eta_2,|\phi-\phi_{\rm{trig}}|>\pi/2}p_T\cos(\phi-\phi_{\rm{trig}})\cdot\frac{1}{\epsilon}\;, $

(1) where all charged particles (
$ 0.15<p_T<10\;{\rm{GeV}}/{\rm{c}} $ ) within the$ \eta $ range that are on the away side ($ |\phi-\phi_{\rm{trig}}|>\pi/2 $ ) of the trigger particle are included. Since the near-side jet is not included in the$ P_{x} $ calculation, the$ \eta $ distribution of the trigger particle is unbiased by the$ P_x $ cut. The inverse of the single-particle relative acceptance×efficiency ($ \epsilon $ ) is used to correct for the single-particle detection efficiency. It depends on the position of the primary vertex along the beam axis$ z_{\rm vtx} $ , collision centrality, particle$ p_T $ ,$ \eta $ and$ \phi $ , and has run period variations [46]. The$ \phi $ -dependence of$ \epsilon_{\phi} $ is obtained, separately for positive and negative$ \eta $ , from the single-particle$ \phi $ distribution normalized to unity on average in each centrality. The$ \eta $ -dependence of$ \epsilon $ varies with$ z_{\rm vtx} $ , centrality and$ p_T $ , and is obtained by treating symmetrized$ {\rm d}N/{\rm d}\eta $ distribution in events with$ |z_{\rm vtx}|<2 $ cm as the baseline, and taking the ratio of the$ {\rm d}N/{\rm d}\eta $ distribution from each$ z_{\rm vtx} $ bin to this baseline. Because our$ P_x $ cut is only used to select a given fraction of events, the absolute efficiency correction is not applied.In this analysis the trigger particle
$ p_T $ range is$ 3<p_T^{\rm{trig}}<10\;{\rm{GeV}}/{\rm{c}}$ . We choose the windows$ -1<\eta< -0.5 $ or$ 0.5<\eta<1 $ for$ P_x $ calculation. Figure 2 shows example$ P_x|_{0.5}^{1} $ distributions for peripheral and central Au+Au collisions. Their difference comes mainly from event multiplicities. For each centrality, we select the 10% of the events with the highest$ -P_x $ to enhance the probability that the away-side jet population is contained in this$ \eta $ region. There is a large statistical fluctuation effect in$ P_x $ , especially in central collisions. The$ P_x $ selection may also be affected by low-$ p_T $ minijets. These effects do not strictly give a symmetric distribution [44]. Nevertheless, we show the reflected data as open circles in Fig. 2(b) to give an order of magnitude estimate of those effects.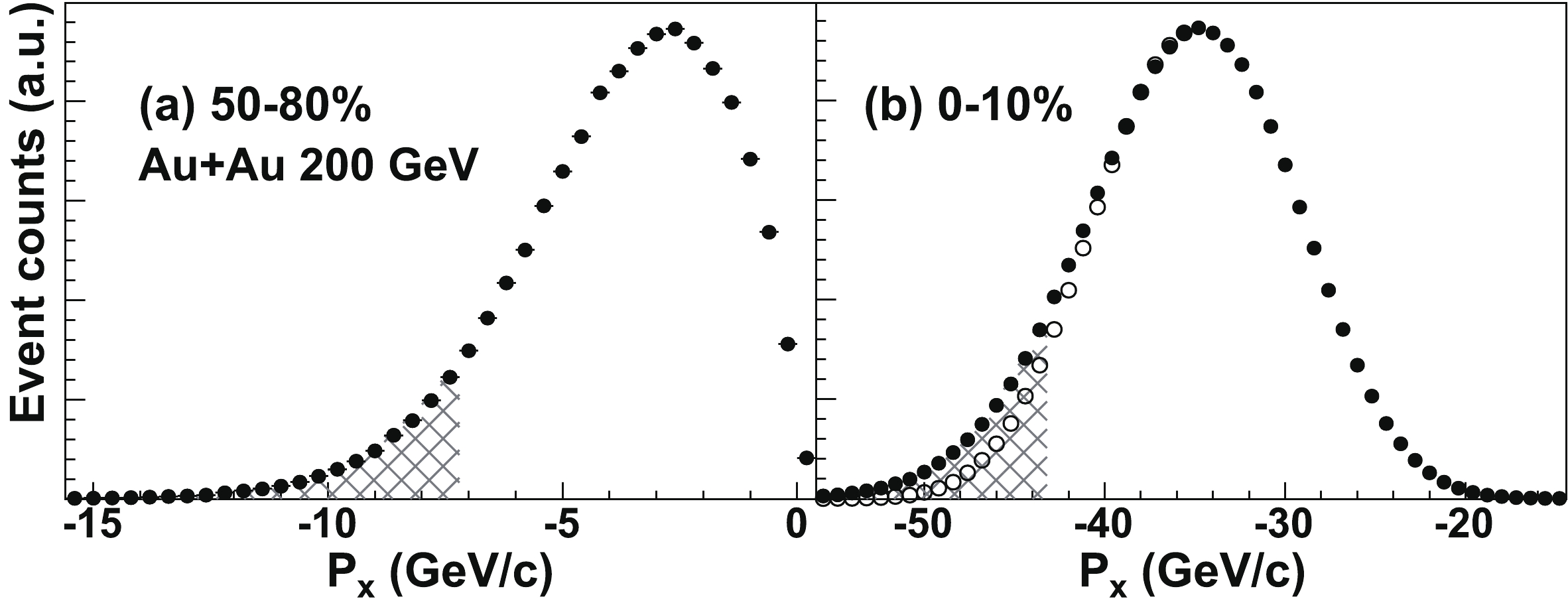
Figure 2. Distributions of the recoil momentum within
$ 0.5<\eta<1 $ ($ P_x|_{0.5}^{1} $ ) from high-$ p_T $ trigger particles of$ 3<p_T^{\rm{trig}}<10\;{\rm{GeV}}/{\rm c}$ in (a) 50%-80% peripheral and (b) 0-10% central collisions. The shaded areas indicate a selection of 10% of events to enhance the away-side jet population inside acceptance. Events from$ |z_{\rm vtx}|<2 $ cm are used; other$ z_{\rm vtx} $ events and$ P_x|_{-1}^{-0.5} $ are similar. The right side of the$ P_x $ distribution is reflected to the left of the maximum, with open circles.In the selected events, we analyze dihadron correlations of associated particles, with respect to trigger particles, in two
$ \eta $ regions symmetric with respect to midrapidity, one close ("close-region") to and the other far ("far-region") from the$ \eta $ window for$ P_x $ (Fig. 1). The dihadron correlation in$ \Delta\phi = \phi_{\rm{assoc}}-\phi_{\rm{trig}} $ , between the associated and trigger particle azimuthal angles, is given by$ \frac{{\rm d}N}{{\rm d}\Delta\phi} = \frac{1}{N_{\rm{trig}}}\cdot\frac{S(\Delta\phi)}{B(\Delta\phi)/B_0}\;, $

(2) where
$ S(\Delta\phi) = \int_{-1}^{+1}{\rm d}\eta_{\rm{trig}}\int_{\rm{region}}{\rm d}\eta_{\rm{assoc}}\frac{{\rm d}^3N}{{\rm d}\eta_{\rm{trig}} {\rm d}\eta_{\rm{assoc}} {\rm d}\Delta\phi}\cdot\frac{1}{\epsilon} $

(3) and
$ B(\Delta\phi) $ is its counterpart from mixed events. The correlations are normalized by the number of trigger particles,$ N_{\rm{trig}} $ . In Eq. (3), "region" stands for close-region or far-region. All the trigger particles with$ |\eta_{\rm{trig}}|<1 $ are integrated. The single-particle relative acceptance×efficiency ($ \epsilon $ ) correction is applied to associated particles. As in the case of$ P_x $ , the absolute efficiency correction is not applied in the correlation measurements because this analysis deals with only the correlation shape, not the absolute amplitude. The mixed-events are formed by pairing the trigger particles in each event with the associated particles from 10 different random events in the same centrality and$ z_{\rm vtx} $ bin. The mixed-event background$ B(\Delta\phi) $ is normalized to unity (via the constant$ B_0 $ ), to correct for residual two-particle acceptance after single-particle efficiency correction.The away-side jet contributes more to the close region than to the far region, owing to the larger
$ \Delta\eta $ gap of the latter (Fig. 1). The anisotropic flow contributions, on the other hand, are on average equal in these two regions that are symmetric with respect to midrapidity. The difference in the close- and far-region correlations, therefore, arises only from jetlike correlations. For$ P_x|_{-1}^{-0.5} $ , the close-region is$ -0.5<\eta<0 $ and the far-region is$ 0<\eta<0.5 $ ; for$ P_x|_{0.5}^{1} $ , they are swapped. The results from these two sets are consistent, and thus combined. We exclude events where both$ P_x|_{-1}^{-0.5} $ and$ P_x|_{0.5}^{1} $ satisfy the respective 10%$ P_x $ cut, because the combined signal would be strictly zero but with a propagated nonzero statistical error.PYTHIA simulations [44] indicate that jet fragmentations are approximately factorized in
$ \eta $ and$ \phi $ . The$ \Delta\phi $ correlations at different$ \Delta\eta $ have approximately the same shape, only differing in magnitude. Thus, the difference between close- and far-region correlations measures the away-side correlation shape. We quantify the shape by a Gaussian width$ \sigma $ determined by fitting. -
The systematic uncertainties of
$ \sigma $ come from several sources. Varying the$ P_x $ cut changes the relative contributions of jets and background fluctuations to selected events, but should not affect the correlation width significantly if the jet sample is unbiased. We vary the$ P_x $ cut from allowing the default 10% of events to 2%, 5%, 15%, 20%, 30% and 50% of events. The calculated systematic uncertainty of$ \sigma $ is 3.4% (one standard deviation).We have assumed that jetlike correlations are factorized in
$ \eta $ and$ \phi $ . There is theoretical [52-54] and experimental evidence [55] that flow may be decorrelated over$ \eta $ , owing to geometry fluctuations. Both these effects would cause uncertainties in attributing the close- and far-region difference purely to jetlike correlations. We vary the close- and far-region$ \eta $ locations and ranges so they have different$ \eta $ gaps in between as well as from the$ P_x $ $ \eta $ window, but are still symmetric with respect to midrapidity. We also vary the$ P_x $ $ \eta $ window location and range. The largest deviation of$ \sigma $ from the default results is approximately half of the statistical error. The calculated systematic uncertainty of$ \sigma $ is 2.0% (one standard deviation) for this source.In addition, we vary the track quality cuts in the analysis. The calculated systematic uncertainty for this source is 5.3% standard deviation in
$ \sigma $ . The final systematic uncertainty is calculated as the quadratic sum of all the sources we studied.The systematic uncertainties on
$ \sigma $ are found to be partially correlated between various centralities and$ p_T^{\rm{assoc}} $ bins. In the difference between central and peripheral collisions,$ \Delta\sigma = \sqrt{\sigma^2_{\rm{cent}}-\sigma^2_{\rm{peri}}} $ , the systematic uncertainties are not simply propagated but obtained in the same way as those on the individual$ \sigma $ 's described above. The same procedure is used to obtain the systematic uncertainty on the linear parameterization of$ \Delta\sigma $ versus$ p_T^{\rm{assoc}} $ . -
Figure 3(a) shows, as an example, the dihadron azimuthal correlations for the close-region and far-region in 10%-30% Au+Au collisions at
$ \sqrt{s_{{NN}}} = 200 $ GeV for trigger$ 3<p_T^{\rm{trig}}<10\;{\rm{GeV}}/{\rm{c}}$ and associated particle$ 1<p_T^{\rm{assoc}}< 2\;{\rm{GeV}}/{\rm{c}}$ . The near-side correlations are almost identical for close- and far-region. The near-side ratio of far- to close-region correlations,$ \alpha $ , are listed in Table 1 and are all approximately unity. This indicates, to a good degree, that near-side jetlike correlations are not biased by the$ P_x $ selection and flow contributions to close- and far-region correlations are indeed equal.$ p_T^{\rm{assoc}} $ /(

$ {\rm{GeV}}/{\rm{c}} $ )

50%-80% 30%-50% 10%-30% 0-10% 0.15-0.5 $ 1.0038\pm0.0007 $ 

$ 1.0036\pm0.0003 $ 

$ 1.0027\pm0.0001 $ 

$ 1.0002\pm0.0001 $ 

0.5-1 $ 1.000\pm0.001 $ 

$ 1.0021\pm0.0003 $ 

$ 1.0006\pm0.0002 $ 

$ 0.9984\pm0.0001 $ 

1-2 $ 1.002\pm0.002 $ 

$ 1.0002\pm0.0006 $ 

$ 0.9994\pm0.0003 $ 

$ 0.9976\pm0.0002 $ 

2-3 $ 0.997\pm0.006 $ 

$ 1.006\pm0.002 $ 

$ 0.9995\pm0.0009 $ 

$ 0.9965\pm0.0008 $ 

3-10 $ 0.99\pm0.01 $ 

$ 0.999\pm0.005 $ 

$ 0.998\pm0.003 $ 

$ 0.999\pm0.003 $ 

Table 1. The near-side ratio of far- to close-region correlations,
$ \alpha $ , averaged over$ |\Delta\phi|<1 $ as a function of$ p_T^{\rm{assoc}} $ and centrality in Au+Au collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV. The trigger particle has$ 3<p_T^{\rm{trig}}<10 \;{\rm{GeV}}/{\rm{c}}$ . Errors are statistical.
Figure 3. (a) Dihadron azimuthal correlations in close-region (solid circles) and far-region (open crosses), as an example, for
$ 3<p_T^{\rm{trig}}<10 \;{\rm{GeV}}/{\rm{c}}$ and$ 1<p_T^{\rm{assoc}}<2\;{\rm{GeV}}/{\rm{c}}$ in 10%-30% Au+Au collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV. (b) The difference between close-region correlation and scaled far-region correlation (see text for detail). The curve is a Gaussian fit with the centroid fixed at$ \pi $ . Errors are statistical.The away-side correlations differ in amplitude and shape, which is caused by the away-side jet contributions. The far-region correlation is scaled by
$ \alpha $ to account for the small near-side difference and then we subtract it from the close-region correlation. The result is shown in Fig. 3(b). The difference measures the away-side jetlike correlation shape. A Gaussian fit centered at$ \Delta\phi = \pi $ is used, for extracting the correlation width. The$ \chi^2 $ values per degree of freedom are all consistent with unity, indicating that the correlation shape is Gaussian. The$ \sigma $ values are tabulated in Table 2.$ p_T^{\rm{assoc}} $ /(

$ {\rm{GeV}}/{\rm{c}} $ )

50%-80% 30%-50% 10%-30% 0-10% 0.15-0.5 $ 0.98\pm0.04\pm0.06 $ 

$ 0.96\pm0.03\pm0.06 $ 

$ 1.07\pm0.03\pm0.07 $ 

$ 0.99\pm0.03\pm0.06 $ 

0.5-1 $ 0.87\pm0.02\pm0.06 $ 

$ 0.84\pm0.02\pm0.06 $ 

$ 0.91\pm0.02\pm0.06 $ 

$ 0.94\pm0.03\pm0.06 $ 

1-2 $ 0.72\pm0.02\pm0.05 $ 

$ 0.79\pm0.02\pm0.05 $ 

$ 0.81\pm0.02\pm0.05 $ 

$ 0.83\pm0.02\pm0.06 $ 

2-3 $ 0.56\pm0.03\pm0.04 $ 

$ 0.67\pm0.03\pm0.04 $ 

$ 0.75\pm0.03\pm0.05 $ 

$ 0.77\pm0.04\pm0.05 $ 

3-10 $ 0.42\pm0.04\pm0.03 $ 

$ 0.59\pm0.05\pm0.04 $ 

$ 0.67\pm0.05\pm0.04 $ 

$ 0.82\pm0.09\pm0.05 $ 

Table 2. Gaussian fit width to away-side jetlike correlations as a function of
$ p_T^{\rm{assoc}} $ and centrality in Au+Au collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV. The trigger particle has$ 3<p_T^{\rm{trig}}<10\;{\rm{GeV}}/{\rm{c}}$ . The first error is statistical and the second is systematic.Figure 4 shows the away-side correlation width (Gaussian
$ \sigma $ ) as a function of centrality, for five$ p_T^{\rm{assoc}} $ bins. The width for the lowest$ p_T^{\rm{assoc}} $ of 0.15-0.5 GeV/c is consistent with a constant over centrality; at this low$ p_T^{\rm{assoc}} $ , the correlations are fairly wide for all centralities, and possible broadening with increasing centrality may not be easily observable. For the four higher$ p_T^{\rm{assoc}} $ bins, the width increases from peripheral to central collisions. The broadening of the correlation function is consistent with jet broadening. However, it is also possible, because the correlation measurement is statistical, that the broadening comes from an increasing dijet acoplanarity (nuclear$ k_T $ effect [56, 57]) with increasing centrality. One possible mechanism of the nuclear$ k_T $ effect is multiple scattering by incident nucleons before the hard scattering between underlying partons. The nuclear$ k_T $ effect gives the hard scattering partons an initial net momentum in the transverse plane, and thus causes a spread in the dijet angular correlation.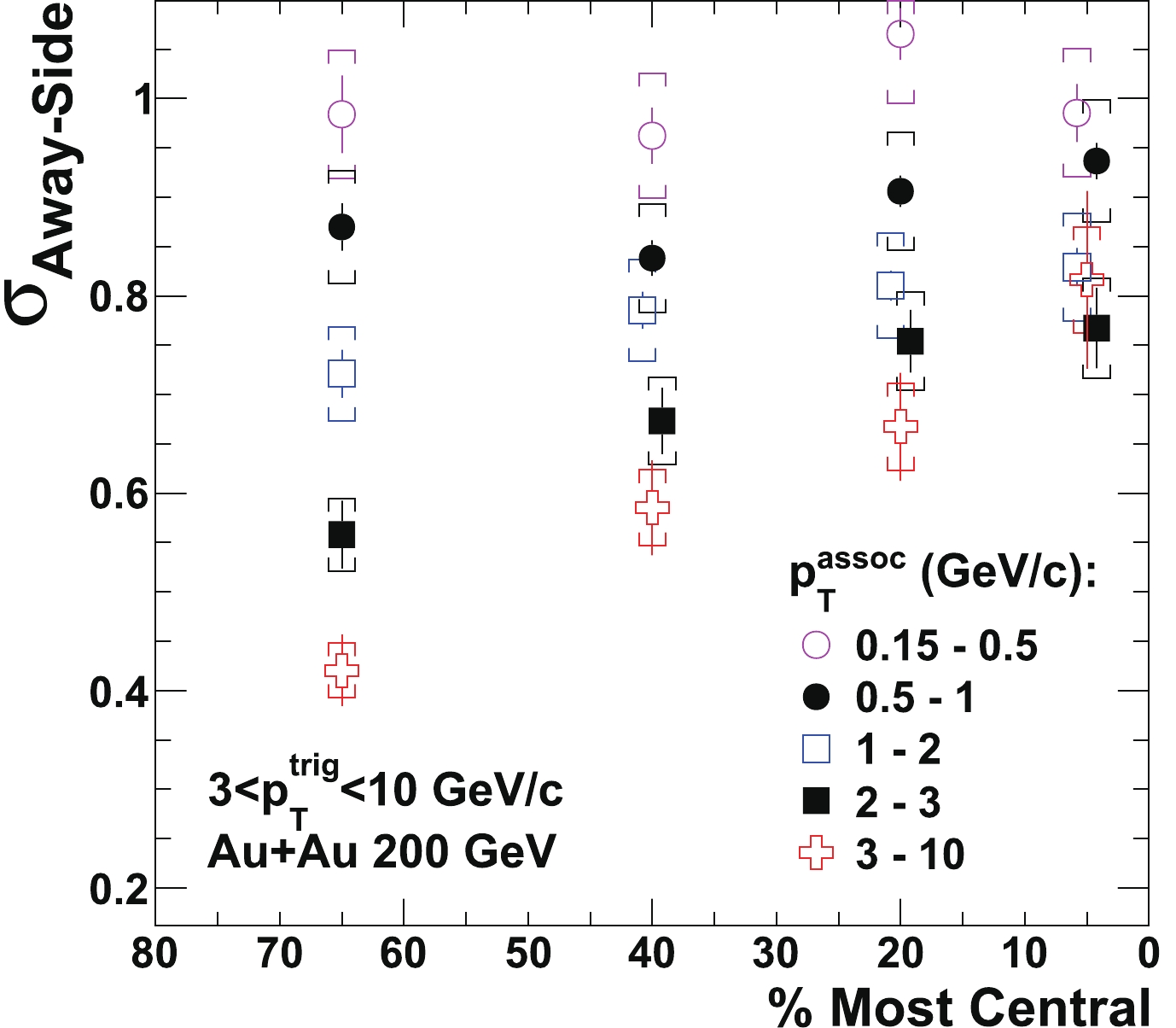
Figure 4. (color online) Away-side jetlike correlation width (Gaussian
$ \sigma $ ) as a function of centrality (0 indicates the most central collisions) for$ 3<p_T^{\rm{trig}}<10\;{\rm{GeV}}/{\rm{c}}$ and various$ p_T^{\rm{assoc}} $ bins in Au+Au collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV. Bars are statistical errors and caps are systematic uncertainties.Figure 5(a) shows
$ \sigma $ as a function of$ p_T^{\rm{assoc}} $ in peripheral and central collisions. In peripheral collisions, the width decreases rapidly with increasing$ p_T^{\rm{assoc}} $ . In central collisions the decrease is less rapid. We quantify the broadening from peripheral to central collisions by$ \Delta\sigma = \sqrt{\sigma^2_{\rm cent}-\sigma^2_{\rm peri}} $ , shown as a function of$ p_T^{\rm{assoc}} $ in Fig. 5(b). The relative broadening is stronger for higher$ p_T $ associated particles. At very low$ p_T^{\rm{assoc}} $ , the jetlike correlation is already quite broad in peripheral collisions, limiting any further broadening in central collisions. At high$ p_T^{\rm{assoc}} $ the initial jetlike correlation is narrow, leaving significant room for broadening in central collisions. In previous STAR dihadron correlation measurements [5, 30], the reported away-side correlations were broader than those reported here, likely because the previous results did not have the high-order harmonic flow backgrounds subtracted. We also note that the reported jet-hadron correlations [40] were measured with a much higher jet$ p_T $ and the extracted widths at low$ p_T^{\rm{assoc}} $ suffer from large flow background uncertainties.
Figure 5. (a) Away-side jetlike correlation width as a function of
$ p_T^{\rm{assoc}} $ for$ 3<p_T^{\rm{trig}}<10\;{\rm{GeV}}/{\rm{c}}$ in 50%-80% peripheral (open circles) and top 10% central (solid circles) Au+Au collisions at$ \sqrt{s_{{NN}}} = 200 $ GeV. (b) The difference between the correlation widths in central and peripheral collisions. Bars are statistical errors and caps are systematic uncertainties.If the away-side correlation broadening is owing to the nuclear
$ k_T $ effect only, without medium-induced jet broadening, then we would have$ \sigma^2_{\rm{cent}} = \sigma^2_{\rm{peri}}+\sigma^2_{k_T} $ . Here,$ k_T $ quantifies the dijet acoplanarity and should ideally not depend on the associated particle$ p_T^{\rm{assoc}} $ . With the wide$ p_T^{\rm{trig}} $ range, it is possible that a higher$ p_T^{\rm{assoc}} $ could bias towards higher$ p_T^{\rm{trig}} $ , hence smaller$ k_T $ effect. To investigate this quantitatively, we fit the data in Fig. 5(b) by a linear function, yielding$ \Delta\sigma\! =\! (0.23\!\pm\!0.09{\rm{(stat.)}}\!\pm \! 0.11{\rm{(syst.)}})+ (0.13\pm 0.04{\rm{(stat.)}}\pm0.05{\rm{(syst.)}})p_T $ ($ p_T $ in GeV/c). This suggests that the nuclear$ k_T $ effect (expected constant or decreasing with$ p_T^{\rm{assoc}} $ ) is not the only source for the observed broadening. There must be contributions from a$ p_T $ dependent effect such as medium induced jet broadening. This conclusion is corroborated by the relatively small nuclear$ k_T $ measured by both PHENIX [58, 59] and STAR [60, 61] We note that the measured broadening is between the associated and trigger particle angles, not directly the angle of the jet fragment from the jet axis. It is the combination of broadening at the trigger particle$ p_T $ and the associated particle$ p_T $ values.A more explicit means to distinguish the jet-medium broadening from the
$ k_T $ effect and other possible mechanisms is to use three-particle correlations [62, 63]. With our method of subtracting anisotropic flow backgrounds, three-particle correlations could shed new light on partonic energy loss mechanisms in relativistic heavy-ion collisions. We leave such studies to future investigations. -
We have reported a measurement of away-side jetlike azimuthal correlation shapes relative to a high-
$ p_T $ trigger particle ($ 3<p_T^{\rm{trig}}<10 \;{\rm{GeV}}/{\rm c}$ ) in Au+Au collisions at$\sqrt{s_{{NN}}} = 200$ GeV by the STAR experiment. We devised a method for a clean and robust subtraction of anisotropic flow backgrounds, using the correlation data itself. Namely, we enhance the away-side jet population in the acceptance by requiring a large recoil momentum$ P_x $ (Eq. (1)), and take the difference of jetlike correlations in regions symmetric with respect to midrapidity but with different$ \Delta\eta $ gaps away from the enhanced$ P_x $ region. The measured Gaussian width of the away-side jetlike correlation increases with increasing centrality in the associated particle$ p_T $ range of$ 0.5<p_T^{\rm{assoc}}<10\;{\rm{GeV}}/{\rm c}$ . The increase is consistent with the medium-induced jet broadening of the trigger and/or associated particles in addition to the nuclear$ k_T $ effect.We thank the RHIC Operations Group and RCF at BNL, the NERSC Center at LBNL, and the Open Science Grid consortium for providing resources and support.
Measurement of away-side broadening with self-subtraction of flow in Au+Au collisions at ${{\sqrt{s_{NN}} = 200}}$ GeV
- Received Date: 2020-03-19
- Available Online: 2020-10-01
Abstract: High transverse momentum (






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: