-
It is widely accepted that all the four kinds of basic interactions will be unified into quantum gravity at the Planck energy scale and that the universe was dominated by quantum gravity at the beginning of creation. The theory describing quantum gravity is far from completion. String theory is one of the efforts. There are many different approaches, such as loop quantum gravity, Ho
$ \check{r} $ ava-Lifshitz gravity, and non-commutative geometry. Explicit Lorentz violation (LV) is common to many of them, while some of them are non-local theories with implicit LV [1, 2].The observable universe is believed to have expanded from a very tiny part of spacetime in the era of quantum gravity domination by inflation. The scale of area with LV expanded so fast as to exceed the horizon in a very short time. Different parts of the region interacting via quantum gravity lose interaction at the instance of expanding out of the horizon, and the Lorentz violation of the small region before inflation is frozen in a large scale after inflation in this manner. The scale may re-enter the horizon during the period of normal expansion, depending on the details of quantum gravity and inflation physics [3].
There are also possible signs of large-scale LV in cosmic observations, e.g., the anisotropies in the low-l multi-pole expansion of the cosmic microwave background (CMB) power spectrum. The normals of the quadrupole and octupole do not coincide with the direction of the dipole, which indicates that the boost transformation from the CMB static frame to the peculiar motion frame is not a simple Lorentz boost [4]. The significant tension between the values of Hubble constant directly measured by the distance ladder method and the measurement by the
$ \Lambda $ CDM model from CMB observation is possibly another sign of physics beyond the standard cosmological model based upon local Lorentz invariant gravitation theory, the$ \Lambda $ CDM model [5].General relativity is a very successful gravitation theory, at least at a small scale. When general relativity is applied to a larger scale, there appear some deviations from its predictions, which are usually not recognized as deviations but as effects caused by unknown energy-momentum distributions named as dark matter and dark energy in turn. One has to take dark energy into account when dealing with cosmic-scale physics. Owing to possible frozen LV at a large scale, an effective theory of gravity at the cosmic scale must take LV into account, and it will be inevitably a non-Einstein gravitation theory because the theory of general relativity is locally Lorentz invariant. Actually, the
$ \Lambda $ CDM model is very successful at explaining most cosmological phenomena by adding a cosmological constant term into Einstein’s theory of gravity,$ \begin{split} {{S}_{\rm E}} = \frac{1}{16\pi G}\int{{{\rm d}^{4}}x}\sqrt{-g}\left( R-2\Lambda \right) \end{split} $

(1) or
$ \begin{split} {{R}_{\mu \nu }}-\frac{1}{2}R{{g}_{\mu \nu }}+\Lambda {{g}_{\mu \nu }} = 8\pi G{{\left( {{T}_{M}} \right)}_{\mu \nu }} \,, \end{split} $

(2) where
$ \Lambda $ is the cosmological constant, which can also be regarded as the vacuum energy density. However, there is an unresolved puzzle related to the cosmological constant when it is regarded as the vacuum energy density: the theoretical prediction of its value is higher than the value fitted based on observations by approximately 54 to 112 orders of magnitude. One has to take fine tuning as a solution, which lowers the confidence level of the model for hard acceptance [6]. The idea of large-scale LV was first proposed in 2015 [7]. The framework of constructing large-scale effective gravity with LV is built as a modified gravity model with the gauge principle via the equivalence principle by utilizing constraint dynamics and the very special relativity (VSR) symmetry [7-10].On the other hand, the low-energy theory of physics describing nature is believed to be an effective quantum field theory derived from a fundamental quantum gravity theory, which is far from being well understood and has many possible candidates. Although string theory can supply many possible links between the fundamental unified theory and the low-energy effective theory, it has an obvious shortage in that there are too many possible vacua, of the order of
$ 10^{500} $ , when compactifying the extra six dimensions to realize a four-dimensional effective low-energy theory. The vacuum energy of different vacua constitute a complex landscape [11]. Anti-de Sitter (AdS)-type vacua from the flux compactification of strings are generic and preserve supersymmetry. To account for the late-time accelerating expansion of the universe, one needs to lift the negative AdS vacuum energy to a meta-stable positive dS one with some unnatural techniques in string theory [12, 13]. However, the low-energy effective field theories built on these meta-stable dS vacua lack UV completion and, hence, are classified as belonging to the swampland, in contrast to the landscape, because they are not supposed to be consistent with quantum gravity or be derivable from the landscape [11, 14]. To explain the accelerating expansion with the$ \Lambda $ CDM model, one seems to need a stable or meta-stable dS vacua to supply a minimum potential energy density as the cosmological constant. Unfortunately, the discrepancy between the swampland condition and inflation excludes the dS type of potential as a favorable one, leaving the quintessence and AdS types as the only allowed potentials [15]. Can the universe with an AdS vacuum expand with acceleration? Is quintessence a fundamental canonical scalar field, or does the quintessence type of potential emerge from another fundamental mechanism? We attempt to investigate this problem from a different perspective within the framework of effective gravity with large-scale LV following pioneering papers [7-10]. -
Take the
$ SIM(2) $ symmetry, a proper subgroup of the Lorentz group, as an example in the language of the tetrad field$ {h_a}^{\mu} $ . One can build local$ SIM(2) $ gravity with the gauge principle by constraining the gauge potential, or the Lorentz connection, to take a value only on$ sim(2) $ algebra. The action for$ sim(2) $ gravity can be taken as$ \begin{split} {{S}_{sim(2)}} =& \frac{1}{16\pi G}\int{{{\rm d}^{4}}x}h\left( {{R}^{ab}}_{ab}+{{\lambda }_{1}}^{\mu }\left( {{A}^{10}}_{\mu }-{{A}^{31}}_{\mu } \right)\right.\\ &\left.+{{\lambda }_{2}}^{\mu }\left( {{A}^{20}}_{\mu }+{{A}^{23}}_{\mu } \right) \right), \end{split} $

(3) where Lagrange multipliers are used to constrain the Lorentz connection to take values on
$ sim(2) $ algebra and$ {h = \det {h^a}_\mu} $ . The Lagrange-multiplier terms contribute an effective angular momentum distribution$ {C_M}_{\rm eff} $ such that$ \begin{array}{l} {{D}_{\nu }}\left( h\left( {{h}_{a}}^{\nu }{{h}_{b}}^{\mu }-{{h}_{a}}^{\mu }{{h}_{b}}^{\nu } \right) \right) = 16\pi G{{\left( {{C}_{M}}+{{C}_{M}}_{\rm eff} \right)}_{ab}}^{\mu }, \end{array} $

(4) where
$ C_M $ is the angular-momentum distribution of the matter source. This equation leads to the torsion-free condition in general relativity in the case of$ C_M = 0 $ , where$ {C_M}_{\rm eff} = 0 $ always holds for the local Lorentz invariance. On the contrary, LV leads to a non-trivial distribution of the torsion tensor even in the case of a scalar matter source, where$ C_M = 0 $ . The variation respect to tetrad fields,$ \dfrac{\delta S_{sim(2)}}{\delta {{h}^{a}}_{u}} $ , yields the equations of motion for tetrad fields,$ \begin{split} {{R}^{a}}_{b}-\frac{1}{2}R{{\delta }^{a}}_{b} = \frac{8\pi G}{{{c}^{4}}}{{\left( {{T}_{M}} \right)}^{a}}_{b} \;, \end{split} $

(5) where
$ {\left(T_M\right)^a}_b $ is the energy-momentum tensor of the matter source. It should be noted that the connection hides in$ {{R}^{a}}_{b} $ , and$ R $ is no longer the torsion-free Levi-Civita connection because of the reason discussed for Eq. (4). Generally, the connection can be decomposed into a torsion-less part and contortion part as$ \begin{array}{l} {{A}^{a}}_{bc} = {{\tilde{A}}^{a}}_{\; \;bc}+{{K}^{a}}_{bc}\,, \end{array} $

(6) where
$ \widetilde{A}_{\; \;bc}^{a} $ is the Levi-Civita connection and$ {{K}^{a}}_{bc} $ is the contortion part [16]. The curvature can be decomposed into three parts with the help of the decomposition of spin connection as$ \begin{array}{l} {{R}^{mn}}_{ab} = {{\tilde{R}^{mn}}}_{\;\;\;\;\;\;ab}+{R_{K}}{{^{mn}}_{ab}}+{{R}_{CK}}{{^{mn}}_{ab}} \;, \end{array} $

(7) where
${\tilde{R}{^{mn}}_{\;ab}}$ and$ {{R}_{K}}{{^{mn}}_{ab}} $ are the curvatures composed of the torsion-free connection and contortion, respectively, while$ {{R}_{CK}}{{^{mn}}_{ab}} $ contains their cross terms. In the geometric unit$ \dfrac{8\pi G}{{{c}^{4}}} = 1 $ , we can rewrite Eq. (13) as$ \begin{split} {{\tilde{R}}^{a}}_{\;\;b}-\frac{1}{2}{{\delta }^{a}}_{b}\tilde{R} = {{\left( T_{\rm eff}+{{T}_{M}} \right)}^{a}}_{b} \;, \end{split} $

(8) where
$ {\tilde{R}}_{c}^{\; \;a} $ and$ \tilde{R} $ are generated by the torsion-free Levi-Civita connection$ {{\tilde{A}}^{a}}_{\; \;bc} $ and$ {T}_{\rm eff} $ collects all the terms involving the contortion$ {{K}^{a}}_{bc} $ :$ \begin{array}{l} {{\left( T_{\rm eff} \right)}^{a}}_{b} = \dfrac{1}{2}{{\delta }^{a}}_{b}\left( {{R}_{K}}+{{R}_{CK}} \right)-\left( {{R}_{K}}{{^{a}}_{b}}+{{R}_{CK}}{{^{a}}_{b}} \right) \; . \end{array} $

(9) The effective energy-momentum tensor
$ T_{\rm eff} $ contributes to the gravitation in addition to the matter contribution$ T_{M} $ and appears as the dark partner of the matter distribution. The non-trivial effective contribution of the contortion to the energy-momentum distribution is expected to be responsible for the dark partner of the matter, The Bianchi identitity guarantees the conservation of$ {T}_{\rm eff} $ with respect to the Levi-Civita connection$ {{\tilde{A}}^{a}}_{\; \;bc} $ .Based upon our analysis of possible frozen large-scale LV, the cosmological observables are actually not Lorentz covariant but still
$ SO(3) $ covariant. Simply restricting the components of the Lorentz gauge field$ {A^a}_{b\mu} $ to be nontrivial only on$ SO(3) $ generators in the construction of a gravitation theory with Lorentz boost violation would result in degenerated dynamics. The reason is that boost transformation is not prohibited at a large scale, because only the Lorentz boost transformation is violated. There have been discussions on the modification of Lorentz algebra at the quantum level by using Hopf algebra or deformed Poincare algebra such as$ \kappa $ -Poincare as well as other quantum gravity models such as Horava-Lifshitz gravity, in which the Lorentz boost is automatically violated.Observing that the Lorentz gauge potentials transform as
$ \begin{array}{l} {{A'}^{a}}_{b\mu } = {{\Lambda }^{a}}_{c}\left( x \right){{A}^{c}}_{d\mu }{{\Lambda }_{b}}^{d}\left( x \right)+{{\Lambda }^{a}}_{c}\left( x \right){{\partial }_{\mu }}{{\Lambda }_{b}}^{c}\left( x \right) \end{array} $

(10) under a local Lorentz transformation
$ \Lambda(x) $ , it is obvious that$ {A'^0}_{i\mu} = {{\Lambda }_{i}}^{j}\left( x \right){{A}^{0}}_{j\mu } $ for a rotation transformation$ {\Lambda\in SO(3)} $ . Hence, the restriction to the Lorentz gauge potentials can be proposed as$ \begin{array}{l} \left({A^{0}}_{1\mu}\right)^2+\left({A^{0}}_{2\mu}\right)^2+\left({A^{0}}_{3\mu}\right)^2 = \left(f_\mu (x)\right)^2, \end{array} $

(11) where
$ f_\mu(x) $ can be regarded as a measurement of the magnitude of the boost violation in some sense, and it is invariant under a local$ SO(3) $ gauge transformation on tetrad fields$ {h_a}^{\mu} $ with respect to the tetrad indices but frame dependent.The action of effective gravity with large-scale LV can then be given by
$ \begin{split} S =& \frac{{{c}^{4}}}{16\pi G}\int{{{\rm d}^{4}}x}h\left( R-2{{\Lambda }_{0}}+{{\lambda }^{u}}\left( {{\left( {{A}^{0}}_{1u} \right)}^{2}}+{{\left( {{A}^{0}}_{2u} \right)}^{2}}\right.\right.\\&\left.\left.+{{\left( {{A}^{0}}_{3u} \right)}^{2}}-f_{u}^{2} \right) \right), \end{split} $

(12) where the repeated superscript and subscript
$ \mu $ of$ \lambda^\mu $ and$ {A^0}_{i\mu} $ , respectively, indicate summation and$ {\Lambda }_{0} $ is the bare cosmological constant given by the vacuum energy density.The variation with respect to tetrad fields,
$ \dfrac{\delta S}{\delta {{h}^{a}}_{u}} $ , gives the equations of motion for tetrad fields,$ \begin{aligned} {{G}^{a}}_{b}\equiv {{R}^{a}}_{b}-\frac{1}{2}R{{\delta }^{a}}_{b}+{{\Lambda }_{0}}{{\delta }^{a}}_{b} = \frac{8\pi G}{{{c}^{4}}}{{\left( {{T}_{M}} \right)}^{a}}_{b} \;, \end{aligned} $

(13) where
$ {\left(T_M\right)^a}_b $ is the energy-momentum tensor of all the matter sources, including both luminous and dark sources. As discussed in Eq. (5),$ {{R}^{a}}_{b} $ and$ R $ are composed of connection with torsion. We can rewrite Eq. (13) in the form of Eq. (8) with a curvature composed only of a torsion-less Levi-Civita connection, and the contortion part contributes effectively as the dark partner of the matter distribution with$ \begin{array}{l} {{\left( T_{\rm eff} \right)}_{c}}^{a} = \left( \dfrac{1}{2}{{\delta }_{c}}^{a}\left( {{R}_{K}}+{{R}_{CK}} \right)-\left( {{R}_{K}}{{_{c}}^{a}}+{{R}_{CK}}{{_{c}}^{a}} \right) \right)-{{\Lambda }_{0}}{{\delta }_{c}}^{a} \; . \end{array} $

(14) At the cosmic scale, the effective energy-momentum tensor
$ T_{\rm eff} $ is expected to contribute to the dark energy effectively and be responsible for the accelerating expansion. In a given basis of the tetrad$ {h_{a}}^{\mu} $ , the equations of motion for connection can be written down explicitly as$ \begin{aligned} {{\cal{D}}_{\nu }}\left( h{{h}_{0}}^{[\nu }{{h}_{i}}^{\mu ]} \right)+\frac{1}{2}\lambda^\mu h{{A}^{0}}_{i\mu }\text{ = 0}, \end{aligned} $

(15) where
$ i = 1,2,3 $ . The repeated superscript and subscript$ \mu $ do not mean summation here, because they are a result of variation of the square of$ {A^0}_{i\mu} $ in Eq. (12) and$ \begin{array}{l} {{\cal{D}}_{\nu }}\left( h{{h}_{i}}^{[\nu }{{h}_{j}}^{\mu ]} \right) = 0 \end{array} $

(16) for the combination of indices
$ i,j $ . With the decomposion of$ {{A^a}_{b\mu}} $ into the Levi-Civita connection$ {\widetilde A^a}_{\;\;b\mu} $ and contortion$ {K^a}_{b\mu} $ in Eq. (6), Eq. (16) can be expressed in detail as$ \begin{array}{*{20}{l}} {K^0}_{12} = {K^0}_{21},&{K^1}_{23} = 0,&{K^2}_{12} = -{K^0}_{10},\\{K^3}_{13} = -{K^0}_{10},& {K^0}_{23} = {K^0}_{32},&{K^2}_{31} = 0,\\{K^3}_{23} = -{K^0}_{20},&{K^1}_{21} = -{K^0}_{20},& {K^0}_{31} = {K^0}_{13},\\{K^3}_{12} = 0,&{K^1}_{31} = -{K^0}_{30},&{K^2}_{32} = -{K^0}_{30}. \end{array} $

(17) Further, Eq. (15) can be expressed in detail as
$ \begin{split} &2{K^0}_{10}{h_0}^\mu+\left({K^0}_{22}+{K^0}_{33}\right){h_1}^\mu-\left({K^1}_{20}+{K^0}_{21}\right){h_2}^\mu +\left({K^3}_{10}-{K^0}_{31}\right){h_3}^\mu+\lambda^\mu\left({A^0}_{10}{h^0}_\mu +{A^0}_{11}{h^1}_\mu+{A^0}_{12}{h^2}_\mu+{A^0}_{13}{h^3}_\mu\right) = 0, \\ &2{K^0}_{20}{h_0}^\mu+\left({K^1}_{20}-{K^0}_{12}\right){h_1}^\mu+\left({K^0}_{11}+{K^0}_{33}\right){h_2}^\mu-\left({K^2}_{30}+{K^0}_{32}\right){h_3}^\mu +\lambda^\mu\left({A^0}_{20}{h^0}_\mu +{A^0}_{21}{h^1}_\mu+{A^0}_{22}{h^2}_\mu+{A^0}_{23}{h^3}_\mu\right) = 0,\\ &2{K^0}_{30}{h_0}^\mu-\left({K^3}_{10}+{K^0}_{13}\right){h_1}^\mu+\left({K^2}_{30}-{K^0}_{23}\right){h_2}^\mu+\left({K^0}_{11}+{K^0}_{22}\right){h_3}^\mu+\lambda^\mu\left({A^0}_{30}{h^0}_\mu+{A^0}_{31}{h^1}_\mu+{A^0}_{32}{h^2}_\mu+{A^0}_{33}{h^3}_\mu\right) = 0. \end{split} $

(18) In fact, the tetrad fields
$ {h_a}^{\mu} $ satisfy Eqs. (17), (18), and (13) as well as the constraint given by Eq. (11) simultaneously, together with the contortion$ {K^a}_{bc} $ and the multiplier$ \lambda $ . To solve the simultaneous equations, one can employ the cosmological principle, which holds in the CMB static reference frame. According to the symmetry requirement of the cosmological principle, the metric for the universe must have the form of the Robertron-Walker spacetime metric,$ \begin{array}{l} {{\rm{d}}s^2 = {\rm{d}}t^2-a(t)^2\left(\dfrac{{\rm{d}}r^2}{1-kr^2}+r^2{\rm{d}}\theta^2+r^2\sin^2\theta\,{\rm{d}}\varphi^2\right)}\, . \end{array} $

(19) The instantaneous co-moving tetrad basis can be read out directly as follows:
$ \begin{split} h^0 =& {\rm{d}}t,\\ h^1 =& \frac{a(t)}{\sqrt{1-kr^2}}\,{\rm{d}}r,\\h^2 =& a(t)r\,{\rm{d}}\theta,\;\\ h^3 =& a(t)r\sin\theta\,{\rm{d}}\varphi\; . \end{split} $

(20) The cosmic media should be a perfect fluid by the analysis of the cosmological principle. The energy momentum
$ T_M $ has the character of a perfect fluid and can be described by the energy density$ \rho $ and pressure$ p $ , i.e., with the diagonal form$ {{\left( {{T}_{M}} \right)}^{a}}_{\text{b}} = {\rm diag}\left( \rho ,-p,-p,-p \right) $ . The perfect-fluid energy-momentum tensor$ T_M $ in Eq. (13) requires$ {{G^a}_{b} = 0,\;\forall a\not = b} $ . One can draw the conclusion that the only possible non-zero independent components of the contortion$ {{K}^{a}}_{bc} $ are$ {{K^0}_{11},{K^0}_{22},{K^0}_{33}} $ , while the others can all be determined to be zero.The cosmological principle also requires that all cosmic physical quantities depend only on the cosmic time
$ t $ , and hence,$ \begin{array}{l} {K^0}_{11} = {K^0}_{22} = {K^0}_{33} = {\mathscr {K}}(t) \end{array} $

(21) are the solutions required. The dependence between
$ {\mathscr {K}}(t) $ and$ f_\mu(x) $ can be derived as$ \begin{split} \left(f_t,f_r,f_\theta,f_\varphi\right) =& \left(a(t){\mathscr {K}}(t)+\dot a(t)\right)\\&\times\left(0, \dfrac{1}{\sqrt{1-kr^2}}, r, r\sin\theta\right). \end{split} $

(22) It is a reasonable result that the only remaining one among the four degrees of freedom for
$ f_\mu(x) $ is expressed by$ {\mathscr {K}}(t) $ , while the other three are used to fix the reference frame$ {h_a}^{\mu} $ . -
Let us denote the contribution to the energy-momentum tensor
$ {{\left( T_{\rm eff} \right)}_{c}}^{a} $ of Eq. (14) in the co-moving frame of the Robertson-Walker universe from the dark partner of a perfect-fluid energy-momentum tensor${{\left( {{T}_{M}} \right)}^{a}}_{\text{b}} = {\rm diag}\left( \rho , -p,-p,-p \right)$ as$ \begin{array}{l} {{T}_{K }}{{^{a}}_{c}}\equiv \left( T_{\rm eff} \right){{^{a}}_{c}} = {\rm diag}({{\rho }_{K}},-{{p}_{K }},-{{p}_{K }},-{{p}_{K }}). \end{array} $

(23) We can obtain
$ \begin{array}{l} {{\rho }_{K }} = -\left( 3{{{\mathscr {K}}}^{2}}+6{\mathscr {K}}\dfrac{{\dot{a}}}{a}-{{\Lambda }_{0}} \right) \end{array} $

(24) and
$ \begin{array}{l} {{p}_{K}} = {{{\mathscr {K}}}^{2}}+4{\mathscr {K}}\dfrac{{\dot{a}}}{a}+2\dot{{\mathscr {K}}}-{{\Lambda }_{0}} \; . \end{array} $

(25) Since astronomical observations reveal that the space of the universe is flat, i.e.,
$ k = 0 $ in the Robertson-Walker metric ansatz (19), we obtain the Friedmann equation modified by large-scale LV:$ \begin{array}{l} {{\left( \dfrac{{\dot{a}}}{a} \right)}^{2}} = \dfrac{\rho +{{\rho }_{K}}}{3} = \dfrac{\rho +{{\Lambda }_{0}}}{3}-{{{\mathscr {K}}}^{2}}-2{\mathscr {K}}\frac{{\dot{a}}}{a} \end{array} $

(26) and
$ \begin{array}{l} \ddot{a} = -\dfrac{a}{2}\left( p+{{p}_{K }}+\dfrac{\rho +{{\rho }_{K }}}{3} \right) = -\dfrac{a}{2}\left( p+\frac{\rho }{3} \right)+\dfrac{1}{3}a{{\Lambda }_{0}}-\dfrac{\rm d}{{\rm d}t}\left( a{\mathscr {K}} \right). \end{array} $

(27) From the modified Friedmann equation given by Eq. (27), the condition for the accelerating expansion of the universe can be easily obtained as
$ {\dfrac{a}{2}\left(p+\dfrac{\rho}{3}-\dfrac{2}{3}\Lambda_0 \right)+ \dfrac{{\rm{d}}}{{\rm{d}}t}\left(a{\mathscr {K}}\right)<0} $ . As discussed in [3], the prediction of LV parameters$ f_\mu(x) $ needs quantum gravity and the inflation model in some detail, rather than the present model. However, it would be suggestive to seek some phenomenological approximations of$ {\mathscr {K}}(t) $ instead of constructing the quantum gravity theory and inflation model in detail at first step. It is inspiring to compare the Friedmann equations of$ \Lambda $ CDM model,$ \begin{array}{l} {{\left( \dfrac{{\dot{a}}}{a} \right)}^{2}} = \dfrac{\rho +{{\rho }_{\Lambda}}}{3} = \dfrac{\rho +{{\Lambda }}}{3} \end{array} $

(28) and
$ \begin{array}{l} \ddot{a} = -\dfrac{a}{2}\left( p+{{p}_{\Lambda }}+\dfrac{\rho +{{\rho }_{\Lambda }}}{3} \right) = -\dfrac{a}{2}\left( p+\frac{\rho }{3} \right)+\dfrac{1}{3}a{{\Lambda }}\;, \end{array} $

(29) with the modified one given by Eqs. (26) and (27), where
$ {{\rho }_{\Lambda }} = \Lambda $ ,$ {{p}_{\Lambda}} = -\Lambda $ ,$ \dfrac{\Lambda}{3{H_0}^2}\approx 0.713775 $ , and$ H_0 $ is the present Hubble constant. It should be noted that$ \Lambda $ in Eqs. (28) and (29) is an observation input or a theoretical input by a more fundamental theory. Once the equation of state (EoS),$ p = w\rho $ , of the cosmic media is given, one can make a prediction on the evolution of the cosmic observables$ a $ ,$ p $ , and$ \rho $ etc. In the modified case of Eqs. (26) and (27), we need one more input,$ {\mathscr {K}} $ , which should be given by a more fundamental theory, quantum gravity, or as an observational input phenomenologically, just like$ \Lambda $ in Eqs. (28) and (29) of the$ \Lambda $ CDM model. Since the$ \Lambda $ CDM model works well phenomenologically, we can employ it to fix the evolution of$ {\mathscr {K}} $ phenomenologically and approximately.Eq. (26) can be rewritten as
$ \begin{array}{l} H ^2 (t) = \dfrac{\rho +{{\Lambda }_{0}}}{3}-{{{\mathscr {K}}}^{2}}-2{\mathscr {K}} H(t), \end{array} $

(30) where the evolution equation for the Hubble constant
$ H(t) = \dfrac{\dot a(t)}{a(t)} $ . Thus, Eq. (28) can be written as$ \begin{array}{l} H ^2 (t) = \dfrac{\rho +{{\Lambda }}}{3}, \end{array} $

(31) with the solution
$ \begin{array}{l} H(t) = \sqrt{\dfrac{\rho +{{\Lambda }}}{3}}\; . \end{array} $

(32) The solutions of Eq. (30) can then be chosen:
$ \begin{array}{l} H(t) = \sqrt{\dfrac{\rho +{{\Lambda }}}{3}}-{\mathscr {K}}(t)\; . \end{array} $

(33) The initial value of
$ {\mathscr {K}}(t) $ can be obtained by comparing Eqs. (26) and (28):$ \begin{array}{l} 2{\mathscr {K}}(t_0)\frac{\dot a(t_0)}{a(t_0)}+{\mathscr {K}}(t_0)^2 = \frac{{{\Lambda }_{0}}}{3}-\frac{{{\Lambda }}}{3}, \end{array} $

(34) where
$ t_0\simeq H_0^{-1} $ is the present moment or the current age of universe and$ H_0 $ is the Hubble constant. Phenomenologically, there are two choices for the initial value of$ {\mathscr {K}}(t) $ :$ \begin{array}{l} {\mathscr {K}}_1 = {{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) \end{array} $

(35) and
$ \begin{array}{l} {\mathscr {K}}_2 = -{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right)\; . \end{array} $

(36) In this scenario, a constraint condition for
$ \Lambda_0 $ ,$ \begin{array}{l} {\Lambda }_{0}\geqslant -0.401\Lambda \approx -\dfrac{2}{5}\Lambda, \end{array} $

(37) must be satisfied to obtain a reasonable evolution of
$ {\mathscr {K}}(t) $ .We can make three kinds of approximations listed as Case A, B, and C to fix the evolution of
$ {\mathscr {K}} $ on the basis of the second Friedmann equation of the$ \Lambda $ CDM model (29).By comparing Eqs. (27) and (29), we can make the first approximation named Case A:
$ \begin{array}{l} \dfrac{\rm d}{{\rm d}t}\left( a{\mathscr {K}} \right) = -\dfrac{1}{3}a\left( \Lambda -{{\Lambda }_{0}} \right). \end{array} $

(38) Suppose the EoS of cosmic media is
$ {p(t) = w(t)\rho(t)} $ . Then, Eqs. (26) and (27) can be converted to the dependence of the evolution$ a(t) $ on$ {\mathscr {K}} $ and$ \Lambda_0 $ $ \begin{split} \frac{\ddot a}{a}+\frac{3w+1}{2}\frac{\dot a^2+k}{a^2} =& -\dot{{\mathscr {K}}}-\frac{3w+1}{2}{\mathscr {K}}^2-(3w+2)\frac{\dot a}{a}{\mathscr {K}}\\&+\frac{w+1}{2}{\Lambda }_{0} \end{split} $

(39) by eliminating
$ p $ and$ \rho $ . By following the same procedure for Eqs. (28) and (29), we obtain the dependence of the evolution$ a(t) $ on$ \Lambda $ as$ \begin{split} \frac{\ddot a}{a}+\frac{3w+1}{2}\frac{\dot a^2+k}{a^2} = \frac{w+1}{2}\Lambda. \end{split} $

(40) We can make the second approximation named Case B by requiring
$ \begin{split} \dot{{\mathscr {K}}}+\frac{3w+1}{2}{\mathscr {K}}^2+(3w+2)\frac{\dot a}{a}{\mathscr {K}} = \frac{w+1}{2}(\Lambda_0-\Lambda)\;, \end{split} $

(41) which relates contortion to
$ w(t) $ .Suppose the dark partner satisfies equation of state
$ {{p}_{K}} = {{w}_{0}}{{\rho }_{K}} $ . Then, we make the third approximation named Case C:$ \begin{array}{l} \left( 3{{w}_{0}}+1 \right){{{\mathscr {K}}}^{2}}+\left( 6{{w}_{0}}+4 \right)\frac{{\dot{a}}}{a}{\mathscr {K}}+2\dot{{\mathscr {K}}} = \left( {{w}_{0}}+1 \right){{\Lambda }_{0}}\;, \end{array} $

(42) from Eqs. (24) and (25).
The evolution of
$ H(t) $ and$ {\mathscr {K}}(t) $ can be determined using Eq. (39), together with one of the approximations Eq. (38), Eq. (41), and Eq. (42) as well as the initial conditions$ H(t_0) = H_0 $ and$ {\mathscr {K}}(t_0) = {\mathscr {K}}_1 $ of Eq. (35) or$ {\mathscr {K}}(t_0) = {\mathscr {K}}_2 $ of Eq. (36).Table 1 summarizes the models of approximation discussed above.
Values of $ {\mathscr {K}}(t_0) $ 

Evolution equation of $ {\mathscr {K}}(t) $ 

Case A1 $ {\mathscr {K}}(t_0)={\mathscr {K}}_1 $ 

$\dfrac{\rm d}{{\rm d}t}\left( a{\mathscr {K} } \right)=-\dfrac{1}{3}a\left( \Lambda -{ {\Lambda }_{0} } \right)$ 

Case A2 $ {\mathscr {K}}(t_0)={\mathscr {K}}_2 $ 

Case B1 $ {\mathscr {K}}(t_0)={\mathscr {K}}_1 $ 

$ \dot{{\mathscr {K}}}+\dfrac{3w+1}{2}{\mathscr {K}}^2+(3w+2)\dfrac{\dot a}{a}{\mathscr {K}}=\dfrac{w+1}{2}(\Lambda_0-\Lambda) $ 

Case B2 $ {\mathscr {K}}(t_0)={\mathscr {K}}_2 $ 

Case C1 $ {\mathscr {K}}(t_0)={\mathscr {K}}_1 $ 

$ \left( 3{{w}_{0}}+1 \right){{{\mathscr {K}}}^{2}}+\left( 6{{w}_{0}}+4 \right)\dfrac{{\dot{a}}}{a}{\mathscr {K}}+2\dot{{\mathscr {K}}}=\left( {{w}_{0}}+1 \right){{\Lambda }_{0}} $ 

Case C2 $ {\mathscr {K}}(t_0)={\mathscr {K}}_2 $ 

Table 1. Models of approximation in large-scale Lorentz violation cosmology.
The evolution of
$ H(t) $ and$ {\mathscr {K}}(t) $ versus$ t $ and$ {{\Lambda }_{0}} $ in all the cases of approximations are presented in Fig. 1 and Fig. 2, where we set$ {w(t)\simeq 0} $ in the EoS of the cosmic media because cold matter dominates the energy density in the period of late-time expansion of the universe and$ w_0 = -0.89 $ and$ w_0 = -1 $ in Case C are selected as examples.
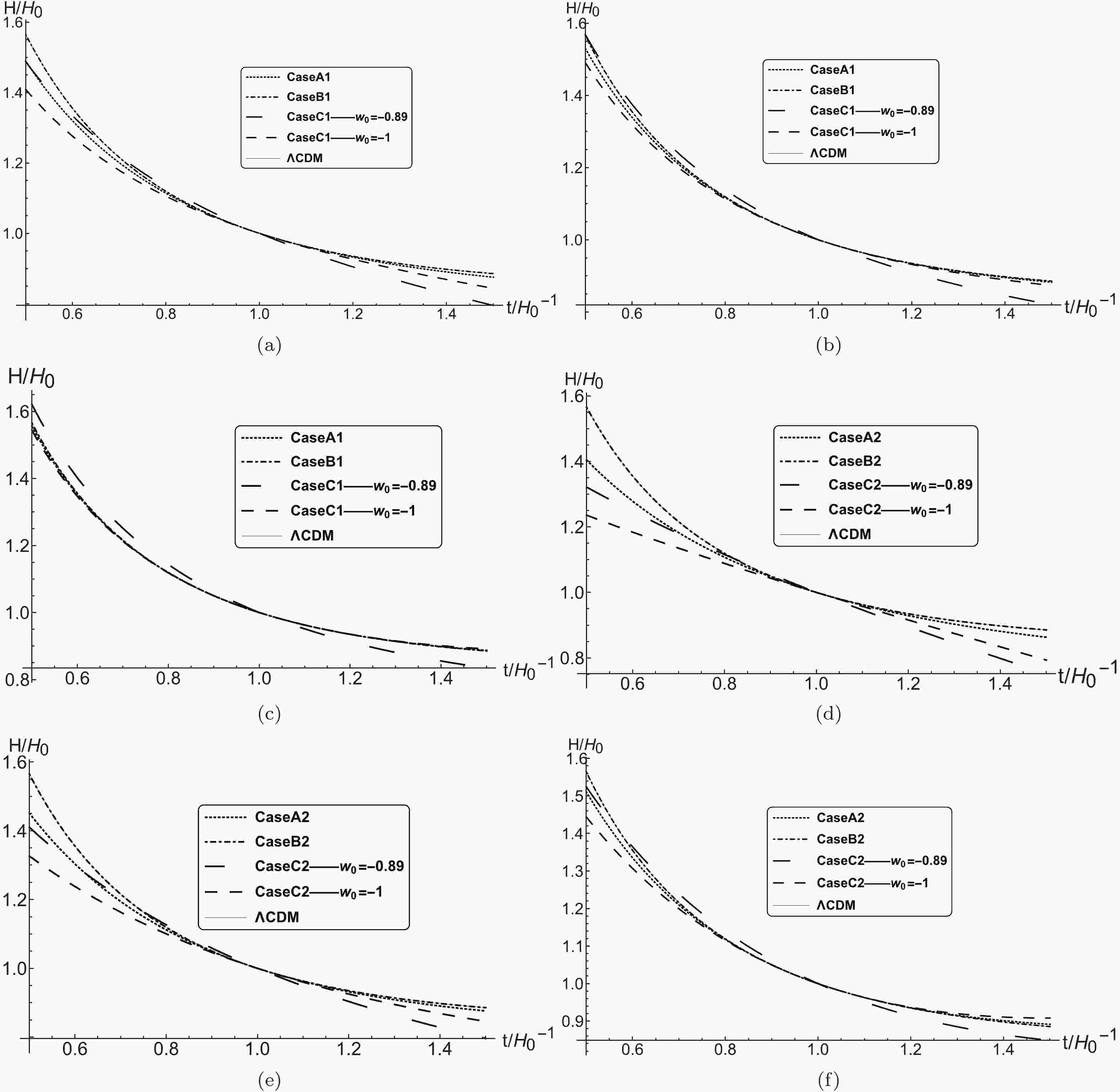
Figure 1. Evolution of the Hubble constant
$ H $ versus$ t $ in the case of the initial value$ {\mathscr {K}}\left( {{t}_{0}} \right) = {{H}_{0}}\left( \pm \sqrt{1-\frac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ and among three cases of approximation and the$ \Lambda {\rm CDM} $ model: (a) and (d)$ \Lambda_0 = -0.2\Lambda $ , (b) and (e)$ \Lambda_0 = 0 $ , and (c) and (f)$ \Lambda_0 = 0.2\Lambda. $ 
Figure 2. Evolution of
$ {\mathscr {K}} $ versus$ t $ in the case of the initial value$ {\mathscr {K}}\left( {{t}_{0}} \right) = {{H}_{0}}\left( \pm \sqrt{1-\frac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ among three case of approximation: (a) and (d)$ \Lambda_0 = -0.2\Lambda $ , (b) and (e)$ \Lambda_0 = 0 $ , and (c) and (f)$ \Lambda_0 = 0.2\Lambda. $ It is apparent that the evolutions of the Hubble constant with
$ t $ in these models are very close and those of Case B and the$ \Lambda {\rm CDM} $ model tend to almost coincide with each other in the long-time evolution. There is clear but small difference between the long-time evolution curves of Case A and the$ \Lambda {\rm CDM} $ model for$ \Lambda_0 < 0 $ , while that between the long-time evolution curves of Case C at$ w_0 = -1 $ and the$ \Lambda {\rm CDM} $ model is slightly larger in the case where the initial value$ {\mathscr {K}}\left( {{t}_{0}} \right) = {{H}_{0}} \left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ . The differences among the evolution curves for$ H(t) $ decrease with the increase of$ \Lambda_0 $ such that those for Case A, Case B, Case C, and the$ \Lambda {\rm CDM} $ model become almost the same. In the long-time evolution of the Hubble constant, the difference between Case A and the$ \Lambda {\rm CDM} $ model decreases as$ \Lambda_0 $ increases, while that between Case C at$ w_0 = -\dfrac{2}{3} $ and the$ \Lambda {\rm CDM} $ model progressively increases. In Case C, the result at$ w_0 = -\dfrac{1}{3} $ is similar that at$ w_0 = -\dfrac{2}{3} $ , and the only difference is that the deviation from the$ \Lambda CDM $ model is larger in the former.In the case where the initial value
$ {\mathscr {K}}\left( {{t}_{0}} \right) = -{{H}_{0}}\left( \sqrt{1-\frac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ , the difference in time evolutions between Case A and the$ \Lambda {\rm CDM} $ model is always smaller than that between Case C and the$ \Lambda {\rm CDM} $ model, irrespective of$ \Lambda_0 $ . The evolution curves of these several models coincide almost identically where the$ \Lambda_0 $ value is approximately zero. The deviations of both Case A and Case C from the$ \Lambda {\rm CDM} $ model increase with the increase of$ \Lambda_0 $ , but the deviation of Case C shows a greater increase than that of Case A.The evolution of
$ {\mathscr {K}}(t) $ with$ t $ for different values of$ {{\Lambda }_{0}} $ is presented in Fig. 2, where the results for Case A and Case B are very close to each other but that for Case C deviates slightly from those of Case A and Case B. Especially in the case where the initial value$ {\mathscr {K}}\left( {{t}_{0}} \right) = {{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ , the results for Case A and Case B are almost the same, while that for Case C differs. We can find that Case C is not a good approximation, probably because$ w_0 $ needs to evolve as well.In the case of non-zero contortion, the world line of a photon is still a light-like geodesic curve as in the Riemann spacetime case, rather than an auto-parallel curve. The redshift formula is the same as in the Lorentz-invariant zero contortion case,
$ 1+z = \frac{{{a}_{0}}}{a} $

(43) and
$ \frac{{\rm d}z}{{\rm d}a} = -\frac{{{a}_{0}}}{{{a}^{2}}},\; $

(44) where
$ a_0 = a(t_0) $ . We can convert$ H $ and$ {\mathscr {K}} $ versus$ t $ to those versus$ z $ ,$ \dot{H}\left( t \right) = H'\left( z \right)\left( -\frac{{{a}_{0}}}{{{a}^{2}}} \right)aH = -\left( 1+z \right)H\left( z \right)H'\left( z \right) $

(45) and
$ \begin{split} \dot{{\mathscr {K}}}\left( t \right) = \frac{{\rm d}{\mathscr {K}}}{{\rm d}a}\frac{{\rm d}a}{{\rm d}t} = {\mathscr {K}}'\left( a \right)aH = -\left( 1+z \right)H\left( z \right){\mathscr {K}}'\left( z \right), \end{split} $

(46) with the relations
$ \begin{split} \dot{H}\left( t \right) = \frac{{\rm d}H}{{\rm d}t} = \frac{{\rm d}H}{{\rm d}a}\frac{{\rm d}a}{{\rm d}t} = H'\left( a \right)aH \end{split} $

(47) and
$ \begin{split} H'\left( a \right) = \frac{{\rm d}H}{{\rm d}a} = \frac{{\rm d}H}{{\rm d}z}\frac{{\rm d}z}{{\rm d}a} = H'\left( z \right)\frac{{\rm d}z}{{\rm d}a}. \end{split} $

(48) By the definition of the luminosity distance
$ d_L $ (see [17]), we can obtain$ \begin{split} d_L(z) = \left(1+z\right)\int^z_0\frac{1}{H(z')}\,{\rm{\rm d}}z'\quad \end{split} $

(49) in the case of
$ k = 0 $ and$ \begin{split} \frac{{\rm{d}}t}{{\rm{d}}z} = -\frac{1}{1+z}\,\frac{{\rm{d}}}{{\rm{d}}z}\left(\frac{d_L}{1+z}\right). \end{split} $

(50) With Eqs. (49) and (50), we can convert the Friedmann equation given by Eq. (39) to the equation for
$ d_L(z) $ and$ {\mathscr {K}}(z) $ versus the redshift$ z $ ,$ \begin{split} \frac{{{\left( 1+z \right)}^{6}}{{d}_{L}}^{\prime \prime }\left( z \right)}{{{\left( \left( 1+z \right){{d}_{L}}^{\prime }\left( z \right)-{{d}_{L}}\left( z \right) \right)}^{3}}}-&\frac{1}{2}\frac{{{\left( 1+z \right)}^{4}}}{{{\left( \left( 1+z \right){{d}_{L}}^{\prime }\left( z \right)-{{d}_{L}}\left( z \right) \right)}^{2}}}-\frac{{{\left( 1+z \right)}^{3}}{{\mathscr {K}}}'\left( z \right)}{\left( 1+z \right){{d}_{L}}^{\prime }\left( z \right)-{{d}_{L}}\left( z \right)} +\frac{\text{2}{{\left( 1+z \right)}^{2}}}{\left( 1+z \right){{d}_{L}}'\left( z \right)-{{d}_{L}}\left( z \right)}{\mathscr {K}}\left( z \right)\\+&\frac{1}{2}{{{\mathscr {K}}}^{\text{2}}}\left( z \right) = {{\Lambda }_{0}}. \end{split} $

(51) Thus, we can perform the three approximations given by Eqs. (38), (41), and (42) to obtain
$ \begin{split} \frac{{{\left( 1+z \right)}^{2}}}{\left( 1+z \right){{d}_{L}}'\left( z \right)-{{d}_{L}}\left( z \right)}{\mathscr {K}}\left( z \right)-\frac{{{\left( 1+z \right)}^{3}}}{\left( 1+z \right){{d}_{L}}^{\prime }\left( z \right)-{{d}_{L}}\left( z \right)}{{\mathscr {K}}}'\left( z \right) = \frac{1}{3}\left( {{\Lambda }_{0}}-\Lambda \right)\;, \end{split} $

(52) $ \begin{split} \frac{4{{\left( 1+z \right)}^{2}}{\mathscr {K}}\left( z \right)-2{{\left( 1+z \right)}^{3}}{K}'\left( z \right)}{\left( 1+z \right){{d}_{L}}'\left( z \right)-{{d}_{L}}\left( z \right)}+{{{\mathscr {K}}}^{2}}\left( z \right) = {{\Lambda }_{0}}-\Lambda \end{split} $

(53) and
$ \begin{split} \frac{2{{\left( 1+z \right)}^{2}}\left( \left( 3{{w}_{0}}+2 \right){\mathscr {K}}\left( z \right)-(1+z){{\mathscr {K}}}'\left( z \right) \right)}{\left( 1+z \right){{d}_{L}}'\left( z \right)-{{d}_{L}}\left( z \right)}+\left( 3{{w}_{0}}+1 \right){\mathscr {K}}{{\left( z \right)}^{2}} = \left( {{w}_{0}}+1 \right){{\Lambda }_{0}}. \end{split} $

(54) A comparisons of the curve of the luminosity distance
$ d_L $ versus the redshift$ z $ among the three models of approximation and the$ \Lambda $ CDM model is presented in Fig. 3.
Figure 3. Comparison of luminosity distance in the case where the initial value
$ {\mathscr {K}}\left( {{t}_{0}} \right) = {{H}_{0}}\left( \pm \sqrt{1-\frac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ among the three cases of approximation and the$ \Lambda {\rm CDM} $ model: (a) and (d)$ \Lambda_0 = -0.2\Lambda $ , (b) and (e)$ \Lambda_0 = 0 $ , and (c) and (f)$ \Lambda_0 = 0.2\Lambda. $ It is observed that, irrespective of the values of
$ {{w}_{0}} $ and$ {{\Lambda }_{0}} $ , the curves of the luminosity distance$ d_L $ versus the redshift$ z $ for Case B and the$ \Lambda {\rm CDM} $ model appear to nearly coincide. The difference between Case A and the$ \Lambda {\rm CDM} $ model and that between Case C at$ w_0 = -1 $ and the$ \Lambda {\rm CDM} $ model decrease with the increase of$ {{\Lambda }_{0}} $ in the case where the initial value$ {\mathscr {K}}\left( {{t}_{0}} \right) = {{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ , but the latter is slightly larger than the former. The difference between Case C and the$ \Lambda {\rm CDM} $ model increases with the increase of$ w_0 $ and reaches a rather large deviation when$ w_0 = -\dfrac{1}{3} $ .The behavior of curves of the luminosity distance
$ d_L $ versus the redshift$ z $ in the case where the initial value$ {\mathscr {K}}\left( {{t}_{0}} \right) = -{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ is similar to that in the case where the initial value$ {\mathscr {K}}\left( {{t}_{0}} \right) = {{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ .The distance modulus is defined as
$ {\mu = 25+5\log_{10}\left(d_L/Mpc\right)} $ [18]. -
By comparing Eqs. (24) and (26), one can introduce the idea of an effective cosmological constant that is responsible for the accelerating expansion of the universe, rather than the bare cosmological constant
$ \Lambda_0 $ :$ \begin{split} {{\Lambda }_{\rm eff}}\left( t \right) = {{\Lambda }_{0}}-3\left(\mathscr K{{\left( t \right)}^{2}}+2{\mathscr {K}}\left( t \right)\frac{\dot{a}\left( t \right)}{a\left( t \right)} \right)\; . \end{split} $

(55) The bare cosmological constant
$ \Lambda_0 $ is simply the vacuum energy density, which plays only a partial role in the accelerating expansion in our approach. It is the non-trivial contortion that eventually determines the accelerating expansion.Phenomenologically,
$ \Lambda_{\rm eff} $ can be regarded as an energy density produced by some auxiliary fields that are responsible for the accelerating expansion, such as the quintessence field [19]. We can consider the action for gravity in the form of$ \begin{array}{l} S_q = \int {\rm d}^4x\sqrt{-g}\left[\dfrac{1}{2}M_{pl}^2R-\dfrac{1}{2}g^{\mu\nu}\partial_{\mu}\phi\partial_{\nu}\phi-V(\phi)\right]\; . \end{array} $

(56) The corresponding energy density for the field
$ \phi $ is$ \begin{array}{l} \rho_{\phi} = \dfrac{{\dot \phi}^2}{2}+V(\phi) \end{array} $

(57) and the pressure of field
$ \phi $ is$ \begin{array}{l} p_{\phi} = \dfrac{{\dot \phi}^2}{2}-V(\phi). \end{array} $

(58) The continuity equation for the field
$ \phi $ is$ \begin{array}{l} \ddot{\phi}+3H\dot{\phi}+V_{,\phi} = 0. \end{array} $

(59) The solution of Eq. (59) yields the evolution
$ \phi(t) $ . In the analog of the LSLV model with quintessence, we have$ \begin{array}{l} \Lambda_{\rm eff}(t) = \dfrac{{\dot \phi}^2(t)}{2}+V(\phi(t)). \end{array} $

(60) Then, we have the relation
$ \begin{split} V\left( \phi \left( t \right) \right) = {{\Lambda }_{\rm eff}}+\frac{{{{\dot{\Lambda }}}_{\rm eff}}}{6H} \end{split}. $

(61) The evolution of
$ V\left( \phi \left( t \right) \right) $ given by$ \Lambda_{\rm eff}(t) $ versus$ t $ bifurcates at a critical value of$ \Lambda_0 $ , named as$ \Lambda_{\rm crit} $ ; i.e.,$ V\left( \phi \left( t \right) \right) $ decreases monotonically with the increase of$ t $ when$ \Lambda_0 \leqslant \Lambda_{\rm crit} $ , while its evolution has a local minimum when$ \Lambda_0 > \Lambda_{\rm crit} $ . Table 2 summarizes the value of$ \Lambda_{\rm crit} $ for all the cases of approximation in consideration. Fig. 5 shows the bifurcation of the evolution of$ V\left( \phi \left( t \right) \right) $ versus t with$ \Lambda_0 $ around$ \Lambda_{\rm crit} $ in all the cases of approximation with both the initial values of$ {\mathscr {K}}(t) $ respectively. We find that for Case C with the first initial value,$ {\mathscr {K}}(t_0) = {{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ ,$ V\left( \phi \left( t \right) \right) $ decreases monotonically with the increase of$ t $ for all values of$ \Lambda_0 $ allowed when$ w_0 >-\dfrac{8}{9} $ , i.e., the solution of$ \Lambda_{\rm crit} $ does not exist in this case. However, the comparison of the theoretical prediction and observation of the luminosity distance modulus reveals that Case C1 at$ w_0 >-\dfrac{8}{9} $ can be ruled out from the observation of the curve of the luminosity distance modulus versus redshift, as shown in Fig. 4. It is reasonable to argue that Case C1 at$ w_0 >-\dfrac{8}{9} $ is not a good approximation to fix the evolution of$ {\mathscr {K}} $ .Initial value of $ {\mathscr {K}}(t) $ 

Critical value of $ \Lambda_0 $ 

Case A $ {\mathscr {K}}\left( {{t}_{0}} \right)={{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ 

−0.05 $ \Lambda $ 

$ {\mathscr {K}}\left( {{t}_{0}} \right)=-{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ 

−0.187 $ \Lambda $ 

Case B $ {\mathscr {K}}\left( {{t}_{0}} \right)={{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ 

−0.071 $ \Lambda $ 

$ {\mathscr {K}}\left( {{t}_{0}} \right)=-{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ 

−0.2144 $ \Lambda $ 

Case C( $ w_0=-1 $ )

$ {\mathscr {K}}\left( {{t}_{0}} \right)={{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ 

0.00001 $ \Lambda $ 

$ {\mathscr {K}}\left( {{t}_{0}} \right)=-{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ 

0.00001 $ \Lambda $ 

Case C $\left( w_0=-\dfrac{8}{9} \right)$ 

$ {\mathscr {K}}\left( {{t}_{0}} \right)={{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ 

0.119 $ \Lambda $ 

$ {\mathscr {K}}\left( {{t}_{0}} \right)=-{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ 

0.075 $ \Lambda $ 

Case C $\left( w_0=-\dfrac{7}{9}\right) $ 

$ {\mathscr {K}}\left( {{t}_{0}} \right)={{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ 

none $ {\mathscr {K}}\left( {{t}_{0}} \right)=-{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ 

0.143 $ \Lambda $ 

Case C $\left( w_0=-\dfrac{2}{3} \right)$ 

$ {\mathscr {K}}\left( {{t}_{0}} \right)={{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ 

none $ {\mathscr {K}}\left( {{t}_{0}} \right)=-{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ 

0.2 $ \Lambda $ 

Case C $\left( w_0=-\dfrac{1}{3}\right) $ 

$ {\mathscr {K}}\left( {{t}_{0}} \right)={{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ 

none $ {\mathscr {K}}\left( {{t}_{0}} \right)=-{{H}_{0}}\left( \sqrt{1-\dfrac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}+1 \right) $ 

0.306 $ \Lambda $ 

Table 2. Critical values of
$ \Lambda_0 $ triggering the transition from the monotonic evolution of$ V\left( \phi \left( t \right) \right) $ to one with a local minimum in different models.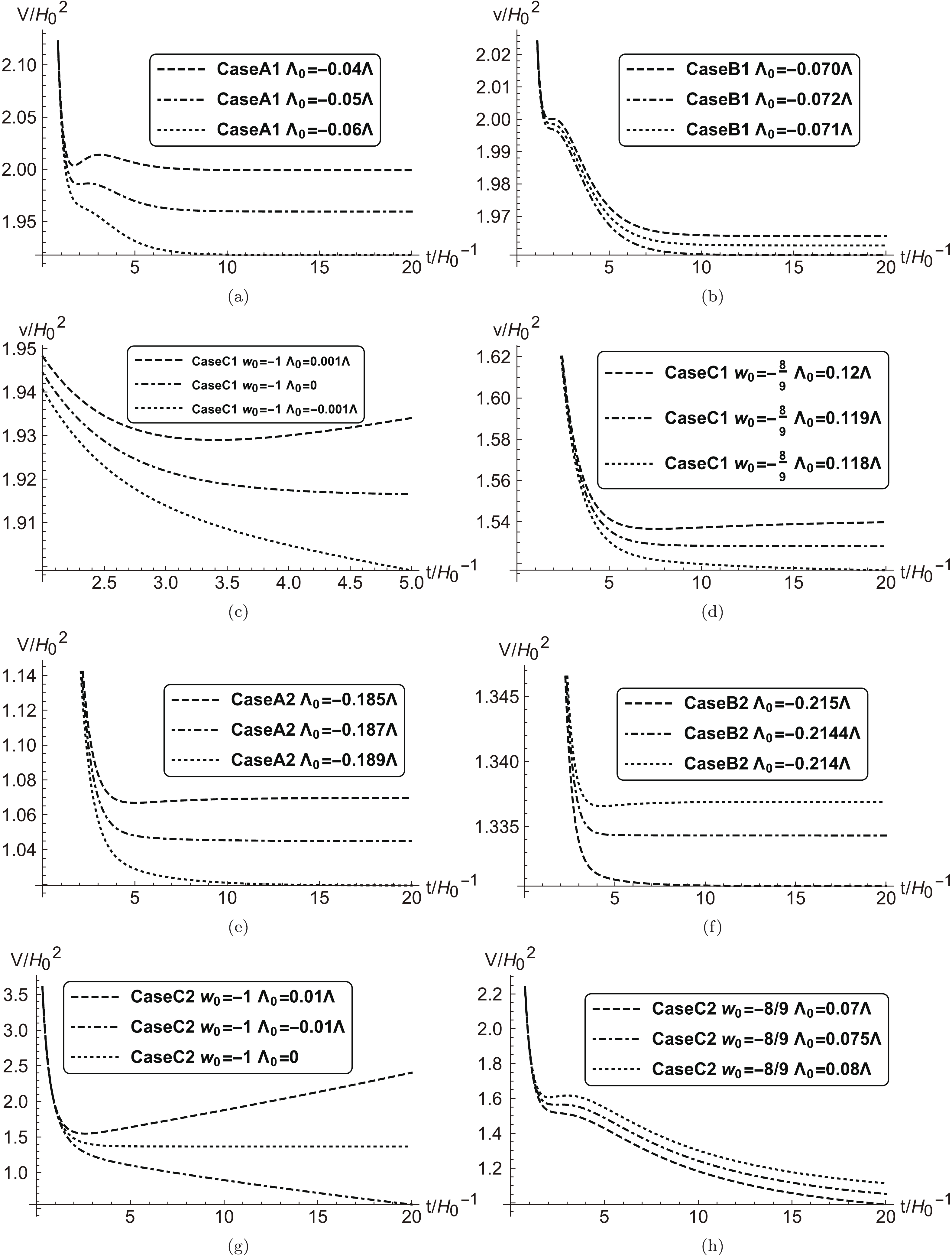
Figure 5.
$ \Lambda_{\rm crit} $ solutions in all the cases with both the initial values$ {\mathscr {K}}\left( {{t}_{0}} \right)={{H}_{0}}\left( \pm \sqrt{1-\frac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right). $ 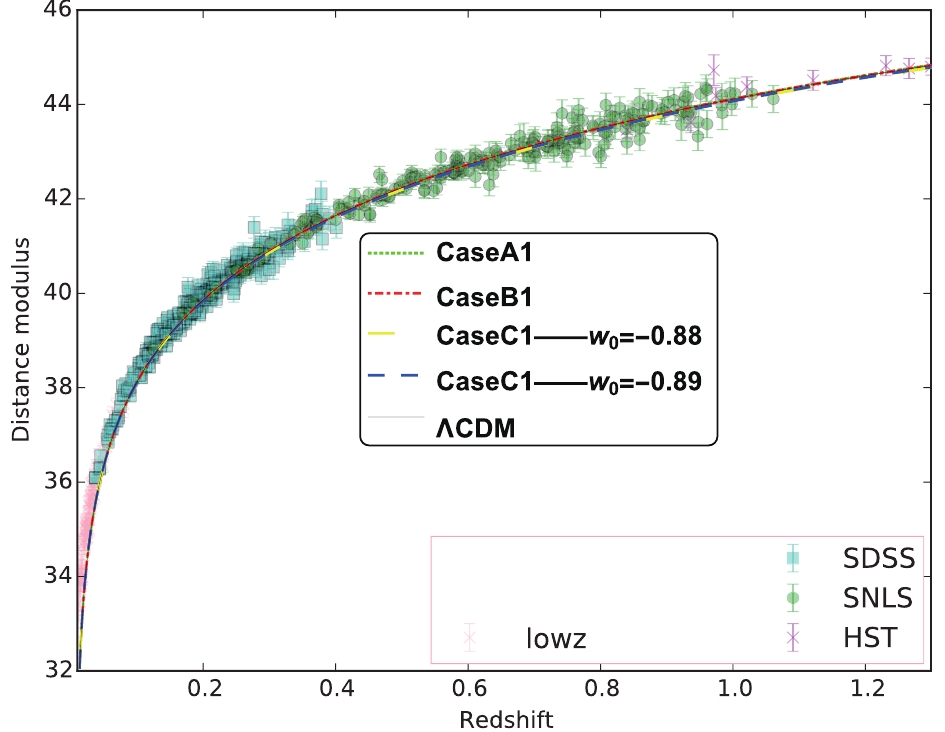
Figure 4. (color online) Comparison between the theoretical prediction of the three cases of approximation and the observation of luminosity distance modulus in the case where the initial value
$ {\mathscr {K}}\left( {{t}_{0}} \right) = {{H}_{0}}\left( \sqrt{1-\frac{\Lambda -{{\Lambda }_{0}}}{3{{H}_{0}}^{2}}}-1 \right) $ for$\Lambda_0 = 0.2\Lambda.$ It can be observed that the solutions of
$ \Lambda_{\rm crit} $ are all around$ \Lambda_0 = 0 $ , the boundary between the string landscape and swampland. We can make a reasonable analysis of the deviation of the$ \Lambda_{\rm crit} $ values from$ \Lambda_0 = 0 $ . All the$ \Lambda_{\rm crit} $ values in Table 2 are obtained with an approximation of the evolution of$ {\mathscr {K}} $ , and we can guess that$ \Lambda_{\rm crit} $ would be exactly zero in a more elaborate model of the evolution of$ {\mathscr {K}} $ . The monotonic$ V(\phi) $ versus$ \phi $ will result in a monotonic$ V\left( \phi \left( t \right) \right) $ versus$ t $ . On the other hand, the appearance of a local minimum in$ V\left( \phi \left( t \right) \right) $ corresponds to a non-monotonic$ V(\phi) $ versus$ \phi $ . This reveals that$ \Lambda_{\rm crit} $ may be the real boundary between the string landscape and swampland.To account for the inflation and the accelerating expansion, the AdS vacua of the string landscape need to be lifted to dS ones by some unnatural mechanisms such as the KKLT or the LVS construction [12, 13]. However, the two criteria on the dS swampland conjecture rule out the meta-stable dS-type vacua as those with which the effective theory with UV completion is built and leave only the possibility of quintessence-like vacua. The result obtained in this paper reveals that large-scale LV can effectively lift the AdS vacua to quintessence-like ones.
-
The KKLT or the LVS construction for uplifting the AdS vacua to dS ones relies on the careful addition of
$ \bar{D_3} $ -branes into the compactification. The tension of$ \bar{D_3} $ -branes in a sufficiently warped background, in the presence of quantum corrections, can be a small enough correction to lift the former AdS vacuum to a positive cosmological constant, without destabilizing the minimum. However, there also exist many cases with no-go theorems to uplift the AdS vacua to dS ones. Several results reveal no-go theorems on dS vacua in string theory constructions, with restrictions on the ingredients used in string theory, which are typically specific combinations of fluxes, D-branes, orientifolds, etc [14]. Moreover, the second criterion on the swampland conjecture excludes the effective theory with meta-stable dS vacua as a theory with UV completion. It seems that accounting for the accelerating expansion and inflation with a simple$ \Lambda {\rm CDM} $ model having a positive cosmological constant is difficult. If the positive cosmological constant originates from the energy density of a vacuum, the construction of such a vacuum is fragile, and the vacuum belongs to the swampland. However, a quintessence-like potential can overcome the restriction from the second criterion of the swampland conjecture and also contribute a decreasing positive vacuum energy density.The result obtained in this paper shows another route to uplift the AdS vacua to an effective quintessence-type vacuum energy that can satisfy the second criterion of the swampland conjecture without adding extra ingredients such as fluxes or D-branes into the modification. The result only relies on the consideration of large-scale LV from quantum gravity frozen by the inflation. Actually, the origin causing accelerating expansion is assorted to the effect of quantum gravity in this scenario. The construction has a UV completion in this sense.
Our approach is also different from the quintessence model, which has a scalar mode as a part of the gravity at a large scale. The quintessence scalar field is either elementary, which needs detection examination, or an effective theory of other elementary physics mechanisms, which needs clarification on its relation with fundamental physics. In our approach, the quintessence field is actually an effective description of the dark-partner contribution by contortion, which is the effect of large-scale LV and can be traced back to the quantum gravity origin.
We employ three kinds of approximations to fix the evolution and magnitude of
$ {\mathscr {K}}(t) $ . However, a more fundamental approach should be given later. We would start with a specific model of quantum gravity and a inflation model to achieve a model with a stronger ability to predict the evolution and magnitude of$ {\mathscr {K}}(t) $ . The LV quantum gravity can be traced along with the inflation, and the frozen large-scale LV can thereby be predicted. The present approach relies on the gauge principle with the local symmetry group as a proper subgroup of the Lorentz group. In fact, the LV can be of types other than the total breakdown of some symmetry generators. The LV can be achieved with a boost transformation differing from Lorentz boost alone. Some discussions assert that the quantum gravity effect can modify the Poincaré algebra into a deformed one, or a Hopf algebra, e.g.,$ \kappa $ -Poincaré (see, e.g., [20]). The gauge principle is not applicable in these cases. The method to introduce LV in long-range effective gravity beyond the gauge principle is under investigation.We strengthen the idea proposed in [3], which stresses on the possibility that the LV in quantum gravity may be frozen at a scale beyond the horizon by the inflation and be subsequently transformed into a large-scale LV, which may play an important role in the evolution of the universe at a late time. In fact, we know that the physics at a much lower energy scale than the Planck scale obeys Lorentz symmetry exactly, and general relativity describes gravitation successfully, at least up to the astronomical scale. Although we understand little about how the Lorentz symmetry emerges from a quantum gravity theory with LV, which is quite challenging and beyond the scope of the present paper, the standard model of particle physics and the gravitation theory of general relativity as well as some ideas beyond the standard model, such as grand unification and SUSY, can provide a good understanding of the physics during the normal expansion period of the universe but not during the late-time accelerating expansion, which seems to need new physics to explain. On the other hand, it is indeed necessary to characterize the transition from large-scale LV to relatively small-scale Lorentz invariance according to our framework. In fact,
$ {\mathscr {K}}(t) $ , the non-trivial component of contortion, is the parameter sought to characterize the magnitude of large-scale LV. The theoretical prediction of its dependence on the length scale and its evolution are highly non-trivial because they depend on the understanding of quantum gravity and details of the inflationary mechanism. However, the parameter$ {\mathscr {K}}(t) $ is actually observable.In most approaches on the extension of general relativity with torsion, the torsion or the contortion cannot propogate and can only be nontrivial in the region of matter-source distribution with spin [21]. The large-scale spacetime must be torsion-free, as is the case for the universe. The spacetime felt by matter motion described by the left-hand side of Eq. (13) is the Riemann-Cartan spacetime, which is determined not only by energy-momentum but also by spin, as in Eq. (4). In our approach, though the torsion caused by frozen large-scale LV propagates neither, it distributes as a shadow of matter distribution and evolves along with the evolution of the universe. Matter moves in a Riemannian spacetime, rather than a Riemann-Cartan one, and interacts with the distribution of torsion in the usual manner of gravitation; i.e., the effective energy-momentum tensor contributed by the contortion distribution participates in the determination of the spacetime curvature, and matter moves along the geodesic line and feels the contortion effect through the spacetime curvature. However, the spin of matter particles can interact with the torsion tensor directly, in addition to the gravitational interaction [22-24]. The large-scale long propagation of particles with spin may exhibit a deviation from the geodesic line, causing the advancement or delay of arrival time with its energy. There are indeed some indication of such events for gamma-ray bursts and neutrinos; the delay differs between gamma rays and neutrinos [25]. Based on our approach of frozen large-scale LV, a detailed investigation of the magnitude of the distorted propagation caused by the large-scale contortion distribution of both the neutrino and light events is ongoing. It is expected that the comparison of observation with prediction will reveal the variation of the large-scale LV magnitude versus the distance scale.
Uplifting of AdS type to quintessence-like potential induced by frozen large-scale Lorentz violation
- Received Date: 2019-12-21
- Accepted Date: 2020-03-13
- Available Online: 2020-08-01
Abstract: The quintessence-like potential of vacuum energy can meet the requirements from both quantum gravity and the accelerating expansion of the universe. The anti-de Sitter (AdS) vacuum in string theory must be lifted to the meta-stable dS vacuum with a positive vacuum energy density to explain the accelerating expansion of the universe. Based on possible large-scale Lorentz violation, we define an effective cosmological constant that depends not only on the bare cosmological constant but also on the Lorentz violation effect. We find that the evolution of the effective cosmological constant exhibits the behavior of the quintessence potential when the bare cosmological constant originates from the string landscape, in contrast to the existence of a local minimum during evolution when the bare cosmological constant is supplied by the swampland. The critical value of the bare cosmological constant is approximately zero for the behavior transition. The frozen large-scale Lorentz violation can uplift the AdS vacua to an effective quintessence-like one in this sense.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: